Prédiction de l'interaction génotype à— environnement par linéarisation et régression PLS-mixte

UNIVERSITE MONTPELLIER II
SCIENCES ET TECHNIQUES DU LANGUEDOC

THESE
pour obtenir le grade de
DOCTEUR DE L'UNIVERSITE MONTPELLIER II

Discipline : Biostatistique
Formation Doctorale : Biostatistique
Ecole Doctorale : Information Structures Systèmes

présentée et soutenue publiquement
par
Ibnou DIENG
le 24 janvier 2007
Titre :

Prediction de l'interaction genotype × environnement par
linearisation et regression PLS-mixte

JURY

M. Robert SABATIER Directeur de Thèse

M. Eric GOZ'E Codirecteur de Thèse

M. Alain CHARCOSSET Rapporteur

M. Jean-Jacques DAUDIN Rapporteur

M. Gilles DUCHARME Examinateur

Mme Christèle ROBERT-GRANIER Examinateur

Résumé: Ce travail porte sur la pr'ediction de l'interaction g'enotype × environnement et est appliqu'e au contexte sah'elien. Après un tour d'horizon des principales m'ethodes d'analyse de la litt'erature, nous proposons la m'ethode APLAT. Le rendement de g'enotypes pr'edit a` l'aide de covariables d'environnement par un modèle de simulation de cultures est d'evelopp'e en s'erie de Taylor a` l'ordre 1 au voisinage du vecteur de paramètres d'un g'enotype de r'ef'erence. Nous nous ramenons alors approximativement a` un modèle lin'eaire o`u la matrice des r'egresseurs est remplac'ee par la matrice des d'eriv'ees partielles par rapport aux paramètres. Le nombre important de paramètres vari'etaux g'en'eralement constat'e chez les modèles de simulation de cultures conduit a` un nombre important de r'egresseurs; d'o`u une estimation par r'egression Partial Least Squares (PLS). Par la suite, nous proposons APLAT-mixte, une extension de APLAT. Pour ce modèle mixte, nous maintenons le rendement des g'enotypes lin'earis'e dans la partie fixe auquel s'ajoute un effet al'eatoire de l'environnement, responsable d'interactions G×E dont il faut estimer la variance. Nous introduisons a` cet effet la technique PLS-Mixte pour estimer les composantes de variance dans un modèle o`u il y a plus de r'egresseurs que d'observations. L'algorithme it'eratif propos'e, qui consiste a` imbriquer la r'egression PLS dans l'algorithme Expectation Maximization (EM), est fond'e sur les m'ethodes de vraisemblance Maximum Likelihood (ML) et Restricted Maximum Likelihood (REML).

Table des matières

1 2

Introduction générale 1.1 Problématique 1.2 Présentation des données de l'étude 1.2.1 L'essai pluriannuel 1.2.2 L'essai multilocal Les méthodes classiques d'analyse des interactions G×E 2.1 Le modèle d'analyse de variance a` deux facteurs 2.1.1 Le modèle 2.1.2 Illustration avec les données de l'essai multilocal . . . 2.2 La méthode de régression conjointe 2.2.1 Le modèle 2.2.2 Illustration avec les données de l'essai multilocal . . . 2.3 La méthode AMMI 2.3.1 Le modèle

4 4 11 12 14 18 22 22 23 26 26 27 28 28

2.3.2 Illustration avec les données de l'essai multilocal . . . . 31

2.4 La régression factorielle 33

2.4.1 Le modèle 33

2.4.2 Illustration avec les données de l'essai multilocal . . . 40

2.5 Un modèle de simulation de cultures : SarraH 42

2.6 Limites des méthodes classiques d'étude des interactions G×E 46

3 La méthode APLAT 48

3.1 La régression Partial least squares 48

3.2 La méthode APLAT : linéarisation autour d'un témoin . . . 52

3.2.1 Le modèle proposé 52

3.2.2 Illustration avec les données de l'essai pluriannuel . . 58

3.2.3 Illustration avec les données de l'essai multilocal . . . 64

3.2.4 Conclusion 64

4 La méthode APLAT-mixte 67

4.1 Le modèle mixte 69

4.2 La régression PLS sur un modèle de variance connue 73

4.3 La méthode PLS-Mixte 74

4.3.1 La méthode PLS-Mixte sur un modèle a` effets aléatoires

indépendants de variances homogènes 75

4.3.2 La méthode PLS-Mixte sur un modèle a` effets aléatoires

corrélés de variances hétérogènes 86

5 Conclusion g'en'erale 104

R'ef'erences cit'ees 110

Annexes 120

A. Modèle de R'egression factorielle 120

B. Article au C.R. Biologie 124

Chapitre 1

Introduction générale

1.1 Problématique

Au Sahel, les pr'ecipitations annuelles ont diminu'e de l'ordre de 20 a` 30 % dans la dernière moiti'e du 20<sup>e</sup> siècle (Baterburry et Warren, 2001) et leur d'eficit y demeure la plus forte contrainte a` l'agriculture (Tucker, 1991).

Dans de telles conditions, les paysans, qui constituent la majorit'e de la population, parviennent difficilement a` g'en'erer des revenus r'eguliers tout en g'erant durablement les ressources naturelles. L'agriculture, qui est pourtant le principal moteur du d'eveloppement 'economique et social du Sahel, ne peut ainsi jouer pleinement son ràole.

Dans ce cadre difficile, le ràole des d'ecideurs ('Etats, ONG, Organismes de coop'eration, Recherche) est de r'epondre a` la demande sociale, principalement »la promotion d'une agriculture productive, diversifi'ee, durable [...]». Ce sont les termes employ'es dans le Cadre strat'egique de s'ecurit'e alimentaire (CSSA), le document de r'ef'erence en matière de s'ecurit'e alimentaire du Comit'e permanent inter-'etats de lutte contre la s'echeresse au Sahel (CILSS).

Ce cadre stratégique qui vise aussi »l'amélioration durable des conditions d'accès des groupes et zones vulnérables a` l'alimentation», a ététraduit en programmes de sécuritéalimentaire pour la plupart des pays sahéliens (CILSS, 2000). Ce document est venu confirmer le mandat déjàattribuéau Centre d'étude régional pour l'amélioration de l'adaptation a` la sécheresse (CERAAS) par le Réseau de recherche sur la résistance a` la sécheresse (R3S) du CILSS.

Le CERAAS est un laboratoire national de recherche a` vocation régionale sous double tutelle. C'est un laboratoire de l'Institut sénégalais de recherches agricoles (ISRA), qui a la mission d'exécuter le programme national de recherche sur l'adaptation des plantes a` la sécheresse. Il est aussi une Base Centre du Conseil ouest et centre africain pour la recherche et le développement agricole (CORAF), chargéde conduire les recherches sur la thématique de l'adaptation des plantes a` la sécheresse et celle de la création variétale.

Le CERAAS conduit des recherches suivant quatre axes principaux :

1. la compréhension de la réponse des plantes;

2. la modélisation du fonctionnement des plantes;

3. l'amélioration de la méthodologie de la sélection

4. l'amélioration des systèmes de culture pour une meilleure adaptation a` la sécheresse.

Au troisième axe, l'objectif est d'identifier et de sélectionner du matériel végétal mieux adaptéa` la sécheresse, stabilisant ainsi le déficit alimentaire dans les pays des régions sèches. Pour atteindre cet objectif, les activités de recherche visent a` fournir des solutions techniques pour réduire l'effet dépressif de la sécheresse sur les productions agricoles. Ces solutions consistent a` proposer des méthodes de sélection, de suivi des cultures et des itinéraires techniques tenant compte du milieu ciblé, qui est soumis a` la contrainte hydrique.

La s'election porte sur des caractères ph'enologiques, physiologiques et mol'eculaires permettant une production am'elior'ee en conditions de d'eficit hydrique par rapport aux cultivars g'en'eralement vulgaris'es. Elle est valid'ee par des essais en plein champ, r'ealis'es dans des conditions qui reflètent la variabilit'e du milieu auquel les vari'et'es sont destin'ees. Ces essais peuvent avoir lieu la même ann'ee, sur plusieurs endroits (essai multilocal) ou sur plusieurs ann'ees, au même endroit (essai pluriannuel) ou sur plusieurs ann'ees, sur plusieurs endroits. Par la suite, nous d'esignerons tous ces types d'essais sous le nom g'en'erique d'essai multienvironnement et emploierons ce terme chaque fois qu'il n'y aura pas d'ambigu·ýt'es et que nous voulons nommer un ensemble d'essais.

Dans cette zone du Sahel a` fort risque climatique, il est souvent constat'e une variabilit'e de l''ecart entre le rendement des g'enotypes lors de ces essais multienvironnements de s'election vari'etale. Cette variabilit'e est connue des s'electionneurs sous le nom d'interaction g'enotype × environnement (G×E) a` laquelle nous nous int'eressons dans ce travail.

Un cas particulier d'interactions 'etant un changement de classement direct des g'enotypes. Si trois g'enotypes A, B et C sont test'es sur plusieurs environnements, nous sommes en pr'esence d'interactions G×E si pour le premier environnement, les g'enotypes se classent A-B-C selon leurs rendements et pour le deuxième environnement, ils se classent par exemple B-A-C. Dans ce cas et même dans le cas plus g'en'eral o`u les diff'erences entre g'enotypes dependent de l'environnement, il sera difficile pour un environnement cible o`u les g'enotypes n'ont pas encore 'et'e test'es, de pr'edire le meilleur g'enotype.

Dune manière g'en'erale, les essais multienvironnements ne peuvent être assez pr'ecis. En effet, en dehors d'une ou de deux vari'et'es t'emoin g'en'eralement reconduites dune ann'ee a` lautre, chaque vari'et'e n'est vue que deux a` cinq ans. Au regard de la forte interaction g'enotype × ann'ee (G×A), ces deux a` cinq ans sont un 'echantillon de taille trop faible. Le s'electionneur doit

souvent extrapoler a` partir de ce nombre d'années faible ou d'un essai multi-local o`u l'interaction génotype x lieu (GxL) ne reproduit qu'imparfaitement l'interaction GxA.

Les interactions GxE gênent donc la sélection variétale et constituent un obstacle aux recommandations éventuellement formulées aux paysans pour l'adoption de cultivars adaptés a` leurs milieux. Une solution est de modéliser ces interactions GxE dans le but de les prédire pour une situation nouvelle en fonction de variables environnementales dont on connaàýt la valeur (ex : nature et profondeur du sol) ou la loi de probabilité(ex : précipitations) (Piepho, Denis et van Eeuwijk, 1998).

Nous proposons alors dans ce travail, une méthode de modélisation des interactions GxE, qui permette de tenir compte de l'impact aléatoire de l'environnement induit principalement au Sahel par une variabilitéclimatique, pour une meilleure prédiction de la réponse des variétés.

Plusieurs méthodes d'analyse des interactions ont étéproposées dans la littérature et sont exposées au chapitre 2. Ces méthodes peuvent être rangées, a` notre sens, en deux catégories : celles qui utilisent les caractéristiques des environnements et celles qui ne les utilisent pas. Pour ces dernières, dont nous pouvons citer la méthode Additive Main effects and Multiplicative Interactions (AMMI) ainsi que la régression conjointe, la critique majeure est qu'elles ne tiennent pas compte justement des environnements cibles pour y prédire le rendement des génotypes. Ce n'est pas adaptédans cette zone du Sahel, car comme nous avions annoncé, les interactions GxE y sont la conséquence principalement de la grande variabilitéclimatique des environnements. Mais ce qui gêne en réalité, c'est la présence de l'interaction GxA qui est imprévisible, au contraire de l'interaction GxL. Talbot (1997) a établi que l'interaction GxAxL est plus importante que l'interaction GxA, ellemême plus importante que l'interaction GxL. C'est certainement le cas au Sahel, o`u la variabilitéclimatique interannuelle est forte. En effet, s'il pouvait

y être possible, pour chaque lieu, de pr'evoir les conditions climatiques d'une ann'ee sur l'autre, il suffirait de mener un essai multilocal sur un ensemble de lieux repr'esentatifs et avec la m'ethode AMMI par exemple, pouvoir pr'edire avec assez de pr'ecision le rendement des cultures. Mais les importantes variations climatiques d'une ann'ee sur l'autre empêchent cette pr'ediction sans passer par la prise en compte des conditions du milieu.

Parmi les m'ethodes qui utilisent les caract'eristiques environnementales, figure la r'egression factorielle, dont une limite est qu'elle suppose une action lin'eaire des environnements sur le rendement. Dans le contexte sah'elien, cette m'ethode utilise le modèle d'analyse de variance a` deux facteurs, g'enotype et environnement, o`u les interactions G×E sont expliqu'ees par des covariables climatiques mesur'ees souvent au pas de temps d'ecadaire voire journalier sur chacun des environnements et des covariables mesur'ees sur chacun des g'enotypes. En g'en'eral, les variables climatiques mesur'ees sur les environnements sont très nombreuses (s'eries temporelles) et la prise en compte de l'ensemble d'entre elles par cette m'ethode est impossible.

Les modèles de simulation de cultures sont aussi utilis'es comme m'ethode de pr'ediction de rendement des cultures tenant compte de l'environnement. Ces modèles ont certes l'avantage d'être plus r'ealistes et considèrent le rendement d'un g'enotype dans un environnement particulier comme une fonction non lin'eaire des paramètres du g'enotype et des caract'eristiques de l'environnement. Ils pr'esentent cependant l'inconv'enient de ne pas être applicables a` tout g'enotype. En effet, les paramètres de tels modèles de simulation de cultures ne sont pour la plupart connus que pour un petit nombre de g'enotypes, car leur 'evaluation demande une exp'erimentation sp'ecifique et des mesures coàuteuses.

La premi`ere méthode proposée : APLAT. Lors d'essais multienviron-
nements, figure g'en'eralement un g'enotype de r'ef'erence dont les paramètres

sont bien connus, dans le but de comparer sa performance aux autres g'enotypes. Tenant compte de l'information souvent disponible pour ce g'enotype de r'ef'erence, nous proposons notre première m'ethode d'estimation qui consiste a` lin'eariser le rendement des g'enotypes pr'edit par un modèle de simulation de cultures autour du vecteur de paramètres de ce g'enotype de r'ef'erence. Le but 'etant d'estimer les paramètres de ces g'enotypes a` l'aide des r'esultats d'essais multienvironnements, sans refaire le travail de »param'etrisation» en station exp'erimentale n'ecessaire a` l'estimation de ceux du t'emoin. Cela per-met de se ramener approximativement a` un modèle lin'eaire o`u la matrice des variables explicatives est remplac'ee par la matrice des d'eriv'ees partielles (sensibilit'es) par rapport aux paramètres.

Cette m'ethode appel'ee Approximation par lin'earisation autour d'un t'emoin (APLAT) est d'ecrite au chapitre 3. Pour estimer ainsi la performance de tout g'enotype i dans un environnement j, nous adjoignons a` la performance de ce g'enotype i pr'edite par un modèle de simulation de cultures pour l'environnement j lin'earis'ee autour du vecteur de paramètres du t'emoin, un biais de ce modèle qui ne d'epend que de l'environnement et une erreur al'eatoire r'esiduelle. Pour que cette m'ethode ait un int'erêt, il faut que les interactions G×E soient bien reproduites par le modèle de simulation de culture, et que la m'ethode d'estimation supporte les abandons de g'enotypes au cours du temps comme cela se pratique habituellement. C'est pourquoi, elle a 'et'e test'ee sur les donn'ees d'un essai pluriannuel men'e sur la station exp'erimentale du CERAAS au S'en'egal o`u tous les g'enotypes n''etaient pas observ'es tous les ans.

Pour la plupart des modèles de simulations de cultures, il existe un nombre important de paramètres pour les g'enotypes. Ces paramètres, g'en'eralement connus pour le g'enotype de r'ef'erence, et que nous cherchons a` r'eestimer pour tout nouveau g'enotype, conduisent a` un nombre important de r'egresseurs

pour notre méthode proposée. Ils ont étéestimés a` l'aide la régression Partial least square (PLS).

La deuxième méthode proposée : APLAT-Mixte. Au chapitre 4, nous étendons la méthode APLAT au cas d'essais a` plusieurs composantes de variance. Pour cette méthode, nous estimons qu'un modèle de simulation de cultures ne permet pas de prendre en compte totalement l'effet aléatoire des interactions G×E, même si nous pouvons concevoir qu'il le permette pour une grande part. Nous rajoutons alors au modèle APLAT un effet résiduel de l'environnement et un effet des interactions G×E aléatoires, dont il faudra estimer les composantes de variance.

Le recours a` un modèle de simulation de culture induit, nous l'avons vu, un nombre important de régresseurs. Comme il s'agit également d'estimer la variance de l'effet de l'environnement et de l'effet des interactions G×E supposés aléatoires, nous nous retrouvons avec un modèle avec un nombre important de régresseurs et des composantes de variance. Nous proposons donc dans ce chapitre, une méthode originale d'estimation des paramètres fixes et des composantes de variance dans un modèle o`u le nombre de régresseurs est important par rapport aux observations. Cette méthode d'estimation, dénommée APLAT-Mixte, se fait par le principe d'une méthode combinée de réduction de dimension et de modèle mixte, que nous avons appeléPLSMixte.

Considérant d'une part les algorithmes itératifs d'estimation des paramètres inconnus dans le cadre du modèle mixte, et d'autre part les techniques de réduction de dimension, nous proposons d'imbriquer la régression PLS dans l'algorithme EM. Puisque nos données d'interaction G×E s'appréhendent a` l'aide d'un modèle o`u les erreurs aléatoires sont corrélées, nous appliquons dans un premier temps cette technique a` des données de NIRS (Near infrared spectroscopy) avec des erreurs indépendantes, o`u nous ne nous occupons que

de la double contrainte de la dimension du modèle et de la pr'esence des composantes de variance. Par la suite, nous nous int'eressons a` r'esoudre le problème suppl'ementaire des erreurs corr'el'ees qui r'esultent des donn'ees de notre probl'ematique d'interaction G×E.

1.2 Présentation des données de l'étude

Les m'ethodes qui ont 'et'e propos'ees ici se sont appuy'ees sur des r'esultats d'essais multienvironnements. Ces exp'erimentations vari'etales, sur quoi finalement repose toute cette 'evaluation du comportement des g'enotypes en rapport avec les caract'eristiques du milieu, sont la base de la s'election vari'etale. Les objectifs de tels essais peuvent être divers et d'ependent des questions auxquelles l'exp'erimentateur veut apporter des r'eponses. Mais l'objectif principal est la comparaison des performances, souvent le rendement, de diff'erents g'enotypes au regard de diff'erentes conditions environnementales.

Plusieurs g'enotypes sont en g'en'eral test'es dans plusieurs environnements et ces derniers sont choisis avec un souci qu'ils soient aussi divers que possible. Le but recherch'e est de couvrir la quasi totalit'e des types d'environnements susceptibles de recevoir les g'enotypes. Ce but est difficile a` atteindre au Sahel tant sont variables, nous l'avons dit, les conditions environnementales d'une ann'ee a` l'autre.

Les donn'ees utilis'ees dans le cadre de cette 'etude proviennent de deux types d'exp'erimentations. D'une part, nous nous sommes servi des r'esultats d'un essai pluriannuel, men'e a` la station exp'erimentale du CERAAS, de 1994 a` 1998. D'autre part, un essai multilocal a 'et'e mis en place durant l'hivernage 2005, sur 11 localit'es. L'hivernage d'esigne la saison des pluies dans les r'egions tropicales. Au S'en'egal, il a lieu chaque ann'ee entre mai et octobre et sa dur'ee varie de trois a` six mois selon un gradient Nord-Sud.

FIG. 1.1 - Localisation du CERAAS et de la station exp'erimentale de Bambey au S'en'egal.

Toutes ces exp'erimentations qui ont donc 'et'e men'ees au S'en'egal, ont concern'e
l'arachide (Arachis hypogaea L.), qui y demeure la principale culture de rente.

1.2.1 L'essai pluriannuel

Cet essai vari'etal n'a concern'e qu'un seul site, la station exp'erimentale du CERAAS situ'ee a` Bambey (14°42 N et 16°28 O). Il est dit pluriannuel et a 'et'e men'e de 1994 a` 1998 (figure 1.1).

Cet essai a 'et'e conduit avec 26 g'enotypes a` cycle de d'eveloppement de 90 jours. Les rendements moyens par g'enotype et par ann'ee sont pr'esent'es dans le tableau 1.1. Tous les g'enotypes ne sont pas observ'es toutes les ann'ees, ce qui est habituel pour les programmes de s'election vari'etale. En effet, le s'electionneur a le loisir au cours de tels programmes, d'enlever certains g'enotypes s'il est av'er'e qu'ils donnent de faibles productions après une ou deux ann'ees d'exp'erimentation. De même, au cours d'un même programme,

le s'electionneur peut tout aussi bien faire entrer de nouveaux g'enotypes, toujours dans le but de les tester.

G'enotype		1994		1995		1996	1997	1998	Moyenne
55-113			1	337,4	1	114,9	351,1	937,9	935,3
55-140			1	236,5		908,2		931,8	1 025,5
55-15			1	234,4	1	052,6			1 143,5
55-16			1	268,4		937,7			1 103,1
55-17			1	246,8		991,6			1 119,2
55-437†		571,3	1	081,0		707,1	421,2	1 074,6	771,1
57-111							401,7	964,7	683,2
57-115							556,5	977,9	767,2
57-120							452,4	1064,0	758,2
57-123							596,7	985,7	791,2
57-125							651,6	1 110,8	881,2
57-126							665,2	1 232,3	948,8
57-14						649,4	244,1		446,8
FLEUR11	1	420,1	1	624,9	1	065,3	941,6	1 098,0	1 230,0
S-45			1	194,3		936,6			1 065,5
S-46					1	001,5	641,4	1 081,8	908,2
SR-1-1		657,8							657,8
SR-1-11		492,0							492,0
SR-1-12		437,7							437,7
SR-1-2		772,7	1	170,1					971,4
SR-1-22		692,2	1	113,3		934,7	474,4		803,7
SR-1-23		582,5							582,5
SR-1-4		563,0	1	205,6		870,9			879,8
SR-1-6		672,8							672,8
SR-1-9		572,7							572,7
US-83		957,7	1	307,0					1 132,4
Moyenne		699,4	1	251,7		930,9	533,2	1 041,8	888,8

† g'enotype de r'ef'erence

Donn'ees de l'essai pluriannuel de 26 g'enotypes d'arachide a` la

TAB. 1.1 - station exp'erimentale de Bambey au S'en'egal de 1994 a` 1998 (rendement en kg ha-').

Le g'enotype de r'ef'erence choisi est le 55-437, une vari'et'e de 90 jours; sa longueur de cycle est la même que celles des autres g'enotypes. Les donn'ees de ce g'enotype sont disponibles pour la dur'ee totale des exp'erimentations, ce qui autorise sa comparaison aux autres vari'et'es utilis'ees dans cet essai.

Le tableau 1.1 r'evèle que les g'enotypes ont des productions moyennes très vari'ees et certains font même plus que doubler leur production d'une ann'ee sur l'autre. Par exemple, le rendement de la vari'et'e 55-437 est de 1 081 kg ha-' en 1995 alors qu'il n'est que de 571,3 kg ha^-'en 1994, soit une augmentation d'un peu moins de 90% entre deux ann'ees cons'ecutives.

Les productions moyennes par ann'ee sont aussi très contrast'ees même si d'une ann'ee sur l'autre, nous n'avons pas les mêmes g'enotypes. L'ann'ee 1995 (1251,7 kg ha^-') est l'ann'ee la plus productive et les g'enotypes qui ont les rendements les plus 'elev'es sur l'ensemble des cinq ann'ees ont tous 'et'e observ'es cette ann'ee. Il s'agit des g'enotypes FLEUR11 avec 1 230 kg ha-', 55-15 avec 1 143,5 kg ha-', US-83avec 1 132,4 kg ha-', etc. L'ann'ee 1997 (533,2 kg ha-') est l'ann'ee la moins productive.

1.2.2 L'essai multilocal

Ces essais ont 'et'e men'es durant l'hivernage 2005 et visent a` mesurer la production et la qualit'e des graines dans des conditions environnementales diff'erenci'ees et connues afin de mod'eliser les interactions G×E.

Pour ces essais, 6 g'enotypes (55-437, FLEUR11, GC 8-35, JL24, 55-128, 55-33) ont 'et'e test'es sur 11 localit'es. Ces localit'es ont 'et'e choisies dans la principale zone de culture de l'arachide au S'en'egal, appel'ee bassin arachidier. Ce bassin a 'et'e divis'e en trois zones a` l'int'erieur desquelles les essais ont 'et'e implant'es : 3 essais dans la zone Nord, 4 dans la zone Centre dont un a` la station exp'erimentale de Bambey et 4 dans la zone Sud dont un a` la station exp'erimentale de Nioro (figure 1.2). Cet 'echantillonnage par stratification a 'et'e mis en place pour tenir compte de la variabilit'e climatique constat'ee dans ce pays selon le gradient Nord-Sud.

Dans chaque localit'e, un dispositif en blocs complets randomis'es avec quatre r'ep'etitions, soit 24 parcelles, a 'et'e adopt'e. La parcelle 'el'ementaire est constitu'ee

FIG. 1.2 - Localisation des sites des essais multilocaux dans le bassin arachidier au S'en'egal durant l'hivernage 2005.

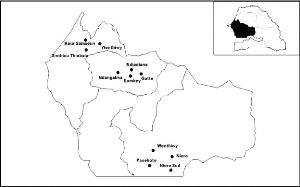
par 5 lignes de 6 m avec un 'ecartement de 50 cm entre les lignes et de 15 cm entre les poquets. Les trois lignes centrales constituent la parcelle utile a` l'int'erieur de laquelle les pr'elèvements de plantes ont 'et'e r'ealis'es.

Le semis a 'et'e effectu'e dès l'installation effective de l'hivernage sur des parcelles avec un pr'ec'edent cultural arachide ou mil. Pour les conditions exp'erimentales, un labour superficiel et un piquetage ont 'et'e effectu'es et le semis fait a` la main quand le sol 'etait humide; deux graines trait'ees au granox ont 'et'e sem'ees par poquet. De l'engrais NPK 6-20-10 a` raison de 150 kg ha^-' a 'et'e appliqu'e a` la lev'ee. Un d'emariage a` un pied par poquet a 'et'e fait vers 10 jours après le semis et enfin, des sarclo-binages et des traitements phytosanitaires ont 'et'e r'ealis'es a` la demande.

Les rendements en gousses et en fanes ont 'et'e mesur'es et un suivi journalier des paramètres climatiques (temp'erature minimale et maximale, humidit'e relative minimale et maximale, vitesse du vent, dur'ee d'insolation) effectu'e. Les rendements moyens par g'enotype et par localit'e sont pr'esent'es dans le tableau 1.2.

Les mesures des données climatiques pour les essais de Nioro et de Bambey
sont celles des postes météorologiques de ces stations. Ces mesures ont servi
aussi pour les sites autour de ces deux localités a` l'exception des mesures

de pluviométrie, réputées plus variables dans l'espace. La localitéde ^Meckhéétait équipée d'une station météorologique portable. Chacun des 11 sites a disposéd'un pluviomètre.

Localit'es		55-128		55-33	55-437		F11	GC-8-35			JL24	Moyenne
Keur Fary		263,0		209,3	189,0		392,5		281,7		239,3		262,5
Keur Samseun		103,7		91,5	119,2		260,9		141,8		151,7		144,8
Sinthiou Thiabala		317,9		198,1	244,0		459,9		275,8		554,2		341,7
Moyenne Nord		228,2		166,3	184,1		371,1		233,1		315,1		249,6
Bambey		248,1		196,6	298,7		472,3		134,0		350,8		283,4
Gatte		121,8		116,0	209,3		261,9		86,3		283,4		179,8
Ndangalma		162,3		202,1	223,9		237,5		183,6		313,8		220,5
Ndiadiane		72,6		107,4	234,9		236,9		159,9		368,7		196,7
Moyenne Centre		151,2		155,5	241,7		302,2		140,9		329,2		220,1
Nioro		928,0		866,3	807,0		856,5		614,1		780,7		808,8
Nioro Sud	1	593,6	1	013,0	670,7	1	115,8	1	115,8	1	255,4	1	127,4
Paoskoto	1	164,0	1	254,2	908,3	1	231,6	1	157,8		712,7	1	071,4
Winthewy		189,2		97,4	369,8		447,3		244,9		528,1		312,8
Moyenne Sud		968,7		807,7	688,9		912,8		783,1		819,2		830,1
Moyenne		469,5		395,6	388,6		543,0		399,6		503,5		450,0

Donn'ees de l'essai multilocal de 6 g'enotypes d'arachide sur TAB. 1.2 - 11 localit'es au S'en'egal durant l'hivernage 2005 (rendement en

kg ha-').

L'examen des données du tableau 1.2 révèle une variabilitéde rendement des génotypes selon les trois principales zones de l'étude : le Nord avec une production moyenne de 249,6 kg ha^-1 et le Centre avec une production moyenne de 220,1 kg ha^-1 s'opposent au Sud qui affiche la meilleure production moyenne avec 830,1 kg ha^-1. A l'intérieur des zones, la variabilitérelative est plus importante au Nord o`u le rendement du génotype le plus productif représente 123,2% de celui du génotype le moins productif et au Centre o`u ce pourcentage est de 133,6%, qu'au Sud o`u il passe a` 40,6%.

Par ailleurs, il est a` noter que le g'enotype FLEUR11 qui a la meilleure production moyenne pour les trois zones (543,0 kg ha^-1), n'est pas le meilleur partout. Il ne donne le meilleur rendement qu'au Nord alors que le g'enotype GC-8-35 domine au Centre et le g'enotype 55-128 au Sud. Ce constat renforce l'id'ee que dans cette zone sah'elienne marqu'ee par une variabilit'e environnementale importante, une recommandation pour le choix de g'enotypes sp'ecifiques aux lieux est pr'ef'erable et plus pertinente qu'une recommandation unique du g'enotype le meilleur en moyenne.

Chapitre 2

Les méthodes classiques

d'analyse des interactions G×E

Dans ce chapitre, nous parlerons des outils classiques d'analyse des interactions G×E et présenterons les modèles de simulation de cultures comme méthode alternative pour prédire le rendement des cultures. Nous allons également soumettre nos données a` ces différentes méthodes présentées et évaluer comment elles prennent en compte les éventuelles interactions décelées. Nous allons toutefois appliquer ces différents modèles uniquement sur les données de l'essai multilocal. En effet, la plupart des méthodes classiques nécessitent des données complètes et seules le sont celles de l'essai multilocal.

Les raisons de la présence des interactions G×E peuvent être de deux ordres. De telles interactions sont, d'une part, attendues en présence d'une large variation des caractéristiques de résistance aux stress des génotypes, le stress hydrique par exemple. D'autre part, en présence, d'une large variation des environnements au niveau de ce même stress. Mais généralement, c'est l'une et l'autre de ces conditions qui les favorisent, même si au Sahel, la grande

variabilit'e climatique y s'evissant dont nous consid'erons qu'elle caract'erise essentiellement les environnements, contribue pour une large part a` la pr'esence de ces interactions.

Le terme g'enotype fait r'ef'erence a` un cultivar, c'est-à-dire un mat'eriel g'en'etique qui peut être homogène ou h'et'erogène et l'environnement a` un ensemble de conditions climatiques, de types de sol et de pratiques culturales d'un essai conduit dans un lieu donn'e, une ann'ee donn'ee (Annicchiarico, 2002).

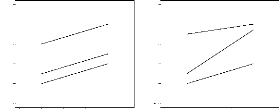
Deux types d'interactions G×E sont a` distinguer (figure 2.1). Les interactions sont dites quantitatives ou noncrossovers, si les classements des g'enotypes entre les diff'erents environnements sont conserv'es mais que l''ecart entre les g'enotypes est modifi'e. Par contre, elles sont dites qualitatives ou crossovers lorsque les classements sont invers'es (Baker, 1988; Baril, 1992).

Dans les essais multienvironnements, il peut être envisag'e de s'electionner les g'enotypes de plus grande production moyenne sur l'ensemble des environnements test'es ou de les choisir en fonction de leurs performances selon les environnements. Pour cela, les informations issues de ces exp'erimentations, sont 'etudi'ees afin d'être synth'etis'ees en dissociant les effets du g'enotype, de l'environnement et des interactions G×E au travers des modèles statistiques (Brancourt-Hulmel, Biarnès-Dumoulin et Denis, 1997).

Plusieurs modèles des interactions G×E ont donc 'et'e propos'es. Dans ce qui suit, nous en ferons un tour d'horizon et en pr'esenterons les principaux : le modèle d'analyse de variance a` deux facteurs, la r'egression conjointe, la m'ethode AMMI, la r'egression factorielle et les modèles de simulation de cultures.

Mais avant de pr'esenter ces diff'erentes m'ethodes fond'ees principalement sur
le modèle d'analyse de variance, il est a` remarquer qu'il est aussi possible
de concevoir, a` travers deux statistiques descriptives, l''etude des interactions

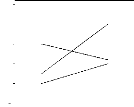
FIG. 2.1 - Types d'interactions G×E pour trois g'enotypes A, B et C. (1) : sans interactions; (2) : interactions quantitatives; (3) : interactions qualitatives.

(1) (2)

1 2 3 4 5 6

environnement

1 2 3 4 5 6

environnement

(3)

1 2 3 4 5 6

renaement

renaement

2 9 4 5 0

A

B

C

A

B

C

A

B

C

C

A

B

renaement

2 9 4 5 0

A

B

C

B

C

A

environnement

G×E pour décrire le comportement des génotypes sur un échantillon d'environnements.

Pour cela, la variabilitéintrinsèque du génotype sur un ensemble d'environnements est étudiée a` l'aide de la variance environnementale S2 i (Becker, 1981; Lin, Binns et Lefkovitch, 1986; Piepho, 1998). L'écart a` la valeur moyenne des performances du génotype, compte tenu du nombre de milieux sur lequel il est testé, représente une mesure de son instabilité. Cette variance environnementale est estimée par

S2 i = _XJ (Yij - Yi.)²/(J - 1) j=1

o`u _Yij est la réponse du génotype i de l'environnement j, _Yi. la moyenne des réponses du génotype i des différents environnements et J le nombre d'environnements. Par la suite, l'opérateur (.) désigne la moyenne sur l'indice qu'il remplace.

Quant a` l'écovalence variétale W i 2 (Becker, 1981; Becker et Léon, 1988), elle est mesurée par la stabilitérelative du génotype et est estimée par

W i 2 = _XJ (Yij - Yi. - Y.j + Y..)² j=1

C'est la somme des carrés des termes d'interaction propres au génotype i. A la différence de S² _i, la somme de carrés W i 2 n'est pas divisée par les degrés de liberté(ddl) correspondants.

Cependant, la liste des méthodes d'étude des interactions G×E présentée dans ce chapitre n'est pas exhaustive. D'autres méthodes, qui ne sont pas décrites ici, existent par ailleurs :

- structuration de l'interaction (Denis et Vincourt, 1982)

- modèles multiplicatifs (Cornelius, Seyedsadr et Crossa, 1992; Crossa, Cornelius, Seyedsadr et Byrne, 1993; Crossa, Cornelius, Sayre et Ortiz-Monasterio, 1995);

- application de l'analyse canonique (Seif, Evans et Balaam, 1979; Calinski, Czajkaet Kaczmarek, 1987);

- variantes des modèles de regression factorielle (Denis, 1988; van Eeuwijk 1992, 1995; van Eeuwijk, Denis et Kang, 1996);

- régression Partial Least Squares (Aastveit et Martens 1986; Talbot et Wheelwright 1989; Vargas, Crossa, Sayre, Reynolds, Ram`ýrez et Talbot, 1998);

- une méthode récente fondée sur l'approche bayésienne (Theobald, Talbot et Nabugoomu, 2002).

2.1 Le mod`ele d'analyse de variance a` deux facteurs

2.1.1 Le mod`ele

Le mod`ele linéaire mixte généralement considérésur les moyennes par génotype et par environnement est le suivant

Yij = m + gi + Ej + (gE)ij + eij (2.1)

o`u Yijest la réponse du génotype i de l'environnement j, m la moyenne générale et gi l'effet fixe du génotype i. L'effet Ej de l'environnement j, l'interaction (gE)ij et le terme d'erreur eij sont supposés aléatoires, iid et indépendants les uns des autres avec

E(Ej) =E[(gE)ij] =E(eij) = 0 et Var(Ej) = ó²_E, Var[(gE)ij] = ó²gE et
Var(eij) = ó²_e

o`u la fonctionE(
·) désigne l'espérance et Var(
·) la variance.

Dans l'optique de prédire la performance des génotypes dans les différents environnements considérés, l'option qui consiste a` prendre les génotypes comme fixes et les environnements comme aléatoires est argumentée par Denis, Piepho et van Euwijk (1997). En effet, ces auteurs justifient ce choix par le fait qu'il s'agit d'étudier un nombre fini de génotypes, d'o`u l'effet génotype fixe. Au contraire, les environnements ne sont pas considérés pour eux-mêmes, mais en tant qu'échantillons dans une population plus vaste d'environnements possibles auxquels les variétés sont destinées. Pour nous, cela s'appliquera aux années plutôt qu'aux lieux.

Les effets principaux du génotype et de l'environnement sont considérés par rapport a` la moyenne générale, alors que le terme d'interaction du modèle représente la variabilitédes performances du génotype avec l'environnement qui n'est pas prise en compte dans les effets additifs du génotype et de l'environnement.

D'après le modèle 2.1, les estimations des effets sont, pour un dispositif équilibré:

bgi = Yi. - Y..

^bEj = Y.j - Y..

^[(gE)_ij = Yij - Yi. - Y.j + Y..

Dans l'estimation des termes du modèle qui portent l'indice j, nous retrouvons _Y.j. Cette moyenne traduit le potentiel de l'environnement. Or l'environnement étant fortement variable au Sahel, les termes en j ne sont pas bien prévisibles a` moins de disposer d'un échantillon de nombreux environnements qui fait généralement défaut. Cependant si nous considérons la différence entre deux variétés i et i^', l'imprévisibilitéde l'effet environnement Ej disparaàýt lors de l'estimation de cette différence, si le dispositif est complet. En effet, il viendra :

Yij - Yi^'j = gi - gi' + (gE)ij - (gE)i'j

Par contre, le problème demeure pour les interactions qu'il faudra modéliser afin de prédire plus finement la différence des performances des génotypes.

2.1.2 Illustration avec les données de l'essai multilocal

Avec le modèle d'analyse de variance a` deux facteurs, génotype et environ-
nement, appliquéaux données de l'essai multilocal, nous sommes intéressés

tout premièrement a` tester la significativit'e des interactions G×E. Dans ce cas, les deux effets principaux sont consid'er'es comme 'etant fixes.

Nous rappelons, que les donn'ees proviennent d'un r'eseau d'essais vari'etaux effectu'es au S'en'egal durant l'hivernage 2005 (tableau 1.2, page 16). Six g'enotypes d'arachide ont 'et'e test'es sur 11 sites dans le bassin arachidier s'en'egalais qui est la r'egion principale de production de cette l'egumineuse.

Le tableau 2.1 fournit les r'esultats de l'analyse de variance a` deux facteurs appliqu'ee a` ces donn'ees.

Effet d.l Somme Carr'e Statistique F Niveau de

de carr'es moyen signification

G'enotype 5 23 2765,0 46 553,0 2,42 0,0485

Environnement 10 8 100 921,7 3 810 092,2 42,1 0,0000

R'esidus 50 962 311,6 19 246,2

Tableau d'analyse de variance des donn'ees des essais multilocaux TAB. 2.1 - de 6 g'enotypes d'arachide sur 11 localit'es au S'en'egal durant l'hivernage 2005.

En n'egligeant dans un premier temps l'interaction, nous concluons qu'au seuil de 5%, les effets g'enotype et environnement sont significatifs. A l'instar de Denis et Vincourt (1982), nous allons 'evaluer et comparer l'ordre de grandeur des r'esidus et l'ordre de grandeur de l'effet g'enotype. Si CM_r est le carr'e moyen des r'esidus, l'ordre de grandeur de ces r'esidus peut être estim'e par vCM_r ; et si CM_g est le carr'e moyen du facteur g'enotype, l'ordre de grandeur de l'effet g'enotype peut être estim'e par ,/CM_g - CM_r/J. Nous notons alors que l'ordre de grandeur des r'esidus (138,7) est grand par rapport a` celui de l'effet g'enotype (15). Il s'agira alors d'essayer de r'eduire ces r'esidus en ajoutant une interaction au modèle additif. L'interaction peut être mise en 'evidence avec la figure 2.2 o`u sont repr'esent'es les rendements des g'enotypes de l'essai multilocal. Les rendements moyens par lieu sont rang'es par ordre croissant et mis en abscisse. Nous constatons sur ce graphique un changement

de classement des variétés d'un site a` un autre. Nous remarquons également que l'écart entre les génotypes augmente avec la moyenne du lieu.

Variation des rendements des six g'enotypes de l'essai multilo-

FIG. 2.2 - cal. En abscisse sont mis, par ordre croissant, les performances moyennes des lieux.

200 400 600 800 1000

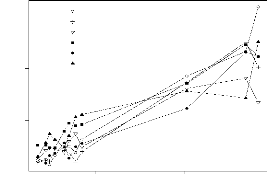
Rendement

500 1000 1500

55-128 55-33 55-437 F11 GC-8-35 JL24

Pour espérer formuler tout de même des recommandations dans ce milieu très contrastépour l'adoption de cultivars les mieux adaptés a` chaque environnement, la solution consiste a` tenter de réduire la part imprévisible de ces interactions en les modélisant; ce qui peut se faire a` travers différentes méthodes que nous allons présenter ci-dessous.

2.2 La methode de regression conjointe

2.2.1 Le modèle

Ce modèle a étéproposépour la première fois par Yates et Cochran (1938). Il
a ensuite étérepris par plusieurs autres auteurs dont les principaux sont Fin-
lay et Wilkinson (1963), Eberhart et Russell (1966) et Perkins et Jinks (1968).

Plutôt proposépour les essais multilocaux que pour les essais pluriannuels, ce modèle pose l'effet des interactions G×E comme une fonction linéaire de l'effet Ej qui représente le potentiel du milieu j pour les génotypes; une valeur positive de Ej traduisant un potentiel élevétandis qu'une valeur négative, un faible potentiel.

L'interaction est de la forme :

(gE)ij = ciEj + dij

o`u bci est le coefficient de la régression pour le génotype i; cette pente caractérise la sensibilitédifférentielle du génotype i au milieu (Denis et Vin-court 1982). Le terme _dij désigne la déviation du modèle, c'est-à-dire les interactions G×E résiduelles.

Ces coefficients bci et la performance moyenne des génotypes sont les paramètres d'intérêt pour une analyse de stabilité. En effet, la performance d'un génotype dans un lieu donnédépend de la performance moyenne des génotypes du lieu et des interactions G×E qui y sont espérées. Une valeur largement positive de bci associée a` une performance moyenne d'un site relativement importante, concourent a` caractériser ce site comme étant favorable. De l'autre côté, un site est considérécomme non favorable si la valeur de bci associée a` la performance moyenne des génotypes de ce site est négative.

Les coefficients bci sont obtenus facilement :

bci =	X ^bEj ^[(gE)ij j
	X^bE^2 j j

Un cas particulier de ce modèle a 'et'e d'evelopp'e par Tukey (1949) : les coefficients c s''ecrivent Kg et l'interaction se r'eduit a` Kg E3.

2.2.2 Illustration avec les données de l'essai multilocal

Les donn'ees sont celles du tableau 1.2 de la page 16. Le tableau 2.2 pr'esente les paramètres mb + bgi et 1 + bci des diff'erents g'enotypes des essais.

G'enotype	mb + bgi	1 + bci
55-128	488,9	1,381
55-33	341,3	1,138
55-437	327,2	0,698
FLEUR11	636,0	0,963
GC-8-35	349,2	1,043
JL24	557,1	0,777

Paramètres estim'es par r'egression conjointe de 6 g'enotypes d'ara-

TAB. 2.2 - chide lors d'essais multilocaux au S'en'egal durant l'hivernage 2005.

Le g'enotype 55-128 qui a la pente (1 + bci) la plus 'elev'ee, est plus sensible aux variations du milieu que la moyenne des g'enotypes des essais, suivi du g'enotype 55-33. En revanche, le g'enotype de r'ef'erence 55-437 et le g'enotype JL24 semblent moins affect'es que la moyenne aux variations du milieu. Quant aux g'enotypes GC-8-35 et FLEUR11 avec des pentes proches de l'unit'e, ils repr'esentent par leurs valeurs, de bonnes indications des variations du milieu.

2.3 La méthode AMMI

2.3.1 Le modèle

La méthode AMMI, Additive main effect and multiplicative interaction, a étéintroduite par Williams (1952) et reprise par Gollob (1968), puis par Mandel (1961, 1971) et par Bradu et Gabriel (1978). Elle fut développée a` l'origine pour les domaines du social et de la physique et son application a` la recherche agricole a étéproposée par Kempton (1984) et Zobel, Wright et Gauch (1988). Mais il faut attendre Gauch (1992) pour qu'elle devienne répandue. C'est une méthode assez générale et Gauch et Zobel (1996) ont soulignéque son champ d'application potentiel va au delàde l'étude

des méthodes d'interactions GxE. Beaucoup d'autres auteurs ont ^étudiéles interactions GxE a` l'aide de cette méthode :Vargas, Crossa, van Eeu-

wijk, Ram`ýrez et Sayre (1999), Yan et Hunt (2001), Ebdon et Gauch (2002a, 2002b), Gonz'alez, Crossa et Cornelius (2003a, 2003b), Gauch (2006).

La méthode AMMI associe l'analyse de variance et l'analyse en composantes principales (ACP). Sont d'abord estimés les effets principaux des variétés et des environnements par une analyse de variance du modèle additif, c'est-àdire du modèle sans les interactions GxE. Ensuite, la partie non additive du modèle est étudiée par une analyse en composantes principales (Crossa, 1990).

L'interaction est décrite de cette façon

(gE)ij = è1á1iâ1j + _è2á2iâ2j + + èháhiâhj

c'est a` dire

Yij = m + gi + Ej + ( _Xh èkákiâkj) + eij

k=1

o`u èk est la valeur singulière du k^e axe (è2 _k 'etant la valeur propre), _áki est le vecteur propre du i^e g'enotype pour le k^e axe, _âkj est le vecteur propre du je environnement pour le k^e axe et avec les contraintes

_X Xá2 ki = Xâ2 kj = 1 et Xákiák^'i = âkjâk^'j = 0

i j i j

Les paramètres du terme d'interaction sont donc estim'es par d'ecomposition en valeur singulière (DVS) de la matrice des r'esidus obtenus après ajustement des deux effets principaux.

Le nombre h de paramètres pour chaque terme multiplicatif de l'interaction qui constitue le nombre d'axes principaux peut être d'etermin'e soit par validation crois'ee (Gauch et Zobel, 1988; Crossa, 1990, Piepho, 1994) o`u les r'ep'etitions sont tour a` tour retir'ees et non les lieux, soit par des tests statistiques (Gollob, 1968; Cornelius, 1993; Piepho, 1995).

Le nombre d'axes principaux retenu est g'en'eralement compris entre z'ero, on parle dans ce cas de AMMI-0 c'est-à-dire du modèle additif et le minimum entre (I - 1) et (J - 1), o`u I constitue le nombre de g'enotypes et J le nombre d'environnements. Le modèle complet (AMMI-F, F faisant r'ef'erence a` full pour full model), avec tous les axes principaux, fournit une estimation parfaite. Mais g'en'eralement, lorsque les interactions G×E sont significatives, les modèles avec un (AMMI-1) ou deux (AMMI-2) axes principaux sont les plus utilis'es a` cause de leur simplicit'e.

Les tests statistiques propos'es pour d'eterminer le nombre optimal d'axes sont tous fond'es sur la statistique t² _k/s² o`u t2 k est l'estimation de la valeur singulière èk obtenue par DVS et s², avec f degr'es de libert'e, est le carr'e moyen des r'esidus du modèle additif divis'e par le nombre de r'ep'etitions par environnement (Piepho, 1995).

Sous l'hypothèse nulle (H0 : èk = 0), les statistiques de tests sont les suivantes :

1. t²_k/s² suit une loi de Fisher a` (J +I-1-2k) et f degrés de liberté(Gollob, 1968)

2. FGH1 = gt²_k/h1fs² suit une loi de Fisher avec h1 et g degrés de liberté, o`u h1 = 2v1u1/v2, g = 2 + 2(f - 2)v1/v2, v1 = u²2 + u²1 + (f - 4)u1 et

v2 = (f - 2)u²₂ + 2u²₁ (Cornelius, 1993) ; u1 et u2 sont des approximations fournies par Cornelius (1980).

3. FGH2 = t²_k/u1s² est distribuée selon la loi de Fisher avec h2 et f degrés de liberté, o`u h2 = 2u²1/u²2 (Cornelius, 1993).

En outre, une statistique de test FR, plus simple a` calculer, a étéproposée par Cornelius et al. (1992). Ce test utilise la somme des carrés résiduels après ajustement du modèle AMMI avec q axes principaux. Sachant que sous l'hypothèse nulle, la somme de carrés résiduels est approximativement une variable de chi-deux, la statistique suivante FR

[ FR = E E(Yij - Yi. - Y.j + Y..)^2 - i j

X q k=1

?t^2 ? /f2s^2 k

suit une distribution de Fisher avec f2 = (J - 1 - q)(I - 1 - q) et f degrés de liberté. La statistique FR significative révèle qu'il y a au moins un axe principal supplémentaire a` prendre en compte en plus des q déjàutilisés.

Dans le cas des essais multienvironnements, il est supposéque les erreurs du modèle sont indépendantes et normalement distribuées avec des variances entre les environnements homogènes. Même si l'indépendance des erreurs peut être assurée par une randomisation des niveaux des facteurs et que les erreurs peuvent être considérées comme gaussiennes, les variances résiduelles sont généralement hétérogènes d'un environnement a` l'autre au Sahel. Or, en présence d'erreurs expérimentales hétérogènes, Piepho(1995) a montréque la statistique de test FR est plus robuste que FGH1, FGH2 et celle de Gollob.

2.3.2 Illustration avec les données de l'essai multilocal

Les données de l'essai multilocal (6 génotypes et 11 sites) ont étésoumises a` la méthode AMMI dans le but d'obtenir l'estimation des performances des génotypes dans les différents environnements. Il est espéréque l'estimation d'un génotype dans un environnement particulier soit plus précise que la simple moyenne des performances de ce même génotype dans les autres environnements o`u il a étéobservé.

Pour ces données, le nombre maximum d'axes principaux a` retenir est égal a` cinq. Pour cela, cinq modèles (AMMI-0 a` AMMI-4) vont être testés étape par étape a` l'aide de la statistique de test FR. Si le modèle AMMI-1 est significatif, c'est-à-dire la statistique associée au premier axe principal est significative, le modèle AMMI-2 est alors testéa` son tour et ainsi de suite jusqu'au modèle AMMI-q non significatif o`u l'on devra s'arrêter. Le meilleur modèle est alors le modèle AMMI-q.

Les valeurs singulières calculées sur les données de l'essai multilocal sont égales a` 723,8 pour le premier axe, 577,6 pour le second, 259,2 pour le troisième, 182,1 pour le quatrième et 66,5 pour le cinquième tandis que le tableau 2.3 montre les vecteurs propres des facteurs pour les quatre premiers axes principaux

Les résultats de la méthode AMMI sont présentés au tableau 2.4. Le test pour le deuxième axe principal est significatif, ce qui signifie qu'il y a au moins un axe supplémentaire intéressant dont il faut tenir compte. Et comme le test pour le troisième axe n'est pas significatif, nous adoptons, pour ces données, le modèle AMMI-3. A la figure 2.3 sont représentés les scores des génotypes et des environnements du deuxième axe principal en fonction de ceux du premier. Ce graphique double, est plus connu sous le nom de biplot (Kempton, 1984). Sur ce graphique, un génotype proche de l'origine présente

Axe 1 Axe 2 Axe 3 Axe 4

Vecteurs propres des g'enotypes pour les 4 axes

55-128	18.0	-7.7	-5.5	1.8
55-33	6.0	11.1	-5.0	-5.0
55-437	-15.6	7.3	-5.6	-0.8
F11	-2.0	4.2	3.7	11.2
GC-8-35	3.8	2.8	12.6	-4.9
JL24	-10.2	-17.8	-0.2	-2.3

Vecteurs propres des environnements pour les 4 axes

Wenthiwy	-9.9	-4.5	3.2	3.3
Niorosud	18.5	-14.9	0.5	-0.4
Paoskoto	12.3	16.2	3.9	0.5
Nioro	2.6	3.1	-13.2	-0.2
Keur Samseun	-1.4	3.1	3.2	-0.1
Keur Fary	1.1	3.1	4.6	1.2
Sinthiou Thiabala	-3.4	-6.4	2.9	2.1
Ndiadiane	-7.5	-1.5	1.4	-6.1
Gatte	-4.9	0.2	-2.4	-1.1
Ndangalma	-3.3	0.8	-0.9	-7.6

TAB. 2.3 - Vecteurs propres des facteurs g'enotype et environnement pour l'essai multilocal.

une faible interaction tandis qu'un genotype qui s'en eloigne est au contraire interactif.

Comme avec la regression conjointe, les genotypes 55-33 et 55-128 presentent de fortes interactions et les genotypes GC-8-35 et F11 semblent les moins interactifs c'est-à-dire les plus conformes au comportement au comportement moyen de l'ensemble des genotypes. Mais au contraire, cette analyse classe les genotypes JL24 et 55-437 parmi les genotypes les plus interactifs alors qu'ils etaient classes parmi ceux qui affichent les plus faibles interactions par la regression conjointe.

FIG. 2.3 - Scores des g'enotypes et des environnements pour le deuxième axe en fonction de ceux du premier.

Score de l'axe 2

-15 -10 -5 0 5 10 15

Ndiadiane Gatte

Wenthiwy

55-128

Sinthiou Thiabala

Nioro Sud

JL24

55-437

Keur Samseun

Bambey

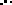
F11

Ndangalma

Keur Fary

Nioro

GC-8-35

55-33

Paoskoto

-15 -10 -5 0 5 10 15 20

Score de l'axe 1

2.4 La r'egression factorielle 2.4.1 Le modèle

C'est le modèle additif auquel trois séries de termes de régression sont ajoutés (Denis, 1980). Ces régresseurs sont des covariables décrivant les génotypes (ex : poids des graines) et les environnements (ex : pluviométrie en aoàut) et aussi l'interaction par les produits deux a` deux de ces régresseurs.

Un modèle similaire de celui de régression factorielle a étéutilisépar Freeman et Perkins (1971) qui n'avaient considéréqu'une covariable associée au facteur milieu non calculée sur les données. Wood (1976), lui, a utiliséune combinaison linéaire de covariables élémentaires liées au milieu.

Effet	d.l		Somme de carrés		Carrémoyen	Statistique F	Niveau de signification
Génotype	5		23 2765,0		46 553,0	2,42	0,0485
Environnement	10	8	100 921,7	3	810 092,2	42,1	0,0000
G×E	50		962 311,6		19 246,2
AMMI axe 1	14		523 953,0		37 425,2	3,1	0,003
AMMI axe 2	12		333 578,0		27 798,1	6,4	0,000
AMMI axe 3	10		67 186,2		6 718,62	2,5	0,057
AMMI axe 4	8		33 172,6		4 146,6	5,6	0,026
Résidus G×E	6		4 422,5
Total	65		929 600

TAB. 2.4 - Tableau d'analyse des données de l'essai multilocal avec la méthode AMMI.

Nous allons pr'esenter le modèle de r'egression factorielle de deux manières diff'erentes. Dans la pr'esentation matricielle, la plus simple, le but est d'expliquer la matrice des observations Y de dimension I ×J a` partir de deux matrices de covariables associ'ees aux deux facteurs 'etudi'es. Dans la pr'esentation indicielle, la plus g'en'erale, les observations Y sont dans un vecteur de longueur IJ.

Nous pouvons disposer en g'en'eral d'un tableau X de p covariables associ'ees
aux g'enotypes et d'un tableau Z de q covariables associ'ees aux environne-

ments. Les matrices X et Z s''ecrivent dans ce cas : x1 1 x2 1 · · · xp 1 z1 1 ? x1 2 x2 2 · · · xp 2 ? ? z1 2 X= Z= ? ? ? ? ? ? ? ? ? ? ... ... ... ????? ... x1I x2 I ··· xp I z1 J

z^21 z2 2 ... z2 J

··· · · · · · ·

zq 1 zq 2 ? ... ????? zq J

La matrice X est de dimension I × p et Z de dimension J × q. Par souci de simplicit'e dans la pr'esentation, nous ne consid'erons alors que le cas d'une unique observation par g'enotype pour un environnement donn'e, qui peut être une moyenne ou une moyenne ajust'ee sur le dispositif de cet environnement. Les matrices X et Z sont consid'er'ees par la suite centr'ees.

Alors le modèle de r'egression factorielle peut se pr'esenter sous forme matricielle, plus commode a` manipuler

2Z^') + XZ^' +g3Z^' + X[^'

Y = 1Im1' _J + (g1 + Xg2)1' _J + 1I(I' ₁ +uEi' 3 + e (2.2)

- Y de dimension I x J est la variable r'eponse

- m est la moyenne g'en'erale

- (g1 + Xg2)1^'

efficients des covariables 1 a` p dans la r'egression de l'effet g'enotype et (g1 1 +uEI' J est l'effet principal du g'enotype o`u (g2 est le vecteur des coles I r'esidus de cette r'egression.

- 1I(i^' 2Z^') est l'effet principal de l'environnement d'ecompos'e de la même

facon

- XZ^' est la partie de l'interaction expliqu'ee par le produit des deux covariables X et Z

-g3Z^' est la partie de l'interaction expliqu'ee par la covariable Z, une fois tenu compte de l'explication fournie par la covariable X

- Xi^'3 est la partie de l'interaction expliqu'ee par la covariable X, une fois tenu compte de l'explication fournie par la covariable Z

Ce modèle 'etant lin'eaire, les proc'edures d'estimation usuelles sont employ'ees, ce qui donne les r'esultats suivants pour l'estimation des paramètres inconnus (voir Annexe A) :

mb = 1^'_IY1J/IJ

bg2 = (X^'X)-¹X^'Y1J/J

bE' 2 = 1^'_IYZ(Z^'Z)^-1/I

I/I - X(X'X)-1X')Y1J/J

bg1 = (II - 1I1^'

bE' 1 = 1^'_IY(IJ - 1J1^' _J/J - Z(Z^'Z)-¹Z^')I

b = (X^'X)-¹X^'YZ(Z^'Z)-¹

I/I - X(X'X)-1X')YZ(Z'Z)-1

bg3 = (II - 1I1^'

bE' 3= (X^'X)^-1X^'Y(IJ - Z(Z^'Z)^-1Z^')

Cependant, cette facon d'ecrire le mod`ele et les calculs qui en decoulent sont lies a` la structure des donnees. En effet, dans ce que nous avons presente, les observations sont supposees àetre dans une matrice a` I lignes et J colonnes, ce qui prevoit cette matrice de donnees compl`ete. Cela s'interpr`ete dans le cas d'un essai multienvironnement par exemple, par le fait que chaque genotype doit àetre present dans chaque environnement. Or la realiteest souvent autre.

Pour les essais o`u toutes les varietes ne sont pas dans tous les environnements, cette methode, qui est ici generalisee avec p covariables associees au facteur genotype et q covariables liees au facteur environnement, peut se presenter sous forme indicielle.

Yij = m (E p

x^iMp + gi) + (E q

zj áq 3 E ) + E p,q

x^p. z^qjã+ e · · (2.3) z pq z3

o`u gi represente la part des effets moyens non expliquee par les covariables X et Ej celle non expliquee par les covariables Z ; x<sup>p</sup><sub>i</sub> etant la valeur de la p<sup>e</sup> covariable associee au genotype i et z<sup>q</sup><sub>j</sub> la valeur de la q<sup>e</sup> covariable associee a` l'environnement j.

Les vecteurs ã =

r1^1 lfp 713^.

, á =

(

á1 ... áq

? ? ? ?

et â =

( â1 ) . âp

sont estimes par regression du vecteur Y des observations, de longueur IJ,
respectivement sur le produit semi-tensoriel ligne (Dieng, 2003) des deux

matrices des covariables, sur la matrice de covariable attach'ee au facteur environnement et sur la matrice de covariable attach'ee au facteur g'enotype. Nous reprenons ci-après la d'efinition du produit semi-tensoriel ligne.

D'efinition 1 Produit semi-tensoriel ligne Si A est une matrice rectangulaire (m,r),

Si B est une matrice rectangulaire (m,s),

A ? B est dit produit semi-tensoriel ligne de A par B. C'est une matrice rectangulaire (m,rs) qui se présente ainsi

a11 · B[1,] ? a21 · B[2,] ? ? ? ? ? ... am1 · B[m,]

a12 · B[1,] a22 · B[2,] ... am2 · B[m,]

· · · · · ·

· · ·

a1r · B[1,] ? a2r · B[2,] ... ????? amr · B[m,]

o`u B[m,] est la m<sup>e</sup> ligne de B. Autrement dit, A ? B est la juxtaposition de tous les produits termes a` termes possibles entre une colonne de A et une colonne de B.

Nous nous servons du produit semi-tensoriel ligne pour obtenir la matrice d'incidence pour l'interaction a` partir des matrices d'incidence des effets simples.

Avec cette pr'esentation indicielle, la r'egression factorielle est effectu'ee en deux 'etapes : d'abord la r'egression des observations sur le produit semitensoriel ligne des deux matrices de covariables et celle sur les deux matrices des covariables auxquelles est ajout'ee par la suite l'estimation des r'esidus de ces r'egressions.

Nous pr'esentons ci-dessous un modèle, plus g'en'eral, o`u tous les paramètres sont estimables en une seule 'etape.

Y = m1IJ + X ·a1 +X·n2 + Z ·b2 +L·Ib2 + X ? Z · (ab)11

- Xn1 est la régression sur les covariables génotypes

+x? Z · (ab)21 + X ?7L· (ab)12 +X?7L· (ab)22 + e

- Y est le vecteur des observations, de longueur IJ

- m1IJ est la moyenne générale des observations

->Xn2 est l'écart des effets génotype a` la régression sur les covariables génotypes,

-7Lb2 est l'écart des effets environnements a` la régression sur les covariables - Zb2 est la régression sur les covariables environnements

Xétant la matrice d'incidence des génotypes

-x?Z(ab)21 est l'effet des covariables environnements modulépar les génotypes - X ? Z(ab)11 est l'effet des covariables environnements modulépar les cova-

environnements,7Létant la matrice d'incidence des environnements

riables génotypes

non expliquépar les covariables génotypes

- X ?L(nb)12 est l'effet des covariables génotypes modulépar les environnements non expliquépar les covariables environnements

-x?7L(ab)22 est l'interaction G×E expliquée ni par les covariables génotypes, ni par les covariables environnements.

Ainsi, les paramètresa1,a2,b2,b2, (ab)11, (ab)21, (ab)12, (rb)22, sont estimés par simple régression linéaire sur les matrices et vecteurs adéquats.

Exemple d'écriture pour un essai multilocal : Pour un essai multilocal de 3 génotypes effectuéen 2 lieux différents o`u nous avons 2 covariables associées au facteur lieu et 1 covariable associée au facteur variété, les vecteurs et matrices se présentent comme suit :

39

?
? ? ? ? ? ? ? ? ? ?

?
? ? ? ? ? ? ? ? ? ?

Y11

Y21

Y31

Y12

Y22

Y32

Y=

?
? ? ? ? ? ? ? ? ? ?

X=

?
? ? ? ? ? ? ? ? ? ?

?
? ? ? ? ? ? ? ? ? ?

?
? ? ? ? ? ? ? ? ? ?

Z=

X=

X111 X211 X311 X121 X221 X321

?
? ? ? ? ? ? ? ? ? ?

?
? ? ? ? ? ? ? ? ? ?

XeZ=

X111Z111 X111Z112 X211Z121 X211Z122 X311Z211 X311Z212 X121Z221 X121Z222 X221Z311 X221Z312 X321Z321 X321Z322

?
? ? ? ? ? ? ? ? ? ?

I

?
? ? ? ? ? ? ? ? ? ?

Z=

1 0 1 0 1 0 0 1 0 1 0 1

Z111 Z112 Z121 Z122 Z211 Z212 Z221 Z222 Z311 Z312 Z321 Z322

1 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0 0 1

?
? ? ? ? ? ? ? ? ? ?

? XeZ= ? ? ? ? ? ? ? ? ? ?	Z111 0 0 Z221 0 0		Z112 0 0 Z222 0 0		0 Z121 0 0 Z311 0
0 0 Z212 X e 0 0 Z322 1		? ? ? ? ? ? ? ? ? ? ?		X111 X211 X311 0 0 0		0 ? 0 0 X121 X221 ? ? ? ? ? ? ? ? ? ? X321

0 0

Z122 0

0 Z211

0 0

Z312 0

0 Z321

0	0	0	0	0
0	1	0	0	0
0	0	0	1	0 I
0	0	0	0	0
0	1	0	0	0
0	0	0	1	0

1 0 0 1 0 0

x? =

?
? ? ? ? ? ? ? ? ? ?

Jusqu'àmaintenant les covariables sont supposées continues. Toutefois, cette méthode est encore valable dans le cas o`u elles sont de type qualitatif. Il suffit de la même manière que l'on passe de la régression a` l'analyse de variance, de remplacer chaque colonne de la matrice de covariables par des colonnes indicatrices des niveaux de la colonne de covariable qualitative considérée (Denis, 1980).

Dans le cas o`u les covariables sont trop nombreuses, différentes méthodes de sélection sont présentées dans (Denis, 1980).

2.4.2 Illustration avec les données de l'essai multilocal

Les données sont celles du tableau 1.2 de la page 16.

Des variables climatiques ont étémesurées quotidiennement sur les sites des essais. Ces variables (pluie, rayonnement solaire, vitesse du vent, etc.) se trouvent en fait plus nombreuses que les essais, ce qui rend impossible leur complète utilisation dans un modèle de régression factorielle. Pour décrire les différents lieux, nous avons uniquement retenu la pluviométrie totale sur le cycle de culture qui, a` notre sens, permet de bien les caractériser.

Pour la covariable génotype, nous pouvons utiliser des indices de tolérance ou de sensibilitéqui font intervenir le rendement en conditions de sécheresse et le rendement en conditions optimales. Mais le mode de calcul de ces indices pénalise très fortement les génotypes a` rendement potentiel élevé; des valeurs

très élevées caractérisent plutôt des génotypes rustiques a` faible productivitéque des génotypes a` rendement stable et élevé(Belhassen, This et Monne-

veux, 1995). Nous privilégions le taux de croissance de culture (C) décrit par Turner, Wright et Siddique (2002) comme étant :

C = (PF + (1,65 PG))/T

o`u PF est le poids des fanes, PG le poids des gousses et T la durée floraisonrécolte. Ce taux permet effectivement de caractériser les génotypes selon leur sensibilitéa` la sécheresse car plus une variétéproduit de biomasse totale et de gousses en un temps relativement court, mieux elle est adaptée a` la sécheresse. Le calcul de C s'est fait sur des données qui n'ont pas servi a` la modélisation de l'interaction G×E.

Les résultats de la régression factorielle tenant compte de la covariable C attachée aux génotypes et de la covariable Pluie liée aux environnements, sont présentés dans le tableau 2.5. La somme des carrés résiduels (751 771,62) est ce qui reste des interactions G×E une fois que nous avons utiliséles covariables pour les interpréter. Sans ces covariables, cette somme des carrés était égale a` 962 311,6 (modèle additif, tableau 2.1 de la page 24).

Effet	d.l		Somme de carrés			Carrémoyen	Statistique F	Niveau de signification
Génotype	5		232	764,98	46	552,99	2,23	0,0725
Environnement	10	8	100	921,68	810	092,17	38,79	0,0000
C×Pluie	1		8	896,50	8	896,50	0,43	0,5181
C×Env.	9		162	944,57	18	104,95	0,87	0,5624
Génotype×Pluie	4		38	698,94	9	674,74	0,46	0,7622
Résidus	36		751	771,62

TAB. 2.5 - Régression factorielle des données de l'essai multilocal.

Nous notons tout de même que les covariables associées aux effets principaux ne sont pas significatives (0,5181 pour le produit des deux covariables, 0,5624 pour la covariable liée a` l'environnement et 0,7622 pour celle liée au facteur génotype). Cela indique que la décomposition de l'interaction n'est pas pertinente avec de telles covariables et qu'il faudrait en sélectionner d'autres. Ce qui pose le problème du choix de covariables caractérisant le mieux le climat des environnements. En effet, face au nombre important de variables climatiques quotidiennement mesurées sur les lieux, se pose la difficultéde

les r'esumer efficacement. Dans ce cas, l'utilisation de modèles de simulation de culture pour les synth'etiser peut être une alternative.

2.5 Un modèle de simulation de cultures : SarraH

Les modèles de simulation de cultures permettent de pr'edire la production de l'ensemble du peuplement v'eg'etal cultiv'e d'une parcelle. Pour cela, ils reproduisent le fonctionnement du système sol-plante-atmosphère et permettent la comparaison de divers itin'eraires techniques en fonction de l'espèce utilis'ee, du type de sol, des donn'ees climatiques, etc. Moyennant un changement d'echelle convenable, ces modèles peuvent alors être utilis'es a` diverses fins : pr'evisions des r'ecoltes et planification de la politique agricole et alimentaire d'un pays, analyse prospective des changements climatiques, protection de l'environnement, etc. (Affholder, 1997).

Au Sahel, les modèles pr'ecurseurs fond'es sur une estimation du bilan hydrique des cultures en cours de cycle, ont 'et'e 'ecrits avant le d'ebut des ann'ees 1980 (Franquin et Forest, 1977). Le bilan hydrique se situe a` l''echelle de la plante ou du champ et permet de comparer les quantit'es d'eau fournies et les quantit'es d'eau utilis'ees par la plante. Il tient aussi compte de la constitution de r'eserves d'eau et des pr'elèvements ult'erieurs sur ces r'eserves. Les apports d'eau fournis par les pr'ecipitations sont mesur'es. Les pertes se composent de la combinaison de l''evaporation et de la transpiration des plantes, plus connue sous le nom d''evapotranspiration.

L''equation du bilan hydrique, sous sa forme la plus g'en'erale, se fonde sur l''equation de conservation de la masse

P = ÄS + D + ETR + R

o`u P d'esigne la pluviom'etrie, ÄS la variation de stock d'eau dans le sol, D le drainage, ETR l''evapotranspiration et R les ruissellements.

L'estimation de l''evapotranspiration peut se faire en deux 'etapes. Pour une culture, l''evapotranspiration en conditions non limitantes d'alimentation hydrique ou 'evapotranspiration maximale (ETM) est d'abord calcul'ee a` l'aide de l''evaporation Bac Classe A (EV A) et du coefficient cultural K^'c caract'eristique de la culture et de son stade de d'eveloppement.

ETM = K^'c × EV A

Ensuite, Eagleman (1971) a propos'e une m'ethode d'estimation de l''evapotranspiration r'eelle qui est fonction de l'evapotranspiration maximale et de l'humidit'e relative du sol.

Doorenbos et Jassam (1979) ont d'evelopp'e une approche de mod'elisation des rendements r'eels fond'ee sur les consommations r'eelles et maximales d'eau et la productivit'e potentielle des cultures. Dans les zones o`u les flux hydriques sont les plus d'eterminants, la mod'elisation du bilan hydrique et la mise en relation de ses paramètres avec la production aboutit a` une estimation bien adapt'ee des rendements des cultures.

Le modèle Arachide bilan hydrique (Arabhy) constitue la première g'en'eration de modèle semi d'eterministe d'evelopp'e par le CERAAS en collaboration avec le CIRAD, pour l'estimation de la production de l'arachide au S'en'egal tenant compte du bilan hydrique (Annerose et Diagne, 1990, 1994). Il ajoute a` la simulation du bilan hydrique des cultures, celle des r'eactions de la plante aux stress hydriques. Ce modèle estime en fin de cycle la production potentielle.

Le modèle de Système d'analyse r'egional des risques agroclimatiques (Sarra) simule des indicateurs hydriques de production (Forest et Clopes, 1991). Ces indicateurs sont fond'es sur la consommation en eau r'eelle et maximale de la plante en relation avec les techniques culturales. Pour ce modèle qui est

utilis'e pour mesurer l'impact du climat sur une culture annuelle, il est suppos'e que la performance d'une culture est une fonction simple d'une combinaison d'indicateurs hydriques cumul'es au cours d'un cycle v'eg'etatif.

Cette première g'en'eration de modèles param'etr'es pour les zones sah'eliennes, utilise en entr'ee une base de donn'ees a` l'echelle locale de la parcelle sur le climat, le sol et les cultures. Ces modèles sont assez simples et sont 'ecrits sans module de bilan de carbone ni prise en compte de la notion de densit'e du peuplement.

Le bilan de carbone est fond'e sur l'assimilation du carbone selon l'interception de l''energie lumineuse en fonction du taux de couverture foliaire et la conversion de la fraction de rayonnement intercept'ee en matière sèche. Associ'e au bilan hydrique, le bilan de carbone constitue un 'el'ement essentiel dans le processus de croissance et de productivit'e des cultures.

Le modèle de simulation de cultures SarraH (Baron, 2002) est quant a` lui, une version plus d'etaill'ee de Sarra et fait intervenir, en plus de la simulation du bilan hydrique, plusieurs autres effets tels que celui de la temp'erature et celui de la radiation solaire sur la production. Il est fond'e sur la notion de l'effets multiplicatif de l'efficience de l'eau (WUE, Water use efficiency) et de l'efficience de l'energie radiative (RUE,Radiation use efficiency) pour simuler l''elaboration des biomasses.

Le modèle SarraH fonctionne au pas de temps journalier et la production de trois types de plantes peuvent y être simul'ee : mil, arachide et palmier. Nous avons pris l'arachide comme plante test pour cette 'etude.

De par la complexit'e inh'erente au système sol-plante-atmosphère, les processus simul'es sont formul'es par des ensembles d''equations que l'on peut regrouper par grand ensembles de (bilan hydrique, ph'enologie, etc.) et optimis'e par sous ensembles de modules ('equations d'ecrivant une 'etape d'un

processus). Le lien entre les modules et les processus s''etablissant au travers
de variables d''etats d'ecrivant la plante, le sol et l'environnement climatique.

D'evelopp'e sous cette approche modulaire, SarraH permet de simuler

- la biomasse initiale qui est fonction de la densit'e de semis et du poids sec moyen d'un grain; ce qui permet de d'eduire la densit'e de peuplement disposant du taux de lev'ee;

- la ph'enologie de la plante qui se d'efinit en plusieurs phases en relation avec la somme de temp'erature : phase v'eg'etative, phase reproductive, phase de maturation des graines. Chaque phase, d'une dur'ee constante, est exprim'ee en temps thermique qui est fonction des temp'eratures maximale, minimale et de base. La temp'erature de base est celle au-dessous de laquelle la plante ne se d'eveloppe pas. Les dur'ees des phases ainsi que la temp'erature de base sont des caract'eristiques vari'etale des plantes simul'ees (pour la vari'et'e d'arachide qui est simul'ee dans SarraH, elle est 'egale a` 13C;

- le bilan hydrique qui d'etermine la dynamique de l'eau dans le sol en fonction des contraintes climatiques ('evaporation du sol) et de la consommation en eau de la plante (transpiration). Cette consommation en eau de la plante permet de d'efinir un frein hydrique qui est le rapport entre la consommation r'eelle et la demande en eau de la plante;

- le bilan de carbone qui d'etermine la fabrication journalière d'assimilats en fonction du coefficient de conversion de l'espèce, du rayonnement intercept'ee et donc de taux de couverture foliaire. A cette production potentielle d'assimilat est appliqu'e le frein hydrique;

- la r'epartition des assimilats, racine, feuille, tige et organes reproducteurs qui 'evolue en fonction des phases ph'enologiques de la plante, ces lois de r'epartition sont fond'ees sur des relations allom'etriques.

2.6 Limites des méthodes classiques d'étude des interactions G×E

Le modèle 2.1, qui correspond a` un modèle d'analyse de variance a` deux facteurs, permet uniquement de tester la significativitédes interactions, mais il ne permet aucunement de les explorer. Dans ce cas, l'information contenue dans ces interactions serait inexploitée si aucune analyse supplémentaire n'était faite (Crossa, 1990). Cette logique sous-tend la modélisation des interactions G×E qui permet alors d'améliorer la prédiction des performances des génotypes dans de nouveaux environnements en contrôlant la variation importante de ces interactions et en l'enlevant de la partie significative du modèle (Gauch, 1990, 1992).

La régression conjointe parait peu adaptée a` cette forte variation d'une année sur l'autre ou d'un site a` l'autre. Cette méthode permet d'interpréter l'interaction par le potentiel du milieu, estimépar l'effet moyen du milieu. Pour un nouveau milieu non encore couvert par une expérimentation, nous n'avons pas d'estimation du potentiel, donc pas de prédiction de l'interaction. De ce fait, elle permet de décrire uniquement les résidus du modèle additif et n'utilise aucune information supplémentaire du milieu pour modéliser l'interaction.

La méthode AMMI est un outil permettant de comprendre des données complexes, notamment celles obtenues dans le cadre des interactions G×E. Cependant, elle n'a qu'un grand intérêt descriptif et constitue une technique appropriée uniquement dans une perspective d'analyse préliminaire. 'Etant donnéqu'une ACP est effectuée sur les résidus du modèle additif, la méthode AMMI permet tout juste d'étudier les corrélations entre composantes principales et covariables de l'environnement et du génotype, alors que le but est de prédire les unes a` partir des autres (Yan et al., 2001). Elle péche ainsi par le fait que cette modélisation de l'interaction se fait sans l'utilisation

des données climatiques des environnements, car, de même que l'analyse de variance, les effets estimés pour les environnements sont imprévisibles.

La régression factorielle, elle, tient compte des conditions climatiques des environnements pour prédire la réponse des génotypes. Mais elle suppose que l'action de l'environnement sur la production est linéaire, ce qui n'est pas certain. De plus, le nombre important de variables climatiques généralement mesurées sur les lieux d'essais fait qu'elles ne peuvent pas être totalement prises en compte par cette méthode.

Il s'agira alors, d'améliorer la prédiction de la performance des génotypes en réduisant l'impact de la variabilitéclimatique sur la précision de cette estimation. Une solution serait de modéliser les variations de la réponse des génotypes en fonction de l'environnement par l'utilisation de modèles de simulation de cultures tels que Diagnostic hydrique des cultures (DHC, Forest et Cortier, 1990), Irrigation scheduling information system (IRSIS, Fao, 1987), SarraH. Seulement, les paramètres de tels modèles ne sont connus que pour un petit nombre de génotypes.

Chapitre 3

La methode APLAT

Ce chapitre traite de notre première m'ethode propos'ee qui consiste a` lin'eariser la performance des g'enotypes pr'edite par le modèle SarraH au voisinage d'un g'enotype de r'ef'erence. Une fois la lin'earisation effectu'ee, l'estimation des paramètres, du fait du nombre important de r'egresseurs dont nous disposions, s'est faite par r'egression Partial least squares. Nous commencerons alors par pr'esenter a` la section 1.1 cette technique de r'egression et terminerons ce chapitre en pr'esentant a` la section 1.2, la m'ethode d'estimation APLAT.

3.1 La regression Partial least squares

La r'egression PLS, Partial least squares est devenue aujourd'hui, une m'ethode très utilis'ee dans le cas des r'egressions sur donn'ees corr'el'ees. Aussi, est-elle une bonne alternative s'il y a plus de r'egresseurs que d'observations (Wold, Albano, Dunn, Esbensen, Hellberg, Johansson, Sjöström 1983; Tenenhaus, 2001).

Un petit nombre de variables appel'ees »facteurs» ou »variables latentes» sont construites l'une après l'autre de façon it'erative et permettent de remplacer l'espace initial des nombreux r'egresseurs par un espace de plus faible dimension. Ces facteurs deviennent les nouvelles variables explicatives dans un modèle de r'egression lin'eaire classique.

Les facteurs sont orthogonaux, et sont des combinaisons lin'eaires des variables explicatives initiales. A ce titre, ils renvoient aux composantes principales de la RCP, R'egression sur composantes principales. Mais alors que ces dernières ne sont calcul'ees qu'àpartir des variables explicatives (et donc sans r'ef'erence a` la variable a` expliquer), les facteurs de la r'egression PLS maximisent les corr'elations successives entre les r'egresseurs et la variable a`

expliquer, tout en maintenant la contrainte d'orthogonalit'e avec ceux d'ejàconstruits.

La r'egression PLS s'effectue selon le principe de l'algorithme NIPALS, Nonlinear estimation by iterative partial least squares d'evelopp'e par Herman Swold (1966) pour l'analyse en composantes principales. Cette r'egression s'inspire de l'approche PLS (Wold, 1975) pour l'estimation des modèles d''equation structurelles reliant plusieurs blocs de variables entre eux.

A pr'esent, pour d'ecrire cette m'ethode, nous nous plaçons dans le cadre du modèle lin'eaire classique. Le vecteur des observations Y de dimension n × 1 est suppos'e suivre le modèle suivant

Y = Xâ + e (3.1)

o`u le vecteur â d'ordre p est le paramètre inconnu a` estimer, X la matrice de dimension n × p des variables explicatives, et le vecteur e un terme d'erreur al'eatoire.

Nous supposerons qu'il n'y a pas de données manquantes et qu'il n'y a qu'une seule variable a` expliquer pour une explication plus claire de la méthode. L'algorithme PLS calcule les variables latentes t1,··· ,th étape par étape. Ces variables latentes th = Xwh sont des combinaisons linéaires des X qui sont orthogonales entre elles et qui maximisent Cov(th, Y) sous la contrainte II wh 11= 1.

A l'étape 1, w1 = (w1 1 · · · w^p₁)^' est solution du problème d'optimisation

? ?

?

max Cov(Xw1, Y) k w1 11= 1

Pour déterminer w1, il suffit d'écrire l'expression du Lagrangien.

L(w1,ë) = Cov(Xw1,Y) - ë(w^' 1w1 - 1)

= w¹ 1Cov(X¹,Y) + ··· + w^p ₁Cov(X^p,Y) - ë[(w¹ 1)² + · · · + (w^p ₁)² - 1]

o`u ë est le multiplicateur de Lagrange associéa` la contrainte.

Les solutions a` ce problème d'optimisation sont obtenues en dérivant L(w1, ë) par rapport a` w¹1,··· , w^p ₁, ë. Les p + 1 équations aux dérivées partielles ou équations normales s'écrivent

? ??????? ???????

Cov(X^1,Y) - 2ëw1 1 = 0 ... Cov(Xp,Y) - 2ëw1 p = 0 (w^11)^2 + ···(w^p 1)^2 = 1

o`u Xp est la p^ecolonne de X

En remplacant dans la dernière équation de ce système les composantes de w1 tirées dans les p premières équations, nous obtenons

[Cov(X¹,Y)/2ë]² + · · · + [Cov(Xp,Y)/2ë]²= 1

D'o`u

X p

j=1

[Cov(X^j,Y)]² = 4ë²

Et

ë = /P[Cov(Xj,Y)]²/2

En reportant cette valeur de ë dans chacune des p premières équations nor-males, nous avons

wj 1 = Cov(Xj,Y)/V/P[Cov(Xj,Y)]²

Ainsi, la première composante t1 = w¹ 1X¹ + · · · + w^p ₁Xp est construite. Puis, il est effectuéune régression simple de Y sur t1

Y = c1t1 + Y1

o`u c1 est le coefficient de régression et Y1 le vecteur des résidus.

S'il reste encore de l'information, il est construit une deuxième variable latente t2?t1. Cette deuxième variable latente est combinaison linéaire des colonnes de X1, résidu de la régression linéaire de X sur t1.

A l'étape 2, w2 = (w1 2 · · · w^p ₂)^' est solution du problème d'optimisation

? ? ?

max Cov(X1w2, Y1) II w2 11= 1

La deuxième variable latente t2 construite, il est effectuéune régression linéaire multiple de Y sur t1 et t2

Y = c1t1 + _c2t2 + Y2

Cette proc'edure it'erative peut ainsi continuer en utilisant les r'esidus Y2, X2 des r'egressions de Y, X sur t1 et t2.

Le nombre de composantes t1,
·
·
· ,tH a` retenir avec H rang(X), peut être d'etermin'e a` l'aide de trois critères : l'ajustement de l''echantillon d'apprentissage (X, Y) par (^bX, ^bY), la pr'ediction sur un 'echantillon externe et la pr'ediction interne aux donn'ees d'apprentissage appel'ee validation crois'ee.

3.2 La méthode APLAT : linéarisation au-tour d'un témoin

Cette m'ethode a fait l'objet d'un article publi'e aux Comptes rendus de l'acad'emie des sciences dont l'original se trouve en Annexe B.

I. Dieng, E. Goz'e, R. Sabatier

Lin'earisation autour d'un t'emoin pour pr'edire la r'eponse de cultures C. R. Biologies 329 (2006) 148-155

3.2.1 Le modèle proposé

Si nous partons du modèle de simulation de cultures, chacune des sorties de ce modèle, le rendement d'un g'enotype i dans un environnement j est la somme :

1. d'un rendement potentiel pr'edit avec le modèle de simulation;

2. d'un biais, esp'erance de l''ecart du potentiel au r'ealis'e;

3. d'une erreur al'eatoire.

Yij = f(Zj, èi) + îj + uij (3.2)

o`u Zj est le vecteur des variables telles que la pluie, la temperature, etc. mesurees sur l'environnement j et èi le vecteur de longueur P des paramètres du genotype i. Nous supposons que le biais îj ne depend que de l'environnement j : il est donc le màeme pour tous les genotypes d'un màeme environnement. L'erreur uij est supposee aleatoire avecE(uij) = 0 et Var(uij) = ó²_u.

Comme dit precedemment, les paramètres des modèles de simulation de cultures ne sont generalement connus que pour un petit nombre de genotypes. Considerons un modèle de simulation de cultures et un genotype de reference dont les paramètres sont connus et appelons è0 le vecteur de ses paramètres. Alors, supposons f de classe C¹ dans un voisinage de è0 et f' derivable sur ce voisinage. De plus supposons èi au voisinage de è0. En pratique, les genotypes dont nous chercherons a` estimer les paramètres seront choisis de telle sorte qu'ils ne soient pas trop eloignes du genotype de reference. Alors, un developpement en serie de Taylor a` l'ordre 1 nous donne :

f(Zj, èi) = f(Zj, è0) +

XP ?f [?è(p) (e^) - è^()) + ? [(èi - è0)^' (èi - è0)] (3.3) p=1 0=00 ,Z=Zj

avec è^(p) _iet è₀^p) la p^e composante du vecteur de paramètres respectivement du genotype i et du genotype de reference.

Posons

X4^p) = [?Zd0=00,Z=Zj

c'est une fonction de l'environnement j, et

â(p) _i= è^(p) i-- è(p)

0

une fonction du g'enotype i.

La fonction X(p)

j est la d'eriv'ee partielle de la sortie du modele de simulation de cultures pour l'environnement j par rapport a` la p^e composante du vecteur de parametres de la vari'et'e de r'ef'erence. Comme la fonction f n'est pas g'en'eralement connue analytiquement, ces sensibilit'es peuvent àetre obtenues par une m'ethode de d'erivation num'erique. Nous avons retenu tout simplement

X(p) = ? f

j [f + hè_,c₎p) ) -- f (èO^p) -- hè_,c_,p))

[BB(P) 0=00,Z=Zj 1

2h (

è,?

Z=Zj

avec h_è(p) ₀tres petit, de l'ordre de è₀^p).10^-4 en pratique. D'autres m'ethodes existent, celle-ci 'etant la plus simple et la plus 'econome en calculs.

Avec ces notations et d'apres les 'equations (3.2) et (3.3) qui permettent d''ecrire

f(Zj, è0) = Y0j -- îj -- u0j

nous pouvons poser, en n'egligeant o [(èi -- è0)^'(èi -- è0)] :

Yij -- Y0j =

XP p=1

X(p) j · â(p) i + oij (3.4)

o`u oij = uij -- u0j.

Ainsi,E(oij) = 0, Var(oij) = 2ó² _u,Cov(oij, oi'j') = 0, mais Cov(oij, oi^'j) = ó² _u.

Si nous disposons de I g'enotypes et de J environnements, nous pouvons poser le modele suivant :

Y -- (Y0 1I) = X
· â + o (3.5)

Le vecteur Y repr'esente le rendement de tous les g'enotypes dans tous les envi-
ronnements, rang'e par environnement et par g'enotype. Si tous les g'enotypes

ont eteobserves une fois dans chaque environnement, ce vecteur est de lon-
gueur IJ. Puis Y^'0 = (Y01 · · · Y0J) et 1I est un vecteur formede 1, de longueur

I.

Le symbole ? designe le produit de Kronecker.

Le vecteur o est un vecteur d'erreur aleatoire. Sa matrice de covariance est de la forme ó²_uÙ avec

		? ? ? ? ? ? ? ? ? ?	ù1	..	.			0	1
	Ù=					ùj
o`u			0				...	ùJ

(

ùj =

2 1 ... 1 2

? ? ? ?

Les matrices Ù et ùj sont carrees de nombre de lignes, respectivement le nombre d'observations de tous les environnements et le nombre d'observations de l'environnement j. La matrice Ù est bloc diagonale tandis que ùj est une matrice form'ee de 1 partout sauf des 2 sur la diagonale. Dans le cas o`u tous les genotypes ont etevus une seule fois dans chaque environnement, Ù est de dimension IJ × IJ et ùj de dimension I × I.

Ensuite,

X = [ X⁽¹⁾ ? II · · · X⁽p⁾ ? II · · · X^(P) ? II

o`u

X(p)' = [ X1p) ... XSp) ]

de longueur J, est le vecteur des derivees des sorties de notre modele de simulation de cultures, SarraH, dans chacun des environnements par rapport au p^e parametre du vecteur de parametres du temoin.

La matrice II est la matrice identited'ordre I, la matrice X⁽p⁾ 0II s'ecrit alors de cette facon :

X(p) 1 ... X(p) ( J )

0

(

1 . 0

0 .. 1

)

=

X(p) 1 ? 0 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? X(p) J 0

... ... 0 ? X(p) 1 ... 0 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? X(p) J

C'est une matrice a` IJ lignes et I colonnes. Par consequent, la matrice X est de dimension IJ x PI.

Enfin

â = [ â(1)' ...â(P)' 1'

avec

â(p)' = [ â1.p) ... â(p⁾ ]

Nous avons proposed'appeler cette methode par l'acronyme APLAT : Ap-
proximation Par Linearisation Autour d'un Temoin. Elle consiste a` appro-
cher, localement, le rendement predit par un modele de simulation de cultures,

par s'erie de Taylor a` l'ordre 1 au voisinage du vecteur de paramètres d'un g'enotype de r'ef'erence. Cette lin'earisation permet, par r'egression lin'eaire, l'estimation des paramètres de ces g'enotypes. Par la suite, la pr'ediction de l''ecart entre le rendement de ces g'enotypes et celui du g'enotype de r'ef'erence dans des environnements nouveaux, c'est a` dire o`u ils ne sont pas encore test'es, pourra se faire si le climat de ces derniers est connu.

Il y a en g'en'eral beaucoup de paramètres dans un modèle de simulation de cultures et peu d'environnements dans un essai multienvironnement, ce qui rend souvent PI grand par rapport a` IJ.

Pour notre exemple, nous avons utilis'e SarraH comme modèle de simulation de cultures. Ce modèle dispose de 61 paramètres fonction du g'enotype. Avec un tel nombre de pr'edicteurs, l'estimation de â s'est faite par r'egression PLS. Ceci permet de r'eduire l'espace des r'egresseurs de rang de X a` k dimensions.

La r'egression PLS, voir section 3.1, s'effectue selon le principe de l'algorithme NIPALS, Nonlinear estimation by Iterative Partial Least Squares, (Tenenhaus, 2001) o`u un ensemble de r'egressions successives par moindres carr'es ordinaires est effectu'e, en même temps que le calcul des composantes.

Ici, la matrice de covariance de o est 'egale a` ó<sup>2</sup> <sub>u</sub>Ù et non a` ó2 uIIJ. La solution serait d'effectuer toutes les r'egressions partielles par moindres carr'es g'en'eralis'es. Mais cette matrice de covariance est inconnue. Elle s''ecrit tout de même a` une constante multiplicative près en fonction de Ù qui elle est connue. La matrice Ù 'etant sym'etrique et semi-d'efinie positive, par d'ecomposition de Cholesky, il existe une matrice ç tel que ç^'ç = Ù^-1.

Si nous multiplions a` gauche tous les termes du modèle 3.5 par ç, nous obtenons le modèle 3.6 dont les erreurs sont ind'ependantes.

çY - ç(Y0 ? 1I) = çX · â + ço (3.6)

En effet, la variance de l'erreur ço s''ecrit

_uçç^-1(ç^')^-1ç^' = ó2

E(çoo^'ç^') = çI(oo^')ç^' = ó² _uçÙç^' = ó² _uç(ç^'ç)^-1ç^' = ó2 uIIJ

â peut alors être estim'e a` l'aide des moindres carr'es ordinaires, appelons âPLS son estimateur.

Le nombre de composantes a` retenir est d'etermin'e par le PRESS, Prediction Error Sum of Squares (Tenenhaus, 2001).

3.2.2 Illustration avec les données de l'essai pluriannuel

Les données

Les donn'ees sont les r'esultats de l'essai pluriannuel (tableau 1.1, page 13). Rappelons que le g'enotype de r'ef'erence est le 55-437, un g'enotype de 90 jours. C'est une vari'et'e largement cultiv'ee au S'en'egal, dans le bassin arachidier, a` ce titre elle a 'et'e pr'esente comme t'emoin dans tous les essais et c'est elle aussi qui a servi pour le param'etrage du modèle SarraH.

Dans ce milieu a` forte variabilit'e des pluies dans l'espace et même dans le temps pour un même lieu, nous avons consid'er'e chacune des 5 ann'ees d'exp'erimentation comme un environnement (figure 3.1).

SarraH a 'et'e utilis'e pour calculer X. Compte tenu du nombre de donn'ees disponibles, seuls deux paramètres (P = 2) ont 'et'e consid'er'es parmi les 61 de SarraH. Le premier paramètre est en fait un coefficient multiplicateur qui agit sur 5 paramètres de SarraH : Coefficient moyen d'angle des feuilles, Coefficient de conversion en assimilat, Coefficient d'efficience d'assimilation des feuilles a` la phase v'eg'etative juv'enile, Coefficient d'efficience d'assimilation

FIG. 3.1 - R'epartition des pluies sur la station de Bambey au S'en'egal de 1994 a` 1998.

MIT

0 50 100 150 200 250

1994 1995 1996 1997 1998

Juin Juillet Août Septembre Octobre

des feuilles a` la première phase de maturation - phase sensible de remplissage des grains - et Coefficient d'efficience d'assimilation des feuilles a` la deuxième phase de maturation - phase non sensible -. Le deuxième paramètre est le poids moyen des gousses.

Validation croisée

Pour valider notre modèle, nous avons r'eserv'e successivement chacune des ann'ees et estim'e les paramètres des g'enotypes sur les ann'ees restantes. Pour chacune des cinq ann'ees, nous avons identifi'e un modèle par la m'ethode APLAT et les rendements observ'es ont 'et'e compar'es a` ceux ainsi pr'edits. Les rendements sont exprim'es en kilogrammes de gousses par hectare.

L''evaluation de la qualit'e de chaque modèle propos'e est faite avec l'erreur
quadratique moyenne de pr'ediction MSEP, Mean Squared Error of Prediction

(Wallach et Goffinet, 1987). La MSEP est utilis'ee comme critère pour comparer diff'erents modèles dont le mod`ele moyen (Colson, Wallach, Bouniols, Denis et Jones, 1995) d'efini pour nos donn'ees par :

Yij = m + gi + Ej + äij (3.7)

o`u m est la moyenne de la population et gi l'effet g'enotype. L'effet Ej de l'environnement j est suppos'e al'eatoire, d'esp'erance nulle et de variance ó²_E. Les erreurs äij sont ind'ependantes, d'esp'erance nulle et de variance ó²ä. De plus, Ej et äij sont suppos'es ind'ependants.

Le modèle moyen n'est rien d'autre que le modèle lin'eaire mixte (2.1) o`u l'interaction al'eatoire G×E, impr'evissible, est fusionn'ee avec le terme d'erreur qui porte les màemes indices i pour le g'enotype et j pour l'environnement.

Nous avons calcul'e les intervalles de confiance des coefficients estim'es par la m'ethode bootstrap (Efron, 1979). Cette technique permet d'estimer la loi inconnue d'un estimateur par une loi empirique obtenue a` partir d'une proc'edure de r'e'echantillonnage fond'ee sur des tirages al'eatoires avec remise des donn'ees. Les intervalles de confiance construits sont de type percentile-t (Aji, Tavolaro, Lantz, et Faraj, 2003).

Soit z(p)?b

i,PLS la variable al'eatoire d'efinie par :

(p)?b
zi,PLS =

(3.8)

ei^?L^bS)

_â(p)?b i,PLS- ⁷A,S

s^?(

o`u _â(p)i,PLS est le (p.i)^e 'el'ement de _eâPLS, il s'agit du p^e paramètre de la i^e vari'et'e
estim'e par la m'ethode PLS. _gL?bS est obtenu au b^e tirage avec b = 1,
·
·
· , B.

de la matrice de variance de

â(p)?b i,PLS.

Soit ^bFB la fonction de répartition empirique des z(pP ^)?b Le fractile d'ordre á,

i LS'

1
B

_XB
b=1

FB (á) est estimépar la valeur ^bt(á) telle que

1n = á

_z(p)?b

Alors un intervalle de confiance percentile-t pour le (p.i)^e élément de ₁3 peut s'écrire :

hs(â(p)i,PLS) t(1 - á) , /R1,3P)LS - s(â(p)i,PLS) · Rá) ] (3.9)

R'esultats

Pour les modeles sans les données respectivement de 1994, 1995 et 1997, le PRESS minimal est atteint avec 6 composantes. Pour les deux autres modeles, le PRESS est minimal avec 9 composantes, mais nous avons réduit leur espace a` 5 dimensions car le PRESS n'y est pas trop différent de ses valeurs minimales (figure 3.2).

Les coefficients des régressions PLS et les intervalles de confiance qui leur sont associés, sont représent'es a` la figure 3.3.

Les MSEP estimées pour les modeles APLAT, sauf celle sans les données de l'année 1998, sont inférieures aux MSEP des modeles moyens correspondants (tableau 4.2). Ce qui signifie que pour ces modeles, prédire le rendement par la méthode APLAT est meilleur que par la moyenne des rendements du passé. Ainsi, 4 fois sur 5, la méthode APLAT s'est révélée meilleure que le modele moyen. Toutefois, cette étude souffre de la faible taille de notre échantillon.

Evolution du PRESS en fonction du nombre de composantes. Le FIG. 3.2 - modèle (-1994) utilise les données sauf celles de l'année 1994 et ainsi de suite.

PRESS

0.0 0.5 1.0 1.5 2.0 2.5

PRESS

Modèle (-1994) : Dim. opt. 6, PRESS=0.051

5 10 15 20

Dim. Mod.

Modèle (-1996) : Dim. opt. 9, PRESS=0.037

5 10 15 20

Dim. Mod.

Modèle (-1995) : Dim. opt. 6, PRESS=0.061

5 10 15 20

Dim. Mod.

Modèle (-1997) : Dim. opt. 6, PRESS=0.034

5 10 15 20

Dim. Mod.

Modèle (-1998) : Dim. opt. 9, PRESS=0.046

5 10 15 20

PRESS

0.0 0.5 1.0 1.5

PRESS

0.0 0.5 1.0 1.5

PRESS

Dim. Mod.

Intervalle de confiance percentile-t a` 95% des coefficients es-
timés. Le modèle (-1994) est sans les données de 1994 et ainsi

FIG. 3.3 - de suite. Sur l'axe des abscisses, les valeurs de chaque paramètre sont rangées par ordre alphabétique de génotype. Le symbole représente l'estimation ponctuelle des coefficients.

0.5 1.0 1.5 2.0 2.5

3

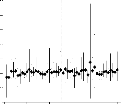
Paramètre 1 Paramètre 2

Modèle (-1994)

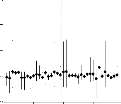
Paramètre 1 Paramètre 2

010 20 30

Modèle (-1996)

Paramètre 1 Paramètre 2

Modèle (-1995)

0 10 20 30

Modèle (-1997)

Paramètre 1 Paramètre

0 10 20 30 50 0 10 20 30

-0.5 0.0 0.5 1.0 1.5 2.0

Modèle (-1998)

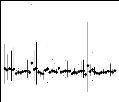
Paramètre 1 Paramètre 2

50

40

30

0 10 20

	APLAT		Modèle moyen
Modèle (-1994)	24	687,3	64	651,6
Modèle (-1995)	5	915,0	7	160,6
Modèle (-1996)	35	446,1	37	814,8
Modèle (-1997)	10	038,3	18	201,1
Modèle (-1998)	118	304,9	84	963,6

MSEP des différents modèles APLAT et modèles moyens corres-

TAB. 3.1 - pondants de l'essai pluriannuel. Le modèle (-1994) est sans les données de 1994 et ainsi de suite.

3.2.3 Illustration avec les données de l'essai multilocal

Les donn'ees sont les r'esultats de l'essai multilocal (tableau 1.2, page 15). Chaque lieu est r'eserv'e et l'estimation des paramètres effectu'ee sur les lieux restants.

Le modèle SarraH a aussi 'et'e utilis'e pour simuler le rendement de la vari'et'e de r'ef'erence dans les diff'erents lieux. Les deux paramètres a` r'eestimer restent les mêmes qu'àla section pr'ec'edente.

Les MSEP estim'es pour les modèles APLAT sont inf'erieures aux MSEP des modèles moyens correspondants, sauf celle sans les donn'ees de Wenthiwy (tableau 3.2). Ainsi, pour cet essai multilocal, la m'ethode APLAT s'est montr'ee meilleure que le modèle moyen 10 fois sur 11 (c''etait 4 fois sur 5 avec l'essai pluriannuel).

3.2.4 Conclusion

Au Sahel, l'interaction G×E est largement due aux al'eas climatiques, dont la probabilit'e peut être estim'ee a` l'aide de longues chroniques de relev'es m'et'eorologiques au sol. Cependant, relier l'interaction G×E et la pluviom'etrie a` l'aide d'un modèle de simulation de cultures n'est habituellement possible que pour des vari'et'es dont on a estim'e les paramètres, au prix d'une

	APLAT		Modèle moyen
Modèle (sans Bambey)	10	289,4	45	374,1
Modèle (sans Gatte)	6	457,1	102	784,7
Modèle (sans Keur Fary)	3	474,2	44	457,9
Modèle (sans Ndangalma)	7	445,7	74	477,6
Modèle (sans Ndiadiane)	12	824,9	99	194,2
Modèle (sans Nioro)	47	015,4	157	989,6
Modèle (sans Nioro Sud)	234	506,4	738	389,6
Modèle (sans Pasokoto)	76	987,8	559	545,3
Modèle (sans Keur Samseun)	1	677,8	120	068,3
Modèle (sans Sinthiou Thiabala)	11	041,1	20	998,8
Modèle (sans Wenthiwy)	80	887,3	48	687,1

TAB. 3.2 - MSEP des différents modèles APLAT et modèles moyens correspondants de l'essai multilocal.

expérimentation spécifique. Le modèle APLAT permet de prédire cette interaction avec les seules données d'une expérimentation multilocale classique, sans autre instrumentation que des stations météorologiques simples.

La méthode APLAT peut être vue ainsi comme un outil d'aide a` la décision pour la sélection au Sahel. Dans l'exemple o`u un sélectionneur doit tester plusieurs génotypes dans un nouvel environnement, cette méthode lui permettra d'écarter d'emblée certains génotypes qui donneront une production faible. En lieu et place de longs essais multilocaux ou pluriannuels ou d'une tentative de paramétrisation d'un modèle de simulation de cultures qui implique un coàut élevé. Son attention sera portée par la suite sur l'ensemble restreint des génotypes retenus avec APLAT o`u il pourra appliquer les schémas classiques de sélection.

Cette méthode évite ainsi de recourir soit a` de longs essais multilocaux et pluriannuels, soit a` la paramétrisation coàuteuse d'un modèle de simulation de culture. De plus, elle permet d'assumer le choix des lieux comme devant expliquer largement la diversitédu milieu plutôt que de la représenter a` travers un sondage équiprobable. En effet, avec APLAT, seuls les résidus de

la modélisation de l'interaction G×E sont aléatoires, et non pas l'interaction toute entière.

Chapitre 4

La méthode APLAT-mixte

Dans ce chapitre, nous partirons de la m'ethode APLAT, qui nous le rappelons, consiste a` lin'eariser autour du vecteur de paramètres d'un g'enotype de r'ef'erence, la r'eponse de g'enotypes pr'edite par un modèle de simulation de cultures.

Notre hypothèse pour cette m'ethode, 'etait qu'un modèle de simulation de cultures, qui est une fonction des paramètres des g'enotypes et des caract'eristiques des environnements o`u nous voulons faire la pr'ediction, permet de capter la majeure partie de l'effet al'eatoire de l'environnement. Ce qui autorise la r'eduction des interactions al'eatoires G×E, et par là, facilite la s'election vari'etale.

Dans cette partie, nous revenons sur cette hypothèse faite en première approximation et consid'erons que certes, si l'al'ea de l'environnement peut être pris en compte par un modèle de simulation de cultures, il ne l'est toutefois pas totalement. Ainsi, si nous pensons toujours pouvoir mod'eliser les variations de la r'eponse d'un g'enotype dans un environnement par le biais de tels modèles de simulation, il subsistera n'eanmoins de l'al'ea environnemental,

responsable d''eventuelles interactions G×E, dont il conviendra d'estimer sa variance, le cas 'ech'eant.

Ce chapitre traite alors de notre deuxième m'ethode mise au point pour estimer les paramètres fixes issus de la lin'earisation du rendement des g'enotypes par le modèle SarraH et les composantes de variance de l'al'ea environnemental restant. Avec les nombreux paramètres de SarraH, ce qui est le cas pour la plupart des modèles de simulation de cultures, nous devons identifier un modèle o`u un nombre important de r'egresseurs et des composantes de variance coexistent. Nous avons a` cet effet, propos'e une m'ethode combin'ee de r'egression PLS et de modèle mixte pour l'estimation des paramètres inconnus. Il s'agit d'une extension de la m'ethode APLAT propos'ee au pr'ec'edent chapitre o`u cette fois-ci, il est not'e la pr'esence d'effets al'eatoires additionnels dont nous nous attacherons a` estimer les variances. Cette m'ethode a 'et'e d'enomm'ee APLAT-Mixte.

Nous d'ebutons ce chapitre par la Section 4.1 o`u nous faisons un retour sur le modèle mixte. Si les composantes de variance 'etaient connues, c'est-àdire s'il y avait uniquement une contrainte a` savoir le nombre important de r'egresseurs par rapport aux observations, une extension de la m'ethode PLS devrait suffire pour r'esoudre le problème. Une telle proc'edure est alors d'etaill'ee a` la Section 4.2. Comme ces composantes sont est en fait souvent inconnues, une m'ethode combin'ee de PLS et d'algorithme EM est pr'esent'ee a` la Section 4.3 pour estimer les paramètres inconnus. Les d'eveloppements de cette m'ethode appel'ee PLS-Mixte, sont fond'es dans un premier temps, sur un modèle mixte o`u des effets al'eatoires sont suppos'es simplement de variance ó<sup>2</sup>I. Pour l''eprouver, nous nous sommes 'eloign'es de nos donn'ees qui ne s'y prêtent pas et avons eu recours a` des donn'ees de NIRS. Ensuite, puisque nos donn'ees d'interaction G×E peuvent être appr'ehend'ees a` travers un modèle mixte o`u les effets al'eatoires sont suppos'es de variance ó²Ä, nous avons adapt'e la m'ethode PLS-Mixte a` ce type de modèle.

4.1 Le modèle mixte

Consid'erons un modèle lin'eaire mixte comme d'ecrit par McCulloch et Searle (2001). Le vecteur des observations Y de dimension n × 1 est suppos'e suivre le modèle suivant :

Y = Xâ + Zu + e (4.1)

o`u â d'ordre p est le vecteur de paramètres des effets fixes, u d'ordre q le vecteur de paramètres des effets al'eatoires, X et Z deux matrices d'incidence connues, et e le vecteur d'erreur al'eatoire.

Dans ce modèle, si nous avons r effets al'eatoires, Zu peut être d'ecompos'e comme suit :

u1 ...

=

Xr k=1

Zkuk

Zu = [ Z1 · · · Z_r ]

u_r

o`u uk d'ordre qk, est le vecteur des effets al'eatoires pour le facteur k avec les suppositions i(uk) = 0, Var(uk) = ó2 kIqk ? k, et Cov(uk,u^' k') = 0 pour k =6 k^',

q= _Xr qk

k=1

Aussi i(e) = 0, Var(e) = ó2 eIn et Cov(uk, e^') = 0 ? k. La fonction i(·) indique l'esp'erance.

En posant u0 = e, q0 = n et Z0 = I_n comme dans la pr'esentation de Rao et Kleffe (1988), l''equation (4.1) devient

Y = Xâ + _Xr Zkuk (4.2)

k=0

et V = _Xr ZkZ^' ió2 k

k=0

L'estimation des paramètres â et ó2 k peut se faire concomitamment au moyen des méthodes de vraisemblance ML, Maximum likelihood ou REML, Restricted or residual maximum likelihood. Pour chacune de ces méthodes, une fonction log-vraisemblance est maximisée par rapport aux paramètres inconnus. La fonction log-vraisemblance pour la méthode ML (REML étant une variation de ML) s'écrit,

l = (-1/2)[log |V| + (Y - Xâ)^'V^-1(Y - Xâ) + n log(2ð)]

En dérivant la fonction l par rapport a` â et a` chacun des ó2 k et en annulant ces dérivées, nous obtenons r + 1 équations pour ó2 k et une équation pour â.

? ? ?

?l/?â = 2X^'V-^1Y - 2X^'V-^1Xâ [ ] ?l/?ó2 k = -(1/2) tr(V^-1V^' k) - (Y - Xâ)^'V^-1V^' kV^-1(Y - Xâ)

oiV' k = ?V/?ó2 k

Les solutions de ce système d'équations ne sont généralement pas obtenues de façon explicite. Pour résoudre ce problème d'optimisation, l'on a recours a` des algorithmes itératifs tels que celui de Newton-Raphson ou l'algorithme EM, Expectation maximization.

Ces deux méthodes d'itérations requièrent des valeurs initiales pour les pa-
ramètres inconnus. L'algorithme EM permet de s'approcher de la région de

l'optimum plus rapidement mais la progression vers l'optimum est lente. Au contraire, celui de Newton-Raphson, malgréqu'il soit instable loin de l'optimum, permet une convergence vers celui-ci beaucoup plus rapidement une fois dans sa région.

L'algorithme de Newton-Raphson utilise un développement de premier ordre de la fonction score c'est-à-dire du gradient de la fonction log-vraisemblance autour de l'estimation du paramètre a` la m<sup>e</sup> itération pour fournir l'estimation a` la (m + 1)^e itération. Chaque étape dans l'algorithme nécessite le calcul de la fonction score et de sa dérivée, la matrice hessienne de la logvraisemblance.

L'algorithme EM (Meng and van Dyk, 1997) permet l'estimation de paramètres dans des modèles avec des données incomplètes. L'argumentaire de l'utilisation de cet algorithme dans le cadre du modèle mixte est fourni en détail par Searle, Cassella et McCulloch (1992, pp. 297-303). Ainsi, les effets aléatoires sont-ils vus comme des données non observées. Searle et al. considèrent alors que si ces effets aléatoires étaient connus, l'estimation des paramètres inconnus pourrait facilement se faire. En effet, il suffirait d'adopter une démarche a` deux étape.

D'abord, estimer la variance de chaque effet aléatoire par

bó2 k = (1/qk) _Xqk (uk - uk)² = (1/qk) _Xqk u2 k = u' kuk/qk k=1 k=1

o`u uk d'ordre qk est supposégaussien d'espérance nulle et de variance ó² k.

Ensuite, déduire ces effets aléatoires supposés connus du vecteur des données Y et appliquer une régression OLS, Ordinary least squares, sur le modèle suivant

Y - _Xr Zkuk ~ N(Xâ, ó2 0In) k=1

Mais comme ces effets al'eatoires ne sont pas connus en r'ealit'e, l'algorithme EM permet de calculer les valeurs conditionnelles de u^'iui a` utiliser a` la place de u^'iui et les valeurs conditionnelles de ui a` la place de ui.

Selon la terminologie de l'algorithme EM, dans le cas du mod`ele mixte, les donn'ees observ'ees Y sont appel'ees donn'ees incompl`etes et Y en plus des effets al'eatoires non observ'es u1, . . . , u_r constituent les donn'ees compl`etes. Nous rappelons ci-dessous cet algorithme pour l'estimation des param`etres fond'ee sur une variation de ML publi'ee par Laird (1982). Les valeurs calcul'ees ók ^2(m) de óz sont obtenues apr`es la m<sup>e</sup> it'eration et sont utilis'ees pour la mise a` jour de la variance V-1(m).

'Etape 0 Poser m = 0 et choisir des valeurs initiales ²⁽⁰⁾

ó_k

'Etape 1 ('Etape-E) Calculer

Q(ó² | ó2(m)) =E_ó2(m)(u^'kuk | Y)

= qkók
· ak

2(m) + 4(m) [Y^'P^(m)ZkZ^'_kP^(m)Y - tr(Z^'_kV-^1(m)Zk)1 o`u P^(m) = V-1(m) - V-1(m)X(X'V-1(m)X~-X'V-1(m)

'Etape 2 ('Etape-M) Determiner ^ó2k(m+1) qui maximise Q(ó² | ó2(m)) c'est-`a-dire,

tel que Q(ó^2(m+1) | ó2(m)) Q(ó² | ó^2(m)). Alors,

ók2(m+1) = E_ó2(m)(ukuk | Y)/qk for k = 0, 1,···, r

'Etape 3 A la convergence c`ad L(ó2k (m+1) | Y) -L(ó2k <sup>(m)</sup> |Y) ç o`u

ç est une quantit'e arbitrairement petite et L la fonction de vraisemblance, prendre bó²_k = ók2(m+1) et alors calculer

X^bâ = X(X^'V-^1(m+1)X)-X^'V-^1(m+1)Y

sinon ajouter 1 a` m et retourner a` l''Etape 1.

A l''Etape-E, calculer l'esp'erance de la vraisemblance conditionnelle fond'ee sur fY,u1,··· ,u_r,la fonction de densit'e des donn'ees compl`etes sachant les donn'ees incompl`etes est 'equivalent a` calculerE_ó2(m)(u^'kuk | Y).

4.2 La r'egression PLS sur un modèle de variance connue

La régression PLS est une méthode d'estimation particulière utilisée pour les modèles linéaires avec l'éventualitén < p. Pour ce type d'analyse, l'objectif est de prédire Y par des combinaisons linéaires des colonnes de X appelées variables latentes. Il est habituellement mis en oeuvre a` l'aide de l'algorithme NIPALS, Nonlinear estimation by iterative partial least squares (Wold 1966; de Jong 1993) o`u le calcul des variables latentes est effectuésimultanément avec un ensemble de régressions par OLS. Cependant, ces régressions sont adéquates seulement dans le cas des erreurs sur Y iid.

L'algorithme PLS appliquéa` un modèle de variance connue est effectuéen remplaçant les régressions OLS sur les variables latentes par des régressions GLS, General least squares, dont voici la description.

1. Centrer et éventuellement réduire X et Y : x0 = X, y0 = Y

2. Pour h = 1,··· ,H avec 1 H rang(X)

(a) Calculer les p-vecteurs wh = [w1 h · · · w^p _h]^' _V/X

o`u wp h = Cov(x^p _h, yh)/ Cov²(x^p _h, yh) et xp h la p^e colonne de xh

p

(b) Normer wh : wh = wh/ wh II

(c) Calculer les variables latentes PLS th = xh-1wh

(d) Calculer ch par régression GLS de _yh-1 sur th

yh-1 = thch + yh o`u Var(yh-1) = V ch =(t^' hV^-1th)^-t^' hV^-1yh-1

(e) Calculer ph par régression de _xh-1 sur th

)-¹_t'

xh-1 = thp' _h + xh d'o`u p' h =(t^' hth hxh-1

(f) Calculer les résidus xh et yh

(g) Alors Y = t1c1 +
·
·
· + _thch + yh

Ainsi, le seul changement par rapport a` l'algorithme PLS classique est le remplacement de la régression OLS par la régression GLS au point 2.(d).

4.3 La méthode PLS-Mixte

Les méthodes de vraisemblances, ML ou REML, comme techniques pour estimer les paramètres fixes et les composantes de variance dans un modèle linéaire mixte, ne sont applicables que dans le cas classique o`u le nombre de régresseurs est faible devant le nombre d'observations, c'est-à-dire n > p. Dans ce cas, comme nous l'avons vu, un algorithme itératif tel que l'algorithme EM est nécessaire pour obtenir l'estimation des paramètres inconnus.

Pour traiter du cas n < p, nous proposons d'imbriquer une méthode de réduction de dimension telle que la régression PLS dans l'algorithme EM. Puisqu'il s'agira d'estimer des composantes de variance dans un contexte de réduction de dimension, nous avons appelécette technique PLS-Mixte.

Avant cette méthode proposée, dans les modèles o`u il y avait plus de régresseurs que d'observations et plusieurs sources de variation, l'estimation des paramètres inconnus se faisait simplement par régression PLS, c'est-à-dire sans

tenir compte précisément des sources de variation. Aussi, avons-nous ^comparél'estimation faite par simple régression PLS a` celle faite par notre méthode en

utilisant le critère MSEP, Mean square error of prediction, dans les différentes applications de ce chapitre. La question de la convergence sera abordée plus loin.

4.3.1 La méthode PLS-Mixte sur un modèle a` effets aléatoires indépendants de variances homogènes

Nous nous plaçons dans le cadre du modèle 4.2 et considérons que n < p. Nous proposons la méthode PLS-Mixte qui consiste donc a` imbriquer une méthode de réduction de dimension telle que la régression PLS dans l'algorithme EM. Cette méthode d'estimation est fondée sur ML et ses variantes. L'estimation par ML est réalisée en maximisant la vraisemblance de Y par rapport aux paramètres inconnus.

Suivant l'algorithme EM, nous prenons des valeurs de départ pour les paramètres inconnus. Ces valeurs permettent de calculer les variables latentes obtenues a` partir du modèle (X, Y) vu que la variance V⁽⁰⁾ est connue, les valeurs initiales ó2(0)

k étant choisies. Sur ces variables latentes, sont calculées les composantes de varianceó²⁽¹⁾

k comme dans le cas classique de l'algorithme

EM. Avec les valeurs ó2(1)

k , ces étapes sont répétées avec les composantes ó2(0)

k

remplacées par les estimations courantes ó2(1)

k . Ce processus itératif est alors

continuéjusqu'àconvergence. Nous décrivons ci-dessous l'algorithme de la méthode proposée avant de le détailler plus loin.

'Etape 1 ('Etape-E) Centrer et reduire X et Y

'Etape 1.1 Reduire la dimension de l'espace des regresseurs en

determinant les h variables latentes T^(m) = [t^(m)

1 · · · t⁽_h :^m)]

vu que la variance V^(m) est connue 'Etape 1.2 Calculer

Q(ó² | ó2(m))

=E_ó2(m)(u^'iuk | Y)

= qkó2(m) k + ó4^(m) [Y^'P^(m)ZkZ^'kP^(m)Y - tr(ZkV^-1(m)Zk)1

o`u P^(m) = V-1(m)-V-1(m)T(m)(T(m)'V-1(m)T(m))-T(m)'V-1(m)

'Etape 2 ('Etape-M) Determiner ^ó2k(m+1) qui maximise E_ó2(m)(u^'iuk | Y) c`ad, tel

que QT(m)(ó^2(m+1) | ó2(m)) % QT(m)(ó² | ó2(m))

_ók2(m+1)

= E_ó2(m)(u^'iuk | Y)/qk pour k = 0, 1, · ··, r

'Etape 3 Si convergence, prendre bó²k = ók2(m+1) et alors calculer

X^-â = X(X^'V-^1(m+1)X)-X^'V-^1(m+1)Y

sinon ajouter 1 a` m et retourner a` 'Etape 1.

Les variables latentes sont ainsi recalculees au debut de chaque iteration dans l'algorithme EM avec les composantes de variance mises a` jour. Cet algorithme de la methode PLS-Mixte fondee sur une variation de ML est detaillede la facon suivante.

'Etape 1 Centrer et reduire X et Y : x0 = X, y0 = Y

'Etape 1.1 Pour h = 1,2, ... , rang(X)

(a) Calculer les p-vector wh = [w¹_h · · · w^p_h]^'

o`u w^p_h = Cov(x^p_h,yh)/ E Cov²(x^p_h, _yh) et x^p_h la p^e

p

colonne de xh

(b) Normer wh : wh = wh/ II wh II

(c) Calculer les variables latentes t(m)

h = xh-1wh

(d) Calculer ch par regression GLS de yh-1 sur t(m)

h

yh-1 = t^(h^m)ch + yh o`u Var(yh-1) = V(m) =

Xr k=0

ZkZ^'kók^2(m)

ch =~t(m)'

h _V-1(m)_t(m) ~-_t(m)'

h V-1(m)yh-1

h

(e) Calculer ph par regression de xh-1 sur t(m)

h
_~-1_t(m)'

xh-1 = t(m)

h p' h + xh d'o`u p' h =~t(m)'

h t(m) h xh-1

h

(f) Calculer les residus xh and yh

(g)

_Xr
i=0

Ziui

Finalement Y = T^(m)C +

o`u ^T(m) =[t^(m)

1 ···t(h ^m)] et C = [c1 · · · ch]^'

'Etape 1.2 Calculer

2m+1)

ó_k⁽ = C r k 2(m) + (ó k(m) / qk) [Y^'P^(m) Z kZ^'_kP^(m)Y - tr (Z'kV -1(m) Zk)1

o`u P^(m) = V-1(m)-V-1(m)T(m)(T(m)'V-1(m)T(m))-T(m)'V-1(m)

'Etape 2 Si convergence, prendre bó2k = ó2k(m+1) ; sinon ajouter 1 a` m

et retourner a` l''Etape 1.1

La procedure REML, quant a` elle, maximise la vraisemblance de certaines combinaisons lineaires des elements de Y par rapport aux param`etres inconnus (McCulloch and Searle, 2001). Notre methode fond'ee sur cette procedure REML est effectuee en remplacant l''Etape 1.2 par

2(m+1)

ó_i = ó^(m) + (ó4^(m) /qi) [Y^'P^(m)ZiZ^'_iP^(m)Y - tr(Z^'_iP^(m)Zi)]

o`u P^(m) reste defini comme ci-dessus.

Convergence de l'algorithme de la m'ethode PLS-Mixte :

Les proprietes de convergence de l'algorithme EM restent valides avec cette methode PLS-Mixte, en particulier sa convergence monotone. Par exemple, pour la monotonocitede l'algorithme EM, nous devons montrer que la fonction de vraisemblance, L(ó² | Y) ne decroit pas apr`es une iteration, c'est-`adire,

LT(m)(ór^m+1) | Y) LT(m-1)(ói ^2(m)| Y) (4.3)

o`u la valeur de la vraisemblance LT(m)(ó<sup>2(m+1)</sup> | Y) est calculee a` la (m + 1)^e

i

iteration en utilisant les valeurs actuelles de T^(m) comme regresseurs et la valeur de la vraisemblance LT(m-1)(ói 2(m) | Y) calculee a` la m^e iteration avec les valeurs de T(m-1)

Pour l'algorithme EM classique, le fait que la vraisemblance augmente a` chaque iteration est un resultat bien connu qui a etemontrepar Dempster, Laird et Rubin (1977) et discuteplus tard par Wu (1983) et par McLachlan et Krishnan (1997).

Nous nous sommes fond'es sur ce resultat pour montrer l'inegalite(4.3). La fonction de densiteconditionnelle des donnees compl`etes [Y, u<sup>'</sup>] o`u u^' = [u^' ₁,· · · ,u^'_r] sachant les donnees incompl`etes Y est egale a`

k([Y,u^'] | Y, ó²) = f[Y,u^']([Y,u^'] | ó²)

f(Y | ó²)

(4.4)

Alors la fonction log-vraisemblance des donnees incompl`etes peut s'ecrire comme suit :

l(ó² | Y) = ln (f(Y | ó²))

= ln (f[Y,u^']([Y, u^'] | ó²)/k([Y, u^'] | Y, ó²))

= ln (f[Y,u^']([Y, u^'] | ó²)) -- ln (k([Y, u^'] | Y, ó²)) = l[Y,u^'](ó² | [Y, u^']) -- ln(k([Y,u^'] | Y, ó²))

L'esperance de cette equation est prise par rapport a` la distribution conditionnelle des donnees compl`etes sachant les donnees incompl`etes, et en utilisant <sup>ó2(m)</sup> a` la place de ó². Ainsi,

E_ó2[l(ó² | Y) | Y1 = lT(m-1)(ó² | Y) (4.5)

= IE_ó2(m) [l[Y,u^'](ó² | [Y,u^']) | Y1

--E_ó2(m) [ln(kT(m-1)([Y,u^'] | Y, ó²)) | Y1

Nous avons, a` l''Etape-E de l'algorithme du mod`ele PLS-Mixte avec une variance connue (section 2.2), la relation suivante :

E_ó2(m) [l[Y,u^'](ó² | [Y,u^']) | Y1 =E_ó2(u^'u | Y)

= QT(m-1)(ó² | ó2(m))

et en posant

GT(m-1)(ó² | ó2(m)) = [E_ó2(m) [ln(kT(m-1)([Y,u^'] | Y,ó²)) | Y1

l'equation (4.5) devient

lT(m-1)(ó² | Y) = QT(m-1)(ó² | ó2(m)) -- GT(m-1)(ó² | ó2(m))

Nous pouvons maintenant calculer

lT(m)(ó^2(m+1) | Y) - lT(m-1)(ó^2(m) | Y) = QT(m)(ó^2(m+1) | ó2(m))

- GT(m)(ó^2(m+1) | ó2(m))

- QT(m-1)(ó^2(m) | ó2(m)) +GT(m-1)(ó^2(m) | ó2(m))

La quantit'e QT(m)(ó^2(m+1) | ó^2(m))-QT(m-1)(ó^2(m) | ó2(m)) est positive car ó2(m+1)

est choisie tel que

QT(m)(ó^2(m+1) | ó2(m)) = QT(m-1)(ó² | ó2(m)) ? ó2

Et, ? ó2

GT(m-1)(ó² | ó2(m)) - GT(m-1)(ó^2(m) | ó2(m)) = E_ó2(m) [ln(kT(m-1)([Y,u^'] | Y, ó²)) | Y]

-E_ó2(m) [ln(kT(m-1)([Y,u^'] | Y,ó^2(m))) | Y]

= ln(1)

= 0

Ce r'esultat est montr'e par McLachlan et Krishnan (1997) pour l'algorithme
EM classique o`u les r'egresseurs sont consid'er'es comme fixes. Ici, la quantit'e

GT(m-1)(ó² | ó2(m)) - GT(m-1)(ó^2(m) | ó2(m))

est prise, ? ó², par rapport aux màemes r'egresseurs T^(m-¹⁾. Ce qui ne change donc pas le r'esultat.

Nous avons alors

lT(m)(ó^2(m+1) | Y) - lT(m-1)(ó^2(m) | Y) ~ 0

La m'ethode PLS-Mixte, utilise entre autres, la technique de r'eduction de dimension. Et dans ce sens, il faudra d'eterminer la dimension du modèle retenue. Pour cela, nous choisissons un nombre maximum h (h < rang(X)) de variables latentes au d'epart. La m'ethode it'erative d'ecrite plus haut permettra de calculer et d'actualiser tour a` tour ces h variables latentes et les composantes de variance. Avec ces composantes de variance estim'ees au final sur le modèle a` h variables latentes, les PRESS, Prediction error sum of squares (Stone 1974), des h sous-modèles avec respectivement 1, 2,
·
·
·, h r'egresseurs sont calcul'es. La dimension retenue est celle du sous-modèle a` plus faible PRESS.

Illustration avec des données de NIRS

Les algorithmes pr'esent'es ci-dessus sont test'es et appliqu'es a` titre illustratif sur un jeu de donn'ees de Rami, Dufour, Trouche, Fliedel, Mestres, Davrieux, Blanchard et Hamon (1998).

Il s'agit d'une population de lign'ees recombinantes de sorgho 'etudi'ee a` la station exp'erimentale de l'INERA au Burkina Faso. Cette population est obtenue par une m'ethode »modified single-seed descent» avec le g'enotype IS 2807 (collection de l'ICRISAT) consid'er'e comme femelle crois'ee avec le g'enotype 249 (collection du CIRAD) consid'er'e comme màale. Cette population de 90 individus fut r'ecolt'ee en 1995 a` la g'en'eration F7, a` partir d'un dispositif exp'erimental en lattice 9x10 avec trois r'ep'etitions.

Nous avons seulement retenu la teneur en prot'eine parmi un ensemble de mesures biochimiques effectu'ees sur les lign'ees, pour nous conformer aux conditions de notre m'ethode; c'est-à-dire qu'il n'est consid'er'e qu'une seule variable a` expliquer.

Pour cette teneur en prot'eine, il a 'et'e utilis'e une m'ethode traditionnelle de mesure, fiable mais longue a` effectuer; les valeurs mesur'ees sur toutes les lign'ees constituent le vecteur Y.

Parallèlement a` cette m'ethode de mesure, la technique NIRS, Near infrared reflectance spectroscopy, beaucoup plus rapide a 'et'e effectu'ee; les spectres d'absorption obtenus pour 1050 longueurs d'onde constituent la matrice X. La s'erie de longueurs d'onde consid'er'ee est constitu'ee d'une s'equence de 400 a` 1098 par 2 (figure 4.1).

FIG. 4.1 - Spectres d'absorption proches de l'infrarouge pour une population de lignées de sorgho récoltées en 1995 a` la Station expérimentale de l'INERA au Burkina Faso.

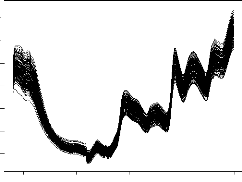
500 1000 1500 2000 2500

absorbance

0.1 02 0.3 0.4 0.5 0.6 0.7

longueurs d'onde

Au delàde notre souci d'utiliser ces donn'ees pour tester et 'eprouver notre m'ethode, l'int'erêt de cette 'etude chez le praticien, pourrait être de calibrer la technique NIRS sur le sorgho pour la teneur en prot'eine dans le but d'obtenir une m'ethode de mesure rapide en tenant compte de la structure particulière de la covariance des erreurs induite par le dispositif exp'erimental.

Pour la mise en oeuvre de la m'ethode PLS-Mixte sur ces donn'ees, il existe cependant des donn'ees manquantes a` savoir la troisième r'ep'etition et trois lign'ees des deux autres r'ep'etitions. Eu 'egard au nombre important de longueurs d'onde (1050) et la corr'elation massive habituellement constat'ee sur les donn'ees de NIRS, nous avons d'ecid'e de conserver syst'ematiquement une longueur d'onde toutes les cinq.

Le modèle consid'er'e pour ces donn'ees s''ecrit comme suit :

Y = Xâ + _Z1u1 + _Z2u2 + e (4.6)

o`u u1 d'ordre 2 est l'effet al'eatoire de la r'ep'etition et u2 d'ordre 20 l'effet al'eatoire du bloc hi'erarchis'e dans la r'ep'etition.

Finalement, la dimension de Y est 174×1 et la dimension de X est 174×210. Aussi, Z1 est une matrice 174×2 et u1 un vecteur 2×1 tandis que Z2 est une matrice 174×20 et u2 un vecteur 20×1.

Les hypothèses pour ce modèle sont par cons'equent

? ???? ????

u1 ~ N(0,ó^21I2) u2 ~ N(0, ó2 2I20) u0 ~ N(0,ó^2 0I174) avec u0 = e

Nous avons donc pour ce modèle, plus de r'egresseurs que d'observations (210 contre 174) et trois composantes de variance a` estimer (ó<sup>2</sup><sub>1</sub> pour l'effet al'eatoire de la r'ep'etition, ó2 2 pour l'effet al'eatoire du bloc et ó2 0 pour l'erreur r'esiduelle al'eatoire). Nous allons donc avoir recours a` la m'ethode PLS-Mixte fond'ee sur ML et sur REML pour estimer les quatres paramètres â, ó² 1, ó2 2 et ó² ₀.

Pour le calcul du PRESS, nous avons, comme annonc'e plus haut, choisi un
nombre maximum de 10 variables latentes. Avec un modèle de dimension 10,

nous avons utilis'e la m'ethode PLS-Mixte pour estimer les trois composantes de variance. Par la suite, pour chacun des sous-modèles de dimension 1 a` 10, nous avons enlev'e successivement chaque lign'ee (dans les deux r'ep'etitions) dont nous avons pr'edit sa teneur en prot'eine par les lign'ees restantes en utilisant une r'egression GLS avec les composantes de variance estim'ees sur le modèle de dimension 10.

Le PRESS d'ecroàýt continuellement avec le nombre de variables latentes pour les deux modèles fond'es sur ML et sur REML quand le nombre de composantes maximum avait initialement 'et'e fix'e a` 10. Cependant, nous avons d'ecid'e pour ces modèles de r'eduire leur espace a` 7 dimensions 'etant donn'e que le PRESS n'y est pas trop diff'erent de ses valeurs minimales (figure 4.2).

FIG. 4.2 - 'Evolution du PRESS selon le nombre de variables latentes quand le nombre maximal de variables latentes avait initialement étéfixéa` dix pour les données de NIRS.

ML REML

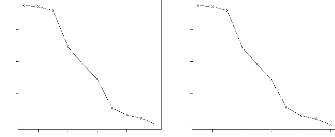
PRESS

20 25 30 35

2 4 6 8 10

2 4 6 8 10

20 25 30 35

PRESS

Par rapport a` l'objectif de cette 'etude, il serait question de s'electionner les r'egresseurs influents. Nous pouvons alors pour cela, consid'erer les coefficients les plus grands en valeur absolue des r'egresseurs pour le modèle s'electionn'e. Nous notons ainsi que les bandes d'absorption localis'ees autour de 2210, 1940, 1690 et 1450 ont les plus grands coefficients (figure 4.3).

FIG. 4.3 - 'Evolution des coefficientsâ^b (modèle (4.6)) selon les différentes longueurs d'onde pour les modèles a` 7 variables latentes fondés sur ML et REML des données de NIRS.

ML REML

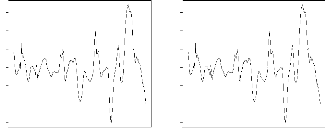
.9 02

02

0.0 0.1

-0 -02 .1 -0

-0.9

02

02

00 0.1

-02 -0.1

500 1000 1500 2000 2500 500 1000 1500 2000 2500

wavelengths wavelengths

Les estimations de ó _k pour ML et pour REML sont montr'ees au tableau 4.1. Nous notons que la variance de l'effet bloc hi'erarchis'e dans la r'ep'etition est deux fois plus faible que celle de l'effet r'ep'etition.

ML REML

ó ₁ 0,11273 0,11276
ó 0,06248 0,06309
ó ₀ 0,46839 0,48917

Estimation des composantes de variance pour les modèles a` 7 va-

TAB. 4.1 - riables latentes fondés sur ML et REML des données de NIRS.

Au tableau 4.2, nous avons le MSEP du modèle 4.6 analys'e par r'egression PLS et le MSEP du même modèle analys'e par la m'ethode PLS-Mixte fond'ee sur ML et sur REML. La pr'ediction par la m'ethode PLS-Mixte, comme nous nous y attendons, de la teneur en prot'eine du sorgho par les bandes d'absorption, quand il y a plusieurs sources de variation, est meilleure que celle faite par simple r'egression PLS.

MSEP

ML 0,64637

PLS-Mixte REML 0,64639

PLS 0,91479

TAB. 4.2 - MSEP des modèles de la méthode PLS-Mixte et de la régression PLS pour les données de NIRS.

Toutefois, la détermination de la dimension optimale a` travers le calcul du PRESS est ici liée a` h, le nombre maximum de variables latentes choisi au départ. En effet, les composantes de variance sont estimées avec les h variables latentes et utilisées par la suite respectivement pour chaque sous-modèle a` 1, 2, ..., h variables latentes pour estimer â et finalement pour calculer les PRESS. Cependant, le choix de h semble ne pas avoir un impact important sur le calcul des PRESS dans notre example. A la figure 4.4, nous avons présentéles valeurs des PRESS calculées pour un nombre maximum de variables latentes choisi initialement pour être égal respectivement a` 10, 20, 30, 40 et 50. L'évolution du PRESS jusqu'àla dixième variable latente n'est quasiment pas affectée par le choix initial du nombre maximum de variables latentes.

4.3.2 La méthode PLS-Mixte sur un modèle a` effets aléatoires corrélés de variances hétérogènes

La méthode PLS-Mixte, présentée ci-dessus et appliquée aux données de NIRS, a étéécrite avec les hypothèses classiques de normalitédes effets aléatoires et surtout de la forme particulière des matrices de variance de ces effets aléatoires. En effet, il a fallu supposer que cette variance pour chaque effet aléatoire Uk était de la forme ó2 kIqk.

Ici, nous allons légèrement relâcher cette hypothèse et considérer que la va-
riance pour chaque effet aléatoire pourrait être de la forme ó2 kAk o`u Ak est

Variation du PRESS selon les dix premières variables latentes

FIG. 4.4 quand le nombre maximum de variables a initialement étéfixéde façon successive a` 10, 20, 30, 40 et 50 pour le modèle fondésur

ML pour les données de NIRS. Le modèle fondésur REML donne des résultats voisins de ceux présentés ici.

ML

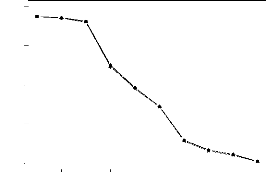
20 25 30 35 40

PRESS

2 4 6 8 10

une matrice quelconque symétrique connue. Nous allons alors voir comment la méthode PLS-Mixte s'écrira avec ces nouvelles données du problème.

Nous nous plaçons toujours dans le cadre du modèle (4.2) que nous allons rappeler.

Y = Xâ + _Xr ZkUk (4.7)

k=0

Nous supposons cette fois-ci donc que Uk ~ N(0, ó2 kÄk), d'o`u V = _Xr ZkÄkZ^' kó² k.

k=0

Avant de présenter notre méthode avec un modèle o`u n < p et la variance
V des observations écrite comme ci-dessus, nous traiterons dans un premier

temps, du cas plus simple n > p o`u nous verrons comment s'effectuent les estimations des paramètres inconnus â et ó2 k a` l'aide de l'algorithme EM fondésur ML.

Le modèle mixte a` effets aléatoires corrélés

L'algorithme EM, nous le rappelons, permet de calculer l'espérance condi-
tionnelle des effets aléatoires sachant les données incomplètes Y. Pour cela, il
est nécessaire d'avoir la loi jointe de Y et u = [ u'1 u' 2 ... u' r ]'. Nous avons

Cov(Y, u' k') = Cov(Xâ + _Xr Zkuk,u^' k') = Zk'Cov(uk',u^' k') = ó2 k'Zk^'Äk^' (4.8)

k=0

car Var(uk) = ó2 kÄk V k, et Cov(uk,u^'k') = 0 pour k =6 k^'.

Ainsi, avec les suppositions du modèle (4.7), la loi jointe de Y et u est gaussienne de la forme .IV(12,Ó) o`u

12 =

Xâ 0 ... 0

? ? ? ? ? et Ó = ?

" # V Cov(Y,u^') Cov(u,Y^') Var(u)

(4.9)

avec Cov(Y,u^') = [ ó2 1Z1Ä1 . . . ó2 rZrÄr ]

?ó²1Ä1Z^'1

?

Cov(u,Y^') = ? ..

? .

ó2 rÄrZ^' r

ó2 1Ä1

et Var(u) = 0 ... 0

ó2 rÄr

Ce qui implique la fonction de densitésuivante

_Pr

fY,u1,··· ,u_r(Y, u1, · · · , u_r) = (2ð)- ¹ k=0 qk|Ó|- 1

o`u

2 2 exp(-¹ ₂Q) (4.10)

[ ] Q = (Y - Xâ)' u' 1 · · · u' Ó-1 r

Y - Xâ u1 ...

(4.11)

u_r

Nous allons donc avec les développements qui vont suivre, trouver les valeurs de |Ó| et de Ó^-1 dans le but de simplifier la densité(4.10). Il s'agira par la suite, de dériver tout simplement cette densité, pour avoir les estimations des paramètres.

Pour calculer |Ó|, nous faisons appel au résultat déjàétabli (Searle et alp 453, 1992) : Si A, B, C et D sont quatre matrices avec les bonnes dimensions, alors

~~~~~

A B C D

~~~~~

= |D||A - BD^-1C|

Ainsi, |Ó| =

~~~~~

V Cov(Y,u^') Cov(u,Y^') Var(u)

~~~~~

= |Var(u)||V - Cov(Y, u^')(Var(u))-^1Cov(u, Y')|

|Var(u)| =

~~~~~~~~

ó^21Ä1 0 ... 0 ó2 rÄr

~~~~~~~~

= |ó^21Ä1| × ··· × |ó^2 rÄr| =

Lr k=1

(ó^2 k)^qk|Äk|

Or,

car chaque matrice Äk est carree de nombre de lignes qk D'autre part,

Cov(Y, u^')(Var(u))^-1Cov(u, Y^')

= [ ó^21Z1Ä1 ··· ó2 rZrÄr ]			ó1^2Ä1^-1 0 · · · 0 ó-2 r Ä	-1 r	ó2 1Ä1Z^' 1 · · · ó^2rÄrZ^'r
=	Xr k=1	ó^2kZkÄkZ^' k

Or,

(Var(u))^-1Cov(u, Y^') =

0
·
·
·

0

_ó-2

r

^Ä

ó²1Ä1Z^'1

·
·
·

ó²_rÄrZ^'_r

^-1

r

_ó-2

1 Ä1-1

=

Z^'₁

·
·
·

Z'r

D'o`u

|Ó| = _Yr (ó²k)^qk|Äk||V - _Xr ó2 kZkÄkZ^' k|

=

_Yr
k=1

k=1 k=1

(ó²k)^qk|Äk||ó²0Ä0|

=

Yr k=0

(ó^2k)^qk|Äk|

Pour calculer Ó^-1, nous utilisons les resultats des inverses generalisees (Searle et al p 450, 1992) et etablissons que

" #

=

0 0

0 (Var(u))-¹

"+

# I

ó,:72Ä:7, ¹ [ I -Cov(Y, u^')(Var(u))^-1

-(Var(u))^-1Cov(u, Y^')

Par ailleurs,

Cov(Y, u^')(Var(u))-¹ = [ Z1 · · ·Zr

Par cons'equent,

Ó-1 = Ó1 ^-1 + Ó-1

2

o`u Ó1 1 =

_ó-2

1 Ä-1

1

?

m ?0

... 0

_ó-2

r Ä-1

r

I

et Ó2 -1 =

-

Z^'1 ...

h h i i ó-2 0 Ä-1 I - Z1 · · · Zr 0

Z' r

Nous allons donc remplacer Ó^-1 par Ó-1

1 +Ó-1

2 dans (4.11) pour avoir la valeur

de Q.

Ainsi,

Q = Q1 + Q2

o`u Q1 = [ (Y - Xâ)^' u^'1 · · · u' Ó-1 r 1

Y - Xi3 u1 ...

u_r

et Q2 = [ (Y - Xâ)^' u^'1 · · · u^'Ó^-1 r 2

Y - Xi3 u1 ... ur

m 0

m ?0

?

? _ó-2

1 Ä-1

1

... 0

r 2Är-1

ó

Q1 = [ (Y - Xâ)^' uc_. · · · u^'_r ]

Y - X_i3
u1

...

ur

= I 0 [ u^'₁ · · · u^'_r ]

		ó-2 1 Ä-1 1 0		... 0 ór^2Är^-1		Y - Xi3 u1 ... ur
= [ u^'1 · · · u^'r ]	ó-2 1 Ä-1 1 0		... 0 ór^2Är^-1		u1 ... ur

u'kÄk 1uk

=

_ó2

k

_Er
k=1

Pour calculer Q2, trouvons d'abord une formule simplifiée de Ó-1

2

I

Ó-1 2 =

-

Z^'1 ... Z^'r

ó 0 ^2Ä,Y1 [ I - [ Z1 ··· Zr ] ]

Ä01 -Ä,y^1 [ Z1 · 1

·· Zr ]

= ó-2 0

-

Z^'1 ... Z^'r

? ? Ä-1 ? 0 ?

Z^'1 ... Z^'r

Ä01 [ Z1 · · · Zr ]

Ainsi Q2 = ó02 [ Q21 Q22 ]

Y - Xi3 u1 ... ur

Z^'1 ... Z^'r

Ä0^-1

?

?

avec Q21 = (Y - Xâ)^'Ä^-1

0 - [ u' 1 · · · u' r ] ? ?

_Ä-1

0 [ Z1 · · · Zr ]

Z' r

Z' 1

...

? ?

et Q22 = -(Y-Xâ)^'Ä^-1

0 [ Z1 · · · Z_r ]+[ u' 1 · · · u' r ] ? ?

D'o`u,

Z^'1

...

Z^'_r

? ?

Q2 = _ó-2 ? r ]

0 _?(Y - Xâ)^'Ä^-1

0 - [ u' 1 · · · u'

? ?

? ?

? _Ä-1 ? (Y - Xâ) ? 0 ?

Z^'1

...

Z^'_r

?
? ? ?

- ó^-2

0

? ?

(Y - Xâ)^'Ä^-1

0 [ Z1 · · · Z_r ] - [ u' 1 · · · u' r ] ? ?

?

? ?Ä-1

0 [ Z1 · · · Zr ]

?

u1

×

... ur

- 2 (Y - Xâ)^'Ä^-1

0 -

_Xr
k=1

!

u' kZ^' kÄ^-1 (Y - Xâ)

ó₀

=

0

- ó^-2 0

(Y - Xâ)^'Ä^-1 0

Xr k=1

Zkuk -

Er k=1

u^'kZ^'kÄ0^-1

Xr k=1

!Zkuk

!

_Xr _Xr

Zkuk - _ó-2 u' kZ^' kÄ^-1 Y - Xâ - Zkuk

0 0

k=1 k=1

- 2 (Y - Xâ)^'Ä^-1 Y - Xâ -

0

_Er
k=1

ó

=

0

! Xr

u' kZ^' kÄ^-1 Y - Xâ - Zkuk

0

k=1

- 2 (Y - Xâ)^'Ä^-1

0 -

_Xr
k=1

= ó 0

= ó^-2 Y - Xâ - 0

Xr k=1

!' Xr Zkuk Ä-1 Y - Xâ - 0 k=

1

Zkuk)

u' kÄ-1

k uk + ó^-2 Y - Xâ -

_ó2 0

k

) !

_X

Zkuk Ä-1 Y - Xâ - Zkuk (4.12)

0

k=1

Q = _Xr

k=1

_Er
k=1

' r

En ajoutant Q1 et Q2, nous obtenons

En remplaçant (4.11) dans (4.9) et en passant au logarithme, nous avons

l = -1 2

X r k=0

log27r -- ) k - k=0 k=1 1 Er (gkiegOlc + loglAkl) -- 1 `-r uk^' Ä^-1u1 qk ' 2 2 L--1 ó2 k

Zkuk) Ä0 ¹ Y

- Xâ-

-2 ó₀

2

Y - Xâ -

_Xr
k=1

EZkuk)

k=

1

1

-

2

X r
k=0

) ¹(qklogó

r r 1.1^' Ä^-1uk

qk log27r -- Nl_c + log|Äk |) - V k k

2 1---/ 2 L--/ ,.,.2

"

k=0 k=0 k

car Y - X0 - _Xr Zkuk = e = u0

k=1

De ce fait, il suffira de d'eriver la fonction l ci-dessus par rapport a` chacun des param`etres inconnus du mod`ele (4.7) pour trouver les estimateurs suivants

= ukÄ_k ¹uk/qk, k = 0,1,· · · r (4.13)

et

XS = X(X^'Ä,y¹X)^-X^'Ä,y¹ Y -

k=1 Zkuk) ) (4.14)

Ainsi, comme les uk ne sont pas connus, nous avons besoin des esp'erances conditionnelles de

u'k _k 1uk

et de

r
Y - Zkuk
k=1

sachant les donn'ees incompl`etes Y.

Pour cela, nous pouvons utiliser le r'esultat suivant : si

_I # _I # _I

x1 u1 V11 V12

~ N ,

x2 u2 V21 V22

alors la loi conditionnelle de x1 sachant x2 est

x1|x2 ~ N[u1 + V12V^-1

22 (x2 - u2), V11 - V12V^-1

22 V21]

Avec uk ~ N(0,ó² _kÄk) et Y ~ N(Xâ,V), nous avons

_I # _I # _I #!

uk 0 ó2 kÄk Cov(uk, Y^')

~ N ,

Y Xâ Cov(Y,u^' k) V

D'apr`es (4.8), il vient

uk|Y ~ N (ó2 )

kÄkZ^' kV^-1(Y - Xâ), ó2 kÄk - ó2 kÄkZ^{' kV-1ó2} kZkÄk

D'o`u

kV^-1(Y - Xâ)

[(uk|Y) = ó2 kÄkZ^' (4.15)

Ensuite, en utilisant le th'eor`eme suivant (Searle p 231, 1987)

Théorème 1

si x ~ N(u, V) alors[(x^'Ax) = tr(AV) + u^'Au ? A

et d'apr`es ce qui pr'ec`ede, nous avons

kÄ^-1 kÄ^-1

E(u' k uk|Y) = tr(ó² kÄ^-1

k Äk - ó4 k ÄkZ^' kV^-1ZkÄk)

+ó⁴k(Y - Xâ)^'V^-1ZkÄ;_cÄ_k ¹ÄkZ^'kV^-1(Y - Xâ)

D'o`u

E(u'kÄ^-1 k uk|Y) = tr(ó²kIqk - ó⁴kZ^'kV^-1ZkÄk) +ó⁴k(Y - Xâ)^'V^-1ZkÄ^'kZ^'kV^-1(Y - Xâ) (4.16)

Nous pouvons alors établir l'algorithme EM dans le cas du modèle linéaire mixte o`u chaque effet aléatoire est de variance ó<sup>2</sup><sub>k</sub>Äk. L'estimation, fondée sur ML, s'effectue en plusieurs itérations. Des valeurs initiales ók <sup>2(0)</sup> et â(0) sont choisies au départ. A la m<sup>e</sup> itération de l''Etape-E, sont calculées les espérances conditionnelles suivantes, a` partir de (4.16),

g(k m) = E(ukÄ_k ¹uk|Y)|₀₌₀(0) _et óZ=óZ(m) (4.17)

= tr(ó_k^(m)I_qk) - ó4(m)

k tr(Z^' kV^-1(m)ZkÄk)

+ók ^4(m) (Y - Xâ^(m))^'V^-1(m)ZkÄ^'kZ^'kV^-1(m)(Y - Xâ^(m)) = qkók + (ó4(m)

2(m) k )

× [ (Y - Xâ^(m))^'V^-1(m)ZkÄ^'kZ^'kV^-1(m) (Y - Xâ^(m)) - tr(Z^'kV^-1(m)ZkÄk)]

Et, a` partir de (4.15)

b(m) =E(Y -

Xr k=1

Zkuk|Y)0=0(0) et ó2 (4.18) k=ó^2(m) k

= Y - _Xr ZkÄkZ;có2k (m)V-1(m)(Y - Xâ^(m)) k=1

= Y - (V^(m) - ó,!,^(m)Ä0)V^-1(m)(Y - Xâ^(m))

= Y - V^(m)V^-1(m)(Y - Xâ^(m)) + ó₀^2(m)Ä0V^-1(m)(Y - Xâ^(m)) = Xâ^(m) + ó₀ ^2(m)Ä0V^-1(m)(Y - Xâ^(m))

A l''Etape-M, pour trouver les estimateurs, il suffit de prendre

ók 2(m+1)

.ik ^m^)/qk (4.19)

= 4,(m) + (4^(m)/qk)

× [(Y - Xâ^(m))^'V^-1(m)ZkÄ;,Z^'kV^-1(m)(Y - Xâ^(m)) - tr(Z^'kV^-1(m)ZkÄk)]

Et, a` partir de (4.14)

Xâ( 1)

= X(X^'Ä,y¹X)^-X^'Ä,y¹ (Xâ^(m) + ó₀ ^2(m)Ä0V^-1(m)(Y - Xâ^(m)) ) (4.20)

= X(X^'Ä^-1

0 X)-X'Ä-1

0 Xâ^(m) + ó₀^(m)X(X^'Ä,y¹X)^-X^'ÄC,¹Ä0V^-1(m)(Y - Xâ^(m)) = Xâ^(m) + 4^(m)X(X^'ĹX)^-X^'V^-1(m)(Y - Xâ^(m))

A la place d'itérer pour obtenir a` la fois les valeurs de â et de ó<sup>2</sup><sub>k</sub>, Laird (1982) suggère de trouver les valeurs de ó<sup>2</sup>k et seulement, a` la fin des itérations, de calculer la valeur de â. En effet, a` la place de calculer V-<sup>1(m)</sup>(Y - Xâ<sup>(m)</sup>) dans l'équation (4.19), il est calculéP<sup>(m)</sup>Y o`u

P^(m) = V-1(m) - V^-1(m)X(X^'V^-1(m)X)^-X^'V^-1(m)

ne depend pas de â.

En effet, si Xâ^(m) etait l'estimation de Xâ, c'est-`a-dire

Xâ^(m) = X(X^'V^-1(m)X)^-X^'V^-1(m)Y

alors

V^-1(m)(Y - Xâ^(m)) = V-1(m)Y - V-1(m)Xâ(m)

= V-1(m)Y - V^-1(m)X(X^'V^-1(m)X)^-X^'V^-1(m)Y = (V-1(m) - V^-1(m)X(X^'V^-1(m)X)^-X^'V^-1(m)) Y

= P^(m)Y

De ce fait, il ne sera pas necessaire de disposer de â^(m) dans les iterations et a`
l''Etape-E. Il ne sera alors plus calculequ'une seule esperance conditionnelle

ó2(m+1) k =

bs^(m) k /qk (4.21)

= ó2k ^(m) + (4(m)/qk) [ Y^'P^(m)ZkÄ^'kZ^'kP^(m)Y - tr(Z^'kV^-1(m)ZkÄk)]

Nous presentons ci-dessous l'algorithme EM fondesur ML appliqueaux effets aleatoires corr'el'es du mod`ele mixte.

'Etape 0 Mettre m = 0 et choisir des valeurs initiales ó2k(0)

'Etape 1 ('Etape-E) Calculer

Q(ó² | ó2(m))

= Eó2(m) (ukÄk ¹uk | Y)

= qkók (Irk2(m) + ^4(m) [Y'P(m)Zk k _Ä' Z' P^(m)Y -- tr(Z^'_kV^-1(m)ZkÄk)1

o`u P(m) = V-1(m) -- V-1(m)X(X'V-1(m)X~-X'V-1(m)

'Etape 2 ('Etape-M) Determiner ^ó2k(m+1) qui maximise Q(ó² | ó2(m)) c'est-`a-dire,

tel que Q(ó^2(m+1) | ó2(m)) ?. Q(ó² | ó^2(m)). Alors,

ók2(m+1) = E 2(m) (ukÄ_i;¹uk | Y)/qk for k = 0,1,
·
·
· , r

'Etape 3 A la convergence c`ad L(ó2k (m+1) | Y) -- L(ó2k (m) | Y) ,.... ç o`u

ç est une quantitearbitrairement petite et L la fonction de vraisemblance, prendre bó²_k = ók2(m+1) et alors calculer

X^-â = X(X^'V^-1(m+1)X)^-X^'V^-1(m+1)Y

sinon ajouter 1 a` m et retourner a` l''Etape 1.

Simulations pour la convergence de l'algorithme EM appliqu'e aux effets al'eatoires corr'el'es du mod`ele mixte :

Pour tester la convergence de cet algorithme et verifier la qualitedes estima-
tions, nous avons effectuedes simulations numeriques. Nous avons considerea` cet effet le modele simple suivant :

Y = X/3 + Z1u1 + Z2u2 + Z0u0 (4.22)

o`u la dimension du vecteur des reponses Y est 120x1, celle de la matrice des observations X est 120x5 et le vecteur ₁3 des parametres fixes est de longueur 5. Aussi, avons-nous suppose

? ???? ????								u1 ~ N(0,ó^21Ä1) u2 ~ N (0, ó2 2Ä2) u0 ~ N (0, ó2 0Ä0)
? o`u Ä1 = ???????	2 1 1 1 1	1 1 1 1 1	1 1 2 1 1	1 1 1 2 1	1 1 1 1 1	? , ???????	? ? ? ? ? ? ? ? ? ? ? Ä2 =		3 1 1 1 1 1	1 2 1 1 1 1	1 1 1 1 1 1	1 1 1 3 1 1	1 1 1 1 3 1	1 1 1 1 1 2	? et Ä0 = I120. ??????????

Nous avons choisi un dispositif équilibréavec le facteur 2 (6 niveaux) hiérarchisédans le facteur 1 (5 niveaux). Les matrices Z1 et Z2 sont donc les matrices

d'incidence correspondantes a` ces deux facteurs tandis que la matrice Z0 est l'identitéd'ordre 120.

Nous présentons au Tableau 4.3 les résultats des simulations obtenues avec le modèle 4.22 sur 300 jeux de données.

	Valeurs simulées	Valeurs estimées
	0,5402 0,8948	Moyenne 0,5380 0,8974	'Ecart-type 0,0937 0,0931
â	0,6476	0,6423	0,0912
	0,9513	0,9526	0,0921
	0,0772	0,0748	0,0933
ó^21	0,4653	0,4241	0,4416
ó2 2	0,2458	0,2471	0,3324
ó2 0	0,9226	0,8874	0,1233

TAB. 4.3 - Résultats des simulations pour un modèle mixte a` effets aléatoires corrélés effectuées sur 300 jeux de données.

Au vu de ces résultats, les valeurs estimées pour les paramètres ne sont pas, en moyenne, éloignées des valeurs simulées.

Le modèle PLS-Mixte a` effets aléatoires corrélés

Nous venons ainsi de voir, a` la section pr'ec'edente, l'estimation des paramètres
fixes et des composantes de variance dans un modèle lin'eaire mixte, a` l'aide
de l'algorithme EM, o`u chaque effet al'eatoire est de variance ó2 kÄk et o`u n > p.

Le cas n < p avec cette même structure de variance des effets al'eatoires, n'ecessite, comme au chapitre pr'ec'edent, d'imbriquer la r'egression PLS, en tant que m'ethode de r'eduction de dimension, a` l'algorithme EM. Nous proposons l'algorithme PLS-Mixte suivant, fond'e sur la variation de ML propos'ee par Laird

'Etape 0 Mettre m = 0 et choisir des valeurs de depart ó2k(0)

'Etape 1 Centrer et reduire X et Y : x0 = X, y0 = Y

'Etape 1.1 For h = 1, 2, ... , rang(X)

(a) Calculer les p-vector wh = [w¹_h · · · w^p_h]^' o`u w^p_h = Cov(x^p_h, yh)/ E Cov²(x^p_h, yh) et x^p_h la p^e

p

colonne de xh

(b) Normer wh : wh = wh/ II wh II

(c) Calculer les variables latentes t(m)

h = xh-1wh

(d) Calculer ch par regression GLS de yh-1 sur t(m)

h

yh-1 = t^(h^m)ch + yh o`u Var(yh-1) = V(m) =

Er k=0

ZkÄk Z'kó2k m)

ch =(t(h ^{m)'V-1(m)t(hm))-t(h} m)'V-1(m)yh-1

(e) Calculer ph par regression de xh-1 sur t(m)

h

xh-1 = t⁽_h ^m)p^'_h+ xh p^'_h =(t(h m)'_t(_hm) )-1t(h m)'xh-1

(f) Calculer les residus xh and yh

(g)

_Er
i=0

Ziui

Finalement Y = T^(m)C +

o`u ^T(m) =[t^(m)

1 ···t(h ^m)] et C = [c1 · · · ch]^'

'Etape 1.2 Calculer

2m+1)

ó_k⁽ = ó2k ^(m) (ók (m) / qk) [YP(m) Z _k Ä^'kZ^'_kP^(m)Y - tr(Z'kV ^-1(m) Zk k)1

o`u P^(m) = V-1(m)-V-1(m)T(m)(T(m)'V-1(m)T(m))-T(m)'V-1(m)

'Etape 2 Si convergence, prendre bó²_k = ó2k(m+1) ; sinon ajouter 1 a` m

et retourner a` 'Etape 1.1

Bien evidemment, le changement par rapport a` l'algorithme de la section precedente concerne l''Etape 1.1 (d) et l''Etape 1.2 o`u l'estimation des ó²_k tient compte de la variance ó²kÄk des effets aleatoires uk.

En resume, les estimations dans le mod`ele PLS-Mixte a` effets aleatoires
corr'el'es ont ete'ecrites de mani`ere explicite. Neanmoins, pour l'algorithme

itératif proposéa` cet effet, la convergence n'a pas étéétablie et est restée locale.

Chapitre 5

Conclusion générale

Nous nous 'etions fix'es comme objectif principal de mod'eliser les interactions G×E en fonction de covariables notamment climatiques observ'ees sur le milieu, avec comme application sa pr'ediction dans une exp'erimentation multienvironnements sah'elienne.

Nous avons commenc'e par exposer les principales m'ethodes existantes dans la litt'erature et montrer leurs limites. Ces m'ethodes ne sont adapt'ees dans le contexte sah'elien que par la prise en compte de la grande variabilit'e climatique du milieu d'une ann'ee sur l'autre. Or, la plupart de ces m'ethodes ne considèrent pas justement les caract'eristiques du milieu pour y pr'edire la performance des g'enotypes. La seule m'ethode a` notre connaissance qui y tient compte - la r'egression factorielle - ne permet pas de g'erer les nombreuses variables climatiques ordinairement mesur'ees sur ces lieux.

Les modèles de simulation de culture ont aussi 'et'e pr'esent'es comme une m'ethode alternative pour 'evaluer le comportement des g'enotypes selon les environnements. Cependant, ces modèles tout comme le modèle SarraH que nous avons utilis'e pour cette 'etude, sont rarement param'etr'es pour plus d'une vari'et'e. Or, pour pouvoir rendre compte des diff'erences de production

des g'enotypes, il est essentiel que les paramètres de ces modèles puissent changer selon les g'enotypes.

Nous proposons en cons'equence la m'ethode APLAT, Approximation par lin'earisation autour d'un t'emoin. Cette m'ethode consiste a` lin'eariser la r'eponse pr'edite par un modèle de simulation de culture de tout g'enotype d'un environnement donn'e autour du vecteur de paramètres connu d'un g'enotype de r'ef'erence. Après cela, certains des paramètres du modèle de simulation de culture, qui peuvent être choisis aux dires d'experts, peuvent être r'eestim'es a` l'aide de cette lin'earisation locale. L'avantage de cette m'ethode est de ne pas n'ecessiter pour tout g'enotype, l'exp'erimentation sp'ecifique indispensable a` la param'etrisation du t'emoin. A l'ensemble de ces exp'erimentations instrument'ees requises pour toute nouvelle vari'et'e d'int'erêt, est substitu'e un essai multilocal classique qu'on aura pris soin de munir de stations m'et'eorologiques simples.

La m'ethode APLAT a 'et'e valid'ee avec les donn'ees d'arachide d'un essai pluriannuel men'e a` la station exp'erimentale du CERAAS au S'en'egal de 1994 a` 1998. Pour ces donn'ees, chacune des ann'ees a 'et'e successivement r'eserv'e et le rendement des g'enotypes pr'edit a` l'aide des ann'ees restantes, d'abord a` l'aide de la m'ethode APLAT, ensuite a` l'aide du modèle moyen. Le modèle moyen est utilis'e pour estimer la performance des g'enotypes pour une ann'ee donn'ee par la moyenne des autres ann'ees. Un modèle qui pr'edit moins bien en moyenne que le modèle moyen n'est pas acceptable. Nous avons trouv'e que quatre fois sur cinq, la m'ethode APLAT s''etait montr'ee meilleure que le modèle moyen.

Ensuite sur les donn'ees de 11 sites d'un essai multilocal men'e durant la saison des pluies de 2005 au S'en'egal, la m'ethode APLAT a fourni une meilleure pr'ediction moyenne du rendement des g'enotypes que le modèle moyen, 10 fois sur 11.

Par la suite, la m'ethode APLAT a 'et'e 'etendue au cas d'essais a` plusieurs composantes de variance, qui devient APLAT-Mixte. Nous avons adjoint au modèle SarraH que nous avions utilis'e pour rendre compte du comportement diff'erenci'e des g'enotypes dans cette situation de variabilit'e environnementale accrue, un effet al'eatoire de l'environnement responsable d'interactions G×E dont il a fallu estimer la variance. Cette m'ethode s'appuie sur la technique PLS-Mixte que nous avons propos'e pour l'estimation des composantes de variance dans le cas o`u il y a plus de r'egresseurs que d'observations. Cette technique PLS-Mixte consiste a` imbriquer la r'egression PLS dans l'algorithme EM et constitue un algorithme it'eratif d'estimation des paramètres inconnus dans le cas du modèle mixte dans un contexte de r'eduction de dimension.

Cette technique PLS-Mixte a 'et'e illustr'ee avec des donn'ees de NIRS obtenues a` partir d'un dispositif exp'erimental en lattice 9×10 o`u l'effet du bloc et l'effet de la r'ep'etition ont 'et'e suppos'es al'eatoires. Sur ces donn'ees, nous avons estim'e les paramètres fixes et les composantes de variance du modèle avec cette m'ethode PLS-Mixte fond'ee sur ML et sur REML. Nous avons compar'e ce type d'estimation a` celui de la r'egression PLS qui 'etait habituellement utilis'ee dans ce genre de situation c'est-à-dire, quand il y avait plus de r'egresseurs que d'observations. Il a alors 'et'e trouv'e que les MSEP de la technique PLS-Mixte fond'ee sur ML et sur REML 'etaient plus faibles que le MSEP de la r'egression PLS faite simplement sans tenir compte des diff'erentes sources de variation.

Nous avons voulu adapt'e la technique PLS-Mixte au cas d'effets al'eatoires corr'el'es et h'et'erogènes. Pour cela, il a d'abord fallu se placer uniquement dans le cadre du modèle mixte avec de tels effets al'eatoires et surseoir au cas de r'eduction de dimension. Ainsi, les estimations des composantes de variance pour ces effets al'eatoires et celles des paramètres ont 'et'e 'ecrits. Sur les simulations effectu'ees pour tester de la convergence et de la qualit'e des ces estimations, nous avons retrouv'e en moyenne des valeurs très proches de

ceux des paramètres inconnus simul'es. Cependant, l'algorithme 'ecrit pour le cas PLS-Mixte avec des effets al'eatoires corr'el'es et h'et'erogènes s'est heurt'e a` des difficult'es de convergence.

Il nous parait n'ecessaire d'attirer l'attention sur les limites de notre travail qui sont multiples. Tout d'abord, la m'ethode APLAT s'appuie essentiellement sur un modèle de simulation de culture. Et a` ce titre, l'efficacit'e de cette m'ethode a` bien g'erer le comportement vari'etal selon les environnements est intrinsèquement li'e a` la capacit'e du modèle de simulation utilis'e a` bien exprimer les interactions G×E.

Ensuite, dans ce travail, il est propos'e de r'eestimer les paramètres des g'enotypes utilis'es dans le cadre d'un modèle de simulation de culture pour pouvoir mieux pr'edire leurs rendements. Or, de tels modèles de simulation disposent g'en'eralement d'un ensemble important de paramètres qui ont 'et'e estim'es seulement pour un t'emoin, au moyen d'exp'erimentations sp'ecifiques. Pour appr'ecier la diff'erence de productivit'e des vari'et'es selon les environnements, il serait n'ecessaire de r'eestimer tous les paramètres pour tout nouveau g'enotype avant l'utilisation de ces modèles. Ce qui peut être complexe et fastidieux. Mais comme tous les paramètres n'agissent pas de la même façon sur la performance des vari'et'es, nous avons propos'e d'en r'eestimer seulement quelques uns. Pour cela, nous avons effectu'e ce tri s'electif par dires d'experts pour gagner du temps et aussi parce qu'en g'en'eral les promoteurs d'un modèle de simulation de culture ont une assez bonne vue du comportement g'en'eral et individuel des paramètres vari'etaux. N'eanmoins, cette prise en compte des connaissances a priori sur les paramètres peut être coupl'ee a` une analyse de sensibilit'e qui permet d'avoir l'impact quantitatif de ces paramètres sur la production des g'enotypes. Une autre voie est d'attacher une loi de probabilit'e aux paramètres, qui permet d'int'egrer les connaissances a priori des experts sur les vari'et'es. Cette m'ethode, non loin de celle que nous avons utilis'e dans le cadre de ce travail, se place dans le cadre bay'esien. Les dires d'experts,

pour chaque paramètre, peuvent ainsi être consid'er'es comme une r'ealisation d'une variable al'eatoire dont on connaàýt la loi a priori. Il s'agira par la suite de prendre comme estimation de chaque paramètre vari'etal l'esp'erance de la loi a posteriori obtenue avec les donn'ees.

Enfin, nous avons utilis'e dans le cadre de cette 'etude des donn'ees d'essais multienvironnements. La courte s'erie de cinq ann'ees de l'essai pluriannuel et le nombre important d'abandons de g'enotypes au cours de cet essai n'autorisent pas de conclure directement quant a` l'efficience de la m'ethode APLAT. A l'essai multilocal, la s'erie 'etait plus longue, 11 lieux, mais ce qui gêne en r'ealit'e au Sahel, c'est moins la variabilit'e climatique entre les lieux que celle d'une ann'ee sur l'autre pour un même lieu. Pour cela, ce qu'il aurait fallu faire si le temps l'avait permis, c''etait de r'ep'eter l'essai multilocal sur deux a` cinq ans tout en diminuant le nombre de lieux. Ce qui est pr'ef'erable a` mener le même nombre d'essais sur plusieurs lieux en une seule ann'ee (Talbot, 1997).

En somme, nous avons propos'e de pr'edire les interactions G×E par lin'earisation d'un modèle de simulation de culture. Dès lors qu'il est possible, pour tout g'enotype, de r'eestimer les paramètres n'ecessaires a` un modèle de simulation de culture, cette m'ethode permet la comparaison de vari'et'es dans des environnements o`u elles n'ont pas 'et'e observ'ees. Bien entendu, pour cela faudrait-il disposer de longues s'eries de donn'ees climatiques pour les lieux. Ces donn'ees climatiques pourront servir alors comme entr'ees d'un modèle de simulation des pluies journalières a` l'exemple du modèle stochastique des chroniques pluviom'etriques d'evelopp'e par Goz'e (1990).

Permettant de mesurer l'impact du changement climatique, cet outil est destin'e en premier lieu aux s'electionneurs du Sahel qui pourront dans des programmes de s'election de courte dur'ee (deux a` cinq ans) r'eduire l'incertitude de la pr'ediction des performances des nouvelles vari'et'es. Adapt'e en outre a` l''echelle de la r'egion et coupl'e a` une m'ethode d'estimation des surfaces

cultivées, il peut être utilisédans le cadre de la prévention des crises alimentaires en Afrique de lOuest, et particulièrement au Sahel. Ainsi, pour chaque année, le rapprochement entre les productions et les besoins prévisionnels peut alimenter le dispositif de veille déjàmis en place par le CILSS avec l'ensemble de ses partenaires techniques dans le cadre de l'alerte précoce, afin de faciliter la prise de décision dans l'élaboration des stratégies alimentaires au Sahel.

R'ef'erences cit'ees

[1] AASTVEIT A.H. et MARTENS H. ANOVA interactions interpreted by partial least squares regression. Biometrics, 1986, 42, 829-844.

[2] AFFHOLDER F. Empirically modelling the interaction between intensification and climatic risk in semi arid regions. Field Crops Research; 1997, 52, 79-93.

[3] AJI S., TAVOLARO S., LANTZ F., FARAJ A. Apport du bootstrap a` la r'egression PLS : application a` la pr'ediction de la qualit'e des gazoles, Oil & Gas Science andTechnology-Rev. IFP, 2003, 58, 599-608.

[4] ANNEROSE D. et DIAGNE M. Caract'erisation de la s'echeresse agronomique en zone semi-aride. Pr'esentation d'un modèle simple d''evaluation appliqu'e au cas de l'arachide cultiv'ee au S'en'egal. Ol'eagineux, 1990, 45, 12, 547-554.

[5] ANNEROSE D. et DIAGNE M. Les modèles de cultures : des outils de la recherche et du d'eveloppement agricole. Arachide Infos, 1994, 5, 5-11.

[6] ANNICCHIARICO, P. Genotype x environment interaction - challenge and opportunities for plant breeding and cultivar recommendations. FAO, Rome, 150 p.

[7] BAKER R.J. Tests for crossover genotype-environmental interactions. Canadian Journal of Plant Science, 1988, 68, 405-410.

[8] BARIL, C.P. Etude de la stabilit'e du rendement chez le bl'e tendre d'hiver.- 170 p. Th : Agronomie : Paris-Sud centre d'Orsay : 1992.

[9] BARON C. Modèle de bilan hydrique et de croissance des plantes cereals: Mil, Sorgho et Arachide. CIRAD, 2002.

[10] BATTERBURY S., WARREN A. The African Sahel 25 years after the great drought : assessing progress and moving towards new agendas and approaches. Global Environmental Change, 2001, 11, 1-8.

[11] BECKER H.C. Correlations among some statistical measures of phenotypic stability. Euphytica, 1981, 30, 835-840.

[12] BECKER H.C. et L'EON J. Stability analysis in plant breeding. Plant Breeding, 1988, 101, 1-23.

[13] BELHASSEN E., THIS D. et MONNEVEUX P. L'adaptation génétique face aux contraintes de sécheresse. Cahiers agricultures, 1995, 4, 251-261.

[14] BRADU D. et GABRIEL K.R. The biplot as a diagnostic tool for models of two-way tables. Technometrics, 1978, 20, 47-68.

[15] BRANCOURT-HULMEL M., BIARNES-DUMOULIN V. et DENIS J.B. Points de repères dans l'analyse de la stabilitéet de l'interaction génotype-milieu en amélioration des plantes. Agronomie, 1997, 17, 219- 246.

[16] CALINSKI T., CZAJKA S. et KACZMAREK, Z. A model for the analysis of a series of experiments repeated at several places over a period of years. I. Theory. Biuletyn Oceny Odmian, 1987, 17/18, 7-33.

[17] CILLS. CSSA, Cadre stratégique de sécuritéalimentaire durable dans une perspective de lutte contre la pauvretéau sahel. CILSS, Ougadougou, 2000, 88 p.

[18] COLSON J., WALLACH D., BOUNIOLS A., DENIS J., JONES J. Mean Squared Error of Yield Prediction by SOYGRO. Agronomy Journal, 1995, 87 , 397-407.

[19] CORNELIUS P.L. Functionc approximating Mandel's tables for the means and standard deviations of the first three roots of a Wishart matrix. Technometrics, 1980, 22, 613-616.

[20] CORNELIUS P.L. Statistical tests and retention of terms in the additive main effects and multiplicative interaction model for cultivar trials. Crop Science, 1993, 33, 1186-1193.

[21] CORNELIUS P.L., SEYEDSADR M.S. et CROSSA J. Using the shifted multiplicative model to search for »separability» in crop cultivar trials. Theoretical and Applied Genetics, 1992, 84, 161-172.

[22] CROSSA J. Statistical analyses of multilocation trials. Advances in agronomy, 1990, 44, 55-85.

[23] CROSSA J., CORNELIUS P.L., SAYRE K. et ORTIZ-MONASTERIO R.J. A shifted multiplicative model fusion method for grouping environments without cultivar rank change. Crop Science, 1995, 35, 54-62.

[24] CROSSA J., CORNELIUS P.L., SEYEDSADR M.S. et BYRNE, P. A shifted multiplicative model cluster analysis for grouping environments without genotypic rank range. Theoretical and Applied Genetics, 1993, 85, 577-586.

[25] de JONG S. SIMPLS : An alternative approach to partial least squares regression. Chemometrics and Intelligent Laboratory Systems, 1993, 18, 251-263.

[26] DEMPSTER A.P., LAIRD N.M. et RUBIN, D.B. Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of the Royal Statistical Society B, 1977, 39, 1-38.

[27] . DENIS J.B. et VINCOURT P. Panorama des méthodes statistiques d'analyse des intéractions génotype x milieu. Agronomie, 1982, 2, 3, 219- 230

[28] DENIS J.B. L'analyse de régression factorielle. Biométrie Praximétrie, 1980, 10, 1-34.

[29] DENIS J.B. Two-way analysis using covariates. Statistics, 1988, 19, 123- 132.

[30] DENIS J.B., PIEPHO H.P. et van EEUWIJK F.A. Modelling expectation and variance for genotype by environment data. Heredity, 1997, 79, 162-171.

[31] DIENG I. Pr'ediction de l'interaction g'enotype x environnement a` partir d'indices vari'etaux de sensibilit'e a` la s'echeresse et de bilan hydrique a` l'aide d'un modèle de r'egression factorielle dans des essais d'arachide au S'en'egal.- 60 p. M'emoire de DEA : Biostatistique : Montpellier II : 2003.

[32] DIENG I.; GOZE E., SABATIER R. Lin'earisation autour d'un t'emoin pour pr'edire la r'eponse des cultures. Comptes Rendus de l'Acad'emie des Sciences Biologies, 2006, 329, 148-155.

[33] DOORENBOS J. et JASSAM A. H. Yield response to water. In Irrigation and drainage Paper 33. FAO, Rome, 1979, pp 193.

[34] EAGLEMAN J.R. An experimentally derived model for actual evapotranspiration. Agricultural meteorology, 1971, 8, 4-3, 385-94.

[35] EBDON J.S. et GAUCH, H.G. Jr. Additive Main Effect and Multiplicative Interaction Analysis of National Turfgrass Performance Trials : I. Interpretation of Genotype x Environment Interaction. Crop Science, 2002a, 42, 489-496.

[36] EBDON J.S. et GAUCH H.G. Jr. Additive Main Effect and Multiplicative Interaction Analysis of National Turfgrass Performance Trials : II. Cultivar Recommendations. Crop Science, 2002b, 42, 497-506.

[37] EBERHART S.A. et RUSSELL W.A. Stability parameters for comparing varieties. Crop Science, 1966, 6, 36-40.

[38] EFRON B. Bootstrap Methods : Another Look at the Jacknife. Annals of statistics, 1979, 7, 1-26.

[39] FAO. IRSIS, Irrigation scheduling information system. FAO, Rome, 1987.

[40] FINLAY K.W. et WILKINSON G.N. The analysis of adaptation in a plant-breeding programme. Australian Journal of Agricultural Research, 1963, 14, 742-754.

[41] FOREST F. et CLOPES A., 1991. Contribution a` l'explication de la variabilitédes rendements d'une culture de ma·ýs plus ou moins intensifiée a` l'aide d'un modèle de bila hydrique amélioré. In Bilan hydrique agricole et sécheresse en Afrique tropicale. France : John Libbey Eurotext, 1991.- pp 3-15.

[42] FOREST F. et CORTIER B. Le diagnostic hydrique des cultures et la prévision du rendement régional du mil cultivédans les pays du CILSS. IRAT/CIRAD/AGRHYMET. IAHS, 1990, 544-557.

[43] FRANQUIN P. et FOREST F. Des programmes pour l'évaluation et l'analyse frequentielle des termes du bilan hydrique. Agronomie Tropicale, Janvier-Mars 1977, XXXII-1, 7-11.

[44] FREEMAN G. H. et PERKINS J. M. Environmental and genotype-environmental components of variability. VIII. Relations between genotypes grown in different environments and measures of these environments. Heredity, 1971, 27, 15-23.

[45] GAUCH H.G. et ZOBEL R.W. 1996. AMMI analysis of yield trials. In Genotype-by-environment interaction. Boca Raton, Floride : M.S. Kang & H.G. Gauch, 1996.- pp 85-122.

[46] GAUCH H.G. et ZOBEL R.W. Predictive and postdictive success of statistical analyses of yield trials. Theoretical and Applied Genetics, 1988, 76, 1-10.

[47] GAUCH H.G. Jr. Statistical Analysis of Yield Trials by AMMI and GGE. Crop Science, 2006, 46 :1488-1500.

[48] GAUCH H.G. Statistical analysis of regional yield trials : AMMI analysis of factorial designs. Amsterdam : Elsevier, 1992.

[49] GAUCH, H.G. Full and reduced models for yield trials. Theoretical and Applied Genetics, 1990, 80, 153-160.

[50] GOLLOB H.F. A statistical model which combines features of factor analytic and analysis of variance techniques. Psychometrika, 1968, 33, 73-115.

[51] GOZE E. Modèle stochastique de la pluviométrie au Sahel - Application a` l'agronomie- Th : UniversitéMontpellier II : 1990.

[52] KEMPTON R.A. The use of biplots in interpreting variety by environment interactions. Journal of Agricultural Science, 1984, 103, 123-135.

[53] LAIRD N. M. Computation of variance components using the EM algorithm. Journal of Statistical Computation and Simulation, 1982, 14, 295-303.

[54] LIN C.S., BINNS M.R. et LEFKOVITCH L.P. Stability Analysis : Where Do We Stand? Crop Science, 1986, 26, 894-900.

[55] MANDEL J. A new analysis of variance model for non-additive data. Technometrics, 1971, 13, 1-18.

[56] MANDEL J. Non-additivity in two-way analysis of variance. Journal of American Statistical Association, 1961, 56, 878-888.

[57] MCCULLOCH C. E. et SEARLE S. R. Generalized, Linear, and Mixed Models. New York: John Wiley & Sons, 2001.

[58] MCLACHLAN G.J. et KRISHNAN T. The EM Algorithm and Extensions. New Jersey : Wiley, 1997.

[59] MENG X.L. et van DYK D.A. Fast EM-type implementations for mixed effects models. Journal of the Royal Statistical Society B, 1998, 60, 559- 578.

[60] MORENO-GONZALEZ J., CROSSA J. et CORNELIUS P.L. Additive Main Effects and Multiplicative Interaction Model : I. Theory on Variance Components for Predicting Cell Means. Crop Science, 2003a, 43, 1967- 1975.

[61] MORENO-GONZALEZ J., CROSSA J. et CORNELIUS P.L. Additive Main Effects and Multiplicative Interaction Model: II. Theory on Shrinkage Factors for Predicting Cell Means. Crop Science, 2003b, 43 :1976- 1982

[62] PERKINS J.M. et JINKS J.L. Environmental and genotype-environmental components of variability. III. Multiple lines and crosses. Heredity, 1968, 23, 339-356.

[63] PIEPHO H.P. Best Linear Unbiased Prediction (BLUP) for regional yield trials : a comparison to additive main effects and multiplicative interaction (AMMI) analysis. Theoretical and Applied Genetics, 1989, 89, 647-654.

[64] PIEPHO H.P. Methods for Comparing the Yield Stability of cropping Systems - A Review. Journal of Agronomy and Crop Science, 1998, 180, 193-213.

[65] PIEPHO H.P., Denis J.B. et van Eeuwijk F.A. Predicting cultivar differences using covariates. Journal of Agricultural, Biological, and Environmental Statistics, 1998, 3, 151-162.

[66] PIEPHO, H.P. Robustness of statistical tests for multiplicative terms in the additive main effects and multiplicative interaction model for cultivar trials. Theoretical and Applied Genetics, 1995, 90, 438-443.

[67] RAMI J. F., DUFOUR P., TROUCHE G., FLIEDEL G., MESTRES C., DAVRIEUX F., BLANCHARD P., et HAMON P. Quantitative trait loci for grain quality, productivity, morphological and agronomical traits in Sorghum (Sorghum bicolor L. Moench). Theorical Applied genetics, 1998, 97, 605-616.

[68] RAO C. R. et KLEFFE J. Estimation of variance components and applications. Amsterdam : North Holland series in statistics and probability, Elsevier, 1988.

[69] SEARLE S. R. Linear models for unbalanced data. New York : John Wiley & Sons, 1987.

[70] SEARLE S. R., CASELLA G. et MCCULLOCH C. E. Variance Components. New York : John Wiley & Sons, 1992.

[71] SEIF E., EVANS J.C. et BALAAM L.N. A multivariate procedure for classifying environments according to their interaction with genotypes. Australian Journal of Agricultural Research, 1979, 30, 1021-1026.

[72] STONE, M. Cross-validatory choice and assessment of statistical predictions. Journal of the Royal Statistical Society B, 1974, 36, 111-147.

[73] TALBOT M. et WHEELWRIGHT A.V. The analysis of genotype x environment interactions by partial least squares regression. Biuletyn Oceny Odmian, 1989, 21/22, 19-25.

[74] . TALBOT M. Resource allocation for selection systems. In : Statistical methods for plant variety evaluation. London : KEMPTON RA, FOX PN, Chapman et Hall, 1997.- pp 162-174.

[75] TENENHAUS M. La Régression PLS : théorie et pratique. Parsi : Tech-nip, 1998.- 254 p.

[76] . THEOBALD C.M., TALBOT M. et NABUGOOMU F. A Bayesian approach to regional and local-area prediction from crop variety trials. Journal of Agricultural, Biological, and Environmental Statistics, 2002, 7, 12-28.

[77] TUCKER C.J., DREGNE H.E., NEWCOMB W.W. Expansion and contraction of the Sahara Desert from 1980 to 1990. Science, 1991, 253, 299-301.

[78] TUKEY J.W. One degree of freedom for non additivity. Biometrics, 1949, 5, 232-242.

[79] TURNER N. C., WRIGHT G. C. et SIDDIQUE K. H. M. Adaptation of grain legumes (pulses) to water-limited environments. Advances in agronomy, 2002, 71, 193-231.

[80] van EEUWIJK F.A. Interpreting genotype-by-environment interaction using redundancy analysis. Theoretical and Applied Genetics, 1992, 85, 89-100.

[81] van EEUWIJK F.A. Linear and bilinear models for the analysis of multi-environment trials. I. An inventory of models. Euphytica, 1995, 84, 1-7.

[82] van EEUWIJK F.A., DENIS J.B. et KANG M.S. 1996. Incorporating additional information on genotypes and environments in models for two-way genotype by environment tables. In Genotype-by-environment interaction. Boca Raton, Floride : M.S. Kang & H.G. Gauch, 1996.- pp 15-49.

[83] VARGAS M., CROSSA J., SAYRE K., REYNOLDS M., RAM`IREZ M.E. et TALBOT M. Interpreting genotype x environment interaction in wheat by partial least squares regression. Crop Science, 1998, 38, 679-689.

[84] VARGAS M., CROSSA J., van EEUWIJK F.A., RAM`IREZ M.E. et SAYRE K. Using partial least squares regression, factorial regression, and AMMI models for interpreting genotype x environment interaction. Crop Science, 1999, 39, 955-967.

[85] WALLACH D., GOFFINET B. Mean Squared Error of Prediction in Models for Studying Ecological and Agronomic Systems. Biometrics, 1987, 43, 561-573.

[86] WILLIAMS E.J. The interpretation of interactions in factorial experiments. Biometrika, 1952, 39, 65-81.

[87] WOLD H. Estimation of principal components and related models by iterative least squares. In Multivariate Analysis. New York : Krishnaiah P.R., Academic Press, 1966, pp 391-420.

[88] WOLD H. Modelling in Complex Situations with Soft Information. Third World Congress of Econometric Society. Toronto, Canada, 1975 August 21-26.

[89] WOLD S., ALBANO C., DUNN W.J., ESBENSEN K., HELLBERG S., JOHANSSON E., SJOSTROM M. Pattern recognition: Finding and

using patterns in Multivariate Data. In : Food Research and Data Analy-
sis. London : Applied Science: Martens H, Russwurm H Jr, 1983 ;147-188.

[90] WOOD J. T. The use of environmental variables in the interpretation of genotype-environment interaction. Heredity, 1976, 37, 1-7.

[91] WU C. F. On the convergence properties of the EM algorithm. The Annals of Statistics, 1983, 11, 95-103.

[92] YAN W. et HUNT W.A. Interpretation of Genotype x Environment Interaction for Winter Wheat Yield in Ontario. Crop Science, 2001, 41, 19-25.

[93] YATES F. et COCHRAN W.G. The analysis of groups of experiments. Journal of Agricultural Science, 1938, 28, 556-580.

[94] ZOBEL R.W., WRIGHT M.J. et GAUCH H.G. Statistical analysis of a yield trial. Agronomy Journal, 1988, 80, 388-393.

Annexe A : Mod`ele de

R'egression factorielle

On dispose de trois matrices : X de dimension I x p est la matrice des co-variables associees au premier facteur (facteur varietepar exemple), Z de dimension J x q est la matrice des covariables associees au deuxieme facteur (facteur lieu) et Y de dimension I x J est la matrice des observations. Les matrices X, Y et Z s'ecrivent ainsi :

x11 ? x21 X= ? ? ? ? ? ... xI1	x12 x22 ... xI2	'' ' ' ' ' '' '	x1p x2p ... xIp )		z11 ? z21 Z= ? ? ? ? ? ... zJ1				z12 z22 ... zJ2	' '' ' ' ' ' ''	z1q z2q ... zJq )
y11 ? y21 Y= ? ? ? ? ? ... yI1				y12 y22 ... yI2		' ' ' ' ' '	' ' '	y1J y2J ... yIJ )

L'idee est d'utiliser les deux matrices de covariables X et Z attachees aux deux facteurs varieteet environnement pour expliquer la matrice Y.

Pour cela, une premiere regression de Y sur X est faite : Y = Xa ^bYX = X(X^/X)^-1X'Y

et RX = Y -

^àYX= (II - X(X^'X)^-1X^')Y

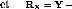
avec II repr'esentant la matrice identit'e d'ordre I et RX la matrice des r'esidus de la r'egression de Y sur X qui est de dimension I × J.

Une deuxième r'egression de àY' X sur Z est faite.

^àY^'_X = Zâ àY'XZ = Z(Z^'Z)-¹Z^{' à}Y^'_X

Ainsi, ^àYXZ = ^àYXZ(Z^'Z)-¹Z^' = X(X^'X)-¹X^'YZ(Z^'Z)-¹Z^'

D'o`u Rà_Yx = ^àYX - ^àYXZ = X(X^'X)-¹X^'Y - X(X^'X)-¹X^'YZ^'(ZZ^')-¹Z Rà_Yx = X(X^'X)^-1X^'Y(IJ - Z^'(ZZ^')^-1Z)

Enfin, une dernière r'egression de RX sur Z est faite.

R^'_X = Zy àR'XZ = Z(Z^'Z)^-1Z^'R^'_X

^àRXZ = RXZ(Z^'Z)^-1Z^' d'o`u ^àRXZ = (IJ - X(X^'X)^-1X^')YZ(Z^'Z)^-1Z^' Ainsi, Y = ^àYXZ + Rà_Yx + _àRXZ + R'esidus,

Posons

^àYXZ = X(X^'X)-¹X^'YZ(Z^'Z)-¹Z^' = XMZ^' (B.1)

RàYx = X(X^'X)-¹X^'Y(IJ - Z(Z^'Z)-¹Z^') = Xâ^' (B.2)

^àYXZ = (IJ - X(X^'X)-¹X^')YZ(Z^'Z)-¹Z^' = áZ^' (B.3)

X et Z peuvent àetre mis sous la forme X = ( 1I X^ÿ ) Z = ( 1J Z^ÿ )

₁' ₁'

avec ./ ) et Z^' = ÿI ) vec X^ÿ se d'eduisant de la matrice X par

X' Z'

centrage des colonnes (de màeme pour ^ÿZ)

! !

1' I 1' I Xÿ

^ÿX^'X = I ( 1I Xÿ ) =

ÿX' _ÿX'1I ÿX' Xÿ

! !

IJ 1'

1 1

IY1J I 1' _IY ^ÿZ( ^{ÿZ' ÿ}Z)-¹ m m' 2

=

J ( ^{ÿX' ÿ}X)-^{1 ÿ}X^'Y1J ( ^{ÿX' ÿ}X)-^{1 ÿ}X^'Y ^ÿZ( ^{ÿZ' ÿ}Z)-¹

1 m1 Mÿ

M=

_!-1

A B = A-1 + FE^-1F^' --FE^-1

Or

B' D --E-1F' E-1

avec E = D -- B^'A^-1B et F = A^-1B

Ici A = I , B = 1'I Xÿ = B^' = ^ÿX^'1I et D = ÿX' Xÿ D'o`u A^-1 = 1I , F = I 1 1' I Xÿ = 0 car X^ÿ centre

et E = ÿX' Xÿ = E^-1 = (^ÿX^' Xÿ) 1.

!-1 1

ÿX'1I ÿX' Xÿ

0

( ^ÿX^{' ÿ}X)

-1

De màeme ( ^ÿZ^'Z)^-1 =

0 ( ^ÿZ^{' ÿ}Z)^-1

1 J 0

D'après l'equation (B.1) M = (X^'X)^-1X^'YZ(Z^'Z)^-1

I 1' I Xÿ 0

Ainsi ( ^ÿX^'X)-¹ = I

=

M=
M=

M= D'o`u

! ! 1 !

1 0 1^' 0

I I Y ( 1J Zÿ ) J

0 ( ^ÿX^' ÿX)-1 ^ÿX^' 0 ( ^ÿZ^{' ÿ}Z)^-1

! 1 !

I 1'

1 _IY 0

( 1J Zÿ ) J

( ^ÿX^{' ÿ}X)^{-1 ÿ}X^'Y 0 ( ^ÿZ^{' ÿ}Z)^-1

I 1'IY1

J I 11'IY Zÿ )

1 0

J

( ^ÿX^{' ÿ}X)^{-1 ÿ}X^'Y1J ( ^ÿX^{' ÿ}X)^-1 ÿX'Y Z^ÿ 0 ( ^ÿZ^{' ÿ}Z)^-1

D'après l'equation (B.2) â^' = (X^'X)^-1X^'Y(IJ -- Z(Z^'Z)^-1Z^')

!

I 1'

( ^ÿX^{' ÿ}X)-¹ ÿX'Y =

1 IY

( ^ÿX^{' ÿ}X)^{-1 ÿ}X^'Y

_1!

0

Z(Z^'Z)^-1 = ( 1J Zÿ ) J = ( 1 J 1J ÿZ( ^ÿZ^{' ÿ}Z)^-1 )

0 ( ^ÿZ^{' ÿ}Z)^-1

!

₁'

Donc Z(Z^'Z)^-1Z^' = ( 1 J 1J ÿZ( ^ÿZ^{' ÿ}Z)^-1 ) J = 1 J 1J1' _J + ÿZ( ^ÿZ^' ÿZ)-1 ÿZ'

ÿZ'

!I11'IY (IJ- 1 J1J1^' _J- ^ÿZ(^ÿZ^'ÿZ)^-1ÿZ^')

D'o`u â^' =

( ^ÿX^{' ÿ}X)^{-1 ÿ}X^'Y

! !

I 1'

1 _IY(IJ- _1J1J1'J - ^ÿZ(^ÿZ^' ÿZ)-1ÿZ') = b'

( ^ÿX^{' ÿ}X)^{-1 ÿ}X^'Y(IJ- _1J1J1'J - ÿZ(ÿZ'ÿZ)-1ÿZ') B'

â' =

D'après l'équation (B.3) á = (II - X(X^'X)^-1X^')YZ(Z^'Z)^-1

X(X^'X)^-1X^' = ( 1I X^ÿ )

!

I 1' 1

I= _I 1 1I1' _I + ÿX( ^ÿX^' ÿX)-1 ÿX' ( ^ÿX^' ÿX)-1 ÿX'

D'o`u a = (II - _1I1I1'I - ÿX(ÿX'ÿX)-1ÿX')( ^1J Y1J Y^ÿZ(^ÿZ^'ÿZ)^-1 )

a = ( (II - _I11I1'I - ^ÿX(^ÿX^'ÿX)-^1ÿX^') _1JY1J (II - _1I1I1'I - ^ÿX(^ÿX^'ÿX)-^{1 ÿ}X^')Y^ÿZ(^ÿZ^{' ÿ}Z)-¹ )
= ( a A )

Ainsi Y = ^àYxZ + RàYX + _àRxZ + R'esidus = XMZ^' + Xâ^' + áZ^' + R'esidus

! ! ^mD'o`uY= ( 1IX) m' 2 J + ( 1I Xÿ ) m1 Mÿ Zÿ B'

! 1' J + ( a A ) Zÿ

!

₁'

Yà = ( 1Im + ^ÿXm1 1Im' ₂ + Xÿ Mÿ ) J + 1Ib^' + ^ÿXB^' + a1' _J + A ÿZ'

ÿZ'

D'o`u

Yà = 1Im1^'_J + ^ÿXm11^' _J+ 1Im' 2 ÿZ' + Xÿ Mÿ ÿZ' + 1Ib^' + ^ÿXB^' + a1^'_J + A ÿZ'

Annexe B : Article au C.R.

Biologie

	C. R. Biologies 329 (2006) 148-155

http://france.elsevier.com/direct/CRASS3/

Biomodélisation / Biological modelling

Linéarisation autour d'un témoin pour prédire la réponse de cultures

Ibnou Dieng ^a,*, Éric Gozé ^b, Robert Sabatier^c

a Centre d'étude régional pour l'amélioration de l'adaptation à la sécheresse, BP 3320, Thiès-Escale, Thiès, Sénégal
b Centre de coopération internationale en recherche agronomique pour le développement, TA 70/09, avenue d'Agropolis,
34398 Montpellier cedex 5, France
c Laboratoire de physique moléculaire et structurale, faculté de pharmacie, 15, avenue Charles-Flahault, 34060 Montpellier, France

Reçu le 18 avril 2005; accepté le 17 janvier 2006
Disponible sur Internet le 9 février 2006
Présenté par Michel Thellier

Résumé

Une nouvelle méthode pour modéliser les interactions génotype x environnement : APLAT. Le rendement de génotypes prédit par un modèle de simulation de cultures est développé en série de Taylor à l'ordre 1 au voisinage du vecteur de paramètres d'un génotype de référence. À l'aide de cette linéarisation locale, l'estimation des paramètres de ces génotypes se fait par régression linéaire des rendements observés sur la sensibilité des sorties du modèle de simulation de cultures par rapport aux paramètres. Pour citer cet article :I. Dieng et al., C. R. Biologies 329 (2006).

(c) 2006 Académie des sciences. Publié par Elsevier SAS. Tous droits réservés.

Abstract

Prediction of crop response by linearisation about control approximation. A new method for modelling genotype x environment interaction: APLAT. The yield predicted by a crop-simulation model is developed as a Taylor series in the neighbourhood of a parameter vector of a control genotype. With this local linearisation, these genotype parameters can be estimated by a linear regression of the observed yield on the derivatives of the crop-simulation model predictions with respect to its parameters. To cite this article: I. Dieng et al., C. R. Biologies 329 (2006).

(c) 2006 Académie des sciences. Publié par Elsevier SAS. Tous droits réservés.

Mots-clés: Linéarisation; Prédiction de la réponse de cultures ; Témoin; Interaction genotype x environnement Keywords: Linearization; Predict responses culture; Control; Genotype x environment interaction

Abridged English version

In Sahel, genotype x environment interactions are often large: this is the justification behind multilocation

* Auteur correspondant.

Adresses e-mail: [e-mail],

[e-mail] (I. Dieng), [e-mail] (É. Gozé), [e-mail] (R. Sabatier).

and pluriannual trials. Because of these sizeable environment effects and interactions, the prediction of an expected yield with a linear mixed model is generally imprecise.

Improving this prediction can be achieved by modelling the environment effect. It is then partly shifted from the random part to the fixed part of a mixed model, by the use of a crop-simulation model like DHC, IRSIS, SarraH... This could not be possible with the empirical

genotype × environment interactions analysis methods like AMMI and joint regression, which do not make use of environmental variables. The factorial regression method does make use of environmental variables; however, it requires their effect on the production to be linear, which might not be the case.

Unfortunately, most crop-simulation models bear a number of parameters, the estimation of which requires a specific and costly experiment. As a consequence, these parameters are usually known, but for a small set of reference genotypes. It would not be sensible to invest in a parameter estimation experiment for every new genotype that is proposed for selection.

To overcome this problem, one can notice that multisite experiments usually share a control variety for which parameters have already been estimated. In this paper, we propose to develop as a Taylor series the modelled response about the parameters of this control genotype. The other genotypes' parameters can then be estimated by a linear regression of the observed yields on the sensitivity to parameters, i.e., on the derivatives of the response with respect to the parameters. With this estimation, one can predict the new genotype responses in environments where they have not been tested. In a given location, this estimation can benefit from the available historic climatic records to estimate a distribution of probable yields.

Let f (Zj,èi) denote the yield of a genotype i predicted by a crop simulation in an environment j and Yij the observed yield. We can write:

Yij = f (Zj ,èi) + îj + uij

where Zj is the vector of the jth environment regressors and èi the P -vector of the ith genotype parameters. The bias îj is that of the crop-simulation model. We suppose that it depends only on environment and is the same for all genotypes in a same environment. The error term uij is supposed random with expectation 0 and variance ó²_u.

Let us consider a control genotype, i.e., whose parameters are known or at least already estimated. Let è0 be the vector of parameters of this control genotype and let us suppose that f is a C¹ class function in a neighbourhood of è0 and f' derivable in this neighbourhood. Moreover, let us suppose èi in the neighbourhood of è0. Then, a Taylor series expansion yields:

f (Zj,èi) = f(Zj,è0) + P_₁ aè(p) è=è0,Z=Zj

EP [ ?f

× (èi (p) - è₀^p))+ ?[(èi - è0)'(è - è0)]

with èi (p) the pth component of the parameters vector

of the ith genotype, è(p)

0 that of the control genotype.

(p) ?

Let X_j = [ ? ^fo(p) |è=è0,Z=Zj ] and âi (p) = èi (p) - è₀^(p)

for p = 1, . . . , P. As f is not known in closed form, one
has to estimate its derivatives by numerical approxima-
tion. The function X^(p) _jis a function of environment j,

while â(p)

i is a function of genotype i. Then, the local

linearization yields:

Yij - Y0j = _~P

p=1

_X(p)

j ·âi ^(p) + ~ij

where _Y0j is the control response in the environment j and eij = uij - u0j. So, E(eij) = 0, V(eij) = 2ó²_u, Cov(eij , ~i~j~) = 0, but Cov(eij, ei^,j) = ó²_u.

This equation can be put in the form of a linear model with correlated errors:

Y - (Y0 ? 1I) = X · â + e

In this equation, Y is the vector of responses of the I genotypes in the J environments, Y'₀ = (Y01 · · · Y0J), 1I is unit vector of size I × 1. The symbol ? indicates the Kronecker product and E is a random error vector. Its covariance matrix is ó²_u? where:

	? ? ? ? ? ? ?	ù1	...
? =		0

and

?

?

0 ? ?

ùj ? ?

..?

.

ùJ

1

2

?

?

ùj = (2₁ . . .

The number of columns of the square matrices ? and ùj are respectively the number of observations for all the environments and the number of observations for environment j.

Also, X = [ X⁽¹⁾ ? II · · · X^(P) ? II ] where X(p)' = [X^(p)

1 ··· X(p)

J ] is a J × 1 vector and II is the I × I unit matrix. The dimension of X is then IJ × PI.

inally, )= [â⁽¹⁾' · · · â⁽"] where â(p), = [ â ^Pit

1

We call this method APLAT for Approximation Par Linéarisation Autour d'un Témoin.

Because of the large number of columns of X, some dimension reduction method like Partial Least Squares regression is necessary. The dimension of the space spanned by the regressors is then reduced from rank of X to k. The PLS regression is usually carried out

with the NIPALS (Nonlinear estimation by Iterative Partial Least Squares) algorithm, where the calculation of the components is performed simultaneously with a set of regressions by ordinary least squares. Here, the error covariance matrix is ó²_u?, not _ó2uIIJ, generalized least squares should be used instead. As ? is symmetric and positive semi-definite, a work around consists in factorizing its inverse, finding a matrix ç such that ç~ç = ?-1.

Then, estimating â by PLS with regressions by generalized least squares is equivalent to consider the model:

çY - ç(Y0 ? 1I) = çX · â + çE

where âPLS is the estimation with regressions made by ordinary least squares.

The number of components is chosen to minimize
the PRESS (Prediction Error Sum of Squares) criterion.
To calculate the confidence interval of the coeffi-

cients, we used a bootstrap technique. Let z(p)~b

i,PLS be the

random variable defined by:

(p)*b

zi, PLS =

_â(p)~b

i,PLS -â(p)

i,PLS

s^*(

_â(p)~b i,PLS)

where

â⁽p⁾

i,PLS is the (p · i)th element of âPLS,â^(p)~b

i,PLS

is obtained at the bth draw with b = 1, . . . , B and

s( àâ(p)~b

i,PLS) is the standard error of â~b PLS. Let ^~FB be

the empirical distribution function of z(p)~b

i,PLS. The frac-

tile FB ¹(á) is estimated by àt(á) such that #{z^(p)~b

i,PLS

~ àt(á)} = áB.

A percentile-t confidence interval for the (p · i)th element of â is in the following form:

~ â(p)

i,PLS -sOilitS ) · àt(1 - á), sOilltS) · àt(á)]

To evaluate the quality of the new model, we compared its MSEP (Mean Squared Error of Prediction) with that of the average model defined for our data as follows:

Yij = m + gi + Ej + äij

where m is the population mean and gi the genotype effect. The term Ej is the year effect and it is assumed random with expectation 0 and variance ó²_E. Errors äij are distributed independently with expectation 0 and variance ó²_ä . The terms Ej and _äij are assumed to be mutually independent.

The data set consists of plant yields of 26 groundnut genotypes. The experiments have been carried out at Bambey (14^?42N and 16^?28W) in Senegal, over a period of five years from 1994 to 1998. The data of each year were kept in turn as a test sample. Yields are expressed in kilograms of pods per hectare.

We used SarraH, a crop simulation model developed by CIRAD in collaboration with CERAAS, to calculate X. Taking into account the available number of data, we estimated two of its varietal parameters.

The PRESS is minimal with six components for models adjusted without the data of 1994, 1995 and 1997. For each of the others, the PRESS is minimal with nine components. However, we decided to keep only five components, as the PRESS was not very different from its minimum value.

The APLAT MSEPs are lower than the average model MSEP, except for prediction of 1998 data. Then the prediction of yield for these models by APLAT was better than that made with the average model four times out of five.

With the APLAT method, the prediction of a genotype in a new environment comes at a relatively low price, using mostly available data, except for the environmental data, which has to be recorded for every site of the experiment, according to the crop-simulation model needs. This method seems promising, but requires additional studies with more numerous data.

1. Introduction

Au Sahel, les interactions genotype × environnement constatées lors des essais multilocaux et pluriannuels sont généralement importantes. Sur les réponses moyennes par variété et par environnement, le modèle linéaire généralement adopté s'écrit :

Yij = m + gi + Ej + (gE)ij + eij (1)

où _Yij est la réponse du génotype i de l'environnement j, m la moyenne générale et gi l'effet fixe du génotype i. L'effet Ej de l'environnement j et l'interaction (gE)ij peuvent être fixes ou aléatoires. Pour l'objectif de prédiction des réponses de génotypes dans l'ensemble des environnements potentiels auxquels ils sont destinés, l'optique aléatoire est plus pertinente. Ainsi, supposons ces deux effets et le terme d'erreur eij aléatoires, iid et indépendants les uns des autres avec E(Ej) = E[(gE)ij] = E(eij) = 0 et V(Ej) = ó² _E, V[(gE)ij] = ó2gE et V(eij) = ó²_e où E(·) et V(·) désignent l'espérance et la variance.

Choisir un génotype i dans un environnement j suppose d'estimer l'espérance de sa performance dans j. La précision de cette estimation est fonction de ó2E, ó2gE et de ó²_e . Dans cette zone du Sahel, l'environnement est variable, c'est-à-dire que ó²_E et ó²_gE sont grands, ce qui

dégrade cette précision. Pour l'améliorer, une solution est de modéliser les variations de _Yij en fonction de l'environnement par l'utilisation de modèles de simulation de cultures tels que DHC [1], IRSIS [2], SarraH [3], etc. De ce fait, une partie de l'effet aléatoire de l'environnement est reportée dans la partie fixe du modèle. Cette approche n'est pas possible avec les modèles classiques de l'interaction génotype × environnement. En effet, la méthode AMMI, Additive Main effects and Multiplicative Interactions [4] ainsi que la régression conjointe [5,6] ne tiennent pas compte des nouveaux environnements pour y prédire les réponses des génotypes. La régression factorielle [4,5] en tient compte, mais suppose que l'action des variables des environnements sur la production est linéaire, ce qui n'est pas certain.

Cependant, les paramètres des modèles de simulation de cultures ne sont pour la plupart connus que pour un petit nombre de génotypes, car leur évaluation demande une expérimentation spécifique et des mesures coûteuses.

L'objectif de cette étude se pose alors en ces termes : comment prédire le comportement de génotypes dans de nouveaux environnements en tenant compte de ces derniers, sans coût excessif ?

2. Le modèle proposé

Si nous partons du modèle de simulation de cultures, chacune des sorties de ce modèle, le rendement potentiel par exemple, peut s'interpréter comme la réponse d'un génotype i dans un environnement j :

Yij = f (Zj,èi) + îj + uij (2)

où Zj est le vecteur des variables telles que la pluie, la température, etc., mesurées sur l'environnement j et èi le vecteur de longueur P des paramètres du génotype i. L'erreur îj est le biais du modèle de simulation de cultures ; nous supposons qu'elle ne dépend que de l'environnement j : elle est donc la même pour tous les génotypes d'un même environnement. Le terme uij est pris aléatoire, avec E(uij) = 0 et V(uij) = ó2 u .

Comme on l'a dit précédemment, les paramètres des modèles de simulation de cultures ne sont généralement connus que pour un petit nombre de génotypes. Considérons un modèle de simulation de cultures et un génotype de référence dont les paramètres sont connus et appelons è0 le vecteur de ses paramètres. Alors, supposons f de classe C¹ dans un voisinage de è0 et f' dérivable sur ce voisinage. De plus supposons èi au voisinage de è0. En pratique, les génotypes dont nous chercherons à estimer leurs paramètres seront choisis de telle sorte qu'ils ne soient pas trop éloignés du génotype de référence. Alors, un développement en série de Taylor à l'ordre 1 nous donne :

f (Zj,èi) = f (Zj,è0) +

~P ~?f ~

?è⁽p⁾)

p=1 è=è0,Z=Zji

× (èi (p) - è(p)

0 ) + ?[(èi - è0)'(èi - è0)]

(³)

(p

avec èi ^(p) et è0 ) la p^e composante du vecteur de paramètres respectivement du génotype i et du génotype de référence.

Posons X^(p) _j=

[ ?f

?è(p) ]è=è0,Z=Zj : c'est une fonction de l'environnement j et â(p)

i = è^(p) i- è(p)

0 une fonc-

tion du génotype i. La fonction X(p)

j est la dérivée partielle de la sortie du modèle de simulation de cultures pour l'environnement j par rapport à la p^e composante du vecteur de paramètres de la variété de référence. Comme la fonction f n'est pas généralement connue analytiquement, ces sensibilités peuvent être obtenues par une méthode de dérivation numérique. Nous avons retenu tout simplement :

X(p) = L?è(p) jè=è0,Z=Zj
~f (è(p)

0 + h_è(p)

₀ ) - f (è^(p)

0 - h_è(p)

₀ ) ~

~

2hè(p) Z=Zj

0

(p

avec hè0 (p) très petit, de l'ordre de è0 ) × 10-⁴ en pra-

tique. D'autres méthodes existent, celle-ci étant la plus simple et économe en calculs.

Avec ces notations et d'après l'Éq. (2), qui permet d'écrire f (Zj,è0) = Y0j - îj - u0j, nous pouvons écrire, en négligeant ?[(èi - è0)'(èi - è0)] :

Yij - Y0j = _~P

p=1

X(p) j · â(p)

i + ^~ij (4)

oùfi eiji = uiji --- u0j.. Ainsi, E(eij)) = 0, V(eij)) = 2ó²_u,, Cov(eij ,, Eijj~) == 0, mais Cov(eij , ~i~j)) = ó²_u..

Si nous disposons de I génotypess et de J environnements, nous pouvons poser le modèle suivant :

Y - (Y0 ? 1I) = X · â + ee (⁵)

Le vecteur Y représente le rendement de tous les génotypess dans tous les environnements ; ilt est de longueur IJ,, Y'₀ = (Y01l ·
· ·
· ·
· Y0J)) et 1I/ est un vecteur formé de 1, de longueur I. Le symbol ? désigne le produit de Kronecker. Le vecteur E est un vecteur d'erreurr aléa-

toire. Sa matrice de covariance est de la forme ó²_u?, avec :

	? ? ? ? ? ? ?	ù1	..
? =		0

où

?

?

. 0 ? ?

ùj ? ?

..?

.

ùJ

2 1

ù j = ( ..?

.

1 2

Les matrices ? et ùj sont carrées de nombre de lignes, respectivement le nombre d'observations de tous les environnements et le nombre d'observations de l'environnement j.

Ensuite, X = [X⁽¹⁾ ? II · · · X^(P) ? II ] où X(p)' = [ X^(p) ₁· · · X(J ^p) ] est de longueur J et II est la matrice identité d'ordre I. La matrice X est donc de dimension IJ × PI.

Enfin, â^~ = [ â(1)~ · · · _â(P )~ ] avec â(p)~ =

[ â(p)

1 · · · â(p)

I ].

Nous proposons d'appeler cette méthode par l'acronyme APLAT : Approximation Par Linéarisation Au-tour d'un Témoin. Elle consiste à approcher, localement, le rendement prédit par un modèle de simulation de cultures, par série de Taylor à l'ordre 1 au voisinage du vecteur de paramètres d'un génotype de référence. Cette linéarisation permet, par régression linéaire, l'estimation des paramètres de ces génotypes. Par la suite, la prédiction de l'écart entre le rendement de ces génotypes et celui du génotype de référence dans des environnements nouveaux, c'est-à-dire où ils ne sont pas encore testés, pourra se faire si le climat de ces derniers est connu.

3. Estimation des paramètres et validation du modèle

Il y a en général beaucoup de paramètres dans un modèle de simulation de cultures et peu d'environnements dans un essai multienvironnement, ce qui rend souvent PI grand par rapport à IJ. Pour notre exemple, nous avons utilisé SarraH comme modèle de simulation de cultures. Ce modèle dispose de 61 paramètres, qui sont fonction du génotype. Avec un tel nombre de prédicteurs, l'estimation de â s'est faite par régression PLS, Partial Least Squares [7]. Il s'agit donc pour nous d'écrire un modèle linéaire de prédiction des rendements des génotypes pour de nouveaux environnements par les sensibilités par rapport aux paramètres des génotypes des sorties d'un modèle de simulation de cultures, fondé sur la construction de composantes orthogonales dans l'image de X. Ceci permet de réduire l'espace des régresseurs de rang de X à k dimensions. La régression PLS s'effectue selon le principe de l'algorithme NI-PALS, Nonlinear estimation by Iterative Partial Least Squares [7], où un ensemble de régressions partielles par moindres carrés ordinaires est effectué, en même temps que le calcul des composantes. Ici, la matrice de covariance de E est égale à ó²_u? et non à ó²_uIIJ . La solution serait d'effectuer toutes les régressions partielles par moindres carrés généralisés. Mais cette matrice de covariance est inconnue. Elle s'écrit tout de même, à une constante multiplicative près, en fonction de ?, qui elle est connue. La matrice ? étant symétrique et semi-définie positive, par décomposition de Cholesky, il existe une matrice ç tel que ç^~ç = ?^-1.

Ainsi, estimer â par PLS avec les régressions partielles par moindres carrés généralisés consiste à poser le modèle suivant :

çY - ç(Y0 ? 1I) = çX · â + çe (6)

où âPLS est l'estimation avec les régressions partielles effectuées par moindres carrés ordinaires.

Dans ce cas, la variance de l'erreur çc s'écrit :

E(ç~E^~ç^~) = çE(ce)ç' = ó²_uç?ç' = ó²_uç(ç'ç)^-1ç^~

2

= ó_uçç

-1(çr)-1ç/ = ó2uIIJ

Le nombre de composantes à retenir est déterminé par le PRESS, Prediction Error Sum of Squares [7].

Nous avons calculé les intervalles de confiance des coefficients estimés par la méthode bootstrap [8]. Cette technique permet d'estimer la loi inconnue d'un estimateur par une loi empirique obtenue à partir d'une procédure de rééchantillonnage fondée sur des tirages aléatoires avec remise des données. Les intervalles de confiance construits sont de type percentile-t [9]. Soit

(p)*b

zi,PLS la variable aléatoire définie par :

(p)*b zi,PLS =

(⁷)

_â(p)~b

i,PLS - â⁽p⁾

i,PLS

s^*(

_â(p)~b i,PLS)

où âi(,pPlS est le (p · i)^e élément de âPLS^, âi(,PL p)*S obtenu

au b^e tirage avec b = 1, . . . , B et s( â(p)~b

i,PLS) l'écart-type

estimé de â~bPLS. Soit 'FB la fonction de répartition empi-

rique des z(p)~b

i,PLS. Le fractile d'ordre á, %¹ (á) est estimé

par la valeur àt(á) telle que :

1
B

_~B
b=1

(p)*b_à= á {zi,PLS t(á)}

Donc un intervalle de confiance percentile-t pour le (p.i)^e élément de â peut s'écrire :

[ â(p)

i,PLS - s~ â(p) ~ · àt(1 - á), â⁽p⁾

i,PLS - s( â(p) ) · àt(á)]

i,PLS i,PLS

(8)

L'évaluation de la qualité du modèle proposé est faite avec l'erreur quadratique moyenne de prédiction MSEP, Mean Squared Error of Prediction [10]. La MSEP est utilisée comme critère pour comparer différents modèles dont le modèle moyen [11], défini pour nos donnés par:

Yij = m + gi + Ej + äij (9)

où m est la moyenne de la population et gi l'effet génotype. L'effet Ej de l'environnement j est supposé aléatoire, d'espérance nulle et de variance ó² _E. Les erreurs _äij sont indépendantes, d'espérance nulle et de variance ó2 ä . De plus, Ej et _äij sont supposés indépendants.

Le logiciel R [12] a été utilisé la fonction qui a servi pour les régression est de J.-F. Durand [13].

4. Les données utiisées

Nous avons des résultats d'essais agronomiques d'arachide menés de 1994 à 1998 sur la station expérimentale du Ceraas, située à Bambey (14^?42N et 16^?28O), au Sénégal. Ces essais pluriannuels ont concerné au total 26 génotypes à cycle de développement de 90 jours et répondaient à l'objectif de recherche de génotypes physiologiquement adaptés à la sécheresse.

La variété de référence choisie est la 55-437, c'est une variété hâtive de 90 jours; elle a donc une longueur de cycle proche de celle des autres variétés utilisées. Elle a été choisie parce que ses données étaient disponibles.

Dans ce milieu à forte variabilité des pluies dans l'espace et même dans le temps pour un même lieu, nous avons considéré chacune des cinq années d'expérimentation comme un environnement (Fig. 1).

Pour valider notre modèle, nous avons réservé successivement chacune des années et estimé les paramètres des génotypes sur les années restantes. Pour chaque année, les rendements observés ont été comparés à ceux prédits par la méthode APLAT. Les rendements sont exprimés en kilogrammes de gousses par hectare.

SarraH a été utilisé pour calculer X. Compte tenu du nombre de données disponibles, seuls deux paramètres (P = 2) ont été considérés parmi les 61 de SarraH. Le premier paramètre est en fait un coefficient multiplicateur qui agit sur cinq paramètres de SarraH : coefficient

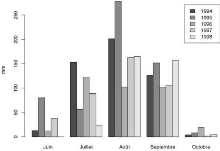
Fig. 1. Répartition des pluies sur la station de Bambey, au Sénégal, de 1994 à 1998.

moyen d'angle des feuilles, coefficient de conversion en assimilat, coefficient d'efficience d'assimilation des feuilles à la phase végétative juvénile, coefficient d'efficience d'assimilation des feuilles à la première phase de maturation, phase sensible de remplissage des grains et coefficient d'efficience d'assimilation des feuilles à la deuxième phase de maturation, phase non sensible. Le deuxième paramètre est le poids moyen des gousses.

5. Résultats

Au Sahel, l'interaction G×E est largement due aux aléas climatiques, dont la probabilité peut être estimée à l'aide de longues chroniques de relevés météo au sol. Cependant, relier l'interaction G×E et la pluviométrie à l'aide d'un modèle de simulation de cultures n'est habituellement possible que pour des variétés dont on a estimé les paramètres, au prix d'une expérimentation spécifique. Le modèle APLAT permet de prédire cette interaction avec les seules données d'une expérimentation multilocale classique, sans autre instrumentation que des stations météo simples.

Pour les modèles sans les données respectivement de 1994, 1995 et 1997, le PRESS minimal est atteint avec six composantes. Pour les deux autres modèles, le PRESS est minimal avec neuf composantes, mais nous avons réduit leur espace à cinq dimensions, car le PRESS n'y est pas trop différent de ses valeurs mini-males (Fig. 2).

Les coefficients des régressions PLS et les intervalles de confiance qui leur sont associés sont représentés sur la Fig. 3.

Les MSEP estimées pour les modèles APLAT, sauf celle sans les données de l'année 1998, sont inférieures aux MSEP des modèles moyens correspondants (Tableau 1). Ce qui signifie que, pour ces modèles, pré-

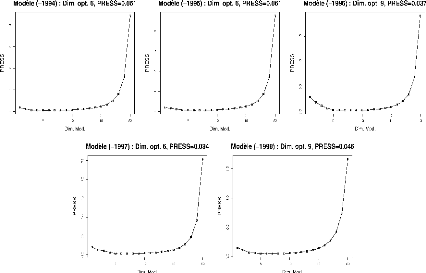
Fig. 2. Evolution du PRESS en fonction du nombre de composantes. Le modèle (-1994) utilise les données, sauf celles de l'année 1994, et ainsi de suite.

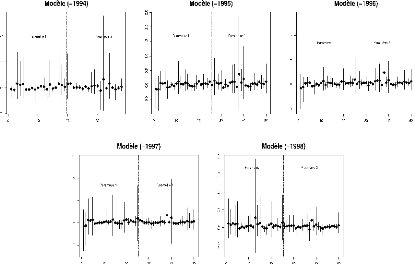
Fig. 3. Intervalle de confiance percentile-t à 95 % des coefficients estimés. Le modèle (-1994) utilise les données, sauf celles de l'année 1994, et ainsi de suite. Sur l'axe des abscisses figurent les génotypes par ordre alphabétique pour chacun des deux paramètres. Le symbole représente l'estimation des coefficients.

Tableau 1

MSEP des différents modèles APLAT et modèles moyens correspon-
dants. Le modèle (-1994) utilise les données, sauf celles de l'année

1994, et ainsi de suite
	APLAT	Modèle moyen
Modèle (-1994)	24687,3	64651,6
Modèle (-1995)	5915,0	7160,6
Modèle (-1996)	35446,1	37814,8
Modèle (-1997)	10038,3	18201,1
Modèle (-1998)	118304,9	84963,6

dire le rendement par la méthode APLAT est meilleur que par la moyenne des rendements du passé. Ainsi, quatre fois sur cinq, la méthode APLAT s'est révélée meilleure que le modèle moyen. Toutefois, cette étude souffre de la faible taille de notre échantillon.

6. Conclusion

La méthode APLAT peut être vue comme un outil d'aide à la décision pour la sélection au Sahel. Dans l'exemple où un sélectionneur doit tester plusieurs génotypes dans un nouvel environnement, cette méthode lui permettra d'écarter d'emblée certains génotypes qui donneront une production faible, en lieu et place d'essais multilocaux ou pluriannuels dans ces environnements contrastés ou d'une tentative de paramétrisation d'un modèle de simulation de cultures qui implique un coût élevé. Son attention sera portée par la suite sur l'ensemble restreint des génotypes retenus avec APLAT, où il pourra appliquer les schémas classiques de sélection.

Cette nouvelle approche semble prometteuse, mais il faut des études supplémentaires. Notamment disposer de données agronomiques plus conséquentes pour l'éprouver.

Remerciements

Nous remercions Danièle Clavel pour les données de l'étude et Jean-Claude Combres pour toutes les discussions autour du modèle SarraH.

Références

[1] AGRHYMET, Bulletins décadaires et mensuels de suivi de la campagne agricole pluviale, Niamey, 1991.

[2] FAO, IRSIS, Irrigation scheduling information system, Rome, 1987.

[3] C. Baron, Modèle de bilan hydrique et de croissance des plantes céréales : Mil Sorgho et Arachide, Cirad, 2002.

[4] M. Vargas, J. Crossa, F.v. Eeuwijk, K.D. Sayre, M.P. Reynolds, Interpreting treatment × environment interaction in agronomy trials, Agron. J. 93 (2001) 949-960.

[5] J.-B. Denis, P. Vincourt, Panorama des méthodes statistiques d'analyse des interactions génotype × milieu, Agronomie 2 (1982) 219-230.

[6] S.A. Eberhart, W.A. Russel, Stability parameters for comparing varieties, Crop Sci. 6 (1966) 36-40.

[7] M. Tenenhaus, La Régression PLS : théorie et pratique, Technip, Paris, 1998.

[8] B. Efron, Bootstrap methods: another look at the jackknife, Ann. Stat. 7 (1979) 1-26.

[9] S. Aji, S. Tavolaro, F. Lantz, A. Faraj, Apport du bootstrap à la régression PLS : application à la prédiction de la qualité des gazoles, Oil Gas Sci. Technol.-Rev. IFP 58 (2003) 599-608.

[10] D. Wallach, B. Goffinet, Mean squared error of prediction in models for studying ecological and agronomic systems, Biometrics 43 (1987) 561-573.

[11] J. Colson, D. Wallach, A. Bouniols, J. Denis, J. Jones, Mean squared error of yield prediction by SOYGRO, Agron. J. 87 (1995) 397-407.

[12] R Development Core Team, R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria, ISBN 3-900051-07-0, 2004, URL http://www.R-project.org.

[13] J.-F. Durand, Calcul matriciel et analyse factorielle des données, université Montpellier-2, Montpellier, France, 2002.