Analyse de l'accès à l'éducation à Kinshasa

Tree description

Number of nodes	25
Number of leaves	13

Decision tree

· cmage < 44,5000 then m13b_ens = Primaire (73,43 % of 399 examples)

· cmage >= 44,5000

o cmage < 52,5000

§ e5_tele < 0,5000

§ depjour$ < 9,2750 then m13b_ens = Primaire (64,93 % of 134 examples)

§ depjour$ >= 9,2750 then m13b_ens = Secondaire (100,00 % of 5 examples)

§ e5_tele >= 0,5000

§ q17_tmen < 4,5000 then m13b_ens = Secondaire (75,00 % of 8 examples)

§ q17_tmen >= 4,5000

§ q17_tmen < 15,5000

§ m15_tec in [Privé,Public conventionné,,]

§ h5_stocu in [Propriétaire,Locataire,Location vente,Logé gratuitement par un tiers,Autre]

§ m8b_reli in [Protestant,Sans religion,Autre chrétien,Autre réligion,Musulman,Kimbanguiste,Animiste] then m13b_ens = Secondaire (53,57 % of 25 examples)

§ m8b_reli in [Catholique] then m13b_ens = Primaire (60,29 % of 68 examples)

§ h5_stocu in [Logé par l'employeur,Logé concession familiale] then m13b_ens = Primaire (86,67 % of 13 examples)

§ m15_tec in [Public non conventionné]

§ cmeduc in [Universitaire,Primaire,Programme non formel,9] then m13b_ens = Secondaire (60,53 % of 32 examples)

§ cmeduc in [Secondaire] then m13b_ens = Primaire (58,82 % of 34 examples)

§ q17_tmen >= 15,5000 then m13b_ens = Primaire (100,00 % of 4 examples)

o cmage >= 52,5000

§ depjour$ < 4,2800

§ e5_tele < 0,5000 then m13b_ens = Primaire (58,72 % of 109 examples)

§ e5_tele >= 0,5000 then m13b_ens = Secondaire (62,82 % of 78 examples)

§ depjour$ >= 4,2800 then m13b_ens = Secondaire (60,14 % of 276 examples)

Computationtime:125ms.
Created at 12/01/2008 17:49:45

a) Matrice de confusion :

C'est un tableau de contingence confrontant les classes obtenues (colonnes) et les classes désirées (lignes) pour l'échantillon. Sur la diagonale principale on trouve donc les valeurs bien classées, hors diagonale les éléments mal classés ; la somme des valeurs sur une ligne donne le nombre d'exemplaires théoriques de la catégorie. Si les classes sont indépendantes, la position de l'erreur n'a aucune signification, si par contre les classes ne sont pas indépendantes, on peut définir une sorte de gradation dans les erreurs. Notre échantillon compte 1911 observations reparties entre les quatre classes. Cette répartition peut être équitable ; ce qui n'est pas une nécessité pour la bonne interprétation.

De la matrice de confusion en annexes ressortent trois indicateurs qu'on définit comme suit :

· Le taux d'erreur global en resubstitution : c'est le ratio entre le nombre d'observations bien classés par rapport par rapport au nombre d'observation de l'échantillon ; Si on considère notre matrice de confusion en annexes, on calcule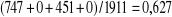. On dira donc que le taux de reconnaissance est d'environ 63%.. Ce qui veut dire que le taux le taux d'erreur est de 37%.

· Le taux d'erreur à priori : c'est le taux d'erreur pour chaque catégorie d'observation ; si on considère chaque classe individuellement, on fait 24% d'erreur pour reconnaître la catégorie « primaire », 45% d'erreur pour reconnaître la catégorie « secondaire ». les autres catégories n'étant pas reconnues.

· Le taux d'erreur à posteriori : c'est le taux de mauvaises classifications par rapport aux bonnes classifications pour une classe donnée. Si on considère le système du point de vue des réponses fournies, lorsqu'on déclare qu'une observation appartient à la catégorie « primaire » on se trompe 387 fois sur 1134 (soit 0,3413), il y a 0,4% de chance que ce soit une observation de la catégorie « programme non formel », 32,5% de chances que ce soit une observation de la catégorie « secondaire » et enfin 0,9% de chance que ce soit une observation de la catégorie « universitaire ». en d'autres termes on dira, le taux de fiabilité pour la catégorie « primaire » est de 65,5%. Par le même type de raisonnement, on trouve les taux de fiabilité des autres catégories. Pour la catégorie « secondaire », on se trompe 326 fois sur 777 (soit 0,4196), il y a 31% de chances que ce soit un élément de « primaire », 0,7% de chance que ce soit un élément de la catégorie « programme non formel », et enfin 10% de chances que ce soit de la catégorie « universitaire ». En d'autres termes, le taux de fiabilité pour la classe « secondaire » est de 58,3%. On ne se trompe pas pour les catégories « programme non formel » et « universitaire ».

b) Détermination de la taille de l'arbre :

L'algorithme utilisé par la méthode CART divise les données en deux échantillons; les informations de ces échantillons se trouvent dans la zone DATA PARTITION de l'arbre en annexes.

· Le premier échantillon, dit d'expansion (growing set) avec 1280 observations, permet de construire l'arbre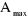. l'objectif est de produire des feuilles aussi pures que possible. Cet arbre minimise RE sur l'échantillon d'expansion. Bien entendu, il ne faut certainement pas utiliser cet arbre pour la prédiction, il est trop spécialisé, il colle exagérément aux données d'expansion, ingérant des informations spécifiques à ce fichier  d'expansion;

· Le deuxième échantillon, dit d'élagage (pruning set) avec 631 observations, sert à réduire l'arbre. l'algorithme réduit peu à peu l'arbre initial et à chaque étape, évalue les performances des sous arbres candidats sur le fichier d'élagage. Nous pouvons ainsi déterminer l'arbre optimal sur cet échantillon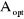. Ici également, l'arbre optimal n'est pas le modèle définitif.

L'arbre sélectionné, est celui que nous allons utiliser pour la prédiction. Le principe est la préférence à la simplicité (parcimonie).

Breiman et al. (1984) proposent de calculer l'écart type SE de 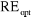correspondant à l'arbre optimal, puis de choisir l'arbre le plus simple dont la réduction de l'erreur set inférieur à. C'est une heuristique comme une autre, le calcul de l'écart type est assez acrobatique et ce seuil est tout à fait arbitraire, nous pourrions prendre comme référence deux fois l'écart type, ou une autre valeur. Le logiciel TANAGRA que nous avons utilisé facilite le calcul par une autre approche que nous ne détaillons pas dans ce travail.

La zone TREE SEQUENCE de notre algorithme indique l'évolution de la réduction de l'erreur RE en fonction du nombre de feuilles de l'arbre, sur le fichier d'élagage. On peut retenir quatre arbres dans cette zone :

1. l'arbre réduit à la racine (Tree with one leaf, the root node) avec une feuille ;

2. l'arbre maximal (maximal tree ,« optimal » tree on growing set) avec 133 feuilles ;

3. l'arbre minimisant RE (optimal tree on the pruning set) achuré en bleu par le logiciel, avec 105 feuilles;

4. l'arbre qui été produit (selected tree) achuré en rouge par le logiciel, avec 13 feuilles.

L'arbre que nous avons construit a 12 noeuds feuilles et 13 noeuds de décision (voir zone TREES SEQUENCE de l'arbre en annexes). Le nombre total de noeuds est tel que renseigné par la zone TREE DESCRIPTION de notre arbre en annexes.

c) Interprétation de l'arbre :

· Accès au primaire :

Remarquons à partir de l'arbre en annexes que la première segmentation des données s'opère sur la variable cmage (âge du chef de ménage) avec un seuil de coupure de 44,5. La deuxième segmentation sur la même variable, cette fois au seuil 52,5. La troisième s'opère sur la variable télévision (e5-télé) au seuil 0,5. La quatrième segmentation sur la taille de ménage (q17-tmen) au seuil 4,5 et la cinquième segmentation s'est faite toujours sur cette même variable ; mais cette fois ci au seuil 15,5. A ce niveau le noeud terminal est pur (avec 100% d'éléments homogènes).

De ce qui suit on dira donc que, si l'âge du chef de ménage est élevé, ce qui détermine l'éducation des enfants ou favorise l'accès au primaire c'est la télévision. Pour ce, manquer de télévision dans le ménage suffit pour favoriser l'accès au primaire.

La taille du ménage intervient lorsque l'âge du chef de ménage est élevé et dans le ménage il y a au moins une télévision. Dans ce cas, les ménages qui ont une petite taille ont la facilité de scolariser leurs enfants. Les autres variables n'interviennent qu'accessoirement.

· Accès au secondaire :

Comme au précédent, la première segmentation se fait sur la variable taille du ménage au seuil 44,5, la deuxième s'opère toujours sur la même variable ; mais cette fois ci au seuil 0,5. La troisième segmentation s'opère sur la variable dépenses journalières en dollar américain (depjour). A ce niveau, le noeud feuille est pur, il ne contient que des observations homogènes.

On dira donc qu'au secondaire, parmi les déterminants de l'accès à l'éducation, l'âge du chef de ménage est le plus décisif, suivi de télévision qui agit positivement cette fois ci et enfin les dépenses journalières qu'effectue le ménage en monnaie américaine.

On peut l'expliquer de cette manière, si l'age du chef de ménage est très élevé, ce qui détermine l'accès au secondaire c'est la télévision. Cette fois, contrairement au niveau primaire, avoir au moins une télévision dans le ménage suffit pour favoriser l'éducation au secondaire. Les dépenses journalières du ménage n'interviennent que lorsque les deux variables ci hauts agissent autrement.

Le niveau universitaire et le programme non formel n'étant pas esquissés par notre algorithme en annexes, nous laissons la tâche aux jeunes chercheurs d'approfondir la recherche dans ce domaine pour la meilleure compréhension du fonctionnement de l'algorithme sous études.

Tableau 14 : Présentation des résultats

Variables	Modèle 1	Modèle 2	Modèle 3	Modèle 4	Modèle 5	Correlation and regression tree
						Primaire	secondaire
Taille du ménage	0 ,041 (-2,04)	0,042 (2,03)				(3)
Téléviseur	0,000 (-4,62)	0,001 (3,47)		0,000 (3,55)		(2)	(2)
Sexe de l'enfant	0,030 (2,16)
Religion du chef de ménage	0,080 (1,75)			0,010 (-2,57)
Sexe du chef de ménage	0,000 (-7,98)
Age du chef de ménage	0,000 (-12,63)	0,000 (6,39)	0,098 (1,65)	0,000 (5,85)	0,098 (1,65)	(1)	(1)
Ecole publique conventionnée	0,018 (2,36)	0,000 (9,96)
Chef a un niveau du type programme non formel	0,000 (-3,94)	0,080 (1,75)
Chef a un niveau secondaire	0,001 (-3,34)
Chef a un niveau universitaire	0,000 (-4,93)	0,070 (1,77)		0,007 (2,72)
Statut d'occupation du logement			0,013 (2,48)		0,013 (2,48)
Part du revenu consacré à l'enseignement			0.014 (-2,45)	0,000 (4,62)	0,014 (-2,45)
Type d'école de l'enfant				0,000 (-5,55)
Dépenses journalières du ménage				0,011 (2,56)			(3)

(.) : Z-statistic pour les régressions logistiques et ordre de détermination pour CART

d) Comparaison des résultats :

Les tableau 14 ci-haut et 15 ci-dessous nous renseignent que toutes les variables décisives dans CART sont significatives dans les régressions logistiques prises de façon détaillée (c'est-à-dire on considère les variables significatives dans chaque régression isolée). A l'exception de la dépense journalière du ménage qui est segmentée dans CART, mais significative seulement à la régression du niveau universitaire.

La part du revenu consacrée à l'enseignement est significative dans la régression du programme non formel et la régression globale, mais n'est pas segmentée dans CART. Pour cela, nous pouvons donc nous assurer que les résultats de ces deux méthodes sont cohérents du point de vue statistique.

Tableau 15 : résultats comparés des régressions logistiques et de la méthode CART

	Modèle logistique			Méthode CART
	Primaire	Secondaire	Niveau global	Primaire	Secondaire
1	Age du chef de ménage	Age du chef de ménage	Age du chef de ménage	Age du chef de ménage (1)	Age du chef de ménage (1)
2	Télévision	Télévision		Télévision (2)	Télévision (2)
3	Taille du ménage	Taille du ménage		Taille du ménage (3)
4	Sexe de l'enfant
5	Religion du chef de ménage
6	Sexe du chef de ménage	Sexe du chef de ménage
7	Type d'école fréquenté	Type d'école fréquenté
8	Education du chef de ménage
9					Dépense journalières du ménage (3)
10			Statut d'occupation du logement
11			Part du revenu consacré à l'éducation

(.) : Ordre de détermination dans CART.