Recalage d'images medicales multimodales par evolution differentielle adaptative

République Algérienne Démocratique et Populaire
Ministère de l'enseignement Supérieur et de la Recherche Scientifique
UniversitéMentouri de Constantine
Facultédes Sciences de l'ingénieur
Département d'informatique

Mémoire

Pour l'obtention du diplôme de Master Professionel en informatique

Option : Sciences et Technologies de l'Information et de la Communication

Recalage d'images médicales multimodales par

évolution différentielle adaptative

Réalisépar :
Aya Belattar

et

Abla Elaggoune

Encadrépar :
Dr. Amer Draa

Année universitaire

2011-2012

i

Remerciements

Nous tenons, avant tout, à remercier en premier lieu `Allah' le tout puissant qui nous a donné le courage et la patience pour achever ce travaille.

Nous tenons, aussi, à remercier notre encadreur Dr. Amer Draa pour ses conseils, ses orientations, son soutien moral et ses qualités humaines.

Nous remercions, également, tous les membres du jury qui ont accepté d'évaluer ce travail.

Finalement, nous remercions toutes les personnes qui, directement ou indirectement, ont contribué à la réalisation de ce mémoire.

.a)eafeace

Ce mémoire est particulièrement dédié :

A mes chers parents

A mes frères « Aymen et Adam »

A mes amis

Et enfin, a tous ceux qui de près ou de loin ont

contribué à ce travail.

ii

Aya

iii

.a)eafeace

A la mémoire de mon père

A ma mère

A toute ma famille en particulier Ghassab Adel,

Ghassab Manar et Chendri Allèl

A mes enseignants, mes collègues, mes amis et en

particulier à mon ami Hamid.

Abla

iv

Rééssuméé

Dans ce travail, une approche à évolution différentielle adaptative pour le recalage d'images médicales multimodales basée sur la maximisation de l'information mutuelle est proposée. Le processus de traitement vise à maximiser l'information mutuelle afin de trouver les paramètres de la meilleure transformation qui permettent la mise en correspondance de deux images.

Nous avons proposé deux nouveaux algorithmes à évolution différentielle pour cette tache de recalage: un algorithme différentiel linéairement adaptatif et un algorithme différentiel périodiquement adaptatif, afin de réaliser un bon compromis entre l'exploration et l'exploitation dans le processus de recherche.

Les résultats obtenu ont prouvé que l'adaptation des paramètres d'ans l'algorithme différentiel le rend meilleur. De plus, à travers l'utilisation d'une formule sinusoïdale pour l'adaptation du facteur d'amplification dans l'opération de mutation, on a pu réduire la complexité algorithmique de l'évolution différentielle de base.

Mottss ccllééss:: Evolution différentielle, Recalage d'images, Information mutuelle, Adaptation de paramètres, Exploration, Exploitation.

Table des matières

v

Remerciement i

Résumé iv

Table des matières v

Liste des figures ix

Liste d'algorithmes xi

Liste d'équations xii

Liste des Tableaux xiii

Introduction générale 1

Chapitre 1 : Recalage d'images médicales

1. Introduction 3

2. Imagerie médicale 3

2.1. Quelque types de modalité 4

2.2. Fusion et recalage 5

3. Recalage d'image 6

3.1. définitions 6

3.2. Types de recalage 7

a) Recalage multi-Modalité 7

b) Recalage de gabarit 7

c) Recalage d'image prises de différents points de vue 7

d) Recalage temporel 7

3.3. Classification des transformations géometriques 8

3.3.1. Transformations linéaire 8

a) Transformations rigides 8

b) Similitudes 8

c) Transformations affines 9

d) Transformations projectives 9

3.3.2 Transformation non linéaire (non rigides) 9

a) Transformations locales non paramétriques 10

b) Transformations locales parametriques 10

vi

3.4. Méthodes de recalage 10

3.4.1. Méthodes géometriques 10

3.4.2. Méthodes iconiques(denses) 12

3.4.3.Méthodes hybride 16

3.5. Information mutuelle et recalage d'image 18

3.5.1. Entropie 18

3.5.2. Entropie conjointe 18

3.5.3. Information mutuelle 19

3.5.4. Avantages et limites de l'utilisation de l'IM 20

4. Recalage et l'imagerie medicale 21

5. Conclusion 23

Chapitre 2 : Métaheuristique d'optimisation

1. Introduction 24

2. Définition 24

2.1. Problémes d'optimisation 24

2.2. Optimum local 24

2.3. Optimum global 25

3. Métaheuristiques 25

4. Classification des metaheuristiques 26

4.1 Métaheuristique a base de population 26

4.1.1. Algorithmes evolutionnaires 27

4.1.2. Optimisation par essaim de particules 31

4.1.3. Optimisation par les colonies de fourmis 32

4.2. Métaheuristique a base de voisinage 34

4.2.1. Recuit simulé 34

4.2.2. Recherche Tabou 35

4.2.3. Méthode de la Descente (Hill-Climbing) 36

4.3. Méthodes hybrides 37

5. Conclusion 37

Chapitre 3 : Évolution différentielle

1. Introduction 38

2. Principe de l'évolution différantielle 38

vii

2.1 Mutation différantielle 38

2.2 Croisement différentiel 39

2.3 Sélection 40

2.4 Critère d'arrêt 40

3.Variantes pour l'évolution differentielle 41

4. Avantages et limites de l'évolution differentielle 42

4.1. Avantages de l'évolution differentielle 42

4.2. Limites de l'évolution differentielle 42

5. Conclusion 43

Chapitre 4 : AED pour le recalage d'image

1. Introduction 44

2. Formulation de problème 44

2.1. Représentation des individus 44

2.2. L'espace de recherche 45

2.2.1 Transformation rigide 45

2.2.2 Transformation rigide avec zoom(similitude) 45

2.2.3 Transformation affine 45

2.3. Fonction objectif 46

2.4. Stratégie de recherche 46

3. Contribution 46

3.1. Algorithme differentiel linéairement adaptatif 48

3.2. Algorithme différentiel périodiquement adaptatif 48

3.3. Résultats expérimentaux 49

3.3.1. Résultat numérique. 49

3.3.2 Analuse qualitative des Résultats. 50

a) Recalage rigide 50

b) Recalage rigide avec zoom 53

4. Interface Graphique. 54

5.Conclusion. 56

Conclusion générale 57

Bibliographie 58

viii

Liste des figures

Figure 1.1 : Évolution de la pratique chirurgicale : de la trépanation à la chirurgie

microscopique 4

Figure 1.2 : Multi modalité fonctionnelle et structurelle pour la compréhension Du

cerveau humain 5

Figure 1.3 : recalage d'image. 7

Figure 1.4 : Transformation rigide 8

Figure 1.5 : Transformation de similitude . 9

Figure 1.6 : Transformation affine. 9

Figure 1.7 : Transformation projective 9

Figure 1.8 : Transformation local. 10

Figure 1.9 : Transformation géométrique : A gauche les primitives sont des points. A

droite la primitive est une surface. 11

Figure 1.10 : Une image et son histogramme . 13

Figure 1.11 : Représentation graphique d'histogramme conjoint 13

Figure 1.12 : Exemple d'histogrammes conjoints obtenus pour (a) des images non

recalées et (b) des images recalées.. 14

Figure 1.13 : Histogramme conjoint de deux IRM cérébrales (coupes coronales

représentés) calculé pour deux transformations différentes 14

Figure 1.14 : Histogramme conjoint d'un couple IRM/scanner (coupes axiales

représentés) calcule pour deux transformations différentes 15

Figure 1.15 : L'entropie, l'entropie conjointe et l'information mutuelle pour deux images

A et B 20

Figure 1.16 : Recalage Multimodal Structurel : alignement d'une image TDM sur une

image IRM 22

Figure 1.17 : Recalage Multimodal Structurel-Fonctionnel : alignement d'une image TEP

(fonctionnelle) sur une image IRM-T2 (structurelle). 22

ix

Figure 1.18 : Recalage multimodal données/atlas : alignement d'un volume TDM sur

l'atlas anatomique de Talairach-Tournoux. 23

Figure 2.1 : Optima locaux et optima globaux d'une fonction a une variable. 25

Figure 2.2 : Classification des métaheuristiques 26

Figure 2.3 : Codage binaire d'un chromosome 28

Figure 2.4 : Codage réel d'un chromosome 29

Figure 2.5 : Détermination du plus court chemin par une colonie de fourmis. (a) Situation initiale, (b) Introduction d'un obstacle, (c) Recherche du chemin optimal,

(d)Prédominance du chemin optimal. 33

Figure 3.1 : Mutation différentielle 39

Figure 3.2 : croisement différentiel : a) croisement binomial, b) croisement exponentiel 40

Figure 4.1 : Un individu pour une Transformation Similitude 44

Figure 4.2 : Recalage rigide multimodale 47

Figure 4.3 : Le meilleur global, le moyen et le minima locaux aux cours du recalage

rigide des images de la figure 4.2. 47

Figure 4.4 : Équation sinusoïdale du facteur Fd. 48

Figure 4.5 : Paire d'image : IRM-Tomographie calculée à rayon X(CTI). 51

Figure 4.6 : Recalage rigide des images de la figure 4.5 par ADE (à gauche), (au milieu) EDLA

et EDPA (à droite) 51

Figure 4.7 : Les graphes d'IM correspondant aux images de la figure 4.5 : : EDA (à gauche

au-dessus), EDLA (à droite au-dessus) et EDPL (milieu au-dessous),. 52

Figure 4.8 : Paire d'image à recaler : à gauche IRM coloré et à droite Scanner 53

Figure 4.9 : Interface de transformation des images de la figure 4.7 53

Figure 4.10 : les graphes d'IM correspondant aux images de la figure 4.7: EDB (à gauche

au-. dessus), EDLA (à droite au-dessus) et EDPL (milieu au-dessous). 54

Figure 4.11 : Interface de transformation similitude avant l'execution. 55

Figure 4.12 : Interface de transformation similitude apres l'execution. 54

x

Liste d'algorithmes

Algorithme 2.1 : Algorithme évolutionnaire génétique 28

Algorithme 2.2 : Optimisation par colonies de fourmis 34

Algorithme 2.3 : Optimisation par le recuit simulé 35

Algorithme 2.4 : Optimisation par la recherche tabou 36

Algorithme 2.5 : Optimisation par la méthode de descente 36

Algorithme 3.1 : Évolution différentielle 41

xi

Liste d'équations

Equation 1.1 : Recalage d'image 6

Equation 1.2 : Transformations rigides 8

Equation 1.3 : Transformation similitude 8

Equation 1.4 : Transformation affine 9

Equation 1.5 : Entropie 18

Equation 1.6 : Entropie conjointe 18

Equation 1.7 : Information mutuelle : Définition 1 19

Equation 1.8 : Information mutuelle : Définition 2 19

Equation 1.9 : Information mutuelle : Définition 3 19

Equation 1.10 : Information mutuelle normalisée 20

Equation 2.1 : Vitesse d'une particule 32

Equation 2.2 : Position d'une particule 32

Equation 3.1 : Mutation différentielle 38

Equation 3.2 : Croisement différentielle 39

Equation 3.3 : Sélection 40

Equation 3.4 : Variantes d'évolution différentielle 41

Equation 4.1 : Transformation rigide 45

Equation 4.2 : Transformation rigide avec zoom 45

Equation 4. 3 : Transformation affine 45

Equation 4.4 : Évolution différentielle linéairement adaptatif (EDLA) 47

Equation 4.5 : Évolution différentielle périodiquement adaptatif (EDPA) 48

xii

Liste des tables

Table 1.1 : Quelques mesures de similarité utiles. 17

Table 4.1 : Résultat numériques des transformations : rigide, rigide avec zoom et affine 50

1

Introduction générale

Le traitement d'images et la vision par ordinateur sont deux disciplines relativement jeunes, mais elles évoluent rapidement. Ces deux domaines de traitement de l'information jouent un rôle très important dans plusieurs contextes : académiques, technologiques et industriels.

Le recalage d'image est un problème classique en vision par ordinateur et un processus fondamental en traitement d'images. Il vise à déterminer la meilleure transformation géométrique qui permet de superposer la plus grande partie commune possible de deux ou plusieurs images prises à différents moments, depuis différents capteurs (recalage multimodale) ou à partir de différents point de vue (recalage monomodale). Le recalage joue un rôle important dans plusieurs applications comme la surveillance de terre agricole à partir d'images satellitaires, la correspondance d'images stéréoscopiques et l'alignement d'images médicales pour le diagnostique.

Pour résoudre le problème de recalage il existe plusieurs techniques. On peut les classer en deux grandes classes : les approches géométriques basées primitives, elles s'appuient sur l'utilisation de primitives géométriques (points, segments, contours, etc.) ; et les approches basées intensité, dites également approches iconiques. Ce deuxième type, approches iconiques, est mieux adapté au recalage d'images multimodales.

Le problème de recalage est connu comme un problème d'optimisation. Pour sa résolution, plusieurs méthodes approchées ont été proposées. Parmi ces méthodes on trouve: le recuit simulé, la recherche taboue, les algorithmes génétiques, les colonies de fourmis et les systèmes immunitaires artificiels.

Dans ce travail, nous proposons un algorithme à évolution différentielle adaptative pour le recalage d'images médicales multimodales en utilisant l'information mutuelle comme mesure de similarité. Deux variantes ont été définies. Dans la première, une adaptation linéaire du facteur d'amplification de l'opération de mutation est utilisée. Dans la deuxième, cette adaptation linéaire est remplacée par une formule sinusoïdale permettant à l'operateur de mutation de changer son rôle périodiquement de l'exploration à l'exploitation et vice versa.

2

Les résultats expérimentaux obtenus de l'application des deux variantes à différentes paires d'images médicales, IRM et PET, ont été comparés avec ceux obtenu de l'application de l'évolution différentielle de base sur les mêmes paires d'images. Cette comparaison a démontré la supériorité de nos deux variantes par rapport à l'algorithme de base au moins au niveau de la complexité algorithmique.

Ce mémoire s'articule donc de la manière suivante :

- Dans le premier chapitre nous expliquons brièvement le problème de recalage

d'images, ses principes de base, ses types et ses domaines d'application.

- Le deuxième chapitre présente le domaine d'optimisation en se concentrant sur les différentes approches proposées dans la littérature pour résoudre les différents problèmes d'optimisation.

- Le troisième chapitre est consacré à la description de l'algorithme de base de l'évolution différentielle, ses variantes, ses limites, et ses avantages.

- Le quatrième chapitre détaille nos contributions pour le recalage d'images médicales, à savoir : l'adaptation linéaire et l'adaptation périodique des paramètres. Dans sa deuxième partie les résultats expérimentaux sont introduits et discutés.

Chapitre 1 :

« Si l'esprit d'un homme s'égare, faites-lui étudier les mathématiques car dans les démonstrations, pour peu qu'il s'écarte, il sera obligé de recommencer »

Francis Bacon.

1. Chapitre 1 Recalage d'images médicales

3

Introduction

A l'évolution des nouvelles techniques occupées à l'interprétation des images par ordinateur, le traitement d'image joue un rôle très important dans plusieurs domaines tels que l'imagerie satellitaire, médicale, industrielle, etc. L'imagerie médicale a connu des techniques efficaces qui permettent d'acquérir et de traiter des images internes du corps humain et d'établir un diagnostic ou même la mise en oeuvre d'une thérapeutique en temps réel comme échographie, IRM, TEP et scanner [Larousse médicale, 2006]. Selon la technique utilisée, on peut distinguer deux types d'images médicales. Les images anatomiques médicales permettant d'obtenir des informations géométriques sur la structure des organes (taille, volume, localisation, etc.). Et les images fonctionnelles permettant d'obtenir une vision sur la fonctionnalité des organes, par exemple le TEP.

Malgré l'efficacité de la vision par ordinateur dans plusieurs domaines, elle reste incapable de visualiser certains objets correctement. Parmi les vieilles problématiques de la vision par ordinateur, on trouve le recalage. Le recalage d'images est un processus qui permet de faire une transformation spatial entre deux ou plusieurs images.

Dans ce chapitre, nous présentons le problème de recalage en imagerie médicale. Nous commençons par une introduction sur l'imagerie médicale. Puis, nous présentons les fondamentaux théoriques du recalage des images : définitions, types, méthodes de recalage les plus pertinentes, mesure de similarités entre images (en se concentrant sur l'information mutuelle). En fin, nous pressentons les différentes applications de recalage en imagerie médicale.

2. Imagerie médicale

De la trépanation à la robotique chirurgicale, la pratique médicale a connu une véritable révolution (Figure 1.1). De nos jours, grâce aux nouvelles techniques d'imagerie, les procédés de traitement se sont modernisés, le diagnostic est devenu plus précis et la qualité des soins est désormais meilleure. Loin des pratiques traditionnelles, où «voir» passait par «ouvrir», aujourd'hui, les radiologues, à l'aide des techniques tomographiques, peuvent diagnostiquer et traiter de façon quasiment non-invasive. Le recours à la chirurgie invasive est devenu la solution de dernier recours [Atif, 2004].

Chapitre 1 Recalage d'images médicales

4

Une trépanation exercée XVI^ième siècle Un chirurgien opérant à l'aide d'un microscope

Figure 1.1 Évolution de la pratique chirurgicale : de la trépanation à la chirurgie microscopique.

Parmi les modalités d'acquisition, on distingue celles qui fournissent des propriétés structurelles (morphologiques) de la zone étudiée (IRM, TDM, X-Ray, etc.), de celles qui restituent des aspects fonctionnels (TEP, TEMP, IRMf, MEG, etc.) [Atif, 2004] (Figure 1.2). Donc, selon la technique utilisée on peut distinguer deux types d'images médicales. Les images anatomiques permettant d'obtenir des informations géométriques sur la structure des organes (taille, volume, localisation, etc.), et les images fonctionnelles permettant d'obtenir une vision sur la fonctionnalité des organes.

2.1. Quelques types de modalité

? L'imagerie par résonance magnétique (IRM) : On distingue deux types d'IRM anatomique et fonctionnelle. L'IRM anatomique permet de visualiser la structure anatomique de tout volume du corps. L''IRM fonctionnelle permet de suivre l'activité d'un organe, à travers l'afflux de sang oxygéné dans certaines de ses zones [Frija et Mazoyer, 2002].

? la Radiologie : La radiologie repose sur l'utilisation des rayons X. Elle s'applique au diagnostic et au traitement des maladies selon différents modalités techniques : La radiographie (Standard), La radioscopie et La tomodensitométrie (scan RX, TDM) [Larousse médicale, 2006].

? la tomographie par émission de positions (TEP) : La TEP renseigne sur la biochimie des organes. Elle fournit des informations sur le fonctionnement des tissus normaux et pathologiques [Frija et Mazoyer, 2002].

? Tomographie d'Émission Mono Photonique (TEMP) : Le principe de la TEMP est de suivre l'évolution dans le corps humain d'un radioélément, qui est dans ce cas un

Chapitre 1 Recalage d'images médicales

5

émetteur naturel de simples photons ã. La TEMP constitue ainsi une technique d'exploration de la perfusion cérébrale [Grova, 2005].

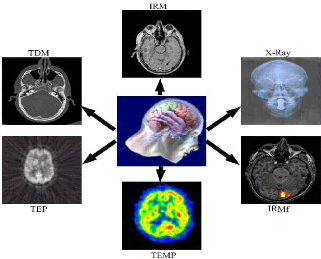
Figure 1.2 Multi modalité fonctionnelle et structurelle pour la compréhension Du cerveau humain

[Atif, 2004].

2.2. Fusion et Recalage

Plusieurs modalités sont parfois utilisées pour effectuer un seul diagnostic. Pour certaines anomalies, le radiologue doit à la fois étudier l'aspect structurel et fonctionnel d'une zone d'intérêt. Or, ces modalités sont en général utilisées avec un décalage dans le temps. Les informations recueillies doivent être alors fusionnées dans un même repère pour permettre d'effectuer les différentes analyses et comparaisons, nécessaires à l'établissent d'un diagnostic précis et efficace [Atif ,2004].

Le développent parallèle des sciences informatiques a fait naître l'idée que des logiciels pourraient aider le praticien dans ce travail. Parmi les besoins les plus courants du praticien se trouvent une variété de tâches de comparaison : comparer des images d'un même patient acquises à des instants différents ou selon des modalités différentes comparer des images de patients différents ou encore comparer une image avec un atlas anatomique ou fonctionnel.

Chapitre 1 Recalage d'images médicales

6

Ces tâches de comparaison relèvent toutes d'une même problématique : le recalage [Roche, 2011].

3. Recalage d'image 3.1. Définitions

? Définition 01 : Le recalage (en Anglais registration) est la tâche qui cherche la meilleure transformation qui permet de superposer la plus grande partie commune possible des images à apparier compte tenu des variations de la scène [Talbi, 2009 ; Brown, 1992].

? Définition 02 : Le recalage d'image est la tâche qui permet d'aligner deux images.

Si on considère ces deux images comme deux matrices notées I1 et I2 où I1 (x, y) et I2 (x, y) sont les intensités des pixels au point dont les cordonnées sont x et y, Alors, le recalage est l'opération qui permet d'estimer les fonctions f et g qui vérifient la relation suivante [Talbi, 2009 ; Brown, 1992] :

I2(x, y)=g (I2 (f(x, y))) (1.1)

Où : f est une fonction à deux dimensions représentant la transformation géométrique et g est une fonction à une dimension représentant la transformation photométrique.

? Définition 03 : Le recalage est la mise en correspondance des images ayant la formule générale [Bloch] :

min f (I1, t(I2)), t C T (1.1)

Où :

I1 et I2 sont les images à recaler (ou informations extraites de ces images), t : transformation, T : ensemble des transformations possibles / admissibles, f : critère de dissimilarité (min) ou de similarité (max).

Chapitre 1 Recalage d'images médicales

7

Figure 1.3 Recalage d'image.

3.2. Types de recalage

On distingue généralement quatre types de recalage [Mashoul, 2004] :

a) Recalage multi-modalité : Traite les problèmes où les images de la même scène sont prises par des capteurs différents.

- Exemple d'application : Intégration d'information de deux images, l'une prise par un

radar et l'autre par un système optique.

b) Recalage de gabarit : Recherche une forme de référence dans une image. - Exemple d'application : Localisation d'une cible par un missile.

c) Recalage d'image prises de différents points de vue : Ce type de recalage requiert souvent des transformations locales afin d'éliminer les distorsions perspectives.

- Exemple d'application : Vision stéréoscopique.

d) Recalage temporel : La mise en correspondances entre deux images prises à des moments différents, ce type de recalage doit accepter les divergences entre les deux images dues aux changements réels dans la scène.

- Exemple d'application : Suivre l'évolution d'une pathologie.

Chapitre 1 Recalage d'images médicales

3.3. Classification des transformations géométriques

3.3.1. Transformation linéaire

Transformations linéaires définie par : X - A_?X + b_? où n est la dimension, A_n est une application linéaire de dimension nxn, et b_n est un vecteur de translation de dimension nx1. Il existe plusieurs types de transformations géométriques linéaires.

a) Transformations rigides

La transformation rigide est la composition d'une rotation et d'une translation. L'hypothèse de rigidité convient au cas où l'on cherche à compenser la différence de positionnement d'un objet par rapport aux capteurs sans tenir compte d'éventuelles déformation des tissus imagés ou de distorsions géométriques créées par les procèdes d'imagerie [Roche, 2011].

La formulation de transformations rigides d'une image 2D est la suivante :

T(x) = Rx + t (1.2)

Où : t est un vecteur 2×1 qui représente la translation, et R est une matrice orthogonale directe 2x2.

8

Figure 1.4 Transformation rigide.

b) Similitudes

Consiste en l'estimation d'un facteur d'échelle isotrope en plus des translations et des rotations. Ce type de recalage conserve les angles et le rapport entre les distances :

T(x)=sRx+t, s>0 (1.3)

s c'est le facteur d'échelle [Brown, 1992].

Chapitre 1 Recalage d'images médicales

Figure 1.5 Transformation de similitude.

c) Transformations affines

Ces transformations autorisent, en plus des rotations et des translations, de prendre en compte un facteur d'échelle anisotrope et de modéliser des cisaillements, elles conservent le parallélisme.

T(x)=A(x)+t (1.4)

Sachant que A est une matrice 2×2 quelconque [Roche, 2011].

Figure 1.6 Transformation affine.

d) Transformations projectives

Les transformations projectives sont utilisées dans le cas où des images 3D sont recalées avec des images 2D acquises au moyen d'une camera, par exemple les images radiologique et les images vidéo [Talbi, 2009].

9

Figure 1.7 Transformation projective.

3.3.2. Transformations non linéaires (non rigides)

Contrairement aux transformations linéaires, les déformations non-rigides sont appliquées localement, c'est à dire que la transformation appliquée en un point peut effectivement être

Chapitre 1 Recalage d'images médicales

différente de celle appliquée à ses voisins. L'amplitude des déformations recherchées est généralement plus faible et localisée. Un nombre important de modèles de déformation non-rigide ont été proposés dans la littérature du recalage. Parmi ceux-ci, on fait la distinction entre les transformations locales non paramétriques et les transformations locales paramétriques [Rubeaux, 2011].

a) Transformations locales non-paramétriques

Dans ce type, la transformation est définie en chaque pixel de l'image. Ces modèles nécessitent l'utilisation d'un terme de régularisation pour contraindre la solution, car le modèle de déformation est totalement libre [Rubeaux, 2011].

b) Transformations locales paramétriques

Des transformations d'ordre plus général pourront être obtenues en perturbant localement la composante globale du mouvement. Les coordonnés de la déformation résiduelle peuvent être modélisées comme des combinaisons linéaires de fonctions élémentaires [Roche 2001].

10

Figure 1.8 Transformation local.

3.4. Méthodes de recalage

On peut distinguer deux approches de recalages : géométrique et iconique. La première est basée sur l'extraction des primitives, et la deuxième est basée sur la mesure de similarité.

3.4.1. Méthodes géométriques

Les méthodes géométriques sont peut être les plus naturelles car elles procèdent de façon analogue à l'esprit humain conscient. Elles sont basées sur l'extraction dans les images de sous-ensembles de points homologues (primitives) qui peuvent être des points, des lignes, des surfaces, des volumes, etc., qu'il s'agit ensuite de mettre en correspondance [Roche, 2011].

Le choix des primitives doit être guidé par un certain nombre de propriétés : détection facile et précise, répartition sur l'ensemble de l'image, robustesse au bruit, aux artefacts et aux

Chapitre 1 Recalage d'images médicales

11

différents changements liés à l'acquisition [Noblet, 2006]. Cependant, la majorité des approches se basent soit sur une sélection manuelle, soit sur une détection semi-automatique des amers (ou primitives géométriques) communs aux deux images, ce qui impose un prétraitement des données pour extraire ces points, lignes ou surfaces d'intérêt [Rubeaux, 2011].

En effet ces méthodes reposent sur deux étapes bien distinctes, qui sont d'ailleurs généralement menés de façons complètement indépendantes : La première étape, dite de segmentation est souvent la plus problématique dès lors que l'on souhaite la réaliser automatiquement. Elle requiert d'extraire des primitives qui soient significatives ce qui peut s'avérer difficile si les images sont fortement bruitées (par exemple, des images ultrasonores). Après la segmentation des primitives la deuxième étape est celle du recalage proprement dit, C'est à dire le calcul d'une transformation spatiale "optimale". Il convient de distinguer le cas où les correspondances entre primitives sont connues à l'avance (primitives labélisées) du cas contraire (primitives non labélisées), très fréquent lorsque la segmentation est automatique [Roche, 2011].

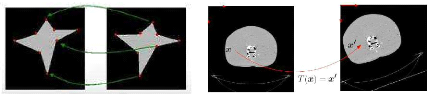
Figure 1.9 Transformation géométrique : A gauche les primitives sont des points. A droite la primitive est une surface.

Avantages et Limites des méthodes géométriques

a) Avantages

On peut résumer les avantages des méthodes géométriques dans les points suivants :

~? Optimisation de la charge calculatoire par la gestion de zones d'images plutôt que de détails sur l'image c'est à dire temps de traitement très réduit, par contre aux méthodes iconiques où le temps de traitement est très élevé [Gardeux, 2008].

~? Utilisation de données déjà issues de l'image et donc plus pertinentes [Gardeux, 2008].

Chapitre 1 Recalage d'images médicales

12

~? Pallier aux problèmes d'artefacts dans les images initiales et des Différences d'intensité entre les 2 images à recaler [Gardeux, 2008].

~? Primitives très informatives [Rubeaux, 2011].

b) Limites

On peut résumer les limites des méthodes géométriques dans les points suivants :

~? Sélection manuelle ou semi-annuelle des primitives, même si plusieurs équipes travaillent sur la conception de méthodes d'identification automatiques [Rubeaux, 2011 ; Noblet, 2006].

~? Le choix des primitives est très arbitraire. Il est difficile de trouver les primitives optimales [Gardeux, 2008].

~? Généralement réservé au recalage monomodal [Rubeaux, 2011].

~? Prétraitement (segmentation) nécessaire [Rubeaux, 2011].

3.4.2. Méthodes iconiques (denses)

Les méthodes iconiques sont des approches bas-niveau. Contrairement aux premières, celles-ci ne nécessitent pas la segmentation préalable des images. Elles consistent essentiellement à optimiser une mesure de similarité fondée uniquement sur des comparaisons locales d'une intensité. Dans ce cas, les primitives guidant le recalage sont des vecteurs 3D contenant la position et l'intensité des pixels (voxels).

On reconnait une méthode iconique à deux propriétés essentielles : D'une part le choix des primitives est complètement arbitraire : tous les voxels sont a priori des candidats valables. D'autre part, les primitives ne sont pas des entités géométriques, elles appartiennent à un espace figuratif différent du monde réel. Ainsi, le critère utilisé pour comparer ces primitives est une mesure de similarité reflétant indirectement une distance géométrique [Talbi, 2009 ; Roche, 2011].

3.4.2.1 Mesure de similarité

Il existe plusieurs mesures de similarité dans la littérature du recalage d'images. La plupart des mesures existantes peuvent être définies à partir d'un histogramme conjoint. D'autres peuvent être appréhendées indépendamment de la notion d'histogramme conjoint [Roche, 2011].

Chapitre 1 Recalage d'images médicales

13

a) Concept d'histogramme conjoint ? Histogramme

La première question posée avant d'expliquer brièvement le concept d'histogramme conjoint : c'est quoi un histogramme d'une image ? L'histogramme des niveaux de gris ou des couleurs d'une image est une fonction qui donne la fréquence d'apparition de chaque niveau de gris (couleur) dans l'image. Il permet de donner une bonne quantité d'information sur la distribution des niveaux de gris (couleur).

Figure 1.10 Une image et son histogramme.

? Histogramme conjoint

Maintenant, nous allons expliquer la notion d'histogramme conjoint : L'histogramme conjoint de deux images I et J est calculé à partir du calcul des fréquences d'apparitions de l'intensité de chaque couple de pixels de même rang de deux matrices de pixels. La figure 1.11 démontre ce processus [Bendaib, 2003].

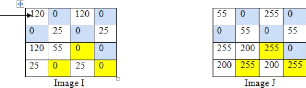
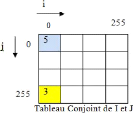
Figure 1.11 Représentation graphique d'histogramme conjoint.

Chapitre 1 Recalage d'images médicales

Figure 1.12 Exemple d'histogrammes conjoints obtenus pour (a) des images non recalées et(b) des

images recalées.

b) Classification des mesures de similarité

Une mesure de similarité est une fonction à valeurs réelles dont l'argument est l'histogramme conjoint, lui-même fonction de la transformation spatiale. Le fondement commun aux nombreuses mesures proposées dans la littérature est l'idée que les intensités de deux images manifestent une cohérence d'autant plus forte que les images sont bien alignées. Le rôle de la mesure de similarité est précisément de donner une signification quantitative à cette notion de cohérence (figures 1.13 et 1.14) [Roche, 2011].

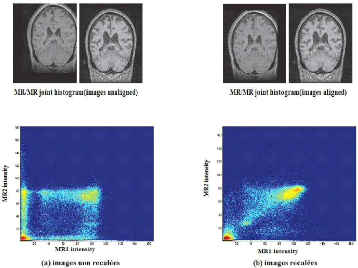
14

Figure 1.13 Histogramme conjoint de deux IRM cérébrales (coupes coronales représentés) calculé
pour deux transformations différentes [Roche, 2011].

Chapitre 1 Recalage d'images médicales

Dans la première situation (a) les couples d'intensité sont répartis dans le plan de façon relativement désordonné. La cohérence est manifestement plus forte dans la deuxième situation (b) où on a la très nette impression que les intensités sont regroupées le long d'une droite.

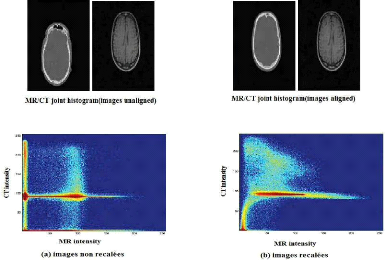
15

Figure 1.14 Histogramme conjoint d'un couple IRM/scanner (coupes axiales représentés) calcule
pour deux transformations différentes.

La situation de recalage (b) donne l'impression visuelle d'un gain de cohérence. Mais la relation entre les intensités n'est clairement plus de type affine lorsque les images sont recalées. La majorité des couples d'intensités est regroupé autour d'une courbe d'allure parabolique. On observe un amas secondaire nettement plus dispersé autour de l'intensité 50 dans l'IRM et 150c dans le scanner. Il n'est pas évident de caractériser une telle relation.

Les mesures de similarités font une hypothèse sur la relation liant les niveaux de gris des deux images à recaler. En général, la nature de cette relation permet de faire une classification des différentes mesures de similarité. Le tableau 1.1 résume les principales mesures de similarité.

Chapitre 1 Recalage d'images médicales

16

3.4.2.2. Avantages et Inconvénients de la méthode iconique

a) Avantages

On peut résumer les avantages des méthodes géométriques dans les points suivants [Gardeux, 2008] :

· On travaille avec toutes les informations portée par l'image. Celle-ci ne subit pas de prétraitement.

· Adapté au recalage multimodal [Rubeaux, 2011].

· Méthode totalement automatique.

c) limites

On peut résumer les limites des méthodes géométriques dans les points suivants :

· Difficulté de lier deux images ayant des niveaux d'intensité différents.

· le problème d'optimisation est bien plus difficile à résoudre que dans le cas des méthodes géométriques à cause de la présence de nombreux minima locaux d'énergie [Noblet, 2006].

· Très grand coût calculatoire de par la nécessité de calculer l'intensité de tous les voxels de l'image [Gardeux, 2008], c'est à dire cette méthode nécessite un temps de traitement important. Pour diminuer le temps de calcule il existe des approches hiérarchiques par construction de pyramides d'images [Noblet, 2006].

· Primitives peu informatives (de bas niveau) [Rubeaux, 2011].

3.4.3. Méthodes hybride

Les méthodes hybrides combinent plusieurs types de caractéristiques extraites des images à Recaler. Le but est d'améliorer la robustesse du recalage en combinant les avantages liés aux caractéristiques utilisées. Trois cas sont envisagés [Rubeaux, 2011] :

a) La combinaison de primitives géométriques de nature différente comme la combinaison de points et de courbe ou la combinaison de courbes et de surfaces.

b) La combinaison de différentes informations issues des niveaux de gris : c'est le cas où le gradient de l'image et l'information des niveaux de gris sont utilisés conjointement.

c) La combinaison des approches géométriques et iconiques.

Chapitre 1 Recalage d'images médicales

17

Nature de la dépendance		Mesure		Formule
Conservation de l'intensité		SDC*		? ??,? (? - ?)^2 ?,?
		SDA*		???,? ~? - ?~ ?,?
Linéaire		Inter-corrélation normalisé		??
				???,? ???? ?,?
		Critère d'Albert*		J ? ??,? (?? ? - ?)^2 ?,?
Affine		Coefficient de corrélation		?? - ???(? - ??) ?
				??,? ???? ?,?
Fonctionnelle		Critère de Woods*		?? ? ?? ???
		Rapport de corrélation*		? ? ?
				?? ??^2 - ??2 ?
Statistique		Entropie conjointe *		-? ??,? ??? ??,??,?
		Information mutuelle		??,? ?
				??? ??,? ???? ?,?
Notations	?? = ? ??,? ? ?? = ???,? ? = ?,? ?? = ???,? ? ?,? ?? = ? ???? ?	??,? ?	?=	? ?? ?? = ?? ??? = ??? - ??? ??? = ??? - ???
		?? = ??,? ???? = ? ?? ? ? ?? ? ??? = ? ??,? ? ? ?,? ? = ??? ? ??? = ? ??,? ? ? ?,? ? ??? = ? ???? ? ^2 - ??^2 ?

Tableau 1.1 Quelques mesures de similarité utiles. Les mesures marqués d'un astérisque * sont à
minimiser. Tandis que les autres sont à maximiser [Roche, 2011].

Chapitre 1 Recalage d'images médicales

18

3.5. Information mutuelle et recalage d'image

L'Information Mutuelle (IM) est née du fruit de travail de Claude Elwood Shannon en1949. En recalage d'images, l'IM fut utilisée pour la première fois et à la même année par deux équipes de recherche. Depuis 1995, la liste des publications qui traitent de cette mesure en recalage ne cesse de s'allonger, et elle est devenue la mesure de référence en recalage d'images médicales multimodales d'intensités inversées [Rubeaux, 2011].

Avant de parler de l'information mutuelle, la notion d'entropie sera d'abord introduite.

3.5.1 Entropie

L'entropie est la quantité d'information contenue dans une série d'événements. Une image A est par exemple constituée d'une série d'événements, des pixels, ayant tous une probabilité pi d'avoir une intensité i. Plus une image n'est complexe, plus son entropie 11(A) est grande. Shannon propose une définition de l'entropie telle que [Lombaert et Thériault, 2005] :

? = ? ?? log 1 = - ? ? ?? ??? ?? (1.5)

? ??

La première expression montre bien que plus un élément est rare, plus il a de signification. Si une image est constituée de pixels de plusieurs tons de gris, l'image transporte une information plus importante qu'une image d'un ton unique. La définition de Shannon de l'entropie indique l'information moyenne que l'on peut s'attendre de chaque élément de l'image [Lombaert et Thériault, 2005].

3.5.2 Entropie conjointe

Si on considère les deux images à recaler comme deux variables aléatoires X et Y, avec ??,? la distribution conjointe correspondante. L'entropie conjointe est formulée comme suit :

???, ?? = ? ?,???,??x, y? log ??,?(x, y) (1.6)

??,?(x, y) est la densité de probabilité conjointe des 2 images.

En effet l'aspect de l'histogramme conjoint reflète directement l'entropie conjointe. L'entropie conjointe est une mesure de dispersion de la distribution conjointe présentée par l'histogramme conjoint. Plus ce dernier est inhomogène, plus l'entropie conjointe est élevée, plus l'alignement est médiocre [Saidonai, 2010].

Chapitre 1 Recalage d'images médicales

19

3.5.3. Information mutuelle

L'information mutuelle MI (A, B) de deux images A, B, possède 3 définitions équivalentes. Chacune d'elles permet d'expliquer différemment l'information mutuelle. La première utilise la différence de l'entropie d'une image A et de l'entropie de la même image A sachant une autre image B [Lombaert et Thériault, 2005] :

MI (A, B) = H (A) - H (AIB) (1.7)

= H (B) - H (BIA)

Ici, H(A) mesure l'information contenu dans l'image A, tandis que H(AIB) mesure la quantité d'information contenu dans l'image A lorsque l'image B est connue. L'information mutuelle correspond donc à la quantité d'information que l'image B possède sur l'image A, ou similairement, la quantité d'information que l'image A possède sur l'image B.

La seconde définition évoque la distance de Kullback-Leibler [Lombaert et Thériault, 2005] :

MI(A, B) = Ea,b pab log pab (1.8)

apb

p

Soit la mesure entre la distribution pab des images A et B et la distribution papb où les images A et B sont indépendantes. Cette définition de l'information mutuelle mesure donc la dépendance des images A et B. Il y aura recalage lorsque les images A et B sont le plus semblables.

La troisième définition de l'information mutuelle est une combinaison des entropies de deux images, s'éparées et jointes [Lombaert et Thériault, 2005] :

MI (A, B) = H (A) + H (B) - H (A, B) (1.9)

Les entropies séparées H(A) et H(B) mesurent la complexité des images A et B. L'entropie jointe H (A, B) mesure la quantité d'information que les images A et B apportent en même temps. Si les images A et B sont proches, une image explique bien la seconde, et l'entropie jointe est minimale.

Studholme a introduit une autre formule normalisée de l'IM pour éliminer l'effet lié à la superposition des images sur la mesure [Lombaert et Thériault ,2005] :

Chapitre 1 Recalage d'images médicales

H(A)+H(B)

MI(X,Y) = (1.10)

H(A, B)

La recherche de la transformation T recalant les images A(x) et B(T (x)) correspond au maximum de la fonction de coût J(T) = MI (A, B) [Lombaert et Thériault, 2005].

20

Figure 1.15 L'entropie, l'entropie conjointe et l'information mutuelle pour deux images A et B

[Saidonai, 2010]

3.5.4. Avantages et limites de l'utilisation de l'IM

a) Avantages

On peut résumer les avantages de l'utilisation de l'IM dans les points suivants [Roche, 2011] :

? Elle est mieux adaptée au problème de recalage multimodal

? Parce qu'elle repose sur des hypothèses faibles concernant la relation entre les intensités des images, l'information mutuelle à toutes les apparences d'une mesure de similarité universelle.

? L'information mutuelle traite les intensités comme des variables purement qualitatives

c'est à dire sans faire intervenir une relation d'ordre dans l'espace des intensités.

b) Limites

On peut résumer les avantages de l'utilisation de l'IM dans les points suivants [Rubeaux, 2011] :

? L'inconvénient majeur de MI, à côté de la charge calculatoire importante, est le risque de tomber sur des optimums locaux lors de la phase d'optimisation itérative et les difficultés confrontées lors de cette phase [Saidonai ,2010].

? Quoique l'information mutuelle soit le critère le plus généraliste, il est déconseillé de l'utiliser dans les cas où des mesures plus restrictives peuvent être utilisées.

Chapitre 1 Recalage d'images médicales

21

? L'IM est reconnue pour être sensible à la zone de recouvrement partiel des données. En effet, lorsque l'on recale des images de modalités différentes, par exemple, il arrive qu'une structure, ou plus généralement qu'une partie des données présente dans une des images ne le soit pas dans l'autre. C'est la notion de recouvrement partiel. Plusieurs critères ont été développés pour répondre à cette problématique. Le plus connu est sans doute l'Information Mutuelle Normalisée (IMN).

? Un désagrément reconnu de l'IM est qu'elle ne fait aucune supposition sur l'information spatiale contenue dans les images à recaler. Traitant les pixels/voxels des images comme des réalisations d'une VA, la localisation spatiale de ces pixels n'entre pas du tout en compte dans l'estimation de l'IM.

? Incorporer une information supplémentaire directement dans l'IM n'est pas simple, car dans la plupart des cas, cela se traduit par la définition d'une IM d'un couple de deux vecteurs aléatoires de dimension 2.

? IM se prémunissant du calcul de l'histogramme conjoint

4. Recalage et l'imagerie médicale

En imagerie médicale, le mot recalage est apparu dans le courant des années soixante-dix. Le recalage est le processus qui vise à apparier des données provenant de sources différentes. Au début, son utilisation se limitait à la seule comparaison des examens acquis avec un décalage temporel. Ces examens provenaient d'une même modalité, en l'occurrence la tomodensitométrie. Ce type de recalage dit monomodal avait pour but une évaluation post-traitement.

Les cliniciens peuvent ainsi évaluer la pertinence d'un traitement en comparant les variations du volume des lésions traitées. Par contre, le besoin de représenter conjointement des informations provenant de plusieurs modalités d'acquisition n'est apparu que vers la fin des années 70, avec l'arrivée de l'IRM. Ce sont à la fois les propriétés physiques et le rendu de ces types de modalités qui ont poussé les chercheurs à combiner les informations fournies par ces techniques, pour pallier le manque d'imageur couvrant tous les aspects d'une forme étudiée. Ce recalage est dit structurel multimodal, puisque les modalités sollicitées ne mettent en exergue que la structure anatomique des zones étudiées (Figure. 1.16). Il intervient davantage dans l'évaluation pré et post-opératoire que dans les comparaisons diachroniques [Atif, 2004].

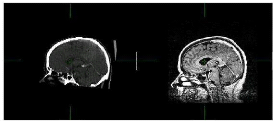
Chapitre 1 Recalage d'images médicales

22

Figure 1.16 Recalage Multimodal Structurel : alignement d'une image TDM sur une image IRM.

Récemment, les chercheurs se sont intéressés à un nouveau type de recalage dit structurel/ fonctionnel, qui fait appel à la fois à des modalités structurelles et fonctionnelles comme son nom l'indique (Figure. 1.17). L'imagerie cérébrale a été et reste le domaine le plus consommateur de ce type de recalage. Par exemple, pour traiter un patient épileptique, aussi bien le CT-scanner, l'IRMf où la scintigraphie est utilisée [Atif, 2004].

La compréhension des processus physiologiques cérébraux passe aussi par le recalage structurel/fonctionnel. On peut alors associer une activation cérébrale à une structure.

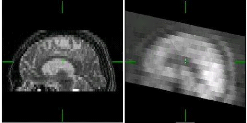
Figure 1.17 Recalage Multimodal Structurel-Fonctionnel : alignement d'une image TEP
(fonctionnelle) sur une image IRM-T2 (structurelle).

Il existe aussi la classe de recalage dite recalage données/atlas. Pour des besoins plus liés à la détection d'anomalies, les données provenant soit d'un seul imageur, soit d'une fusion multimodale, sont recalées avec un atlas numérique préalablement établi. L'utilisation de l'atlas peut aussi servir de critère de recalage comme c'est le cas pour l'atlas de Talairach/Tournoux (figure 1.18).

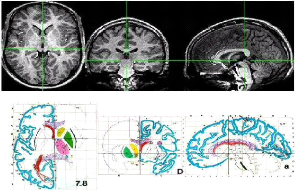
Chapitre 1 Recalage d'images médicales

23

Figure 1.18 Recalage multimodal données/atlas : alignement d'un volume TDM sur l'atlas
anatomique de Talairach-Tournoux.

Finalement, On peut évoquer le recalage multi-sujet. La fusion de données provenant de sujets différents est utile pour la construction d'atlas anatomiques et pour d'éventuelles études statistiques sur une population. Ce type de recalage est d'autant plus intéressant qu'il constitue la brique de base de la détection automatique des anomalies [Atif, 2004].

5. conclusion

Dans ce chapitre on a présenté le problème de recalage dans l'imagerie médicale : ses principes, ses types et ses méthodes. Aussi, on a expliqué la notion de mesure de similarité en donnant à l'information mutuelle plus d'importance parce qu'on l'a choisi comme mesure de similarité dans notre travail.

Le problème de recalage peut être formulé sous forme de problème d'optimisation. La recherche de la solution optimale est une tâche très couteuse voire impossible à affecter par les méthodes exhaustives. Ceci a favorisé le développement des méthodes approchées dont le principe est de trouver une solution acceptable, qui n'est pas forcement l'optimale mais en un temps raisonnable, en utilisant des processus stochastiques. Nous allons utiliser un algorithme d'évolution différentielle pour le recalage multimodal des images médicales en maximisant l'information mutuelle. Dans le prochain chapitre nous allons présenter les problèmes d'optimisation et les métaheuristiques destinées à la résolution de ces problèmes.

Chapitre 2 :

«J'espère prouver que la nature possède les moyens et les facultés qui lui sont nécessaires pour produire elle-même ce que nous admirons en elle.»

Jean Baptiste de Monet, chevalier de LAMARCK.

1. Chapitre 02 Métaheuristique d'optimisation

24

Introduction

L'Optimisation est l'une des branches les plus importantes des mathématiques appliquées modernes, et de nombreuses recherches. La résolution de problèmes d'optimisation est devenue un sujet central en recherches opérationnelles. Il existe deux classes de base des méthodes d'optimisation : exactes et approchées.

Les méthodes exactes sont des méthodes permettant de trouver une solution optimale en temps fini mais elles sont incapables de résoudre les problèmes trop complexes parmi les méthodes exactes on distingue : la programmation dynamique, la programmation linéaire et les algorithmes avec retour arrière [Layeb, 2010]. Contrairement aux méthodes exactes, les méthodes approchées ne procurent pas forcément une solution optimale, mais seulement une bonne solution (de qualité raisonnable) en un temps de calcul aussi faible que possible [Troudi, 2006], il existe une partie importante de méthodes approchées connues sous le nom de métaheuristiques.

Les métaheuristiques sont des méthodes approchées d'optimisation basées sur la bio-inspiration. Plusieurs classifications des métaheuristiques sont été proposées. La plupart distinguent globalement deux catégories : les métaheuristiques à base de population et les métaheuristiques à base de voisinage.

2. Définitions

2.1. Problèmes d'optimisation

Un problème d'optimisation se définit comme un problème de minimisation ou de maximisation, c'est à dire on cherche une solution de valeur optimale, minimale, si on minimise la fonction objectif, ou maximale, si on la maximise [Troudi, 2006].

Il existe plusieurs problèmes d'optimisations : problème mono ou multi objectif, problème combinatoire ou a variables continues, problèmes statistiques ou dynamiques, etc. [Boudieb, 2008].

2.2. Optimum local

Une solution s S est un optimum local si et seulement si' il n'existe pas de solution 0 voisinage v(s) de s, dont l'évaluation est de meilleure qualité que s, soit [Devarenne, 2007 ; Layeb, 2010]:

Chapitre 02 Métaheuristique d'optimisation

25

s0 ( )

s0 Dans le cas problème de minimisation s0 Dans le cas d un probleme de maximisation avec l ensembledes solution voisines de

2.3. Optimum global

Une solution est un optimum global à un problème d'optimisation s'il n'existe pas d'autres solutions de meilleure qualité. La solution s* S est un optimum global si et seulement si :

s ?S Dans le cas d'un problème de minimisation

Dans le cas d^'un probleme de maximisation

La figure 1.3 schématise la courbe d'une fonction d'évaluation en faisant apparaître l'optimum global et local [Devarenne, 2007 ; Layeb, 2010].

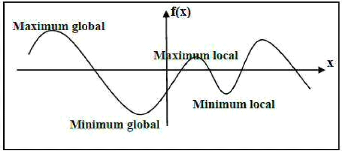
Figure 2.1 Optima locaux et optima globaux d'une fonction a une variable.

3. Métaheuristiques

Les métaheuristiques sont des algorithmes stochastiques itératifs qui progressent vers un optimum global. Il existe de nombreuses métaheuristiques allant de la simple recherche locale à des algorithmes plus complexes de recherche globale [Layeb, 2010]. Donc on peut distinguer deux catégories des méthodes heuristiques : les méthodes locales et les méthodes globales.

Les méthodes locales celles qui convergent vers un minimum local. Ces méthodes, appelées aussi méthodes de recherche par voisinages [Layeb, 2010]. On trouve plusieurs méthodes locales parmi elles on peut citer : le recuit simulé, la recherche tabou, etc.

Chapitre 02 Métaheuristique d'optimisation

26

Les méthodes globales sont des méthodes qui permettent d'atteindre un ou plusieurs optima globaux. Ces méthodes sont appelées aussi méthodes à base de population [Layeb, 2010]. Parmi elles on peut distinguer : les algorithmes génétiques, les algorithmes à évolution différentielle, les colonies de fourmis, etc.

4. Classification des métaheuristiques

On distingue plusieurs classifications des métaheuristiques dans ce chapitre nous présentons une classification mono objectif des métaheuristiques d'optimisation. La figure 2.2 résume cette classification.

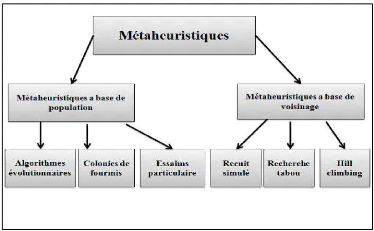
Figure 2.2 Classification des métaheuristiques [Collette, 2002 ; Troudi, 2006].

4.1. Métaheuristique a base de population

Les méthodes à base de population utilisent la population comme un facteur de diversité. Parmi ces méthodes on distingue les algorithmes évolutionnaires (algorithmes génétiques, algorithme a évolution differentielle), les colonies de fourmis, les algorithmes basés sur l'essaim de particule, etc .

4.1.1. Algorithmes evolutionnaires

Les Algorithmes Evolutionnaires (AEs), sont des algorithmes basés sur le concept de la selection naturelle élaborée par Charles Darwin [Koza, 1999]. On distingue quatre types d'AEs : les algorithmes genetiques(AG), les strategies d'évolution (SE), la programmation

Chapitre 02 Métaheuristique d'optimisation

27

évolutionnaire (PE) et la programmation génétique (PG) [Benlahrache, 2007]. Dans ce qui suit, nous présentons les algoritmes génetiques et les algorithmes a évolution différantielle.

A. Algorithmes génétiques

Les algorithmes génétiques sont une abstraction de la théorie de l'évolution. Ce sont des algorithmes d'optimisation stochastique (aléatoire) fondés sur les mécanismes de la sélection naturelle de Darwin et sur les méthodes de combinaison des gènes introduites par Mendel pour traiter des problèmes d'optimisation.

Les algorithmes génétiques sont appliques dans des différents domaines comme : L'optimisation de fonctions numériques difficiles (discontinues, etc.), traitement d'images (alignement de photos satellites, reconnaissance de suspects, etc.), optimisation d'emplois du temps, apprentissage des réseaux de neurones, etc.

A .1.Éléments des algorithmes génétiques

Gène: Un gène est le plus petit élément dans l'AG. Généralement, il correspond à un seul symbole (0 ou 1 dans le cas de codage binaire).

Chromosome : Un chromosome est constitué d'une suite finis de gènes.

Individu : un individu est une forme qui est le produit de l'activité des gènes. Pour un AG, il est réduit à un chromosome et on l'appelle donc chromosome ou individu pour désigner un même objet [Laboudi, 2009].

Population : une population est un ensemble d'individus.

Génération: une génération est un ensemble des opérations qui permettent de passer d'une population à une autre. Ces opérations sont : sélection des individus de la population courante, croisement, mutation et enfin l'évaluation des individus de la nouvelle population.

A.2. Fonctionnement générale d'un algorithme génétique

Le principe général du fonctionnement d'un algorithme génétique standard est présenté par l'algorithme suivant [Souquet et Radet, 2004]:

Chapitre 02 Métaheuristique d'optimisation

28

Algorithme 2.1 : Algorithme évolutionnaire génétique

Début

Initialiser la population initiale P.

Évaluer P.

Tant Que(Pas Convergence) faire

P ' = Sélection des Parents dans P

P ' = Appliquer Opérateur de Croisement sur P '

P ' = Appliquer Opérateur de Mutation sur P '

P = Remplacer les Anciens de P par leurs Descendants de P '

Évaluer P

Fin Tant Que

Fin

A.3.Mécanismes de fonctionnement d'un AG

A.3.1.Codage des chromosomes

Les chromosomes de la population doivent être codés selon le problème présent, donc le choix de codage est très important. Parmi les techniques utilisées pour coder les individus, on distingue les codages : binaire et réel.

? Codage binaire

Le codage binaire permet de coder le chromosome par une chaine binaire, chaque gène de ce chromosome est représenté par une valeur binaire 0 ou 1. Certainement, ce codage le plus utilisé car il possède plusieurs avantages, parmi lesquels, on trouve qu'il permet la création d'opérateurs de croisement et de mutation facilement.

1

0

0

1

1

Figure 2.3 Codage binaire d'un chromosome.

? Codage réels

Ce type de codage permet d'utiliser des nombres réels pour coder les gènes des individus de la population. Le codage réel est plus pratique que le codage binaire car, il est plus proche à l'environnement des problèmes à résoudre.

Chapitre 02 Métaheuristique d'optimisation

29

2

4

6

5

3

Figure 2.4 Codage réel d'un chromosome.

A.3.2. Initialisation de la population

L'initialisation sert à constituer la population initiale. C'est une étape très importante car si la population n'est par uniformément répartis au départ, l'évolution risque de se concentrer sur un optimum local [Labed, 2006].

A.3. 3.Évaluation

Pendant les étapes d'évaluation, la fonction d'évaluation est calculée pour chaque individu, le but est d'évaluer chaque individu par rapport à un problème donné. Les individus ayant la valeur de la fitness la plus élevée seront appelés les meilleurs individus, le choix d'une fonction d'évaluation appropriée au problème est critique [Labed, 2006].

A.3.4.Sélection des parents

L'idée générale de cette étape basée sur la sélection parmi est que tous les individus de la population les parent qui assureront la reproduction, la probabilité de survivre d'un individu sera directement relié à son efficacité au sein de la population. Il existe des différents principes de sélection, parmi eux on peut citer:

? Sélection par roulette Wheel (loterie biaisée)

La sélection par roulette est basée sur la division de la roulette en secteurs, chaque secteur correspond à un individu, en tourne la roulette n fois pour sélectionner n individus. Les individus ayant la plus grande valeur de fitness auront plus de chance d'être choisis [Souquet et Radet, 2004].

? Sélection élitiste

Cette méthode consiste à sélectionner les meilleurs n individus de la population après l'avoir triée de manière décroissante selon leurs fitness [Souquet et Radet, 2004].

? Sélection par tournois

Cette méthode consiste à sélectionner deux individus aléatoirement pour s'évaluer, puis on sélectionner le meilleur individu et on répète ce processus n fois pour obtenir n individus de population P. La variance de cette technique est élevée [Souquet et Radet, 2004 ; Laboudi,

Chapitre 02 Métaheuristique d'optimisation

30

2009]. En effet, on peut accorder plus ou moins de chance aux individus peu adaptés [Laboudi, 2009].

A.3.5.Croisement

Pour enrichir la diversité de la population il faut faire un croisement, car s'il n y a pas de croisement les enfants sont exactement des copies de leurs parents. L'operateur de croisement se déroule en trois étapes : au début il faut faire un choix aléatoire de deux parents et on choisir un ou plusieurs points de croisements, ensuite on échange les valeurs des deux parents par rapport de ce point de croisement. Il existe plusieurs types de croisement à point, à 2point ou à plusieurs points.

A.3.6.Mutation

L'operateur de mutation consiste à modifier aléatoirement avec une certaine probabilité la valeur d'un gène à partir d'une seule chaîne initiale, cet opérateur garantit la diversité de la population. On distingue plusieurs types de mutation selon le type de codage utilisé, dans le codage binaire il consiste simplement à changer un 0 en un 1 ou l'inverse. La probabilité Pm de mutation est généralement choisi très faible (?comprise entre 0.01 et 0.001) [Souquet et Radet, 2004].

A.3.7.Remplacement

Cet opérateur est basé, comme l'opérateur de sélection, sur la fitness des individus. Son rôle consiste à déterminer les chromosomes parmi la population courante constituant la population de la génération suivante. Cette opération est appliquée après l'application successive des opérateurs de sélection, de croisement et de mutation. On trouve essentiellement 2 méthodes de remplacement différentes : Le remplacement stationnaire et le remplacement élitiste.

A.4.Critères d'arrêts

Pour arrêter l'algorithme génétique il ya plusieurs critères d'arrêt sont possibles. On peut arrêter l'algorithme s'il n'y a pas un changement de la fonction de fitness d'une population pour un nombre de génération spécifié. On peut aussi arrêter l'algorithme lorsque le nombre de génération est atteint ou lorsque le temps spécifique s'écoule.

Chapitre 02 Métaheuristique d'optimisation

31

Chapitre 02 Métaheuristique d'optimisation

A.5.Avantages et désavantages d'AG

a) Avantages d'AG

On peut citer les avantages d'AGs dans les points suivants [Moutairou, 2009 ; Whitley, 1994 ; Yoon et al., 1994 ; Draa, 2011]:

- Il fait un bon équilibre entre l'exploration et l'exploitation de l'espace de recherche. - La recherche de l'optimum est globale.

b) Désavantages d'AG

On peut citer les limites d'AGs dans les points suivants [Moutairou, 2009 ; Whitley, 1994 ; Yoon et al., 1994 ; Draa, 2011] :

- Les algorithmes génétiques convergent rapidement vers une solution locale dans les premiers stades, mais la convergence vers une solution optimale peut nécessiter plus de temps.

- La qualité des résultats obtenus est tributaire de l'ajustement des paramètres de l'algorithme (à savoir, les probabilités de croisement et de mutation) qui est souvent empirique.

B. Évolution Différentielle

L'évolution différentielle est un algorithme développé par Storn et Price en 1995, qui est basé sur population. Il utilise les mêmes opérateurs de l'algorithme génétique : croisement, mutation et sélection, car il est inspiré par ces algorithmes, mais il basé sur une nouvelle stratégie de mutation. Dans le chapitre suivant nous essayerons d'étudier cet algorithme en détail, car c'est le noyau de notre approche pour le recalage.

4.1.2. Optimisation par essaim de particules

L'optimisation par essaim de particules (en Anglais Particle Swarm Optimization PSO) est une technique d'optimisation globale stochastique développée par Eberhart et Kennedy en 1995 [Kennedy et al., 1995], qui utilise une population de solutions potentielles (particules) pour développer une solution optimale au problème. Le degré d'optimalité est mesuré par une fonction fitness (aptitude) définie par l'utilisateur. Cette technique est inspirée par le comportement social des essaims d'oiseaux, ces animaux caractérisent par le concept

32

d'intelligence commune où chaque particule ne possède qu'une information partielle de son environnement qui collectivement permet de gérer intelligemment le groupe [Barrette, 2008].

Les particules sont les individus et elles se déplacent dans l'hyperespace de recherche. Le processus de recherche est basé sur deux règles [Dutot, Olivier] :

1. Chaque particule est dotée d'une mémoire qui lui permet de mémoriser le meilleur point par lequel elle est déjà passée et elle à tendance à retourner vers ce point.

2. Chaque particule est informée du meilleur point connu au sein de son voisinage et elle va tendre à aller vers ce point.

? Modèle d'optimisation par essaim de particules de base

L'essaim se compose d'un certain nombre de particules qui se déplacent dans l'espace de recherche, chaque particule p possède deux variables d'état où : x(t) est la position courante et v(t) est la vitesse courante, il possède aussi une petite mémoire où : p(t) est la meilleure position précédente, et g(t)est la meilleure p(t) de toutes les p?N(p) [Chikhi, 2010].

Les expressions suivantes pour les positions et les vitesses des particules dans le prochain pas de temps sont données par ces équations récursives :

#177; 1	=	#177;	1 #177; 2	2.1
#177; 1	=	#177;	#177; 1	2.2

Où , qui limite chaque coordonnée de v(t) à V= [-vmax, vmax] et C1, C2 qui déterminent

l'influence de p(t) et g(t) dans la formule de mise à jour de vitesse [Chikhi, 2010].

L'algorithme de PSO possède plusieurs avantages. En effet, est un algorithme simple a implémenter, très efficace dans la recherche global, facile à paralléliser pour le traitement concurrent et enfin il possède très peu de paramètres à régler. Cependant, il possède certaines limites comme le taux de convergence lente à l'étape de la recherche locale [Nebti, 2005], et le problème de convergence prématurée dans le cas où le taux de convergence est rapide.

4.1.3. Optimisation par les colonies de fourmis

L'optimisation par colonie de fourmis est une technique d'optimisation basée sur la population. Elle a été introduite pour la première fois par Dorigo. Les algorithmes de colonies de fourmis sont nés d'une constatation simple : les insectes sociaux, et en particulier les fourmis, résolvent naturellement des problèmes complexes. Un tel comportement est possible

Chapitre 02 Métaheuristique d'optimisation

car les fourmis communiquent entre elles de manière indirecte par le dépôt de substances chimiques, appelées phéromones, sur le sol. Ce type de communication indirecte est appelé stigmergie¹ [Cooren, 2008].

La principale illustration de ce constat est donnée par la « Figure 2.14 ». On voit sur cette Figure que, si un obstacle est introduit sur le chemin des fourmis, les fourmis vont, après une phase de recherche, avoir tendance à toutes emprunter le plus court chemin entre le nid et l'obstacle. Plus le taux de phéromone à un endroit donné est important, plus une fourmi va avoir tendance à être attirée par cette zone. Les fourmis qui sont arrivées le plus rapidement au nid en passant par la source de nourriture sont celles qui ont emprunté la branche la plus courte du trajet. Il en découle donc que la quantité de phéromones sur ce trajet est plus importante que sur le trajet plus long.

Ces algorithmes utilisés pour résoudre plusieurs problèmes comme le problème de voyageurs de commerce.

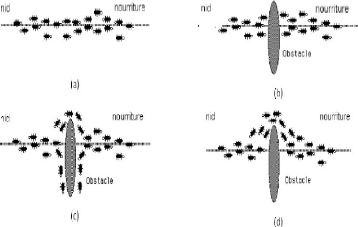
33

Figure 2.5 Détermination du plus court chemin par une colonie de fourmis. (a) Situation initiale, (b) Introduction d'un obstacle, (c) Recherche du chemin optimal, (d) Prédominance du chemin optimal.

¹Interactions sociales indirectes

Chapitre 02 Métaheuristique d'optimisation

34

Chapitre 02 Métaheuristique d'optimisation

35

Algorithme 2.2 : optimisation par colonies de fourmis

Début

Initialiser les traces à 0 pour toute décision possible d

Tant qu'aucun critère d'arrêt n'est satisfait faire

Construire AI solutions en tenant compte de la force gloutonne et de la trace

Mettre à jour les traces ainsi que la meilleure solution rencontrée;
Fin tant que

Fin

4.2.Métaheuristique a base de voisinage

Les méthodes à base de voisinage (ou méthodes de recherche locale) sont des méthodes qui travaillent sur un seul point de l'espace de recherche à un instant donné.

4.2.1. Recuit simulé

La méthode du Recuit Simulé (RS) a été proposée par des chercheurs d'IBM en 1983 [KIR, 83], cette méthode est une technique de recherche locale fondée sur une analogie entre un processus physique (recuit) et le problème d'optimisation. Cette méthode en tant que métaheuristique s'appuie en effet sur des travaux visant a simulé l'évolution d'un solide vers son état d'énergie minimale.

Le recuit simulé s'appuie sur l'algorithme de Métropolis-Hastings, qui permet de décrire l'évolution d'un système thermodynamique. Par analogie avec le processus physique, la fonction à minimiser deviendra l'énergie E du système. On introduit également un paramètre fictif, la température T du système.

L'algorithme du recuit simulé part d'une solution donnée, et la modifie itérativement jusqu' à le refroidissement du système. Les solutions trouvées peuvent améliorer le critère que l'on cherche à optimiser, on dit alors qu'on a fait baisser l'énergie du système, comme elles peuvent les dégrader. Si on accepte une solution améliorant le critère, on tend ainsi à chercher l'optimum dans le voisinage de la solution de départ [Layeb, 2010].

La méthode du Recuit Simulé possède plusieurs avantages, c'est une méthode générale et facile à programmer et se produit des solutions de bonne qualité, mais elle peut présenter quelque limite comme le problème de temps de calcul excessif dans certaines applications et le nombre important de paramètres à ajuster [Saha, 2010].

Algorithme 2.3Optimisation par le recuit simulé

Début

Déterminé une configuration aléatoire S

Choix des mécanismes de perturbation d'une configuration

Initialiser la température T

Tant que la condition d'arrêt n'est pas atteinte faire

Tant que là l'équilibre n'est pas atteint faire

Tirer une nouvelle configuration S'

Appliquer les règles de metropolis

Si f(S') < f(S)

Smin = S'

fmin = f(S')

Fin Si

Fin Tant que

Décroitre la température

Fin Tant que

Fin

4.2.2. Recherche Tabou

La recherche tabou est une métaheuristique de recherche locale a été présentée par Fred Glover en 1986, l'idée est de passe d'une solution valide a une autre les deux solutions sont dites alors voisines. L'ensemble des solutions que l'on peut atteindre à partir d'une solution s'appellera alors un voisinage.

On commence par l'initialisation d'un liste vide de longueur maximale, cette liste contiendra tous les mouvements que l'on a déjà effectué et deviennent donc interdits, cette méthode permet d'éviter de tomber dans un cycle de mouvement répétitives, donc à chaque itération, on va choisir le meilleur mouvement possible dans le voisinage de la solution actuelle sans faire de mouvement contenus dans la liste tabou «liste de mouvements interdits».

Dans sa forme de base, l'algorithme de recherche tabou présente l'avantage de comporter moins de paramètres que l'algorithme de recuit simulé. Cependant, l'algorithme n'étant pas toujours performant, il est souvent approprié de lui ajouter des processus d'intensification et/ou de diversification, qui introduisent de nouveaux paramètres de contrôle [Glover et al., 1997 ; Cooren, 2008]. L'algorithme général de la recherche tabou est le suivant [Rodriguez-Tello et al, 2005] :

Chapitre 02 Métaheuristique d'optimisation

Algorithme 2.4Optimisation par la recherche tabou

Début

S = solution initiate

Best = S

Répéter

Sbest = meilleur voisin de S

si(fitness(Sbest) < fitness (Best)) Alors

Best = Sbest

Mise à jour de la liste Tabou

S = Sbest ;

Jusqu'à(critère de fin est vérifié)

Retourner Best ;

Fin

4.2.3. Méthode de la Descente (Hill-Climbing)

Cette méthode est très simple et ancien, elle procède de manière itérative, en choisissant à chaque itération un point dans le voisinage de la solution courante. S'il est meilleur c'est à dire il améliore la solution courante, il devient la nouvelle solution courante, sinon un autre point est choisi, et ainsi de suite c'est à dire que ce procédé est répété aussi long temps que la valeur de la fonction objectif diminue. La recherche s'interrompe des lors qu'un minimum local de f est atteint [Troudi, 2006].

La méthode de Hill climbing possède plusieurs avantages, c'est une méthode intuitive et simple mais présenté aussi quelque limite comme le problème de minimum local et la lenteur de la méthode [Layeb, 2010].

Algorithme 2.5 : Optimisation par la méthode de descente

Début

Générer et évaluer une solution initiale s

Tant que La condition d'arrêt n'est pas vérifiée faire

Modifier s pour obtenir s' et évaluer s'

Si (s'est meilleure que s) alors

Remplacer s par s'

Fin si

Fin tant que

Retourner s

Fin

36

Chapitre 02 Métaheuristique d'optimisation

37

4.3 Méthodes hybrides

Une autre façon d'améliorer les performances d'un algorithme ou de combler certaines de ses lacunes consiste à le combiner avec une autre heuristique [Talbi, 2000 ; Benlahrache, 2007]. Les algorithmes hybrides sont considérés parmi les méthodes les plus puissantes pour résoudre les problèmes d'optimisation. Cette puissance réside dans la combinaison des deux principes de recherche de meilleure solution, fondamentalement différents. Il existe plusieurs types d'hybridation parmi eux, on peut citer: l'hybridation entre les méthodes de recherche globale et locale, l'hybridation entre les métaheuristiques et les méthodes exactes et l'exécution en parallèle qui consiste à lancer en parallèle l'exécution de la même métaheuristique.

5. Conclusion

Dans ce chapitre nous avons présenté des méthodes approchées utilisées pour la résolution de problèmes d'optimisations connues sous le titre de métaheuristique. Les métaheuristiques sont des méthodes stochastiques qui visent à résoudre un large panel de problèmes, le but visé par ces méthodes est d'explorer l'espace de recherche efficacement afin de déterminer des solutions (presque) optimales, elles ont rencontrées un vif succès grâce à leur simplicité d'emploi mais aussi à leur forte modularité. Malgré les bons effets des métaheuristiques, elles peuvent donner de mauvais résultats.

La performance d'une métaheuristique dépend de plusieurs facteurs. La limite majeure de métaheuristique dépend du paramétrage, car il existe très peu de règles universelles permettant de connaître le paramétrage idéal et généralement, seules l'expertise et l'expérience de l'utilisateur permettront de faire un choix.

Dans le chapitre suivant, nous présentons une méthode basée-population appelée algorithmes à évolution différentielle (ED). C'est cette approche qu'on va étendre pour la résolution du problème de recalage d'images médicales.

Chapitre 3 :

«If evolution really works, how come mothers only have two hands? »

Milton Berle

1. Chapitre 3 Évolution différentielle

38

Introduction

Évolution Différentielle (ED) est une heuristique de recherche introduite par Storn et Price en 1997. C'est un algorithme d'optimisation globale simple mais très efficace. Et qui fut initialement créé pour résoudre des problèmes continus. L'ED est aussi devenu un outil puissant pour résoudre les problèmes d'optimisation qui se posent dans les applications financières (pour l'ajustement des modèles sophistiqués et pour effectuer la sélection du modèle) [Ardia, Boudt, 2011] et dans les applications en temps réelle [Draa, 2011].

Dans ce qui suit, nous expliquons l'algorithme à évolution différentielle, nous donnons ses principes, ses variantes, ses avantages et ses limites.

2. Principe de l'évolution différentielle

Évolution différentielle a été conçue comme une méthode de recherche parallèle, directe, et stochastique. L'idée générale de cet algorithme est basée sur l'utilisation d'une nouvelle stratégie de mutation. Elle consiste à ajouter la différence vectorielle pondérée entre deux individus à un autre. Ensuite, une opération de croisement entre l'individu mutant et l'individu correspondant de la population aura lieux. Finalement, une sélection gloutonne entre ces deux, le père et le fils, va décider lequel des deux, ayant la meilleure fitness, survivra dans la prochaine génération [Draa, 2011].

Dans sa version de base il existe trois paramètres : la taille de la population NP, le taux de croisement CR et le facteur de différence F.

Les individus (solutions) sont représentés par des vecteurs M-dimensionnels de valeurs réelles, où M est le nombre des paramètres à optimiser et NP est la taille de la population. Un algorithme à évolution différentielle peut être présenté comme suit [Ston, price, 1997] :

2.1. Mutation différentielle

Une opération de mutation consiste à créer un nouvel individu fils correspondant à un individu père à partir de trois autres individus choisis aléatoirement selon l'équation (3.1) [Ston, price, 1997] :

, #177;1 = 1, #177; ( 2, 3, ) (3.1)

Où : i, r1, r2, r3 {1,...... NP} sont des entiers mutuellement différents, et F est un facteur

constant réel positif servant à contrôler la variation différentielle ( 2, 3, ).

Chapitre 3 Évolution différentielle

Le principe de cette mutation est illustré dans la figure 3.1.

2.2 Croisement différentielle

Le croisement est introduit en vue d'augmenter la diversité de la population, il combine l'individu mutant obtenu par l'opération de mutation avec l'individu cible pour générer

un individu d'essai selon l'équation (3.2) [Ston, price, 1997] :

, 0,1 > (0, ) . (3.2)

39

,

Où : (0, 1) est un nombre aléatoire entre 0 et 1, et CR [0, 1] est le taux de croisement.

L'ajout de la condition 0, . permet d'éviter de créer des clones en s'assurant que les

nouvelles solutions aient au moins une composante issue du vecteur mutant [Mathieu, 2008].

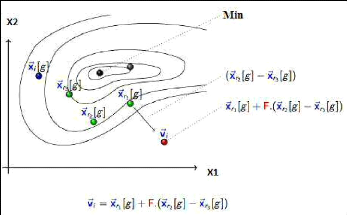
Figure 3.1 Mutation différentielle [Dutech, 2010].

Ce croisement (développé par Stone et Price) est appelé croisement binomial. Il existe un autre type de croisement fréquemment utilisé dans des variantes plus récentes de l'ED que celle de Storn et Price, c'est le croisement exponentiel. Dans ce type de croisement, à partir d'une position choisie aléatoirement, T composants successifs de l'individu mutant, sont transmis à l'individu d'essai [Draa, 2011], comme le montre la figure 3.2.

Chapitre 3 Évolution différentielle

40

2.3 Sélection

Pour la sélection, toutes les solutions dans la population ont la même chance d'être sélectionnées comme des parents, selon la fonction d'adaptation. La sélection entre l'individu cible et l'individu d'essai, va décider lequel des deux individus survivra dans la prochaine génération, selon la qualité de leurs finesses, comme indiqué dans l'équation suivante [Ston, price, 1997 ; Draa, 2011 ; Neggaz et Benyettou] :

X= , < ( )

> ( ) (3.3)

,

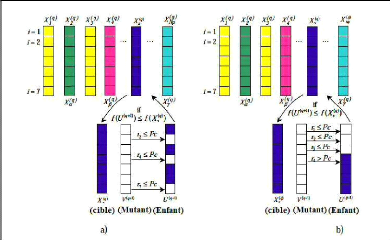
Figure 3.2 Croisement différentiel : a) croisement binomial, b) croisement exponentiel
[Purcina, Saramago, 2008].

2.4Critère d'arrêts

Le critère d'arrêt d'un AED est généralement l'un des suivants :

a) Temps écoulé : L'algorithme s'arrête s'il n'y a pas un changement de la fonction fitness d'une population pour un nombre de génération spécifié [Kajee-Bagdadi, 2007].

b) L'obtention de la qualité requise de la fonction d'adaptation [Draa, 2011].

c) Nombre maximal de génération : L'algorithme s'arrête quand le nombre maximal de génération est atteint [Kajee-Bagdadi, 2007].

Chapitre 3 Évolution différentielle

Le principe général du fonctionnement d'un algorithme à évolution différentielle est présenté par l'algorithme suivant :

Algorithme 3.1 Évolution différentielle (ED)

,

Début

G 1

Choisir NP, F et CR

PG initialiser la population aléatoirement

Tant que (le critère d'arrêt n'est pas atteint) Faire Pour (chaque individu , de PG) Faire

Choisir les parents auxiliaires , , , et

Créer l'individu enfant	,	en utilisant la mutation et le
Croisement différentiels Appliquer la sélection + + Meilleur( Fin Pour G G+ 1 Fin tant que Fin			, , , )

DE/rand to best /1:

, = , + , , ) + ( 1, 2, . (3.4)

41

3. Variantes pour l'évolution différentielle

L'algorithme à évolution différentielle est connu sous la forme DE/x/y/z, où la variable x est le vecteur de base pour la mutation. La sélection de ce vecteur est purement aléatoire (rand), mais il existe également deux autres versions permettant de favoriser le meilleur vecteur (best), (rand-to-best). La variable y détermine le nombre de vecteurs de différences utilisés dans la mutation de x. La variable z est le mode de croisement utilisé, exponentiel (exp) ou binomial (bin).

Les variantes d'AEDs diffèrent généralement entre eux par le type de mutation utilisé qui permet être résumés dans les équations suivants [Ston, price, 1997 ; Neggaz et Benyettou] :

DE/rand/1 :

= 3, + 2, . (3.4) , 1,

DE/best /1 : , = , + 2, . (3.4)

1,

DE/rand/2 : DE/best /2 :

= 1, + 3, ) + ( 4, 5, . (3.4) , 2, = , + 2, ) + ( 3, 4, . (3.4) , 1,

Chapitre 3 Évolution différentielle

Où :

,

42

: Individu de la génération courante G.

x : ensemble de population et F : constante de mutation [0,2].

, , 1, , _2, , _3, , _4, ,, sont aléatoirement choisis dans la génération courante.

4. Avantages et limites de l'évolution différentielle

4.1 Avantages de l'évolution différentielle

On peut citer les avantages d'évolution différentielle dans les points suivants [Das et Suganthan, 2011 ; Draa, 2011 ; Karaboga, Okdem, 2004] :

- L'ED est plus simple à implémenter qu'autres approches évolutionnaires. Pour cette raison est le plus utilisé par les non-informaticiens.

- Trouver le minimum global réel quel que soit les valeurs de paramètres initiales et convergence rapide.

- On peut contrôler AED sans difficultés car il possède un nombre de paramètres de contrôles limité (CR, F et NP dans la version de base).

- La complexité spatiale de l'ED est réduite, quand on la compare à d'autres algorithmes performants célèbres tels que le CMA-ES. Cette caractéristique permet d'étendre l'ED pour résoudre des problèmes d'optimisation de grandes dimensions.

- Malgré sa simplicité, l'évolution différentielle offre des performances remarquablement meilleures que celles offertes par plusieurs autres approches d'optimisation, notamment les AEs et le PSO.

4.2 Limites de l'évolution différentielle

Malgré son efficacité et sa robustesse, l'ED souffre principalement des limites

suivantes [Draa, 2011] :

- Comme tous autres algorithmes d'optimisation, la performance d'AED est très

sensibles des valeurs des paramètres F, CR et NP.

- le choix des paramètres est très dépendant du problème à résoudre.

- Le problème de convergence prématurée.

- Comme tout autre AE, la performance d'un AED se détériore avec la croissance de

la dimension de l'espace de recherche.

Chapitre 3 Évolution différentielle

43

? Dans, l'évolution différentielle, le concept de voisinage, concept clé dans les stratégies d'évolution est manquant.

5. Conclusion

Dans ce chapitre on a présenté l'évolution différentielle : ses principes, son comportement général, quelques variantes de l'évolution différentielle ont été abordées, ainsi que ses avantages et ses limites.

Dans le chapitre suivant, nous présenterons deux nouveaux algorithmes à évolution différentielle pour le recalage d'images, à savoir : un algorithme différentiel linéairement adaptatif et un algorithme différentiel périodiquement adaptatif.

Chapitre 4 :

« Savoir où l'on veut aller, c'est très bien ; mais il faut encore montrer qu'on y va »

Emil ZOLA

1. Chapitre 4 Contributions

44

Introduction

Ce chapitre est consacré à la description de nos deux contributions, à savoir: adaptation linéaire et adaptation périodique des paramètres pour le recalage d'images médicales multimodales. L'application de nos algorithmes pour déférents types de transformations (rigide, rigide avec zoom et affine) est décrite dans la première partie du chapitre. Dans sa deuxième partie, le chapitre analyse et discute les différents résultats expérimentaux.

2. Formulation de problème

Le problème traité dans ce travail peut être formulé comme suit. Étant données deux image I1 et I2 obtenues de capteur identiques (recalage monomodale), ou différents (recalage multimodal), il s'agit de trouver la transformation géométrique T qui permet d'aligner correctement les deux images.

Les algorithmes proposés, basés sur l'évolution différentielle, permettent d'estimer la transformation géométrique T. Il s'agit d'une approche iconique puisque les deux algorithmes considèrent la totalité de l'information photométrique contenue dans les images.

Pour ce faire, on doit d'abord définir d'une représentation des solutions adoptée, d'une mesure de similarité qui permet une évaluation quantitative de la relation entre deux images lors de leur superposition, et d'une stratégie de recherche.

2.1. Représentation des individus

Formellement, les individus dans un Algorithme à Évolution Différentielle (AED) sont représentés par des vecteurs Narg-dimensionnels de valeurs réelles xi V i E [1, Np] , où: Narg est le nombre des paramètres à optimiser et Np est la taille de la population. La longueur de chaque individu dépend du type de la transformation recherchée.

10.3

23.56

30.50

0.8

Figure 4.1 Un individu pour une Transformation Similitude.

Chapitre 4 Contributions

45

2.2. Espace de recherche

Nous avons appliqué notre algorithme dans les trois transformations Suivantes.

2.2.1 Transformation rigide

Dans ce type de transformation qui est la composition d'une translation et d'une rotation, on a trois paramètres : dx, dy pour la translation et ? pour la rotation, la nouvelle position (?', ?') d'un point (?2, ?2) de la deuxième image est calcule comme suit :

?

?'_ (d?l (c??? ????) (x2) ?' -- _\d?l + `--???? ????) `Y2) 4.1

Les paramètres dx et dy appartiennent à l'intervalle [-20, 20] tandis que ? appartient à l'intervalle [-50, 50] degré. Un individu encode les trois paramètres : dx, dy, ?. Donc il s'agit alors de chercher dans l'espace R³ les valeurs des paramètres donnant la meilleure superposition des deux images.

2.2.2 Transformation rigide avec zoom (similitude)

Cette transformation formée par la combinaison d'une translation, une rotation et un changement d'échelle S (agrandissement ou réduction), la nouvelle position de chaque pixel dans l'image résultante (?', ?') d'un point (?2, ?2) de l'image à recaler est calcule comme suit :

?

?'\ _ (^d?l (c?se ????).(x2)
?')^--\"YI^+S~ `--???? ????/`?2/ 4.2

Le facteur d'échelle s appartient à l'intervalle [0, 2]. Un individu encode donc les quatre paramètres : dx, dy, ? et S. Donc il s'agit alors de chercher dans l'espace R⁴ les valeurs des paramètres donnant la meilleure superposition des deux images.

2.2.3. Transformation affine

Pour la transformation affine, l'individu encode les six paramètres : ??, ??, ?11 , ?12, ?21, ?22 tel que chaque point dans l'image I2 est calculé à partir de sont correspondant dans I1 comme suit :

??1 _ (d?l ?' -- \d?) + ?

?11 ?21

?12) ?22/

(x2 `Y2?

4.3

Les paramètres ?11 , ?12, ?21, ?22 appartiennent à l'intervalle [-2, 2].

Chapitre 4 Contributions

46

2.3. Fonction objectif

Pour l'évaluation d'une transformation, on a besoin d'une mesure de similarité. Il existe plusieurs mesures de similarité parmi lesquelles nous citons : le coefficient de corrélation, le critère quadratique, la corrélation croisée normalisée, etc. Ces mesures sont simples et facile à programmer mais ne sont pas adaptées au cas d'un recalage multi modale où les images ont des structures similaires mais des caractéristiques différentes. L'information mutuelle est l'une des mesures adaptée à la comparaison d'images multi sources. Elle est définie par l'expression :

IM (I1, I2) = H (I1) + H (I2) - H (I1, I2)

Les entropies séparées H(I1) et H(I2) mesurent la complexité des images I1 et I2. L'entropie jointe H (I1, I2) mesure la quantité d'information que les images I1 et I2 apportent en même temps. Comme nous avons dit dans le premier chapitre, L'information mutuelle est maximale dans le cas d'une totale dépendance, et minimale dans le cas contraire.

2.4. Stratégie de recherche

L'information mutuelle est maximale dans le cas d'une parfaite superposition. Donc, l'idée est de définir une stratégie de recherche ayant pour objectif de maximiser cette mesure. Le problème revient donc à explorer l'ensemble des paramètres pour maximiser cette mesure.

3. Contributions

L'algorithme à évolution différentiel de base, comme déjà mentionné dans le chapitre précédent, soufre du problème de convergence prématurée. Par exemple, la figure 4.3 montre l'évolution de l'information mutuelle équivalente au recalage des images de la figure 4.2. On peut bien voir que l'algorithme de base souffre du problème des minima locaux. Ceci est principalement causé par le fait qu'avec le temps, les individus deviennent égaux à cause de l'impact de l'opérateur de mutation et donc, la mutation différentielle sera incapable de créer la diversité au sein de la population.

Pour résoudre ce problème, on a proposé deux nouvelles extensions de l'AED. Ces deux variantes sont nommées respectivement : Evolution Différentielle Linéairement Adaptative (EDLA) et Evolution Différentielle Périodiquement Adaptative (EDPA). Dans ce qui suit, ces deux variantes seront expliquées.

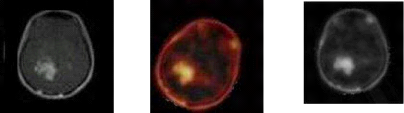
Chapitre 4 Contributions

47

Image de référence Image d'entrée Image Résultat

Figure 4.2 Recalage rigide multimodale.

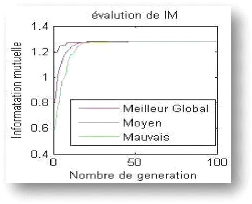
Figure 4.3 Le meilleur global, le moyen et le minima locaux aux cours du recalage rigide des images de la figure 4.2

3.1. Evolution Différentielle Linéairement Adaptative (EDLA)

Dans cette variante, nous avons défini les deux facteurs de mutation (Fd) et de croisement (Fc), généralement donnés come des constantes dans la version de base, par les deux équations linéaires suivantes :

?

?? = ????? - ?????? - ????? ? * ??/???? = ????? + ?????? - ????? ? * ??/?? (4.1)

Où ?? ? ?????? , ????? ? = ?0.5,1? et ?? ? ?????? , ????? ? = ?0.5,1?. It : itération en cours et Ng : le nombre maximum de générations.

Chapitre 4 Contributions

48

On voit bien de cette formule que Fd décroit avec le temps et Fc accroît avec le temps.

3.2. Evolution différentielle périodiquement adaptatif (EDPA)

Dans la deuxième de nos contributions, le facteur de mutation Fd est contrôlé par l'équation sinusoïdale suivante :

iFd = sjn(f * j) * j/Ng 4.2

Fc = 0

Où : j E{1,...... Ng}; Ng : est le nombre maximal de génération ; et f est la fréquence. Le signe de facteur de mutation représente la direction de graph.

Dans cette contribution nous avons initialisé le facteur de croisement (Fc) à la valeur 0. Puisque l'équation périodique est capable de gérer l'équilibre entre l'exploration et l'exploitation.

Comme le montre la figure 4.4, le facteur Fd change sa direction d'évolution d'une façon périodique. Ce qui donne lieu à une bonne balance entre l'exploitation et l'exploration.

L'avantage principal de cette deuxième approche est qu'on a pu éliminer l'opérateur de croisement de l'algorithme. Donc, une complexité algorithmique réduite est associé à cette deuxième variante.

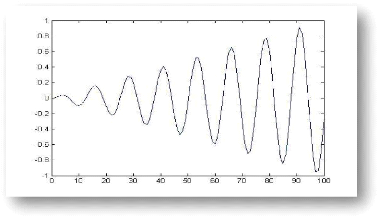
Figure 4.4 Équation sinusoïdale du facteur Fd

Chapitre 4 Contributions

49

3.3. Résultats expérimentaux

Le but de cette section est d'évaluer les performances des deux contributions à travers leur application sur des paires d'image de test. Des comparaisons statistiques sont fournies pour pouvoir comparer nos approches avec l'algorithme différentiel de base.

3.3.1. Résultats numériques

On présente ici quelques résultats numériques pour les trois types de transformations rigide, rigide avec zoom et affine. Pour chaque paire d'image, les algorithmes AED, EDLA et EDPA sont exécutés 30 fois pour les deux premiers types de recalage et 5 fois pour le cas du recalage affine (car plus de temps de calcul est nécessaire pour ce dernier). On donne la moyenne (moy), l'écart type (STD) et le médian (médian) de la valeur de l'information mutuelle sur l'ensemble des 30 exécutions ainsi que la meilleure (meilleurIM) et la mauvaise (mauvaisIM) valeur de l'information mutuelle. Ces résultats sont présentés dans le tableau 4.1.

? Le choix des paramètres :

Dans l'algorithme de base, Nous avons fixé le facteur de mutation Fd par la valeur 0.6301 et le facteur de croisement Fc par la valeur 0.7122. Ces valeurs sont tirées de la littérature, à base de travaux actant sur le réglage de paramètres de l'ED de base.

Nous avons utilisé une population (Np) de 20 individus, ces individus sont représentés par des vecteurs de 3, 4 et 6 variables réelles (pour différents types de transformation). Le nombre d'itérations a été choisi d'être 20, 50 et 100 pour le recalage rigide, la similitude et l'affine respectivement.

Les valeurs des paramètres propres aux contributions sont fixées empiriquement comme suit. Dans la première variante, EDLA, les bornes supérieures et inférieure des valeurs de Fd et de l'Fc sont égales à 0.9 et 0.4 respectivement. Dans la deuxième variante, la fréquence f de l'équation sinusoïdale est choisie d'être égale à 1/5.

50

Chapitre 4 Contributions

Paire d'images	AED			EDLA			EDPA
	Moy	STD	Médian	Moy	STD	Médian	Moy	STD	Médian
			MeilleurIM			MeilleurIM			MeilleurIM
			MauvaiseIM			MauvaiseIM			MauvaiseIM
PI1	1.1174	0.1043	1.1530 1.2169 0.8621	1.2777	3.4510e-004	1.2777 1.2782 1.2771	1.2762	0.0012	1.2765 1.2777 1.2744
PI2	0.9031	0	0.9031 0.9031 0.9031	1.1474	0.1581	1.2235 1.2360 0.7873	0.9480	0.0516	0.9360 1.0897 0.8772
PI3	1.0142	0.0279	1.0140 1.0496 0.9718	0.5220	0.2614	0.3536 0.9807 0.4573	0.7054	0.0974	0.7160 0.8542 0.6108

Tableau 4. 1 : Résultats numériques des transformations : rigide et rigide avec zoom et affine.

Le tableau 4.1 montre bien que les deux nouveaux Algorithmes EDLA et EDPA ont presque la même performance et donnent dans la majorité des cas (transformations rigide et similitude) de meilleurs résultats par rapport à l'ED de base. Aussi, on a gagné un opérateur dans la deuxième variante, EDPA ; et donc moins de temps de calcul sera nécessaire avec des performances similaires ou meilleures que l'algorithme de base.

3.3.2 Analyse qualitative des résultats

Dans cette section nous donnons quelques résultats qualitatifs des différentes approches.

a. Recalage rigide

Les figures 4.5 et 4.6 représentent respectivement, une paire d'images à être recalée et les résultats d'application des différentes variantes sur cette paire d'images dans le cas rigide.

Chapitre 4 Contributions

Image référence

Image d'entrée

Figure 4.5 Paire d'image : IRM-Tomographie calculée à rayon X(CTI).

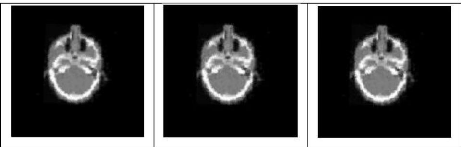
ADE : IM final : 1.037

EDLA : IM final: 1.034

EDPA : IM final: 1.037

51

Figure 4.6 Recalage rigide des images de la figure 4.5 par ADE (à gauche), (au milieu) EDLA et

EDPA (à droite).

D'une autre part, les graphes de la figure 4.7 présente à quel point les deux variantes proposées dans ce travail sont capable d'offrir un bon compromis entre exploration et exploitation. Il est claire des graphes de cette figure que la troisième approche est meilleure dans sa recherche des solutions : elle permet au même temps une bonne exploration de l'espace de recherche, et une préservation de la diversité de la population.

Chapitre 4 Contributions

Figure 4.7 les graphes d'IM correspondant aux images de la figure 4.6 : EDA (à gauche au-dessus), EDLA (à droite au-dessus) et EDPL (milieu au-dessous)

52

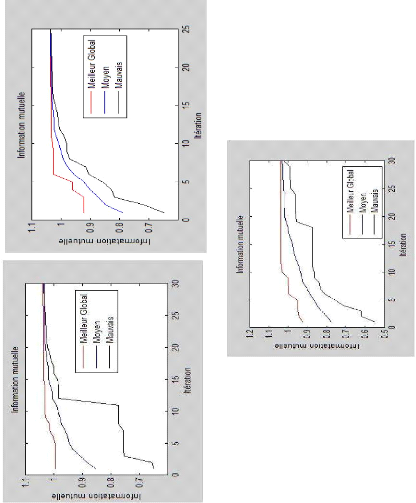
Chapitre 4 Contributions

b. Recalage rigide avec zoom

Les figures 4.8 et 4.9 représentent respectivement, une paire d'images à être recalée et les résultats d'application des différentes variantes sur cette paire d'images dans le cas de similitude. Une autre fois, la figure 4.10 montre la supériorité de la deuxième variante en termes de garantie du bon équilibre entre exploitation et exploration.

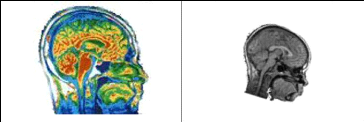
Image référence

Image recalé

Figure 4.8 : Paire d'image à recaler : à gauche IRM coloré et à droite Scanner.

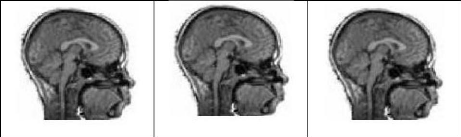
ADE : IM final : 1.3256

EDLA: IM final : 1,3268

EDPA : IM final : 1.3230

53

Figure 4.9 Recalage rigide avec zoom des images de la figure 4.8.

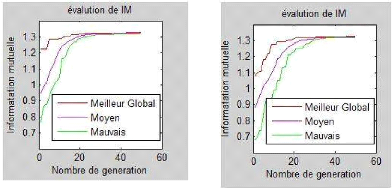
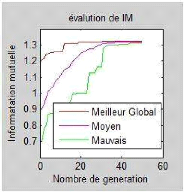
Chapitre 4 Contributions

54

Figure 4.10 les graphes d'IM correspondant aux images de la figure 4.9: EDB (à gauche au-dessus),
EDLA (à droite au-dessus) et EDPL (milieu au-dessous).

5. Interface Graphique

Une interface graphique permettant de faciliter la tâche de réglage de paramètres au médecin, qui n'est pas familier avec l'outil de développement (Matlab dans ce travail), a été développée. Cette interface permet : l'accès aux de images à être recalée, le réglage des paramètres et le lancement de la recherche de la meilleure transformation. Les figures 4.11 et 4.12 représente respectivement l'interface graphique de l'application avant et après exécution de l'algorithme en question.

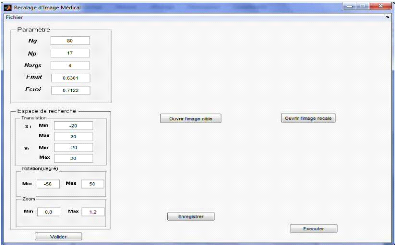
Chapitre 4 Contributions

55

Figure 4.11 : Interface de transformation similitude avant l'exécution.

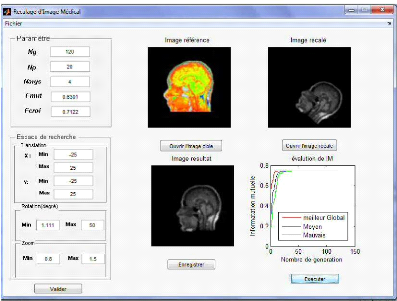
Figure 4.12 : Interface de transformation similitude après l'exécution.

Chapitre 4 Contributions

56

6. Conclusion

Dans ce chapitre deux nouvelles variantes de l'algorithme à évolution différentielle pour le recalage d'images médicales multimodales ont été proposées. Dans la première variante, une adaptation linéaire du facteur de mutation et de la probabilité de croisement est adoptée. Dans la deuxième, on a utilisé une adaptation sinusoïdale du facteur de mutation, et on n'a pas appliqué le croisement, car la mutation par facteur d'amplification périodiquement adapté a permis d'assurer le bon équilibre entre exploitation et exploration. Ceci a donné lieu à une complexité algorithmique relativement réduite.

Dans l'ensemble, les résultats expérimentaux ont montré que les deux approches proposées sont meilleures ou au moins concurrentes à l'évolution différentielle de base dans le cas du recalage d'images médicales multimodales.

57

Conclusion générale

Dans ce travail, nous avons traité un problème d'optimisation très important dans le domaine de traitement et d'analyse d'images médicales. Il s'agit du recalage d'images médicales multimodales. Nous avons choisi l'algorithme de l'évolution différentielle (ED) comme un algorithme d'optimisation de base, et l'avons étendu pour avoir deux nouvelles variantes: L'évolution Différentielle Linéairement Adaptative (EDLA) et l'Evolution Différentielle Périodiquement Adaptative (EDPA).

Une approche iconique basée sur la maximisation de l'information mutuelle a été adoptée, vu qu'elle est la plus adaptée au cas des images médicales multimodales.

Les trois variantes, algorithme de base et les deux contributions, ont été testés sur différentes paires d'images médicales multimodales. Chaque variante a été exécuté 30 fois (excepte 5 pour le cas affine) et la moyenne, l'écart-type et la médiane ont été calculés. A base de ces mesures statistiques, des comparaisons et des analyses ont été offertes. Les résultats obtenus ont démontré que les deux nouvelles variantes sont meilleures dans la majorité des cas que la variante de base.

Une difficulté majeure qu'on a rencontré lors de la réalisation de ce travail était le besoin à des supports de calculs puissants, vu la complexité algorithmique élevée des approches iconiques (calcul de l'information mutuelle). Même avec un processeur CORE I5, l'exécution reste trop lente.

Comme perspective, nous voulons étendre nos contributions pour la résolution d'autres problèmes réels ou académiques, ainsi que la réalisation d'une étude plus fine de leurs performances.

Bibliographie

[Ardia, Boudt, 2011] D. Ardia, K.Boudt, C.Peter, M.Mullen and B.G. Peterson, « Differential Evolution with DE optimé », the R Journal Vol. 3/1, ISSN 2073-4859, 2011.

[Atif, 2004] J.Atif, « Recalage non-rigide multimodal des images radiologiques par Information mutuelle quadratique normalisée», Thèse de doctorat, Université de Paris XI - Orsay, 2004.

[Barrette, 2008] M.Barrette, « Methode de Comparaison Statistique des Performances D'algorithmes Évolutionnaire », Mémoire, École de Technologie Supérieure, Université du Québec 2008.

[Bendiab, 2003] E.Bendiab, « Recalage d'image par système immunitaires », Mémoire de magistère, Universite Mentouri, Constantine.

[Benlahrache, 2007] N.Benlahrache, « Optimisation Multi-Objectif Pour l'Alignement Multiple de Séquences », Mémoire de magistère, Université Mentouri, Constantine, 2007.

[Bloch] I.Bloch, « Recalage d'images 2D et 3D », Présentation, Ecole Nationale Supérieur des Communications - CNRS UMR 5141 LTCI, Paris-France.

[Boudieb, 2008] D.boudieb, «Application des algorithmes évolutionnaires en optimisation géométrique de forme », Mémoire de magistère, Université M'Hamed Bougara, Boumerdes, 2008.

[Brown, 1992] L.G.Brown, « A suvery of image registration techniques », ACM Computing Survey, 1992.

[Cooren, 2008] Y.Cooren, « Perfectionnement d'un algorithme adaptatif d'Optimisation par Essaim Particulaire. Applications en génie médical et en électronique », Thèse de doctorat, Université de Paris, 2008.

[Collette, 2002] Y. Collette et P. Siarry, « Optimisation multiobjectif. Eyrolles », 2002. [Chikhi, 2010] S.Chikhi, « systèmes complexes », cours sac master 1 stic, 2010.

[Das et Suganthan, 2011] S.Das, et P. N.Suganthan, « Differential Evolution: A Survey of the State-of the-Art. », IEEE Trans. Evolutionary Computation, 2011.

[KIR, 83] S. Kirkpatrick, C.D. Gellat et M.P. Vecchi, « Optimization by simulated anealing », Science, 1983.

[Devarenne, 2007] I.Devarenne, « Études en recherche locale adaptative pour l'optimisation combinatoire », Thèse de doctorat, 2007.

[Draa, 2011] A. Draa , « Modèles pour les systèmes complexes adaptatifs pour la résolution de problèmes : Automates cellulaires apprenants quantiques et évolution différentielle quantique », Thèse de doctorat, Université Mentouri, Constantine, 2011.

[Dutot, Olivier] A.Dutot, D.Olivier, « Optimisation par essaim de particules Application au problème des n-Reines», document, Université du Havre.

[Dutech, 2010] A.Dutech, « Méta-heuristiques pour l'optimisation : Differential Evolution et Particle Swarm Optimisation. », Séminaire MAIA, LORIA, Mai 2010. http://www.loria. fr/~dutech/Papier/pres_optim_maia_100503.pdf.

[Faugeras, 1993] O.Faugeras, « Three Dimensional Computer Vision. The MIT Press »,1993.

[Frija et Mazoyer, 2002] G.Frija, B.Mazoyer, site web de la Fondation pour la recherche médicale, 2002. www.frm.org.

[Gardeux, 2008] V.Gardeux, « Recalage d'image et méthodes d'optimisation », 2008.

[Grova, 2005] C.Grova, « Simulations réalistes de données de tomographie d'émission monophotonique (TEMP) pour l'évaluation de méthodes de recalage TEMP/IRM utilisant des mesures statistiques de similarité : application dans le contexte de la fusion de données en épilepsie», Thèse de doctorat, Université De Rennes I, 2005.

[Kajee-Bagdadi, 2007] Z. Kajee-Bagdadi, «Differential Evolution Algorithms for Constrained Global Optimization», A thesis submitted to the Faculty of Science, University of the Witwatersrand, Johannesburg in fulfillment of the requirements for the degree of Master of Science, 2007.

[Karaboga, OKDEM, 2004] D.Karaboga, S.OKDEM «A Simple and Global Optimization Algorithm for Engineering Problems: Differential Evolution Algorithm», Department of Computer Engineering, Erciyes University, Kayseri-TURKEY, 2004.

[Purcina, Saramago, 2008] L.A.Purcina, P.Saramago, « Differential Evolution Applied to the Solution of Large Linear Systems », In ICEO, 2008.

[Kennedy et al., 1995] J. Kennedy, R.C. Eberhart, « Particle Swarm Optimisation », Proceedings of the IEEE International Conference on Neural Networks, IEEE, Press, 1995.

[Koza, 1999] J.R.Koza, Bennett, F.H., Andre, D., and Keane, M.A, « Genetic Programming III: Darwinian Invention and Problem Solving », Morgan Kaufmann, 1999.

[Larousse médicale, 2006] Larousse médicale, 2006.

[Labed, 2006] S.Labed, « Systèmes Complexes Adaptatifs Application au traitement des images », Université Mentouri, Constantine, 2006.

[Laboudi, 2009] Z.Laboudi, « Évolution d'automates cellulaires par algorithmes génétiques quantiques sur un environnement parallèle », Mémoire de magistère, Université Mentouri de Constantine, 2009.

[Layeb, 2010] A.Layeb, « Utilisation des Approches d'Optimisation Combinatoire pour la Vérification des Applications Temps Réel », Thèse de doctorat, Université Mentouri, Constantine, 2010.

[Lombaert et Thériault, 2005] H.Lombaert, J.Thériault, « Recalage par maximisation de l'information mutuelle », Rapport de projet, Ecole polytechnique de Montréal, 2005.

[Mashoul, 2004] S.Mashoul, « Optimisation par les systèmes complexes pour le recalage et la mise en correspondance en analyse d'image », Thèse de doctorat, Université Mentouri, Constantine, 2004.

[Nebti, 2005] S.Nebti, « Optimisation Par Écosystème Artificiels : Application à La

Segmentation D'images », Mémoire de magistère, Université Mentouri, Constantine, 2005.

[Neggaz et Benyettou] N.Neggaz, A.Benyettou, « Recalage des images médicales par les algorithmes évolutionnaires », Article, Université des Sciences et de la Technologie d'Oran, Oran.

[Noblet, 2006] V.Noblet, « Recalage non rigide d'images cérébrales 3D avec contrainte de conservation de la topologie», Thèse de doctorat, Université Louis Pasteur, Strasbourg, 2006.

[Roche, 2011] A.Roche, « Recalage d'images médicales par inférence statistique» Université de NICE - SOPHIA ANTIPOLIS, Version 2011.

[Rodriguez-Tello et al, 2005] E.Rodriguez-Tello, and LERIA J.K. Hao, « Recherche Tabou Réactive pour le Problème de l'Arrangement Linéaire Minimum », Proceedings of the ROADEF, 2005.

[Rubeaux, 2011] M.Rubeaux, « Approximation de l'information mutuelle basée sur le développement d'Edgeworth : application au recalage d'images médicales», Thèse de doctorat, Université DE RENNES 1 sous le sceau de l'Université Européenne de Bretagne, 2011.

[Saha] A.Saha, « Résolution des Problèmes Multi Objectifs à Base de Colonies de Fourmi», Université de Batna.

[Souquet et F.G .Radet, 2004] A.Souquet, F.G.Radet, «Algorithmes Génétiques», Thèse de fin d'année, 2004.

[Ston, Price, 1997] R.Ston, K.Price, «Differential Evolution - A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces», Journal of Global Optimization, Kluwer Academic Publishers, Printed in the Netherlands, 1997.

[Talbi, 2000] E-G.Talbi, «Une taxinomie des métaheuristiques hybrides», ROADEF'2000, 2000.

[Talbi, 2009] H.Talbi, « Algorithmes évolutionnaires quantiques pour le recalage et la segmentation multi objectif d'images », Thèse de doctorat, Université Mentouri, Constantine, 2009.

[Troudi, 2006] F.Troudi, « Résolution du problème de l'emploi du temps : Proposition d'un algorithme évolutionnaire multi objectif », Mémoire de magistère, Université Mentouri, Constantine 2006.