III.5. Pertinence de la normalisation dans la
conception d'une Base de données relationnelle
III.5.1. Redondance d'un attribut
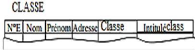
Prenons un cas pratique d'un modèle relationnel obtenu
pour représenter les données relatives à l'inscription des
élève dans une classe se soit réduit à une seule
table (suite à une mauvaise conception du modèle
entité-association) :
57
Une pareille conception entraîne des difficultés
de redondance des informations. On s'aperçoit en effet que
l'intitulé de la classe est répété pour chaque
élève, et qu'il est identique pour tous les élèves
inscrits dans la même classe. Cet attribut est donc redondant, et il est
préférable de stocker ces informations, relatives à une
classe, dans une table séparée.
III.5.2. Anomalies de mutation
En conséquence, le schéma
précédent n'est pas satisfaisant car il engendre certaines
anomalies lors des opérations de mise à jour, d'insertion et de
suppression des données (anomalies dites de mutation).
? Si par exemple on modifie l'intitulé d'une classe
dans un tuple (ex. de "Etude de la Vie" en "Etude du Vivant"), ce même
intitulé devra être changé pour tous les autres
élèves concernés, sans quoi cette classe possédera
plusieurs intitulés différents (anomalie de mise à
jour).
? Si une nouvelle classe se crée, elle ne pourra pas
être ajoutée dans la table sans y inscrire immédiatement
des élèves, car la clé primaire (N°E) ne peut
être laissée vide. Cette anomalie d'insertion peut être
gênante, par exemple, parce que le stockage d'informations sur la
nouvelle formation (maquette, intervenants, ...) doit pouvoir intervenir avant
toute inscription d'élève.
? Si l'on supprime tous les élèves de la table
(par exemple parce qu'ils ont tous eu leur diplôme !), on perd du
même coup toutes les informations relatives aux promotions (anomalie de
suppression).
Ces termes définis, soulignons qu'à l'instar des
anomalies de mutation, une base de données relationnelle doit stocker un
ensemble de schémas relationnels sans redondance inutile et sans
comportement anormal des relations lors des opérations de mise à
jour. Cependant la théorie de la normalisation des relations a
été associée au modèle relationnel.
III.6. Dépendances fonctionnelles et
normalisations des relations
III.6.1. Dépendance fonctionnelle :
définitions
La notion de dépendance fonctionnelle (DF) a
été introduite par Codd en 1970, elle permet de
caractériser des relations qui peuvent être
décomposée sans perte d'information. Tout d'abord, sa
formalisation mathématique découle de l'observation des
rôles de cardinalité simple (au plus égale à 1). En
intégrant sa pratique, intuitivement, une DF traduit le fait que
58
les valeurs de certains attributs sont nécessairement
déterminées (fixées) lorsque le sont celles d'autres
attributs.
Partant de cela, on dit qu'un attribut ou un ensemble
d'attributs Y est fonctionnellement dépendant d'un autre (ensemble d')
attribut(s) X si, à chaque valeur prise par X correspond une valeur
unique de Y. Autrement dit, des valeurs identiques de X impliquent des valeurs
identiques de Y. Cette dépendance est notée X--Y.
Avec une particularité, qu'une propriété
remarquable des clés d'identification est que, justement, tout attribut
non-clé dépend fonctionnellement de la clé, puisque
celle-ci identifie chaque tuple de manière unique.
Mais avant cela, une des propriétés de la DF est
la transitivité : X--Y et Y--Z X--Z. On dit qu'un attribut Z est
transitivement dépendant d'un attribut X s'il existe un attribut Y tel
que X--Y et Y--Z, et aussi que X ne dépend pas fonctionnellement de
Y.
| 


