Quantum key distribution theory and practice

1.3 Cryptosystem

In terms of Key, we can define also two kinds of cryptosystems for the security of data in the society. In both, we will try to say something about algorithm, keys and mathematic definition if is possible.

1.3.1 Symmetric Cryptosystem. A symmetric cryptosytem, is called also a private key use same key for encryption and decryption. In order to get a symmetrics cryptosystem, we must define tree algorithms, the generator of keys, the encryption and decryption.

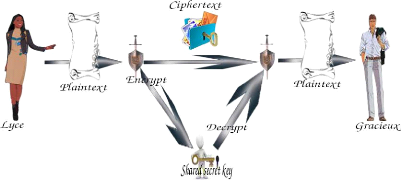
Section 1.3. Cryptosystem Page 4

Figure 1.1: Symmetric Cryptosystem

1.3.2 Keys Generator algorithm. The generator Keys algorithm produce a key with random l bits. The mathematics relation is given by:

G(l) = k

.

1.3.3 Encryption Algorithm. Many definition can be given around the encryption word. As said [MVOV96];The encryption is a function including e E k such that we can define uniquely a bijection from P a set of plaintext to C set of cipher and is denoted by C(p). This algorithm makes cipher of the message with a key generated by the generator keys algorithm, it is defined by:

C(P) = c.

1.3.4 Decryption algorithm. A function is called Decryption function if and only if V k E K, ? Dk a bijection function goes from C to P. This function as the same to recover the plaintext using the cipher, so the relation is given by:

Dk(c) = P.

This function can be writing as

Dk(CP) = P.

That is the main way to encrypt and decrypt using symmetrics cryptosystems. Certaintly, we are talking about security but in all thing, there are what we call drawback and advantages.

1.3.5 Advantages. In private key distribution, there exist a restruction to keep secret a key, that key is shared from one side to the other side with availability to both side, just two actors in the process can know how it look like. That ensure a communication channel, this implementation is easy, less complexity for implementation in hardware.

1.3.6 Drawback. The private key cipher has a big problem, it is the key management. When we are dueling with this such cryptosystem, the length of the message is the same as the length of the cipher. So to generate a key for a person, you may produce a key for each message that you want to send. When we have an algorithm which makes ciphers one bit by one bits it is called Stream cipher and other use to encrypt n bits directly and we call it Block cipher.

Section 1.3. Cryptosystem Page 5

D = Cdmod(N)

1.3.7 Same Private Key Cipher.

1. Block Cipher : The most popular block cipher use for security are:

(a) DES define by Data Encryption Standard;

(b) IDEA ;

(c) AES define by Advanced Encryption Standard.

2. Examples of Stream Cipher: There are many stream cipher

(a) Pseudo-Vernam or XOR operator. We know that when we are talking around computing information in computer, the unit is a bit. That bits in full it means Binary digit is a composition of 0 and 1.

(b) RC4 is ciphering byte by byte.

(c) Vigenere cipher

1.3.8 Asymmetric Cryptosystem. The asymmetric cryptosystem or the public key cipher is quite different to private cipher. The public Key distribution as we named it in other word. This algorithm is the most popular in terms of utilization. The asymmetric cryptosystem includes a new notion of signature for key verification. Alice will send a message to Bob using the private Key when Bob will get the message, using same mathematic operation, he can know immediately if Alice send the message or not. All private Key have a corresponding public key. By definition, asymmetric cryptosystem is an algorihm using differents keys to encrypt and decrypt a message, also you can not derive the decryption key from the encryption key. According to [STI06], the signature is define as a set quintuplet (P, A, K, S, V ) verifying: P is a finite set of plaintext; A a finite set of signatures; K a finite set of Keys such that V k E K, sigk E S is a verification function corresponding verk E V . So, the signature function is a map

sigk P -p A,

and the verication function is a map define by:

verk P x A ?p {True,False},

{Which verify Vx E P and y E A verk = T rue if y = sig(x); False if y = sig(x).

Diffie and Hellman at Stanford University achieved an astounding breakthrough in 1976 by coming up with a method that addressed symmetric cryptosystem problems and that was radically different from all previous approaches to cryptography, going back over four millennia [STI06].

1.3.9 Base of RSA algorithm. Diffie-Hellman came up with the concept of public-key cryptography. One of the first cryptographic algorithm that meet the requirements for public-key systems was the RSA algorithm developed by Ron Rivest, Adi Shamir, and Len Adelman. A typical size of n is 1024 bits, or 309 decimal digits. Thus, the plaintext is encrypted in blocks, with each block having a binary value less than some number n. That is, the block size must be less than or equal to log₂(n); in practice, the block size is k bits, where 2^k< n <2^k+¹. The encryption and decryption for public Key algorithm are given by modulo operation.

C = M^emod(N).

This is an encryption function and

Section 1.4. Diffie-Hellman Key Exchange Page 6

crypto-Recovered.jpg

Figure 1.2: ASymmetric Cryptosystem

is the decryption function. The Key generator: The key generator is the most important for RSA security. It is the generator of private key and public keys.

? p,q ? Z, ? N such that N = pq,