Quantum key distribution theory and practice

Quantum Key Distribution : Theory and Practice

Grace Mupoyi Ntuala ( [e-mail])
African Institute for Mathematical Sciences (AIMS)

Senegal

Supervised by: Dr. Kassem Kalach
[e-mail]

Institute for Quantum Computing

13 June 2015

Submitted in Partial Fulfillment of a Masters II at AIMS

Abstract

Information security has increasingly been important for individuals and organizations. For example, secure communications in financial, commercial and military applications are vital. Cryptography is the science of all aspects of information security. In particular, public-key cryptography is necessary to provide secure communications over the Internet.

Unfortunately, based on the assumed difficulty of some mathematical problems, public-key cryptography (includes ECDSA, ElGamal, and RSA schemes), would be broken with either advances in algorithms or the advent of quantum computers. On the other hand, quantum cryptography, based on the laws of quantum physics, provides perfect security even against the most general quantum attacks.

Quantum key distribution (QKD), a branch of quantum cryptography, allows two legitimate parties to expand a previously shared secret over a public quantum channel. Importantly, eavesdropping can now be detected, this is impossible in classical cryptography. Although many QKD protocols have been proposed, they all face technological challenges in practice, thus making them not suitable in many applications. In this project, we survey the most promising protocols, and compare them from theoretical and practical point of view. In particular, we study how and where they can be practical, and try to propose new applications.

i

Declaration

I, the undersigned, hereby declare that the work contained in this essay is my original work, and that any work done by others or by myself previously has been acknowledged and referenced accordingly

Grace Mupoyi Ntuala,

ii

Contents

Abstract i

EPIGRAPHY 1

INTRODUCTION 1

1 Classical Cryptography 2

1.1 Definition 2

1.2 Security concepts 3

1.3 Cryptosystem 3

1.4 Diffie-Hellman Key Exchange 6

1.5 Information Theory 7

2 Fundamentals of Quantum Mechanics 8

2.1 Polarization 8

2.2 Circular polarization 9

2.3 Heisenberg Uncertainty principle 10

2.4 Entanglement 11

2.5 No-cloning Theorem 12

3 QKD protocols 14

3.1 QKD with classical notion 14

3.2 Main operation of key exchange technic of QKD 14

3.3 Assumption and protocol 16

3.4 Protocols Using Heisenberg's 16

3.5 Entaglement base to protocol 18

3.6 Attacks on a QKD channel 19

4 QKD implementation technologies 21

4.1 Sources for QKD 21

4.2 Detectors 23

5 QKD Application 25

5.1 Network 25

5.2 Databases future work 30

CONCLUSION 1

References 4

EPIGRAPHY

1

The best thing is in the thorns

by Jean Kanyinda Bidiku

1

INTRODUCTION

Naturally, human had a desire to communicate secretly since the beginning of civilization. Many ancient societies Egypt, India, china, Japan, developped methods of secret communication like globaly a new science where the goal was to keep with innovations and evolution that science progressed and Stephen Weisner proposed a new concept of crypthograhy in conjonction with a quantum mechanics, a subfield of quantum physics, and it was publish in a seminal paper titled Conjugate coding. But in 1983, with SIGACT News, Stephen Weisner proposition was eventually published in that document, he showed how two messages can be stored or transmited by encoding in two conjugate observable, Using physical notion, such as linear or circular polarization so that either of which may be recieveed and decoded. The physical notion cannot use both in the same time.

After SIGACT News published Weisner proposition of quantum conjugate coding, the field red team of quantum cryptography red was created. Using Weisner work, there are same peoples based on it 1984, charles H. Bernnett of the IBM, Thomas J. Watson research center and Gilles Brassard come up with a concept of secure communication based on conjugate observable. After six years, an other person proposed a different approach to quantum key distribution which is based on pecullar quantum correlations known as quantum entanglement. We may know that after people developped classical crytography one of the most promising. They wanted to find other way to keep secret message which will be more secure since RSA crypto-system have a high level of security with a discrete logarithm, factoring, or Diffie-Hellmann problem, quantum cryptography come with a QKD to solve this problem and that provide a small size of key between sender and receiver.

The combination of cryptography and quantum mechanics notions give this new field a condition to be a power field in terms of security. As this field used a photon as matter for transmission message and the two notions of quantum mechanics use in this field have an ability to detect any kinds of attack in the channel. In general, quantum cryptography have a goal which is to perform tasks that are impossible with conventional cryptography. Quantum cryptography has an avantage since the security is based on physical laws such no-cloning theorem, heisenberg principle. Having those notion which QKD as tool of quantum cryptography, quantum bit and quantum coin tossing, quantum cryptography was prove that this cryptography is unconditionally secure.

In our thesis we will talk about Quantum Key Distribution and we will develop five chapters. In the first chapter we will discuss about classical cryptography, in second chapter, we will focus on fundamental of quantum mechanics, in the third we will try to speak about QKD protocols. Chapter four we will focussed on the different implementations of QKD and in the last chapter we will talk about QKD applications. At the end of this thesis, we will propose, as a contribution in this new field of security, a new application of QKD in Business Intelligence. We hope there will be an outcome for a new generation of Business Intelligence.

2

1. Classical Cryptography

In this section, we will talk around all notions in cryptography. Since longtime, in the world to keep secret message was very important. That trick in mind has been with us since we moved out of caves, started living in groups and decided to take this civilization idea seriously. As soon as there were different groups or tribes, the idea that we had to work against each other surfaced and proliferated, along with rank violence, secrecy, and crowd manipulation. The earliest forms of cryptography were found in the cradle of civilization, which comes as no surprise, the regions currently encompassed by Egypt, Greece and Rome. In Rome when Julius Cesar Emperor, wanted to send a message through the war to inform his army generals about something, he was writing a message covertly by shifting the alphabet letters so that if another person foundn'ta message can not understand what is going on just the intendedreceiver would knows how to read the message.

1.1 Definition

Cryptography is a word coming from Grec which is divide by two parts Cryptus which is mean Keep (Secret) and Graphy is define as written. By those Grec words we define Crytography as a way to keep secret a message (Written) using some mathematics notions, principaly number theory. other way, cryptography is a way and techniquess to study how to make secure information using mathematical notions with concepts such as confidentiality, data integrity, entity authentication and data origin authenticate.

1.1.1 Mathmaticaly. We define Cryptography as a set of five G = (P, C, Ck, Dk, k) where

1. G is our main set of cryptography;

2. P is a the clear message that we want to keep secret;

3. C is a finite set of text blocks can be digit

4. Ck is an encryption function;

5. Dk is a function of decryption;

6. k is the key, that we use to keep secret a message.

According to [STI06], in order to define just cryptography as a way to secure message, there is also other words which are related to Cryptography.

1. Cryptogramme is one way use through the media (newspaper, magazine, so on) to keep secret a message. Is technic, is based on an encryption message is just a shifting of letters.

2. Cipher is a secret way to write a message using subtitution or transposition of letter specially in form of symbol.

3. Cryptanalysis is a science where people analysis a cryptogram with goal to decrypt a message keep there.

4. Cryptology is science wich combine cryptography and cryptanalysis.

5.

Section 1.2. Security concepts Page 3

Cryptolect is a secretive language form used by a subculture dissimiller for a message.

This field is remaind not new for all persons but most of people use cryptography without knowing that they use this field of science to keep secret a message, communication whatsoever. Authentification, confidentiallity, non-repudiation and integrity those are conditions if you need a good security of message in term of secrecy. These conditions in the other way is called primitive function, because its make sure the security of information using some mathematical notions.

1.2 Security concepts

Let's define those concepts:

1. The authentification is a function that ensure verification that the person who are communicate are still the same people. All time we are dealing with this function, we are still answer in same important questions. The answer in those question, make a new functions which are connect directly in the security system where its make a verification of certification, control of access, the key manager, proof of knowledge and proof of disclosure

2. Integrity is a function use for data verification that is if during the transmission the data stay the same as in the beginning. To do it, one part must have the ability to detect data manipulation by unauthorized parties.

3. Non-repudiation, this service in the security of information, is the most important such that when someone use or send data, the system registers an action and after, we can verify the information and reconstruct the scheme of communication so that the person cannot lie the action he did. It means also the disponibility of information in the system.

4. Confidentiality is a function or service used to verify the content of information, if there are not modification on it. (goal to keep) from the persons who are authorized.

Cryptography, science including all security for sharing datas, use those principals in terms of safety. As we defined a cryptography as a set G of five elements, to secure a message or to provide the writing to become unreadable, to apply those concepts in terms of implementation, we use the most import element which is a key in the set G. To build a good secure system, we need to compute a good secure key. To build this key, we follow a mathematics concept of modulo in Z. For that, we have two kind of Keys: a private and public key. Around those two types, we define what we call cryptosystem.

1.3 Cryptosystem

In terms of Key, we can define also two kinds of cryptosystems for the security of data in the society. In both, we will try to say something about algorithm, keys and mathematic definition if is possible.

1.3.1 Symmetric Cryptosystem. A symmetric cryptosytem, is called also a private key use same key for encryption and decryption. In order to get a symmetrics cryptosystem, we must define tree algorithms, the generator of keys, the encryption and decryption.

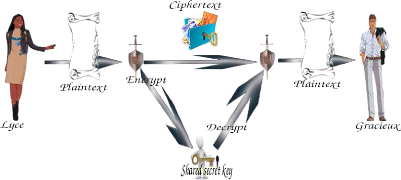
Section 1.3. Cryptosystem Page 4

Figure 1.1: Symmetric Cryptosystem

1.3.2 Keys Generator algorithm. The generator Keys algorithm produce a key with random l bits. The mathematics relation is given by:

G(l) = k

.

1.3.3 Encryption Algorithm. Many definition can be given around the encryption word. As said [MVOV96];The encryption is a function including e E k such that we can define uniquely a bijection from P a set of plaintext to C set of cipher and is denoted by C(p). This algorithm makes cipher of the message with a key generated by the generator keys algorithm, it is defined by:

C(P) = c.

1.3.4 Decryption algorithm. A function is called Decryption function if and only if V k E K, ? Dk a bijection function goes from C to P. This function as the same to recover the plaintext using the cipher, so the relation is given by:

Dk(c) = P.

This function can be writing as

Dk(CP) = P.

That is the main way to encrypt and decrypt using symmetrics cryptosystems. Certaintly, we are talking about security but in all thing, there are what we call drawback and advantages.

1.3.5 Advantages. In private key distribution, there exist a restruction to keep secret a key, that key is shared from one side to the other side with availability to both side, just two actors in the process can know how it look like. That ensure a communication channel, this implementation is easy, less complexity for implementation in hardware.

1.3.6 Drawback. The private key cipher has a big problem, it is the key management. When we are dueling with this such cryptosystem, the length of the message is the same as the length of the cipher. So to generate a key for a person, you may produce a key for each message that you want to send. When we have an algorithm which makes ciphers one bit by one bits it is called Stream cipher and other use to encrypt n bits directly and we call it Block cipher.

Section 1.3. Cryptosystem Page 5

D = Cdmod(N)

1.3.7 Same Private Key Cipher.

1. Block Cipher : The most popular block cipher use for security are:

(a) DES define by Data Encryption Standard;

(b) IDEA ;

(c) AES define by Advanced Encryption Standard.

2. Examples of Stream Cipher: There are many stream cipher

(a) Pseudo-Vernam or XOR operator. We know that when we are talking around computing information in computer, the unit is a bit. That bits in full it means Binary digit is a composition of 0 and 1.

(b) RC4 is ciphering byte by byte.

(c) Vigenere cipher

1.3.8 Asymmetric Cryptosystem. The asymmetric cryptosystem or the public key cipher is quite different to private cipher. The public Key distribution as we named it in other word. This algorithm is the most popular in terms of utilization. The asymmetric cryptosystem includes a new notion of signature for key verification. Alice will send a message to Bob using the private Key when Bob will get the message, using same mathematic operation, he can know immediately if Alice send the message or not. All private Key have a corresponding public key. By definition, asymmetric cryptosystem is an algorihm using differents keys to encrypt and decrypt a message, also you can not derive the decryption key from the encryption key. According to [STI06], the signature is define as a set quintuplet (P, A, K, S, V ) verifying: P is a finite set of plaintext; A a finite set of signatures; K a finite set of Keys such that V k E K, sigk E S is a verification function corresponding verk E V . So, the signature function is a map

sigk P -p A,

and the verication function is a map define by:

verk P x A ?p {True,False},

{Which verify Vx E P and y E A verk = T rue if y = sig(x); False if y = sig(x).

Diffie and Hellman at Stanford University achieved an astounding breakthrough in 1976 by coming up with a method that addressed symmetric cryptosystem problems and that was radically different from all previous approaches to cryptography, going back over four millennia [STI06].

1.3.9 Base of RSA algorithm. Diffie-Hellman came up with the concept of public-key cryptography. One of the first cryptographic algorithm that meet the requirements for public-key systems was the RSA algorithm developed by Ron Rivest, Adi Shamir, and Len Adelman. A typical size of n is 1024 bits, or 309 decimal digits. Thus, the plaintext is encrypted in blocks, with each block having a binary value less than some number n. That is, the block size must be less than or equal to log₂(n); in practice, the block size is k bits, where 2^k< n <2^k+¹. The encryption and decryption for public Key algorithm are given by modulo operation.

C = M^emod(N).

This is an encryption function and

Section 1.4. Diffie-Hellman Key Exchange Page 6

crypto-Recovered.jpg

Figure 1.2: ASymmetric Cryptosystem

is the decryption function. The Key generator: The key generator is the most important for RSA security. It is the generator of private key and public keys.

? p,q ? Z, ? N such that N = pq,

1.4 Diffie-Hellman Key Exchange

Diffie-Hellman is the first asymmetric encryption algorithm, invented in 1976, using discrete logarithms in a finite field. It allows two users to exchange a secret key over an insecure medium without any prior secrets. This Public-Key is based on the discrete logarithm in finite field which is hard to solve. In general, we consider a Diffie-Hillman protocol secure when an appropriate mathematical group is used.

Diffie-hellman key-exchange is a way that two persons agree about a number without the third person knows the number. This method is the same quite than Elgamal public-key encryption because the security is based on discrete logarithme and Diffie-Hellman problem [Mer07]. This key-Exchange methode use a group notion denoted by G. Diffie-Hellman the choose number by Alice and Bob still secret Eve in classical scheme can be in the middle understand the communication, she couldn't know the secrete number. The Diffie-Hellman is define also as (DHP) given a prime p, a generator g of Z* p and element ga mod (p) and g^b mod (p),find g^abmod(p). We need to find a generator

1. Alice and Bob will choose the finite group where they will play the security game and generate a generator

2. Alice will choose randomly a number and compute ga

3. Bob must do the same thing than Alice but will choose b as a natural number and compute gb

4. Alice will compute (gb)a

Section 1.5. Information Theory Page 7

5. Bob, he will compute (g^a)^b

For the Diffie-Hellmann protocole, the secret values of Alice and Bob, a and b, must be big numbers. There are steps for encryption which Alice and Bob will follow if they want to share secret messages without Eavesdropper knows.

Note: The computation must be difficult from Alice to solve Bob's private key and from Bob to solve Alice's private key. If the computation is easy, that allows Eve simply to substitute her own private, public key pair, plug Bob's public key into her private key, produce a fake shared secret key, and share it in both sides.

1.5 Information Theory

In our century, the information is still in order the most important in all part of life (societies, entreprises, millitaries) and there are some assumption which expect that if you know to manipulate an information you can do many things. So, people developped a concept in information named Information theory. The principal actor for this theory is nammed Claude Shannon who in 1949 published a article with a title »Communication Theory of Secrecy Systems» in the bell System newspaper that made a big influence in cryptography science. With Shannon theory, we are now able to make a quantification of our information.

8

2. Fundamentals of Quantum Mechanics

Classical physics failed to explain phenomenon such as the black body radiation and presence of spectral lines in the spectrum of absorption and emission of some atoms. A new theory known as quantum mechanics arised in the 20^th century and gave a satisfactory explanation of those phenomenon. A conceptual difference between this new theory and classical mechanics is the desapperences of the full description of the trajectory of a particle. Indeed, in quantum mechanics, one speaks of the probability of the particle to be at a certain position at a given time. Quantum mechanics is a physical theory that discribes some systems where h is not negligible anymore. It is especially efficient to describe physical phenomena at molecular scales and above (except at high energies such that solar energy. We need to take into account relativistic effects). We will recall the five postulat of quantum mechanics

1. The knowledge of state of quantum system is completely known in normalizable vector of a hilbert space H usually denoted |?(t)i;

2. The correspondance principle: to any physical observable corresponds an hermitian operator which acts on the vectors of a hilbert space;

3. If we have a initial state ái, the probability that it is at the final state áf is given by

Páf = |háf|áii|², (2.0.1)

If the system is in the state á, the mean value of the measure of an observable is given by

h ^àAi = há| ^àA|ái. (2.0.2)

4. Projection of quantum states Let a_n be an eigenvalue of an operator A and is the output of measurement at time t and let ö be its associated eigenstate. The state of the system after the measure is projected on the eigenspace associated to a_n.

5. Time evolution of state öt is given by the schrödinger equation

in ? ?t|ö, ti = ^àH|ö,ti. (2.0.3)

One notices that H is the generator of time translation and is called the hamiltonian is the

operator is associated to the energy of the system and the hermitian have a dimension tw.

2.1 Polarization

First, we will present the polarization of a classical electromagnetic field and translate it in the frame of quantum mechanics. According to Maxwell's equations in the vacum, we observed that light is a transverse electromagnetic wave which means that the electromagnetic field is perpendicular to the direction of propagation of the wave. To simplify, we will consider a monocromatic wave which propagates along the z-axis :

E~ = ^~E_ocos(ùt - kz + ?), (2.1.1)

Section 2.2. Circular polarization Page 9

E_x =

Eo _v2coswt; (2.2.1)

2r

where w is a vibration frequency, |E_o| is the amplitude, k is the wave vector given by k = À , and À

is the wavelenght. The vibration frequency is given with the relation

w = c x k, (2.1.2)

here c is the speed of light and ? is the phase at the origine. The electomagnetic field is polarized in the plane perpendicular to the direction of propagation thus we let z = 0.

2.1.1 Linear polarization. In the linear polarization, the electric field describe a straight line in a single direction which is the direction of propagation. The mathematical relation is given by:

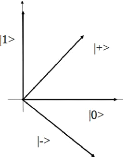
E_x = E0cosOcoswt, (2.1.3)

E_y = E0sinOcoswt. (2.1.4)

With Malus law, in the output of the polarization, the electric field is proportionnal to the square of the intensity.

I' = Icos²(O - á). (2.1.5)

If O = á - ð 2 that imply in the output of the analyzer, we will not get any light.

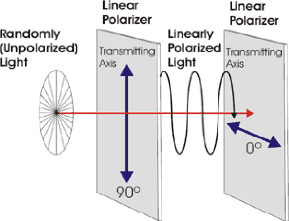
Figure 2.1: Linear polarization

The orientation of a linearly polarized electromagnetic wave is defined by the direction of the electric field vector

2.2 Circular polarization

The second polarization is circular, when the electric field describes a circle in the plane during the propagation of the wave along z. The wave is polarized circularly if

Section 2.3. Heisenberg Uncertainty principle Page 10

E_o

E_y =

Section 2.4. Entanglement Page 11

_v2 sinùt. (2.2.2)

This is a general cas of polarization, where the polarization of electromagnetic radiation such that the

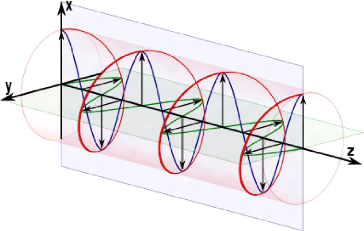
Figure 2.2: Circular polarization

tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to the direction of propagation. The mathematical definition is

ÇA cos ùt )

Ê= ;
B sin ùt

with A =6 B and A, B =6 0. satisfy to

_{ÇX )2 ÇY )2}

+ = 1. (2.2.3)

A B

2.3 Heisenberg Uncertainty principle

People are interrested in quantum mechanics such that they made many research, experiences and found new concepts which clarify the theory of quantum. In 1927, Werner Heisenberg discovered Heisenberg Uncertainty Principle. Quantum system is a system which calls mesure, hermitian operators, and observable, as define previously. Quantum mechanics is applied to the microscopic domain of particle and its the principle for complementarity [NAZ02] of two states, momentum and position. In general, Heisenberg Uncertainty Principle is given by any hermitian operators denoted by x and p, where x describes the position and p the momentum of particle in certain coordonate. This principle simutaneously increase the position and the momentum, it is impossible to measure a position without disturbing momentum, and vice versa. This principle can be called a principle of complementarity [NAZ02]; when the momentum is increased, the position decreases and when the position increase the

momentun decreass (distribution is proportionnal). In general, the Heisenberg Uncertainty Principle is given by the following formula:

~

ÄxÄp_x = ₂. (2.3.1)

Note that Ä symbol is what we call Uncertainty. The uncertainty principle is taken as a limitation of quantum preparation (states)[BHL07]. There are many application on it such that in signal processing with Fourrier transformation but the one domain that is interesting to us is cryptography. We will see how this notion is applied in cryptography. In this figure the uncertainty momentum is given by Äv is

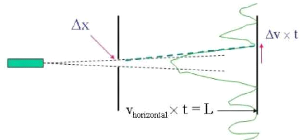
Figure 2.3: Heisenberg Uncertainty Principle

still the same as Äp.

2.4 Entanglement

We describe that quantum mechanics include states but those states are characterized in two [Sar], pure and mixed state which are define by any linear operator acting on H called density operator, satisfies the following properties:

1. ñ is define positive ñ 0;

2. tr(ñ) = 1

For the following conditions, we describe other conditions for a state. Pure state are define when ñ² = ñ and ñ² > ñ. i.e when we have a pure state we have always an unique state vector. In the hilbert space it is expressed as a projection operator on |ø). For the mixed state, the definition is quite different than the pure state. The mixed state is a combination of pure states. Entanglement notion is defined as an inseparable state in quantum mechanics, it can be taken as two states which are commited that means [A,B] = 0. In more details, let's consider corresponding Hilbert spaces on the state A and B where we write respectively HA and HB. The composite system is a product HA®HB. If the first can be represented by |ø)A and the second by |ø)B, the product is given by |ø)A ® |ø)B. Those states in binary notation will take |ø)A = {|0)A, |1)A} and |ø)B = {|0)B, |1)B}, thus the basical representation

Section 2.5. No-cloning Theorem Page 12

of entanglement using binary representation is:

_v2

1

_v2

1 (|0iA|0iB + |1iA|1iB); (2.4.1)

(|0iA|0iB - |1iA|1iB). (2.4.2)

)

| ?i|?i - |?i|?i

(2.4.7)

The quantization notation is what we will use more in the next point where we will go through and more details in quantum protocols.

2.5 No-cloning Theorem

With those main values which is differenciate by a sign, the bits can be shift to get a four maximal

entaglement states otherwise we get the Bell basis,

1

|ö+i = v2(|00i + |11i, (2.4.3)

1

|ø+i = v2(|01i + |10i, (2.4.4)

1

|ö-i = v2(|00i - |11i), (2.4.5)

1

|ø-i = v2(|01i - |10i). (2.4.6)
Bell said : The probabilities of outcomes of the measurements of certain quantum-mechanical observables on one system are not immediately influenced by the kinds of measurements directly made on a second system, which is sufficiently spatially separated from the first. Choosen a quantization axis, the entanglement state is given with spins up or down example

1

|ø-i =

v2(

Having a classical information, we can share it to differents entities without any problem. We can duplicate the information. But in quantum information such operation seems quite impossible. In 1982, Wootters, Zurek and Deiks stated a no-cloning theorem which profound an implication in quantum computing and its related field [NAZ02] of quantum cryptography. With a quantum state choosen from a given set of possible states can be cloned perfectly only if the states in the set that are mutually orthogonal. But if a set of states is orthogonal, the states are related to each other in the same way that classical alternatives are related to each other. There is none of the ambiguity that typically charactarizes the relation among quantum states. This is what we meant when we said cloning is possible only if the information being cloned is essentially classical. More explaination can be found [NAZ02]

2.5.1 Characteristics of no-cloning theorem. After many experience, the following characteristics come up to make a point in the security of the message without using a error

/The no-cloning theorem use to prevents using a classical error technic on quantum states.(Enable to create a backup copies of states )

/The quantum measurement is impossible. That means the state in quantum area can not be diplucate. /The no-cloning theorem does not prevent superluminal communication via quantum entanglement, as cloning is a sufficient condition for such communication, but not a necessary one.

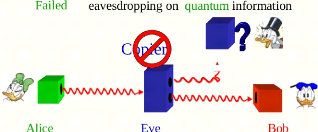
Section 2.5. No-cloning Theorem Page 13

Figure 2.4: No-cloning

14

3. QKD protocols

QKD in short mean Quantum Key Distribution was invented by Bernett and Brassard in 1984, this innovation was recognized as a main key-technology for our century. There are many questions which are still asked like you can see in the publication of [SRS12]. QKD use same classical notions learnt from public-key cryptosystem such as management of keys and their creation, the activation, assignment, building (to identities), escrow, as well revocation and destruction. The experiment of QKD did with people and organisation, like work of Tanaka et al. in 2008. It shows that the randomness for QKD keys still a vital security of subsequent applications based on these keys. Till now, this field has many questions which brings innovations in security science. In this section, we will try to focus our mind in QKD protocols, give details relate to the basis of each protocols. As we showed it previously, such technic requires a knowledge in quantum mechanic, particularly in light.

3.1 QKD with classical notion

That QKD is a new tool in the toolbox of cryptographers, does not excludes classical notion for security concepts as defined in other section. To share data, informations or messages using QKD, we need to use cipher; most of the times the QKD network uses One-time-Pade¹ cipher. For interaction between different parties, we may need to establish three mains phases to secure communication; this is deeply explained in the litterature of [SML10]

1. Key agreement : This phase is about the agreement of sharing private key between parties

2. Authentification : Second phase is to be sure that the message received comes from a particular party to avoid the attack of man-in-the middle²

3. Key usage : Once the key security is etablished, it can be used for encryption, further authentification or other cryptographic proposes

Every day cryptography is improving. People come up with new tools; after discovering a problem in one cryptosystem, they want to improve that and the cryptography system base on public-key, which is more used in the community, are retooled with new and standards algorithms over the coming years. That give a big opportunity to incorporate QKD as a new tool offering fundamentally new security features. QKD is based in quantum mechanics notion, it provides two kinds of protocols which use Heisenberg Uncertainty Principal and quantum Entanglement.

3.2 Main operation of key exchange technic of QKD

Based on Vernam code, this cipher required the use of key which provide only authorized parties suppose to know and the key are renewed this is an idea of the rapport of [KDB⁺]. All QKD have two phases

¹One-time-pade is a crypto-system where the key is used once for sharing data

²Man-in-the middle : Its the attack of Eavesdropper when she is placed in the middle of the channel and when the transmission of message come, she will take it decrypt and send it to Bob without Bob knowing that the message was decrypted and when Bob will reply to Alice she will do the same

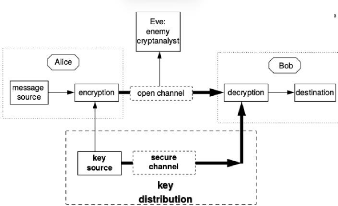
Section 3.2. Main operation of key exchange technic of QKD Page 15

Figure 3.1: Key distribution in conventional cryptography

1. Firstly, Alice will send to Bob a signals ³ to measure.

2. Secondly, Alice and Bob will deliver to check the result of measure⁴

For this two phases, QKD use two channels one for quantum signal build with optical fiber and the classical channel for classical communication which is public. The above figure explain the principe of

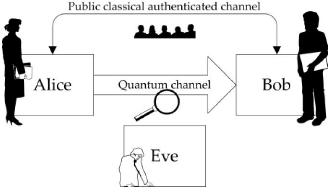
Figure 3.2: Principe of QKD

QKD. In the next point, we will talk about which kind of QKD can be found in practice. There exist two kinds of QKD based in quantum mechanics notions which are HUP⁵ and the Entanglement.

³The signals that we are talking is quantum (other talk instead of quantum they use soap bubble) ⁴To check the result of measurement, they use the classical way

⁵Heisenberg Uncertainty principle

Section 3.3. Assumption and protocol Page 16

3.3 Assumption and protocol

Untill now the research considered a QKD as the only one key exchange which is secure. After their experience and verification, they came up with same characteristics to show us that this system stayed a secure system and the eternel system secure. Let us enumerate them.

1. This system give an guarantee to detect the Eve presence in the channel;

2. The key is absolutely secure that does not depend to the complexity of the algorithm or the technology used by Eavesdropper to attack.

Having those assumptions with a properties of quantum mechanics, quantum cryptography provide two kinds of protocols. All the protocols are able to detect the Eavesdropper in the channel and have the unconditional security.

3.4 Protocols Using Heisenberg's

There are many protocols using this notion of HUP but for us, we will focus on those which are more used and discovered before. We may have in mind that all the protocols follow the same structure⁶.

Prepare and send protocol

After Weisberg publish a paper where he introduced the concept of quantum mechanics in communication, Bernett and Bassard in 1984 come up with a new revolutionnary idea which was the first proposal of QKD protocol using totaly HUP (based on quantum properties) notion. This protocol is the oldest for quantum cryptography, based on basis⁷ which are quite related to the polarization notion. We have the rectilinear and the diagonal basis for BB84. Quantum protocol can be describe in two steps or phases, quantum and classical one. Let us describe firstly quantum phase and classical phase after.

Quantum phase

Any message passing through in the computer are converted into zeroes and ones which are the informatic unity in classical information theory. In BB84, there exist a correspondant unity for quantum information to express information. Using Dirac notation, we express the information unity with a braket as |øi, |1i or |xi and its call qubits ⁸. Other definition, we call a qubit a superposition of zeroes and ones (|00i, |01i, |10i) , is described by complex number with an argument 1 belong the set

{á|0i + /3|1i : |á|² + |/3|² = 1;á,/3 ? C}, (3.4.1)

we take |0i and |1i as two references qubits, corresponding to two orthogonal states in a quantum system.

⁶Structure means the fonctionnality is the same but few differents we can find but in general is the same

⁷BB84 is the main protocol and the remaind follow the way that its works the difference is few certain have a difference just in basis used to send the information

⁸Quantum bits

Section 3.4. Protocols Using Heisenberg's Page 17

Figure 3.3: Transmission photon by Alice to Bob

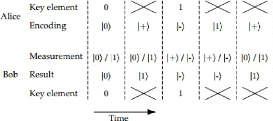
Figure 3.4: Detection of photon by Bob using states measurement

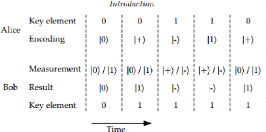
1. In BB84, Alice sends a sequence of photon to Bob, each independantly choose one of the four polarization (the four polarization are vertical, horizontal, 45% and 135% you can have an idea checking the figure down).

2. For each polarization, Bob will choose one base for measurement to achieve the result

3. Bob will records the result and his measurement bases and after, he will publicly acknowledges his receipt other signal.

Classical phase

In this phase the entities have a following steps

1. Alice broadcasts her bases of measurement, Bob broadcasts his bases of measurements

2. Alice and Bob discard all events where they use different bases for a signal

3. To test for tempering, Alice randomly choose a fraction, if all remaining events as test events, she publicly broadcasts their position and polarization

4. Bob broadcasts the polarizations of the test events

Section 3.5. Entaglement base to protocol Page 18

Figure 3.5: Data transmit between two parties using basis

5. Alice and Bob compute the error rate of the test events. If the compution of error rate is large than some prescribed threshold value, say 11% they about otherwise, they proceed to the next step (This step is where Alice and Bob detect Eve presence)

6. Alice and Bob each convert the polarization data of all remaining data into a binary string called a raw key. They can perform classical post-procesing such as error correction and privacy amplification to generate a final key.

With quantum mechanics properties, the security is a efficiency and the Eavesdropper can use any method of attack Alice and Bob will detect her. The work of [Zha09] explain other notion for the efficiency security.

3.4.1 B92 protocol . This protocol is a derivative of BB84 protocol. It was proposed by Charles Bernett in 1992. B92 have the same function then BB84 but the difference is just the half part of fonctionality from BB84. The encoding of one state for example |ø) composed by {|0), |1)} we can encode each element of the set in this way the first element in the set will be encode with rectilinear basis which is correspond to 0^o and |1) encode in diagonal basis this according to [Hai14]. There exist also other variants QKD protocols using the notion of Heisenber Uncertainty Principale as you can see in many book where they are talking about QKD like [Hai14]. We can enumerate other protocols using Heisenberg like, Six-State Protoco(SSP) proposed by Posquinucci, Gusin in 1999 the different with BB84 instand of two state and here the use one.

3.5 Entaglement base to protocol

The protocol using entanglement are called entanglement-based protocols, Ekert protocols or EPR protocols. This protocols was discovered by Arthur Ekert at 1991. EPR protocols use pairs of photons which are entangled. The pairs photons entangled can be produced by both Alice and Bob or other person. The main idea for E91, is to use three possible states and testing no violability of Bell inequality that to detect the evesdropper in the channel. The entanglement protocol follows three steps:

1. The imposibility for Alice to preduct which polarization she will get as a result;

2.

Section 3.6. Attacks on a QKD channel Page 19

Secondly, If Alice and Bob carry out polarization of measurement they will not have a perfect correlated answers but same will be correlated;

3. Last is the Eavesdropper will be detect for every tentative by Bob and Alice.

Figure 3.6: QKD entanglement protocol

We may need to mention that as quantum cryptography is dueling with light (photon), the transmission of informations between terminals using QKD for security implies appropriate devices for connexion. So, the transmission in this field is done by a channel call quantum channel and is composed by optical fiber. When Arthur Ekert proposed the protocol, he based the assumption that Alice and Bob can test the Bell's inequality by verifying the entanglement of particle. This assumption allows that the generation of is secure key still possible as long as the entanglement is verified. This part have more explanation in [QQL10a]

3.6 Attacks on a QKD channel

Since we said that quantum cryptography have a sure security, that did not avoid in mind of people to find a way to attack. In classical cryptography, we can mention attacks like brute force, frequency there are many attacks. Is still the same for quantum cryptography, people developed some attacks concepts but till now quantum cryptography is still not crackable. Let us list some attacks used.

1. Individual attack : This attack as you can guess by the name, is an attack acting in each qubit in the channel. The systems for this attack are prepared separately (independantly). An example for this attack is an intercept - resend;

2. The collective attacks : The difference from the first one is to perform Eavesdropper result. That will joint a measurement to get more information

3. Coherent attack : This attack one of the powerfull attack that Eve can use because it has all possible things that she can do. Here, she has to do an albitrairy preparation of joint state (entanglement) where the interaction of each qubit must be before the measure being joint in the channel.

The figures below will describe a little bit the explanation of each attack for QKD.

Section 3.6. Attacks on a QKD channel

Page 20

Eve individuel Mea urerneal

Bob

A1iaa

Ere AeciI

Figure 3.7: Indivivual Attack

Light Moe

·

Alice

Source

Eve Cal led we Measuremeal

Big Aael1lie

J

Figure 3.9: Cohence attack

Figure 3.8: Collectif attack

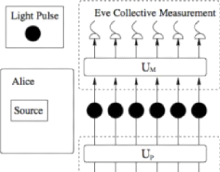
Light Plc

·

Eve Collective Mesiuirrrnc ll

ars^'

Alice

Some

Bob

Manor

Eve Collrcti.ve Ancitie

21

4. QKD implementation technologies

Implementation is a way to express an idea. Classically all ideas along communication are protocols. There are softwares built for interchange of messages and there exist many protocols which have dif-ferents functions. To build such software, is what we call implementation. We named protocols like : http, Smtp, ftp. In quantum, we described the implementation of BB84 which is privilegie protocol composed by two sets of non-orthogonal basis and four polarizations. The security of protocols in quantum cryptography depend on the production of single photon. There is an art for implementing a new technology with QKD. We will need same notions like the notions of single photon EPR¹ photon source and photon stabilized interferometer. Those notions are so important for the implementation of QKD technologies. Quantum technology allows us to organise and control the components of a complex system governed by the laws of quantum physics. We have two imperatives driving quantum technology:

1. Technological innovation of miniaturisation,

2. Performance over the classical framework.

Since many years, human did act with matter, they could explain many phenomenon like periodic table, atoms but they were not be able to manipulate the behavior of semiconductors. In the second, we see the implication of human. There are appropriate tools for QKD like sources and detectors are the mains tools for implementing the QKD technology.

4.1 Sources for QKD

There exist many sources for a QKD. That sources correspond to the technologies that you want to implement.

1. Single photon : This is a main element for implementation, the photons have been used in some other fields like quantum optics and quantum communications. People did experience to perfect a photon applying a single photon for those subfield of quantum. Photon-gun which is a single-photon, is a unique photon sources. This elements is given significative progress achieved in the last decade. In term of emitting information, the number of photons prove to precise certain number of matters for transmission. There are some experiments that allows application of laser but indeed, the laser cannot produce photon number states because the implementation source for a QKD need a special kind of photon. It is why we are talking about single-photon, that must have a precise number of photons. This can be understood as follows: the gain medium of a conventional laser contains a large number of individual atoms or molecules and each of them has a certain probability to emit a photon during a fixed time period as said in [QQL10a]. It was found that a single-photon include atoms or ion gas phase, organic molecules, colour center in crystals, semiconductor, nanocrystals, quantum dots.

2. EPR photon pair : For this source, the main problem is the efficent production of photon. The use of entanglement photon pair allow optical processes and the production of photon pairs need

¹EPR : Ekert Protocol

Section 4.1. Sources for QKD Page 22

a spontaneous parametric down-conversion (SPDC). The conversations of energy and momentum imply that the generated daughter photons are entangled in spectral and spatial domains. The production of photon pair here, have two steps using the main toll which is non-linear crystal. Let's see how its look like the production of photon pair by the figure below.

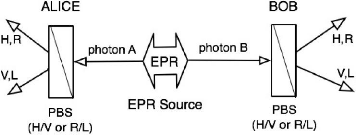
Figure 4.1: EPR source

(a) Firstly, the first crystal can be selected to phase match vertical pump photon with horizontal down-converted photon pair

(b) Secondly, the second one will be chosen to phase match horizontal pump down-converted photon pair

The two crystals will be done with 45 % that to get a high quality of polarization entangle.

3. Attenuated Laser This source, is where Eavesdrpper use same probability notion to get the information in the quantum channel. The difference between the first source is the use of linear relation also, we stay using single-photon. Laser is used as an attack for Eavesdropper. To produce single-photon for high quality, this model of source have certains probability to get non-zero probability to get more or than one photon. This experience did by people is called photon number Splitting (PNS) attack. The functionnality of this attack can be describe well in the article of [QQL10b]. It can be detected by testing quantum channel during QKD process.

Figure 4.2: Laser source

Section 4.2. Detectors Page 23

4.2 Detectors

[QQL10b] The quantum channel is so powerfull, that it avoid all attempt for eavesdropping including error in that channel, error are related in noises for that, in our point, we will present two technologies for quantum states detection for a QKD system.

1. Single photon detector :

We know that there exist many protocols for a QKD but for us, we will try to take one of them which will be BB84 one of the usual protocol used for experiment. Detectors need main elements like a single-photon detector (SPD), photomultiplier tube (PMT) and more recently they add a new device called superconductive single-photon detector (SSPD) for a high performance of detection. This detector follow

(a) Receiving an incoming photon, the SPD have a efficiency probability for detection which its determined by intrinsic quantum and coupling losses of the detector.

(b) Dark counts are detection events registered by a SPD while no actual photon hits it. Due to its random, the QBER contributed by dark count event 50%.

(c) The registers of photon have an operation in the detector b, the dead time of the single-photon sending by Alice.

(d) The detector have an output action due to the electrical pulse in time domain. This action is fructuation of a SPD.

Figure 4.3: SPD

Figure 4.4: SPD detector composition

2. The Optical homodyne detector :

This detector used in the implementation of GMCS² QKD protcol, there is not a difference with the classical coherent communication system. The detector here act as follow.

(a) When the sender encode information using one of the subfield of quantum (As this is about light);

(b) The receiver will recover the complete information;

(c) The receiver will interfering the signal with a local oscillator;

To discover that Eve attack's, we focus on one basical requirement of homodyne detector which is limited shot noise in the quantum scheme. This requirement call a strong local oscillator. This

²GMCS is a one QKD protocol which mean Gaussian-Modulated Coherent States

Section 4.2. Detectors Page 24

detector compare to SPD, the optical homodyne have a higher efficiency and a larger bandwidth and a strong local oscillator for production of interference. Those differences enumerated are big enough to detect in the high speed photo diode. We must know that the detection efficiency is a function of the wavelenght of the incoming and to build homody, we have same challenges for implemantation in QKD.

The first challenge is to find stability of signal and local oscillator between Alice and Bob that are from the same laser and that will propagate through the same optical fiber. Secondly, as we said in the beginning of this points and mention the use of GMCS QKD protocol, the balance detection scheme is commonly employed to remove the DC background.

25

5. QKD Application

We have seen the importance of quantum cryptography and the tools related to that field. Now, we reach the point where we will describe two main points: the first point is on QKD applications in network and the second point is related to databases; particularly Business Intelligence (datawerouse). In the last section of this chapter, we will try to propose a new application of QKD, which is to combine a data warehouse with a QKD.

5.1 Network

We know that to share information between two entities, we need connexion and for that, there existe same models which were build by people and published after second world war by ARPA-NET project. That project was a PETENGONE project in second world war it was impossible for them to share or contact other bases for sharing data so the upcome of network idea. A network by definition is a group of two or more computers (Equipments) systems linked together..

A network follow a model and that model allows an implication of several steps which are called layers. Let us talk little bit about the composition of layer.

5.1.1 Model. In network, there exist two kinds of models that according to the convention of IEEE¹, The OSI and TCP/IP model. The OSI model is composed by seven layers and TCP/IP is composed with four layers. For our part QKD, we will be more interest in OSI model and try to explain how the QKD was implemented in the OSI model and how its works in this model also were precisely researchers implemented in classical model to become a quantum model. You can see in the figures how the models look like.

Figure 5.1: Network Model

5.1.2 Integration of QKD in the OSI model layers. In the begining of 21^st century, people used the genius idea to implement a QKD in the OSI model and this implementation was focus in some types of layers. The layers where QKD was implemented are session layer, network layer and the data link loyer. Those layers seem are more important.

The combination of QKD with other protocols in OSI model, is for an efficiency related to quantum field.

¹IEEE (Institute of Electrical and Electronics Engineers) is a organisation where all networks conventions are approved

Section 5.1. Network Page 26

Section 5.1. Network Page 27

We have a combination with a TLS/SSL in the session layer, in the network layer where more result are related to the connexion, the QKD find a cohabitation with an IPSEC protocol, the combination gives a new kind of protocol called SEQKEIP and the last layer, we have a Q3P is the mixage of QKD with PPP protocol.

Implementing a QKD in OSI model, give an explanation that the QKD network technology might be an essential part of modern security schemes for high performance distributed computing application. This implementation of secure scheme in OSI model was a project funded F6 called SECOQC which is a global network and the meaning is given by Secure Communication based on Quantum Cryptography. This project was developped by BBN technology, DARPA, researchers of Harvard University, Boston University in 2014. The combination give us the sophisticated protocol and QKD network architecture.

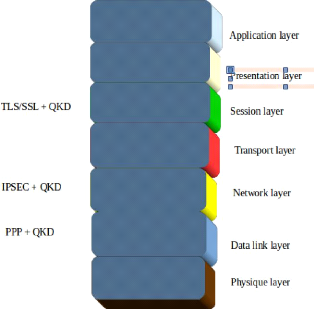
Figure 5.2: QKD implementation in OSI model

There exist a system which coordonate various network tools such that standard, open, general proposed protocols all those compose a system architecture and the system is called a grid. Grid computing is emerging as a modern technology to fulfill the high performance. Computing requirement of users, institutions and business organization world wide that was clear in [KX]

5.1.3 Functionality. In this point, we used a paper of [EAA]. The example take, is the integration of QKD in TLS/SSL for secure a transaction. That is related with online-commerce and palpaye classically, we have a secure server and protocol Htpps, the connection use TLS/SSL mode.

/This protocol ensure a integrity of the message and the encryption using point-to-point connection

between client and server. The combination of TLS/SSL with QKD is called QSSL and can be described as two principal modes. The first modes is about authentification of two sides which are communicating, that communication is in QKD.

The client and server after authentification, the following main operation continue to complete the generation of key size negociation and in the end of the operation of generating key size, the change-cipher-spec and finished messages can be exchanged.

The second method called the handshaking this method is a pre-shared keys initialization based on the previous model-1, the transactions (messages) are inserted before the transmission of change-cipher-spec and finished message.

The protocol QSSL has been added in the SSL record protocol. For this quantum cryptography with a principal toll QKD, can be integrated within SSL/TLS. In SSL, we have an additional parameter which is the Alert Protocol. Let us describe the fields than the messages follow in quantum cryptography and the fields can be represented in table where we will summarise

1. Describe the message use in public exchange phase of the QKD protocol with a type of 2 bytes

2. Specification of QKD protocol used type 1 bytes

3. Allows the use of more than one version of certain QKD protocol version 1 byte

4. length (4 bytes) the length of the messages is in bytes.

5. Jo. no 2 bytes QSSL session all operation multiple QKD protocol instance belong on it.

6. Authentification 1 bytes : specification of the message whether is authentificated. The idea of this point was taken in the article [EAA]

Type	Protocol	Version
	Length
Job no	Authentication	Encoding
	Content
	Tag

/The integration of QKD in network layers. The network layer is important because in this layer, when we want to ensure a point-to-point connection between two distinct people and to determine a data travel, the layer has a capacity to find the short way and quick one using some parameters for the reach the destinator. There are the most important job for this layer in OSI model and for the communication. The OSI model use what we call IPSEC² with a comming of QKD in 2003, BBN technologies found a way to integrate a QKD with the IPSEC protocol and that combination give the another current protocol named SEQKEIP³.

The new protocol which act with a main toll of quantum cryptography, has one idea in this construction and the idea is to stick, to traditional IPSEC and ISAKMP⁴. Those protocols, you can have some deep information like how its works in web site of RFC 2409, this is what we called norm RFC. QKD with

²Internet Protocol security

³Secure Quantum Key Exchange Internet Protocol

⁴Internet Security Association and Key Management Protocol

Section 5.1. Network Page 28

IPSEC gives a SEQKEIP, to build simply, we have to define two phases of Internet Key Exchange and that its the same as the use of ISAKMP mechanics, that takes an advantage to QKD in order to build a pratical protocol.

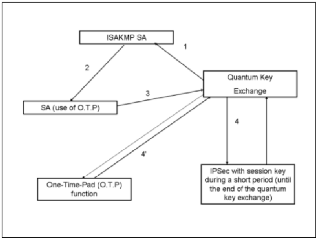
SEQKEIP have three mains in functionnality or phases: phase 1 is the negociation of the ISAKMP SA, phase 2 is negociation of SA and the last is phase 0, in this Alice and Bob will share the first secret key as adding in the phase. SEQKEIP have three modes, Quantum mode, Main mode, Quick mode. All those modes correspond to the phases listed in top. Quantum mode include quantum cryptography with a key exchange in phase 0, during the negociation phase of IASKMP SA, we can assimilate this phase to main mode and when we have the negociation of SA, the corresponding relation in SEQKEIP is the quick mode.

We can now explain how SEQKEIP works. We will see in the next figure, the action are numerated.

1. The fixation parameters of our protocol, that will be done with ISAKAMP SA and SA in other way is the combination of main mode and quick mode.

2. The implication of QKD using key Exchange with or either one-time-pad function

3. In last part, is the use of traductional symmetric cryptography algorithms for exchange of data.

We must put in mind that this operation, the lifetime of session key is so very short. Its equal to the time need to exchange the secret key using quantum cryptography. Whitout QKD, IPSEC work in the same manner. The idea of the quantum cryptography is to sift completely to the unconditional security function (QKD and OTP). You can find many explanation on [STH]

/Integration of QKD in data link : The data link provide the physical address service to the upper layer and is the only one add a queue to ensure the validation of data. This layer provide physical adress

Figure 5.3: SEQKEIP functionality

Section 5.1. Network Page 29

which is MAC address to the equipment. In classical part of network, the protocol used in this layer is PPP⁵ adding in this a quantum notion, we will leave a classical communication and will reach quantum networking. The combiation of PPP with QKD that provide a new protocol call Q3P.

The integratin of QKD in data link, provide some steps to achieve the right information. The steps that we list in this part we get inspiration in the writing of [EAA]. Let us illustrate brievely which steps for Q3P :

1. In this first step, we have an action of dead, establish, authentification. The three actions are identical to PPP, that mean the first phase pass through 3. The negociation of Encryption start just after the authentification operation for two nodes and the parameters are negociated also

2. The second phase is if the encryption key functions successfull, the requirement, the QKD phase will directly start. The encryption negociation is along the Key length and the TTL⁶ by sending a proper ECP⁷ packet

3. The quantum cryptography exchange will start directly with one goal to share a secret key in both nodes, that the goal of QKD. The encryption algorithm will be shared and the TTL of the key. The key that we get will be used in the network phase.

4. The data are sending through the channel, it is enciphered using the key production in the previous step and the algorithm also.

The following enumerate all the steps of Q3P. As we said that the TTL is short so far that when the

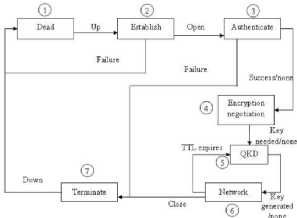
Figure 5.4: Q3P

TTL is expired, a new QKD phase start automatically. You can see in the picture how can we be build a network with the same equipment and include a QKD implementation in that network.

⁵PPP: Point-to-Point Protocol ⁶TTL: Time to life

⁷Ecryption Control Protocol

Section 5.2. Databases future work Page 30

Figure 5.5: Quantum network Architecture

5.2 Databases future work

The second point in this part will be related to the data, using a way of storage and some other notions study by many researchers for data. The main one is what we call databases. Its can be defined as a collection of element which are follow the same conditions like integrity and the data have an exhoustivity.

There exist two kinds of databases, relational and the decisional databases. The first one is related to some mathematics notions (Union,Intersection) and to build it we need to use the MERISE method or UML. But MERISE is enough to build such thing and the second is so oriented decision for market battle and to build it, we must have firstly the operational database before the decisional.

A decisional Database have many subfield or spelling like a dataware house, data mining, data mark those database are oriented decision.

A Business Intelligence is the way that we use computing technologies spotting, digging-out and analyzing big data for business like a revenues products, costs and incomes. The B.I is caratecrize by historical off operation. The B.I is build for to give a best understanting in the market and the evolution or relationship between products.

5.2.1 Tolls of B.I. When we build a B.I for an structure, we are not again in relational area but we are in the decisional area. This area is called in other way DSS (i.e Decision System Support in short DSS). The general key categories of business Business Intelligence are:

1. Spreadsheets

2. Reporting and querying software

3. OLAP

4.

Section 5.2. Databases future work Page 31

Digital dashboards

5. Datamining

6. Data warehouse

7. Local information system

In all those tools listed for a BI, they have a same goal which is to help people to have a synthetique representation of the data in the entreprise, to select and present a usefull datas, provide easy consultation tool for users and to produce data according the need of users, Thus to take a decision.

To have a full B.I for example a data warehouse, we need to represent the informations in dimension and measure. Dimension is defined as a object that we need to get an information like date of production, designation of article, name of the establishment and the measure is the object in the entreprise which is reprensented in term of quantity like price, amounts. The representation of the data for taking the decision by the decider is in cube. The need of B.I are related to the diversification of the entrenprise, different place in the country or outside. Let show a example of cube. In this part of our these, we are not going to speak about all notions related to B.I but our goal is to find a way using a tool of quantum cryptography the QKD precisely, to make secure a B.I for all Data Base Management System. As you

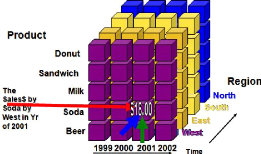
Figure 5.6: Data cube

can see in this figure, we can have many dimensions in the B.I that are according to the need of the entreprise and this allows for the entreprise to stay competitive in the market. To build a data cube, firstly we need to have a knowledge in how to construct an operation data base, the use of UML⁸ with all details diagrams and so on. The notion of how to build a operator database you can read those books [Bar05], [GG08] and for building the cube you can find more details and understand the notion of measure and dimension in [KR02]. With a data cube, we can do operations like,zoom up and zoom down. The B.I have three main steps for the data to be analysed. We will see it in the next figure and try to explain the functionality of all the part briefly and for us, will be focus on an element in the B.I architecture not all elements but just one element where we will try to figure out our assumption for applying QKD in all DSS like oracle, SQL-Server, PostGre.

In this picture, we can see the full steps follow by datas before the decider have information which he needs and starts to decide.

⁸UML : Unifield Modeling language

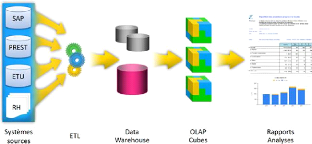
Section 5.2. Databases future work Page 32

Figure 5.7: B.I Architecture

For us, the main thing is to describe the object ETL where we will study deeply the composition of ETL and try to propose a new application of QKD in Business Inteligence.

As a definition, ETL (Extract-Transform-Load ) is an intelligent informatic technology which provide a massive a sychronization of information from one entite to another. The letter of ETL is define like :

1. Extracts : To extract the data from homogeneous or heterogeneous data sources

2. Transform : To transform the data for storing it in proper format or structure for querying and analysis propose.

3. Load : The load is for the final target where the data must reach its can be a data mark, an operational data store, or a data warehouse

We know that many structures have a need for security. As we show it in our thesis, a quantum cryptographic cryptosystem provide an unconditional security. In our future work, we want to go deeply in this topic and try to propose a new kind of business intelligence which can be called a Q.B.I (Quuantum Business Intelligence). The integration of a QKD in the B.I can be done in ETL because in that element we have three operations which is Reading, Mapping and Writting.

1

CONCLUSION

The combination of quantum mechanic with cryptography has given rise to a new field which is quantum cryptography. In this project, we started by introducing the basic cryptographic notions, namely encryption/decryption, one type of cryptosystems and Diffie-Hellmann Key-Exchange.

As this field make a jonction with physics, in our second part, we studied some notions related to quantum mechanics as polarization, Heisenberg Uncertainty Principle, quantum entanglement and the no-cloning theorem where we explained the use of those notions. The notions developed in the second section of this project, are the basic and important one to understand physics notions used in quantum cryptography and those notions allow us to introduce a Quantum Key Distribution Protocols (QKD), QKD as a main element in quantum cryptography, follow by Quantum Key Distribution implementation technologies. We also gave some examples and come up with the last point related to Quantum key Distribution applications.

Indeed, we reach our last point by taking one example of application SECOQC which is a quantum network. In this application, BBN Technolgy with Havard University and others groups developed new protocols for quantum area in the F6 project. The protocols was developped in OSI model, using the composition of the model, the researchers added a new componant in the classical protocols acting with specific layers. As in session layer, they added a QKD in TLS/SSL and the combination give the QSSL protocol again they added in network layer, they combine two protocols nammed IPSEC plus QKD and they found a new protocol called SEQKEIP. The last one is data link where they found other name like Q3P, which is the composition of QKD with a protocol Point-to-point protocol. This is one of the applications of quantum cryptography. All the applications and technologies are possible by the way of single photon and single detector. The only way they are used for transmitting information through quantum network is an optical fiber.

2

Acknowledgements

I express my sincere thanks to the AIMS-NEI and AIMS-Senegal family, for funding, providing me with an opportunity to study and all the necessary facilities for completion of my work in good condition.

I place on record, sincere gratitude to my supervisor Dr. Kassem Kalach, from Institue for Quantum Computing. I am extremely thankful and indebted to him for his expertise, sincere and valuable guidance extended to me.

Big thanks to my father Jean Kanyinda Bidiku and mother Jeanne Ngomba Bitota for helping and supporting me since i was borned till now. Thanks to my sisters Lydie Gambwalemba Galubadi-a-Lemba, Fidele Kapinga Kalonji, Ruth Muambi Kanyinda, Esther Mbombo Kanyinda, Dorcas Ngomba Kanyinda.

I thanks my tutor Miss. Bernadette Faye for her help, constructive criticism, encouragement and support during my essay phase.

I also thank my colleagues and all tutors, one and all, who directly or indirectly, have lent their hand in this venture.

3

References

[AD11] Atsushi Yabushita and Department of Electrophy, Schemes to generate entangled photon

pairs via spontaneous parametric down conversion, May 2011.

[Bar05] Franck Barbier, UML 2 et MDE: ingnierie des modles avec tudes de cas, Dunod, Paris, 2005

(French).

[BHL07] Paul Busch, Teiko Heinonen, and Pekka Lahti, Heisenberg's uncertainty principle, Physics

Reports 452 (2007), no. 6, 155-176.

[EAA] Mohamed Elboukhari, Abdelmalek Azizi, and Mostafa Azizi, Integration of Quantum Cryp-

tography in the TLS Protocol: Reality and Perspectives, MICS 10, 2-4.

[GG08] Joseph Gabay and David Gabay, UML 2 analyse et conception: mise en oeuvre guide avec

tudes de cas, 2008.

[Hai14] Mart Haitjema, A survey of the prominent quantum key distribution protocols, URL:

http://www. cse. wustl. edu/ jain/cse571-07/ftp/quantum ( 18.10. 2013), 2014.

[KDB⁺] E. Karpov, T. Durt, F. Vanden Berge, N. J. Cerf, and T. dHondt, Cryptographie quantique,

White paper, 10.

[KR02] Ralph Kimball and Margy Ross, The data warehouse toolkit: the complete guide to dimen-

sional modeling, 2nd ed ed., Wiley, New York, 2002.

[KX] Muhammad Mubashir Khan and Jie Xu, Applications of QKD Network for High Performance

Distributed Computing.

[Mer07] N. David Mermin, Quantum computer science an introduction, Cambridge University Press,

Cambridge, 2007 (English).

[MVOV96] Alfred J. Menezes, Paul C. Van Oorschot, and Scott A. Vanstone, Handbook of applied cryptography, CRC press, 1996.

[NAZ02] Olaf Nairz, Markus Arndt, and Anton Zeilinger, Experimental verification of the Heisenberg uncertainty principle for fullerene molecules, Physical Review A 65 (2002), no. 3 (en).

[NC10] Michael A. Nielsen and Isaac L. Chuang, Quantum computation and quantum information,

10th anniversary ed ed., Cambridge University Press, Cambridge ; New York, 2010.

[QQL10a] Bing Qi, Li Qian, and Hoi-Kwong Lo, A brief introduction of quantum cryptography for engineers, arXiv preprint arXiv:1002.1237 (2010).

[QQL10b] , A brief introduction of quantum cryptography for engineers, arXiv preprint

arXiv:1002.1237 (2010).

[Sar] Debasis Sarkar, Quantum Entanglement- Fundamental Aspects.

[Sar14] Mohan Sarovar, Introduction to quantum key distribution, October 2014.

[Sca09] Valerio Scarani, Quantum information: primitive notions and quantum correlations, arXiv

preprint arXiv:0910.4222 (2009).

REFERENCES Page 4

[SML10] Douglas Stebila, Michele Mosca, and Norbert Ltkenhaus, The case for quantum key distri-

bution, Quantum Communication and Quantum Networking, Springer, 2010, pp. 283-296.

[SRS12] Peter Schartner, Stefan Rass, and Martin Schaffer, Quantum Key Management, APPLIED

CRYPTOGRAPHY AND NETWORK SECURITY, 2012, p. 227.

[SSL09] Douglas Stebila, Douglas Stebila, and Norbert Ltkenhaus, The Case for Quantum Key

Distribution, 12.

[STH] M. A. Sfaxi, I. Tashi, and S. Ghernaouti Hlie, How QKD can improve the security level of

future e-commerce transaction, Proc. 18th European Regional International Telecommunication Society Conf.(ITS2007), Citeseer, pp. 1-12.

[STI06] Douglas R. STINSON, Cryptography theory and practice third edition, chapman & Hall

/CRC, Taylor & Francis Group, 2006 (English).

[Tan13] Xiaoqing Tan, Introduction to Quantum Cryptography, Theory and Practice of Cryptography

and Network Security Protocols and Technologies (Jaydip Sen, ed.), InTech, July 2013, p. 1 (en).

[VA06a] Gilles Van Assche, Quantum cryptography and secret-key distillation, Cambridge University

Press, Cambridge ; New York, 2006.

[VA06b] , Quantum cryptography and secret-key distillation, Cambridge University Press,

2006.

[Zha09] Yi Zhao, Quantum cryptography in real-life applications: assumptions and security, Ph.D.

thesis, University of Toronto, 2009.