Le développement de la filière cacao et son incidence sur la gestion des terroirs forestiers en zone de Beni

ANNEXE : Essai analytique de la production du cacao

Le modèle multiple de la production en fonction de la superficie, du rendement, du

prix et du nombre des planteurs s'écrit de la manière suivante :

Y = f (S, R, P, NP)

Avec S comme superficie, R étant le rendement moyen, P tel que prix moyen, et NP étant le nombre des planteurs. De ce qui précède, la formulation de notre modèle se présente comme suit :

Y = a+â1S+â2R+â3P+â4NP+å

Sur base des données du tableau numéro 10, d'après nos calculs via Eviews, les résultats suivants se sont présentés :

Dependent Variable: PROD

Method: Least Squares (Gauss-Newton / Marquardt steps)

Date: 10/03/21 Time: 13:53

Sample: 2008 2020

Included observations: 13

PROD=C(1)+C(2)*SUP+C(3)*RDM+C(4)*PRIX+C(5)*NPLANT

	Coefficient	Std. Error t-Statistic	Prob.
C(1)	-57066.62	4278.022 -13.33949	0.0000		C(2)
4.158822	0.767410 5.419297	0.0006	C(3)
9095.775	787.1575 11.55522	0.0000	C(4)
0.000808	0.003259 0.247966	0.8104	C(5)
3.408623	1.351929 2.521303	0.0357
R-squared	0.994881	Mean dependent var	41374.08
Adjusted R-squared	0.992322	S.D. dependent var	31834.63
S.E. of regression	2789.549	Akaike info criterion	18.98887
Sum squared resid	62252664	Schwarz criterion	19.20616
Log likelihood	-118.4277	Hannan-Quinn criter.	18.94421
F-statistic	388.7086	Durbin-Watson stat	0.443558
Prob(F-statistic)	0.000000

Source : nos calculs via Eviews

De ce tableau, les critères d'information ont pour objet d'estimer la quantité de notre information. De tout ce qui se présente, le critère de Schwarz est de 19.2 et celui d'Akaike reste de 18.9. Étant qu'ils se présentent par des valeurs minimales, le moindre carré ordinaire nous servira certainement de modèle contrairement à d'autres.

124

Pour voir la présence ou absence de l'homoscedasticité, le tableau suivant nous y éclaire.

Heteroskedasticity Test: White

F-statistic	0.786836	Prob. F(4,8)	0.5648
Obs*R-squared	3.670424	Prob. Chi-Square(4)	0.4524
Scaled explained SS	0.848984	Prob. Chi-Square(4)	0.9318

Test Equation:

Dependent Variable: RESID^2 Method: Least Squares

Date: 10/03/21 Time: 20:17 Sample: 2008 2020

Included observations: 13

Variable	Coefficient	Std. Error t-Statistic	Prob.
C	3949622.	4370876. 0.903623	0.3926
(SUP)^2	0.054975	0.084728 0.648845	0.5346
(RDMT)^2	132737.3	133397.9 0.995048	0.3489
(PRIX)^2	4.40E-07	1.68E-06 0.261805	0.8001
(NPLANT)^2	-0.418952	0.238493 -1.756669	0.1170
R-squared	0.282340	Mean dependent var	4788666.
Adjusted R-squared	-0.076490	S.D. dependent var	5508783.
S.E. of regression	5715584.	Akaike info criterion	34.23901
Sum squared resid	2.61E+14	Schwarz criterion	34.45630
Log likelihood	-217.5536	Hannan-Quinn criter.	34.19435
F-statistic	0.786836	Durbin-Watson stat	1.034061
Prob(F-statistic)	0.564838

Source : nos calculs via Eviews.

Vu que nous utilisons le test de White pour analyser la présence de l'homoscedasticité dans notre série multiple. De ce tableau, R² de la régression auxiliaire est égal à 0,282340. Et que TR² est de 3,670424 qui est supérieur à 0,4524 ; nous concluons qu'il a hétéroscedasticité.

De ce qui précède, le tableau suivant présente le test d'autocorrélation Breusch-Godfrey dans les variables résiduelles.

125

Breusch-Godfrey Serial Correlation LM Test:

F-statistic 5.188817 Prob. F(1,7) 0.0568

Obs*R-squared 5.534140 Prob. Chi-Square(1) 0.0186

Test Equation:

Dependent Variable: RESID

Method: Least Squares

Date: 10/03/21 Time: 21:31

Sample: 2008 2020

Included observations: 13

Presample missing value lagged residuals set to zero.

Variable Coefficient Std. Error t-Statistic Prob.

C(1)	2546.399	3641.650 0.699243		0.5070	C(2)
0.094183	0.623089 0.151155	0.8841		C(3)
-228.4487	645.5516 -0.353881	0.7338		C(4)
-0.000266	0.002643 -0.100671	0.9226		C(5)
-0.353517	1.106203 -0.319577	0.7586
RESID(-1)	0.765500	0.336056 2.277898		0.0568
R-squared	0.425703	Mean dependent var		-1.02E-11
Adjusted R-squared	0.015491	S.D. dependent var		2277.657
S.E. of regression	2259.947	Akaike info criterion		18.58811
Sum squared resid	35751512	Schwarz criterion		18.84885
Log likelihood	-114.8227	Hannan-Quinn criter.		18.53451
F-statistic	1.037763	Durbin-Watson stat		1.328767
Prob(F-statistic)	0.464194

Source : nos calculs via Eviews.

De ce tableau test, R² est égal à 0,425703 avec 13 observations et 4 coefficients selon les variables d'études. Alors GB= (13-4)0,425703.

GB= 3,831327 qui est 0,0186. Nous concluons qu'il y a une autocorrélation des erreurs et qu'au moins un des coefficients est significativement différent de zéro.

Les figures suivantes le montrent clairement.

			126	^100,000 ^80,000 ^60,000 ^40,000 ^20,000 ^0
^4,000 ^2,000 ^0 ^-2,000 ^-4,000 ^-6,000
	^08 09 10 11 12 13 14 15 16 17 18 19 20
			^Residual Actual Fitted

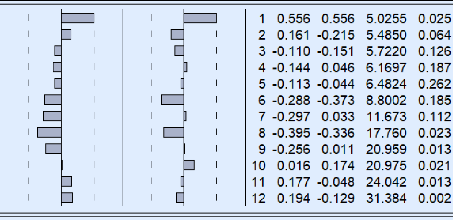
De toutes ces représentations résiduelles, l'histogramme le montre d'avantage avec certaines spécificités :

127

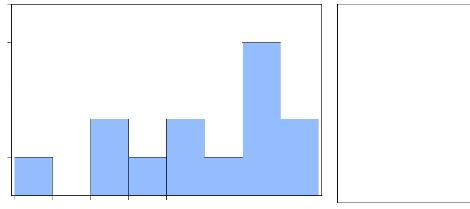
⁵

⁴

³

²

¹

⁰

^{-5000 -4000 -3000 -2000 -1000 0 1000 2000 3000}

^{Series: Residuals}

^{Sample 2008 2020}

^{Observations 13}

^Mean ^Median ^Maximum ^Minimum ^Skewness ^Kurtosis ^Jarque-Bera ^Probability

Le VIF et matrice de covariance se sont présenté comme suit :

Variance Inflation Factors Date: 10/03/21 Time: 15:40 Sample: 2008 2020

Included observations: 13

Variable	Coefficient Uncentered Centered Variance VIF VIF
C(1)	18301469	30.57464	NA		C(2)
0.588918	61.50857	19.65585	C(3)
619616.9	39.80814	1.409847	C(4)
1.06E-05	57.70129	17.20140	C(5)
1.827712	66.56848	9.805758

Covariance Analysis: Ordinary Date: 10/03/21 Time: 15:35 Sample: 2008 2020

Included observations: 13

Covariance Correlation t-Statistic	NPLANT	PRIX RDM SUP
NPLANT	3211426.
	1.000000
PRIX	1.62E+09	9.69E+11
	0.917680	1.000000
	7.660296

128

RDM	898.9182	305103.1	1.361988
	0.429818	0.265526	1.000000
	1.578824	0.913439
SUP	7474914.	4.26E+09	1650.046	19978444
	0.933204	0.967494	0.316321	1.000000
	8.613053	12.68838	1.105905

De tout ce qui précède, en violation des hypothèses de base, le modèle qui explique la production du cacao en zone de Beni est globalement à estimer par la méthode des moindres carrés généralisés.

Le modèle multiple de la production en fonction de la superficie, du rendement, du prix et du nombre des planteurs s'écrit de la manière suivante :

Y = f (S, R, P, NP)

Avec S comme superficie, R étant le rendement moyen, P tel que prix moyen, et NP étant le nombre des planteurs.

Nous y avons utilisé la méthode des moindres carrés généralisés pour résoudre les problèmes de violation des hypothèses de base sur la présentation de l'autocorrélation et de l'hétéroscedasticité dans les erreurs. Ce qui approxime le MCO par le MCG.

129

Dependent Variable: PROD

Method: Generalized Linear Model (Newton-Raphson / Marquardt steps)

Date: 10/04/21 Time: 10:54

Sample: 2008 2020

Included observations: 13

Family: Normal

Link: Identity

Dispersion computed using Pearson Chi-Square

Convergence achieved after 1 iteration

Coefficient covariance computed using observed Hessian

	Coefficient	Std. Error z-Statistic	Prob.
C(1)	-57066.62	4278.022 -13.33949	0.0000		C(2)
4.158822	0.767410 5.419297	0.0000	C(3)
9095.775	787.1575 11.55522	0.0000	C(4)
0.000808	0.003259 0.247966	0.8042	C(5)
3.408623	1.351929 2.521303	0.0117
Mean dependent var	41374.08	S.D. dependent var	31834.63
Sum squared resid	62252664	Log likelihood	-119.0835
Akaike info criterion	19.08976	Schwarz criterion	19.30705
Hannan-Quinn criter.	19.04510	Deviance	62252664
Deviance statistic	7781583.	Restr. deviance	1.22E+10
LR statistic	1554.834	Prob(LR statistic)	0.000000
Pearson SSR	62252664	Pearson statistic	7781583.
Dispersion	7781583.

Source : nos calculs via Eviews.

Avec correction d'hétéroscedasticité, utilisant les observations 2008-2020 (T = 13) Variable dépendante: PROD

	Coefficient		Erreur Std		t de Student	p. critique
const	-56166,0		2667,27		-21,06	<0,0001
SUP	4,56553		0,512596		8,907	<0,0001
RDMT	9,25964		0,656202		14,11	<0,0001
PRIX	0,000299110		0,00171247		0,1747	0,8657
NPLANT	2,62409		0,958454		2,738	0,0255
Somme carrés résidus		13,77198		Éc. type régression			1,312059
R2		0,998724		R2 ajusté			0,998086
F(4, 8)		1565,543		P. critique (F)			1,32e-11
Log de vraisemblance		-18,82117		Critère d'Akaike			47,64233
Critère de Schwarz		50,46708		Hannan-Quinn			47,06172
rho		0,598850		Durbin-Watson			0,449645
Moyenne var. dép.		41374,16		Éc. type var. dép.			31834,58
Somme carrés résidus		68149497		Éc. type régression			2918,679

Source : nos calculs avec Gretl

Modèle de l'estimation de l'étendue : 2008 - 2020 avec Écart-type du résidu = 2918,68

130

Etant donné que nous nous sommes servis de la méthode linéaire généralisée dont son F test calculé est supérieur au F théorique, notre modèle est adapté en terme de sa specification.De tout compte fait, nous concluons que la production du cacao en zone de Beni est expliquée par le rendement lié à la fertilité du sol, la superficie emblavée aussi y joue un rôle et le nombre des planteurs plus que le prix suite à la pérennité de la culture et non pas à l'oscillation du prix vue que ce marché est monopsonique à 99,8724% étant donné que notre R2 normal et ajusté sont respectivement de 0,998 et 0,998086. Ce qui se laisse concevoir que les autres variables synthétisées par le terme de l'erreur å expliquent la production en petit pourcentage.

D'où, la matrice de coefficient de covariation se présente comme suit :

const	SUP	RDMT	PRIX	NPLANT
7,11435e+006	444,959	-1256,92	0,798687	-700,865	const
	0,262755	-0,00513108	-0,000551310	-0,263129	SUP
		0,430600	-2,03388e-005	-0,269724	RDMT
			2,93254e-006	-0,000294111	PRIX
				0,918633	NPLANT

Source : nos calculs via Gretl

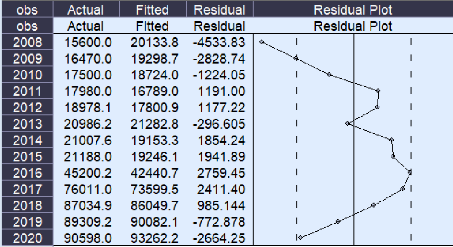
Quant à la prévision des productions, le tableau suivant le montre mieux pour l'intervalle de confiance de 95%, t (8, 0,025) = 2,306.

Obs	PROD	prédiction	éc. type	intervalle de 95%
2008	15600,0	20745,4	1329,07	(17680,6, 23810,3)
2009	16470,0	19923,5	1238,58	(17067,3, 22779,7)
2010	17500,0	19430,5	1017,17	(17084,9, 21776,0)
2011	17980,0	17169,8	699,425	(15557,0, 18782,7)
2012	18978,1	17996,0	545,349	(16738,4, 19253,6)
2013	20986,2	21187,2	412,310	(20236,4, 22137,9)
2014	21008,6	19317,3	509,317	(18142,8, 20491,8)
2015	21188,0	19048,6	1244,11	(16179,7, 21917,5)
2016	45200,2	43523,5	1427,31	(40232,1, 46814,9)
2017	76010,9	74966,1	2069,37	(70194,2, 79738,1)
2018	87034,9	86238,7	1230,13	(83402,0, 89075,4)
2019	89309,2	89491,0	976,376	(87239,5, 91742,5)
2020	90598,0	94112,6	3158,84	(86828,4, 101397,)

131

	PROD	ajusté	résidu
2008	15600,0	20745,4	-5145,42
2009	16470,0	19923,5	-3453,50
2010	17500,0	19430,5	-1930,45
2011	17980,0	17169,8	810,158
2012	18978,1	17996,0	982,068
2013	20986,2	21187,2	-200,963
2014	21008,6	19317,3	1691,25
2015	21188,0	19048,6	2139,35
2016	45200,2	43523,5	1676,65
2017	76010,9	74966,1	1044,82
2018	87034,9	86238,7	796,158
2019	89309,2	89491,0	-181,782
2020	90598,0	94112,6	-3514,65

Source : Nos calculs via Gretl

De ceci, le graphique de la production avec ses prévisions se présente comme suit :

132

De ce qui se présente, la normalisation des résidus s'est présenté dans le graphique

suivant :

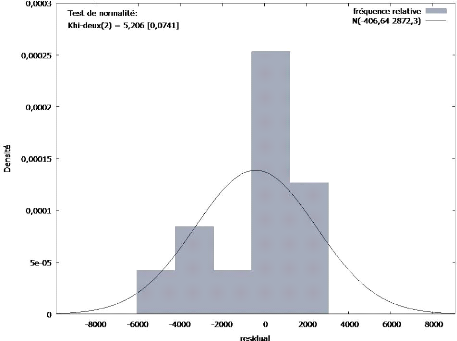
En bref, Par un modèle de correction d'hétéroscedasticité, les coeffiscients viennent : D'où, avec Y = a+â1S+â2R+â3P+â4NP+åcomme formulation de notre modèle se présente comme suit :

GLM PROD=C(1)+C(2)*SUP+C(3)*RDMT+C(4)*PRIX+C(5)*NPLANT

Substituted Coefficients:

Y= PROD = - 56166 + 4,7 SUP+ 9,26 RDMT+ 0,0003 PRIX+ 2,62 NPLANT

Voilà l'analyse économétrique finie par élaboration d'un modèle de production du cacao a conclu cette section. La droite estimée est spécifiée pour la production en zone de Beni et cela par un modèle linéaire à hétéroscedasticité corrigé.

133

Sommaire

EPIGRAPHE ii

DEDICACE iii

REMERCIEMENT iv

RESUME v

ABSTRACT vii

INTRODUCTION 1

I. PROBLEMATIQUE 1

II. HYPOTHESE 5

III. CHOIX ET INTERET DU SUJET 6

IV. OBJECTIFS DU TRAVAIL 7

V. METHODES 8

VI. DELIMITATION DU SUJET 9

VII. SUBDIVISION DU TRAVAIL 9

VIII. DIFFICULTES RENCONTREES 9
CHAPITRE I : REVUE DE LA LITTERATURE SUR LA FILIERE ET CHAINE DE VALEUR, LA

TRANSFORMATION DU MILIEU RURAL, LA GESTION DE TERROIR ET LE CACAOYER .. 10

I.1. Notions de chaine de valeur et de filière agricole 10

I.1.1. Origine et évolution des concepts « filière » et « chaine de valeur » 10

I.1.2 Définition des concepts filières et chaines de valeur 13

I.2. Développement et structuration de filière 22

I.2.1. Aperçu générale sur le développement rural 22

I.2.2. Théories de développement et de structuration de la filière 25

I.3. Notions sur la gestion de terroirs 28

I.3.1. Essai définitionnel 28

I.3.2. Structure du terroir 29

I.3.4. Gestion du terroir et aménagement du terroir 31

I.4. Le Cacaoyer 35

I.4.1. Historique 36

I.4.2.Botanique 36

I.4.3. Classification 38

I.4.4. Description 38

I.4.5. Parasites et ennemis du cacaoyer 39

I.4.6.Lutte contre les maladies et ravageurs du cacaoyer 40

107

134

I.4.7. La Production Du Cacaoyer 41

I.5. Conclusion du chapitre 44

CHAPITRE II. STRUCTURATION ET DEVELOPPEMENT DE LA FILIERE « CACAO » EN

ZONE DE BENI 46

2.1. Présentation de la zone de Beni 46

2.2. Structuration de la chaine de valeur « Cacao » 50

2.2.1. Histoire de la filière « cacao » en RDC et expérience des firmes intervenants de la filière 50

2.2.2. Expérience de la Société ESCO-KIVU 52

2.2.3. Expérience de la Société de Commerce et d'Agriculture du Kivu SCAK 63

2.2.4. Venue et appui de Virunga Origins Chocolate à la filière 67

2.3. Le développement de la filière « cacao » 73

2.3.1. Production 74

2.3.2. Autres maillons de la chaine de valeurs 77

2.3.3. Fonctionnement de la filière 78

2.4. Identification, analyse des acteurs de la filière « cacao » et contraintes de son développement 79

2.4.2. Analyse fonctionnelle de la filière « cacao » à Beni 82

2.4.3. Analyse SWOTT de la filière « cacao » à Beni 83

2.3. Conclusion du chapitre 84

CHAPITRE III. INCIDENCE DU DEVELOPPEMENT DE LA FILIERE CACAO SUR LA

GESTION DES TERROIRS FORESTIERS EN ZONE DE BENI 85

3.1. Itinéraire agronomique cacaoyère à Beni et prise de conscience paysanne du risque 86

3.1.1. Mode d'acquisition et gestion des terres en zone de Beni 86

3.1.2. Préparation de la zone d'exploitation, semis et maintenance du cacaoyer en Zone de Beni90

3.1.3. Production et contraintes courues par les paysans 92

3.1.4. Mesures de Maintenance productive de l'exploitation cacaoyère. 94

3.1.5. Prise de conscience et initiative communautaire face à la cacao-déforestation 95

3.2. Vulgarisations sur les bonnes pratiques culturales : acteurs et interventions publique 97

3.2.1. Vulgarisations sur les bonnes pratiques culturales cacaoyères 98

3.2.2. Contraintes de l'intervention publique-privée dans la vulgarisation 100

3.2.3. Prise de conscience : Acteurs publics-privés face à la cacao-déforestation et initiatives

palliatives 101

3.3. Analyse de la réglementation du secteur agricole et forestier 102

3.3.1. Analyse des relations et limites entre code forestier et code agricole 102

3.3.2. Interaction entre code forestier et code agricole : quelle efficacité pour un cacao durable ?

135

3.4. Recommandations critiques personnelles 108

3.5. Conclusion du chapitre 111

CONCLUSION GENERALE 113

LISTE DES FIGURES 115

LISTE DES GRAPHIQUES 116

BIBLIOGRAPHIE 117

ANNEXE : Essai analytique de la production du cacao 123