Mesure de l'efficacité technique des banques commerciales de la CEMAC (Communauté Economique et monitaire de l'Afrique Centrale )

Communauté Economique et 911onitaire de l'Afrique Centrale

(CEMAC)

Institut Sous régional de Statistique et d'Economie Appliquée
(ISSEA)
Organisation Internationale

BP : 294 Yaoundé CAMEROUN Tel : [phone]

911émoire rédigi en vue de l'obtention du diplôme d'Inginieur d'Application de la Statistique,
Option Gestion

Rédigé par :
KWAYEP DIMOU Leonnel

me Ingénieur d'Application de la Statistique de 4^' Année

Elève 4e

Soutenu publiquement le 13 juin 2007 devant le jury composé de : Dr. Wilfrid GRANGER : Président

Dr. es Sciences Économiques, Conseiller du Directeur Général de l'ISSEA

M. Jeannot NGBANZA : Rapporteur

Ingénieur Statisticien Économiste, Directeur de la Formation Continue à l'ISSEA

M. Séverin Yves KAMGNA : Directeur de Mémoire

Ingénieur Statisticien Économiste, Chef du Service des Prévisions Macroéconomiques au siège de la BEAC

Juin 2007

DÉDICACE

Je dédie ce travail :

I A la mémoire de mon père M. DIMOU ANDRE

I A ma mère Mme DIMOU née SELEU GEORGETTE

I A mes frères HANGOUA ELVIS et NDJODJE CHRISTIAN

I A ma tante Mme TCHEUDZEU ELISABETH

I A maman METCHA CECILE

REMERCIEMENTS

Nous tenons ici à exprimer notre reconnaissance et notre immense gratitude à :

M. Leoncio F. ESSONO NZE OYANA, Directeur Général de l'ISSEA, et à travers lui tout le personnel de l'Institut pour la qualité des enseignements reçus.

M. Séverin Yves KAMGNA, Chef du Service des Prévisions Macroéconomiques à la BEAC, qui a bien voulu guider nos premiers pas sur les sentiers de la recherche. Malgré vos multiples occupations, vous avez toujours trouvé un moment à nous consacrer. Recevez ici l'expression de nos sincères remerciements.

M. Robert NGONTHE, Directeur des études du 3^ème cycle à l'ISSEA, pour son soutien et ses multiples conseils durant toute notre formation.

M. Dieudonné KINKIELELE, Directeur des études des 1^er et 2^ème cycles à l'ISSEA, pour son soutien et pour la rigueur qu'il nous a inculqué tout au long de notre cursus.

M. Sébastien DJIENOUASSI et Mlle Arlette WOKAM pour m'avoir soutenu tout au long de ce travail. Toute notre reconnaissance.

Mlle Alvine TCHAMKO pour l'amour et l'affection dont j'ai bénéficié tout au long de ce travail.

M. Joubert NGUETSE dont les critiques et suggestions ont permis d'améliorer la qualité de ce travail.

Tout ceux qui ont relu ce document, particulièrement Mlle Carine METASSE et Mlle Carine NZEUYANG.

Tous nos camarades de promotion plus particulièrement Guy Paulin TEKOMBONG, Jules Roland WOGUIA, Eric Maturin NKAMGNIA, pour le soutien amical accordé tout au long de notre formation.

Mes frères et amis particulièrement Anicet SEIGNING, Guy Martial NGANGKAM, Honoré LATA, pour m'avoir soutenu et encouragé durant toute ma formation à l'ISSEA.

Nous ne saurions terminer sans rendre un vibrant hommage à tous ceux qui, bien que n'ayant pas été cités ici, ont fait en sorte que ce travail soit mené à terme.

TABLE DES MATIÈRES

DÉDICACE I

REMERCIEMENTS II

LISTE DES TABLEAUX, FIGURES ET GRAPHIQUES V

LISTE DES ABRÉVIATIONS VI

AVANT-PROPOS VII

RÉSUMÉ VIII

INTRODUCTION GÉNÉRALE 1

Chapitre 1 : APERÇU DU SYSTÈME BANCAIRE DE LA CEMAC 4

Section 1 : PRÉSENTATION GÉNÉRALE 4

1.1 Typologie des institutions financières de la CEMAC 4

1.1.1 La Banque Centrale 4

1.1.2 Les banques Créatrices de Monnaie (BCM) 5

1.1.3 Les Autres Institutions Bancaires (AIB) 5

1.1.4 Les Institutions Financières Non Bancaires (IFNB) 5

1.2 L'activité des banques commerciales de la CEMAC 5

1.2.1 L'intermédiation financière 7

1.2.2 La création monétaire 8

1.2.3 La gestion des moyens de paiements 9

Section 2 : ÉVOLUTION DU SYSTÈME BANCAIRE DE LA CEMAC 10

2.1 Crise et restructuration du système bancaire 10

2.1.1 Les causes de la crise 10

2.1.2 Les restructurations du système bancaire 11

2.2 La politique de libéralisation financière 13

2.2.1 La politique monétaire avant 1990 13

2.2.2 La nouvelle politique monétaire (après 1990) 14

2.2.3 La Commission Bancaire de l'Afrique Centrale (COBAC) 15

2.3 Surliquidité des banques et faiblesse du financement bancaire dans la CEMAC 17
Chapitre 2 : DE L'EFFICACITÉ ÉCONOMIQUE A LA MESURE DE L'EFFICACITÉ

TECHNIQUE 19

Section 1 : CONCEPT D'EFFICACITÉ ÉCONOMIQUE 19

1.1 L'efficacité technique 19

1.2 L'efficacité allocative (efficacité prix) 21

1.3 Décomposition de l'efficacité économique 21

Section 2 : LES MÉTHODES D'ESTIMATION DE L'EFFICACITÉ TECHNIQUE 24

2.1 La méthode d'enveloppement des données 25

2.1.1 Le modèle à rendements d'échelle constants 26

2.1.2 Le modèle à rendements d'échelle variables 29

2.2 L'approche Free Disposall Hull (FDH) 31

2.3 L'approche de la frontière stochastique 32

Chapitre 3 : MESURE DE L'EFFICACITÉ TECHNIQUE DES BANQUES COMMERCIALES DE LA CEMAC PAR LA METHODE DEA 37

Section 1 : APPROCHE MÉTHODOLOGIQUE 37

1.1 Spécification input-output bancaire 37

1.1.1 L'approche par la production 37

1.1.2 L'approche par l'intermédiation 37

1.2 Les données et les variables 38

1.3 Présentation du modèle empirique 40

Section 2 : ANALYSE DES RÉSULTATS 41

2.1 Analyses descriptives 42

2.1.1 Evolution des scores moyens annuels et mensuels 42

2.1.2 Analyses suivant l'année 47

2.2 Analyse en composantes principales (ACP) et classification des banques de la

CEMAC 50

Chapitre 4 : ANALYSE ÉCONOMÉTRIQUE DES DÉTERMINANTS DE L'EFFICACITÉ TECHNIQUE 55

Section 1: PRÉSENTATION DU MODÈLE 55

1.1 Choix du modèle empirique 55

1.2 Spécification du modèle 56

Section 2: ESTIMATION DU MODÈLE ET INTERPRÉTATION DES RESULTATS 57

2.1 Estimation du modèle 57

2.2 Interprétation des résultats 58

CONCLUSION ET RECOMMANDATIONS 61

RÉFÉRENCES BIBLIOGRAPHIQUES 64

ANNEXES 66

LISTE DES TABLEAUX, FIGURES ET GRAPHIQUES

Liste des tableaux

Tableau 1.1 : Banque en activité au 31 décembre 2004 6

Tableau 1.2: Situation des dépôts et des crédits au 31 mars 2005 (en Mds de FCA) 8

Tableau 1.3 : Ventilation des crédits bruts par type de clientèle au 31 décembre 2 004 (en millions) 9

Tableau 1.5 : Besoins de financement du système bancaire par Etat en 1 990 (En milliards de Fcfa) 11

Tableau 1.6 : Banques en liquidation en fin 1 996 12

Tableau 1.7 : Signification des cotes SYSCO 17

Tableau 2.1 : Nombre de banques de l'échantillon par pays 38

Tableau 3.2 : Evolution des scores moyens d'efficacité 42

Tableau 3.3 : Score d'inefficacité moyen entre 2001 et 2004 44

Tableau 3.4 : Nombre de banques techniquement efficaces suivant l'hypothèse de rendements d'échelle.

47

Tableau 3.5 : Classement des banques suivant le score moyen d'efficacité technique pure 48

Tableau 3.6 : Moyennes mensuelles des scores de l'échantillon 50

Tableau 3.7 : Tableau des valeurs propres 51

Tableau 3.8 : Résultats du modèle 58

Liste des figures

Figure 2.1 : Frontière de production et rendements d'échelle 20

Figure 2.2 : Efficacité technique et allocative : cas de deux intrants 22

Figure 2.3 : Changement de la proportion d'utilisation des inputs de la firme P 23

Figure 2.4 : Illustration de la mesure de l'efficacité technique par la méthode DEA 25

Figure 2.5 : Illustration de la domination entre firmes dans l'approche FDH 31

Figure 2.6 : frontière de production par l'approche FDH 32

Figure 2.7 : frontière de production stochastique : décomposition du terme d'erreur 33

Figure 3.1 : Illustration de l'intermédiation financière des banques commerciales 39

Figure 3.2 : Arbre hiérarchique issu de l'algorithme de Ward 53

Liste des graphiques

Graphique 3.1 : Evolution des scores moyens d'efficacité 43

Graphique 3.2 : Evolution des scores moyens annuels d'efficacité 44

Graphique 3.3 : Evolution des scores moyens mensuels d'efficacité 46

Graphique 3.4 : Score moyen par pays et par an 49

Graphique 3.5 : Projection des individus sur les deux premiers facteurs 52

LISTE DES ABRÉVIATIONS

AIB : Autres Institutions Bancaires

AIBE : Autres Institutions Bancaires Eligibles au refinancement de la BEAC

AIBNE : Autres Institutions Bancaires Non Eligibles au refinancement de la BEAC

BCM : Banques Créatrices de Monnaie

BEAC : Banque des Etats de l'Afrique Centrale

CEMAC : Communauté Economique et Monétaire de l'Afrique Centrale CLC : Crédit Lyonnais Cameroun

COBAC : Commission Bancaire de l'Afrique Centrale

CRS : Constant Returns to Scale

DEA : Data Envelopment Analysis

FCFA : Franc de la Coopération Financière en Afrique

FDH : Free Disposall Hull

IAS4 : Ingénieur d'Application de la Statistique, ^4ième année

IFNB : Institutions Financières Non Bancaires

ISSEA : Institut Sous-régional de Statistique et d'Economie Appliquée

MCO : Moindres carrés ordinaires

Mds : Milliards

RCA : République Centrafricaine

REC : Rendement d'échelle constant

REV : Rendement d'échelle variable

SCB : Société Camerounaise de Banque

SYSCO : Système de Cotation

TCM : Taux Créditeur Minimum

TDM : Taux Débiteur Maximum

VRS : Variable Returns to Scale

AVANT-PROPOS

L'ISSEA est un établissement public inter-étatique créé dans le cadre des organismes spécialisés de la CEMAC, ayant pour mission la formation et le perfectionnement des cadres Statisticiens et Economistes de la sous région. Il comprend trois cycles : le cycle des Techniciens Supérieurs de la Statistique (TSS), le cycle des Ingénieurs d'Application de la Statistique (IAS) et le cycle des Ingénieurs Statisticiens Economistes (ISE).

Les étudiants de 4ème année du cycle des Ingénieurs d'Application de la Statistique sont astreints à rédiger et à soutenir publiquement un mémoire de fin de scolarité. Ce mémoire qui marque le début d'une initiation à la recherche, est l'occasion idoine pour eux de valoriser les enseignements reçus durant leur formation.

C'est dans ce cadre qu'intervient le présent document qui est le fruit de nos recherches sur le thème « Mesure de l'efficacité technique des banques commerciales de la CEMAC ». Le choix de ce thème se justifie par la place prépondérante qu'occupe les banques commerciales dans les économies de la sous région où les marchés financiers existants sont encore dans un état embryonnaire. En effet, en l'absence de marché financier, le financement de l'activité économique provient essentiellement des crédits bancaires. C'est conscient de cette réalité que nous avons voulu à travers ce travail, apporter notre modeste contribution à l'évaluation des performances techniques du secteur bancaire sous régional. Pour parvenir à nos fins, nous avons eu recours à l'une des méthodes les plus utilisées pour évaluer les performances des unités de production notamment la méthode DEA (Data envelopment analysis). Nous nous sommes donc attelés tout au long de ce travail à mesurer empiriquement le niveau d'efficacité technique des banques commerciales de la CEMAC et à détecter les déterminants de cette efficacité.

L'oeuvre humaine étant entachée d'imperfections, nous n'avons pas la prétention d'avoir cerné tous les contours de ce sujet. Nous restons donc ouvert à toutes critiques et suggestions visant l'amélioration de la qualité de ce travail.

RÉSUMÉ

En Afrique Centrale, comme dans la plupart des pays en voie de développement, les banques occupent une place de choix dans le financement de l'activité économique à travers le processus d'intermédiation financière. Leur rôle consiste donc à collecter des ressources auprès des agents à capacité de financement, pour les mettre à la disposition des agents à besoin de financement à travers des crédits. Par ce processus de transformation de leurs ressources, les banques concourent au financement des investissements qui génèrent la croissance économique. Depuis déjà une décennie, on assiste dans la sous région à une situation où les banques regorgent suffisamment de ressources et n'octroient que très peu de crédits. Ce qui nous fait penser que les banques de la CEMAC semblent ne pas gérer optimalement les ressources mises à leur disposition.

L'objet de cette étude est d'évaluer empiriquement sur la période allant de 2001 à 2004, les niveaux d'efficacité technique de 24 banques commerciales dans la sous région, et de détecter les principaux déterminants de ces niveaux. La méthode DEA est utilisée pour estimer des scores mensuels d'efficacité technique de chacune des banques de l'échantillon sur toute la période. Les scores ainsi obtenus sont régressés sur certains ratios de la gestion bancaire, afin de détecter les variables sur lesquelles on pourrait agir, pour améliorer l'efficacité des banques dans la transformation de leurs ressources en crédits.

Les banques commerciales sur toute la période de l'étude, n'ont produit en moyenne que 36,9 % de la quantité de crédits qu'elles auraient pu produire à partir de leurs ressources, si elles opéraient toutes à rendements d'échelle constants. Sous hypothèse de rendements variables, elles n'ont produit que 69,3 % de la quantité de crédits qu'elles étaient susceptibles de produire à partir de leurs ressources. Ces résultats confirment le fait que les banques produisent des quantités de crédits inférieures à ce qui est techniquement possible à partir des ressources dont elles disposent. Leurs sous-productions sont beaucoup plus liées à un problème d'échelle sous optimale qu'à un problème de mauvaises pratiques de gestion. On constate également que les pratiques de gestion des banques n'ont pas beaucoup varié durant la période de l'étude. Ce travail révèle aussi que plus les banques accumulent des créances douteuses dans leur portefeuille de crédits, plus elles sont techniquement inefficaces. La crainte de ne pas pouvoir récupérer leurs créances est le principal facteur qui justifie le comportement frileux des banques. Un autre résultat de cette étude est que plus les fonds propres d'une banque deviennent importants, plus elle est efficace dans la transformation de ses ressources en crédits. Par contre,

une trésorerie pléthorique pour une banque pourrait s'interpréter comme la manifestation d'une inefficacité dans la transformation de ses ressources.

Pour améliorer l'efficacité technique des banques, plusieurs axes d'actions sont envisageables, notamment l'amélioration du cadre juridique dans lequel évolue l'activité bancaire, la mise en place par les banques d'outils appropriés pour l'évaluation du risque, le

renforcement des fonds propres dans l'actif total des banques et la création de structures ^d'appuipour l'élaboration de projets d'investissements bancables.

.

INTRODUCTION GÉNÉRALE

La fin des années 80 dans la plupart des pays de la CEMAC est marquée par une grave crise du secteur bancaire dont la manifestation la plus apparente a été la liquidation de plusieurs établissements de crédits. Cette crise était le résultat d'une conjoncture économique déprimée du fait de la baisse des cours des produits de base exportés sur lesquels reposait l'économie des pays de la sous région, du rôle prépondérant joué par l'Etat en tant qu'actionnaire majoritaire dans la plupart des banques, de l'inefficacité du dispositif de surveillance existant et d'une mauvaise gestion des établissements bancaires. Pour y remédier, les autorités monétaires de la sous région ont entrepris des reformes portant sur le renforcement du cadre réglementaire et prudentiel, la libéralisation de l'activité bancaire, ainsi que de nombreuses mesures de restructuration du système bancaire. C'est ainsi que la commission bancaire de l'Afrique Centrale (COBAC) voit le jour en janvier 1993 en tant qu'organe supranational de supervision des établissements de crédits. Elle s'est immédiatement dotée dès sa création d'un dispositif prudentiel lui permettant d'apprécier la santé financière des établissements de crédit afin de prendre des mesures correctives en cas de nécessité. Ce qui semble avoir porté fruit dans la mesure où les faillites bancaires ont pratiquement disparue et les banques semblent être bien portante du moins financièrement.

A partir du deuxième semestre de 1994, suite à la dévaluation du franc CFA, les banques commerciales de la CEMAC se retrouvent dans une situation de surliquidité pouvant être appréhendé à travers le coefficient de liquidité¹ dont la valeur dans la sous région s'élève à 217,5 % en 1995. Elles bénéficient ainsi d'importantes ressources pouvant leur permettre de s'impliquer davantage dans le financement de l'activité économique et contribuer ainsi au développement des économies de la sous région. Curieusement, on a plutôt l'impression au regard de l'évolution comparée des ressources collectées et des crédits octroyés durant cette dernière décennie², que les banques s'éloignent de plus en plus du financement des investissements. Leur préférence est plutôt orientée vers des emplois de trésorerie et l'offre de services à la clientèle pour

¹ C= Actif liquide / Passif exigible à court terme ~ 100 %

² Les dépôts collectés par l'ensemble du système bancaire se sont accrus de 128,2 % de 1 994 à 2004 alors que durant la même période, les crédits bruts à l'économie n'ont évolué que de 56 %.

lesquels elles prélèvent d'importantes commissions. Cette frilosité des banques à financer les investissements quoi que disposant suffisamment de ressources, est un constat assez alarmant dans la mesure oü le crédit bancaire constitue dans la sous région l'une des principales sources de financement de l'activité économique, les marchés financiers étant encore inopérants. On évolue ainsi dans un environnement oü le besoin d'investissement n'est pas entièrement satisfait par la production bancaire. Pourtant les banques regorgent de ressources en abondance. La question qui nous interpelle alors est celle de savoir si dans ce contexte de surliquidité, les banques exploitent optimalement les ressources mises à leur disposition ? Autrement dit les banques sont elles techniquement efficaces dans la transformation de leurs ressources en crédits ? L'efficacité technique est entendue ici comme l'habileté pour une banque à obtenir le maximum de crédits possibles à partir des ressources dont elle dispose, pour une technologie donnée. Ce niveau maximum de production possible étant déterminé au regard des performances de banques similaires. Le choix de définition de l'efficacité étant opéré, on pourrait également rechercher les déterminants de l'efficacité technique des banques commerciales de la CEMAC.

L'objectif général de ce travail est de mesurer les niveaux d'efficacité technique des banques commerciales de la CEMAC et de détecter les facteurs explicatifs de ces niveaux.

Pour atteindre cet objectif, on passera par les objectifs spécifiques ci-après :

1' Evaluer les niveaux d'efficacité technique des banques de notre échantillon en attribuant à chacune d'elles un score d'efficacité compris entre 0 et 1.

1' Etablir le lien existant entre les scores obtenus et les variables explicatives potentielles de l'efficacité technique des banques.

Ce sujet présente un double intérêt :

1' Il fait ressortir les variables sur lesquelles on pourrait agir pour améliorer l'efficacité des banques commerciales dans la transformation de leurs ressources en crédits.

1' Il peut également servir de tremplin à des études similaires, en l'occurrence, les facteurs explicatifs de l'efficacité technique des établissements de microfinances que nous n'abordons pas ici.

Deux hypothèses sous-tendent cette étude à savoir :

1' Les banques commerciales de la CEMAC sont techniquement inefficaces dans la transformation de leurs ressources en crédits : elles produisent en deçà de ce qu'elles sont susceptibles de produire à partir des ressources dont elles disposent ;

1' Plus les banques accumulent des créances douteuses, plus elles sont techniquement inefficaces.

Nous avons eu recours à la méthode DEA (Data envelopment analysis) pour mesurer les niveaux d'efficacité technique de 24 banques commerciales de la CEMAC sur la période 2001-2004. Le choix de cette méthode non paramétrique se justifie par l'incertitude de la relation fonctionnelle liant les inputs et les outputs dans le secteur bancaire. Pour cerner les facteurs explicatifs des niveaux d'efficacité des banques, nous avons estimé un modèle de régression linéaire. Ce modèle a pour variable expliquée les scores d'efficacité et comme variables explicatives, les déterminants potentiels de l'efficacité technique des banques. Les données utilisées pour l'estimation des scores et l'analyse des déterminants de l'efficacité technique, proviennent du Secrétariat Général de la COBAC.

Pour atteindre nos objectifs, nous avons structuré notre travail en quatre chapitres : le premier chapitre présente le système bancaire de la CEMAC et son évolution depuis la crise des années 80. Le deuxième chapitre quant à lui présente les concepts d'efficacité ainsi que les principales méthodes utilisées dans la littérature pour mesurer l'efficacité technique des unités de production. Au troisième chapitre, la méthode DEA est utilisée pour estimer les scores d'efficacité technique des banques commerciales de notre échantillon sur la période de l'étude. Le quatrième chapitre est consacré à l'analyse économétrique des déterminants de l'efficacité technique des banques et à quelques recommandations visant l'amélioration de l'efficacité des banques dans la transformation de leurs ressources en crédits.

Chapitre 1 : APERÇU DU SYSTÈME BANCAIRE DE LA CEMAC

L'objet de ce chapitre est la présentation du système bancaire de la CEMAC (section 1) à travers ses éléments constitutifs, ainsi qu'un aperçu de l'évolution de l'activité bancaire dans la CEMAC depuis la crise des années 80 (section 2). Un système bancaire peut se définir comme un ensemble de banques, d'autres établissements financiers et d'une banque centrale qui entretiennent des relations financières de créances et d'engagements les uns vis-à-vis des autres ainsi que vis-à-vis des agents non financiers (Mathis, 1992).

Section 1 : PRÉSENTATION GÉNÉRALE

1.1 Typologie des institutions financières de la CEMAC

La Banque des Etats de l'Afrique Centrale (BEAC) classifie les institutions financières composant le secteur financier des pays membres de l'Union Monétaire de l'Afrique Centrale en quatre groupes : la Banque Centrale, les Banques Créatrices de monnaie (BCM), les Autres Institutions Bancaires (AIB), et les Institutions Financières Non Bancaires (IFNB).

1.1.1 La Banque Centrale

Le dictionnaire d'économie et des faits économiques et sociaux contemporains définit la banque centrale comme étant une banque située au sommet de la hiérarchie du système bancaire et jouant un rôle essentiel dans le processus de création monétaire en émettant la monnaie centrale qui est composée des billets de banque et du solde créditeur des comptes des banques commerciales et du trésor dans ses livres, ces avoirs en compte pouvant être convertis en billets.

La Banque des Etats de l'Afrique Centrale (BEAC) est un établissement multinational regroupant six Etats membres : le Cameroun, le Gabon, la République Centrafricaine, le Congo, le Tchad et la Guinée Equatoriale. Créée le 22 novembre 1972, la BEAC émet la monnaie de l'Union et en garantit la stabilité. Elle a pour missions de:

1' définir et conduire la politique monétaire applicable dans les pays membres de l'Union ; 1' conduire les opérations de change ;

1' détenir et gérer les réserves de change des pays membres ;

1' promouvoir le bon fonctionnement du système des paiements dans l'Union.

1.1.2 Les banques Créatrices de Monnaie (BCM)

Les BCM acceptent les dépôts à vue disponibles par chèques et utilisés comme moyens de paiement. C'est dans cette catégorie que se situent les banques commerciales.

1.1.3 Les Autres Institutions Bancaires (AIB)

Les AIB regroupent tous les autres établissements bancaires qui, contrairement aux BCM, n'acceptent pas des dépôts à vue disponibles par chèques. On peut les regrouper en deux catégories :

~ Les Autres Institutions Bancaires Eligibles au Refinancement de la BEAC (AIBE)

Ce sont tous les autres établissements à caractère bancaire qui sont admis au refinancement de la Banque Centrale et qui reçoivent des dépôts d'épargne et à terme sans toutefois contracter des engagements sous forme de dépôts à vue transférables par chèques. Il s'agit essentiellement de certaines banques de développement, des institutions bancaires de financement de l'habitat social (Crédit Foncier...), etc.

~ Les Autres Institutions Bancaires Non Eligibles au Refinancement de la BEAC (AIBNE)

Ce sont les établissements bancaires de même nature que ceux définis précédemment sauf que ces institutions ne recourent pas au refinancement de l'Institut d'Emission. On dénombre dans cette catégorie les Caisses d'Epargne Postale et certaines banques spécialisées.

1.1.4 Les Institutions Financières Non Bancaires (IFNB)

Les IFNB sont des établissements qui ne collectent pas de dépôts du public mais qui participent d'une certaine manière au financement de l'économie. Il s'agit essentiellement des compagnies d'assurances et de réassurances, des établissements de crédit-bail et de leasing, des sociétés financières et de participation, etc.

1.2 L'activité des banques commerciales de la CEMAC

A la fin de l'année 2004, le système bancaire de la CEMAC comptait 33 banques en activité dont 10 au Cameroun, 3 en Centrafrique, 4 au Congo, 6 au Gabon, 3 en Guinée équatoriale et 7 au Tchad. Le tableau ci-dessous présente les différentes banques en activité dans la CEMAC ainsi que la structure de leur capital en décembre 2004.

Tableau 1.1 : Banque en activité au 31 décembre 2004

Pays	Etablissement	Capital social (million CFA)	Structure du capital des banques (%)
			Etat	Etranger	Privés nationaux
Cameroun (10banques)	BICEC	3 000	37,25	62,75	0
	Crédit Lyonnais Cameroun S.A	6 000	35	65	0
	SGBC	6 250	25,60	58,08	16,32
	Standard Chartered Bank Cameroon	7 000	0	100	0
	Afriland First Bank	4 500	0	20	80
	Amity Bank Cameroon	4 000	0	0	100
	Citibank Cameroon N.A	3 163	0	100	0
	Commercial Bank of Cameroon	7 000	0	15	85
	Union bank of Cameroon PLC	5 000	0	7,13	92,87
	Ecobank Cameroun S.A	2 500	0	79,60	20,40
Centrafrique (3 banques)	Banque Populaire Maroco-Centrafricaine	2 000	37,50	62,50	0
	Banque Internationale pour la Centrafrique	1 500	9,33	50	40,67
	Commercial Bank Centrafrique	1 500	10	59,50	30,50
Congo (4 banques)	Cofipa Investment Bank Congo	3 000	10	77,43	12,57
	Crédit Lyonnais Congo S.A	2 222	9,99	81	10,01
	BGFIBANK Congo	5 000	0	85	15
	La Congolaise de Banque	4 000	11	25	64
Gabon (6 banques)	BICIG	12 000	26,35	46,67	26,98
	Banque Gabonaise de développement	25 200	69,01	30,99	0
	BGFIBANK Gabon	25 065	8	14	78
	CITIBANK N.A. Gabon	1 000	0	100	0
	Union Gabonaise de banque	5 000	25	74,20	0,80
	Financial Bank Gabon	1 250	1,58	70	28,42
Guinée Equatoriale (3 banques)	BGFIBANK-Guinée Equatoriale	1 500	15	55	30
	SGB-GE	1 740	31,80	57,24	10,96
	CCEI Bank Guinée Equatoriale	3 500	10	77	13
Tchad (7 banques)	Banque Agricole du Soudan au Tchad	869	0	100	0
	Banque commerciale du Chari	3 000	50	50	0
	Commercial Bank Tchad	4 020	17,48	77,93	4,59
	Banque internationale pour l'Afrique au Tchad	3 000	0	80,60	19,4
	Société Générale Tchadienne de Banque	1 100	20	76	4
	Financial Bank Tchad	1 850	0	100	0
	BSIC	2 000	0	100	0

Source : COBAC (rapport d'activité 2004)

Le tableau ci-dessus laisse entrevoir qu'en décembre 2004, l'actionnariat des banques des Etats de la CEMAC est majoritairement constitué d'apports privés nationaux ou étrangers. Cette main mise limitée de l'Etat sur les banques commerciales dans la CEMAC pourrait s'expliquer par la libéralisation financière du secteur bancaire ayant fait suite à la crise bancaire des années 1980.

L'activité des banques commerciales peut s'analyser en trois fonctions principales : l'intermédiation financière, la création monétaire, et la gestion des moyens de paiement.

1.2.1 L'intermédiation financière

L'intermédiation financière est l'activité par laquelle une banque met en relation les agents économiques à excédent de financement avec ceux à déficit de financement. Elle consiste pour une banque à collecter des ressources auprès des agents à excédent de financement, pour les mettre à la disposition des agents à déficit de financement qui en manifestent le besoin. Cette activité qui constitue la fonction fondamentale des banques commerciales, se justifie par les imperfections sur le marché des capitaux, caractérisées par des coûts de transactions élevés liés à la finance directe, l'incohérence entre les objectifs des agents à capacité de financement recherchant généralement des placements à court terme et ceux des agents à déficit de financement désirant des financements à long terme, et l'asymétrie d'information existante sur le marché. On distingue généralement deux formes d'intermédiation : l'intermédiation de représentation et l'intermédiation de transformation. Dans l'intermédiation de représentation, le rôle de l'intermédiaire financier est semblable à celui d'un courtier sur le marché financier. La banque dans ce cas collecte et/ou exécute les ordres de ses clients sur le marché ou alors se convertit en acheteur et revendeur de titres. L'intermédiation de transformation quant à elle consiste pour la banque à collecter des ressources ou dépôts auprès de la clientèle lui permettant l'octroi des crédits. La banque dans ce cas transforme les dépôts en crédits et cette opération affecte nécessairement son bilan. Les marchés financiers de la sous région étant encore dans un état embryonnaire, c'est l'intermédiation de transformation qui est pratiquée par les banques commerciales dans la CEMAC. Le tableau ci-dessous donne la situation des dépôts et des crédits effectués par les banques des différents Etats au 31 Mars 2005.

Tableau 1.2: Situation des dépôts et des crédits au 31 mars 2005 (en Mds de FCA)

Pays	Dépôts de la clientèle	Proportion des dépôts (%)	Crédits bruts à la clientèle	Proportion des crédits (%)
Cameroun	1 234	52,58	920	53,05
RCA	35	1,49	60	3,46
Congo	179	7,63	95	5,48
Gabon	613	26,12	440	25,38
Guinée Equatoriale	176	7,49	93	5,36
Tchad	110	4,69	126	7,27
Total	2 347	100	1 734	100

Source : COBAC

D'après les données du tableau ci-dessus, le système bancaire camerounais constitue à lui seul 52,58 % du montant total des dépôts et 53,05 % du montant total des crédits dans la sous région. Le système bancaire gabonais constitue pour sa part 26,12 % du total des dépôts et 25,38 % du total des crédits. Les deux systèmes bancaires représentent ainsi à eux seuls près de 79 % du marché bancaire de la CEMAC en termes de collecte de dépôts et de distribution de crédits.

1.2.2 La création monétaire

L'une des particularités des banques commerciales et qui les distingue des autres institutions financières est le pouvoir qu'elles ont de créer de la monnaie. La création monétaire correspond à une augmentation de la masse monétaire, entendue comme étant l'ensemble des moyens de paiements mis à la disposition des agents non financiers. Dans le processus de création monétaire, ce sont les « crédits qui font les dépôts » (Patat J., 1993). La banque dans ce cas octroi des crédits non plus à partir des dépôts collectés, mais plutôt à partir de la monnaie centrale provenant d'une autre banque à travers le marché interbancaire ou de la banque centrale. Ces crédits vont générer de nouveaux dépôts en augmentant ainsi la masse monétaire. La création monétaire peut également se faire à travers des opérations sur devises étrangères. Dans ce cas, l'augmentation de la masse monétaire correspond à la quantité de monnaie étrangère convertie en monnaie nationale par la banque. On distingue généralement trois principales sources de création monétaire, encore dénommées contreparties de la masse monétaire³ : le crédit à l'économie, les créances nettes sur l'Etat et les créances sur l'extérieur. Le crédit à l'économie représente l'ensemble des crédits octroyés aux agents non financiers autres que l'Etat. Le tableau ci-dessous présente la ventilation des crédits bruts par type de clientèle au 31 décembre 2004.

³ D. Plihon (page 45)

Tableau 1.3 : Ventilation des crédits bruts par type de clientèle au 31 décembre 2004 (en millions)

	Crédit à l'Etat	Crédit à l'économie		Crédits aux non résidents	Autres créances	Total
Cameroun	9 033		828 563	26 649	9 402	873 647
RCA	4 264		55 531	316	77	60 188
Congo	22 392		82 566	1 531	488	106 977
Gabon	39 080		393 279	25 614	5 156	463 129
Guinée E.	5 180		63 197	26 318	717	95 412
Tchad	20 450		85 745	4 297	1 778	112 270
CEMAC	100 399	1	508 881	84 725	17 618	1 711 623
Proportion	5,87		88,15	4,95	1,03	100

Source : COBAC

Il ressort du tableau ci-dessus que les créances sur l'économie représentent en 2004 la principale source de création monétaire dans la sous région, constituant à elle seule 88,15 % du total des créances des banques sur la clientèle. Le secteur productif reste donc le principal bénéficiaire des crédits octroyés par les banques de la CEMAC. Les créances sur l'Etat ne constituent pour leur part que 5,86 % du total des crédits distribués par les banques à leur clientèle.

1.2.3 La gestion des moyens de paiements

Les moyens de paiements sont constitués par les billets et pièces de la banque centrale (monnaie fiduciaire), et les dépôts à vue (monnaie scripturale). Un moyen de paiement permet à un agent économique d'effectuer des règlements dans ses transactions avec les autres agents. La banque centrale est chargée de l'émission des billets et pièces métalliques dont elle contrôle la quantité en circulation. Les banques gèrent les dépôts à vue qui constituent également de la monnaie pouvant être retirée immédiatement par les déposants, et dont la circulation est assurée par des instruments tels que les chèques bancaires, les virements bancaires, les effets de commerce, etc.

Section 2 : ÉVOLUTION DU SYSTÈME BANCAIRE DE LA CEMAC

Nous aborderons dans cette section l'évolution du système bancaire de la CEMAC, de la crise des années 80 à la surliquidité systémique observée dans la sous région, en passant par la politique de libéralisation financière des années 90.

2.1 Crise et restructuration du système bancaire

Le système bancaire de la CEMAC a connu à la fin des années 80, une crise dont la manifestation la plus apparente a été la fermeture de nombreux établissements de crédits. Cette partie a pour but de présenter les causes de cette crise ainsi que les solutions adoptées pour y remédier.

2.1.1 Les causes de la crise

On peut regrouper les facteurs à l'origine de la crise en deux groupes : les facteurs externes et les facteurs internes.

a. Les facteurs externes

Ils sont liés à la conjoncture économique déprimée, à l'inefficacité du dispositif de surveillance bancaire et aux défaillances du système juridique.

La baisse des cours des matières premières dont dépendaient la plupart des économies de la sous région a créé un déficit au niveau du budget de l'Etat. Pour combler ce déficit, le trésor public fait appel au financement bancaire, accumulant ainsi la dette intérieure. L'Etat ne pouvant plus honorer ses engagements, porte atteinte à la liquidité bancaire, provoquant ainsi une réduction du niveau des dépôts privés. Les banques ne pouvant entrer en possession de la plupart de leurs créances, se retrouvent dans une situation d'illiquidité et sont incapables de faire face à leurs engagements vis-à-vis de la clientèle.

Par ailleurs, le dispositif de surveillance bancaire mis en place ne jouait pas véritablement son rôle, n'usant pas de son pouvoir de sanction pour remette sur les rails les banques en dérapage.

Sur le plan juridique,le système était peu favorable à l'activité bancaire, ce système étant incapable de sévir face à des débiteurs bénéficiant de protections politiques.

b. Les facteurs internes

Les facteurs internes étaient liés à une mauvaise gestion des établissements de crédits. Selon Mathis J. (1992), les erreurs de gestion sont de deux sortes à savoir la distribution de crédit à des entreprises non rentables et le gonflement excessif des frais généraux . En effet, les banques prenaient des énormes risques en octroyant des crédits sans étudier préalablement la

rentabilité des projets auxquels ils étaient destinés. De plus, le gonflement des frais de personnel par les organes dirigeants a eu des répercussions sur la rentabilité des banques, en réduisant leurs marges bénéficiaires.

2.1.2 Les restructurations du système bancaire

Pour remédier à la crise du système bancaire, les autorités monétaires ont entrepris des mesures de restructurations entrant dans l'une des trois catégories suivantes : le traitement des banques en difficultés, les mesures spécifiques à l'ensemble du secteur bancaire et les mesures de politique économique générale (Mathis J., 1992).

a. La première restructuration (1989 - 1992)

Elle consistait essentiellement à liquider les établissements gravement touchés par la crise et à restaurer la liquidité, la solvabilité, et la rentabilité de ceux restés en activité.

Les autorités monétaires ont procédé à la liquidation de l'actif des banques en situation d'insolvabilité profonde et au financement de celles dont la viabilité à terme paraissait certaine. Certains créanciers des banques, en particuliers les petits déposants, se sont vus rembourser par le biais des structures de liquidation (la Société de Recouvrement des Créances dans le cas du Cameroun par exemple). L'Etat qui était le principal débiteur des banques en liquidation, s'est engagé à rembourser une partie des dépôts des entreprises publiques, des particuliers, ainsi que le refinancement consenti par la banque centrale à ces banques. Les bilans des banques ont été corrigés afin de pallier aux erreurs de gestion du passé. La comparaison des bilans avant et après corrections fait apparaître une accumulation des déficits de gestion correspondant à d'importants besoins de financement. Le tableau ci-dessous donne la répartition des besoins de financement du système bancaire dans son ensemble et par Etat. Le total s'élevait à plus de 540 Milliards de FCFA.

Tableau 1.5 : Besoins de financement du système bancaire par Etat en 1990 (En milliards

de Fcfa)

Pays	Cameroun	RCA	Tchad	Gabon	Guinée Equatoriale	Congo
Banques à liquider	185,1			1,3		15
Banques à réhabiliter	305,3
Banques en liquidation		2,5				17
Banques à restructurer		7,6				2,5
Banques inactives			1,8		3,5
Banques à assainir			4,2
Total	490,4	10,1	6	1,3	3,5	34,5

Source : COBAC

Le système bancaire Camerounais est celui qui présentait le plus grand besoin de financement, soit près de 90 % du financement nécessaire dans la sous-région.

Malgré toutes ces mesures, le système bancaire de la CEMAC va connaître de nouvelles secousses qui conduiront les autorités monétaires à entreprendre une deuxième restructuration

b. La deuxième restructuration (après 1992)

Cette deuxième restructuration qui vient pallier aux insuffisances de la première, consistait essentiellement en l'adoption de mesures visant la transformation du secteur bancaire, notamment la mise en place de la Commission Bancaire de l'Afrique Centrale (COBAC) pour assurer un meilleur contrôle de la liquidité, de la solvabilité et de la rentabilité des banques. Cette deuxième phase de restructuration aboutit d'une part à la liquidation de certaines banques qui malgré la dernière restructuration, demeuraient en situation très critique, et d'autre part à la réhabilitation et à la privatisation des autres. Le tableau ci-dessous donne la liste des banques en liquidation dans la CEMAC en fin 1996.

Tableau 1.6 : Banques en liquidation en fin 1996

Pays	Etablissements
Cameroun (11 banques)	Crédit Agricole du Cameroun (CAC) Banque Méridien BIAO Cameroun First Investment Bank (FIB) International Bank of Africa (IBAC) Banque internationale pour le commerce et l'industrie du Cameroun (BICIC) Portefeuille de banques géré par la SRC ( Société Camerounaise de banques, Cam Bank, Banque Camerounaise de développement ,Paribas Cameroun, Bank of Credit and Commerce, BIAOC)
Centrafrique (4 banques)	Banque Nationale de développement (BND) Banque Centrafricaine d'Investissement (BCI) Banque Centrafricaine de Crédit Agricole (BCAD) Banque Nationale Centrafricaine de dépôts (BNCD)
Congo (2 banques)	Banque Commerciale Congolaise (BCC) Banque Nationale de développement du Congo (BNDC)
Gabon (3 banques)	Banque du Gabon et du Luxembourg (BGL) Banque privée de Gestion et du Crédit (BPGC) Bank of Credit and Commerce International (BCCI)
Guinée Equatoriale (2 banques)	Banco de Credito y Desarollo (BCD) Guinext Bank
Tchad (1 banque)	Banque pour le Commerce et l'industrie du Tchad (BICIT)

Source : COBAC (rapport d'activité 1996)

Parmi les banques restées en activité, certaines présentaient de bonnes perspectives de redressement et d'autres éprouvaient toujours d'importants besoins de financement à cause d'une insuffisance de fonds propres. Ainsi, sur les 31 banques en activité dans la zone à cette période, 11 présentaient une situation relativement saine, 11 ont des équilibres financiers fragiles et 9 étaient dans une situation critique avec des fonds propres négatifs.

2.2 La politique de libéralisation financière

La crise qui a profondément bouleversé le système bancaire de la CEMAC à la fin des années 80 et dans les premières années de la décennie passée, a conduit les autorités avec le concours des institutions de Bretton Woods, à mettre en oeuvre une nouvelle politique de libéralisation financière comportant essentiellement deux volets dont l'un monétaire et l'autre bancaire.

Sur le plan monétaire, une nouvelle politique monétaire est mise en place portant sur l'abandon du contrôle direct du crédit au profit de mécanisme d'intervention plus respectueux du marché, la remise en cause partielle de la fixation administrative des taux débiteurs et créditeurs des banques, et la modernisation du système financier par la création d'un marché interbancaire.

Sur le plan bancaire, la politique de libéralisation financière a consisté, d'une part, à créer une instance supranationale de contrôle de l'activité bancaire notamment la Commission Bancaire de l'Afrique Centrale (COBAC) et, d'autre part, à renforcer les règles prudentielles.

2.2.1 La politique monétaire avant 1990

La politique monétaire est un ensemble de mesures prises par la banque centrale, visant à faire varier la quantité de monnaie présente dans l'économie afin d'agir indirectement sur la valeur de la monnaie nationale, sur la production, l'investissement, la consommation et l'inflation⁴.

Les instruments de politique monétaire utilisés par la BEAC avant 1990 concernent notamment les taux d'intérêt, le contrôle quantitatif du crédit, et le contrôle sélectif du crédit.

a. La politique des taux d'intérêt

Jusqu'en 1990, trois taux sont applicables par la BEAC dans ses concours aux banques: le taux d'escompte normal, le taux d'escompte préférentiel et le taux de pénalité. Le taux d'escompte préférentiel concerne essentiellement les crédits de campagne, les crédits aux PME nationales, et les crédits aux organismes sans but lucratif. Il vaut 5 % en 1987 et 6,5 % en 1989. Le taux de pénalité s'applique en cas de violation des normes de plafonnement établies. Il vaut 16 % en 1987.

⁴ Encarta 2006

b. Le contrôle quantitatif du crédit

Cette politique dite d'encadrement de crédit consiste pour la BEAC à limiter le volume de crédit à l'économie en fixant des normes aux crédits distribués par les banques, et en plafonnant le refinancement des banques par la banque centrale ainsi que les concours de la banque centrale aux trésors nationaux.

c. Le contrôle sélectif du crédit

Il s'agit d'une politique sélective du crédit adoptée par la BEAC, qui s'appuie sur trois instruments : les taux d'intérêt différenciés, la sélectivité des plafonds de réescompte et les limites individuelles. La BEAC cherche à travers cette politique, à apporter un appui aux secteurs jugés prioritaires constitués par les Petites et moyennes entreprises (PME) nationales, les campagnes agricoles, l'habitat social, etc....

2.2.2 La nouvelle politique monétaire (après 1990)

A partir de 1991, la BEAC assouplit progressivement la nature dirigiste de sa politique monétaire sur plusieurs fronts :

v' elle abandonne sa politique d'encadrement du crédit qui lui permettait de contrôler le volume de crédit à l'économie et d'agir sélectivement sur sa distribution. Cette politique présentait le défaut intrinsèque de figer la situation relative des banques en entravant le développement des banques les plus dynamiques et en compromettant celles nouvellement créées ;

v' elle modifie sa pratique de réescompte qui manquait de souplesse pour les banques car l'échéance des effets ne correspondait pas nécessairement à la durée de leurs besoins de trésorerie et fait recours au système d'avances sur titres, plus souple, dont le plafond trimestriel est fixé par pays et le taux d'intérêt par le Gouverneur de la banque centrale.

v' elle institue en juillet 1991, la programmation monétaire dans chaque Etat ;

v' elle créé en juillet 1994 un marché monétaire sous-régional avec un compartiment interbancaire, qui permet ainsi aux banques confrontées aux besoins de liquidité, de pouvoir combler leur déficit auprès de celles disposant de liquidités en excès, à des conditions librement débattues et sous le contrôle de la banque centrale. Le marché interbancaire constitue avec le système d'avances sur titres, les deux seules voies de refinancement des banques ;

v' elle libéralise partiellement les taux d'intérêt sur les dépôts et les crédits en adoptant deux taux d'intérêts jouant le rôle de bornes notamment un Taux Créditeur Minimum⁵ (TCM) et

⁵ Les taux d'intérêt créditeurs sont les taux qui rémunèrent les dépôts de la clientèle. Le TCM est de 5 % en 2004.

un Taux Débiteur Maximum⁶ (TDM) et fixés par le Gouverneur de la banque centrale. Le TCM s'applique obligatoirement dans le cas de placements à moins d'un an et d'un montant inférieur à 5 000 000 F CFA. A l'exception de ce type de placement, les banques fixent librement leurs taux créditeurs. Pour les opérations de crédit à la clientèle,les banques sont autorisées à fixer librement leurs taux débiteurs dans la limite du plafond fixé par la banque centrale.

La politique de libéralisation financière a consisté également à reformer le dispositif de supervision des établissements de crédit notamment à travers les conventions du 16 Octobre 1990 et du 17 janvier 1992 portant création de la Commission Bancaire de l'Afrique Centrale (COBAC) et harmonisation de la réglementation bancaire en Afrique Centrale.

2.2.3 La Commission Bancaire de l'Afrique Centrale (COBAC)

La Commission Bancaire de l'Afrique Centrale est un organe supranational de réglementation et de contrôle de l'activité bancaire dans la sous-région. Mise en place en janvier 1993 par les Etats de la CEMAC, elle est dotée de compétences diverses en matière de réglementation et assure quatre fonctions principales : une fonction administrative, une fonction réglementaire et normative, une fonction de surveillance et de contrôle, et une fonction juridictionnelle.

a. Les fonctions de la COBAC

1' La fonction administrative

La COBAC est chargée de délivrer des avis conformes aux agréments des établissements de crédit et de leurs dirigeants. Aucun établissement de crédit ne peut démarrer ses activités sans autorisation préalable de la COBAC. En cas de carence constatée dans la direction d'un établissement de crédit, la COBAC peut procéder à la nomination d'un administrateur provisoire à la tête de cet établissement. La COBAC peut également nommer un liquidateur dans tout établissement qui cesse d'être agrée.

1' La fonction réglementaire et normative

Afin de contrôler l'équilibre de la structure financière de ses assujettis, La COBAC est chargée de définir le plan et les procédures comptables applicables aux établissements de crédit, et les normes prudentielles de gestion.

⁶ Les taux d'intérêt débiteurs constituent des primes de risque et permettent de taxer les crédits accordés à la clientèle. Le TDM est de 18 % en 2004.

1' La fonction de surveillance et de contrôle

La COBAC est chargée de veiller à l'application par les établissements de crédit de la réglementation bancaire à travers les contrôles sur pièces et les contrôles sur place qu'elle organise.

1' La fonction juridictionnelle

La COBAC est un organe juridictionnel capable de prononcer des sanctions disciplinaires à l'encontre de ses assujettis pour tout manquement constaté, sans préjudice des sanctions que pourront prendre les autorités judiciaires nationales.

b. Le dispositif prudentiel de la COBAC⁷

La COBAC a mis en place en mars 1993, des normes prudentielles lui permettant de mieux apprécier la liquidité et la solvabilité des établissements de crédit placés sous son contrôle. Elle s'est également dotée d'un système de cotation des banques (SYSCO) axé sur le respect des normes établies.

1' Les normes de solvabilitéLa solvabilité d'une banque est sa capacité à faire face à ses engagements vis-à-vis de ses

créanciers au moyen de ses ressources propres. Il existe cinq normes permettant de contrôler la solvabilité des banques.

· Le ratio de couverture de risques qui oblige les établissements de crédit de justifier en permanence que leurs fonds propres nets couvrent au moins 8% de l'ensemble de leurs concours y compris ceux aux Etats.

· Le ratio de division des risques interdit à une banque de s'engager en faveur d'un seul client pour un montant supérieur à 75% de ses fonds propres nets et en faveur de ses gros clients pour un montant de crédit supérieur à 800 % de ses fonds propres nets.

· Le ratio de couverture des immobilisations contraint les banques à financer leurs immobilisations à 100 % par leurs ressources permanentes.

· La limitation des prises de participation au capital d'entreprises qui oblige les établissements de crédit à ne pas participer au capital d'une entreprise à plus de 15 % de ses fonds propres nets, l'ensemble des participations ne pouvant dépasser 75 %.

· La limitation des concours octroyés aux actionnaires, associés, dirigeants,

administrateurs et personnel à 15% des fonds propres nets.

⁷ Cf. site de la BEAC

1' Les normes de liquiditéLa liquidité d'une banque mesure sa capacité à faire face à ses engagements à vue ou à

très court terme. Deux normes ont été établies afin de contrôler la liquidité des banques.

· Le ratio de liquidité contraint les établissements de crédit à justifier en permanence qu'elles disposent de ressources immédiatement disponibles et susceptibles de couvrir la totalité de leurs dettes à échoir dans un mois au plus.

· Le ratio de transformation à long terme est le rapport entre les emplois et engagements à plus de 5 ans d'échéance d'un établissement de crédit et ses ressources de même terme, retenues au numérateur et dont le taux à observer est fixé à 50%.

1' Le système de cotation des banques (SYSCO)

Le système de cotation des banques a été mis en place par la COBAC pour évaluer les performances des banques par rapport au respect des normes réglementaires et prudentielles. Il établit pour chaque banque, une cote pouvant aller de 1 à 4C et reflétant sa situation financière, en adoptant la classification ci-dessous :

Tableau 1.7 : Signification des cotes SYSCO

Cotes			Signification	1
		Situation financière solide	2
		Bonne situation financière	3
		Situation financière fragile, dont
3A 3B 3C		Légèrement fragile Moyennement fragile Très fragile	4
		Situation financière critique, dont
4A 4B 4C		Critique Très critique Irrémédiable

Source : COBAC

2.3 Surliquidité des banques et faiblesse du financement bancaire

dans la CEMAC

Au cours de ces dernières années, l'embellie des économies de la sous région a eu un impact direct sur la croissance de la liquidité des banques. En effet, l'accroissement des recettes d'exportations pétrolières suite à la flambée des cours mondiaux de pétrole, s'est traduit par une augmentation de la masse monétaire dans la sous région. Ce surplus de monnaie a eu comme conséquence un accroissement des réserves bancaires, conduisant ainsi à la surliquidité des banques. Il y a lieu de souligner également comme cause de la surliquidité, l'amélioration de la

gestion bancaire suite au processus de restructuration ayant assaini le secteur. En effet, les banques sortant d'un long processus d'assainissement sont devenues prudentes dans la prise du risque, ce qui a contribué à une contraction du volume des crédits distribués.

Face à cette situation, on s'attendrait à ce que les banques s'impliquent davantage dans le financement de l'économie, disposant suffisamment de ressources. Très curieusement, les banques se plaisent dans cette situation de surliquidité et ne financent que très peu l'économie. En effet, au cours de la décennie passée (1994-2004), la croissance des crédits dans la zone n'a pas suivi celle des dépôts. Les dépôts se sont accrus de 128,2 % tandis que les crédits à l'économie n'ont connu qu'une augmentation de 56 %. Les banques préfèrent orienter leurs ressources vers des emplois de trésorerie moins risqués que les crédits.

Fort de ce constat, il y a lieu de s'interroger sur la qualité de la gestion des ressources bancaires dans la CEMAC. En effet, une présomption d'inefficacité des banques dans la transformation de leurs ressources en crédits demeure ainsi palpable. La seule façon d'en avoir le coeur net est donc d'évaluer empiriquement les niveaux d'efficacité des banques dans la transformation de leurs ressources en crédits. Cette évaluation nécessitant l'application de méthodes appropriées, la méthode DEA est retenue dans le cadre de cette étude pour évaluer les niveaux relatifs d'efficacité technique des banques de la CEMAC. Mais avant de nous lancer dans cette évaluation, il serait judicieux de présenter le concept d'efficacité technique ainsi que les principales méthodes utilisées pour la mesurer.

Chapitre 2 : DE L'EFFICACITÉ ÉCONOMIQUE A LA MESURE DE

L'EFFICACITÉ TECHNIQUE

L'objectif de ce chapitre est de présenter le concept d'efficacité économique dans sa double dimension technique et allocative, ainsi que les différentes méthodes permettant d'estimer les frontières d'efficacité technique. Ainsi, après avoir précisé à quoi renvoie le concept d'efficacité économique (section 1), nous passerons en revue les principales méthodes utilisées pour évaluer l'efficacité technique des unités de production en examinant les avantages et les limites de chacune d'elles ( section2).

Section 1 : CONCEPT D'EFFICACITÉ ÉCONOMIQUE

Dans la littérature, l'efficacité économique est composée de l'efficacité technique et de l'efficacité allocative. L'efficacité technique s'intéresse à la façon dont le processus de production transforme les inputs en outputs. Par contre, l'efficacité allocative met l'accent sur la manière dont les inputs sont combinés étant donné leurs prix relatifs.

1.1 L'efficacité technique

L'efficacité technique mesure l'aptitude d'une unité de production à obtenir le maximum d'outputs possible à partir d'une combinaison d'inputs et d'une technologie de production données (définition « orientée output >>⁸), ou son aptitude à réaliser un niveau d'output donné à partir des plus petites quantités d'inputs possibles (définition « orientée input >>⁹). L'inefficacité technique correspond donc soit à une production en deçà de ce qui est techniquement possible pour une quantité d'inputs et une technologie données, ou à l'utilisation de quantités d'inputs au dessus du nécessaire pour un niveau d'output donné.

Si on tient compte du type de rendement dans lequel s'effectue la production, l'efficacité technique peut elle-même être décomposée en une efficacité technique pure et une efficacité d'échelle^10.. L'efficacité technique pure reflète la manière dont les ressources de l'unité de production sont gérées. En revanche, l'efficacité d'échelle détermine si l'unité de production opère à une échelle optimale ou non. L'échelle optimale est entendue ici comme étant la

⁸ Elle répond à la question : de combien peut-on accroître les quantités d'outputs sans toutefois modifier les quantités d'inputs utilisées ?

⁹ Elle répond à la question : de combien les quantités d'inputs peuvent être proportionnellement réduites, sans qu'il y ait changement des quantités d'outputs produits ?

¹⁰ Cf. Farrell (1 957) cité par O. JOUMADY (2000)

meilleure situation à laquelle peut parvenir l'unité de production en augmentant proportionnellement la quantité de tous ses facteurs.

Pour illustrer cette décomposition¹¹, considérons le cas d'une banque qui produit un output y à partir d'un seul input x (figure 2.1) en supposant la technologie de production à rendements d'échelle variables. Une technologie est à rendements d'échelle variables si à la suite d'une augmentation proportionnelle de tous les facteurs de production, la production varie dans une proportion différente. Par contre, elle est à rendements d'échelles constantes si une augmentation proportionnelle de tous les facteurs de production entraîne une augmentation de la production dans la même proportion.

La frontière des possibilités de production est représentée par la courbe à rendements d'échelle variables (REV). Sous l'hypothèse de rendements d'échelle constants, cette frontière est représentée par la droite REC.

Figure 2.1 : Frontière de production et rendements d'échelle

REC

y

A' REV

x

Source : JOUADY O. (2000)

A

O

A»

A'''

Au point A''', la banque est techniquement capable de produire la même quantité d'output en utilisant moins d'inputs. Elle est par conséquent inefficace dans la mesure où elle peut réaliser une économie d'inputs correspondant à A»A'''. Le niveau d'efficacité technique

pure est le rapport	AA	''		. L'efficacité d'échelle quant à elle est fournie par la distance entre les
	'''

¹¹ Extraite de O. JOUMADY (2000)

frontières REC et REV et est mesurée par le rapport	AA	'		. Le produit de l'efficacité technique
	''

AA '
AA '''

pure et de l'efficacité d'échelle représentant l'efficacité technique totale, donne le rapport

et correspond à la mesure de l'efficacité technique dans le cas de rendements d'échelle constants.

1.2 L'efficacité allocative (efficacité prix)

L'efficacité allocative provient du fait que les facteurs de productions ne sont pas gratuits, ils ont un coût. De ce fait, en choisissant son programme de production, la firme doit en plus des paramètres techniques, tenir compte de leurs prix relatifs sur le marché.

L'efficacité allocative mesure ainsi l'aptitude de l'unité de production à combiner ses inputs dans des proportions optimales compte tenu de leur prix relatif sur le marché et du budget alloué pour les acquérir. Ainsi, pour une famille de combinaisons de facteurs permettant la réalisation d'un niveau de production donné, la meilleure combinaison allocativement, est celle qui est obtenue à moindre coût. L'inefficacité allocative provient donc de l'utilisation des facteurs de production dans des proportions ne minimisant pas les coûts compte tenu de leur prix sur le marché.

Il ressort des deux notions abordées ci-dessus que pour une unité de production, la combinaison optimale des facteurs de production est celle qui s'obtient à moindre coût et qui permet d'obtenir le maximum d'outputs possible compte tenu de la technologie utilisée. L'unité de production dans ce cas est dite économiquement efficace dans la mesure où elle utilise la meilleure combinaison d'inputs possible dans son processus de production. L'inefficacité économique intègre donc l'inefficacité technique et l'inefficacité allocative.

1.3 Décomposition de l'efficacité économique

La décomposition de l'efficacité économique en efficacité technique et allocative est illustrée par Farrell¹² à partir d'une fonction de production d'une firme combinant par exemple les facteurs capital et travail pour produire un produit donné. L'approche de Farrell illustrée cidessous suppose les rendements d'échelle constants et se place dans le cas d'une définition « orientée input ».

12 L'approche de Farrell exposée ici est extraite de Nabil A. et Robert R [2000]

Figure 2.2 : Efficacité technique et allocative : cas de deux intrants Capital S

P

A

Q

R

Q' S'

A'

O

Travail

Source : Nabil A. et Robert R. (2000)

Sur la figure ci-dessus, SS' est un isoquant représentant l'ensemble des combinaisons des facteurs capital et travail permettant à une firme techniquement efficace, de produire une unité d'output. Tout point de la figure en dehors de SS' est techniquement inefficace pour ce niveau de production donné. Le point Q représente une firme techniquement efficace dont les quantités de capital et de travail utilisées sont proportionnelles¹³ à celles de la firme située au point P. Si on suppose que la firme Q parvient à produire la même quantité d'outputs que la firme P en

utilisant seulement une fraction OQ OP

des facteurs de production, le niveau d'efficacité technique

OQ

de la firme P est défini par le ratio . Ainsi, ce ratio est égal à 1 pour une firme techniquement

OP

efficace c'est-à-dire située sur SS'. Le degré relatif d'inefficacité technique de la firme quant à

et correspond à la quantité d'inputs pouvant être économisée

QP

OP

lui, est mesuré par le rapport

¹³ On démontre mathématiquement que le coefficient de proportionnalité est OQ

sans qu'il y ait une réduction du niveau de la production. Cependant, pour que la firme soit économiquement efficace, il faudrait en plus qu'elle combine ses facteurs de production dans des proportions lui permettant de minimiser leurs coûts étant donné leurs prix relatifs. Ainsi, sur la figure ci-dessus, si AA' représente la courbe d'isocoût¹⁴ associée au niveau de dépense dont dispose la firme pour acquérir ses facteurs de production, c'est le point Q' et non Q qui est donc

OP

¹⁴ Dans la théorie microéconomique, pour des prix de facteurs donnés, l'isocoût associé à une dépense est le lieu des combinaisons de facteurs qui correspondent à cette dépense.

le point optimal de production. C'est le point où le rapport des productivités marginales des
facteurs de productions est égal au rapport des prix. Q' et Q étant situés sur SS', leur efficacité
technique est de 100 % mais les coûts de production au point Q' ne représentent que la fraction
de ceux au point Q. L'efficacité allocative ou efficacité prix de la firme Q est donc mesurée

OR
OQ

OR

.

OQ

par le rapport

Si la firme P (figure 2.3) change la proportion d'utilisation de ses inputs en les combinant dans des quantités proportionnelles à celles données au point Q' ( en passant de P à P'), tout en gardant le même indice d'efficacité technique, elle améliore ses coûts de production par le

OR OR

rapport . L'efficacité allocative de P est donc défini comme étant le rapport .

OQ OQ

Figure 2.3 : Changement de la proportion d'utilisation des inputs de la firme P

Capital S

P

A Q

R P'

Q' S'

A'

O

Travail

Source : L'auteur (d'après Farrell)

Les coûts de production de la firme techniquement et allocativement efficace Q' ne

représentent qu'une fraction OR OP

OR OQ OR de ceux de P. Ce ratio = × , qui est le produit de OP OP OQ

l'efficacité technique et de l'efficacité allocative au point P, mesure le niveau d'efficacité économique de la firme P.

Nous allons nous restreindre dans la section suivante, à l'exploration des méthodes permettant la mesure de l'efficacité technique, en nous attardant sur les principales méthodes utilisées dans la littérature.

Section 2 : LES MÉTHODES D'ESTIMATION DE L'EFFICACITÉ TECHNIQUE

La première tâche à accomplir lorsqu'on désire évaluer l'efficacité technique d'une unité de production est la construction d'une frontière de production, de profit ou de coût. Dans la pratique, cette frontière de référence n'est pas connue et doit être estimée empiriquement, grâce aux données de l'échantillon observé à partir d'unités similaires placées dans les mêmes conditions que l'unité étudiée et présentant les meilleures performances. L'efficacité d'une unité de production se définit donc par rapport aux unités de l'échantillon placées sur la frontière estimée et présentant les meilleures performances. Des scores d'efficacité sont ainsi attribués à toutes les unités de l'échantillon avec comme valeur 1 pour celles situées sur la frontière. Les unités en dehors de la frontière ont des scores strictement compris entre 0 et 1. Selon Forsund et al [cités par Nabil A. et Robert R ; (2000), p.4], « La distance dont une firme se situe en deçà de sa frontière de production et de profit, et la distance dont elle se situe au dessus de sa frontière de coût, peuvent être considérées comme des mesures de l'inefficacité ».

L'estimation d'une frontière de production, de profit ou de coût nécessite l'application de méthodes appropriées. Ces méthodes sont regroupées dans la littérature en deux grandes catégories notamment les approches paramétriques et les approches non paramétriques. Les approches paramétriques spécifient une forme fonctionnelle particulière à la frontière estimée. Ces fonctions peuvent être de type Cobb-Douglas, CES, Translog, etc. Elles peuvent être déterministes ou stochastiques. Les approches déterministes considèrent tout écart entre la frontière estimée et les données observées comme découlant entièrement de l'inefficacité. Par contre, l'approche stochastique décompose l'écart entre la frontière estimée et les données observées en deux composantes dont l'une aléatoire et l'autre découlant de l'inefficacité. Les approches non paramétriques ne font aucune supposition concernant la forme de la frontière estimée. Elles se basent sur la programmation mathématique pour construire la frontière d'efficacité et sont toutes déterministes. Les principales méthodes d'estimations de la frontière d'efficacité technique qui feront ici l'objet d'une présentation sont au nombre de 3 dont 2 approches non paramétriques notamment la méthode d'enveloppement des données et le Free Disposall Hull (FDH), et une approche paramétrique notamment l'approche de la frontière stochastique.

2.1 La méthode d'enveloppement des données

Plus connue sous son appellation en anglais « Data Envelopment Analysis (DEA) », la méthode d'enveloppement des données est une méthode déterministe non paramétrique d'estimation de fonctions frontières, qui suppose l'ensemble des possibilités de production comme étant un ensemble convexe.

La mesure de l'efficacité technique par la méthode DEA peut être faite suivant deux orientations. La première orientation tournée vers la maximisation des outputs est appliquée lorsque l'on cherche à augmenter les quantités d'outputs sans changer les quantités d'inputs utilisées. Par contre, l'orientation tournée vers la minimisation des inputs est appliquée lorsque l'on cherche à diminuer proportionnellement les quantités d'inputs sans modifier les quantités d'outputs.

La méthode DEA s'appuie sur les techniques de programmation linéaire pour estimer une frontière de production d'un échantillon d'observations. Cette frontière de production se situe au sommet des observations et correspond aux unités de l'échantillon les plus performantes. Elle enveloppe l'ensemble des observations de telle sorte que les unités moins performantes se situent en dessous de l'enveloppe. L'efficacité technique d'une unité de l'échantillon correspond ainsi à la distance qui la sépare de l'enveloppe. Elle est une efficacité relative dans la mesure où elle dépend des unités les plus performantes de l'échantillon. La figure ci-dessous permet d'illustrer cela dans le cas d'un échantillon d'unités utilisant un seul input pour produire un seul bien avec les rendements d'échelle supposés non constants.

D

A

X⁰P XP Input (X)

B

P

C E

Figure 2.4 : Illustration de la mesure de l'efficacité technique par la méthode DEA Output (Y)

Y^*P
Y⁰P

O

Source : Ekuh Ngwese R. et Mbaku Mbah D. [2006]

Sur la figure ci-dessus, les unités de production A, B, C, D et E constituent l'enveloppe de référence par rapport à laquelle est évaluée l'efficacité technique des autres unités de l'échantillon. Elles correspondent aux unités les plus performantes de l'échantillon observé et leur efficacité technique est par définition égale à 1. Le point P n'étant pas sur la frontière, représente une firme techniquement inefficace. En effet, à partir de la quantité d'input XP dont elle dispose, elle est techniquement susceptible de produire la quantité Y* P d'output supérieure à celle qu'elle réalise Y0 P . Son efficacité technique dans ce cas vaut Y0 P / Y* P < 1 et correspond au rapport de la quantité d'output qu'elle produit à partir de la quantité d'input XP , par la quantité maximale qu'elle pourrait produire à partir de cette même quantité d'input au regard des meilleures unités de l'échantillon. Cette façon de mesurer l'efficacité technique correspond à une orientation output. La firme peut également produire la quantité Y0 P en utilisant moins d'inputs notamment une quantité X⁰P < XP . Son efficacité technique dans ce cas vaut X⁰P / XP < 1 et correspond à une orientation input. Selon Fare et Lovell (1978) [Cités par Coelli T. (1996)], les indices d'efficacité technique orientation output et orientation input sont égaux dans le cas de rendements d'échelle constants et différents dans le cas de rendements d'échelle variables. Cependant, notons que les unités de production situées sur la frontière estimée sont les mêmes quelque soit l'orientation choisie.

Le programme linéaire permettant la construction de la frontière d'efficacité dépend du type de rendement dans lequel s'effectue la production. On distingue ainsi le modèle à rendements d'échelle constants (ou modèle CRS¹⁵) et celui à rendements d'échelle variables (ou modèle VRS¹⁶) qui sont présentés ci-dessous.

2.1.1 Le modèle à rendements d'échelle constants

Le modèle CRS (orientation input) attribué à Charnes et al (1978) est basé sur la maximisation pour une firme donnée, du ratio correspondant à la somme pondérée de ses outputs sur la somme pondérée de ses inputs et considéré comme étant une mesure de son efficacité technique. Ainsi, si on dispose d'un échantillon de N unités de production, de K inputs et M outputs, pour chacune de ces unités, la mesure de l'efficacité de l'unité " i " de l'échantillon est donnée par le programme de maximisation ci-dessous :

¹⁵ Constant Returns to Scale.

¹⁶ Variable Returns to Scale

M >2

, u Y m m i

~ 1

Max (u, v) h i= m , i =1, ..., N

K

k i
,

v X

k

>2

k 1

Sous les contraintes

~

~

~

~

~

~

M

~ u Y

m 1

= =

1 j=1, 2, ... , N

K

~ k 1 =

vkXk, j

m m, j

L u , v 0

=

m k

où h_i est l'indice d'efficacité de l'unité de production " i "

m et k sont respectivement l'indice des outputs et l'indice des inputs ;

Xk , i et Y_m, _i représentent respectivement le ^kième input et le ^mième output de l'unité " i "; Xk , j et Y_m, j représentent respectivement le ^kième input et le ^mième output de l'unité " j " avec j = 1,2, ..., N ;

u_m et vk sont des paramètres à estimer et représentent respectivement les coefficients

de pondération des outputs et des inputs.

L'objectif de ce programme est de déterminer les coefficients de pondération um et vk qui maximisent l'indice d'efficacité de l'unité " i " en s'assurant que cet indice évalué pour toutes les autres unités avec les mêmes coefficients um et vk , est inférieur ou égal à 1 signifiant que toutes les unités de l'échantillon sont situées sur ou en dessous de la frontière estimée.

La résolution du programme ci-dessus tel qu'il a été formulé, n'est pas chose aisée. Toutefois, ce programme peut être transformé en un programme linéaire en posant pour tout i

K

k k , i >i: v X k=1

1 . Le programme devient alors :

M

Max u Y

m m , i

>

m=1

Sous les contraintes :

K

~

v X 1

=

k k,i

~~

~

k 1

=

M K

~

~

~

u Y - v X 0

=

m m,i k k,i

m 1

= k 1

=

L u , v 0

=

m k

La forme duale équivalente de ce programme linéaire, peut s'écrire :

ö i

~- + ë =

N

~ Y Y 0

m,i j m,j

j 1

=

~

N

ö ? ë =

X ~ X 0

~ i k,i j k,j

~ë = ⁰

Sous les contraintes

~

Min

j 1

=

~ j

Ott X est un vecteur de dimension N de coefficients à estimer ;

ö_i est un scalaire compris entre 0 et 1 qui prend la valeur 1 pour une unité de production

située sur la frontière. Il représente pour l'unité de production " i ", la fraction de ses ressources qu'elle utilise optimalement.

La première contrainte signifie que le choix des coefficients Xj doit être tel que la somme pondérée des outputs de toutes les unités de production de l'échantillon soit au moins égal à l'output de l'unité étudiée. La seconde contrainte quant à elle suppose que pour une unité de

production située sur la frontière ( ö_i =1), la somme pondérée des quantités d'inputs utilisées par toutes les unités de production est au plus égale à la quantité d'inputs de l'unité étudiée.

La valeur ö_i solution du programme ci-dessus constitue une mesure de l'efficacité technique de la firme " i " dans le cas d'une orientation input. Ce programme linéaire est donc résolu N fois pour chacune des unités de l'échantillon et une valeur ö_i est obtenue pour chaque

unité correspondant à son score d'efficacité technique.

Le programme linéaire équivalent à celui ci-dessus et permettant d'obtenir l'indice d'efficacité technique dans le cas d'une orientation output est le suivant :

Max (1 i N)

ö = =

i

~ - ë =

N

~ X ~ X 0 k,i j k,j

j 1

Sous les contraintes

=

~

~- ö + ë =

N

Y ~ Y 0

~ i m,i j m,j

j 1

=

~ j

~ë = ⁰

Ott 1 < öi < 8 est un scalaire tel que 1/ öi (compris entre 0 et 1) détermine le score d'efficacité de l'unité de production "i".

Le modèle CRS permet d'obtenir une mesure de l'efficacité technique totale sans distinguer l'efficacité technique pure de l'efficacité d'échelle.

2.1.2 Le modèle à rendements d'échelle variables

Selon Coelli et al. (1998), (cités par Nabil A. et Robert R) « L'hypothèse de rendements d'échelle constants n'est appropriée que si toutes les unités de production opèrent à un niveau d'échelle optimal. L'imperfection de la concurrence, les contraintes financières diverses, etc., pourraient faire en sorte qu'une unité de production n'opère pas à un niveau d'échelle optimal ». L'hypothèse de rendements variables paraît ainsi plus vraisemblable que celle de rendements constants. La prise en compte de rendements non constants dans la mesure de l'efficacité technique (orientation input) proposée par Banker et al. (1984) s'obtient en ajoutant

N

au programme dual précédent, une contrainte de convexité programme ci-dessous: Min (1 i N) ö ? ? i N Y + ë ? ~ Y 0 m,i j m,j j 1 = N

~= 1, on obtient alors le ë j j=1

ö ? ë =

X ~ X 0

i k,i j k,j

~ ë =

N

~ ~ j

~

Sous les contraintes

~~

~

j 1

=

1

j 1

=

~ ë = 0

j

La résolution du programme ci-dessus permet d'obtenir l'indice d'efficacité technique de l'unité de production étudiée dans le cas de rendements d'échelle variables et dans une orientation input. Cet indice (score) constitue une mesure de l'efficacité technique pure de l'unité étudiée. L'efficacité d'échelle de l'unité étudiée s'obtient en comparant cet indice à celui obtenu par le modèle CRS.

La mesure de l'efficacité technique dans le cas d'une orientation output s'obtient à travers la résolution du programme linéaire ci-dessous, obtenu en ajoutant au modèle CRS

N

orientation output, la contrainte de convexité

~j ë = 1 : j=1

Max (1 i N)

ö = =

i

N

X - ë =

~ X 0

k,i j k,j

j 1

=

N

? ö + ë =

Y ~ Y 0

i m,i j m,j

~ ë =

N

~ ~ j

~

Sous les contraintes

~~

I

j 1

=

1

=

ë =

j

j 1

~ 0

Le score d'efficacité de l'unité de production « i » est déterminé par la grandeur 1/ öi

comprise entre 0 et 1.

Avantages et limites de la méthode DEA

Dans la littérature, la méthode DEA présente plusieurs avantages dont la détermination de l'efficacité technique sans aucune hypothèse à priori concernant la forme fonctionnelle de la frontière estimée. Elle est de ce fait une méthode particulièrement adaptée en cas d'incertitude sur la forme fonctionnelle de la technique de production étudiée. De plus, elle ne fait aucune restriction concernant la distribution de l'inefficacité et permet la mesure de l'efficacité technique même dans un cadre multi-output/multi-input c'est-à-dire dans le cas de firmes combinant plusieurs inputs pour produire plusieurs outputs différents. La méthode DEA est également adaptée dans le cas de petits échantillons.

La méthode DEA présente également des limites notamment le fait d'attribuer tout écart par rapport à la frontière à de l'inefficacité. Elle ne fait ainsi aucune distinction entre l'inefficacité provenant de facteurs aléatoires et l'inefficacité du processus de production. Cette omission de l'aléa semble irréaliste et conduit à une surévaluation de l'inefficacité technique. Une autre limite majeure attribuée à la méthode DEA est son extrême sensibilité aux valeurs extrêmes et aux erreurs de mesure. En effet, une seule valeur extrême est susceptible de décaler la frontière d'efficacité. La principale limite de la méthode DEA est que l'indice d'efficacité d'une unité de production obtenu à partir de cette méthode est une grandeur relative et non absolue. Il dépend de l'échantillon dans lequel est évalué l'unité considérée. La méthode DEA mesure l'efficacité d'une unité par rapport aux meilleures unités de l'échantillon observé. L'on pourrait être techniquement efficace dans un échantillon (score égal à 1) et ne plus l'être dans un autre.

Une autre méthode non paramétrique de mesure de l'efficacité technique courante dans la littérature est l'approche Free Disposall Hull (FDH).

2.2 L'approche Free Disposall Hull (FDH)

L'approche FDH développée par Deprins, Simar et Tulkens (1984) considère la frontière de production comme étant la frontière de l'enveloppe de libre disposition de l'échantillon observé et contrairement à la méthode DEA, ne fait aucune hypothèse de convexité de l'ensemble des possibilités de production. Elle permet d'estimer la frontière de production sans aucune hypothèse à priori concernant sa forme ou sa nature. Cette frontière de production est constituée par l'ensemble des unités de production dominantes dans l'échantillon observé. Une unité de production est dominante si elle domine éventuellement d'autres unités et n'est ellemême dominée par aucune unité. Si elle ne domine aucune unité et n'est elle-même dominée par aucune autre, alors elle devient dominante par défaut et est déclarée techniquement efficace. La domination d'une unité de production sur une autre dans ce contexte signifie son aptitude à produire plus d'outputs en utilisant moins d'inputs que cette autre unité. Une unité de production qui est dominée par au moins une autre unité de l'échantillon est considérée comme étant inefficace. La figure ci-dessous permet d'illustrer cela dans le cas d'un échantillon de firmes produisant un seul output à partir d'un seul input.

Figure 2.5 : Illustration de la domination entre firmes dans l'approche FDH Output

A

B

C

O XA XB XC Input

Source: Simar L. and Wilson P. (2006)

Sur la figure ci-dessus, la firme A parvient à produire plus d'output que B en utilisant une quantité d'inputs XA inférieure à la quantité XB utilisée par B. La firme B est donc dominée par A et est déclarée techniquement inefficace. La firme A par contre n'est dominée par aucune autre firme de l'échantillon. Elle est donc déclarée techniquement efficace et constitue un point dominant de l'échantillon faisant partie de la frontière d'efficacité. Par le même raisonnement, on conclut que la firme C est dominée par A et B et est par conséquent inefficace. Schématiquement, pour une unité de production donnée dans l'échantillon observé, l'ensemble

des unités qu'elle domine représente la partie inférieure droite à l'unité et délimitée par l'axe des inputs et les traits en pointillé sur la figure.

La frontière de production dans l'approche FDH se présente ainsi comme une fonction linéaire en escalier reliant l'ensemble des points dominants de l'échantillon tel que l'illustre la figure ci-dessous. Toutes les unités de production de l'échantillon sont situées soit sur la frontière, soit en dessous de la frontière. Tous les points de la frontière sont déclarés techniquement efficaces.

Figure 2.6 : frontière de production par l'approche FDH

Output

D

C

A

B

O Input

Source: Simar L. and Wilson P. (2006)

Les points A, B, C, D représentés ci-dessus, sont les unités dominantes de l'échantillon observé et constituants la frontière de production. La mesure de l'efficacité des unités de ce même échantillon à partir de la méthode DEA conduirait à un nombre plus restreint de points sur la frontière dû à l'hypothèse de convexité de l'ensemble des possibilités de production.

Avantages et limites de la méthode FDH

Le principal avantage de l'approche FDH est qu'il ne fait aucune restriction à priori concernant la forme ou la nature de la frontière de production.

L'inconvénient de l'approche FDH est le fait de déclarer un très grand nombre d'unités de production comme étant efficaces. Elle n'est donc pas appropriée dans le cas de petits échantillons dans la mesure où elle pourrait déclarer la totalité des unités comme étant efficaces.

2.3 L'approche de la frontière stochastique

L'approche stochastique est une approche paramétrique qui spécifie une forme fonctionnelle particulière à la fonction de production, de profit ou de coût. Elle considère que les performances d'une unité de production sont influencées par deux types de facteurs notamment

internes et externes. Les facteurs internes sont ceux qui malgré leur influence, sont contrôlables par l'unité de production. A contrario, les facteurs externes affectent les performances des unités de production favorablement ou défavorablement, en échappant totalement à leur contrôle. Les pénuries des intrants, les catastrophes naturels, le changement de politique économique sont autant de facteurs incontrôlables pouvant affecter les performances d'une unité de production. La crise économique dans la sous-région ayant affecté le système bancaire à la fin des années 80 en est un exemple palpable. L'approche stochastique prend en compte l'effet des facteurs externes dans son terme d'erreur. En effet, elle décompose l'écart entre les observations et la frontière estimée en deux composantes indépendantes dont l'une aléatoire, prend en compte l'effet des facteurs externes et les erreurs de mesure des variables utilisées dans l'estimation de la fonction frontière, et l'autre représente l'inefficacité technique de l'unité de production étudiée. L'hypothèse admise dans la littérature¹⁷ est que la composante aléatoire suit une distribution normale symétrique tandis que la composante d'inefficacité suit une distribution asymétrique définie positivement pour une fonction de coût et négativement pour une fonction de production. On admet couramment que la composante d'inefficacité suit une loi sémi normale. La figure ci-dessous permet d'illustrer cette décomposition de l'erreur dans le cas d'une firme produisant un seul produit à partir d'un seul intrant X.

Figure 2.7 : frontière de production stochastique : décomposition du terme d'erreur

Q

B2

U2

B1

U1

B

A2

E1

A1

E2

A

x

Source : GUARDA P. et ROUABAH A. (1999)

17 Cf. GUARDA P. et ROUABAH A. [1999]

Sur la figure ci-dessus, A est une firme techniquement inefficace car étant en dessous de la frontière de production estimée. L'écart entre la firme A et la frontière peut se décomposer en E1 et E2. Le premier terme E1 est dû à une inefficacité technique de la firme A qui ne gère pas optimalement ses ressources. Cette mauvaise gestion des ressources fait en sorte que la firme se situe au point A1 au lieu de A2. Au point _A1, la firme subit l'effet d'un choc exogène défavorable et matérialisé par E2, qui la ramène à sa position actuelle c'est-à-dire au point A. Les effets combinés E1 et E2 sont donc à l'origine de l'écart entre A2 et A.

Le point B2 par contre étant situé au dessus de la frontière d'efficacité, représente une firme techniquement surefficace dans la mesure ott elle produit au-delà de la quantité maximale espérée au regard de la technologie qu'elle utilise. L'écart entre la firme B et la frontière dans ce cas se décompose en U1 et U2. La composante U1 représente l'inefficacité technique de la firme liée à la gestion de ses ressources. Elle fait en sorte que la firme se situe au point B au lieu de B1. Etant au point B, la firme subit l'effet d'un choc exogène favorable qui la propulse au-delà de la frontière d'efficacité c'est-à-dire au point B2 ott elle se situe actuellement.

L'une des particularités de l'approche stochastique par rapport aux autres approches, est le fait d'admettre qu'une firme sous l'influence de facteurs exogènes favorables, est capable de se situer au-delà de sa frontière de production. Ce qui n'est pas possible avec les approches non paramétriques qui considèrent toutes les firmes de l'échantillon situées soit sur la frontière, soit en dessous de la frontière.

Le modèle d'estimation de la fonction de production stochastique initialement proposé par Aigner, Lovell et Schmidt (1977) [d'après Tim Coelli (1996)] dans le cas d'un échantillon en coupe instantanée est le suivant :

Y i = Xi â + íi - ui

Ott Yi est la production (ou le logarithme de la production) de la i^ème firme de l'échantillon ;

Xi un vecteur ligne des quantités d'inputs (ou une transformation de ce vecteur) de la ième firme de l'échantillon ;

â est un vecteur colonne de paramètres inconnus ;

v _i ~N(0, a _v ) est le terme aléatoire iid suivant une loi normale symétrique ;

2

u i ~	N(0, a u ) 2		est le terme d'inefficacité technique suivant une loi sémi-normale

et supposé positif.

Ce modèle de départ ayant été longtemps utilisé empiriquement a connu de nombreuses mutations concernant notamment l'hypothèse de distribution du terme d'inefficacité technique

ou encore un élargissement du modèle dans le cas des données de panel. Ce qui a conduit à une définition analytique de la fonction de production stochastique comme suit :

Y = f ( X )exp(V -U )

Ott f est une fonction exprimant la manière dont les inputs sont transformés en outputs ; Y est le vecteur d'outputs ;

X est le vecteur d'inputs ;

V la composante aléatoire du terme d'erreur ;

U la composante représentant l'inefficacité technique ;

f(X) exp (V) est la fonction de production frontière associée ;

Exp (-U) reflète l'inefficacité technique relative à la frontière stochastique (U=0). Jondrow et al. (Cités par Nabil A. et Robert R ; 2000) ont montré qu'en assignant d'avance à V la forme d'une distribution normale (V--~N(0, 2

ó _v)) et à U celle d'une loi sémi-

normale (U--~ N(0, 2

ó _u) ), les paramètres de la fonction frontière peuvent être estimés à l'aide de la fonction de vraisemblance suivante :

K K

1 / 2 - 1 - 1 2

Ln KLn

î = = KLn ó + Ó -

~ Ln F W - k

~ W ²

ð

(2 / ) [1 ( )] 1 / 2 ott

k ëó ó

k = 1 k=1

W = U + V;

ó = (ó²u + ó²v)^1/2 ; ë = le ratio ó²u/ó²v ;

F = la fonction de densité de la distribution normale ; K = le nombre de firmes dans l'échantillon.

En estimant la moyenne conditionnelle de la distribution Uk sachant Vk, l'indice d'efficacité technique de la firme « k » est donnée par :

EFF^k = E (Uk?Wk) = åk + ó* {f (-åk / ó*) [1 - F (-åk / ó*] -1}; k = 1, . . ., K ott ó* = (ó2uó2v/ó2) 1/2 ;

åk = (-óu² Wk) / ó² ;

f = la fonction de densité de la distribution normale standard.

Avantages et limites de l'approche stochastique

On reconnaît comme avantage à l'approche stochastique, le fait de prendre en compte dans son terme d'erreur, l'effet des facteurs exogènes pouvant influencer l'unité de production. Elle permet ainsi de distinguer l'inefficacité technique de l'inefficacité due à l'influence de facteurs indépendants de l'unité de production. L'approche stochastique est aussi avantageuse lorsque la technologie de production est connue d'avance.

Une limite de l'approche stochastique est qu'une mauvaise spécification de la forme fonctionnelle de la frontière d'efficacité engendrerait nécessairement un biais sur les mesures d'efficacité obtenues. Une autre limite est le fait que l'hypothèse concernant la distribution de la composante d'inefficacité du terme d'erreur dont dépendent les résultats de l'estimation, est choisi arbitrairement.

Après cette présentation du concept d'efficacité technique et des principales méthodes utilisées pour la mesurer, il convient d'adopter l'une d'entre elles, pour évaluer empiriquement l'efficacité technique des banques commerciales de la CEMAC. Le choix de la méthode non paramétrique d'enveloppement des données dans le cadre de cette étude se justifie par l'incertitude sur la relation fonctionnelle liant les inputs et les outputs dans le secteur bancaire.

Chapitre 3 : MESURE DE L'EFFICACITÉ TECHNIQUE DES BANQUES COMMERCIALES DE LA CEMAC PAR LA METHODE DEA

L'objectif de ce chapitre est de mesurer l'efficacité technique des banques commerciales de la CEMAC grâce à la méthode DEA. Cette mesure de l'efficacité technique des banques commerciales nécessite au préalable que soit clairement défini ce qui constitue les inputs et les outputs bancaires. Ainsi, après avoir défini les inputs et les outputs retenus dans le cadre de cette étude, et présenté le modèle empirique utilisé pour l'estimation des scores d'efficacité technique (section 1), nous analyserons les résultats obtenus (section 2).

Section 1 : APPROCHE MÉTHODOLOGIQUE

1.1 Spécification input-output bancaire

On distingue dans la littérature principalement deux approches permettant d'identifier les inputs et les outputs bancaires, en l'occurrence l'approche par la production et l'approche par l'intermédiation.

1.1.1 L'approche par la production

L'approche par la production considère une banque comme étant un producteur de services aux clients déposants (ouverture et gestion des comptes) et emprunteurs (prêts accordés), à partir des inputs que sont le capital (immobilisations), et le travail (salaires). La production est mesurée en unité physique par le nombre de comptes ouverts par la banque pour gérer les dépôts et les crédits¹⁸.

1.1.2 L'approche par l'intermédiation

Cette approche met l'accent sur le rôle des banques dans la collecte des dépôts du public et sa transformation en prêts et autres actifs, et évalue la production en unité monétaire. Elle considère donc les inputs bancaires comme étant constitués des dépôts de la clientèle et autres ressources du marché, ainsi que les coûts opératoires et les outputs comme étant les prêts et autres activités génératrices de revenus.

L'approche par l'intermédiation est choisie dans le cadre de cette étude parce qu'elle s'avère être la plus appropriée dans l'évaluation de l'efficacité de l'intermédiation financière.

¹⁸ Cf. Abdelaziz ROUABAH, 2002

Nous retenons ainsi trois inputs notamment les dépôts à vue, les dépôts à terme et les dépôts publics, et quatre outputs notamment les crédits à long terme, les crédits à moyen terme, les crédits à court terme et les crédits à l'Etat.

1.2 Les données et les variables

Les données mensuelles utilisées dans cette étude proviennent de la base du Secrétariat Général de la COBAC et concernent un échantillon de 24 banques des six Etats membres de la CEMAC sur la période 2001-2004. Les noms des banques ont été codés pour des raisons de confidentialité. Nous disposons ainsi de 24x12 points d' observations chaque année et de 24x12x4 points d'observations sur toute la période, permettant la construction d'une frontière de production et l'estimation des scores d'efficacité mensuels des banques observées. L'échantillon choisit ne couvre pas la totalité des banques de la sous-région, pour des raisons de disponibilité des données relatives à certaines banques sur la période d'étude. Le tableau ci-dessous donne la répartition du nombre de banques de l'échantillon par pays.

Tableau 2.1 : Nombre de banques de l'échantillon par pays

Pays	Cameroun	RCA	Congo	Gabon	Guinée E.	Tchad		Total	Nombre de banques
^8/10	^3/3	^1/4	^5/6	^2/3	5/7	24

Source : L'auteur

Il ressort du tableau ci-dessus qu'à l'exception du Congo où ne figure qu'une seule banque dans l'échantillon sur les quatre en activité durant la période d'étude, l'échantillon comporte plus de 50 % des banques des autres Etats de la CEMAC.

Les variables retenues pour l'estimation de l'efficacité technique des banques, sont au nombre de sept dont quatre outputs et trois inputs. Elles correspondent à la fonction d'intermédiation financière des banques.

a- Les inputs

· Les dépôts à vue

Les dépôts à vue sont des dépôts pouvant être retirés immédiatement par les déposants et sans préavis.

· Les dépôts à terme

Les dépôts à terme sont des dépôts ne pouvant être restitués aux déposants qu'après une certaine échéance.

· Les dépôts publics

Les dépôts publics par opposition aux dépôts privés (dépôts à vue et dépôts à terme) englobent les dépôts du gouvernement et des administrations publiques .

b- Les outputs

· Les crédits à court terme

Les crédits à court terme sont des crédits dont l'échéance peut aller d'un jour à deux ans.

· Les crédits à moyen terme

Les crédits à moyen terme ont une échéance de deux à sept ans.

· Les crédits à long terme

Les crédits à long terme ont une échéance pouvant aller de sept à vingt ans.

· Les crédits à l'Etat

Ce sont les crédits consentis par les banques au gouvernement et aux administrations publiques.

La fonction d'intermédiation financière des banques est illustrée à travers le graphique ci- dessous :

Figure 3.1 : Illustration de l'intermédiation financière des banques commerciales

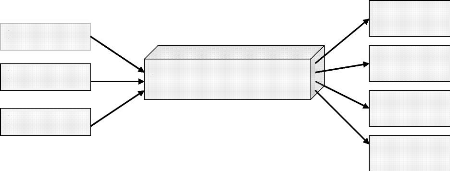
Dépôts à vue

Dépôts à terme

Dépôts publics

Banques commerciales

Crédits à moyen terme

Crédits à long terme

Crédits à l'Etat

Crédits à court terme

Source : L'auteur

Nous allons donc sur la base de ces variables, mesurer l'efficacité technique des 24 banques de notre échantillon. L'efficacité technique de chacune des banques de l'échantillon est évaluée mensuellement par un score compris entre 0 et 1 sur toute la période d'étude, de tel sorte qu'on obtienne 48 scores mensuels pour chaque banque de janvier 2001 à décembre 2004.

1.3 Présentation du modèle empirique

Le modèle empirique utilisé dans cette étude pour mesurer l'efficacité technique des banques commerciales de notre échantillon est un modèle à rendements d'échelle variables. Le choix de ce modèle se justifie par le fait qu'il permet de distinguer l'efficacité technique pure de l'efficacité d'échelle. L'orientation choisie est une orientation tournée vers la maximation des outputs qui à notre avis semble plus appropriée au contexte dans lequel évolue l'activité bancaire dans la sous-région. En effet, on assiste dans la sous-région à une situation où les banques commerciales sont surliquides, mais s'impliquent très peu dans le financement des investissements. Une augmentation de la production bancaire à partir des ressources disponibles paraît à notre avis l'option idéale pour les économies de la sous-région qui souffrent énormément du problème de manque de financement. Le programme linéaire permettant d'estimer l'efficacité technique des banques de l'échantillon est présenté ci-dessous :

Max ö _i (1 = i = 288)

288

X - ë =

X 0

1,i j 1,j

j 1

=

288

X - ë =

~ X 0

2,i j 2,j

j 1

=

288

X - ë =

~ X 0

3,i j 3,j

j 1

288

? ö + ë ?

Y ~ Y 0

i 1,i j 1,j

j 1

=

288

=

~- ö + ë =

Y ~ Y 0 ~ i 2,i j 2,j

j 1

=

~ 288

? ö + ë ?

Y ~ Y 0

i 3,i j 3,j

j 1

=

288

ö + ë =

Y ~ Y 0

i 4,i j 4,j

288

j 1 =

1

~ ë =

j

j 1 = L ë = j

0 (1 j 288) = =

où X1 , i ; X2 , i et X3 , i représentent respectivement les dépôts à vue, les dépôts à terme et les dépôts publics collectés par l'unité de l'échantillon observé au ième rang ;

Y1, i ; Y2, i ; Y3, i et Y4, _i représentent respectivement les crédits à court terme, les crédits à moyen terme et les crédits à long terme distribués par l'unité de l'échantillon observé au ième

rang ;

öi est un scalaire (1 < öi < 00) tel que 1/ öi ( 0 < 1/ öi < 1) détermine le score d'efficacité

de l'unité au ième rang d'observation.

Ce programme linéaire est donc résolu 24x12 fois chaque année et permet d'obtenir un score d'efficacité mensuel pour chaque banque.

La résolution du programme linéaire ci-dessus, permettant l'estimation des scores, est faite à l'aide du logiciel de programmation linéaire DEAP version 2.1 développé par Tim Coelli (1996). DEAP est un programme DOS qui peut être exécuté à partir du gestionnaire de fichiers de WINDOWS. L'exécution du programme requiert au préalable que soient crées un fichier de données et un fichier d'instruction. Une fois ces deux fichiers créés, il suffit pour l'utilisateur de spécifier le nom du fichier d'instruction au programme exécutable afin que ce dernier génère automatiquement le fichier de résultats. Le fichier de données est un fichier de type texte dans lequel les données sont entrées sous forme d'une matrice et suivant un ordre bien précis. Chaque ligne de la matrice correspond aux valeurs des inputs ou des outputs d'une unité observée, listées de la gauche vers la droite en commençant d'abord par les outputs et ensuite les inputs. La matrice de données comporte ainsi autant de ligne que d'observations. Les colonnes de la matrice correspondent de la gauche vers la droite respectivement aux valeurs des outputs et des inputs de toutes les unités observées. Le fichier d'instruction est également un fichier de type texte. Le fichier de résultat quant à lui, toujours de type texte, affiche les scores d'efficacité technique pour toutes les unités observées et calcule également la moyenne de ces scores sur la période d'étude.

Les scores mensuels calculés pour toutes les banques commerciales de notre échantillon figurent en annexe1 de ce document.

Section 2 : ANALYSE DES RÉSULTATS

Les résultats obtenus dans le cadre de cette étude supposent que toutes les banques de l'échantillon sont placées dans les mêmes conditions c'est-à-dire qu'elles utilisent les mêmes inputs pour produire les mêmes outputs, elles sont soumises aux mêmes normes règlementaires, etc. Ces résultats supposent également la technologie constante (absence de progrès technique) durant la période d'étude.

2.1 Analyses descriptives

2.1.1 Evolution des scores moyens annuels et mensuels

Le tableau ci-dessous présente les niveaux moyens annuels d'efficacité technique totale obtenus par l'ensemble de l'échantillon sur la période d'étude, ainsi que leur décomposition en efficacité technique pure et en efficacité d'échelle.

Tableau 3.2 : Evolution des scores moyens ^{d'efficacité}

Période	Totale	Pure	Echelle
2001	0,451	0,693	0,660
2002	0,385	0,700	0,568
2003	0,259	0,657	0,395
2004	0,382	0,723	0,531
2001-2004	0,369	0,693	0,538

Source : COBAC, nos calculs

Il ressort de ce tableau que l'indice moyen d'efficacité technique totale des banques s'est établi à 0,369 sur la période de l'étude. Ce résultat signifie qu'en moyenne, sous l'hypothèse de rendements d'échelle constants, les banques de la CEMAC n'ont produit que 36,9 % de la quantité d'outputs qu'elles auraient pu produire à partir de leurs ressources. En supposant les rendements plutôt variables, le niveau moyen d'efficacité technique s'est établi à 0,693 signifiant que les banques n'ont produit en moyenne sur la période d'étude que 69,3 % de ce qu'elles étaient capables de produire à partir de leurs ressources. Ces résultats confirment notre hypothèse selon laquelle les banques commerciales de la CEMAC ne sont pas optimales dans la gestion de leurs ressources. Elles produisent en deçà de ce qu'elles sont susceptibles de produire à partir des ressources et de la technologie dont elles disposent. Le score moyen d'efficacité d'échelle sur la période d'étude s'est élevé à 0,538, signifiant que sous hypothèse de rendements variables, les banques déclarées techniquement efficaces n'ont produit que 53,8 % de la quantité de crédits qu'elles auraient pu produire si elles opéraient à rendements constants. Ce résultat laisse entrevoir que les banques commerciales de la CEMAC souffrent énormément de problèmes d'inefficacité d'échelle. Il montre en effet qu'en moyenne, le rythme de croissance des crédits a été inférieur à celui des dépôts durant la période d'étude. Ce qui confirme le fait que les banques soient surliquides mais n'octroient que très peu de crédits.

La graphique 1 ci-dessous permet une meilleure appréciation de l'évolution des scores moyens annuels sous différentes hypothèses de rendements d'échelle.

Graphique 3.1 : Evolution des scores moyens d'efficacité

Score moyen d'efficacite

_0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1

0

2001 2002 2003 2004

Année

Technique totale Technique pure Echelle

Source : COBAC , nos calculs

Ce graphique révèle que le niveau moyen d'efficacité technique pure reste pratiquement constant sur toute la période de l'étude. On remarque juste une légère baisse entre 2002 et 2003 ainsi qu'une légère hausse entre 2003 et 2004. Sa valeur est relativement élevée dans la mesure où elle se situe au dessus de 0,5 sur toute la période de l'étude. Cette constance de l'indice d'efficacité technique pure montre que les pratiques de gestion des banques n'ont pas beaucoup varié durant la période de l'étude.

Par ailleurs, le niveau moyen d'efficacité technique totale dont la valeur est restée toujours inférieure à 0,5 décroît considérablement entre 2001 et 2003 avant de connaître une remontée moins que proportionnelle entre 2003 et 2004. Le niveau moyen d'efficacité d'échelle quant à lui, a connu une évolution quasiment identique à celle du niveau moyen d'efficacité totale sur toute la période de l'étude. On peut donc affirmer au regard de ces constats que l'efficacité d'échelle explique pratiquement à elle seule, l'évolution de l'efficacité technique totale des banques sur la période de l'étude.

Les banques commerciales de la CEMAC ont beaucoup plus souffert entre 2001 et 2004 de problèmes d'inefficacité d'échelle¹⁹ que de mauvaises pratiques de gestion. Leurs sous productions sont beaucoup plus liées à un problème d'échelle sous optimale qu'à un problème de mauvaises pratiques de gestion. Il ressort du tableau 3.3 ci-dessous que le niveau moyen d'inefficacité totale sur toute la période s'est établi à 0,631 signifiant que sous hypothèse de

¹⁹ Indice d'inefficacité = 1- indice d'efficacité

rendements constant, les banques commerciales de la CEMAC auraient pu accroître proportionnellement leur volume de crédit de 171 %²⁰ en maintenant le niveau des dépôts constant. Sous hypothèse de rendements variables, cet accroissement s'élève plutôt à 44,3 %.

Tableau 3.3 : Score d'inefficacité moyen entre 2001 et 2004

Période	Totale	Pure	Echelle
2001	0,549	0,307	0,340
2002	0,615	0,300	0,432
2003	0,741	0,343	0,605
2004	0,618	0,277	0,469
2001-2004	0,631	0,307	0,462

Source : COBAC, nos calculs

L'inefficacité d'échelle quant à elle, s'est établie sur la période de l'étude à 0,462 signifiant que les banques déclarées techniquement efficaces sous hypothèse de rendements variables, pourraient accroître leur volume de crédit de 85,8 % sans changer la quantité de dépôts utilisés si elles opéraient à rendements constants.

Graphique 3.2 : Evolution des scores moyens annuels d'inefficacité

Score moyen d'ineffficacite

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1

0

2001 2002 2003 2004

Année

Inefficacité totale Inefficacité pure

Inefficacité d'échelle

Source : COBAC, nos calculs

²⁰(0,631/0,369)*100=171

A la lumière de ce graphique, il ressort que c'est en 2003 que les banques de la CEMAC ont été en moyenne plus techniquement inefficaces car c'est l'année où toutes les courbes du graphique atteignent leur maximum. Il ressort également de ce graphique que l'inefficacité pure n'a pas beaucoup varié sur toute la période d'étude avec une valeur relativement faible et oscillante autour de 0,3. Ce qui témoigne le fait que les pratiques de gestion des banques n'ont presque pas changé tout au long de la période. L'inefficacité pure a atteint sa plus grande valeur en 2003 et sa plus petite valeur en 2004. C'est donc en 2003 que les banques de la CEMAC ont enregistré les plus mauvaises pratiques de gestion contrairement à 2004 où les pratiques de gestion ont été les plus bonnes.

L'inefficacité d'échelle a été croissante de 2001 à 2003 où elle a atteint son point culminant avant de décroître de 2003 à 2004. Ce qui veut dire qu'en moyenne entre 2001 et 2003, le rythme de croissance des crédits a été inférieur à celui des dépôts, en étant lui même décroissant. Autrement dit, le rythme de croissance des crédits en 2001 a été inférieur à celui des dépôts en 2001. De même, le rythme de croissance des crédits en 2002 a été inférieur à celui des dépôts en 2002, et également inférieur au rythme de croissance des crédits de 2001. Enfin, le rythme de croissance des crédits en 2003 a été inférieur à celui des dépôts en 2003, et également inférieur au rythme de croissance des crédits de 2001 et 2002. La décroissance de l'inefficacité d'échelle observée entre 2003 et 2004 signifie que le rythme de croissance des crédits en 2004 a été supérieur à celui de 2003.

L'inefficacité totale présente une évolution semblable à celle de l'inefficacité d'échelle sur toute la période. L'évolution de l'inefficacité pure étant pratiquement constante sur toute la période, l'évolution de l'inefficacité totale est en grande partie expliquée par l'évolution de l'inefficacité d'échelle.

Le graphique ci-dessous donne l'évolution des scores moyens mensuels d'efficacité technique pure et d'échelle pour l'ensemble de l'échantillon sur toute la période.

Graphique 3.3 : Evolution des scores moyens mensuels d'efficacité

_0,9

0,8

0,6

0,4

0,3

0,2

0,0

0,7

0,5

0,1

Technique pure Echelle

M o is

Source : COBAC, nos calculs

Il ressort de ce graphique qu'à l'exception des mois d'avril 2002 et de septembre 2003 où l'on observe quelques variations brusques, le score moyen mensuel d'efficacité technique pure a connu une évolution presque stationnaire tout au long de la période, oscillant entre 0,6 et 0,8. Ce qui confirme le fait qu'entre 2001 et 2004, il n'y ait pas eu un grand changement au niveau de la gestion des ressources bancaires dans la CEMAC. Les pratiques de gestion sont restées presque les mêmes tout au long de cette période. La meilleure performance du système a été réalisée en décembre 2004 avec un score moyen de 0,8 contrairement à septembre 2003 où le système a connu sa plus faible performance avec un score moyen qui s'est établi à 0,44.

Ce graphique laisse également entrevoir que le score moyen d'efficacité d'échelle a connu une évolution presque stationnaire durant l'année 2001, avant de chuter en janvier 2002 où sa valeur s'est établie à 0,55. Son évolution a été également presque stationnaire durant l'année 2002 avec une valeur toujours comprise entre 0,5 et 0,6 et signifiant une contre performance des banques comparativement à l'année 2001. C'est en 2003 que les banques commerciales de l'échantillon ont beaucoup plus souffert de problèmes d'inefficacité d'échelle avec un score oscillant autour de 0,4 et atteignant sa plus faible valeur 0,36 en septembre 2003. En 2004, le score a évolué presque stationnairement avec une valeur toujours comprise entre 0,5 et 0,6 sur toute l'année.

On constate ainsi que c'est en septembre 2003 que les banques commerciales de l'échantillon ont été le plus techniquement inefficaces dans la transformation de leurs ressources. Elles ont réalisé un score d'efficacité totale de 0,2 signifiant qu'en septembre 2003, les banques de l'échantillon n'ont produit en moyenne que 20 % de ce qu'elles auraient pu produire à partir de leurs ressources si elles opéraient toutes à rendements d'échelle constants.

2.1.2 Analyses suivant l'année

Le tableau ci-dessous donne la répartition du nombre de banques déclarées techniquement efficaces c'est-à-dire situées sur la frontière d'efficacité, sous différentes hypothèses de rendements d'échelle.

Tableau 3.4 : Nombre de banques techniquement efficaces suivant l'hypothèse de rendements d'échelle.

Mois	2001		2002		2003		2004
	REC	REV	REC	REV	REC	REV	REC	REV
Janvier	1	8	1	5	0	5	1	3
Février	1	5	1	3	0	3	2	9
Mars	3	5	2	3	1	4	1	3
Avril	3	3	0	2	2	4	0	0
Mai	2	5	1	4	0	1	1	4
Juin	1	7	1	7	0	5	1	3
Juillet	0	0	1	4	2	3	3	4
Août	2	4	0	4	1	5	1	2
Septembre	2	3	2	8	2	5	0	2
Octobre	2	5	1	5	1	5	2	5
Novembre	1	5	1	5	1	8	0	6
Décembre	2	8	1	8	1	7	1	7

Source : COBAC, nos calculs

On remarque que l'on retrouve beaucoup plus de banques sur la frontière lorsque l'hypothèse de rendements variables est admise. Ce qui signifie que certaines banques techniquement efficaces sous l'hypothèse de rendements variables ne le sont plus lorsque l'on suppose les rendements plutôt constants. D'où l'importance du choix de l'hypothèse de rendements d'échelle dans le calcul des scores d'efficacité.

On observe également qu'aucune banque de l'échantillon n'a été techniquement efficace en juillet 2001 et en Avril 2004. C'est en février 2004 qu'on obtient sous hypothèse de rendements variables, le plus grand nombre de banques sur la frontière d'efficacité soit 37,5 % des banques de l'échantillon. Par contre, le plus grand nombre de banques sur la frontière d'efficacité sous hypothèse de rendements constants ne représente que 12,5 % des banques de l'échantillon.

Le classement des banques commerciales de l'échantillon suivant le score moyen d'efficacité technique pure obtenu sur toute la période, figure dans le tableau ci-dessous :

Tableau 3.5 : Classement des banques suivant le score moyen d'efficacité technique pure

Banque	2001 2002 2003 2004 2001-2004					Rang
Gab4	0,984	0,979	0,999	0,977	0,985	1er
Gab1	0,989	0,989	0,979	0,952	0,977	2ème
Gab3	0,988	0,963	0,984	0,879	0,954	3ème
Cam5	0,967	0,757	0,809	0,956	0,873	4ème
Cam3	0,853	0,795	0,873	0,957	0,870	5ème
Gab2	0,811	0,923	0,838	0,831	0,851	6ème
Cam1	0,832	0,845	0,788	0,863	0,832	7ème
Cam4	0,754	0,763	0,890	0,892	0,825	8ème
Cam7	0,764	0,777	0,751	0,976	0,817	9ème
Tcd2	0,723	0,882	0,780	0,831	0,804	10^ème
Tcd3	0,721	0,687	0,814	0,843	0,766	11^ème
Cam2	0,647	0,793	0,846	0,667	0,738	12^ème
Gab5	0,573	0,858	0,784	0,695	0,728	13^ème
Gnq1	0,931	0,838	0,290	0,754	0,703	14^ème
Cam8	0,423	0,739	0,656	0,826	0,661	15^ème
Caf3	0,845	0,629	0,517	0,597	0,647	16^ème
Tcd4	0,189	0,758	0,780	0,822	0,637	17^ème
Tcd1	0,596	0,615	0,560	0,708	0,620	18^ème
Caf1	0,877	0,526	0,353	0,442	0,550	19^ème
Caf2	0,495	0,414	0,477	0,541	0,482	20^ème
Cam6	0,607	0,478	0,251	0,502	0,460	21^ème
Tcd5	0,460	0,395	0,278	0,216	0,338	22^ème
Cog8	0,443	0,190	0,215	0,238	0,271	23^ème
Gnq2	0,152	0,198	0,261	0,377	0,247	24^ème
Moyenne	0,693	0,700	0,657	0,723	0,693
Ecart type	0,24	0,23	0,26	0,23	0,21

Source : COBAC, nos calculs

Il ressort de ce tableau que sous hypothèse de rendements variables, Gab4 a été la banque la plus performante techniquement sur toute la période de l'étude. C'est elle qui a réalisé la meilleure gestion de ressources entre 2001 et 2004. Elle a en effet produit en moyenne sur toute la période 98,5 % de ce qu'elle aurait pu produire à partir de ses ressources. Contrairement à elle, Gnq2 est la banque qui a été la moins performante sur toute la période avec un score moyen qui s'est établi à 0,247. Ce tableau révèle également que la plus faible performance moyenne enregistrée par l'ensemble des banques en 2003 pourrait s'expliquer par la chute flagrante de la Gnq1 dont le score moyen est passé de 0,838 à 0,290 entre 2002 et 2003. La Gnq1 a connu un parcours médiocre dans la transformation de ses ressources en crédits durant l'année 2003, comparativement aux autres années. Ce qui signifie qu'en 2003, il y a eu un grand changement dans sa façon de gérer ses ressources.

On constate également que c'est en 2003 que la dispersion entre les scores moyens des banques a été la plus accentuée avec un écart type dont la valeur s'est établie à 0,26. On observe aussi à la lumière de ce tableau que l'écart type des scores moyens n'a pas considérablement varié tout au long de la période. Ce qui témoigne le fait qu'il n y'ait pas eu une grande différence dans le comportement des banques relativement à la façon de gérer leurs ressources entre 2001 et 2004. L'examen du tableau ci-dessus montre que les banques gabonaises et camerounaises semblent dans l'ensemble être les plus performantes de l'échantillon. La figure ci-dessous est la représentation des scores moyens par pays et par an.

Graphique 3.4 : Score moyen par pays et par an

0,90

0,80

0,70

0,60

0,50

0,40

0,30

0,20

0,00

0,10

1,00

Cameroun RCA Congo Gabon Guinnée Equatoriale Tchad Ensemble

2001 2002 2003 2004

source : COBAC, nos calculs

On constate effectivement à la lumière de ce graphique que durant les quatre années de l'étude, les banques gabonaises ont réalisé en moyenne les scores les plus élevés. Elles sont suivies par les banques camerounaises dont le score moyen n'a presque pas varié entre 2001 et 2003. On remarque que les scores moyens des banques gabonaises et camerounaises sont nettement au dessus des scores moyens de l'ensemble des banques de l'échantillon sur toute la période. Par contre, les scores moyens de la Cog8 et des banques equato guinéennes sont restés toujours inférieur au score moyen de l'ensemble des banques sur toute la période. Les banques tchadiennes (respectivement centrafricaines) quant à elles, à l'exception de 2001, présentent des scores moyens supérieurs (respectivement inférieurs) à ceux de l'ensemble des banques de l'échantillon.

2.2 Analyse en composantes principales (ACP) et classification des

banques de la CEMAC

L'analyse en composantes principales est une méthode d'analyse des données appliquée sur un tableau rectangulaire individus-variables où N individus sont décrits par P variables quantitatives. Elle a pour but d'obtenir un résumé synthétique des informations contenues dans le tableau de données. Elle permet ainsi d'analyser les proximités entre les individus, les corrélations entre les variables, les individus et les variables simultanément.

Notre objectif dans cette analyse est de pouvoir regrouper les banques qui ont eu des performances similaires durant toute la période de l'étude. Nous disposons ainsi d'un tableau rectangulaire²¹ comportant 24 banques décrites chacune par 48 scores mensuels sur toute la période de l'étude. Les moyennes mensuelles des scores pour tout l'échantillon sur toute la période de l'étude sont consignées dans le tableau ci-dessous.

Tableau 3.6 : Moyennes mensuelles des scores de l'échantillon

Janv 01	Févr 01	Mars 01	Avr 01	Mai 01	Juin 01	juil- 01	Août 01	Sept 01	Oct 01	Nov 01	Déc 01
0,716	0,660	0,687	0,718	0,704	0,714	0,695	0,695	0,700	0,672	0,657	0,693
Janv 02	Févr 02	Mars 02	Avr 02	Mai 02	Juin 02	juil- 02	Août 02	Sept 02	Oct 02	Nov 02	Déc 02
0,660	0,718	0,665	0,496	0,753	0,739	0,736	0,722	0,730	0,704	0,703	0,770
Janv 03	Févr 03	Mars 03	Avr 03	Mai 03	Juin 03	juil- 03	Août 03	Sept 03	Oct 03	Nov 03	Déc 03
0,684	0,669	0,661	0,669	0,605	0,679	0,685	0,692	0,444	0,654	0,729	0,715
Janv 04	Févr 04	Mars 04	Avr 04	Mai 04	Juin 04	juil- 04	Août 04	Sept 04	Oct 04	Nov 04	Déc 04
0,688	0,771	0,706	0,693	0,714	0,711	0,724	0,693	0,721	0,728	0,720	0,803

Source : COBAC, nos calculs

L'application d'une ACP normée à notre tableau rectangulaire sous le logiciel SPAD nous a permis d'obtenir les résultats suivants :

²¹ Voire annexe

Mémoire rédigé et soutenu par Leonnel DIMOU KWAYEP 50

Tableau 3.7 : Tableau des valeurs propres

Mois	Numéro	Valeur Propre	Pourcentage	Pourcentage ^cumulé
Janvier	1	27,71	57,74	57,74
Février	2	5,93	12,36	70,10
Mars	3	3,38	7,06	77,16
Avril	4	1,86	3,88	81,04
Mai	5	1,58	3,29	84,.33
Juin	6	1,23	2,58	86,91
Juillet	7	1,10	2,31	89,22
Août	8	0,97	2,04	91,26
Septembre	9	0,92	1,92	93,18
Octobre	10	0,74	1,54	94,72
Novembre	11	0,57	1,19	95,91
Décembre	12	0,40	0,83	96,75

Source : COBAC, nos calculs

L'inertie totale du nuage des individus et des variables dans une ACP normée est égale au nombre de variables actives (48 dans notre cas). L'examen du tableau des valeurs propres cidessus permet de constater que le premier axe factoriel avec une inertie de 27,71 explique 57,74 % de l'inertie totale du nuage. Le deuxième axe quant à lui n'explique que 12,36 % de l'inertie du nuage. Les deux premiers axes factoriels expliquent ainsi à eux seul 70,10 % de l'inertie totale du nuage. Nous pensons que ce pourcentage d'inertie cumulée est satisfaisant pour pouvoir mener nos interprétations à partir des deux premiers axes factoriels. D'autre part, si chacune des 24 banques contribuait à part égale à la détermination des axes, la contribution de chacune devrait être de 100/24 = 4,16 % pour la détermination de chaque axe.

La matrice donnant les coordonnées des variables sur les axes factoriels (en annexe2) laisse entrevoir que la quasi-totalité des variables sont corrélées positivement au premier facteur. Ce qui signifie que pour toutes les banques bien représentées sur cet axe avec une coordonnée positive, les scores mensuels ont été supérieurs aux moyennes mensuelles pratiquement sur toute la période de l'étude. De même, pour toutes les banques bien représentées sur cet axe, mais plutôt avec une coordonnée négative, les scores mensuels ont été inférieurs à la moyenne presque sur toute la période de l'étude. L'examen du nuage des banques ci-dessous permet de constater que le premier axe factoriel oppose deux groupes de banques à gauche et à droite de l'origine. Le premier groupe situé à droite de l'origine est constitué essentiellement de banques camerounaises et gabonaises dont la plupart ont eu des scores mensuels supérieurs aux moyennes mensuelles des scores sur toute la période.

Graphique 3.5 : Projection des individus sur les deux premiers facteurs

Source : COBAC, nos calculs

Le deuxième groupe situé à gauche de l'origine est constitué essentiellement des banques des autres Etats de la CEMAC. Les banques de ce groupe qui sont bien représentées sur le premier facteur, ont eu des scores mensuels inférieurs aux moyennes mensuelles des scores sur toute la période.

Le deuxième axe factoriel quant à lui oppose également deux groupes de banques au dessus et en dessous de l'origine. La matrice des coordonnées des variables sur les axes factoriels montre que toutes les variables correspondants à l'année 2001 sont négativement corrélées au deuxième facteur. Ce qui signifie que pour les banques bien représentées sur cet axe avec une coordonnée négative, les scores mensuels ont été supérieurs aux moyennes mensuelles durant toute l'année 2001. Il s'agit notamment des banques gabonaises situées en dessous de l'origine dont les contributions sur le deuxième facteur sont supérieures à la contribution moyenne de ce facteur. De manière analogue, les banques bien représentées sur cet axe plutôt avec une coordonnée positive, ont eu des scores mensuels inférieurs aux moyennes mensuelles durant toute l'année 2001. L'on constate que la quasi-totalité des autres variables sont faiblement et positivement corrélées au deuxième facteur.

L'ACP permet donc de distinguer dans l'ensemble deux grands groupes :

v' Les banques gabonaises et camerounaises (et certaines banques Tchadiennes), dont la plupart ont eu des scores élevés pratiquement sur toute la période de l'étude ;

v' Les banques des autres Etats de la CEMAC dont certaines ont eu des scores tantôt élevés, tantôt faibles, et d'autres des scores faibles sur toute la période de l'étude.

La figure ci-dessous représente l'arbre hiérarchique obtenu en appliquant l'algorithme de Ward à notre tableau rectangulaire constitué des banques en ligne et des scores mensuels en colonne.

Figure 3.2 : Arbre hiérarchique issu de l'algorithme de Ward

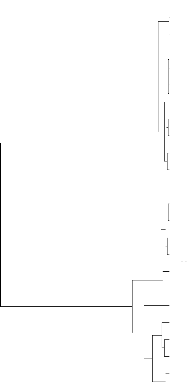
Gab4

Gab1

Gab3

Gab2

Cam3

Cam1

Cam5

Cam7

Cam4

Tcd3

Tcd2

Tcd4

Gab5

Cam2

Cam8

Tcd1

Cog8

Gnq2

Gnq1

Cam6

Tcd5

Caf2

Caf3

Caf1

Source : COBAC, nos calculs

Cet arbre met effectivement en évidence une similarité entre la plupart des banques gabonaises et camerounaises ainsi que certaines banques tchadiennes. En effet, en adoptant un regroupement en trois classes, on constate que la première classe est essentiellement constituée

de banques gabonaises et camerounaises ainsi que de deux banques tchadiennes. La deuxième classe quant à elle, est constituée essentiellement de banques camerounaises et tchadiennes, et d'une banque gabonaise (la moins performante au Gabon). Enfin la dernière, comporte toutes les banques centrafricaines et équato-guinéennes, ainsi que l'unique banque congolaise de notre échantillon. On retrouve également dans cette classe, une banque camerounaise (la moins performante au Cameroun), et une banque tchadienne (la moins performante au Tchad).

En définitive, il ressort de ce chapitre que les banques commerciales de la CEMAC ne gèrent pas optimalement les ressources mises à leur disposition. Elles produisent des quantités de crédits inférieures à ce qui est techniquement possible à partir des ressources dont elles disposent. Ce qui justifie le fait que la production des crédits bancaires semble ne pas couvrir entièrement les besoins d'investissements dans la sous-région. Ce chapitre révèle également que les banques gabonaises et camerounaises semblent avoir été dans l'ensemble les plus efficaces dans la transformation de leurs ressources en crédits entre 2001 et 2004.

L'investissement productif étant le moteur de la croissance économique, il convient donc afin d'assurer son financement, de rechercher les facteurs sur lesquels on pourrait agir pour améliorer l'efficacité technique des banques de la CEMAC. Ce qui nous amène à estimer le modèle économétrique présenté au chapitre suivant.

Chapitre 4 : ANALYSE ÉCONOMÉTRIQUE DES DÉTERMINANTS

DE L'EFFICACITÉ TECHNIQUE

Ce chapitre a pour but de mettre en exergue les variables explicatives des niveaux d'efficacité technique pure des banques commerciales de la CEMAC sur la période de l'étude à travers une analyse économétrique. Pour y parvenir, nous estimerons un modèle linéaire multiple ayant comme variable dépendante le score d'efficacité technique pure, et comme variables explicatives, certains ratios de gestion nous semblant pertinents. Ainsi, après l'estimation et l'interprétation des résultats du modèle (section 1), nous proposerons quelques solutions à mettre en oeuvre pour améliorer l'efficacité technique des banques commerciales dans la sous-région (section 2).

Section 1: PRÉSENTATION DU MODÈLE

1.1 Choix du modèle empirique

Il existe dans la littérature principalement deux méthodes de modélisation des déterminants de l'efficacité technique à savoir le modèle Tobit ou Logit et la régression linéaire utilisant les moindres carrés ordinaires (MCO). L'inconvénient d'un modèle Tobit dans l'estimation des déterminants de l'efficacité technique est qu'il requiert une hypothèse concernant l'interdépendance des scores les uns par rapport aux autres, condition qui n'est pas vérifiée.

Nous avons donc eu recours dans le cadre de cette étude à un modèle de régression linéaire en considérant comme variable dépendante les scores d'efficacité technique pure et comme variables explicatives potentielles, certains ratios de gestion des banques jugés pertinents dans l'explication des scores. Nous n'avons pas pris en compte dans un souci de simplification, la présence d'éventuels effets spécifiques individuels ou temporels dans l'explication des scores. En effet, notre objectif étant d'identifier les facteurs de la gestion bancaire qui déterminent les scores en un mois donné, nous avons travaillé en considérant une banque comme deux individus différents lorsqu'on passe d'un mois à l'autre. Ce qui veut dire que notre modèle a été estimé à partir de 1152 = 24×48 observations différentes de janvier 2001 à décembre 2004.

1.2 Spécification du modèle

Le modèle retenu dans le cadre de cette étude est un modèle linéaire multiple dont la forme est la suivante :

Yi = 31X1i + 32X2i + 33X3i +...+~kXki + ci , i = 1,2,...,1152

Ott Y est un vecteur de dimension 1152×1 représentant les scores mensuels d'efficacité technique pure des banques sur toute la période de l'étude.

X1i, X2i, X3i, ..., _Xki représentent respectivement les k variables explicatives exogènes et potentielles des scores de la banque " i ".

Les variables explicatives utilisées dans l'estimation de ce modèle représentent quatre ratios de gestion bancaire à savoir :

v' Le ratio créances douteuses/ total crédits (CDTC) qui donne la proportion des créances douteuses dans le total des crédits octroyés par la banque. Les créances douteuses sont des crédits accordés par la banque, mais qui n'ont pas été remboursés par les bénéficiaires. La raison du non remboursement pouvant être l'insolvabilité, le refus délibéré de rembourser, etc ;

v' Le ratio fonds propres/ total crédits (FPTC) qui est utilisé par la COBAC pour limiter les risques pris par les banques ;

v' Le ratio fonds propres/ total actif (FPTA) qui détermine la proportion des ressources propres de la banque dans ses avoirs ;

v' Le ratio excédent de trésorerie/ total actif (EBTA) qui donne la proportion de l'excédent de liquidité dont dispose la banque dans ses avoirs.

La spécification du modèle empirique d'estimation des déterminants de l'efficacité technique est dont la suivante :

Yi = 30 + 31CDTCi + 32FPTCi + 33FPTAi + 34EBTAi + ~i , i = 1,2,...,1152

C'est ce modèle qui nous a permis de mettre en exergue les facteurs pouvant influencer la transformation des ressources bancaires en crédits. Afin de corriger une éventuelle autocorrélation des erreurs du modèle, nous avons introduit le terme AR (1) dans le modèle.

Les données utilisées pour l'estimation de ce modèle sont issues du secrétariat Général de la COBAC.

Section 2: ESTIMATION DU MODÈLE ET INTERPRÉTATION DES RESULTATS

2.1 Estimation du modèle

Le modèle présenté ci-dessus a été estimé à l'aide du logiciel Eviews5 sur des données mensuelles de janvier 2001 à décembre 2004. Les résultats de l'estimation figurent dans le tableau ci-dessous. Avant de ce lancer dans l'interprétation de ces résultats, il convient de ce rassurer qu'un certain nombre d'hypothèses sont vérifiées.

1' Le test de Jarque Bera

Ce test permet de vérifier que les résidus du modèle suivent une loi normale. L'hypothèse nulle est que tous les résidus sont normaux. On l'accepte à un seuil de confiance donné si la p-value est supérieure à ce seuil. Le test de Jarque Bera réalisé dans le cas de ce modèle (annexe3) montre que tous les résidus sont normaux au seuil 5 %.

1' Le test de Durbin Watson

Le test de Durbin Watson permet de vérifier s'il y'a autocorrélation entre les résidus du modèle. Une statistique de Durbin Watson proche de 2 comme c'est le cas dans ce modèle où DW = 2,188 signifie qu'il y'a absence d'autocorrélation entre les résidus du modèle.

1' Le test de Fischer

Ce test permet de vérifier la significativité globale du modèle. L'hypothèse nulle est définie par la nullité de l'ensemble des coefficients du modèle. Pour un seuil de confiance donné, si la p-value est inférieure au seuil, on rejette l'hypothèse nulle. Dans le cas contraire, on l'accepte. La p-value dans le cas de ce modèle nous permet de constater qu'il est globalement significatif au seuil 5 %.

1' Le test de Student

Ce test permet de vérifier la significativité des coefficients du modèle pris individuellement. L'hypothèse nulle est définie par la nullité du coefficient considéré. Pour un seuil de confiance donné, si la p-value est inférieur à ce seuil, on rejette l'hypothèse nulle. La p-value dans le cas de ce modèle montre que tous les coefficients du modèle sont significatifs au seuil 5%.

Tableau 3.8 : Résultats du modèle

Dependent Variable: SCORE

Sample (adjusted): 2001M01 2004M12 Cross-sections included: 24

Total observations: 1152

Variable	Coefficient Std. Error t-Statistic		Prob.
C	-0.144	0.006 -20.742	0.000
CDTC	-0.724	0.024 -30.129	0.000
FPTC	-0.149	0.019 -7.756	0.000
FPTA	0.477	0.033 14.098	0.000
EBTA	-0.262	0.015 -16.927	0.000
AR(1)	0.373	0.028 13.279	0.000
R-squared	0.669	Mean dependent var	-0.268
Adjusted R-squared	0.668	S.D. dependent var	0.133
S.E. of regression	0.076	Akaike info criterion	-2.290
Sum squared resid	6.591	Schwarz criterion	-2.263
Log likelihood	1293.188	F-statistic	453.727
Durbin-Watson stat	2.188	Prob(F-statistic)	0.000
Inverted AR Roots	.37

Source : COBAC, nos calculs

2.2 Interprétation des résultats

v' Le R² ou coefficient de détermination

Le coefficient de détermination représente la proportion de la variance totale expliquée par le modèle. En effet, plus le R² est proche de 1, meilleur est l'ajustement global du modèle. La valeur du R² dans ce modèle vaut 0,67 et signifie que le modèle n'explique que 67 % de la variance des scores d'efficacité technique pure. Cela pourrait être dû au fait que le modèle ne prenne pas en compte toutes les variables susceptibles d'expliquer les scores d'efficacité ou encore à des erreurs de mesure sur les variables retenues dans le modèle.

v' La proportion des créances douteuses dans le total des crédits (CDTC)

Le signe négatif de cette variable dans le modèle signifie qu'elle agit négativement sur l'efficacité des banques dans la transformation de leurs ressources. Plus la proportion des créances douteuses dans le total des crédits augmente, moins la banque transforme les dépôts en crédits. Plus précisément, toutes choses égales par ailleurs, une augmentation de 1 % de la proportion des créances douteuses dans le total des crédits, entraînerait une diminution du score d'efficacité technique pure de 72,4 %. Ce qui confirme notre hypothèse selon laquelle, plus les

banques accumulent des créances douteuses, plus elles deviennent réticentes à octroyer des crédits et sont ainsi techniquement inefficaces.

Les créances douteuses reflètent en effet la mauvaise qualité des demandeurs de crédits qui une fois entrer en possession d'un crédit bancaire, ne parviennent pas ou refusent délibérément de rembourser. Elles traduisent également la situation de l'environnement dans lequel évolue l'activité bancaire. En effet, une accumulation des créances douteuses pourrait être la manifestation d'une incapacité des banques à procéder au recouvrement de leurs créances due à un dysfonctionnement de l'appareil judiciaire. Cela pourrait traduire aussi le financement d'un nombre élevé de projets d'investissement non viables, mal montés, ne présentant aucune perspective de rentabilité.

v' Le ratio des fonds propres sur le total des crédits (FPTC)

Cette variable influence négativement l'efficacité des banques dans la transformation de leurs ressources en crédits. Son signe négatif traduit le fait que plus la proportion des fonds propres dans le total des crédits est élevé, moins la banque transforme ses ressources en crédits. Avec un coefficient de régression de - 0,149, une augmentation de ce ratio de 1 % toutes choses égales par ailleurs, entraînerait une diminution du score d'efficacité de 14,9 %. On constate ainsi que l'influence de cette variable sur le score d'efficacité est moindre que celle de la variable précédente. Connu sous le nom de ratio de couverture des risques, la valeur minimale de ce ratio a été fixée à 8 % par la COBAC. Ce qui signifie que toutes choses égales par ailleurs, les banques les plus optimales dans la transformation de leurs ressources seront celles pour qui ce ratio aura la valeur de 8 %.

v' Le ratio des fonds propres sur le total des actifs (FPTA)

Ce ratio qui représente la proportion des fonds propres de la banque dans l'ensemble de ses ressources, semble améliorer son efficacité dans la transformation de ses ressources en crédits. En effet, ce ratio agit positivement sur le score d'efficacité signifiant que plus la proportion des fonds propres dans les actifs d'une banque augmente, plus cette banque est efficace dans la transformation de ses ressources. Autrement dit, plus une banque est solvable, plus elle est techniquement efficace. Plus précisément, toutes choses égales par ailleurs, une augmentation de 1% de la proportion des fonds propres dans l'actif total améliorerait le score d'efficacité de 47,8 %. Ce résultat pourrait s'expliquer par le fait que plus les fonds propres d'une banque sont importantes, plus elle peut accorder des crédits à court , moyen et long terme sachant qu'elle dispose suffisamment de ressources propres pouvant lui permettre de couvrir l'ensemble des risques inhérents .

v' Le ratio excédent de trésorerie sur le total des actifs (EBTA)

La trésorerie peut être considérée comme l'ensemble des liquidités dont dispose la banque à un moment donné. L'excédent de trésorerie constitue le solde positif entre les emplois et les ressources de trésorerie. Le signe négatif de ce ratio signifie que plus la part de l'excédent de trésorerie dans les actifs d'une banque augmente, moins la banque est efficace dans la transformation de ses ressources. De manière formelle, toutes choses égales par ailleurs, une augmentation de 1 % de ce ratio, provoquerait une réduction du score d'efficacité de 26,2 %.

Une trésorerie pléthorique pour une banque pourrait donc s'interpréter comme la manifestation d'une inefficacité dans la transformation de ses ressources. Ce résultat pourrait s'expliquer par le fait que les banques préfèrent plutôt orienter leurs ressources dans les emplois de trésorerie (placements auprès de la Banque Centrale et chez les correspondants résidents et non résidents), moins rémunérateurs que les crédits à la clientèle mais peu risqués.

CONCLUSION ET RECOMMANDATIONS

L'objectif de ce mémoire a été d'évaluer empiriquement les niveaux relatifs d'efficacité technique de 24 banques commerciales de la CEMAC sur la période allant de janvier 2001 à décembre 2004, et de rechercher les facteurs de la gestion bancaire susceptibles d'expliquer les niveaux obtenus. Pour ce faire, nous avons estimé grâce à la méthode DEA, des scores mensuels d'efficacité technique de chaque banque sous différentes hypothèses de rendements d'échelle. Une fois ces scores obtenus, nous avons fait ressortir à travers l'estimation d'un modèle linéaire multiple, l'influence de certains ratios de la gestion bancaire sur les scores d'efficacité technique pure. Ce qui a permis d'aboutir aux résultats suivants :

v' Sous hypothèse de rendements constants, l'efficacité technique moyenne de l'ensemble des banques de l'échantillon sur toute la période de l'étude s'est établie à 0,369. Ce qui signifie qu'entre 2001 et 2004, ces banques n'ont produit en moyenne que 36,9 % de la quantité de crédits qu'elles auraient pu produire à partir de leurs ressources si elles opéraient toutes à rendements d'échelle constants. En d'autres termes, elles auraient pu accroître proportionnellement leur volume de crédit de 171 % en maintenant le niveau des dépôts constant si elles opéraient toutes à rendements d'échelle constants.

v' Sous hypothèse de rendements variables, l'efficacité technique moyenne s'est plutôt établie à 0,693 sur toute la période de l'étude. Ce qui veut dire que durant cette période, les banques n'ont produit en moyenne que 69,3 % de la quantité de crédits qu'elles étaient susceptibles de produire à partir de leurs ressources. Autrement dit, elles auraient pu accroître proportionnellement leur volume de crédits de 44,3 % en maintenant le niveau des dépôts constant.

v' C'est en septembre 2003 que les banques ont été le plus techniquement inefficaces. Elles n'ont produit en moyenne que 20 % de ce qu'elles auraient pu produire à partir de leurs ressources si elles opéraient toutes à rendements d'échelle constants.

v' Les banques ont beaucoup plus souffert entre 2001 et 2004 de problèmes d'inefficacité d'échelle que de mauvaises pratiques de gestion. Leurs sous productions sont beaucoup plus liées à un problème d'échelle sous optimale qu'à un problème de mauvaises pratiques de gestion. En effet, le score moyen d'efficacité d'échelle a été de 53,8 % sur toute la période tandis que celui d'efficacité technique pure reflétant les pratiques de gestion s'est établi à 69,3 %. Les pratiques de gestion des banques n'ont pas beaucoup variées durant la période de l'étude au regard de l'évolution des scores moyens d'efficacité technique pure.

v' Les banques gabonaises et camerounaises semblent avoir été dans l'ensemble les plus performantes dans la transformation de leurs ressources entre 2001 et 2004 dans toute la sous région.

1' Le risque encouru par les banques, évalué par la proportion des créances douteuses dans le total des crédits accordés est au centre du processus de transformation des ressources bancaires dans la sous région. En effet, plus les banques accumulent des créances douteuses, plus elles deviennent réticentes à octroyer des crédits.

1' La proportion des fonds propres dans l'ensemble des actifs des banques, semble également être un facteur clé dans le processus de transformation des dépôts en crédits. En effet, plus la part des fonds propres d'une banque dans ses ressources augmente, plus elle est efficace dans la transformation de ses ressources.

1' Une trésorerie pléthorique pour une banque pourrait s'interpréter comme la manifestation d'une inefficacité dans la transformation de ses ressources. En d'autres termes, plus la part de l'excédent de trésorerie dans les actifs d'une banque augmente, moins elle est efficace dans la transformation de ses ressources.

1' Une proportion de fonds propres dans le total des crédits élevée pour une banque semble être également la manifestation d'une inefficacité dans la transformation de ses ressources. Autrement dit, plus la proportion des fonds propres dans le total des crédits augmente, moins la banque est techniquement efficace.

Face à ces résultats, plusieurs axes d'actions sont envisageables pour l'amélioration de l'efficacité des banques dans la transformation de leurs ressources. Nous évoquons ici celles qui nous paraissent les plus importantes.

RECOMMANDATIONS

L'analyse des déterminants de l'efficacité technique pure montre que le risque encouru par les banques est au centre du processus de transformation des ressources bancaires en crédits. La crainte de ne pas pouvoir récupérer leurs créances serait le principal facteur qui justifie le comportement frileux des banques. Fort de ce constat, nous suggérons quelques mesures d'incitations à mettre en oeuvre pour une amélioration des niveaux d'efficacité technique des banques de la sous région à savoir :

v' L'amélioration du cadre juridique

L'amélioration du cadre juridique dans la CEMAC est primordiale pour redynamiser le processus de transformation des ressources bancaires. En effet, le montant élevé des frais de

justice, la lenteur des procédures juridiques de recouvrement des créances, la partialité des décisions de justice qui favorisent certains débiteurs au détriment des banques, l'impunité dont jouissent certains clients influents, la corruption régnant dans le milieu juridique, sont autant de facteurs qui entravent le processus de transformation des ressources bancaires en crédits. Tous ces facteurs susmentionnés font en sorte que les banques soient réticentes à financer l'activité économique bien que disposant suffisamment de ressources.

V' La mise en place d'outils appropriés d'évaluation du risque

Nous suggérons aux banques de mettre en place des outils appropriés pour l'évaluation du risque au lieu de s'abstenir à octroyer des crédits. Les banques devraient en réalité examiner minutieusement les demandes de crédits qu'elles reçoivent afin d'extirper du lot de ces demandes celles présentant moins de risque.

V' Le renforcement des fonds propres dans le total de l'actif des banques

Nous recommandons aux banques de toujours maintenir un niveau de fonds propres considérable dans leurs actifs. Pour ce faire, elles pourraient par exemple faire appel à de nouveaux actionnaires ou augmenter la part des bénéfices non distribués.

V' La création de structures pour l'élaboration de projets d'investissements bancables

L'une des raisons évoquées par la plupart des banques par rapport à leur comportement frileux est l'absence de projets d'investissements bancables et viables. En effet, les banques se plaignent que les projets d'investissements qui leur parviennent de la part des opérateurs économiques ne remplissent pas tous les conditions nécessaires pour être financés. Nous suggérons donc aux Etats de la CEMAC de promouvoir la création de structures pour l'élaboration de projets d'investissements bancables. Ces structures devraient accompagner les investisseurs potentiels dans le processus d'élaboration de leur projet d'investissement de la phase de conception du projet à la recherche des financements.

En définitive, il ressort de cette étude que malgré tout le processus de restructuration mis en oeuvre par les autorités monétaires pour assainir le secteur bancaire dans la sous région, la plupart des banques éprouvent encore des difficultés à transformer leurs ressources en crédits. La production de crédits bancaires dans la sous région reste encore inférieure à ce qui est techniquement possible. La vocation fondamentale des banques étant le financement de l'activité économique à travers des prêts aux agents économiques qui manifestent le besoin, beaucoup d'efforts restent encore à faire dans la sous région.

RÉFÉRENCES BIBLIOGRAPHIQUES

BEAC [2004], Statistiques monétaires des Etats de la CEMAC. Bourbonnais R. [2003], Econométrie, 5^e édition, DUNOD, Paris. Claude J. S. [1994], Les banques, Edition la Découverte, Paris.

COBAC [1994], Rapport d'activité. COBAC [1996], Rapport d'activité. COBAC [1998], Rapport d'activité. COBAC [1999] , Rapport d'activité. COBAC, Rapport d'activité, 2004.

Coelli T. [1996], A guide to DEAP Version 2.1: A Data Envelopment Analysis (computer) Program, CEPA Working Paper 96/08.

Dictionnaire d'économie et des faits économiques et sociaux contemporain [1999], Editions Foucher, Paris.

Ekuh Ngwese R. et Mbaku Mbah D. [2006] , Measuring the efficiency of Cameroon commercial banks - An application of Data Envelopment Analysis , School of Business Economics and Law, Göteborg University, Master Thesis N° 2005: 9.

Guarda P. et Rouabah A. [1999], Efficacité et performance des banques en Europe : une analyse "stochastic frontier" sur des données en panel, WORKING PAPER n°99-5.

Joumady O. [2000], Efficacité et productivité des banques au Maroc durant la période de libéralisation financière : 1990 - 1996, 17èmes journées Internationales d'Economie Monétaire et Bancaire, Lisbonne.

Mathis J. [1992] , Monnaie et banques en Afrique francophone , Edicef, Paris.

Nabil A. et Romain R. [2000], Mesure de l'efficacité technique : Revue de la littérature, CREA.

Patat J. P.[1993], Monnaie, institutions financières et politiques monétaires, Edition Economica. Plihon D. [2000], La monnaie et ses mécanismes, Editions la Découverte & Syros, Paris.

Rouabah A. [2002], Economies d'échelle, économie de diversification et efficacité productive des banques Luxembourgeoises : une analyse comparative des frontières stochastiques sur données en panel, WORKING PAPER n°3 ;

Samer Y. S. and Vacher J. [2007], Banking Sector Integration and Competition in CEMAC , IMF Working Paper, WP/07/3.

Simar L. et Wilson P.W. [2006], Statistical inference in Nonparametric Frontier Models: Recent Developments and perspectives, inter-university Attraction pole, Phase V, N° P5/24.

Villarmois O. [2001], Le concept de performance et sa mesure : un état de l'art, Les cahiers de la Recherche, CLAREE.

Wheelock C. D. et Wilson W. P. [1995], Evaluating the efficiency of commercial banks: does our view of what banks do matter? , Review jult/august.

Sites internet

http// : www.beac.int. http// : www.izf.int.

Mémoires

Pandong Armand [2005], le système bancaire de la CEMAC, mémoire de fin de formation en vue du diplôme d'Ingénieur d'Application de la Statistique, ISSEA.

Macha Kana Doriane [2006], Modélisation de la défaillance du système bancaire de la CEMAC, mémoire de fin de formation en vue du diplôme d'Ingénieur d'Application de la Statistique, ISSEA.

Defo Wafo Sylvain [2006], Efficacité technique de l'activité de production des produits vivriers vendus à Yaoundé et Douala, mémoire de fin de formation en vue du diplôme d'Ingénieur d'Application de la Statistique, ISSEA.

ANNEXES

ANNEXE 1

MATRICE DES SCORES 2001

	Janvier			Février			Mars			Avril			Mai			Juin
	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle
Cam1	0,11	0,872	0,126	0,102	0,814	0,125	0,101	0,912	0,111	0,092	0,825	0,112	0,088	0,786	0,112	0,116	0,847	0,137
Cam2	0,075	0,591	0,126	0,086	0,606	0,142	0,082	0,622	0,131	0,086	0,692	0,124	0,074	0,628	0,117	0,076	0,643	0,118
Cam3	0,16	0,717	0,223	0,163	0,706	0,232	0,201	0,776	0,259	0,172	0,755	0,228	0,206	0,844	0,244	0,247	1	0,247
Cam4	0,1	0,656	0,153	0,135	0,716	0,188	0,097	0,568	0,171	0,132	0,738	0,179	0,139	0,792	0,175	0,126	0,809	0,155
Cam5	0,862	1	0,862	0,781	0,984	0,793	0,895	0,988	0,906	1	1	0,666	0,892	0,96	0,929	1	1	1
Cam6	0,568	1	0,568	0,279	0,344	0,811	0,57	1	0,57	0,625	0,938	0,666	0,332	0,363	0,914	0,585	1	0,585
Cam7	0,811	1	0,811	0,694	1	0,694	0,67	0,792	0,846	0,573	0,816	0,702	0,585	0,703	0,832	0,5	0,564	0,887
Cam8	0,199	0,498	0,399	0,097	0,357	0,273	0,109	0,374	0,292	0,141	0,376	0,373	0,119	0,371	0,32	0,164	0,422	0,389
Caf1	0,738	0,744	0,992	0,683	0,735	0,93	0,799	0,837	0,954	0,796	0,832	0,956	0,813	0,851	0,955	0,754	0,785	0,961
Caf2	0,579	0,58	0,999	0,647	0,655	0,987	0,493	0,496	0,994	0,474	0,481	0,985	0,507	0,524	0,969	0,478	0,495	0,966
Caf3	0,516	0,628	0,822	0,401	0,446	0,9	0,649	0,985	0,659	0,633	0,796	0,795	0,762	0,912	0,835	0,671	1	0,671
Cog8	0,091	0,467	0,194	0,095	0,467	0,203	0,118	0,467	0,252	0,178	0,467	0,38	0,29	0,467	0,62	0,182	0,209	0,871
Gab1	0,603	1	0,603	0,622	1	0,622	0,365	0,916	0,399	0,576	0,978	0,589	0,538	1	0,538	0,517	1	0,517
Gab2	0,455	0,673	0,676	0,451	0,669	0,675	0,458	0,675	0,679	0,499	0,792	0,63	0,392	0,691	0,567	0,379	0,724	0,524
Gab3	0,616	1	0,616	0,677	1	0,677	0,658	1	0,658	0,536	0,999	0,536	0,459	0,997	0,461	0,402	0,946	0,425
Gab4	0,784	0,826	0,949	1	1	1	1	1	1	1	1	1	1	1	1	0,914	1	0,914
Gab5	0,143	0,483	0,297	0,262	0,501	0,524	0,225	0,485	0,463	0,274	0,576	0,476	0,274	0,576	0,476	0,311	0,629	0,494
Gnq1	1	1	1	0,936	0,936	1	1	1	1	0,708	0,955	0,741	0,874	1	0,874	0,724	0,872	0,83
Gnq2	0,114	0,118	0,965	0,07	0,082	0,845	0,071	0,096	0,744	0,072	0,101	0,718	0,154	0,163	0,943	0,08	0,099	0,802
Tcd1	0,331	0,497	0,666	0,307	0,503	0,61	0,053	0,065	0,821	0,337	0,525	0,641	0,438	0,542	0,807	0,534	0,658	0,812
Tcd2	0,507	0,645	0,786	0,655	0,811	0,808	0,735	0,853	0,861	0,915	0,976	0,938	1	1	1	0,978	1	0,978
Tcd3	0,679	1	0,679	0,831	1	0,831	1	1	1	1	1	1	0,99	1	0,99	0,826	0,873	0,946
Tcd4	0,164	0,193	0,849	0,212	0,212	1	0,164	0,174	0,945	0,138	0,183	0,755	0,131	0,192	0,682	0,14	0,192	0,729
Tcd5	0,382	1	0,382	0,302	0,302	0,999	0,396	0,408	0,97	0,412	0,432	0,953	0,475	0,523	0,907	0,335	0,362	0,926

Mesure de l'efficacité technique des banques commerciales de la CEMAC

MATRICE DES SCORES 2001 (Suite)

	Totale	Juillet Pure	Echelle	Totale	Août Pure	Echelle	Totale	Septembre Pure	Echelle	Totale	Octobre Pure	Echelle	Totale	Novembre Pure	Echelle	Totale	Juin Pure	Echelle
Cam1	0,097	0,74	0,131	0,107	0,848	0,126	0,067	0,578	0,115	0,097	0,824	0,118	0,093	0,933	0,099	0,121	1	0,121
Cam2	0,064	0,568	0,113	0,075	0,688	0,11	0,082	0,735	0,112	0,073	0,625	0,117	0,079	0,676	0,116	0,081	0,688	0,118
Cam3	0,245	0,919	0,267	0,243	0,978	0,249	0,217	0,981	0,222	0,196	0,858	0,229	0,164	0,772	0,213	0,216	0,928	0,233
Cam4	0,119	0,823	0,145	0,103	0,732	0,141	0,112	0,803	0,14	0,085	0,612	0,14	0,114	0,827	0,138	0,193	0,971	0,199
Cam5	0,918	0,957	0,959	0,943	0,964	0,979	0,907	0,943	0,962	0,939	0,961	0,977	0,797	0,847	0,941	1	1	1
Cam6	0,645	0,917	0,703	0,393	0,47	0,834	0,33	0,37	0,892	0,289	0,327	0,882	0,242	0,27	0,897	0,256	0,29	0,881
Cam7	0,416	0,549	0,757	0,551	0,62	0,89	0,601	0,945	0,635	0,56	0,588	0,952	0,56	0,593	0,944	0,984	1	0,984
Cam8	0,167	0,422	0,397	0,139	0,389	0,359	0,19	0,419	0,454	0,208	0,384	0,542	0,15	0,369	0,408	0,354	0,692	0,511
Caf1	0,833	0,857	0,971	1	1	1	1	1	1	1	1	1	0,923	0,93	0,993	0,944	0,951	0,993
Caf2	0,503	0,521	0,965	0,418	0,457	0,914	0,374	0,456	0,821	0,405	0,457	0,886	0,361	0,403	0,896	0,371	0,409	0,907
Caf3	0,693	0,818	0,848	0,653	0,881	0,741	0,687	0,939	0,732	0,612	0,735	0,833	0,817	1	0,817	0,896	1	0,896
Cog8	0,208	0,212	0,981	0,222	0,308	0,719	0,491	0,767	0,64	0,482	1	0,482	0,246	0,259	0,951	0,209	0,225	0,927
Gab1	0,432	0,98	0,441	0,446	1	0,446	0,479	1	0,479	0,464	1	0,464	0,452	0,993	0,455	0,56	1	0,56
Gab2	0,405	0,763	0,531	0,511	0,883	0,578	0,616	0,991	0,622	0,634	1	0,634	0,527	0,889	0,593	0,765	0,984	0,778
Gab3	0,428	0,977	0,438	0,447	1	0,447	0,461	0,971	0,475	0,493	0,971	0,508	0,527	1	0,527	0,525	1	0,525
Gab4	0,959	0,976	0,982	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
Gab5	0,343	0,621	0,552	0,559	0,637	0,877	0,326	0,719	0,453	0,269	0,534	0,503	0,3	0,599	0,501	0,233	0,521	0,446
Gnq1	0,657	0,829	0,793	0,595	0,761	0,783	0,778	0,887	0,878	0,831	0,935	0,888	0,845	1	0,845	0,988	1	0,988
Gnq2	0,055	0,11	0,5	0,182	0,2	0,912	0,235	0,263	0,893	0,236	0,265	0,888	0,064	0,157	0,408	0,067	0,167	0,4
Tcd1	0,553	0,768	0,72	0,727	0,961	0,756	0,302	0,449	0,674	0,544	0,814	0,668	0,764	1	0,764	0,203	0,367	0,552
Tcd2	0,791	0,896	0,883	0,684	0,787	0,87	0,311	0,479	0,65	0,309	0,445	0,695	0,268	0,37	0,725	0,235	0,408	0,575
Tcd3	0,58	0,639	0,908	0,441	0,49	0,9	0,419	0,422	0,994	0,363	0,395	0,918	0,372	0,372	1	0,442	0,465	0,949
Tcd4	0,109	0,159	0,687	0,112	0,131	0,852	0,095	0,118	0,801	0,186	0,19	0,979	0,229	0,233	0,979	0,289	0,289	1
Tcd5	0,402	0,668	0,602	0,441	0,492	0,895	0,494	0,567	0,872	0,206	0,206	1	0,281	0,283	0,993	0,266	0,281	0,947

Mesure de l'efficacité technique des banques commerciales de la CEMAC

MATRICE DES SCORES 2002

	Janvier			Février			Mars			Avril			Mai			Juin
	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle
Cam1	0,22	0,971	0,23	0,185	0,898	0,206	0,182	0,85	0,214	0,008	0,042	0,19	0,152	0,863	0,177	0,152	0,871	0,174
Cam2	0,12	0,675	0,181	0,139	0,652	0,214	0,143	0,708	0,201	0,124	0,577	0,215	0,137	0,753	0,182	0,133	0,746	0,178
Cam3	0,21	0,763	0,27	0,199	0,743	0,268	0,21	0,759	0,277	0	0,002	0,185	0,211	0,866	0,244	0,185	0,88	0,211
Cam4	0	0	0,223	0,225	0,686	0,327	0,332	0,857	0,387	0	0	0,29	0,321	0,942	0,34	0,402	1	0,402
Cam5	0,48	0,764	0,623	0,506	0,747	0,678	0,504	0,759	0,665	0,468	0,683	0,686	0,478	0,751	0,636	0,501	0,749	0,67
Cam6	0,23	0,33	0,694	0,337	1	0,337	0,265	0,405	0,655	0,24	0,396	0,606	0,289	0,508	0,569	0,339	0,491	0,691
Cam7	0,37	0,577	0,639	0,623	0,891	0,699	1	1	1	0,24	0,396	0,606	0,854	0,891	0,959	0,746	0,796	0,937
Cam8	0,2	0,673	0,293	0,198	0,625	0,316	0,226	0,615	0,368	0,246	0,799	0,308	0,233	0,719	0,324	0,322	0,906	0,356
Caf1	0,21	0,424	0,5	0,715	1	0,715	0,333	0,455	0,731	0,407	0,421	0,967	0,445	0,471	0,945	0,457	0,489	0,933
Caf2	0,28	0,419	0,668	0,268	0,409	0,655	0,234	0,43	0,543	0,189	0,358	0,528	0,232	0,445	0,522	0,265	0,424	0,626
Caf3	0,36	1	0,359	0,332	0,467	0,71	0,32	0,366	0,873	0,016	0,018	0,842	0,716	1	0,716	0,355	0,368	0,962
Cog8	0,11	0,115	0,995	0,095	0,157	0,604	0,089	0,123	0,726	0,016	0,018	0,842	0,065	0,066	0,99	0,042	0,044	0,97
Gab1	0,2	0,953	0,209	0,176	0,953	0,185	0,254	0,993	0,255	0,228	0,968	0,235	0,221	1	0,221	0,262	1	0,262
Gab2	0,44	1	0,442	0,384	0,944	0,407	0,426	0,995	0,428	0,089	0,329	0,27	0,381	0,976	0,391	0,403	1	0,403
Gab3	0,2	0,934	0,218	0,209	0,939	0,223	0,231	0,926	0,249	0,225	0,902	0,249	0,179	0,863	0,207	0,224	1	0,224
Gab4	0,96	1	0,963	0,935	0,987	0,947	0,891	0,935	0,953	0,88	0,915	0,962	0,831	0,941	0,883	0,827	0,966	0,856
Gab5	0,36	0,523	0,683	0,359	0,55	0,653	0,211	0,503	0,42	0,451	0,867	0,52	0,509	0,906	0,562	0,79	1	0,79
Gnq1	1	1	1	1	1	1	1	1	1	0,958	0,973	0,984	0,82	1	0,82	0,817	1	0,817
Gnq2	0,08	0,194	0,427	0,083	0,189	0,439	0,041	0,149	0,276	0,039	0,144	0,27	0,051	0,158	0,321	0,038	0,159	0,239
Tcd1	0,4	0,732	0,543	0,395	0,728	0,542	0,433	0,851	0,509	0,034	0,042	0,822	0,416	0,758	0,548	0,419	0,757	0,554
Tcd2	0,39	0,846	0,462	0,402	0,863	0,466	0,496	1	0,496	0,496	0,993	0,5	0,444	0,937	0,474	0,462	0,944	0,49
Tcd3	0,97	1	0,972	0,643	0,755	0,851	0,05	0,086	0,578	0,038	0,056	0,685	0,916	0,963	0,951	1	1	1
Tcd4	0,45	0,629	0,721	0,508	0,642	0,792	0,701	0,85	0,825	0,139	1	0,139	1	1	1	0,796	0,895	0,89
Tcd5	0,28	0,308	0,918	0,367	0,413	0,887	0,312	0,335	0,93	0,139	1	0,139	0,302	0,303	0,996	0,237	0,251	0,946

Mesure de l'efficacité technique des banques commerciales de la CEMAC

MATRICE DES SCORES 2002 (Suite)

Juillet			Août			Septembre			Octobre			Novembre			Décembre
Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle
0,168	0,88	0,191	0,138	0,816	0,169	0,202	1	0,202	0,218	1	0,218	0,194	0,953	0,204	0,209	0,997	0,21
0,202	0,904	0,224	0,198	0,901	0,22	0,159	0,833	0,191	0,194	0,902	0,215	0,218	0,939	0,232	0,2	0,931	0,215
0,204	0,911	0,223	0,173	0,847	0,204	0,197	0,925	0,213	0,183	0,924	0,198	0,195	0,916	0,213	0,228	1	0,228
0,342	0,929	0,368	0,331	0,896	0,37	0,41	0,921	0,445	0,513	1	0,513	0,437	0,96	0,456	0,353	0,96	0,367
0,535	0,79	0,677	0,554	0,783	0,708	0,457	0,732	0,625	0,419	0,738	0,567	0,446	0,772	0,577	0,579	0,821	0,705
0,534	0,75	0,713	0,461	0,554	0,832	0,359	0,384	0,934	0,296	0,316	0,936	0,265	0,28	0,948	0,299	0,324	0,922
0,533	0,569	0,935	0,554	0,608	0,911	0,401	0,683	0,587	0,53	0,911	0,582	0,754	1	0,754	0,902	1	0,902
0,332	0,896	0,371	0,282	0,791	0,357	0,278	0,742	0,374	0,271	0,706	0,384	0,263	0,646	0,407	0,312	0,749	0,416
0,325	0,484	0,672	0,474	0,558	0,85	0,429	0,489	0,876	0,458	0,5	0,916	0,552	0,558	0,988	0,378	0,467	0,81
0,185	0,403	0,46	0,188	0,397	0,473	0,162	0,355	0,455	0,172	0,361	0,477	0,199	0,416	0,479	0,293	0,549	0,534
0,367	0,374	0,983	0,411	0,431	0,954	0,415	0,741	0,56	0,653	0,984	0,664	0,579	0,802	0,722	0,644	1	0,644
0,037	0,043	0,86	0,083	0,176	0,474	0,054	0,137	0,398	0,054	0,128	0,421	0,071	0,269	0,265	0,422	1	0,422
0,246	1	0,246	0,245	1	0,245	0,277	1	0,277	0,253	1	0,253	0,259	1	0,259	0,277	1	0,277
0,364	0,98	0,371	0,32	0,923	0,346	0,396	1	0,396	0,359	0,944	0,38	0,393	1	0,393	0,333	0,982	0,339
0,246	1	0,246	0,231	0,995	0,233	0,272	1	0,272	0,244	1	0,244	0,223	1	0,223	0,217	1	0,217
1	1	1	0,989	1	0,989	1	1	1	1	1	1	1	1	1	1	1	1
0,789	0,997	0,791	0,795	1	0,795	0,764	1	0,764	0,736	0,959	0,767	0,753	0,992	0,759	0,933	1	0,933
0,861	1	0,861	0,856	1	0,856	1	1	1	0,182	0,209	0,87	0,373	0,424	0,88	0,398	0,445	0,893
0,04	0,167	0,237	0,058	0,335	0,172	0,039	0,187	0,21	0,043	0,209	0,206	0,045	0,184	0,246	0,053	0,3	0,176
0,443	0,786	0,564	0,4	0,718	0,558	0,355	0,639	0,556	0,299	0,55	0,543	0,24	0,453	0,528	0,187	0,365	0,513
0,414	0,853	0,485	0,428	0,86	0,498	0,634	1	0,634	0,437	0,737	0,593	0,407	0,67	0,608	0,7	0,876	0,8
0,76	0,892	0,852	0,656	0,772	0,85	0,554	0,671	0,825	0,656	0,759	0,864	0,565	0,672	0,841	0,579	0,615	0,941
0,531	0,761	0,698	0,454	0,664	0,684	0,538	0,66	0,815	0,552	0,625	0,883	0,554	0,622	0,89	0,705	0,75	0,939
0,286	0,289	0,988	0,29	0,291	0,994	0,413	0,429	0,962	0,426	0,436	0,978	0,314	0,344	0,911	0,344	0,345	0,998

Mesure de l'efficacité technique des banques commerciales de la CEMAC

MATRICE DES SCORES 2003

	Janvier			Février			Mars			Avril			Mai			Juin
	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle
Cam!	0,111	0,826	0,134	0,08	0,708	0,113	0,089	0,743	0,12	0,084	0,715	0,118	0,091	0,793	0,115	0,121	0,777	0,155
Cam2	0,086	0,629	0,137	0,109	0,738	0,148	0,192	1	0,192	0,155	0,836	0,185	0,093	0,684	0,136	0,177	0,916	0,194
Cam3	0,215	0,778	0,277	0,215	0,728	0,295	0,228	0,713	0,319	0,232	0,786	0,295	0,217	0,847	0,256	0,297	0,865	0,343
Cam4	0,21	1	0,21	0,221	1	0,221	0,2	1	0,2	0,195	0,982	0,199	0,221	0,949	0,233	0,219	0,948	0,231
Cam5	0,35	0,814	0,43	0,26	0,763	0,341	0,259	0,72	0,36	0,281	0,734	0,382	0,311	0,748	0,416	0,25	0,769	0,325
Cam6	0,167	0,245	0,682	0,271	0,276	0,98	0,157	0,238	0,659	0,157	0,236	0,664	0,234	0,24	0,977	0,142	0,178	0,795
Cam7	0,37	0,976	0,379	0,35	0,941	0,372	0,396	1	0,396	0,403	0,953	0,423	0,227	0,62	0,366	0,173	0,58	0,298
Cam8	0,225	0,691	0,326	0,219	0,659	0,332	0,237	0,656	0,361	0,263	0,697	0,377	0,23	0,614	0,375	0,283	0,684	0,414
Caf!	0,301	0,428	0,702	0,213	0,356	0,598	0,201	0,326	0,617	0,225	0,282	0,797	0,17	0,297	0,573	0,212	0,365	0,582
Caf2	0,219	0,556	0,395	0,214	0,554	0,385	0,217	0,535	0,406	0,141	0,414	0,341	0,142	0,455	0,312	0,143	0,458	0,311
Caf3	0,496	0,868	0,571	0,501	1	0,501	0,367	0,507	0,723	0,276	0,301	0,918	0,203	0,267	0,761	0,209	0,288	0,726
Cog8	0,215	1	0,215	0,033	0,199	0,168	0,008	0,072	0,117	0,005	0,067	0,067	0,005	0,068	0,079	0,007	0,072	0,092
Gab!	0,316	1	0,316	0,259	1	0,259	0,248	0,99	0,25	0,268	1	0,268	0,237	0,986	0,24	0,318	1	0,318
Gab2	0,275	0,94	0,292	0,232	0,929	0,249	0,193	0,878	0,22	0,229	0,924	0,248	0,232	0,882	0,263	0,289	1	0,289
Gab3	0,19	1	0,19	0,16	0,979	0,163	0,126	0,958	0,132	0,179	1	0,179	0,213	1	0,213	0,179	1	0,179
Gab4	0,854	1	0,854	0,862	0,999	0,863	1	1	1	1	1	1	0,77	0,987	0,78	0,886	1	0,886
Gab5	0,117	0,848	0,138	0,126	0,728	0,172	0,166	0,853	0,195	0,143	0,55	0,26	0,133	0,461	0,289	0,43	1	0,43
Gnq!	0,053	0,103	0,517	0,059	0,113	0,523	0,059	0,11	0,534	1	1	1	0,061	0,302	0,204	0,132	0,645	0,205
Gnq2	0,03	0,18	0,169	0,035	0,212	0,167	0,034	0,299	0,115	0,034	0,311	0,108	0,028	0,258	0,109	0,031	0,328	0,094
Tcd!	0,137	0,425	0,322	0,175	0,527	0,332	0,166	0,526	0,316	0,185	0,582	0,317	0,174	0,54	0,323	0,186	0,573	0,325
Tcd2	0,268	0,747	0,359	0,298	0,841	0,355	0,35	0,948	0,37	0,318	0,854	0,373	0,323	0,843	0,383	0,438	0,96	0,456
Tcd3	0,181	0,491	0,369	0,349	0,76	0,46	0,389	0,847	0,459	0,375	0,856	0,438	0,326	0,751	0,434	0,382	0,87	0,439
Tcd4	0,255	0,514	0,496	0,361	0,703	0,513	0,227	0,639	0,355	0,245	0,657	0,373	0,225	0,638	0,353	0,261	0,732	0,357
Tcd5	0,217	0,368	0,591	0,201	0,333	0,603	0,198	0,3	0,66	0,241	0,307	0,784	0,231	0,298	0,776	0,239	0,281	0,851

Mesure de l'efficacité technique des banques commerciales de la CEMAC

MATRICE DES SCORES 2003 (Suite)

Juillet			Août			Septembre			Octobre			Novembre			Décembre
Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle
0,095	0,939	0,101	0,145	0,952	0,153	0,002	0,021	0,072	0,132	0,984	0,134	0,136	1	0,136	0,17	1	0,17
0,102	0,731	0,139	0,142	0,898	0,158	0,244	1	0,244	0,117	0,895	0,131	0,093	1	0,093	0,115	0,824	0,14
0,322	0,954	0,337	0,309	0,919	0,336	1	1	1	0,318	0,889	0,357	0,364	1	0,364	0,368	1	0,368
0,182	0,924	0,197	0,217	0,975	0,223	0	0	0,132	0,24	1	0,24	0,251	1	0,251	0,203	0,905	0,224
0,336	0,776	0,433	0,407	0,81	0,502	0,258	0,681	0,378	0,367	0,896	0,409	0,505	1	0,505	0,607	1	0,607
0,298	0,322	0,925	0,233	0,33	0,706	0,007	0,011	0,69	0,235	0,305	0,771	0,217	0,309	0,702	0,287	0,326	0,88
0,312	0,845	0,369	0,312	0,845	0,369	0	0	0,205	0,183	0,556	0,33	0,312	0,845	0,369	0,312	0,845	0,369
0,31	0,675	0,459	0,278	0,707	0,393	0,295	0,696	0,424	0,001	0,006	0,24	0,363	0,789	0,461	0,642	1	0,642
0,268	0,397	0,675	0,238	0,361	0,66	0,213	0,36	0,591	0,204	0,344	0,594	0,2	0,34	0,588	0,233	0,376	0,618
0,147	0,456	0,323	0,133	0,444	0,299	0,146	0,417	0,35	0,16	0,448	0,358	0,173	0,501		0,177	0,488	0,362
0,183	0,286	0,637	0,207	0,292	0,707	0,409	0,672	0,608	0,435	0,675	0,644	0,508	0,703	0,723	0,282	0,339	0,832
0,009	0,068	0,133	0,01	0,092	0,104	0,016	0,097	0,161	0,02	0,11	0,184	0,026	0,123	0,211	0,116	0,612	0,189
0,319	0,991	0,322	0,377	1	0,377	0,171	0,803	0,213	0,36	1	0,36	0,298	0,973	0,306	0,355	1	0,355
0,203	0,858	0,236	0,262	0,958	0,274	0,091	0,442	0,206	0,079	0,393	0,201	0,256	0,928	0,275	0,23	0,928	0,248
0,163	0,989	0,164	0,193	1	0,193	0,17	1	0,17	0,176	0,956	0,184	0,193	1	0,193	0,167	0,929	0,18
1	1	1	1	1	1	1	1	1	1	1	1	0,866	1	0,866	1	1	1
0,192	0,775	0,248	0,367	1	0,367	0,106	0,544	0,195	0,577	1	0,577	0,203	0,868	0,234	0,174	0,786	0,221
0,128	0,321	0,4	0,162	0,382	0,425	0,008	0,057	0,137	0,041	0,145	0,282	0,026	0,156	0,165	0,029	0,143	0,2
0,038	0,349	0,109	0,03	0,32	0,094	0,027	0,213	0,126	0,018	0,24	0,075	0,023	0,206	0,111	0,023	0,215	0,107
0,19	0,566	0,335	0,202	0,618	0,326	0,046	0,215	0,213	0,298	0,785	0,379	0,258	0,737	0,351	0,214	0,62	0,345
0,453	0,933	0,485	0,444	0,951	0,467	0,033	0,136	0,245	0,298	0,785	0,379	0,308	0,759	0,406	0,256	0,602	0,425
0,436	1	0,436	0,436	1	0,436	0,068	0,257	0,263	0,402	1	0,402	0,331	0,964	0,343	0,344	0,966	0,356
1	1	1	0,104	0,484	0,214	0,515	1	0,515	0,989	0,989	1	1	1	1	0,973	1	0,973
0,199	0,282	0,705	0,2	0,28	0,715	0,018	0,039	0,459	0,168	0,287	0,585	0,171	0,3	0,571	0,152	0,262	0,579

Mesure de l'efficacité technique des banques commerciales de la CEMAC

MATRICE DES SCORES 2004

	Janvier			Février			Mars			Avril			Mai			Juin
	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle
Cam1	0,208	0,873	0,239	0,202	0,866	0,233	0,158	0,862	0,183	0,22	0,875	0,251	0,184	0,855	0,215	0,16	0,874	0,183
Cam2	0,113	0,545	0,206	0,124	0,528	0,235	0,155	0,561	0,276	0,146	0,556	0,263	0,146	0,571	0,255	0,128	0,557	0,229
Cam3	0,564	0,963	0,586	0,461	0,851	0,542	0,445	0,847	0,526	0,525	0,965	0,544	0,491	0,948	0,518	0,484	0,964	0,502
Cam4	0,241	0,921	0,261	0,278	1	0,278	0,275	1	0,275	0,233	0,907	0,257	0,233	0,894	0,26	0,223	0,869	0,257
Cam5	0,559	0,981	0,57	0,535	0,981	0,545	0,413	0,937	0,441	0,513	0,97	0,529	0,648	0,96	0,675	0,637	0,867	0,734
Cam6	0,385	0,389	0,989	0,439	0,442	0,994	0,414	0,431	0,962	0,565	0,643	0,88	0,339	0,364	0,931	0,414	0,423	0,98
Cam7	0,984	1	0,984	1	1	1	0,995	1	0,995	0,454	0,742	0,611	0,983	1	0,983	1	1	1
Cam8	0,33	0,818	0,404	0,378	0,828	0,457	0,385	0,79	0,487	0,441	0,875	0,504	0,441	0,847	0,521	0,444	0,84	0,528
Caf1	0,322	0,478	0,674	0,236	0,379	0,621	0,292	0,418	0,698	0,261	0,36	0,725	0,277	0,369	0,75	0,404	0,515	0,784
Caf2	0,318	0,613	0,518	0,308	0,559	0,55	0,288	0,536	0,538	0,249	0,486	0,511	0,237	0,466	0,508	0,273	0,511	0,535
Caf3	0,676	1	0,676	0,515	1	0,515	0,382	0,422	0,906	0,279	0,341	0,819	0,247	0,308	0,804	0,425	0,527	0,807
Cog8	0,039	0,121	0,322	0,119	0,426	0,279	0,053	0,191	0,278	0,034	0,111	0,306	0,061	0,185	0,329	0,02	0,089	0,226
Gab1	0,252	1	0,252	0,221	1	0,221	0,256	0,968	0,265	0,211	0,951	0,222	0,363	1	0,363	0,374	1	0,374
Gab2	0,189	0,822	0,229	0,222	0,875	0,253	0,219	0,887	0,247	0,175	0,788	0,222	0,182	0,779	0,234	0,18	0,814	0,222
Gab3	0,222	0,898	0,247	0,159	0,835	0,19	0,179	0,821	0,217	0,178	0,905	0,197	0,367	1	0,367	0,142	0,736	0,193
Gab4	1	1	1	1	1	1	1	1	1	0,963	0,992	0,971	0,837	0,978	0,856	0,95	0,977	0,972
Gab5	0,17	0,564	0,302	0,629	0,85	0,74	0,244	0,672	0,363	0,276	0,741	0,373	0,314	0,783	0,401	0,267	0,755	0,354
Gnq1	0,043	0,153	0,279	0,636	1	0,636	0,339	0,565	0,6	0,455	0,627	0,726	0,497	0,674	0,738	0,658	0,795	0,828
Gnq2	0,034	0,192	0,176	0,044	0,213	0,207	0,058	0,219	0,263	0,056	0,218	0,258	0,134	0,58	0,232	0,178	0,341	0,523
Tcd1	0,381	0,746	0,51	0,42	0,795	0,528	0,441	0,834	0,529	0,437	0,825	0,53	0,397	0,769	0,516	0,396	0,747	0,53
Tcd2	0,465	0,891	0,522	0,505	1	0,505	0,481	0,959	0,502	0,404	0,809	0,499	0,429	0,851	0,504	0,428	0,87	0,492
Tcd3	0,17	0,383	0,443	0,54	1	0,54	0,562	0,954	0,589	0,498	0,908	0,549	0,387	0,741	0,522	0,486	1	0,486
Tcd4	0,72	0,902	0,798	0,427	0,809	0,527	0,459	0,849	0,541	0,409	0,814	0,502	1	1	1	0,494	0,763	0,647
Tcd5	0,223	0,268	0,831	0,23	0,267	0,861	0,186	0,232	0,8	0,171	0,225	0,762	0,161	0,211	0,763	0,156	0,219	0,716

Mesure de l'efficacité technique des banques commerciales de la CEMAC

MATRICE DES
SCORES 2004
(Suite)

Juillet			Août			Septembre			Octobre			Novembre			Décembre
Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle	Totale	Pure	Echelle
0,171	0,875	0,196	0,175	0,846	0,207	0,181	0,879	0,205	0,177	0,849	0,208	0,142	0,827	0,172	0,17	0,88	0,194
0,166	0,634	0,262	0,194	0,735	0,264	0,151	0,607	0,249	0,189	0,712	0,265	0,147	1	0,147	0,21	1	0,213
0,461	0,963	0,479	0,426	0,987	0,431	0,542	0,999	0,542	0,663	1	0,663	0,396	1	0,396	0,43	1	0,427
0,237	0,931	0,254	0,199	0,785	0,253	0,227	0,824	0,275	0,219	0,878	0,249	0,189	0,788	0,239	0,22	0,9	0,238
0,781	1	0,781	0,66	0,863	0,765	0,513	0,933	0,55	0,625	1	0,625	0,898	1	0,898	0,8	0,98	0,808
0,499	0,607	0,822	0,66	1	0,66	0,494	1	0,494	0,255	0,257	0,99	0,27	0,271	0,998	0,19	0,2	0,947
1	1	1	1	1	1	0,797	0,969	0,823	1	1	1	0,982	1	0,982	1	1	1
0,389	0,852	0,457	0,376	0,851	0,442	0,405	0,786	0,515	0,378	0,822	0,46	0,415	0,768	0,541	0,42	0,84	0,504
0,271	0,4	0,678	0,28	0,399	0,703	0,36	0,502	0,717	0,334	0,46	0,728	0,393	0,516	0,761	0,44	0,51	0,858
0,238	0,452	0,526	0,269	0,489	0,55	0,244	0,516	0,472	0,294	0,551	0,534	0,305	0,621	0,491	0,4	0,69	0,588
0,476	0,492	0,968	0,44	0,453	0,972	0,5	0,5	0,999	0,433	0,434	0,998	0,712	1	0,712	0,69	0,69	0,997
0,091	0,201	0,455	0,052	0,16	0,327	0,037	0,096	0,383	0,072	0,175	0,414	0,036	0,095	0,381	0,51	1	0,513
0,319	0,914	0,349	0,344	0,926	0,371	0,308	0,869	0,354	0,323	0,891	0,363	0,314	0,905	0,346	0,29	1	0,288
0,144	0,772	0,187	0,162	0,762	0,212	0,227	0,939	0,242	0,203	0,878	0,231	0,177	0,815	0,217	0,2	0,84	0,241
0,172	0,907	0,19	0,159	0,798	0,199	0,133	0,896	0,149	0,138	0,915	0,151	0,129	0,901	0,143	0,1	0,94	0,106
1	1	1	0,916	0,967	0,947	0,744	0,955	0,779	0,959	0,968	0,991	0,779	0,944	0,825	0,92	0,95	0,972
0,278	0,715	0,389	0,304	0,734	0,414	0,288	0,72	0,4	0,4	0,736	0,543	0,158	0,498	0,318	0,21	0,57	0,361
0,469	0,685	0,684	0,444	0,554	0,801	0,952	1	0,952	1	1	1	0,666	1	0,666	0,8	1	0,795
0,15	0,462	0,326	0,168	0,353	0,476	0,171	0,365	0,467	0,181	0,484	0,374	0,179	0,379	0,471	0,23	0,72	0,324
0,362	0,679	0,533	0,295	0,593	0,498	0,323	0,633	0,51	0,317	0,624	0,507	0,316	0,65	0,486	0,29	0,61	0,484
0,333	0,72	0,462	0,318	0,733	0,434	0,269	0,657	0,409	0,347	0,862	0,402	0,319	0,794	0,402	0,35	0,82	0,428
0,437	0,909	0,481	0,345	0,758	0,455	0,422	0,889	0,475	0,354	0,806	0,439	0,327	0,767	0,426	0,44	1	0,443
1	1	1	0,543	0,657	0,826	0,295	0,559	0,528	0,965	1	0,965	0,335	0,549	0,61	0,88	0,96	0,911
0,154	0,203	0,757	0,154	0,221	0,698	0,148	0,213	0,694	0,111	0,165	0,669	0,127	0,191	0,664	0,13	0,18	0,706

ANNEXE 1I

		Coordonnées des variables actives				Corrélations des variables actives avec les facteurs						Coordonnées des variables actives				Corrélations des variables actives avec les facteurs
Libellé de la variable		Axe 1		Axe 2		Axe 1		Axe 2		Libellé de la variable		Axe 1		Axe 2		Axe 1	Axe 2
janv-01		0,42		-0,66		0,42		-0,66		janv-03		0,58		0,09		0,58	0,09
févr-01		0,75		-0,43		0,75		-0,43		févr-03		0,81		0,21		0,81	0,21
mars-01		0,53		-0,67		0,53		-0,67		mars-03		0,83		0,34		0,83	0,34
avr-01		0,66		-0,65		0,66		-0,65		avr-03		0,89		0,10		0,89	0,10
mai-01		0,69		-0,59		0,69		-0,59		mai-03		0,89		0,24		0,89	0,24
juin-01		0,69		-0,58		0,69		-0,58		juin-03		0,88		0,27		0,88	0,27
juil-01		0,62		-0,65		0,62		-0,65		juil-03		0,86		0,41		0,86	0,41
août-01		0,67		-0,58		0,67		-0,58		août-03		0,89		0,23		0,89	0,23
01-sept		0,50		-0,61		0,50		-0,61		03-sept		0,43		0,25		0,43	0,25
01-oct		0,44		-0,58		0,44		-0,58		03-oct		0,70		0,24		0,70	0,24
01-nov		0,64		-0,52		0,64		-0,52		03-nov		0,85		0,39		0,85	0,39
déc-01		0,74		-0,43		0,74		-0,43		déc-03		0,74		0,46		0,74	0,46
janv-02		0,68		-0,21		0,68		-0,21		janv-04		0,77		0,19		0,77	0,19
févr-02		0,70		-0,38		0,70		-0,38		févr-04		0,85		0,01		0,85	0,01
mars-02		0,76		0,01		0,76		0,01		mars-04		0,90		0,25		0,90	0,25
avr-02		0,21		0,06		0,21		0,06		avr-04		0,89		0,22		0,89	0,22
mai-02		0,87		0,06		0,87		0,06		mai-04		0,83		0,39		0,83	0,39
juin-02		0,89		0,17		0,89		0,17		juin-04		0,91		0,15		0,91	0,15
juil-02		0,85		0,07		0,85		0,07		juil-04		0,87		0,31		0,87	0,31
août-02		0,88		0,02		0,88		0,02		août-04		0,80		0,12		0,80	0,12
02-sept		0,90		-0,04		0,90		-0,04		04-sept		0,80		-0,14		0,80	-0,14
02-oct		0,84		0,13		0,84		0,13		04-oct		0,86		0,25		0,86	0,25
02-nov		0,88		0,08		0,88		0,08		04-nov		0,83		-0,13		0,83	-0,13
déc-02		0,65		0,13		0,65		0,13		déc-04		0,57		0,22		0,57	0,22
			Coordonnées des individus actifs				Contributions des individus actifs				Cosinus carrés des individus actifs
Identificateur	Distance à l'origine		Axe 1		Axe 2		Axe 1		Axe 2		Axe 1		Axe 2
Caf1	43,86		-4,16		-4,47		2,61		14,01		0,40		0,45
Caf2	32,27		-5,36		0,62		4,32		0,27		0,89		0,01
Caf3	45,14		-1,61		-3,10		0,39		6,73		0,06		0,21
Cam1	22,31		3,82		-0,25		2,19		0,04		0,65		0,00
Cam2	14,72		0,96		1,25		0,14		1,09		0,06		0,11
Cam3	29,04		4,59		0,13		3,17		0,01		0,73		0,00
Cam4	32,63		3,97		1,48		2,37		1,54		0,48		0,07
Cam5	26,44		4,23		-1,42		2,69		1,41		0,68		0,08
Cam6	73,87		-5,83		-2,48		5,11		4,33		0,46		0,08
Cam7	30,18		3,45		0,56		1,79		0,22		0,39		0,01
Cam8	21,99		-0,47		3,47		0,03		8,45		0,01		0,55
Cog8	153,24		-11,11		-0,74		18,57		0,38		0,81		0,00
Gab1	50,23		6,81		-0,88		6,98		0,54		0,92		0,02
Gab2	25,04		4,13		-0,09		2,56		0,01		0,68		0,00
Gab3	44,15		6,11		-1,10		5,61		0,85		0,84		0,03
Gab4	52,95		7,02		-0,72		7,40		0,37		0,93		0,01
Gab5	18,86		0,97		2,19		0,14		3,36		0,05		0,25
Gnq1	61,79		0,08		-4,74		0,00		15,80		0,00		0,36
Gnq2	134,17		-10,91		2,98		17,89		6,25		0,89		0,07
Tcd1	20,73		-1,45		0,49		0,32		0,17		0,10		0,01
Tcd2	23,45		2,96		0,41		1,31		0,12		0,37		0,01
Tcd3	32,81		2,36		0,68		0,84		0,32		0,17		0,01
Tcd4	57,91		-1,10		6,84		0,18		32,86		0,02		0,81
Tcd5	104,22		-9,43		-1,11		13,38		0,87		0,85		0,01

ANNEXE III

Series: Standardized Residuals Sample 2001M01 2004M12 Observations 1152

Mean		4.88e-13
Median		-0.000988
Maximum		0.295968
Minimum		-0.317852
Std. Dev.		0.076611
Skewness		0.072037
Kurtosis		2.987871
Jarque-Bera		0.979022
Probability		0.612926
140 120 100 80 60 40 20 0

-0.250 -0.125 -0.000 0.125 0.250