3-4-2-3 Relation entre déformation et
déplacement
La déformation est déduite des expressions
(3.8) et (3.13). Soit :
E=
du dx=
11[-1 1]C9A~
9A~D = B Ue (3-17)
La matrice B reliant les déformations de
l'élément à ses déplacements nodaux est
alors
 = 11[ 1 1]
(3-18)
3-4-2-4 Matrice de rigidité d'une barre dans le
plan
La forme de la matrice de rigidité 2
e de l'élément dans le
repère local est donnée par l'expression (3.5). La matrice
d'élasticité D se réduit au scalaire E (module de Young du
matériau). Soit, après intégration :
|
Ke = A*E
1
|
[1I~
I ~ J (3-19)
|
3-4-2-5 Matrice de masse d'une barre dans le plan
La matrice de masse Me dans le repère
local est déterminée à partir de l'expression (2.6). Soit,
après intégration :
Me =
p*A*1 [2 11 (3-2 )
6 2
L'expression de la matrice masse telle qu'elle est
obtenue en (3.20) est appelée masse cohérente ou répartie.
Il est possible de concentrer la masse de l'élément en ses
extrémités. On attribue à chacun des deux noeuds la
moitié de la masse totale de l'élément soit :
Me
KF#FB
~ H
= J ~~~~~~
3-4-2-6 Transformation dans le repère
global
Soit uxi , uyi , uxj et uyj les déplacements
aux noeuds i et j
exprimés dans le repère global (figure 3.5). La
relation entre les déplacements exprimés dans le repère
local et ceux exprimés dans le repère global est donnée
par :
1xi =uxi cx+ uyi
cy (3-22)
1xj =uxj cx+ uyj
cy
Oil cx et cy sont les cosinus directeurs définis
par :
~ ~
cx= B (xj-xi) et cy=
B (yj-yi) ~~~~~~
Avec l la longueur de l'élément
calculée à partir des coordonnées des noeuds. Soit
:
l=*(xj -- x02 + (yj -- yi)2 (3-24)
Sous forme matricielle, on écrit :
9A
C9A~
u31
La matrice transformation du repère local au
repère global est :
9A~D =CRA R& 9&
RA R&D S 9A T ~~~~~~
T = rcx cy 001
0 0 cx cy (3-26)
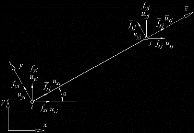
Figure 3-5 : élément dans le repère
global
La matrice de rigidité exprimée dans le
repère global sera déduite de la matrice de rigidité
exprimée dans le repère local par la relation [2],
[7]:
Ke = Tt
Ke T (3-27)
De même, la matrice de masse de
l'élément barre dans le plan exprimée dans le
repère global est donnée par l'expression.
Me = Tt Me T
(3-28)
3-4-2-7 Charges appliquées sur les
éléments
Dans le cas d'une charge répartie q sur un
élément, celle-ci est rapportée aux noeuds
d'extrémités. Le vecteur de charge nodale correspondant est
:
Fer = f
Nt q ds (3-29)
Pour une charge uniformément répartie sur
un élément poutre dans le plan (figure 3.6), le vecteur de
charges nodales équivalent est :
B
Fer= q f 0 Nt dl
(3-3 0)
Pour une barre de treillis, la notion de charge
répartie transversale n'est pas cohérente avec la théorie,
la modélisation de type barre ne prenant pas en compte la raideur
flexionnelle. La force répartie d'une barre doit être
modélisé par deux forces, concentrées aux noeuds
d'extrémités, statiquement équivalentes au poids total de
la barre (figure 3.6)
Fer = [0
-(121
0 (121] (
3-31)

Figure 3-6 : force répartie sur une barre
Soit un tronçon donné du pylône, le
vent agit uniformément sur toutes les barres du
tronçon.
- qH est la pression statique du vent,
- Sp la surface pleine du tronçon, celle qui est
en contact avec le vent, - Si, la surface totale, les vides
étant obturés
Suivant [5],
el =Sp/Si (3-32)
cI est généralement compris entre 0.08 et
0.35. Pour les constructions prismatiques, le coefficient de trainée est
égal à : [5]
Ct = 3.20 - 2.0 ( 3-33)
L'action d'ensemble T s'exerce sur tous les
éléments du tronçon (figure3-7). Cette action est ensuite
répartie sur les membrures (figure 3.8) et devient T/2.l
où l est la longueur de la membrure. En
appliquant la formule (3-31), on transforme cette force linéique en
force ponctuelle (figures 3-9 et 3-10). Le même travail est fait pour les
autres tronçons. La figure 3-9 est l'illustration d'un tronçon du
pylône sous l'action du vent.
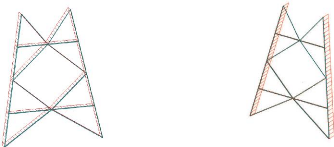
Figure 3-8 : force répartie sur les barres Figure 3-7 :
force répartie sur les membrures

Figure 3-10 : force nodale Figure 3-9 : force nodale
| 


