Conception d'une application pour le calcul et la simulation des efforts sur les pylônes

Dédicaces

Le présent travail est dédié à:

- mon feu papa M. Donfack Bernard,

- ma maman Mme Donfack Marceline.

Remerciements

Je tiens tout d'abord à remercier la société ORANGE Cameroun et le département déploiement et patrimoine de m'avoir accueilli durant ces quatre mois et de m'avoir donné l'opportunité, à travers mon stage, de découvrir plus profondément le métier d'ingénieur à travers des visites de sites très intéressantes.

Ma vive gratitude aux Dr. AMBA Jean Chills et Dr MOUSSA Sali, qui ont encadré ce travail académiquement, avec beaucoup d'engagement.

Je remercie M. Joseph Alain Mailli, Chef de Département déploiement et patrimoine de ORANGE CAMEROUN, M. Jocelle TOUKA TCHANA, Chef Service déploiement Littoral/Ouest et Mme Roukia ABAKAKA administrateur du département pour tous les efforts qu'ils ont fourni pour me permettre de travailler dans de bonnes conditions. J'ai beaucoup apprécié leur compagnie et j'espère que notre amitié durera longtemps.

Je remercie tout particulièrement mon encadreur professionnel M. Christian MBOCKO, de m'avoir guidé et conseillé tout au long de ce stage.

Je remercie le chef de département de technologie de construction industrielle de la FGI M. NYATTE NYATTE JEAN de m'avoir conseillé depuis mon entrée à la FGI en 2008.

Je remercie tous mes frères et soeurs (JEAN PIERRE, EMMANUEL, MATHIAS, MAURICE, LUCIENNE, JONAS ET OLIVIER) et mon tuteur MAHONDE Achile pour leurs soutiens inconditionnels.

Mes remerciements vont à l'endroit de ceux qui ont participé à la réussite de mon parcours scolaire; il s'agit de ma famille, mes enseignants, mes amis et mes camarades de classe.

Je remercie les personnes avec lesquelles j'ai travaillées au quotidien : l'ingénieur Bernard BASSEMEL, les techniciens René ESSIGA et Hugues NGOUEN. Je suis très reconnaissant du temps qu'ils m'ont consacré car ils ont ainsi enrichi mon apprentissage pendant ce stage.

Résumé :

Les pylones font partie des structures qu'on peut qualifier de structures discrètes en forme de barres ou poutres. La technique de calcul de ces structures a connu ces dernières années un développement considérable. La méthode des éléments finis est de nos fours un outil puissant permettant de modéliser ces systèmes, et ce a des co~ts raisonnables ; avec en prime un temps de calcul réduit .Dans cette optique, une application a été développée avec pour obfectif le calcul des déplacements et des rotations en tête du pylone, les contraintes et les forces axiales dans les barres ainsi que les réactions a la base du pylone. Les obfectifs visés sont les suivants :

- permettre a tout le personnel du département « déploiement et patrimoine » de ORANGE CAMEROUN qu'ils soient ingénieurs ou non de rapidement vérifier si un pylone de hauteur donnée peut être implanté dans une région donnée.

- Améliorer la qualité de service dans le territoire camerounais.

Pour cela, une interface graphique a été intégrée a l'application et l'ensemble a été programmé sur « MATLAB 2007b ».

Un exemple de vérification a été fait pour un pylone de 36 mètres par la méthode analytique et sur Robot millénium 2010. Les résultats obtenus sont en adéquation avec les calculs analytiques effectués au moyen de la méthode des forces, ceci avec une erreur inférieure a 1%.

Les même observations ont été faites pour ce qui est de la confrontation des résultats analytiques avec ceux du progiciel « ROBOT MILLENIUM ».

Abstract

Pylons are part of structures which we can qualify as discreet structures in the form of bars or beams. The technical of calculation of these structures had a considerable development these last years. The method of finite elements analysis is nowadays a powerful tool alowing to model these systems, and in it reasonable costs; with a reduces time in calculation .In this optics, an application was developed with objective, the calculation of the displacements and the rotations movement sat the head of the pylon, the stress and the axial force in the bars as well as the reactions to the base of the pylon. The targeted objectives are the following:

-	To allow all the staff of the department "deploiement et patrimoine "of ORANGE CAMEROON

whether engineers or not to quickly verify if a pylon of given height can be implanted in a given region. - Improve the quality of service in the Cameroonian territory.

For that purpose, a graphical interface was integrated into the application and the whole set was programmed on "MATLAB 2007b ".

A verification example was made for a 36 meter pylon by the analytical method and on Robot millennium 2010. The results obtained are in adequacy with the analytical calculations made by means of the method of the forces, this with an error lower than 1 %.

The same observations were made as for the confrontation of the analytical results with those of the software package "ROBOT MILLENNIUM ".

A		aire de la section transversale
Ct		coefficient de trainée
Cr		coefficient de réduction des pressions
E		module de Young
F		force en général
fy		limite élastique du matériau
iv		rayon de giration
Km		effet de masque
Ks		coefficient de site
Lcr		longueur de flambement dans le plan considéré
L		longueur de l'élément
Nb,Rd		valeur de calcul de la résistance au flambement
NRd		valeur de calcul de la résistance à l'effort normal
N		effort normal
N Ed		valeur de calcul de l'effort de traction
Q		Actions variables
Qk		Valeurs caractéristiques des actions variables
qH		pression du vent corrigée
Si		surface totale d'un tronçon, les vides étant obturés
Sp		surface pleine d'un tronçon
T		action d'ensemble sur un tronçon
a		facteur d'imperfection
~		effet de dimension
~~		Élancement réduit dû au flambement
ë1		valeur d'élancement pour déterminer l'élancement réduit
~		facteur de distribution
ãÌ0,ãÌ1:		coefficients partiels de sécurité de résistance
A	section de l'élément
B	matrice reliant les déformations de l'élément à ses déplacements nodaux
Ce	matrice de localisation de l'élément e
cx, cy	cosinus directeur suivant x et y
D	matrice d'élasticité
E	module de Young du matériau
~~~~~~	Vecteur des forces extérieures exprimé dans le repère local
Fe	vecteur des forces extérieures de l'élément e exprimé dans le repère global
F	vecteur des forces aux noeuds de la structure
f xi	composante du vecteur de forces au noeud i suivant l'axe local ~~
f yi	composante du vecteur de forces au noeud i suivant l'axe local ji~
G	module de cisaillement du matériau
It	moment d'inertie de torsion
~~~~~~	matrice de rigidité de l'élément e exprimée dans le repère local
Ke	matrice de rigidité de l'élément e exprimée dans le repère global
K	matrice de rigidité de la structure
L	longueur de l'élément
~~ e	matrice de masse de l'élément e exprimée dans le repère local
Me	matrice de masse de l'élément e exprimée dans le repère global
M	matrice de masse de la structure
N	matrice d'interpolation reliant les déplacements d'un point intérieur de l'élément aux déplacements nodaux
q	charge répartie sur l'élément
R	réactions inconnues engendrées par les appuis
T	matrice de transformation du repère local au repère global
~^~e	vecteur de déplacements aux noeuds de l'élément e exprimé dans le repère local
Ue	vecteur de déplacements aux noeuds de l'élément e exprimé dans le repère global
U	vecteur de déplacements nodaux de la structure
uxi	composante du vecteur de déplacements au noeud i suivant l'axe local ~~
u yi	composante du vecteur de déplacements au noeud i suivant l'axe local jii
~~	dérivée seconde du vecteur de déplacements nodaux de la structure
ue (x,y)	déplacements à l'intérieur de l'élément e exprimés en fonction de x et y
u (x)	déplacement le long de l'axe x
~	déformation de l'élément
p	masse volumique du matériau constituant l'élément
a:	contrainte dans la barre
wi	pulsation propre correspondant au mode propre élastique de rang i
w	pulsation
pi	déphasage correspondant au mode propre élastique de rang i
H:	énergie potentielle totale de la structure
He	énergie potentielle de l'élément e

Sigles et abréviations

ART : agence de régulation des télécommunications AUTO STABLE (pylône)

Mât autoportant

AZIMUT

L'azimut est la direction principale d'émission d'une antenne. Il est exprimé en degrés et est compté positivement dans le sens horaire, en partant du nord (azimut 0°).

BTS : Base Transceiver Station - Station de base émettrice-réceptrice

La BTS est le premier élément électronique « vu » par le téléphone, elle se trouve près des antennes, dans une baie métallique. La BTS est constituée de nombreuses cartes électroniques qui organisent la liaison entre le téléphone et le réseau GSM.

CHARGE EN TETE : Somme des surfaces au vent de toutes les antennes placées sur le pylône. DEPOINTAGE : Angle de rotation maximale que peut subir l'entête du pylône

FH : Faisceau Hertzien

Un FH est une liaison hertzienne assurée par deux antennes en visibilité directe et à très faible diagramme d'ouverture, ce mode de transmission est très souvent utilisé pour la liaison Abis.

GSM : Global System for Mobile communications - Système global de communications mobiles

Le GSM est une norme dont le contenu dépasse 10 000 pages et qui a débuté en 1979. Le développement de la première phase de cette norme s'est terminé en 1990, alors que les premiers réseaux ouvraient en Europe. Cette norme de télécommunications mobiles de 2ème génération, choisit la transmission numérique avec multiplexage temporel (TDMA).

M.E .F : méthode des éléments finis

MS : Mobile Station - Station mobile, téléphone portable

Téléphone mobile dans un réseau de téléphonie mobile GSM. NSS : Network Sub-System - Sous-système réseau

OCM : Orange Cameroun Mobiles

FIGURE 1-1 : ORGANISATION DE L'ENTREPRISE ........................................................................................... 4
FIGURE 1-2 : SITE DE TELECOMMUNICATION ................................................................................................. 9

FIGURE 1-3 : ANTENNE GSM 10

FIGURE1-4 : ANTENNE FH 10

FIGURE 1-5 : VUE D'ENSEMBLE D'UN PYLONE HAUBANE 12

FIGURE 2-1 : PYLONE AUTO STABLE DE 54 M: VUE EN ELEVATION ET AERIENS 16

FIGURE2-2 AERIENS 17

FIGURE 2-3 : DESCRIPTION D'UN TRONÇON 18

FIGURE 2-4 : TYPE DE TRONÇONS A UTILISER 19

FIGURE 2-5 : ALGORITHME DE CALCUL DU COEFFICIENT DE REDUCTION ........... 30

FIGURE 2-6 : ALGORITHME DE DIMENSIONNEMENT AU FLAMBAGE ........................ 32

FIGURE 3-1 : DISCRETISATION EN ELEMENTS FINIS D'UN TREILLIS PLAN 34

FIGURE 3-2 : GEOMETRIE D'UN ELEMENT BARRE 38

FIGURE 3-3 : MODELISATION D'UN ELEMENT BARRE 38

FIGURE 3-4 : ELEMENT BARRE DANS LE PLAN (I ,X,Y) 39

FIGURE 3-5 : ELEMENT DANS LE REPERE GLOBAL 42

FIGURE 3-6 : FORCE REPARTIE SUR UNE BARRE 43

FIGURE 3-7 : FORCE REPARTIE SUR LES MEMBRURES 43

FIGURE 3-8 : FORCE REPARTIE SUR LES BARRES 43

FIGURE 3-11 : ELEMENT POUTRE EN TORSION 44

FIGURE3-9 : FORCE NODALE 44

FIGURE 3-10 : FORCE NODALE 44

FIGURE 3-12 : ORGANIGRAMME D'ANALYSE LINEAIRE PAR LA M.E.F. D'UNE STRUCTURE A DE

POUTRES 50

FIGURE 3-13 : ETAPES DE REALISATION DE L'INTERFACE 54

FIGURE3-14 : OUTIL GUIDE 55

FIGURE 4-1 : INTERFACE DE L'APPLICATION 57

FIGURE 4-2 : MAILLAGE DU PYLONE 58

FIGURE 4-3 : PYLONE DEFORME A L'ECHELLE 10 59

FIGURE 4-4 : CHOIX DE LA REGION ET ANTENNES 59

FIGURE 4-5 : LISTING DES CORNIERES 60

FIGURE 4-6 : AFFICHAGE DES RESULTATS 61

FIGURE 4-7 : DEPLACEMENT EN TETE DU PYLONE 61

FIGURE 4-8 : AFFICHAGE PERIODES PROPRES 62

FIGURE 4-9 : RESULTAT DIMENSIONNEMENT 62

FIGURE 4-10 REACTIONS AU NIVEAU DE LA BASE DU PYLONE 63

TABLEAU 1-1 : IDENTIFICATION D'OCM ............................................................................................................. 4
TABLEAU 1-2 : PRESENCE D'ORANGE EN AFRIQUE ..................................................................................... 5
TABLEAU 1-3 : COUT DE REALISATION D'UN SITE ......................................................................................... 8

TABLEAU 2-1 : COMBINAISONS DES TYPES DE TRONÇONS 19

TABLEAU 2-2 : HAUTEUR DES TRONÇONS 19

TABLEAU 2-3 : COMBINAISONS D'ACTIONS A L'ELS 23

TABLEAU 2-4 : COMBINAISONS D'ACTIONS A L'ELS 23

TABLEAU 2-5 : PRINCIPALES ZONES CLIMATIQUES AU CAMEROUN 24

TABLEAU 2-6 : TYPE DE SITE 25

TABLEAU 2-7 : CALCUL DE LA CHARGE EN TETE D'UN PYLONE 27

TABLEAU 4-1 : RESULTATS DES REACTIONS 66

TABLEAU 4-2 : RESULTAT DU CALCUL DES CONTRAINTES 67

TABLEAU 4-3 : RESULTAT DU CALCUL DES CONTRAINTES (SUITE) ......................... 68

TABLEAU 4-4 : RESULTAT DU CALCUL DES CONTRAINTES (SUITE) ......................... 69

TABLEAU 4-5 : RESULTAT DU CALCUL DES CONTRAINTES (SUITE) 70

TABLEAU 4-6 : RESULTAT DU CALCUL DES CONTRAINTES (SUITE) ......................... 71

TABLEAU 4-7 : RESULTAT DU CALCUL DES CONTRAINTES (SUITE) ........................ 72

TABLEAU 4-8 : RESULTAT DU CALCUL DES CONTRAINTES (FIN) .............................. 73

TABLEAU 4-9: RESULTAT DU CALCUL DES DEPLACEMENTS 73

TABLEAU 4-10 : COMPARAISON DES RESULTATS 73

Sommaire pages

Dédicaces i

Remerciements ii

Résumé ...iii

Abstract . .iv

Notations . v

Sigles et abréviations ...vi i i

Liste des figures . x

Liste des tableaux . xii

Sommaire xii

Introduction générale ..1

chapitre-1 : Présentation générale de l'entreprise (*) 3

1-1 Historique et naissance 3

1-2 Missions 3

1-3 Actionnariat 3

1-4 Organisation de l'entreprise 4

1-5 Identification 4

1-6 Quelques activités du département déploiement et patrimoine 5

1-7 Présence de Orange en Afrique 5

1-8 Étapes de construction du site 5

1-8-1 Commande de l'opérateur 5

1-8-2 Contenu de l'étude 6

1-9 Réalisation 7

1-9-1 Gros oeuvre 7

1-9-2 Installation et test du matériel 8

1-9-3 Mise en route 8

1-9-4 Coût 8

1-10 Les difficultés et solutions proposés 9

1-11 Site de télécommunication 9

1-11-1 Le relais 9

1-11-2 Le pylône 11

1-12 Restriction de l'étude 13

1-12-1 Type de pylônes à traiter 13

1-12-2 Modèle 14

1-13 Conclusion 14

chapitre-2 Différentes normes de construction des pylônes 15

2-1 Introduction 15

2-2 Prise de connaissance des pylônes à étudier 16

2-3 L'Eurocode 3 20

2-3-1 Introduction 20

2-3-2 Définition des états limites 20

2-3-3 Représentation des actions 21

2-3-4 Combinaisons d'actions 22

2-4 Charges appliquées au pylône 23

2-4-1 Combinaisons des actions 23

2-5 Les normes du vent 24

2-5-1 La zone où se situe la construction : 24

2-5-2 La hauteur de la construction 24

2-5-3 Le site où se situe la construction : ks 25

2-5-4 L'effet de dimension: ö 25

2-5-5 L'effet de masque: km 25

2-5-6 De la forme de la construction : Ce - Ci 25

2-5-7 Des actions dynamiques: 3 25

2-6 Détermination de la pression de calcul du vent 26

2-7 Action d'ensemble sur le pylône 26

2-8 Dimensionnement 28

2-8-1 L'analyse globale du premier ordre 28

2-8-2 Vérification de la résistance des sections transversales de classe 3. 29

2-8-3 Algorithmes de vérifications 31

2-9 Conclusion 32

chapitre-3 Formulation des éléments finis 33

3-1 Introduction 33

3-2 Concept de base de la méthode des éléments finis 34

3-2-1 La formulation élémentaire au niveau de l'élément fini 35

3-2-2 La formulation globale au niveau de la structure complète 35

3-3 Démarche de formulation éléments finis 35

3-3-1 Discrétisation de la structure en éléments finis 35

3-3-2 Construction de l'approximation nodale par sous domaine 36

3-3-3 Etablissement de la relation entre déformations et déplacements 36

3-3-4 Etablissement de la relation entre contraintes et déformations 36

3-3-5 Calcul des matrices élémentaires. 36

3-3-6 Assemblage des matrices élémentaires 37

3-4 Elément fini barre 37

3-4-1 Définition 37

3-4-2 Formulation de l'élément barre dans le plan 39

3-5 Formulation d'un élément poutre en torsion 44

3-5-1 La matrice de rigidité 44

3-6 Résolution en analyse statique 45

3-6-1 Systèmes d'équations linéaires 45

3-6-2 Prise en compte des conditions de déplacement imposé 45

3-6-3 Résolution du système linéaire 46

3-6-4 Calcul des efforts 47

3-7 Résolution en analyse modale 48

3-7-1 Système d'équations aux valeurs propres 48

3-7-2 Résolution du système aux valeurs propres 49

3-8 Algorithmes de résolution 49

3-8-1 Lecture des données 50

3-8-2 Traitement des données 51

3-8-3 Calcul de la solution 52

3-9 Création de l'interface graphique 53

3-9-1 Etapes de conception 54

3-9-2 Outil guide 54

3-9-3 Programmation du guide 55

3-10 Conclusion 56

chapitre-4 Application à un pylône de 36 mètres 57

4-1 Introduction 57

4-2 Affichage (maillage) du pylône 58

4-3 Choix de la région et de l'antenne 59

4-4 Choix des cornières 60

4-5 Affichage des résultats 61

4-6 Périodes propres du pylône : zone de texte 62

4-7 Vérification du dimensionnement 62

4-8 Réactions à la base du pylone 63

4-9 Confrontation avec la méthode analytique 63

4-9-1 Principe de la méthode analytique 63

4-9-2 Calcul des erreurs moyennes 65

4-9-3 Conclusion 73

Conclusion générale 75
Bibliographie

Annexes

Les pylônes font partie de ces structures que l'on qualifie de structures discrètes à cause de leur composition en éléments barres ou poutres assemblées par soudures ou rivetage en des points appelés <<noeuds>>, et soumises à des forces extérieures. Le calcul analytique de ces structures est fastidieux, voir impossible à cause du nombre élevé de barres et de leurs connectivités. La méthode des éléments finis est apparue avec la nécessité de résoudre ces problèmes de calcul complexes dans un contexte où le développement massif de l'informatique permettait d'automatiser le traitement de gros systèmes d'équations. Presque tous les logiciels de calcul des structures (ROBOT MILLENIUM, SAP 2000 etc.) utilisent la méthode des éléments finis pour déterminer les contraintes, les déplacements dans les structures, etc.

Ces logiciels ne sont pas d'une manipulation aisée, ils exigent une bonne formation pouvant aller jusqu'à un an ; ne peut les utiliser efficacement que celui qui a une maitrise dans le domaine du calcul des structures. Ces logiciels ne sont pas destinés à une structure particulière puisque, selon le type de structure que l'on veut concevoir, il faut adapter la méthode de calcul ainsi que le logiciel appropriés. Tous les calculs se font de façon automatique, en conséquence, une petite erreur de la part du manipulateur peut conduire à des résultats aberrants, surtout si celui-ci n'est pas un utilisateur confirmé. Parfois ces logiciels sont dotés d'un nombre de fonctionnalités très impressionnantes, pas toujours très utiles, parfois redondantes, qui peuvent éventuellement davantage égarer l'utilisateur.

Pour cela, la nécessité de développer des programmes de calcul beaucoup plus simples et adaptés pour certaines applications spécifiques permet d'atteindre les résultats escomptés tout en nécessitant les temps d'adaptation et de formation relativement courts pour les utilisateurs.

L'objectif de ce travail est de concevoir un code, de calcul statique et modal par la méthode des éléments finis pour des pylônes. Ce code programmé en matlab version 2007b, sera baptisé << GENIE >> et permettra de faire une estimation des contraintes dans toutes les barres et de mettre en évidence, le déplacement et la rotation en tête du pylône selon la norme européenne

Eurocode 3. Le calcul sera effectué suivant une analyse globale du premier ordre qui permet de déterminer la distribution des sollicitations à l'intérieur des différents composants de la structure. Il est à noter que l'architecture de << GENIE >> offre la possibilité d'ajout de nouveaux modules pour d'autres types d'application.

Sans disposer de toutes les fonctionnalités disponibles dans les logiciels commerciaux (analyse élasto-plastique, temporelle etc.), GENIE se veut tout de même une alternative crédible à ces logiciels pour la conception des pylônes. En effet, dans de nombreux cas, un nombre limité de fonctionnalités est nécessaire. Pour cette raison, la programmation de << GENIE >> s'est apaisantie sur ces fonctionnalités de base, en veillant à ce que l'interface utilisateur soit la plus claire possible.

Ce travail est développé en quatre chapitres.

Dans le chapitre 1, est faite une présentation générale l'entreprise. Il est question ici de donner tous les renseignements inhérents à l'entreprise ; nous allons faire un état de lieu du département ou s'est déroulé le stage.

Dans le chapitre 2, nous présentons toutes les normes relatives à la construction des pylônes à savoir : les normes Eurocodes et les normes NV 65.

Dans le chapitre 3, les formulations éléments finis utilisées dans l'application GENIE pour modéliser des pylônes sont présentées. Les modèles, les théorèmes, les équations, les formules théoriques ainsi que les algorithmes sont présentés.

Dans le chapitre 4, une présentation des résultats et de l'interface graphique développée est faite. Un exemple de calculs statique et modal est traité en vue de calculer les contraintes et les déplacements sur le pylône.

1-1 Historique et naissance

ORANGE fut lancé sur le marché britannique en avril 1994 par Hutchison Whampoa groupe originaire de Hong Kong, avec pour objectif de devenir l'opérateur de référence en matière de communications mobiles. C'est alors le quatrième opérateur sur ce marché déjà très saturé. Pour atteindre son objectif, ORANGE doit donc se démarquer radicalement. Les trois acteurs déjà présents sur ce marché pratiquaient à l'époque une tarification complexe et élevée. Pour les contrer, ORANGE se forge une identité forte et innove en proposant des forfaits simples, moins chers et avec des services supplémentaires. ORANGE est lancée à Hong Kong en septembre 1998, et passe de la quatrième à la première place du marché. En 1999, ORANGE prend pied en Afrique et donc au Cameroun avec la libéralisation du secteur de la télécommunication avec pour appellation société camerounaise des mobiles « mobilis » et c'est depuis juin 2002 que mobilis est devenu ORANGE CAMEROUN MOBILE. Il est présent sur beaucoup de pays africains et occupe le deuxième rang au Cameroun derrière MTN. [12]

1-2 Missions

OCM est une société privée dont l'objectif est de fournir Les services de communication mobile et d'accès au réseau internet sur le plan national et international. Tout ceci avec des interfaces assurant une qualité de service optimale

1-3 Actionnariat

- OCM : 69.8% ;

- Société de droit Camerounais: 29.5% ;

- Personnes physiques représentant les intérêts du groupe: 0.7%.

(*) Informations de 2009 non encore mises à jour.

Chapitre 1 : présentation générale de l'entreprise

1-4 Organisation de l'entreprise

service Design et
planification des
infrasr uct ures

département
Ingénierie
système

département
déploiement
patrimoine

Service
centre/ nord

responsable
infrastructure
littoral

technicien site
littoral

Département
radio

Service
littoral/o uest

responsable
infrastructure
o uest

technicien site
o uest

q ualité et
méthodes

Administrateur

Direction des
ventes

Direction d u
système
d'information

Direction des
resso urces
h umaines

Direction d u
développement
résea u

Direction
technique et
informatiq ue

direction
générale

Direction des
opérations de
maintenance

Direction de
controle de
gestion

direction d u
service client

Figure 1-1 : organisation de l'entreprise

1-5 Identification

Tableau 1-1 : identification d'OCM

Raison sociale	ORANGE CAMEROUN MOBILE
Statut juridique	société anonyme (SA)
Date de création (mobilis)	28 mai 1999
Date de mise en service du réseau	février 2000
Dénomination OCM	04 juin 2002
Siege social	rue franqueville BP. 1864 douala -Cameroun
Capital social	15 010 000 000 francs cfa
Directeur général	Jean BARDET
Logos

1-6 Quelques activités du département déploiement et patrimoine

Le département déploiement et patrimoine est celui qui s'occupe de la négociation, du suivi de la construction et de la maintenance des sites de téléphonie. Il supervise les travaux des soustraitants, parmi ces travaux, nous pouvons citer :

- La négociation des sites, - La construction des sites,

- L'électrification des sites,

- La remise à niveau des sites, - La bibandisation.

1-7 Présence de Orange en Afrique

Tableau 1-2 : présence d'orange en Afrique

pays	opérateur	Nombre de clients (millions)	Part de marché (%)	rang
Cameroun	Orange	2,137	42	^2è
Cote d'ivoire	Orange	4	42.5	1er
Egypte	mobinil	20	51.9	1er
Madagascar	Orange	3.8	63.2	1er
Guinée équatoriale	Orange guinée équatoriale	<<< 1
Ile Maurice	Orange	0.552	59	1er
Kenya	Orange Kenya	0.6	5	3ème
Ouganda	Orange Ouganda	<<< 1	/	/
Tunisie	Orange Tunisie	0.676	8	3ème
mali	orange	2	80	1er

1-8 Étapes de construction du site

1-8-1 Commande de l'opérateur

Pour des raisons commerciales ou par imposition de l'agence de régulation des télécommunications (ART), Orange définit de nouvelles zones à équiper, pour cela, il commande à un sous-traitant spécialisé (CAMUSAT, CARTEL, SAGEMCOM ...) la réalisation d'une étude pour de nouveaux emplacements de relais. L'opérateur définit une zone de quelques kilomètres en zone rurale ou de quelques centaines de mètres en ville où devra se trouver le

relais, il définit aussi les besoins de couverture, la capacité en trafic, les fréquences utilisées (900, 1800, 1900- 2200 MHz).

1-8-2 Contenu de l'étude

1-8-2-1 Recherche des emplacements

Le sous-traitant cherche des emplacements pour le site, qui seront classés par ordre de priorité par l'opérateur.

1-8-2-2 Début de la négociation (survey)

Quand des emplacements ont été trouvés, le sous-traitant s'occupe de la négociation avec le propriétaire. C'est cette phase la plus délicate, puisque les propriétaires sont très réticents pour accueillir des antennes. Cette négociation dure tout au long de l'étude, et après la visite technique qui définit la position des baies et des antennes, une proposition est faite au propriétaire. Si la négociation s'est bien déroulée, le montant de la location (qui peut aller d'une centaine à un million de francs par mois) payé par l'opérateur est fixé et un accord de principe est signé.

1-8-2-3 Visite technique (draft)

Les services d'Orange font une visite technique sur place, pour définir le type d'antenne et leurs positions. Le sous-traitant fait lui aussi des relevés pour prévoir l'installation du matériel et des chemins de câbles.

1-8-2-4 Dossier technique (avant projet détaillé)

L'opérateur donne les spécifications générales du site au sous-traitant, qui va établir un dossier technique minimal contenant les plans, descriptifs des travaux, position sur le cadastre. Une fois le dossier retourné à l'opérateur, celui-ci va le compléter en faisant des simulations pour choisir définitivement le type d'antennes, leur orientation, azimut etc.

1-8-2-5 Démarches administratives

Le sous-traitant prend connaissance du dossier complet et accomplit les démarches nécessaires. Il fait les demandes administratives pour la réalisation des travaux (permis de construire, demande de travaux). Si l'un des ces agréments n'est pas donné, le site doit être abandonné ou modifié de manière à devenir conforme et ainsi obtenir les autorisations nécessaires.

1-8-2-6 Dossier technique complet

Une fois toutes les autorisations obtenues, un dossier technique définitif est renvoyé à l'opérateur qui vérifie que tout corresponde bien aux spécifications techniques initiales. Les travaux devront suivre scrupuleusement ce dossier.

1-8-2-7 Décision finale

L'opérateur étudie le dossier et vérifie que la négociation effectuée avec le propriétaire (prix d'achat, location) est convenable. Si tout est bon, l'accord de financement est donné, l'opérateur et le propriétaire concluent la négociation (signature du bail, acte de vente) et les travaux peuvent débuter.

1-9 Réalisation

Le sous-traitant choisi par Orange organise les travaux, il les réalise entièrement ou peut en sous-traiter une partie à des entreprises spécialisées dans les gros oeuvres, l'installation du pylône, etc.

1-9-1 Gros oeuvre

Cette étape doit permettre l'accès au site en question. S'il s'agit d'une région difficile d'accès, il faudra au préalable mettre en place un chemin praticable par les engins nécessaires à l'installation du pylône et autres matériels. Si le site se trouve sur un toit d'immeuble, il faudra sécuriser les abords du toit et préparer à accueillir les antennes et les BTS. C'est à ce moment-là que seront faites les fondations en ciment destinées à supporter le pylône et les baies.

1-9-2 Installation et test du matériel

Le sous-traitant installe les antennes dans les azimuts et inclinaisons définis, met en place les câbles et prépare la structure pour accueillir les baies ; il s'occupe aussi de la sécurité du site, pour protéger les personnes qui seront amenées à y travailler (garde-fous, rampe d'accès, échelle d'accessibilité.

Un technicien de l'entreprise qui fournit les BTS se rend sur place, pour terminer l'installation des baies. Il achève les derniers branchements : alimentation électrique, connexion des antennes et procède aux premiers essais en collaboration avec une personne du centre de supervision de l'opérateur, pour vérifier le bon fonctionnement et la bonne configuration de la BTS et des antennes, secteur par secteur.

Orange organise une visite qui lui permet de vérifier la conformité du site aux spécifications du dossier technique. Si le site est conforme, le sous-traitant est payé. [13]

1-9-3 Mise en route

Le site ouvre en exploitation, il est surveillé par le service optimisation de l'opérateur qui procède à des réajustements notamment au niveau de la puissance, pendant les premiers mois de fonctionnement. Des interventions peuvent avoir lieu sur le site pour affiner les réglages.

1-9-4 Coût

Tableau 1-3 : Gout de réalisation d'un site

Ouverture de chemins d'accès, clôture du site, terrassement, construction des locaux techniques, tableau électrique	15	000 000 FCFA
Pylône et installation	24	000 000 FCFA
Antennes GSM, antenne HH et câbles coaxiaux	10	000 000 FCFA
Installation et configuration d'une baie avec 1 TRX par secteur.	50	000 000 FCFA
Total	99	000 000 FCFA

Il est à noter que les coûts de réalisation varient suivant la nature du site : pylône existant, terrain difficilement accessible, capacité du site, nombre d'antennes. Lors de la location de terrain, le loyer mensuel varie d'une centaine à un million de francs, suivant l'emplacement. Ici, nous donnons une valeur approximative de ce coût.

1-10 Les difficultés et solutions proposés

Il est donc difficile pour un personnel de ORANGE de donner les spécificités mécaniques quant au pylône qui sera mis sur pied car peu de personnels sont du domaine du génie civil ou du génie mécanique. La communication peut paraitre difficile entre l'employé de l'opérateur et le sous traitant. Nous nous proposons de mettre sur pied un outil de vérification des pylônes, facile d'utilisation et accessible à tout le personnel quelque soit son domaine de compétence et son niveau hiérarchique.

1-11 Site de télécommunication

Un site de télécommunication est globalement composé de deux éléments majeurs : le relais et le pylône.

Figure 1-2 : site de télécommunication

1-11-1 Le relais

Le relais sert d'intermédiaire entre le téléphone mobile (MS) et le sous système réseau qui regroupe l'ensemble des éléments de gestion des mobiles et d'acheminement des

communications. Nous allons voir dans cette partie les caractéristiques principales d'un relais GSM, ainsi que sa composition, d'une manière assez simplifiée. [13]

1-11-1-1 Les antennes

Les antennes sont les composantes les plus visibles du réseau. On les voit un peu partout, souvent sur des hauts pylônes, sur des toits d'immeubles, contre des murs, à l'intérieur des bâtiments. Il arrive assez souvent qu'elles soient invisibles puisque camouflées, pour des raisons esthétiques, à proximité de bâtiment. Nous donnons ici quelques caractéristiques des antennes.

Figure 1-4 : antenne FH Figure 1-3 : antenne GSM

a. Fréquence d'utilisation

La caractéristique la plus importante d'une antenne, aussi appelée aérien, est la bande de fréquences supportée ; c'est-à-dire les fréquences que l'antenne pourra émettre et recevoir. Sur les sites GSM, on trouve des antennes qui émettent seulement en 900 MHz, seulement en 1800 MHz ou des antennes bi-bandes 900 et 1800 MHz.

b. Directivité

La deuxième caractéristique importante est la directivité sur le plan horizontal, c'est en fait la ou les direction(s) dans laquelle l'antenne va émettre.

c. Azimut

Chaque antenne est dirigée dans une direction déterminée par des simulations, de manière à couvrir exactement la zone définie (annexe 1.a). La direction principale de propagation de l'antenne, c'est-à-dire la direction dans laquelle l'antenne émet à sa puissance la plus importante est dirigée dans l'azimut établi. L'azimut est un angle qui se compte en degrés, positivement dans le sens horaire, en partant du nord (0°). De cette façon, l'azimut 90° correspond à l'est, l'azimut 180° au sud, etc.

1-11-1-2 La BTS

La BTS est le premier élément électronique actif du réseau GSM, vu par le mobile. C'est l'élément intermédiaire qui reçoit des informations, donne des ordres et les exécute. Elle est logée dans un abri (annexe 1.b).

Elle est constituée de :

a. Baie

La baie est une grande armoire métallique, parfaitement blindée électriquement, hermétique, climatisée en saison sèche et chauffée en saison des pluies pour conserver une température de fonctionnement constante. Une baie est modulaire, elle contient des emplacements pour des cartes électroniques qui sont ajoutées suivant les besoins du site (annexe 1.c).

b. Alimentation

L'alimentation de la baie se fait avec la tension du réseau alternatif. Ensuite, le transformateur convertit cette tension en une tension continue pour l'alimentation de tous les éléments de la BTS, qui peut consommer jusqu'à une trentaine d'ampères en fonctionnement à plein régime. Des batteries sont associées à cette alimentation, pour permettre un fonctionnement de plusieurs heures en cas de coupure de courant.

1-11-2 Le pylône

Le pylône est la structure porteuse à treillis de section triangulaire ou carrée ayant pour seul rôle de supporter et de maintenir en équilibre les antennes. Les spécificités des pylônes sont les suivantes : [14]

1-11-2-1 Les pylônes haubanés

Conçue pour supporter des charges légères et moyennes, elles sont stabilisées à différents niveaux sur sa hauteur par des haubans ancrés au sol. Ce type de pylône est construit lorsqu'on dispose d'un grand espace ou alors si le pylône est de grande taille. L'ensemble de pylônes haubanés se présentent sous forme triangulaire, présentent une conception haubanée treillis. Les pylônes haubanés sont conçus pour des hauteurs allant de 20 à 150m. Chaque pylône est équipé d'une variété d'accessoires comprenant des plates-formes, des supports d'antennes, des dispositifs de sécurité, des kits de balisage, un kit de protection contre la foudre et autres.

Figure 1-5 : vue d'ensemble d'un pylône haubané

1-11-2-2 Les pylônes autostables à quatre pieds

C'est un pylône autoportant de quatre pieds constitué d'éléments conçu suivant un modèle de base carré. Ce pylône est capable de supporter des charges moyennes et lourdes. Le pylône autostable carré est conçu pour des hauteurs allant de 20 à 120m. Le pylône angulaire carré peut être équipé d'une variété d'accessoires tels que des plates-formes, des supports d'antennes, des dispositifs de sécurité, des kits de balisage, un kit de protection contre la foudre et autres. L'ensemble des accessoires de pylônes de télécommunication peuvent être installés à une hauteur et une orientation souhaitées conformément aux exigences du client.

1-11-2-3 Les pylônes autostables à trois pieds

Ce sont des pylônes autoportants à trois pieds constitués d'éléments triangulaires conçus suivant un modèle de base triangulaire. Le pylône de communication est capable de supporter des charges moyennes et lourdes. Il est conçu pour des hauteurs allant de 20 à 70m. Tous les pylônes peuvent être fournis avec une variété d'accessoires tels que des plates-formes, des supports d'antennes, des dispositifs de sécurité, des kits de balisage, un kit de protection contre la foudre et autres. L'ensemble de ces accessoires de pylônes d'antenne peuvent être installés à une hauteur et une orientation souhaitées conformément aux exigences du client.

Figure 1-3 : vue d'ensemble d'un pylône auto stable à quatre pieds

1-12 Restriction de l'étude

1-12-1 Type de pylônes à traiter

Durant toute cette étude, seuls les pylônes auto stables carrés seront traités, les hauteurs seront les suivantes : 36 mètres, 54 mètres et 72 mètres.

1-12-2 Modèle

Le pylône est soumis uniquement à l'action des antennes et du vent, les longueurs des barres sont relativement courtes. Ces efforts ne sont pas de nature à créer des efforts de flexions considérables. Par conséquent, les barres du pylône ne seront sollicitées qu'en traction ou compression. Les liaisons entre les barres ne sont que des rotules sans frottement constituant les noeuds. Nous supposerons également que : [1]

- Les forces extérieures sont appliquées uniquement aux noeuds (pour la force du vent, elle est linéaire et sera appliquée sur les noeuds correspondants).

- Les poids propres des barres sont négligeables devant les forces extérieures.

Le modèle de structure que nous adoptons est donc le treillis plan.

Nous allons nous intéresser à une seule face, puisque le pylône est symétrique. Les profilés sont les cornières à ailes égales. La limite d'élasticité est de 235 Mpa pour toutes les barres sauf les membrures. La limite d'élasticité des membrures est de 275 Mpa.

Le vent agit dans deux directions principales : l'une normale à la face qui porte l'antenne et l'autre suivant une diagonale de la structure.

Les pylônes sont supposés être construits uniquement sur le territoire camerounais.

1-13 Conclusion

Nous avons l'état des lieux au sein du département « déploiement et patrimoine » de OCM et toutes les étapes de construction d'un site de télécommunication.

chapitre-2 Différentes normes de construction des

pylônes

2-1 Introduction

Les pylônes que nous nous proposons de calculer sont constitués totalement des produits laminés. Ces produits laminés sont constitués des profilés, des tôles etc. La réalisation de telles structures s'effectue suivant des normes de conception qui permettent d'obtenir un ouvrage assurant la sécurité des personnes et des biens et bénéficiant d'une durabilité cohérente avec l'investissement consenti.

Dans ce travail, nous nous intéressons au calcul basé sur les normes NV65 et les normes structurales Eurocodes 3 partie 3-1 applicables aux pylônes et mats haubanés. Ainsi, dans ce chapitre nous présentons les exigences relatives à la résistance mécanique des sections transversales et à la stabilité des éléments de ce type de structures. L'ensemble de ces exigences est intégré dans le code GENIE en vue de réaliser un diagnostic faisant suite à une analyse globale qui permet de déterminer la distribution interne des sollicitations pour les différents composants du pylône.

Nous nous limiterons aux profils laminés de classe 3. Nous supposerons, aussi, étudier des sections brutes sans trous de fixation.

2-2 Prise de connaissance des pylônes à étudier

Figure 2-1 : pylône auto stable de 54 m: vue en élévation et aériens

Balisage

Figure 2-2 aériens

Figure 2-3 : description d'un tronçon

Les pylônes à étudier sont de type auto stable carrés destinés à supporter plusieurs types d'antennes dont la charge en tête est connue. Les faces du pylône sont des quadrilatères et les sections sont variables ; la partie inférieure est en tronc de pyramide et la partie supérieure est parallélépipédique. Il se compose de plusieurs tronçons variables selon la taille du pylône. Un tronçon est toute partie d'un pylône subdivisé verticalement dans le but de déterminer les aires projetées et la traînée aérodynamique. Les tronçons sont souvent, mais pas nécessairement, compris entre des intersections de membrures et de contreventements principaux. Pour l'analyse globale, il convient de s'assurer que la hauteur du pylône est subdivisée en un nombre suffisant de sections pour obtenir une modélisation représentative de la structure. En fonction de la hauteur du pylône, il faut juxtaposer les tronçons convenables, ainsi les combinaisons de ces tronçons sont les suivantes :

Les tronçons de base à utiliser sont les suivants :

Figure 2-4 : type de tronçons à utiliser
Tableau 2-1 : combinaisons des types de tronçons

Hauteur du pylône				Type de tronçons
36 mètres				4 - 4 - 4	- 4	- 4	- 5	- 6
54 mètres			2 - 2	4 4	4	4	4	4 5	- 6
72 mètres	2		- 2 -4	4 4 4	4	4	4	4	4 5	- 6

Les hauteurs de ces tronçons sont les suivantes :

Tableau 2-2 : hauteur des tronçons

Type de troncon	1	2	3	4	5	6
Hauteur en mètres	3 ou 4	6	6	6	2	4

2-3 L'Eurocode 3

2-3-1 Introduction

Les Eurocodes constituent un ensemble intégré de normes européennes pour la conception des structures de bâtiments et ouvrages de Génie Civil. Ils ont une importance essentielle à la fois pour le secteur de la conception des ouvrages et pour l'industrie du bâtiment et des Travaux Publics.

L'objet des Eurocodes est de codifier des méthodes communes de vérification des structures qui, mises à la disposition des États, constitueront une référence technique et commerciale dans le domaine du génie civil.

L'application des Eurocodes permet de bénéficier d'une présomption favorable du respect des prescriptions de sécurité, de stabilité et de durabilité des constructions en service, ainsi que d'une sécurité au feu, dans la mesure où ils permettent de déterminer les performances des structures ou des éléments structuraux vis-à-vis de toutes ces exigences.

L'Eurocode 3 définit les exigences de résistance, d'aptitude au service et de durabilité des structures an acier et est subdivisé en différentes parties :

Les Eurocodes sont publiés par les Organismes Nationaux de Normalisation et complétés dans chaque pays, par des Annexes Nationales. L'Annexe Nationale contient des informations relatives à des paramètres qui sont à déterminer au niveau national (par exemple, les données climatiques).

2-3-2 Définition des états limites

C'est un état au delà duquel la structure ne satisfait plus aux critères de dimensionnement pertinent.

Pour un ouvrage, un état limite est un état au delà duquel une exigence n'est plus satisfaite.

2-3-2-1 États limites ultimes

Chaque état limite ultime est associé à une ruine ou un effondrement total ou partiel de la structure considérée qui met en cause la sécurité des personnes. Sur le plan pratique, les modes de ruine considérés sont :

- la perte d'équilibre statique de la structure ou de l'une de ses parties, considérée comme un corps rigide, couvrant les phénomènes de renversement, de soulèvement et de glissement avec ou sans frottement ;

- la défaillance par déformation excessive, par transformation de la structure ou de l'une quelconque de ses parties en mécanisme, par rupture, par perte de stabilité.

- la défaillance due à la fatigue ou autres effets dépendant du temps.

2-3-2-2 États limites de service

Les états limites de service sont associés à des situations de la structure (ou de certaines de ses parties) rendant l'usage de la structure impossible dans le cadre des exigences définies lors de son projet (exigences de fonctionnement, de confort pour les usagers ou d'aspect).

Ces états limites de service comprennent :

- les déformations affectant défavorablement l'exploitation de l'ouvrage ou provoquant des dommages aux finitions ou superstructures (bardage, couverture, etc.) ;

- les vibrations pouvant incommoder les occupants, endommager le bâtiment ou limiter son efficacité fonctionnelle.

2-3-3 Représentation des actions

Les actions sont, généralement, classées en actions permanentes, actions variables et actions accidentelles [4].

a. Les actions permanentes (notées G) sont des actions dont la durée d'application est égale à la durée de vie de la structure ; elles peuvent être constantes ou connaître de faibles variations au cours du temps.

b. Les actions variables (notées Q) sont des actions à occurrences discrètes plus ou moins ponctuelles dans le temps ou à caractères (intensité, direction, etc.) variables dans le temps et non monotones (neige, vent, température, houle par exemple).

Les principales valeurs représentatives d'une action variable qui peuvent intervenir dans les combinaisons d'actions sont :

- la valeur caractéristique, notée Qk

- la valeur de combinaison, notée i0Qk ;

- la valeur fréquente, notée yr1Qk ;

- la valeur quasi permanente, notée iir2Qk ;

Les coefficients yr dépendent de la nature de la charge (exploitation, neige ou vent) et sont fixés dans l'Eurocode 1.

c. Les actions accidentelles (notées A) qui sont parfois de courte durée d'application et de caractère aléatoire (explosions, chocs, incendie par exemple).

La valeur de calcul d'une action est obtenue en faisant le produit de sa valeur caractéristique par un coefficient partiel de sécurité, majorant variable selon l'action considérée

2-3-4 Combinaisons d'actions

Pour les états limites ultimes, les valeurs de calcul des effets des actions doivent être combinées en appliquant les règles de combinaisons suivantes [4] :

Situations de projet durables et transitoires :

E ~YG,j*Gkj +Y Q,1*Qk,1+E i> 1 YQ,i* 1110,i *Qk,i (2-1)

Situations de projet accidentelles :

E ~YGAj*Gkj + Ad + 1111,1*Qk,1+E i> 12,i *thi,i (2-2)

Où

- Gk, j valeurs caractéristiques des actions permanentes ;

- Q k,1 valeur caractéristique d'une action variable jugée prépondérante ; - Q k,i valeurs caractéristiques des autres actions variables ;

- A d valeur caractéristique de l'action accidentelle ;

- yG, j coefficient partiel de sécurité appliqué à l'action permanente G k, j ;

- yGA, j coefficient partiel de sécurité appliqué à k, j G dans le cas de situations accidentelles ;

- yQ,i coefficient partiel de sécurité appliqué à l'action variable Q k,i ; - w0, 1111, w2 coefficients dépendant de la nature de la charge.

Pour les états limites de service, on définit les expressions suivantes [4] Combinaison rare E ~ Gk,j +Qk,1+E ~> 10,i Qk,i Combinaison fréquente E ~ Gk,j +1111,1Qk,1+E i> 12,i Combinaison quasi-permanente E ~ Gk,j +Ei> 1 1112,i Qk,i

(2-3) (2-4) ( 2-5)

2-4 Charges appliquées au pylône

- Cas 1 : poids des antennes,

- Cas 2 : vent normal suivant Dx : le vent agit normalement à une face,

- Cas 3 : vent normal suivant Dxy : le vent agit normalement à une diagonale du pylône.

2-4-1 Combinaisons des actions

2-4-1-1 Calcul à l'ELU

Durant ce travail, les combinaisons seront les suivantes : [11]

Tableau 2-3 : combinaisons d'actions à l'ELS

combinaison	nom	Type d'analyse	Nature de la combinaison	définition
1	Comb1	Analyse linéaire	ELU	1.35* « cas1 »+1.50* « cas2 »
2	Comb 2	analyse linéaire	ELU	1.35* « cas1 »+1.50* « cas3 »

2-4-1-2 Calcul à l'ELS

Tableau 2-4 : combinaisons d'actions à l'ELS

combinaison	nom	Type d'analyse	Nature de la combinaison	définition
1	Comb3	Analyse linéaire	ELS	1* « cas1 »+1* « cas2 »
2	Comb 4	Analyse linéaire	ELS	1* « cas1 »+1* « cas3 »

2-5 Les normes du vent

On admet que le vent a une direction d'ensemble moyenne horizontale. L'action du vent sur un ouvrage et sur chacun de ses éléments dépend des caractéristiques suivantes [5] :

2-5-1 La zone où se situe la construction :

On définit une pression dynamique de base normale _q10. Selon les données climatiques, le

Cameroun est découpé en huit zones jouissant des mêmes caractéristiques climatiques. L'étude

des vents de surface montre que le Cameroun est soumis à deux types de vents principaux [10]:

- Quadrant sud-ouest, c'est le vent océanique vecteur de flux humide.son influence est primordiale une bonne partie de l'année dans le sud Cameroun alors qu'il n'est ressenti qu'en saison de pluies dans le nord du pays.

- Quadrant nord - est : c'est l'harmattan, souverain dans le nord du pays pendant plus de six mois est encore ressenti en saison sèche au sud de l'Adamaoua et en particulier dans les régions de l'ouest. Le découpage est le suivant :

Tableau 2-5 : principales zones climatiques au Cameroun

Zones climatiques (principale ville de la zone)	Altitude moyenne (m)	Vitesse maximale observée (m/s)	Pression dynamique de base à la hauteur de 10 m au dessus su sol (Pa)
1. Yaoundé	850	31	1243
2. Kribi	19	30	1163
3. douala	850	32	1324
4. Bertoua	700	45	2618
5. Bamenda	1700	21	570
6. N'Gaoundéré	1200	58	4349
7. Garoua	400	50	3232
8. Maroua	600	50	3232
2-5-2 La hauteur de la construction La pression qH qui s'exerce à une hauteur H (exprimée en m), s'exprime : qH = 2.5 H+18 H+6 0 q10				(2-6)

2-5-3 Le site où se situe la construction : ks

Tableau 2-6 : type de site

Type de site	exemples	ks
Site protégé	Fond de cuvette bordé de collines sur tout son pourtour et protégé ainsi pour toutes les directions du vent	0.8
Site normal	Plaine ou plateau de grande étendue pouvant présenter des dénivellations peu importantes, de pente < 10%	1
Site exposé	Littoral sur une profondeur de 6km, sommet des falaises, iles ou presqu'iles étroites, vallées étroites où le vent s'engouffre, montagnes isolées ou élevées, et certains cols	1.35

2-5-4 L'effet de dimension: 6

L'action du vent s'exerçant sur une paroi n'est pas uniforme en raison des tourbillons locaux (plus faible plus la surface est grande). On tient pour cette raison compte de ce phénomène par l'utilisation du coefficient ö, dit coefficient de réduction des pressions dynamiques [Annexes 2].

2-5-5 L'effet de masque: km

De manière générale, on ne tient pas compte des effets de masque dus aux autres constructions masquant partiellement ou intégralement la construction étudiée. On utilise alors k_m = 1.

2-5-6 De la forme de la construction : Ce - Ci

Dans le cadre de notre étude, ce coefficient est pris égal à 1 selon [11]

2-5-7 Des actions dynamiques: 13

Aux effets statiques précédemment définis s'ajoutent des effets dynamiques qui dépendent des caractéristiques mécaniques et aérodynamiques de la construction. Ces actions dynamiques dépendent entre autres de la fréquence propre fondamentale de vibration de la construction et sont caractérisées par le coefficient de majoration ~ (pour les actions parallèles à la direction du vent) [5].

~ = O (1+ ~. T) (2-7)

~ : Coefficient de réponse fonction de la période T du mode fondamental « Annexe 2-b »

~ : Coefficient de pulsation dépendant de la hauteur H de chaque niveau considéré. << Annexe 2- c>>

0 = 1 pour les constructions prismatiques [11]

Les périodes calculées dans le cadre de ce projet sont très faible et donc ~ est presque nul. On prendra ~ =1 selon [11]

2-6 Détermination de la pression de calcul du vent.

La pression statique de calcul du vent est finalement donnée par la formule suivante:

q =q10*o*ks*km*Cr * ~ (2-8)

2-7 Action d'ensemble sur le pylône

Cette action permet de calculer les éléments principaux assurant la stabilité de l'ouvrage. L'action d'ensemble du vent soufflant dans une direction donnée sur une construction est la résultante géométrique de toutes les actions sur les différentes parois. Pour le cas des pylônes, il s'agit de la composante horizontale T qui est la Traînée, produisant un effet d'entraînement et de renversement ;

T=q*Ct*Sp (2-9)

Ct =Le coefficient de trainée << voir chapitre3, § 4 >> Sp = surface pleine de la paroi << voir chapitre3, § 4 >>

2-7-1-1 Action d'ensemble sur les antennes

Seules les antennes FH et GSM (figures 1-3 et 1-4) seront prises en considération dans le dimensionnement des pylônes. La prise au vent de ces antennes s'effectue de la façon suivante: pour chaque antenne, suivre les étapes suivantes :

- calculer sa surface effective Sa (fonction de la forme de l'antenne);

- repérer sa position P par rapport au pied du pylône ;

- relever le coefficient de trainée Ct correspondant en fonction de son azimut; - déterminer la surface équivalente :

Seq = Ct. Sa. P/H (2-1 0)

Où H est la hauteur du pylône ;

% appliquer la même opération pour toutes les antennes et sommer ces surfaces : cette surface est appelé charge en tête du pylône. Cette surface correspond à celle d'une antenne fictive placée sur l'entête du pylône.

% Il faut multiplier la charge en tête par la pression dynamique en tête pour avoir la force qui sera appliquée horizontalement à l'en tête du pylône. Si on note _Feq la force créée par l'antenne, on aura

Feq = Ct. QH. Seq (2-11)

Cette force est appliquée normalement sur les deux noeuds supérieurs au vent. Le tableau ci-contre récapitule le calcul de la charge en tête d'un pylône.

Tableau 2-7 : Calcul du coefficient de trainée sur les antennes

Azimut	0	15	30	45	60	75	90	105	120	135	150	165	180
Ct	1.312	1.289	1.222	1.122	1.037	0.696	0.644	0.742	0.821	0.94	0.987	1.066	1.148

Tableau 2-8 : calcul de la charge en tête d'un pylône

Antenne de transmission
Quantité	Diamètre (m)		Sa (m^2)	Coef de trainée	position	Hauteur du pylône	Seq1 (m^2)
ni	di		Pi.di^2/4	Cti	Pi	H	Sai.Pi/H
Antenne radio
Quantité	longueurs		Sa	Coef de trainée	position	H (m)	Seq2
mi	L i	li	Li.li	Cti	Pi	H	Sai.Pi/H
Surface en tête totale (m^2)							Seq1 +Seq2

L'antenne placée sur l'en tête du pylône crée une excentricité qui provoque un moment de torsion sur les membrures. Ce moment est égal à la force en tête multiplié par cette excentricité. L'excentricité est prise forfaitairement égale à 50 cm. [11]

La surface en tête du pylône sera donc la somme des surfaces des antennes GSM et FH. La surface en tête étant connue, il suffit de la multiplier par la valeur de la pression correspondante à la hauteur du pylône pour avoir la force. A cette force de vent, s'ajoute le poids propre de l'antenne et le moment crée par l'excentricité des antennes.

2-8 Dimensionnement

L'instabilité à vérifier est le flambement. Il est très important de vérifier que les éléments comprimés (barres comprimées de treillis) présentent une sécurité suffisante vis à vis du flambement car celui-ci se produit sans prévenir et entraîne souvent non seulement la propre ruine de l'élément, mais aussi celle de tout le pylône.

2-8-1 L'analyse globale du premier ordre

Le but de l'analyse globale est d'abord de déterminer la distribution des sollicitations à l'intérieur des différents composants du pylône. Le comportement mécanique du pylône sous les charges qui lui sont appliquées est traité par GENIE en utilisant la méthode des éléments finis. Le calcul est basé sur la théorie linéaire ou au premier ordre des poutres qui suppose les hypothèses suivantes :

- les déplacements des sections sont petits : les équations d'équilibre statique sont écrites en prenant en compte la géométrie de la structure non déformée ;

- le matériau, notamment l'acier, a un comportement élastique linéaire : effort et déformation sont proportionnels et il y a réversibilité c'est-à-dire que la structure revient à son état initial dès que la perturbation qui l'en a écartée disparaît ;

- les assemblages sont idéalisés sous la forme d'assemblages rotulés.

2-8-2 Vérification de la résistance des sections transversales de classe 3.

2-8-2-1 Traction

La valeur de calcul de l'effort de traction _NED dans chaque section transversale doit satisfaire la condition suivante [4]:

NED ~ #$%&

'~ (2-12)

Où A est l'aire de la section transversale, fy est la limite élastique du matériau et 7M0 est le coefficient partiel de sécurité portant sur la résistance mécanique du matériau caractérisée par sa limite élastique. Ce coefficient est actuellement être pris égal à 1

2-8-2-2 Compression

La valeur de calcul de l'effort de compression _NEd dans chaque section transversale de classe 1, 2 ou 3 doit satisfaire la condition suivante [4]:

NED ~ #$%&

'~ (2-13)

2-8-2-3 Résistance au flambement - Elément comprimé

Le flambement est le mode de ruine prépondérant et le plus dangereux des composants comprimés. Il se traduit par une déformation de flexion brutale du composant à partir d'un niveau donné de l'effort de compression. Une barre comprimée doit donc être vérifiée vis-à-vis du flambement de la façon suivante:

N Ed ~ N b,Rd (2-14)

Où Nb,Rd est la valeur de calcul de la résistance de la barre comprimée au flambement. Pour des sections transversales de classe 1, 2 ou 3 on a [4]:

N b,Rd = x.A.fy

YM1 (2-15)

Où YM1 est le coefficient partiel de sécurité de résistance et qui vaut 1.1. [4]

x est le coefficient de réduction pour le mode de flambement. Il est donné par la formule

x= (13402- .2

mais z = 1.0 ( 2-16)

où (p = 0.5 [1+ a ( A - 0.2) + A²]

a est un facteur d'imperfection, pour les cornières à ailes égales, il est égal à 0.49 [2]: A est l'élancement réduit donné par:

A = X / X1 (2-17)

X1 =ð ( E / fy)^0.5 (2-18)

I, = Ler/iv (2-19)

iv est le rayon de giration suivant l'axe concerné, déterminé à partir des caractéristiques brutes de la section.

Figure 2-5 : Algorithme de calcul du coefficient de réduction

2-8-2-4 Vérification aux états limites de service

° Flèches horizontales

La flèche en tête du pylône doit être inférieure à h/200 où h est la hauteur du pylône [4] et [11]. ° Twist

Cet angle doit être inférieur au dépointage imposé par OCM

2-8-3 Algorithmes de vérifications

Dans cette partie, nous donnons l'algorithme du processus de diagnostic basé sur l'Euro code 3 à partir de toutes les vérifications présentées précédemment. L'ensemble de ces algorithmes est intégré dans GENIE. La figure (2.6) donne un aperçu global sur le diagnostic imposé par l'Eurocode 3. L'analyse linéaire par GENIE permet de déterminer les valeurs de calcul des efforts dans les barres, les déplacements aux noeuds et les fréquences propres de la structure. Ces valeurs sont utilisées pour la vérification d'états limites ultimes et d'états limites de service pour chaque élément de la structure.

Section mauvaise

Figure 2-6 : algorithme de dimensionnement au flambage

2-9 Conclusion

Dans ce chapitre nous avons présenté les exigences relatives au calcul des différentes contraintes et à la stabilité des éléments des structures tendues ou comprimées (treillis plans). Le calcul des sollicitations dans les éléments est basé sur l'analyse globale élastique linéaire ou analyse au premier ordre

chapitre-3 Formulation des éléments finis

3-1 Introduction

Les pylônes que nous calculons font partie des structures discrètes qui sont composées d'éléments barres assemblées par boulonnage en des points appelés «noeuds», et soumises à des forces extérieures que sont : la pression due au vent, le poids propre du pylône et des antennes. Sous l'effet de ces forces, le pylône peut se déformer et des contraintes internes dans chaque élément peuvent se manifester. Cette dernière est entièrement définie par les caractéristiques géométriques de la section courante (aire, module d'Young etc.) et la géométrie de la fibre moyenne. Les efforts appliqués à chaque barre sont schématisés comme charges ponctuelles. Les sollicitations résultantes sont obtenues sous la forme d'un seul effort (effort axial) en chaque point de la fibre moyenne. Des relations simples reliant l'effort aux caractéristiques géométriques de la section permettent de déduire les contraintes dans la section. L'application de la théorie des poutres à des structures simples comme les treillis simples, conduit à des solutions analytiques complètes. En revanche, pour les structures plus complexes comme le pylône, le recours à une méthode numérique est nécessaire telle que la méthode aux éléments finis qui est systématiquement et aisément programmable. Le problème de l'analyse linéaire des structures formées de poutres par la méthode des éléments finis est bien connu. Nous nous limiterons, ici, à évoquer les formulations éléments-finis utilisées dans le GENIE avec les références nécessaires pour l'analyse statique et modale des structures de type treillis plans obtenus par assemblage de barres articulées aux extrémités. Les éléments d'un treillis ne travaillent qu'en traction ou compression. Ils sont modélisés par des éléments finis de type barres (figure 3-1).

Figure 3-1 : discrétisation en éléments finis d'un treillis plan

3-2 Concept de base de la méthode des éléments finis

La méthode des éléments finis (M.E.F.) est un des outils les plus efficaces et les plus généraux pour l'analyse des structures dans de nombreux secteurs de l'industrie : aérospatial, automobile, nucléaire, génie civil, construction navale, mécanique, constructions off-shore, etc. Dans le domaine du calcul des structures, la M.E.F. est une technique à caractère pluridisciplinaire qui met en oeuvre des connaissances relevant de plusieurs disciplines de base telles que la mécanique des structures, l'analyse numérique et l'informatique appliquée. Les bases théoriques de la M.E.F. reposent d'une part sur les méthodes énergétiques de la mécanique des structures et d'autre part sur les méthodes d'approximation spatiale des fonctions. La M.E.F. est basée sur une décomposition du domaine dans lequel on désire effectuer la simulation en sous-domaines de forme géométrique simple appelés « éléments finis » pour lesquels on procède à des approximations nodales des champs de déplacements ou de contraintes qui prennent en général la forme de fonctions polynomiales. L'ensemble de ces éléments constitue ce que l'on appelle le maillage du domaine. Ces éléments sont liés par un nombre fini de conditions de continuité, exprimées en certains points communs à plusieurs éléments appelés `noeuds'. Ce sont les méthodes classiques du calcul des structures, méthode des déplacements et méthode des forces, qui sont à la base de la M.E.F. Selon que l'on approxime le champ des contraintes ou le champ des déplacements, on crée le modèle contrainte ou le modèle déplacement. Le modèle déplacement semble plus commode à mettre en oeuvre car il s'adapte généralement mieux aux problèmes de calcul des structures et sera adopté dans ce qui suit. Dans la méthode des déplacements, la formulation du problème est faite en fonction des déplacements aux noeuds qui sont les inconnues cinématiques. La structure est préalablement discrétisée en éléments finis. Le

calcul est conduit suivant deux niveaux de formulation : élémentaire au niveau de l'élément fini et globale au niveau de la structure complète.

3-2-1 La formulation élémentaire au niveau de l'élément fini

Pour chaque élément et dans un repère local, on choisit une fonction d'interpolation qui représente la variation des déplacements à l'intérieur de cet élément en termes de déplacements nodaux. Puis, on calcule pour chaque élément ses matrices de rigidité et de masse ainsi que son vecteur des forces. Ces caractéristiques élémentaires sont transformées par la suite dans le repère global de la structure.

3-2-2 La formulation globale au niveau de la structure complète

Elle consiste à rechercher pour la structure complète l'expression matricielle de l'énergie potentielle en fonction des déplacements inconnus en tous les noeuds de la structure. Cette étape nécessite l'assemblage des matrices de rigidité et de masse et les vecteurs forces et déplacements de la structure à partir des caractéristiques élémentaires (matrices de rigidité et de masse et vecteurs forces et déplacements de chaque élément).

3-3 Démarche de formulation éléments finis

L'analyse des structures de type treillis peut s'effectuer en considérant d'abord le comportement de chaque partie (élément barre) indépendamment puis en assemblant ces parties de telle façon que l'équilibre des forces et la compatibilité des déplacements soient satisfaits en chaque noeud. [2] et [7]

Dans la suite, toutes les grandeurs vectorielles et matricielles relatives à la base locale de l'élément sont surlignées d'une barre.

3-3-1 Discrétisation de la structure en éléments finis

C'est l'ensemble des opérations à effectuer pour établir le modèle mathématique de calculs représentant au mieux la structure réelle. Pratiquement cette idéalisation consiste du point de vue topologique, à ramener la structure à une géométrie simple ; c'est ainsi qu'on réduit les éléments unidimensionnels à leur axe et on définit les conditions d'appuis et les charges. Au

point de vue rhéologique, elle consiste à choisir la loi constitutive du matériau et à déterminer les constantes qui définissent cette loi.

3-3-2 Construction de l'approximation nodale par sous domaine

Pour chaque élément, on choisit une fonction d'interpolation qui représente la variation des déplacements u^e (x, y) à l'intérieur de cet élément en termes de déplacements nodaux I^le. Ce modèle peut être représenté de façon commode par une expression polynomiale contenant un coefficient inconnu pour chaque degré de liberté. Soit, [2] et [7]

u^e (x, y) = N t ~le ( 3-1)

Où N est la matrice d'interpolation reliant les déplacements d'un point intérieur de l'élément aux déplacements nodaux.

3-3-3 Etablissement de la relation entre déformations et déplacements

Il s'agit ici de trouver la matrice B reliant les déformations 8 de l'élément à ses déplacements nodaux U^le. Cette relation est exprimée par :

{ e }= Â Ul^e (3-2)

3-3-4 Etablissement de la relation entre contraintes et déformations

Pour un matériau élastique linéaire, les contraintes a sont des fonctions linéaires des déformations E. Elles sont exprimées par l'expression :

{0 }= D { e } (3-3)

Où D est la matrice d'élasticité.

3-3-5 Calcul des matrices élémentaires.

Cette étape constitue la partie la plus importante du problème. Les déplacements U^e aux noeuds sont déterminés de telle façon que les contraintes engendrées dans l'élément équilibrent le chargement extérieur Fe, c'est-à-dire que :

/l^e Il^e = P^e ( 3-4)

Il^e est la matrice de rigidité de l'élément exprimée dans le repère local. Elle est déduite de l'énergie de déformation de l'élément et exprimée par [2] et [7] :

k^e=f _vB^t D B dv (3-5)

Il faut aussi calculer la matrice de masse M^e de chaque élément. Cette matrice est déduite de l'énergie cinétique de l'élément. Dans le repère local de l'élément, cette matrice est donnée par l'expression [2], [7]

M^e=f _vpN^t N dv ( 3-6)

où p est la masse volumique du matériau constituant l'élément.

Finalement, on exprime les matrices K~ e_, me, Ue et F^e dans le repère global défini pour toute la structure.

3-3-6 Assemblage des matrices élémentaires

La phase de l'assemblage consiste à construire les matrices K, M et F de la structure complète à partir des matrices élémentaires K^e, M^e, U~^e _et F~^e exprimées dans le repère global, des différents éléments en sommant les énergies de déformation et cinétique de chaque élément. Pour une structure formée de barres, on ne peut pas sommer les matrices directement, car elles ne sont pas exprimées en fonction des mêmes variables. Pour chaque élément, il faut localiser la position des variables nodales dans le vecteur des déplacements de l'ensemble des noeuds de la structure. Cette opération consiste à ranger les termes des matrices élémentaires dans une matrice globale.

Exemple d'assemblage : [6]

Il y a lieu de remarquer lors de l'assemblage des deux systèmes élémentaires que les composantes qui correspondent au noeud n occupent les positions 2×n et 2×n-1 dans la matrice globale. On généralise ainsi cet assemblage en calculant une table de localisation à partir de la table des connectivités.

3-4 Elément fini barre

3-4-1 Définition

Géométriquement, une barre correspond à un solide orienté dans la direction x (repère local). Les dimensions dans le plan (y--z) normal à x sont relativement petites par rapport à la

dimension longitudinale (figure 3-2). Un élément fini barre (figure 3-3) schématise un composant d'une structure qui travaille uniquement en traction ou compression. C'est généralement un élément à 2 noeuds, qui comporte 3 inconnues ou degrés de liberté (d.d.l.) par noeud représentant les composantes de son déplacement dans l'espace.

Figure 3-2 : géométrie d'un élément barre

Figure 3-3 : modélisation d'un élément barre

Les principales hypothèses pour un élément barre rectiligne qui ne travaille qu'en traction ou compression sont :

- Petits déplacements

, U

, (M, t) = u

(x, t) x

( 3-7)

- Déformations en petits déplacements :

s =

Ou Ox

(3-8)

- Loi de Hooke dans un milieu isotrope homogène élastique :

a = E E

( 3-9)

avec a, la contrainte dans la barre et E est le module de Young du matériau. En intégrant les contraintes sur la section A, nous obtenons la loi de comportement intégrée des barres:

n(x) = E A E (3-1 0)

Où n(x) est l'effort normal dans la barre dû à la force nodale F.

3-4-2 Formulation de l'élément barre dans le plan

3-4-2-1 Identification du problème

Considérons un élément barre dans le plan défini par deux noeuds i et j, de longueur L et de section uniforme A (figure 3-4).

Figure 3-4 : élément barre dans le plan (i ,x,y)

Dans le repère local (i,.,~ y), on note par u_xi et 1~xj les déplacements aux noeuds i et j, et

~	~
par f xi et f		xj les forces aux noeuds i et j. Le vecteur force relatif à l'élément e est donné par :

xj f^~yj] (3-11)

~

~

~

F^e= [ f

xi fyi f

Le vecteur déplacement est donné par:

U^~e= [U_xi U_yi U_xj U_yj] (3-12)

~ ~

Dans le cas qui nous occupe, f_yi fyj, U_yj et U_yj sont nuls puisque l'élément barre ne travaille qu'en traction ou compression.

3-4-2-2 Fonction d'interpolation

Pour un problème statique, lorsque l'élément est chargé au niveau de ses noeuds, l'effort normal est uniforme. Compte tenu des relations (3.8) et (3.10), la solution u(x) sera linéaire. Pour chercher cette solution, nous allons utiliser une approximation polynomiale linéaire de la forme :

u(x) = N1 fixi + N2 fixj (3-13)
où N1 et N2 sont les coordonnées naturelles.

Nous identifions aux noeuds i (x=0) et j (x=L) la valeur de l'approximation des déplacements axiaux. Nous en déduisons :

N1= 1- ^x_i et N2= ^x_i (3-14)

Sous forme matricielle nous écrivons :

U(x)=Nt U^e = [1- A _B A B]C9A~

9A~D (3-15)

La matrice N d'interpolation reliant les déplacements d'un point intérieur de l'élément aux déplacements nodaux est donc :

_{N= [1-} x x]t (3-16)

/ /

3-4-2-3 Relation entre déformation et déplacement

La déformation est déduite des expressions (3.8) et (3.13). Soit :

E=

du dx⁼

¹₁[-1 1]C^9A~

9A~D = B Ue (3-17)

La matrice B reliant les déformations de l'élément à ses déplacements nodaux est alors

 = ¹₁[ 1 1] (3-18)

3-4-2-4 Matrice de rigidité d'une barre dans le plan

La forme de la matrice de rigidité 2 ^e de l'élément dans le repère local est donnée par l'expression (3.5). La matrice d'élasticité D se réduit au scalaire E (module de Young du matériau). Soit, après intégration :

Ke = A*E 1

[^1I~ I ~ J (3-19)

3-4-2-5 Matrice de masse d'une barre dans le plan

La matrice de masse M^e dans le repère local est déterminée à partir de l'expression (2.6). Soit, après intégration :

_Me =

p*A*1 [2 11 (3-2 )

⁶ 2

L'expression de la matrice masse telle qu'elle est obtenue en (3.20) est appelée masse cohérente ou répartie. Il est possible de concentrer la masse de l'élément en ses extrémités. On attribue à chacun des deux noeuds la moitié de la masse totale de l'élément soit :

M^e

KF#FB

~ H

= J ~~~~~~

3-4-2-6 Transformation dans le repère global

Soit uxi , uyi , uxj et uyj les déplacements aux noeuds i et j exprimés dans le repère global (figure 3.5). La relation entre les déplacements exprimés dans le repère local et ceux exprimés dans le repère global est donnée par :

1xi =uxi ^cx+ _uyi c_y (3-22)

1xj =uxj ^cx+ _uyj c_y

Oil cx et cy sont les cosinus directeurs définis par :

~ ~

cx= _B (xj-xi) et cy= _B (yj-yi) ~~~~~~

Avec l la longueur de l'élément calculée à partir des coordonnées des noeuds. Soit :

l=*(xj -- x02 + (yj -- yi)2 (3-24)

Sous forme matricielle, on écrit :

9A

C9A~

u31

La matrice transformation du repère local au repère global est :

9A~D =CRA R& 9&

RA R&D ^S _9A T ~~~~~~

T = rcx cy 001

0 0 cx cy (3-26)

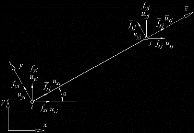
Figure 3-5 : élément dans le repère global

La matrice de rigidité exprimée dans le repère global sera déduite de la matrice de rigidité exprimée dans le repère local par la relation [2], [7]:

K^e = T^t K^e T (3-27)

De même, la matrice de masse de l'élément barre dans le plan exprimée dans le repère global est donnée par l'expression.

Me = _Tt Me T (3-28)

3-4-2-7 Charges appliquées sur les éléments

Dans le cas d'une charge répartie q sur un élément, celle-ci est rapportée aux noeuds d'extrémités. Le vecteur de charge nodale correspondant est :

Fe_r = f N^t q ds (3-29)

Pour une charge uniformément répartie sur un élément poutre dans le plan (figure 3.6), le vecteur de charges nodales équivalent est :

B

Fe_r= q f 0 Nt dl (3-3 0)

Pour une barre de treillis, la notion de charge répartie transversale n'est pas cohérente avec la théorie, la modélisation de type barre ne prenant pas en compte la raideur flexionnelle. La force répartie d'une barre doit être modélisé par deux forces, concentrées aux noeuds d'extrémités, statiquement équivalentes au poids total de la barre (figure 3.6)

Fe_r = [0 -⁽¹₂¹ 0 ⁽¹₂¹] ( 3-31)

Figure 3-6 : force répartie sur une barre

Soit un tronçon donné du pylône, le vent agit uniformément sur toutes les barres du tronçon.

- qH est la pression statique du vent,

- Sp la surface pleine du tronçon, celle qui est en contact avec le vent, - Si, la surface totale, les vides étant obturés

Suivant [5],

el =Sp/Si (3-32)

cI est généralement compris entre 0.08 et 0.35. Pour les constructions prismatiques, le coefficient de trainée est égal à : [5]

Ct = 3.20 - 2.0 ( 3-33)

L'action d'ensemble T s'exerce sur tous les éléments du tronçon (figure3-7). Cette action est ensuite répartie sur les membrures (figure 3.8) et devient T/2.l

où l est la longueur de la membrure. En appliquant la formule (3-31), on transforme cette force linéique en force ponctuelle (figures 3-9 et 3-10). Le même travail est fait pour les autres tronçons. La figure 3-9 est l'illustration d'un tronçon du pylône sous l'action du vent.

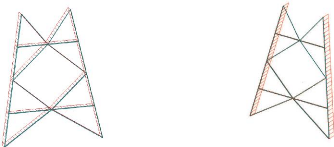
Figure 3-8 : force répartie sur les barres Figure 3-7 : force répartie sur les membrures

Figure 3-10 : force nodale Figure 3-9 : force nodale

3-5 Formulation d'un élément poutre en torsion

3-5-1 La matrice de rigidité

Considérons la poutre représentée à la figure (3-11) sollicitée par un moment de torsion mx.

Figure 3-11 : Elément poutre en torsion

La rotation varie linéairement le long de la longueur de la poutre et peut être exprimée de la manière suivante :

Ox = N1 Oxi+N2 Oxj (3-34)

oil N1 et N2 sont les coordonnées naturelles définies par l'expression (3.14). L'angle á de torsion le long de l'élément est donné par :

d0x

á = dx

¹,[-1 1][ t] = (3-35)

Le moment de torsion mx est exprimé par :

m_x= G It á = G It ¹,[-1 1] (3-36)

oil It est le moment d'inertie de torsion et G est le module de cisaillement du matériau. En assimilant le moment m_x à la contrainte ó, les matrice B et D sont données par :

D = G It ( 3-37)

 = / 1

[ 1 1] (3-38)

Compte tenu de l'expression (3.5), la matrice de rigidité de l'élément fini poutre en torsion exprimée dans le repère local est :

_Ke = G*₁ It [ --1 1 -. 1 --11 (3-39)

3-6 Résolution en analyse statique

3-6-1 Systèmes d'équations linéaires

L'analyse statique consiste à calculer la réponse statique linéaire d'une structure soumise à des charges ponctuelles ou réparties. Dans le cas statique l'énergie potentielle s'écrit [7]:

Ð=¹U^tK U -U^t F (3-40)

2

Les extremums de cette énergie sont :

??/ ?U = KU - F = 0 (3-41)

D'où:

KU = F (3-42)

La résolution de ce système linéaire permet de déterminer le vecteur U des déplacements inconnus. On calculera par la suite, les réactions, les efforts et les contraintes dans les éléments de la structure

3-6-2 Prise en compte des conditions de déplacement imposé

Dans l'expression l'équation (3-42), la matrice de rigidité K de la structure est singulière. Cela implique qu'il existe des déplacements qui doivent être éliminés en introduisant les conditions aux limites cinématiques. Avant de résoudre ce système d'équations pour déterminer le vecteur U des déplacements inconnus, il faut donc prendre en compte les conditions aux limites. Pour appliquer cette condition, on élimine les lignes et les colonnes correspondants dans les matrices K et M ainsi que du vecteur F.

3-6-3 Résolution du système linéaire

La résolution du système permet de déterminer le vecteur Ui des déplacements inconnus. En pratique, la matrice K à laquelle on aboutit est de grande taille. Le coût de la résolution numérique de ces systèmes d'équations est une partie significative du coût global de l'analyse. Il existe des méthodes de résolution appropriées qui tirent profit du caractère symétrique de la topologie de la matrice de rigidité. La matrice présente quelques propriétés intéressantes qui peuvent être exploités pour résoudre efficacement le système [3]:

- Symétrique,

- Définie positive (toutes les valeurs propres sont positives), - Disposée en bande autour de la diagonale,

- A diagonale dominante,

- La matrice K est très bien conditionnée (conditionnement =1).

Pour que la matrice remplisse les conditions ci-dessus, il est important de bien numéroter les noeuds. Pour les structures à deux dimensions, la matrice de rigidité a généralement la forme de la bande matrice si les points nodaux sont bien numérotés, tel que la largeur de la bande de la matrice de rigidité soit plus étroite. Et donc les problèmes de stockage peuvent être réduites et les équations sont résolues en utilisant la méthode d'élimination directe au lieu des itérations, la largeur de la bande pour une structure assemblée d'éléments finis est trouvée par l'équation générale suivante [9]:

L = 2[mn + ( n -1)]+1 (3-43)

m : La différence maximale entre deux noeuds d'un même élément fini.

n : Nombre de degrés de liberté pour chaque noeud.

Exemple de numérotations:

Numérotation horizontale :

Dans cet exemple tel que la numérotation des points nodaux est horizontale, la largeur de la bande de la matrice pour une structure à deux dimensions vaut : L=19

Numérotation verticale

Dans cet exemple tel que la numérotation des points nodaux est verticale, la largeur de la bande de la matrice pour une structure à deux dimensions vaut: L = 23

Donc la largeur de la bande est minimale dans le premier système de numérotation c'est à dire la numérotation horizontale, elle sera donc adoptée dans la suite de ce travail.

La méthode la plus pratique pour résoudre ce genre de problème est celle de CHOLESKY (voir. chapitre 3, § 8).

3-6-4 Calcul des efforts

Les efforts intérieurs se calculent élément par élément à partir des déplacements exprimés dans le repère local de l'élément. Ils sont obtenus en écrivant les équations élémentaires d'équilibre ; soit en statique pour un élément,

~^~ei = Ke ~~e i (3-44)

La somme des efforts exercés sur un noeud doit être nulle. Nous pouvons donc tester la précision de la résolution du système en calculant les résidus d'équilibre locaux. Les contraintes sont calculées à partir des efforts en fonction de la forme et des dimensions de la section transversale.

3-7 Résolution en analyse modale

3-7-1 Système d'équations aux valeurs propres

La recherche des fréquences et modes naturels d'une structure s'appelle l'analyse modale. L'énergie potentielle Ð totale de la structure due aux vibrations libres de l'élément est : [6]

n =₂¹U^t K U ₊1 Ut MU
^·
· (3-45)

2

Les extremums de cette énergie sont donnés par la relation :

· · an/ aU = MU

+ KU = 0 (3-46)

Et l'équation matricielle associée à l'analyse électrodynamique pour un régime libre est définie

par :

·
·

MU

+ KU = 0 (3-47)

Les solutions recherchées pour l'équation sont régies par une loi temporelle et, pour autant que la matrice de rigidité soit non singulière, sont de type harmonique

u(t) = p a cos (wt - co) (3-48)

a, 03 et (p sont des nombres réels dénotant respectivement l'amplitude de référence, la pulsation et la phase de la fonction. Cette relation traduit physiquement que chaque d.d.l. de la structure suit un mouvement en phase avec tous les autres déplacements généralisés. Compte tenu de cette expression, l'équation (3 - 47) associée au régime libre devient :

(K - co²M) p = 0 (3-49)

Ce système homogène de n équations linéaires admet n solutions non triviales pi (i = 1,2,..., n) telles que soient vérifiées les équations :

(K - co²iM) pi = 0 i = 1, 2, ..., n ( 3-5 0)

alors que

ui = pi ai cos (coi t - (pi) (3-51)

est le mode propre élastique de rang i à amplitude de référence ai et de déphasage (pi. En termes de mécanique des structures le vecteur pi est le vecteur modal et coi est la pulsation propre associée, mesurée en rd/s. Les grandeurs co sont les racines de l'équation algébrique suivante

det (K - w²M) = 0 (3-52)

3-7-2 Résolution du système aux valeurs propres

La résolution d'un système aux valeurs propres est beaucoup plus coûteuse que celle d'un problème statique. En fait, il s'agit d'un problème non linéaire, et beaucoup de méthodes s'appuient sur la résolution d'une succession de systèmes linéaires, en interne. De nombreux algorithmes performants ont été développés pour l'extraction numérique des caractéristiques modales d'une structure. Pour la résolution du système, nous avons utilisé la méthode de factorisation QR qui est un sous module de matlab. Cette méthode est généralement considérée comme étant la plus robuste et la plus performante pour déterminer l'ensemble des valeurs propres quand les matrices structurelles sont de petite taille ou à grande largeur de bande [3] et [6]

3-8 Algorithmes de résolution

La mise en oeuvre d'un programme d'éléments finis pour les structures d'assemblage de barres nécessite en premier lieu une bonne organisation du fichier de données. Le programme destiné au calcul de notre pylône doit avoir une structure qui permet d'effectuer trois grandes tâches : lecture de données, traitement des données, calcul de la solution et affichage des résultats. Ce processus peut être décrit par l'organigramme de la figure.

Figure 3-12 : Organigramme d'analyse linéaire par la M.E.F. d'une structure à de poutres

3-8-1 Lecture des données

La partie du programme destinée à la lecture des données doit pouvoir construire des variables pour la géométrie du pylône, la charge en tête du pylône, le poids des antennes, la zone géographique, les cornières à utiliser et le chargement extérieur. La géométrie concerne la hauteur du pylône, les sections de base et d'en tête, la charge en tête du pylône qui est la somme

de toutes les surfaces des antennes placées sur le pylône telle que calculée au tableau 2-7. La zone géographique fait intervenir la zone où est placé le pylône. Les cornières sont entrées sous forme d'une matrice de 13 lignes correspondant aux 13 tronçons du pylône le plus haut soit celui de 72 mètres et 5 colonnes, les colonnes représentent les cornières à utiliser pour les membrures, les diagonales, les traverses, les raidisseurs diagonales et les raidisseurs traverses respectivement. Ces données sont entrées sur l'interface de GENIE.

3-8-2 Traitement des données

Il s'agit ici de construire les éléments nécessaires dont a besoin le programme d'éléments finis : il s'agit de :

3-8-2-1 Les coordonnées et les connectivités de tous les noeuds du pylône

Les coordonnées et les connectivités de tous les noeuds sont calculées pour chaque type de tronçon en fonction de sa grande base, sa petite base et sa hauteur. Le programme combine les tronçons selon la hauteur du pylône en ajoutant aux ordonnées des tronçons la hauteur du tronçon précédent.

Exemple :

Soit pour un pylône de 36 mètres qui est constitué successivement de 5 tronçons de type 4, un tronçon de type 5 et un tronçon de type 6. (Figure 2-4)

- Etape1 : Les coordonnées et les connectivités de tous les noeuds du premier

tronçon sont connues, il faut recalculer ces coordonnées et ces connectivités 4 fois en modifiant à chaque fois les grande et petite bases et en ajoutant aux ordonnées la hauteur des tronçons précédents. Après ces opérations, le pylône aura une taille de 30 mètres.

- Etape 2 : Nous ajoutons le tronçon de type 5 tout en augmentant aux ordonnées de
ce tronçon la hauteur de 30.

- Etape 3 : On termine en ajoutant le tronçon de type 6 en augmentant également à

ses ordonnées la hauteur de 32 mètres.

Cette fonction que nous appelons « schéma » est décrite en annexe 3-a. Le même travail est fait pour les autres pylônes de hauteurs différentes.

La fonction « plotmesh » (annexe 3-g) permet d'afficher le pylône qui est une figure du maillage, elle permet donc, avec le tracé de la structure saisie, une vérification visuelle des éléments et des noeuds :

3-8-3 Calcul de la solution

Une fois la géométrie saisie, on peut calculer les matrices de rigidité et de masse assemblées. On crée une fonction << truss2dKM » (annexe 3-i) pour les deux matrices et à la fois. Les variables d'entrée communes aux deux matrices sont : la hauteur, la base, l'en tête, la pression à 10 mètres, la charge en tête, la masse des antennes, le tableau des cornières, le coefficient de site et la direction du vent

On ajoute les modules d'élasticité pour la matrice de rigidité et les masses volumiques pour la matrice de masse.

Il est à remarquer qu'on initialise les matrices de rigidité et de masse avec des matrices creuses (sparse). L'avantage qu'offre les matrices creuses est que seuls les éléments non nuls sont sauvegardés en mémoire. MATLAB est équipé d'une structure de données et de plusieurs fonctions pour prendre en charge toutes les opérations matricielles sur ce type de matrices et d'une façon pratiquement imperceptible pour l'utilisateur. Pour la construction de ces matrices, on introduit ici une table de localisation Li qu'on calcule avec la fonction << localise » (annexe 3- b) et qu'on utilise à la place de la table des connectivités pour l'assemblage des matrices. Pour le calcul des matrices élémentaires << fonction truss2dke » (annexe 3-h), on a besoin de connaitre les coordonnées des noeuds, leurs sections, la densité de l'acier et le module de Young. La longueur et les cosinus directeurs de l'élément sont calculés à partir des coordonnées de ses noeuds, ces longueurs, cosinus et sinus sont par la fonction << etlen » (annexe 3-c)

3-8-3-1 Résolution du système discret

a. Système linéaire KU =F

Les conditions d'appuis sont l'ensemble des déplacements nuls aux niveaux des appuis. La matrice K initialement est singulière. Le vecteur << nul » dans le fichier de données est utilisé pour spécifier les degrés de liberté à bloquer. Pour appliquer cette condition, on élimine les lignes et les colonnes des matrices de rigidité et de masse ainsi que du vecteur force puisque le

Chapitre3 : Formulation des éléments finis chargement est saisi pour tous les noeuds y compris ceux d'appuis. Cette opération rend la matrice K régulière. Voir fonction « deldofs » (annexe 3-d)

La factorisation de Cholesky, consiste, pour la matrice symétrique définie positive K, à déterminer une matrice triangulaire inférieure L telle que : K=LL^T. La matrice L est en quelque sorte une « racine carrée » de A. Nous nous servons de la fonction matlab « chol » pour décomposer la matrice K en un produit de fonction triangulaire inférieure et supérieure. Soit K=L*L^T, il suffit de résoudre successivement les systèmes linéaires triangulaires supérieures et inférieures directement, une fois la solution calculée, il faut ajouter les déplacements des noeuds bloqués, voir fonction « addfos » (annexe 3-e).

b. Calcul des forces aux noeuds

Une fois les déplacements obtenus, il faut parcourir toutes les barres en multipliant ces déplacements par les matrices de rigidités élémentaires correspondantes. Cette fonction s'appelle « Trussforces » (annexe 3-f).

3-8-3-2 Résolution modale

On peut calculer les modes propres de la structure avec la fonction « eigs » qui résout le système

[K -- w² M] ~ = 0 ( 3-53)

Elle prend en argument d'entrée les deux matrice K et M et retourne comme résultat deux matrices : l'une orthogonale pour les vecteurs propres et l'autre diagonale pour les valeurs propres. Les modes propres sont donc les colonnes de la matrice des vecteurs propres et les périodes propres sont données par :

T = 2r/w. (3-54)

3-9 Création de l'interface graphique

L'outil GUI Matlab offre la simple possibilité de programmer des interfaces utilisateur dont le développement est relativement simpliste. Chaque objet (boutons, graphiques, listes) est défini par un certain nombre de fonction et de propriétés. Les fonctions sont utilisées pour

exécuter la construction de l'objet, ainsi que les événements le concernant (appui sur un bouton, choix dans une liste...). La fonction la plus intéressante est la fonction de << Callback >> qui est appelée lors d'une action de l'utilisateur sur l'objet. Les propriétés de l'objet sont stockées dans une structure de données. On y accède avec les fonctions << set >> et << get >>. Afin de passer toutes ces propriétés de fonction en fonction, mais aussi de pouvoir définir et stocker des variables globales, une super structure appelée << handles >> est utilisée dans le programme.

3-9-1 Etapes de conception

Il est clair que l'interface graphique passe par un certain nombre d'étapes : [8]

- Planification: délimitation du problème à résoudre,

- Analyse : Rassembler les équations mathématiques nécessaires

- Le Cahier de charges : définir les fonctions et tâches en détails : Enumérer les

différentes tâches voulues et rassembler les données nécessaires,

- La Conception : compléter le cahier de charge avec les détails de conception,

- Développer le design,

- Exemples d'écran (taille des fenêtres...),

- Disposition des boutons,

- Les couleurs, la forme d'écriture.

Description Du Problème		Analyse Du Problème		Algorithme		Programme		Interface Graphique

Figure 3-13 : étapes de réalisation de l'interface

3-9-2 Outil guide

Le GUIDE est un outil graphique qui regroupe tout ce dont le programmeur à besoin pour créer une interface graphique de façon intuitive. [15]

Figure 3-14 : outil guide

Le placement des objets est réalisé par sélection dans la boite à outils, mise en place et mise à dimension à la souris. Un double-clique sur chaque objet permet de faire apparaître un menu avec les propriétés de cet objet. Leur modification et l'aperçu de ces modifications sont immédiats. Au final, le code est généré automatiquement et l'interface est enregistrée sous deux fichiers portant le même nom mais dont les deux extensions sont .fig et .m. Le premier contient la définition des objets graphiques. Le second contient les lignes de code qui assurent le fonctionnement de l'interface graphique.

3-9-3 Programmation du guide

Nous avons gardé à l'esprit sept principes qui ont guidé la création de l'interface :

- L'utilisateur doit avoir le contrôle: l`utilisateur doit sentir que c`est lui qui a l`initiative d`une action.

- Etre direct: les différentes fonctions sont visuellement intuitives.

- La Cohérence: l`utilisateur ne doit pas passer beaucoup de temps à prendre connaissance notre application.

- L'esthétique:

- La simplicité: l'application est facile d`apprentissage et d`usage. L'utilisateur a l`accès à toutes les fonctions et informations de l`application, et la manipulation reste aussi simple que possible.

Nous avons testé plusieurs fois l'application avec différents intrants.

3-10 Conclusion

Dans ce chapitre, nous avons présenté les formulations élémentaires et globales utilisées dans cette application pour l'analyse statique et modale de calcul des pylônes par la méthode des éléments finis. La formulation élémentaire consiste à déterminer une fonction d'interpolation qui représente la variation des déplacements à l'intérieur de l'élément en termes de déplacements nodaux puis à calculer, pour chaque élément, ses caractéristiques élémentaires : matrice de rigidité, matrice de masse et vecteur des forces. La formulation globale consiste à rechercher, pour la structure complète, l'expression matricielle de l'énergie potentielle en fonction des déplacements inconnus en tous les noeuds de la structure. Ceci nécessite l'assemblage des caractéristiques élémentaires (matrices de rigidité, de masses, vecteurs forces) de tous les éléments. Ainsi, à partir des formulations énergétiques, nous aboutissons à un système d'équations linéaires qui régissent le comportement statique et modal de la structure.

chapitre-4 Application à un pylône de 36 mètres

4-1 Introduction

Un exemple de calcul statique et modal est traité pour le calcul des efforts internes, du déplacement en tête et des modes propres. Les résultats obtenus sont confrontés à ceux de la méthode analytique et au logiciel ROBOT MILLENIUM 2010. Nous traitons donc un pylône auto stable de 36 mètres. Toutes les données sont entrées sur l'interface ci-contre :

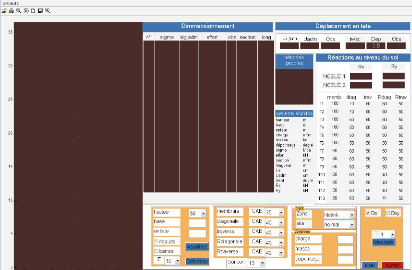
Figure 4-1 : interface de l'application Les données suivantes sont entrées :

- Base : 5 m

- Entête : 1m

- Charge entête : 20 m2

- Masse de l'antenne : 900 kg

- Type de site : protégé - Zone : Yaoundé

- Dépointage : 0.8°

- Direction du vent : Dx

4-2 Affichage (maillage) du pylône

Tout d'abord, il faut sélectionner la hauteur du pylône à construire dans << hauteur >>, entrer les sections de << base >> et d' << entête >>. Il est aussi possible de visualiser les numéros des noeuds et des barres. A ce stade, il faut cliquer sur << visualiser >> pour voir s'afficher le pylône à l'extrême gauche.

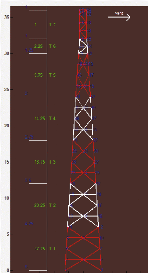
Figure 4-2 : maillage du pylône

Sur le schéma, on lit directement les surfaces totales des différents tronçons, les longueurs des tronçons etc.

Un clic sur l'onglet << déformée >> affiche la déformée du pylône selon l'échelle choisie. Cette touche fonctionne seulement si la charge en tête, la masse du pylône sont remplies.

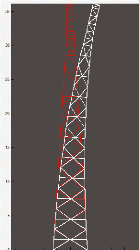
Figure 4-3 : pylône déformé à l'échelle 10

Le pylône initial est en rouge et celui déformé en blanc.

4-3 Choix de la région et de l'antenne

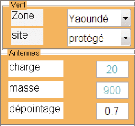
Figure 4-4 : choix de la région et antennes

Après avoir choisi la zone et le type de site, il faut entrer la charge en tête en mètres carrés, la masse en kg et le dépointage en degré ; par défaut, le dépointage est égal à 0.5°.

4-4 Choix des cornières

Pour chaque tronçon, choisir les cornières de la membrure, la diagonale, la traverse, le raidisseur- diagonale et le raidisseur-traverse correspondant à au tronçon désiré. La saisie est interactive puisque l'on visualise directement les changements sur le tableau suivant :

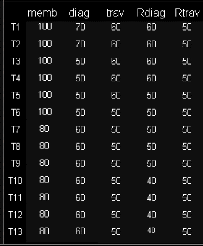
Figure 4-5 : listing des cornières

4-5 Affichage des résultats

Figure 4-6 : affichage des résultats

Il faut préciser la direction du vent, choisir le tronçon dont on veut afficher les résultats et un clic sur << résultats ». On observe ceci :

Figure 4-7 : déplacement en tête du pylône

- Ux : déplacement horizontal de l'en tête du pylône en centimètres, soit 19.10 cm,

- Uadm : déplacement limite imposé par [4] et [11], il vaut h/200 soit 36 m /200 = 18 cm où h est la hauteur du pylône

- Obs : zone de texte à deux états : si Ux est inférieur à Uadm, le message affiché est << bon », dans le cas contraire, la réponse est << non », on constate bien que 19.10 est supérieure à 18.

- Twist : rotation due à la torsion des membrures à l'en tête du pylône en degré,

- Dép désigne le dépointage c'est-à-dire la rotation maximale en tête du pylône, il est fourni dans le cahier de charge et est compris entre 0.3° et 1°,

- Obs fonctionne exactement comme celui décrit précédement.

4-6 Périodes propres du pylône : zone de texte

Figure 4-8 : Affichage périodes propres Ce sont les périodes de vibration propre du pylône en secondes

4-7 Vérification du dimensionnement

Figure 4-9 : résultat dimensionnement

A chaque fois que la contrainte est inférieure à la contrainte admissible, un message << bon >> apparait dans la colonne << obs >> et << non >> dans le cas contraire. Un message apparait aussi en rouge ou en vert selon que le tronçon est incorrect ou correct.

4-8 Réactions à la base du pylone

Figure 4-10 réactions au niveau de la base du pylône

Ce sont les réactions au niveau du sol :

Rx désigne la réaction horizontale et Ry la réaction verticale ; le noeud 1 désignant celui de gauche et le noeud 2 celui de droite.

4-9 Confrontation avec la méthode analytique

Une fois les résultats obtenus, nous passons au niveau de la vérification qui consiste à confronter simultanément nos résultats et ceux obtenus par la méthode analytique, ensuite positionner nos résultats par rapport obtenus par ROBOT MILLENIUM (annexe 4)

4-9-1 Principe de la méthode analytique

Cette méthode est basée sur le fait que chaque noeud isolé doit être en équilibre. Sur chaque barre, l'effort est nécessairement sur l'axe reliant les deux articulations. Par le fait même, les forces sur un noeud sont toujours concourantes. Donc, les efforts se rencontrent sur le noeud. En plus, on a vu que l'on ne peut pas charger un treillis sur une barre mais plutôt sur le noeud donc, on en arrive à un système de forces concourantes autour des noeuds [1].

Rapportons le plan du treillis à un repère orthonormé (O,x,y). Soit A un noeud relié à Ai par des barres Bi = AAi. Désignons par :

- F(x,y) la résultante des forces extérieures appliquées au noeud A.

:::;

- cIi l'angle polaire du vecteur AA i par rapport à (Ox),

- Ni l'effort normal dans la barre, Ni est supérieure à zéro si la barre travaille en traction et inférieure à zéro si la barre travaille en compression

y

Ai

Ni

~i

Bi

A

x

Si ^^:;i est la force exercée par la barre Bi sur le noeud A, on constate que la mesure

algébrique sur l'axe i:^; i est Ni en intensité et en signe. L'équilibre des forces appliquées s'écrit :

~^:;i + ~ U^::;i = :; . ( 4-1)

En décomposant sur les deux axes, on obtient

X + Ni.cos (cDi) =0 (4-2)

Y + Ni.sin (cDi) =0 (4-3)

On répète cette opération sur chaque noeud de la structure.

On obtient les réactions en projetant verticalement les efforts des barres reliés à la base du pylône.

Pour avoir la flèche en tête du pylône, on utilise le théorème de Pasternak qui stipule que le déplacement en un noeud d'une structure isostatique à treillis est donné par l'expression suivante :

Aj =

(4 4)

- N désigne la sollicitation intérieure (effort normal) de la structure

- ^~0 j , la sollicitatation due à une force unité placée au point d'application de la charge dans la direction de celle-ci.

Dans le cas de notre pylône, on a vu que les effforts normaux sont constans le long d'une barre, d'où l'expression devient :

(4 5)

Aj =

4-9-1-1 Comparaison des résultats

Les calculs effectués par la méthode analytique sont exacts. Nous nous proposons de calculer l'erreur moyenne commise par les deux méthodes numériques (calculs faits par GENIE et ROBOT MILLENIUM) ensuite de les comparer à la méthode analytique, ceci a pour but non seulement de vérifier la justesse de nos résultats, mais aussi de les positionner par rapport au logiciel commercial le plus utilisé.

4-9-2 Calcul des erreurs moyennes L'erreur moyenne est calculée ainsi :

em =	~ ei ` ~ N ~4-6~

e_m = erreur moyenne,

ei = erreur relative entre la grandeur calculée numériquement (GENIE, ROBOT MILLENNIUM) et la grandeur calculée analytiquement.

N = nombre de barres, de noeuds ou de réactions d'appui.

4-9-2-1 Calcul des réactions au sol

Tableau 4-1 : résultats des réactions

		Rx (kN)	Erreur relative	Ry (kN)	Erreur relative
Noeud 1	Calcul par la méthode analytique	-30.14		-334.18
	Calcul par GENIE	-30.12	0.06%	-334.15	0.01%
	Calcul par robot	-30.49	1.16%	-333.79	0.12%
Noeud 2	Calcul par la méthode analytique	-31.36		345.90
	Calcul par GENIE	-31.36	0%	345.9	0%
	Calcul par robot	-31.01	1.12%	345.79	0.3%

4-9-2-2 Calcul des contraintes

Tableau 4-2 : résultat du calcul des contraintes

Barre	Méthode analytique	Calcul de GENIE	Erreur relative	Calcul de ROBOT	Erreur relative
1	171.38	171.37	0.01%	171.47	0.05%
2	11.93	11.91	0.17%	12.41	4.02%
3	-12.55	-12.56	0.08%	-12.12	3.43%
4	-177.34	-177.34	0.00%	-177.82	0.27%
5	-1.86	-1.85	0.54%	-1.85	0.54%
6	171.36	171.37	0.01%	171.47	0.06%
7	0	0.00	0.00%	0	0.00%
8	-11.59	-12.00	3.54%	-11.59	0.00%
9	11.38	11.39	0.09%	11.86	4.22%
10	-177.35	-177.34	0.01%	-177.82	0.27%
11	165.17	165.15	0.01%	165.45	0.17%
12	11.33	11.32	0.09%	10.89	3.88%
13	-12.36	-12.35	0.08%	-12.86	4.05%
14	-171.12	-171.00	0.07%	-171.2	0.05%
15	-1.85	-1.85	0.00%	-1.85	0.00%
16	165.2	165.15	0.03%	165.45	0.15%
17	0	0.00	0.00%	0	0.00%
18	-11.85	-11.81	0.34%	-12.3	3.80%
19	10.84	10.84	0.00%	10.43	3.78%
20	-171.2	-171.00	0.12%	-171.2	0.00%

Tableau 4-3 : résultat du calcul des contraintes (suite)

Barre	Méthode analytique	Calcul de GENIE	Erreur relative	Calcul de ROBOT	Erreur relative
21	158.66	158.66	0.00%	158.65	0.01%
22	11.12	11.11	0.09%	11.7	5.22%
23	-11.82	-11.84	0.17%	-11.4	3.55%
24	-164.6	-164.59	0.01%	-165.01	0.25%
25	-1.94	-1.94	0.00%	-1.85	4.64%
26	158.66	158.66	0.00%	158.65	0.01%
27	0	0.00	0.00%	0	0.00%
28	-11.35	-11.30	0.44%	-10.93	3.70%
29	10.63	10.62	0.09%	11.21	5.46%
30	-164.6	-164.59	0.01%	-165.01	0.25%
31	152.12	152.10	0.01%	152.29	0.11%
32	10.54	10.55	0.09%	10.2	3.23%
33	-11.7	-11.69	0.09%	-12.35	5.56%
34	-157.9	-157.89	0.01%	-157.92	0.01%
35	-1.94	-1.94	0.00%	-1.93	0.52%
36	152.12	152.10	0.01%	152.29	0.11%
37	0	0.00	0.00%	0	0.00%
38	-11.19	-11.18	0.09%	-11.82	5.63%
39	10.09	10.11	0.20%	9.79	2.97%
40	-157.9	-157.89	0.01%	-157.92	0.01%

Tableau 4-4 : résultat du calcul des contraintes (suite)

Barre	Méthode analytique	Calcul de GENIE	Erreur relative	Calcul de ROBOT	Erreur relative
41	145.17	145.16	0.01%	144.94	0.16%
42	20.7	20.71	0.05%	21.88	5.70%
43	-22.05	-22.04	0.05%	-21.33	3.27%
44	-151.06	-151.07	0.01%	-151.3	0.16%
45	-1.74	-1.73	0.57%	-1.93	10.92%
46	145.17	145.16	0.01%	144.94	0.16%
47	0	0.00	0.00%	0	0.00%
48	-21.42	-21.40	0.09%	-20.55	4.06%
49	20.14	20.15	0.05%	21.07	4.62%
50	-151.06	-151.07	0.01%	-151.3	0.16%
51	137.9	137.89	0.01%	138	0.07%
52	20.45	20.47	0.10%	19.31	5.57%
53	-22.74	-22.72	0.09%	-23.76	4.49%
54	-143.62	-143.63	0.01%	-143.5	0.08%
55	-1.73	-1.73	0.00%	-1.72	0.58%
56	137.9	137.89	0.01%	138	0.07%
57	0	0.00	0.00%	0	0.00%
58	-22.29	-22.28	0.04%	-23.25	4.31%
59	20.14	20.16	0.10%	19.07	5.31%
60	-143.62	-143.63	0.01%	-143.5	0.08%

Tableau 4-5 : résultat du calcul des contraintes (suite)

Barre	Méthode analytique	Calcul de GENIE	Erreur relative	Calcul de ROBOT	Erreur relative
61	129.78	129.79	0.01%	129.49	0.22%
62	21.64	21.63	0.05%	22.74	5.08%
63	-23.1	-23.11	0.04%	-21.86	5.37%
64	-135.65	-135.64	0.01%	-135.92	0.20%
65	-1.69	-1.69	0.00%	-1.72	1.78%
66	129.78	129.79	0.01%	129.49	0.22%
67	0	0.00	0.00%	0	0.00%
68	-23.06	-23.08	0.09%	-21.88	5.12%
69	21.8	21.70	0.46%	22.7	4.13%
70	-135.66	-135.64	0.01%	-135.92	0.19%
71	120.78	120.78	0.00%	120.97	0.16%
72	22.76	22.78	0.09%	21.36	6.15%
73	-25.43	-25.42	0.04%	-26.59	4.56%
74	-126.4	-126.39	0.01%	-126.22	0.14%
75	-1.68	-1.69	0.60%	-1.67	0.60%
76	120.8	120.78	0.02%	120.97	0.14%
77	0	0.00	0.00%	0	0.00%
78	-26.02	-26.01	0.04%	-27.13	4.27%
79	23.51	23.53	0.09%	22.2	5.57%
80	-126.35	-126.39	0.03%	-126.22	0.10%

Tableau 4-6 : résultat du calcul des contraintes (suite)

Barre	Méthode analytique	Calcul de GENIE	Erreur relative	Calcul de ROBOT	Erreur relative
81	109.9	109.80	0.09%	109.43	0.43%
82	26.67	26.68	0.04%	28.08	5.29%
83	-28.5	-28.40	0.35%	-28.79	1.02%
84	-115.58	-115.57	0.01%	-115.97	0.34%
85	-1.65	-1.60	3.03%	-1.59	3.64%
86	109.78	109.80	0.02%	109.49	0.26%
87	0	0.00	0.00%	0	0.00%
88	-30.47	-30.47	0.00%	-30.48	0.03%
89	28.85	28.84	0.03%	28.55	1.04%
90	-115.58	-115.57	0.01%	-115.97	0.34%
91	95.82	95.83	0.01%	94.31	1.58%
92	32.92	32.94	0.06%	32.74	0.55%
93	-36.38	-36.36	0.05%	-33.48	7.97%
94	-101.23	-101.20	0.03%	-102.71	1.46%
95	-1.65	-1.60	3.03%	-1.66	0.61%
96	95.8	95.83	0.03%	95.56	0.25%
97	0	0.00	0.00%	0	0.00%
98	-41.56	-41.54	0.05%	-41.55	0.02%
99	38.3	38.28	0.05%	38.29	0.03%
100	-101.23	-101.20	0.03%	-102.71	1.46%

Tableau 4-7 : résultat du calcul des contraintes (suite)

Barre	Méthode analytique	Calcul de GENIE	Erreur relative	Calcul de ROBOT	Erreur relative
101	-16.94	-16.93	0.06%	-16.63	1.83%
102	78.8	78.79	0.01%	78.8	0.00%
103	46	46.10	0.22%	46.05	0.11%
104	-92.32	-92.35	0.03%	-92.33	0.01%
105	-1.48	-1.49	0.68%	-1.52	2.70%
106	78.8	78.79	0.01%	78.8	0.00%
107	-51.98	-51.99	0.02%	-51.96	0.04%
108	-75.99	-75.99	0.00%	-76	0.01%
109	55.91	55.93	0.04%	55.85	0.11%
110	108.86	108.84	0.02%	108.72	0.13%
111	-79	-79.00	0.00%	-79.2	0.25%
112	-84.97	-84.99	0.02%	-89.22	5.00%
113	0	0.00	0.00%	0	0.00%
114	42.76	42.79	0.07%	42.52	0.56%
115	77.25	77.22	0.04%	77.46	0.27%
116	-84.96	-84.99	0.04%	-89.22	5.01%
117	-1.69	-1.68	0.59%	-1.66	1.78%
118	42.69	42.79	0.23%	42.52	0.40%
119	-75.48	-75.45	0.04%	-75.71	0.30%
120	-20.42	-20.44	0.10%	-20.13	1.42%

Tableau 4-8 : résultat du calcul des contraintes (fin)

Barre	Méthode analytique	Calcul de GENIE	Erreur relative	Calcul de ROBOT	Erreur relative
121	0	0.00	0.00%	0	0.00%
122	-4.87	-4.77	0.00%	-4.89	2.52%
123	56.44	56.21	0.04%	59.58	5.96%
124	-20.55	-20.44	0.10%	-20.13	1.42%
125	-70.42	-70.26	0.01%	-70.21	0.06%

4-9-2-3 Calcul du déplacement en tête

Tableau 4-9: résultat du calcul des déplacements

Methode analytique	GENIE	Erre ur relative	ROBOT	Erre ur relative
19.21 cm	19.11 cm	0. 52%	19.40 cm	0.99%

Après avoir calculés toutes les grandeurs par les trois méthodes, il nous reste à comparer les résultats. Les comparaisons sont effectuées dans le tableau suivant :

Tableau 4-10 : comparaison des résultats

réactions		contraintes		Déplacement en tête
GENIE	ROBOT	GENIE	ROBOT	GENIE	ROBOT
0.02%	0.61%	0.15%	1.76%	0.52%	0.99%

4-9-3 Conclusion

Les exemples présentés dans ce chapitre ont permis d'évaluer la qualité des résultats de calcul fournis par GENIE. Les résultats obtenus suite à l'analyse statique ont été comparés à ceux calculés par la méthode analytique et nous ont permis de nous positionner par rapport au

logiciel de calcul en construction métallique ROBOT MILLENIUM 2010.Dans l'ensemble des résultats, GENIE propose une erreur relative inférieure à 1%. ROBOT MILLENIUM présente une erreur relative supérieure à celle de GENIE. Cela place les résultats de GENIE dans la marge acceptable. Le code GENIE sans disposer de toutes les fonctionnalités de ROBOT MILLENIUM est tout de même une alternative crédible de dimensionnement des pylônes autostables.

Conclusion générale

GENIE, objet de ce travail, destiné au calcul et à la simulation des efforts sur les pylônes constitue un problème à caractère pluridisciplinaire nécessitant de mettre en oeuvre des connaissances relevant de plusieurs domaines tels que la méthode des éléments finis, les normes de dimensionnement en construction métallique, le calcul numérique et la programmation informatique. Dans un premier temps, nous avons présenté la méthode des éléments finis utilisée dans l'analyse élastostatique et modale des pylônes construits par GENIE. Ces pylônes sont discrétisés en barres avec une approximation basée sur la méthode des déplacements. Ensuite, nous avons présenté les exigences des normes Eurocode 3 et NV 65 relatives à la construction des pylônes. Ces exigences sont intégrées dans le code GENIE pour faciliter et automatiser le calcul. Enfin, nous avons présenté une interface graphique qui a été développé sur le logiciel matlab 2007b à travers l'outil guide en utilisant sa librairie. Signalons que l'architecture de GENIE assure une maintenance facile du code et permet d'ajouter de nouveaux modules pour répondre aux besoins, en évolution permanente, à la fois industriels et de recherche scientifique. Un exemple d'application traité démontre la validité du code réalisé dans le cadre de ce travail. Nous avons procédé aux calculs statique et modal d'un pylône de 36 mètres. Les résultats obtenus ont été approuvés par La méthode analytique et le logiciel ROBOT MILLENIUM 2010.

Au terme de ce travail, il nous semble intéressant d'envisager quelques perspectives :

° Extension des types de pylônes comme le dimensionnement des pylônes tubulaires et les pylônes tripodes,

° Nous pouvons aussi ajouter une fonction économique qui va rechercher pour un pylône donné, les cornières optimales,

° L'interface utilisateur basé sur le GUI matlab pourrait être améliorée en ajoutant d'autres fonctions graphiques (icônes) pour faciliter davantage les opérations de post-traitement.

Bibliographie

[1] SERGES LAROZE, Mécanique des structures.2, Toulouse - 2005, 191p.

[2] PIERRE THOMAS, Eléments finis pour l'ingénieur, Paris -2006, 448 p.

[3] MANFRED GILLI, méthodes numériques, Genève - 2006, 132 p.

[4] J. MOREL, calcul des structures selon l'eurocode 3, Lyon - 2005, 331 p.

[5] Règles NV 65, Règles de calcul définissant les effets de la neige et du vent sur les constructions et annexes, Avril 2000, 224 p

[6] A SEGHIR, éléments finis barres dans méthode d'éléments finis, BEJAIA- 2008, 3-11

[7] JC AMBA, cours d'éléments finis, FGI, 2010

[8] PATRICK MARCHAND AND O. THOMAS HOLLAND, Graphics and GUIs with MATLAB

[9] HAMRIT Fareh analyse des structures discrètes par la méthode des éléments finis, mémoire d'ingénieur université de M'sila ,158p.

[10] Direction de la météorologie-République du Cameroun, « unités climatiques et leurs caractéristiques, 2008

[11] avant projet détaillés de la société CARTEL (compagnie africaine de réalisation en télécommunication)

[12] site de recherche : http://fr.wikipedia.org/wiki/Orange %28entreprise%29 date de visite:20/11/2011

[13] les relais GSM: http://www.juliendelmas.com, date de visite: 30/11/2011

[14] mer télécom : http://www.mer-group.com/?CategoryID=549&ArticleID=220: date de visite : 30/11/2011

[15] interfaces graphiques : http://briot-jerome.developpez.com/matlab/tutoriels/introductionprogrammation-interfaces-graphiques/ date de visite: 30/11/2011

Annexes

Annexe 1 : quelques éléments d'un site de télécommunication Annexe 1.a : lecture des azimuts

Annexe 1.b : BTS

Annexe 1.c : Baie

Annexe 2 : quelques données de la norme NV 65 Annexe 2-a: coefficient de réduction

Annexe 2-b : coefficient de réponse

Annexe 2-c : coefficient de pulsation

Annexe 3 : Fonctions essentielles utilisées dans le code

Annexe 3-a : coordonnées et connectivités entre les noeuds.

function [t,p]=schema36(B,H) %

%cette fonction dessine le pylone %B: longueur des bases

%H:hauteur du pylone

%t:table de connectivité %p:coordonnées des noeuds %tsopgo clovis, faculte de genie industriel

%

[t,p]=type4(B(1),B(2),H(1));

for i=2:7

if i<6

[T,P]=type4(B(i),B(i+1),H(i)); elseif i==6

[T,P]=type5(B(i),B(i+1),H(i));

else

[T,P]=type6(B(i),B(i+1),H(i));

end

T=T+size(p,1)-2;

P=P(3:size(P,1),:);

P(:,2)=P(:,2)+sum(H(1:i-1));

t=[t;T]; p=[p;P];

end

return

Annexe 3-b: localisation de la matrice élémentaire dans la matrice globale

function L = Localise(t)

%calcul de la localisation de la matrice elementaire % dans la matrice globale

% t : table de connectivités de l'element % L : table de loacalisation

%

% tsopgo clovis,faculte de genie industriel

nne = length(t);

for i= 1:nne

L([2*i1 2*i]) = [2*t(i)1 2*t(i)];

end

return

annexe 3-c: longueurs et cosines directeurs des barres

function [ds,c,s] = EltLen(XY)

%

% Calcul de la longueur, du cos et du sin de la matrice de rotation pour un

% element barre à deux noeuds (x1,y1) (x2,y2)

% c : cosinus de l'angle

% s : sinus de l'angle

% XY: cordonnées des noeuds XY = [x1,y1; x2,y2]

%

% tsopgo clovis,faculte de genie industriel

dx = XY(2,1) - XY(1,1);
dy = XY(2,2) - XY(1,2);

ds = sqrt(dx^2 + dy^2);

c = dx/ds; s = dy/ds; return

annexe 3-d: élimination des noeuds bloqués

function A = DelDOFs(A,L)

% A = DelDOFs(A,L)

%

% A : matrice globale après assemblage

% L : liste des degrés de liberté à éliminer % tsopgo clovis faculté de genie industriel

L = sort(L); % tri de la liste des DDL

n = length(L); % longueur de L

if (size(A,2) == 1) % cas d'un vecteur

for i = n:-1:1 % parcourir L à partir du plus grand indice

A(L(i)) =[] ; % suppression de la composante associée au DDL

courant

end

else % cas d'une matrice

for i = n:-1:1

A(L(i),:) =[] ; % suppression de la ligne L(i)

A(:,L(i)) =[] ; % suppression de la colonne L(i)

end end return

annexe 3-e : ajout des noeuds bloqués

function U = AddDOFs(U,L)

%

% U = K \ F : FE solution

% L : Table de localisation des noeuds d'appuis

%

%tsopgo clovis faculté de génie industriel

[m,n] = size(L);

L = reshape(L,m*n,1); L = L(find(L));

L = sort(L);

n = length(L);

for i = 1:n

U = AddToVect(U,L(i),0);

end

U = U';

return

annexe 3-f : calcul des efforts normaux

function [F,R] = TrussForces(t,p,A,E,U)

% F : forces axiales dans les barres

% R : forces aux niveaux des noeuds = réactions dans le cas d'appuis % t : table de connectivités des éléments

% p : table des coordonnées des noeuds

% A : sections des éléments

% E : modules d'élasticité

% U : solution en déplacement

%

% tsopgo clovis, faculte de genie industriel

net = size(t,1); % nombre d'éléments total

nnt = size(p,1); % nombre de noeuds total

R = zeros(2*nnt,1); % Forces aux noeuds

for ie = 1:net % boucle sur les éléments

L = localise(t(ie,:)); % table de localisation

ke = truss2dKe(p(t(ie,:),:),A(ie),E); % matrice élémentaire

ue = U(L); % déplacements des noeuds

fe = ke*ue; % forces élémentaires dans (oxy)

R(L) = R(L) + fe; % tous les éléments liés au noeud

[L,c,s] = EltLen(p(t(ie,:),:)); % les cosinus directeurs

F(ie,:) = -( c*fe(1) + s*fe(2) ); % rotation au repère local

end % fin de boucle

return

annexe 3-g : maillage du pylône

function plotmesh(haut,base,entete,EltLabels,NodeLabels)

%

% cette fonction dessine le pylone

% haut: hauteur du pylone

% base: longueur de la base

% entete: longueur de l'entete

% NodeLabels : vaut true pour afficher les éléments

% EltLabels : vaut true pour afficher les noeuds

% color : couleur des lignes

% % %tsopgo clovis, faculte de genie industriel

%

axis equal

[hauteur, D,d,H,B]=geom(haut,base,entete);

[t,p]=schema(B,H); Net = size(t,1); for ie = 1:Net

XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','r','linewidth',2)

if(EltLabels)

x = mean(XY(:,1));

y = mean(XY(:,2));

axis equal text(x,y,num2str(ie),'color','g')

end

end

Np = size(p,1); if(NodeLabels) for i=1:Np

text(p(i,1),p(i,2),num2str(i),'color','b')

end

end

if hauteur ==36; for ie = 21:40

XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','w','linewidth',2)

end

for ie = 61:80

XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','w','linewidth',2)

end

for ie = 101:108

XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','w','linewidth',2)

end

elseif hauteur ==54;

for ie = 1:26

XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','w','linewidth',2)

end

for ie = 53:72

XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','w','linewidth',2)

end

for ie = 93:112

XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','w','linewidth',2)

end

for ie = 133:152
XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','w','linewidth',2)

end

for ie = 173:180

XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','w','linewidth',2)

end

elseif hauteur ==72;

for ie = 27:52

XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','w','linewidth',2)

end

for ie = 73:92

XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','w','linewidth',2)

end

for ie = 113:132

XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','w','linewidth',2)

end

for ie = 153:172
XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','w','linewidth',2)

end

for ie = 193:212

XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','w','linewidth',2)

end

for ie = 234:241

XY = p(t(ie,:),:);

X = [XY(:,1)];

Y = [XY(:,2)]; line(X,Y,'color','w','linewidth',2)

end

end

X=[-D -D];

Y=[-0.5 sum(H)+0.5];

line(X,Y,'color','w')

h=[0 H];

B = num2str(B,'%10.2f');

B=str2num(B);

x=[-D -1.5*D];

y=[0 0];

line(x,y,'color','w')

text(-1.6*D,0.45,num2str(B(1)),'color','b')

z1=[0.5*D+1 0.5*D+4]; z2=[sum(h)-1 sum(h)-1]; t1=[0.5*D+3.5 0.5*D+4]; t2=[sum(h)-1.5 sum(h)-1]; t3=[sum(h)-0.5 sum(h)-1];

line(z1,z2,'color','w','linewidth',2) line(t1,t2,'color','w','linewidth',2)

line(t1,t3,'color','w','linewidth',2)

text(0.5*D+2,sum(h)-0.4,'vent','color','w')

for i= 1:length(H)

s=0.5*(B(i+1)+B(i))*H(i); y=[sum(H(1:i)) sum(H(1:i))]; line(x,y,'color','w')

text(-D+0.3,sum(h(1:i))+0.5*h(i+1),'T','color','g') text(-D+0.9,sum(h(1:i))+0.5*h(i+1),num2str(i),'color','g') text(-1.35*D,sum(h(1:i))+0.5*h(i+1),num2str(s),'color','g') text(-1.6*D,sum(H(1:i))+0.45,num2str(B(i+1)),'color','b')

end

return

annexe 3-h: matrice de rigidité élémentaire

function [ke,L] = truss2dKe(XY,A,E)

%

% Calcul de la matrice elementaire pour un

% element barre à deux noeuds (x1,y1) (x2,y2) % A : section de l'element

% E : module d'élasticité

% XY: cordonnées des noeuds XY = [x1,y1; x2,y2] % L:longueur de la barre

%tsopgo clovis, faculte de genie industriel

[L,c,s] = EltLen(XY); % longueur et orientation de l'élément

cc = c*c; % cos(angle)^2

cs = c*s; % cos(angle)*sin(angle)

ss = s*s; % sin(angle)^{^}2

ke = (A*E/L) * [ cc cs -cc -cs % matrice élémentaire Ke

cs ss -cs -ss -cc -cs cc cs cs ss cs ss

];

return

Annexe 3- i : programme principal

function [P,R,sigma,Ux,Umax,Rx1,Ry1,Rx2,Ry2,T,U,t,p,A,ba,Long,fy,obs,alpha] = truss2dKM(haut,base,entete,q,sa,masse,cornieres,ks,direct)

% haut: hauteur du pylone

% base: longueur de la base

% entete: longueur de l'entete % q:pression à 10 mètres du sol % sa: charge en tete du pylone % masse: masse des antennes

% cornières: matrice des cornières à utiliser

% ks: coefficient de site % direct:direction du vent

% P:vecteur des efforts normaux % R:réactions au niveau du sol

% sigma: vecteur des contraintes

% Ux: valeur de la flèche en tete du pylone

% Umax: déplacement maximal en tete du pylone

% RX, RY: valeurs des réactions au niveau du sol

% T: périodes propres

% U: vecteur déplacement % t : table de connectivités des éléments

% p : table des coordonées des noeuds

% A : sections des éléments (des barres)

% ba :numéros des barres

% long :longueur des barres % fy :contraintes maximales

% obs:vecteur à deux états: "oui" si sigma < fy et "non" sinon

% alpha: angle de rotation en tete

%tsopgo clovis, faculte de genie industriel

%

clc % effacer tout le contenu de la

fenetre de commande

[B,Al,A,si,sp,dens,E,G,H,Fv,Fp,t,p,iv,fy,Iw]=traitement(haut,base,entete,q,co rnieres,ks,direct);

if direct==0 %direction du vent qui vaut 0 pour

le vent

Fv=Fv/1.41; % diagonal et 1 pour le vent normal

end %fin de la boucle

qa=1.3*2.5*q*sa*(sum(H)+16)/(sum(H)+58); % frce du vent dur les antennes

net = size(t,1); %nombre de barres

nnt = 2*size(p,1); % nombre de noeuds, 2 signifie le

nombre de degré de liberté

K = sparse(nnt,nnt); % initialisation des matrices de

rigidité, d'inertie, et des forces

Kw = zeros(nnt,nnt); % par des matrices creuses nulles

M = sparse(nnt,nnt); FV = sparse(nnt,1); FP = sparse(nnt,1); Mw = sparse(nnt,1);

Fp=2*Fp; % prise en compte des barrres

latérales

FV(end -3) = FV(end-3)+0.5*qa; %ajout du poids des antennes

Long=zeros(net,1); %initialisation des longueurs des

barres

for i = 1:net %début de boucle sur les éléments

ti = t(i,:); %table de connectivité et de

Li = localise(ti); %localisation de l'élément courant

[Ke,l] = truss2dKe(p(ti,:),A(i),E);%matrice de rigidité élémentaire kw=((81e+9)*Iw(i)/l)*[1 0 -1 0;... %matrice de rigidité élémentaire 0 0 0 0;-1 0 1 0;0 0 0 0]; %en torsion

Long(i)=l;

Me = truss2dMe(p(ti,:),A(i),dens);%matrice masse élémentaire fe=Fv(i)*l*[0.5;0;0.5;0];

Fe=-Fp(i)*[0;0.5;0;0.5];

K(Li,Li)	=	K(Li,Li) +	Ke;
Kw(Li,Li)	=	Kw(Li,Li)	+ kw;
M(Li,Li)	=	M(Li,Li) +	Me;

%assemblage de la fonction K %assemblage de la matrice kw %assemblage de la matrice M

FV(Li) = FV(Li) + fe; %assemblage de la matrice FV

% FP(Li) = FP(Li) + Fe; %assemblage de la matrice FP

end %fin de la boucle

Long = num2str(Long,'%10.2f'); %choix du format d'affichage

Long=str2num(Long); %des longueurs

Mw(end-2)= 0.1*qa; %valeur du moment en tete

poids=masse*9.81; %poids des antennes

nul=1:4; %noeuds encastrés

K = DelDOFs(K,nul); %application

M = DelDOFs(M,nul); %des

FV = DelDOFs(FV,nul); %conditions

Mw = DelDOFs(Mw,nul); %aux

Kw = DelDOFs(Kw,nul); %limites

[y,kk]=chol(K); %décomposition

[yw,kk]=chol(Kw); %de cholesky

angle=yw'\Mw; %angle de

angle=yw\angle; %rotation

alpha= angle(end2)*180/3.14; %en tete du pylone

alpha = num2str(alpha,'%10.2f'); %normaux

alpha=str2num(alpha);

x=y'\FV; %calcul de

U=y\x; %la solution

U = AddDOFs(U,nul); %ajout des DDl des noeuds encastrés

Ux=100*U(end-1); %calcul de la flèche en tete

Ux = num2str(Ux,'%10.2f');

Ux=str2num(Ux);

Umax=sum(H)/2; %déplacement maximal

FP(end)=FP(end)-0.5*poids;

FP(end-2)=FP(end-2)-0.5*poids;

FP = DelDOFs(FP,nul); %conditions aux limites

U1=y'\(1.33*FP+1.5*FV);

U1=y\U1;

U1 = AddDOFs(U1,nul); % Ajouter les DDL des noeuds encastré

[phi, omega2] = eigs(K,M); % modes propres

omega = sqrt(diag(omega2)); % pulsations

T = 2*pi./sort(omega); % périodes propres par ordre croissant

T = num2str(T,3); % et choix du format d'affichage

[P,R] = TrussForces(t,p,A,E,U1); %calcul

sigma=(1e-6)*P./A %des éfforts

sigma = num2str(sigma,'%10.2f'); %normaux

sigma=str2num(sigma); %des contraintes

ba=1:length(t(:,1));

Rx1=R(1)/1000; %des réactions

Rx2=R(3)/1000; %et choix du format

Ry1=R(2)/1000; %d'affichage

Ry2=R(4)/1000;

Rx1 = num2str(Rx1,'%10.2f'); Rx1=str2num(Rx1);

Rx2 = num2str(Rx2,'%10.2f'); Rx2=str2num(Rx2);

Ry1 = num2str(Ry1,'%10.2f'); Ry1=str2num(Ry1);

Ry2 = num2str(Ry2,'%10.2f'); Ry2=str2num(Ry2);

%%%%% DIMMENSIONNEMENT %%%%%%

lam=Long./iv; %calcul de lamda

lam1=93.9*sqrt(235./fy); %de lamda 1

lba=lam./lam1; %de lamda barre

fi=0.5*(1+0.49*(lba-0.2)+lba.*lba); %de phi

ki=fi+sqrt(fi.*fi-lba.*lba); %de ki

ki=1./ki; %et

simax=ki.*fy./1.1; %de sigma max

for i=1:net % boucle de

if (lba(i)>0.2 && sigma(i)<=0) %vérification

fy(i)= simax(i); %des contraintes

end % fin

end % de la boucle

%%%%% FIN DU DIMENSIONNEMENT %%%%

P=P/1000; %conversion de la force en kN

P = num2str(P,'%10.2f'); %choix du format d'affichage

P=str2num(P); %de l'effort

fy = num2str(fy,'%10.2f'); %et de

fy=str2num(fy); %l'effort maximal

obs=100*ones(net,1); %affichage

sigma=troncon(sigma,H); %de la contrainte

P=troncon(P,H); %de l'effort normal

A=A*1e+6;

A=troncon(A,H); %de la section

ba=troncon(ba,H); %des numéros des barres

Long=troncon(Long,H); %des longueurs

fy=troncon(fy,H); %de la contrainte maximale

obs=troncon(obs,H); %et de l'observation en fonction de la

hauteur

return %fin de la fonction

Annexe 4 : pylône dans robot millénium

Annexe 4-a : vue en élévation du pylône (numéro des noeuds et des barres)

Annexe 4-b : déformée du pylône

Annexe 4-c valeur des réactions

Annexe 4-d : quelques valeurs des contraintes et déplacements