Analyse et modélisation d'un glissement de terrain. Cas de Sidi Youcef (Béni Messous, Alger )

République Algérienne Démocratique et Populaire
Ministère de l'enseignement supérieur et de la
Recherche scientifique
Centre Universitaire Khemis Miliana
Institut des sciences de la terre et de la nature

En vue de l'obtention du diplôme de Master
Domaine : Sciences de la Terre et l'Univers
Spécialité : Géotechnique

Présenté par :

+ AISSA Mohamed Hamza.
+ HADDOUCHE Khadidja.

Devant le jury composé de :

· M ^elle BELHADJ Fatima Zohra Examinatrice.

· M^r HAMDANE Ali Président.

· M^me FILALI Mira Promotrice.

· M^r MEBROUK Faouzi Examinateur.

Promotion 2010/2011

[Tapez un texte]

ÈÇÈÓ

æ áßÔãáÇ

Ï?ÏÍÊ æ á?áÍÊáÇ ÇÐ äã

íÓ?ÆÑáÇ ÏáÇ

.

2

ã

10200

ÜÈ ÊÍÇÓã ÊÑÏÞ íÐáÇ

. äÚ ãÌäÊ ÏÞ íÊáÇ ÈÞÇæÚáÇ ìáÚ ÁæÖáÇ ÁÇÞáÅ Úã ÚæÞæ

íÑæÑÖáÇ äã äÇß ÇÐá æ Þ?Òä?Ç ÈÈÓÊ ä ÇäÔ äã É?áæÍÊ É?Ìæáæ?Ì ÉÚ?ÈØ ÉÞØäãáÇ åÐá

ÇÐß æ ÉÞØäãáá É?ÎÇäãáÇ æ É?Ìæáæ?ÌæÑÏ?áÇ ÊÇ?ØÚãáÇ ìáÅ ÉÇÖ?ÇÈ ÉÑ?Î?Ç åÐ äã áß ÉÓÇÑÏ

. ÉÈÑÊáá É?ß?äÇß?ãæ?Ò?áÇ ÊÇÒ?ããáÇ

íÊáÇ æ (<1) íãÊÍ ÉÈÑÊ Þ?ÒäÇ áßÔã ãÇã Çää ÊÊÈË ÊãÊ íÊáÇ äÇã?Ç Ê?ãÇÚã ÊÇÈÇÓÍ áß

. (뇂

. . .

Ê?æãÍáÇ

ÊÇØÞÇÓÊáÇ) É?ÌÑÇÎ Ê?ãÇÚã ÏæÌæ í ÖÎäÊ

. ÓæÓã ??? Ó?Óß?È ÈæáÓæ?Ì äÇã?Ç ????? ÉÈÑÊáÇ Þ?ÒäÇ : ?????? ÊÇãáß

Résumé :

Cette étude consiste en une analyse d'un glissement de terrain survenue dans une zone de
10200 m² située à Sidi Youcef dans la commune de Beni Messous dont le but est de connaître
le fond du problème en déterminant les causes déclenchantes, et les conséquences probables.

Cette région est caractérisée par une nature géologique métamorphique qui favorisant les mouvements de terrain. C'est pour cela qu'il est nécessaire d'étudier et d'analyser toutes les données géologiques, hydrogéologiques et climatiques de la région, ainsi les caractéristiques physico -mécaniques du terrain.

Tous les calculs réalisés ont montré qu'on est en face d'un terrain instable ce qui se traduit par un coefficient de sécurité très faible (<1) et qui peut diminuer encore plus en présence de facteurs extérieurs (précipitations, surcharges etc).

Mots-clés: Glissement de terrain, Coefficient de sécurité, GEOSLOPE, PLAXIS, Beni Messous.

Abstract :

This study analyses the landslide that happened in an area of 10200 m² which is located in Sidi Youcef, Beni Messous municipality. Our main aim from this analyse is to know the problem, its causes and its consequences.

This region has metamorphic geological nature, it can provide landslide therefore it was necessary to study it, in addition to the hydrogeological and climatic data of this zone and physico ?mecanic characteristics of the soil.

All the security coefficient calculates improved that we are in front of landslide trouble. It can be decreased (<1) with the presence of external factors (rains, loads...etc).

Key words: landslide, security coefficient, GEOSLOPE, PLAXIS, Beni Messous.

Table de matière

Liste des tableaux i

Listes des figures et des photos ii

Tableau de notations vi

INTRODUCTION GENERALE

CHAPITRE I : Généralités sur les mouvements de terrain

I-1- Introduction

	.3
I-2- Les mouvement des terrains et les différents types	4
I-2-1- Les mouvements rapides et discontinus	4
I-2-2- Les mouvements longs et continus	7
I-2-3- Types de Glissement	9
I-3- Origines et causes des glissements de terrain	12
I-3-1- Les causes augmentant les moments moteurs	12
I-3-2- Les causes diminuant les moments résistants	13
I-4- Les phases des Glissement	13
I-4-1- Glissements de terrain actifs	.14
I-4-2- Glissement de terrain réactifs	14
I-4-3- Glissement de terrain inactifs	14
I-5- Quelques exemples des glissements de terrain	.14
I-5-1- Dans le monde	14
I-5-2- En Algérie	17
I-6- Techniques et moyens de confortement	20
I-6-1- Généralités	20
I-6-2- Les différentes techniques	20
Conclusion	33

CHAPITRE II : Méthodes de calcul des glissements de terrain

II-1-Introduction .35

II-2-Généralités sur l'analyse de la stabilité .36

II-2-1-Notion de facteur de sécurité 36

II-2-2-Les différentes méthodes de calcules 37

II-3-Rupture plane 38

II-3-1-Pente semi-infinie terrain sec 38

II-3-2-Pente semi-infinie avec écoulement 39

II-4-Rupture circulaire 40

II-4-1-Méthode d'équilibre limite 40

II-4-2-Méthode des éléments finis 55

II-5-Présentation de l'outil numérique utilisé 56

II-5-1-Présentation du code PLAXIS 56

II-5-2-Présentation du logiciel Geoslope- GEOSTUDIO 61

CHAPITRE III : Cadre géologique et hydrogéologique

III-1- Introduction .65

III-2- Description du site 65

III-2-1- Situation géographique .65

III-2-2- Situation géologique 66

III-2-3- Situation hydrologique et hydrogéologique .68

III-2-4- Climat .69

III-2-5- Sismicité 73

Conclusion 75

IV-1-

CHAPITRE IV : Etude de glissement de terrain

Introduction 77

IV-2- Etat des lieux .78

IV -3- Résultats des investigations géotechniques 82

IV -3-1- Sondages carottés 82

IV -3-2- Résultats des pénétromètres dynamique 91

IV -3-3- Résultat de l'essai préssiométrique 97

IV -3-4- Résultats des essais d'identification 99

IV -3-5- Résultats des essais mécaniques 104

Conclusion 107

CHAPITRE V : Calculs et vérifications

V-1-Introduction

	110
V- 2-Détermination du coefficient de sécurité Fs	.110
V-2-1-Calcul de facteur de sécurité manuellement	..110
V-2-2-Calcul à l`aide des logiciels	..112
V-2-2-1- Calcul par GEOSLOPE	.112
V-2-2-2- Calcul par le code PLAXIS	...116
V-2-3- Récapitulatif des résultats de calcul	.127
V-3- Moyen de confortement	128
Synthèse et recommandation	132

CONCLUSION GENERALE

ANNEXE

ANNEXE A 134

ANNEXE B 143

Liste des tableaux

Tableau I.1 Classification selon l'activité en fonction de l'évaluation de la vitesse 12

moyenne de glissement a long terme.

Tableau I. 2 Classification selon la profondeur de la surface de glissement. 12

Tableau II.1 Fs en fonction de grandeurs par rapport à une grandeur limite. 36

Tableau II.2 Valeur de FS en fonction de l'état de l'ouvrage. 37

Tableau II.3 Nombre de stabilité de TAYLOR. 43

Tableau III.1 Valeurs du coefficient d'accélération de zone selon le RPA99 (version 74

2003).

Tableau IV.1 Résultats d'essai préssiométrique. 97

Tableau IV.2 Résultats d'analyse granulométrique. 102

Tableau IV.3 Résultats des essais d'identification physiques. 102

Tableau IV.4 Résultats d'essai de cisaillement à la boite. 104

Tableau IV.5 Récapitulation des résultats d'essais. 107

Tableau V.1 Caractéristiques des couches de terrain. 110

Tableau V.2 Les résultats de calcul en état vierge. 111

Tableau V.3 Les résultats de calcul en état entièrement saturé. 112

Tableau V.4 Valeur de coefficient de sécurité avec les différentes méthodes. 113

Tableau V.5 Valeur de coefficient de sécurité avec les différentes méthodes. 114

Tableau V.6 Valeur de coefficient de sécurité avec les différentes méthodes. 115

Tableau V.7 Valeur de coefficient de sécurité avec les différentes méthodes. 115

Tableau IV.8 Récapitulatif des données de calcul. 115

Tableau V. 9 Présentation des informations de calcul. 119

Tableau V.10 Présentation des informations de calcul. 121

Tableau V.11 Présentation des informations de calcul. 124

Tableau V.12 Présentation des informations de calcul. 126

Tableau V.13 Récapitulation des résultats de calcul du code PLAXIS. 126

Tableau V.14 Récapitulation globale des résultats de calcul. 127

Tableau V.15 Présentation des résultats de calcul. 130

Liste des figures et des photos

Figure I.1 Les chutes de blocs et les écroulements 5

Figure I.2 Progression d'un effondrement 6

Figure I.3 Le phénomène du fluage. 7

Figure I.4 L'affaissement. 8

Figure I.5 Processus de glissement de terrain 9

Figure I.5. a Glissement plan 10

Figure I.5.b Glissement rotationnel 10

Figure I.5.c Glissement rotationnel simple 11

Figure I.5.d Glissement rotationnel complexe. 11

Figure I.6 Différentes phases de l'activité d'un glissement de terrain. 13

Figure I.7 Coupe géologique du Climat De France 19

Figure I.8 Chargement au pied d'un talus. 21

Figure I.9 Les différents procédés de modification géométrique. 22

Figure I.10 Tranchées drainantes 24

Figure I.11 Eperons drainantes 24

Figure I.12 Les drains subhorizontaux 25

Figure I.13 Mur de soutènement 27

Figure I.14 Paroi de palplanche. 28

Figure I.15 Principe de la technique terre armée. 29

Figure I.16 Schéma de principe d'un tirant d'ancrage injecté 30

Figure II.1 Notations pour le calcul de la stabilité d'une pente 38

Figure II.2 Notations pour le calcul de la stabilité d'une pente avec écoulement 39

Figure II-3 Schéma représentatif des forces appliqué sur un bloc 41

Figure II.4 Illustration des forces appliquée dans la méthode des coins. 44

Figure II.5 Exemple d'une rupture circulaire 45

Figure II.6 Forces appliquées sur une tranche dans la méthode de Bishop. 47

Figure II.7 Forces appliquées sur une tranche dans la méthode de Fellenius 48

Figure II.8 La représentation des forces sur une tranche 50

Figure II.9 Représentation des forces sur une tranche. 51

Figure II.10 Résultante des forces parallèles 52

Figure II.11 Représentation de toutes les forces inconnues sur une tranche dans la 53

méthode de Spencer.

Figure II.12 Les coordonnées pour une surface de rupture non circulaire utilisée dans la 53

méthode de Spencer.

Figure II.13 Représentation graphique des forces sur une tranche 54

Figure II.14 Définition du module d'Young E. 57

Figure II.15 Résultats d'essais triaxiaux drainés et le modèle Élastoplastiques de type 58

Mohr-Coulomb.

Figure II.16 Organigramme de la structure du code PLAXIS 60

Figure II.17 Les menus disponibles sur logiciel SLOPE/W 63

Figure III.1 Situation géographique de la commune de Beni Messous. 65

Figure III.2 Carte géologique d'Alger 67

Figure III.3 Carte hydrogéologique de la région d'Alger 71

Figure III.4 Profil de variation des températures moyennes de l'air 1995-2005 (d'après 72

ONM).

Figure III.5 Précipitations annuelles 1995-2005 (d'après ONM). 73

Figure III.6 Carte de zonage sismique de l'Algérie 74

Figure IV.1 Log de sondage Sc1. 83

Figure IV.2 Log de sondage Sc2 84

Figure IV.3 Log de sondage Sc3 85

Figure IV.4 Log de sondage Sc4 86

Figure IV.5 Log de sondage Sc5 87

Figure IV.6 Log de sondage Sc6 88

Figure IV.7 Plan d'implantation 89

Figure IV.8 Coupe géotechnique du site. 90

Figure IV.9 Pénétrogramme P1 91

Figure IV.10 Pénétrogramme P2 92

Figure IV.11 Pénétrogramme P3 93

Figure IV.12 Pénétrogramme P4 94

Figure IV.13 Pénétrogramme P5 95

Figure IV.14 Pénétrogramme P6 96

Figure IV.15 Le log préssiométrique 98

Figure IV.16 Courbe granulométrique. 99

Figure IV.17 Courbe granulométrique 100

Figure IV.18 Courbe granulométrique 101

Figure IV.19 Abaque de plasticité de Casagrande. 103

Figure IV.20 L'essai de cisaillement à la boite 105

Figure IV.21 L'essai de cisaillement à la boite 106

Figure V.1 Le modèle géométrique adopté 113

Figure V.2 La position du centre et du cercle de glissement dans le modèle géométrique. 113

Figure V.3 La position du centre et du cercle de glissement dans le modèle géométrique. 114

Figure V.4 La position du centre et du cercle de glissement dans le modèle géométrique. 114

Figure V.5 La position du centre et du cercle de glissement dans le modèle géométrique. 115

Figure V.6 Le modèle géométrique. 116

Figure V.7 Le maillage déformé du talus. 117

Figure V.8 Les contraintes maximales de cisaillement. 118

Figure V.9 Les déplacements totaux. 118

Figure V.10 Le modèle géométrique avec la prise en compte des surcharges. 119

Figure V.11 Le maillage déformé du talus et bâtiment. 120

Figure V.12 Les contraintes maximales de cisaillement. 120

Figure V.13 Les déplacements totaux. 121

Figure V.14 Le maillage déformé du talus. 122

Figure V.15 Les pressions interstitielles 122

Figure V.16 Les contraintes maximales de cisaillement 123

Figure V.17 Les déplacements totaux. 123

Figure V.18 Le maillage déformé du talus et bâtiment. 124

Figure V.19 Les contraintes maximales de cisaillement. 125

Figure V.20 Les déplacements totaux. 125

Figure V.21 La position des pieux dans le talus. 128

Figure V.22 Le maillage déformé du talus. 129

Figure V.23 Les déplacements totaux après confortement. 129

Figure V.24 Plan de coffrage et de ferraillage 131

Liste des photos :

Photo I.1 Les coulées boueuses. 5

Photo I.2 Morphologie de la zone de glissement de Villatina Medellin en Colombie. 15

Photo I.3 Glissements de La Leona près de San Vicente (a) et de Las Collinas (b) au 16

Salvador.

Photo I.4 Glissement de terrain à Belouizdad. [2002]. 17

Photo I.5 Rue de Verdun. [2002]. 18

Photo I.6 Le glissement de la route des abattoirs 18

Photo I.7 L'implantation des plantes dans un talus. 26

Photo I.8 Un versant stabilisé par clouage. 31

Photo I.9 L'utilisation du géotextile en jouant un double rôle le drainage et le 32

renforcement du talus.

Photo III.1 Localisation du site étudié 66

Photo IV.1 Situation du glissement 77

Photo IV.2 Vue du versant et les bermes de sécurité approximé de la CW 45. 78

Photo IV.3 Décalage du dallage périphérique (après affaissement) par rapport à la longrine. 79

Photo IV.4 Affaissement au niveau de la chaussée 80

Photo IV.5 Affaissement du dallage entre les bâtiments 2 et 3. 80

Photo IV.6 Affaissement de la partie aval du chaussée et basculement des gardes corps. 81

Photo IV.7 Aperçu sur les traces des fuites d'eau des réseaux. 81

Photo IV.8 Aperçu sur les mouvements du talus 82

Liste de notations

â: L'angle du talus.

C : Cohésion.

C_c : coefficient de courbure. C_u : coefficient d'uniformité. E : Module de Young.

EM : Module préssiometrique. FS : Coefficient de sécurité. Id : Poids volumique sèche. yh : Poids volumique humide. ysat : Poids volumique saturé. IC : Indice de consistance.

IP : Indice de plasticité. í: Coefficient de poisson. PL : Pression limite_.

Rp: Résistance a la pointe. ? : Angle de frottement.

t : Contrainte tangentielle. w : Teneur en eau.

wL : Limite de liquidité. wP : Limité de plasticité. ?Msf : Coefficient de réduction.

Introduction générale

Les glissements de terrain sont parmi les mouvements de masse les plus spectaculaires et les plus fréquents, dont l'apparition provoque des déformations de la croûte terrestre. Ils se développent dans un massif de sols meubles ou de roches tendres et se produisent dans des circonstances très variées, affectant les ouvrages construits par l'homme (déblais et remblais) ou tout simplement, des pentes naturelles.

Face à une telle situation, l'entreprise des études adéquates et les moyens de confortement efficaces devient indispensable.

La région d'Alger a connue cet aléa qui a provoqué de graves dégâts.

Le développement de la population algérienne ces derniers années, et sa concentration dans le Nord du pays en particulier dans la capitale ou pratiquement tous les terrains stables ont été bâti, ce qui a poussé à projeter différentes constructions et ouvrages sur des terrains en pentes qui sont parfois instables ou ils deviennent instables après l'intervention de l'homme suite à des travaux de terrassements, travaux en pied des talus,...etc, ce qui engendre des catastrophes de glissement de terrain, des pertes humaines et des dégâts matériels inestimables.

C'est dans ce cadre que s'inscrit notre étude comme une modeste contribution à l'étude et la prévention de ce phénomène, en prenant comme exemple le glissement de terrain survenue au lieu dit Sidi Youcef dans la commune de Beni Messous -Wilaya d'Alger-.

Notre travail a été articulé en cinq chapitres:

· Dans le premier chapitre on a illustré les différents types des mouvements de terrain,

les causes déclenchant, avec quelques exemples dans le monde en générale et en Algérie en particulier avec les moyens de confortement utilisés.

· Dans le deuxième chapitre on a exposé principalement les méthodes de calcul de stabilité à savoir: les méthodes d'équilibre limite et les méthodes des éléments finis et on a présenté et décrit deux outils numériques utilisés dans la modélisation et calcul de la stabilité des talus .

· Dans le troisième chapitre on a fait une description géologique, hydrogéologiques, hydrologique ainsi qu'une étude géotechnique réalisé à partir des résultats d'essais collectés dans le laboratoire.

· Dans le quatrième chapitre on a analysé les résultats d'essais effectués au laboratoire. Après une brève description du matériau étudié.

· Dans le cinquième chapitre on a introduit une approche nous permettant de donner un
modèle de ce glissement en utilisant le code PALXIS et le programme GEOSLOPE.

Chapitre I :

Généralités sur les mouvements de terrain

I-1-INTRODUCTION:

Les problèmes de stabilité des pentes se rencontrent fréquemment dans la construction des routes, des canaux, des digues et des barrages. En outre certaines pentes naturelles sont ou peuvent devenir instables. Une rupture d'un talus peut être catastrophique et peut provoquer des pertes en vies humaines et matériels ainsi que des dégâts naturelles considérables.

Les mouvements de terrain sont très variés, par leur nature (glissements de terrains, éboulements rocheux, coulées de boues, effondrements de vides souterrains, affaissements, gonflement ou retrait des sols,...etc.) et par leur dimension (certains glissements, comme celui de la Clapière dans les Alpes Maritimes, peuvent atteindre plusieurs dizaines de millions de m³).

Pour éviter un glissement, il est important d'installer des moyens de surveillance sur le site jugé instable ou peuvent être également procéder aux moyens de confortement adéquats, en prennent compte tous les facteurs aussi bien liée au mouvement (dimension, géométrie) et les facteurs extérieurs telle que les écoulements et l'altération...etc. pour empêcher tout déplacement de masse.

I-2- LES MOUVEMENTS DE TERRAIN ET LES DIFFERENTS TYPES :

On regroupe sous l'appellation de " mouvement de terrain " tous phénomènes affectant une masse de sols ou roches et le faire déplacer d'un état à un autre d'une manière lente et

superficielle qui se résulte de l'effet des actions de gravité, l'alternance de " gel/dégel ", ou d'une manière rapide et profonde résultant de l'érosion favorisée par l'action de l'eau et de l'homme c'est pour cela qu'il y a une multitude de mouvement de terrain ^[1].

Il existe de nombreuses classifications des mouvements de terrain; Selon la vitesse de déplacement, deux ensembles peuvent être distingués: les mouvements lents et les mouvements rapides.

Seuls les mouvements rapides sont directement dangereux pour l'homme. Leurs conséquences sont d'autant plus graves que les masses déplacées sont importantes.

Les conséquences des mouvements lents sont essentiellement socioéconomiques ou d'intérêt public.

I-2-1-Les mouvements rapides et discontinus :

a) Les écroulements et chutes de blocs:

Ils résultent de l'évolution de falaises allant, selon les volumes de matériaux mis en jeu, de la simple chute de pierres (inférieur à 0,1m³), à l'écroulement catastrophique supérieur à dix millions de m³ avec, dans ce dernier cas, une extension importante des matériaux éboulés et une vitesse de propagation supérieure à cent kilomètre par heure.

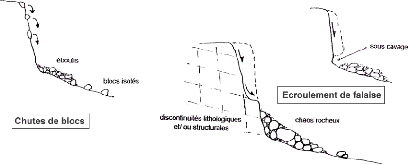
Figure I-1: Les chutes de blocs et les écroulements ^[1].

b) Les coulées boueuses:

Phénomènes caractérisés par un transport de matériaux sous forme plus ou moins fluide.

Photo I-1 : Les coulées boueuses.

Les coulées ont lieu dans des formations argileuses, ou a granulométrie très fine (marnes, schiste argileux, flysch argileux ) fissurées ou saturées a plasticité moyenne.

c) Les effondrements:

Déplacements verticaux instantanés de la surface du sol par rupture brutale de cavités souterraines préexistantes, naturelles ou artificielles (mines ou carrières), avec ouverture d'excavations.

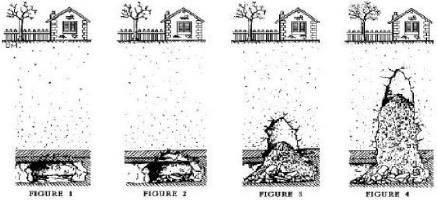
Figure I-2 : Progression d'un effondrement.

I- 2-2- Les mouvements lents et continus :

a) Le fluage :

Il se caractérise par des mouvements lents, et des vitesses faibles, dans ce cas, il est difficile de mettre en évidence une surface de rupture.

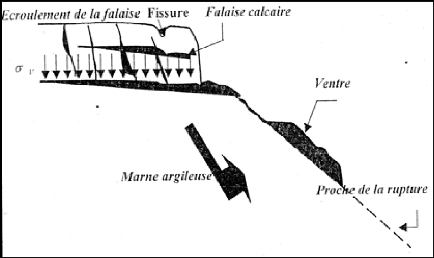
Figure I-3 : Le phénomène du fluage.

Le mouvement se produit généralement sans modification des efforts appliqués (contrairement aux glissements). Ce type de mouvement peut : soit se stabiliser, soit évolué vers une rupture.

b) Les affaissements:

Evolution des cavités souterraines dont l'effondrement est amorti par le comportement souple des terrains superficiels.

Figure I-4 : L'affaissement.

Ces cavités peuvent être:

- Des vides naturels par dissolution de roches solubles, calcaires, gypses...etc. - Des ouvrages souterrains exécutés sans précaution.

- Des carrières souterraines (calcaire, craie, mines de sel, de charbon...etc.).

c) Les glissements de terrain [2] :

Il s'agit d'un déplacement relatif d'un volume du sol par rapport au reste du massif selon
une surface de glissement quelconque dont la morphologie est décrite par le schéma suivant :

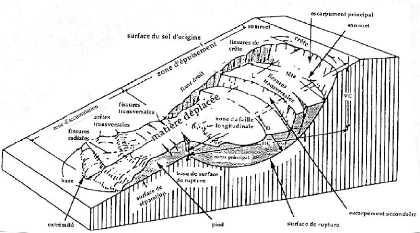
Figure I-5 : Processus de glissement de terrain ^[3].

Argiles Limons Substratum

Ils peuvent intéresser les couches superficielles ou être très profonds (plusieurs dizaines de mètres): dans ce dernier cas, les volumes de terrain en jeu peuvent être considérables.

I-2-3-Types de glissement :

I-2-3.1.Glissement plan :

Ce type de glissement se produit lorsque, le massif en pente est constitué de sols par exemple meubles reposant sur un substratum, ou encore lorsque la longueur de la surface de rupture potentiel est très grande par rapport à l'épaisseur du terrain.

La taille de tels glissements est très variable et peut comprendre des surfaces allant de quelques mètres carrés à plusieurs kilomètres carrés.

Les zones de flysch, les schistes marno -calcaires ou les schistes métamorphiques sont les formations les plus sujettes à ce genre de glissement.

Figure I-5.a : Glissement plan.

I-2.3.2.Glissement rotationnel :

Lors de glissement rotationnel, la masse se déplace vers l'aval le long d'une surface de rupture circulaire. Habituellement, les glissements de ce type sont de faible volume et le déplacement des matériaux est limité.

Route Talus Marnes

Figure I-5.b : Glissement rotationnel.

Ils se produisent principalement dans des terrains meubles homogènes surtout argileux et silteux ^[4]

On distingue deux classes de glissement rotationnel :

a) Glissement rotationnel simple :

La surface de rupture à une forme simple et peut être assimilée à un cylindre dans la plupart des cas.

Il comprend :

· en tête des fissures de traction,

· un escarpement correspondant au départ de la surface de glissement.

· à la base, un bourrelet formé par des matières glissées.

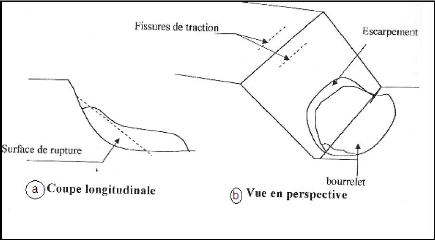
Figure I-5.c : Glissement rotationnel simple. b) Glissement rotationnel complexe :

Il s'agit de glissements multiples « emboîtés » les uns dans les autres, dus à la suppression de la butée provoquée par le glissement précédent, ce qui entraîne ainsi des glissements successifs remontant vers l'amont.

Figure I-5.d : Glissement rotationnel complexe.

*Les glissements de terrain se différencient aussi par leur vitesse et par leur profondeur estimée de la surface de glissement:

*Vitesse moyenne de glissement :

Glissement	Vitesse de glissement
Substabilisé, très lent	0 - 2 cm/an
Peu actif, lent	2 - 10 cm/an
Actif (ou lent avec phases rapides)	> 10 cm/an

Tableau I-1 : Classification selon l'activité en fonction de l'évaluation de la vitesse moyenne
de glissement a long terme.

*Profondeur de glissement :

Glissement	Surface de glissement
Superficiel	0 - 2 m
Semi profond	2 - 10 m
Profond	> 10m

Tableau I-2 : Classification selon la profondeur de la surface de glissement. I-3- ORIGINE ET CAUSES DES GLISSEMENTS DE TERRAIN:

En règle générale, les glissements sont dus à des modifications soit dans les moments résistants, soit dans les moments moteurs. Il y a rupture lorsque les moments moteurs sont supérieurs ou égale aux moments résistants, d'origine naturelle ou anthropique.

I-3- 1- Les causes augmentant les moments moteurs :

- Augmentation de la hauteur d'une pente.

- Enlever le sol au pied de la pente.

- Ajouter une charge au sommet.

- Abaisser le niveau d'eau a l'extérieur de la pente.

- Augmentation de la pression d'eau dans les fissures de traction.

- Augmentation du poids volumique par saturation. - Séisme ou charge dynamique.

I-3- 2- Les causes diminuant les moments résistants :

- Augmentation de la pression interstitielle. - Liquéfaction des sols.

- Gonflement des sols et annulation de la succion. - Altération lessivage.

- Rupture progressive (fluage).

I-4- PHASES DES GLISSEMENTS:

Les glissements de terrain se caractérisent par des phases d'activité variables : des périodes de vitesse de glissement plus élevée avec des phases de calme apparent.

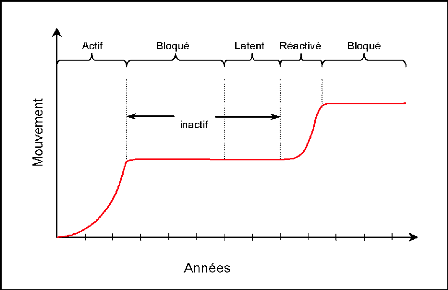
Figure I-6 : Différentes phases de l'activité d'un glissement de terrain.

1. Glissements de terrain actifs :

Un glissement de terrain est considéré comme actif si un mouvement peut être constaté. Le déplacement peut être minime, les déformations de moins d'un millimètre étant toutefois difficilement détectables.

Les glissements actifs comprennent les glissements présentant des vitesses plus ou moins constantes à long terme tout comme les glissements avec des phases successives d'accélérations.

2. Glissements de terrain réactivés :

Désigne les glissements de terrain qui quittent une phase inactive pour entrer dans une phase active. Habituellement, les glissements de terrain réactivés se déplacent le long d'une surface de glissement existante.

3. Glissements de terrain inactifs [5] :

Désigne les glissements de terrain restés immobiles pendant plusieurs années. Ceux-ci se subdivisent en quatre catégories :

*Glissements bloqués.

*Glissements latents.

*Glissements abandonnés.

* Glissements stabilisés.

I-5- QUELQUES EXEMPLES DES GLISSEMENTS DE TERRAIN :

I-5-1- A travers le monde :

I-5-1-1-Glissement de Villatina Medellin en Colombie [6]. :

Le glissement a eu lieu en 1987 au quartier de Villatina Medellin qui est localisé sur le flanc oriental de l'aval du Rio Medellin. Il est l'une des grandes catastrophes naturelles qui ont eu lieu en Colombie dans une zone urbaine. Le nombre des victimes a été entre 450 et 500, avec plus de 120 maisons détruites.

Le glissement est parti de la zone de dunites (roches argileuses fracturées) qui a une pente supérieure à 20%, il est descendu en suivant la ligne de plus forte pente (Photo ².2)

Photo I-2: Morphologie de la zone de glissement de Villatina Medellin en Colombie ^[6].

I-5-1-2-Glissements de La Leona et de Las Coiinas au Salvador :

A la suite d'un tremblement de terre de magnitude 7.6 à l'échelle Richter survenu en 2001 au large des cotes du Salvador, deux glissements de terrain se sont produits : le glissement de La Leona près de San Vicente et le glissement de Las Collinas (Photo I.3).

a/ La Leona

b/ Las Collinas
Photo I-3 : Glissements de La Leona près de San Vicente (a) et de Las Collinas (b) au
Salvador [6].

Le glissement de La Leona s'est produit au kilomètre 53 de la route Panaméricaine sur un versant de pente moyenne égale à 22° présentant une paroi raide à sa base, de hauteur égale à environ 120 m et de largeur de l'ordre de 250 m. L'instabilité s'est développée sur une épaisseur de l'ordre de 25 m, son volume est compris entre 500 000 et 700 000 m³.

La zone du glissement est formée de coulées de basalte datant du Pliocène et de nombreuses brèches de pente qui témoignent de l'existence d'anciennes phases de glissement. Ce glissement de terrain a la particularité de s'être produit sur le site d'un ancien glissement.

Le glissement de Las Collinas est caractérisé par un escarpement qui se situe à une altitude de 1075 m, dans une zone de pente moyenne égale à 32°. La largeur de l'instabilité est de l'ordre de la centaine de mètres (80-120 m) et la distance parcourue par la masse instable est estimée à 735 m. Le volume de cette instabilité est de l'ordre de 200 000 m³. Le soubassement de la zone du glissement est constitué de dépôts de laves et de pyroclastes indurés. Cette formation est recouverte de deux niveaux plus récents : une couche de cendres volcaniques sur laquelle repose une couche de dépôts pyroclastiques peu consolidés et lâches dont la Terra Blanca.

I-5-2- En Algérie :

Le problème des glissements de terrain est couramment rencontré en Algérie et ce depuis fort longtemps. On rappelle :

I-5-2-1- Glissement de terrain à Constantine:

A côté des catastrophes naturelles qui ont ébranlé des villes algériennes ces dernières années, Constantine est touchée par les phénomènes des glissements de terrain.

Selon les services de la Wilaya, le phénomène affecte une superficie de cent vingt hectares abritant quinze mille logements avec une population estimée à cent mille habitants.

Il en est ainsi de la rue Kitouni, de l'avenue Belouizdad et de certaines des ruelles qui leur sont adjacentes, ou encore de l'avenue Rahmani et du côté de Bellevue., la mosquée EmirAbdelkader, et les cités de Bardo, Siloc, Aïn El Bey, Boussouf et Zaouch, la liste n'est tout de même pas close.

Ce phénomène semble du à la conjonction d'un certain nombre de causes: fragilité naturelle des lieux, infiltration des eaux pluviales, mais surtout à la vétusté de réseau de distribution d'eau qui entraîne dans le sous-sol une perte très importante, et qui mine alors les fondations des habitations.

Photo I-4: Glissement de terrain à Belouizdad. [2002].

Photo I-5: Rue de Verdun. [2002].

Cet immeuble blanc (haut de la rue de Verdun) avec de fausses fenêtres, est totalement vide et fermé. Il est démoli ^[4].

I-5-2-2-Glissement des abattoirs Ténès (Chlef) [v] :

Le glissement des abattoirs Ténès, se trouvant sur un talus de 10 m environ de hauteur. Ce glissement a été provoqué dans les années 80 sous l'effet des infiltrations souterraines ayant fait déplacer la masse de remblai composée d'alluvions récentes.

Photo I-6 : Le glissement de la route des abattoirs.

L'étude a été réalisée par la DTP (Antenne de Chlef), ou une solution a été dégagée consistant a recharger le pied du talus tout en proposant des murs de soutènement reposant sur des pieux ancrées a plus de 25m de profondeur, mais cette solution n'a pas été réalisé.

Par conséquent, de grave préjudices ont été observés sur le terrain, dont la partie se trouvant en haut du talus a été complètement déplacée et touchant même les fondations des bâtiments se trouvant a coté de l'emprise.

I-5-2-3- Glissement d'Ain El Hammam (Tizi-Ouzou) [2] :

Il s'agit d'un méga glissement qui a touché une grande zone située a Ain El Hammam dans la wilaya de Tizi-Ouzou. La zone touchée par ce glissement est d'environ 10ha de surface.

Outre l'étendue importante de ce glissement, il a eu des conséquences néfastes sur une bonne partie de l'ancienne ville d'Ain El Hammam, Pour deux raisons : la grande étendue et l'impact exigent des solutions adéquates à ce méga glissement

I-5-2-4- Les glissements de terrain dans la région d'Alger [4] :

Ils affectent essentiellement les marnes plaisanciennes (collines du sahel), et d'une façon importante les assises astiennes, mais peu importante pour les formations métamorphiques :

Au niveau de Télemly, les ruptures de réseaux (AEP et eaux usées) traversant les zones instables participent à aggraver l'instabilité.

Dans le cas du glissement de Climat du France, la non-surveillance des drainages réalisés risque de voir se redévelopper les mouvements de terrain (Figure I-7) :

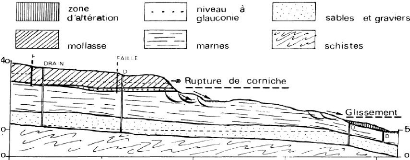
Figure I-7 : Coupe géologique du Climat de France.

La réalisation des constructions et villas en zones pentues, c'est le cas de Bouzaréah dont le risque de l'instabilité à cause de la schistosité et de la fissuration.

Et d'autres glissements tels que le Parc zoologique, à Ben Aknoun et à Ouled Fayet.

Dans la plus part des cas, l'homme est la cause principale dans ces instabilités suite a la méconnaissance de la géologie de la région.

I-6-TECHNIQUES ET MOYENS DE CONFORTEMENT :

I-6-1-Généralités :

Le confortement des talus est défini comme l'ensemble des méthodes qui servent a stabilisés la masse de terrain instable.

La méthode de confortement choisie doit répondre aux exigences suivantes :

· Coté résistance : la méthode doit assurer la stabilité du talus, ainsi le mode de
renforcement ne génère aucun risque d'augmenter les efforts moteur de notre talus.

· Coté économique : le mode de renforcement doit être le moins coûteux et le plus disponible dans le marché, car il y a des modes de renforcement qui nécessitent une importation, en règle générale on utilise ce qui est disponible (locale) et moins coûteux.

· Coté technologique (ouvrabilité et maniabilité): la méthode de renforcement doit être simple et ne demande qu'un minimum d'effort ainsi qu'on peut la réaliser facilement.

I-6-2-Les différentes techniques :

D'une manière générale, les méthodes de confortement peuvent être regroupées en trois catégories :

1- La modification géométrique :

Les conditions de stabilité étant directement liées à la pente du terrain, pour cela la modification géométrique et morphologique s'impose en premier lieu, elle peut être envisagée par plusieurs méthodes selon la nature du problème.

On peut citer :

1-1- Le déchargement en tête :

Le déchargement en tête de glissement consiste à venir terrasser dans la partie supérieure. Il en résulte une diminution du poids moteur et, par conséquent, une augmentation du coefficient de sécurité.

La méthode de dimensionnement consiste en un calcul de stabilité le long de la surface de rupture déclarée en prenant en compte la modification de géométrie en tête. 1-2- Le chargement en pied :

Le chargement en pied d'un glissement est une technique souvent utilisée, généralement efficace. L'ouvrage, également appelé banquette, berme ou butée, agit par contre balancement des forces motrices. Pour qu'il soit fiable, il faut réaliser un ancrage dans les formations sous-jacentes en place.

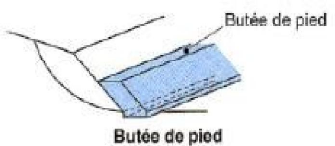
Figure I-8 : chargement au pied d'un talus.

Comme dans le cas d'un ouvrage de soutènement, le dimensionnement doit justifier de la stabilité au renversement et la stabilité au glissement sur la base.

1-3- Le reprofilage :

Ce procédé s'apparente au déchargement en tête : il consiste a un adoucissement de la pente moyenne. Ce type de traitement est spécifiquement bien adapté aux talus de déblais, et il est de pratique courante. Notons que l'exécution de risbermes a l'avantage d'améliorer la stabilité par rapport a une pente unique et de créer des voies d'accès pour l'entretien ou des travaux complémentaires. L'adoucissement de la pente est généralement mal adapté aux versants naturels instables car il met en jeu des volumes de sol très importants.

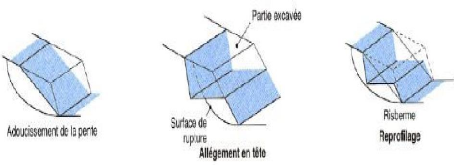
Figure I-9 : les différents procédés de modification géométrique.

2- La substitution :

La substitution totale consiste à venir purger l'ensemble des matériaux glissés ou susceptibles de glisser, et à les remplacer par un matériau de meilleure qualité.

Cela permet de reconstituer le profil du talus initial. Il importe de vérifier la stabilité au cours des phases de travaux et celle du talus définitif dans lequel on prend en compte les caractéristiques du matériau de substitution et du matériau en place.

La substitution de matériaux glissés suppose que l'on connaisse le volume de matériaux concerné, que l'on excave plus profondément que la surface de rupture, et que

l'on réalise des redans afin d'assurer un bon accrochage entre le substratum et le sol d'apport. La tenue des talus provisoires de la purge dépend des conditions de terrassement, de la météorologie, des hétérogénéités locales.

Des substitutions partielles sont souvent employées, sous forme de bêches ou de contreforts discontinus. Le coefficient de sécurité de la pente ainsi traitée peut être estimé en prenant la moyenne pondérée des coefficients de sécurité de la pente avec et sans substitution [8].

3- Le drainage :

Dans la plupart des cas de glissement, l'eau joue un rôle moteur déterminant. Elle peut être un facteur occasionnel de glissement, sinon la cause principale de celui-ci, le drainage est recommandé dans la majorité des cas.

En outre, l'implantation d'un dispositif de drainage est souvent moins coûteuse que

les autres méthodes de stabilisation. L'efficacité d'un système de drainage est liée en particulier à la nature et l'hétérogénéité des terrains.

Les méthodes de drainage habituelles consistent en général à :

· capter les eaux de surface,

· Eviter les ruissellements et infiltrations dans les zones instables,

· diminuer les pressions interstitielles en profondeur en abaissant la nappe

· Améliorer l'écoulement des eaux dans les structures.

Parmi ces méthodes, on trouve les techniques suivantes :

3-1- Les tranchées drainantes :

Les tranchées drainantes sont des structures allongées, disposées

perpendiculairement aux écoulements afin de rabattre le niveau de la nappe.

Leur mode de réalisation consiste à creuser à la pelle, des tranchées de plusieurs mètres de profondeur (entre 4 à 6 m) et une largeur d'environ un mètre (0,8 à 1,20m). On met des tubes en P.V.C ; on les remplit avec des matériaux drainant le tout est protégé par un géotextile anti-contaminant (voir la figure I.10).

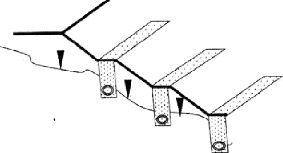
Figure I-10 : tranchées drainantes.

3-2- Les éperons drainants :

Les éperons drainants sont des excavations étroites (environ 1m), mais qui peuvent atteindre une profondeur supérieure à 7m.

Leur mode d'exécution consiste à creuser des tranchées de plusieurs mètres, parallèlement à la pente du talus avec engins mécaniques, sans qu'elles soient trop espacées pour assurer un bon drainage, ensuite ces tranchées sont remplies en matériaux granulaires grossiers (voir la figure I.11).

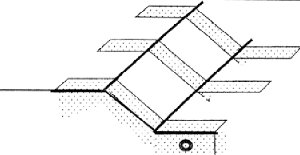
Figure I-11: Eperons drainantes.

3-3- Les drains subhorizontaux

Cette technique consiste à réaliser des puits ou des tubes de petits diamètres légèrement inclinés (5%) vers l'extérieur pour permettre l'écoulement de l'eau au sein du terrain.

Leur exécution présente des difficultés liées par exemple à la longueur du drain à réaliser dans le cas de terrains à faible pente.

Cette technique est utilisée quand la nappe est trop profonde pour être atteinte par des drains superficiels.

La meilleur justification de l'utilisation de drains subhorizontaux est le cas d'un aquifère assez perméable (sable, roche extrêmement fracturée) dont l'émergence est masquée par des terrains moins perméables (éboulis argileux). Le rayon d'action de chaque drain est faible.

La méthode est souvent inefficace dans des formations argileuses (trop faible perméabilité, circulation trop diffuse). Toutefois, le rabattement de la nappe, si faible soit-il, pourra suffire dans certains cas.

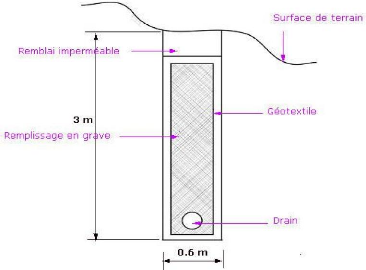
Figure I-12 : les drains subhorizontaux 3-4- Les drains verticaux :

Les drains verticaux sont utilisés pour l'amélioration des sols saturés en eau (ex : terrain silteux ou argileux). La technique consiste à foncer verticalement dans le terrain,

suivant un maillage déterminé, un drain préfabriqué. Au moment de sa mise en service, le drain transport l'eau du terrain jusqu'au surface. La surcharge est apportée en générale par un remblai de pré-chargement ^[8].

4- La végétalisation :

La végétation possède un rôle stabilisateur mécanique par enracinement dans le sol. C'est une méthode écologique et économique qui consiste à stabiliser le sol avec des plantations appropriées au terrain et à l'environnement.

Photo I-7 : l'implantation des plantes dans un talus.

5- Les éléments résistants :

Ces procédés ne s'attaquent pas à la cause des mouvements mais visent à réduire ou à arrêter les déformations. Elles sont intéressantes dans les cas où les solutions précédentes (modification géométrique et drainages) ne peuvent pas être techniquement ou économiquement mises en oeuvre. La compatibilité des déplacements du sol et des structures doit être prise en compte lors du choix de ce type de technique.

5-1- Les ouvrages de soutènement :

Il existe plusieurs types d'ouvrages destinées à résister à la poussée des terres on distingue : les ouvrages rigides (murs en béton armé, en béton...) et les ouvrages flexibles (rideau de palplanches).

5-1-1- Les murs de soutènements :

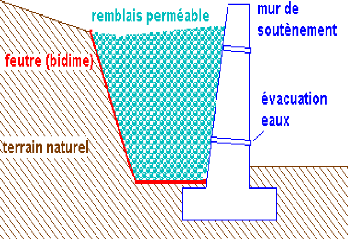
Figure I-13: Mur de soutènement.

Les murs de soutènements sont les ouvrages réalisés dans le but de stabiliser un talus instable utilisant leurs poids propres ou leurs rigidités, Il existe deux types d'ouvrages :

· Les murs poids

· Les murs souples.

5-1-2- Les rideaux de palplanches :

Les rideaux de palplanches sont utilisés en soutènement provisoire ou permanent. Cette technique est applicable dans tous les terrains meubles.

Ces rideaux sont auto stables pour une hauteur de terre à soutenir de 3 à 4 mètres. Au delà ils doivent être ancrés. L'un des avantages de cette technique est la rapidité d'exécution. Par contre leur utilisation pose des problèmes particuliers en site urbain en raison des nuisances crées par le fonçage à proximité d'habitations.

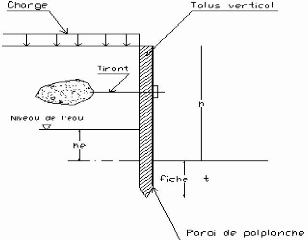
Figure I-14: Paroi de palplanche.

5-1-3- La terre armée [9]:

La terre armée fut mise au point par H.VIDAL en 1963. Cette technique de renforcement de remblais consiste en association de trois éléments principaux à savoir :

v' un sol : plus ou moins frottant constituant la majeure partie du remblai et devant posséder un certain nombre de caractéristiques mécaniques.

v' des inclusions : horizontales et linéaires appelées "armatures" qui jouent le rôle d'éléments de renforcement.

v' un parement : anciennement métallique, aujourd'hui plutôt constitué d'éléments béton préfabriqués (écailles), dont la fonction mécanique est très limitée.

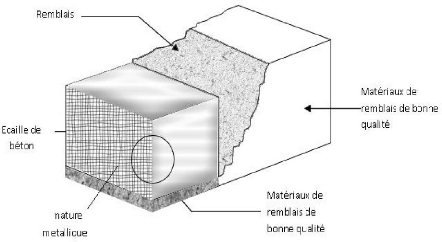
Figure I-15 : principe de la technique terre armée.

5-2-Les tirants d'encrage :

Le principe de base consiste à mobiliser un certain volume de terrain ou de rocher encaissant, afin de rétablir ou de renforcer la stabilité d'une fondation, au glissement ou au soulèvement.

Un tirant est constitué par une armature continue au diamètre d'une trentaine ou quarantaine de millimètres (barre unique ou faisceau de barres, tube, fils ou torons parallèles, câble,) scellée dans un forage sur une partie de sa longueur, par injection de coulis ou de mortier de scellement, ou ancrée mécaniquement dans un terrain.

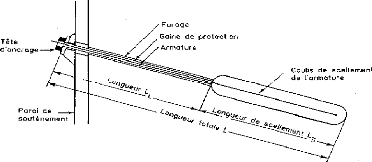
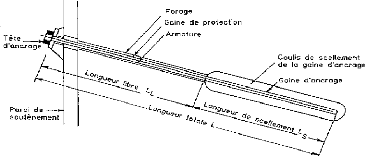
Figure I-16: Schéma de principe d'un tirant d'ancrage injecté

5-3-Le clouage :

Désignée aussi par le terme cloutage. Les armatures, généralement métalliques, sont déposées perpendiculairement aux lignes de glissements éventuelles. La technique repose sur un transfert des efforts du sol vers les barres par mise en butée du terrain. Il en résulte une cohésion apparente du sol clouté, ce qui explique le succès du procédé.

Photo I-8 : Un versant stabilisé par clouage.

5-4-Les géotextiles :

Les géotextiles sont des produits textiles à bases de fibres polymères utilisées au contact du sol dans le cadre d'application dans le domaine de la géotechnique et du génie civil. Leurs domaines d'utilisation sont très vastes et concernent aussi bien la géotechnique routière, les centres de stockage des déchets, les aménagements hydrauliques, la stabilisation des sols et le renforcement des fondations....etc.

Les principales fonctions des géotextiles sont :

> La séparation : éviter l'interpénétration des sols de nature et de granulométrie différente (en vue de maintenir leurs performances initiales).

> La filtration : assurer le passage de l'eau perpendiculairement au plan de la nappe en retenant les particules de sol.

> Le drainage : assurer le passage de l'eau dans le plan de la nappe.

> Le renforcement : améliorer la résistance d'un massif de sol dans lequel il est inclus.

> La protection : protéger une structure fragile (géomembrane) contre des éléments poinçonnant.

> La lutte contre l'érosion : limiter les mouvements des particules de sol en surface causés par l'eau ou le vent ^[10].

Photo I-9 : L'utilisation du géotextile en jouant un double rôle le drainage et le renforcement
du talus.

CONCLUSION :

A travers ce chapitre, on déduit que le glissement de Sidi Youcef est l'un des cas d'instabilité rencontrés dans la région d'Alger, a cause de l'action anthropique des constructions et de terrassement en zone pentue.

Chapitre II :

Méthodes de calcul de glissement de terrain

II-1- INTRODUCTION :

Le danger de l'apparition d'un glissement peut être estimé par l'analyse de la variation du facteur de sécurité en fonction de la forme et de la position de la surface possible de glissement pour laquelle le facteur de sécurité a la valeur minimum qui représente la surface critique de rupture

Nous allons nous efforcer de montrer le mécanisme qui conduit à la rupture de certains talus ou pentes naturelles. Nous verrons les méthodes de calcul qui permettent d'évaluer si un talus est stable ou non.

Il existe plusieurs méthodes dans la littérature. Elles apparaissent en général trop simples et trop figées ou trop élaborées et de maniement délicat. Ces dernières diffèrent entre elles par les conditions d'équilibre statique utilisées et par les hypothèses admises pour annuler l'indétermination statique du problème.

II-2 - GENERALITES SUR L'ANALYSE DE STABILITE [11] :

II-2 -1- Notion de facteur de sécurité :

Le principe de calcul de stabilité des talus consiste à déterminer le facteur de sécurité Fs par lequel il faut diviser la résistance de la surface de glissement pour que la masse potentiellement stable soit à la limite de l'équilibre. Ce facteur peut être décrit de la façon suivante :

Qrnax

Fs = Q

Avec :

Q: cette valeur définit la sollicitation vectorielle ou tensorielle appliquée au massif (force H, force V, moment M).

Qmax: valeur maximale de Q.

Le facteur de sécurité pourrait être calculé, pour un paramètre sélectionné, en prenant le ratio de la valeur à la rupture, par la valeur calculée sous les conditions de projet de ce

paramètre, ce dernier peut être un rapport de forces, de moments, de grandeurs par rapport à une grandeur limite comme le montre le tableau II-1 :

Définition		Formule	Rapport de contraintes
F=ômax/ô		Rapport de forces
F=Erésist/Emoteur		Rapport de moments
F=Mresist/Mmoteur		Rapport de grandeurs
Par ex: H/Hmax

Tableau II-1 : Fs en fonction de grandeurs par rapport à une grandeur limite. On distingue deux manières différentes d'utiliser les méthodes de calcul:

· Dans la première, le glissement a déjà eu lieu, il s'agit d'une valeur de Fs inférieure ou égale à 1, dans ce cas la surface exacte est connue et on cherche à déterminer, pour Fs = 1, les caractéristiques correspondantes.

· La deuxième, la plus fréquente, consiste à déterminer la marge de sécurité disponible et adopter les solutions adéquates pour améliorer la sécurité de l'ouvrage en répondant à des exigences en fonction de l'emploi des talus.

Choix de la valeur du coefficient de sécurité dans le calcul de stabilité :

Le facteur de sécurité minimal Fs adopté est assez rarement inférieur à 1.5. Il peut quelquefois être égal à 2, voire à 2.5 pour des ouvrages dont la stabilité doit être garantie à tout prix (grand risque pour les personnes, site exceptionnel), ou pour des méthodes dont l'incertitude est grande (analyse en contrainte totale avec risque d'erreur sur la valeur de la cohésion drainé Cu).

Pour certains sites peu importants ou pour certains ouvrages courants, et lorsqu'il n'y a pas de risque pour la vie humaine, on peut accepter des valeurs plus faibles pendant un moment très court ou pour des fréquences faible : 1.2 voire 1.1.

Le tableau ci-dessous, nous donne les valeurs de FS en fonction de l'importance de l'ouvrage et des conditions particulières qui l'entoure :

FS		Etat de l'ouvrage	<1
Danger		1.0-1.25
sécurité contestable		1.25-1.4
sécurité satisfaisante pour les ouvrages peu importants sécurité contestable pour les barrages, ou bien quand la rupture serait catastrophique		>1.4
satisfaisante pour les barrages

Tableau II-2 : Valeur de FS en fonction de l'état de l'ouvrage. II-2 -2 - Les différentes méthodes de calcul :

Un autre choix important, qui dépend des moyens que l'on peut mettre en oeuvre, doit être posé entre une méthode modélisant toute la masse de sol (méthode des éléments finis) et une méthode cinématique, définissant une surface de rupture par exemple (méthode d'équilibre limite). Cependant, avec les possibilités d'analyse d'un grand nombre de courbes de rupture potentielles, les deux approches se rejoignent.

Le comportement global de la pente correspond à quatre mécanismes qui se traduisent par des déplacements du sol différemment répartis :

· Pré-rupture : où le comportement du sol est élasto-viscoplastique et où le massif est un milieu continu, sans zone de discontinuité, les déformations sont quasi homogènes

· Rupture : où une partie du massif se déplace par rapport à l'autre, le modèle de sol est élasto-plastique, voire rigide-plastique ;

· Post-rupture : où une partie du sol se déplace sur l'autre, comme un écoulement visqueux et avec une vitesse appréciable ;

· Réaction : quand la partie du sol ayant déjà glissé et s'étant stabilisée, le mouvement reprend sur une surface, suivant un comportement rigide-plastique; La distinction entre ces quatre mécanismes est fondamentale pour une étude fiable des pentes, et ceci va bien sûr influer sur le choix d'une méthode de calcul.

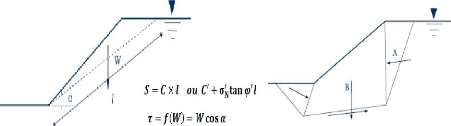
II-3- RUPTURE PLANE [12]:

II-3-1-Pente semi-infinie terrain sec :

Soit un élément de volume de sol ABCD de hauteur H et de largeur b qui glisse sur sa base CD.

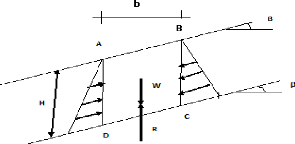
Figure II-1: Notations pour le calcul de la stabilité d'une pente.

Les diagrammes triangulaires le long d'AD et le long de BC sont égaux et opposés. On considère que la réaction R du terrain est égale au poids W de l'élément ABCD. Cette réaction se décompose en une composante normale à la face DC notée N et une composante parallèle à la face DC notée T.

N = WX cos â = ãX bX HX cos â. T = WX sin â = ãX bX HX sinâ.

On déduit les contraintes moyennes le long de CD :

ó =N / (b / cos â) = ãX HX cos² â

ô= T/(b / cos â) = ãX HX sinâX cos â.

En retenant comme critère de rupture par glissement la loi de coulomb :

ô = ó tg ö + C il vient:

ãX HX sinâX cos â= ãX HX cos² âX (tg ö + C).

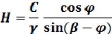
D'ou l'on tire l'expression suivante :

Si â <ö.

L'application de l'équation donne pour H <0 donc aucune

ligne de glissement ne peut se produire et la pente est stable d'où :

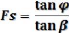
Si â = ö

L'expression donne pour H une valeur théoriquement infinie et la pente est en état d'équilibre limite donc

Fs = 1.

Si â >ö

Le talus est instable et l'équation de H permet d'apprécier la profondeur maximum prise par la ligne de glissement.

II-3-2-Pente semi-infinie avec écoulement :

Soit une pente semi-infinie qui est le lieu d'un écoulement parallèle à la pente à la profondeur z :

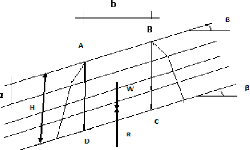
Figure II-2 : Notations pour le calcul de la stabilité d'une pente avec écoulement.

Les diagrammes de poussée des terres le long de AD et le long de BC sont considères égaux et opposés. On en contrainte moyenne le long de DC pour calculer l'équilibre. On déduit les contraintes effectives moyennes appliquées le long de CD :

Fs Tmax T =l	=	((Yh × z) + (Ysat -- Yw)(H -- z)) cos^2 # × tan p' + C^'
		((Yh × z) + Ysat × (H -- z)) sin # × cos #

ômax : résistance au cisaillement du sol ;

ô: contraintes de cisaillement s'exerçant le long de la surface. II-4- RUPTURE CIRCULAIRE :

II -4-1- METHODE D'EQUILIBRE LIMITE :

L'étude de la stabilité des pentes est d'une importance primordiale dans le dessin des excavations, des digues, des barrages, des autoroutes, etc. En général, la méthode universellement utilisée est celle de l'équilibre limite .On considère l'aptitude au glissement d'un certain volume de sol au voisinage de la pente.

II -4- 1-1- Principe :

Pour illustré le principe on va étudier l'équilibre d'un bloc sur une pente avec un angle quelconque, on considère uniquement l'action de la force dus au poids propre de la masse qui conduit le bloc a ce déplacer. On dit que le bloc est en équilibre si la somme des forces internes égale à 0.

La composante du W qui rend ou bien qui met le bloc en mouvement est : Wsin á La composante du W entre la base du bloc et la surface de glissement est : Wcosá

La contrainte appliquée normale à la surface de contact est : ó = (F)/ A. telle que F = W cos á ó = (W cos á)/ A.

A : la surface de contacte.

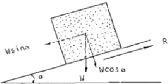
Figure II-3 : Schéma représentatif des forces appliqué sur un bloc.

La contrainte tangentielle (cisaillement) est définie par le critère de rupture de Coulomb : ô = c + ó tg ö

ô = c + ((W cos á)/ A) tg ö.

La force de cisaillement (R = ô.A) qui résiste au glissement. L'égalité avec le critère donne : R = cA+ (W cos á) tg ö.

L'équilibre de la masse est satisfait lorsque la force qui cause le mouvement est en égalité avec la force opposée qui stabilise la masse, donc :

R = W sin á => W sin á = cA+ (W cos á) tg ö

Si :

C = 0 => W sin á = (W cos á) tg ö. Et si á = ö =>W sin á = W sin á (le bloc est en équilibre)

II -4-1- 2- Hypothèses classiques de la méthode de l'équiibre limite [13] : La méthode est basée sur les hypothèses suivantes :

- Le problème est supposé bi-dimensionnel.

- Il existe une ligne de glissement.

- Le coefficient de sécurité F traduit l'écart entre l'état d'équilibre existant et l'état d'équilibre limite :

- Le sol est considère comme ayant un comportement rigide plastique avec le critère de Coulomb ô = C + ó tg ö. La rupture, si elle a lieu, se produit en tout point d'une ligne de glissement continue en même temps (pas de rupture progressive) .

- Le coefficient de sécurité F traduit l'écart entre l'état d'équilibre existant et l'état d'équilibre limite :

Fs= _ôlim /ô = (C + ó tg ö) / (C + ó tg ö_c)

A Fs peuvent être associés deux autres coefficients de sécurités :

> L'un relatif à la cohésion : F_c = C /C_c

> L'autre à l'angle de frottement : F_ö = tg ö / tg ö_c.

II-4-1-3- Méthode d'analyse globale :

. Méthode de TAYLOR (1948) ou méthode du cercle de frottement [14]:

Lors d'une étude d'équilibre d'une pente infinie, le poids du sol contribue aux forces déstabilisatrices alors que la cohésion c_u contribue aux forces d'équilibre. Ainsi, la cohésion C_u et inversement proportionnelle au poids volumique du sol ã. Elle est donnée par la formule suivante :

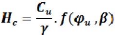
Pour que cette expression soit correcte de point de vue dimension, la fonction f (ö_u ,â) doit être une fonction sans dimensions.

=l Cu ~

km/m^2 Firm. km/m2 1-Wu ,~)sans ~imension

TAYLOR (1948) exprima cette fonction f(ö_u ,â) par un nombre appelé nombre de stabilité S_n ou N_s

En s'appuyant sur le principe de la méthode de cercle de frottement, TAYLOR publia le coefficient de stabilité d'un talus homogènes en fonction de ö_u et â sous forme de tableaux et d'abaques ABQ 2.1. Pour ö_u =0 et â< 53° la valeur de S_n dépends aussi du coefficient de profondeur Df ou (Df .H) est la profondeur de la couche de sol ferme.

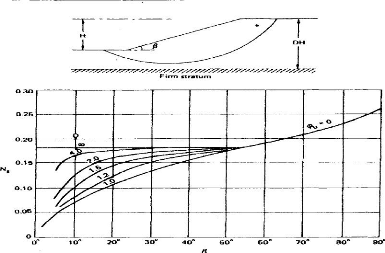
Abaque 1 : Coefficient de stabilité de TAYLOR

Â	Ö
	0°	5°	10°	15°	20°	25°
90°	0.261	0.239	0.218	0.199	0.182	0.166
75°	0.219	0.195	0.173	0.152	0.13	0.117
60°	0.191	0.162	0.138	0.116	0.097	0.079
45°	0.170	0.136	0.108	0.083	0.062	0.044
30°	0.156	0.110	0.075	0.046	0.025	0.009

15°

0.145

0.068

0.023

-

-

-

Tableau II-3 : Nombre de stabilité de TAYLOR.

II-4-1-4- Méthode de l'équilibre des forces [15] :

. La méthode de Coin :

Il s'agit d'une méthode approximative. La masse sur le plan de rupture potentiel est séparée en une série de coins et l'équilibre de chaque coin est considéré.

> Équilibre des forces horizontales et verticales.

> On doit cependant faire une hypothèse sur l'inclinaison de la force entre les coins : 10^o < d < 15^o - d = 0^o conservateur.

ces appliquée dans la méthode des coins.

- En A et B, on voit que en plus de la translation du bloc sous son propre poids, il y'aurai des efforts à chacune des extrémités.

- En A semblable à pousser sur un mur

- En B semblable à buté sur un mur

- On retrouve donc deux façons de traiter ce problème.

- D'abord on fait l'équilibre des forces sur les blocs où on

considère toutes les masses, incluant celles à l'extérieur.

- Problème : il faut maintenant considérer l'interaction des coins. - On assume un facteur de sécurité de départ. Résolution par

polygone des forces du coin 1 (on obtient R12). R21 étant égal à

R12, le polygone des forces du coin2 doit fermer si équilibre.

- Si le polygone ne ferme pas, il faut assumer un autre Fs.

II-4-1-5- Méthode de l'équilibre des moments [11]:

. Méthodes faisant appel à des hypothèses sur la valeur des efforts inter tranches :

Le principe de base de toutes ces méthodes est de découper le volume de sol étudié en un certain nombre de tranches et d'appliquer les différentes forces comme le montre à titre indicatif la figure. Toutes ces méthodes ont en commun la même difficulté qui est de trouver à la fois:

· la surface critique;

· les contraintes normales et tangentielles le long de cette surface;

· le facteur de sécurité (sur le critère de rupture) en partant des équations d'équilibre.

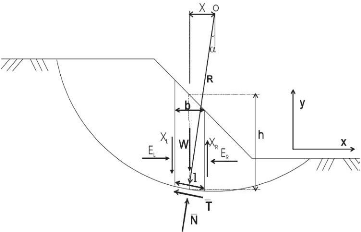
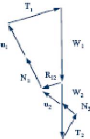
Figure II-5: Exemple d'une rupture circulaire.

Comme on peut le voir sur la figure, les forces agissant sur la tranche peuvent être définies comme suit :

W = poids total de la tranche de largeur b et de hauteur h

N, T = composantes normale et tangentielle de la force agissant à la base de la tranche

X, E = composantes verticale et horizontale des forces inter tranches.

b = épaisseur de la tranche (b=l.cosá)

á = angle que fait la base de la tranche avec l'horizontale R = rayon du cercle de rupture de centre o

l = longueur du plan de glissement de la tranche

x = bras de levier du poids des terres Définissons les efforts comme suit:

N=ól et m T=ô l

Où ô _m est la contrainte de cisaillement mobilisée à la base de la tranche qui peut être exprimée par:

T

T_m = FS

Où ô est donnee par l'equation de Mohr- Coulomb: ô =c'+ (ó?u) tanö'

Fs est le facteur de securite par lequel la resistance au cisaillement du sol doit être reduite pour amener la masse de sol dans un etat d'equilibre limite.

Il vient alors:

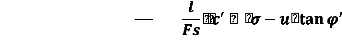
T

T = l

Fs

=

Ou :

1

T=Fs 1'l+ (N

- uI) tan q

~

Pour une tranche:

· En projetant verticalement toutes les forces:

N cos a + T sin a = W - (XR - XL)

Si on remplace T par sa valeur on obtient:

ER - EL = Nin a -

1 [~~~ + (~~ - ~~) ~~~ ~'] ~~~ ~ ~~

On peut definir le coefficient de securite comme suit:

1. soit on le definit à partir de l'equilibre moment de toutes les forces et on va le designer par Fm;

2. soit on le definit à partir de l'equilibre global des forces horizontales, les unes tendant à bouger la masse de sol, les autres tendant à la stabiliser, et on va le designer par Ff. Equilibre global des moments:

ÓW.x = ÓT.R et si on remplace T par sa valeur et x par R siná :

Fes` =

?W sina

?[E'l + (W - ul)tan to

'

Equilibre global des forces:

En absence de tout chargement de la masse de sol etudiee:

~ ER - EL = 0

~XR - XL = 0

D'où, l'equation donne:

~ ?N

hin a

~

?[~~~ + (~

~~ =

- ut) tan q^']cos a

1- Bishop:

I [~~ +

Fs & - u)tan to'

Au contraire de la methode de Fellenius, Bishop prend en consideration les forces entre

tranches ; et de même façon que la première methode :

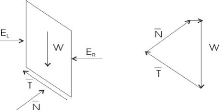
Figure II-6: Forces appliquées sur une tranche dans la méthode de Bishop. La force verticale totale W_n + ?T

~?~~

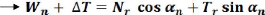
~~ + ?~ - sin a_n

Fs

tan (I) sin a_n

N, =

cos ~~ + Fs

La somme des moments :

n=p n=p

n=1 n=1

~ ~~ ~ ~~~ ~~ = ~ ~~ ~ (~ + ~~ ~~~ ~) (? ~~)(~) ? i_n

? (~?~~ + (~ ~~~ ~~ - ~ ? ~~)) ~~~ ~

~~~

~~~

~~ = --

? ~~ ~~~ ~~

~~~
~~~

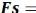
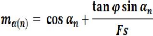
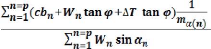
2- Fellenius :

Fellenius suppose en général, que les forces entre tranches peuvent être négligées, parce qu'elles sont parallèles aux bases des tranches. Ce faisant, on ne respecte cependant pas le principe de Newton d'égalité de l'action et de la réaction, et suggère que la résultante des forces qui agissent sur chaque tranche est nulle dans la direction normale.

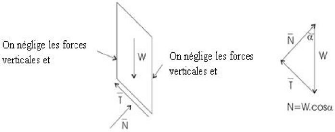
Forces sur une tranche :

Figure II-

7: Forces

appliquées

sur une

tranche dans la méthode de Fellenius

Si la tranche est en équilibre, ces forces doivent satisfaire les 3 conditions d'équilibre. Les inconnus et équations pour un système de n tranches est :

· n équations des moments pour chaque tranche; ÓM = 0.

· n équations des forces verticales pour chaque tranche; ÓFy = 0 3n.

· n équations des forces horizontales pour chaque tranche; Ó Fx = 0.

Les équations de translations ou d'équilibre donnent respectivement :

>

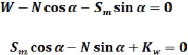
Verticalement :

> Horizontalement : Expression oil les termes ( S_m sin a, S_m cosa) présente l'effet de l'eau a l'amont et a l'aval et K_w l'effet des séismes, ces termes seront négligés par la suite pour des raisons de

simplifications des calculs, ce qui donne l'expression « La méthode de Fellenius simplifiée ». Avec les suggestions de « Fellenius », l'évaluation de la contrainte normal pour tous les points le long de la ligne de glissement, sont devenues possibles et on a :

Ni = Wi cos ai - Ui?Li

Connaissant la valeur de N_i et les paramètres C,cp du sol, devraient possible d'évaluer la force en chaque point d'élément du massif :

Si = Ni tan (I) + C?LT = (Ni cos ai - Ui?Li) +

Cb

cos ai

Par conséquent le moment autour du centre du cercle des forces résistantes à :

n n

~ Cb

SiR = l R (Ni cos ai - Ui?Li ) +

cos ai

i=1 i=1

De même le moment autour du centre du cercle des forces motrices à :

n

n

n

~ Wixi = Wi sin aiR = R1W sin ai

i=1

i=1

i=1

Comme on à mentionner auparavant, le coefficient de sécurité relatif au cercle de rupture choisit est défini comme le rapport entre les moments résistants et les moments moteurs par rapport a " O ", il vaut donc

F_s = ? ~~~ + (~~ ~~~ ~~ - ~~~~) ~~~ ~

~

~~~

? Wi sin ai

~

~~~

Autre simplification :

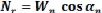
Equilibre des forces :

La force de cisaillement résistant :

~f?L7 Tr = rd?Ln = Fs La contrainte effective normale, ó'		1 =lFs + a^' tan (p)?Ln
Nr = ?Ln	Wn cos an
	?Ln

La somme des moments autour de O

n=p n=p

n=1 n=1

~~~ ~ ~~~ ~~ = ~ ~~ ~ ( ~ + ~~ ~~~ ~~ ~~~ ~)?~~ ~ ?L_n

? (~?~~ + ~~ ~~~ ~~ ~~~ ~)

~~~

~~~

~~ =? En=1 ^n=P W_n sin ^an

II-4-1-6--Méthodee del'équilibree des forces et des moments :

·Méthodess faisant deshypothèsess sur lalignee depousséee^[16]1 : 1- Jambugénéralisée::

La méthode généralisée de Jambu (Jambu 1973)considèree les deux forces inter-tranches et suppose une ligne de pousséeafinm dedéterminerr une relation des forces inter-tranches. ^Parconséquent,, le coefficient de sécurité devient une fonction complexeàa la fois avec les forces inter-tranches :

FigureII-88 : Lareprésentationn des forces sur une ^tranche?(t'tt + (~ --- u/)tann v^')sinn a

FS ^=l?(W - {~2 - Ti}tann _a ^+l ?(E22 --- El)¹

Demême,, la force totale normaleàa la base (N) devient une fonction de la force inter tranche de cisaillement (T) comme:

N =	~~ ~~ - (~~ - ~~) - ~ ~ ~ (~~~ - ~~ ~~~ ~') ~~~ ~~ 2- Jambu simplifié :

La méthode simplifiée de Jambu est un indice composite basé sur des surfaces de cisaillement (c'est-à-dire non circulaire) et le coefficient de sécurité est déterminé par l'équilibre des forces horizontales. Comme dans la méthode de Bishop, la méthode considère les forces inter-tranches normales, mais néglige les forces de cisaillement (T). La base de la force normale (N) est déterminé de la même manière que dans la méthode de Bishop et le coefficient de sécurité est calculé par:

Fs =	?(V/ + (N - u/) tan ~') l cos a ? Wtan a + ? ?E

Figure II-9: Représentation des forces sur une tranche.

? ?E = El - E2 (Zéro s'il n'y a pas de force horizontale).

Jambu introduit un facteur de correction ( f₀ ), dans le coefficient de sécurité F₀ ,

pour tenir compte des effets des forces inter-tranches de cisaillement. Avec cette modification, la méthode de Jambu corrigé donne un coefficient de sécurité supérieur, comme:

Oil :

F =

Ff = foF0

_?(P(t' + (P - u)tanv')

n_a

? pb tan a

Et :

~~ = ~~~² ~(~ + ~~~ ~ ~~~ ~~ F

C'est un facteur de correction qui varie en fonction de la profondeur à la longueur de la masse de la terre glissante et du type de sol.

P=W/b=contrainte totale verticale ;

b= largeur d'une tranche.

· Méthodes faisant appel à des hypothèses sur l'orientation des efforts inter tranches :

1- Méthode de spencer :

La méthode de Spencer est initialement présentée pour les surfaces de rupture circulaire, mais la procédure peut être facilement étendu aux surfaces de rupture non circulaires.

Spencer (1967) a mis au point deux équations de coefficient de sécurité, l'un à l'égard de l'équilibre des forces horizontales et un autre à l'égard de l'équilibre de moment. Il a adopté un rapport constant entre les forces inter- tranches de cisaillement et normal.

[Tapez un texte]

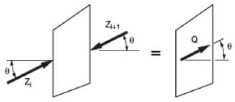
Figure II-10: Résultante des forces parallèles L'équation de l'équilibre des forces:

1Qi = ⁰

Et :

Qi = Zi -- Zi-Fi

Parce que les forces inter tranche sont supposées être parallèles, Q_i , Z_i , et Z_i + ₁ ont la même direction et Q_i est tout simplement est la différence scalaire entre les forces intertranches de gauche et de droite de la tranche

Figure II-11: Représentation de toutes les forces inconnues sur une
tranche dans la méthode de Spencer.

L'équation d'équilibre des moments est exprimée par la relation :

1QEirb sin 0 -- yQ cos 0) = 0

Figure II-12: Les coordonnées pour une surface de rupture non circulaire utilisée dans la
méthode de Spencer.

Après une série de calcul Spencer a trouvé une expression réduite pour le coefficient de sécurité comme suite :

( 2 = ~~~ ~~~ ~~~~ ~~~ ~~~~~?~

cos(_o)l[sin(l-O)tan epll

~ ~~(~~ ~~~ ~~~~ ~~~ ~~~?~)(~~~~~

F ~ )

Méthodes Morgenstern et Price.

La méthode de Morgenstern et Price aussi satisfaire à la fois les forces et les moments et suppose une fonction des forces inter-tranches. Selon Morgenstern - Price (1965), l'inclinaison des forces inter-tranches peut varier par une fonction arbitraire (f (x)) comme:

7' = f(i)RE

Les forces considérées sont indiquées dans la figure:

Figure II-13: Représentation graphique des forces sur une tranche.

Oil :

f(x) : Fonction des forces inter-tranches qui varie continuellement le long de la surface de rupture,

A : Facteur d'échelle de la fonction supposée.

La méthode propose tout type assumant la fonction de la force, par exemple un demisinus, trapézoïdal ou autre. Les relations de la force normale à la base (N) et les forces intertranches (E, T) sont les mêmes que dans la méthode générale de Jambu. Pour une fonction de force, les forces inter-tranches sont calculées par la procédure d'itération jusqu'à ce que, F_f est

égal à F_m dans les équations

?[{c^f/+(1--u/)tan vr}_{cos cc}]

F

=

l

f ? {ig-- (1'2 --Ti)}Itan a+?(IE2 --Ei )l

Et

~~ = ?(~~~~(~~~~) ~~~ ~~

?W sin a

En générale cette méthode :

· Considère les deux forces inter tranches,

· suppose une fonction des forces inter-tranches f (x),

· Permet la sélection de la fonction des forces inter tranches,

· Le coefficient de sécurité est calculé à la fois par les équations d'équilibres des forces et des moments.

II-4-2- METHODES DES ELEMENTS FINIS:

Hypothèses de calcul et modèles numériques

Le choix des hypothèses de calcul et, notamment, d'un modèle de comportement pour chaque sol présent sous l'ouvrage à étudier doit tenir compte des contraintes économiques et de délai de l'étude (durée des calculs, temps passé par les ingénieurs à réaliser l'étude numérique), et aussi des informations disponibles sur les différents aspects du problème. Par ailleurs, une trop grande complexité du modèle numérique peut créer des risques d'erreurs importants et rendre l'exploitation des calculs compliqués à cause du nombre des variables calculées.

La modélisation par éléments finis d'un ouvrage est donc constituée par un ensemble d'hypothèses, toujours simplificatrices, et la mise en oeuvre d'une suite de modèles, chacun plus ou moins approché :

· modèle géométrique (maillage, limites entre les couches, discontinuités, etc.) .

· modèle de charge (estimation des forces et des pressions, des déplacements imposés, définition du phasage des travaux, conditions aux limites, décomposition en incréments pour la résolution en comportement non linéaire, etc.) .

· modèle hydraulique (sol saturé, état initial, écoulement permanent ou transitoire, position de la surface libre, consolidation, etc.).

· modèles de matériaux (élasticité, élastoplasticité, viscoplasticité, etc.) ;

· modèle d'évolution (choix des pas de temps à considérer, historique des charges) .

· modèles de structures (poutres, coques, plaques, élasticité, élastoplasticité, etc.) .

· modèles d'interaction sol-structures (lois d'interface, modules de réaction, etc.).

Ces hypothèses ne sont pas fondamentalement différentes de celles de toutes les études géotechniques, mais la complexité plus grande des modèles de calcul oblige à fixer plus de conditions et à déterminer plus de paramètres que dans les calculs courants.

Pour que les résultats demeurent réalistes, les hypothèses de calcul ne doivent pas négliger les aspects essentiels d'un problème : par exemple, on ne peut négliger les aspects mécaniques liés au frottement dans la modélisation d'un pieu, ni les effets du front de taille dans la modélisation du creusement d'un tunnel, ni les effets des écoulements transitoires dans les sols peu perméables, etc.

On peut se permettre beaucoup d'hypothèses et d'approximations seulement si l'on a bien repéré et modélisé les caractères essentiels du comportement de l'ouvrage étudié. En général, l'observation d'ouvrages réels permet de mettre en évidence ces caractères essentiels ^[17].

II-5-PRESENTATION DE L'OUTIL NUMERIQUE UTILISE :

II-5-1- Présentation du code PLAXIS :

II-5-1-1-Généralités :

Dans sa version originale, le code de calcul par éléments finis PLAXIS traite la stabilité des digues en terre. Dans sa version actuelle, il permet de traiter différents types de problèmes géotechniques (fondations, tunnels, ouvrages de soutènement, etc.), les calculs s'effectuant en déformations planes (Analyse bidimensionnelle ou Analyse 2D) ou en déformations axisymétriques (Analyse tridimensionnelle ou Analyse 3D).

L'algorithme général de résolution des équations non linéaires du code PLAXIS s'effectue selon un processus itératif permettant de déterminer à chaque pas de temps de calcul les champs de déplacements, de vitesses et d'accélérations correspondantes aux chargements appliqués ; l'équilibre résultant rapidement.

Les modèles de calcul implémentés dans le code PLAXIS couvrent pratiquement l'ensemble des aspects théoriques et expérimentaux du comportement des sols courants

(élasticité linéaire de Hooke, pour simuler le comportement des structures rigides massives placées dans le sol ; plasticité parfaite isotrope de type Mohr-Coulomb pour simuler le comportement de la plus part des sols fins ; élastoplasticité de type hyperbolique avec écrouissage en cisaillement pour simuler le comportement des sables et des graves, mais aussi des argile et des limons ; élastoplasticité de type Cam Clay pour simuler le comportement des argiles molles normalement consolidées ; viscoplasticité pour simuler le comportement des sols mous en fonction du temps (fluage et consolidation).

Aussi se limitera-t-on ci après à ne décrire que le modèle de Mohr-Coulomb intéressant l'objet de la présente étude. Ce modèle est utilisé comme une première approximation du comportement des sols. Il comporte cinq paramètres :

? Le module d'Young E: défini soit par le module tangent initial E0, soit par le module sécant à 50% de la résistance en compression _E50 (Figure II-14).

Figure II-14 : Définition du module d'Young E.

? Le coefficient de Poisson n : évalué par l'intermédiaire du coefficient de pression des terres au repos K0=í/ (1- í) pour un chargement gravitaire, dont les valeurs sont comprises entre 0.3 et 0.4.

? La cohésion c: nulle (C=0) pour les sables, mais constante non nulle (C?0) ou évoluant avec la profondeur pour les argiles.

? L'angle de frottement interne ö : qui conditionne la résistance au cisaillement des sols;

? L'angle de dilatance ø : nul (ø= 0) pour des sols argileux qui ne montrent aucune dilatance, mais non nul (ø? 0) pour les sables dont la dilatance dépend de leur densité et de leur angle de frottement. Pour les sables siliceux, ø= ö ?30.

Ces paramètres peuvent être aisément identifiés sur des résultats d'essais triaxiaux classiques [17].

Figure II-15 : Résultats d'essais triaxiaux drainés et le modèle
Élastoplastiques de type Mohr-Coulomb.

Pour la prise en compte des interactions squelette - eau interstitielle dans la réponse du sol, le code PLAXIS distingue entre les comportements drainé et non drainé :

· Pour le comportement drainé, aucune surpression interstitielle n'est générée. C'est évidemment le cas pour des sols secs et pour des sols totalement drainés du fait de leur forte perméabilité ou à cause d'un faible accroissement du chargement. Cette option peut aussi être utilisée pour simuler le comportement des sols à long terme (fluage et consolidation) ;

· Pour le comportement non drainé, les surpressions interstitielles sont complètement générées.

L'écoulement de l'eau interstitielle peut parfois être négligé du fait des faibles perméabilités ou à cause d'une vitesse de chargement élevée. Toutes les couches considérées comme non drainées se comporteront ainsi, même si la couche ou une partie de celle-ci se trouve audessus de la nappe phréatique.

Dans PLAXIS, une analyse de la sécurité peut être menée en réduisant les caractéristiques mécaniques du sol. Ce procédé s'appelle "Phi-c reduction". Dans cette approche, les caractéristiques tanö et c du sol sont réduites progressivement jusqu'à l'apparition de la rupture. Le coefficient total appelé coefficient de réduction ?Msf permet de définir la valeur des caractéristiques du sol à une étape donnée de l'analyse :

~ ~~~ = tan ~~~~~é~ = Cdonné~

tan 'Pré~uit ~~é~~~~

Où les caractéristiques notées "donnée" se référent aux valeurs initiales des propriétés des matériaux et les caractéristiques notées «réduit» se rapportent aux valeurs réduites utilisées au cours de l'analyse. Contrairement aux autres coefficients, ?Msf vaut 1.0 au début d'un calcul pour utiliser les valeurs non réduites des caractéristiques des matériaux. Le coefficient de

sécurité global est déterminé comme suit :

rEsistance lisponible

F E E valeur le lEIM_sfEEllalrupture

rEsistance làllalrupture

Cette approche ressemble à la méthode de calcul de coefficients de sécurité adoptée conventionnellement dans les analyses de rupture circulaire (méthodes des tranches).

II-5-1-2- L'interface du code PLAXIS :

Le code PLAXIS est divisé en quatre sous-programmes (PLAXIS-Input, PLAXISCalculations, PLAXIS-Output and PLAXIS-Curves).

· PLAXIS-Input: le sous programme Input appelé aussi le pré-processing programme contient les toutes facilités nécessaires à la création et modifications des modèles géométriques, à l'engendrement des maillages des éléments finis et à la définition des conditions initiales.

· PLAXIS-Calculations: le processing programme ou le sous programme de calculs contient les facilités utiles à la définition des phases et au commencement de la procédure de calcul des éléments finis.

· PLAXIS-Output: ou le programme post-processing contient les facilités pour la visualisation des résultats de la phase de calculs, comme les déplacements au niveau des noeuds, les contraintes les forces au des éléments structuraux etc.

· PLAXIS-Curves: le sous-programme curve sert à la construction des courbes de chargement - déplacement, des chemins de contraintes, en plus de divers autres diagrammes.

II-5-1-3- Structure du code PLAXIS [18] :

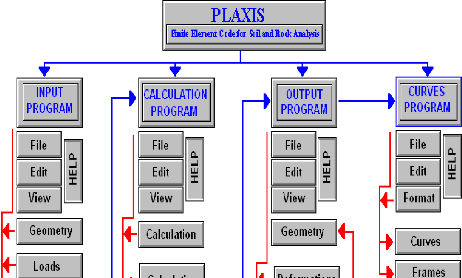
Figure II-16 : Organigramme de la structure du code PLAXIS.

II-5-2-Présentation du logiciel Géoslope Géostudio :

II-5-2-1-Généralités :

Géostudio est un logiciel de calcul géotechnique permet de traiter les différents problèmes du sol comme le glissement des terrains, le tassement, la consolidation, les infiltrations des eaux dans le corps de la digue d'un barrage et d'autres problèmes liés a la géotechnique. Plusieurs programmes sont intégrés dans la fenêtre générale du logiciel :

SEEP/W : Permet de calculer les infiltrations des eaux.

SIGMA/W : Permet d'analyser les problèmes de la relation contraintes -déformations. QUAKE/W : Permet de définir le comportement d'un terrain sous l'effet d'un séisme. TEMP/W : Permet d'analyser les problèmes géotechniques du sol.

SLOPE/W : c'est le programme qui nous intéresse dans la présente étude.

Le programme de calcul SLOPE est un programme d'analyse de la stabilité des pentes, basée sur la théorie d'équilibre limite qui consistes à respecter les deux règles de la stabilité statique, c'est-à-dire il faut satisfaire les conditions d'équilibres des moments et d'équilibre des forces.

Cette analyse consiste à calculer un facteur de sécurité en visualisant les résultats graphiques du volume instable correspondant.

Les méthodes de calcul du facteur de sécurité intégrées dans SLOPE sont la méthode de Fellinius, de Morgenstern-price, de Jumbo et celle de Bishop simplifiée, et enfin"la méthode des éléments finis" qu'on peut le trouver dans la partie logique " SIGMA/W ".

Elles permettent de calculer un coefficient de sécurité vis-à-vis d'un type de rupture bien défini. Le modèle géométrique est subdivisé en tranches verticales en 2D. Il exécute plusieurs méthodes de recherches automatiques du centre de rotation de la surface de glissement potentiel jusqu'à atteindre le plus faible coefficient de sécurité.

II-5-1-2-Le fonctionnement du logiciel :

Le présent logiciel comme touts les autres programmes de calcul sert à fournir des résultats issus d'un nombre défini des paramètres, donc il est nécessaire de suivre les étapes suivantes pour l'achèvement de l'opération de calcul :

1. Define:

Cette étape est très importante car on va définir le problème et introduire les différentes données spécifiques au problème en vigueur.

Set

· la délimitation de la surface du travail

· La définition de l'échelle

· La définition des réseaux

· La détermination du zoom

· La fixation d'axes

Keyln

· La spécification des méthodes d'analyses

· La spécification des options d'analyse

· La définition des propriétés du sol

Draw

· Le dessin des points

· Le dessin des lignes

· La détermination de ligne piézométrique

· Le dessin du rayon de la surface de rupture

· Le dessin des réseaux de la surface de rupture

Sketch

· La réalisation de l'esquisse du problème

· Etiquetage du sol

· Rajout d'un titre d'identification du problème

· Eclaircir les ténèbres d'identification

Modify: cette instruction permet aux utilisateurs de rajouter, éliminer, supprimer et modifier des objets dans le problème.

Tools : à l'aide de cette icône on peut vérifier toutes les données de ce problème ^ainsifaciliter l'accès pour sa résolution. Saving : dès l'achèvement du processus de définition du problème, il faut sauvegarder ces données sous forme d'un fichier.

2. Solve :

C'est l'étape de résolution du problème, à l'aide des méthodes classiques et la méthode des éléments finis et a partir des données introduites, on détermine le coefficient de sécurité Fs.

3. Contour :

C'est l'étape chargée de traduire les différents résultats sous une forme graphique; et afficher ces résultats ^[19].

Figure II-17 : Les menus disponibles sur logiciel SLOPE/W

Chapitre III :

Cadre géologique et hydrogéologique

III-1-INTRODUCTION :

Notre étude consiste à analyser un glissement de terrain, pour cela, différentes données ont été collecté auprès de laboratoire LCTP, en plus d'une synthèse des travaux géologique et hydrogéologique sur le site.

III-2-DESCRIPTION DU SITE:

III-2-1-Situation géographique :

La commune de Beni Messous est une subdivision administrative de la Daïra de Bouzaréah et qui se situe à l'Ouest d'Alger. Elle est limitée :

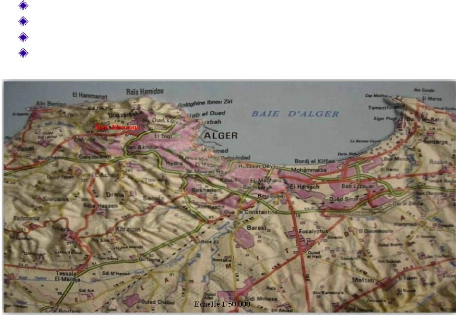
Au Nord par la commune de Hammamet.

Au Sud par la commune de Chéraga et la commune de Dely Brahim. A l'Est par la commune de Bouzaréah.

A l'Ouest par la commune de Ain Bénian.

Figure III-1 : Situation géographique de la commune de Beni Messous (Direction générale
des forets, Alger).

La commune compte une population de 19407 selon les statistiques de 2004 faites par l'office national des statistiques d'Alger.

Le site étudié se trouve au Nord Ouest de la commune, le glissement a eu lieu dans la cité des 384 logements sur l'axe de la CW 45.

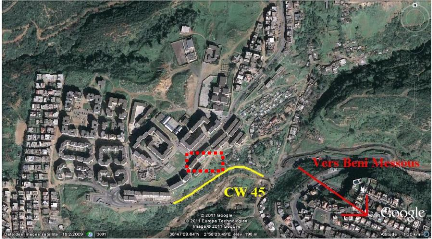
Photo III-1 : Localisation du site étudié (Image satellitaire par Google Earth). III-2-2-Cadre géologique de la région :

La géologie de Beni Messous est variée partant du Primaire au Tertiaire

a. Le primaire : [Tapez un texte]

Figure 111-2 : Carte geologique de la region d'Alger.

Correspond au massif Bouzaréah qui s'étend sur une longueur de 20 km et sa largeur maximale est de 6 km selon une direction Est -Ouest. Ce massif est métamorphique, constitué principalement par des schistes cristallophylliens. Il est très tectonisé, boisé et recoupé par un réseau de thalwegs profonds, sa topographie est très accidentée et son sommet qui culmine à 407 m constitue le point le plus haut de la région.

b. Le tertiaire :

Marqué par une lacune de l'Eocène et de l'Oligocène, il recouvre en discordance le substratum métamorphique.

Le Miocène inférieur (Burdigalien) :

Formé de grés et poudingues, ils affleurent d'Alger à la commune de Beni Messous, et plongent vers le sud sous les formations plaisanciennes.

Les grés grossiers et peu fissurés, débutent par un poudingue mal cimenté remaniant sur 1 à 2 m des éléments du massif ancien et qui renferment des lits de gravier discontinues.

Le Pliocène inférieur (Plaisancien) :

Rencontré dans le sud de la commune de Beni Messous et il affleure aussi dans le Sahel et au Télémly. Il est essentiellement argilo -marneux. Ces faciès verdâtres et bleutés sont dénommés <<marnes bleues du plaisancien» ^[20].

III-2-3-Cadre hydrologique et hydrogéologique :

Puisque le socle métamorphique est rattaché aux nappes phréatiques du Sahel, il existe une présence d'eau qui se manifeste sous forme de résurgences (sources) ou de nappe aquifère. Il s'agit d'une eau localisée dans les fissures, diaclases et fractures qui peut s'accumuler dans les zones d'altération superficielle plus ou moins épaisses.

Les grés et poudingues Burdigalien contiennent une nappe qui s'épanche par quelques petites sources descendant vers l'oued de Beni Messous. Cette nappe liée dans la zone de l'affleurement à la nappe phréatique des terrains anciens, se met en charge vers le sud sous les marnes bleues.

De petites nappes libres existent aussi, elles sont alimentées exclusivement par la pluviométrie et s'écoulent vers la mer.

On note que l'oued de Beni Messous, dont l'origine est à l'Est de la commune de Bouzaréah, traverse les communes de Béni-Messous et Chéraga (avec une longueur de 11.5 km et un débit moyen de 0.245m³/s), et débouche du coté Ouest dans la baie d'EL Djamila au niveau de la plage << Les Dunes » [21].

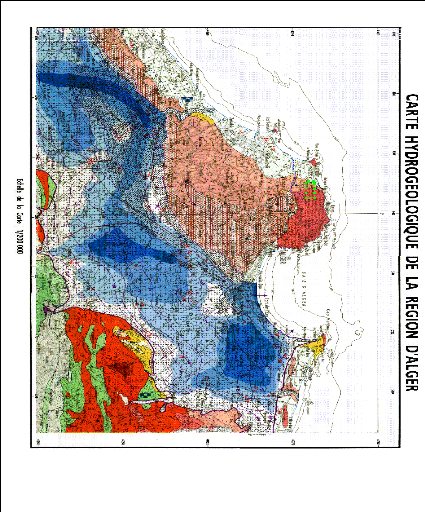
Légende

Figure III-3: Carte hydrogéologique de la région d'Alger (Extrait de la carte HD, secrétariat
d'état a l'hydraulique, Birmandrais, Alger).

III-2-4-Climat :

III-2-4-1-La température :

Deux saisons dominent dans la région de Béni-Messous; une saison chaude qui s'étale de Juin à Octobre, où les températures moyennes de l'air varient entre 20^°C et 27^°C avec une température maximale en Août et se rafraîchissent en Novembre et une autre saison qui débute en Décembre et s'achève en Mars, où les températures moyennes varient entre 11^°C et 18^°C avec une température minimale en Janvier.

Sur la figure suivante nous pouvons apprécier la variation moyenne des températures maximales et minimales entre 1995 et 2005.

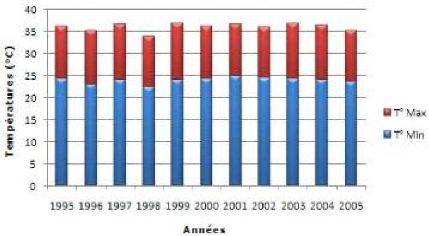
Figure III-4: Profil de variation des températures moyennes de l'air 1995-2005 (d'après
ONM).

III-2-4-2-La pluviométrie :

À Béni-Messous, les pluies sont fréquentes en automne et en hiver et diminuent dès la fin du printemps et deviennent presque nulles en été.

Deux saisons humides se distinguent : l'une allant du mois de Novembre au mois de Février où la moyenne mensuelle maximale atteint 93 mm et l'autre plutôt sèche allant du mois de Juin au mois d'Octobre avec un minimum de 1,95 mm.

Il existe cependant, une période transitoire entre Mars et Mai où les précipitations moyennes varient entre 45 et 64 mm.

La figure suivante indique les précipitations annuelles entre 1995 et 2005.

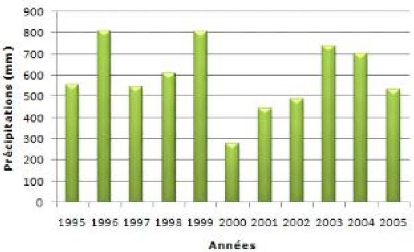
Figure III-5: Précipitations annuelles 1995-2005 (d'après ONM). III-2-5-Sismicité :

La wilaya d'Alger est l'une des régions propices aux activités sismiques. En se basant sur la sismicité historique, l'Algérie a été subdivisée en quatre zones macrosismiques (RPA99 modifié en 2003) :

· Zone 0 : sismicité négligeable.

· Zone I: sismicité faible.

· Zone II: sismicité moyenne.

· Zone III: sismicité élevée.

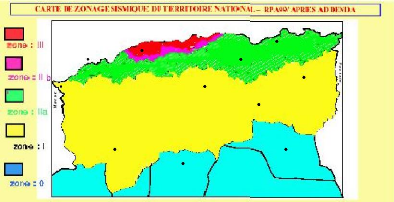
Tlemcen

Oran

Sidi Belabes

El Bayd El

Aghouat

Tiaret

Chlef

Alger

Boumerdes Blida Setif

Djelfa

Msila

Biskra

Mila

Tebessa

El Oued

Annaba

Figure III-6: Carte de zonage sismique de l'Algérie (Source : RPA 2003).

La région de Beni Messous est classée dans la zone III, et l'ouvrage est considéré comme un ouvrage courant ou d'importance moyenne qui correspond au groupe 2:

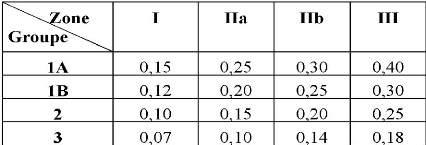
Tableau III-1 : Valeurs du coefficient d'accélération de zone selon le RPA99 (version 2003).

Sur la base de ces deux informations, le coefficient d'accélération sismique A est égale à A = 0,25g.

Avec g=9,81m/s² accélération de la pesanteur.

CONCLUSION :

A travers ce chapitre on déduit que la région de Beni Messous est caractérisée par une géologie variée d'âge différent.

La sismicité de la région est élevée, donc elle est menacée par plusieurs types d'instabilité.

Chapitre IV :

Etude de glissement de terrain de Sidi Youcef

IV-1-INTRODUCTION :

Le LCTP a fait un constat des lieux le 06/10/2010 suite a une demande d'expertise sollicitée par le DTP d'Alger après l'apparition du glissement.

Ensuite, on a effectué des visites en date du 29/12/2010 et 22/03/2011, afin de constater les mouvements du talus, ces derniers se traduisent par l'affaissement de la partie avale de la chaussée.

IV-2-ETAT DES LIEUX :

Un glissement a eu lieu dans le site de Sidi Youcef qui s'étend sur une surface de 10200m² selon une direction N.O -S.E, au niveau de la cité des 384 logements.

Le processus de glissement du talus en contrebas de cette cité semble être bien enclenché et risque d'évoluer rapidement notamment sous l'effet :

+ Des infiltrations des eaux de surface à partir des fissures et des escarpements des chaussées et des eaux provenant des fuites dans les réseaux d'assainissement et d'alimentation en eau potable.

+ De la poussée au vide due à l'aspect abrupt du talus.

Le bâtiment 1 situé immédiatement en amont de ce talus présente déjà les premiers signes de déstabilisation (fissures au niveau des maçonneries de la façade principale) et peut même s'effondrer sous l'effet d'une évolution du glissement ou de facteurs exceptionnels (séisme, crues ...).

La stabilité des autres bâtiments avoisinants peut être aussi menacée à court ou moyen terme par l'évolution de ce glissement.

Ces désordres du talus ont toutefois, évolué pendant la période pluvieuse et ont entraîné la déformation partielle de la chaussée.

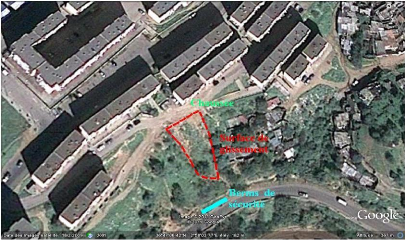
B3 B2
B1

Photo IV-1 : Situation du glissement (Image satellitaire par Google Earth).

Photo IV-2 : Vue du versant et les bermes de sécurité approximé de la CW 45.

A travers nos visites techniques au site glissé, nous avons constaté les dégradations suivantes :

· Un affaissement très important au niveau du dallage périphérique du bâtiment 1 donnant naissance à un décalage de 20 à 30 cm entre la longrine périphérique du bâtiment et le dallage.

· Apparition des fissures diagonales au niveau des maçonneries de la façade principale du bâtiment 1.

· Fissures multidirectionnelles importantes au niveau de la chaussée de la voie desservant le bâtiment 1.

· Affaissement du dallage de la voie entre les bâtiments 2 et 3.

· Affaissement de la partie avale de la chaussée avec d'importants escarpements (allant jusqu'à 1 m) en cascades et basculements des garde-corps de la chaussée.

· Fuites d'eau provenant probablement des réseaux d'assainissement et d'eau potable de la cité.

· Un important suintement d'eau sur le talus du CW 45 en contre bas de la cité.

17 cm

25 cm

Photo IV-3 : décalage du dallage périphérique (après affaissement) par rapport à la longrine.

Photo IV-4 : affaissement au niveau de la chaussée.

Photo IV-5 : Affaissement du dallage entre les bâtiments 2 et 3.

Photo IV-6: Affaissement de la partie aval du chaussée et basculement des gardes corps.

Photo IV-7 : Aperçu sur les traces des fuites d'eau des réseaux.

Photo IV-8 : Aperçu sur les mouvements du talus.

IV-3- RESULTAT DES INVESTIGATIONS GEOTECHNIQUES :

Les données utilisées dans cette étude ont été collectés au niveau du laboratoire LCTP. Differentes essais ont été réalisées In-situ et en Laboratoire. Ces derniers ont été effectués après l'apparition du glissement en 2008.

IV-3 - 1- Sondages carottés :

Six (06) sondages carottés on été réalisés dans le site :

+ Sondage Sc 01 :

0.00 - 3.50 m : Remblais.

3.50 -7.50 m : Argile schisteuse graveleuse avec des traces d'oxydation de couleur brunâtre à grisâtre.

7.50 - 9.50 m : Fragments de schiste de couleur grisâtre.

9.50 - 13.70 m: Schiste très altéré dans une matrice argileuse avec des traces d'oxydation et des débris de calcite.

13.70 - 30.00m : Schiste avec des débris de calcite grisâtre.

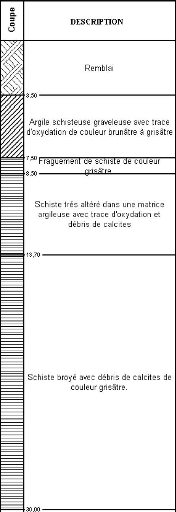
Figure IV-1 : Log de sondage Sc1.

+ Sondage Sc 02 :

0.00 - 3.00 m : Remblais.

3.00 - 9.50 m : Argile schisteuse avec des traces d'oxydation de couleur brunâtre à grisâtre. 9.50 - 12.00 m : Schiste friable, altéré grisâtre.

12.00 - 30.00 m: Schiste altéré grisâtre.

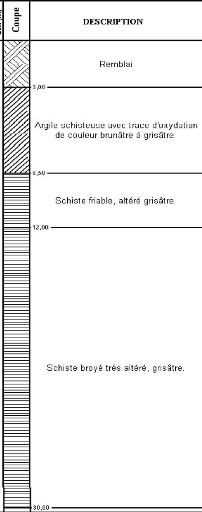
Figure IV-2: Log de sondage Sc2.

+ Sondage Sc 03 :

0.00 - 2.00 m : Remblais.

2.00 - 3.00 m : Conglomérat de mauvaise qualité.

3.00 - 20.00 m : Schiste avec débris de calcite de couleur grisâtre.

Figure IV-3: Log de sondage Sc3.

+ Sondage Sc 04 :

0.00 - 1.50 m : Remblais.

1.50 - 3.70 m : Grés de couleur grisâtre avec passage sableux entre 2.20 et 3.00 m.

3.70 - 20.00 m : Schiste avec débris de calcite de couleur grisâtre.

Figure IV-4: Log de sondage Sc4.

+ Sondage Sc 05 :

0.00 - 1.30 m : Remblais.

1.30 - 10.00 m : Schiste très altéré dans une matrice argileuse et très oxydé.

Figure IV-5: Log de sondage Sc5.

+ Sondage Sc 06:

0.00-0.20m : Remblais.

0.20-10.00m : Schiste broyé avec de calcites de couleur grisâtre.

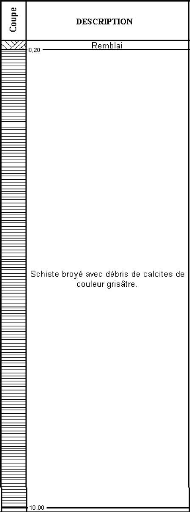
Figure IV-6 : Log de sondage Sc6.

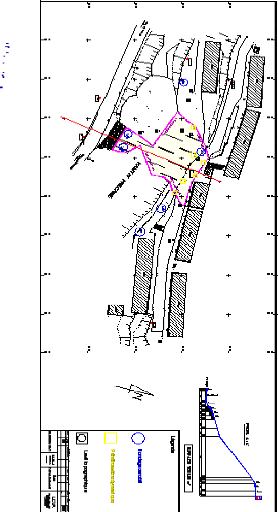
Figure IV.7 : Plan d'implantation.

Ces sondages nous permettent de tracer la coupe géotechnique :

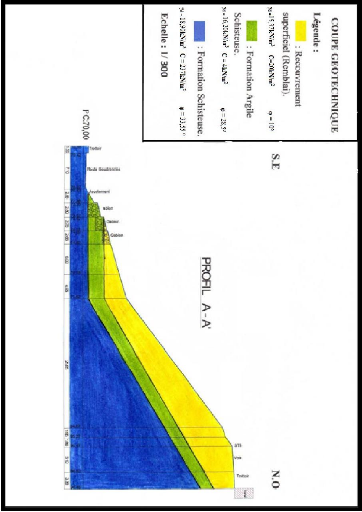
Figure IV-8: Coupe géotechnique du site.

III-3-2- Résultats des pénétromètres dynamiques:

Six (06) pénétromètres dynamiques ont été réalisés, l'implantation des pénétromètres dynamiques (Figure IV.7), et les pénétrogrammes sont les suivants :

+ Pénétromètre P01 : Cet essai enregistre une résistance de pointe moyenne entre 0.50 m et 1.50 m, cette résistance chute ensuite de façon assez significative de 2.00 m à 5.00 m, puis progresse de façon très rapide et régulière et atteint le refus à 6.40 m pour une résistance de pointe de 546 bars.

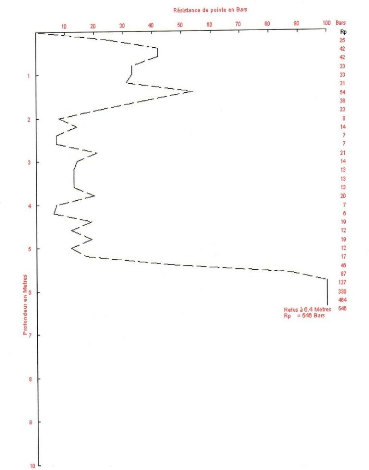
Figure IV-9: Pénétrogramme P1.

+ Pénétromètre P02 : Cet essai enregistre une première pointe non significative à 0.30 m puis chute de façon subite et atteint des valeurs nulles à très faible entre 1.30 m et 3.80 m. Il reprend une progression très rapide et régulière pour atteindre le refus à 6.60 m avec une résistance de pointe de 546 bars.

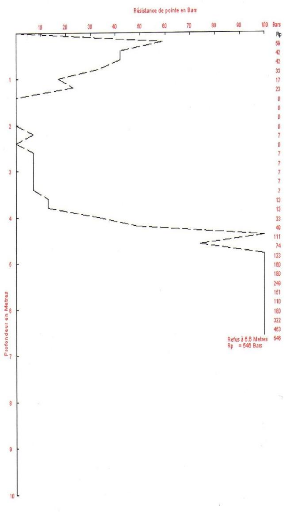
Figure IV-10: Pénétrogramme P2.

+ Pénétromètre P03 : Cet essai a la même allure que le précédent, il enregistre une pointe non significative (accidentelle) entre 0.50 m et 1.20 m puis chute de façon subite et atteint des valeurs nulles à très faible entre 1.60 m et 4.80 m. Il croit ensuite rapidement et atteint le refus à 7.80 m pour une résistance de pointe de 516 bars.

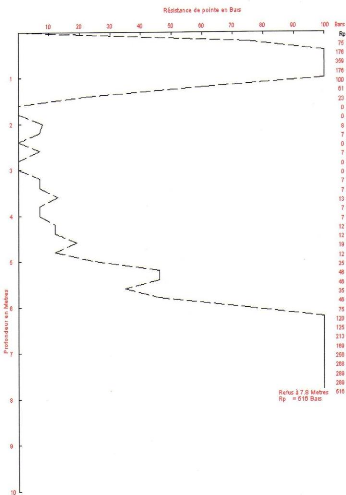
Figure IV-11: Pénétrogramme P3.

+ Pénétromètre P04 : Cet essai a lui aussi la même allure que les deux précédents, il enregistre une pointe non significative (accidentelle) à 0.80 m puis chute de façon subite et atteint des valeurs nulles à très faible entre 1.60 m et 6.00 m. Il croit ensuite rapidement et atteint le refus à 8.20 m pour une résistance de pointe de 516 bars.

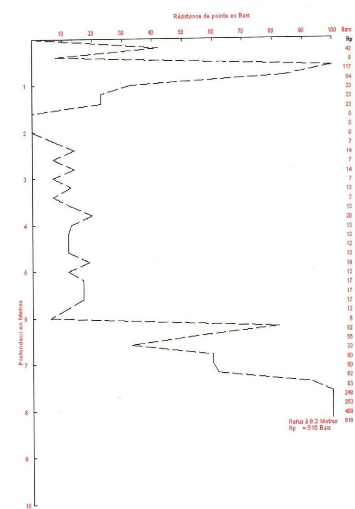
Figure IV-12: Pénétrogramme P4.

+ Pénétromètre P05 : Cet essai enregistre une croissance rapide et régulière de la résistance et atteint le refus à 0.80 m pour une résistance de pointe de 836 bars. Cette

résistance de pointe et ce refus sont probablement de nature accidentelle dûe à la rencontre d'un bloc rocheux (béton, roche).

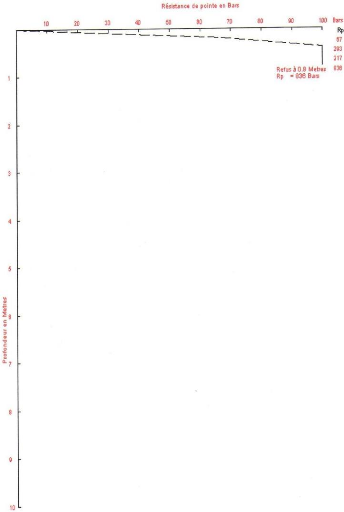
Figure IV-13: Pénétrogramme P5.

+ Pénétromètre P06 : Cet essai enregistre une pointe non significative jusqu'à 0.50m puis décroît de façon irrégulière et prend des valeurs faibles à médiocres jusqu'à 3.50

m de profondeur. Au delà la résistance croit de façon rapide et régulière et atteint le refus à 7.40 m pour une résistance de pointe de 516 bars.

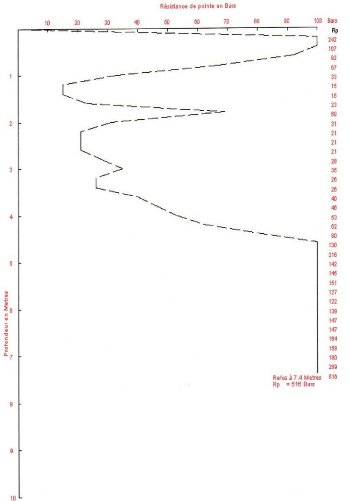
Figure IV-14: Pénétrogramme P6.

Conclusion :

A partir de l'analyse des résultats et en corrélation avec les coupes lithologiques du site, on déduit ce qui suit :

> La couche du remblai et d'argile schisteuse enregistre des valeurs de Rp assez faible, ce qui provoque un problème d'instabilité dans le site.

> Les valeurs élevées du Rp jusqu'au refus sont enregistrées au niveau de la couche schisteuse.

> Enfin, le substratum correspond au schiste, sur lequel repose une couche de remblai et d'argile schisteuse d'épaisseur moyenne de 7m. Ce qui coïncide avec les données géologiques du site.

IV-3-3-Résultats de l'essai préssiométrique :

L'essai préssiométrique qui a été réalisé dans la région de Sidi Youcef a donné les résultats suivants :

Profondeur (m)	EM (bars)	PL (bars)		EM/PL	1
432	14.7	29.38		2
167	11.7	14.27		3
123	12	10.25		4
170	13.9	12.23

Tableau IV-1 : Résultats d'essai préssiométrique.

Interprétation des résultats :

Le rapport _EM/PL est supérieur à 9, ce qui explique que le terrain est en état de surconsolidation.

On a les relations suivantes :

EM ~Oy

E =

~

Avec á = 2/3 pour une roche altérée.

~~~~~ PL Anoy

c_~ = =

Kb Kb

Avec Kb = 5,5 en générale. On a l'équation de Cassan :

~~ - P0 = 2. 5 × 2

q-24 ~ ~ =

4 × (~~~~~ ~~~ - 1og2. ~ + 61og2) log2

On aura les résultats suivants :

E = 334.5 bars. C_u = 2.37 bars. ö =33,55°.

Figure IV-15: Le log préssiométrique.

IV-3-4-Résultats des essais d'identification :

a. Granulométrie :

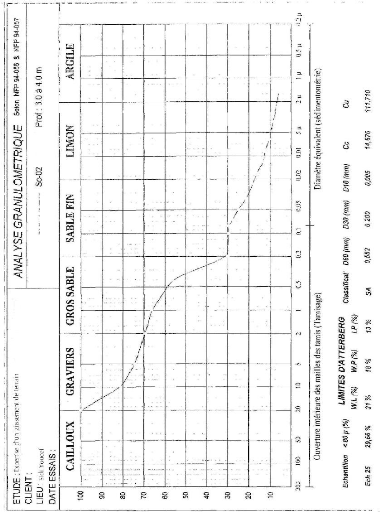
Figure IV-16: Courbe granulométrique.

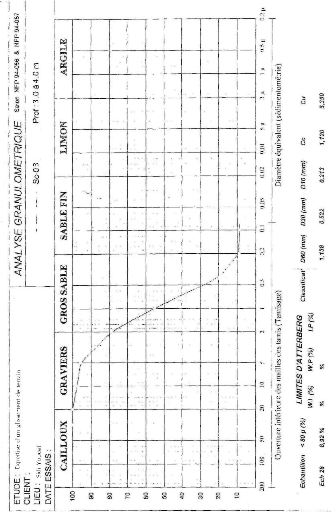
Figure IV-17: Courbe granulométrique.

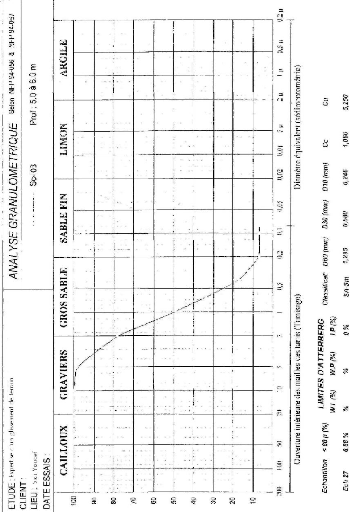
Figure IV-18: Courbe granulométrique.

N° de sondage	Profondeur (m)	5mm	2mm	0,08mm	20um	2um	<80um	Cc		Cu	Sc 02
3,00 ? 4,00	74	70	30	17	7	29,66%	14,67	111,71		Sc 03
3,00 ? 4,00	95	79	9	-	-	8,92%	1,12	5,35
5,00 ? 6,00	98	77	7	-	-	6,88%	1,060	5,25

Tableau IV-2 : Résultats d'analyse granulométrique.

Commentaire et interprétation :

L'analyse de ces résultats indique que plus de 50% des éléments >80um, donc on est en face d'un sol grenue.

Selon la classification LCPC :

?Le sol du Sc 02 a la profondeur de 3,00 à 4,00 m est classé comme SA.

?Le sol du Sc 03 a la profondeur de 5,00 à 6,00 m est classé comme SA?Sm. ?Le terrain est hétérogène.

Avec :

SA : sable argileux.

SA-Sm : sable argileux, sable propre mal gradué.

b.Détermination des paramètres physiques :

Les résultats d'identification sont regroupés dans le tableau suivant :

N° de	Profondeur	w(%)	wsat(%)	Sr(%)	wL	Ip	ãd	ãh(t/m^3)		ãsat(t/m^3)	sondage
(m)						(t/m^3)				Sc 02
3,00 ? 4,00	13,61	23,67	57,49	31	13	1,62	1,85	2,003		Sc 03
3,00 ? 4,00	11	15,02	73,23	-	-	1,89	2,1	2,173

Tableau IV-3 : Résultats des essais d'identification physiques.

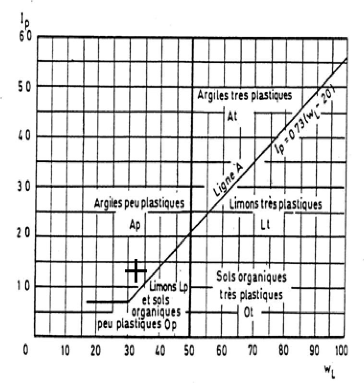
Figure IV-19 : Abaque de plasticité de Casagrande

Commentaire et interprétation :

· Les densités sèches des couches d'argile schisteuse et de schiste varient de 1,62 à 1,89 t/m³.

· A partir des caractéristiques du Sc 02, IC = 1,33 et IL = - 0,33, donc IC >1 et IL<0, donc le sol est en état solide.

· A partir des caractéristiques Ip et wL et l'abaque de Casagrande on est dans une Argile peu Plastique (Ap).

IV-3-5-Résultats des essais mécaniques :

Essai de cisaillement rectiligne :

Deux (02) essais de cisaillement on été réalisés, dont les résultats sont dans le tableau suivant :

N° sondage	Profondeur (m)	Type d'essai	C (bars)	ö (°)
Sc 01	6,50 ? 6,90	Uu	0,04	28,5
Sc 01	10,50 ? 10,70	Uu	0,00	22,27

Tableau IV-4 : Résultats d'essai de cisaillement à la boite (Par le LCTP).

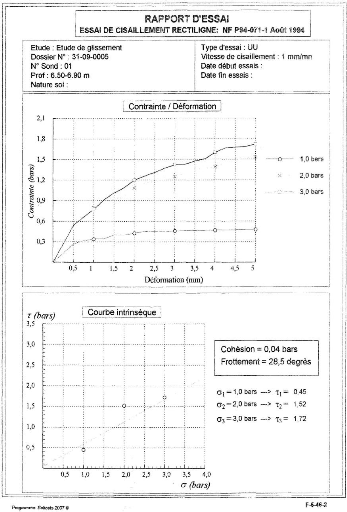
Figure IV-20: L'essai de cisaillement à la boite.

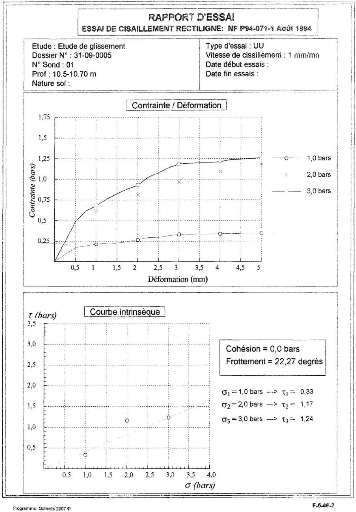
Figure IV-21: L'essai de cisaillement à la boite.

CONCLUSION :

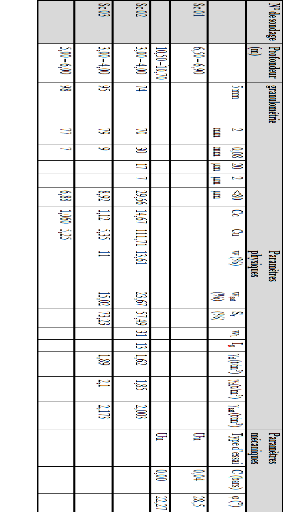
Tableau IV.5 : Recapitulation des resultats d'essais.

? On remarque que l'ensemble des essais a été limité sur quelques sondages, compte tenue de la récupération des échantillons.

? La couche d'argile schisteuse présente des caractéristiques géotechniques trop faibles, à cause de l'altération qui se présente sous forme des traces d'oxydation.

? La couche schisteuse possède des caractéristiques géotechniques élevées, donc cette couche est stable.

Chapitre V :

Calculs et vérifications

V- 1-INTRODUCTION :

Dans cette partie, en vue d'analyser et de modéliser le glissement, deux logiciels de calcul ont été utilisé : le GEOSLOPE et le PLAXIS, avec la détermination du coefficient de sécurité.

V- 2- DETERMINATION DU COEFFICIENT DE SECURITE FS :

La série des calculs effectuée vise à déterminer les valeurs du coefficient de sécurité par la méthode de Fellenius et par les logiciel ; GEOSLOPE et PLAXIS (Phi-c reduction).

Quatre combinaisons de calcul ont été envisagées :

Un premier calcul (variante N°01) dans lequel le talus est analysé sous l'action de son poids propre ou bien en état vierge.

Un second calcul (variante N°02), on prend en compte les surcharges des bâtiments situés en amont du talus.

Un troisième calcul (variante N°03), dont le niveau d'eau est supposé atteindre le terrain naturel (talus entièrement saturé) pour simuler les infiltrations et les fuites d'eau en surface.

Un quatrième calcul (variante N°04), dans lequel les effets combinés des eaux et les surcharges.

Le tableau suivant regroupe les caractéristiques des différentes couches du terrain :

	ãd (kN/m^3)	ãh (kN/m^3)	ãsat (kN/m^3)	C (kN/m^2)	ö °	E (kN/m^2)	í
Remblai	15,37	17,00	19,51	20	10	4800	0,33
Argile schisteuse	16,20	18,50	20,03	4	28,5	10000	0,33
Schiste	18,90	21,00	21,73	237	33,55	33450	0,30

Tableau V-1 : Caractéristiques des couches de terrain. V- 2-1-Calcul de facteur de sécurité manuellement :

D

nd = H

Avec :

D=30m

H=26.75m

30

nd = 26. ~5 = iE. iE2

Donc le nd <2 ; alors la ligne de glissement passe par le pied.

D'après l'abaque XI-17 (abaque de détermination du cercle de rupture) on a : á0= 37°.

â0=26°

Le calcul manuel se fait avec la méthode de Fellenius, dont la figure en annexe montre la localisation du cercle et du rayon de glissement, ainsi les différentes tranches.

Les résultats de calcul sont indiqués dans les deux tableaux suivants :

N i	?i	Wi	Wicos^2?i	Ub	(Wicos^2?i-Ub) tgö	[Cb + (Wicos^2?i-Ub) tg ö1/cos?i	Wisin?i
1	62°	843,61	185,93	0	31,04	145,35	744,86
2	53°	2039,62	738,71	0	289,01	541,51	1628,91
3	39°	2186,1	1380,31	0	604,8	821,76	1378,76
4	27°	1942,2	1541,9	0	725,11	853,79	881,74
5	21°	675,18	588,47	0	248,79	306,01	241,96
6	- 9°	259,515	253,16	0	111,35	150,04	- 40,6

Tableau V-2 : Les résultats de calcul en état vierge.

v Etat vierge: v Avec surcharges:

Fs3524[38 = 4832,63 3524, 38

=0,73

Fs =			= 0, 69

Avec les surcharges Q = 220kN/m²

Ni	?i	Wi	Wicos^2?i	Ub	(Wicos^2?i-Ub) tg ö	[Cb + (Wicos^2?i-Ub)tg ö]1/cos?i		Wisin?i	1
62°	843,61	185,93	128.76	100,95	294,26	744,86		2
53°	2039,6 2	738,71	206.41	401,08	727,54	1628,91		3
39°	2186,1	1380,31	206.41	716,87	965,21	1375,76		4
27°	1942,2	1541,9	206.41	837,18	979,30	881,74		5
21°	675,18	588,47	130.26	319,51	381,68	241,96		6
-9°	259,51 5	253,16	48.7	137,45	176,39	-40,6

Tableau V-3 : Les résultats de calcul en état entièrement saturé.

v Prise en compte des infiltrations :

2818,46

Fs =			= 0. 58

v Couplage hydromécanique :

2818, 46

Fs =			= 0.55

V-2-2-Calcul a l'aide des logiciels :

V-2-2-1-Calcul par GEOSLOPE :

Le calcul s'effectue par les variantes précédentes avec les différentes méthodes de calcul (Fellenius, Bishop, Jambu,.....etc). La position de cercle de glissement est choisie automatiquement (AUTO LOCATE).

La position des cercles de glissement et les résultats de calcul de chaque variante sont présentés ci-après :

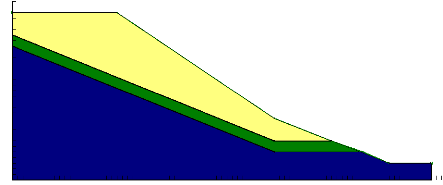
32

31

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 ²⁶ ₂₇ ²⁸ ₂₉ ³⁰ 31 32 33 34 35 ³⁶ ₃₇ ³⁸ 39 40 ⁴¹ 42 43 ⁴⁴ ₄₅ ⁴⁶ 47 48 49 50 51 52 53 ⁵⁴ ₅₅ ⁵⁶ 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 ⁷⁶ 77 78 79 80 81 82

hauteur

30

29

28

27

26

25

24

23

22

21

20

19

18

17

16

15

14

13

12

11

10

9

8

7

6

5

4

3

2

0

1

longueur

Figure V-1 : Le modèle géométrique adopté.

v Etat vierge :

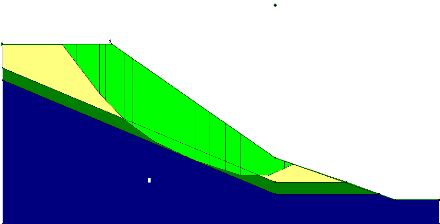
1

6

7

3

4

3

5

8 9

¹0 11

3

12

0.844

Figure V-2 : La position du centre et du cercle de glissement dans le modèle géométrique.

	Fellenius	Bishop	Morgenstern & Price		Jambu	Fs
0,79523	0,84338	0,84426	0,79533

Tableau V-4 : Valeur de coefficient de sécurité avec les différentes méthodes.

v Prise en compte des surcharges :

[Tapez un texte]

0.683

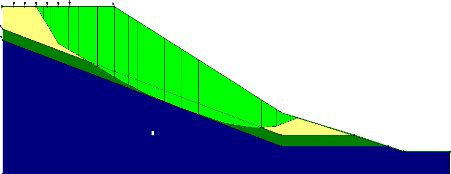
3

1 14 15 16 17 18 19

3

3

5

8 9

4

10 11

12

Figure V-3 : La position du centre et du cercle de glissement dans le modèle géométrique.

	Fellenius	Bishop	Morgenstern & Price	Jambu
Fs	0,62393	0,64929	0,64977	0,60586

Tableau V-5 : Valeur de coefficient de sécurité avec les différentes méthodes. + La prise en compte des infiltrations des eaux :

0.510

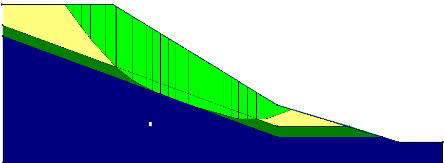
1 2

6

7

3

4

3

5

8 9

10 11

3

12

Figure V-4 : La position du centre et du cercle de glissement dans le modèle géométrique.

	Fellenius	Bishop	Morgenstern & Price	Jambu
Fs	0,50997	0,56053	0,56333	0,5243

Tableau V-6 : Valeur du coefficient de sécurité avec les différentes méthodes. + Couplage hydromécanique :

[Tapez un texte]

0.447

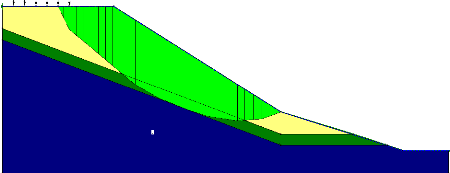
1 14 15 16 17 18 19 2

6

7

3

4

3

5

8 9

10 11

3

12

Figure V-5 : La position du centre et du cercle de glissement dans le modèle géométrique.

	Fellenius	Bishop	Morgenstern & Price	Jambu
Fs	0,42388	0,44507	0,44992	0,41749

Tableau V-7 : Valeur de coefficient de sécurité avec les différentes méthodes. + Récapitulatif des résultats de GEOSLOPE :

	Méthode	Variante N°01	Variante N°02	Variante N°03	Variante N°04
GEOSLOP	Fellenius	0,79523	0,62393	0,50997	0,42388
	Bishop	0,84338	0,64929	0,56053	0,44507
	Morgenstern &Price	0,84426	0,64977	0,56333	0,44992
	Jambu	0,79533	0,60586	0,5243	0,41749

Tableau V. 8 : Récapitulatif des données de calcul.

Commentaires et interprétation :

> On remarque que tous les coefficients de sécurité sont inférieurs à 1, donc le talus est

considéré comme instable et que les facteurs extérieurs : les infiltrations et les surcharges accentue le problème ce qui se traduit dans les calculs par une diminution du facteur de sécurité

> Le facteur de l'eau joue un rôle très important dans le processus de glissement par rapport aux surcharges; a titre d'exemple Fs = 0,50 avec la nappe, et Fs = 0,62 avec les surcharges par la méthode de Fellenius.

La comparaison entre les calculs manuels et les calculs par le GEOSLOPE génère un écart n'excède pas 0,1 dans tous les cas.

IV-2-2-2-Le calcul par le code PLAXIS :

+ Etat vierge :

Présentation du modèle géométrique :

[Tapez un texte]

La figure suivante présente le modèle géométrique (modèle de référence) retenu pour le calcul. Le nombre des éléments choisi est de 6 noeuds ce qui est fiable avec le problème traité. Les conditions aux limites imposées sont définies par des déplacements horizontaux sur les bords latéraux et par des déplacements verticaux sur la base inférieure du modèle (substratum) nuls.

20 m 30 m 30 m

6

5

7

10

30 m

4

y

3

2

0 x 1

8 9

11 12

80 m

Figure V-6 L èle géométrique.

Le code PLAXIS offre la possibilité de faire une exploitation détaillée des calculs sous forme des tableaux et courbes. La figure V.7 représente le maillage déformé du talus, les contraintes de cisaillement (figure V.8), les déplacements totaux (figure V.9) :

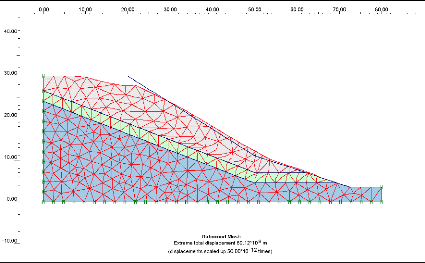
Figure V-7: Le maillage déformé du talus.

[Tapez un texte]

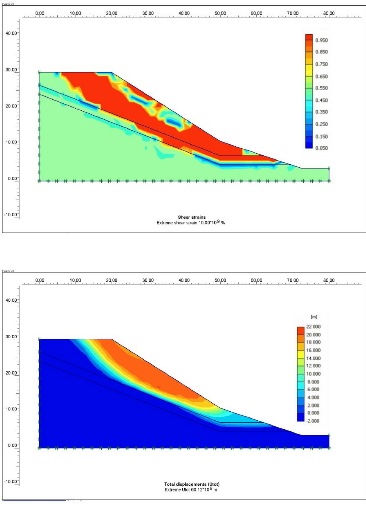
Figure V-8: Les contraintes maximales de cisaillement

Figure V-9: Les déplacements totaux.

Ainsi le PLAXIS offre des informations sur l'étape des calculs, et le coefficient de sécurité Fs (Tableau V.9) :

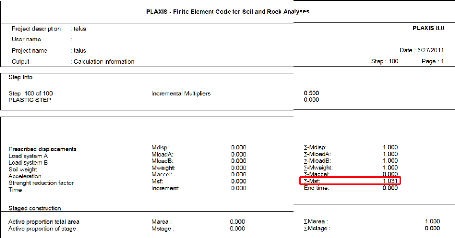
Tableau V-9: Présentation des informations de calcul. Prise en compte des surcharges :

Le modèle géométrique est semblable au modèle de référence avec la présence d'une construction éloignée de 8m de la tête du talus, pour la prise en compte du poids des bâtiments

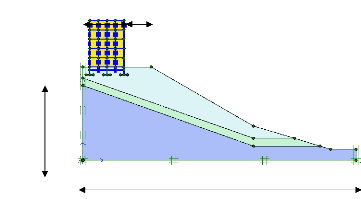
10 m 8 m

03613⁵01 1 ³⁸¹²⁴³ ₀ 3

935135411421247834
733135311411246732
6 30135111401248631

1245528

5

₁₁

39

1352

29

6 13 ⁴ 49 18 ⁴ 44 14 25 27 26

24223 211920

7

171516

5

10

Figu

30 m re V10 : Le mod èle

y

0 x 1

4

8 9

11 12

3

2

géométrique avec la ⁸⁰sm mpte des surcharges.

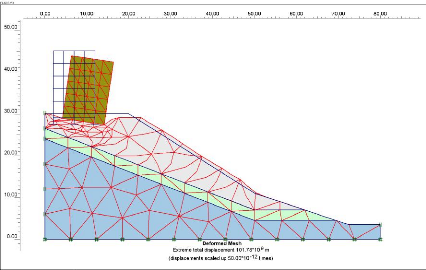
Figure V-11: le maillage déformé du talus et bâtiment.
Figure V-12: Les contraintes maximales de cisaillement.

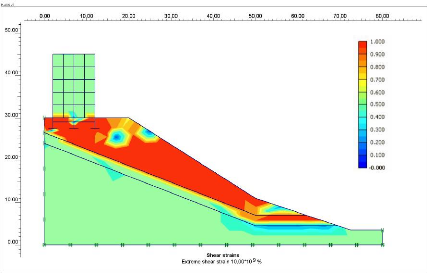
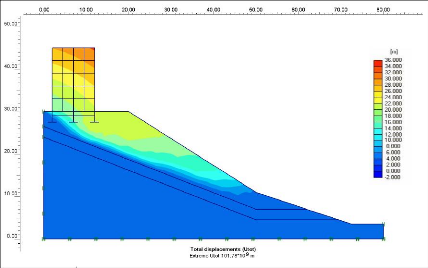
Figure V-13: Les déplacements totaux.

Tableau V-10: Présentation des informations de calcul.

+ La prise en compte des infiltrations des eaux :

Le modèle géométrique est le même, sauf qu'on détermine le niveau de la nappe en surface.

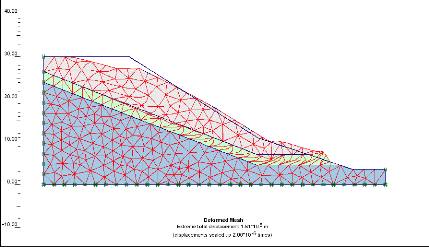
Figure V-14: Le maillage déformé du talus.

Figure V-15: Les pressions interstitielles.

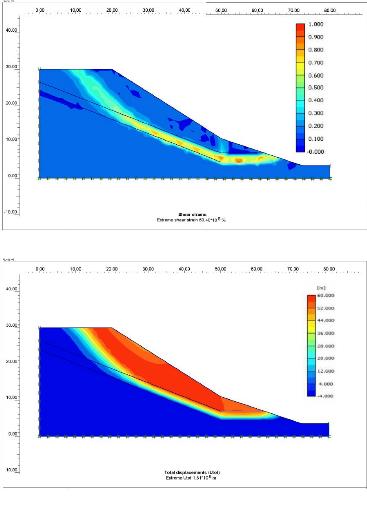
Figure V-16: Les contraintes maximales de cisaillement.

Figure V-17: Les déplacements totaux.

Tableau V-11 : Présentation des informations de calcul. + Couplage hydromécanique :

Ce modèle est le plus proche de la réalité, dont le double effet des surcharges et d'eau s'impose.

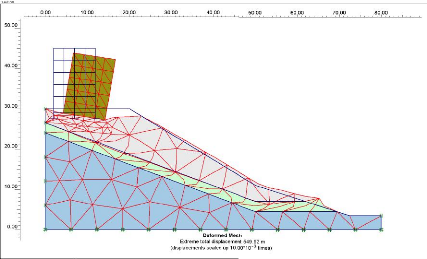
Figure IV-18: Le maillage déformé du talus et bâtiment.

Figure V-19: Les contraintes maximales de cisaillement.

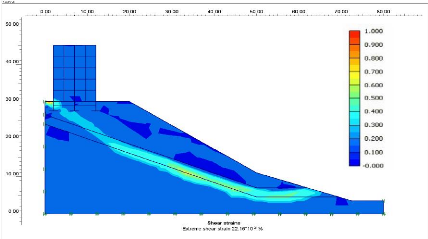
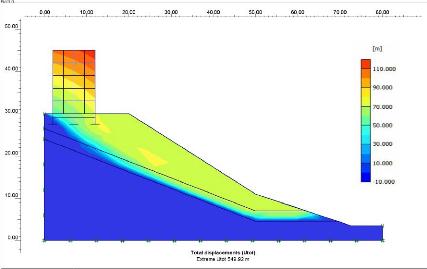
Figure V-20: Les déplacements totaux.

Tableau V-12: Présentation des informations de calcul. + Récapitulatif des résultats de code PLAXIS :

	Variante N°01	Variante N°02	Variante N°03	Variante N°04
Coefficient de sécurité Fs	1,031	0,658	0,519	0,450
Modèle	Mohr-Coulomb	Mohr-Coulomb	Mohr-Coulomb	Mohr-Coulomb
Comportement	Non drainé	Non drainé	Non drainé	Non drainé

Tableau V-13 : Récapitulatif des résultats de calcul du code PLAXIS. Interprétation des résultats :

Variante N°01 :

> L'analyse des résultats confirme les calculs précédents, et que le talus a été instable

avant la construction des bâtiments.

> Les déplacements du talus sont très importants, et les contraintes de cisaillement sont très importantes au niveau de la deuxième couche (de 3 à 5.5m), ce qui explique que la couche d'argile schisteuse constitue un plan favorable au processus de glissement.

Variante N°02 :

> Le coefficient de sécurité Fs = 0,658, donc l'influence de la structure suite aux

mouvements du versant.

> Un déplacement important est observé au niveau de la structure, ce qui traduit que la construction est elle aussi affectée par les mouvements du versant.

Variante N°03 :

> Le coefficient de sécurité Fs subit une diminution considérable de 1,031 à 0,519, ce

qui explique l'importance de l'eau dans le phénomène du glissement de terrain. [Tapez un texte]

> Le volume de terrain déplacé est plus important qu'en état vierge, avec une concentration des contraintes de cisaillement maximales au niveau de la deuxième couche.

Variante N°04 :

> L'effet mixte de l'eau et des surcharges génère une diminution du coefficient de sécurité (Fs = 0,450).

> Les déplacements et les contraintes de cisaillement deviennent importants au niveau de la première et la deuxième couche ce qui se traduit par un déplacement d'un grand volume.

> Les désordres observés au niveau des constructions sont plus important.

V-2-3-Récapitulatif des résultats de calcul :

L'outil	Méthode	Variante N°01	Variante N°02	Variante N°03	Variante N°04
Manuel	Fellenius	0,73	0,69	0,58	0,55
GEOSLOPE	Fellenius	0,79523	0,62393	0,50997	0,42388
	Bishop	0,84338	0,64929	0,56053	0,44507
	Morgenstern &Price	0,84426	0,64977	0,56333	0,44992
	Jambu	0,79533	0,60586	0,5243	0,41749
PLAXIS	c- phi réduction	1,031	0,658	0,519	0,450

Tableau V-14 : Récapitulation globale des résultats de calcul.

V-3- MOYEN DE CONFORTEMENT :

Sur la base des résultats de calcul effectuées, on a constater que l'eau et les surcharges sont a l'origine de l'instabilité du talus, mettant donc le site dans un état critique avec des coefficients de sécurité considérablement faibles.

Il apparaît que la stabilisation du talus peut être assurée par plusieurs méthodes, mais le choix de la méthode de confortement convenable doit tenir compte de l'aspect technicoéconomique.

Notre choix repose sur le procédé d'un rideau de pieux, compte tenu de la nature du terrain et les dimensions du talus qui atteint 30m de hauteur.

On procède à la réalisation d'un rideau de pieux sur toute la surface instable, une série en amont avec 15 m de longueur, l'autre en aval avec 11 m de longueur. Le diamètre de chaque pieu est de 1m.

Le critère du choix de la longueur de pieu est basé sur la profondeur de la couche schisteuse qui est stable, donc le pieu doit être suffisamment ancré dans cette dernière.

Ainsi la série en amont vise à conforter les bâtiments, qui risquent avec une forte probabilité de basculer et la série en aval a pour but d'arrêter le mouvement du terrain.

Les figures suivantes illustrent l'état du talus après confortement :

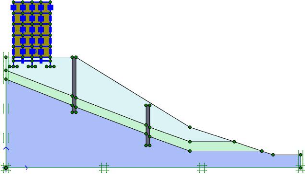
10³⁶135⁰1 1 ³⁸12⁴³10³7

935135411421247

411246

6 ³⁰135¹11⁴⁰12⁴⁸6³¹

1245528

7

33

529

135³

11

8

7

1352

11 3

9

6 13 ⁴ ₄₉₁₈ ⁴ 44 14 59 5

25 27 26

7

242223 211920 171516

10

⁶¹57

⁶⁰56

6362

5855

⁶⁶69

4

⁶⁵68

y

6467

3

2

0 x 1

8 9

11 12

34

32

Figure V-21 : La position des pieux dans le talus.

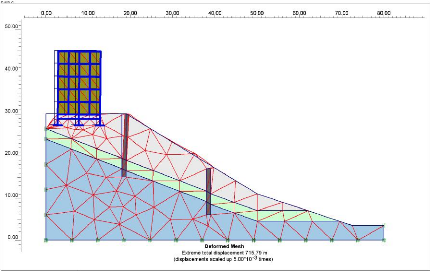
Figure V-22 : Le maillage déformé du talus.

Figure V-23 : Les déplacements totaux après confortement.

Tableau V-15: Présentation des résultats de calcul.

Commentaires et interprétation :

> On remarque une augmentation du coefficient de sécurité (F_s = 1,683), ce qui signifie que le procédé de confortement est efficace.

> La figure V-23 montre une diminution des déplacements du talus, ce qui confirme une autre fois l'efficacité du procédé.

Figure V.24 : Plan de coffrage et de ferraillage.

SYNTHESE ET RECOMMANDATION :

Le calcul de la stabilité a été effectué par plusieurs méthodes et par différentes variantes pour arriver à une analyse comparative entre les résultats ainsi de savoir l'influence de chaque facteur sur le processus de glissement.

Les résultats obtenus dans ce chapitre révèlent que le terrain est instable dans tous les cas étudiés en particulier dans le couplage hydromécanique.

A ce titre, il a été impératif de trouver une solution face a ce problème ; une solution réaliste et qui répond aux exigences technico- économiques.

Le confortement avec un rideau de pieux semble bien efficace dans ce cas, ainsi la réparation des fuites des eaux d'assainissement en prenant des précautions particulier dans le mode d'exécution.

La résolution du problème n'est pas définitive, car il faut prendre en considération quelques précautions telles que le mode de réalisation et les conditions du chantier.

D'autre part, il est indispensable de réparer les fuites des réseaux d'assainissement et d'alimentation en eau potable en veillant à utiliser des conduites souples.

Conclusion générale

Notre projet, a pour but d'étudier et analyser la stabilité d'un talus situé dans la commune de Beni Messous (Sidi Youcef), qui s'étend sur une surface de 10200m² et qui menace les constructions qui se trouve en tête du versant.

Cette région est caractérisée par des formations géologiques diverses, la masse qui est en mouvement est constituée d'un remblai et d'une argile schisteuse.

Le talus, caractérisé par une pente de 28°; est constitué d'un sol hétérogène (Argile schisteuse et schiste).

A partir des essais in situ et en laboratoire et d'après les résultats obtenus on déduit que la couche d'argile schisteuse a des caractéristiques géotechniques de mauvaise qualité ce qui se traduit par :

. Faible cohésion (C=4KN/m²).

. Faible résistance à la pointe (Rp <10 bars).

L'analyse du problème a permis de mettre en évidence un coefficient de sécurité très faible (< 1.4) et qui aura tendance à diminuer en présence des eaux souterrains et d'infiltrations pouvant aller jusqu'à une valeur de 0.41, et surtout en période de grande pluviométrie.

Ce talus nécessite des travaux de confortement afin de le stabiliser et minimiser au maximum le déplacement.

Le soutènement proposé est les rideaux des pieux qui sont caractérisés par un coût raisonnable et une mise en oeuvre plus ou moins facile.

Les caractéristiques des rideaux issues de notre étude sont comme suit :

-Une série en amont avec 15 m de longueur, l'autre en aval avec 11 m de longueur. -Le diamètre de chaque pieu est de 1 m.

-L'espacement entre chaque pieu est de 1,2 m.

-De préférence un coulage sur place.

Pour qu'on s'assure plus de la fiabilité du rideau proposé on a utilisé le code PALXIS qui a donné des résultats satisfaisantes dont le coefficient de sécurité, après avoir réalisé le soutènement, aura une valeur égale a 1,683 (>1,4), ce qui signifie que le talus est devenu stable.

Les différents problèmes rencontrés au cours du projet ont été axés principalement sur le manque des données et quelques documentations tel que la carte topographique, une carte géologique récente....etc. Au niveau des essais on a constaté l'absence d'un système de surveillance tel que les inclinomètres.

Enfin, nous espérons avoir contribué, même partiellement à résoudre le problème de la stabilité du site, et qu'il sera un point de départ à notre vie professionnelle.

Références bibliographiques

[1] : J.Costet, G.Sanglerat (1983)- Cours pratique de mécanique des sols 2 -"calcul des ouvrages"- "troisième édition Dunod ".

[2] : DJAFRI.N, TOUMI.Z ?Mémoire d'ingéniorat-- : Etude d'Un Méga Glissement à Ain el Hamame wilaya de Tizi Ouzou promotion 2010.

[3] : M. Ventura ESCARIO, Luc-Amaury GEORGE, Richard S. CHENEY, Kazuya YAMAMURA et Al --GLISSEMENTS DE TERRAIN-- << Techniques d'évaluation du risque » Comité technique AIPCR des Terrassements, Drainage, Couche de Forme (C12)1997.

[4] : LADGHEM CHIKOUCHE Fadila (2009)- Mémoire de magistère-<< Prévention du risque mouvement de terrain par l'utilisation des paramètres géotechniques ».

[5] : Département fédéral de l'environnement, des transports, de l'énergie et de la communication (DETEC) Office fédéral de l'environnement Division Prévention des dangers Septembre 2009.

[6] : AFPS (2001). Le séisme du 13 janvier 2001 au Salvador. Rapport de mission de l'association Française du Génie Parasismique.

[7] : MOKADDEM Redhouane, MERKOUNE Boubakr - mémoire d'ingéniorat- << Etude d'un glissement de terrain à Tenès près de l'abattoir»- Université Hassiba Ben Bouali-Chlef- (2005/2006).

[8] : BENTAIBA.F, HENDI.F.Z --Mémoire d'ingéniorat-- << Etude de la stabilité au glissement d'un terrain devant recevoir le projet de 47 logements à Chéraga-Alger»Université Saad Dahleb Blida (2009/2010).

[9] : François Schlosser << mur expérimental en terre armée » Bulletin de liaison des laboratoires routiers des ponts et chaussées. Aout - septembre 1979.

[10] : Ouvrages de protection contre les risques naturels et ouvrages en sites instables : Utilisation de matériaux grossiers : Renforcement par géosynthétiques -ouvrages de référence.

[11] : http://bictel.ulg.ac.be/ETD-db/collection/available/ULgetd-06062008 160721/unrestricted/Masekthese.pdf - Jean-Pierre MASEKANYA- Stabilité des pentes et saturation partielle Etude expérimentale et modélisation numérique- Thèse présentée en vue de l'obtention du grade de Docteur en Sciences de l'Ingénieur.

[12] : Eric GERVREAU (Maitre de conférence à l'Université de Cergy Pontoise)- GEOTECHNIQUE << calcul des ouvrages »-Gaëtan Morin Editeur 2000.

[13] : Abdelkader BENAISSA (Mars 2003) -GLISSEMENT DE TERRAIN- << calcul de stabilité » 2^ème édition OPU -Ben Aknoun- Alger.

[14] : Noureddine CHALGHOUM (2006)- Les ouvrages de soutènement en mécaniques des sols -1^ère édition -Publication de l'université Badji Mokhtar -Annaba.

[15] : http://www.pages.usherbrooke.ca/gci730/gci730/chapitre5.pdf.

[16] : http://www.4shared.com/ref/6090239/1.

[17] : Jean-Pierre et Philippe MESTAT Lois de comportement et modélisation des sols (c) Techniques d'Ingénieur.

[18] : AHMED SEDDIKI- ANALYSE DE LA STABILITE DES PENTES SOUS SEISME - Présenté pour l'obtention du diplôme de Magister Spécialité: Génie Civil Option : Géotechnique Promotion : 2007/2008.

[19] : MALLOUK Hanen, << La Résistance Au Glissement D'un Tronçon De La route Nationale N° 16 D'EL-MACHROUHA Menant à Annaba » Mémoire d'ingéniorat-Promotion 2007/2008.

[20] : Khaled BENALLAL et Kamel OURABIA -Monographie géologique et géotechnique de la région d'Alger- (Recueil de notes). OPU 1988.

[21] : Fateh TARMOUL << Détermination de la pollution résiduelle d'une station d'épuration par lagunage naturel "cas de la lagune de Beni-Messous" » par l'Institut des Sciences de la Mer et de l'Aménagement du Littoral DEUA.

Annexe

Sondage Sc 01 : Caisse 01 profondeur 0.00m-7.50m

Sondage Sc 01 : Caisse 02 profondeur 7.50m-15.00m
Sondage Sc 01 : Caisse 03 profondeur 15.00m-22.50m

Sondage Sc 01 : Caisse 04 profondeur 22.50m-30.00m

Sondage Sc 02 : Caisse 01 profondeur 0.00m-7.50m
Sondage Sc 02 : Caisse 02 profondeur 7.50-15.00m

Sondage Sc 02 : Caisse 03 profondeur 15.00-22.50m

Sondage Sc 02 : Caisse 04 profondeur 22.50-30.00m
Sondage Sc 03 : Caisse 01 profondeur 0.00-7.50m.

Sondage Sc 03 : Caisse 02 profondeur 7.50-15.00m

Sondage Sc 04 : Caisse 01 profondeur 0.00-7.50m

Sondage Sc 04 : Caisse 02 profondeur 7.50-15.00m

Sondage Sc 04 : Caisse 03 profondeur 15.00m-20.00m.

Sondage Sc 05 : Caisse 01 profondeur 0.00m-5.00m

Sondage Sc 05 : Caisse 02 profondeur 5.00m-10.00m

Sondage Sc 06 : Caisse 01 profondeur 0.00m-5.00m

Sondage Sc 06 : Caisse 02 profondeur 5.00m-10.00m

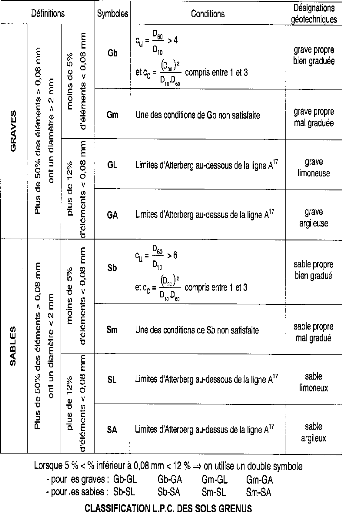
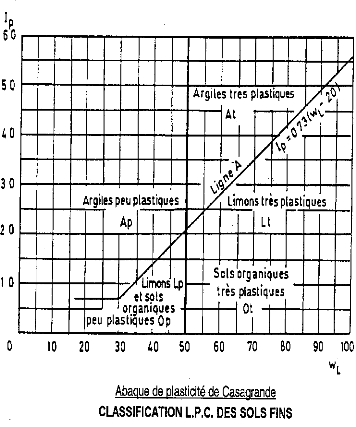
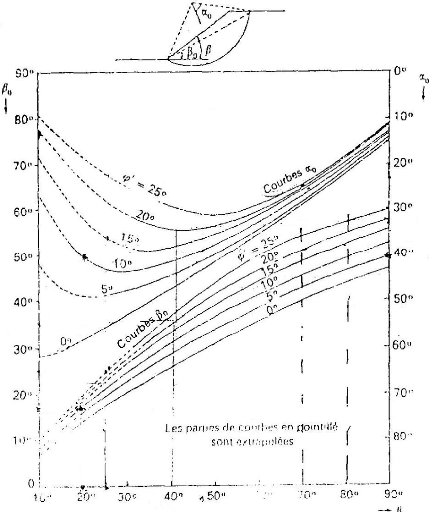
L'abaque XI-17 (abaque de détermination du cercle de rupture).

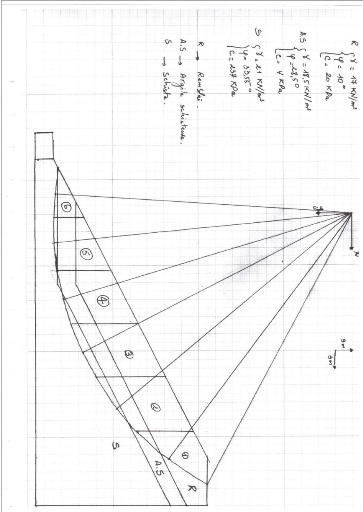
Figure : Localisation du cercle et du centre de glissement.
Illustrations d'utilisation du code PLAXIS

Illustrations d'utilisation du programme GEOSLOPE

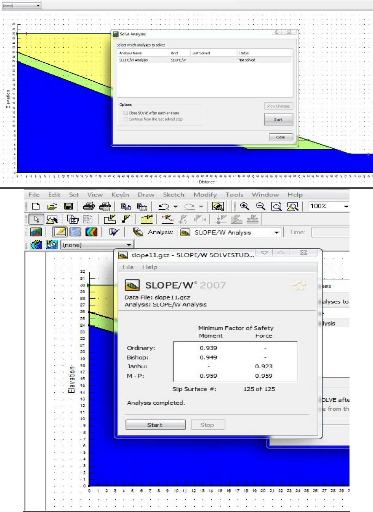
Les efforts appliqués sur une tranche
L'état vierge :

Slice 1 - Ordinary Method

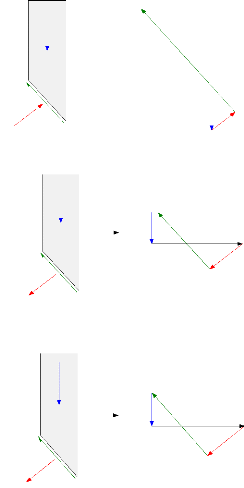
45.924

24.504

51.523

19.398

Slice 1 - Janbu Method

27.279

48.082

19.398

51.523

Slice 1 - Bishop Method

56.904

12.477

19.398

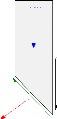
Slice 1 - Morgenstern-Price Method

19.398

46.537

2.0375

46.415

21.921

Avec écoulement :

Slice 1 - Ordinary Method

29.147

16.941

101.45

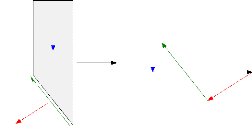
49.682 71.345

29.147

88.836

Slice 1 - Bishop Method

Slice 1 - Janbu Method

53.761 74.904

29.147

88.836

Slice 1 - Morgenstern-Price Method

44.999 72.456

29.147

3.6611

78.565

24.981

126.81

220

08.22

Avec les surcharges :

Slice 1 - Ordinary Method

Slice 1 - Bishop Method

220

24.981

249.34

129.92

135.56

Slice 1 - Janbu Method

139.05

4.7532

220

140.55

Slice 1 - Morgenstern-Price Method

24.981

243.23

33.62

129.92

24.981

244.06

220

Avec écoulement et les surcharges :

Slice 1 - Ordinary Method

29.147

16.941

101.45

49.682

71.345

29.147

88.836

Slice 1 - Janbu Method

29.147

53.761 74.904

88.836

Slice 1 - Bishop Method

Slice 1 - Morgenstern-Price Method

29.147

78.565

3.6611

44.999 72.456