II.2. Analyse des
résultats
L'analyse de nos résultats fera recours à
plusieurs techniques statistiques. Nous allons citer successivement le
coefficient de corrélation r de Bravais-Pearson, le coefficient
de corrélation r de Spearman-Brown,l'anova,le test de
comparaison des moyennes de Student,le test de signification des
différences des moyennes de Student et enfin, le coefficient de
corrélation multiple R
II.2.1. Le coefficient de
corrélation r de Bravais Pearson
Le coefficient de corrélation s'obtient par la formule
(Robert, 1993) :
 soit par la formule soit par la formule
 ou ou 
La covariance s'obtient par la formule
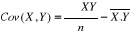
Quant à la variance, elle s'obtient par
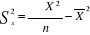
Et l'écart type S est la racine carrée de la
variance. Rappelons que la moyenne des X s'obtient par la formule 
II.2.2. Le coefficient de
corrélation r de Spearman Brown
Est employé pour trouver le coefficient de
corrélation du test entier lorsqu'on a fait usage de la méthode
de bissection, le split half. Ce coefficient s'obtient par la formule
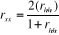
Où r est le coefficient de chaque
moitié. (Lukoba,2006)
II.2.3. L'analyse de la
variance
Déroulement technique du test :
1. nous calculons la moyenne observée m de
l'échantillon n ;
2. nous calculons la moyenne générale
observée M(moyenne pondérée des m) ;
3. nous calculons les sommes des carrées relatives aux
parts des variances observées et regroupons les résultats comme
indiqués dans ce tableau :
|
Source
|
SCE
|
ddl
|
CM
|
Rapport F
|
|
Facteur A (interclasses)
|
|
p -1
|
|
|
|
Résiduelle ou Erreur (interclasse)
|
|
N-p
|
|
|
|
Total
|
|
N-1
|
|
|
Notations : SCE représente la Somme des
Carrés des Ecarts;
CM représente le Carré
moyen ;
ddl représente le Degré de
Liberté.
4. nous entrons dans la table F de Snédecor avec les
degrés de liberté (p-1) en ligne et (N-p) en ligne. Pour la
prise de décision, si 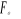 est supérieur à est supérieur à 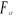 nous rejetons l'hypothèse nulle selon laquelle, les moyennes
sont égales. Cela nous amène à accepter l'hypothèse
alternative selon laquelle, il existerait une différence entre les
moyennes. nous rejetons l'hypothèse nulle selon laquelle, les moyennes
sont égales. Cela nous amène à accepter l'hypothèse
alternative selon laquelle, il existerait une différence entre les
moyennes.
II.2.4. Test de comparaison des
moyennes de Student
Déroulement technique du test :
· nous calculons les moyennes observées  ; ;
· nous les rangeons par ordre croissant dans un tableau
à double entrée ;
Nous calculons les différences des moyennes des
colonnes qr de Student par la formule
 = =   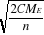 
Notes : Rappelons que cette étape vient
après le test d'anova qui fournit le 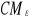 qui est le carré moyen dû à l'erreur, qui est le carré moyen dû à l'erreur,
La valeur t se retrouve sur la table t de
Student.
· nous comparons les résultats des
différences des moyennes à la valeur observée du qr ;
si la valeur observée est supérieure à la valeur critique
qr, nous rejetons l'hypothèse nulle ; dans le cas contraire,nous
l'acceptons.(Dagnelie,1998)
S'il arrive que deux ou plusieurs moyennes ont une
différence très significative ou significative, nous ferons
recours au test bilatéral de comparaison des moyennes ì et ì et ì . .
| 


