Etude du modèle mécaniste dit à quatre (4) flux proposée par Yeoh et al (2008) pour la prédiction du transfert de chaleur dans la région d'ébullition sous saturée.

REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET POPULAIRE MINISTERE DE L'ENSEIGNEMENT SUPERIEUR ET DE

LA RECHERCHE SCIENTIFIQUE

En vue de l'obtention du diplôme
Master en génie mécanique

Option : énergétique

Thème :

Remerciements

Je remercie profondément mon promoteur Mr FERROUK Mohamed d'avoir proposé ce thème, d'accepter de me encadrer et ainsi pour sa disponibilité et l'aide qu'il m'a apporté au cours de ce travail.

Je remercie également les membres de jury d'avoir accepté de me faire l'honneur d'examiner ce modeste travail.

J'adresse aussi mes remerciements à tous mes enseignants depuis le primaire.

TABLE DES MATIERES

Remerciements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .i
Dédicace. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .i

Table des matières . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ii Liste des figures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iv Liste des tableaux . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . vi Nomenclature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . vii

Introduction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

Chapitre 1: Notions fondamentales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1. Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.1. Grandeurs caractéristiques d'un écoulement diphasique . . . . . . . . . . . . . . . . . . . . . . . 4 1.3. Configuration d'écoulement et régime d'ébullition . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.3.1. Ebullition en vase clos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

1.3.2. Ebullition en convection forcée à l'intérieur d'un tube chauffant . . . . . . . . . . . . . . 10

Chapitre II : Transfert de chaleur en écoulement diphasique à l'intérieur d'un tube

vertical. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

2.1. Le transfert de chaleur dans un tube chauffant à flux imposé . . . . . . . . . . . . . . . . . . . 16 2.1.1. Convection forcée monophasique liquide . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

2.1.2. Début d'ébullition locale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

2.1.3. Début d'ébullition locale développée . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 2.1.3.1 Ebullition locale fortement sous-saturée . . . . . . . . . . . . . . . . . . . . . . . .. 20 2.1.3.2 Ebullition locale faiblement sous-saturée . . . . . . . . . . . . . . . . . . . . . . .. 21

2.2. Le phénomène de la crise d'ébullition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

2.2.1. Crise d'ébullition à faible titre (caléfaction) . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.2.2. Crise d'ébullition a titre élevée (assèchement) . . . . . . . . . . . . . . . . . . . . . . . . . 23

Chapitre III : Les modèles mécanistes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25

3.1. Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

3.2 Principaux modèles mécanistes les plus récents . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

3.2.1. Modèles de Kurul et Podowski . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
3.2.2. Modèles de Basu et al . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
3.2.3. Modèle de Yeoh et al . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33

3.2.3.1 Modélisation de différents paramètres . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

3.2.3.2 Forces appliquées à une bulle de vapeur en croissance. . . . . . . . . . . . . . . . 37

Chapitre IV : Programmation de Modèle de Yeoh et al en langage fortran . . . . . . . . . 46

4.1. Description de la géométrie du canal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

4.2. L'objectif . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48

4.3. Procédure de calcul . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59 4.4. Organigramme de programme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50

Chapitre V : Résultats obtenus et discussions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 5.1. Cotes des régimes d'ébullitions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

5.1.1. Influences de la vitesse massique de l'écoulement et la densité du flux imposée sur

la configuration d'écoulement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56

5.2. Prédiction des rayons Rd et RL .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60

5.2.1. Représentation graphique des résultats de l'application du bilan des forces. . . . 61

5.2.2. Variation des rayons Rd et RL . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . 62

5.3. Prédiction des temps de détachement

Liste des figures

Figure Page

1.1 Courbe de Nukiyama. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

1.2 Configurations d'écoulement et régimes de transfert de chaleur associés

pour un flux de chaleur pariétal faible. . . . . . . . . . . . . . . . . . . . . 11

1.3 Carte d'ébullition des différentes régions d'écoulement pour un flux de

chaleur imposé. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .13

1.4 Carte d'ébullition des différentes régions d'écoulement pour une température

. de la paroi imposée 14

2.1 Différents régimes de transfert thermique associés aux différentes régions

. d'écoulement. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

2.2 Schématisation de l'ébullition nucléée sous-saturée. . . . . . . . . . . . . . 17

2.3 Evolution de la température moyenne de fluide et de la paroi dans les trois

. premiers régimes 19

2.4 Différents mécanismes de crise d'ébullition à faible titre (caléfaction). . . . .23

3.1 Schématisation de la répartition des flux de modèle de Kurul et podowski. . .26

3.2 Répartition axiale des flux de chaleur selon l'ONB et l'OSV. . . . . . . . . .29

3.3 Schématisation des scénarios 1,2 et 3 de Basu et al. . . . . . . . . . . . . . .31

3.4 Illustration schématiques de mécanisme de départ, glissement et détachement

. de la bulle de vapeur sur la paroi chauffante 36

3.5 Les forces intervenantes sur la bulle de vapeur l'instant de détachement. . . . 37

3.6 Glissement de la bulle sur la paroi. . . . . . . . . . . . . . . . . . . . . . . .44

4.1 Description de la géométrie de canal. . . . . . . . . . . . . . . . . . . . . . .47

4.2 Méthode itérative pour le calcul de flux pariétal. . . . . . . . . . . . . . . . .48

4.3 Méthode itérative pour le calcul de la température de paroi. . . . . . . . . . .48

5.1 Variation ZNB, ZFDB ^et _ZSC en fonction de flux pariétal ~. . . . . . . . . . 57

5.2 ZNB, ZFDB ^et _ZSC en fonction de vitesse massique d'écoulement G. . . . . .58

5.3 Solution graphique approchée de rayon de détachement de la bulle de vapeur

59

. par application du bilan des forces projeté sur yy'

5.4 Solution graphique approchée de rayon de décollage de la bulle de vapeur par

. application du bilan des forces projeté sur xx' 59

5.7 Variation de la longueur de glissement en fonction de vitesse spécifique

. d'écoulement. 63

5.8 Variation de flux d'amorçage d'ébullition nucléée _'1'WONB dans le canal. . . 63

5.9 Evolution des températures de fluide et de la paroi chauffante avec absence

66

. d'ébullition dans le canal.

5.10 Evolution des températures de fluide et de la paroi chauffante avec existence

. de régime d'ébullition local dans le canal 68

5.11 : Evolution de coefficient d'échange h le long du canal. . . . . . . . . . . . . 69

5.12 : Variation de contribution de quatre flux de modèle de Yeoh dans le canal. . 70

Liste des tableaux

Table page

5.1 L'influence des paramètres (G, Ö) sur la configuration du régime

d'ébullition sous-saturée. . . . . . . . . . . . . . . . . . . . . . . . . . . . 57

5.2 Prédiction des rayons de détachement et de décollage en fonction

de la vitesse spécifique de l'écoulement. . . . . . . . . . . . . . . . . . . . . 60

5.3 Prédiction des temps de détachement, glissement, décollage et la longueur de

glissement en fonction de vitesse spécifique d'écoulement. . . . . . . . . . . 62

5.4 Prédiction des températures de fluide et de la paroi chauffante avec absence

. d'ébullition dans le canal. . . . . . . . . . . . . . . . . . . . . . . . . . . . .65

5.5 Prédiction des températures de fluide et de la paroi chauffante avec existence de

. régime d'ébullition local dans le canal. . . . . . . . . . . . . . . . . . . . . . 67

Nomenclatures

Une lettre peut avoir plusieurs significations. Toutefois le contexte n'autorisera aucune confusion.

A Section. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . [m²]

Atc Fraction de l'aire occupée par les bulles de vapeur [m²]

Asl Fraction de la section influencée par glissement des bulles de vapeur [m²]

b Taux d'accroissement de la bulle [-]

Cp Chaleur spécifique [kJ/kg K]

Csf Constante empirique [-]

Cf Constante empirique [-]

Dhy Diamètre hydraulique [m]

D Diamètre moyen de la bulle de vapeur [m]

F Facteur empirique dans l'équation de Chen [-]

F(M) Constantes empiriques [-]

Fd Force de la traînée ( drag force) [N]

Fdu Force d'expansion de la bulle (growth force) [N]

Fb Force de flottabilité (buoyancy force) [N]

Fsl Force de portance (shear-lift force) [N]

F_s Force de tension superficielle [N]

Fcp Force de pression de contact [N]

G Débit spécifique [kg/m² s]

Gsl Taux de cisaillement adimensionné [-]

g Constante de la gravitation [m/s²]

h Coefficient d'échange thermique [kW/m²K]

h2ph Coefficient d'échange double phase [kW/m²K]

hLO Coefficient d'échange simple phase liquide [kW/m²K]

i Enthalpie [kJ/kg]

iLG Chaleur latente de vaporisation [kJ/kg]

k Conductivité thermique [W/m K]

K l'aire d'influence effective des bulles [m²]

L Longueur du canal [m]

Lsl Longueur de glissement [m]

M? Débit massique [kg/s]

M Masse molaire [kg/mole]

Na Densité des sites de nucléation [sites/m²]

n Exposant [-]

P Pression [Mpa]

Q Débit volumique [m3/s]

r Rayon de la bulle [m]

1? La première dérivée temporelle du rayon de la bulle [m /s]

1· La seconde dérivée temporelle du rayon de la bulle [m /s²]

rD Rayon des bulles aux détachement [m]

rL Rayon des bulles aux décollage [m]

t Temps [s]

tgr Temps de croissance [s]

tsl Temps de glissement [s]

tL Temps de décollage [s]

t_w Temps d'attente [s]

T

	Température	[°K]
TW	Température de paroi	[°K]
ÄT	Différence de température	[°K]
ub	Vitesse d'écoulement	[m/s]
uô	Vitesse de frottement de la paroi	[m/s]
u+	Vitesse adimensionnelle	[m/s]
v	Volume	[m^3]
X	Titre réel	[-]
Xth	Titre thermodynamique	[-]
x	Distance à la paroi	[m]
x+	Epaisseur adimensionnelle de la couche thermique limite	[m]
y	Coordonné cartésienne le long de canal	[m]

Lettres grecques

Á fraction de vide [-]

áL diffusivité thermique du liquide

[-]

â titre volumique [-]

Ö_e le flux net de chaleur par évaporation [Kw/m²]

Öj c le flux de chaleur monophasique par convection forcée [Kw/m²]

Ötc le flux de conduction instationnaire lors du détachement

ou décollage des bulles de leur site de nucléation [Kw/m²]

Ötc,sl le flux de conduction instationnaire lors du glissement des bulles [Kw/m²]

Ö_~ densité du flux de chaleur [Kw/m²]

ì viscosité dynamique [Ns/m2]

è angle d'inclinaison de la bulle [-]

ñ masse volumique [kg/m3]

ó tension superficielle [N/m]

ô_w contrainte de cisaillement à la paroi [N /m²]

[-]

8 tend vers l'infini

Nombres adimensionnels

J_a Nombre de Jakob

Pe Nombre de Peclet

Pr Nombre de Prandtl

Re Nombre de Reynolds

ReL Nombre de Reynolds du liquide

Reb Nombre de Reynolds de la bulle

Nu Nombre de Nusselt

We Nombre de Weber

Xtt paramètre de Martinelli

Indices

b au centre de l'écoulement (bulk)

d détachement (departure)

F fluide

flow écoulement

G vapeur

i entrée (inlet)

L liquide

L décollage (lift-off)

LO simple phase liquide

n non - ébullition

nb ébullition nucléée (nucleate boiling)

SPL simple phase liquide

SUB sous refroidie

W paroi (wall)

Abréviations

cb ébullition convective (convective boiling)

CFD Computational fluid dynamics

fc convection forcée (forced convection)

MAX maximal

MIN minimal

ONB début d'ébullition nucléée (onset of nucleate boiling)

SAT saturation

SC sous refroidie

SCB ébullition sous refroidie (subcooling boiling).

Introduction

Le phénomène d'ébullition sous saturée ou locale intervient dans divers applications industrielles, dans les grandes installations thermiques (centrales électriques, complexes sidérurgiques ou raffineries) ou dans les petits et moyens équipements (microprocesseurs, moteurs à combustion interne, ...), dans le développement des systèmes de refroidissement modernes, les performances croissantes en puissance conduisent à des charges thermiques considérables sur les surfaces chauffantes. De tels systèmes présentant des limitations sur la surface d'échange disponible pour le transfert de chaleur, du débit du fluide caloporteur et sur les températures admissibles des parois qui ne peuvent être refroidis que par le passage contrôlé du fluide caloporteur du régime simple phase liquide au régime d'ébullition nucléée.

Sous certaines conditions appelées `'conditions critiques» la vapeur produite forme une barrière thermique entraînant une montée brusque de la température, le flux thermique critique provoque une dégradation brutale du coefficient de transfert de chaleur pouvant entraîner la fusion de la paroi chauffante. Ce phénomène est appelé »crise d'ébullition».

La crise d'ébullition est un phénomène brutal et destructif qu'il faut à tout prix éviter son apparition dans les systèmes thermiques, selon les conditions de l écoulement, il existe deux types de crise d'ébullition :

- crise d'ébullition à faible titre appelée aussi »caléfaction». - crise d'ébullition à titre élevé appelée »assèchement».

Les systèmes faisant intervenir le phénomène d'ébullition en fonctionnement normal dissipent et permettent d'extraire de grande quantité de chaleur à des écarts des températures faibles. ce mode de transfert de chaleur par ébullition à un coefficient d'échange sensiblement augmenté, est associé à un phénomène d'évaporation très complexe mal compris et mal défini à ce jour et constitue un grand défit pour les développeurs des codes CFD (Computational Fluid Dynamic). Pour son application dans l'ingénierie,

Beaucoup de corrélations modélisant ce phénomène à partir de banques de données issus des expériences, et à l'aide d'outils d'analyse statistique, en fonction des paramètres d'influence judicieusement choisis et mesurés : la géométrie, la puissance, débit, etc. Cette approche présente deux inconvénients :

- Son coût élevé et le manque de généralité.

- Les corrélations développées ne sont pas applicables en dehors du domaine d'application correspondant aux conditions de l'expérience.

En effet, les chercheurs ont tentés une deuxième méthode consiste à identifier les mécanismes physiques qui provoquent le phénomène, cette approche requiert une modélisation réaliste du phénomène complexe de l'ébullition relatif au transfert de chaleur diphasique. , plusieurs modèles mécaniste on étés développés (modèle Basu et al, Kurul et Podowski et Yeoh et al).

Dans ce travail, nous nous intéressons à l'étude du modèle mécaniste dit à quatre (4) flux proposée par Yeoh et al (2008) pour la prédiction du transfert de chaleur dans la région d'ébullition sous saturée.

Pour ce faire, on a structuré notre mémoire en cinq (05) chapitres. Dans le premier chapitre sert à rappeler de notions fondamentales et de grandeurs caractéristique d'un écoulement diphasique ainsi qu'à la description des régimes d'ébullition et régions d'écoulements rencontrés dans le cas d'ébullition en vase clos et dans le cas d'un tube chauffant. Dans le deuxième chapitre, nous scrutons les régimes d'ébullition dont une étude particulière aux régimes d'ébullitions sous-saturée en donnant les différentes corrélations qui régissent le transfert de chaleur dans ces régions. Le chapitre trois (3) passe en revue les différents modèles mécanistes actuels dont une étude particulière de modèle de Yeoh. Le quatrième (4) chapitre est consacré à décrire la méthode de calcul et en utilisant ce modèle pour élaboration d'un programme en langage Fortran dont l'objectif principal est la prédiction de coefficient d'échange thermique dans les régions sous-refroidies. Le dernier est consacrer à la discutions des résultats prédis par ce modèle et on finira par une conclusion générale.

Chapitre I

Notions Fondamentales

1.1. Définitions :

1.1.1 Rappel sur l'ébullition :

L'ébullition est une vaporisation prenant place au sein d'un liquide, généralement dû à un apport de chaleur. La vaporisation provoque la formation des bulles. Lorsque ces dernières sont formées directement dans le liquide, on parle de nucléation homogène. Lorsque. Lorsqu'elles sont formées en paroi d'une surface chauffée, les bulles de la vapeur peuvent être formées par nucléation hétérogène dans le cas d'une surface extrêmement lisse ou le plus souvent à partir de germes précurseurs de vapeur piégés dans les microcavités de la paroi. C'est ce dernier type d'ébullition qu'on observe généralement et qui est celui traité dans les travaux de recherches sur lesquels notre travail est basé.

Lors de l'ébullition hétérogène, la source de chaleur provient de la paroi. Pour que le phénomène de vaporisation ait lieu, il faut que la température de la paroi dépasse la température de saturation de liquide _Tsat correspondante au pression du liquide. Plus les températures de la paroi et celle du liquide environnant les bulles seront élevées, plus la vaporisation sera forte. Ainsi, l'intensité de la vaporisation dépendra de la surchauffe à la paroi.

1.2 Grandeurs caractéristiques d'un écoulement diphasique :

· La température de saturation :

C'est la température pour laquelle il y a équilibre entre la phase liquide et la phase vapeur pour une pression donnée, à condition que la pression soit constante à une valeur inférieure à la pression critique. On l'appelle aussi température d'ébullition parce que l'ébullition ou la condensation se produit à cette température qu'on note

-sat .

· La pression de saturation : La pression de saturation _PSAT est la pression pour laquelle l'ébullition ou la condensation se produit pour une température donnée.

· La surchauffe : La surchauffe représente la quantité positive entre la température T_w

de la paroi et la température de saturation Tsat.

ATsat = Tw -- Tsat (1.1)

· Le sous refroidissement : Le sous refroidissement représente la quantité positive entre la température de saturation T_sat et la température T_w de la paroi.

AT_sub = T_sat -- T_w Ellin (1.2)

· La fraction ou le taux de vide : Pour une section A perpendiculaire à l'ecoulement, la fraction de vide est le rapport entre la surface occupee par la vapeur AG sur la surface totale de la section occupee par la vapeur et le liquide A=AG + AL

A = (AG ) / A (1.3)

· Le titre massique : Le titre massique ou reel est egal au rapport du debit massique de la vapeur sur le debit massique total.

_r, GG

=

G

=l apGuG

(1.4)

(1-a)p_LuL+ap_GuG

X = _l MG

M

· Le titre thermodynamique : Il est caracterise par la quantite de gaz calculee pour les ecoulements diphasique (liquide-vapeur) avec changement de phase.

im-iLs im-iLs

Xth = l =l (1.5)

iGs^-iLs iLG

Où _iLS ^et _iGS sont les enthalpies specifiques du liquide et de vapeur à l'etat de saturation.

iLG : est la chaleur latente de vaporisation.

i(z) : est l'enthalpie specifique du fluide au point z.

D'après les definitions de X et Xth on notera que :

Pour un ecoulement monophasique de liquide sous-sature (Tl < TSAT) : X = 0 et Xth< 0 Pour un ecoulement monophasique de vapeur surchauffee (TG > TSAT) : X = 1 et Xth >1 Pour un ecoulement diphasique de liquide et de vapeur avec TL = TG = TSAT : X=Xth

· Le titre volumique : C'est le rapport du debit volumique de vapeur au debit volumique total

13 = QG (1.6)

Q

Où Q et QG sont le debit volumique total et de la phase de vapeur respectivement.

· Le débit spécifique : C'est le rapport du debit massique total à la section de passage.

M? (1.7)

G =l

A

· La vitesse réelle : C'est la vitesse à laquelle la phase évolue réellement le long de la conduite. Elle est le rapport du débit volumique à la section de passage occupée par la phase.

W ~ = ~~

AG , W ~ = ~~

AL (1.8)

1.3 Configuration d'écoulement et régimes d'ébullitions :

Dans cette partie, nous présentons les différentes configurations d'écoulement qui apparaissent lors de l'ébullition en convection forcée à l'intérieur d'un tube chauffée. Avant de passer à l'ébullition en convection forcée, il est bon de rappeler les différents régimes d'ébullitions observés lors de l'ébullition en convection en vase clos.

1.3.1. Ebullition en vase clos :

Nukiyama (1934, [19]) fut l'un des premiers à caractériser les différents régimes d'ébullition, qui sont fonction de la surchauffe et de la densité du flux thermique transmis à la paroi ?_w. La figure 1.1 représente une courbe d'ébullition ou courbe de Nukiyama (la courbe présentée est plus générale que la courbe originale de Nukiyama, celle-ci ayant été obtenue à flux imposé, courbes pointillées). Pour les plus faibles flux, il n'y a pas d'ébullition, c'est le régime de convection naturelle. Lorsque le flux augmente, l'ébullition se déclenche.

Le transfert thermique est accru par rapport à la convection naturelle. Au fur et à mesure que l'on augmente le flux de chaleur, le taux de nucléation augmente et les bulles deviennent de plus en plus grosses. On atteint ensuite un régime d'ébullition nucléée développée où la paroi est couverte en grande partie par les bulles. On peut augmenter le flux de chaleur jusqu'à une valeur ? max, nommée flux critique, où une très brutale augmentation de la température de paroi est observée lors d'un chauffage à flux imposé (courbe pointillée). La paroi est alors isolée par une couche de vapeur, c'est le régime d'ébullition en film.

En diminuant le flux de chaleur, l'ébullition en film sera maintenu jusqu'à atteindre le flux ? min, en dessous duquel la paroi sera remouillée, sa température diminuera rapidement (courbe pointillée) et l'on entrera à nouveau dans le régime d'ébullition nucléée. Lorsque la température de paroi est imposée, un régime d'ébullition de transition apparaît au-delà du flux critique. Le flux de chaleur diminue lorsque la surchauffe augmente jusqu'à ? min et la formation d'un film de vapeur stable.

La figure ci-dessous représente le flux de chaleur échangé entre la paroi chauffante et le liquide en fonction de l'écart de température entre ces deux milieux (TW - TSAT) et elle illustre les différents régimes rencontré en fonction de la

surchauffe. On peut clairement identifier les différents régimes d'ébullition en vase, dans un dispositif à puissance contrôlée. On remarque 5 régimes distincts de transfert de chaleur par ébullition.

Figure 1.1: courbe de Nukiyama (1934, [19]).

·Régime a-b :

Bien que la température de la paroi soit légèrement supérieure à celle de saturation, mais il n'y a pas encore apparition des bulles et le fluide demeure intégralement sous forme liquide. Pour qu'il y ait l'ébullition, il faut que la surchauffe dépasse une certaine valeur pour amorcer le développement des germes de nucléation. Ici l'échange se fait seulement par convection naturelle et le coefficient d'échange peut être calculé avec des corrélations classiques correspondant à ce régime. La température de l'eau reste pratiquement constante pendant l'ébullition donc on remplace

TAT par T₈ .

Le flux de chaleur transmis par convection naturelle au fluide est :

TW - T₈ : est le gradient de température entre la paroi et l'eau.

· Régime b-e : ébullition nucléée à bulles séparées

Dans ce régime il y a présence des bulles mais elles sont séparées. Ces bulles montent en colonnes à partir des points isolés de la paroi que l'on appelle les sites de nucléation, elles deviennent nombreuses si on augmente l'écart de température.

Le coefficient d'échange h correspondant à cette région dépend de la nature du liquide, de la pression, de la géométrie et de l'état de la surface de l'élément chauffant. La puissance échangée est plus importante que celle du régime précédent.

· Régime e-f : ébullition nucléée avec colonnes continues

Le flux évacué est soutenu par la chaleur latente de vaporisation mais il croit très lentement cela à cause de la multiplication des bulles qui se fusionnent pour créer des poches de vapeur isolant la paroi chauffante et l'empêchant à s'irriguer par de l'eau.

Il existe un grand nombre de corrélations reliant la surchauffe à la paroi au flux thermique pariétal pour l'ébullition nucléée. Dans cette section, nous n'en mentionnerons que quelques-unes parmi les plus couramment utilisées qui modélisent le flux de chaleur en fonction de la surchauffe _(?TSAT) de l'ébullition nucléée.

? Yamagata (1995, [14]):

à été le premier à mettre en évidence l'influence des sites de nucléation sur le transfert de chaleur qui est donnée par la formule suivante :

?_W = c × ?T~~~

~ × N ~ (1.10)

a et b sont deux constantes (a=1,2 et b=1/3 approximativement)

c: Coefficient qui dépend de la combinaison fluide-matériau de la surface.

N : Densité de sites de nucléation, elle est donnée par la formule empirique suivante:

N = 1,2 × 10 × ?^~p

P : Pression exprimée en bars.

Ö est de la forme: ? = h ÄTs~.F^''

n : Une constante (pour l'eau :3 < n < 4)

· Corrélation de Rohsenow (1965, [27]) :

C'est probablement la corrélation la plus célèbre. Elle apparaît dans Rohsenow (1962). Il considère que la croissance et le détachement des bulles d'une paroi induisent un mouvement de convection au sein du liquide qui est le mode de transfert de chaleur dominant entre la paroi et le fluide.

?_w = ìLi~G ~~(ñ~~ñ~) ~/~ ~

~~~~ Ä~~~~

ó ~ ~~ (1.11)

~~~ ~~~ ~~~

Les indices L et G se rapportent au liquide et à la vapeur à l'état de saturation.

Le coefficient Csf et l'exposant n dépendent de la combinaison surface/liquide.

(Csf = 0,013 et n = 1 pour les combinaisons inox/eau et cuivre/eau).

· Corrélation de Cooper (1965, [27]) :

Devant la difficulté d'utilisation de la relation de Rohsnow. Cooper (1984) à proposé la corrélation dimensionnelle suivante pour la détermination du coefficient d'échange h.

h = 40P;^~.~2LogE.(-Log P)^r0.5.m_^0..?_w^2/3 (1.12)

Avec : M masse molaire du liquide, h en [W/m².K], P~ la pression réduite (rapport de la pression à la pression critique), ?_w en [W/m².], å [um] la rugosité de la paroi.

· Au point f :

Dans ce point la couche de vapeur isolante est continue, elle isole complètement le liquide de la surface chauffante, l'échange se fait seulement à travers cette couche ; ce qui explique la difficulté de transfert de chaleur. Le point f s'appelle point critique (crise d'ébullition ou flux thermique critique).

Nous donnons ci-après deux corrélations permettant d'évoluer ce flux critique :

· Corrélation de Kutateladze (1974, [14]): il a proposé une expression pour évaluer le flux critique en vase, en utilisant l'analyse dimensionnelle.

~/~ ~ ~ ~ ~ i~~ñ~ ~ó~(ñ~~ñ~) ~ñ~~ñ~ Ö~~~ = ñ~~ ~ ñ~ ~ ~~

(1.13)

? Corrélation de Zuber (1974, [24]) : Zuber a obtenu une relation

expérimentale analogue à la précédente en utilisant l'analyse de la stabilité hydrodynamique :

1/4

Ömax = 0,149 i~~ ñ~ Fó~(ñ~~ñG)

ñG~ ~ (1.14)

Au delà du point critique, on peut rencontrer deux cas : -le chauffage est à flux de chaleur imposé:

Dans ce cas, le transfert à travers la couche de vapeur est incapable d'évacuer le flux ainsi imposé ce qui fait croitre d'une manière considérable la température de la paroi ou de l'élément chauffant jusqu'au point de fusion, et on passe directement au point h.

- la température de la paroi chauffante est imposée :

· Régime f-g : ébullition de transition

Dans ce cas, selon la température de fusion de la paroi chauffante par rapport à celle imposée, on peut avoir ou non la destruction de l'élément par assèchement. Cette région est décrite par courbe en pointillé ce qui explique la diminution du flux thermique échangé, Ce régime peut être aléatoire et instable.

· Régime g-h : ébullition en film

En plus de la convection paroi-vapeur, l'évacuation de la chaleur se fait par rayonnement à cause de la faible conductivité thermique de la pellicule (film) de vapeur isolant la paroi. Ce régime est dit aussi ébullition pelliculaire.

1.3.2. Ebullition en convection forcée dans un tube chauffant :

Dans un écoulement bouillant vertical dont la paroi est chauffée de manière uniforme, on peut situer plusieurs configurations; ces dernières sont discernées par la répartition spatiale de la quantité de vapeur présente dans l'écoulement qui évolue en fonction des conditions thermo-hydrauliques de l'écoulement à la paroi. Chacune des configurations d'écoulements est également caractérisée par un ou plusieurs régimes d'échange thermique à la paroi.

Dans la figure 1.2, le tube est alimenté en liquide très sous-saturée à l'entrée et de longueur suffisante pour assurer un écoulement en vapeur surchauffée à la sortie.

Figure 1.2 : Configurations d'écoulement et régimes de transfert de chaleur associés
pour un flux de chaleur pariétal faible (1977, [1]).

On distingue sept régions différentes le long de ce tube (A à G) : 'Region A:

Région simple phase liquide (single phase liquid flow), C'est la première région à l'entrée du canal où l'échange de chaleur entre la paroi et le fluide se fait par convection forcée en simple phase liquide.

'Region B:

C'est la région d'écoulement à bulles (bubbly flow). En premier lieu, les bulles de vapeur se forment au voisinage de la paroi dont la température est voisine à celle de saturation, puis elles s'arrachent et se condensent au centre du tube où le liquide n'a pas encore atteint la température de saturation. Dans cette région, on rencontre plusieurs termes décrivant les modes d'échange thermique, on citera : l'ébullition locale, l'ébullition sous-refroidie et l'ébullition nucléée sous-saturée.

'Region C:

C'est la région d'écoulement à bouchon ou à poches (Plug-flow ou slugflow).Comme son nom l'indique, il y a formation des poches de vapeur au centre du tube par le regroupement d'un nombre important de bulles. Dans cette zone, si le flux de chaleur est très important, l'apparition des bulles se multiplient et elles prennent du volume puis se rejoignent pour former une couche de vapeur au voisinage de la paroi, constituant une barrière à l'échange thermique. C'est le phénomène de la crise d'ébullition à faible titre (la caléfaction), un phénomène destructif qu'il faut éviter.

'Region D:

C'est la région d'écoulement annulaire (annular-flow), les poches de vapeur s'agglomèrent au centre et forment des manchons enchainés en queue leu-leu, ces manchons de vapeur se rejoignent à leurs tours pour créer un cylindre de vapeur au centre du tube entouré du liquide annulaire.

'Region E:

C'est la région d'écoulement annulaire avec entrainement. De fines gouttelettes liquide sont entrainées par de la vapeur, parfois de la vapeur se condense et se dépose sur le film liquide. Lorsque l'écoulement annulaire se stabilise, on voit un film annulaire liquide à la paroi entraîné par la vapeur au centre. Le film liquide annulaire se dissipe peu à peu par vaporisation. Lorsqu'il disparait complètement, on assiste à un phénomène de crise d'ébullition à titre élevé qu'on appelle aussi assèchement (dry out).

'Region F: C'est la région d'écoulement à brouillard (Mist Flow), Le film liquide à complètement disparu. Cette région est caractérisée par le brouillard formé de microscopiques gouttelettes liquides en suspension dans la vapeur. Ici la température du fluide dépasse celle de la saturation.

'Region G:

C'est la région d'écoulement simple phase vapeur (sèche), le transfert de chaleur paroi-fluide est calculé par les lois classiques de la convection forcée.

Les configurations d'écoulements et les régimes de transfert thermique que nous venons de décrire peuvent être repérés différemment en fonction des conditions initiales de l'écoulement. Les cartes d'ébullition « idéalisées » tracées par Collier illustrent les différents régimes qui peuvent avoir lieu dans un tube chauffant vertical pour un flux de chaleur imposé (refroidissement des coeurs de réacteurs nucléaires, moteur à combustion interne, tubes électroniques,...) (Figure 1.3) et pour un gradient de température paroi-fluide (TW _-TSAT) donné ou imposé (Figure 1.4).

Les paramètres thermo-hydraulique de l'écoulement (le débit spécifique G, la température d'entrée Ti du fluide, la pression P dans le tube, la géométrie du canal), influent considérablement sur la configuration et les régimes d'écoulement dans le tube.

Le cas traité par la figure 1.2 est représenté par la courbe en bas (en bleu) de la figure 1.3 (Flux faible) qui permis d'avoir toutes les différentes régions de l'écoulement de A à G. Cette situation correspond à des conditions de faible flux et de faible débit spécifique.

Figure 1.3 : Carte d'ébullition des différentes régions d'écoulement pour un flux d
chaleur imposé (1981, [4])

Figure 1.4 : Carte d'ébullition des différentes régions d'écoulement pour un
température de la paroi imposée (1981, [4]).

Chapitre II

Le transfert de chaleur en écoulement

diphasique à l'intérieur d'un tube vertical

chauffé uniformément

2.1. Le transfert de chaleur dans un tube chauffant à flux imposé :

La figure (2.1) illustre le cas d'un écoulement bouillant dans une conduite vertical dont la paroi est chauffé de manière uniforme, l'eau entre en sous saturation à l'extrémité inferieur de tube chauffant et sort totalement évaporée, nous analysons les différents régimes de transfert thermique associés aux différentes régions d'écoulement.

Figure 2.1 : différents régimes de transfert thermique associés aux différentes régions
d'écoulement (1995, [26]).

On distingue six régimes différentiés par leurs modes de transfert thermique.

L'évolution des températures de la paroi et de fluide en fonction de la cote Z pour les trois premiers régimes depuis la région d'écoulement simple phase liquide jusqu'à celle d'écoulement à bouchons .

Pour ne pas sortir du cadre de notre étude, On se limitera à la description des trois premiers régimes de transfert thermique (I, II et III) où une attention particulière est accordée à l'ébullition nucléée sous-saturée.

Figure 2.2 : Evolution de la température moyenne de fluide et de la paroi

dans les trois premiers régimes (1981, [4]).

2.1. 1 Convection forcée monophasique liquide :

La première région s'étale de l'entrée du canal jusqu'à la section de la cote (ZONB) où apparaissent à la paroi les premières bulles de vapeur car la température de la paroi est proche de celle de la saturation (fig 2.2). Le transfert de chaleur se fait en convection forcée entre la paroi et le liquide. Pour ce mode, Il existe des relations régissant les évolutions de la température et de flux thermique en fonction de nombre

de Nusselt (Nu), nombre de Reynolds (R_e) et le nombre de Prandtl (Pr), ces relations donnent des résultats acceptables et proches des résultats expérimentaux.

Le flux échangé dans cette région est donné par :

? = hLO ÄTL (2.1)

Où ÄTL est la différence de température entre la température de la paroi interne du tube et la température moyenne du fluide à la cote z depuis l'entrée du tube.

Et _hLO est le coefficient d'échange simple phase en convection forcée qui est calculé en fonction du nombre de Nusselt :

NU ~L

hLO = (2.2)

~

Pour un écoulement laminaire, Nu est donné par la corrélation de Rohsenow et Choi (1995, [21]):

Nu = hLoD = 4

kL

(2.3)

En régime turbulent, plusieurs corrélations ont été proposées, chacune possède un domaine de validité.

La plus célèbre est celle donnée par la corrélation de Dittus-Boelter [12]:

~

~.~

hLoD

Nu = = 0.023 (GD ~~~ ì

ì~ ) k 1L ~ (2.4)

~~

Incopera & De Witt (1934, [13]) :

~

O.~ O,4

Nu = 0.027 (GD (CP ì

ì~ ) k i 3 (ìL

ì~th (2.5)

Ces corrélations sont valables pour un écoulement ascendant dont le rapport z/D > 50, Re >10000 et 0,7 = Pr = 160.

Gnielinski (1983, [11]):

ECV2 11Re-10001Pr

El El El (2.6)

1+12EIVCV2Vr2 / 3 -1) ^LIDDL

Avec : DOD ¹ IIIIMEIMEE10 (2.7)

4

Et YDL est un paramètre tenant compte de la longueur chauffée donné par :

YDL El [DM (D)2 /31 (2.8)

Cette corrélation est valable dans les domaines suivants :

z/D =1, 2300 < Re <10⁶ et 0,6 = Pr = 2000.

2.1.2 Ebullition nucléée sous saturée ou l'ébullition locale :

A une cote donnée de la paroi chauffante (fin de la région simple phase), la température de la paroi devient suffisante pour déclencher la nucléation (Onset of Nucleate Boiling ou ONB). A cette cote débute l'ébullition nucléée sous-saturée associée à un changement de configuration d'écoulement avec l'apparition de l'écoulement à bulles (bulles attachées à la paroi dans un premier temps). La température du liquide à la paroi est alors supérieure de quelques degrés à la température de saturation tandis que la température du liquide au coeur de l'écoulement tend vers la température de saturation.

Selon l'allure de la fraction vide (figure 2.2) ou la fig 2.3, on a :

- la cote Z_n ou Z_nbmarque le début d'ébullition nucléée ;

- la deuxième région (II) se décompose en deux sous régions :

- La région d'ébullition partielle, dite aussi région »fortement sous saturée»

- La région d'ébullition développée (faiblement sous saturée).

2.1.3. Début d'ébullition locale (Onset of Boiling) Zn ou Zonb :

La cote (Z_n) ou Z_onb ( fig : 2.3) marque le passage de la région I (simple phase)

vers la région II (ébullition locale). Cette limite est difficile à déterminer à cause de
l'estimation de la surchauffe du fluide nécessaire à la création de la bulle de vapeur.

Par contre, la limite inferieure de cette temperature necessaire pour l'amorçage de l'ebullition nucleee peut être calculee à l'aide de la correlation de Davis and Anderson (1988, [25]) :

.131 (80" 4)TSAT)^°.15

1(1TSAT)mb (2.9)

IcLhLGPGJ

Et la valeur limite du flux _'PONB (onset of nucleate boiling) necessaire pour amorcer l'ebullition nucleee est donnee par Steiner (1988) [25]:

rcrPGhLO

²⁰"TSATILG

'PONB =

(2.10)

TSAT en K et le rayon critique de la bulle _rcr est egal à 0.3 × 10^-6 m. 2.1.4 Ebullition locale partielle (fortement sous saturée) :

Elle se situe entre la cote _Zn, et ZFDB , region d'ebullition locale partielle, où la

surchauffe de la paroi (T -- TSAT) est suffisante pour l'initiation de petites bulles

attachees à la paroi et qui disparaissent très rapidement en se condensant au centre de

liquide dont la temperature TF(z) est inferieure à celle de la saturation, donc les
bulles n'atteignant pas la region d'ebullition sous refroidie complètement developpee
et elles participent au transfert thermique en cedant la quantite de chaleur procuree
lors de l'evaporation à la paroi au fluide par condensation. La fraction du flux de
chaleur utilisee pour la formation de vapeur est insignifiante et le flux total transfere
dans ce regime est estime par Bowring comme la somme de trois modes de transfert
simultanes qui correspondent à trois mecanismes distincts:

- la chaleur latente des bulles vapeurs produites puis par condensation en fin d'accroissement (Ö_e),

- par convection due à l'agitation du film thermique sous l'action des bulles (Öa),

- par convection dans le liquide où la turbulence simple phase (ÖSPL). Bowring (1977, [1]) :

Ow = (I)_e + (I)_a + (I)SPL (2.10)

D'après Bowring :

'PscB = (I)e + ⁽I⁾a (2.11)

L'équation (2.10) s'écrit :

Ow = ?SPL + ?SCB (2.12)

OA la composante simple phase _(ÖSPL) est donnée par :

ÖSPL=hLO(TSAT^-TL(z)~ (2.13)

Et _(ÖSCB) est le flux de chaleur transféré par nucléation des bulles :

ÖSCB=hscB( TW(z) - TSAT) (2.14)

2.1.5 Ebullition locale développée (faiblement sous saturée) :

- Le début d'ébullition locale développée ZFDB :

La cote ( ZFDB) marque le passage entre la région d'ébullition locale partielle et la

région d'ébullition locale développée (figure 2.2). La prédiction de cette transition oA a lieu le détachement des bulles est important pour le calcul des pertes de pression. On distingue plusieurs modèles pour sa prédiction, selon le détachement qui est contrôlé thermiquement, le détachement provoqué hydro-dynamiquement et le détachement combinant les deux mécanismes. Parmi les modèles les plus recommandé on suggère d'utiliser le modèle à mécanismes combinés de Saha et Zuber [7], qui ont proposé une corrélation simple pour le calcul du point de détachement des bulles. La sous saturation au point de détachement est donnée par :

?T~~~(~~~~) = 0.0022 Ö~ .~ Ph= 70 000 (2.15) xi, ?TsuBITFDB ) l = 153.8 Öw .c Ph > 70 000 (2.16) G ~pL

c.piph

P₆ = (Nombre de peclet) (2.17)

KL

Les corrélations les plus répandues qui permettent de calculer le transfert de chaleur dans la région FDB sont données par :

Jens et Lottes (1983, [14]):

(~~ - ~~~~)	= 25 ~~ ~.~Se_f /6 2	(2.15)
Pour : Öw=6,31 MW/m^2
Thom et al (1965, [26]):
(~~ - TSAT) =	22.65 ~~ ~.~ ~~~ /~ ~	(2.16)
Pour : Öw > 6,31 MW/m^2.

2.2. Le phénomène de la crise d'ébullition :

Consécutive à un changement de configuration d'écoulement diphasique, la crise d'ébullition sensible à de nombreux paramètres géométriques et thermohydrauliques, elle correspond à une dégradation importante du coefficient d'échange paroi-écoulement se qui engendre à son tour une augmentation de la température de la paroi due au déficit du transfert thermique, et par conséquence elle peut conduire à la fusion de la paroi chauffante (burn out), il existe deux types de crises d'ébullition, crise d'ébullition à faible titre appelée caléfaction (Departure from Nucleate Boiling, DNB) rencontrée à la fin d'ébullition nucléée sous-saturée et la crise d'ébullition à titre élevé appelée assèchement (Dry out) rencontrée à l'épuisement du film liquide dans l'écoulement annulaire, on note que la crise d'ébullition à faible titre est la plus destructive par rapport à la deuxième.

2.2.1. Crise d'ébullition a faible titre (caléfaction) :

Dans les systèmes à flux de chaleur imposés (refroidissement des coeurs des réacteurs nucléaires, moteur à combustion interne, tubes électroniques, ...) l'élément chauffant peut alors atteindre des températures supérieures à son point de fusion et se dégrader brutalement. Cet état de destruction ou limite de destruction est désigné par collier (1971, 1981) par le terme <<burnout ». la limite de destruction survient généralement avec un certain retard par rapport aux limites de la caléfaction (DNB) et de l'assèchement <<dryout» comme le montre la figure 2.5. le terme de flux thermique

critique « Critical Heat Flux (CHF)» est utilisé pour désigner les deux types de crise d'ébullition.

Les conséquences de la crise d'ébullition à faible titre sont beaucoup plus graves que l'assèchement. Les principaux mécanismes conduisant à son apparition sont au nombre de trois (voir la figure ci-après) :

Figure2.3 : Différents mécanismes de crise d'ébullition à faible titre `'caléfaction»
(2009, [8]).

1 - L'accumulation des bulles de vapeur prés de la paroi chauffante. Le recouvrement de la paroi par bulles empêche tout contacte avec le liquide.

2 - Des efforts de surchauffe locales de la paroi aux emplacements des sites de

nucléation dues à la formation et à l'accroissement des bulles de vapeur, sous des conditions défavorable à leur détachement.

3 - Formation des taches sèches pendant le passage de gros bouchons de vapeur en régime d'écoulement avec bouchons.

2.2.2. Crise d'ébullition a titre élevée (assèchement) :

L'assèchement est moins dangereux si l'on compare à la caléfaction en termes d'impact brutal sur les matériaux, mais à long terme, il peut provoquer la fatigue des matériaux. La configuration de l'écoulement menant à la crise d'ébullition est de type annulaire, constituée d'un film liquide en contact avec la paroi et d'un coeur de vapeur contenant des gouttelettes. L'échange de chaleur est effectué par convection forcée au travers du film liquide conduisant à l'évaporation progressive de celui-ci ; l'assèchement est alors consécutif à la vaporisation complète de ce film et conduit à une configuration d'écoulement de type écoulement à gouttelettes. Les mécanismes conduisant à l'assèchement sont assez bien connus.

Chapitre III

Les modèles mécanistes

Dans le chapitre précédent, nous avant présenté quelques corrélations donnant le flux appliqué à la paroi en fonction du coefficient d'échange. Toutes les corrélations ne sont valables que dans les mêmes conditions expérimentales où elles sont établies, leurs utilisations en dehors du domaine de validité sont déconseillées.

Le manque de généralité et du coût élevé de l'approche empirique, les chercheurs ont exploité une autre voie en développant des modèles mécanistes basés sur l'identification des mécanismes régissant le transfert diphasique. Les modèles mécanistes actuels qui et de plus ils sont tous développés pour les conditions d'un tube vertical chauffé uniformément.

Les corrélations empiriques sont basées sur une exploitation statistique de résultats expérimentaux souvent associée à des considérations physiques tandis que les modèles mécanistes sont, en premier lieu, basés sur des considérations phénoménologiques enrichies par des données expérimentales, ce qui leurs donnes un caractère réel.

Ces dernières années, avec le développement de l'informatique et des techniques expérimentales, plusieurs chercheurs ont tenté une approche théorique basée sur la description des mécanismes régissant les phénomènes de transfert de chaleur pariétaux car ils modélisent a priori plus finement et précisément les transferts de chaleur pariétaux.

En particulier, ils modélisent le flux de chaleur pariétal en flux de chaleur sensible et flux de chaleur latent net «représentant» respectivement la quantité de chaleur dédiée au réchauffement du liquide et la quantité de chaleur nette pour la génération des bulles de vapeur quittant la paroi.

3.1- les modèles mécanistes :

Plusieurs modèles mécanistiques ont été développés, on peut citer le modèle de Chen (1963, [2]) ou celui Boiring (1977, [1]). Ces modèles ou ceux qui en dérivent ont généralement une bonne capacité à estimer les flux thermiques en régime d'ébullition nucléée en bulles isolées. Néanmoins, lorsqu'on est en régime d'ébullition pleinement développée, l'interaction entre les sites de nucléation ou entre les bulles va jouer un rôle de plus en plus important.

Ces mécanismes d'interaction sont très mal connus rendant le développement d'un modèle mécanistique adapté à l'ébullition nucléée pleinement développée très difficile.

3.2 Principaux modèles mécanistes les plus récents :

Nous présentons, dans cette section, trois modèles mécanistes de l'ébullition nucléée qui nous ont paru pertinents :

> le modèle de Kurul et Podowski (1990,[18]), > le modèle de Basu et al. (2005, [18]),

> le modèle de Yeoh et al. (2008, [18]).

3.2.1 Modèle de Kurul et podowski :

a) Description du modèle :

Ce modèle mécaniste est très largement cité dans la littérature se base sur une répartition du flux pariétal en trois contributions.( modèle à trois (3) flux ).

Ö_w = Öfc -' _Ötc -' Ö_e (3.1)

avec :

· Öfc le flux de chaleur monophasique par convection forcée,

· Ötc le flux de chaleur par conduction instationnaire (quenching ou trempe),

· Ö_e le flux net de chaleur par évaporation.

Fig 3.1 : Schématisation de la répartition des flux de modèle de Kurul et podowski.

Le modèle de Kurul et Podowski comporte :

- une inconnue principale, i.e. soit la température de la paroi Tw soit le flux

pariétal Ö,4,.

- Et quatre paramètres qui nécessitent d'être modélisés :

> le diamètre de décollage des bulles Dl,

> la densité de sites actifs de nucléation Na,

> la fréquence de nucléation f,

> et le coefficient d'échange monophasique par convection forcée hfc.

b) Répartition des flux de chaleur de modèle de Kurul et podowski :

* Le flux de convection forcée Of_t :

Öfc = Afc hfc(T,4, -T~) (3.1)

avec :

· Afc : fraction de l'aire de la paroi non-influencée par les bulles.

La fraction de l'aire non-influencée _Afc est calculée à partir de la fraction de l'aire influencée par les bulles _Atc. Cette dernière correspond à la somme des aires de projection des bulles sur la paroi :

_D2

Aft = 1- _Atc= 1-7rN4 a / (3.2)

Avec :

Dl : diamètre de décollage des bulles.

* Le flux de conduction instationnaire Ötc :

2k

-- (ll'_w VI

Ötc= Aft t_w f 7

¹, (3.3)

E71/tw

avec :

· f la fréquence moyenne de décollage des bulles,

· t_w le temps d'attente entre le décollage d'une bulle et la formation d'un
nouvel embryon de bulle.

Le temps d'attente t_w est calculé à partir du temps d'attente entre le décollage de deux bulles _tcyc (temps d'un cycle de nucléation) et de la durée de la croissance d'une bulle tl :

f = 1/tcyc ; tw = tcyc-tl

Kurul et Podowski (1990) considèrent que le temps nécessaire à la croissance d'une bulle tl est négligeable devant t_w. On obtient alors :

t_w ~ tcyc = f ~1/t_w

* Le flux net d'évaporation Ö_e :

· f la fréquence de décollage des bulles,

· Vb le volume des bulles au décollage,

· hlg la chaleur latente d'évaporation,

· Na la densité de site de nucléation sur la paroi chauffante.

Modélisation des paramètres principaux de ce modèle :

* Le diamètre de décollage d'une bulle Dl :

L'expression développée alors par Kurul et Podowski est la suivante :

Dl = 10^-4 (Tl _-Tsat) +0,0014 (3.5)

» Il concerne exclusivement les écoulements eau/vapeur.

* La densité de sites actifs de nucléation N_a :

L'expression de la densité de site de nucléation Na utilisée par Kurul et Podowski (1990,) est celle de Lemmert et Chwala (1977) :

(3.6)

* La fréquence de nucléation f :

Kurul et Podowski (1990) utilisent l'expression de Ceumern et Lindenstjerna (1977) pour calculer la fréquence de nucléation f :

(3.7)

3.2.2 Le modèle de Basu et al :

· Description du modèle :

Ce modèle mécaniste plus récent que celui de Kurul et Podowski est basé sur une phénoménologie plus fine de l'ébullition nucléée pariétale et prend notamment en compte le phénomène de glissement des bulles le long de la paroi chauffante et son impact sur la répartition des flux de chaleur. Il est, contrairement au modèle de Kurul et Podowski, dépendant de la topologie de l'écoulement et s'appuie donc sur les deux sous-régimes de l'ébullition nucléée sous-saturée délimités par :

· le déclenchement de l'ébullition nucléée (ONB) et par

· l'apparition significative de la vapeur (OSV) (fig : 3.2).

Le calcul de la répartition du flux de chaleur pariétal entre chaleur sensible et chaleur latente est différent de celui du modèle de Kurul et Podowski. En effet, le calcul de convergence vers la température de la paroi est indépendant du flux net d'évaporation ; ce dernier est obtenu dans un second temps à partir de cette température de la paroi.

Fig 3.2 : répartition axiale des flux de chaleur selon l'ONB et l'OSV [2].

On distingue trois régions :

- Region I :

Avant l'ONB. Il n'y a pas de création de vapeur et l'échange de chaleur entre la paroi et le liquide s'effectue au travers d'un flux de convection forcée Öf c.

- Region II :

Entre l'ONB et l'OSV. Des bulles de vapeur apparaissent et grossissent sur la paroi ; toutefois, il n'y a pas de création nette de vapeur dans cette zone : tout le flux pariétal est (au final) transmis au liquide sous forme de chaleur sensible. Ce flux de chaleur est modélisé comme un flux de convection forcée entre l'écoulement et la

paroi un coefficient d'échanges «amélioré» _h~Fc ( = 1.3 _hFC ) prenant en compte

l'augmentation de la rugosité de la paroi due à la présence des bulles. - Region III :

Basu à considéré 3 scénarios (voir figure 3.3) en fonction de la longueur de glissement (!~), la distance entre deux cite de nucléation (s) et la densité des sites actifs de nucléation (N_a).

Fig 3.3 : schématisation des scénarios du modèle de Basu et al.

Afin de ne pas alourdir la rédaction de ce mémoire, les répartitions des flux du modèle de Basu et al dans la troisième région ne seront pas développées.

3.2.3 Le modèle de Yeoh et al :

Ce modèle est en faite une amélioration de modèle de podowski qui passe de trois flux à quatre flux avec introduction de la notion glissement des bulles dédié par Basu et al.

a\- Description du modèle :

Yeoh et al proposent un modèle d'ébullition nucléée basé sur la répartition des flux du modèle de Kurul et Podowski, tout en introduisant la notion de glissement des bulles sur la paroi proposée par Basu et al. Néanmoins, cette prise en compte du glissement des bulles est limitée par le fait que le modèle de Yeoh et al. Ne traite pas la coalescence des bulles sur la paroi.

b\- Répartition des flux de chaleur de modèle de Yeoh et al :

Ce modèle de type «Kurul et Podowski amélioré» passe alors de trois (3) à quatre (4) flux, le quatrième étant un flux de conduction instationnaire lors du glissement des bulles sur la paroi :

· Öf c : le flux de chaleur monophasique par convection forcée,

· Ötc : le flux de conduction instationnaire lors du détachement ou décollage des bulles de leur site de nucléation,

· Ötc,sl : le flux de conduction instationnaire lors du glissement des bulles,

· Ö_e : le flux net de chaleur par évaporation.

De manière identique au modèle de Kurul et Podowski, le flux de chaleur pariétal correspond à la somme de ces flux.

?~?~ = ?~fc ?~?~ ?~tc ?~tc,?~1

(3.16)

c\- Modélisation de modèle de yeoh et al

* Le flux de convection forcée Öf c

Le flux de chaleur transmit au fluide par convection forcée est donnée par :

Öfc = Afchfc(Tw -- T)

(3.17)

La fraction de l'aire non-influencée par les bulles _Afc est calculée à partir de celle influencée par les bulles Atc :

(K ^ð14)t1_wf1+ (K ð d) III -- t_wf) I+ N_agKD tl_w

mi²

Atc ^=l _RfNa [ 4

4 )

(3.18)

D'oA :
	Afc = 1 -- Atc	(3.19)

Le coefficient de transfert thermique convectif _hfc est calculé en utilisant la corrélation de Dittus-Boelter :

ki o4

hf, = l 00I23 1Re^ors Pr (3.20)

p_h 1 1

OA :

Pr1 = (CP ì) ; 1Re1 = l (ñi d

k 1 ì_i )₁

Cette corrélation est valable pour un écoulement ascendant dont le rapport L/Dh>50, Re >10000 et 0,7 = Pr = 160.

* Le flux de conduction instationnaire (1)t, :

Lors du détachement ou décollage des bulles de leur site de nucléation. Ce flux est calculé par les auteurs comme un flux de conduction instationnaire appliqué sur la fraction de l'aire influencée par les bulles _24tc se détachant ou décollant de leur site actif de nucléation. Il est pondéré par le facteur de réduction Rf afin de différencier les bulles décollant et les bulles glissant sur la paroi :

^2 Ö~~ = 2 ~ ~~ñ~~~~ ð~~ ~T~ - T R N ~ K ~ð~~ ~ ~ t f	(3.21)
~ 2 ~ ~~ñ~~~~ ð ~~ (T - T) R N ~ ~ð~~ ~ ~ (1 - t f )

* Le flux de conduction instationnaire influencé par le glissement des bulles

Otcs/

Lors du glissement des bulles sur la paroi. Ce flux est également calculé comme un flux de conduction instationnaire classique rapporté à la fraction de l'aire influencée par les bulles _24tc glissant sur la paroi. Il est également multiplié par le facteur de réduction Rf :

Ötcs1 = 2 ~ ~~ ñ~ ~~~ ð~~ ( T - T ) R N ~ l K D t f ~ + 2 ~ ~~ ñ~ ~~~ ð ~~ ( T - T ) R N ~ f t ~ð ~~~ ~ ~ ( 1 - t f )

(3.22)

* Le flux net d'évaporation (P_e

Ce flux est calculé exactement comme celui du modèle de Basu et al, et se différencie donc du modèle de Kurul et Podowski par l'utilisation du facteur de réduction Ri :

_IrD1^3 Öe = l RfNafa: 6 119ghfg

(3.23)

3.2.3.1 Modélisation de différents paramètres : Le modèle de Yeoh et al. Comporte :

* une inconnue principale : soit la température de la paroi T_w , soit le flux pariétal, (I)_w.

* plusieurs paramètres qui nécessitent d'être modélisés.

1- le diamètre de détachement des bulles Dd

2- le diamètre de décollage des bulles Dl

3- la densité de sites actifs de nucléation N_a

4- le coefficient d'échange monophasique par convection forcée hi c

5- le temps de croissance d'une bulle sur son site actif de nucléation t_g

6- le temps de glissement de la bulle sur la paroi t₅1

7- le temps de décollage de la paroi t₅1

8- le temps d'attente entre le détachement (ou décollage) d'une bulle son site actif de nucléation et l'apparition d'un nouvel embryon de vapeur sur ce même site t_w

9- la distance de glissement 1₅ Les autres paramètres sont des données thermo hydrauliques de l'écoulement.

a. Diamètre de détachement Ddet de décollage D1 :

Fig3.4:Illustration schématiques de mécanisme de détachement, glissement et
décollage de la bulle de vapeur sur la paroi chauffante (2008, [10]).

L'évaluation de diamètre de détachement et de décollage des bulles de la paroi s'appuie sur la résolution d'un bilan des forces agissant à une bulle de vapeur isolée grossissant sur une paroi chauffante (figure 3.5).

1- Différentes forces appliqués sur la bulle :

Elles peuvent être décomposées en deux catégories :

1. les forces statiques, qui existent même en absence d'écoulement autour de la bulle,

2. les forces hydrodynamiques, qui due à l'existence de l'écoulement

Ces forces sont schématisées sur la figure ci-dessous :

Fig3.5 : Les forces intervenantes sur la bulle de vapeur l'instant de détachement
(2008, [10]).

2- Modélisation de différentes forces : - La force de traînée Fqs :

La force de traînée s'oppose au mouvement relatif de la bulle.

Fqs = ⁶C?~ðì?~ur

(3.24)

?~¹

?~

Oil : C?~ = 12 3 + ?~( 12 ?~?~ coef?~icient de trainé. n=0 ; ?~?~?~ = ?~?~d(?~?~?~?~?~)

Rej,?~ + 0.796?~?~ ?~?~

- La force de portance Fsl :

C'est une force liée à la non-uniformité de l'écoulement et/ou à la dissymétrie de la bulle qui engendre une réaction perpendiculaire à la vitesse relative de la bulle.

1 F?~?~ = C?~ñ?~u^2ðr^2 2	(3.25)
CL = 3.877Gç ( 1 ?~ + 0.014G?~^2) Re?~		1 ^4 Coefficient de portance.

Oil Reb , ReF sont les nombres de Reynolds de la bulle et de fluide, respectivement.

G_s est le taux de cisaillement adimensionné donné par la relation suivante :

G₅ = ?~du r

dx?~x=r u (3.26)

La valeur de la vitesse u ainsi que sa dérivée spatiale ( ?~'

?~?~ ) quand x = r, sont

calculées en utilisant l'expression analytique de Reichardt pour l'écoulement simple phase liquide (régime turbulent):

u+ = ?~

U_ô

1 ln(1 + K x^?~) + c ?~1 - exp (- ?~?~ ÷ ?~ - ?~?~ ÷ exp (- ?~?~

= 3 ?~?~ (3.27)

Oil :

K

u : Vitesse de fluide à l'épaisseur (x) de la couche sous refroidie (m/s).

u : Vitesse adimensionnelle en fonction de l'épaisseur adimensionnelle (x⁺) qui est donnée par :

~+ = ñ_~ ~_ô ~ (3.28)

U1,u1k

U1, : Vitesse de frottement à la paroi (m/s), Elle est déterminée à partir de

u_ô = u1,bu1k ( ~

2.36 in ~ei J-4.39) (3.29)

Avec _ul,bulk est la vitesse moyenne de liquide au centre de l'écoulement.

- La force de flottabilité Fb :

Cette force est la résultante de la poussée d'Archimède et du poids s'exerçant sur la bulle. Elle est donnée par :

~ Fb = rðg (ñi - ñg) ~

(3.30)

- La force de croissance Fdu :

C'est une force liée à l'inertie du liquide environnant la bulle mis en mouvement par l'accélération ou la croissance de celle-ci.

Elle est déterminée suivant la corrélation de Zeng et al, qui ont considéré une bulle hémisphérique en phase de croissance dans un liquide visqueux, la corrélation est la suivante :

Fdu = -ñ1ðr~ (~ ~ Cr? + rr·~

(3.31)

Où la constante empirique C est introduite pour tenir compte de la présence de la
paroi, en basant sur la comparaison des données expérimentales disponibles, Zeng et al

ont proposé la valeur C_~ = 20/3.

L'évolution temporelle du rayon des bulles r(t), ainsi leurs dérivées r? et r ·

nécessaire dans la relation de la force de croissance sont obtenus en considérant le
modèle proposé par Zuber (1961, [1]), r(t) est corrélé en fonction du nombre de Jakob
(Ja), la diffusivité thermique pour la phase liquide (ç_i) et la constante empirique b par

la relation suivante :

r(t) = ~~ v~ ~~ ~~~~ (3.32)

OA :

ja= 0ñp1cP (nrw^-TsA)=1 k l

; 41 ^=lñ_ghloo Pl-pll

L'équationn (3.31) devient ^:
	FMau= El-^-- 36PbEV4/4ð, /	(3.33)

La constante empirique b,d'aprèss Zuber, est au voisinage de un(b1)) pourun ⁿécoulementt vertical.

- La force de tension superficiell F. : I

La force de tension de surface est une force capillaire qui maintient la bullesur r la paroi ets'opposee au détachement et décollage de celle-ci. Elle agit au niveau dela a ligne de contact entre la paroi etl'interfacee liquide/vapeur.

F_sx =l- ~_w0" _aⁿ _f3[cos/3 ---sin1 a] l

Fs= E(3.34))

r(ax-()=1

11111Mk_gy=El E--d_wo^- _{7r2(Ed_f30} [cos0/3+lsin M ] El

Enréalité,, lediamètree de contact d_w , 0 et0^'évoluentt au cours dedéveloppement t

de la bulle. Plusieurs auteurs ondonnée& des valeurs issues del'expérimental..

Pour le modèle de Yeoh, les valeurs de ~~, 0 et 0' ont été donnée 0.09mm, 5^l et

10° respectivement.

á l= è + 0^' ; 13 I= è -- 0'

- La force de pression de contact F_cp:

La force de pression de contact résulte de la différence de pression entre l'intérieur et l'extérieur de la bulle et correspond à la composante normale à la paroi du bilan total des forces de pression qui s'exercent sur la bulle :

	~ Fci, = d^cr)i^ndw	de la dynamique appliqué à une	(3.35) bulle s'écrit : (3.36)
	1 -- 5r 4
	Le principe fondamental
ÓF 1= Fs + Fdu +		d
		= Fs1 + Fos + Fb + Fci, I Pg dt (9bUb)

Le bilan des forces statiques et dynamiques projetées sur les deux axes ox et oy, s'écrit :

d

/x: ÓFx 1 = Fs_x + _Fs1 + _Fdu. + _Fcp I= Pg dt (9b.~b) (3.37)

d

/y : ÓF_y 1= _Fsy + Fb + _Fduy + _Fqs I= Pg dt (9b.12b) (3.38)

Dans le cas de faible rapport de densité ( ñ: << 1 l ), les forces d'inerties sont

négligeables.

Dans le cadre des écoulements verticaux, l'équation selon x gouverne le phénomène de décollage des bulles de la paroi tandis que l'équation selon y permet de décrire le détachement des bulles de leur site actif de nucléation ainsi que le glissement de celles-ci sur la paroi.

La détermination de diamètres de détachement et de décollage s'appuis sur la résolution de ces deux équations

Diamètre de détachement (Dd) :

La bulle est attachée sur son site de nucléation, elle est inclinée d'un angle è due à la force hydrodynamique et hydrostatique de l'écoulement et grandit jusqu'un volume critique du détachement Vd , la bulle alors quitte son site de nucléation.

Le diamètre de détachement (Dd) correspondant au volume Vd est défini comme suit :

Dd = l 2l (3vd)1/3 (3.39)

\ 4ð I

Le diamètre au détachement Dd s'obtient donc par la résolution de l'équation suivante :

Fb + _Fsy + _Fdu sin ₀ + Fqs = 0 (3.40)

Le diamètre de décollage (DL)

Au moment de glissement, la bulle se redresse (sans inclinaison, 0 = 0) elle prend

davantage de volume le long de la surface chauffante mais sans la quitter jusqu'à ce que la force de portance _Fsl (voir la) est suffisante pour faire la décoller de la surface. Au point de détachement.

Le diamètre de décollement (DL) correspondant au volume VL est défini comme suit :

D L = l 2l (3:) ^1/13 (3.41)

Le diamètre au décollage DL s'obtient donc par la résolution de système d'équation suivant :

Fs1 + _Fdu cosO + F_cp + F_sx = 0 (3.42)

b- Le temps d'attente t_w [1]:

C'est le temps nécessaire à la reconstitution de la couche limite thermique, suite au glissement et/ou au décollage des bulles, est défini par :

c- La fréquence de nucléation f :

La fréquence de nucléation f est définie de manière classique comme dans le modèle de Basu et al :

d- La densité de sites actifs de nucléation Na :

La densité de sites actifs de nucléation utilisée dans ce modèle est, comme pour Kurul et Podowski :

e- La longueur de glissement l_s :

Elle est approximée à l'aide de la corrélation de Maity utilisée dans le modèle

de nucléation de Basu et al :

Fig 3.6 : Glissement de la bulle sur la paroi [3].

f- La fraction de l'aire influencée par le glissement des bulles Asl :

Elle correspond à la fraction de l'aire balayée par les bulles lors de leur glissement sur la paroi et s'exprime en fonction des diamètres de détachement et décollage.

0 est l'angle d'inclinaison de la bulle de vapeur.

· D51 le diamètre moyen des bulles pendant leur glissement,

'sI = ('d + D1) / 2 (3.52)

h- Le facteur de réduction Rf : Il est calculé de la même manière que celui du modèle de Basu et al :

5 1

Rf = = (3.53)

t_s 1 JfN~

S : la distance entre deux cite de nucléation.

i- Le paramètre K

Ce paramètre permet de rendre compte de la zone d'influence effective des bulles. Il est pris égal à 1,8 pour ce modèle [2]:

K = 1.8

Chapitre IV

Programmation du Modèle de Yeoh en langage

FORTRAN

4.1. Description de la geometrie du canal :

Il s'agit de deux tubes coaxiaux places verticalement (figure ci-contre). Le tube interieur est en acier chauffe par effet joule genere un flux de chaleur parietal uniforme, ce dernier est refroidi par ecoulement d'eau a travers l'espace annulaire, dans des conditions qui sont rencontres dans les systemes de refroidissement par les liquides.

-Les dimensions du canal sont :

D_i El DElmmIZIEED, El EICIffinmEbt2 El Elm.

Dans le cas d'un chauffage uniforme a la paroi du tube interieur, les parametres independants (figure 4.1) influencant sur le transfert de chaleur t sont (Collier & Thome,1994) :

- le debit spécifique G, la

- temperature d'entrée T_in du fluide,

- la pression p du système,

- le diametre hydraulique D_i

- et la longueur L du tube.

Figure 4-1 : Description de la geométrie de canal.

4.2. L'objectif :

L'objectif principal de notre etude est de mettre au point un programme informatique permettant de predire pour une pression dorm& et un flux de chaleur parietal impose la distribution de temperature en paroi 7'_w Ilk El de tube chauffe et celle du fluide le long du canal pour &valuer le coefficient d'echange thermique en utilisant le modele mecaniste de Yeoh. Ce dernier a ete &labor& pour les regions de transfert de chaleur sous-saturee (temperature de fluide est inferieur a la temperature de saturation correspondante a la pression P, region monophasique liquide et la region en ebullition locale).

Le coefficient h est calcule directement a partir du flux &change (O_w) et le gradient de temperature lies par cette relation :

cr._w

DOTS El (4.1)

111Twftli-PCFAIIIIII

4.3. Procédure de calcul :

Les modèles de type mécaniste sont généralement utilisés dans les codes de calcul CFD (Computational Fluid Dynamics) car ils modélisent à priori plus finement les transferts de chaleur pariétaux. Ces modèles ont la particularité de pouvoir être résolus à l'aide des méthodes numériques grâce au développement de l'utile informatique.

L'ensemble de ces modèles d'ébullition nucléée comporte généralement deux inconnues principales moyennées spatialement et temporellement :

- la température de la paroi ÖW , - la densité du flux pariétal T _W ,

Ces modèles peuvent donc être résolues en imposant l'une de ces deux inconnues

- à partir du flux pariétal Ö_w si la température de la paroi T_w est imposée.

Figure 4.2: Méthode itérative pour le calcul de flux pariétal.

- ou à partir de la température de la paroi T_w quand le flux pariétal Ö_w est imposé,

Figure 4.3: Méthode itérative pour le calcul de la température de paroi.

111111 Dans le cadre de cette étude, le flux pariétal est imposé (qui est le cas pour les générateurs de vapeur, les chaudières et les gaines de combustible des réacteurs nucléaires, ...); la température de la paroi est donc la seule inconnue du modèle.

I

On suppose une température de paroi quelconque, puis on calcule les différents paramètres et le flux pariétal global à partir de cette supposition. Si les deux flux sont égaux, c'est qu'on a trouvé la bonne température de paroi. Sinon, on augmente ou on diminue la température de paroi supposée et on réitère (Voir figure 4.3). En tenant compte des dimensions du canal (figure 4.1) décrites précédemment, la nature de fluide et les conditions initiales à l'entrée.

Cote des déférentes régions d'ébullitions:

Utilisant le bilan thermique, On peut déterminer les cotes Zonb, ZFDBet Zpar la relation

suivante :

0:13_w × S = T? (hi(Z) -- hiniet) = G × A(hi(Z) -- hiniet) (4.1)

Dans notre cas, il s'agit d'un écoulement annulaire entre deux tubes de diamètres intérieur

et extérieur Di_n , _Dex respectivement.

D'où :

S : la section chauffée S = ir _Din.Z . . . . . . . . . . . . . . . (i)

A : section du canal A = ir( Dex² -- Di_n²)/4 . . . . . . . . . . . (ii)

hi(~) : L'enthalpie du liquide a la cote z du canal.

Remplaçant les équations (i) et (ii) dans l'équation (4.1), on obtient :

Ö_wir Din.Znb = Gir( Dex² -- Din²)(hi(Znb) -- hiniet)/⁴ . . . . . . . (iii)

Après le développement de l'éq (iii), on aboutit à la formule suivante :

Znb =( (Ti -- Tsat) + (Tsat -- Tin) ^)GCPi( Dex² -- Din²)/⁴DinÖw.

=( _ATsatonb + ATsuB in)GCPi( Dex² -- Din²)/⁴DinÖw. (4.2)

ATsatoNB : Surchauffe nécessaire pour amorçage de l'ébullition nucléée (équation 2.9)

ATsuB in : Le sous-refroidissement à l'entré du canal.

Cote _ZFDB ^et Zsc :

Utilisant l'équation (4.1), on obtient :

ZFDB = (hFDB -- hin) E ( Dex² -- Din²)/⁴DinÖw. (4.3)

Sc =( hFsat -- hin) E ~ D_ex ² -- Di_n²)/ 4Di_n0:13_w. (4.4

L'enthalpie du fluide _(hFDB) et à l'état de saturation (hF_sat) serons obtenus à l'aide des

tables thermodynamiques de l'eau et sa vapeur en fonction des températures TFDB et Tsat.

Les propriétés thermo-physiques de l'eau et sa vapeur évolues dans le canal, afin de pouvoir connaitre l'évolution de température de fluide et de la paroi le long de canal, on subdivise le canal en plusieurs sous région et on calcul le flux nécessaire pour l'amorçage de l'ébullition nucléée _(0:13WONB) (eq 2.10) correspondant aux propriétés thermo physique

de fluide pour chaque cote Zi de canal.

Donc, en fonction des conditions initiales et le flux imposé, le programme peut suivre l'un des deux chemins (voir figure 4.4):

a- M_w < Ow_oNBi : pas d'ébullition au niveau de la cote Zi :

Le transfert de chaleur ce fait uniquement par convection forcée, c'est le régime monophasique liquide, le coefficient de transfert de chaleur est calculé directement par la relation (2.4)

b- [O_w > Ow_oNBi : existence d'ébullition au niveau de Zi :

En utilise le modèle mécaniste de yeoh qui postule que le flux de chaleur pariétal

est la somme de quatre (4) flux (0:13f_c, 0:13_e, 0:13t_c, _0:13tc,s~) pour la détermination des

températures de fluide et de paroi. Le coefficient de transfert de chaleur est calculé directement par la relation (4.1)

Programme FORTRAN 2000

Début

J = J + 1

4.4. Organigramme de programme :

Entré de données géométriques du
canal et les conditions initiales

Lecture des données

Calcul des propriétés thermo-physiques du
fluide à l'état de saturation pour la pression
P.

j = 1

l'état de saturation : P, _TSAT, VF, VG, CpF, CpG, HF, HG, KL, KG,

Impression des propriétés thermo-physiques du fluide à

ìL, ìG

A

G (J) = 100 + (j-1) * 100

Calcul des propriétés thermo-hydrauliques à la
vitesse G (J) : ReL, PrL, ReyL et hFC.

1

N = 1

B

N = N + 1

ÖW (N) =100 + (N-1)×100

K = K+1

C

K = 1

Z (K) = Z₀ + (K -- 1) × n

n : Le pas (n = 0.01) [m]

Calcul de _ÖONB (J, K)

0_w(N) > ⁰0NB(J,K)

Oui Non

Existence du régime diphasique

Transfert en convection forcée
simple phase liquide

Calcul les cotes des differences regions :

z_nb(J, N), zFDB(J, N) et z(J, N)

3

2

Calcul des propriétés thermo-physiques du
l'eau et sa vapeur à la cote Z(K) du canal pour
la pression P.
HFZ, HGZ, TFZ, VFZ, VGZ, SIGMAZ, visfz,

Calcul des propriétés thermo-physiques du
l'eau à la cote Z(K) du canal pour la
pression P.
HFZ, TFZ, VGZ, SIGMAZ, visfz ,....

4

5

Region I
(monophasique)

Même procedure
que simple

h

Calcul HFC (J, N, K)
(Par la correlation de
Bittus Boeter)

Z(K) > Z_nb(J, N )

Oui Non

Region II (diphasique)

Tw(N ) *

~~, ~~, Rf , f, ...

Tw(J, N ,K) *

(I) * (I) * (I)^* + (I) * (DW EI) *

fc e tc tcEs1

(DW (J, N ) * = (DW (N )

Oui

Non

6

Tw(N ) = Tw(J, N ) *

5 6

Impression des résultats:

z_nbE(J, N), zFDB (J, N) et z_sc(J, N)

TW (J, N, K), h_Yeoh (J, N, K).

Impression des résultats:

z_nb(J, N), zFDB(J, N) et z_sc(J, N)

TW (J, N, K), Hfc (J, N, K).

Impression des résultats:
TW (J, N, K), HFC (J, N, K).

C

Non

Z() Zsc. (J, N)

Oui

B

N = 6

Non

A

Oui

Non

J = 12

Oui

Fin

Figure 4-4 : Organigramme du programme

Chapitre V

Résultats obtenus et discutions

5.1. Cotes des différents régimes d'ébullitions:

5.1.1. Influences de la vitesse massique de l'écoulement et la densité du flux imposée sur les limites d'ébullition :

Les résultats tabulés ci-après sont calculées pour les conditions d'entrées suivantes :

P =0.13 Mpa, Tin = 80 °K.

L'eau entre avec un sous refroidissement Tsub = T,t - Ti_n= 387.5 - 353 = 33.5 °K

- La configuration d'écoulement est très sensible à la variation de la vitesse massique et la densité de flux imposé (figure 5.2). L'augmentation de la vitesse d'écoulement dans le tube engendre l'intensification de la turbulence, aussi engendre l'expansion de la longueur du régime d'ébullition locale, par contre l'augmentation de la densité du flux thermique favorise l'apparition de l'ébullition a des cotes plus faibles et rétrécie la longueur des régions d'ébullitions.

- A flux imposé élevé et à des faibles vitesses spécifiques d'écoulement, l'ébullition aura lieu a l'entrée du canal et la région monophasique liquide est très réduite (figure 5.1).

Ow = 150 Kw/m^2
G [Kg/s.m^2]	ZNB [m]			ZFDB [m]	Zsc [m]
100	0.619			1.184	3.961
200	0.774			1.480	4.951
300	0.928			1.776	5.941
400	1.083			2.706	6.931
500	1.238			3.696	7.921
600	1.393			4.685	8.911
700	1.547			5.675	9.902
800	1.702			6.665	10.892
900	1.857			7.655	11.882
1000	2.012			8.645	12.872
1100	2.166			9.635	13.862
1200	2.321			10.625	14.852
Ow = 300 Kw/m^2
100	0.345			1.292	3.067
200	0.518			1.365	3.834
300	0.605			1.437	4.600
400	0.691			2.144	5.367
500	0.777			2.910	6.134
600	0.821			2.910	6.134
700	0.864			3.676	6.900
800	0.950			4.442	7.667
900	1.036			5.208	8.434
1000	1.123			6.974	9.201
1100	1.209			7.741	9.967
1200	1.295			8.507	10.734
~~		=	450 Kw/m^2
100	0.247			0.929	2.405
200	0.308			1.261	3.006
300	0.370			1.354	3.607
400	0.432			1.513	4.208
500	0.493			1.787	4.809
600	0.555			2.187	5.411
700	0.617			2.788	6.012
800	0.678			3.388	6.613
900	0.740			3.989	7.214
1000	0.802			4.590	7.815
1100	0.863			5.191	8.417
1200	0.925			5.792	9.018
~~		=	600 Kw/m^2
100	0.195			0.564	2.109
200	0.244			0.829	2.637
300	0.293			1.095	3.164
400	0.342			1.509	3.692
500	0.391			2.002	4.219
600	0.439			2.524	4.746
700	0.488			3.051	5.274
800	0.537			3.577	5.801
900	0.586			4.104	6.328
1000	0.635			4.631	6.856
1100	0.683			5.158	7.383
1200	0.732			5.685	7.911
~~		=	800 Kw/m^2
100	0.155			0.277	1.191
200	0.194			0.322	1.488
300	0.233			0.466	1.786
400	0.272			0.730	2.083
500	0.311			0.834	2.381
600	0.349			1.038	2.679
700	0.388			1.242	2.976
800	0.427			1.485	3.274
900	0.466			1.648	3.572
1000	0.505			1.851	3.869
1100	0.544			2.054	4.167
cPw = 1000 Kw/m^2
100	0.002			0.1906	0.858
200	0.005			0.263	1.072
300	0.009			0.316	1.287
400	0.016			0.417	1.501
500	0.031			0.595	1.716
600	0.043			0.782	1.930
700	0.058			1.069	2.145
800	0.072			1.216	2.359
900	0.087			1.429	2.574
1000	0.101			1.643	2.788
1100	0.116			1.856	3.002
1200	0.129			2.002	3.217

Table 5-1: L'influence des paramètres (G, Ö) sur la configuration des régimes
d'écoulement sous-saturée.

Figure 5.1 : Variations des cotesZ_nb, ZFDB et Z₅ en fonction de flux pariétalck.

Figure 5.2 : Variations des cotesZ_nb , _ZFDB et Z₅ en fonction de vitesse massique

d'écoulement G.

5.2. Prédiction des rayons rD et rL :

Dans le cas des écoulements verticaux, la projection de bilan de forces selon x gouverne le phénomène de décollage des bulles de la paroi tandis que sa projection selon y permet de décrire le détachement des bulles de leur site actif de nucléation et le glissement de celles-ci sur la paroi.

La prédiction des rayons des bulles sont calculés Pour les conditions d'entrées suivantes :
vitesse massique d'écoulement G = 250 Kg/s.m², pression dans le canal P = 0.143 MPa,

température d'entrée Tin = 97 °C et un flux de chaleur pariétal ~~ = 500 ~w/n².

5.2.1. Représentation graphique du bilan des forces agissant sur la bulle de

vapeur :

Les résultats obtenus pour les rayons de détachement des bulles de leurs sites et de décollage de la paroi sont représentés sur les figures (5.3) (5.4) respectivement :

Fig 5.3 : solution graphique approchée de rayon de détachement de la bulle de vapeur par
application du bilan des forces projeté sur yy'

Figure 5.4 : solution graphique approchée de rayon de décollage de la bulle de vapeur par
application du bilan des forces projeté sur xx'

5.2.2. Variation des rayons Rd et RL :

Les rayons des bulles calculés par application du bilan de forces et pour différentes vitesses spécifiques d'écoulement sont donnés dans le tableau (5.2) et représentés sur la figure (5.5) :

G [Kg/S.m2]	RD [m]	RL [m]
100	0.0004023	0.0012551
200	0.0003171	0.0009318
300	0.0002264	0.0007168
400	0.0002053	0.0006557
500	0.0001972	0.0004699
600	0.0001891	0.0004082
700	0.0001812	0.0002338
800	0.0001735	0.0002211
900	0.0001658	0.0002165
1000	0.0001582	0.0002142
1100	0.0001508	0.0002128
1200	0.0001434	0.0002119
1300	0.0001360	0.0002113
1400	0.0001288	0.0002108
1500	0.0001216	0.0002105

Tableau 5.2: Prédiction des rayons de détachement et de décollage en fonction de la vitesse
spécifique de l'écoulement.

La variation des rayons de détachement et de décollage sont inversement proportionnel à la vitesse spécifique d'écoulement (figure 5.5) qui est logiquement acceptable de faite que le détachement des bulles de vapeur de la surface provoqué essentiellement par la force de trainé qui est proportionnelle à la vitesse d'écoulement (éq 3.24); de même pour le décollage qui est provoqué essentiellement par la force de portance qui est proportionnelle au carré de la vitesse d'écoulement (éq 3.25).

Figure 5-5: Allures de rayon de détachement et de décollage en fonction de G.

L'écart entre ces deux rayons est important dans la gamme des faibles vitesses mais

les deux rayons modelés lb et l sont rapprochés ( lb ~ l ) de plus en plus avec

l'augmentation de la vitesse.

5.3. Prédiction des temps de détachement ( t~), décollage ( t~) , glissement ( t~~) et la

longueur de glissement ( Lsi) :

Pour les mêmes conditions d'entrées précédentes, la prédiction de ces temps

ggr,al ^~t _lsi sont déduits par remplacement des rayons Nd ~~ N/ calculés (Table 5.2) dans

l'équation de Zuber (éq 3.32) et la longueur de glissement et calculée par la correlation de Maity (éq 3.49)

Temps G	Temps de Croissance tGR [s]	Temps de Décollage tL [s]	Temps de glissement tSL [s]	Longueur de glissement LSL[m]
100	0.27	0.84	0.57	0.122
200	0.27	0.68	0.41	0.124
300	0.26	0.56	0.30	0.125
400	0.25	0.45	0.20	0.138
500	0.25	0.38	0.13	0.149
600	0.24	0.35	0.11	0.173
800	0.23	0.31	0.08	0.197
1000	0.22	0.27	0.05	0.219
1200	0.21	0.23	0.02	0.244
1400	0.21	0.22	0.01	0.269
1500	0.20	0.21	0.01	0.295

Tableau5.3:temps de détachement, glissement, décollage et la longueur de glissement en
fonction de vitesse spécifique d'écoulement.

La figure (5.6) illustre qu'en augmentant la vitesse d'écoulement, le processus de détachement-décollage devient plus vite de faite que la bulle de vapeur ne dure pas longtemps sur sont site d'où une augmentation de la fréquence de nucléation.

Figure 5.6: Variation de temps de détachement, glissement et décollage des bulles de vapeu
en fonction de la vitesse spécifique de l'écoulement.

Figure 5-7 : Variation de la longueur de glissement en fonction de la vitesse spécifique
d'écoulement.

5.4. Prédiction de coefficient d'échange thermique :

Les résultats obtenus ci-dessous sont calculées pour les conditions d'entrées suivantes : P =0.13 Mpa, G = 1000 Kg/s.m², Tin = 80 °K.

L'eau entre avec un sous refroidissement Tsub = 7',t - _7'in= 387.5 - 353 = 33.5 °K

D'après les conditions précédentes, le canal comporte le régime d'ébullition local si le flux

imposé est supérieur à1'Pw0NB LI 111 131111 aM 2.

5.4.1. Prédiction des températures de paroi et de fluide et le coefficient d'échange thermique le long du canal :

a / - flux imposé faible : 'Pw 1L 111 1Kw ar² 1:

Pour les conditions précédentes (P =0.13 Mpa, G = 1000 Kg/s.m², Tin = 80 °K), le début du régime d'ébullition locale aura lieu à la cote Zn= 2.012m .Donc le canal de longueur L = 2m ne comporte pas le régime d'ébullition local (voir table 5.1).Le transfert de chaleur sera donc par convection forcée.

	Transfert de chaleur par convection force
Cote du canal [m]	Température De la paroi Tw [°K]		Température moyenne De fluide Tf [°K]		Coefficient de transfert chaleur h
0.00	361.2		353.0		HFC = 7306.935 [Kw/m2K]
0.10	361.4		353.3
0.20	361.5		353.5
0.30	361.7		353.7
0.40	361.9		353.9
0.50	362.1		354.1
0.60	362.3		354.3
0.70	362.5		354.5
0.80	362.7		354.7
0.90	362.9		354.9
1.00		363.1		355.1		HFC ? 7306.935 [Kw/m^2K]
1.10		363.3		355.3
1.20		363.5		355.5
1.30		363.7		355.7
1.40		363.9		355.9
1.50		364.1		356.1
1.60		364.3		356.3
1.70		364.5		356.5
1.80		364.7		356.7
1.90		364.8		356.9
2.00		365.0		357.1

Table 5.4 : Prédiction des températures de fluide et de la paroi chauffante avec absence
d'ébullition dans le canal.

Figure 5.9 : Evolution des températures de fluide et de la paroi chauffante en absence
d'ébullition dans le canal.

b /- flux imposé : cP~ > 150 Kw/n²:

Le canal comporte le régime d'ébullition locale (Voir figure 5.8)

Les résultats tabulés ci-après sont calculées pour les conditions d'entrés suivantes :

P =0.143 Mpa, G = 1000 Kg/s.m², Tin = 80 °K, ~w = 900 KW/fl²

L'eau entre avec un sous refroidissement Tsub = Tsat - T1~= 387.5 - 353 = 33.5 °K

	Zone I : Transfert de chaleur monophasique
Cote du canal [m]	Température De la paroi Tw [°K]		Température De fluide Tf [°K]		Coefficient de transfert chaleur h[Kw/m2K]		Pourcentage des différents flux du modèles de Yeoh. %
							Öfc		Ö		Ötc		Ötc[s1
0.00	377		353		8334.976		100 %		0 %		0 %		0 %
0.10	383		354.4		8297.347		100 %		0 %		0 %		0 %
0.20	387		355.7		8314.309		100 %		0 %		0 %		0 %
0.30	391		357		8343.480		100 %		0 %		0 %		0 %
Znb =0.358	Zone II : Transfert de chaleur diphasique
0.40	389		358.3		8953.275		81.24%		11.57%		2.76%		4.43%
0.50	389		359.6		9004.960		80.78%		11.88%		2.80%		4.54%
0.60	390		360.9		9167.107		79.34%		12.42%		3.07%		5.17%
0.70	391		362.2		9337.288		77.88%		12.94%		3.37%		5.81%
0.80	391		363.5		9404.894		75.81%		13.80%		3.74%		6.65%
0.90	392		364.7		9589.964		74.30%		14.28%		4.06%		7.36%
1.00	392		366.0		9783.715		72.78%		14.74%		4.40%		8.09%
1.10	393		367.3		9986.303		72.09%		15.13%		4.48%		8.30%
1.20	393		368.6		10081.764		70.54%		15.57%		4.84%		9.05%
1.30	394		369.9		10301.892		68.99%		15.98%		5.20%		9.83%
1.40	394		371.2		10531.656		68.20%		16.41%		^5.31%		10.08%
1.50	395		372.5		10653.359		67.43%		16.41%		5.31%		10.08%
1.60	395		373.7		10903.234		66.62%		16.80%		5.69%		10.88%
1.70	396		375.0		11045.859		65.77%		17.25%		5.81%		11.17%
1.80	396		376.3		11318.109		64.17%		17.63%		6.21%		11.99%
1.90		397		377.6		11601.804		62.59%		17.98%		6.60%		12.82%
2.00		397		378.9		11782.885		61.63%		18.46%		6.75%		13.16%

Table 5.5 : Prédiction des températures de fluide et de la paroi chauffante avec existence de
régime d'ébullition local dans le canal.

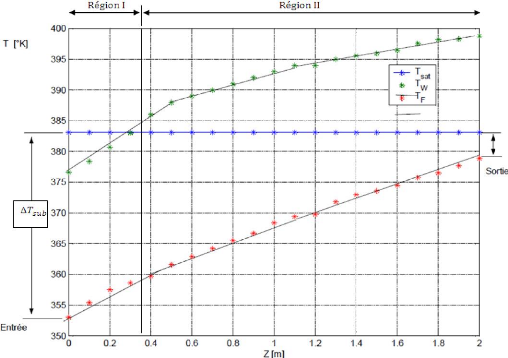
Figure 5.10 : Evolution des températures de fluide et de la paroi chauffante avec existence
de régime d'ébullition local dans le canal.

Le canal est alimenté en liquide très sous-saturée à l'entrée (LTSUb = 31.1 °C) et de

longueur suffisante afin de bien observer graphiquement (Voir Figure 5.10) la transition de régime monophasique liquide au régime d'ébullition local.

Pour les conditions d'entrée précédentes (G = 1000 Kg/s.m², _LTSUb =31.1 °C) , le début d'ébullition aura lieu à Z=0.358 m où la température de paroi vaut 389.0 °K.

En examinant l'évolution de la température de paroi le long du tube, la surchauffe de la paroi nécessaire pour initier l'ébullition nucléée est de ÄTSAT 5°C, l'eau quitte le canalavec un sous refroidissement de _LTSUb 5.1 °C.

Figure 5.11 : Evolution du coefficient d'échange _(hyeoh) le long du canal pour une vitesse
spécifique de 1000 Kg/S.m².

A partir de _1nb , l'écart des températures paroi-fluide diminue pour un flux de chaleur uniforme (figure 5.10) ce qui explique l'accroissement coefficient d'échange thermique dans la région d'ébullition locale (figure 5.11), ce qui prouve l'importance de l'ébullition en transfert thermique.

5.4.2. Distribution des différents flux du modèle de Yeoh et al:

Figure5.12 : Variation de contribution de quatre flux de modèle de Yeoh dans le canal.

Pour un flux uniforme, la contribution des flux dus à l'évaporation ( Ö_e, _Ö~~ ~~ Ö~~,~~) augmentent, par contre le flux de convection forcée (Ö_e) diminue (l'apparition de la vapeur devient de plus en plus forte dans les zone avancée de l'ébullition nucléée (Voir figure 5.12).

Conclusion

Conclusion

Pour mener à bien notre étude, il a fallu en premier lieu maitriser le langage de programmation FORTRAN.

Le modèle mécaniste présenté par Yeoh et al (2008, [10]).a été étudié en détail et une étude bibliographique sur les écoulements diphasiques (eau vapeur) à un seul constituant à été menée. Les différents modèles mécanistes et corrélations permettant de modéliser le transfert de chaleur sont présentés dans ce mémoire.

Le modèle de Yeoh possède l'avantage de prendre en compte la notion de glissement des bulles comme le modèle de Basu que nous avons d'ailleurs pu montrer lors de notre étude que son impact est non négligeable. En plus, il se base sur une modélisation plus simple comme celle de Kurul et Podowski qui permet de calculer la répartition de tous les flux de chaleur en une seule étape ; de plus, il s'appuie sur la résolution d'un bilan des forces qui nous permet d''evaluer les diamètres de détachement et de décollage en s'appuyant sur des considérations physiques. Par conséquent, cette approche est plus adaptable à la configuration des écoulements étudiés et possède donc un caractère plus «universel» que les corrélations empiriques de la littérature telles que celles utilisées par le modèle de Basu et al.. De plus, elle permet d'accéder à d'autres paramètres tels que le temps de croissance, le temps de décollage des bulles et la longueur de glissement des bulles.

Comme les autres modèles, le modèle de Yeoh est loin d'être «complets» physiquement, en revanche, il existe des phénomènes intervenants lors de la formation des bulles de vapeur qui ne sont pas pris en compte comme:

- La coalescence des bulles de vapeur sur la paroi.

- L'effet de la condensation au sommet de la bulle de faite que le liquide autour d'elle est sous-saturée.

En perspective, le programme de calcul basé sur le modèle de Yeoh réalisé ne dépend pas du canal, il est applicable à d'autres configuration géométriques (circulaire, rectangulaire, ...) que celle étudié dans ce mémoire (section annulaire). En plus, il est applicable à d'autre fluides à condition d'implémenter les tables de propriétés thermodynamique appropriées dans le programme.

Références:

[1] - Bowring, R.W. A new Mixed flow cluster dryout correlation (1977).

[2] - Chen, J. C. A correlation for boiling heat transfer to saturated fluids in convective flow'. Presented at 6th National Heat Transfer Conference, Boston (1963).

[3] - COLLIER, J. G. AND THOME, J. R. Convective boiling and condensation - Third edition. Oxford Science Publications (1994).

[4] - Collier, J. G. Convective boiling and condensation, 2nd Edition, McGrawHill Book Company (1981).

[5] - Collier, J.G. & Thome, J.R. Convective Boiling and Condensation, 3rd Edition, Oxford University Press, New York (1994).

[6] - Davis, E. J. & Anderson G. H. The incipience of nucleate boiling in forced convection flow (1966).

[7] - Dittus, F. W. and Boelter. Univ. Calif. (Berkeley) (1930).

[8] FERROUK .M : Contribution à l'étude de la crise d'ébullition à faible titre''Caléfaction'' (2009).

[9] - Forster, H. & K., Zuber, N. Growth of a vapor bubble in superheated liquid (1954).

[10] - G.H.Yeoh, `Fundamental consideration of wall heat partition of vertical subcooled boiling flows `(2008).

[11] - Gnielinski. Forced Convection in Ducts, Heat Exchange Design Handbook (1983).

[12] - Groeneveld, D. C. & Snoek, C. W. A comprehensive examination of heat transfer Correlation suitable for reactor safety analysis, in Multiphase Science and Technology (1986).

[13] - Incopera & De Witt. Fundamentals of heat and mass transfer, Edition 3 (1990).

[14] - JENS, W. H., AND LOTTES, P. A. Analysis of heat transfer burnout, pressure drop, and density data for high-pressure water. Tech. rep., Argonne National Laboratories (1974).

[15] - J.F.Sacadura, Initiation aux transferts thermiques, 6e tirage (2000).

[16] - L.Z Zeng, J.F. Klausner, D.M. Bernhard, R. Mei, A unified model for the prediction of bubble detachment diameter in boiling systems-II. Flow boiling, Int. J. Heat Mass Transfer (1976).

[17] - Martinelli, R. C. Heat transfer to Molten metal's (1947).

[18] - Michel Montout: `Contribution au développement d'une Approche Prédictive Locale de la crise d'ébullition', (2009).

[19] - Nukiyama S. `Maximum and minimum values of heat transmitted from metal to boiling water under atmospheric pressure (1934).

[20] - Plummer, D., N., `Post critical heat transfer to flowing liquid in a vertical tube' , Ph. D. thesis, Mass . Inst. Technol (1974).

[21] - Rousseau, J. C. Transferts de chaleur associés à l'ébullition ou à la condensation des corps purs sur des parois, dans Techniques de l'ingénieur (1995).

[22] - Stiener & al., A wall heat transfer model for subcooled boiling flow, International Journal of Heat and Mass Transfer (1988).

[23] - Steiner, D. & Taborek, J. Flow Boiling Heat Transfer in Vertical tubes Correlated by an Asymptotic Model' (1992).

[24] - Saha, P. & Zuber. Point of net vapour generation and vapour void fraction in subcooled boiling (1974).

[25] - Shah, M. M. Chart correlation for saturated boiling heat transfer : Equations and further study (1982).

[26] - Thom, J. R. S. et al. Boiling in subcooled water during flow up heated tubes or annular (1975).

[27] - W. M. Rohsenow, Heat transfer with evaporation, in : Heat transfer-A Symposium held at the university of Michigan (1965).

Annexe

Propriétés thermo-physiques de l'eau et de sa vapeur à l'état de saturation : Pour une pression de 0.1 Mp

Pf_sat = 372.8 (°K) ~ = 0.05899 (N/M)

rr = 0.10431E-02 (M3/KG) ~~ = 1.694023 (M3/KG)

lPf = 4.216 (KJ/KG MI P =I 2.0IM (KJ/KGMI

g

hf = 4IM.4I4 MIJ/KG =I 26I74.9I5IEEKJ/KG

g

K F = 0.678 (W/M K) ~~ = 0.0248 (W/M K)

pf = 0.2829E-03 (N S/M) ft_g = 0.12E-04 (N S/M)

CI

Pour une pression de 0.15 Mpa

CI

TSAT = 384.5 (°K) ~ = (N/M)

rr = 0.10527E-02 (M3/KG) ~~ = 1.159357 (M3/KG

IlL'Pf = 4.232 (KJ/KG MI P =I 2.128I (KJ/KGMI

g

hf = 467.08 (KJ/KG) h~ = 2693.11 (KJ/KG)

K F = 0.682 (W/M K) ~~= 0.0260 (W/M K)

of = 0.2514E-03 (N S/M) #_g = 0.13E-04 (N S/M)

Pour une pression de 0.2 Mpa

Pf_sat = 393.4 (°K) ~ = 0.05493 (N/M)

rr = 0.10605E-02 (M3/KG) Y_g = 0.885735 (M3/KG

lPf = 4.247 (KJ/KG K) r g = 2.175 (KJ/KG K)

hf = 504.68 (KJ/KG) h_g = 2706.24 (KJ/KG)

Yr = 0.684 (W/M K) ~~ = 0.0270 (W/M K)

k = 0.2316E-03 (N S/M) N = 0.13E-04 (N S/M)