Subventions cotonnières des pays développés et distorsions sur le marche mondial : une approche par le modèle vectoriel a correction d'erreur

REPUBLIQUE DU BENIN

*****

MINISTERE DE L'ENSEIGNEMENT SUPERIEUR ET DE LA FORMATION PROFESSIONNELLE (MESFP)

******

UNIVERSITE D'ABOMEY - CALAVI (UAC)

******

FACULTE DES SCIENCES ECONOMIQUES ET DE GESTION (FASEG)

MEMOIRE DE MAITRISE ES-SCIENCES ECONOMIQUES

******

******

OPTION : ECONOMIE

Année académique : 2004-2005

SUBVENTIONS COTONNIERES DES PAYS DEVELOPPES ET DISTORSIONS SUR LE MARCHE MONDIAL : UNE APPROCHE PAR LE MODELE VECTORIEL A CORRECTION D'ERREUR

THEME :

tttttt

Réalisé et soutenu par :

ALAVO Odilon Modeste & AVOUTOU Mathieu

Sous la Direction de :

Fulbert GERO AMOUSSOUGA

Professeur

Juin 2006

LA FACULTE N'ENTEND DONNER AUCUNE APPROBATION NI IMPROBATION AUX OPINIONS EMISES DANS LES MEMOIRES.

CES OPINIONS DOIVENT ETRE CONSIDEREES COMME PROPRES À LEURS AUTEURS.

DEDICACES

Ø A mon père HENRI ALAVO

Sincères gratitudes pour avoir cru en moi et fait de moi ta raison d'espérer. Que tes prières et ton soutien ne soient pas vains.

Ø A ma mère JOSEPHINE ALAVO née ATCHEKPE, grâce à l'éducation rigoureuse que tu m'a donnée, j'ai pu entreprendre de belles choses. J'espère que tu trouveras en ce mémoire le fruit des efforts et sacrifices que tu as su déployer pour moi.

Ø A mes oncles et tantes : ATCHEKPE Alphonse, ATCHEKPE Antoine, SOSSOU Bernadette, SOSSOU Nestor, SOSSOU Janvier, SOSSOU Marcelin.

Ø A tous mes frères et soeurs, cousins et cousines, neveux, nièces, particulièrement à Léopold ALLAVO, vous m'avez toujours soutenu, que ce qui a commencé se perpétue.

Ø A Marie Ange DIKEBIE sur mon chemin parsemé d'embûches, tu était là pour m'aider à me relever quand je tombais. Sincères gratitudes à toi.

Modeste Odilon ALAVO

· A ma mère Aminatou BEHANZIN qui s'est sacrifiée entièrement pour sauver ma vie et me donner les mêmes chances que les autres enfants.

Que Dieu, le tout Puissant me permette de te voir longtemps.

· A mon père Paul S. AVOUTOU

Ton souci permanent de voir tous tes enfants réussir m'a été d'un grand secours. Que Dieu te garde longtemps près de nous.

· A mes grands parents Tessilimi BEHANZIN et Bintou MANDJOGBE qui m'ont accordé tout leur amour depuis ma naissance jusque là. Longue vie à vous.

· A tous mes oncles et tantes, particulièrement Wassiatou et Salimatou BEHANZIN pour m'avoir secouru quand ma mère et moi étions en difficulté. Mille reconnaissances.

· A ma belle mère HOUNGBO Louise ; A tous mes frères et soeurs, cousins et cousines, neveux et nièces, singulièrement Armandine AVOUTOU pour tout ce que vous avez fait pour moi.

Amour fraternel.

Mathieu AVOUTOU

REMERCIEMENTS

Ce travail a été réalisé grâce aux multiples conseils et collaborations de certaines personnes à qui nous tenons à adresser nos sincères remerciements.

v Au professeur Fulbert GERO AMOUSSOUGA. Vous avez accepté la direction de ce mémoire malgré vos multiples occupations. Recevez ici nos sincères gratitudes.

v A Monsieur Fousséini Traoré du Centre d'Etude et de Recherches sur le Développement International (CERDI). Vos conseils et explications nous ont permis d'améliorer ce travail et d'avoir une maîtrise de nombreux concepts. Vous avez toute notre reconnaissance.

v A Monsieur Augustin DADE, Assistant du Secrétaire Technique de la CNDLP / Ministère des Finances et de l'Economie, enseignant à la FASEG vous n'avez ménagé aucun effort pour nous aider dans les estimations malgré votre emploi du temps assez chargé. Toute notre reconnaissance.

v Aux professeurs du Département d'Economie vous nous avez donné la chose la plus précieuse qu'est la connaissance. Sincères gratitudes à vous.

Nous adressons également nos vifs et sincères remerciements à :

- Mr BEHANZIN T. COWIOU pour avoir mis son outil informatique à notre disposition.

- Messieurs, ANATO Gilbert, Hermann AVAHOUIN pour nous avoir hautement aidés dans la saisie du document. Qu'ils acceptent ici nos sincères remerciements.

v A tous ceux qui nous ont aidé d'une manière ou d'une autre à la réalisation de cette oeuvre. Merci pour tout.

Modeste ALAVO et Mathieu AVOUTOU.

LISTE DES SIGLES ET ABREVIATIONS

ADF	Augmented Dickey Fuller
AOC	Afrique de l'Ouest et du Centre
ATPSM	Agricultural Trade Policy Simulation Model
ATV	Accord sur les Textiles et les Vêtements
CAF	Coût-Assurance-Frêt
CCIC	Comité Consultatif International du Coton
CE	Communauté Européenne
CMA	Conférence des Ministres de l'Agriculture
CNUCED	Conférence des Nations Unis sur le commerce et le développement
CV	Critical Value
DF	Dickey Fuller
FAO	Food and Agriculture Organization
GATT	General Agreement on Tariffs and Trade
GTAP	Global Trade Analysis Project
ICAC	International Cotton Advisory Committee
INRA	Institut National de la Recherche Agronomique
MCO	Moindres Carrés Ordinaires
MGS	Mesure Globale de Soutien
MVCE	Modèle Vectoriel à Correction d'erreur
NEPAD	New Partnership for Africa's Development
OMC	Organisation Mondial du Commerce
PAC	Politique Agricole Commune
PFC	Production Flexibility Contracts
PIB	Produit Intérieur Bruit
PMA	Pays Moins Avancé
SMC	Subventions et les Mesures Compensatoires
UE	Union Européenne
UEMOA	Union Economique et Monétaire Ouest Africaine
USA	United States of América
USDA	United States Department of Agriculture
VA	Valeur Ajoutée
VAR	Vecteurs Auto Régressifs
WCA	West and Central Africa

LISTE DES TABLEAUX

TABLEAU 1 : RESUME DES RESULTATS ISSUS D'ETUDES

ANTERIEURES...............................................................25

TABLEAU 2 : RESULTATS DES TESTS DE STATIONNARITE

EN NIVEAU....................................................................35

TABLEAU 3 : RESULTATS DES TESTS DE STATIONNARITE EN

DIFFERENCE PREMIERE..................................................36

TABLEAU 4 : RESULTATS DU TEST ADF SUR LE RESIDU DE LA

RELATION DE LT............................................................37

TABLEAU 5 : RESULTATS DE LA RECHERCHE DU NOMBRE OPTIMAL DE

DECALAGES....................................................................37

TABLEAU 6 : RESULTATS DU TEST DE LA TRACE....................................35

TABLEAU 7 : ESTIMATION DU MVCE................................................... .41

TABLEAU 8 : DECOMPOSITION DE LA VARIANCE....................................45LISTE DES FIGURES

FIGURE 1 : DERIVATION DE LA COURBE DE DEMANDE

D'IMPORTATION DE NATION............................................15

FIGURE 2 : DERIVATION DE LA COURBE D'OFFRE

D'EXPORTATION D'ETRANGER.......................................16

FIGURE 3 : EQUILIBRE MONDIAL......................................................16

FIGURE 4 : EFFETS D'UN DROIT DE DOUANE.......................................17

FIGURE 5 : EFFETS D'UN SUBSIDE A L'EXPORTATION ........................19

FIGURE 6 : EFFETS DES SUBVENTIONS DES PAYS

DEVELOPPES SUR LE PRIX MONDIAL

DU COTON ET LES QUANTITES PRODUITES ........................ .20

FIGURE 7 : EVOLUTION DE PRC, NSUB, PRO, CONS, PRP

(EN LOGARITHME)..............................................................38

FIGURE 8 : REPONSE DU PRIX DU COTON A UN CHOC

SUR LES SUBVENTIONS........................................................43

FIGURE 9 : REPONSE DE LA CONSOMMATION MONDIALE

A UN CHOC SUR LES SUBVENTIONS.......................................44

FIGURE 10 : REPONSE DE LA PRODUCTION MONDIALE A UN

CHOC SUR LES SUBVENTONS............................................44

RESUME

Les subventions agricoles des pays développés sont fréquemment désignées comme responsables des distorsions observées sur le marché mondial des produits agricoles- principalement de la baisse des prix des produits en question-. Le cas du coton a donné lieu à l'un des plus vifs débats notamment à l'Organisation Mondiale du Commerce (OMC). Ce travail essaie d'approcher cette question à travers un Modèle Vectoriel à Correction d'Erreur (MVCE).L'analyse par les fonctions de réponses impulsionnelles et par la décomposition de la variance a quant à elle confirmé les résultats du MVCE.

Les principaux résultats sont alors que les subventions ne créent pas de distorsions en terme de prix et de consommation, sauf en terme de production.

Afin d'apprécier parfaitement l'impact des politiques de subventions ; les études futures devront prendre en compte les données sur les subventions chinoises puis incorporer dans leur modèle toutes formes de mesures incitatives à la production et à l'exportation tout en séparant subventions à la production d'un côté et subventions à l'exportation de l'autre.

SSSSSOMMAIRESSOMMAIRE

SOMMAIRE

Introduction Générale

Chapitre I : CADRE THEORIQUE ET METHODOLOGIQUE DE L'ETUDE

Section 1 : De la Problématique à la revue de littérature

Section 2 : Méthodologie de la recherche

Chapitre II : RESULTATS DE L'ETUDE ET ENJEUX

Section 1 : Etude de la cointégration et estimation du MVCE

Section 2 : Confirmation des résultats, interprétations, limites et suggestions

Conclusion Générale

Bibliographie

Annexes

Table des matières

INTRODUCTION GENERALE

Le 30 Avril 2003, quatre pays d'Afrique sub-saharienne - le Bénin, le Burkina Faso, le Mali et le Tchad- ont déposé au comité de l'agriculture de l'OMC un document intitulé « Réduction de la Pauvreté : initiative sectorielle en faveur du coton ». Faisant suite à la grave crise traversée par leur secteur cotonnier en 2001 - 2002, il s'agit d'une proposition visant à supprimer progressivement les subventions des pays développés qui provoquent des distorsions sur le marché mondial. C'est à Cancùn durant les travaux de la 5^ème réunion ministérielle de l'OMC que la proposition a été examinée. Elle est originale pour plusieurs raisons : d'abord parce qu'il s'agit d'une initiative de quatre petits pays africains qui introduisent dans l'agenda de la négociation commerciale multilatérale une discussion sur un problème urgent les concernant directement. Ensuite parce qu'ils ne demandent pas dans leur initiative une aide au développement supplémentaire ou un traitement spécial et différencié mais tout simplement l'application des règles de base du système commercial international avec la suppression des subventions qui provoquent des distorsions sur les prix.

Sur le plan des principes, il est difficile pour les principaux pays pourvoyeurs de subventions, essentiellement les Etats-Unis (USA) et l'Union européenne (UE), de contester la légitimité de la démarche des pays africains, a fortiori lorsqu'il s'agit d'un différend aussi symbolique opposant quatre pays moins avancés (PMA) parmi les plus pauvres du monde aux deux superpuissances commerciales.

Pourtant, c'est une fin de non recevoir qui a été donnée à l'initiative sectorielle en faveur du coton à Cancùn et le dossier a sans doute participé à l'échec global de la Ministérielle.

Alors que les membres de l'OMC s'efforçaient à relancer la négociation commerciale internationale (conférence de décembre 2005 par exemple), on peut se demander qu'elles sont les chances de l'initiative sectorielle sur le coton d'aboutir.

La faible et récente remontée des cours mondiaux a quelque peu affaibli la position des pays africains qui justifient leur proposition par l'urgence de la situation et l'impact sur la pauvreté de la distorsion des prix. Pour autant cette embellie conjoncturelle n'enlève rien à l'existence de dispositifs de soutien qui lors d'une nouvelle crise aboutiraient aux mêmes conséquences qu'en 2001-2002 à savoir des subventions record, une surproduction et un effondrement des prix pénalisant les producteurs africains (qui exportent l'essentiel de leur production et n'ont pas les mêmes soutiens en cas de chute des prix).

Pour les pays de l'Initiative sectorielle la question des subventions au coton est capitale dans la mesure où le coton représente environ 30 à 40% de leurs revenus à l'exportation et sa contribution au PIB de ces quatre économies va de 5 à 10%. Le problème est d'autant plus important que les cours du coton aujourd'hui sont très faibles.

La réalité ainsi décrite justifie l'intérêt pour le dossier sur les subventions et la nécessité de réfléchir sur les effets réels de ces subventions sur le marché mondial. C'est donc dans ce registre que s'inscrit la présente étude.

La question de l'impact des subventions au coton a déjà donné lieu a de nombreuses études que ce soit le fait d'organisations non gouvernementales (OXFAM, 2002), d'institutions internationales - comme la FAO - (Poonyth et al, 2004) ou de chercheurs indépendants (Shepherd, 2004). Cependant, aucune de ces études n'a réellement encore pris en compte les subventions européennes. Les outils d'analyse mobilisés sont essentiellement des modèles d'équilibre général calculable, les modèles d'équilibre partiel et l'économétrie avec des résultats pour le moins contradictoires. Cette étude renoue avec l'approche économétrique, tout en tenant compte des subventions européennes, mais cette fois ci en utilisant une technique nouvelle dans ce domaine de recherche : la cointégration à la Johansen et le modèle vectoriel à correction d'erreur (MVCE).

La présente étude compte trois chapitres ; le premier concerne le cadre théorique et présente les différentes étapes de la construction du modèle ; le second s'attarde sur le débat autour des subventions et la classification des subventions par boîte en soulignant les arguments ayant motivés le choix des pays subventionneurs ; le troisième chapitre quant à lui présente, analyse les résultats des estimations et aborde pour finir la rubrique des limites et suggestions.

CHAPITRE I : CADRE T

CHAPITRE I : CADRE THEORIQUE ET METHODOLOGIQUE DE L'ETUDE

CHEORIQUE DE L'ETUDE

Ce premier chapitre comprend deux sections. La première section présente les fondements sur lesquels repose la présente étude à savoir : la problématique, les objectifs, les hypothèses de recherche et la revue de littérature. La seconde section quant à elle présente le modèle retenu et définit la démarche méthodologique qu'on entend suivre pour atteindre nos objectifs.

Section 1 : De la Problématique à la revue de littérature

PARAGRAPHE 1 : Problématique, objectifs et hypothèses de

recherche

A. Problématique et intérêt de l'étude

1. Problématique

L'effet des subventions cotonnières dans le monde en général et des pays développés en particulier sur les marchés mondiaux représente une question centrale.

En effet, le sujet semble récurrent dans les négociations commerciales Nord-Sud, notamment celles engagées au sein de l'Organisation Mondiale du Commerce (OMC) (Conférence de Doha, Conférence de Cancùn). Sur un plan plutôt juridique, les experts de l'OMC viennent de donner récemment raison au Brésil suite à une plainte déposée par ce pays contre les Etats- Unis, premier pays subventionneur du monde. Parler des subventions avec une telle acuité aujourd'hui nous amène à croire qu'il s'agit d'un phénomène nouveau. Pourtant, ce n'est pas le cas.

En effet, en s'inspirant des fondements théoriques de l'analyse économique, on se rend compte que les subventions n'ont pas toujours fait l'objet d'une telle attention, car de par le monde, en tant que politique commerciale agricole, elles ont été utilisées pour stabiliser dans certains cas les revenus des agriculteurs et dans d'autres relancer la production. C'est le cas par exemple de la communauté  Européenne (CE) en 1970, qui dans le cadre de la politique Agricole Commune (PAC) garantissait des prix élevés aux agriculteurs européens en rachetant les produits agricoles chaque fois que les prix tombaient en dessous d'un certain seuil d'intervention. Cette politique a eu pour conséquence la stabilisation des revenus des agriculteurs et la stimulation de la production, en l'occurrence celle du blé où des stocks furent constitués (12 millions de tonne de blé)^1(*) afin de maintenir stable les prix.

Aujourd'hui, le problème est tout autre.Les pays riches à savoir les Etats-Unis et l'Union Européenne (notamment la Grèce et l'Espagne), deux superpuissances subventionnent le coton qui fait l'objet de transactions internationales et qui constitue une culture d'exportation, sinon la principale culture d'exportation de certains pays de l'Afrique de l'Ouest et du Centre (AOC), faisant partie des moins avancés au monde (BENIN, BURKINA FASO, MALI, etc....). Ces pays ont un avantage comparatif dans la production de coton, avec des coûts, qui environnent 30 cents par livre contre le double aux Etats-Unis^2(*).

Par contre, les subventions ont pour vocation de réduire les coûts de production des producteurs des pays aisés et par ricochet de fausser les calculs de l'avantage commercial dont profitaient les nombreux producteurs africains. Si l'on suppose qu'a coûts de production bas, prix bas, une question s'impose : Quel est le lien entre les politiques commerciales agricoles des pays développés et les cours mondiaux du coton ?

Les subventions du coton qui étaient pratiquement négligeables pendant la campagne 95/96 ont atteint un niveau record en 2001-2002, soit 5,8 milliards de dollar dont environ 4,3 milliards pour les Etats Unis et l'UE^3(*). Aussi les cours du coton en l'espace de cinq ans (1997-2002) ont-ils diminué de 50% pour atteindre 35 cents la livre lors de la campagne 2001-2002^3(*). C'est pendant cette campagne que les cours du coton se sont effondrés à leur niveau le plus bas en termes réels, depuis l'invention de l'égreneuse en 1793^3(*).

Cette simultanéité ne signifie pas forcément une relation de cause à effet, si ce n'est une forte présomption d'une hausse de la production (voire une surproduction) et d'une distorsion des prix liée aux subventions. Au regard de cela, les pays de l'AOC sont engagés à porter loin le différend commercial entre eux et les pays développés car selon eux, les subventions au coton sont la source de leur malheur et créent nécessairement des distorsions - raison à les éliminer-. Au nom des distorsions évoquées on peut citer :

- des distorsions en terme de prix;

- des distorsions en terme de production et de consommation.

Pour les pays producteurs de coton les distorsions en terme de prix évoquent principalement l'effondrement des prix du coton. Cette chute de prix est généralement associée à un manque à gagner pour les producteurs^4(*) (pertes en recettes d'exportation) et hypothèque les chances de sortir de pauvreté de beaucoup de ménages ruraux^5(*). En outre, les producteurs africains espèrent que même si la distorsion en terme de prix n'était pas avérée, au moins en terme de production ou de consommation cela pourrait se vérifier afin de trouver des motifs crédibles au débat initié à l'OMC.

Le présent mémoire tente d'apporter des éléments de réponse aux questions suivantes :

-L'accroissement des subventions des pays riches est -il à l'origine de la chute des prix tel que supposé par les producteurs de l' AOC ?

-Cet accroissement des subventions est-il lié à une perte en terme de recettes d'exportation pour les producteurs de coton de l'AOC et du Bénin en particulier ?

-Les subventions des pays riches ont -elles une réelle influence sur les volumes produits et consommés de coton dans le monde ?

Les éléments de réponse à ces questions font l'objet des paragraphes suivants du présent mémoire dont le but est d'analyser les distorsions éventuelles provoquées par les subventions cotonnières des pays développés.

2. Intérêt de l'étude

Les interrogations ci- dessus énumérées constituent les préoccupations autour desquelles est bâtie la présente étude et permettront de valider ou non sur le plan empirique, les différentes constructions théoriques quant à l'analyse de l'impact des subventions des pays développés sur le marché mondial du coton, et c'est là un intérêt de l'étude.

Par ailleurs, l'étude présente l'intérêt de conforter ou non la position du BENIN, du BURKINA FASO, du MALI et du TCHAD qui dans un document intitulé : « Réduction de la pauvreté :Initiative sectorielle en faveur du coton » ont fait savoir que le premier pas, sinon l'action salutaire dans la résolution de la crise de leur filière serait la suppression sans condition de tous les soutiens à la production en trois(03) ans (2004-2006) et ensuite les compensations financières tant que les subventions ne sont pas éliminées.

B. Objectifs et hypothèses de recherche

1. Objectifs

Objectif général

Le présent travail vise à analyser les distorsions sur le marché provoquées par les subventions cotonnières des pays développés.

Objectifs spécifiques

Il s'agira précisément dans le cadre de cette étude de :

- Analyser l'effet des subventions sur le prix mondial du coton;

- Analyser le poids des subventions sur les volumes produits et consommés de coton dans le monde;

- Mesurer l'effet des subventions des pays riches en 2001-2002^6(*) sur les recettes d'exportations des producteurs de l'AOC et du Bénin en particulier.

2. Hypothèses de recherche

H1- L'élimination des subventions entraîne une élévation du prix mondial du coton.

H2- La suppression des subventions réduit la production et la consommation mondiale du coton.

H3- L'existence des subventions des pays développés en 2001-2002 a contribué à la perte de recettes d'exportation pour les producteurs africains de coton.

PARAGRAPHE 2 : Revue de littérature

Ce paragraphe débute avec des réflexions sur le problème de la réduction des subventions et nous renseigne sur la classification par boîte des subventions. Ensuite, nous abordons les développements théoriques et empiriques de l'impact des subventions sur le marché mondial.

A. Problématique de la réduction des subventions et

Catégorisation des subventions

1. Problématique de la réduction des subventions

Les négociateurs du Gatt^7(*) (et de l'OMC qui lui a succédé) avaient pensé que le problème du coton pourrait être réglé par l'accord sur les textiles et vêtements (ATV) qui doit éliminer les quotas à l'importation (janvier 2005). A l'issue de l'Uruguay Round^8(*), une garantie supplémentaire a été instaurée en limitant les soutiens à l'agriculture définis par la « Mesure Globale de Soutien » (MGS) ; Mais, comme cette mesure couvre les soutiens accordés à l'ensemble des produits agricoles, elle permet aux gouvernements de maintenir leurs soutiens aux produits considérés comme politiquement les plus sensibles. Un pays peut donc respecter ses engagements auprès de l'OMC en maintenant son soutien aux producteurs de coton (voire même en l'augmentant) si cette action est compensée par une diminution des subventions pour d'autres produits politiquement moins sensibles. Le calcul du MGS n'est pas simple. Il faut tout d'abord déterminer qu'il s'agisse d'une subvention comme définie par l'accord sur les subventions et les mesures compensatoires (SMC). Il faut ensuite classer les subventions en fonction de leurs « effets de distorsions des échanges » en les répartissant entre les boîtes bleue, verte et orange. Ce classement par boîte est issu d'un compromis. D'un côté, il était reconnu que les gouvernements avaient des obligations envers leurs agriculteurs et qu'ils devaient veiller à la conservation de l'environnement. De l'autre, il était désirable que ces obligations puissent être remplies sans créer de distorsions, sur le marché mondial qui causeraient un préjudice grave à des tierces parties.

Les mesures allant dans la boîte bleue ont été définies dans l'accord MGS. Ce sont par exemple, les paiements aux planteurs visant à réduire leur production en fonction de surfaces prédéterminées. Mais le problème clé a été la répartition entre boîtes verte et orange, en particulier en ce qui concerne les subventions accordées par les Etats-Unis à leurs producteurs de coton. Comme les subventions éligibles à la boîte verte ne doivent créer que des distorsions minimales, elles ne sont pas plafonnées. Par contre, les subventions créant des distorsions significatives vont dans la boîte orange et ce sont les seules prises en considération dans le MGS qui est plafonné. La logique ayant conduit à établir une distinction entre boîtes verte et orange s'est malheureusement trouvée affaiblie par la clause « de minimis ». Cette dernière permet en effet de classer dans la boîte verte une subvention qui, de par sa nature, aurait du aller dans la boîte orange, pour autant que la dite subvention soit inférieure à un certain montant. Nous verrons par la suite, que cette clause fût utilisée à profit par les Etats-Unis. Il faut savoir que l'innovation notable de la loi agricole américaine de 1996 fût l'institution de paiements découplés effectués sur la base de « production flexibility contracts, (PFC) » .L'exploitant qui avait produit une Quantité donnée de coton (Q) lors de la période de référence (antérieure à 1996) pouvait ainsi recevoir en 1996 et au cours des cinq années suivantes un paiement dont le montant dépendait seulement de la quantité prédéterminée Q. Le paiement était découplé car son montant ne dépendait pas de la quantité de coton produite en l'année courante. L'exploitant était assuré de recevoir son chèque même s'il ne plantait pas de coton cette année là. Comme ces paiements étaient découplés, ils étaient éligibles à la boîte verte. Une subvention liée à un désastre naturel était également éligible à la boîte verte. Mais, si une subvention formellement accordée au titre d'un désastre naturel l'était en fait, afin de compenser les producteurs pour la chute des cours mondiaux, elle devrait aller dans la boîte orange.

Pourtant, en suivant l'accord conclu à l'issue de l'Uruguay Round, les Etats-Unis devaient réduire les subventions de la boîte orange de 20% par rapport à 1986-1988, ce qui établissait une limite annuelle de 19,1 milliards de dollar pour 2000-2002. On est, néanmoins, en droit de croire que cette limite sera respectée dans la lettre, sinon dans l'esprit. Elle le sera grâce à un transfert massif de la boîte orange à la boîte verte.

C'est ainsi que selon deux experts américains, le coût annuel des programmes éligibles à la boîte verte serait passé de 26 milliards de dollars de 1986-1988 à 50 milliards de dollars dix ans plus tard^9(*). Selon ses mêmes experts, les subventions de la boîte orange auraient augmenté de 44% en 1999 et 2000 sans le recours à la clause « de minimis ». Force est de reconnaître alors qu'en dépit de son appellation, cette clause à donc eu des conséquences majeures. Par ailleurs la loi agricole de 2002 modifie la nature de plusieurs types de subventions. D'une part, elle introduit des mesures anticycliques qui paraissent bien relever de la boîte orange. D'autre part, elle permet aux producteurs de remplacer l'ancienne période de référence par la période de 1998-2001 s'ils considèrent qu'ils obtiendront ainsi un contrat de flexibilité (PFC) plus avantageux. Ainsi le planteur qui avait augmenté sa production de coton au cours des dernières années pourra bénéficier au titre du PFC de paiements plus importants que celui qui avait réduit sa production. Certains experts considèrent que le choix d'une nouvelle période de référence aurait pour effet de rompre le découplage invoqué pour le PFC et que les paiements effectués sous ce titre devraient être classés dans la boîte orange à partir de 2002/2003.

2. catégorisation des subventions

Classification par boîte des subventions

La boîte verte 

Les aides autorisées car«découplées». Elle regroupe des aides dont l'effet sur la production ou sur des distorsions de concurrence sur les échanges est nul ou très faible ; il n'y a pas d'obligation de réduction si ces aides sont découplées de l'acte productif ou/ et soumises à des conditions strictes ou/et des aides à caractère général et collectif ou/et des aides aux producteurs à caractère social ou environnemental. Force est de reconnaître que les critères de classement sont assez sévères, deux conditions fondamentales figurent au point 1 de l'annexe II de l'accord agricole^10(*) : Pas de soutien aux prix et financement par les contribuables et pas de transferts aux consommateurs. Il faut en plus que l'aide s'inscrive dans un des 12 points définis par l'annexe qui autorisent ces aides ; si c'est un programme de service public, il s'agit de services tels que recherche, formation, infrastructures, stocks de sécurité et aide alimentaire interne ; il s'agit de versements aux producteurs, c'est soit un soutien découplé au revenu avec des critères d'attribution bien définis au cours d'une période, avec un montant indépendant du type ou volume de production, sans obligation de production ; indépendante du prix des facteurs de production; soit un programme de garantie de revenu, d'assurance récolte ou d'ajustement des structures (cessation d'activité, retrait de ressources productives, aides aux investissements) soit des programmes d'aides aux régions défavorisées et de protection de l'environnement.

La boîte bleue 

Les aides transitoires associées à un contrôle de l'offre. Base de l'accord UE/USA de 1992, elle a été créée pour abriter les aides directes compensatoires instituées par la reforme de la PAC (et les deficiency payments nord- américains d'avant 1996). Ces aides doivent être associées à un programme de limitation de la production ; fondées sur la superficie, le rendement ou le nombre de têtes, elles sont peu découplées aux produits mais du fait de la fameuse clause de paix entre l'UE et les Etats-Unis, elles échappent à une réduction et à une action contentieuse tant que la somme totale de toutes les boîtes de soutien reste inférieure au montant de 1992 et qu'elles ne provoquent pas de dommages chez un partenaire.

La boîte orange 

Les aides interdites soumises à réduction, cette boîte concerne toutes les autres aides et donc en particulier toutes les interventions sur les marchés et les autres restrictions ou subventions aux exportations. Il existe des clauses de minimum toléré : ne sont pas astreintes à réduction des aides à un produit représentant moins de 5% de la valeur de la production ou des aides générales de moins de 5% de la valeur totale de la production agricole.

Source : tirée du site de l'INRA (France) et complétée par nos soins. Disponible sur le site : www.inra.fr

B. Approche théorique et empirique de l'impact des subventions sur le marché mondial

Pour bénéficier des éclairages de la flopée de travaux effectués sur ce sujet, un aperçu critique tant des principales réflexions théoriques que des analyses et études empiriques sur l'impact des subventions sur le marché mondial est présenté.

Cette synthèse des diverses analyses sur les effets des subventions et leur estimation n'est sans doute ni exhaustive, ni suffisante. Elle a en revanche la préoccupation majeure de présenter sous un angle critique les grands axes de la multitude des travaux sur le sujet.

1. Approche théorique de l'impact des

Subventions

L'architecture théorique sur les subventions a été ébauchée par Krugman P. et M. Obstfeld (2001). Dans leur démarche, ils ont fait ressortir l'effet des droits de douane sur les prix qui n'est rien d'autre que l'effet inverse de celui des subventions sur les prix. Afin de mieux appréhender l'impact des subventions sur le marché mondial, une attention sera consacrée à celui des droits de douane. Dans la séquence consacrée aux droits de douane nous montrerons comment s'obtiennent les courbes de demande d'importation et d'offre d'exportation sans omettre bien évidemment de montrer les effets du droit de douane.

Supposons qu'il y a deux pays, Nation et Etranger, tous deux consommant et produisant du «coton » qui peut être transporté sans coût entre les pays. Dans chaque pays, le « coton » constitue une industrie compétitive dans laquelle les courbes d'offre et de demande sont fonction du prix du marché. Comme il est normal, l'offre et la demande dans Nation dépendront du prix exprimé en termes de la monnaie de Nation ; l'offre et la demande dans Etranger dépendront du prix exprimé en termes de la monnaie de Etranger. Nous supposons aussi que le taux de change entre les monnaies n'est pas affecté par les mesures de politique commerciale quelle qu'en soit la nature. Nous pouvons donc exprimer les prix sur les deux marchés en termes de la monnaie de Nation.

Le commerce se développera sur pareil marché si les prix avant l'échange sont différents. Supposons qu'en l'absence d'échange, le prix du « coton » soit plus élevé dans Nation, que dans Etranger. Laissons maintenant les pays procéder au commerce international :

Comme le prix du « coton » dans Nation excède le prix dans Etranger, les vendeurs se mettront à expédier du « coton » d'Etranger à Nation. L'exportation du « coton » en augmente le prix dans Etranger et en abaisse le prix dans Nation jusqu'au moment où la différence de prix est éliminée.

Pour déterminer le prix mondial et les quantités échangées, il est commode de définir deux nouvelles courbes : la courbe de demande d'importation pour Nation et la courbe d'offre d'exportation pour Etranger.



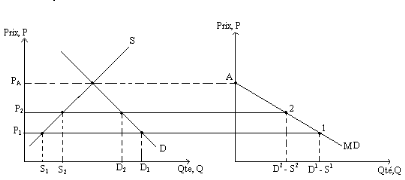
Figure 1:Dérivation de la courbe de demande d'importation de Nation.

Source : Economie internationale, Paul R. Krugman et Maurice Obstfeld, 3^éme édition

La courbe de demande d'importation est descendante car la quantité d'importation demandée diminue au fur à mesure que le prix s'accroît



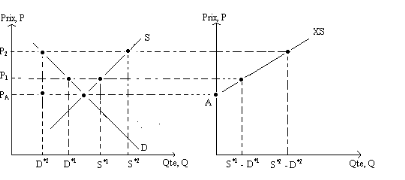
Figure 2: Dérivation de la courbe d'offre d'exportation d'Etranger

Source : Economie internationale, Paul R. Krugman et Maurice Obstfeld, 3^ème édition

Cette courbe est ascendante car l'offre de biens disponibles pour l'exportation s'accroît au fur et à mesure que le prix monte. L'équilibre mondial se réalise lorsque la demande d'importation de Nation est égale à l'offre d'exportation de Etranger



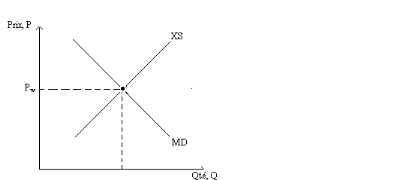
Figure 3: Equilibre mondial

Source : Economie internationale, Paul R. Krugman et Maurice Obstfeld, 3^ème édition

P_w est le prix d'équilibre, celui pour lequel la demande d'importation est égale à l'offre d'exportation d'étranger.

En ce qui concerne l'effet du droit de douane,(03) graphiques sont mis en relief afin d'illustrer ce phénomène



Figure 4: Effets d'un droit de douane

Source : Economie internationale, Paul R. Krugman et Maurice Obstfeld, 3^ème édition

Du point de vue de celui qui livre les biens, le droit de douane ressemble tout à fait à un coût de transport. Si Nation impose une taxe de 2$ sur tout boisseau de « coton » importé, les vendeurs se refuseront à y livrer le « coton » à moins que la différence de prix entre les deux marchés soit au moins de 2$.

La figure 4 illustre les effets d'un tarif spécifique de t$ par unité de « coton » (t dans la figure). En l'absence de droit de douane, le prix du « coton » serait égal à P_w à la fois dans Nation et dans Etranger (1 dans le graphique central, qui représente le marché mondial). Avec le droit de douane en place, cependant, les vendeurs ne voudront pas expédier du « coton » d'Etranger dans Nation à moins que le prix dans Nation n'excède le prix dans Etranger d'au moins t$. Si aucune quantité de « coton » n'est transportée, il y aura une demande excédentaire de « coton » dans Nation et une offre excédentaire dans Etranger. Par conséquent, le prix dans Nation augmente et le prix dans Etranger diminue jusqu'à ce que la différence de prix soit t$.

Le droit de douane augmente le prix dans Nation à P_T et diminue le prix dans Etranger à P_T^* = P_T - t. Les producteurs de Nation produisent du « coton » à un prix plus élevé, tandis que les consommateurs en demandent moins : de la sorte, une quantité plus faible d'importation est demandée dans Nation (mouvement de 1 à 2 sur la droite MD). Dans Etranger, le prix plus bas conduit à une réduction de l'offre et à un accroissement de la demande : de la sorte, il en résulte une offre plus faible d'exportation (mouvement de 1 à 3 sur la droite XS). Ainsi le volume de « coton » échangé décline de Q_w, le volume dans un régime de libre échange, à Q_T, le volume avec un droit de douane. Au volume d'échange Q_T, la demande d'importation de Nation est égale à l'offre d'exportation d'Etranger avec P_T - P_T^* = t. On retiendra donc que le droit de douane établi par Nation augmente le prix dans Nation et baisse le prix dans Etranger. Le volume échangé se réduit.

Dans la seconde séquence réservée aux subventions, nous citerons encore l'analyse de Paul R. Krugman et Maurice Obstfeld puis nous passerons à l'analyse théorique proprement dite de l'impact des subventions des Etats-Unis et de l'Union Européenne sur le marché mondial.

En effet, la notion de subvention est abordée par ces auteurs en utilisant le terme subside à l'exportation. Pour ces derniers, le subside à l'exportation est un paiement fait à une firme ou un individu qui vend les biens à l'étranger. Comme le droit de douane, le subside à l'exportation peut soit être spécifique (une somme déterminée par unité vendue) ou ad valorem (une certaine proportion de la valeur exportée).

Lorsque le gouvernement attribue un subside à l'exportation, les vendeurs exporteront le bien jusqu'au point où le prix intérieur excède le prix à l'étranger du montant du subside. - Les effets sur les prix d'un subside à l'exportation sont exactement l'inverse de ceux d'un droit de douane -.



Figure 5: Effets d'un subside à l'exportation

Source : Economie internationale, Paul R. Krugman et Maurice Obstfeld, 3^ème édition

Le prix dans le pays d'exportation s'accroît de P_w à P_s. Toutefois, comme le prix dans le pays d'importation tombe de P_w à P_s^*, la hausse du prix est moindre que le subside. Dans le pays d'exportation, les consommateurs font une perte, les producteurs font un gain et le gouvernement perd puisqu'il doit faire la dépense correspondant au subside. La perte des consommateurs est la surface a + b ; le gain des producteurs est la surface a + b + c ; le subside du gouvernement est la surface b + c + d + e + f + g. La perte nette du bien être est par conséquent la somme des surfaces b + d + e + f + g. On note que les surfaces b et d représentent respectivement les pertes de distorsion de consommation^11(*) et de production^12(*) -ce même effet se produit avec le droit de douane-.

Dans la mesure où les exportations américaines représentent 40% des exportations mondiales et que celles de l'UE, 5% -soit pour les pays développés 45% des exportations mondiales- le cadre théorique sous- jacent à notre étude : subventions des pays développés et distorsions sur le marché mondial, repose essentiellement à travers l'analyse néoclassique standard en équilibre partiel, sur la théorie du grand pays (USA + UE) - price maker-. Graphiquement on a la configuration suivante :



Figure 6: Effets des subventions des pays développés sur le prix mondial du coton et les quantités produites

Source : nous mêmes (2006)

Partant d'une situation où le prix mondial est P₀^w, et les exportations EX0, le grand pays (ici les USA + UE) subventionne ses exportations d'un montant forfaitaire unitaire (S), cela entraîne sur le marché domestique, un relèvement du prix aux consommateurs, qui devront accepter de payer le prix mondial augmenté de la subvention (P₁^W +S) pour que les producteurs soient indifférents entre vendre sur le marché domestique et exporter. Pour les producteurs, cette subvention (S) a les mêmes conséquences qu'une baisse du coût marginal de production sur les quantités exportées d'un montant identique. Ainsi la courbe d'offre d'exportation de (USA+UE) se déplace vers le bas (passage X0 à X1 sur le marché mondial)^13(*) et on enregistre un accroissement du volume des exportations. Etant donné que la courbe de demande mondiale à laquelle font face les Etats- Unis, la Grèce et l'Espagne n'est pas infiniment élastique, les (USA + UE) étant globalement price maker, cette offre excédentaire d'exportation(X₁ - X₀ = AB + CD) entraîne toutes choses égales par ailleurs une baisse du prix mondial (passage de P₀^w à P₁^W). Ainsi, tandis que le prix mondial qui prévaudra sera P₁^W, l'exportateur des pays riches lui touchera (P₁^W +S).

La même analyse peut être menée en raisonnant en terme de prix mondial sur le marché domestique (USA + UE). Dans cette optique, pour un même prix mondial, les consommateurs des pays riches paient plus cher le coton (déplacement vers la gauche de la courbe de demande, qui devient D') et, pour un même prix mondial, les producteurs touchent plus (déplacement vers la droite de la courbe d `offre, qui devient O'). Ainsi, tout se passe comme si le nouveau prix d'équilibre d'autarcie était P₁^a, prix à partir duquel les (USA + UE) deviennent exportateurs. C'est ce jeu qui fausse les règles de la concurrence en incitant à la surproduction. Le schéma ci-dessus étant censé représenter la situation actuelle sur le marché mondial du coton, on s'attend, de façon symétrique, à avoir les effets inverses (réduction des quantités produites et relèvement du prix mondial) dans l'hypothèse d'une réduction des subventions.

2. Approche empirique de l'impact des

Subventions

De nombreuses études ont été consacrées à l'effet des subventions - dont notamment américaines sur le prix international du coton-. Nous retiendrons principalement pour des raisons de simplicité deux d'entre elles, reposant chacune sur des méthodologies différentes.

2.1. L'étude de Goreux

Notre intérêt pour cette étude repose sur le fait qu'elle est couramment citée lors des débats publics par les autorités, les acteurs de la filière cotonnière ouest africaine et du centre pour dénoncer les effets pervers des subventions des pays développés et surtout les Etats- Unis sur le cours du coton et les recettes d'exportation.

Cette étude, commanditée par la conférence des ministres de l'Agriculture des pays d'Afrique de l'Ouest et du centre (CMA/OAC), repose sur un modèle d'équilibre partiel. Le raisonnement est le suivant :

- A partir d'un prix mondial d'équilibre établi par la confrontation de l'offre et de la demande mondiale, on simule une élimination des subventions (celles portant sur les cinq dernières années avant l'étude);

- L'élimination des subventions entraîne alors une réduction de l'offre mondiale d'exportation car les exportateurs auparavant subventionnés ne toucheront plus que le prix mondial (déplacement vers le haut et vers la gauche de la courbe d'offre d'exportation);

- Un nouveau prix d'équilibre- plus élevé que le précédent- s'établit ainsi sur le marché mondial, en fonction de la demande mondiale et de la nouvelle offre ;

-Les quantités et le prix d'équilibre sont ensuite calculés algébriquement en résolvant simultanément les équations d'offre et de demande mondiales.

Cette démarche a l'avantage de la simplicité. Elle permet en outre- ce qui fait l'objet de l'étude- d'évaluer quantitativement les gains potentiels en recettes d'exportation pour un groupe de pays considéré. Les simulations effectuées avec le modèle donnent, suivant les élasticités d'offre et de demande retenues une augmentation de l'indice A de Cotlook ( indicateur du marché mondial des prix du coton ) de l'ordre de 2, 9 à13,4% et un gain de recettes d'exportation. Ainsi pour (Eo= 0.5 et Ed= -0,1) on note une augmentation de l'indice A de 12% et des recettes d'exportation de 250 millions de dollars sur la période 1997/1998- 2001/2002.

Cependant plusieurs limites sont inhérentes à ce genre d'analyse, entre autres :

- comme toute approche d'équilibre partiel, elle repose sur l'hypothèse ceteris paribus et néglige de ce fait les autres marchés, en particulier celui des produits concurrents du coton - comme les fibres synthétiques -;

- les résultats obtenus reposent essentiellement sur les élasticités d'offre et de demande retenues. Une façon intéressante de procéder consiste à les estimer économétriquement. Faute de procéder à une telle estimation, l'auteur retient plutôt les valeurs allant de 0,15 à 0,90 pour l'élasticité de l'offre et de -0,05 à -0,6 pour la demande. Bien qu'évitant les restrictions théoriques également inhérentes à l'économétrie- comme la formulation d'hypothèses sur les élasticités-, la démarche de l'auteur reste néanmoins sujet à critique dans la mesure où la même valeur de l'élasticité est retenue pour les pays.

Pour certains auteurs, l'utilité scientifique d'un modèle est déterminée par sa capacité à faire des prédictions qui seront après confrontées à la réalité. Pourtant les prédictions du modèle Goreux (2003a) telles qu'elles se tiennent sont difficiles à tester. En ce sens qu'elles réclament que les pays riches acceptent d'éliminer leurs subventions- ce qui n'est pas sur le point d'être observé maintenant - c'est cette situation qui amène certains auteurs dont notamment Benjamin Shepherd à dire que l'étude de Goreux n'est pas empirique dans un sens réel, mais elle est plutôt une traduction de la théorie à l'algèbre et finalement aux nombres.

2.2. L'étude de Shepherd (2004)

Cette étude visait à évaluer l'impact d'une réduction des seules subventions américaines sur le prix mondial du coton. Cependant, contrairement à l'étude précédente, celle-ci fait plutôt appel à l'outil économétrique. Le modèle estimé est un modèle vectoriel autorégressif (VAR) standard. Les variables retenues sont le prix mondial du coton, les variations de stocks mondiaux, les subventions américaines, la production et la consommation mondiale du coton. Une fois le modèle estimé, l'auteur trouve que les subventions américaines agissent beaucoup plus sur la production et les stocks que sur les prix. De même, en procédant à une décomposition de la variance, il apparaît que les variations de prix sont davantage dues aux variations de la demande qu'à celles des subventions. Enfin, en retenant différents scénarios de réduction du volume des subventions (10%,50% et 90%), il aboutit au résultat -plutôt surprenant - que même une réduction de 90% des subventions n'aurait qu'un effet limité, voire nul, sur les prix. Toutefois, force est de noter que pour apprécier les relations de causes à effets entre les variables en scène, B. Shepherd s'est penché sur la causalité à la Granger (les variables sont prises deux à deux) et a effectué des simulations- à l'aide des fonctions de réponses impulsionnelles- de l'effet de réduction des subventions sur les autres variables considérées. Il ne s'est donc pas intéressé à l'analyse multivariée de la cointegration à la Johansen. Pourtant cette approche est réputée comme étant mieux adapté aux VAR puisqu'elle prend en compte les inter-relations entre les variables et permet si les conditions sont réunies d'établir le MVCE.

En outre, certaines variables utilisées par Shepherd ne nous semblaient pas judicieuses. Le prix mondial a été approximé par l'indice de Liverpool qui n'est pas le meilleur indicateur du marché mondial du coton. La prise en compte des variations de stocks dans le modèle pourrait conduire à un double emploi car la consommation n'est rien d'autre que la production +/- les variations de stocks. Or le modèle prend déjà en compte la production et la consommation. Ensuite, le marché cotonnier a été traité comme étant indépendant des autres marchés, en particulier celui des produits concurrents (la fibre synthétique). C'est donc ce qui justifie la prise en compte du prix du polyester dans le modèle finalement retenu.

D'autres études récentes notamment (Poonyth et al, 2004) essaient également d'évaluer l'impact des subventions- de tous les pays subventionneurs cette fois-ci- sur le prix mondial et les volumes échangés du coton. Cette dernière tentative utilise le modèle ATPSM (Agricultural Trade Policy Simulation Model) développé conjointement par la FAO et la CNUCED. Les auteurs trouvent qu'une réduction complète des subventions dans tous les pays aboutirait à un relèvement de 3,1% à 5% du prix mondial suivant les valeurs des élasticités de l'offre et de la demande.

Tableau 1: Résumé des résultats issus d'études antérieures

Auteurs	Méthodes	Effets sur le prix mondial (%)	Préjudice pour les agriculteurs WCA (million $ E.-U)
ICAC (2002)	Equilibre partiel	29 ,7	274
Goreux (2003a)	Equilibre partiel	2,9 - 13,4	37 - 254
Reeves et al (2001)	Equilibre général (GTAP)	10,70	76
Tockarick (2003)	Equilibre partiel	2,8	26
Shepherd (2004)	Modèle économétrique VAR	Pas d'effet significatif	Un gain dérisoire pour les agriculteurs WCA
Poonyth et al (2004)	Equilibre partiel (ATPSM)	3,1- 5	___

Source : FAO (2004) complété par nos soins

- informations non disponibles

- WCA : West and Central Africa (Afrique de l'Ouest et du Centre)

Il ressort comme observation de ce tableau (1) que la plupart des études concourent aux mêmes résultats concernant les prix et les préjudices, c'est à dire une augmentation des prix et un relèvement des recettes d'exportation si les subventions étaient éliminées. Sauf l'étude de B.Shepherd fait ressortir le fait que les subventions peuvent ne pas avoir l'effet pervers préétabli sur les prix et par conséquent sur les recettes d'exportation (pertes). Il apparaît clairement que les méthodes diffèrent (VAR, modèle d'équilibre partiel, ATPSM...), car l'objetif des études n'est pas le même. Cependant, même pour un même objectif, il arrive que les résultats diffèrent du fait notamment des hypothèses formulées sur la valeur des paramètres (comme des élasticités).

Section 2 : Méthodologie de la recherche

La démarche méthodologique adoptée dans la présente étude se situe à deux niveaux ; elle concerne d'une part la présentation du modèle et d'autre part la méthode d'analyse. C'est dire que dans un premier temps, un point sur les principales variables de l'étude, la période de l'étude et les sources des données est fait. Ensuite, la méthode d'analyse qu'on entend utiliser est clairement abordée.

PARAGRAPHE 1: Présentation du modèle

A. Le modèle retenu

Le modèle standard VAR n'a pas été motivé par une quelconque théorie économique particulière et n'a pas une quelconque interprétation économique évidente ; avec chaque variable simplement reformulée comme une fonction de ses propres valeurs antérieures et celles d'autres variables endogènes. Toutes les variables sont initialement considérées comme endogènes ; ce qui veut dire qu'aucun ordre causatique n'est imposé sur les données a priori. En des termes plus concrets, ce que le modèle VAR nous donnera dans ce cas précisera simplement une sténographie de représentation mathématique d'un groupe de variables considéré comme décrivant les travaux du marché cotonnier mais sans l'imposition précédente d'idées découlant des théories économiques considérées comme gouvernant les relations inter-variables. Nous reprenons à quelques nuances près le modèle de B. Shepherd en corrigeant les insuffissances dont nous avions parlées plus haut. Ce modèle VAR(q) se présente sous forme matricielle comme suit :



Sous forme développée, on a :



Avec constante et nombre de retards

Pour l'utilisation du modèle toutes les variables sont exprimées en logarithme.

B. Définition des variables^14(*)

Prix du coton (PRC)

PRC (p_t ): le prix mondial du coton approché par l'indice A de Cotlook. Cotlook est une agence d'information spécialisée, basée au royaume- uni à Liverpool. Cet indice exprimé en US-Cents^15(*)/ Livre^16(*) est la moyenne des cinq cotations les plus basses parmi un ensemble de cotations représentatives d'origines très diversifiées, rapportées au stade CAF nord - Europe.

Cette variable est capitale dans notre étude dans la mesure où les distorsions évoquées sur le marché du coton font principalement allusion à la chute des cours mondiaux du coton.

Production mondiale du coton ( PRO)

PRO (o_t) : représente la quantité de coton produite dans l'ensemble du monde et est exprimée en million de bales^17(*).

La prise en compte de cette variable s'explique par le fait que le prix de tout bien est déterminé par son offre (l'offre découlant de la production).

Consommation mondiale du coton (CONS)

CONS (d_t ) : représente la quantité de coton consommée dans l'ensemble du monde et est exprimée en million de bales.

Cette variable est très déterminante dans la demande mondiale du coton. Elle est donc assimilée à la demande du coton. Le choix de cette variable est expliqué par le fait que la demande d'un bien influence nécessairement son prix.

Subventions des pays riches (NSUB)

NSUB (s_t) : les subventions américaines et européennes. Les subventions américaines sont approximées par les paiements totaux du gouvernement tels qu'apparaissant dans les USDA Cotton and Wool Yearbook (2003). Les subventions européennes quant à elles sont approchées par les aides pour la production du coton.

C'est la variable clé de notre modèle. Elle est considérée comme étant à l'origine des distorsions observées sur le marché mondial du coton.

N.B : la conversion en dollars des subventions européennes exprimées en Euro à été possible grâce aux bases de données historiques de taux de change disponibles sur le  site : www.oanda.com.

Prix du Polyester (PRP)

PRP (f_t ) : le prix international du polyester. On rappelle que le polyester est la principale fibre concurrente du coton. Partant, on s'attend à ce que les fluctuations du prix du polyester influencent le prix du coton. Il est exprimé en dollars par kilogramme.

C. Période de l'étude et sources des données.

1. Période de l'étude

L'arsenal des données est composé des observations annuelles entre 1970 et 2003 ; c'est à dire 34 observations.

2. Sources des données

Les données utilisées dans le cadre de cette étude sont des données secondaires, tirées sur des bases de données existantes ou dans des journaux spécialisés.

Les variables retenues viennent alors de diverses sources, ainsi :

- Le prix mondial du coton approximé par l'indice A de Cotlook provient de la base de données de l'agence Cotlook (précisément du site www.cotlook.com);

- La consommation mondiale et la production mondiale de coton sont tirées du USDA Cotton and Wool Yearbook, 2003,table 15 ;

- Le prix du polyester provient du USDA Cotton and Wool Yearbook, 2003, table 12 ;

- Les subventions américaines proviennent du USDA Upland Cotton Factsheet, 1 January 2003, table "summary of basic data" complèté par le "Government Payments by crop year";

- Les subventions européennes quant à elles proviennent du "Official journal of the European Union, Special Report N° 13/2003", table 4.

PARAGRAPHE 2 : Méthode d'analyse

Pour apprécier les relations qui existent entre les différentes variables de notre modèle, nous allons estimer le modèle vectoriel à correction d'erreur - après avoir dans un premier temps fait les tests de diagnostic sur les données (stationnarité et cointégration) - par le logiciel E.Views. Ensuite, nous allons vérifier la justesse des résultats du MVCE par l'analyse des fonctions de réponses impulsionnelles et de la décomposition de la variance. Pour finir, nous comptons utiliser le modèle d'équilibre partiel de Goreux (2003a) pour évaluer l'éventuelle perte des recettes d'exportation des producteurs de l'AOC en 2001/2002.

A. Tests de diagnostic sur les données

Notre analyse débute par l'étude de la stationnarité des variables. Pour ce faire, on procède aux tests de racine unitaire développés par Fuller (1976) et Dickey et Fuller ( 1979, 1981). Cette analyse nous permet de déterminer l'ordre d'intégration des différentes variables retenues. On dit qu'une série est intégrée d'ordre (d) si sa différence d ième est stationnaire ; c'est-à-dire intégrée d'ordre 0. Après la détermination de l'ordre d'intégration, si les variables en scène sont intégrées d'ordre1 [I(1)], cela voudrait dire qu'il existerait un risque de cointégration entre les variables. Cette présomption de cointégration ne serait confirmée qu'après étude de la stationnarité du résidu obtenu à l'issue de l'estimation par les MCO de la relation de long terme ( L_T ) suivante :

LPRC_t = á₀ + á₁ LNSUB_t + á₂ LCONS_t + á₃ LPRO_t + á₄ LPRP_t + å_t



Où å_t est le terme d'erreur.

Le test ADF permet de juger de la stationnarité du résidu. A la suite de la confirmation de la stationnarité du résidu, on peut conclure que les variables sont cointégrées. Du fait qu'il s'agit d'un modèle multivarié on pourrait ne pas avoir un seul vecteur de cointégration. Ce qui fait appel à la représentation vectorielle à correction d'erreur qui n'est rien d'autre que l'approche cointégrée du VAR.

B. Estimation du MVCE

Les grandes étapes relatives à l'estimation d'un MVCE sont les suivantes :

Etape1 : détermination du nombre de retards p du modèle. Plusieurs critères servent à discriminer entre les retards (Akaike, Hannan- Quinn, Schwarz). Nous retenons le critère de Schwarz qui donne un nombre de retard inférieur à celui de Akaike. Ce choix se justifie par le fait que dans le modèle VAR un nombre élevé de retards réduit le nombre d'observations. Ceci est d'autant plus ressenti lorsque les séries ne sont pas longues. Le nombre de retards obtenu est donc celui qui minimise la fonction de Schwarz :

SC(h) = Ln( SCR_h / n) + hLn n /n

SCR_h = somme des carrés des résidus pour le modèle à h retards

n = nombre d'observations

Ln = logarithme népérien

Etape 2 : test de Johansen permettant de connaître le nombre de relations de cointégration. Johansen a proposé deux statistiques pour déterminer le nombre de vecteurs de cointégration : le test de la Trace et le test de la valeur propre maximale. Nous retenons celui de la Trace qui est plus usité par rapport à l'autre.

L'hypothèse nulle testée est : r = q, c'est-à-dire qu'il existe au plus r vecteurs de cointégration. On rejette l'hypothèse nulle de r relations de cointégration lorsque la statistique de la Trace est superieure à sa valeur critique. Plusieurs cas pourraient se présenter : r = 0 ; 0 < r < K ; r =K avec K = nombre de variables du modèle.

Lorsque 0< r < K, cela signifie que les variables sont cointégrées de rang r et qu'il existe donc r relations de cointégration. Un modèle à correction d'erreur peut alors être estimé.

Par ailleurs pour effectuer le test de la Trace, la spécification à retenir dépend de :

- L'absence ou la présence de constante dans le modèle à correction d'erreur,

- L'absence ou la présence de constante et de tendance dans les relations de cointégration.

Etape 3 : Identification des relations de cointégration, c'est à dire des relations de long terme entre les variables. A cette étape, on choisit les relations de long terme qui nous donnerons des écarts types relativement faibles et les relations adéquates.

Etape 4 : estimation par la méthode du Maximum de Vraisemblance du modèle vectoriel à correction d'erreur et validation avec les tests usuels : significativité des coefficients et vérification du signe et de la significativité des termes à correction d'erreur. A cette étape, la méthode du Maximum de Vraisemblance reprend l'estimation de la relation de long terme estimée par les MCO et fournit les équations de court terme.

Après l'estimation du MVCE, on s'intéresse à l'analyse dynamique par les fonctions de réponses impulsionnelles et à la décomposition de la variance de manière à voir si ces deux outils d'analyse supplémentaires confirment les résultats du MVCE.

Enfin, pour mesurer l'éventuelle perte de recettes d'exportation des pays de l' AOC producteurs de coton en 2001/2002, on compte procéder comme suit :

- utiliser l'élasticité prix des subventions fournie par la relation de court terme (du MVCE) estimée par la méthode du Maximum de Vraisemblance pour déterminer le nouveau prix p' sans subvention.

-Ensuite, intégrer ce nouveau prix p' dans le modèle d'équilibre partiel développé par L.Goreux (voir annexe 2) pour apprécier l'augmentation des recettes d'exportation à la suite de la suppression des subventions.

Chapitre II : RESULTATS DE L'ETUDE ET ENJEUX

CHAPITRE III : ANALYSE S RESULTATS ET

Ce dernier chapitre livre dans la première section les principaux résultats de la méthodologie adoptée. Dans la section suivante, deux instruments d'analyse supplémentaires sont utilisés pour juger la fiabilité des résultats du MVCE. Ensuite, cette section se ferme avec la rubrique des interprétations, limites et suggestions.

Section 1 : Etude de la cointégration et estimation du MVCE

PARAGRAPHE 1 : Etude de la cointégration

A. Vérification des conditions préalables à l'analyse de la cointégration

La méthode de cointégration à la johansen exige que les variables soient toutes intégrées d'ordre 1[I (1)]. Cela signifie qu'elles ne sont pas stationnaires en niveau alors que leurs différences premières le sont.

La stationnarité de la variable est jugée à partir de la comparaison entre les statistiques DF (Dickey Fuller) ou ADF (Augmented Dickey Fuller) et les valeurs critiques tabulées par Mackinnon (Mackinnon critical value = CV). L'alternative d'hypothèses qui se présente à l'issue du test est la suivante :

H₀ : racine unitaire ou non stationnarité  

H₁ : non racine unitaire ou stationnarité

Dans la mesure où les valeurs critiques sont négatives, la règle de décision est la suivante :

Si DF ou ADF CV, on rejette l'hypothèse nulle de non stationnarité.

Si DF ou ADF CV, on accepte l'hypothèse nulle de non stationnarité.

Les tests sont appliqués en niveau puis en différence première au cas où il y aurait présence de racine unitaire à ce premier stade.

Test de Stationnarité

Par souci de synthèse, compte tenu du nombre important des tests appliqués, le tableau ci-dessous résume les résultats des tests de racine unitaire appliqués en niveau à l'ensemble des variables.

L'étude considère le seuil de 5% pour la validation des différentes hypothèses.

Tableau 2: Résultats des tests de stationnarité en niveau

test	Type de modèle	LPRC		LCONS		LNSUB		LPRO		LPRP
		t	CV à 5%	t	CVà5%	t	CVà5%	t	CVà5%	t	CVà5%
ADF(1)	M1	-3,890	-2,955	-0,558	-2,955	-2,460	-2,955	-1,403	-2,955	-2,682	-2,955
	M2	-3,816	-3,556	-1,696	-3,556	-3,298	-3,556	-3,657	-3,556	-2,200	-3,556
	M3	0,376	-1,951	2,635	-1,951	1,328	-1,951	1,008	-1,951	0,486	-1,951
ADF(3)	M1	-2,153	-2,962					-0,693	-2,962
	M2	-2,234	-3,567					-1,853	-3,567
	M3	-0,139	-1,952					1,863	-1,952
Résultats		LPRC n'est pas I(0)		LCONS n'est pas I(0)		LNSUB n'est pas I(0)		LPRO n'est pas I(0)		LPRP n'est pas I(0)

Source : nous mêmes (2006)

I (0) = intégré d'ordre 0 ou stationnaire en niveau ; ADF(1) = DF

M₁ = modèle avec constante

M₂ = modèle avec constante et tendance

M₃ = modèle sans constante et sans tendance

Les variables LCONS, LNSUB, LPRP se sont révélées non stationnaires en niveau au retard d'ordre 1 (ADF (1) CV). Par contre, LPRC et LPRO présentent une non stationnarité partielle en niveau au retard d'ordre 1.c'est à dire (M₃ pour LPRC) et (M₁ et M₃ pour LPRO). En passant au retard d'ordre 3, on se rend compte qu'elles ne sont pas stationnaires car ADF (3) CV.

En effet une variable est stationnaire en niveau lorsqu'elle l'est quelque soit le retard.

Conclusion : les variables sont non stationnaires en niveau.

Probablement donc qu'elles sont intégrées d'ordre 1.

L'examen de la stationnarité se poursuit en différence première et les résultats sont fournis par le tableau suivant :

Tableau 3: Résultats des tests de stationnarité en différence première

Test	Type de Modèle	DLPRC		DLCONS		DLNSUB		DLPRO		DLPRP
		t	CVà5%	t	CVà5%	t	CVà5%	t	CVà5%	t	CVà5%
ADF(1)	M1	-5,256	-2,959	-3,920	-2,959	-6,152	-2,959	-7,829	-2,959	-4,320	-2,959
	M2	-5,464	-3,561	-3,850	-3,561	-6,562	-3,561	-7,703	-3,561	-4,386	-3,561
	M3	-5,307	-1,952	-2,967	-1,952	-5,637	-1,952	-7,281	-1,952	-4,259	-1,952
résultats		LPRC est I (1)		LCONS est I (1)		LNSUB est I (1)		LPRO est I (1)		LPRP est I (1)

Source : nous-mêmes (2006)

D (x_t) = x_t - x_{t - 1} avec D = Opérateur différence

Les résultats du test de racine unitaire en différence première montrent la stationnarité pour toutes les variables ADF (1) < CV.

Les variables sont donc toutes cointégrées d'ordre 1.

Conclusion : il y a donc présomption de cointégration entre les variables.  

On estime alors la tendance de L_T suivante par les MCO.

LPRC = ₀ + ₁ LNSUB + ₂ LCONS + ₃ LPRO + ₄ LPRP + _t

Le résultat obtenu grâce au logiciel E. views se présente comme suit :

LPRC = 3,24311 + 0,577263 LNSUB - 0,389138 LCONS

3,493253^* -0,906615

- 1,049172 LPRO + 0,598625 LPRP

- 2,544426^* 3,740229^*

_* significatif à 5%

On étudie ensuite, la stationnarité des Résidus recueillis. Le tableau suivant rend compte des résultats du test de racine unitaire appliqué sur le résidu.

Tableau 4: Résultats du test ADF sur le résidu de la Relation de L_T

Variable	ADF	Valeur critique à 5%	Valeur critique à 10%	Résultat
Résidu	-6,595	-2,955	-3,6496	Stationnarité des Résidus

Source : nous-mêmes (2006)

Conclusion : il y a donc confirmation de la possibilité de cointégration des variables

Comme dans notre cas, il s'agit d'un modèle multivarié, on pourrait ne pas avoir un seul vecteur de cointégration. Cela fait appel à la représentation vectorielle à correction d'erreur. On utilise alors une approche cointégrée du VAR à la Johansen.

B- Détermination du nombre optimal de retard et

Cointégration à la Johansen

1. Détermination du nombre optimal de retard

La détermination du nombre optimal de retard constitue la première étape du processus conduisant au (MVCE). Nous utilisons alors le critère de Schwarz comme évoqué plus haut dans notre méthodologie. Les différentes valeurs obtenues pour différents nombres de retards (1à 4) sont consignées dans le tableau suivant :

Tableau 5: Résultats de la Recherche du nombre optimal de décalages

Nombre de retards	1	2	3	4
Valeurs du critère de Schwarz	-9,450	-8,303	-7,400	-6,524

Source : Nous-mêmes (2006)

Le nombre de retards qui minimise le critère de Schwarz est alors 1.

2. Cointégration à la johansen

Après la détermination du nombre optimal de retard, on procède au test de Johansen pour déterminer le nombre de relations de cointégration. Pour ce faire, nous utilisons la statistique de la trace.

Pour retenir la spécification convenable nous analysons l'évolution des courbes univariées des différentes variables dans le temps.



Figure 7 : Evolution de PRC, NSUB, PRO, CONS, PRP (en logarithme)

Source : Nous-mêmes (2006)

L'allure de ces différentes courbes montre que les variables considérées présentent des tendances et des constantes.

Nous effectuons alors le test de la trace en supposant la présence de constante et de tendance dans les relations de cointégration et la présence de constante dans le modèle à correction d'erreur.

Les résultats du test de la trace figurent dans le tableau n° 6.

Tableau 6: Résultats du test de la trace

Statistique de la trace	Valeur critique à 5%	Valeur critique à 1%	Hypothèse nulle de r relations de cointégration
85,14212 54,84738 30,62966 14,54330	68,52 47,21 29,68 15,41	76,07 54,46 35,65 20,04	None Au plus 1 Au plus 2 Au plus 3

Source : Nous-mêmes (2006)

On rejette l'hypothèse nulle d'au plus 2 relations de cointégration (30,62 29,68) au seuil de 5%. En revanche, on accepte l'hypothèse nulle selon laquelle il existe au plus 3 relations de cointégration entre les cinq variables considérées (14,543 15,41). Ces trois relations sont les suivantes :

LPRC = 0,340221 LNSUB + 2,589041 LCONS

(0,19966) (1,42312)

- 4,176708 LPRO + 0,936895 LPRP + 4,290731

(1,47951) (0,18836) + _t (1)

LPRC = 102,3871 LCONS - 114,2834 LPRO + 11,08932 LPRP

(519,847) (588,769) (55,3197)

+ 14,00792 + _t (2)

LPRC = 1,131846 LPRO - 0,109288 LPRP - 0,117378 + _t

(0,05883) (0,04861) (3)

Les valeurs entre parenthèses représentent les écarts types.

L'équation 1 est la seule ayant attribuée un coefficient non nul à la variable clé de notre modèle (les subventions). En plus, elle présente des écarts types faibles.

L'équation 3 qui présente aussi des écarts types faibles élimine deux variables (les subventions et la consommation mondiale) qui sont d'une grande importance dans cette étude. Nous retenons de fait l'équation 1 comme notre relation de long- terme.

ANALYSE DE LA RELATION DE L_T

LPRC = 0,340221 LNSUB + 2,589041 LCONS - 4, 176708 LPRO
(1,70402)(*)	(-1,81927)**	(2,82303)(*)
+ 0,936895 LPRP + 4,290731 + t
(- 4,97407)*

Les valeurs entre parenthèses sont les t de student.

Elles indiquent que la production et le prix du polyester expliquent significativement à long terme le prix du coton. Par contre, les subventions et la consommation expliquent dans une moindre mesure le prix du coton car elles ne sont pertinentes qu'à un seuil de 10%. Les rapports de long terme établis peuvent ne pas être vérifiés à court terme. L'étude de la relation de court terme repose sur l'estimation des paramètres du modèle vectoriel à correction d'erreur qui intègre les dynamiques de court et de long terme.

PARAGRAPHE 2 : Estimation et analyse du MVCE

A. Estimation

Dans la mesure où nous avons cinq variables, le MVCE comportera 5 équations. Les résultats obtenus par le logiciel E.views sont présentés dans le tableau n° 7.

Tableau 7: Estimation du MVCE

Relation normalisée de LT de l'équation 1
LPRC(-1)	1.000000
LNSUB(-1)	-0.340221
	(0.19966)
	(-1.70402)
LCONS(-1)	-2.589041
	(1.42312)
	(-1.81927)
LPRO(-1)	4.176708
	(1.47951)
	(2.82303)
LPRP(-1)	-0.936895
	(0.18836)
	(-4.97407)
C	-4.290731
Correction d'erreur	D(LPRC)	D (LNSUB)	D (LCONS)	D(LPRO)	D(LPRP)
CointEq1	-0.408546	-0.049574	-0.022115	-0.121356	0.000784
	(0.19035)	(0.16979)	(0.02553)	(0.05467)	(0.08981)
	(-2.14633) *	(-0.29197)	(-0.86612)	(-2.21988) *	(0.00873)
D(LPRC(-1))	-0.316397	0.301299	-0.087310	0.379427	0.210096
	(0.18775)	(0.16748)	(0.02518)	(0.05392)	(0.08859)
	(-1.68519)	(1.79904)	(-3.46676)*	(7.03654)*	(2.37164)
D(LNSUB(-1))	0.118426	-0.259614	-0.024495	-0.244631	0.040542
	(0.24860)	(0.22175)	(0.03335)	(0.07140)	(0.11729)
	(0.47638)	(-1.17074)	(-0.73457)	(-3.42636)*	(0.34565)
D(LCONS(-1))	1.195784	0.800612	0.014164	-0.548300	0.663415
	(1.30534)	(1.16439)	(0.17510)	(0.37489)	(0.61590)
	(0.91607)	(0.68758)	(0.08089)	(-1.46255)	(1.07715)
D(LPRO(-1))	-0.087055	0.237999	0.085543	0.428219	-0.045992
	(0.62141)	(0.55431)	(0.08336)	(0.17847)	(0.29320)
	(-0.14009)	(0.42936)	(1.02623)	(2.39938)*	(-0.15686)
D(LPRP(-1))	-0.022968	-0.083023	-0.014327	-0.206414	0.345722
	(0.38538)	(0.34376)	(0.05169)	(0.11068)	(0.18183)
	(-0.05960)	(-0.24151)	(-0.27714)	(-1.86495)**	(1.90132)
C	0.001501	0.028548	0.017616	0.022661	-0.005370
	(0.04367)	(0.03895)	(0.00586)	(0.01254)	(0.02060)

Sources : nous-mêmes (2006) ; *significatif à 5% ;**significatif à 10%

Dans le tableau n° 8 cointéq 1 désigne les résidus, retardés d'une période, de la relation de cointégration préalablement trouvée (relation 1). Les premiers chiffres entre parenthèses désignent les écarts types et les seconds, les t de student des coefficients estimés.

B. Analyse des résultats du MVCE

Les résultats issus du tableau n° 8 montrent que le terme à correction d'erreur est négatif et significativement différent de zéro dans les relations relatives à (DLPRC) et à (DLPRO). Pour (DLCONS) le terme à correction d'erreur est négatif mais non significatif. Par contre, pour DLPRP le terme à correction d'erreur est positif et significatif ce qui est difficilement interprétable. Par ailleurs, il ressort du tableau que le prix du coton n'est influencé à court terme par aucune des variables du modèle. Sauf par ses valeurs passées dans une moindre mesure (au seuil de 10%). Le tableau montre un lien positif entre les subventions et le prix du coton mais non significatif. Quant à la production, elle est influencée positivement et significativement par le prix du coton à court terme. Alors que les subventions l'explique significativement mais négativement. Par ailleurs, on remarque que la production dépend de ses valeurs passées à court terme.

En ce qui concerne la consommation, elle est influencée négativement et significativement par le prix du coton à court terme. Il ressort aussi que les subventions n'exercent aucune influence à court terme sur la consommation.

Section 2 : Confirmation des résultats, interprétations, limites et suggestions

PARAGRAPHE 1 : Confirmation des résultats du MVCE

Le modèle vectoriel à correction d'erreur étant un modèle VAR (donc dépourvu de fondements théoriques), il est nécessaire d'utiliser d'autres formes d'analyse en vue de confirmer la fiabilité de ses résultats. Ici nous retenons les fonctions de réponses Impulsionnelles et la décomposition de la variance.

A. Fonctions de réponses impulsionnelles

Les modèles VAR sont souvent analysés au travers de leur dynamique via la simulation des chocs sur les innovations du modèle.

En effet, les fonctions de réponses Impulsionnelles permettent d'analyser l'effet d'un choc d'une innovation sur les valeurs courantes et futures des variables endogènes. Nous stimulons donc un choc sur l'innovation des subventions. Les fonctions de réponses Impulsionnelles du prix du coton (LPRC), de la consommation (LCONS) et de la production (LPRO) à ce choc sont reportées sur les figures ci-dessous.



Figure 8: Réponse du prix du coton à un choc sur les subventions.

Source : nous-mêmes (2006)



Figure 9: Réponse de la consommation mondiale à un choc sur les subventions

Source : nous-mêmes (2006)



Figure 10: Réponse de la production mondiale à un choc sur les subventions

Source : nous-mêmes (2006)

De la figure n° 8, il ressort qu'un choc positif sur les subventions se traduit par une fonction de réaction positive et presque nulle du prix du coton. Les prix sont quasi-insensibles aux variations de subventions.

D'après la figure n° 10, on observe qu'a la suite d'un choc positif sur les subventions, la production fluctue sur les 10 périodes.De la période 1 à 2, cette fonction de réaction est décroissante. Tandis qu'elle devient croissante sur la période 2 à 5 avant de décroître à nouveau sur la période 5 à 7.

La figure n° 9 montre que la consommation reste totalement insensible à la suite d'un choc positif sur les subventions.

Conclusion : l'analyse dynamique suivant les fonctions de réponses impulsionnelles confirme que les subventions n'influencent pas le prix et la consommation.

En outre, elle montre que les subventions agissent bel et bien négativement sur la production mais seulement entre la période (1à 4). Après cette période, on peut dire que la production réagit plutôt positivement au choc positif sur les subventions.

B. Décomposition de la variance

L'analyse par la décomposition de la variance traduit la contribution de chaque variable à la composition de la variance de la variable endogène. Les résultats de la décomposition de la variance des variables LPRC, LPRO, LCONS sont consignés dans le tableau suivant :

Tableau 8: Décomposition de la variance

Variable exogène Variable endogène	LPRC	LNSUB	LCONS	LPRO	LPRP	Période
LPRC	75,24749	2,386898	4,093908	5,637912	12,63379	10
LPRO	37,22760	7,301368	13,22719	20,63755	21,60629	10
LCONS	20,34288	0,259059	78,75606	0,392540	0,249458	10

Source : nous-mêmes (2006)

En procédant à la décomposition de la variance on constate que les variations du prix du coton sont davantage dues aux variations de ses valeurs passées et dans une proportion relativement plus faible à une variation du prix du polyester. Par contre, on observe que les subventions n'influencent presque pas le prix du coton.

En ce qui concerne la production, ses variations sont dues essentiellement aux variations du prix du coton, des valeurs passées de la production et du prix du polyester. Par ailleurs, on remarque que les subventions expliquent les variations de la production dans une proportion plus grande que son influence sur le prix du coton.

Quant à la consommation, ses variations sont largement expliquées par ses valeurs passées. En outre, on remarque que les subventions n'expliquent pas du tout les variations de la consommation.

Conclusion : L'analyse par la décomposition de la variance tout comme les fonctions de réponses impulsionnelles confirment les résultats du modèle vectoriel à correction d'erreur.

PARAGRAPHE 2 : Interprétations, limites, et suggestions

A. Interprétations des résultats

De l'analyse de nos résultats, il ressort que les subventions n'influencent pas le prix mondial du coton que ce soit à court ou long terme. Cela infirme donc notre hypothèse de départ. Toutefois, ce résultat plutôt surprenant n'est pas nouveau. Il rejoint les conclusions des travaux de certaines études comme celles de B. Shepherd et de la Banque Mondiale (2004). Par ailleurs, le modèle prix^18(*) du CCIC qui s'est révélé un modèle à forte capacité prévisionnelle - en matière de prévision du prix du coton - ne prend pas en compte les subventions. C'est-à-dire que si les subventions avaient un impact significatif sur le prix, le modèle ne serait pas aussi fiable. Tout porte à croire qu'en définitive les subventions des pays riches n'influencent pas le prix du coton et que les pays de l'AOC se trompe de cible. Une raison pouvant justifier l'insensibilité du prix du coton aux variations des subventions est probablement la nature de ces dernières. En effet, les subventions intégrées dans le modèle sont en majorité composées de subventions à la production. Pourtant, théoriquement il est démontré que ce sont les subventions à l'exportation qui créent des distorsions en terme de prix.

Considérant la relation entre les subventions et la production, il ressort de nos analyses que les subventions expliquent la production mais pas dans le sens escompté. Cela voudrait dire qu'à la suite de la suppression des subventions des pays développés, les pays africains producteurs de coton et non subventionneurs réagiraient (augmentation de la production) plus que proportionnellement à la chute de la production dans les pays qui subventionnent (USA + UE). Ce qui peut s'expliquer par le fait que les pays de l'AOC dispose d'un avantage comparatif dans la production du coton.

Par ailleurs, si les subventions n'ont pas eu un impact significatif sur la consommation, cela paraît normal dans la mesure où si les subventions devaient influencées la consommation, se serait à travers le prix. Or notre modèle n'a pas pu montrer l'influence négative escomptée des subventions sur les prix.

En ce qui concerne les pertes en recettes d'exportations, il s'avère impossible de les évaluer par le modèle envisagé. Ceci parce que nous ne pouvons pas nous fier à l'élasticité prix des subventions fournie par le MVCE (relation positive et non significative entre le prix et les subventions). On ne peut donc plus prétendre une perte de recettes d'exportation imputable aux subventions au travers d'une chute des prix.

B. Limites et suggestions

1. Limites et perspectives

La présente étude, sans remettre en cause essentiellement ses résultats comporte des limites en certains points.

- Notre variable de subventions n'est certainement qu'une Proxy des soutiens accordés aux producteurs cotonniers américains et européens. Il conviendrait de chercher d'autres variables pertinentes comme les différentes formes d'aide accordées par ces pays à leurs producteurs. Les garanties de crédit à l'exportation pourraient également être prises en compte.

- Notre étude n'a pas pris en compte les subventions chinoises. Pourtant la Chine est le deuxième pays qui subventionne le plus le coton après les Etats-Unis. Ceci est dû au fait que les données relatives aux subventions chinoises sont peu connues ; à telle enseigne que la politique de subvention de la Chine est difficilement appréciable.

- En outre, il existe plusieurs sources de données concernant les variables clés du marché cotonnier. On peut citer entre autres : les sources de données de la FAO, du CCIC, de USDA (ministère américain de l'Agriculture-US Departement of Agriculture-) et le COMTRADE (Base de données des Nations Unies relative au commerce des produits de base). Les études ultérieures pourraient s'employer à comparer les résultats provenant de ces différentes sources. Pour notre part, le choix de la base de données de l'USDA s'explique par la conformité et l'existence de données sur une longue période.

- Notre étude n'a par ailleurs, pas évaluée la performance du modèle en terme de prévision, à travers notamment les statistiques comme la moyenne carré des erreurs ou la moyenne des erreurs absolues.^19(*)

- Enfin, le modèle VAR étant un modèle qui requiert beaucoup de données afin d'améliorer la précision des estimateurs ; l'ajout d'une information supplémentaire est toujours la bien venue. C'est pour cette raison que les travaux prochains devront s'intéresser à l'économétrie bayésienne. Cette méthode d'estimation consiste en l'absence de séries longues à aller chercher de l'information « en dehors » des données. Cela passe en partie par la formulation d'hypothèses a priori sur les paramètres d'intérêt (ici les coefficients du modèle VAR), puis de les combiner avec les informations contenues dans les données pour trouver l'estimateur a posteriori bayésien.

2. Suggestions

Notre étude n'a pas complètement pu montrer l'effet pervers des subventions en terme de distorsion sur le marché mondial. Serait-ce une raison valable pour remettre systématiquement en cause les revendications des producteurs de coton de l'AOC ? Certainement non. En effet, ces pays peuvent se tromper de cible mais pas de combat. C'est ce que énonçait une étude de la Banque Mondiale en ces termes : « les pays en développement sont davantage victimes de barrières tarifaires et d'un accès aux marchés insuffisant que des subventions aux producteurs » (Banque Mondiale, 2004). Aussi, force est de notifier que les producteurs africains disposent d'un avantage comparatif certain dans la production du coton- ce qui justifie leur spécialisation-. Il est donc légitime et rationnel de revendiquer une libéralisation immédiate. La libéralisation souhaitée est déterminante pour le succès des reformes internes envisagées et en phase d'exécution.

En ce qui concerne les reformes internes, il s'agira pour les pays de l'AOC et le Bénin en particulier d'accélérer le processus de libéralisation et de privatisation de leurs structures. Cependant, il faut garder en vue l'idée selon laquelle le marché doit être privatisé mais réglementé (Eric Hazard, 2004). La réforme en question doit s'effectuer sur des bases saines. Elle doit permettre : d'approvisionner les producteurs de coton en intrants de bonne qualité et à coûts raisonnables dans les délais adéquats ; de résoudre le problème de retard dans le paiement des producteurs ; d'instaurer un professionnalisme dans la filière.

Par ailleurs, une autre solution endogène serait de valoriser notre coton par le biais de la transformation locale. En effet, l'UEMOA s'est fixée comme objectif de valoriser 25% de la production d'ici 2010. Ce souci vise bien évidemment à atténuer les effets de la volatilité des cours internationaux du coton brute en le valorisant. De facto, il devrait aussi permettre aux pays AOC de se positionner sur un segment de la filière où la valeur ajoutée (VA) est la plus importante. Le souci de créer de la valeur ajoutée n'est pas nouveau. Des pays comme le Pakistan et la Chine, principaux producteurs et exportateurs dans le passé ont aujourd'hui connu un tel développement dans le secteur textile qu'ils sont devenus importateurs nets. De l'Angleterre du XIX^ième siecle (dont la révolution industrielle a débuté dans le secteur du coton), à l'Ile Maurice dans les années 1970, le secteur textile a, dans un grand nombre d'expériences et de développement, été le secteur clé de l'industrialisation (et comme on le voit dans le cas de l'Ile Maurice indépendamment d'une production locale de coton brut).

L'UEMOA, quant à elle a connu un succès mitigé : « au cours de la période 1981/82, le Bénin et le Burkina Faso, la Côte d'Ivoire et le Mali transformaient 22% de leur production locale ; 20 ans plus tard, ils n'en transformaient que 5% »^20(*). Au nom des raisons qui expliquent l'échec de cette stratégie, on peut citer :

- Le manque de capitaux suffisant pour investir dans le segment de la transformation industrielle ;

- Les infrastructures (mauvais états des routes et des aéroports, coûts de fournitures en électricité très élevés...) pour accueillir une technologie de pointe sont le plus souvent inadaptées ;

- Le capital humain ne semble pas toujours disponible ;

- Certains pré requis tels que la bonne gouvernance, l'intégrité restent absents.

Pour corriger ces blocages, des marges de manoeuvre existent. La volonté politique des Etats (AOC) et du BENIN en particulier reste le principal levier pour l'action. Par ailleurs, il serait à la fois dommage et aberrant de ne pas profiter des politiques de développement et d'infrastructures (Accords de Partenariat Economique avec l'UE, NEPAD, Stratégie de Réduction de la Pauvreté...) pour relever le défis de la transformation locale de la fibre, en investissant dans un secteur industriel moderne. Parallèlement, le secteur traditionnel pourra lui aussi être soutenu afin d'occuper une « niche » à haute valeur ajoutée, celle du tissu coton manuel.

Pour finir, la nécessité d'une diversification des économies africaines s'impose. Elle est souhaitable dans le sens où la trop grande dépendance du PIB d'un pays à l'égard d'une seule matière première dont le cours est très volatile est un frein à la croissance. Turnovsky et al (1998) montrent que différents types de volatilité affectent la croissance d'un pays parmi lesquels, la volatilité des termes de l'échange et de la production. La concentration de l'activité économique dans un secteur comme le coton accroît ces deux types de volatilité. La solution serait alors pour les pays africains de réduire leur « dépendance » vis-à-vis du coton en développant d'autres filières, par exemple (la filière manioc,arachide, du riz...). Ce raisonnement pose néanmoins un problème fondamental. Une diversification de l'Economie ne signifie pas une substitution d'une filière à une autre et encore moins la condamnation d'une filière qui (fonctionne en Afrique sub-sahérienne et a pu joué un rôle dans la diminution de la pauvreté) - le coton - à une hypothétique filière dont l'issue n'est pas encore certaine.

CONCLUSION GENERALEsion Générale

Cette étude visait à évaluer l'impact éventuel des subventions des pays riches sur le marché mondial du coton. Les principaux résultats qui s'en sont dégagés peuvent être résumés comme suit :

L'analyse par le modèle vectoriel à correction d'erreur montre que les subventions ne créent aucune distorsion en terme de prix et de consommation, mais seulement au niveau de la production. Elle indique aussi que les subventions n'ont pas pu contribuer à une perte de recettes d'exportation pour les producteurs de coton de l'AOC lors de la campagne cotonnière 2001 / 02.

L'analyse par les fonctions de réponses impulsionnelles et la décomposition de la variance a confirmé les résultats du MVCE.

Par ailleurs, le résultat relatif à l'effet des subventions sur le prix mondial du coton, quoique surprenant n'est pas nouveau. Il vient confirmer des travaux antérieurs sur la question à savoir les études de B. Shepherd et celles de la Banque Mondiale. Toutefois, de tels résultats pourraient résulter d'une mauvaise appréciation des politiques de subventions internes des pays subventionneurs. Mais dans tous les cas, afin de ne pas être victime de la chute et de la volatilité des cours mondiaux, il appartient aux pays africains producteurs de coton, tel que le BENIN de poursuivre les réformes entamées dans leur filière, de chercher à créer de la valeur ajoutée en transformant une partie du coton produit localement et finalement de diversifier leur économie de manière à être peu tributaire d'un seul produit.

IOGRAPHIE

BIBLIOGRAPHIE

BANQUE MONDIALE (2002),

`'Perspectives Cotonnières''

Bulletin Occasionnel de la Banque Mondiale sur les Enjeux et les Options de la Réformes Politiques dans la Filière Coton, Juillet 2002.

BANQUE MONDIALE (2004)

`'Global Economic Prosjects 2004''

Realizing the Development Promise of the Doha Agenda.

BENIN, BURKINA FASO, MALI et TCHAD (2003),

`'Poverty Reduction:

Sectoral Initiative in Favour of Cotton'', WTO Doc. TN / AG / 4, 16 May 2003.

BIDAUX A, BIO GOURA S.(2005),

`'Etude sur le Mécanisme

d'Approvisionnement et de Distribution des Intrants Agricoles au BENIN'' AIC-BENIN,Décembre 2005.

DGAE (2004)

`' le Coton et l'Economie Béninoise'',

DGAE, Avril 2004

DICKEY, D. A et FULLER, W. A (1979)

«Distribution of the Estimators

for Autoregressive Time Series with a Unit Root'', Journal of the American Statistical Association, 74,PP. 427-431.

DICKEY, D. A et FULLER, W. A (1981),

`'Likelihood Ratio Statistics

for Autoregressive Time Series with a Unit Root'' Econometrica, 49, PP. 1057-1072.

DROESBEKE J. J, FINE J. et SAPORTA G, ed, (2002), `'Méthodes

Bayésiennes en statistique'', Techniq.

ESTUR , G. (2003),

`'le Coton Africain dans le Marché

Mondial'', Comité Consultatif International du Coton, 3 Mars 2003.

FAO (2004),

`' the Impact of Domestic and Trade Policies on the

World Cotton Market'', FAO Commodity and Trade Policy Research Working Paper N° 8, ROME.

GOREUX, L. (2003a),

`'Préjudices Causés par les Subventions

des Pays Développés aux Filières Cotonnières de l'AOC'', OMC, Genève, 25 Mars 2003.

GOREUX, L. (2003b),

`'les Producteurs de Coton des Pays

CFA face aux Subventions Américaines et Européennes'', Juillet 2003

GOREUX, L. (2004),

`' le Coton après Cancùn'' Mars 2004.

HAZARD, E. (2003),

`'le Coton AOC et son Insertion dans

les Echanges Internationaux'', Enda Prospectives Dialogues Politiques, 19 Juillet 2003.

ICAC (2002),

`'Production and Trade Policies Affecting the

cotton Industry'' Washington, D. C, USA, ICAC.

JOHANSEN, S. (1995),

`'Likelihood - Based Inference in

Cointegrated Vector Auto regressive Models'', Oxford: Oxford University Press.

KOOP G. (2003),

`'Bayesian Econometrics'', West Sussex, John

Wiley et Sons.

KRUGMAN P., OBSTFELD M. (2001),

`'Economie Internationale''

Edition de Boeck Université, 2001.

MIROUDOT, S. (2004),

`'Quel Avenir Pour l'Initiative

Sectorielle en Faveur du Coton après l'Echec de Cancùn'', Mars 2004.

OXFAM (2002),

`'Cultivating Poverty: the Impact of US Cotton

Subsidies on Africa'', Briefing paper 30.

POONYTH. D, SARRIS A, SHARMA R et SHUI S (2004),

`'The

Impact of Domestic and Trade Policies on the World Cotton Market'', Commodity and Trade Policy research working paper, N° 8, ROME, FAO.

REEVES. G, VINCENT D., et WYATT S. (2001),

`'Trade Distorsions

and Cotton Markets:Implications for Australian Cotton Producers'', Narrabri, NSW: Cotton Research and Development Corporation.

SHEPHERD B. (2004),

`' The Impact of US Subsidies on the

World Cotton Market: a Reassessment'', Groupe d'Economie Mondiale, Paris.

SUMMER, D. (2003),

`' A Quantitative Simulation Analysis of the

Impacts of US Cotton Subsidies on Cotton Price and Quantities'', SUMMER, 2003.

TOKARICK, S. (2003),

`'Measuring the Impact of Distorsions

in Agricultural Trade in Partial and General Equilibrium'', WP/03/110, Washington, DC, USA, FMI.

TURNOVSKY, S. et al (1998),

''Volatility and Growth in

Development Economies: some Numerical Results and Empirical Evidence'', University of Washington.

ANNEXES

ANNEXES

ANNEXE 1 : De la stationnarité des variables à la décomposition de la variance

1- Analyse de la stationnarité des variables

TEST ADF

PRIX DU COTON

ADF(1) d=0 avec constante

ADF Test Statistic	-3.890850	1% Critical Value*		-3.6496
		5% Critical Value		-2.9558
		10% Critical Value		-2.6164
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRC)
Method: Least Squares
Date: 04/19/06 Time: 21:34
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRC(-1)	-0.586962	0.150857	-3.890850	0.0005
D(LPRC(-1))	0.056695	0.156408	0.362479	0.7196
C	2.484321	0.633789	3.919790	0.0005
R-squared	0.354284	Mean dependent var		0.019029
Adjusted R-squared	0.309752	S.D. dependent var		0.222224
S.E. of regression	0.184626	Akaike info criterion		-0.451904
Sum squared resid	0.988521	Schwarz criterion		-0.314492
Log likelihood	10.23047	F-statistic		7.955706
Durbin-Watson stat	2.048334	Prob(F-statistic)		0.001760

ADF(1) d=0 avec constante et trend

ADF Test Statistic	-3.816645	1% Critical Value*		-4.2712
		5% Critical Value		-3.5562
		10% Critical Value		-3.2109
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRC)
Method: Least Squares
Date: 04/19/06 Time: 21:37
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRC(-1)	-0.578010	0.151445	-3.816645	0.0007
D(LPRC(-1))	0.022866	0.160764	0.142235	0.8879
C	2.507332	0.635475	3.945601	0.0005
@TREND(1970)	-0.003426	0.003633	-0.942832	0.3538
R-squared	0.374153	Mean dependent var		0.019029
Adjusted R-squared	0.307099	S.D. dependent var		0.222224
S.E. of regression	0.184981	Akaike info criterion		-0.420659
Sum squared resid	0.958103	Schwarz criterion		-0.237442
Log likelihood	10.73054	F-statistic		5.579802
Durbin-Watson stat	2.079191	Prob(F-statistic)		0.003949

ADF(1) d=0 ni constante ni trend

ADF Test Statistic	0.376847	1% Critical Value*		-2.6369
		5% Critical Value		-1.9517
		10% Critical Value		-1.6213
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRC)
Method: Least Squares
Date: 04/19/06 Time: 21:38
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRC(-1)	0.003575	0.009486	0.376847	0.7089
D(LPRC(-1))	-0.129207	0.181248	-0.712872	0.4814
R-squared	0.012172	Mean dependent var		0.019029
Adjusted R-squared	-0.020756	S.D. dependent var		0.222224
S.E. of regression	0.224519	Akaike info criterion		-0.089255
Sum squared resid	1.512258	Schwarz criterion		0.002354
Log likelihood	3.428079	F-statistic		0.369655
Durbin-Watson stat	2.059941	Prob(F-statistic)		0.547768

ADF(3) d=0 avec constante

ADF Test Statistic	-2.153936	1% Critical Value*		-3.6661
		5% Critical Value		-2.9627
		10% Critical Value		-2.6200
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRC)
Method: Least Squares
Date: 04/19/06 Time: 21:43
Sample(adjusted): 1974 2003
Included observations: 30 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRC(-1)	-0.483622	0.224530	-2.153936	0.0411
D(LPRC(-1))	-0.004410	0.198614	-0.022204	0.9825
D(LPRC(-2))	-0.169328	0.178103	-0.950730	0.3508
D(LPRC(-3))	0.170741	0.164437	1.038337	0.3091
C	2.041210	0.949371	2.150064	0.0414
R-squared	0.342753	Mean dependent var		-0.003746
Adjusted R-squared	0.237593	S.D. dependent var		0.206571
S.E. of regression	0.180369	Akaike info criterion		-0.436611
Sum squared resid	0.813326	Schwarz criterion		-0.203078
Log likelihood	11.54916	F-statistic		3.259363
Durbin-Watson stat	1.637849	Prob(F-statistic)		0.027836

ADF(3) d=0 avec constante et trend

ADF Test Statistic	-2.234711	1% Critical Value*		-4.2949
		5% Critical Value		-3.5670
		10% Critical Value		-3.2169
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRC)
Method: Least Squares
Date: 04/19/06 Time: 21:44
Sample(adjusted): 1974 2003
Included observations: 30 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRC(-1)	-0.506474	0.226640	-2.234711	0.0350
D(LPRC(-1))	-0.039123	0.202837	-0.192881	0.8487
D(LPRC(-2))	-0.223665	0.188284	-1.187912	0.2465
D(LPRC(-3))	0.113067	0.176593	0.640270	0.5281
C	2.214749	0.971146	2.280553	0.0317
@TREND(1970)	-0.004060	0.004435	-0.915416	0.3691
R-squared	0.364927	Mean dependent var		-0.003746
Adjusted R-squared	0.232620	S.D. dependent var		0.206571
S.E. of regression	0.180956	Akaike info criterion		-0.404264
Sum squared resid	0.785886	Schwarz criterion		-0.124025
Log likelihood	12.06397	F-statistic		2.758190
Durbin-Watson stat	1.607444	Prob(F-statistic)		0.041727

ADF(3) d=0 ni constante ni trend

ADF Test Statistic	-0.139022	1% Critical Value*		-2.6423
		5% Critical Value		-1.9526
		10% Critical Value		-1.6216
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRC)
Method: Least Squares
Date: 04/19/06 Time: 21:45
Sample(adjusted): 1974 2003
Included observations: 30 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRC(-1)	-0.001164	0.008374	-0.139022	0.8905
D(LPRC(-1))	-0.267751	0.166890	-1.604359	0.1207
D(LPRC(-2))	-0.349782	0.167675	-2.086070	0.0469
D(LPRC(-3))	0.115463	0.173361	0.666025	0.5113
R-squared	0.221221	Mean dependent var		-0.003746
Adjusted R-squared	0.131362	S.D. dependent var		0.206571
S.E. of regression	0.192526	Akaike info criterion		-0.333610
Sum squared resid	0.963719	Schwarz criterion		-0.146783
Log likelihood	9.004146	F-statistic		2.461862
Durbin-Watson stat	1.705462	Prob(F-statistic)		0.085004

ADF(1) d=1 avec constante

ADF Test Statistic	-5.256104	1% Critical Value*		-3.6576
		5% Critical Value		-2.9591
		10% Critical Value		-2.6181
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRC,2)
Method: Least Squares
Date: 04/19/06 Time: 21:47
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LPRC(-1))	-1.473714	0.280382	-5.256104	0.0000
D(LPRC(-1),2)	0.275638	0.186182	1.480479	0.1499
C	0.018399	0.039606	0.464546	0.6458
R-squared	0.610834	Mean dependent var		-0.002085
Adjusted R-squared	0.583036	S.D. dependent var		0.340189
S.E. of regression	0.219669	Akaike info criterion		-0.101622
Sum squared resid	1.351128	Schwarz criterion		0.037151
Log likelihood	4.575138	F-statistic		21.97433
Durbin-Watson stat	1.867322	Prob(F-statistic)		0.000002

ADF(1) d=1 avec constante et trend

ADF Test Statistic	-5.464718	1% Critical Value*		-4.2826
		5% Critical Value		-3.5614
		10% Critical Value		-3.2138
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRC,2)
Method: Least Squares
Date: 04/19/06 Time: 21:48
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LPRC(-1))	-1.639556	0.300026	-5.464718	0.0000
D(LPRC(-1),2)	0.375419	0.196430	1.911208	0.0666
C	0.139774	0.094990	1.471460	0.1527
@TREND(1970)	-0.006636	0.004737	-1.400903	0.1726
R-squared	0.637204	Mean dependent var		-0.002085
Adjusted R-squared	0.596893	S.D. dependent var		0.340189
S.E. of regression	0.215988	Akaike info criterion		-0.107272
Sum squared resid	1.259575	Schwarz criterion		0.077759
Log likelihood	5.662712	F-statistic		15.80733
Durbin-Watson stat	1.840482	Prob(F-statistic)		0.000004

ADF(1) d=1 ni constante ni trend

ADF Test Statistic	-5.307806	1% Critical Value*		-2.6395
		5% Critical Value		-1.9521
		10% Critical Value		-1.6214
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRC,2)
Method: Least Squares
Date: 04/19/06 Time: 21:49
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LPRC(-1))	-1.462507	0.275539	-5.307806	0.0000
D(LPRC(-1),2)	0.270785	0.183358	1.476809	0.1505
R-squared	0.607834	Mean dependent var		-0.002085
Adjusted R-squared	0.594311	S.D. dependent var		0.340189
S.E. of regression	0.216679	Akaike info criterion		-0.158460
Sum squared resid	1.361542	Schwarz criterion		-0.065945
Log likelihood	4.456133	F-statistic		44.94832
Durbin-Watson stat	1.867560	Prob(F-statistic)		0.000000

SUBVENTION

ADF(1) d=0 avec constante

ADF Test Statistic	-2.460223	1% Critical Value*		-3.6496
		5% Critical Value		-2.9558
		10% Critical Value		-2.6164
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LNSUB)
Method: Least Squares
Date: 04/19/06 Time: 21:51
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LNSUB(-1)	-0.203906	0.082881	-2.460223	0.0201
D(LNSUB(-1))	-0.166002	0.165226	-1.004695	0.3234
C	1.780182	0.705094	2.524745	0.0173
R-squared	0.200248	Mean dependent var		0.039240
Adjusted R-squared	0.145093	S.D. dependent var		0.180744
S.E. of regression	0.167118	Akaike info criterion		-0.651175
Sum squared resid	0.809923	Schwarz criterion		-0.513763
Log likelihood	13.41881	F-statistic		3.630626
Durbin-Watson stat	2.158259	Prob(F-statistic)		0.039161

ADF(1) d=0 avec constante et trend

ADF Test Statistic	-3.298779	1% Critical Value*		-4.2712
		5% Critical Value		-3.5562
		10% Critical Value		-3.2109
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LNSUB)
Method: Least Squares
Date: 04/19/06 Time: 21:52
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LNSUB(-1)	-0.566268	0.171660	-3.298779	0.0026
D(LNSUB(-1))	0.017501	0.172082	0.101702	0.9197
C	4.574276	1.352271	3.382661	0.0021
@TREND(1970)	0.015942	0.006749	2.362048	0.0254
R-squared	0.333129	Mean dependent var		0.039240
Adjusted R-squared	0.261678	S.D. dependent var		0.180744
S.E. of regression	0.155305	Akaike info criterion		-0.770380
Sum squared resid	0.675352	Schwarz criterion		-0.587163
Log likelihood	16.32608	F-statistic		4.662374
Durbin-Watson stat	2.034771	Prob(F-statistic)		0.009149

ADF(1) d=0 ni constante ni trend

ADF Test Statistic	1.328150	1% Critical Value*		-2.6369
		5% Critical Value		-1.9517
		10% Critical Value		-1.6213
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LNSUB)
Method: Least Squares
Date: 04/19/06 Time: 21:53
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LNSUB(-1)	0.005153	0.003880	1.328150	0.1941
D(LNSUB(-1))	-0.177670	0.179347	-0.990650	0.3298
R-squared	0.024459	Mean dependent var		0.039240
Adjusted R-squared	-0.008059	S.D. dependent var		0.180744
S.E. of regression	0.181471	Akaike info criterion		-0.514985
Sum squared resid	0.987948	Schwarz criterion		-0.423376
Log likelihood	10.23975	F-statistic		0.752168
Durbin-Watson stat	2.140734	Prob(F-statistic)		0.392675

ADF(1) d=1 avec constante

ADF Test Statistic	-6.152996	1% Critical Value*		-3.6576
		5% Critical Value		-2.9591
		10% Critical Value		-2.6181
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LNSUB,2)
Method: Least Squares
Date: 04/19/06 Time: 21:54
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LNSUB(-1))	-1.638514	0.266295	-6.152996	0.0000
D(LNSUB(-1),2)	0.372849	0.173461	2.149477	0.0404
C	0.060200	0.032486	1.853121	0.0744
R-squared	0.659507	Mean dependent var		-0.004803
Adjusted R-squared	0.635186	S.D. dependent var		0.283353
S.E. of regression	0.171144	Akaike info criterion		-0.600852
Sum squared resid	0.820132	Schwarz criterion		-0.462079
Log likelihood	12.31321	F-statistic		27.11686
Durbin-Watson stat	1.777302	Prob(F-statistic)		0.000000

ADF(1) d=1 avec constante et trend

ADF Test Statistic	-6.562313	1% Critical Value*		-4.2826
		5% Critical Value		-3.5614
		10% Critical Value		-3.2138
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LNSUB,2)
Method: Least Squares
Date: 04/19/06 Time: 21:56
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LNSUB(-1))	-1.785594	0.272098	-6.562313	0.0000
D(LNSUB(-1),2)	0.456134	0.175018	2.606209	0.0147
C	0.173112	0.073756	2.347075	0.0265
@TREND(1970)	-0.005951	0.003516	-1.692507	0.1021
R-squared	0.692167	Mean dependent var		-0.004803
Adjusted R-squared	0.657963	S.D. dependent var		0.283353
S.E. of regression	0.165716	Akaike info criterion		-0.637172
Sum squared resid	0.741465	Schwarz criterion		-0.452142
Log likelihood	13.87617	F-statistic		20.23662
Durbin-Watson stat	1.778922	Prob(F-statistic)		0.000000

ADF(1) d=1 ni constante ni trend

ADF Test Statistic	-5.637301	1% Critical Value*		-2.6395
		5% Critical Value		-1.9521
		10% Critical Value		-1.6214
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LNSUB,2)
Method: Least Squares
Date: 04/19/06 Time: 21:56
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LNSUB(-1))	-1.478849	0.262333	-5.637301	0.0000
D(LNSUB(-1),2)	0.293343	0.174982	1.676418	0.1044
R-squared	0.617747	Mean dependent var		-0.004803
Adjusted R-squared	0.604566	S.D. dependent var		0.283353
S.E. of regression	0.178182	Akaike info criterion		-0.549681
Sum squared resid	0.920717	Schwarz criterion		-0.457166
Log likelihood	10.52006	F-statistic		46.86606
Durbin-Watson stat	1.791056	Prob(F-statistic)		0.000000

CONSOMMATION

ADF(1) ; d=0 ; Avec constante

ADF Test Statistic	-0.558113	1% Critical Value*		-3.6496
		5% Critical Value		-2.9558
		10% Critical Value		-2.6164
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LCONS)
Method: Least Squares
Date: 03/20/06 Time: 18:40
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LCONS(-1)	-0.019541	0.035013	-0.558113	0.5811
D(LCONS(-1))	-0.079801	0.186219	-0.428536	0.6714
C	0.101903	0.151144	0.674208	0.5055
R-squared	0.018612	Mean dependent var		0.016097
Adjusted R-squared	-0.049070	S.D. dependent var		0.032577
S.E. of regression	0.033366	Akaike info criterion		-3.873476
Sum squared resid	0.032286	Schwarz criterion		-3.736064
Log likelihood	64.97562	F-statistic		0.274996
Durbin-Watson stat	1.993101	Prob(F-statistic)		0.761534

ADF(1) ; d=1 ; Avec constante

ADF Test Statistic	-3.920111	1% Critical Value*		-3.6576
		5% Critical Value		-2.9591
		10% Critical Value		-2.6181
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LCONS,2)
Method: Least Squares
Date: 03/20/06 Time: 18:58
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LCONS(-1))	-1.097341	0.279926	-3.920111	0.0005
D(LCONS(-1),2)	0.005917	0.191300	0.030929	0.9755
C	0.017634	0.007682	2.295392	0.0294
R-squared	0.541928	Mean dependent var		-0.000787
Adjusted R-squared	0.509209	S.D. dependent var		0.048721
S.E. of regression	0.034132	Akaike info criterion		-3.825386
Sum squared resid	0.032620	Schwarz criterion		-3.686613
Log likelihood	62.29349	F-statistic		16.56288
Durbin-Watson stat	1.985804	Prob(F-statistic)		0.000018

ADF(1) ; d=0 ; Avec Trend et constante

ADF Test Statistic	-1.696559	1% Critical Value*		-4.2712
		5% Critical Value		-3.5562
		10% Critical Value		-3.2109
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LCONS)
Method: Least Squares
Date: 03/20/06 Time: 18:48
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LCONS(-1)	-0.206428	0.121675	-1.696559	0.1009
D(LCONS(-1))	0.012603	0.190372	0.066200	0.9477
C	0.845869	0.487703	1.734394	0.0938
@TREND(1970)	0.003552	0.002220	1.600109	0.1208
R-squared	0.100833	Mean dependent var		0.016097
Adjusted R-squared	0.004494	S.D. dependent var		0.032577
S.E. of regression	0.032503	Akaike info criterion		-3.898475
Sum squared resid	0.029581	Schwarz criterion		-3.715258
Log likelihood	66.37560	F-statistic		1.046644
Durbin-Watson stat	1.987690	Prob(F-statistic)		0.387341

ADF(1) ; d=1 ; Avec Trend et constante

ADF Test Statistic	-3.850168	1% Critical Value*		-4.2826
		5% Critical Value		-3.5614
		10% Critical Value		-3.2138
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LCONS,2)
Method: Least Squares
Date: 03/20/06 Time: 18:59
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LCONS(-1))	-1.097462	0.285043	-3.850168	0.0007
D(LCONS(-1),2)	0.006256	0.194855	0.032105	0.9746
C	0.018505	0.014827	1.248099	0.2227
@TREND(1970)	-4.83E-05	0.000698	-0.069201	0.9453
R-squared	0.542009	Mean dependent var		-0.000787
Adjusted R-squared	0.491121	S.D. dependent var		0.048721
S.E. of regression	0.034755	Akaike info criterion		-3.761047
Sum squared resid	0.032614	Schwarz criterion		-3.576017
Log likelihood	62.29624	F-statistic		10.65105
Durbin-Watson stat	1.986426	Prob(F-statistic)		0.000085

ADF(1) ; d=0 ; Ni Trend et constante

ADF Test Statistic	2.635461	1% Critical Value*		-2.6369
		5% Critical Value		-1.9517
		10% Critical Value		-1.6213
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LCONS)
Method: Least Squares
Date: 03/20/06 Time: 18:50
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LCONS(-1)	0.004042	0.001534	2.635461	0.0132
D(LCONS(-1))	-0.090075	0.183899	-0.489808	0.6278
R-squared	0.003230	Mean dependent var		0.016097
Adjusted R-squared	-0.029996	S.D. dependent var		0.032577
S.E. of regression	0.033062	Akaike info criterion		-3.920423
Sum squared resid	0.032792	Schwarz criterion		-3.828815
Log likelihood	64.72678	F-statistic		0.097203
Durbin-Watson stat	1.989165	Prob(F-statistic)		0.757369

ADF(1) ; d=1 ; Ni Trend et constante

ADF Test Statistic	-2.967966	1% Critical Value*		-2.6395
		5% Critical Value		-1.9521
		10% Critical Value		-1.6214
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LCONS,2)
Method: Least Squares
Date: 03/20/06 Time: 19:03
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LCONS(-1))	-0.710131	0.239265	-2.967966	0.0060
D(LCONS(-1),2)	-0.186298	0.184224	-1.011258	0.3203
R-squared	0.455732	Mean dependent var		-0.000787
Adjusted R-squared	0.436964	S.D. dependent var		0.048721
S.E. of regression	0.036558	Akaike info criterion		-3.717486
Sum squared resid	0.038758	Schwarz criterion		-3.624971
Log likelihood	59.62104	F-statistic		24.28253
Durbin-Watson stat	2.104406	Prob(F-statistic)		0.000031

PRODUCTION

ADF(1) d=0, avec constante

ADF Test Statistic	-1.403881	1% Critical Value*		-3.6496
		5% Critical Value		-2.9558
		10% Critical Value		-2.6164
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRO)
Method: Least Squares
Date: 03/20/06 Time: 19:23
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRO(-1)	-0.136825	0.097462	-1.403881	0.1710
D(LPRO(-1))	-0.239482	0.175644	-1.363452	0.1832
C	0.608687	0.421022	1.445736	0.1590
R-squared	0.144691	Mean dependent var		0.013868
Adjusted R-squared	0.085705	S.D. dependent var		0.097728
S.E. of regression	0.093446	Akaike info criterion		-1.813799
Sum squared resid	0.253234	Schwarz criterion		-1.676386
Log likelihood	32.02078	F-statistic		2.452944
Durbin-Watson stat	2.244308	Prob(F-statistic)		0.103701

ADF(1) d=0, avec trend et constante

ADF Test Statistic	-3.657865	1% Critical Value*		-4.2712
		5% Critical Value		-3.5562
		10% Critical Value		-3.2109
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRO)
Method: Least Squares
Date: 03/20/06 Time: 19:26
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRO(-1)	-0.875278	0.239287	-3.657865	0.0010
D(LPRO(-1))	0.158223	0.193829	0.816303	0.4212
C	3.540497	0.960768	3.685069	0.0010
@TREND(1970)	0.014524	0.004405	3.296828	0.0027
R-squared	0.383864	Mean dependent var		0.013868
Adjusted R-squared	0.317849	S.D. dependent var		0.097728
S.E. of regression	0.080716	Akaike info criterion		-2.079293
Sum squared resid	0.182422	Schwarz criterion		-1.896076
Log likelihood	37.26869	F-statistic		5.814832
Durbin-Watson stat	1.898679	Prob(F-statistic)		0.003207

ADF(1) d=0, ni trend ni constante

ADF Test Statistic	1.008255	1% Critical Value*		-2.6369
		5% Critical Value		-1.9517
		10% Critical Value		-1.6213
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRO)
Method: Least Squares
Date: 03/20/06 Time: 19:28
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRO(-1)	0.003968	0.003936	1.008255	0.3214
D(LPRO(-1))	-0.293699	0.174683	-1.681323	0.1031
R-squared	0.083046	Mean dependent var		0.013868
Adjusted R-squared	0.052480	S.D. dependent var		0.097728
S.E. of regression	0.095129	Akaike info criterion		-1.806704
Sum squared resid	0.271486	Schwarz criterion		-1.715095
Log likelihood	30.90726	F-statistic		2.717005
Durbin-Watson stat	2.316510	Prob(F-statistic)		0.109719

ADF(1) d=1, avec constante

ADF Test Statistic	-7.829995	1% Critical Value*		-3.6576
		5% Critical Value		-2.9591
		10% Critical Value		-2.6181
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRO,2)
Method: Least Squares
Date: 03/20/06 Time: 19:31
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LPRO(-1))	-2.012004	0.256961	-7.829995	0.0000
D(LPRO(-1),2)	0.554769	0.162033	3.423793	0.0019
C	0.028998	0.015314	1.893508	0.0687
R-squared	0.753568	Mean dependent var		6.14E-05
Adjusted R-squared	0.735965	S.D. dependent var		0.159970
S.E. of regression	0.082200	Akaike info criterion		-2.067565
Sum squared resid	0.189190	Schwarz criterion		-1.928792
Log likelihood	35.04725	F-statistic		42.81071
Durbin-Watson stat	2.147420	Prob(F-statistic)		0.000000

ADF(1) d=1, avec trend et constante

ADF Test Statistic	-7.703165	1% Critical Value*		-4.2826
		5% Critical Value		-3.5614
		10% Critical Value		-3.2138
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRO,2)
Method: Least Squares
Date: 03/20/06 Time: 19:32
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LPRO(-1))	-2.015330	0.261624	-7.703165	0.0000
D(LPRO(-1),2)	0.555696	0.164824	3.371449	0.0023
C	0.037155	0.034195	1.086580	0.2868
@TREND(1970)	-0.000451	0.001681	-0.267977	0.7908
R-squared	0.754221	Mean dependent var		6.14E-05
Adjusted R-squared	0.726913	S.D. dependent var		0.159970
S.E. of regression	0.083597	Akaike info criterion		-2.005705
Sum squared resid	0.188688	Schwarz criterion		-1.820674
Log likelihood	35.08842	F-statistic		27.61830
Durbin-Watson stat	2.148584	Prob(F-statistic)		0.000000

ADF(1) d=1, ni trend ni constante

ADF Test Statistic	-7.281950	1% Critical Value*		-2.6395
		5% Critical Value		-1.9521
		10% Critical Value		-1.6214
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRO,2)
Method: Least Squares
Date: 03/20/06 Time: 19:34
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LPRO(-1))	-1.883832	0.258699	-7.281950	0.0000
D(LPRO(-1),2)	0.483108	0.164425	2.938169	0.0064
R-squared	0.722012	Mean dependent var		6.14E-05
Adjusted R-squared	0.712426	S.D. dependent var		0.159970
S.E. of regression	0.085786	Akaike info criterion		-2.011591
Sum squared resid	0.213416	Schwarz criterion		-1.919076
Log likelihood	33.17966	F-statistic		75.32110
Durbin-Watson stat	2.006281	Prob(F-statistic)		0.000000
ADF(3) d=0 ni constante, ni tendance
ADF Test Statistic	1.863045	1% Critical Value*		-2.6423
		5% Critical Value		-1.9526
		10% Critical Value		-1.6216
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRO3)
Method: Least Squares
Date: 04/30/06 Time: 16:03
Sample(adjusted): 1974 2003
Included observations: 30 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRO3(-1)	0.007286	0.003911	1.863045	0.0738
D(LPRO3(-1))	-0.539531	0.195159	-2.764570	0.0103
D(LPRO3(-2))	-0.621773	0.187619	-3.314012	0.0027
D(LPRO3(-3))	-0.136872	0.199691	-0.685418	0.4991
R-squared	0.372457	Mean dependent var		0.012972
Adjusted R-squared	0.300049	S.D. dependent var		0.100878
S.E. of regression	0.084398	Akaike info criterion		-1.982980
Sum squared resid	0.185199	Schwarz criterion		-1.796153
Log likelihood	33.74469	F-statistic		5.143814
Durbin-Watson stat	2.061301	Prob(F-statistic)		0.006320
ADF(3) d=0 avec constante et tendance
ADF Test Statistic	-1.854966	1% Critical Value*		-4.2949
		5% Critical Value		-3.5670
		10% Critical Value		-3.2169
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRO2)
Method: Least Squares
Date: 04/30/06 Time: 16:03
Sample(adjusted): 1974 2003
Included observations: 30 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRO2(-1)	-0.620161	0.334325	-1.854966	0.0759
D(LPRO2(-1))	-0.056106	0.322056	-0.174211	0.8632
D(LPRO2(-2))	-0.308226	0.247981	-1.242943	0.2259
D(LPRO2(-3))	0.034046	0.216241	0.157446	0.8762
C	2.512003	1.333844	1.883282	0.0718
@TREND(1970)	0.010588	0.006150	1.721655	0.0980
R-squared	0.454336	Mean dependent var		0.012972
Adjusted R-squared	0.340656	S.D. dependent var		0.100878
S.E. of regression	0.081913	Akaike info criterion		-1.989454
Sum squared resid	0.161035	Schwarz criterion		-1.709215
Log likelihood	35.84181	F-statistic		3.996619
Durbin-Watson stat	2.007358	Prob(F-statistic)		0.008855
ADF(3) d=0 avec constante
ADF Test Statistic	-0.693628	1% Critical Value*		-3.6661
		5% Critical Value		-2.9627
		10% Critical Value		-2.6200
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRO1)
Method: Least Squares
Date: 04/30/06 Time: 16:11
Sample(adjusted): 1974 2003
Included observations: 30 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRO1(-1)	-0.067965	0.097985	-0.693628	0.4943
D(LPRO1(-1))	-0.493323	0.205695	-2.398323	0.0243
D(LPRO1(-2))	-0.589613	0.193687	-3.044157	0.0054
D(LPRO1(-3))	-0.130488	0.201452	-0.647737	0.5231
C	0.325599	0.423619	0.768611	0.4493
R-squared	0.386944	Mean dependent var		0.012972
Adjusted R-squared	0.288854	S.D. dependent var		0.100878
S.E. of regression	0.085070	Akaike info criterion		-1.939668
Sum squared resid	0.180924	Schwarz criterion		-1.706135
Log likelihood	34.09502	F-statistic		3.944819
Durbin-Watson stat	2.048737	Prob(F-statistic)		0.012880

PRIX DU POLYESTER

ADF(1) d=0, avec constante

ADF Test Statistic	-2.682483	1% Critical Value*		-3.6496
		5% Critical Value		-2.9558
		10% Critical Value		-2.6164
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRP)
Method: Least Squares
Date: 03/20/06 Time: 19:36
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRP(-1)	-0.185097	0.069002	-2.682483	0.0119
D(LPRP(-1))	0.341595	0.157073	2.174756	0.0379
C	0.778026	0.286140	2.719037	0.0109
R-squared	0.270769	Mean dependent var		0.015572
Adjusted R-squared	0.220478	S.D. dependent var		0.107905
S.E. of regression	0.095270	Akaike info criterion		-1.775150
Sum squared resid	0.263213	Schwarz criterion		-1.637738
Log likelihood	31.40241	F-statistic		5.383968
Durbin-Watson stat	1.963681	Prob(F-statistic)		0.010269

ADF(1) d=0, avec trend et constante

ADF Test Statistic	-2.200966	1% Critical Value*		-4.2712
		5% Critical Value		-3.5562
		10% Critical Value		-3.2109
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRP)
Method: Least Squares
Date: 03/20/06 Time: 19:38
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRP(-1)	-0.186631	0.084795	-2.200966	0.0361
D(LPRP(-1))	0.343429	0.169645	2.024396	0.0526
C	0.783060	0.330304	2.370725	0.0249
@TREND(1970)	7.43E-05	0.002302	0.032288	0.9745
R-squared	0.270796	Mean dependent var		0.015572
Adjusted R-squared	0.192667	S.D. dependent var		0.107905
S.E. of regression	0.096954	Akaike info criterion		-1.712688
Sum squared resid	0.263203	Schwarz criterion		-1.529471
Log likelihood	31.40300	F-statistic		3.466019
Durbin-Watson stat	1.963455	Prob(F-statistic)		0.029372

ADF(1) d=0, ni trend ni constante

ADF Test Statistic	0.486757	1% Critical Value*		-2.6369
		5% Critical Value		-1.9517
		10% Critical Value		-1.6213
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRP)
Method: Least Squares
Date: 03/20/06 Time: 19:39
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
LPRP(-1)	0.002192	0.004504	0.486757	0.6300
D(LPRP(-1))	0.297459	0.172075	1.728654	0.0942
R-squared	0.084862	Mean dependent var		0.015572
Adjusted R-squared	0.054357	S.D. dependent var		0.107905
S.E. of regression	0.104931	Akaike info criterion		-1.610565
Sum squared resid	0.330316	Schwarz criterion		-1.518957
Log likelihood	27.76905	F-statistic		2.781930
Durbin-Watson stat	1.851040	Prob(F-statistic)		0.105740

ADF(1) d=1, avec constante

ADF Test Statistic	-4.320814	1% Critical Value*		-3.6576
		5% Critical Value		-2.9591
		10% Critical Value		-2.6181
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRP,2)
Method: Least Squares
Date: 03/20/06 Time: 19:41
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LPRP(-1))	-0.915207	0.211814	-4.320814	0.0002
D(LPRP(-1),2)	0.278626	0.177534	1.569423	0.1278
C	0.015995	0.018824	0.849751	0.4027
R-squared	0.417048	Mean dependent var		0.002114
Adjusted R-squared	0.375408	S.D. dependent var		0.130781
S.E. of regression	0.103357	Akaike info criterion		-1.609481
Sum squared resid	0.299117	Schwarz criterion		-1.470708
Log likelihood	27.94696	F-statistic		10.01569
Durbin-Watson stat	1.992261	Prob(F-statistic)		0.000523

ADF(1) d=1, avec trend et constante

ADF Test Statistic	-4.986836	1% Critical Value*		-4.2826
		5% Critical Value		-3.5614
		10% Critical Value		-3.2138
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRP,2)
Method: Least Squares
Date: 03/20/06 Time: 19:42
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LPRP(-1))	-1.061729	0.212906	-4.986836	0.0000
D(LPRP(-1),2)	0.335780	0.170421	1.970292	0.0591
C	0.095390	0.042569	2.240845	0.0335
@TREND(1970)	-0.004290	0.002089	-2.053866	0.0498
R-squared	0.495819	Mean dependent var		0.002114
Adjusted R-squared	0.439799	S.D. dependent var		0.130781
S.E. of regression	0.097885	Akaike info criterion		-1.690135
Sum squared resid	0.258699	Schwarz criterion		-1.505104
Log likelihood	30.19709	F-statistic		8.850725
Durbin-Watson stat	2.121695	Prob(F-statistic)		0.000300

ADF(1) d=1, ni trend ni constante

ADF Test Statistic	-4.259375	1% Critical Value*		-2.6395
		5% Critical Value		-1.9521
		10% Critical Value		-1.6214
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPRP,2)
Method: Least Squares
Date: 03/20/06 Time: 19:43
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(LPRP(-1))	-0.885773	0.207958	-4.259375	0.0002
D(LPRP(-1),2)	0.267491	0.176199	1.518114	0.1398
R-squared	0.402014	Mean dependent var		0.002114
Adjusted R-squared	0.381394	S.D. dependent var		0.130781
S.E. of regression	0.102861	Akaike info criterion		-1.648536
Sum squared resid	0.306831	Schwarz criterion		-1.556020
Log likelihood	27.55230	F-statistic		19.49614
Durbin-Watson stat	1.977665	Prob(F-statistic)		0.000128

Conclusion : toutes les variables sont intégrées d'ordre 1 : il y a présomption de cointégration

2-Estimation de la tendance de LT par la méthode des MCO (à la Engle-Granger) : Estimation de EQ/LT

Dependent Variable: LPRC
Method: Least Squares
Date: 04/19/06 Time: 21:16
Sample: 1970 2003
Included observations: 34
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	3.024311	0.722924	4.183444	0.0002
LNSUB	0.577263	0.165251	3.493253	0.0016
LCONS	-0.389138	0.429220	-0.906615	0.3721
LPRO	-1.049172	0.412342	-2.544426	0.0165
LPRP	0.598628	0.160051	3.740229	0.0008
R-squared	0.630597	Mean dependent var		4.180170
Adjusted R-squared	0.579645	S.D. dependent var		0.259579
S.E. of regression	0.168297	Akaike info criterion		-0.591115
Sum squared resid	0.821396	Schwarz criterion		-0.366650
Log likelihood	15.04896	F-statistic		12.37626
Durbin-Watson stat	1.623121	Prob(F-statistic)		0.000005

Stationnarité des résidus :

ADF Test Statistic	-6.595528	1% Critical Value*		-3.6496
		5% Critical Value		-2.9558
		10% Critical Value		-2.6164
*MacKinnon critical values for rejection of hypothesis of a unit root.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(RESID3)
Method: Least Squares
Date: 04/25/06 Time: 12:40
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Variable	Coefficient	Std. Error	t-Statistic	Prob.
RESID3(-1)	-1.344164	0.203799	-6.595528	0.0000
D(RESID3(-1))	0.485885	0.148773	3.265953	0.0028
C	0.011472	0.023340	0.491505	0.6268
R-squared	0.606844	Mean dependent var		0.007869
Adjusted R-squared	0.579730	S.D. dependent var		0.203433
S.E. of regression	0.131882	Akaike info criterion		-1.124758
Sum squared resid	0.504393	Schwarz criterion		-0.987346
Log likelihood	20.99614	F-statistic		22.38108
Durbin-Watson stat	2.164398	Prob(F-statistic)		0.000001

Conclusion : Confirmation de la possibilité de cointégration des variables

3- Détermination du nombre de retard

Date: 05/11/06 Time: 15:46
Sample(adjusted): 1971 2003
Included observations: 33 after adjusting endpoints
Standard errors & t-statistics in parentheses
	LPRC	LNSUB	LPRO	LCONS	LPRP
LPRC(-1)	0.205257	0.274352	0.242383	-0.082652	0.255119
	(0.19352)	(0.15647)	(0.06694)	(0.03065)	(0.09499)
	(1.06066)	(1.75334)	(3.62082)	(-2.69683)	(2.68573)
LNSUB(-1)	0.303332	0.344130	-0.238073	0.009668	0.051107
	(0.20291)	(0.16407)	(0.07019)	(0.03214)	(0.09960)
	(1.49490)	(2.09747)	(-3.39179)	(0.30084)	(0.51311)
LPRO(-1)	-1.268494	-0.259161	0.401130	0.098791	-0.379355
	(0.46881)	(0.37907)	(0.16217)	(0.07425)	(0.23012)
	(-2.70577)	(-0.68368)	(2.47351)	(1.33058)	(-1.64850)
LCONS(-1)	0.357396	1.367578	0.978226	0.821134	0.388632
	(0.45644)	(0.36907)	(0.15789)	(0.07229)	(0.22405)
	(0.78301)	(3.70551)	(6.19557)	(11.3593)	(1.73459)
LPRP(-1)	0.293807	-0.049724	-0.029107	0.075944	0.661992
	(0.20572)	(0.16634)	(0.07116)	(0.03258)	(0.10098)
	(1.42821)	(-0.29894)	(-0.40902)	(2.33100)	(6.55578)
C	3.491248	-0.123557	-0.497207	0.311607	-0.131247
	(0.97673)	(0.78976)	(0.33787)	(0.15469)	(0.47944)
	(3.57441)	(-0.15645)	(-1.47159)	(2.01443)	(-0.27375)
R-squared	0.512180	0.874628	0.903856	0.979403	0.899236
Adj. R-squared	0.421843	0.851411	0.886052	0.975589	0.880576
Sum sq. resids	0.807513	0.527949	0.096627	0.020254	0.194566
S.E. equation	0.172939	0.139834	0.059823	0.027389	0.084889
F-statistic	5.669659	37.67185	50.76589	256.7778	48.19041
Log likelihood	14.39504	21.40686	49.42621	75.20757	37.87760
Akaike AIC	-0.508790	-0.933749	-2.631891	-4.194398	-1.931976
Schwarz SC	-0.236698	-0.661657	-2.359799	-3.922306	-1.659884
Mean dependent	4.202674	8.514157	4.328230	4.329735	4.141739
S.D. dependent	0.227442	0.362761	0.177220	0.175300	0.245644
Determinant Residual Covariance		2.25E-12
Log Likelihood		208.3760
Akaike Information Criteria		-10.81067	-10.82271	-11.10134	-11.42893
Schwarz Criteria		-9.450204	-8.303478	-7.400730	-6.524736
Date: 05/11/06 Time: 15:55
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Standard errors & t-statistics in parentheses
	LPRC	LNSUB	LPRO	LCONS	LPRP
LPRC(-1)	0.054017	0.167893	0.296354	-0.122028	0.177222
	(0.23839)	(0.21391)	(0.07140)	(0.03788)	(0.11618)
	(0.22659)	(0.78486)	(4.15080)	(-3.22144)	(1.52541)
LPRC(-2)	-0.191853	0.220860	-0.154710	0.068977	0.028441
	(0.33366)	(0.29940)	(0.09993)	(0.05302)	(0.16261)
	(-0.57499)	(0.73768)	(-1.54820)	(1.30103)	(0.17491)
LNSUB(-1)	0.235207	0.339353	-0.260789	-0.034177	0.061208
	(0.25571)	(0.22945)	(0.07658)	(0.04063)	(0.12462)
	(0.91982)	(1.47896)	(-3.40530)	(-0.84115)	(0.49116)
LNSUB(-2)	0.215523	-0.167257	0.105220	0.024496	0.042116
	(0.26916)	(0.24152)	(0.08061)	(0.04277)	(0.13117)
	(0.80072)	(-0.69251)	(1.30527)	(0.57275)	(0.32107)
LPRO(-1)	-0.954584	-0.712120	0.579659	0.023316	-0.315089
	(0.68804)	(0.61739)	(0.20606)	(0.10933)	(0.33531)
	(-1.38740)	(-1.15344)	(2.81303)	(0.21327)	(-0.93969)
LPRO(-2)	-0.086501	0.056477	-0.361435	-0.066581	-0.234434
	(0.56393)	(0.50602)	(0.16889)	(0.08961)	(0.27483)
	(-0.15339)	(0.11161)	(-2.14005)	(-0.74305)	(-0.85303)
LCONS(-1)	0.992224	1.459671	0.196767	0.966773	1.336411
	(1.27334)	(1.14259)	(0.38136)	(0.20233)	(0.62056)
	(0.77923)	(1.27751)	(0.51597)	(4.77820)	(2.15357)
LCONS(-2)	-1.307031	0.567750	0.766128	0.024890	-0.830475
	(1.19682)	(1.07392)	(0.35844)	(0.19017)	(0.58326)
	(-1.09209)	(0.52867)	(2.13742)	(0.13088)	(-1.42385)
LPRP(-1)	0.631784	-0.151012	-0.212215	0.027226	0.965613
	(0.42568)	(0.38197)	(0.12749)	(0.06764)	(0.20745)
	(1.48419)	(-0.39535)	(-1.66462)	(0.40252)	(4.65467)
LPRP(-2)	-0.185877	0.070733	0.262675	0.013697	-0.333759
	(0.34410)	(0.30877)	(0.10306)	(0.05468)	(0.16770)
	(-0.54018)	(0.22908)	(2.54887)	(0.25052)	(-1.99026)
C	4.960554	-0.142300	-0.237564	0.376907	-0.032798
	(1.30409)	(1.17018)	(0.39056)	(0.20722)	(0.63554)
	(3.80384)	(-0.12161)	(-0.60826)	(1.81891)	(-0.05161)
R-squared	0.523496	0.853348	0.941023	0.982867	0.910389
Adj. R-squared	0.296590	0.783514	0.912939	0.974708	0.867718
Sum sq. resids	0.618896	0.498322	0.055512	0.015626	0.146991
S.E. equation	0.171672	0.154044	0.051414	0.027278	0.083663
F-statistic	2.307101	12.21965	33.50710	120.4683	21.33473
Log likelihood	17.72283	21.18987	56.30421	76.58685	40.72389
Akaike AIC	-0.420177	-0.636867	-2.831513	-4.099178	-1.857743
Schwarz SC	0.083670	-0.133020	-2.327667	-3.595331	-1.353897
Mean dependent	4.221048	8.541905	4.336001	4.337954	4.158327
S.D. dependent	0.204689	0.331079	0.174250	0.171523	0.230030
Determinant Residual Covariance		4.41E-13
Log Likelihood		228.1634
Akaike Information Criteria		-10.82271
Schwarz Criteria		-8.303478
Date: 05/11/06 Time: 15:57
Sample(adjusted): 1973 2003
Included observations: 31 after adjusting endpoints
Standard errors & t-statistics in parentheses
	LPRC	LNSUB	LPRO	LCONS	LPRP
LPRC(-1)	-0.245937	0.068784	0.234987	-0.165855	0.086595
	(0.21720)	(0.29678)	(0.08511)	(0.04853)	(0.14591)
	(-1.13228)	(0.23177)	(2.76082)	(-3.41779)	(0.59348)
LPRC(-2)	0.413556	0.159916	-0.119117	0.079895	0.183662
	(0.38810)	(0.53028)	(0.15208)	(0.08671)	(0.26071)
	(1.06560)	(0.30157)	(-0.78324)	(0.92144)	(0.70446)
LPRC(-3)	-1.104008	0.034854	-0.075947	-0.064501	-0.224231
	(0.34948)	(0.47751)	(0.13695)	(0.07808)	(0.23477)
	(-3.15903)	(0.07299)	(-0.55457)	(-0.82611)	(-0.95512)
LNSUB(-1)	0.367848	0.401346	-0.205604	-0.010779	0.099138
	(0.21292)	(0.29093)	(0.08344)	(0.04757)	(0.14304)
	(1.72761)	(1.37953)	(-2.46417)	(-0.22659)	(0.69310)
LNSUB(-2)	0.036283	-0.409798	0.029598	0.002050	0.046809
	(0.28917)	(0.39511)	(0.11332)	(0.06461)	(0.19426)
	(0.12547)	(-1.03716)	(0.26120)	(0.03173)	(0.24097)
LNSUB(-3)	0.144111	0.243795	0.174075	0.065224	-0.048788
	(0.24170)	(0.33025)	(0.09471)	(0.05400)	(0.16237)
	(0.59624)	(0.73821)	(1.83788)	(1.20785)	(-0.30048)
LPRO(-1)	-2.500951	-0.862791	0.491919	-0.049179	-0.798061
	(0.81222)	(1.10978)	(0.31828)	(0.18146)	(0.54562)
	(-3.07917)	(-0.77744)	(1.54555)	(-0.27102)	(-1.46266)
LPRO(-2)	0.751703	0.243756	-0.073719	0.045987	-0.065033
	(0.68931)	(0.94184)	(0.27012)	(0.15400)	(0.46306)
	(1.09052)	(0.25881)	(-0.27292)	(0.29861)	(-0.14044)
LPRO(-3)	-0.479734	-0.183035	-0.150010	-0.101153	-0.292767
	(0.51487)	(0.70350)	(0.20176)	(0.11503)	(0.34588)
	(-0.93175)	(-0.26018)	(-0.74350)	(-0.87936)	(-0.84645)
LCONS(-1)	2.869136	0.947850	0.106287	0.942211	1.890448
	(1.24666)	(1.70338)	(0.48852)	(0.27852)	(0.83747)
	(2.30146)	(0.55645)	(0.21757)	(3.38289)	(2.25734)
LCONS(-2)	-5.020108	0.446684	1.106218	0.146441	-1.307816
	(1.58014)	(2.15904)	(0.61920)	(0.35303)	(1.06149)
	(-3.17700)	(0.20689)	(1.78652)	(0.41481)	(-1.23205)
LCONS(-3)	2.453802	0.502073	-0.624952	-0.215713	0.355910
	(1.03224)	(1.41041)	(0.40450)	(0.23062)	(0.69343)
	(2.37717)	(0.35598)	(-1.54501)	(-0.93537)	(0.51326)
LPRP(-1)	0.620927	0.055480	-0.173332	0.043248	1.019617
	(0.36526)	(0.49907)	(0.14313)	(0.08160)	(0.24537)
	(1.69998)	(0.11117)	(-1.21100)	(0.52997)	(4.15546)
LPRP(-2)	0.411054	-0.336099	0.172165	0.007776	-0.445740
	(0.49126)	(0.67124)	(0.19251)	(0.10976)	(0.33001)
	(0.83673)	(-0.50071)	(0.89432)	(0.07085)	(-1.35067)
LPRP(-3)	0.096060	0.277100	0.076103	0.044549	0.273411
	(0.34335)	(0.46915)	(0.13455)	(0.07671)	(0.23066)
	(0.27977)	(0.59065)	(0.56561)	(0.58075)	(1.18537)
C	7.149779	0.751159	0.182226	0.772576	0.547116
	(1.43402)	(1.95939)	(0.56194)	(0.32038)	(0.96333)
	(4.98582)	(0.38336)	(0.32428)	(2.41142)	(0.56794)
R-squared	0.786643	0.839456	0.958332	0.985682	0.912131
Adj. R-squared	0.573286	0.678912	0.916665	0.971363	0.824261
Sum sq. resids	0.242786	0.453267	0.037282	0.012119	0.109564
S.E. equation	0.127223	0.173833	0.049854	0.028424	0.085465
F-statistic	3.686976	5.228821	22.99948	68.84061	10.38053
Log likelihood	31.18113	21.50445	60.22302	77.64150	43.51409
Akaike AIC	-0.979427	-0.355126	-2.853098	-3.976871	-1.775103
Schwarz SC	-0.239305	0.384997	-2.112976	-3.236748	-1.034980
Mean dependent	4.233784	8.565974	4.342848	4.346090	4.178243
S.D. dependent	0.194759	0.306775	0.172699	0.167965	0.203870
Determinant Residual Covariance		5.95E-14
Log Likelihood		252.0708
Akaike Information Criteria		-11.10134
Schwarz Criteria		-7.400730
Date: 05/11/06 Time: 16:01
Sample(adjusted): 1974 2003
Included observations: 30 after adjusting endpoints
Standard errors & t-statistics in parentheses
	LPRC	LNSUB	LPRO	LCONS	LPRP
LPRC(-1)	-0.226373	0.542015	0.184618	-0.162003	-0.000788
	(0.43478)	(0.58920)	(0.17405)	(0.09883)	(0.32041)
	(-0.52066)	(0.91992)	(1.06069)	(-1.63918)	(-0.00246)
LPRC(-2)	0.549416	0.215517	-0.168977	0.052860	0.080895
	(0.43932)	(0.59534)	(0.17587)	(0.09986)	(0.32375)
	(1.25062)	(0.36201)	(-0.96080)	(0.52933)	(0.24987)
LPRC(-3)	-0.938749	0.370471	0.056750	-0.104554	-0.233053
	(0.49139)	(0.66591)	(0.19672)	(0.11170)	(0.36213)
	(-1.91038)	(0.55634)	(0.28848)	(-0.93603)	(-0.64357)
LPRC(-4)	-0.019533	0.578245	-0.172632	0.056250	-0.142389
	(0.65439)	(0.88679)	(0.26197)	(0.14875)	(0.48224)
	(-0.02985)	(0.65206)	(-0.65898)	(0.37815)	(-0.29526)
LNSUB(-1)	0.441311	0.260112	-0.212714	-0.021185	0.097884
	(0.28327)	(0.38387)	(0.11340)	(0.06439)	(0.20875)
	(1.55793)	(0.67760)	(-1.87579)	(-0.32901)	(0.46890)
LNSUB(-2)	0.016328	-0.310667	0.073766	0.001531	0.077325
	(0.32863)	(0.44534)	(0.13156)	(0.07470)	(0.24218)
	(0.04968)	(-0.69759)	(0.56070)	(0.02050)	(0.31929)
LNSUB(-3)	0.230263	0.129316	0.063591	0.101209	-0.075947
	(0.36134)	(0.48967)	(0.14465)	(0.08214)	(0.26628)
	(0.63725)	(0.26409)	(0.43961)	(1.23221)	(-0.28521)
LNSUB(-4)	-0.121277	-0.405189	0.111100	-0.073903	0.078171
	(0.33098)	(0.44853)	(0.13250)	(0.07524)	(0.24391)
	(-0.36642)	(-0.90337)	(0.83849)	(-0.98228)	(0.32049)
LPRO(-1)	-2.477442	0.073842	0.372196	0.065756	-0.904958
	(1.12731)	(1.52767)	(0.45129)	(0.25625)	(0.83076)
	(-2.19767)	(0.04834)	(0.82474)	(0.25661)	(-1.08932)
LPRO(-2)	0.568162	0.184654	-0.488380	0.116314	-0.393010
	(1.17650)	(1.59433)	(0.47098)	(0.26743)	(0.86701)
	(0.48293)	(0.11582)	(-1.03694)	(0.43493)	(-0.45330)
LPRO(-3)	-0.385009	-0.304832	0.088451	-0.240408	-0.264362
	(0.79768)	(1.08098)	(0.31933)	(0.18132)	(0.58784)
	(-0.48266)	(-0.28200)	(0.27699)	(-1.32585)	(-0.44972)
LPRO(-4)	-0.332337	0.199262	-0.159839	0.160311	-0.268490
	(0.66419)	(0.90008)	(0.26589)	(0.15098)	(0.48947)
	(-0.50036)	(0.22138)	(-0.60114)	(1.06180)	(-0.54853)
LCONS(-1)	3.188688	1.247296	0.039658	0.887472	1.547912
	(1.43578)	(1.94570)	(0.57478)	(0.32637)	(1.05808)
	(2.22088)	(0.64105)	(0.06900)	(2.71921)	(1.46294)
LCONS(-2)	-4.653193	0.296322	1.607146	0.062645	-0.758469
	(2.30862)	(3.12853)	(0.92420)	(0.52478)	(1.70131)
	(-2.01558)	(0.09472)	(1.73896)	(0.11937)	(-0.44582)
LCONS(-3)	2.693801	0.700174	-1.382048	-0.348192	0.093905
	(2.40267)	(3.25599)	(0.96185)	(0.54616)	(1.77062)
	(1.12117)	(0.21504)	(-1.43686)	(-0.63753)	(0.05303)
LCONS(-4)	-0.298093	0.418181	0.545769	0.145026	0.294286
	(1.33842)	(1.81377)	(0.53581)	(0.30424)	(0.98634)
	(-0.22272)	(0.23056)	(1.01859)	(0.47668)	(0.29836)
LPRP(-1)	0.573966	-0.079010	-0.210639	0.043197	0.902372
	(0.44493)	(0.60295)	(0.17812)	(0.10114)	(0.32789)
	(1.29000)	(-0.13104)	(-1.18257)	(0.42711)	(2.75207)
LPRP(-2)	0.192267	-0.323267	0.341200	0.052700	-0.194420
	(0.62844)	(0.85163)	(0.25158)	(0.14285)	(0.46312)
	(0.30594)	(-0.37959)	(1.35623)	(0.36891)	(-0.41981)
LPRP(-3)	0.302981	-0.691553	-0.167577	0.016095	0.158251
	(0.72023)	(0.97602)	(0.28833)	(0.16372)	(0.53076)
	(0.42067)	(-0.70854)	(-0.58121)	(0.09831)	(0.29816)
LPRP(-4)	-0.159187	0.304551	0.260099	-0.008189	0.209983
	(0.40673)	(0.55118)	(0.16282)	(0.09245)	(0.29973)
	(-0.39138)	(0.55254)	(1.59742)	(-0.08858)	(0.70056)
C	5.598849	-4.751686	0.856996	0.838139	2.253647
	(3.46637)	(4.69746)	(1.38768)	(0.78795)	(2.55450)
	(1.61519)	(-1.01154)	(0.61757)	(1.06369)	(0.88223)
R-squared	0.847344	0.879766	0.967549	0.988648	0.896895
Adj. R-squared	0.508108	0.612579	0.895436	0.963421	0.667774
Sum sq. resids	0.172065	0.315987	0.027575	0.008891	0.093445
S.E. equation	0.138269	0.187376	0.055353	0.031430	0.101896
F-statistic	2.497799	3.292700	13.41705	39.18994	3.914493
Log likelihood	34.84806	25.73061	62.31225	79.29084	44.00557
Akaike AIC	-0.923204	-0.315374	-2.754150	-3.886056	-1.533705
Schwarz SC	0.057634	0.665464	-1.773312	-2.905218	-0.552866
Mean dependent	4.230377	8.580462	4.349803	4.354332	4.197379
S.D. dependent	0.197147	0.301038	0.171178	0.164336	0.176782
Determinant Residual Covariance		6.82E-15
Log Likelihood		276.4339
Akaike Information Criteria		-11.42893
Schwarz Criteria		-6.524736

Conclusion : p=1.

4 et 5- Test de cointégration et Identification du nombre de relation

Démarches préliminaires pour le choix du type d'estimation :



Conclusion : les variables présentent des tendances et des constantes

Estimation

Date: 04/19/06 Time: 21:08
Sample: 1970 2003
Included observations: 32
Test assumption: Linear deterministic trend in the data
Series: LPRC LNSUB LCONS LPRO LPRP
Lags interval: 1 to 1
	Likelihood	5 Percent	1 Percent	Hypothesized
Eigenvalue	Ratio	Critical Value	Critical Value	No. of CE(s)
0.611985	85.14212	68.52	76.07	None **
0.530836	54.84738	47.21	54.46	At most 1 **
0.395104	30.62966	29.68	35.65	At most 2 *
0.343720	14.54330	15.41	20.04	At most 3
0.032762	1.065957	3.76	6.65	At most 4
*(**) denotes rejection of the hypothesis at 5%(1%) significance level
L.R. test indicates 3 cointegrating equation(s) at 5% significance level
Unnormalized Cointegrating Coefficients:
LPRC	LNSUB	LCONS	LPRO	LPRP
-0.945457	0.321664	2.447826	-3.948896	0.885794
-1.516209	0.587783	-3.439992	1.888552	0.622787
-0.765169	1.473529	-3.287545	0.822495	0.262914
-0.514963	-0.371339	-1.444340	1.713768	1.238298
-0.128405	-0.106953	1.615928	-0.247785	-0.311950
Normalized Cointegrating Coefficients: 1 Cointegrating Equation(s)
LPRC	LNSUB	LCONS	LPRO	LPRP	C
1.000000	-0.340221	-2.589041	4.176708	-0.936895	-4.290731
	(0.19966)	(1.42312)	(1.47951)	(0.18836)
Log likelihood	200.7397
Normalized Cointegrating Coefficients: 2 Cointegrating Equation(s)
LPRC	LNSUB	LCONS	LPRO	LPRP	C
1.000000	0.000000	-37.42325	43.05829	-4.709709	-9.056512
		(193.217)	(218.834)	(20.5612)
0.000000	1.000000	-102.3871	114.2834	-11.08932	-14.00792
		(519.847)	(588.769)	(55.3197)
Log likelihood	212.8486
Normalized Cointegrating Coefficients: 3 Cointegrating Equation(s)
LPRC	LNSUB	LCONS	LPRO	LPRP	C
1.000000	0.000000	0.000000	0.700911	-0.619779	-4.663857
			(0.19598)	(0.16195)
0.000000	1.000000	0.000000	-1.603080	0.100418	-1.989950
			(0.32894)	(0.27181)
0.000000	0.000000	1.000000	-1.131846	0.109288	0.117378
			(0.05883)	(0.04861)
Log likelihood	220.8917
Normalized Cointegrating Coefficients: 4 Cointegrating Equation(s)
LPRC	LNSUB	LCONS	LPRO	LPRP	C
1.000000	0.000000	0.000000	0.000000	4.407756	-22.46227
				(14.2290)
0.000000	1.000000	0.000000	0.000000	-11.39825	38.71748
				(29.9442)
0.000000	0.000000	1.000000	0.000000	-8.009287	28.85866
				(21.7943)
0.000000	0.000000	0.000000	1.000000	-7.172860	25.39327
				(19.3764)
Log likelihood	227.6304

6- Estimation par le MV du MVCE

Une seule relation de cointégration

Date: 04/19/06 Time: 20:47
Sample(adjusted): 1972 2003
Included observations: 32 after adjusting endpoints
Standard errors & t-statistics in parentheses
Cointegrating Eq:	CointEq1
LPRC(-1)	1.000000
LNSUB(-1)	-0.340221
	(0.19966)
	(-1.70402)
LCONS(-1)	-2.589041
	(1.42312)
	(-1.81927)
LPRO(-1)	4.176708
	(1.47951)
	(2.82303)
LPRP(-1)	-0.936895
	(0.18836)
	(-4.97407)
C	-4.290731
Error Correction:	D(LPRC)	D(LNSUB)	D(LCONS)	D(LPRO)	D(LPRP)
CointEq1	-0.408546	-0.049574	-0.022115	-0.121356	0.000784
	(0.19035)	(0.16979)	(0.02553)	(0.05467)	(0.08981)
	(-2.14633)	(-0.29197)	(-0.86612)	(-2.21988)	(0.00873)
D(LPRC(-1))	-0.316397	0.301299	-0.087310	0.379427	0.210096
	(0.18775)	(0.16748)	(0.02518)	(0.05392)	(0.08859)
	(-1.68519)	(1.79904)	(-3.46676)	(7.03654)	(2.37164)
D(LNSUB(-1))	0.118426	-0.259614	-0.024495	-0.244631	0.040542
	(0.24860)	(0.22175)	(0.03335)	(0.07140)	(0.11729)
	(0.47638)	(-1.17074)	(-0.73457)	(-3.42636)	(0.34565)
D(LCONS(-1))	1.195784	0.800612	0.014164	-0.548300	0.663415
	(1.30534)	(1.16439)	(0.17510)	(0.37489)	(0.61590)
	(0.91607)	(0.68758)	(0.08089)	(-1.46255)	(1.07715)
D(LPRO(-1))	-0.087055	0.237999	0.085543	0.428219	-0.045992
	(0.62141)	(0.55431)	(0.08336)	(0.17847)	(0.29320)
	(-0.14009)	(0.42936)	(1.02623)	(2.39938)	(-0.15686)
D(LPRP(-1))	-0.022968	-0.083023	-0.014327	-0.206414	0.345722
	(0.38538)	(0.34376)	(0.05169)	(0.11068)	(0.18183)
	(-0.05960)	(-0.24151)	(-0.27714)	(-1.86495)	(1.90132)
C	0.001501	0.028548	0.017616	0.022661	-0.005370
	(0.04367)	(0.03895)	(0.00586)	(0.01254)	(0.02060)
	(0.03437)	(0.73288)	(3.00730)	(1.80680)	(-0.26061)
R-squared	0.338084	0.203830	0.445777	0.717695	0.375007
Adj. R-squared	0.179224	0.012749	0.312763	0.649942	0.225008
Sum sq. resids	1.013322	0.806295	0.018233	0.083583	0.225589
S.E. equation	0.201328	0.179588	0.027006	0.057821	0.094992
F-statistic	2.128192	1.066723	3.351364	10.59279	2.500072
Log likelihood	9.834004	13.49063	74.11802	49.75638	33.87040
Akaike AIC	-0.177125	-0.405664	-4.194877	-2.672274	-1.679400
Schwarz SC	0.143504	-0.085034	-3.874247	-2.351644	-1.358770
Mean dependent	0.019029	0.039240	0.016097	0.013868	0.015572
S.D. dependent	0.222224	0.180744	0.032577	0.097728	0.107905
Determinant Residual Covariance		2.45E-12
Log Likelihood		200.7397
Akaike Information Criteria		-10.04623
Schwarz Criteria		-8.214061

Représentation

Estimation Proc:

===============================

EC 1 1 LPRC LNSUB LCONS LPRO LPRP @ C

VAR Model:

===============================

D(LPRC) = A(1,1)*(B(1,1)*LPRC(-1) + B(1,2)*LNSUB(-1) + B(1,3)*LCONS(-1) + B(1,4)*LPRO(-1) + B(1,5)*LPRP(-1) + B(1,6)) + C(1,1)*D(LPRC(-1)) + C(1,2)*D(LNSUB(-1)) + C(1,3)*D(LCONS(-1)) + C(1,4)*D(LPRO(-1)) + C(1,5)*D(LPRP(-1)) + C(1,6)

D(LNSUB) = A(2,1)*(B(1,1)*LPRC(-1) + B(1,2)*LNSUB(-1) + B(1,3)*LCONS(-1) + B(1,4)*LPRO(-1) + B(1,5)*LPRP(-1) + B(1,6)) + C(2,1)*D(LPRC(-1)) + C(2,2)*D(LNSUB(-1)) + C(2,3)*D(LCONS(-1)) + C(2,4)*D(LPRO(-1)) + C(2,5)*D(LPRP(-1)) + C(2,6)

D(LCONS) = A(3,1)*(B(1,1)*LPRC(-1) + B(1,2)*LNSUB(-1) + B(1,3)*LCONS(-1) + B(1,4)*LPRO(-1) + B(1,5)*LPRP(-1) + B(1,6)) + C(3,1)*D(LPRC(-1)) + C(3,2)*D(LNSUB(-1)) + C(3,3)*D(LCONS(-1)) + C(3,4)*D(LPRO(-1)) + C(3,5)*D(LPRP(-1)) + C(3,6)

D(LPRO) = A(4,1)*(B(1,1)*LPRC(-1) + B(1,2)*LNSUB(-1) + B(1,3)*LCONS(-1) + B(1,4)*LPRO(-1) + B(1,5)*LPRP(-1) + B(1,6)) + C(4,1)*D(LPRC(-1)) + C(4,2)*D(LNSUB(-1)) + C(4,3)*D(LCONS(-1)) + C(4,4)*D(LPRO(-1)) + C(4,5)*D(LPRP(-1)) + C(4,6)

D(LPRP) = A(5,1)*(B(1,1)*LPRC(-1) + B(1,2)*LNSUB(-1) + B(1,3)*LCONS(-1) + B(1,4)*LPRO(-1) + B(1,5)*LPRP(-1) + B(1,6)) + C(5,1)*D(LPRC(-1)) + C(5,2)*D(LNSUB(-1)) + C(5,3)*D(LCONS(-1)) + C(5,4)*D(LPRO(-1)) + C(5,5)*D(LPRP(-1)) + C(5,6)

VAR Model - Substituted Coefficients:

===============================

D(LPRC) = - 0.4085463551*( LPRC(-1) - 0.3402205817*LNSUB(-1) - 2.589040839*LCONS(-1) + 4.176707946*LPRO(-1) - 0.9368954394*LPRP(-1) - 4.290730878 ) - 0.3163970841*D(LPRC(-1)) + 0.1184264556*D(LNSUB(-1)) + 1.195783779*D(LCONS(-1)) - 0.08705458523*D(LPRO(-1)) - 0.02296766631*D(LPRP(-1)) + 0.001500734796

D(LNSUB) = - 0.04957379141*( LPRC(-1) - 0.3402205817*LNSUB(-1) - 2.589040839*LCONS(-1) + 4.176707946*LPRO(-1) - 0.9368954394*LPRP(-1) - 4.290730878 ) + 0.301299125*D(LPRC(-1)) - 0.2596136987*D(LNSUB(-1)) + 0.8006116274*D(LCONS(-1)) + 0.2379992104*D(LPRO(-1)) - 0.08302317248*D(LPRP(-1)) + 0.02854829442

D(LCONS) = - 0.02211463955*( LPRC(-1) - 0.3402205817*LNSUB(-1) - 2.589040839*LCONS(-1) + 4.176707946*LPRO(-1) - 0.9368954394*LPRP(-1) - 4.290730878 ) - 0.0873100742*D(LPRC(-1)) - 0.02449539672*D(LNSUB(-1)) + 0.01416385047*D(LCONS(-1)) + 0.08554264835*D(LPRO(-1)) - 0.01432669387*D(LPRP(-1)) + 0.01761599735

D(LPRO) = - 0.1213556337*( LPRC(-1) - 0.3402205817*LNSUB(-1) - 2.589040839*LCONS(-1) + 4.176707946*LPRO(-1) - 0.9368954394*LPRP(-1) - 4.290730878 ) + 0.3794270341*D(LPRC(-1)) - 0.2446314623*D(LNSUB(-1)) - 0.5482998201*D(LCONS(-1)) + 0.428219454*D(LPRO(-1)) - 0.2064141313*D(LPRP(-1)) + 0.02266051657

D(LPRP) = 0.000783830909*( LPRC(-1) - 0.3402205817*LNSUB(-1) - 2.589040839*LCONS(-1) + 4.176707946*LPRO(-1) - 0.9368954394*LPRP(-1) - 4.290730878 ) + 0.2100964483*D(LPRC(-1)) + 0.04054244061*D(LNSUB(-1)) + 0.6634154436*D(LCONS(-1)) - 0.04599184447*D(LPRO(-1)) + 0.3457220482*D(LPRP(-1)) - 0.005369653458

Test de résidus



Fonctions de réponses impulsionnelles.



Décompositions :

Variance Decomposition of LPRC:
Period	S.E.	LPRC	LNSUB	LCONS	LPRO	LPRP
1	0.177950	100.0000	0.000000	0.000000	0.000000	0.000000
2	0.224737	92.76315	0.042907	0.999760	4.614941	1.579239
3	0.250415	81.64260	1.541987	1.922280	7.687241	7.205891
4	0.279786	78.01703	2.556988	2.665882	6.681592	10.07851
5	0.312732	78.98321	2.305599	3.113555	5.626746	9.970885
6	0.338014	78.45788	2.128654	3.385928	5.722191	10.30535
7	0.359041	76.68254	2.264889	3.607509	6.055721	11.38934
8	0.380362	75.66115	2.429385	3.813191	5.921598	12.17467
9	0.401919	75.49406	2.421548	3.974179	5.688267	12.42194
10	0.421696	75.24749	2.386898	4.093908	5.637912	12.63379
Variance Decomposition of LNSUB:
Period	S.E.	LPRC	LNSUB	LCONS	LPRO	LPRP
1	0.158735	1.727629	98.27237	0.000000	0.000000	0.000000
2	0.211557	9.389397	89.45837	1.133594	0.000221	0.018419
3	0.249446	7.309824	90.40773	1.662055	0.508587	0.111809
4	0.286149	5.704806	91.39929	1.829460	0.615525	0.450921
5	0.318708	5.322459	91.59296	2.015113	0.513564	0.555902
6	0.346523	5.359920	91.45440	2.175593	0.460590	0.549492
7	0.372013	5.094383	91.58242	2.265670	0.482608	0.574915
8	0.396723	4.775078	91.77324	2.323489	0.493404	0.634787
9	0.420109	4.613206	91.86129	2.381447	0.473461	0.670592
10	0.441875	4.545254	91.88159	2.433958	0.457278	0.681925
Variance Decomposition of LCONS:
Period	S.E.	LPRC	LNSUB	LCONS	LPRO	LPRP
1	0.023870	1.220395	2.175287	96.60432	0.000000	0.000000
2	0.038378	19.32826	0.892465	79.76153	0.000652	0.017094
3	0.046280	21.25906	0.614073	77.73385	0.361234	0.031782
4	0.052034	19.46435	0.538843	79.23361	0.549189	0.214012
5	0.057577	19.47363	0.475963	79.31863	0.463928	0.267847
6	0.062942	20.38253	0.398314	78.58309	0.398431	0.237633
7	0.067730	20.48185	0.344025	78.54152	0.408756	0.223850
8	0.072080	20.21356	0.309885	78.80697	0.427827	0.241757
9	0.076222	20.19296	0.284794	78.85738	0.411439	0.253424
10	0.080211	20.34288	0.259059	78.75606	0.392540	0.249458
Variance Decomposition of LPRO:
Period	S.E.	LPRC	LNSUB	LCONS	LPRO	LPRP
1	0.051107	37.44247	17.99844	9.310427	35.24866	0.000000
2	0.060785	29.44052	16.35456	9.025741	43.74565	1.433534
3	0.064338	33.24483	15.32760	9.753118	39.04924	2.625215
4	0.078964	43.27088	11.66073	8.390601	25.93073	10.74706
5	0.087501	40.74812	10.80146	9.396841	24.10128	14.95229
6	0.091811	37.85349	9.850822	11.01503	25.20354	16.07712
7	0.095812	37.53976	9.050009	11.99559	24.06529	17.34935
8	0.101722	38.47024	8.260245	12.22775	21.90811	19.13365
9	0.107136	38.08169	7.757711	12.62038	20.88908	20.65113
10	0.111343	37.22760	7.301368	13.22719	20.63755	21.60629
Variance Decomposition of LPRP:
Period	S.E.	LPRC	LNSUB	LCONS	LPRO	LPRP
1	0.083962	5.190848	2.631411	0.648278	4.129500	87.39996
2	0.152715	20.91790	1.275266	0.338137	3.258430	74.21027
3	0.205261	19.92680	0.953353	0.873190	2.220944	76.02571
4	0.249917	16.89389	0.687501	1.222509	1.742035	79.45407
5	0.290051	15.82977	0.533596	1.443802	1.691697	80.50113
6	0.325633	15.82930	0.476776	1.600689	1.704477	80.38875
7	0.357278	15.62293	0.450008	1.699759	1.631533	80.59577
8	0.386469	15.22558	0.413819	1.765444	1.558848	81.03630
9	0.413902	14.98052	0.381863	1.819542	1.532055	81.28602
10	0.439633	14.89579	0.362796	1.864895	1.523117	81.35340
Ordering: LPRC LNSUB LCONS LPRO LPRP

ANNEXE 2 :Approche mathématique et graphique de l'étude de Goreux(2003a)

P= prix mondial du coton défini par l'indice A^21(*) exprimé en cents par livre

S_i = subvention accordée par le gouvernement du pays i en cents par livre

Q_i = quantité de coton produit par le pays i en milliers de tonnes

Q_J = quantité de coton produite sans subvention par le pays j en milliers de tonnes

Q = quantité de coton produite dans l'ensemble du monde en milliers de tonnes

E₀ = coefficient d'élasticité de l'offre ( positif)

E_d = coefficient d'élasticité de la demande (négatif)

Ln = Logarithme

i = Indice caractérisant les pays à subventions Etats-Unis, Chine, UE (Grèce et Espagne)

j = Indice caractérisant les pays sans subventions : reste du monde

a_1. Prix et les quantités produites après l'élimination des subventions

Quand les subventions sont éliminées dans le pays i, le prix reçu par le producteur tombe de P +S_i à P et la production de Q_i à Q_i' défini par l'équation (1)

Ln (Q_i'/ Q_i) = E₀ * ln (P/ (P + S_I) (1)

L'opération est répétée pour chacun des quatre pays afin de calculer la quantité qui serait retirée du marché mondial par l'équation (2). On obtient ainsi l'amplitude de la translation horizontale vers la gauche de la courbe d'offre mondiale (figure 3B)

Q - Q' = SUM (Q_i- Q_i') (2)

Le déplacement vers la gauche de la courbe d'offre mondial provoque une hausse du prix mondial de P à P' qui conduit à une réduction de la demande Q - Q'' et une augmentation de la production

(Q''- Q') qui sont, respectivement, définies par les équations (3) et (4)

Ln (Q''/ Q) = E_d * Ln (P'/ P) (3)

Ln (Q''/ Q') = E₀ * Ln (P'/ P) (4)

Sachant q'un nouvel équilibre ne peut être obtenu que si l'équation (5) est satisfaite

Q - Q'= ( Q - Q'') + (Q''- Q') (5)

Pour des variations suffisamment faibles, on peut déduire des équations (3), (4) et (5), l'équation (6) qui permet de calculer le nouveau prix d'équilibre P'.

E₀ * Ln (P'/ P) - E_d * Ln (P'/ P) = Ln (Q''/ Q') - Ln (Q''/ Q)

Ln ((Q''/Q') . (Q /Q'')) = (E₀ - E_d ) . Ln (P'/P)

Ln (Q /Q') = ( E₀ - E_d) . Ln (P'/P) (6)

Connaissant l'augmentation des prix, on peut calculer l'augmentation de la production dans les pays j qui n'étaient pas subventionnés

Ln ( Q_j''/ Q_j ) = E₀ . Ln (P'/P) (7)

Pour les pays i qui étaient subventionnés, l'augmentation de la production causée par la hausse des prix de P à P' est calculée comme indiqué dans l'équation (7). Elle doit être combinée avec la réduction de la production précédemment calculée par l'équation (1) afin d'obtenir la production Q_i'' qui prévaudrait dans le pays i après élimination des subventions. Cette valeur est donnée par l'équation (8)

Q_i''/ Q_i = (Q_i''/ Q_i') . (Q_i'/ Q_i) (8)

a₂ Augmentation des revenus et des recettes d'exportations en AOC

Les pays non subventionnés ont été précédemment caractérisés par l'indice j. Comme il s'agit maintenant de calculer les gains d'un sous-groupe des pays non subventionnés, on caractérisera les pays de l'AOC par l'indice a.

L'augmentation de revenu net de l'AOC est due à deux facteurs. Tout d'abord, la production avant l'élimination des subventions ( Q_a ) est, après leur élimination, vendue au prix P' supérieur à P ce qui conduit au gain défini par l'équation (9).

Ensuite, pour ce qui est de la production additionnelle, les pays bénéficient du surplus du producteur défini par le triangle séparant le nouveau prix P' de la courbe d'offre qui est supposée mesurer le coût de la production additionnelle ; ce gain est défini par l'équation (10)

Q_a. (P'- P) (9)

0,5. (Q_a''- Q_a). (P'- P) = 0,5P. Q_a[(P'/P)-1] . [(Q_a''/ Q_a)-1] (10)

L'addition de ces deux termes donne l'accroissement du revenu net des filières AOC qui peut s'écrire :

R_a''- R_a = P . Q_a. [( P'/P)-1] [(1+ 0,5 . ((Q_a''/ Q_a)-1)] (11)

où P'/P est obtenu de l'équation (7) et Q_a''/ Q_a de l'équation (8).

L'augmentation des recettes d'exportation X_a'' - X_a est aussi décomposée de deux éléments_.

L'augmentation des recettes brutes X_ab'' - X_ab est donnée par l'équation (12) :

X_ab'' - X_{ab =} Q_a . (P'- P) + (Q_a'' - Q_a) . P'= Q_a''. P' - Q_a .P (12)

L'augmentation des recettes nettes X_an'' - X_an est donnée par l'équation (13)

X_an'' - X_{an =} Q_a . (P'- P) +(1-m) . (Q_a'' - Q_a) . P' (13)

Où m est une fraction obtenue en divisant le coût des importations additionnelles requises par la valeur de la production additionnelle.



TABLE DES MATIERES

DEDICACES ............................................................................................................................... II

REMERCIEMENTS.................................................................. IV

LISTE DES SIGLES ET ABREVIATIONS.................................... V

LISTE DES TABLEAUX...............................................................VII

LISTE DES FIGURES...............................................................VIII

RESUME.................................................................................IX

SOMMAIRE.............................................................................. X

INTRODUCION GENERALE........................................................ 1

CHAPITRE I CADRE THEORIQUE ET METHODOLOGIQUE

DE L'ETUDE ......................................................... 4

Section 1 : De la problématique à la revue de littérature.............5

PARAGRAPHE 1 : Problématique, objectifs et

hypothèses de recherche........................... ..5

A- Problématique et intérêt de l'étude ..................... ..5

1 - Problématique.................................................. 5

2- intérêt de l'étude............................................. .. 8

B- objectifs et hypothèses de recherche..................... ...8

1- objectifs......................................................... ... 8

2- hypothèses de recherche...................................... .9

PARAGRAPHE 2 : Revue de littérature ..................... ...9

A- Problématique de la réduction des

subventions et catégorisation des subventions...................9

1- Problématique de la réduction des subventions ..........9

2- Catégorisations des subventions........................ .... 12

B- Approche théorique et Empirique de

l'Empirique de l'Impact des subventions

Sur le marché mondial ........................................... 14

1- Approche théorique de l'Impact des subventions ...... 14

2- Approche Empirique de l'Impact des subventions ...... 21

2-1 L'étude de Goreux (2003 a) ........................ 21

2-2 L'étude de Shepherd (2004) ........................ 23

Section 2 : Méthodologie de la recherche .............................. 26

PARAGRAPHE1 :Présentation du modèle ..................... 26

A- Le modèle retenu ................................................ 26

B- Définition des variables....................................... .27

C- Période de l'étude et sources des données .....................29

1- Période de l'étude .................................... 29

2- Sources des donnés .................................... 29

PARAGRAPHE 2 :Méthode de d'analyse........................ .29

A- Tests de diagnostic sur les données .........................30

B- Estimation du MVCE...........................................30

CHAPITRE II : RESULTATS DE L'ETUDE ET ENJEUX ..............33

Section 1 : Etude de la cointégration et estimation du MVCE ... ..34

PARAGRAPHE 1 : Etude de la cointégration ....................34

A- Vérification des conditions préalables

à l'analyse de la cointégration .....................................34

B- Détermination du nombre optimal de

retard et cointégration à la Johansen ..............................37

1- Détermination du nombre optimal de retard ......... .37

2- Cointégration à la Johansen.............................. ..38

PARAGRAPHE 2 : Estimation et analyse du MVCE ......... .40

A- Estimation ...................................................... .40

B- Analyse des résultats du MVCE...............................42

Section 2 : Confirmation des résultats,

interprétations, limites et suggestions ................................. ...........43

PARAGRAPHE 1 : Confirmation des résultats du MVCE ... ..43

A- Fonctions de réponses Impulsionnelles ......................43

B- Décomposition de la variance .............................. ..45

·PARAGRAPHE 2 : Interprétations, limites et suggestions ... ..46

A- Interprétations des résultats ................................. ..46

B- Limites et suggestions....................................... ..47

1- limites et perspectives ....................................... .47

2- Suggestions .......................................................48

Conclusion générale ................................................................52

Bibliographie ........................................................................53

Annexes ..................................................................... XI

Annexes 1 : De stationnarité des variables à la

décomposition de la variance ......................................................XII

Annexes 2 : Approche mathématique et

graphique de l'étude de Goreux (2003 a) .......................................XLI

* ¹"Economie internationale" par Paul Krugman et Maurice Obstfeld, édition de Boeck Université 2001

* ², ³ ,⁴"quel avenir pour l'initiative sectorielle en faveur du coton après l'échec de cancùn» par Sébastien Miroudot, Mars 2004

* ³ «coton africain dans le marché mondial, communication présentée par Gérald Estur, statisticien du Comité consultatif international sur le coton (CCIC), 3 mars à Bamako.

* ⁴ Voir le coton après Cancùn, Louis Goreux, mars 2004.

* ⁵ "Perspectives cotonnières", bulletin occasionnel de la banque mondiale sur les enjeux et les options de reforme politique dans la filière coton, juillet 2002

* ⁶ On rappelle que la campagne cotonnière 2001-2002 a été marquée par la chute sans précédent des cours mondiaux du coton. Aussi, on pourra mesurer les pertes en recettes d'exportation dues aux subventions en 2001-2002 si le lien négatif entre les subventions et le prix mondial est confirmé

* ⁷ "pour éviter le retour aux désordres commerciaux de l'entre-deux-guerre, les pays occidentaux ont conclu en octobre 1947 un accord général sur les tarifs douaniers et le commerce (General Agreement on Tariffs and Trade - GATT) permettant de supprimer progressivement tous les obstacles aux échanges internationaux"

* ⁸ «Uruguay Round, commencé en 1986 et adopté en 1993, prévoit la création d'une organisation mondiale du commerce ( OMC) qui se substituera au GATT »Il prévoit aussi la réduction des subventions aux exportations agricoles, une nouvelle réduction des droits de douane et le demantelèment progressif de l'accord multifibres.

* ⁹ tiré de «préjudices causés par les subventions aux filières cotonnières de l' AOC, Louis Goreux, 25 mars 2003

* ¹⁰ « il s`agit ici des accords relatifs aux dispositions de la politique agricole commune(PAC) »  .

* ¹¹ La perte de distorsion de consommation résulte du fait que les consommateurs consomment une quantité trop faible du bien.

* ¹² La perte de distorsion de production résulte du fait que la subvention amène les producteurs domestiques à produire une trop grande quantité du bien.

* ¹³ si on avait le prix domestique en ordonnée sur le marché mondial, c'est la courbe de demande mondiale qui serait déplacée vers la droite. L'effet restant bien sûr le même pour les producteurs des pays riches.

* ¹⁴ Dans la suite, on utilisera PRC, PRO, CONS, NSUB, PRP respectivement à la place de p_t, o_t, d_t, s_t, f_{t qui} avaient été utilisées à cause de la complexité du modèle.

* ¹⁵ Le Cent est la centième division du dollar (1$= 100 cents)

* ¹⁶ La livre ( pound ou Ib) est une unité de mesure angloxasonne qui vaut 0,4536 kg.

* ¹⁷ 1 bale, est égal à 480 Ib.

* ²² significatif à 5% significatif à 10%

* ¹⁸ Le modèle présente un R² près de 0.8, avec des paramètres estimés significatifs. En plus, les prévisions relatives à la campagne 1999-2000 s'écarte seulement de 2 cents de la valeur observée.

* ¹⁹ « mean absolute errors » et « mean squared errors »

* ²⁰ Louis Goreux, « les producteurs de coton des pays CFA face aux subventions américaines et européennes » juillet 2003

* ²¹ L'indice A de cotlook est un indicateur sans précédent du marché mondial des prix du coton