From pricing to rating structured credit products and vice-versa

1.2.4 Structured Non-Correlation Products

Unlike CSO tranches, the value of which relies heavily on correlation assumptions linking default probabilities on single names, a range of «correlation-free» structured credit products has emerged since 2004. Constant Proportion Portfolio Insurance (CPPI) and Constant Proportion Debt Obligation (CPDO) products reference CDS portfolios, but their joint-loss distribution is not tranched among investors.

Constant Proportion Debt Obligation: «the more you lose, the more you bet»

First introduced by ABN-Amro in S2 2006, a Constant Proportion Debt Obligation is a security whose principal and coupons are rated AAA by rating agencies such as S&P and Moody's and that pays to the noteholder quarterly EURIBOR/LIBOR coupons plus a spread around 100-200 bps depending on issuing market conditions. Such a return is achieved by selling credit protection on credit indices or on a portfolio of single-name CDS in an amount that is adjusted dynamically throughout the transaction's lifetime: this dynamic «leverage» function can reach as much as 15 times the initial notional.

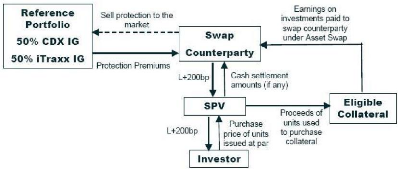
Figure 1.3: Structuring of a first-generation CPDO, referencing credit indices

Let us define the following variables at time t in order to summarize the few investment guidelines that rule the CPDO's behaviour:

· A = Notional of the security;

· NPV = Net Present Value of the security;

· MtM = Marked-to-Market value of all long positions on credit indices and/or single-name CDS;

· Collat = Value of the assets collateralized in the transaction to serve the EURIBOR/LIBOR component of the coupon;

· CA = Balance of the Cash Account of the structure; in particular, can be affected by default losses;

· TRV = Target Redemption Value of the security;

· PVNotional = Present Value of the security's Notional as discounted per the risk-free discount curve;

· PVCoupons = Present Value of the future coupons of the security discounted as per the risk-free discount curve;

· PVFees = Present Value of the future running fees to be paid by the noteholder and discounted as per the risk-free discount curve;

· TNE = Target Notional Exposure in credit indices or single-name CDS;

· F = Shortfall Multiplier, assumed to be constant in this example;

· lb = Lower Bound cash-out threshold, expressed as a percentage of the security's notional;

· TL = Target Leverage function.

The aim of the structure is to increase the security's NPV in order to hit the TRV (a «lock-in» event: in this case, the credit portfolio is unwound and the proceeds of the transaction are high enough to cover all future promised coupon, fee and principal payments until maturity by construction of the TRV aggregate. At the same time, the structure must avoid any «lock-out» event, which takes place when the security's NPV hits a fixed percentage lb, usually around 10%, of the security's notional N.

As long as no lock-in nor lock-out event has occured, the leveraging mechanism described hereafter expresses the Target Leverage function TL(t) as a linearly increasing function of the structure's shortfall, defined as the difference between the TRV and the NPV:

NPV (t) = MtM(t) + Collat(t) + CA(t) TRV (t) = PV Notional(t) + PV Coupons(t) + PV Fees(t) TNE(t) = F · (TRV (t) - NPV (t)) T NE(t) T L(t) = A

(1.2)

In other words, the CPDO's leveraging mechanism enables the structure to increase its credit exposure when the shortfall increases, i.e. when the security's NPV incurs MtM or default losses: «the more you lose, the more you bet». Conversely, MtM gains translate into a reduction in the structure's credit exposure.

Constant Proportion Portfolio Insurance: placing greedy but secured bets

Originally designed for equity underlyings, Constant Proportion Portfolio Insurance (CPPI) products referencing credit-linked assets have developped in the past three years. Unlike CPDOs, CPPIs are principal-protected at maturity. In other words, the investor will always receive the notional of the security at its maturity, whereas the CPDO noteholder can end up with as little as lb% of his initial investment.

The CPPI is a security whose principal is protected at maturity and whose coupons
can be rated by S&P and/or Moody's and/or Fitch. Similarly to CPDOs, the rated

CPPI pays to the noteholder quarterly EURIBOR/LIBOR coupons plus a spread around 50-100 bps depending on issuing market conditions. This return is achieved by selling protection on a portfolio of single-name CDS in an amount that is adjusted dynamically during the transaction's lifetime. This dynamic «leverage» function can reach as much as 10-12 times the initial notional.

Notations introduced earlier to describe the CPDO structure remain valid hereafter. In addition, we define the following variables at time t:

· BF = Bond Floor: value of a risk-free zero-coupon bond maturing at the legal maturity of the security;

· R = Reserve;

· RM = Reserve Multiplier.

A CPPI lock-out event happens whenever the security's NPV hits the Bond Floor BF. A lock-in event is the same as for CPDOs. The leveraging mechanism is different however: the CPPI's target leverage function TL is an increasing function of the Reserve R, defined as the difference between the security's NPV and BF.

R(t) = NPV (t) - BF(t) TNE(t) = RM · R(t) TNE(t) TL(t) = A

(1.3)

The CPPI's leveraging mechanism enables the structure to increase its credit exposure when the reserve increases, i.e. when either the security's NPV increases due to MtM gains or its BF rises as a result of lower interest rates. The more money you make, the more you can afford losing by increasing your bets.