From pricing to rating structured credit products and vice-versa

Chapter 1

Structured credit products: a

business review

1.1 Introduction

Credit derivatives markets have been consistently among the fastest growing areas of capital markets in recent years: 2006 year-end ISDA survey shows outstanding notionnal of 34,000 USD Bio for all credit derivatives contracts, up from 8,000 USD Bio in 2004. Such a growth was fueled by the appetite of various types of investors for credit risk and relied upon the ability of investment banks to repackage credit risk into synthetic structured products.

Before going into the details of modeling and pricing such credit derivatives, we shall describe the principles of the main products that can then be used as building blocks for more sophisticated ones. They share the same underlying risk, that is the credit risk of one or several reference entities, whether it be a corporate company, a financial institution or even a soveriegn entity:

· Single-name Credit Default Swaps (CDS) are to credit derivatives markets what single-name equity stocks are to equity derivatives markets;

· Collateralized Synthetic Obligations (CSO) aim at tranching credit risk on an entire portfolio of reference entities, hence creating correlation risk;

· Constant Proportion Dynamic Portoflio Obligations (CPDO) and Constant Proportion Portfolio Insurance (CPPI) products allow investors to take credit risk on diversified portfolios of single names while avoiding first-order correlation risk;

· Vanilla options on credit indices started trading as liquidity in underlying CDS contracts and standardized CSO tranches was increasing.

1.2 Elementary building blocks

1.2.1 Credit Default Swaps

A Credit Default Swap (CDS) is a contract whereby counterpart A (the «protection
seller») receives a periodic premium from counterpart B (the «protection buyer») and
agrees to protect the latter against the default of entity C (the «reference entity»).

In the event of default, counterpart A would pay counterpart B the notional amount of a reference obligation (which could be a bond or a loan) issued by entity C and receive the reference obligation.

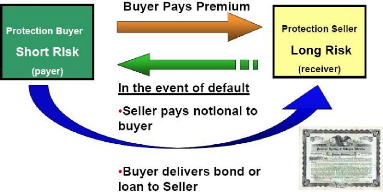
Figure 1.1: Cash flows of a Credit Default Swap with physical delivery

CDS are quoted in terms of spread (measured in basis points) over an Inter Bank Offered Rate (EURIBOR or LIBOR depending on the currency). Assuming a constant recovery rate R for the underlying obligation, we can easily express this spread as a function of the survival cumulative distribution function S0(.) of the reference entity defined as follows under the risk neutral probability measure Q. Let r be the continuous random variable modelling the instant of default:

?t ? R⁺,S0(t) = Q(r = t)

By construction, for a given notional amount N, a fixed recovery rate R, a contract maturity of T_n and risk-free bond prices B(0, Ti), i ? {1, .., n}, the market spread at inception of a given CDS is determined such that the present value of the premium leg (the «fixed leg») equals that of the default leg (the «variable» leg):

_Xn B(0, Ti) · E^Q [N(1 - R)1{Ti-1=ô=Ti} ~

i=1

_Xn B(0,Ti) · N(1 - R) · [S0(Ti-1) - S0(Ti)]

i=1

[ Xn ]

= EQ B(0, Ti)sN¹{ô=Ti}

i=1

_Xn B(0, Ti) · sN · (Ti - Ti-1) · S0(Ti)

i=1

As a result, the CDS spread s is given by the following formula, where D0(Ti) := B(0, Ti)S0(Ti) denotes the risky bond price: