4. Kovarianz
Offensichtlich weisen manche Anlageobjekte ähnliche
Kursverläufe (und damit Risiko-Rendite-Profile) auf, andere hingegen
scheinen sich eher gegenläufig zu verhalten. Um die Enge des Zusammenhangs
z.B. zwischen zwei verschiedenen Aktien X und Y zu ermitteln, bedient man sich
der Kovarianz:
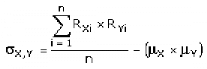
sX,Y = Kovarianz der Aktien X und Y
RXi = Rendite der Aktie X in Periode i
RYi = Rendite der Aktie Y in Periode i
uX = Mittelwert der Renditen der Aktie X
uY = Mittelwert der Renditen der Aktie Y
n = Anzahl der betrachteten Perioden
5. Beta-Faktor
Als Maß für die absolute Flatterhaftigkeit
(Schwankungsbreite) einer Aktie haben wir bereits die Volatilität kennen
gelernt. Als Maß für den Vergleich der Flatterhaftigkeit einer Aktie
gegenüber einem Vergleichswert (z.B. einer anderen Aktie oder einem Index)
verwendet man hingegen den Beta-Faktor. Dieser misst also die relative
Schwankungsbreite einer Aktie
Mathematisch wird der Beta-Faktor aus dem Verhältnis der
Kovarianz der betrachteten Aktie mit dem Vergleichswert und der quadrierten
Volatilität des Vergleichwerts berechnet

Mit ;
bX,V = Beta-Faktor der Aktie X in Bezug auf den
Vergleichswert V
sX,V = Kovarianz der Renditen der Aktie X und des
Vergleichswerts V
sV = Volatilität der Renditen des Vergleichswerts
V
Ist der Beta-Faktor genau gleich 1, so entspricht die
Schwankungsbreite des betrachteten Wertes exakt der des Vergleichswert. Dies
ist natürlich insbesondere dann der Fall, wenn die betrachtete Aktie X und
der Vergleichswert V identisch sind.
5. Korrelationskoeffizient
Die Güte eines Beta-Faktors misst man mit Hilfe des
Korrelationskoeffizienten
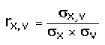
Der Korrelationskoeffizient kann prinzipiell nur Werte zwischen
-1 und 1 annehmen
Ist rX,V genau gleich 1, so liegt eine
vollständige positive Korrelation zwischen der Aktie X und dem
Vergleichswert V vor, d.h. jeder Anstieg des Vergleichswertes V führt
stets zu einem Ansteigen der Aktie X im Verhältnis des Beta-Faktors
Ist rX,V genau gleich -1, so liegt eine
vollständige negative Korrelation zwischen der Aktie X und dem
Vergleichswert V vor, d.h. jeder Anstieg des Vergleichswertes V führt
unweigerlich zu einem Absinken der Aktie X im Verhältnis des
Beta-Faktors
III. Optimales Portfolio
Um es gleich vorweg zu sagen: Wer hier von der Portfolio-Theorie
ein Kochrezept für die optimale Geldanlage schlechthin erwartet wird
leider enttäuscht. Es gibt keine absolut optimale Geldanlage, sondern nur
ein persönlich ideales Portfolio, das die individuellen Wünsche,
Rahmenbedingungen und Neigungen des Investors berücksichtigt.
Daher kann auch nicht oft genug betont werden, dass Geldanlage
immer nur nach eingehender persönlicher Analyse - im Idealfall gemeinsam
mit einem Anlageberater der Hausbank oder mit einem unabhängigen
Finanzberater - erfolgen sollte.
Dennoch kann die Portfolio-Theorie helfen, wenn es um die schon
andiskutierte Problematik des individuell optimalen Mischungsverhältnisses
zweier Aktien geht.
Wenden wir uns dazu nochmals unserem Beispiel mit den A- und
C-Aktien zu. Wir erinnern uns an die risikoeffiziente Linie im
Rendite-Volatilitäts-Diagramm. Zeichnen wir nun zusätzlich zu dieser
Linie noch unsere Indifferenzkurve in das Diagramm so erhalten wir folgende
Darstellung.

Genau dort, wo sich die beiden Linien schneiden ist das
individuell optimale Portfolio. Der Grund leuchtet schnell ein: Portfolios die
link oberhalb der blauen Indifferenzkurve liegen würden, wären dem
Investor sicher recht, da sie mehr Rendite bei weniger Volatilität bieten.
Aber die möglichen Kombinationen von A- und C-Aktie lassen dies nicht zu.
Punkte rechts unterhalb der Indifferenzkurve wären zwar durch geeignete
A-C-Kombinationen möglich, aber dem Investor nicht sicherlich nicht
gelegen, da sie bei gleicher Rendite weitaus höhere Volatilitäten
aufweisen.
Wir sehen aber sehr deutlich: Dieser Investor wird sich nicht
für das Varianz-Minimale-Portfolio von 60:40 A:C Aktien entscheiden.
Aufgrund seiner individuellen Risikobereitschaft - ausgerückt in der
Indifferenzkurve - wird er ein A-C-Mischungsverhältnis von etwa 40:60
für sein Depot realisieren.
Die gleichen Prinzipien funktionieren natürlich auch bei den
exponentiellen

Was aber, wenn es keinen eindeutigen Schnittpunkt zwischen der
Indifferenzkurve und der risikoeffizienten Linie gibt?
Betrachten wir zunächst einmal den Fall, dass die
Indifferenzkurve vom Niveau her tiefer liegt und es somit zwei Schnittpunkte
gibt:

In einem solchen Fall wird der Anleger sicherlich bereit sein,
seine Indifferenzkurve so
lange "anzuheben", bis es nur noch einen Schnittpunkt gibt, da er
so - bei gleicher Volatilität - eine höhere Rendite erzielen kann,
als er ursprünglich erzielen wollte.
Anders sieht es jedoch aus, wenn die Indifferenzkurve vom Niveau
her höher liegt und es gar keinen Schnittpunkt gibt:

Hier hat der Investor nur zwei Möglichkeiten:
· Entweder beißt er aud die Zähne und senkt seine
Indifferenzkurve vom Niveau her so lange ab, bis es einen eindeutigen
Schnittpunkt gibt, d.h. er reduziert - bei gleicher Volatilität - seine
Rendite-Forderungen an ein Portfolio.
· Oder er muss andere Aktien-Kombinationen untersuchen, mit
denen er ein höheres Risiko-Rendite-Profil erreichen kann und deren
risikoeffiziente Portfolio-Kombinationen entsprechend vom Niveau her höher
liegen.
Weitere moderne Instrumente der Portfolio-Theorie
Alpha
Alpha misst den relativen durch einen Asset Manager beigebrachten
Mehrwert verglichen mit einem Marktindex, unter Voraussetzung des Marktrisikos
eines Portfolios.
Ein positives Alpha ist die zusätzliche Rendite, die ein
Investor für die Übernahme eines Risikos anstelle der Marktrendite
erhält. So bedeutet zum Beispiel ein Alpha von 1.0, dass ein Portfolio
eine Rendite erzeugt hat, die 1% höher liegt, als sein Beta voraussagen
würde. Ein Alpha von -1.0 bedeutet, dass ein Portfolio eine Rendite
erzeugt hat, die 1% tiefer liegt, als erwartet würde.
Alpha vernachlässigt das gesamte Volatlitätsrisiko und
es wird angenommen, dass der Manager ein diversifiziertes Portfolio hat. Die
Diversifikation kann mittels R-Quadrat gemessen werden. Ein R-Quadrat von
weniger als 50 macht das Alpha-Rating eines Manager praktisch bedeutungslos.
Alpha kann sich von Quartal zu Quartal dramatisch verändern.
R-Quadrat
R-Quadrat misst, wie gut ein Portfolio im Vergleich zu einem
Marktindex (wie etwa dem S&P 500 Index) diversifiziert ist. R-Quadrat kann
von Null bis 100 gehen. Ein Wert von 100 zeigt eine perfekte Korrelation mit
dem Marktindex an. Bei einem Portfolio mit einem R-Quadrat von 0.85 können
85% des Risikos des Portfolios dem Markt angerechnet werden und 15% des Risikos
beruhen auf anderen Faktoren (d.h. Sicherheit oder Sektorwahl).
Sharpe-Ratio
Die Sharpe-Ratio bestimmt, wie viel Risiko ein Manager
einging, um die historische Rendite des Portfolios zu erreichen. Sie wird
berechnet, indem man die Differenz zwischen der Rendite eines Portfolios und
einer risikofreien Rendite (gemessen an einer Treasury-Bill) nimmt und diese
durch die Standardabweichung des Portfolios dividiert. .Wenn zum Beispiel ein
Portfolio eine Sharpe-Ratio von 1.30 hatte und der Marktindex eine Sharpe-Ratio
von 1.00 hat, dann hat das Porfolio eine um 30% höhere Rendite als der
Index verglichen mit dem risikofreien Satz erbracht. Die Sharpe-Ratio kann ein
nützliches Mittel zum Vergleich verschiedener Portfolios sein, um den Wert
zu bestimmen, den ein Asset Manager beigebracht hat.
Up/Down Capture Ratio
Dieses Instrument zeigt den prozentualen Anteil an der
Markt-Performance - wie zum Beispiel dem S&P 500 Index -, den der Asset
Manager gewonnen hat. Dieser Wert wird berechnet, indem man die Rendite der
Perfomance des Managers durch die Rendite des Marktindexes dividiert.
Rendite des Managers
Up/down Capture Ratio =
Rendite des Marktindexes
Die Up Capture Ratio wird über Quartalsperioden berechnet,
in denen der Marktindex eine positive Rendite generiert hat, die Down Capture
Ratio für Quartale, in denen der Markt negative Renditen macht. So hat zum
Beispiel ein Portfolio Manager mit einer Up Capture Ratio von 120% 120% der
Rendite des Indexes gewonnen, wenn dieser an Wert zugelegt hat (eine um 20%
höhere Rendite als der Index). Ein Portfolio Manager mit einer Down
Capture Ratio von 120% hat 120% mehr als die Rendite des Indexes gewonnen, als
dieser zurückging (um 20% schlechter als der Index).
Die Up/Down Capture Ratio ist nur ein Instrument, um die
Performance eines Portfolio Managers zu bewerten. Doch zusammen mit anderen
Instrumenten kann es ein hilfreiches Mittel sein, um festzustellen, ob ein
bestimmter Manager und sein oder ihr Portfolio hinreichend auf dem jeweiligen
Risiko/Rendite Profil abgestützt sind.
Information Ratio
Die Information Ratio misst den durch einen
Portfolio Manger hinzugefügten Wert. Diese Kennzahl zeigt die auf das Jahr
umgerechnete Rendite eines Portfolios über dem Marktindex im
Verhältnis zum auf das Jahr umgerechneten Tracking Error.
Tracking Error
Der Tracking Error misst, wie eng die Portfolio-Performance eines
Asset Managers sich am Markt bewegt. Der Tracking Error wird berechnet, indem
man die Standardabweichung der Differenzen innerhalb der Renditen des
Portfolios zu den Quartalsrenditen des Markts bestimmt. Wenn das Portfolio sich
nahe am Markt bewegt, hat es einen geringen Tracking Error.
Efficient Frontier
Der Efficient Frontier ist ein Graph, der eine Menge von
Portfolios wiedergibt, welche die Renditen auf jeder Stufe des Portfoliorisikos
(oder der Renidtenvolatilität) vergleichen. Laut der modernen
Portfolio-Theorie gibt es für jedes Asset-Portfolio eine Efficient
Frontier, welche verschieden gewichtete Kombinationen der Assets des Portfolios
wiedergibt, die die maximal möglich erwartete Rendite auf jeder Stufe des
Porfoliorisikos wiedergeben.
Scattergrams
Ein Scattergram ist eine graphische Repräsentation des
Risiko/Rendite-Profils eines Asset Managers innerhalb einer Peergroup oder
einem zugehörigen Martkindex, üblicherweise über einen Zeitraum
von 5 oder 10 Jahren. Diese Graphen zeigen die auf das Jahr umgerechneten
Renditenwerte des Portfolios des Managers relativ zum Risiko, wiedergegeben
durch die Standardabweichung. Scattergrams können Investoren helfen die
Performance eines Asset-Managers auf Grundlage ..... zu bewerten.
Literaturverzeichnis
Akdogan, H Akdogan [( 1997) ] : International Security Selection
under Segmentation : Theory and Application ; in : Journal of Portfolio
Management, Fall 1997, S : 82-92
Bernstein, P.L. [Bernstein (1992)] the great Beta Deâata,
in: Journal of Portfolio Management, Fall 1992, S. 42-56
Camer J:E / Rudolph , B. ( Hrsg.) [ Cramer u.a ( 1992) ] Handbuch
Anlageberatung und Vermögensverwaltung, Frankfurt Main : Fritz- Knapp-
Verlag
Elton, E.J / Gruber, M.J. [ Elton u.a. ( 1995) ] : Modern
Poetfolio Theory and Investment analysis, fifth eddition, New York : John Wily
& Sons, Inc. 1995
FTSE - International ( Hrsg.) : FTSE Global classification
System, Version 1.4, London Mars 2000
Goldman Sachs ( Hrsg.) : Global Portfolio Strategy- Stay Global -
Sector Correlations Still Rising, a be- weekly focus London 2000
Markowitz H. [ Markowitz ( 1994) ] : Portfolio selection, in :
Journal of finance, Vol. 7 , No. 1, Mars 19952. S.34-77
Morgan Stanley Capital International ( Hrsg.) [ Morgan Stanley
Capital Inaternational ( Mars 1998) : Methodology and Index Policy, New York,
Mars 1998
Sharpe, E.F. : Capital Asset Prices: A theory of Market
Equilibrium under Volatility of Risk. In : Journal of Finance, Vol.21, November
1964
Bruce I. Jacobs, Kenneth N. Levy
Equity Management:
Quantitative Analysis for Stock Selection
Eine Sammlung der Aufsätze
und Beiträge von Markowitz und seinen Zeitgenossen aus dem Journal of
Portfolio Management, dem Journal of Investing und dem Financial Analysts
Journal.
Franz-Josef Leven, Christoph Schlienkamp
Erfolgreiches Depotmanagement
Ich habe selten ein Buch
gesehen, in dem die Grundlagen der Portfolio-Theorie so
"populärwissenschaftlich" (im positivsten Sinne) und anschaulich
erklärt werden.
| 


