Portfoliotheorie/ Diversification im Swiss Performance
Index ( SPI)
I Difinition: Die Portfoliotheorie
Die Portfolio ist ein Teilgebiet der Finanzierung und untersucht
das
Investitionsverhalten an
Kapitalmärkten (z. B.
Aktienmarkt). Die Portfoliotheorie versucht, anhand
mathematischer Modelle die optimale Zusammensetzung eines Wertpapierdepots zu
bestimmen. Dazu werden die Kombinationen aus erwartetem Gewinn und Risiko
für einzelne Wertpapiere ermittelt und mit der Risikobereitschaft des
Anlegers in Beziehung gesetzt. Da sich Aktien und Rentenpapiere durch sehr
unterschiedliche Risiken auszeichnen, wurden für das Management der
entsprechenden Portfolios unterschiedliche Strategien entwickelt . Die
Portfoliotheorie geht auf
Harry M. Markowitz (
Portfolio Selection) zurück und
unterstellt bestimmte Annahmen an das Verhalten von
Investoren und erzielt so gewisse
Aussagen über das Investitionsverhalten.
1. Zielsetzung
Auch wenn die moderne Portfoliotheorie bereit mehr als 50
jahre alt ist sind ihren Grundaussagen auch für Heute noch Basiswekzeuge
im Portfoliomanagement . Der Ziel der Portfoliotheorie ist es,
Handlungsanweisungen zur bestmöglichen Kombination von Anlagealternativen
zur Bildung eines optimalen
Portfolios zu geben. In diesem optimalen
Portfolio werden die Präferenzen des Anlegers bezüglich des
Risikos und des
Ertrags sowie die
Liquidität berücksichtigt.
Dadurch soll das Risiko eines Wertpapierportfolios, ohne eine Verringerung der
zu erwartenden Rendite, minimiert werden. Notwendige Voraussetzung hierbei ist,
dass die Wertpapiere nicht vollständig
korreliert
2. Annahmen.
Die Portfoliotheorie unterstellt einen
Investor, der sich in seinem Verhalten
ausschließlich an Zahlungsgrößen orientiert und sein
Vermögen mehren will. Er handelt
rational und
nutzenmaximierend: Das bedeutet, er
informiert sich über die Gegebenheiten des
Kapitalmarktes und entscheidet sich, indem er
Chancen und Risiken gegeneinander abwägt. Dabei scheut er das Risiko man
spricht hier auch von
Risikoaversion Risikoaverses Verhalten
bedeutet, dass ein höheres Risiko nur dann in Kauf genommen wird, wenn der
erwartete Ertrag überproportional steigt. Über die Frage, welche
Information aus den beobachtbaren Daten des Marktes gewonnen werden kann, hat
es in der Finanzierung eine intensive Debatte gegeben (zurückgehend auf
die bahnbrechenden Arbeiten von
Eugene Fama zur
Informationseffizienz).
Um die Analyse zu vereinfachen, nimmt man weiter an, dass der
Kapitalmarkt
vollkommen ist.
Kern der Portfoliotheorie ist die Unterscheidung in
systematisches und unsystematisches Risiko. Dem systematischen Risiko sind alle
Wertpapiere am Markt unterworfen, es kann somit nicht wegdiversifiziert werden
und ist das Risiko des Anlegens selbst. Das unsystematische Risiko hingegen ist
das Risiko, das sich durch
Diversifikation, also mit steigender Anzahl
an Wertpapieren verringern lässt. Daher können Anleger für
dieses Risiko am Markt keine Prämie erwarten.
II Portfolio Selection
In einer rationalen welt ist es unangezweiflt , dass ein Anlger
bei der Wahl von zwei anlagenalternativen diejenigen wählt, deren Risio
bei gleicher zu erwartender Randite kliener ist, man spricht in diesem
zusammenhang von der Risikoaversion des anlegers
Die auf Harry Markowitz zurückgehenden Erkenntnisse
erweitern im kern das Denken über die Allocation von Vermögen von
eindimensionalen Renditeaspekt zum zweidimonsionalen Rendite- Risiko-Aspekt.
Der name Markowitz und das phenomen von Divesifiacation1. sind
untrennbar. Ist man sich vor Markowitz Aufsatz bereits der sogenannte naiven
Derversifivcation2 Bewusst gewesen, nicht alle auf eine karte zu spielen,
sondern sein vermögen auf meherer Anlegen gut zu verteilen. Die
herausforderung ist es Matematisch nachzuweisen, das diese möglichkeit
gibt.
Anlagen so kombineiren, dass man unter Einschluss von Anlagen
deren Erträge sich wechsil seitig nicht proportional und
ungleichläufig, ein Porfilo erhält, welches bei den gleichen
Renditeerwartung ein niedriges Risiko mit sich führt.
Harry Markowitz hat gelingt einein systhematischen Prozess zu
difinierenn, wie man unter kenntnisse von dreier emprischen Kennzahlen und zwar
der erwateten Rendite der Einzelnen Anlagen, deren empirischen
Standardabweichung und jeweiligen Korrelationen Zwischen eizelnen Renditen von
der jeweiligen Anlagealternativen, ein so gennannt optimales und
risikoreduzierenden Wertpapierportfolio abauen kann.( Effizientes)
Nachfolegenden werden die drei fondamentalen Bgeriffen der
porfolio Selection Theorie, und nämlich Rendite, Risiko und Korrolation
erläutert.
1.Rendite
Man difiniert den Begrifff Rendite als relatives mass für
den Erfolg oder miss erfolg eine Investition bezogen auf einne difiniert
Zeitraum
In den Moderne Portfolio Theorie wird der Ex-Post Rendite Linear
und kontinuirlich gerchnet werden, sie berchenet den Erfolg am Ende er Zeitraum
aud der Basis alle informationen über die zahlungen und Wertenwicklugen
der Investionprodkten.5
Die zufällige Rendite basiert auf dem Ex-post begriff
-interpritiert diesen aber zu beginn der Renditeperiode als Zufallsvariable.
Harry Markowitz bedient sich bei der abbauen von der optimale protfolio diese
Renditebegriffs am anfang der investitionenperiode .
In fall der Vertteilung dieser Zufallsvariablen, nimmt mann der
Eifachheit der Modellierung hablber hfige kontinuierliche Renditen, um dem
wunsch der modernen Portfoliotheorie unterstellen Normaverteilung von Renditen
gerecht zu werden6 .
Die nommaleverteilunghypothese stellt eine Basisprämisse der
Modell dar , den diese Verteilung lässit sich durch die oben genannten
zwei pararamter erwartete Rendite und Standardabweichung vollständig
darstellen.
Über die additive Verkettung der kontinuirlichen Rendite hat
man glangt zum mehrperiodischen Renditebegriff. Diese Rendite ist auf grund des
Grenzwertsatzes normal verteilt.
Die kontinuerliche Rendite wird wie folgende 9 berchenet

Die kontinuierliche Renditen haben den Vorteil, dass gleiche
absolute Abweichungen von Renditen nach oben und nach unten auch gleiche
prozentuale Folgen haben.
Zb wann eine Aktien von CHF 38- auf CHF 49 steigt und wieder auf
CHF 38 fällt , weißt additive Verkettung der beiden kontinuierlichen
Renditen ln ( 49/ 38) und ln ( 38/49) eine Rendite von Null aus. Was der
absoluten Wertentwicklung der Anlage über mehrere Perioden entspricht10
Die lineare Renditeberchnung wird anhand nachsthender Formel
vorgenommen


Man verwendet das arithmische Mittel der Historichen Renditen der
bercheneten gleiche periode um das EX post basiserte Zufälligue Rendite zu
kommen. Man bezeichnet es als erwartete rendite aber eigentliche eine
geschätzte Zufallvariable sein soll.

Mit n = Anzahl der perioden
Die Rendite eines protfolios aus meheren Wertpapieren stzt sich
aus den Summen aller Eizelerträge zusammen, oder der Rentiesparche tu
bleiben als die gewicht summe de einzelrendite

Mit n= Anzahl der Wert papier

2. Volatilität
Mit dem Begriff Risiko bezeichnet man daher die Unsicherheit, mit
der die erwarteten Renditen auch wirklich eintreten. Je stärker das Risiko
einer Anlageform ist, um so stärker schwankt die Wertentwicklung im
Zeitverlauf. Das Instrument um diese Unregelmäßigkeit oder
Flatterhaftigkeit der Renditeentwicklungen zu messen ist die sogenannte
Volatilität.
Wir betrachten, dass das Risiko ist das bewusste eingehen der
Möglichkeit eines Verlustes im Negativfall. Man hat jedoch die
Möglichkeit diese Schwankungen mit Investments zu nutzen, die dieses
können und unter Beweis stellen, oder die Verluste unkontrolliert
größer werden zu lassen, wobei man wieder viel Zeit benötigt,
um diesen auszugleichen.

Die Standardabweichung misst, wie stark die einzelnen Renditen
der Perioden um den Mittelwert (Erwartungswert) schwanken. Die quadrierte
Standardabweichung, also s2 wird in der Mathematik auch als Varianz
bezeichnet. Die Varianz lässt sich zwar leichter errechnen, mit Hilfe der
Standardabweichung lassen sich aber "griffigere" Aussagen bezüglich der
Risikohaftigkeit einer Anlageform treffen.
Erster geht von einer Unmöglichkeit der Vorhersagbarkeit
zukünftiger Renditen aus, letzter arbeit mit wahrscheinlichlichkeiten
zukünfiger Renditeenwicklungen. In dieser Arbeit wird aus Gründen der
Modellierbarkeit mit dem begriff ders Risikos gearbeitet, wobei die in diesem
zuammenhang stehenden Wahrscheinlichkeiten aus einperiodischen Historischen
Renditeenwicklungen ( linearer Berchnung) resultieren.
Da ferner auch die moderne portfoliotheorie rein quantitiver
Natur ist, wird der Risikoaspekt von Ester in verschierdene Momente der
Wahrscheinlichkeitsverteilungen eingeteilt.
3. Varianz einzlener Wertpapiere
Die Varianz wird ausgerechnet von den durchschinttliche
quadrierten Abweichungen der Historischen Renditen zur erwarteten Rendite.
Emprichen Varianz

Mit
n = Anzahl der Perioden
Um auf die gleiche Dimension wie die erwartete Rendite zu
gelangen, nimmt man die Wurzel der empirischen Varianz und erhält so die
empirischen Standardabweichung

Um die Volatilität zu bekommen muss man ersten dieses Werte
anannualisieren,Da die Renditen häfig als p.a Zahlen dargestellet werden,
ist das dazugehörige Risiko für die gleiche periode als p.a.
darzustellen. Das sin un zwek bei der Annualisierung besteht darin in der
einfachen Verwendungsmöglichkeit zur Ermittlung weitere kennzahlen,
für deren meit auf annualisierte Daten zurückzugreifen.

 p.a.
p.a.

Mit T1= Jahr
Mit T2 = periode der zur Stabweichung zugrundeleigenden
Renditen.
N.b Die transformation täglichen Renditen wird in
verschiedenen Weise vorgenommen . Häufig findet man als Faktor v 250 da
man gehet man davon aus das die 250 handelstagen pro Jahr .
4. Kovarianz
Offensichtlich weisen manche Anlageobjekte ähnliche
Kursverläufe (und damit Risiko-Rendite-Profile) auf, andere hingegen
scheinen sich eher gegenläufig zu verhalten. Um die Enge des Zusammenhangs
z.B. zwischen zwei verschiedenen Aktien X und Y zu ermitteln, bedient man sich
der Kovarianz:
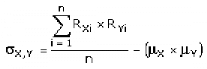
sX,Y = Kovarianz der Aktien X und Y
RXi = Rendite der Aktie X in Periode i
RYi = Rendite der Aktie Y in Periode i
uX = Mittelwert der Renditen der Aktie X
uY = Mittelwert der Renditen der Aktie Y
n = Anzahl der betrachteten Perioden
5. Beta-Faktor
Als Maß für die absolute Flatterhaftigkeit
(Schwankungsbreite) einer Aktie haben wir bereits die Volatilität kennen
gelernt. Als Maß für den Vergleich der Flatterhaftigkeit einer Aktie
gegenüber einem Vergleichswert (z.B. einer anderen Aktie oder einem Index)
verwendet man hingegen den Beta-Faktor. Dieser misst also die relative
Schwankungsbreite einer Aktie
Mathematisch wird der Beta-Faktor aus dem Verhältnis der
Kovarianz der betrachteten Aktie mit dem Vergleichswert und der quadrierten
Volatilität des Vergleichwerts berechnet

Mit ;
bX,V = Beta-Faktor der Aktie X in Bezug auf den
Vergleichswert V
sX,V = Kovarianz der Renditen der Aktie X und des
Vergleichswerts V
sV = Volatilität der Renditen des Vergleichswerts
V
Ist der Beta-Faktor genau gleich 1, so entspricht die
Schwankungsbreite des betrachteten Wertes exakt der des Vergleichswert. Dies
ist natürlich insbesondere dann der Fall, wenn die betrachtete Aktie X und
der Vergleichswert V identisch sind.
5. Korrelationskoeffizient
Die Güte eines Beta-Faktors misst man mit Hilfe des
Korrelationskoeffizienten
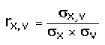
Der Korrelationskoeffizient kann prinzipiell nur Werte zwischen
-1 und 1 annehmen
Ist rX,V genau gleich 1, so liegt eine
vollständige positive Korrelation zwischen der Aktie X und dem
Vergleichswert V vor, d.h. jeder Anstieg des Vergleichswertes V führt
stets zu einem Ansteigen der Aktie X im Verhältnis des Beta-Faktors
Ist rX,V genau gleich -1, so liegt eine
vollständige negative Korrelation zwischen der Aktie X und dem
Vergleichswert V vor, d.h. jeder Anstieg des Vergleichswertes V führt
unweigerlich zu einem Absinken der Aktie X im Verhältnis des
Beta-Faktors
III. Optimales Portfolio
Um es gleich vorweg zu sagen: Wer hier von der Portfolio-Theorie
ein Kochrezept für die optimale Geldanlage schlechthin erwartet wird
leider enttäuscht. Es gibt keine absolut optimale Geldanlage, sondern nur
ein persönlich ideales Portfolio, das die individuellen Wünsche,
Rahmenbedingungen und Neigungen des Investors berücksichtigt.
Daher kann auch nicht oft genug betont werden, dass Geldanlage
immer nur nach eingehender persönlicher Analyse - im Idealfall gemeinsam
mit einem Anlageberater der Hausbank oder mit einem unabhängigen
Finanzberater - erfolgen sollte.
Dennoch kann die Portfolio-Theorie helfen, wenn es um die schon
andiskutierte Problematik des individuell optimalen Mischungsverhältnisses
zweier Aktien geht.
Wenden wir uns dazu nochmals unserem Beispiel mit den A- und
C-Aktien zu. Wir erinnern uns an die risikoeffiziente Linie im
Rendite-Volatilitäts-Diagramm. Zeichnen wir nun zusätzlich zu dieser
Linie noch unsere Indifferenzkurve in das Diagramm so erhalten wir folgende
Darstellung.

Genau dort, wo sich die beiden Linien schneiden ist das
individuell optimale Portfolio. Der Grund leuchtet schnell ein: Portfolios die
link oberhalb der blauen Indifferenzkurve liegen würden, wären dem
Investor sicher recht, da sie mehr Rendite bei weniger Volatilität bieten.
Aber die möglichen Kombinationen von A- und C-Aktie lassen dies nicht zu.
Punkte rechts unterhalb der Indifferenzkurve wären zwar durch geeignete
A-C-Kombinationen möglich, aber dem Investor nicht sicherlich nicht
gelegen, da sie bei gleicher Rendite weitaus höhere Volatilitäten
aufweisen.
Wir sehen aber sehr deutlich: Dieser Investor wird sich nicht
für das Varianz-Minimale-Portfolio von 60:40 A:C Aktien entscheiden.
Aufgrund seiner individuellen Risikobereitschaft - ausgerückt in der
Indifferenzkurve - wird er ein A-C-Mischungsverhältnis von etwa 40:60
für sein Depot realisieren.
Die gleichen Prinzipien funktionieren natürlich auch bei den
exponentiellen

Was aber, wenn es keinen eindeutigen Schnittpunkt zwischen der
Indifferenzkurve und der risikoeffizienten Linie gibt?
Betrachten wir zunächst einmal den Fall, dass die
Indifferenzkurve vom Niveau her tiefer liegt und es somit zwei Schnittpunkte
gibt:

In einem solchen Fall wird der Anleger sicherlich bereit sein,
seine Indifferenzkurve so
lange "anzuheben", bis es nur noch einen Schnittpunkt gibt, da er
so - bei gleicher Volatilität - eine höhere Rendite erzielen kann,
als er ursprünglich erzielen wollte.
Anders sieht es jedoch aus, wenn die Indifferenzkurve vom Niveau
her höher liegt und es gar keinen Schnittpunkt gibt:

Hier hat der Investor nur zwei Möglichkeiten:
· Entweder beißt er aud die Zähne und senkt seine
Indifferenzkurve vom Niveau her so lange ab, bis es einen eindeutigen
Schnittpunkt gibt, d.h. er reduziert - bei gleicher Volatilität - seine
Rendite-Forderungen an ein Portfolio.
· Oder er muss andere Aktien-Kombinationen untersuchen, mit
denen er ein höheres Risiko-Rendite-Profil erreichen kann und deren
risikoeffiziente Portfolio-Kombinationen entsprechend vom Niveau her höher
liegen.
Weitere moderne Instrumente der Portfolio-Theorie
Alpha
Alpha misst den relativen durch einen Asset Manager beigebrachten
Mehrwert verglichen mit einem Marktindex, unter Voraussetzung des Marktrisikos
eines Portfolios.
Ein positives Alpha ist die zusätzliche Rendite, die ein
Investor für die Übernahme eines Risikos anstelle der Marktrendite
erhält. So bedeutet zum Beispiel ein Alpha von 1.0, dass ein Portfolio
eine Rendite erzeugt hat, die 1% höher liegt, als sein Beta voraussagen
würde. Ein Alpha von -1.0 bedeutet, dass ein Portfolio eine Rendite
erzeugt hat, die 1% tiefer liegt, als erwartet würde.
Alpha vernachlässigt das gesamte Volatlitätsrisiko und
es wird angenommen, dass der Manager ein diversifiziertes Portfolio hat. Die
Diversifikation kann mittels R-Quadrat gemessen werden. Ein R-Quadrat von
weniger als 50 macht das Alpha-Rating eines Manager praktisch bedeutungslos.
Alpha kann sich von Quartal zu Quartal dramatisch verändern.
R-Quadrat
R-Quadrat misst, wie gut ein Portfolio im Vergleich zu einem
Marktindex (wie etwa dem S&P 500 Index) diversifiziert ist. R-Quadrat kann
von Null bis 100 gehen. Ein Wert von 100 zeigt eine perfekte Korrelation mit
dem Marktindex an. Bei einem Portfolio mit einem R-Quadrat von 0.85 können
85% des Risikos des Portfolios dem Markt angerechnet werden und 15% des Risikos
beruhen auf anderen Faktoren (d.h. Sicherheit oder Sektorwahl).
Sharpe-Ratio
Die Sharpe-Ratio bestimmt, wie viel Risiko ein Manager
einging, um die historische Rendite des Portfolios zu erreichen. Sie wird
berechnet, indem man die Differenz zwischen der Rendite eines Portfolios und
einer risikofreien Rendite (gemessen an einer Treasury-Bill) nimmt und diese
durch die Standardabweichung des Portfolios dividiert. .Wenn zum Beispiel ein
Portfolio eine Sharpe-Ratio von 1.30 hatte und der Marktindex eine Sharpe-Ratio
von 1.00 hat, dann hat das Porfolio eine um 30% höhere Rendite als der
Index verglichen mit dem risikofreien Satz erbracht. Die Sharpe-Ratio kann ein
nützliches Mittel zum Vergleich verschiedener Portfolios sein, um den Wert
zu bestimmen, den ein Asset Manager beigebracht hat.
Up/Down Capture Ratio
Dieses Instrument zeigt den prozentualen Anteil an der
Markt-Performance - wie zum Beispiel dem S&P 500 Index -, den der Asset
Manager gewonnen hat. Dieser Wert wird berechnet, indem man die Rendite der
Perfomance des Managers durch die Rendite des Marktindexes dividiert.
Rendite des Managers
Up/down Capture Ratio =
Rendite des Marktindexes
Die Up Capture Ratio wird über Quartalsperioden berechnet,
in denen der Marktindex eine positive Rendite generiert hat, die Down Capture
Ratio für Quartale, in denen der Markt negative Renditen macht. So hat zum
Beispiel ein Portfolio Manager mit einer Up Capture Ratio von 120% 120% der
Rendite des Indexes gewonnen, wenn dieser an Wert zugelegt hat (eine um 20%
höhere Rendite als der Index). Ein Portfolio Manager mit einer Down
Capture Ratio von 120% hat 120% mehr als die Rendite des Indexes gewonnen, als
dieser zurückging (um 20% schlechter als der Index).
Die Up/Down Capture Ratio ist nur ein Instrument, um die
Performance eines Portfolio Managers zu bewerten. Doch zusammen mit anderen
Instrumenten kann es ein hilfreiches Mittel sein, um festzustellen, ob ein
bestimmter Manager und sein oder ihr Portfolio hinreichend auf dem jeweiligen
Risiko/Rendite Profil abgestützt sind.
Information Ratio
Die Information Ratio misst den durch einen
Portfolio Manger hinzugefügten Wert. Diese Kennzahl zeigt die auf das Jahr
umgerechnete Rendite eines Portfolios über dem Marktindex im
Verhältnis zum auf das Jahr umgerechneten Tracking Error.
Tracking Error
Der Tracking Error misst, wie eng die Portfolio-Performance eines
Asset Managers sich am Markt bewegt. Der Tracking Error wird berechnet, indem
man die Standardabweichung der Differenzen innerhalb der Renditen des
Portfolios zu den Quartalsrenditen des Markts bestimmt. Wenn das Portfolio sich
nahe am Markt bewegt, hat es einen geringen Tracking Error.
Efficient Frontier
Der Efficient Frontier ist ein Graph, der eine Menge von
Portfolios wiedergibt, welche die Renditen auf jeder Stufe des Portfoliorisikos
(oder der Renidtenvolatilität) vergleichen. Laut der modernen
Portfolio-Theorie gibt es für jedes Asset-Portfolio eine Efficient
Frontier, welche verschieden gewichtete Kombinationen der Assets des Portfolios
wiedergibt, die die maximal möglich erwartete Rendite auf jeder Stufe des
Porfoliorisikos wiedergeben.
Scattergrams
Ein Scattergram ist eine graphische Repräsentation des
Risiko/Rendite-Profils eines Asset Managers innerhalb einer Peergroup oder
einem zugehörigen Martkindex, üblicherweise über einen Zeitraum
von 5 oder 10 Jahren. Diese Graphen zeigen die auf das Jahr umgerechneten
Renditenwerte des Portfolios des Managers relativ zum Risiko, wiedergegeben
durch die Standardabweichung. Scattergrams können Investoren helfen die
Performance eines Asset-Managers auf Grundlage ..... zu bewerten.
Literaturverzeichnis
Akdogan, H Akdogan [( 1997) ] : International Security Selection
under Segmentation : Theory and Application ; in : Journal of Portfolio
Management, Fall 1997, S : 82-92
Bernstein, P.L. [Bernstein (1992)] the great Beta Deâata,
in: Journal of Portfolio Management, Fall 1992, S. 42-56
Camer J:E / Rudolph , B. ( Hrsg.) [ Cramer u.a ( 1992) ] Handbuch
Anlageberatung und Vermögensverwaltung, Frankfurt Main : Fritz- Knapp-
Verlag
Elton, E.J / Gruber, M.J. [ Elton u.a. ( 1995) ] : Modern
Poetfolio Theory and Investment analysis, fifth eddition, New York : John Wily
& Sons, Inc. 1995
FTSE - International ( Hrsg.) : FTSE Global classification
System, Version 1.4, London Mars 2000
Goldman Sachs ( Hrsg.) : Global Portfolio Strategy- Stay Global -
Sector Correlations Still Rising, a be- weekly focus London 2000
Markowitz H. [ Markowitz ( 1994) ] : Portfolio selection, in :
Journal of finance, Vol. 7 , No. 1, Mars 19952. S.34-77
Morgan Stanley Capital International ( Hrsg.) [ Morgan Stanley
Capital Inaternational ( Mars 1998) : Methodology and Index Policy, New York,
Mars 1998
Sharpe, E.F. : Capital Asset Prices: A theory of Market
Equilibrium under Volatility of Risk. In : Journal of Finance, Vol.21, November
1964
Bruce I. Jacobs, Kenneth N. Levy
Equity Management:
Quantitative Analysis for Stock Selection
Eine Sammlung der Aufsätze
und Beiträge von Markowitz und seinen Zeitgenossen aus dem Journal of
Portfolio Management, dem Journal of Investing und dem Financial Analysts
Journal.
Franz-Josef Leven, Christoph Schlienkamp
Erfolgreiches Depotmanagement
Ich habe selten ein Buch
gesehen, in dem die Grundlagen der Portfolio-Theorie so
"populärwissenschaftlich" (im positivsten Sinne) und anschaulich
erklärt werden.



