5. Les modèles économétriques
5.1 Modèle de Poisson
La distribution de probabilité suivant la loi de poisson
est donnée selon la formule suivante:
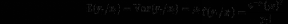
Dans ce modèle de régression, nous supposons que la
population est hétérogène avec des Xi
covariés, et ?i est spécifié comme
, où i = 1, . . ., N indice des observations dans
l'échantillon.
Les effets de la réforme, sont définis comme la
variation relative du nombre prévisionnel de visites chez le
médecin, elle est calculée comme suit :
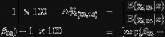
Le modèle de Poisson peut être critiqué
sur un certain nombre points :
- Il ne permet pas d'observer
l'hétérogénéité, d'autres modèles,
tels que le Modèle binomialnégatif ou le modèle
Poisson-log-normal fournissent des estimateurs plus efficaces, (Winckelmann
2000).
- Il ne tient pas compte de la structure du panel de
données. Il y a jusqu'a cinq observations pour une personne
donnée, la présence d'un individu spécifique en termes
d'hétérogénéité, entraîne la
nullité de l'hKpSphèOe d'inHépG1LanGe de
l'échantillon.
Alternativement, on pourrait supposer une dépendance
entre les effets individuels et leur covariance.
(QIinQ L] L'indice du modèle de
régression de Poisson (et ses généralisations) implique
que la moyenne est donnée et tous les autres aspects de la distribution
sont bien déterminés. En particulier, la réforme ne peut
pas avoir des effets différents dans les différentes parties de
la distribution.
5.2 Modèle binomial négatif
/II mSTIèpI pSi[[SF LérifiI
p'égYpité [QiLYFtI : Espérance =
Variance dans la distribution

Cependant, un tel modèle comporte une hypothèse
très restrictive sur la variance.
Dès lors, il néglige la « surdispersion »
Ifti[tYFt TIYF[ p'échantillon ce qui conduirait à la
nonvalidité TII[ tI[t[ TI'inférence. Pour remédier
à cette situation, cette hypothèse peut être
relâchée en supposant une forme fonctionnelle alternative de la
variance telle que :

Ce modèle est désigné sous le nom de
modèle binomial négatif ou Negbin3. Il offre tous les
avantages du modèle de Poisson mais il est plus flexible.
Cependant, un tel modèle ignore une des
caractéristiques essentielles des variables dépendantes, i.e.
p'IftT[tIFcI TI'QFI différence qualitative entre les
réponses nulles et les réponses positives.
5.3 Modèles structurels
il s'agit d'une structure de modèle hurdle (Mullahy, 1986)
l'estimation est la suivante :
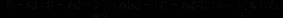
Pour fermer le modèle, il faut préciser f1 et
f2.
J1 comprend
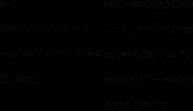
J2 comprend Poisson, binomial négatif, Poisson
log-normal
Le modèle hurdle est populaire dans la
littérature de la santé, il donne une interprétation
structurelle qui s'entend avec l'intuition d'une structure de double
décision, du processus de demande. La première décision de
contact est prise indépendamment par le patient, alors que le traitement
et l'orientation de décision est influencée par le
médecin.
Deb et Trivedi ont observé une incompatibilité
entre les hypothèses du modèle et l'état des
données. Les consultations médicales sont mesurées par
période et non par stade de la maladie.
3 Notation proposée par Cameron et Trivedi.
En outre, les personnes en bonne santé consultent aussi
les médecins. Deb et Trivedi préconisent le modèle mixture
finie dans le but d'opérer une distinction entre les patients
fréquents et les moins fréquents.
6. Résultats
La moyenne du nombre de visites trimestrielle chez un
médecin a diminué de 2,66 à 2,35 visites entre 1996 et
1998. Les visites annuelles ont diminué de 11 % entre 1996 et 1998.
Déclin entre 1995 et 1996, et une augmentation de 2 %
entre 1998 et 1999. Ainsi, la diminution importante du nombre de visites
coïncide clairement avec le calendrier de la réforme. Aussi, pour
le compte de 1999, la réforme est allée de pair avec une
augmentation du nombre de visites, ceci est compatible avec l'hypothèse
d'un effet comportemental (abrogation de la réforme).
Tout au long de la période de l'étude, il y a
une large part des non-visiteurs. Cette proportion est plus
élevée en 1998, quand elle atteint 37 % de la population, il y a
une augmentation de plus 4,4 pts par rapport en 1996.
La moyenne d'âge a augmenté de moins d'un an
entre 1995 et 1999. Cela laisse penser que f'éU}aXtfffoX1X'Ost1Ras
1éQEfffbré. Une raison à cela est que les1jeEXes1eXQrIIXt
1daXs1f'éU}IXtfffoX1et 1 les personnes âgées fe1qEftteXL,
1fa1foErU}eLI 1d'kgL 1ItaXt1F0-60 ans.
Le taux de chômage de la population est lié
à1 'état de la conjoncture. En effet, il retrace
approximativement le taux réel de chômage qui a atteint 11 % en
1997 en Allemagne. Fait intéressant, les statistiques indiquent une
amélioration générale de l'état de santé de
la population entre 1996 et 1998. La proportion des personnes pratiquant le
sport a augmenté de 25 à 31%, bien que ces moyennes restent
très volatiles. La proportion des personnes déclarant une bonne
santé a augmenté de 56 à 60 %, alors que la proportion des
personnes déclarant un mauvais état de santé a
diminué, passant de 14 à 13 %. Ces tendances sont importantes
pour deux raisons. Tout d'abord, l'amélioration de la qualité des
soins de santé pourrait être en mesure d'expliquer en partie la
diminution du nombre de visites chez un médecin.
Deuxièmement, ces améliorations apportent quelques
éléments prouvant que les réformes, ont réussi
à maîtriser les coûts, mais en fait ont pu aggraver la
situation sanitaire générale. Les estimations du modèle de
Poisson, avec prise en compte des effets spécifiques individuels
appellent les remarques suivantes :
La plupart des effets sont robustes pour la
spécification du modèle, et de nombreux résultats sont
communs à ceux qu'on trouve ailleurs dans la littérature. Les
hommes ont moins visité les médecins que les femmes. Sur la base
du modèle de Poisson, le nombre de visites a diminué de 9,9 %
entre 1996 et 1998.
Six autres modèles ont été estimés
en utilisant les mêmes données : binomial négatif,
Poisson-log - Normal, hurdle- binomial négatif, mixture finie binomial
négatif à deux composantes, modèle à multi
composantes, et le modèle probit-Poisson-log-normal.
Deb et Trivedi (2002) ont conclu la supériorité
du modèle mixture finie sur le modèle hurdle.
Il y a plusieurs façons d'exercer une discrimination
entre les modèles. Certains de ces modèles sont imbriqués
(comme le modèle de Poisson et le modèle binomial
négatif), la plupart d'entre eux ne le sont pas (par exemple mixture
finie, le hurdle binomial négatif et le modèle multi
épisodes)
Les valeurs du maximum de vraisemblance des différents
modèles montrent que le ratio de test de vraisemblance rejette
clairement le modèle de Poisson contre les autres modèles.
Pour sélectionner le meilleur modèle parmi les
sept, une simple comparaison des maximums de vraisemblance (Likelihood) est un
premier indicateur.
Il convient de souligner que les résultats corroborent
les conclusions de Deb et Trivedi (2002) que le modèle mixture finie
Binomial négatif surpasse le modèle hurdle binomial
négatif.
La taille et la composition des effets de la réforme,
mesurés par le pourcentage de réduction du nombre de visites chez
le médecin, pour chacun des modèles appellent les remarques
suivantes : Les estimations pour le modèle de base (modèle de
poisson et binomial négatif), avec ou sans observation d}hI
pI ropI RI JpI , sont toutes dans le même rang,
allant de 9,9 à 10,4 %. Ces estimations sont nettement au-dessus de
celle (e l}I tF(p (e Lauterbach et al, Pour rappel leur étude
a montré une baisse de 4,5 %.
Comment réconcilier ces deux conclusions ? Il est
possible que les différences ont trait aux faibles taux de
réponse dans l'enquête, ou la manière dont les questions
ont été posées par le GSOEP.
Les modèles structurels répondent à cette
question de différences (}élasticités dans
différentes parties de la distribution. Les résultats confirment
effectivement qu'un tel effet est présent, cela est le plus
évident dans le modèle probit-Poisson-log-normal.
Cette réduction est plus forte à gauche de la
distribution : la probabilité (}JffITTFer au mñns une visite a
diminué d'environ 6,7 % entre 1996 et 1998, alors que le nombre de
visites prévisionnel R}J diminué que d'environ 2,6 %.
| 


