Existence globale de solutions à symétrie sphérique du système d'Einstein-Klein-Gordon.

Année Académique 2018-2019

EXISTENCE GLOBALE DE SOLUTIONS

A SYMÉTRIE SPHÉRIQUE DU

SYSTÈME D'EINSTEIN-KLEIN-GORDON

Mémoire présenté et soutenu publiquement en vue de

l'obtention du diplôme de MASTER en

Mathématiques

Option: Analyse et Applications

rédigé par

TEYANG Franck Modeste
Matricule: 12V0212
Sous la direction du :
Pr.NOUNDJEU Pierre
Maître de conférences
Université de Yaoundé I

Mémoire de MASTER



Université de Yaoundé 1

? Remerciements ?

Je souhaite évidemment en tout premier lieu remercier le professeur Noundjeu Pierre. Il a été pour moi un encadreur exemplaire, toujours disponible malgré un emploi du temps parfois extrêmement chargé. Il a su m'encadrer, me guider, me conseiller et me faire partager son savoir mathématique et son enthousiasme, même lorsque les choses pouvaient paraître mal engagées. Pour tout cela, je lui suis très reconnaissant.

Comme ce mémoire est l'aboutissement de plus de cinq années d'études, c'est l'occasion pour moi de remercier tous les enseignants qui ont influencé mon parcours et m'ont fait prendre goût aux mathématiques, ici à l'université de Yaoundé I ou encore, plus tôt, au lycée de Fotouni.

Il est maintenant temps de remercier mes amis et camarades de classe, anciens et actuels, et plus particulièrement ceux du département de Mathématiques de l'université de Yaoundé I. Merci à Kungne Hervé et à Bedong Amassoumou pour leur précieux aide qui m'ont permis à débloquer certains problèmes. Merci également à Zotsa Brice et à Kuate Collins pour tous les conseils avisés, tant en LateX que vis à vis du déroulement de nos mémoire. Merci à Matial Djomgang, à Ferdinand Tchoumeni et à Diane Kipuguie pour la bonne humeur, à Djoko Charly, pour ses conseils et toutes les discussions intéressantes que l'on a pu avoir du fait de la connexité de nos domaines de recherche. Je n'oublie pas de remercier très sincèrement Xavier Kamgang et Sedric Ngomseu pour leur soutien moral et financier. Bien sûr, je ne peux terminer ces quelques lignes sans évoquer ma famille, et notamment ma mère Pascaline Sodannelle Kengni, que je ne pourrai jamais suffisamment remercier pour m'avoir toujours encouragé, m'avoir soutenu, et avoir toujours su me dire ce que j'avais besoin d'entendre lors des inévitables moments de découragement. Merci pour l'éducation que tu as su me prodiguer, et notamment pour l'ouverture d'esprit que tu as su me transmettre. Merci à mes deux grandes soeurs Blandine et Cendrine pour leur soutien et encouragement.

Mémoire de MASTER



Université de Yaoundé 1

? Résumé ?

Les équations d'Einstein décrivent en relativité générale comment la matière et l'énergie modifient la géométrie de l'espace-temps. Dans ce mémoire, nous prouvons l'existence globale et l'unicité de solutions à symétrie sphérique du système couplé d'équations non linéaires d'Einstein et de Klein-Gordon (EKG) pour des petites données initiales. Par un changement de fonctions inconnues, nous transformons ce système en une équation intégro-différentielle non linéaire du premier ordre que nous résolvons en utilisant le théorème du point fixe dans un espace de Banach.

Mots clés : Relativité générale, Équations d'Einstein, Espace-temps à symétrie sphérique, équation intégro-differentielle.

Mémoire de MASTER



Université de Yaoundé 1

? Abstract ?

The Einstein equations describe in general relativity how matter and energy modify the geometry of spacetime. In this dissertation, we prove the global existence and uniqueness of spherical symmetric solutions to the coupled Einstein and nonlinear Klein-Gordon system (EKG) for small initial data. By a change of unknown functions, we transform this system into a nonlinear first-order integro-differential equation that we solve by using the fixed-point theorem in a Banach space.

Keywords : General relativity, The Einstein equations, Spherically symmetric spacetime, integro-differential equation.

Mémoire de MASTER

iv

Université de Yaoundé 1

? Table des matières ?

Résumé i

Abstract ii

Introduction 1

1 PRÉLIMINAIRES 2

1.1 Espace de Banach 2

1.2 Théorème de Cauchy-Lipschitz 3

1.3 Quelques notions de géométrie différentielle 4

1.4 Rappels de géométrie lorentzienne 10

1.4.1 Dérivée covariante d'un champ de tenseurs 15

2 ÉQUATION INTEGRO-DIFFÉRENTIELLE NON LINÉAIRE OBTE-

NUE DU SYSTÈME D'EKG 18

2.1 Espace-temps à symétrie sphérique 18

2.1.1 Système d'EKG 21

2.2 Réduction du système d'EKG en une équation intégro-différentielle du

premier ordre 25

3 THÉORÈME D'EXISTENCE ET D'UNICITÉ POUR L'ÉQUATION INTEGRO-DIFFÉRENTIELLE NON LINÉAIRE DU PREMIER ORDRE

28

3.1 Cardre fonctionnel 28

3.2 Théorème d'existence et d'unicité (théorème principal) 29

3.2.1 Éléments de preuve du théorème d'existence de d'unicité 30

Table des matières

3.2.2 Preuve du lemme 3.1 31

3.2.3 Preuve du lemme 3.2 44

3.3 Preuve du théorème d'existence et d'unicité 51

Conclusion 52

Annexe 53

Bibliographie 55



Mémoire de MASTER

Mémoire de MASTER

1

Université de Yaoundé 1

* Introduction *

Des observations astronomiques font état non seulement de l'existence de matières cachées mais aussi d'énergies sombres. Pour mieux les décrire, considérons un champ scalaire réel, solution de l'équation dite de Klein-Gordon; En présence du champ gravitationnel, nous avons le système d'EKG. La recherche d'une solution globale en temps d'un tel système est difficile en général; C'est la raison pour laquelle on suppose diverses symétries telles que la symétrie sphérique, la symétrie axiale, la symétrie cylindrique et bien d'autres en vue de rendre compréhensibles les preuves. On se fixe la tâche de rechercher une solution de ce système à symétrie sphérique. C'est-à-dire que l'espace-temps recherché est de la forme (R⁴,g), avec g définie par :

ds² = -e^-2"du² - 2e"^+ëdudr + r²(dè² + sin² èdö²)

Pour mener à bien cet objectif, nous transformons comme dans les travaux de Dongho Chae [2], le système d'EKG en une équation intégro-différentielle non linéaire du premier ordre, puis nous utilisons le théorème du point fixe et un contrôle de solutions du système caractéristique associé à cette équation. De ce fait, notre travail s'articule comme suit : Tout d'abord au premier chapitre, nous définissons les notions importantes pour la bonne manipulation de ce système d'équations, ensuite dans le second chapitre, nous réduisons notre système d'EKG en une équation intégro-différentielle non linéaire du premier ordre et enfin dans le troisième chapitre, nous énonçons et prouvons notre théorème principale qui conduira à l'existence globale de solution pour notre équation intégro-différentielle.

* *

* *

Chapitre Un

Mémoire de MASTER

2

Université de Yaoundé 1

PRÉLIMINAIRES

1.1 Espace de Banach

Définition 1.1.1 : (Espace vectoriel normé)

Un espace vectoriel normé est la donnée d'un espace vectoriel E sur K (K = R ou C) et d'une application Y.Y : E --* R₊ vérifiant:

· Vx E E, YxY = 0 ? x = 0

· Vx,y E E, Yx + yY = YxY + YyY

· Vx E E, VA E K, YAxY = SASYxY

On note (E, Y.Y) l'espace vectoriel normé muni de la norme Y.Y

Définition 1.1.2 : (Espace métrique) Un espace métrique est un ensemble E non vide muni d'une application d : E x E -* R₊ vérifiant pour tout triplet (x, y, z) E E³ :

a) d(x,y) = 0 ? x = y

b) d(x,y) = d(y,x)

c) d(x,z) = d(x,y) + d(y,z)

Une telle application est appelée distance sur E et le couple (E, d) est appelé espace métrique.

Exemple 1.1 : Tout espace vectoriel normé (E, Y.Y) est un espace métrique (E, d) pour la distance d(x, y) = Yx - yY.

Définition 1.1.3 : (Suite de Cauchy)

On dit d'une suite _(xn)n de (E, Y.Y) qu'elle est de Cauchy si

Vå > 0 N_E E N tel que Vp, q E N p, q = N_E Ô Yx_p - x_qY < å

1.2. Théorème de Cauchy-Lipschitz

ce qui revient à

bå > 03N_E E N tel quebp, q E N p,q >_ N_E = d(x_p,x_q) < å

lorsque l'on est dans un espace métrique (E, d).

Définition 1.1.4 : (Espace métrique complet)

On dit qu'un espace métrique (E, d) est complet si tout suite de Cauchy de E converge dans E.

Définition 1.1.5 : (Espace de Banach)

Un espace vectoriel normé (E, 11.11) est dit de Banach s'il est complet.

Exemple 1.2 : D'espace de Banach

L'espace des fonctions f : R²₊ ? R bornées admettant des dérivées partielles bornées muni de la norme

I^??x^,

f(xy)I+ sup I _n f(x, y)I

0=x,y<oo y

11f1 1= sup If(x, y)1 + sup

0=x,y<oo 0=x,y<oo

Mémoire de MASTER

3

est un espace de Banach.

Théorème 1.1.1 : (Théorème du point fixe de Banach)

Soit (E, d) un espace métrique complet, f une application strictement contractante de (E, d) vers (E, d) i.e : 3k E]0,1[ tel que bx, y E E, d(f(x), f(y) <_ kd(x, y). Alors f admet un unique point fixe dans E c'est-à dire qu'il existe un unique point x E E tel que f(x) = x.

Preuve : Voir [5]
·

1.2 Théorème de Cauchy-Lipschitz

Définition 1.2.1 : (Application lipschitzienne)

Soient M et N deux espaces métriques et f une application de M dans N. Soit k un réel strictement positif. Alors f est k-lipschitzienne si

d(f(x), f(y)) <_ kd(x,y), b x, y E M

k est appelé constante de Lipschitz de f.

Mémoire de MASTER

4

1.3. Quelques notions de géométrie différentielle

Définition 1.2.2 : (Application globalement lipschitzienne)

Soit E un espace de Banach, U un ouvert de R x E. Une application f définie de U dans E est dite globalement lipschitzienne par rapport à x E E s'il existe k > 0 telle que

Yf(t,x) - f(t,y) ~ kYx - yY, V(t,x), (t,y) E U

Définition 1.2.3 : (Application localement lipschitzienne)

Soit E un espace de Banach, U un ouvert de R x E. Une application f définie de U dans E est dite localement lipschitzienne par rapport à x E E si pour tout (t0, x0) E U, il existe V E v(t0, x0) dans U et une constante strictement positive k tels que f/V soit k-lipschitzienne par rapport à la variable x.

Théorème 1.2.1 : (Cauchy-Lipschitz)

Soient E un espace de Banach et f une application continue d'un ouvert I xU de RxE dans E. On suppose que pour t fixé, l'application x z? f(t, x) est localement lipschitzienne. Alors pour tout point (s0, y0) E I xU, il existe I0 xU0 voisinage de (s0, y0) dans I xU tel que pour tout (t0, x0) E I0 xU0, il existe une unique solution x(t) de l'équation x^'(t) = f(t, x(t)) définie sur I0 avec la condition initiale (t0, x0).

Preuve : Voir [5] Ì

1.3 Quelques notions de géométrie différentielle

Définition 1.3.1 : (Espace topologique)

Soit E un ensemble non vide, O une famille de parties de E vérifiant:

(i) 0,E E O

(ii) VA,B E O, A n B E O

(iii) _V(Oi)i?I C O, _Ui?IOi E O

Le couple (E, O) est appelé espace topologique et O est ensemble des ouverts de E.

Définition 1.3.2 : (Espace topologique séparé)

Un espace topologique (E, O) est dit séparé(au sens de Hausdorff) si Vx, y E E tels que x ~ y, il existe U E O contenant x et V E O contenant y avec U n V = 0

Mémoire de MASTER

5

1.3. Quelques notions de géométrie différentielle

Dans la suite, lorsqu'il n'y aura pas d'ambiguïté, nous noterons tout simplement E pour désigner un espace topologique.

Définition 1.3.3 : (Espace séparable)

E est dite à base dénombrable d'ouverts s'il possède un sous ensemble dénombrable dense dans E

Exemple 1.3 : Pour l'espace topologique Rⁿ, on a Qⁿ comme partie dénombrable dense.

Définition 1.3.4 : (Application de classe C°°)

Soit n E N, Sl un ouvert non vide de Rⁿ. Soient x = (x1, ...., x_n) E Rⁿ et á =

(á1, , á_n) E Nⁿ un multi-indice.

Soit f : Sl --p C une application. On dit que f est de classe C^k, k E N si Vá E Nⁿ tel que

lál = k, D^áf existe et est continue avec lál = á1 + á2 + + á_n et D^á =

?x^á1

1 ?xá2

2 ...?xán

_n .

f est de classe C^°° si elle est de classe C^k Vk E N.

?lál

Définition 1.3.5 : (Carte locale)

Soit E un espace topologique.On appelle carte locale de dimension n sur E la donnée d'un couple (U,ö) tel que :

i-) U est un ouvert de E.

ii-) ö est un homéomorphisme de U vers ö(U) g Rⁿ.

L'ouvert U est le domaine de la carte et pour p E U, ö(p) = (x¹(p), , xⁿ(p)) E Rⁿ. Les

xⁱ(p) ,i = 1, 2, ...., n sont appelés coordonnées locales du point p.

Définition 1.3.6 : (Cartes compatibles)

Deux cartes (U, ö) et (V,ø) sur E sont dites C^k -compatibles si U n V = 0 ou lorsque l'application ø ö-¹ : ö(U n V ) -* ø(U n V ) est un C^k- difféomorphisme.

Définition 1.3.7 : (Atlas)

Un atlas de dimension n (n E N^*) sur E de classe C^k (k E N) est un ensemble A = {(U_á, _öá)á?Ë} de cartes de dimension n tel que :

- Les ouverts U_á recouvrent E ;

- Toutes les cartes de A sont C^k- compatibles deux à deux.

Mémoire de MASTER

6

1.3. Quelques notions de géométrie différentielle

Un atlas permet donc de définir des coordonnées locales partout sur E. On dit que deux atlas sont équivalents si leur union est encore un atlas c'est-à-dire que A = {(U_á, _á)á?A} et B = {(Vâ, _öâ)â?A} sont équivalents si toutes les cartes (U_á, _á) et (Vâ, çbâ) sont compatibles deux à deux.

Définition 1.3.8 : (Structure différentiable)

Une structure différentiable de dimension n sur E est une classe d'équivalence d'atlas de dimension n de E.

La relation d'équivalence R ici étant : pour deux atlas A et B, ARB si et seulement si toutes les cartes de A et B sont deux à deux compatibles.

En pratique, on définit une structure différentiable en donnant un atlas représentant la classe.

Définition 1.3.9 : (Variété topologique, sous-variété)

Une variété topologique de dimension n(n E N^*) est un espace topologique séparé dont chaque point possède un voisinage ouvert homéomorphe à Rⁿ.

Un sous-ensemble M de Rⁿ est appelé sous-variété de Rⁿ de dimension in (in < n) de classe C^k si ?x E M, il existe un ouvert U de Rⁿ contenant x et çb : U -? çb(U) ? Rⁿ de classe C^k tels que çb(U n M) = çb(U) n R^m.

Définition 1.3.10 : (Variété différentielle)

Une variété différentielle de classe C^k et de dimension n est un espace topologique séparé muni d'un atlas maximal (au sens de l'inclusion) de classe C^k et dans lequel toutes les cartes sont de dimension n.

Définition 1.3.11 : (Courbe différentielle en un point)

Soit M une variété différentiable et I une partie non vide de R contenant 0, x un point de M. Une courbe différentielle de M en x est une application différentielle

c : I -? M

t--?c(t)

telle que c(0) = x. F = c(I) c M est appelé arc paramétré de M et le couple (I, c) est une paramétrisation de la courbe F.

Mémoire de MASTER

7

1.3. Quelques notions de géométrie différentielle

Définition 1.3.12 : (Courbes tangentes en un point)

Deux courbes c1 et c2 passant par x sont dites tangentes si pour toute carte locale (U, ö) d'une variété différentielle M, on a :

cents ····

····

c1(0) = c2(0) = x dt(ö c1)(0) = d

d dt(ö c2)(0)

.

Par la suite, on définit la relation R sur l'ensemble des arcs paramétrés de M par _c1Rc2 si et seulement si les courbes c1 et c2 sont tangentes.

R ainsi définie est une relation d'équivalence et une classe d'équivalence suivant la relation R est définie par :

c_x : C⁸(M) Ð? R

d

g z? [c]_x(g) = _dtg(x)

Définition 1.3.13 : (Vecteur tangent- Espace tangent)

Soit M une variété différentielle et x E M. Un vecteur tangent à M en x est une classe d'équivalence pour la relation R définie ci-dessus.

L'espace tangent à M en x est l'ensemble des vecteurs tangents à M en x.C'est un espace vectoriel de même dimension que M et est noté T_xM.

Soit M une variété différentielle de dimension n Définition 1.3.14 : (Fibré tangent)

TM = U x?M

({x} x TxM) est une variété différentielle de dimension deux fois la dimen-

sion de M et est appelé fibré tangent à M.

Définition 1.3.15 : (Champ de vecteurs)

Un champ de vecteurs sur M est une application

X : M Ð? TM

x z? X(x) = X_x E T_xM

telle que H X = idM (H étant la projection canonique).Un champ de vecteurs est dit différentiable si l'application qui le définit est C⁸.On note par X(M) l'ensemble des champs de vecteurs différentiables définis sur M.

Mémoire de MASTER

8

1.3. Quelques notions de géométrie différentielle

Théorème 1.3.1 : Un champ de vecteurs différentiable X est une dérivation sur C^°°(M) ce qui revient à dire que les deux propriétés suivantes sont vérifiées :

i-) Va, b E R, Vg, h E C^°°(M), X(ag + bh) = aX(g) + bX(h)

ii-) Vg,h E C^°°(M), X(hg) = hX(g) + gX(h)

Preuve : Voir [7] Ì

Définition 1.3.16 : (Produit de deux champs de vecteurs)

Soient X et Y deux champs de vecteurs. Le produit de X par Y est donné par:

XY (g) = X(Y (g)), Vg E C^°°(M)

.

Proposition 1.3.1 : le produit de deux champs de vecteurs n'est pas une dérivation. Preuve : Soient X et Y deux champs de vecteurs. On a pour tout h,g E C^°°(M), on a :

XY (gh) = X(Y (gh)) = X(gY h + hYg)

= gX(Y h) + Y hX(g) + hX(Yg) + Y gX(h) = gXY (h) + hXY (g) + Y hX(g) + Y gX(h)

Mais,

g(XY )h + h(XY )g = gX(Y h) + hX(Yg)

.Il vient que, XY (gh) ? g(XY )h + h(XY )g.
·

Définition 1.3.17 : (Crochet de Lie) Soit M une variété différentiable.

On appelle crochet de Lie de deux champs de vecteurs X et Y ,le champs de vecteurs noté [.,.] et défini par:

[.,.] :X(M) x X(M) ? X(M) (X,Y ) '-? [X,Y ] = XY - Y X

Remarque 1.3.1 : L'opérateur crochet définit une dérivation sur C^°°(M). En coordonnées locales, on a :

n n

[X,Y ] = Q Q (Xj?jY i - Y ^j?jXⁱ)` ?i

i=1j=1

a

axi

où ?i =

Mémoire de MASTER

9

1.3. Quelques notions de géométrie différentielle

Définition 1.3.18 : (Dérivée de Lie)

La dérivée de Lie d'un champ de vecteurs X par rapport à un autre champ de vecteurs Y est le champ de vecteurs LX(Y ) défini par : LX(Y ) = [X, Y ]

Définition 1.3.19 : (Applications n-linéaires)

Soient n E N^*, E1, E_n et F des K-espaces vectoriels, K = R ou C.Une application

f : E1 x x E_n -* F est dite n-linéaire si elle est linéaire par rapport à chacune de ses

n facteurs.

Lorsque F = K, on dit que f est une forme linéaire sur E1 x x E_n

Remarque 1.3.2 : Lorsque E1 = E2 = ....E_n = E et F = K, on dit f est une forme n-linéaire sur E

Définition 1.3.20 : (Tenseur élémentaire)

Soient E et F deux K-espaces vectoriels(K = R ou C), x E E et y E F.On appelle tenseur élémentaire, l'application :

x ® y :E^* x F^* -* K

(á,i) 1---* á(x).i(y)

où "." désigne le produit scalaire et E*, F^* désignant respectivement les duals algébriques

de E et F.

Définition 1.3.21 : (Produit tensoriel)

Soient E et F deux K-espaces vectoriels, x E E et y E F.On appelle produit tensoriel de E par F, l'ensemble E ® F défini par :

E®F={x®y;xEE,yEF}

Dans tout ce qui suivra, M désigne une variété différentiable de dimension n. Définition 1.3.22 : (Tenseur covariant)

Un tenseur du type (⁰) ou p-fois covariant au point x E M est une forme p-linéaire p

sur T_xM.

On désigne par ®^pT_x^* M = TP l'espace des p-formes linéaires sur T_xM.

Exemple 1.4 : Un tenseur 2-fois covariant ou du type (⁰₂) est une forme bilinéaire sur

T_xM x T_xM

1.4. Rappels de géométrie lorentzienne

Définition 1.3.23 : (Tenseur contravariant)

Un tenseur de type (^q₀) ou q- fois contravariant au point x E M est une forme q-linéaire sur T_x^*M, où T_x^*M est le dual algébrique de T_xM.

On désigne par ®qT_xM = T^q_x0 l'espace de toutes les q-formes linéaires sur T_x^*M. Définition 1.3.24 : (Tenseur mixte)

Un tenseur du type (^q) ou tenseur p-fois covariant et q-fois contravariant au point p

x E M est une p-forme linéaire sur T_xM et q- forme linéaire sur T_x^*M.

On désigne par ®^q_pT_xM = T^qxp l'ensemble des tenseurs du type (^q) au point x E M.

p

Définition 1.3.25 : (Fibré tensoriel)

On appelle fibré tensoriel, la variété différentielle T_p^q M définie par :

T_p^qM = ux?M({x} x T^qxp)

.

Définition 1.3.26 : (Champ de tenseur)

Un champ de tenseur de type (^q) sur M est une application

p

T:M--*T_pqM xi-?T(x)

où T(x) = (x, t_x) t_x E T^qxp.

1.4 Rappels de géométrie lorentzienne

Convention de sommation d'Einstein :

Soient E un espace vectoriel de dimension finie n sur K et B = {e1, e2, , e_n} une base de

E. Soit x E E alors, x =

n Q i=1

xiei ; xi E K.

Mémoire de MASTER

10

L'indice i sur lequel on effectue la sommation est appelé indice muet. La convention de sommation d'Einstein consiste à supprimer le symbole de sommation ? et d'indiquer l'indice muet apparaissant en bas et en haut. Ainsi l'écriture de x E E dans la base B

devient : x = xⁱei avec i E {1, 2, , n}.

Dans toute la suite, V4 désigne la variété différentiable de dimension 4, le corps de base R. On adopte la convention de sommation d'Einstein où les indices grecs á, â, ã, .... sont les éléments de {0,1, 2, 3} et les indices latins i, j, k, .... les les éléments de {1, 2, 3}.

1.4. Rappels de géométrie lorentzienne

Définition 1.4.1 : (Variété Lorentzienne)

Une variété Lorentzienne est la donnée du couple (M, g) où M est une variété différentielle de dimension 4 et g un champ de tenseur covariant de type 2 et de classe C⁸ sur M appelé métrique et vérifie:

i-) g est symétrique;

ii-) ?x E M, g induit sur T_xM une forme bilinéaire non dégénérée

g_x : T_xM x T_xM ? R;

iii-) g est de signature (+, -, -, -) ou (-, +, +, +) et on dit que g est de signature hyperbolique.

Remarque 1.4.1 : 1-) Dans la définition précédente, iii-) signifie que à g ,on associe une forme quadratique admettant une décomposition en un carré positif et trois carrés négatifs ( ou en un carré négatif et trois carrés positifs ).

2-) Dans un repère _(eá)á de V4, g s'écrit en coordonnées locales g = g_áâdx^ádxâ. On dit alors que g est une matrice carrée d'ordre 4 dont les composantes sont les g_áâ.On note alors g = (gáâ)á,â. g étant par définition inversible, son inverse g-¹ est noté (g^áâ)á,â et on a : g^áãg_ãâ = 8á â (symbole de Kronecker) avec gáâ = gâá. Mais on a aussi comme dans [3] g^áâg_áâ = dimV4 = 4.

Définition 1.4.2 : (Repère orthonormé)

Le repère _(eá)á est dit orthonormé dans (V4,g) si g s'écrit de la forme :

3

g = ds^2= (dx^0)^2-

Q á=1

(dx^á)^2

3

dont de signature (+, -, -, -) ou de la forme g = ds^2= -(dx^0)^2+

Q á=1

(dx^á)^2dont de signature

Mémoire de MASTER

11

(-, +, +, +). Un événement x E V4 est représenté par (x⁰, xⁱ) avec x⁰ = t appelé coordonnée temporelle et xⁱ coordonnées de l'espace. Ainsi pour tout système de coordonnées locales dans V4, x⁰ représente le temps t et xⁱ l'espace. Cette représentation vient de Minkowski (1908).

Définition 1.4.3 : (Espace-temps)

Un espace-temps est la donnée d'un couple (M,g) où (M,g) est une variété Lorent-zienne.

1.4. Rappels de géométrie lorentzienne

Exemple 1.5 : 1.) L'espace-temps de Minkowski

(118⁴,g) est l'espace-temps de Minkowski où la métrique g dite de Minkowski est définie

3 3

par : g = -(dt)^2 +

(dx^i)^2 ou g = (dt)^2 -

(dx^j)^2 avec les matrices de g dans la base

i=1 j=1 canonique de 118^4 données respectivement par : 2.) L'espace-temps de Sitter

' -1 0 - - - - - - - - 0 » 0

0 1 0 0

0 0 1 0

0 « 0 -- -- -- -- -- -- -- -- 0 1 ·

et

' 1 0 - - - - - - - - 0 » 0

0 -1 0 0

0 0 -1 0

0 « 0 -- -- -- -- -- -- -- -- 0 -1 ·

(118 × S³, h) est l'espace-temps de Sitter. S³ désigne la sphère unité de 118⁴ et la métrique h s'écrit : h = dt² - a²ch²(^t_a)[dw² + sin²w(d0² + sin²0d?²)] avec : t E 118 ,w E 118₊ , a E 118^* , 0 < 0 < 7r , 0 < cp < 27r. h a pour signature (+,-,-,-) avec h00 = 1, h11 = -a²ch²(^t_a) , h22 = -a²ch²(^t_a)sin²w , h33 = -a²ch²(^t_a)sin²wsin²0 et les autres coefficients sont tous nuls. 3. L'espace-temps de Schwarzschid

La métrique de Schwarzschild est définie par :

r )dt² + (1 - ^2m)^-1dr² + r²(d0² + sin² 04²) r

2m

avec pour signature (-, +, +, +) ; g00 = -(1

gSchw = -(1

2m

2m

) , g11 = (1- )-¹ , g22 = r² , g33 = r² sin² 0

r r

et tous les autres coefficients nuls.

Remarque 1.4.2 : Un élément u de _TxV4 est encore appelé vecteur contravariant et ses composantes dans une base _(eá)á ^de _TxV4 sont notées u^á i.e : u = u^áe_á. Un élément u* de _Tx*V4 est encore appelé vecteur covariant et ses composantes dans la base duale (0^á)_á de _(eá)á sont notées u^*_á, i.e u^* = u^*_á0^á. On sait que g = g_x : TxV4 × TxV4 ? 118 est une forme bilinéaire symétrique dont ?u , v E _TxV4, u fixé, l'application v H g(u, v) est une forme linéaire sur _TxV4, donc u^* = g(u, .) E T_x^* V4.

On a : u^* = u^*_á0^á où u^*_á = u^*(e_á). D'où :

_u*

á = u^*(e_á) = g(u, e_á) = u^âg(eâ,e_á) = gáâu^â

Par analogie avec l'inverse g^áâ qui est une forme bilinéaire symétrique sur T_x^* V4, on associe à tout vecteur covariant u^* E T_x^* V4 un vecteur contravariant par uâ = g^áâu^*_á. Ainsi g

Mémoire de MASTER 12

Mémoire de MASTER

13

1.4. Rappels de géométrie lorentzienne

permet d'associer canoniquement à tout vecteur contravariant u un vecteur covariant u* et réciproquement. Par la suite,u sera identifié à u^* et on parlera de u tout simplement et de ses composantes covariantes u_á et contravariantes uâ liées par les relations u_á = gáâu^â et u^á = g^áâuâ.

La généralisation de ce résultat aux tenseurs d'ordre p quelconques est immédiate car un

tenseur est une combinaison de tenseurs élémentaires de la forme x1 ? x2 ? ? x_p . On a
donc : Táâ = gáãgâuT^ãu , T^áâ = g^áãgâuT_ãu , T_â^á = g^áuT_uâ , T_â^á = gâuT uá

Définition 1.4.4 : (Métrique Riemannienne)

Une métrique Riemannienne sur une variété différentiable M est une application g E C⁸(M) telle que ?x E M, g(x) est un produit scalaire sur T_xM (l'ensemble des vecteurs tangents à M en x).

Définition 1.4.5 : (Variété Riemannienne)

Une variété Riemannienne est la donnée d'un couple (M, g) où M est une variété différentiable et g une métrique Riemannienne.

Définition 1.4.6 : (Connexion linéaire et Symboles de Christoffel) Une connexion linéaire sur V4 est la donnée d'une application

? : TV4 * T^*V4 ? TV4
v H ?v

définie sur les champs de tenseurs différentiables sur V4 et vérifie pour toute fonction différentiable

cents ····

····

?(u + v) = ?u + ?v (linéarité) ?fu = df ? u + f?u (règle de Leibnitz)

(1.1)

?v est appelé la dérivée covariante (ou la différentielle absolue) de v. Si v = v^áe_á dans la base _(eá)á ^de _TxV4 alors de (1.1), on déduit que ?v = v^á?e_á + dv^á ? e_á. Les composantes locales du tenseur mixtes ?v notées ?_ávâ sont donc données par :

?_áv^â = 8_áv^â + Fâ áñvñ (1.2)

Les coefficients Fâ áñ de la relation (1.2) sont appelés symboles de Christoffel associés à la connexion ?.

1.4. Rappels de géométrie lorentzienne

Remarque 1.4.3 : Les composantes covariantes locales du tenseur ?v notées _?ávâ sont données par

?ávâ = aávâ - ^ñ_áâvñ

_

où 8J_á = ?

?xá

Remarque 1.4.4 : 1.) ?(df) est un tenseur symétrique et par commutativité de la dérivée partielle seconde,on déduit que ^ñ_áâ = ñâá.

2.) La dérivée covariante de la métrique g est nulle c'est-à-dire ?g = 0 et on déduit que

Oñgáâ - ^u_ñáguâ - ^u_ñâgáu = 0 i.e âñgáâ = ^u_ñáguâ + ^u_ñâgáu (1.3)

Proposition 1.4.1 : Les coefficients de Christoffel en coordonnées locales s'obtiennent du tenseur métrique par :

ñ áâ =

1 2

g^ñu(aáguâ + aâgáu - augáâ) (1.4)

Mémoire de MASTER

14

Preuve : D'après (1.3) on a :

aáguâ = ^ñ_áugñâ + ^ñ_áâguñ
aâgáu = ^ñâ_ágñu + ^ñâ_ugáñ
augáâ = ^ñ_uágñâ + ñ uâgáñ

Et donc

g^ñuaáguâ = ^ñ_áug^ññugñâ + ^ñ_áâg^ñuguñ = ^ñáu^8uâ + ñáâ

g^ñuaâgáu = ^ñâ_ág^ñugñu + ^ñâ_ug^ñugáñ = ^ñ_âá + ^ñâ_uä^uá

uáäu ^â+ ñâuäuá

g^ñuaugáâ = ^ñ_uág^ñugñâ + ^ñâ_ug^ñugáñ = ñ

Ainsi,

g^ñu(aáguâ + aâgáu - augáâ) = ^ñ_áâ + ^ñ_áâ + ^ñ_áâ + ^ñ_âá - ñ âá - ñ áâ = 2ñ áâ

D'où le résultat. Ì

Mémoire de MASTER

15

1.4. Rappels de géométrie lorentzienne

1.4.1 Dérivée covariante d'un champ de tenseurs

Soient _(eá)á la base naturelle de T_q^p V4 et (è^á)_á sa base duale alors, on peut montrer (voir [6]) que si

_Tá1....áp

e 0....0e ? èâ¹ ? .... ? èâq

â1....â_q á1 a_n

est un tenseur de type ^q
· quelconque, alors sa dérivée covariante p

?íT

á1....áp â1....âq eá1 ? .... ? eá_p ? è^â1 ? .... ? èâq

est un tenseur de type

q p + 1 ·

donné par

?íTá1.... _â1....= ?íT á1....

â1....+ á1íñTñ.... â1....+ - ñ íâ1T á1....

ñ.... - ....

où les termes comprenant les symboles sont au nombre de q avec un signe + (un terme pour chaque indice contravariant) et au nombre de p avec un signe - (un terme pour chaque indice covariant).

Exemple 1.6 : Pour un tenseur de type

^11 ·

?íTâ^á =?_íT_â^á + á íñTâñ - ^ñ_íâTñ^á

Définition 1.4.7 : (Tenseur de courbure)

Le tenseur de courbure ou tenseur de Riemann _Rãuáâ associé à la connexion linéaire ? est un tenseur de type ¹₃
· sur V4 défini localement par :

Rãuáâ = ?á^ã_uâ - ?â^ã_uá + ^ñ_uâ^ãñá - ñ uáã (1.5)

âñ

Proposition 1.4.2 : Le tenseur courbure _Rãuáâ est antisymétrique par rapport aux indices á, â c'est-à-dire

Rã = -R^ã

uáâ uâá

Preuve : De (1.5), on a :

Rãuáâ = ?á^ã_uâ - ?â^ã_uá + ^ñ_uâ^ãñá - ^ñuá^ãâ_ñ

et

Rãuâá = ?â^ã_uá - ?á^ã_uâ + ^ñuá^ã_ñâ - ^ñ_uâ^ãáñ

et comme ã áâ = ãâá, on a le résultat. Ì

Mémoire de MASTER

16

1.4. Rappels de géométrie lorentzienne

Définition 1.4.8 : (Torsion d'une connexion)

On appelle torsion de la connexion linéaire ?, le tenseur T de type (¹ ₂) de composantes

locales :

T ã áâ = [ã áâ - [ãâá

Théorème 1.4.1 : (Théorème fondamental de la géométrie Riemannienne)

Sur une variété Riemannienne quelconque ( en particulier sur la variété Riemannienne (V4, g)), il existe une et une seule connexion linéaire vérifiant:

1-) ? est sans torsion c'est-à-dire T = 0;

2-) ? est g-métrique compatible avec g c'est-à-dire ?g = 0

Preuve : Voir [7] Ì

Définition 1.4.9 : (Connexion de Levi-Civita)

Une connexion linéaire vérifiant le théorème 1.3.1 est appelée connexion Riemannienne ou connexion de Levi-Civita.

Proposition 1.4.3 : (Identité de Bianchi)

?ñRã _áâu + ?âRã _áuñ + ?uRã áñâ = 0

Preuve : Voir [7] Ì

Définition 1.4.10 : (Tenseur de Ricci)

Le tenseur de Ricci est le tenseur de composantes locales Ráâ = Rã áãâ obtenu par contraction de l'indice supérieur et du deuxième indice inférieur du tenseur de courbure. Son expression en fonction des coefficients de Christoffel est :

Ráâ = 3ã[ã áâ - ?â[ã _áã + [ñ áâ^[ã ñã - [ñáã[ã âñ.

Ce tenseur est souvent noté Ricc(g).

Proposition 1.4.4 : Le tenseur de Ricci est un tenseur symétrique c'est-à-dire :

Ráâ = Râá

Mémoire de MASTER

17

1.4. Rappels de géométrie lorentzienne

Preuve : En considérant différentes contractions des indices du tenseur de courbure, on

a :

Ráâ = Rã áãâ

= g^ãñRñáãâ = -g^ãñRáñãâ (d^'après la proposition 1.3.2)

= g^ãñRñáâã = Rã âãá (toujours d^'après la proposition 1.3.2)

= Râá

Définition 1.4.11 : (Courbure Riemannienne)

La courbure Riemannienne R de (V4, g) est le scalaire obtenu par contraction des deux indices du tenseur de Ricci.

Il est défini par:

R = g^áâR_áâ

Proposition 1.4.5 : Par contraction de l'identité de Bianchi, on obtient :

?ñRáu - ?âRñá + ?uRã áñâ = 0

Par une autre contraction, on a :

?^ãSãu =0, où ?ã =g^ãó?óSãu ^et Sáâ = Ráâ - 1 ₂gáâR (1.6)

Mais aussi

?_ãSãu = 0 avec S^áâ = R^áâ - 1 2gáâR

Preuve : Voir [ 6] . Ì

Définition 1.4.12 : Le tenseur _Sáâ défini par la relation (1.6) est appelé tenseur d'Ein-stein et est souvent noté S(g) et on a donc

1

S(g) = Ricc(g) - ₂gR

.

* *

* *

Chapitre Deux

Mémoire de MASTER

18

Université de Yaoundé 1

ÉQUATION

INTEGRO-DIFFÉRENTIELLE

NON LINÉAIRE OBTENUE DU

SYSTÈME D'EKG

La théorie de la relativité générale [Einstein, 1915] identifie la gravitation à la courbure de l'espace-temps issue de la présence de la matière et de l'énergie. D'après la formule consacrée, la matière dit à l'espace-temps comment se courber et l'espace-temps dit à la matière comment se mouvoir.

Le but de ce chapitre est d'exprimer la métrique dans l'espace-temps à symétrie sphérique définie par Christodoulou. D (1999) puis transformer le système d'équation non linéaire couplé d'EKG en une équation intégro-différentielle de premier ordre.

2.1 Espace-temps à symétrie sphérique

Définition 2.1.1 : (Variété Riemannienne symétrie sphérique)

Soit (M,g) une variété Riemannienne de dimension 3. (M,g) est dite à symétrie sphérique si :

1-) La variété M est représentée par une carte (U, ço) avec ço(U) = R³ ou l'extérieur d'une boule ouverte de R³ centrée en un point O. On définit par p, , ç les cordonnées sphériques dans ço(U) telles que si x, y, z sont les coordonnées canoniques(locales) de R³, on a les relations usuelles suivantes : x = psinesinç, y = psine cosç, z = pcose

.

Mémoire de MASTER

19

2.1. Espace-temps à symétrie sphérique

2-) Dans cp(U),on a : p = p0 = 0, 0 < e < 7r, 0 = ç < 27r, la métrique g est représentée par

e^h(P⁾dp² + f²(p)(de² + sin² edç²) (2.1)

où f et h sont des fonctions positives strictement croissantes.

La métrique (2.1) est la forme générale de la métrique invariante par rotation dans R3 centrée en O.

Remarque 2.1.1 : Le choix de la coordonnée r donnée par r = f(p) s'appelle le choix standard; ce choix est toujours possible lorsque f est une fonction croissante.

Définition 2.1.2 : (Métrique symétrique-sphérique dans l'espace-temps )

Considérons l'espace-temps (V4,'y) avec V4 contenu dans R³ x R tel que un point (quelconque) de V4 soit représenté par (x, t). Supposons que les sous-ensembles Mt = {t}xR³ sont des sous-variétés d'espaces, désignons par gt la métrique Riemannienne induite par 'y sur Mt. Les trajectoires des vecteurs â/ât étant supposées de même nature, L'espace-temps est dit à symétrie sphérique si :

i-) Toute variété Mt est une représentation de l'extérieur R³ - Bt de la boule ouverte Bt de R³ centrée à l'origine. Toute variété (Mt, gt) est à symétrique sphérique. Dans R3 - Bt, la métrique gt en coordonnées standards est

gt = ea(r,t)dr2 + r²(de² + sin² edç²)

ii-) Pour tout t, la longueur 'y et le représentant de la projection sur Mt du vecteur âlât tangent sont tous deux invariants dans le groupe de rotations défini ci-dessus.

On admet que sur V4, la métrique est de la forme

ds² = 'y_u dxudx^v = gQ + r²(de² + sin²edç²)

où 'yuv = guv et gQ est la métrique Lorentzienne sur la variété quotient Q(de dimension 2) sur V4 sous l'action de SO(3) groupe des rotations centrées à l'origine r = 0 de l'espace euclidien R³. La fonction 47rr² est l'aire des orbites des sphères S² du groupe SO(3) des isométries de 'y. Christodoulou considère le cas où la frontière de la variété quotient Q (de dimension 2) est représentée comme un sous-ensemble de R₊ x R₊ suivant les coordonnées u = 0 et r = 0 avec la métrique gQ de la forme

gQ = -e^2Adu² - 2e^v+~`dudr

2.1. Espace-temps à symétrie sphérique

où í et ë sont des fonctions de u et de r ; ce qui est équivalent à

gQ = -(e^ídu + e^ëdr)² + e^2ëdr²

ce qui donne la forme d'une métrique Lorentzienne. Ainsi la métrique ã est donc de la forme :

ds² = ã_uídxudx^í = -e^2ídu² - 2e^í+ëdudr + r²(dè² + sin²èdö²) (2.2)

Pour toute la suite , nous supposons que í et ë sont des fonctions de u et r qui tendent chacune pour tout u = 0 fixé vers 0 lorsque r -p +00 pour avoir un espace-temps asympto-tiquement plat.

Remarque 2.1.2 : Lorsque í = ë = 0, on parle de l'espace-temps de Minkowski.

La matrice ã et la matrice inverse ã-¹ associées à la métrique (2.2) sont définies respectivement par :



-e

et

1

0

1

'

- - - - - - - -

»

'

- - - - - - - -

»

r2 sin² è

0 ^-e-í-ë 0 0

-í-ë e-2ë 0 0

1

0 0 _r2

1

0 0 0

-e^2í -e^í+ë 0 0

-e^í+ë 0 0 0 0 0 r² 0

0 0 0 r² sin² è

Mémoire de MASTER

20

Lemme 2.1 : Les symboles de Christoffel non nuls de la métrique (2.2) sont :

P^uuu = -?íev-~` + ? (í + ë) Pr_r = ? (í + ë)

?r au Or

u -í-ë = -2ë

Pèè = re Pèè^r -re

Puöö = r sin2 èe-í-ë Pröö = -r sin² èe^-2ë

P^rur r = Pr u Or ^uu or

= ?í _eí-ë Pr = ?í e2(í-ë) -

?u ? (í + ë)e^í-ë

Pè -- P^è -- 1 rè - èr - r

Pèöö = - cos è sin è

1

P-P =coteB BC P-

P= _rrö ^--Or

Preuve : On applique la formule (1.4).
·

Mémoire de MASTER

21

2.1. Espace-temps à symétrie sphérique

Lemme 2.2 : Les composantes du tenseur de courbure de Ricci non nulles associées à la métrique (2.2) sont :

?2í+ (^av)² _ av âa + 2 ?í _e2(v-a) + _ev-a [-2 ? (í + ë) - ?2 (í + ëd

?r² ?r ?r ?r r ?r L

Ruu r Ou OrOu
Rèè = e^-2ë [r ?ë?r - ^?íRöö = r ?ë

?r
· - 1 + 1 ?r - ?í

?r
· - 1 sin² èe^-2ë + sin² è

2

Rur = Rru = ~?2í

?r2 + ^?í - ?í ?ë ?r ~ e^í-ë - ?²í 2 ?

?r
· ?r + 2 ?í ?r?u - ?2ë Rrr = _?r(í + ë)

?r r ?r?u r

Preuve : Il suffit d'appliquer la formule (1.5). Ì

2.1.1 Système d'EKG

Le système d'équations non linéaire couplé d'Einstein et de Klein-Gordon est définit en coordonnées locales par :

cents ·····

·····

(2.3)

0p+1

Ruí - 12guíR = 8ðTuí

u

Tuí=0u0í-12guígáâ0á0â-pg + ^í 1

?0

où p E [j, +8[, j = 3 ou 4, 0 : IR₊ × 1[$₊ --? 1[$ et 0_á := où á E {u, r, è, ö}, _Ruí est le

?á

tenseur de Ricci qui permet de retrouver l'accélération à partir de l'état de repos d'une sphère de particules entourant une masse ponctuelle, _guí le tenseur métrique, _Tuí le tenseur énergie-impulsion dont l'expression dépend du choix de la matière et R = g^áâR_áâ la courbure riemannienne scalaire.

Définition 2.1.3 : (Tenseur d'Einstein)

Le tenseur Suí = Ruí - 12guíR est appelé tenseur d'Einstein dénommé en l'honneur à Albert Einstein en géométrie différentielle. Il est utilisé pour exprimer la courbure d'une variété pseudo-riemannienne. En relativité générale, il permet de décrire comment le champ gravitationnel est affecté par la présence de la matière.

Lemme 2.3 : Ruí peut s'écrire

Ruí = 8ð0u0í + 8ð guí p + 1

0p+1

Mémoire de MASTER

22

2.1. Espace-temps à symétrie sphérique

Preuve : La relation (2.3) donne par contraction :

gáâ(Ráâ -1

₂gáâR) = 87rg^áâT_áâ = 87rT

où T = g^áâT_áâ et puisque g^áâR_áâ = R et g^áâg_áâ = 4, on aura :

4

R - ₂R = 87rT

c'est-à-dire R = -87rT. Or

T = g^áâT_áâ = g^áâ(Ö_áÖâ - 1 ₂gáâg^uíÖuÖí - gáâ

p + 1Öp+1)

= g^áâÖ_áÖâ - 4 ₂g^áâÖáÖâ - gáâgáâ

p + 1 Öp+1

_Öp+1

= 4

g^áâÖ_áÖâ -p + 1

Mais toujours de la relation (2.3), on a aussi

1

Ruí = ₂guíR + 87rT_uí

1

= ₂g_uí(-87rT) + 87rT_uí

= -47rguíT + 87rTuí 4 = -47rguí(-g^áâÖáÖâ - p + 1

Ö^p+1) + 87rTuí

167r

= 47rguíg^áâÖáÖâ + p + ₁guíÖ^p+1 + 87rT_uí

= 47rguíg^áâÖáÖâ + ^16ð g_uvÖ^p+1 + 87r(Ö Ö_í - 1 guvg^áâÖáÖâ - guí Öp+1)

p + 1 2 p+ 1

_Öp+1

87rg_uí

= 87rÖ_uÖ_í +

p + 1

d'où le résultat. Ì

Proposition 2.1.1 : Pour l'équation (2.3), le tenseur énergie-impulsion est à divergence nulle c'est-à-dire :

?_uTu^í = 0

Cela traduit qu'un objet suivant une géodésique conserve son énergie.

L'équation de la conservation d'énergie ?_uTu^í = 0 doit souvent être complétée par d'autres équations vérifiées par les quantités physiques apparaissant dans T.

Mémoire de MASTER

23

2.1. Espace-temps à symétrie sphérique

Preuve : En effet, en appliquant à l'équation (2.3) la dérivée covariante, on obtient : ?_u(Ru^í - ₂gu^íR) = 8ð?_uTu^í

1

Or de (1.6) on a ?_ãSãu = 0 avec S^áâ = R^áâ - ¹₂g^áâR, on déduit donc que

?_íTu^í = 0 Ì

Proposition 2.1.2 : Ö est solution de l'équation dite de Klein-Gordon :

jÖ = Öp

où jÖ = ?ça_çÖ si et seulement si il y a conservation d'énergie.

Preuve : En effet :

T uí = guçg^íñT_çñ

1_a g~1P

= 9uçgíñ r Ö_P -- 2g~lPgáâÖ~Q + 1 OP+1l

LL p JJ

1l

= guçgíñ [?_çÖ?_ñÖ - ₂gçñg^áâ?áÖ?âÖ - +^ñ₁Ö^p+1] (car ?_çÖ = Ö_ç)

^p

donc,

?_uTu^í = guçg^íñ?_u(?_çÖ?_ñÖ) - ₂guçg^íñg_çñg^áâ?_u(?_áÖ?âÖ) - _guç_gíñ gçñ

1 p + ₁(p + 1)ÖpÖ_u
= guçg^íñ?_u?_çÖ?_ñÖ + guçg^íñ?_çÖ?_u?_ñÖ - ₂g^áâg^íñSu

1 ñ (?u?áÖ?âÖ + ?áÖ?u?âÖ) - S^í_çguçÖ^pÖ_u
= g^íñ(guç?_u?_ç)Ö?_ñÖ + guçg^íñ?_çÖ?_u?_ñÖ - ₂g^áâgu^í(?_u?_áÖ?âÖ + ?áÖ?u?âÖ) - gu^íÖpÖ_u 1

= g^íñ?ç?_çÖ?_ñÖ + guçg^íñ?_çÖ?_u?_ñÖ - gu^âg^áí?_u?_áÖ?âÖ - gu^íÖ^pÖ_u

= g^íu j Ö?_uÖ - gu^íÖp?_uÖ

= gu^íÖ_u(jÖ - Ö^p)

Ainsi, ?_uTu^í = 0 ? jÖ - Öp = 0 car gu^íÖ_u = g^uuÖ_u + g^urÖ_u + g^ruÖ_r + g^rrÖ_r ? 0 . Ì
Définition 2.1.4 : (d'Alembertien associé à une métrique)

L'opérateur j de la proposition 2.1.2 s'appelle le d'Alembertien et est souvent noté j_ã lorsqu'il est associé une métrique ly et est défini par

j_ãÖ = H-2 1 a_á( SãS¹² ryu^í 0_íÖ)

où 1'y1 est la valeur absolue du déterminant de la matrice représentée par ly pour la métrique (2.2) dans la base (du, dr, de, dç) et les ryu^í, u , v E {u, r, e, 0} les composantes de la matrice inverse de ly dans cette même base.

2.1. Espace-temps à symétrie sphérique

Proposition 2.1.3 : Le d'Alembertien j_ã associé à la métrique ã définit par (2.2) peut s'écrire

í ?²O 1 ?O 2~ ?²O2 ?í ?ë ?O

jO = -2e- - + + e + + -

¹

ã

?u?r r ?u ?r² r ?r ?r ?r

Preuve : En utilisant la matrice ã et la matrice inverse ã-¹ de la métrique (2.2) définies

en on a :

j_ãO = SãS- ² ?ë(SãS¹² ãu^í?_íÖ )

= r^-2 sin-1 ^èe-í-ë [(r² sin èe^í+ë × -e^-í-ëO_u)_r + (r² sin èe^í+ë × -e^-í-ëO_r)_u + (r² sin èe^í+ë × e^-2ëO_r)_rl

= r^-2 sin^-1 èe^-í-ë(-2r sin èO_u - r² sin èOur - r² sin _èOru + 2r sin èe^í-ëO_r + r² sin è ? (í - ë)e^í-ëO_r

?r

+ r² sin èe^í-ëO_rr)

= -2r^-1e^-í-ëO_u - e^-í-ëO_ur - e^-í-ëO_ru + 2r^-1e^-2ëO_r + ??r(í - ë)O_re^-2ë

+ O_rre^-2ë

[Örr

?í - ^?ë
·¹_ -2e^-í-ë _%oOur + _r-1 e-2ë + ~_r + 2r^-1O_rJ

?r ?r

?²O1 ?O r Ou
· _L f ?²O 2 ?í ?ë?O l

= -2e^-í-ë ?u?r + + e-2ë ?r² r + + ?r ?r
· ?r

Propriété 2.1.1 : La composante {rr} de (2.3) est

?í + ?r

?ë ?r

= 4ðr

(^?O1^2 ?Or) (2.4)

Preuve : Des Lemme 2.2 et Lemme 2.3, nous avons :

2 ?í₊ ?ë
· = Rrr = 8ðO_rO_r + 8ðgrrOp+1

r ?r ?r p + 1

et comme grr = 0, on a	?í + ?r	?ë	= 4ðr	2 ?~ ·
		?r			Ì

Mémoire de MASTER

24

Proposition 2.1.4 : De (2.4), on a :

8 2

í + ë = -4ð _f s0
· ds (2.5)

r

Preuve : En effet puisque í et ë tendent vers 0 lorsque r tend vers l'infini, en intégrant (2.4) sur l'intervalle [r, +8[, on a :

+8 2

-(í + ë) = 4ð s^?O
· ds

Jrr ?s Ì

Mémoire de MASTER

25

2.2. Réduction du système d'EKG en une équation intégro-différentielle du premier ordre

C'est-à-dire

+8 2

í + ë = -4ð _f s^4: ds (2.6)

r ?s

Propriété 2.1.2 : La composante {èè} ou {??} de (2.3) est donnée par

?í ?ë

?r ?r

1 (e^2ë - 1) = -8ðre2ë

p + 1 (Ö)^p+1 (2.7)

r

Preuve : Des Lemme 2.2 et Lemme 2.3, on a :

e-2ë r ?ë

?r - ?í

?r
· - 1 + 1 = Rèè = 8ðÖèÖè + 8ðgèè

p + 1 (Ö)p+1

et puisque Ö := Ö(u, r) et gèè = r², on déduit que

e-2ë r ?ë

?r - ?í

?r
· - 1 + 1 = 8ðr2

p + 1 (Ö)p+1

donc

?í ?ë ¹(e^2ë - 1) = -8ðre2ë

- - (Ö)^p+1

?r ?r r p + 1 Ì

2.2 Réduction du système d'EKG en une équation intégro-différentielle du premier ordre

Comme dans [2], nous désignons par h la fonction

?

h := _?r(rÖ).

Alors en utilisant

1 r

f(u, r) := r f f(u, s)ds, (2.8)

nous avons facilement

? h, _?rÖ = ^h_r^h. (2.9)

Posons

g = e^í+ë, (2.10)

et

g = e^í-ë. (2.11)

2.2. Réduction du système d'EKG en une équation intégro-différentielle du premier ordre

Proposition 2.2.1 : En combinant (2.6) et (2.10), on obtient

g = exp [-4ð _J (h - h)2 ^ds ] (2.12)

r

Preuve : (immédiate) Ì

Proposition 2.2.2 : En combinant (2.7) et (2.11), on obtient

g = g (p ⁸ 1)r Jo r s2 %ohé^p+1 gds (2.13)

Preuve :

_?r[r(g - g)] = g - g + r?g- ?g
·

?r ?r

r Jo

En injectant (2.7) dans cette égalité et en utilisant (2.9) on obtient :

?

[r(g g)] = eí-ë 1 rr gds + r 1 e2ë - 1 8ðre2ë (h)p+1 e^í-ë + 1 ^r gds - 1 eí+ë

?r r o r r p + 1 r² o r

eí-ë - 1

r

gds+r

~

[?r^í ?r
· e r v-a + r2 Jo gds - _re

í+ë 1

1

2 jãh = - rg	?h + ?u	g ?h g - rg ?r g	h - h r2 +	h - h	(h - h) ^8ð %ohép+1 p + 1
				r2

r

8ðr2 í+~ r

r Jo gds + e^í+ë - eí-ë

= e^í-ë - 1

p+ 1 (hé^p+1 + r Jo gds - eí+ë

p + 1 %ohép+1 eí+ë

8ðr²

p + 1 %ohé^p+1 g

8ðr²

En intégrant cette dernière égalité, sur [0, r[, on obtient :

8ðr 2 p+1

r(§-

g) = - p + 1 _Jo s %ohé gds

Soit

g= g

8ð

(p +

Ì

1)r Jo s2 %ohé^p+1 gds

r

Lemme 2.4 : Le d'Alembertien j_ã défini à la proposition 2.1.3 peut encore s'écrire :

Mémoire de MASTER

26

2.2. Réduction du système d'EKG en une équation intégro-différentielle du premier ordre

Preuve : En utilisant les relations (2.9), (2.10) , (2.11) et (2.7) on a :

j_ãÖ = -2e^-í-ë ?2Ö

?u?r + 1 ?Ö ?u
· + e-2ë ~?2Ö

?r2 + 2 r + ?í

?r - ?ë ?r
· ?Ö ?r ~

r

= -2e-í-ë ?u ? ?Ö ?r + 1 r Ö
· + e-2ë ? ?r ^?Ö ?r
· + 2 r + ?í

?r - ?ë ?r
· ?Ö ?r

= -2e-í-ë ? OEh-h1h`+e-2ë?

h ` + e-2+ 2 ?í - ?ë
· h - h

?u r r ?r r r ?r ?r r

-2ë

2_e-í-ë

= -

r

?h + e

?u

OE-h - h + 1 ?h - 1 ?h` + e-2ë 2 - 1 + 1 e2ë - 8ðre2ë _%ohép+1 h - h

r²r?r r?r r r r p + 1 r

-2ë ~-h - h

r2 + h - h

r2 e2ë - (h - h)8ðe2ë

p + 1 %ohép+1

?h

+

r ?u

2_e-í-ë

=

_e-2ë

r ?r

?h + e

?h +

rg ?u

?h g

-

?r g

h - h

r2 +

(h - h) ^8ð %ohép+1 p + 1

g rg

h - h

_r2

2

= -

Mémoire de MASTER

27

d'où le résultat. Ì

Définition 2.2.1 : (Opérateur différentiel)

Dans le reste du travail, nous introduisons l'opérateur différentiel D qui est un opérateur différentiel le long des rayons lumineux entrants défini par :

g

2

?

?r

?

D = ?u

Théorème 2.2.1 : L'équation de Klein-Gordon obtenue à la proposition 2.1.2 peut s'écrire comme une équation intégro-différentielle non linéaire du premier ordre en h

Dh = (h - h) [g-g

2r - 4ðrg

p + 1 %ohé^p+1~ - 1 ₂rg %ohé^p (2.14)

Preuve : De la proposition 2.1.2, on a :

j_ãh = %ohé^p

mais grâce au Lemme 2.4, on a :

%ohé^p = jãh =

2 ?h g ?h gh - h h - h 8ðp+1 rg?u^+rg?r g r2 + r2 - (h - h)p + 1 %ohé

rg ?h

2 ?u - g ?h

?r
· + h - h

r2 1- g_g
·-(h-h) 8ð

p + 1 %ohép+1

2

2 1

= - Dh + _r2g (h - h)(g - g) - (h - h) p+^8ð 1 %ohép+1
rg

ainsi,

2 Dh = 1 (h - h)(g - g) - (h - h) ^8ð %ohé^p+1 - %ohé^p

rg r²g p + 1

et donc

Dh = 1 (h - h)(g - g) - (h - h) p + 1 4ðrg %ohé^p+1 - 1 2rg %ohé^p 2rÌ

* *

* *

Chapitre Trois

Mémoire de MASTER

28

Université de Yaoundé 1

THÉORÈME D'EXISTENCE ET

D'UNICITÉ POUR L'ÉQUATION

INTEGRO-DIFFÉRENTIELLE

NON LINÉAIRE DU PREMIER

ORDRE

Le but de ce chapitre est de démontrer que l'équation intégro-différentielle (2.14) avec pour condition initiale h(0, r) = h0(r) possède une unique solution dans C¹([0, +8[×[0, +8[). Pour cela, nous procéderons par la méthode du point fixe de Banach.

3.1 Cardre fonctionnel

Comme dans les travaux de Dongho Chae [2], nous définissons les espaces: Définition 3.1.1 : Soit j E {3, 4}. Désignons par X l'espace des fonctions défini par

X = {h(.,.) E C¹([0, +8[×[0, +8[) : YhYX < 8}

où

YhYX = sup u=0

sup r=0 (1 + r + u)^j^-1Sh(u, r)S + (1 + r + u)j V?h ôr (u, r)V

Définition 3.1.2 : Soit l'espace des fonctions X0 défini par:

X0 = {h(.) E C¹([0, +8[) : YhYX0 < 8}

3.2. Théorème d'existence et d'unicité (théorème principal)

où

YhYX0 = sup

r=0 (1 + r)^j-1Sh(r)S + (1 + r)j V?h ?r (r)V 

et Yh0YX0 = d.

Définition 3.1.3 : Soit l'espace Y contenant X défini par :

Y = {h(.,.) E C([0,+8[x[0,+8[) : YhYY < 8}

où

YhYY = sup u=0

sup TM(1 + r + u)^j-1Sh(u,r)Sú r=0

Proposition 3.1.1 : Y est un espace métrique complet pour la distance induite par la norme Y.YY .

Preuve : En effet, considérons C¹(1[8₊x1[8₊) comme l'espace des fonctions f : 1[8₊x1[8₊ 1[8

bornées et admettant des dérivées partielles bornées. Ainsi en munissant C¹(1[8₊ x 1[8₊) de la norme

V ? _?xf(x,y)V+ sup V _?yf(x, y)V

0=x,y<oo

YfY = sup Sf(x,y)S + sup

0=x,y<oo 0=x,y<oo

Mémoire de MASTER

29

il est un espace de Banach. Soit (hⁿ)_n une suite de points de Y qui converge vers h dans Y , alors hⁿ est C¹, hⁿ₀(r) = hⁿ(0, r) et YhⁿYY < +8 donc h est aussi C¹, h0(r) = lim hⁿ₀(r) = lim hⁿ(0, r) = h(0,r) et il existe N E N tel que bn = N, Yhⁿ - hYY = 1 c'est-à-dire YhYY = 1+YhⁿYY < +8 donc h E Y . Ainsi Y est un fermé du Banach (C¹(1[8₊x1[8₊),Y.Y) et donc un espace métrique complet pour la distance d définit par d(f, g) = Yf -gYY bf, g E Y

3.2 Théorème d'existence et d'unicité (théorème principal)

Le théorème suivant donne l'existence et l'unicité de solution pour l'équation intégro-différentielle non linéaire du premier ordre

Théorème 3.2.1 : Soit j E {3, 4}. Supposons que la donnée initiale h0 E C¹([0, +8[), où h0(r) = h(0,r) telle que h(0,r) = O(r-(j-¹)) et ^?_?rh(0,r) = O(r-j). Notons

d = Yh(0,.)YX₀

Mémoire de MASTER

30

3.2. Théorème d'existence et d'unicité (théorème principal)

.Alors il existe ä > 0 tel que si d < ä, alors il existe une unique solution globale h E C¹([0, +8[×[0, +8[) de l'équation intégro-différentielle non linéaire (2.14) pour p E [j, 8[ avec h0 la donnée initiale.Cette solution vérifie

1h(u, r)1 = M(1 + r + ^u)-(j-1) , I?h ?r (u, r)V= M(1 + r + u)^-j. (3.1)

De plus,nous avons e^í , e^ë --> 1 et l'espace-temps devient plat quand u --> +8

Remarque 3.2.1 : Nous déduisons du Théorème 3.2.1 que si h E C¹([0, 8[×[0, 8[) alors h(u,.) est localement C¹ sur [0, 8[ pour u = 0 fixé. Considérons la formule

r

ö(u, r) = 1 f h(u, s)ds

, la fonction qui à s H h(u, s) étant continue sur [0,r], par la formule de la moyenne, il existe c_r E [0,r] tel que h(u, c_r) = r1 f0 r h(u, s)ds en faisant r --> 0, on a c_r --> 0; on déduit donc que ö(u, 0) = h(u, 0) pour tout u = 0.Donc

1 r r

ö(u, r) - ö(u, 0) = r S ₀ h(u, s)ds - S 0 h(u, 0)ds)

1 r

r S 0 (h(u, s) - h(u, 0))ds

1 r

I Is

r Jo Jo ?ódóds

Nous avons donc

1ö(u, r) - ö(u, 0)1 = r supI

2 0<s<rI?h(u, s)

et

sup

0<r<ä

?s

V

?ö(u, r) I = 1 _sup I?h(u, r) I M(ä, u) < 8 ?r 2 0<r<ä ?r

pour tout u = 0. Ceci combiné avec (2.4), nous déduisons que í + ë est localement lipschitzienne sur 1[8₊ pour u = 0 fixé. Des relations (2.10) et (2.13) les fonctions g et g sont aussi localement lipschitziennes.

3.2.1 Éléments de preuve du théorème d'existence de d'unicité

Pour démontrer le théorème 3.2.1, nous allons insister le plus sur le cas j = 3, et donc p E [3, 8[ . Les principaux changements d'estimations pour le cas j = 4 doivent être soulignés. Nous considérons l'application h H .7^-(h), qui est définie comme une solution de l'équation différentielle non linéaire du premier ordre

D.7- = (.7- - h) [^g-_2r^g - 4ðr9 (h)^p+1] - ¹₂rg (h)^p (3.2)

p +

3.2. Théorème d'existence et d'unicité (théorème principal)

avec la condition initiale

F(h)(0,r) = h(0,r) (3.3)

Notons B(O,x) = {f E X : fYX = x}. Alors il est clair que B(O,x) c X c Y . On a les deux lemmes suivants :

Lemme 3.1 : Soit x > 0 tel que d < x. Alors,

F : B(O, x) ? B(O, x)

.

Lemme 3.2 : Il existe = î(x) E]0, 1[ tel que

YF(h1) - F(h2)YY = îYh1 - h2YY

pour tout h1 , h2 E Y . C'est-à- dire que F est contractante dans Y . Alors le théorème du point fixe de Banach, fournit l'existence d'un unique point fixe h E Y tel que F(h) = h.

Prouvons ces deux lemmes qui vont jouer un rôle capital pour la démonstration du théorème principal le Théorème 3.2.1.

3.2.2 Preuve du lemme 3.1

Fixons YhYX = x.

Soit r(u) = X(u; r0) la solution de l'équation différentielle ordinaire. Nous pouvons avoir grâce au Théorème 1.2.1 (théorème de Cauchy-Lipschitz)

dr = - du

1 2

g(u,r), r(0) = r0 (3.4)

Mémoire de MASTER

31

Notons r1(u1) = X(u1, r0), alors (3.4) donne après une intégration sur [0, u1]

1 u1

r1 = r0 - 2 S 0 g(u, X(u; r0))du. (3.5)

En utilisant cette caractéristique, nous pouvons représenter F au moyen d'une intégrale comme suit

^u1 2r - 4ðrg

F(u1, r1) = h(0, r0)exp oeS 0 ~g - g p + 1 %ohé^p+1~ du^'

X

+ Su1 ^u12r - 47rrg 0 exp (S u ~g - g p + 1 (h)^p+^1] du^' [f]X du. X

(3.6)

Mémoire de MASTER

32

3.2. Théorème d'existence et d'unicité (théorème principal)

où

f=-

[1 4ðgr p+1 1 p-1
2r(g ^g) p+ 1 %ohé ₂rg %ohé ] h. (3.7)

En effet :

Posons A(u) = h(u, r(u))expoef ^u1

_u g - g

2r - 4ðrg

p + 1 %ohé^p+1~ du^'. Alors X

dA(u) du

^u12r - 4ðrg = Dh exp oeS u g - g p + 1 %ohé^p+1~ du^' X - h g - g 2r - 4ðrg p + 1 %ohé^p+1~exp oeS u g - g ^u12r - 4ðrg p + 1 %ohé^p+1~ du^' X r g-- g4ðrg p+1 1 pl ~1 g- g4ðrg p+1 ' = j (h - h) [ 2r + 1 %ohé ]-2 rg %ohé } expoef[ 2r + 1 %ohé]dull P 1 P X

h g - g - 4ðrg (hé^p+ⁱ] expoef u1 g - g - 4ðrg %ohé^p+1 du^'

[ 2r p + 1 [ 2r p + 1 ]X

= -h[g - g 4ðrg _%ohép+1 ¹ rg(h)^p-1 - g - 4ðrg %ohé^p+1 du^'

2r p+1 2 ] expoef~1 [⁹2r p + 1 ]X

Par une intégration sur [0, u1], on a :

A(u1) = A(0) ₊4 f ^u1oe-h [^g-_2r^g-⁴+^r9 %ohé^p+1 + 2rg(h)^p-1] expoef u1 [g2rg p+r9 %ohé^p+1~ du^' du

X

^u1 2r - 4ðrg

= h(0, r(0))exp oeS 0 g - g p + 1 %ohé^p+1~ du^'

X

+ f0

^u1 oe-h g - g

2r - 4ðrg p+1%ohép+1 + ¹₂rg(h)^p-1] exp oef g - g

^u1 2r - 4ðrg

p + 1 %ohé^p+1~ du^' du

X

d'où le résultat.

?.7"

.

?r

Pour j = 3, on a :

Dans ce qui va suivre, nous chercherons une majoration de .7" et de

= V¹_r

f^rh(u,s)ds

V

1
· ~

ü Jo (1 + s + s)2(1 + s + u)²Sh(u,s)Sds

r

1 r YhYX ds = x (3.8)

ü
· for

(1 + s + u)² (1 + u)(1 + r + u)

et

s

Sh(u,r) - h(u, r^')S = f ,r V _?s (u, s)I ds = x _Jr'r (1 + s+ u)³

x 1 1

2 (1 + r^' + u)^{2 -}(1 + r + u)2 (3.9)

3.2. Théorème d'existence et d'unicité (théorème principal)

De là, nous avons

]dr^'

1 r

S(h - h)(u, r)S = r S 0 Sh(u, r) - h(u, r^')Sdr^'

=

S0

x rr 1 1

2r Jo L1 + r^' + u)^2-(1 + r + u)²

xr

2(1 + r + u)²(1 + u)

(3.10)

Donc

00 (h -_r h)2 2 002 _x2

24

_Jo

dr =(3.11)

4(1 + u)² (1+ s + u)4ds = 24(1 + u)2 =

Ceci combiné avec (2.12) donne

ð4x² g(u, 0) = exp[- (3.12)

24(1 + u)4] = exp ~-^ðx2

6 ~

En utilisant (2.12)(en dérivant g par rapport à r) et en utilisant l'inégalité (3.10) on a

fr?g rr (h - h)² ðx2 rr s
(u,$)~ds = 4ðds J ds
(~Js Jr'r' s (1 + u)² r' (1+s+u)⁴
ðx² r 1

3(1 + u)2 ~ r'

(1 + r^' + u)3 - (1 + r + u)3 ~ + ðx2

6(1 + u)2 ~ 1 (1 + r^' + u)^{2 -}(1 + r + u)2 ~

(3.13)

Et on obtient

(g - g)(u,r)S¹ = rJo r Sg(u,r)- g(u,r')Sdr'= 1 f r f'r S4g (u,s)Sds
·dr'

ð x2 r r ' r

3r(1 + u)2 _Jo L1 + r^' + u)³ (1 + r + u)³

6r(1 + u)2 Jo (1 + r^' + u)² (1 + r + u)² ð

=

+

]dr^' ]dr^'

x2 r

1 1

Mémoire de MASTER

33

ðx²(r³ - r² - ur²)

6r(1 + u)^3(1 + r + u)3 +	ðx^2r^2
	6r(1 + u)^3(1 + r + u)^2

ðx²(r³ - r² - ur² + r² + ur² + r³)

=

6r(1 + u)³(1 + r + u)³ ðx²r²

(3.14)

3(1 + u)³(1 + r + u)³

3.2. Théorème d'existence et d'unicité (théorème principal)

S0

ds

Nous avons aussi grâce à l'inégalité (3.8) et du fait que g = 1

r _xp+1r

2

s

p

=

2(h)

(1 + u)p⁺¹ (1 + s + u)p⁺¹

+1gds L

_xp+1 r _s2

= (1 + u)p+1 ^S (1 + s + u)^4ds 0

_xp+1 1+r+u 1

(1 + u)p⁺¹ ji+u t4 [(1 + u)² + t² - 2t(1 + u)] dt

= xp+1 _r r3 - 3r(1 + u)

(1 + u)p⁺¹ 3(1 + u)(1 + r +u)³]

_xp+1_r3

= (3.15)

3(1 + u)p⁺²(1 + r + u)³

Donc de (2.13) puis de (3.14) et (3.15) on a

8ð r

Sg - gS = Sg - gS + r(p + 1) S 0 s2ShSp+1gds

8ðxp⁺¹r²

3(p + 1)(1 + u)p⁺²(1 + r + u)³

ðx²r²

= + 3(1 + u)³(1 + r + u )3

M(x² + xp⁺¹)r²

= Car p = 3 (3.16)
(1 + u)³(1 + r + u)³

où M est une constante indépendante de x, u et r. (3.16) avec (3.8) donne

L r Jo u1 [g2rg ^p+ 1 %ohé^p+1du = M(x^2+ xp^+1) Jo u1 2(1 + u)^3(1 + r + u)^3 x

du

r

1

]_X^du

+

4ð up + 1 Jo

8 1 8 1

= M(x² + xp+1)S 2(1 + u)5du + ð S (1 + u)7du (car p = 3)

0 0

ð +

6

M(x² + xp⁺¹)

= 8

= M(x² + xp⁺¹) (3.17)

En utilisant (2.13), (3.12) et (3.15), on a

8ð /,r

J

g = g(u, 0) r(p + 1) o

s²(h)p⁺¹gds

ðx² 8ðxp⁺¹r²

= exp[

6 ] ^-3(p + 1)(1 + u)p⁺²(1 + r + u)³

Mémoire de MASTER

34

exp[

ðx^28ðxp^+1 6 ] - (3.18) 3(p + 1)

Soit x1 une racine de l'équation

exp[-^ðx2] - 8ðxp+1 (3.19)

6 3(p + 1) = 0

Mémoire de MASTER

35

3.2. Théorème d'existence et d'unicité (théorème principal)

Alors la fonction

k = k(x) = exp[-^ðx2 ] - 8ðxP+1 (3.20)

6 3(p + 1)

vérifie 0 < k = 1 pour tout x E [0, x1[ ; en effet k est décroissante sur [0, x1[, on a

0 = x < x1 = k(0) = k(x) > k(x1)

Et comme k(0) = 1 et k(x1) = 0, on a le résultat. De (3.16), on a

1 4ðrg

SfS = 2rS(g - g)SShS + p + 1 ShS^P+2 + ₂rgShS^P

1

= A1 + A2 + A3. (3.21)
De (3.8) et (3.16) nous avons

M(x³ + xP+2) (puisque r < 1 + r + u) (3.22)

2(1 + u)⁴(1 + r + u)³

M(x³ + xP⁺²)r

A1 =< 2(1 + u)⁴(1 + r + u)⁴

Toujours de (3.8) et du fait que de (2.12), g = 1, on a

4ðrxP⁺²

A2 = (p+1)(1+u)P+2(1+r+u)P+2

4ðxP⁺²

= 4(1 + u)P⁺²(1 + r + u)P+1 car p = 3
4ðxP⁺²

= (3.23)

4(1 + u)³(1 + r + u)²

et

rxP A3 = = 2(1 + u)P(1 + r + u)P	4ðxP
	4(1 + u)P(1 + r + u)P-^1

4ðxP =(3.24)

4(1 + u)³(1 + r + u)²

Nous notons que si j = 4, une estimation de A2 et A3 est :

4ðxP⁺²

A2 = (3.25)

4(1 + u)³(1 + r + u)³

4ðxP ( )

A3 = (3.26)
4(1 + u)³(1 + r + u)³

En combinant (3.21) , (3.22), (3.23) et (3.24), on obtient

SfS = 2(1 + u)⁴(1 + r + u)3 + 4(1 + u)³(1 + r + u)3 + 4(1 + u)³(1 + r + u)²

M(x³ + xP⁺²) 4ðxP⁺² 4ðxP

= 3.27
M(x³ + xP + xP⁺²)

(1 + u)³(1 + r + u)2 ( )

Mémoire de MASTER

36

3.2. Théorème d'existence et d'unicité (théorème principal)

Dans le cas où j = 4, de (3.24) on a

M(x³ + xP + xP⁺²)

SfS = (3.28)

(1 + u)³(1 + r + u)³

Grâce au Théorème 1.2.1, on peut poser r(u) = X (u; r1) et des relations (3.18) et (3.20), nous avons

1ru' 1

r(u) = r1 + 2 J §oû, X (u^'; r0))du^' = r1 + ₂(u1 - u)k (3.29)

et puisque k ?]0,1] pour x ? [0, x1[,

u k u1

1 + r(u) + u = 1 + ₂ + r1 + ₂(u1 - u) = k(1 + ₂ + r1)

k

= ₂(1 + r1 + u1) (3.30)

Donc

S0 u1u1 M(x³ + xP + xP⁺²)

[f]_X Sdu =fdu L1 + u)³(1 + r + u)²]_X

M(x³ + xP + xP+2) 8 du

= k²(1 + r1 + u1)2 Jo (1 + u)³

M(x³ + xP + xP+2) (3.31)

2k²(1 + r1 + u1)²

En utilisant (3.29), on obtient

k

r0 = r(0) = r1 + ₂u1 (3.32)

et puisque k ?]0,1] pour x ? [0, x1[, nous avons de (3.1)

d d d

Sh(0,r0)S = (1 + r0)2 =(3.33) (1 + r1 + k 2u1)2 = k²(1 + r1 + u1)²

En combinant (3.6), (3.17), (3.31) et (3.33), nous obtenons

W

SF(u1, r1)S = Sh(0, r0)Sexpoef ^u1 WL 2rg - 4+r9 ] du^'

p X

u1 ^u1 2r - 4ðrg

+ S 0 exp oeS _u W~g - g p + 1 ~ W du^'S [f]_X Sdu

X

M(d + x³ + xP + xP⁺²)exp[M(x² + xP⁺¹)] =3.34

2k²(1 + r1 + u1)2 ( )

Posons maintenant

G(u, r) = F

ar (u, r)

avec

?h

G(0, r0)

= ?r (0, r0)

3.2. Théorème d'existence et d'unicité (théorème principal)

En différenciant (3.2) par rapport à r,on a :

? 1 ?g ?.~ ₌OE?F ?h _f 1 4ðr 1

Dg(u1, r1) = ?r(D.r) ⁺2?r?r ?r ?r [_2r(g-g)-_{p +}9(h)^P+1J
g_h p -r?g h P_- p ?h h p-1 ₊1?g?.~

2 %o ) 2?r %o ) 2rg?r %o ) 2?r?r

1_r ? g - g ?h ₎P 4ðg p+1 4ðr ?g ₎P+1
+ - hé 2 ?r(g - g) - 2r2 - 4ðrg _?r ^%oh) p + 1 ^%ohé-p + 1 ?r %oh)

= 1 4ðrg p+1 1 ?g
[2r(g-g)- p + 1 ^%ohé +2?r]g

1 ? g - g 4ðg p+1 ?h P 4~rr âg ^p+1 %o.r hé

+ (g - g) - - %ohé - 4ðrg %ohé - (h)
2r ?r

2r² p + 1



?

1?

r p +

r

+ ~4ðrg

p + 1 %ohé^p+1 - 1 ?g

2r(g - g) - p ₂rg %ohép-1~ ?h

?r - g 2 %ohé^p - r ?r %ohé^p (3.35)

2

Comme précédemment, nous résolvons l'équation linéaire (3.35) en g, utilisant la caractéristique introduite dans (3.29) pour obtenir :

?h u1 4ðrg p+1 1 ?g 'g(u1,r1)=?r(0,r0)expoeJo [¹2r⁽g-g)-p+1 ^%ohé +2?r]Xdu

u1 u1 ?g
+ S 0 exp oeS u ~ 1 2r(g - g)- 4ðrg

p + 1 %ohé^p+1 + 1 du^' _[f1]X du (3.36)
2 ?r X

où

f1 1 ? (9 9) g - g -- 47rg (h)^p+1 -- 47rrg^Oh (h)^P -- 4irr âg

= (h)^P+i (1 - hé

[2r?r 2r² p + 1 ?r p + 1 ?r

+ ~4ðrg

p + 1 %ohé^p+1 - 1 ?g
2r(g - g) - p ₂rg %ohép-1~ ?h

?r - g 2 %ohé^p - r ?r %ohé^p (3.37)

2

En effet :

Mémoire de MASTER

37

?g

Donc en utilisant la formule

, on a de la relation (3.14), (3.15), (3.8) et du fait

g - g r

?r

3.2. Théorème d'existence et d'unicité (théorème principal)

Posons B(u) = G(u,r(u))exp oe? ^u1

_u [21( p +rg %ohé^p+1 + ^12. _?9]_Xdu^'. Alors,

d _duB(u) = DGexp oef_u^u1

1 4ðrg p+1 1 ?g '

é _[2r(g ^g) p + 1 %oh + 2 ?r]X du

- 1 4ðrg p+1 1 ?g _u1 4ðrg p+1 1 ?g,~[ _2r(g g)p + 1 %ohé + 2 ?r ] expYI _2r(g g) p + 1 %ohé + 2 ?r ]_X du

'l

4ðrg p+1 1 ?g

=G[12r(g-g)- _p+1 %ohé +_2?r]exp{...} - ^g₂ %ohé^p + r?g

?r %ohé^p
· exp {...}

2

1 ? g - g P 4ðg

+ %oF - hé 2r ?r(g ^g) 2r2 - 4ðrg^âh %ohé - %ohép+1 4ðr ?g - %ohé^p+1]exp{...}
?



1?

r p + 1 p +

r

+ ~4ðrg

p+1 %ohé^p+1 - 1 2r(g - g)- ^p ₂rg %ohép-1~ ?h

?r exp{...}

-G[

1 4ðrg p+1 1 ?g
2r(g-g)- p + 1 %oh) +_2?r]exp{...} = ~ 1 ?r(g - g) - g - g

? 2r2 - 4ðg

p + 1 %ohé^p+1 - 4ðrg ?h

?r %ohé^p - 4ðr ?g ?r %ohé^p+1~ %oF - hé exp {...}

2r p + 1

+ [

4ðrg p+1 1 p p-1 ?h g p r ?gp
p + 1 %ohé - _2r(g - g) ₂rg %ohé ] ?r 2 ^%ohé 2 ?r %ohé exp {...}

et intégrant membre à membre sur [0, u1] la dernière égalité, nous avons, puisque B(u1) =

G(u1, r1) = 0,

?F

B(0) = G(0, r0) = ?r (0, r0)

, nous avons le résultat.

Or, nous déduisons de (3.37), puisque 0 < g = 1

Sf1S = oeS 1 ?2r?r(g - g)S 2r2

+ Sg - gS + p + 4ð ShSp⁺¹ + 4ðr ^?h ShSp + p+ 4ðr ShSp⁺¹ V^?g_rV (SFS + ShS)

1 ?r 1 ?

+[

(3.38)

Sg - gS + pgrShS^p-1 + ^4ðr _ShSp+1] ^?h + ¹ShS^p+^rS^?gSShS^p 2r 2 p + 1 ?r ^W 2 2 ?r
= (B1 + B2 + B3 + B4 + B5)(SFS + ShS) + (B6 + B7 + B8) W?h

?r W+ B9 + B10

En dérivant (2.13) par rapport à r on a

?g ?g + ?r ?r

(p f^rs²ShSp⁺¹gds - 9(3.39)81)r2 +

Mémoire de MASTER

38

3.2. Théorème d'existence et d'unicité (théorème principal)

que g < 1

~^gS < Sg - ^gSr⁺(p81)r2 _Jo^rs²ShSp⁺¹ds + p₊1ShSp⁺¹

ðx^2r < 3(1 + u)^3(1 + r + u)3 + 8ðxp^+1r	8ðxp^+1r
	3(p + 1)(1 + u)p^+2(1 + r + u)^3

+ (p + 1)(1 + u)p⁺¹(1 + r + u)p⁺¹

M(x² + x⁴ + xp⁺¹)r

< (3.40)
(1 + u)³(1 + r + u)³

En différenciant g définit par la relation (2.12) puis en utilisant (3.10), nous avons

< 4ðSh - hS2 < ðx2r

?r r (1+u)²(1+ r+u⁴V^?gV (3.41)

En combinant (3.40) et (3.41), on déduit que

1 ? M(x² + x⁴ + xp⁺¹⁾ ðx²

B1 := V2r?r(g ^g)V 2(1 + u)³(1 + r + u)^{3 +}2(1 + u)²(1 + r + u)⁴

< M(x² + x⁴ + xp+1) (3.42)
- (1 + u)²(1 + r + u)³

M(x² + xp⁺¹)

De (3.16), on a

B2 := Sg - gS

2r2 < 2(1 + u)³(1 + r + u)³

< (3.43)
M(x² + x⁴ + xp⁺¹)

(1 + u)²(1 + r + u)³

De (3.8) on a

4ð 4ð xp+1

B3 :=

ShS^p+1 <

p + 1 p + 1 (1 + u)p⁺¹(1 + r + u)p⁺¹

Mémoire de MASTER

39

ðxp⁺¹

< (1 + u)³(1 + r + u)³

< M(x² + x⁴ + xp+1) (3.44)

- (1 + u)²(1 + r + u)³

?h h - h

Puisque = , (3.8) et (3.10) donnent :
?r r

B4 := 4ðr W8_h^hShS^p <_r_4ðr^Sh_r^hSShS^p

x < 4ðr 2(1 + u)(1 + r + u)^2 4ðxp^+1	xp
	(1 + u)p(1 + r + u)p

<

<

2(1 + u)p⁺¹(1 + r + u)p⁺² 2ðxp⁺¹

(1 + u)³(1 + r + u)³
M(x² + x⁴ + xp⁺¹)

< (3.45)

(1 + u)²(1 + r + u)³

3.2. Théorème d'existence et d'unicité (théorème principal)

De (3.8) et (3.41), on a

B _ 4ðr _ShSP+ âg < 47rr xP⁺¹ ðx²r

=

5 p+1 V?rV p + 1 (1 +

¹ u)P⁺¹(1 + r + u)P⁺¹ (1 + u)²(1 + r + u)⁴
4ð²xP⁺³r²

(p + 1)(1 + u)P⁺³(1 + r + u)P⁺⁵

4ðxP⁺³

= (1 + u)P⁺³(1 + r + u)P+3 (car p + 1 > ð et r² = (1 + r + u)²)

=

4ðxP⁺³

(1 + u)³(1 + r + u)³

M(x² + x⁴ + xP⁺³) =(3.46)

(1 + u)²(1 + r + u)³

Comme précédemment, les relations (3.8) et (3.16) impliquent

B6 + B7 := Sg - gS

2r

p + grShS^P-1 = M(x² + xP⁺¹⁾r. pxP-¹r

2 2(1 + u)³(1 + rll ++ u)³ 2(1 + u)P-¹(1 + r + u)P-¹

M(x² + xP-¹ + xP⁺¹)r

= (3.47)

(1 + u)²(1 + r + u)²

De (3.8), on a

4ðrS _IP+1 4ðr xP+1

B8 := p + 1 h p + 1 (1 + u)P⁺¹(1 + r + u)P⁺¹

ðxP⁺¹r

= (1 + u)²(1 + r + u)2 car p + 1 = 4

M(x² + xP-¹ + xP⁺¹)r

=

(3.48)

(1 + u)²(1 + r + u)²

Des relations (3.8) et (3.41), on a :

2

B9 + B10 :=

?

S

S

V?

1 r

r x r xP

₂

g xP 7r

h

P + 2

rV ShSP = 2(1 + u)P(1 + r + u)P + 2 (1+ u)²(1 + r + u)⁴ (1 + u)P(1 + r + u)P

_xP

= 2(1+u)P(1+r+u)P+ _xP

= 2(1 + u)³(1 + r + u)4 +

ðxP⁺²r²

2(1+u)P⁺²(1+r+u)P⁺⁴ ðxP⁺²

2(1 + u)³(1 + r + u)⁴

Mémoire de MASTER

40

M(x³ + xP + xP⁺²)

= 3.49

(1 + u)³(1 + r + u)4 ( )
En utilisant inégalités (3.42) - (3.42), (3.8) et (3.10), nous obtenons

5M(x² + x⁴ + xP⁺¹ + xP⁺³) 2M(x² + xP-¹ + xP⁺¹)Sh - hS M(x³ + xP + xP⁺²)

(1 + u)²(1 + r + u)³ (1 + u)²(1 + r + u)2 + (1 + u)³(1 + r + u)⁴



SS

S

f1

h

) +

5M(x² + x⁴ + xP⁺¹ + xP⁺³) 6M(x³ + x⁵ + xP + xP⁺² + xP+4) + M(x³ + xP + xP⁺²⁾ r

(1 + u)²(1 + r + u)³ (1 + u)³(1 + r + u)4 ¹ (1 + u)³(1 + r + u^l)⁴

(3.50)

+

SFS

3.2. Théorème d'existence et d'unicité (théorème principal)

Maintenant, en utilisant l'inégalité le long de la caractéristique comme dans les relations (3.29) et (3.30), nous savons que

k

1 + r(u) + u = ₂(1 + r1 + u1) (3.51)

et nous obtenons donc en général pour tous entiers naturels q , s et t, il existe m ? Z tels que :

u1

u1 1 du

Jo _x [(1+u)t(l+r+u)q-s _X

=

Lrs

(1+u)t(1+r+u)q du

~

=

=

Mémoire de MASTER

41

2q-s 8 du

2m

00

du

kq-^s(1 + r1 + u1)q-s Jo (1 + u)^t

k^m(1 + r1 + u1)m fo (1 + u)q-s+t-m avec m = q - s

2m

= (3.52)

k^m(q - s + t - m)(1 + r1 + u1)^m

S0

pour q - s + t - m > 1. En appliquant (3.52) sur chaque terme de la majoration de f1 (pour le premier terme on prend t = 2, q = 3, m = 1, ets = 0, pour le deuxième t = m = 3, q = 4, et s = 0 pour le troisième t = m = 3, q = 4, et s = 1) obtenue en (3.50), nous avons :

1

u

1

L1 + u)²(1 + r + u)3]X du

u1

du

_o

S _[f1]X Sdu = SF(u1, r1)S5M(x² + x⁴ + x^p+1 + xp+3)

+ 6M(x³ + x⁵ + x^p + x^p+2 + xp+4) JoL1 + u)³(1 + r + u)⁴

1

X

1



u

( 3 P ^P+2)_o L₁

r

+ M x +x +x + u)³(1 + r + u)4 du

X

10M(x² + x⁴ + xp⁺¹ + xp⁺³)

=

4k(1 + r1 + u1)³

sup TM(1 + r1 + u1)²SF(u1,r1)Sú 0=u1,r1<8

48M(x^3 + x^5 + xp + xp^+2 + xp^+4) + + 4k^3(1 + r1 + u1)^3

M(x^3 + xp + xp^+2) 3k^3(1 + r1 + u1)^3

5M²(d + x³ + xp + xp⁺²)(x² + x⁴ + xp⁺¹ + xp⁺³)exp[M(x² + xp⁺¹)]

= de (3.34) 4k³(1 + r1 + u1)³

13M(x³ + x⁵ + xp + xp⁺² + xp⁺⁴)

+ (3.53) k³(1 + r1 + u1)³

Dans le cas où j = 4, nous avons

S0

u1 10M²(d + x³ + xp + xp⁺²)(x² + x⁴ + xp⁺¹ + xp⁺³)exp[M(x² + xp⁺¹)]

S _[f1]X Sdu = 3k⁴(1 + r1 + u1)⁴
40M(x³ + x⁵ + xp + xp⁺² + xp⁺⁴)

+

(3.54)

k⁴(1 + r1 + u1)⁴

3.2. Théorème d'existence et d'unicité (théorème principal)

De (3.8), on a :

V

4ðrg %ohé^p+1V < 4ðrxp+1
p + 1 (p + 1)(1 + u)p⁺¹(1 + r + u)p⁺¹
4ðxp⁺¹

< (p + 1)(1 + u)p⁺¹(1 + r + u)p

M(x² + x⁴ + xp⁺¹) <(3.55)

(1 + u)4 ,

de (3.16), on a

V

^g-gV < M(x² + xp⁺¹) 2r (1 + u)⁵
M(x²

(1 + u)4+1) (3.56)

et de (3.40), on a

V

I M(x² + x⁴ + xp⁺¹)r _?r' < (1 + u)³(1 + r + u)³ M(x² + x⁴ + xp⁺¹) <car r < 1 + r + u

(1 + u)³(1 + r + u)²

( )

M(x² + x⁴ + xp⁺¹)

< (3.57)
(1 + u)⁴

En combinant (3.55), (3.56) et (3.57), nous obtenons

Wf_o [ 2r

1

u

1du

4ðrg%oh < M(x² + x⁴ + xp⁺¹)f⁸

1 ⁽1 + u)⁴

+ M(x² xp+1) °° du fo (1 + u)⁴

8 du

+ M(x² + x⁴ + x^p+1)

S

0 (1 + u)⁴

< M(x² + x⁴ + x^p+1) (3.58)

De (3.1) et de (3.32) on a pour tout x E [0,x1[

V?h

?r (0, r0)V₍₁ < ~ihoYX03 < 3 1+8d+ul 3 (3.59)

( 0)k( )

. Dans le cas où j = 4, on a

V^?h(0_'r0)V

Ilh0YX0 k4 1 + ^6d u 4 (3.60)

Or ( _o)4 <( 1 ₁)

Donc des relations (3.54), (3.58), (3.59) et du fait que



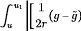
W4ðrg p+1 1?-, , u1 1 4ðrg p+1 1 ?g du'

p + 1 ^%ohé _+2?r]X du'

u = o Wr

2r(9-g)- p + 1 ^%ohé +2Or]X

1 4ðrg p+1 1 ?g '

_fu

[2r(9 g) _

p+1`

+ 1 ~hé + 2 ?r ]_X du

< fu¹1 47rrg p+1 1 ?g '
[2r(g--g)- p + 1 ^%ohé _+2?r]X du

Mémoire de MASTER

fuu1W[21r(g -g)

42

3.2. Théorème d'existence et d'unicité (théorème principal)

on a de (3.53)

SÇ

nn⁽⁽ V_a^h_r (0,r0)S +f:
' (u1,r1)S < S _[f1]X Sdu
·exp[M(x² + x⁴ + x^p+1)]
8d

= k³(1 + r1 + u1)3 exp[M(x² + x⁴ + x^p+1)] 13M(x³ + x⁵ + xp + xp⁺² + xp⁺⁴)

+ exp[M(x² + x⁴ + x^1+p)] k³(1 + r1 + u1)³

5M²(d + x³ + xp + xp⁺²)(x² + x⁴ + xp⁺¹ + xp⁺³)exp[M(x² + xp⁺¹)]

+ exp[M(x² + x⁴ + x^1+p)] 4k³(1 + r1 + u1)³

(3.61)

et par une simplification, nous obtenons

Sy(

1, 1)I_ 16M²(d + x³ + x⁵ + xp + xp⁺²)(1 + x² + x⁴ + xp⁺¹ + xp+3) _P[ ( 2 4 1+p)]
u r < k³(1 + r1 + u1)3 ex 2M(x +x +x

(3.62)

En combinant (3.34) et (3.62), nous avons donc

Y.7-(h)YX = sup u1=0

sup r1=0

{(1 + r1 + u1)^2S.7-(u1,r1)S + (1 + r1 + u1)^3Sy(u1,r1)S}

=

Mémoire de MASTER

43

2k2(d + x³ + xp + xp⁺²)exp[M(x² + x¹⁺p)] M

16M²

+ _k3 (d + x³ + x⁵ + xp + xp⁺²)(1 + x² + x⁴ + x¹⁺p + xp⁺³)exp[2M(x² + x⁴ + xp⁺¹)]

(3.63)

Puisque pour tout x ?]0, x1], 0 < k = 1 alors, k³ = k² et comme on peut toujours trouver M1 et M2 deux réels strictement positifs fonctions de M(par exemple M1 = 17M² et M2 = 2M) tels que

M1

Y.7-(h)YX = k3 (d+x³+x⁵+x^p+x^p+2)(1+x²+x⁴+x^1+p+x^p+3)exp[M2(x²+x⁴+x^p+1)] (3.64)

Des relations (3.54) et (3.60) nous déduisons pour le cas j = 4 qu'il existe N1 , N2 des réels strictement positifs tels que

N1

Y.7-(h)YX = k4 (d+x³+x⁵+x^p+x^p+2)(1+x²+x⁴+x^1+p+x^p+3)exp[N2(x²+x⁴+x^p+1)] (3.65) Soit L la fonction définie par

xk³exp[-M2(x² + x⁴ + xp⁺¹)]

L(x) = M1(1 + x² + x⁴ + xp⁺¹ + xp+3) - (x³ + x⁵ + xp + xp⁺²) (3.66)

Alors on a L(0) = 0, L(x1) < 0, L^'(0) > 0, et L^' est continue sur [0,x1]. Donc il existe x0 ?]0, x1[, tel que L^'(x) > 0 pour tout x ? [0, x0] c'est-à-dire que L est croissante sur

3.2. Théorème d'existence et d'unicité (théorème principal)

[0,x0]. Pour tout x ?]0, x0[,

M1

Y.7-(h)YX = k3 (d + x³ + x⁵ + x^p + x^p+2)(1 + x² + x⁴ + x^1+p + x^p+3)exp[M2(x² + x⁴ + x^p+1)]

= dM1

k3 (1 + x² + x⁴ + x^1+p + x^p+3)exp[M2(x² + x⁴ + x^p+1)]

M1

+ _k3 (x³ + x⁵ + x^p + x^p+2)(1 + x² + x⁴ + x^1+p + x^p+3)exp[M2(x² + x⁴ + x^p+1)]

= x

d + x³ + x⁵ + xp + xp+2

L(x) + x³ + x⁵ + xp + xp+2 grâce à (3.66)

nous déduisons que II.7-(h)IIX = x si d < L(x). Donc pour d < L(x), .7-(h) ? B(O, x).

3.2.3 Preuve du lemme 3.2

Nous allons à présent montrer que l'application h H .7^-(h) est contractante dans Y . Soient h1 et h2 deux solutions de (3.2) avec h1(0, r) = h2(0, r). Supposons que

max{IIh1IIX,IIh2IIX} = x < x1

Posons È = .7-(h1) - .7-(h2) ; h1, h2 ? X et notons pour l = 1, 2 gl := g(hl) et .7-l := .7^-(hl).

Alors, nous obtenons d'une part

D.7-1

47r

= (.7-1 - h1) [g1 2rg1 - +g1 (h1)^p+1] - ¹₂rg1 (h1)^p

p

et d'autre part

D.7-2 = (.7^-2 - h2) g2 - g2

2r - 4ðrg2

p + 1 (h2)^p+1]- _12rg2 (h2)^p

puis on déduit de ces deux relations

DÈ = D(.7-1 - .7-2) = (.7-1 - h1) [g1 -g1 4ðrg1 (h )p+1] ¹ _(h )p

p

-

2r + 1 1

₂rg1 1

Mémoire de MASTER

44

- (.7^-2 - h2) [^g2-_2r^g2 - 4ðrg2

p + 1 (h2)^p+1] + _12rg2 (h2)^p

3.2. Théorème d'existence et d'unicité (théorème principal)

. Ainsi,

1 1

DÈ = _2r(g1 -g2)h2 + _2r(g1 -g1)(È - h1 - h2)

1 4ðrg1

+ 2r(g1 - g2 - g1 + g2)(F2 - h2) - p + 1 (h1)p⁺¹(È - h1 + h2) 4ðrp+1

+ p + 1 [g2 %oh2é - g1 %oh1é^p+1]+^r₂(g2 - g1)h1

- ₂(h1^p - h2^p)

= ~ 1 2r(g1-g1)- 4ðrg1

p + 1 (h1)p+1~(È-h1+h2)+ 1 2r( g1- g2)h2+ 1 _2r(g1-g2- g1+ g2)(F2-h2)

4ðr p₎
+ p + 1 g2 %oh2é^p+1 - g1 %oh1é^p+1~ + r ₂(g2 - g1)h1 p - r ₂(h1^p - h2

Posons

y = Yh1 - h2YY

Comme précédemment, grâce au Théorème 1.2.1, nous allons utiliser la caractéristique Xl := Xl(u, r) définie par

dr = - du

gl(Xl(u, r), u); r(0) = r0

Mémoire de MASTER

45

où l = 1, 2. Ainsi, nous pouvons représenter È comme

È(u1,r1) = J exp [_2r(g1 -g1) - +~1 (h1)^p+1] du^'[ø]_X1 du

o p xl

1 1 1

, où ø est après réarrangement des termes

ø _=2r(g1-g2)h2 + _2r [g1 -g1 - (g2 -g2)]F2 - 2r [g1 -g1 - (g2 -g2)]h2

- (h1- h2) g1 - 2r g1 - 4ðrg1

p + 1 (h1)^p+1~ + p ^4ðr + 1 g2 %oh2é^p+1 - g1 %oh1é^p+1~ + r p₎

₂(g2 - g1)h1 p - r 2(h1 p - h2

. Or

1 1

SøS = _2rSg1 -g2SSh2S + _2rSg1 -g1 - (g2 -g2)SSF2S 1

2r V + Sh1 - h2SS^4ðrg1

+ 2rSg1 - g1 - (g2 - g2)SSh2S + Sh1 - h2SVg1 - g1 p + 1 SSh1Sp+1

4ðr

p_S

+ p + 1 Ug2 %oh2é^p+1 - g1 %oh1é^p+1U + r ₂Sg2 - g1SSh1^pS + r ₂Sh1^p - h2

:= D1 + D2 + ... + D8. (3.67)

3.2. Théorème d'existence et d'unicité (théorème principal)

Nous allons à présent chercher une majoration des termes D1 , D2 , ... , D8. Pour cela, nous remarquons que :

1 r

Sh1 - h2S < f

Sh1 - h2Sds

r

1 r Jo^r (1 + s + u)2S(h1 - h2)(u,s)Sds

<

1 r

sup 0=u,s<°°

{(1 + s + u)^2S(h1 - h2)(u, s)S} f r o (1 + ^ds^s+ u)^2

Mémoire de MASTER

46

1 r ds

= Yh1 - h2YY r J^ro (1 + s + u)²

y

(3.68)

(1 + u)(1 + r + u)

et

Sh1 - h2 - (h1 - h2)S < Sh1 - h2S + Sh1 - h2S

< y + y

(1 + r + u)² (1 + u)(1 + r + u)

2y

(3.69)

(1 + u)(1 + r + u)

En utilisant (3.10) et (3.68), nous déduisons que

TSh1 - h1S² - Sh2 - h2S²T < S(h1 - h2) - (h1 - h2)S(h1 - h1 + h2 - h2)S

< (1 + u)(1 + r + u) 2(1 + r + u)²(1 + u) + 2(1 + r + u)²(1 + u)

2y xr xr ]
2xyr

(3.70)

(1 + u)²(1 + r + u)³

Comme

-4ð S r (h1 - h1)^2ds

°° _s< 0

, nous avons

Sg1 - g2S = Vexp[-4ð f ^°°(h1 - h1)^2ds]- exp[-4ð _f ^°°(h2 - h2)²d^s_JV < 4ð f °° s S_h1- h1S² - Sh2 - h2S² ds

< ^8ð(1 + u)²(1 + s + u)3 ds

r°° xy

r

4ðyx (3.71)

< (1 + u)²(1 + r + u)²

Mais, nous pouvons noter

1

h^p₁ - h^p₂ = p(h1 - h2) _f (th1 + (1 - t)h2)^p-1dt (3.72)

0

3.2. Théorème d'existence et d'unicité (théorème principal)

et

Sh^p₁ - h^p₂S < pSh1 - h2S(Sh1S + Sh2S)^p-1

yp < × (1 + u)(1 + r + u)	2p-1xp-1
	(1 + u)p-^1(1 + r + u)p-^1

yp2p-¹xp-¹

(3.73)

(1 + u)p(1 + r + u)p

donc

V^r₂(h^p1 - h^p₂)V = ^r₂Sh^p₁ - h^p₂S

r

< 2

yp2p-¹xp-¹

(1+u)p(1+r+u)p ryp2p-²xp-¹

(1+u)p(1+r+u)p

ryp2p-²xp-¹ <(3.74)

(1 + u)p(1 + r + u)p-¹

D'autre part, nous avons

1 r 4ðxy rr ds

Sg₁ - g₂S < r fSg1 - g2Sds r(1 + u)² Jo (1 + s + u)²

4ðxy <(3.75)

(1 + u)³(1 + r + u)

et de la relation (3.8) puis du fait que g1 < 1, g2 < 1, on a

p+¹)USg2h2^p+1 - g1h1^p+1S = U(g2 - g1)h2^p+1 + g1(h2^p+1 - h1

p+1_S

+ Sh2 p+1 - h1

< 2Sh2S^p+1

< (1 + u)p⁺¹(1 + r + u)p+1 + (1 + u)p⁺¹(1 + r + u)p⁺¹

2xp⁺¹ y(p + 1)2pxp

2p(p + 1)y(xp + xp⁺¹)

< (3.76)
(1 + u)p⁺¹(1 + r + u)p⁺¹

Or des relations (3.75) et (3.76), nous avons

8ð r p+1Sds

S g1 - g2S < Sg1 - g2S + (p + 1)r S 0 s²Sg2h2^p+1 - g1h1

4ðxy

< (1 + u)³(1 + r + u) +

4ðxy

< (1 + u)³(1 + r + u) +

8ð ^rr s 2p(1 + p)y(xp + xp+1) ds

(p + 1)r ^Jo (1 + u)p⁺¹(1 + s + u)p⁺¹

2p⁺³ðy(xp + xp+1) r _s2
r(1 + u)p+1 1 Jo (1 + s + u)4 ds

2p⁺³ðy(xp + xp⁺¹)r² 3(1 + u)p⁺²(1 + r + u)³

4ðxy

(1 + u)³(1 + r + u) +

4ðxy

< (1 + u)³(1 + r + u) +

2p⁺³ðy(xp + xp⁺¹) r(1 + u)p+1 1

r3 - 3r(1 + u) 3(1 + u)(1 + r + u)³

<

My(x + xp + xp⁺¹)r

Mémoire de MASTER

47

(3.77) (1 + u)³(1 + r + u)

3.2. Théorème d'existence et d'unicité (théorème principal)

De la relation (3.77) et (3.8), nous obtenons D1 = 1 g1 - g21^1h21 2r My(x + xp + xp^+1)r = (1 + u)^3(1 + r + u)		1h21 2r
My(x + xp + xp^+1) < (1 + u)^3(1 + r + u)	x
	(1 + u)(1 + r + u)

My⁽x² + xp⁺¹ + xp⁺²)

(1 + u)⁴(1 + r + u)2 .(3.78)

De (3.70), on a :

1 1g1 - g2 - (g1 - g2)1 <_r Jor ^fr

1 ?

?s(g1 - g2)1dsdr^'

4ð I^rf^r_s h1 - h11² - h2 - h21² dsdr^'

r

< 8 Jo d
7rx r r s

r(1 + u)² Jr^, (1+s +u)^3dr'

4ðrxy

(3.79)

(1 + u)³(1 + r + u)²

En utilisant les relations (3.73) et (3.79), nous avons :

1 1 8ð r 2 p+1 p+1

2r1g1 -g1 - (g2 -g2)1 < 2r1g1 - g2 - (g1 - g2)1 + r(p + 1) _Jo s Ih1 - h2 1ds

1 4ðrxy 1 2p+3ðyxpr s2

· 2r (1+u)³(1+r+u)^{2 +}2r r(p + 1)(1 + u)p+1 ^S (1 + s + u)p+1ds~ 0

2ðxy

< (1 + u)³(1 + r + u)2 +

2ðxy

< (1 + u)³(1 + r + u)2 +

1 2p+3ðyxp ,rr s2

2r r(p + 1)(1 + u)p⁺¹ Jo (1 + s + u)^4ds

1 r 2p+3ðyxpr2

2r 3(p + 1)(1 + u)p⁺²(1 + r + u)3 ~

M(x + xp)y

< (1 + u)³(1 + r + u)2 .(3.80)

Des relations (3.80) et (3.34), nous avons

1

D2

= 2r1g1 -g1 - (g2 -g2)11F21

M(x + xp)y1F21

<

(1 + u)³(1 + r + u)²

M(x + xp)y =sup {(1 + r + u)²1F2(u,r)1}

(1 + u)³(1 + r + u)⁴ 0=u,r<8

Myâ(x)

(3.81)

< 2k²(1 + u)³(1 + r + u)⁴

Mémoire de MASTER

48

Où â est définit par

â(x) = (x + x^p)(d + x³ + x^p + x^p+2)exp[M(x² + x^p+1)] (3.82)

3.2. Théorème d'existence et d'unicité (théorème principal)

Des relations (3.80) et (3.8), on obtient

1 _

D3 = 2rSg1 -g1 - (g2 -g2)SSh2S

yM(x + xP) < (1 + u)^3(1 + r + u)^2	x
	(1 + u)(1 + r + u)

yM(x² + xP+1) (3.83)

(1 + u)⁴(1 + r + u)³

De (3.16) et (3.68), nous avons

D4 = Sh1 - h2S Vg1 - g1

2r V

1 M(x² + xP⁺¹)r²

2r (1 + u)³(1 + r + u)3 ~

<

- (1 + u)(1 + r + u)

y

Mémoire de MASTER

49

M(x² + xP⁺¹)y

< (3.84)

- (1 + u)⁴(1 + r + u)³

Des relations (3.8) et (3.68),

47rrg1 P+1

D5 = Sh1 - h2 V p + 1 Vh1S

< y - (1 + u)(1 + r + u)	47rrxP^+1
	(p + 1)(1 + u)P^+1(1 + r + u)P^+1

<

47ryxP⁺¹

(p + 1)(1 + u)P⁺¹(1 + r + u)P MyxP⁺¹

<

(3.85)

(1 + u)P⁺¹(1 + r + u)³

De la relation (3.76), on a :

47rr P+1 P+1

D6 p + 1 Ug2 %oh2é - g1 %oh1é

MxP-¹y

< (1 + u)P⁺¹(1 + r + u)³

MxP-¹y <(3.86)

(1 + u)P(1 + r + u)²

De (3.71) et (3.8), on obtient r PS D7 = 2Sg2 - g1SSh1 47ryxr < X (1 + u)^2(1 + r + u)^2	xP
	(1+u)P(1+r+u)P

47ryxP⁺¹r

(1 + u)P⁺²(1 + r + u)P⁺² 47ryxP⁺¹

(1 + u)P⁺²(1 + r + u)P⁺¹ MxP⁺¹y

<

(1 + u)P⁺²(1 + r + u)⁴

(3.87)

Mémoire de MASTER

50

3.2. Théorème d'existence et d'unicité (théorème principal)

De la relation (3.77), on a :

r P P

D8 = ₂Ih1 - h2 ^P1

ryp2P-²xP-¹

= (1 + u)P(1 + r + u)P-¹

yMxP-¹ =(3.88)

(1 + u)P(1 + r + u)²

Remarque 3.2.2 : Pour le cas où j = 4, D1 , D2 , D3 , D4 , D5, D6, D7 peuvent avoir les mêmes majorations que dans le cas j = 3.

Dans le cas j = 4, nous avons

MxP-1y ( )

D8 3.89
<_ (1 + u)P(1 + r + u)³

De l'inégalité 1 + r(u) + u = ¹₂k(1 + r1 + u1) et de l'intégrale (forme générale) définie en (3.52), nous avons

S0

u1 u1

S[?]XSdu = S 0 [(D1 + D2 + ... + D8)]Xdu

C3y[â(x) + x² + xP-¹ + xP⁺¹ + xP⁺²] =(3.90)

k³(1 + r1 + u1)²

avec C3 > 0 dépendant de M.

Pour le cas j = 4, on déduit de (3.88) qu'il existe 0₃ > 0 dépendant aussi de M tel que

S0

u1 u1

S[?]XSdu = S 0 [(D1 + D2 + ... + D8)]Xdu

+ xP-¹ + xP⁺¹ + xP⁺²]

03y[â(x) + _x2 =(3.91)

k³(1 + r1 + u1)³



Comme en (3.17), on peut trouver C4 > 0 tel que

ru, 1 4

rg

Jo [2r(

1

1)

+ 1

(h1)P⁺¹] du = C4(x² + xP⁺¹) (3.92)

En combinant (3.90), (3.92) puis la définition de O, on obtient

ð

1

g

-g

-p

(1 + u1 r1)²1/3(u1, r1)1 = (1 + r1 + u1)2 ^u1 exp{f u1 [_2r(91 -91₎ - ~ð+g1 1 (h1)^P+1~ du'} _[?]X1 duW

X1

= (1 + r1 + u1)² × exp[C4(x² + x^P+1)] × C3y[â(x)k3(1 + rP+ u1)2+1 + xP⁺²]

yC3[â(x) + x² + xP-¹ + xP⁺¹ + xP+2] exp[C4(x² + x^P+1)] (3.93)

k3

3.3. Preuve du théorème d'existence et d'unicité

sup

r1=0

. On déduit de (3.93) que

11011Y = sup

u1=0

{(1 + r1 + u1)²1O(u1,r1)1}

yC3[â(x) + x² +xp-¹ + xp⁺¹ + xp⁺²]

< exp[C4(x² + x^p+1)] (3.94)

k3

Ainsi en posant

G⁽x) = C3[â(x) + x² + x3 ¹ + xp⁺¹ + xp+2] exp[C4(x² + x^p+1)], (3.95)

on obtient finalement

11011Y < G(x)y (3.96)

Or G est une fonction positive, croissante dans [0, x0[ et G(0) = 0, et il existe x2 E]0, x0] tel que G(x) < 1 pour tout x E]0, x2] ; ainsi pour 11h11X < x2 l'application h H ..7"(h) est contractante dans Y donc prendre î = G(x).

3.3 Preuve du théorème d'existence et d'unicité

Pour ä = L(x), nous déduisons du théorème 1.1.1 et de la relation (3.96) que l'équation (2.14) possède une unique solution h dans Y . Et comme cette solution vérifie la relation (3.1), nous déduisons l'unicité de solution dans X. Mais cette unique solution h vérifie 11h11X < x2 donc pour tout u = 0, r = 0, ,

(1 + r + u)^j-11h(u,r)1+ (1 + r + u)^jl^?h(u,r)1 < x2

?r

ce qui implique

{ (1 + r + u)j-^11h(u, r)1 < x22 (1 + r + u)jS^?h ?r (u,r)S < x22

?

cents ···· ····

Ih(u,r)1 < x2 2 (1 + r + u)-(j-1) S?h ?r (u,r)S < x22 (1 + r + u)-j

On a

Mémoire de MASTER

51

x2

donc la relation (3.1) en prenant C = 2 .

Montrons à présent que pour tout r = 0, e^ë , e^í tendent vers 1 lorsque u ? +8 Nous avons de la relation (3.11)

8 0 < 4ð fSh-hl^2ð2x2

d^ss(1 + u)⁴

donc

lim

u?+8

4ð _f 1h - hl^2ds 8

_s= 0

pour tout r > 0 fixé et avec la relation (2.12), nous avons

lim g = 1

u?+8

Mémoire de MASTER

52

3.3. Preuve du théorème d'existence et d'unicité

.

D'autre part de la relation (3.16), on a : lim u-++00		Sg - gS = 0
d'où	lim u-++00		g= 1

. Finalement des relations (2.10) et (2.11) nous avons

lim eí+ë = 1 et lim eí-ë = 1

u-++00 u-++00

on conclut que e^í et e^ë tendent vers 1 lorsque u ? +8 ce qui termine la preuve du théorème

3.2.1.

Mémoire de MASTER

53

Université de Yaoundé 1

? Conclusion ?

Rendu au terme de ce travail dans lequel il était question de montrer l'existence et l'unicité de solution du système non linéaire d'Einstein et de Klein-Gordon pour la métrique à symétrie sphérique, il se dégage que les équations d'Einstein se sont réduites en une équation intégro-différentielle non linéaire du premier ordre. Pour arriver à ce résultat, nous avons pris le soin de définir dans le premier chapitre des notions requises pour la meilleure compréhension du probleme. Dans le second chapitre, nous avons effectué des manipulations et des calculs qui ont conduit à l'établissement de cette équation, puis au dernier chapitre, nous avons énoncé et démontré un théorème qui conduit à l'existence globale et à l'unicité de solution pour cette équation.

Cependant, le cas d'un champ scalaire complexe n'a pas été examiné dans ce travail. D'une part, ça serait une perspective intéressante de pencher pour une étude analogue au cas réel; D'autre part, on peut considérer le cas des particules chargées et se demander si les résultats obtenus ne peuvent pas s'étendre au système d'Einstein-Klein-Gordon-Maxwell à symétrie sphérique; Et enfin, le cas p ? [0, 3[ reste à investiguer.

? Annexe ?

_Öp+1

Nous avons grâce au lemme 2.3 :

Ruu = 8ðÖ2 _u + 8ð guu p + 1

e2í = 8ðÖ^2 - 8ð p + 1

Öp+1 (3.97)

_Öp+1

Rur = 8ðÖ_uÖ_r + 8ð gur

p + 1

eí+ë = 8ðÖuÖr - 8ð p + 1

Öp+1 (3.98)

Des relations (3.98) et (3.99) nous avons :

Ruu - e^í-ëR_ur = 8ðÖ²_u - 8ðÖ_rÖ_ue^í-ë (3.99)
D'autre part du Lemme 2.2, nous avons

eí-ë + ^?ë(3.100)

(?í
?u ?u)

Ruu - e^í-ëR_ur = -

r

2

Mémoire de MASTER

54

Université de Yaoundé 1

En combinant (3.100) et (3.101), nous avons

2 _eí-ë ?í

-?u + ?ë

?u
· = 8ðÖ²_u - 8ðÖ_rÖ_ue^í-ë (3.101)

r

En utilisant les relations (2.9) et (2.11), (3.102) peut encore s'écrire

2 ?í + ?ë = 8ð ?h ?h h - h

r^g(?u ?u) ?u

?u ^g r

Remarque 3.3.1 : De la relation (3.102), nous pouvons conclure que les deux autres

équations obtenues grâce à _Ruu ^et _Rur du système d'équations d'EKG donné par la relation

?í ?ë

(2.3) aident à trouver une définition de + en fonction de Ö.

?u ?u

Mémoire de MASTER

55

Université de Yaoundé 1

? Bibliographie ?

[1] ANDREW S.GOETZ, "The Einstein-Klein-Gordon equations, wave Dark Matter, and the Tully-Fisher Relation ".Ph.D. Durke university,8jul 2015.ar Xiv : 1507.02626v1 [gr-qc].

[2] DONGHO CHAE, "Global existence of spherically symmetric solutions to the coupled Einstein and nonlinear Klein-Gordon system", 22 October 2001. Online at stacks.iop.org/CQG/18/4589.

[3] EGARD ELBAZ, Cosmologie, Ellipses (1992).

[4] FRÉDERIC PAULIN , Topologie, Analyse et calcul différentiel ,version préliminaire,cours de troisième année E.N.S (2008-2009).

[5] S. BENZONI-GAVAGE, Calcul différentiel et équations différentielles, Dunod, Paris, 2010

[6] LUC BLANCHET, introduction à la relativité générale, Institut d'Astrophysique de Paris, UMR 7095 du CNRS, Université Pierre et Marie Curie, 98bis boulevard Arago, 75014 Paris, France September 17, 2009 .

[7] Y.CHOQUET-BRUHAT, Géométrie différentielle et systèmes extérieures, Dunod, Paris, 1968.