5.2 Adaptation des algorithmes génétiques
au problème
5.2.1 Codage des données
Nous définissons le chromosome comme étant un
vecteur V de taille 15, composé de trois parties :
- Partie une : Un vecteur de taille 5 de
composante bivalentes ( 1 si la station de compression est en marche, 0
sinon).
- Partie deux: Un vecteur de taille 5 de
composantes entières( le nombre de turbocompresseurs en marche dans la
station de compression correspondante).
- Partie trois : Un vecteur de taille 5 de
composantes entières( les vitesses de rotation des turbocompresseurs
dans les stations de compression).
La structure d'un individu est présentée dans la
figure ci-dessous.

FIGURE 5.1 - La structure d'un
individu.
5.2.2 Population initiale
On génère n solutions réalisables du
problème, obtenues par l'heuristique NSCM, qui constituera une
population initiale pour l'algorithme génétique.
Vu que les constantes n'influencent pas sur la solution, on va
pas les considérer dans l'éva-luation des individus, ce qu'on
appelle fitness.
86
5.2. ADAPTATION DES ALGORITHMES GÉNÉTIQUES
AU PROBLÈME
5.2.3 Évaluation
Procédure Évaluation ( E
: nT C, S, q, H, Eta: matrice; S : f : matrice, Z :
vecteur)
Début
Pour i := 1 à n
faire
Y := 0
Pour j := 1 à 5
faire
|
f (i,j] :=
|
H [i,j] !
Q ·
1000
24·Eta[i,j] ;
|
Y := Y +f [i,j];
Fait;
Z [i] := Y ;
Fait;
Fin.
5.2.4 Sélection
La sélection des individu pour la reproduction se fait
par la sélection de deux individus aléatoirement. Pour chaque
paire d'individus tirées aléatoirement on compare et on
sélectionne le meilleur, ce qui produit deux parents P1 et
P2. L'étape sélection est décrite dans la
partie (1) de la procédure croisement.
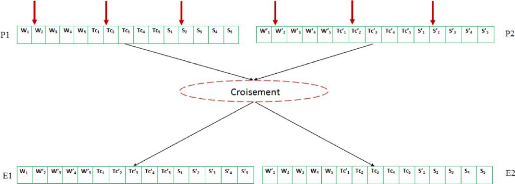
5.2.5 Croisement
Dans notre cas, nous avons utilisé le croisement en un
point. Pour effectuer ce type de croisement sur des chromosomes, on tire
aléatoirement une position de croisement dans chacun des parents. On
échange ensuite les deux chaînes terminales de chacun des deux
chromosomes, ce qui produit deux enfants E1 et E2. Pour ce
qui est du probabilité de croisement nous avons choisi
Pc = 0.9.
87
5.2. ADAPTATION DES ALGORITHMES GÉNÉTIQUES
AU PROBLÈME
Procédure Croisement ( E : P1, P2 :
vecteur; S : P 1, P 2, E1, E2, H1, H2, q1, q2, Eta1, Eta2 :
vecteur)
Début
Pour i := 1 à n faire
/* Partie(1)*/
t := random(n);
u := random(n);
minimum :=min (Z [t],Z [u]);
Si (minimum=Z [t]) alors indice1 :=t
Sinon indice1 :=u;
v := random(n);
w := random(n);
minimum :=min(Z [v],Z
[w]);
Si (minimum=Z [v]) alors
indice2 :=v
Si non indice2 :=w;
Pour k := 1 à 15
faire
P 1[k] := B[k,indice1];
P 2[k] := B[k,indice2];
Fait;
/* Partie(2)*/
r := random[0,1]; Si (r <
pc) alors
s := random(5);
Pour k := 1 à s - 1
faire E1[k] := P 1[k] ;
E2[k] := P 2[k];
E1[k + 5] := P 1[k +5] ;
E2[k +5] := P 2[k +5]; E1[k
+ 10] := P 1[k + 10] ; E2[k +10] :=
P 2[k +10]; Fait;
Pour k := s à 5
faire E1[k] := P 2[k];
E2[k] := P 1[k];
E1[k +5] := P 2[k +5];
E2[k +5] := P 1[k +5]; E1[k
+10] := P 2[k +10]; E2[k + 10] :=
P 1[k + 10] ;
Fait;
Pour k := 1 à 5
faire
|
P [i,2k] :=
|
'Q2 '
(P [i,2k - 1])2 -
R[K] · D5
;
se[k]
|
y
|
?
??????????????
|
|
|
?
???????????
? ??
|
|
|
P [i,2k +1] :=
|
|
+1
|
|
|
|
Fait; Si non
- Garder les deux parents P1 et P2; Fsi;
Fait; Fin.
88
5.2. ADAPTATION DES ALGORITHMES GÉNÉTIQUES AU
PROBLÈME
89
5.2. ADAPTATION DES ALGORITHMES GÉNÉTIQUES AU
PROBLÈME
On aura le résultat suivant:
| 


