3.5 Approche de modélisation
Pour permettre la résolution du problème
relatif à la perte de charge à travers la canalisation, la
présentation de la modélisation mathématique, les
paramètres, les variables, les contraintes, ainsi que la fonction
objectif serons définies dans ce qui suit.
La détermination d'un régime de fonctionnement
optimal des stations de compression nécessite le choix de la station de
compression à mettre en marche ainsi que le nombre de compresseurs qui
fonctionnent dans cette station choisie. D'autre part, pour chaque compresseur
en fonction on détermine le débit, la vitesse et la hauteur
adiabatique de telle sorte à minimiser l'énergie en respectant
son domaine de fonctionnement.
3.6 Données et paramètres du
problème
3.6.1 Données du problème
Présentation de la ligne GZ1 40»
La ligne de transport du gaz naturel GZ1 a été
réalisée en 1976/1979 sur une distance de 507 km pour
relier le gisement de gaz naturel de Hassi R'mel et le terminal de
raffinerie à Arzew.
Cette ligne fait partie d'un faisceau de canalisations de
pétrole, de gaz et de condensât. Elle se dirige à partir de
nord-ouest de Hassi R'mel vers l'ouest à Arzew.
GZ1 dispose de cinq stations de compression comme l'illustre
la Figure 3.1 : SC1 Timzhert (Laghouat), S M'seka (Laghouat), SC3 Medarreg
(Tiaret), SC4 Djebel Nador (Tiaret) et SC5 Kenenda (Relizane)
réparties sur la ligne assurant la mise sous pression du fluide
gazeux nécessaire à son écoulement, entrainées par
4 compresseurs centrifuges (voir Figure 3.2), les cinq stations de compression
consomment du gaz.

FIGURE 3.1 - Présentation de GZ1
FIGURE 3.2 - Schéma d'une station de
compression
37
3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME

Q = 5,747× 10-4 ·F
·
|
tv
|
) P 2
i - eseijP 2
Tb j
F?????? ??????? ·
D2,5
·
Pb Tm · Leij · G
· Z
|
|
avec
38
3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME
3.6.2 Définition des paramètres du
problème
I. Équation de chute de pression (perte en
charge)
La formule de perte de charge dans un tronçon "ij"
s'exprime de la façon suivante : [11]
Q2
P 2
i -eseijP j 2 = Rij.D5,
avec
· Pi : Pression initiale (entrante) dans le
tronçon (Kpas).
· Pj : Pression terminale (sortante) sur le
tronçon (Kpas).
· Q : Débit du gaz (m3/
jour).
· D : Diamètre intérieur du gazoduc
(mm).
· Rij : Constante qui dépend des
paramètres du tronçon.
· e : Base de logarithme népérien
(e=2,718...).
· seij une constante qui prend en
considération l'altitude de la conduite, sans unité,
définie par la formule suivante:
"Hj - Hi #
seij = 0,0684.G ,
Tf Z
avec
· Hi : L'altitude en amont de tronçon
(m).
· Hj : L'altitude en aval de tronçon
(m).
· Tf : La température finale du gaz K
(273,15+C°).
Cette constante sera calculée à partir de
l'équation du débit de la manière suivante:
II. Équation de calcul du débit
Q
L'equation de calcul du débit s'exprime de la
façon suivante: [11]
39
3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME
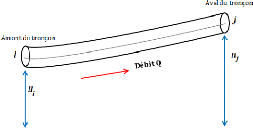
FIGURE 3.3 - Schéma d'un
tronçon ij
· Q : Débit du gaz
(m3/jours).
· Pb : Pression de base (Kpas).
· Tb :Température de base K
(273,15 + C° ).
· G : Gravité du gaz.
· Z : Facteur de compressibilité (sans
unité),
· Tm : Température moyenne du
gaz dans la conduite K (273,15 + C°).
2
· F = v avec ë :
facteur de friction.
ë
· Pi : Pression initiale dans le tronçon
(Kpas).
· Pj : Pression terminale sur le tronçon
(Kpas).
· D : Diamètre intérieur de la
conduite (mm).
· e : Base de logarithme népérien
(e=2,718...).
· Leij : Longueur équivalente qui prend en
considération la différence de l'altitude
entre l'amont et l'aval du tronçon.
L.(eseij - 1)
Leij = ,
seij
Transformation de l'équation de flux pour avoir la
formule de chute de pression, pour déterminer le coefficient
Rij.
1. On calcule Q2
Tb ) i - eseijP 2
F?????? P 2 j ???????
D5.
Q2 = (5,747)2 x
10-8 F2
Pb Tm Leij G Z
3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME
2. On fait sortir la formule de perte en
charge
?
???????????????
2
Pi2 - eseijP2 =
Q2
j D5
On pose A = 10-8 ×
(5,747)2 et B = Tb
Pb)
3. On fait sortir le coefficient Rij
?
????
.
G ·Tm ·Leij
·Z ?????
Tb !2 ????
(5,747)2 ·10-8 ·
· F2 ? ?
Pb
|
Rij =
|
G ·Tm ·Leij
·Z
|
|
|
A·B·F2 .
|
D'où la perte de charge sera exprimée comme suit
:
Q2
P 2
i -eseijPj 2 =Rij.D5.
4. Le facteur de compressibilité
On dit qu'un fluide est compressible, si pour une quantité
massique donnée de gaz qui occupe un volume donnée V1,
dans les conditions de pression et de
température(P1,T1), occupe un autre volume V2
en changent les conditions de (P1,T1) à
(P2,T2). [12]
Cette propriété de gaz est
représentée par le facteur de compressibilité Z
qui est exprimé en fonction de la température, la
pression et la composition de gaz.
Il exister plusieurs méthodes pour le calcul du facteur de
compressibilité, on peut citer la méthode de CNGA
(California Natural Gas Association), qui est la plus simple
et rapide en termes de calcul.[11]
1
Z =
?
?????
1+
?
?????
Pm ×
344,4(10)1,785×d
T 3,825 m
11
,
avec :
.
40
Pm : Pression moyenne (Kpas).
. Tm : Température moyenne K
(273,15+C?).
. d : Densité relative du gaz.
41
3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME
5. Nombre de Reynolds
Un paramètre important pour caractériser le type
de mouvement des fluides circulant dans un gazoduc, le nombre de Reynolds
dépend du débit massique M, le diamètre intérieur
du gazoduc, la densité et la viscosité du gaz, il peut être
calculé par la relation: [11]
4M
Re = ðDu,
· Re : nombre de Reynolds (sans unité).
· M : Le débit massique, M = Q x
ñ.
Q : Le débit volumique.
ñ : La masse volumique de gaz, (ñ
= 0,78).
· ð = 3,14...
· D : Diamètre intérieur du gazoduc.
· u : La viscosité du gaz (Kg/m.s), (u
= 1,25 x 10-5).
6. Coefficient de friction
Coefficient de résistance hydraulique établit
par Darcy, il est calculé de la même manière que pour les
liquides. Le calcul du coefficient de friction peut se faire par
l'intermédiaire de la formule suivante : [11]
/158 \
Re + 2 · Rug
ë = 0,067 ,
D
· Re : nombre de Reynolds (sans unité).
· Rug: La Rugosité de la conduite (mm), Rug
= 0,015.
42
3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME
7. Puissance de compression
La formule qui calcule la puissance d'un compresseur
nécessaire pour comprimer un débit Q est la suivante : [11]
" /Pj !m j
286,76
Wa = mG T1 - 1 ,
Pi
·
· m =
y
Wa : Puissance d'un compresseur
(joule/kg). y -1 , avec
y : Le rapport de chaleur spécifique qui vaut
1,28.
· T1 : Température d'aspiration de gaz (K)
.
· Pi : Pression d'aspiration (Kpas) .
· Pj : Pression de refoulement (Kpas).
8. Hauteur adiabatique
La Hauteur adiabatique caractérise la puissance
absorbée par le compresseur pour comprimer le gaz en supposons que la
transformation est adiabatique. [11]
|
" /Pj !m j
286,76
Had = mG T1.g - 1
Pi
|
.
|
Remarque:
On obtient la formule précédente en multipliant la
formule de la puissance de compression par g, où g =
9,
81m3.kg-1.s-2.
43
3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME
| 


