Optimisation du transport du gaz par canalisation.

Remerciements

Nous remercions Allah tout puissant de nous avoir donné le courage, la force et la volonté pour la réalisation de ce mémoire.

Nos vifs remerciements sont adressés à notre encadreur Mme.MESLEM Kahina(USTHB) pour nous avoir guidés et soutenus dans l'élaboration et la réalisation de ce travail. Qu'elle trouve ici l'expression de nos sincères remerciements.

Nous témoignons une reconnaissance particulière à notre encadreur Mr. LEFGOUNE Madjid chef de département Gestion Flux Gaz (SONATRACH TRC) pour nous avoir proposé le thème de cette étude, soutenu et surtout de nous avoir accueillis au sein du TRC, pour sa disponibilité, temps et patience qu'il nous a accordés, en nous facilitant la compréhension des clauses de travail, le côté technique et le fonctionnement sur le plan pratique.

Nous tenons également à remercier les membres du jury: Mr.BOUROUBI Sadek (Professeur USTHB) le président de jury et Mme.BENYAHIA TANI Nesrine (Université Alger3) d'avoir accordé de leurs temps précieux pour expertiser notre travail, nous espérons qu'ils en soient satisfaits.

Nous tenons à exprimer notre gratitude à Mr.MEZGHICHE Abdelhak (USTHB) pour sa disponibilité, son aide et ses conseils.

Nos profonds remerciements s'adressent également à l'ensemble du personnel du SONA-TRACH (TRC) et en particulier Mr.LAALAM Boualam, Mr. SAHEB Lyes et Mme. KARA Nachida qui nous ont facilité l'accomplissement de notre tâche, ainsi que l'ensemble des enseignants qui nous ont formé au cours de notre cursus à l'USTHB.

Nous voudrions également remercié du fond de coeur notre camarade Mr. LABRECHE Mustapha pour sa gentillesse, sa patience, son aide et sa disponibilité, nous voudrions aussi lui témoigner notre reconnaissance pour nous avoir fait découvrir le plaisir de travailler avec LATEX, sans oublier nos collègues et amis.

Finalement, nous remercions toute personne ayant contribué de près ou de loin à l'éla-boration de ce mémoire, sans oublier tous ceux qui nous ont encouragé le long de notre parcours universitaire.

Dédicaces

Je dédie ce modeste travail à :

Ma chère mère, celle qui m'a donnée le sens de vie, celle qui a toujours été là pour moi,
et qui n'a pas cessé de prier pour moi et de m'encourager,
que Dieu me la garde.

Mon très cher père, qui m'a toujours soutenue et aidée à affronter les difficultés.
A ma chère grand mère.

A mes chères frères Yahia, Adel et mes soeurs : Fatima, Mariem.

A mon amie et mon binôme Soumaya, merci pour sa présence et pour avoir
su m'écouter durant ces années. Ainsi qu'à son adorable famille.

A tous mes chers amis pour leur amitiés, leur encouragement, leur soutien :

Mina, BEN BIDA Gania, LABANE Hayet, Sihem, Nadjou, Selma (gm), Amina(gm), Massouda et

Chahrazed

A tous ceux qui sont chères et dont je n'ai pas cité le nom.
A tous mes camarades de la promotion sortante 2015.

Soumia

Dédicaces

Je dédie ce modeste travail à :

Ma chère mère, pour ses sacrifices depuis qu'elle m'a mis au monde,
et qui n'a pas cessé de prier pour moi et de m'encourager,
et qui a su m'entourer de toute son affection et son amour,
que Dieu me la garde.

Mon très cher père, qui a veillé, tout au long de
ma vie, à ce que je n'eusse besoin de rien, que Dieu le protège.

A mon frère Abes, mes soeurs : Hadjer, Manel, Asma et son fils Anis.

A mon binôme Soumia, qui avec sa patience a tant donné pour que nous achevions ce travail dans les meilleur conditions, ainsi que toute sa famille.

A tous mes chers amis.

A tous mes camarades de la promotion sortante 2015,
et a tous ceux qui me sont chers.

Soumaya

Table des matières

Introduction générale

1	Présentation de la SONATRACH				14
	1.1		Introduction		14
	1.2		Historique		14
	1.3		Description du groupe pétrolier SONATRACH		15
	1.4		Organisation de la SONATRACH		16
			1.4.1 Structures opérationnelles		16
			1.4.2 Structures fonctionnelles		17
	1.5		Organigramme de la SONATRACH		18
	1.6		Présentation de l'activité Transport par canalisation TRC		19
			1.6.1 Missions de l'activités de TRC		19
			1.6.2 Le transport au sein de la chaîne hydrocarbures		20
			1.6.3 Organigramme de l'Activité TRC		21
			1.6.4 Patrimoine de l'Activité TRC		22
			1.6.5 Quantités livrées		22
2	Définitions et généralités				23
	2.1		Introduction		23
	2.2		Généralités sur les hydrocarbures		23
			2.2.1 Gaz naturel		23
	2.3		Description d'un réseau de transport du gaz		25
			2.3.1 Les gazoducs		25
			2.3.2 Terminal de départ et d'arrivée		27
				2.3.3 La station de compression: un maillon essentiel du transport		27
				2.3.4 Les compresseurs		29
		2.4		Calculs hydrauliques : Définitions		31
3		Problématique et Modélisation				33
		3.1		Introduction		33
		3.2		Position du problème		33
		3.3		Étude de l'existant		34
		3.4		Modélisation du problème		35
		3.5		Approche de modélisation		36
		3.6		Données et paramètres du problème		36
				3.6.1 Données du problème		36
				3.6.2 Définition des paramètres du problème		38
				3.6.3 Modélisation des courbes caractéristiques des compresseurs		43
				3.6.4 Estimation des valeurs de la hauteur adiabatique et du rendement
				adiabatique		45
		3.7		Formulation mathématique du problème		50
				3.7.1 Les hypothèses du problème		50
				3.7.2 Définition des données		51
				3.7.3 Paramètres du modèle		51
				3.7.4 Contraintes		52
				3.7.5 L'objectif		55
				3.7.6 Evaluation du modèle		57
		3.8		L'état de l'art		59
				3.8.1 Introduction		59
				3.8.2 Les différentes approches de modélisation et de résolution de "Gaz
				Pipeline Fuel Consumption Minimisation Problem (GPFCMP)" . . . .		59
4		Méthode de résolution				62
		4.1		Introduction		62
		4.2		La programmation non linéaire mixte en nombres entiers		63

4.2.1 Qu'est ce qu'un programme MINLP ? 63

4.2.2 Technique de résolution 64

4.3 Les méthodes approchées 65

4.3.1 Les heuristiques classiques 65

4.3.2 Les métaheuristiques 67

4.4 Le recuit simulé 68

4.4.1 Présentation 68

4.4.2 L'analogie entre le recuit physique et le recuit simulé 69

4.4.3 Paramètres opérationnelles 69

4.4.4 Principe de RS : 70

4.4.5 Algorithme général du Recuit simulé 71

4.5 Les algorithmes génétiques 72

4.5.1 Présentation 72

4.5.2 L'analogie entre la génétique biologique et algorithme génétiques . 72

4.5.3 Le principe d'un algorithme génétique 73

4.6 Schéma des méthodes approchées 78

4.7 Démarches Hybrides 78

5 Résolution du problème 80

5.1 Adaptation d'une heuristique au problème 80

5.1.1 Principe de l'heuristique 80

5.1.2 Procédure de l'heuristique 81

5.1.3 Organigramme de l'heuristique 84

5.2 Adaptation des algorithmes génétiques au problème 85

5.2.1 Codage des données 85

5.2.2 Population initiale 85

5.2.3 Évaluation 86

5.2.4 Sélection 86

5.2.5 Croisement 86

5.2.6 Mutation 89

5.3 Heuristique de réparation 91

	5.4	5.3.1 Organigramme de l'adaptation des AG au problème Adaptation du recuit simulé au problème	92 93
		5.4.1 Initialisation	93
		5.4.2 Paramètres opérationnelles	93
		5.4.3 Voisinage	93
		5.4.4 Principales étapes	93
		5.4.5 Organigramme d'adaptation de recuit simulé au problème	95
6	Description informatique		96
	6.1	Introduction	96
	6.2	C'est quoi le Delphi?	96
	6.3	Présentation de l'application	97
		6.3.1 Description de l'application	97
		6.3.2 Utilisation de l'application	97
	6.4	Résultats de l'application	112
		6.4.1 Comparaison des résultats obtenus avec les données réelles	117

Conclusion générale Bibliographie Annexe

Table des figures

1.1	La chaîne de production des hydrocarbures	17
1.2	Schéma organisationnel et fonctionnel de la SONATRACH. 18
1.3	Le processus du transport des hydrocarbures	20
1.4	Organigramme de l'Activité TRC	21
2.1	Consommation mondiale de gaz naturel, 2007-2035	24
2.2	Chaine de transport par gazoduc	25
2.3	Le gazoduc GALSI de Hassi R'mel vers Castilionne Della Pescia (Italie)	26
2.4	Une station de compression avec quatre machines(turbocompresseurs)	28
2.5	Un compresseur centrifuge	30
2.6	Schéma de fonctionnement d'un compresseur centrifuge	31
2.7	Schéma d'un tube	32
2.8	La perte de charge	32
3.1	Présentation de GZ1	37
3.2	Schéma d'une station de compression	37
3.3	Schéma d'un tronçon ij	39
3.4	La carte de fonctionnement d'un compresseur	43
3.5	Le rendement adiabatique théorique en fonction du débit et de la vitesse	50
3.6	Représentation de la ligne étudiée	52
3.7	Schéma de la ligne	60
4.1	Le processus de l'analyse du système	62
4.2	Sélection par roulette	75
4.3	Sélection par tournoi (entre deux individus)	75

4.4 Croisement en un point 76

4.5 La mutation 76

4.6 Schéma d'hybride de bas niveau 78

4.7 Schéma d'hybride de Haut niveau 79

5.1 La structure d'un individu. 85

5.2 Organigramme d'adaptation de récuit simulé au problème 95

6.1 Logo 97

6.2 Fenêtre de lancement de l'application 98

6.3 Saisie du mot de passe 98

6.4 Fenêtre principale du l'application 99

6.5 Menu "Données" 99

6.6 sous-menu "calcul moindres carrées" 100

6.7 Les calculs par moindres carrées 100

6.8 sous-menu "Conditions opératoires" 100

6.9 Conditions opératoires 101

6.10 sous-menu "Caractéristiques du gazoduc" 101

6.11 Caractéristiques du gazoduc 102

6.12 sous-menu "Caractéristiques des compresseurs" 102

6.13 Caractéristiques des compresseurs 102

6.14 Menu "Calcul perte de charge" 103

6.15 fenêtre "Calcul perte de charge" 103

6.16 sous-menu "Options" 104

6.17 sous-menu "Sites web" 104

6.18 Bouton "Résolution" 104

6.19 La fenêtre "Résolution" 105

6.20 Le champ correspondant au débit 105

6.21 Le champ correspondant aux méthodes de résolution 105

6.22 Résolution par l'heuristique 106

6.23 Résolution par l'algorithme génétique 107

6.24 Résolution par le récuit simulé 107

6.25 Barre d'outils 108

6.26 Champ correspondant à l'affichage de la configuration optimale 108

6.27 Affichage de la quantité consommée ainsi que sa proportion 109

6.28 Bouton "Voir la ligne" 109

6.29 La fenêtre "Voir la ligne" 109

6.30 Bouton "Aide" 110

6.31 La fenêtre "Aide" 110

6.32 Bouton "Apropos" 111

6.33 La fenêtre "A propos" 111

6.34 Résolution par l'heuristique 112

6.35 Résolution par l'algorithme génétique 113

6.36 Résolution par le recuit simulé 114

Liste des tableaux

3.1	Résultats obtenue par estimation	49
4.1	Analogies recuit physique / recuit simulé	69
4.2	Analogie génétique biologique/algorithme génétiques	72
6.1	Résultats obtenus par l'application	115
6.2	Comparaison entre les données réelles et les résultats obtenus par l'optimisa-
	tion	117
6.3	Caractéristiques de la ligne GZ1. 122
6.4	Profil Altimétrie	122
6.5	Caractéristiques des compresseurs. 123
6.6	Caractéristiques de gaz naturel. 123

Introduction générale

Le gaz naturel joue un rôle énergétique croissant. L'importance de ses réserves et les avantages qu'il présente sur le plan de l'environnement favorisent son utilisation, notamment dans des secteurs à forte valeur ajoutée : industrie de précision, production d'électri-cité.

Les coûts techniques de production, de traitement et surtout de transport du gaz naturel restent toutefois élevés et représentant un handicap. Cette difficulté est d'autant plus réelle que la part des réserves de gaz naturel situées en mer ou dans des zones plus éloignées au consommateur.

Pour transporter des quantités de plus en plus importantes sur des distances toujours plus grande, le système de transport de gaz naturel par canalisation reste le mode le plus utilisé à travers le monde. Les compagnies gazières s'intéressent, d'une manière régulière, à réduire les coûts d'investissement et les charges d'exploitation pour le développement et le maintien de leurs réseaux.

Dans notre étude, nous nous intéressons à la minimisation des charges d'exploitation dans le transport du gaz naturel. En effet, l'acheminement du gaz dans le réseau passe par divers dispositifs de la conduite. le gaz perd en pression suite aux frottements avec la paroi de la canalisation, cette perte en pression est compensée par les stations de compression qui élèvent la pression de gaz.

Pour comprimer le gaz à travers les stations, ces dernières ont besoins de consommer une quantité de gaz prélevée à partir de la canalisation. Dans notre pays, elles consomment beaucoup de gaz naturel, plus de 600 millions de m³/an, soit un coût de 130 millions de dollars par an.

L'objectif de notre étude, est donc de chercher une meilleure solution qui permet de minimiser la quantité de gaz consommée par les stations de compression de telle sorte à satisfaire la demande en transport.

Pour mener à bien notre projet nous avons élaboré le plan suivant:

· Le premier chapitre servira à faire une brève présentation de l'entreprise SONATRACH, ses activités, ses objectifs, ainsi que la branche TRC.

· Dans le deuxième chapitre, nous donnons quelques généralités sur le gaz naturel et les termes techniques utilisés dans ce mémoire.

· Le troisième chapitre propose la problématique et l'objectif assigné à notre travail, ainsi que la modélisation du problème.

· Le quatrième chapitre est réservé aux méthodes de résolution du problème proposé.

· Le cinquième chapitre porte sur l'adaptation des méthodes de résolutions au problème étudié.

· Le sixième chapitre porte sur la description générale de l'application informatique.

· Enfin, nous terminons notre travail par une conclusion générale portant sur ce qui a été élaboré.

14

Chapitre 1

Présentation de la SONATRACH

1.1 Introduction

SONATRACH est une compagnie algérienne et un acteur internationale majeur dans l'industrie des hydrocarbures, c'est une compagnie de recherche, d'exploration, de transport par canalisation, de transformation et de commercialisation des hydrocarbures et leurs dérivés. Elle intervient également dans d'autres secteurs tels que les énergies nouvelles et renouvelables, le dessalement de l'eau de mer, la génération électrique. Elle exerce ses métiers en Algérie et partout dans le monde où des opportunités se présentent.

Elle a pour missions de valoriser de façon optimale les ressources nationales d'hydrocar-bures et de créer des richesses au service du développement économique et social du pays.

1.2 Historique

SONATRACH : plus d'un demi-siècle d'existance ...

La Société Nationale de Transport et de Commercialisation des Hydrocarbures SONATRACH a été crée par le décrit N°63/491 du 31 décembre 1963 paru au journal officiel du 10 nou-vombre 1964. Ces missions on été élargies le 22 Septembre 1966 pour s'étendre à tous les domaines de l'industrie pétrolière, la recherche et le transport des hydrocarbures.[18] La nationalisation des hydrocarbures le 24 février 1971 a poussé SONATRACH à prendre en main le destin pétrolier et gazier du pays.

15

1.3. DESCRIPTION DU GROUPE PÉTROLIER SONATRACH

Aujourd'hui et après sa restructuration en 1981, SONATRACH garde les principales fonctions du secteur des hydrocarbures à savoir :[18]

· L'exploitation, le forage et la production.

· Le transport des hydrocarbures.

· Le traitement et la liquéfaction du gaz naturel.

· La commercialisation des hydrocarbures liquides et gazeux.

1.3 Description du groupe pétrolier SONATRACH

· Principales activités:

- L'exploration.

- La production.

- Le transport terrestre et maritime des produits pétroliers.

- La commercialisation et le partenariat en amont et en aval dans le domaine des

hydrocarbures liquides et gazeux.

· Forme juridique: Société par action (SPA).

· Effectif de SONATRACH : 48 789 agents en 2013. [18]

Durant la période 2009-2013, l'effectif permanent à enregistré une évolution qualitative (accroissement des effectifs universitaires, diminution des effectifs exécution).

· Production totale d'hydrocarbures en 2013 : 187 millions TEP .[16]

· Chiffre d'affaires à l'exportation en 2013 : plus de 63 milliard de dollars.

· La production de gaz naturel en 2013 : 127,2 milliards de m³.

· Position du groupe Sonatrach sur le plan international [18]

Le groupe pétrolier et gazier est classé 1^eren Afrique et 12^eme dans le monde en 2013.

- Quatrième exportateur mondial de Gaz Naturel Liquéfié (GNL).

- Troisième exportateur mondial de Gaz Pétrole Liquéfié (GPL).

- Cinquième exportateur de Gaz Naturel(GN).

16

1.4. ORGANISATION DE LA SONATRACH

1.4 Organisation de la SONATRACH

1.4.1 Structures opérationnelles

Les activités opérationnelles exercent les métiers du groupe et développent son potentiel d'affaires tant en Algérie qu'à l'étranger. Les activités opérationnelles, qui sont placées sous l'autorité d'un vice-président sont: [18]

- Activité « Amont (AMT) » :

L'activité Amont couvre les activités de recherche, forage et la production d'hydrocar-bures. Elles sont assurées par Sonatrach seule, ou en association avec d'autres compagnies pétrolières.

- Activité « Transport par Canalisation (TRC) » :

Au sien du groupe Sonatrach, l'activité Transport par Canalisation TRC est en charge de l'acheminement des hydrocarbures, (pétrole brut, gaz, GPL et condensât), depuis les zones de production jusqu'aux zones de stockage, les ports pétroliers et les unités de transformations, via des canalisations dédiés à chaque produit.

- Activité « Aval (AVL) » :

Elle prend en charge l'élaboration et la mise en ouvre des politiques de développement et d'exploitation de l'aval pétrolier et gazier. Elle a pour missions essentielles l'exploi-tation des installations existantes de liquéfaction de gaz naturel et de séparation de GPL, de raffinage, de pétrochimie et de gaz industriel.

- Activité commercialisation "COM" : chargée d'assurer la valorisation et l'écoulement de la production sur le marché national et internationale.

17

1.4. ORGANISATION DE LA SONATRACH

La figure ci-dessous montre bien ces activités

FIGURE 1.1 - La chaîne de production des hydrocarbures

1.4.2 Structures fonctionnelles

Elles sont organisées en cinq Directions Coordination Groupe sous l'autorité d'un directeur:

· Direction Ressources Humaines et Communication « RHC ».

· Direction Activité Centrale « ACT ».

· Direction Stratégie Planification et Economie « SPE ».

· Direction Finance « FIN ».

· Direction activités Internationales « INT » (nouvelle direction créée en 2006). et quatre directions centrales :

· Direction Audit Groupe « ADG ».

· Direction Juridique « JUR ».

· Direction Santé, sécurité en Environnement « HSE ».

· Direction Techniques et Développement « TEC» (nouvelle direction créée en 2006).

1.5. ORGANIGRAMME DE LA SONATRACH

1.5 Organigramme de la SONATRACH

FIGURE 1.2 - Schéma organisationnel et fonctionnel de la SONATRACH.

18

Note : les flèches indiquent les interactions et les flux d'informations.

19

1.6. PRÉSENTATION DE L'ACTIVITÉ TRANSPORT PAR CANALISATION TRC

1.6 Présentation de l'activité Transport par canalisation TRC :

Le transport par canalisation est un mode de transport de matières gazeuses, liquides, solides ou polyphasiques, réalisé au moyen de conduites constituant généralement un réseau ou système de transport. [18]

L'activité Transport par Canalisation assure l'acheminement des hydrocarbures, pétrole brut, gaz, GPL et condensât depuis les zones de production jusqu'aux zones de stockage, aux complexes GNL et GPL, aux raffineries, aux ports pétroliers ainsi que vers les pays importateurs. Elle dispose un réseau de canalisations de près de 19599 km en 2013 contre 19063 en 2012, soit une augmentation de 536 km suite à la réception du GR4 et répartis comme suit: [18]

- Des gazoducs d'une longueur de 9689 km. - Des oléoducs d'une longueur de 9910 km.

1.6.1 Missions de l'activités de TRC

La branche de transport par canalisation a pour mission:

- La gestion et l'exploitation des ouvrages concentrés et les canalisations de transport des hydrocarburs.

- La coordination et le contrôle de l'exécution des programmes de transport arrêtés en fonction des impératifs de production et de commercialisation.

- La maintenance, l'intervention et la protection des ouvrages concentrés et canalisation de transport des hydrocarburs.

- La conduite des études, la réalisation et la gestion des projets de développement du réseau.

1.6. PRÉSENTATION DE L'ACTIVITÉ TRANSPORT PAR CANALISATION TRC

1.6.2 Le transport au sein de la chaîne hydrocarbures

Le transport par canalisation constitue le maillon intermédiaire entre l'amont de l'acti-vité pétrolière et gazière et les activités en aval en matière de transformation, de traitement des hydrocarbures et leur commercialisation. C'est une étape charnière dans la chaîne des hydrocarbures.

20

FIGURE 1.3 - Le processus du transport des hydrocarbures

21

1.6. PRÉSENTATION DE L'ACTIVITÉ TRANSPORT PAR CANALISATION TRC

1.6.3 Organigramme de l'Activité TRC

L'organigramme de la société est représenté comme suit:

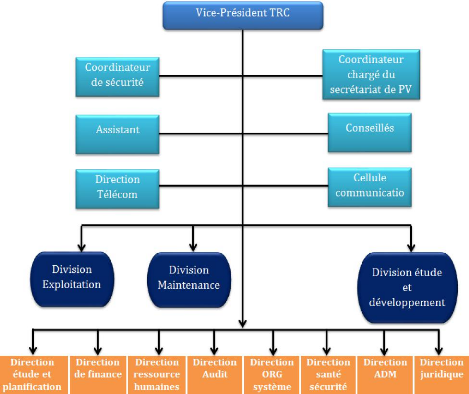
FIGURE 1.4 - Organigramme de l'Activité TRC

22

1.6. PRÉSENTATION DE L'ACTIVITÉ TRANSPORT PAR CANALISATION TRC

1.6.4 Patrimoine de l'Activité TRC

· TRC dispose de 34 canalisations dont 11 sont réservées au pétrole brut, 3 pour le condensât, 4 pour le GPL et 16 pour le gaz naturel.

· 357 millions TEP en Pétrole.

· 82 stations de pompage et de compression.

· 300 machines principales d'une puissance total de plus de 2 millions CV , (où 1 CV=0.00073550 MW).

· 127 bacs de stockage d'une capacité de design de 4.3 millions TEP.

· 03 ports pétroliers d'une capacité opérationnelle de 320 MTA.

· 03 bases principales de maintenance.

· 01 Centre National de Dispatching Gaz (CNDG) Hassi R'mel.

· 01 Centre de Dispatching des Hydrocarbures Liquides (CDHL) Haoud El Hamra.

· 01 Centre de Stockage et Transfert des Huiles (CSTH).

1.6.5 Quantités livrées

Les quantités évacuées en 2013 sont réparties comme suit [18]

· Pétrole brut: 47,9 Millions Tonnes.

· Gaz naturel: 80,2 Milliards m³.

· Condensât: 8,6 Millions Tonnes.

· GPL : 6,4 Millions Tonnes.

Le réseau de transport par canalisation compte 16 gazoducs, avec une capacité de transport de 357 million TEP.

Depuis la mise en service des 02 gazoducs transcontinentaux, Enrico Matei (reliant l'Algérie à l'Italie via la Tunisie) et Pedro Duran Farrel (reliant l'Algérie à l'Espagne via le Maroc), de nouveaux projets de construction de gazoducs sont en cours de réalisation afin de répondre notamment à une demande croissante du marché européen.[18]

23

Chapitre 2

Définitions et généralités

2.1 Introduction

Confrontées à une problématique d'optimisation liée au transport des hydrocarbures, plus précisément les stations de compression, nous présenterons dans ce chapitre la terminologie nécessaire avant de décrire la problématique et ses facettes.

2.2 Généralités sur les hydrocarbures

Les hydrocarbures sont des molécules organiques exclusivement composées de carbone et d'hydrogène. Ils sont inflammables, à l'image du pétrole et du gaz naturel , deux carburants importants. Par ailleurs, ils ne se mélangent pas à l'eau.

2.2.1 Gaz naturel

a- Description du gaz

Le gaz naturel est incolore, inodore, insipide, sans forme particulière et plus léger que l'air. Il se présente sous sa forme gazeuse au dessus de -161°C. Le gaz naturel est un mélange d'hydrocarbures légers comprenant du méthane, de l'éthane, du propane, des butanes et des pentanes. Cependant, son composant principal est le méthane(au moins 84,87%). Il possède une structure d'hydrocarbure simple, composée d'un atome de carbone et quatre atomes d'hydrogène CH4. Issu de la dégradation d'anciens organismes vivants, il est souvent pré-

2.2. GÉNÉRALITÉS SUR LES HYDROCARBURES

sent dans les mêmes zones de production que le pétrole à des profondeurs allant de 1000 à 6000 mètres sous terre, il est extrait par forage. Trois pays se partagent plus de 50% des réserves mondiales de gaz naturel : la Russie (27%), l'Iran (15%) et le Qatar (14%).

Les Caractéristiques principales du gaz naturel sont les suivantes :

· Densité : 0.656 par rapport à l'air.

· Masse volumique: 0.78 kg/ m³.

· La capacité énergétique du gaz naturel est appelée Pouvoir Calorifique Supérieur (PCS) : 9482 Kcal/ m³.

b- Utilité du gaz naturel

Le gaz naturel est la troisième source d'énergie la plus utilisée dans le monde (aprés le pétrole et le charbon), principalement dans:

- la production de chaleur pour la cuisson et le chauffage.

- le secteur industriel, comme matière première pour l'industrie chimique (pétrochimie et raffinage).

- la production d'électricité.

- les transports : le gaz naturel pour véhicules (GNV) est de plus en plus utilisé pour les transports publics urbains comme les bus ou les camions-bennes.

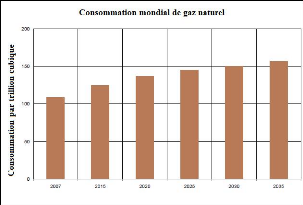
24

FIGURE 2.1 - Consommation mondiale de gaz naturel, 2007-2035

25

2.3. DESCRIPTION D'UN RÉSEAU DE TRANSPORT DU GAZ

2.3 Description d'un réseau de transport du gaz

Le transport du gaz consiste à l'acheminer depuis la zone d'extraction jusqu'à la zone de consommation afin d'alimenter les réseaux de distribution.

A l'échelle nationale ou internationale, le transport du gaz relie les gisements aux réseaux de distribution de manière efficace, généralement invisible et en toute sécurité, les moyens de transport du gaz doivent parfois couvrir de longues distances et traverser plusieurs frontières afin de relier les pays producteurs aux pays consommateurs. Il existe deux moyens complémentaires pour transporter le gaz efficacement:

- les gazoducs.

- la transformation en gaz naturel liquéfié (GNL).

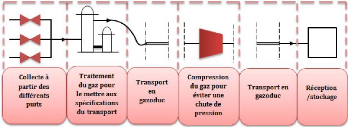
FIGURE 2.2 - Chaine de transport par gazoduc

2.3.1 Les gazoducs

Ils sont le moyen de transport du gaz naturel le plus utilisé car ils sont fiables et rentables. Des tubes d'acier sont soudés pour former une canalisation pouvant atteindre plus de 3 000 kilomètres de long. Le diamètre de ces tubes varie entre 20" à 48" (1"pouce"=2.54cm).

Pour des raisons de sécurité et d'environnement, les gazoducs sont le plus souvent enterrés (de 1 à 1.5 mètre). Cependant, dans les régions désertiques ou lorsque le sol est gelé (ex : pergélisol), le gazoduc est installé à même le sol. Les gazoducs sous-marins sont posés au fond de l'océan.

26

2.3. DESCRIPTION D'UN RÉSEAU DE TRANSPORT DU GAZ

Chaque gazoduc à sa particularité c'est pour cela qu'il faut affecter à chaque conduite ses propres caractéristiques tels que :

· Les tronçons.

· La longueur en kilomètres.

· Le diamètre en pouce.

· le produit qu'il transporte.

· Le nombre de stations de compression.

· La provenance et la destination. Il existe deux types de gazoducs

· Gazoducs Amont: Les lignes amont transportent le gaz produit par les gisements vers les Centres de Dispatching.

· Gazoducs Aval : Les lignes Aval transportent le gaz acheminé par les Gazoducs Amont est dispatché vers les principales installations gazières nationales au nord ainsi que les clients de Sonatrach (Espagne,Italie).

FIGURE 2.3 - Le gazoduc GALSI de Hassi R'mel vers Castilionne Della Pescia (Italie)

27

2.3. DESCRIPTION D'UN RÉSEAU DE TRANSPORT DU GAZ

2.3.2 Terminal de départ et d'arrivée

· Terminal de départ

Un terminal de départ est un point source sert à exploiter le gaz via le réseau principal, il

est essentiellement constitué de :

- Une gare de lancement de racleur pour nettoyer périodiquement la conduite.

- Un réseau de tuyauterie.

- Un banc de filtration.

- Un banc de régulation qui a pour but de régler la pression au départ du gazoduc pour

permettre l'exploitation à des valeurs basses de débits.

- Un banc de comptage.

· Terminal arrivée

Un terminal arrivée est un point de livraison où se terminent un ou plusieurs gazoducs

principaux, il est constitué principalement de :

- Une gare de réception de racleur de nettoyage.

- Un réseau de tuyauterie.

- Un terminal d'arrivé peut également comporter un bacs de stockage.

2.3.3 La station de compression : un maillon essentiel du transport

Situées sur des intervalles réguliers sur les gazoducs (tous les 120 à 150 km), les stations de compression servent à compenser les pertes de pression dues au déplacement du gaz naturel. En effet, en circulant dans les canalisations, le gaz naturel est ralenti par le frottement sur les parois, entraînant une baisse de pression. Les stations de compression permettent de redonner de la pression au gaz naturel afin que celui-ci soit transporté sur de grandes distances et dispose d'une pression suffisante pour être livré aux points de cession (réseaux de distribution et industriels).

Elles rassemblent plusieurs compresseurs qui aspirent le gaz à basse pression pour le rejeter à une pression importante.

28

2.3. DESCRIPTION D'UN RÉSEAU DE TRANSPORT DU GAZ

Une station de compression est constitué principalement de :

· Plusieurs turbocompresseur (un compresseur entrainé par une turbine à gaz).

· Des aéroréfrigérateurs.

· Deux turbogénérateur.

· Un bâtiment de contrôle.

· Un bâtiment de service et de logistique.

· Une base de vie.

· Un bac d'eau et une pompe d'incendie.

FIGURE 2.4 - Une station de compression avec quatre machines(turbocompresseurs)

Les aéroréfrigérants

Les aéroréfrigérants sont des échangeurs de chaleur servant à baisser la température du gaz à la sortie des compresseurs jusqu'à 60^?, afin de prévenir la détérioration du gazoduc. Il est prévu un nombre de deux aéroréfrigérants par compresseurs.

29

2.3. DESCRIPTION D'UN RÉSEAU DE TRANSPORT DU GAZ

2.3.4 Les compresseurs

· La compression du gaz naturel

La pression d'arrivée du gaz naturel à une station de compression est appelée pression d'aspiration, et la pression de gaz sortante d'une station est appelée pression de refoulement. On les notera respectivement _Pasp ^et Pref.

La compression du gaz est un processus destiné à réaliser une augmentation de la pression d'aspiration _Pasp à la pression de refoulement Pref.

La variation de température n'est qu'une conséquence d'accroissement de la pression

des circonstances dans lesquelles s'effectue la compression. La compression peut s'effectuer

dans des machines fonctionnant suivant des principes divers.

Il existe deux types de compresseurs:

- Compresseurs à piston.

- Compresseurs centrifuges.

Dans notre travail, on n'utilise que les compresseurs centrifuge montés en parallèle.

· Compresseur centrifuge

Les compresseurs centrifuges transforment l'énergie mécanique de rotation en augmentation de pression du gaz. Autrement dit, ils transforment la vitesse en pression et sont les plus utilisés dans l'industrie des pipelines, en raison de leur domaine d'application, de leur prix moins élevé, de leur souplesse d'exploitation et de leur bon rendement qui varie dans l'intervalle suivant [0.70 - 0.85]. [11]

Les paramètres qui permettent le choix des compresseurs sont:

- Le débit du gaz à comprimer.

- La pression de refoulement.

- Le taux de compression.

30

2.3. DESCRIPTION D'UN RÉSEAU DE TRANSPORT DU GAZ

FIGURE 2.5 - Un compresseur centrifuge

· Principe de fonctionnement d'un compresseur centrifuge

Le compresseur tourne à vitesse élevée dans laquelle une ou plusieurs roues fournissent l'énergie nécessaire au transfert du gaz. Lorsque cette énergie doit être importante, il est nécessaire de prévoir plusieurs roues conduisant parfois à l'amélioration de ces machines par plusieurs étages de compression.

L'augmentation de pression est assurée par les roues, les diffuseurs et les canaux de retour. La vitesse de rotation de la roue soumet le gaz à une force centrifuge qui se traduit par une augmentation de vitesse, de pression et de température dans la roue. Le diffuseur puis le canal permet de ramener le gaz dans la roue suivante en gagnant encore de la pression par rapport à celle de sortie par ralentissement de la vitesse du gaz.

Les compresseurs centrifuges demandent une pression minimale et une autre maximal

· Pression de d'aspiration (pression minimale) : c'est la pression minimale exigée par les compresseurs pour qu'ils fonctionnent.

· Pression de refoulement (pression maximale) : c'est la pression maximale avec laquelle les stations refoulent le gaz.

31

2.4. CALCULS HYDRAULIQUES : DÉFINITIONS

FIGURE 2.6 - Schéma de fonctionnement d'un compresseur centrifuge

2.4 Calculs hydrauliques : Définitions

· Débit

Un Débit est le quotient de la quantité du fluide qui traverse une section droite de la conduite par la durée de cet écoulement, on a deux types de débit:

1. Débit massique M

si Am est la masse de fluide qui a traversé une section droite de la conduite pendant le temps At de cet écoulement, le débit massique est défini comme suit :

Am

M = Unité : kg/s
At

2. Débit volumique Q

Si AV est le volume de fluide qui a traversé une section droite de la conduite pendant le temps At de cet écoulement, le débit volumique est défini comme suit:

AV

Q = Unité: m³/s
At

· Le diamètre D

On définie le diamètre d'un gazoduc par la formule suivante

[ ~

Dext.^2.54

D = - 2.e

100

Où

D : Le diamètre intérieur du tube en mètre.

Dext : Le diamètre extérieur du tube qui est donné en pouces.

e : épaisseur de la paroi du tube en mètre.

Il faut aussi préciser que: 1 pouce=0.0254 m

2.4. CALCULS HYDRAULIQUES : DÉFINITIONS

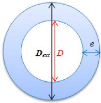
FIGURE 2.7 - Schéma d'un tube

· La perte de charge

Lors de son transport dans les gazoducs, le gaz subit des frottements avec les parois des canalisations. Ce qui fait perdre de la pression au gaz et cette perte est appelée perte de charge. C'est le phénomène le plus problématique du transport de gaz et de là provient une des difficultés du problème. En effet, sans la perte de pression induite par ce phénomène, le gaz circulerait très facilement dans les gazoducs.

32

FIGURE 2.8 - La perte de charge

33

Chapitre 3

Problématique et Modélisation

3.1 Introduction

Le gaz naturel est devenu, ces dernières années, un véritable enjeu mondial. Sa demande s'accroit de jour en jour et pour fournir cette énergie aux différents usagers les compagnies gazières s'intéressent d'une manière régulière à réduire les coûts d'investissement et les charges d'exploitation, les montants engagés par ces compagnies sont importants, donc une amélioration dans les frais d'investissements et les charges d'exploitation peut impliquer des montants substrats importants. De ce fait ces compagnies doivent assurer le transport du gaz aux consommateurs d'une manière à réduire les coûts du transport pour le développement et le maintien de leurs réseaux.

Dans ce cadre, l'Algérie avec des réserves gazières importantes, doit profiter de cette conjecture favorable. Le système de transport par canalisation est largement développé à travers les grandes régions de notre pays.

3.2 Position du problème

L'acheminement du gaz naturel dans le réseau de transport passe par divers dispositifs constitués de pipes, de régulateurs, de valves et de compresseurs. Le gaz naturel est introduit avec une pression importante.

34

3.3. ÉTUDE DE L'EXISTANT

Le gaz perd en pression suite au frottement avec la cloison des canalisations quand le gaz les traverse. La perte de compression est compensée par les stations de compression qui élèvent la pression.

L'objectif de cette étude est de déterminer dans une première étape, le choix des stations à mettre en marche, et dans une deuxième étape le nombre de compresseurs qu'il faut faire fonctionner à fin de minimiser la quantité de gaz consommer par les stations de compression en service tout en respectant les conditions d'exploitation, à partir d'un débit Q donné à l'entrée d'une station de compression avec une pression d'aspiration _Pasp, une pression de refoulement Pref.

3.3 Étude de l'existant

Dans la pratique, l'opérateur de la station de compression ajuste et essaye d'avoir le débit par l'arrêt des turbocompresseurs ou par le contrôle ou l'ajustement des vitesses des turbocompresseurs par son expérience, l'essentiel est de satisfaire la demande des clients et les caractéristiques des compresseurs sans tenir comptent de l'énergie consommée.

35

3.4. MODÉLISATION DU PROBLÈME

3.4 Modélisation du problème

La modélisation mathématique est une phase importante pour décrire, analyser et prédire le comportement des systèmes dans différents domaines du monde réel et les résoudre. Il y a beaucoup de types différents de modèles mathématiques, les plus utilisée en recherche opérationnelle sont les modèles d'optimisation.

Un modèle d'optimisation en recherche opérationnelle est une construction mathématique. Cette dernière est constituée de trois composantes principales :

- Variables de décision: L'étape la plus importante dans la construction d'un modèle est le choix des variables qui vont présenter les décisions à prendre.

- Contraintes : Un ensemble des paramètres qui limitent le modèle réalisable, avec des équations ou des inéquations composées des variables de décision.

- Fonction objectif: Une fonction qui définit l'objectif à atteindre, elle sert à déterminer la meilleure solution au problème d'optimisation. L'objectif du problème peut être de minimiser ou de maximiser cette fonction jusqu'à l'optimum.

36

3.5. APPROCHE DE MODÉLISATION

3.5 Approche de modélisation

Pour permettre la résolution du problème relatif à la perte de charge à travers la canalisation, la présentation de la modélisation mathématique, les paramètres, les variables, les contraintes, ainsi que la fonction objectif serons définies dans ce qui suit.

La détermination d'un régime de fonctionnement optimal des stations de compression nécessite le choix de la station de compression à mettre en marche ainsi que le nombre de compresseurs qui fonctionnent dans cette station choisie. D'autre part, pour chaque compresseur en fonction on détermine le débit, la vitesse et la hauteur adiabatique de telle sorte à minimiser l'énergie en respectant son domaine de fonctionnement.

3.6 Données et paramètres du problème

3.6.1 Données du problème

Présentation de la ligne GZ1 40»

La ligne de transport du gaz naturel GZ1 a été réalisée en 1976/1979 sur une distance de 507 km pour relier le gisement de gaz naturel de Hassi R'mel et le terminal de raffinerie à Arzew.

Cette ligne fait partie d'un faisceau de canalisations de pétrole, de gaz et de condensât. Elle se dirige à partir de nord-ouest de Hassi R'mel vers l'ouest à Arzew.

GZ1 dispose de cinq stations de compression comme l'illustre la Figure 3.1 : SC1 Timzhert (Laghouat), S M'seka (Laghouat), SC3 Medarreg (Tiaret), SC4 Djebel Nador (Tiaret) et SC5 Kenenda (Relizane) réparties sur la ligne assurant la mise sous pression du fluide gazeux nécessaire à son écoulement, entrainées par 4 compresseurs centrifuges (voir Figure 3.2), les cinq stations de compression consomment du gaz.

FIGURE 3.1 - Présentation de GZ1

FIGURE 3.2 - Schéma d'une station de compression

37

3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME

Q = 5,747× 10-^4·F ·

tv

) P 2 i - eseijP 2 Tb j ^F?????? ??????? · D2,5 · Pb Tm · Leij · G · Z

avec

38

3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME

3.6.2 Définition des paramètres du problème

I. Équation de chute de pression (perte en charge)

La formule de perte de charge dans un tronçon "ij" s'exprime de la façon suivante : [11]

Q2

P 2

i -eseijP j 2 = Rij._D5,

avec

· Pi : Pression initiale (entrante) dans le tronçon (Kpas).

· Pj : Pression terminale (sortante) sur le tronçon (Kpas).

· Q : Débit du gaz (m³/ jour).

· D : Diamètre intérieur du gazoduc (mm).

· Rij : Constante qui dépend des paramètres du tronçon.

· e : Base de logarithme népérien (e=2,718...).

· seij une constante qui prend en considération l'altitude de la conduite, sans unité, définie par la formule suivante:

"Hj - Hi #

seij = 0,0684.G ,

Tf Z

avec

· Hi : L'altitude en amont de tronçon (m).

· Hj : L'altitude en aval de tronçon (m).

· Tf : La température finale du gaz K (273,15+C°).

Cette constante sera calculée à partir de l'équation du débit de la manière suivante:

II. Équation de calcul du débit Q

L'equation de calcul du débit s'exprime de la façon suivante: [11]

39

3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME

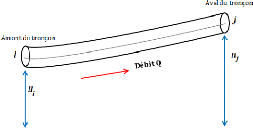
FIGURE 3.3 - Schéma d'un tronçon ij

· Q : Débit du gaz (m³/jours).

· Pb : Pression de base (Kpas).

· Tb :Température de base K (273,15 + C^° ).

· G : Gravité du gaz.

· Z : Facteur de compressibilité (sans unité),

· T_m : Température moyenne du gaz dans la conduite K (273,15 + C^°).

2

· F = v avec ë : facteur de friction.

ë

· Pi : Pression initiale dans le tronçon (Kpas).

· Pj : Pression terminale sur le tronçon (Kpas).

· D : Diamètre intérieur de la conduite (mm).

· e : Base de logarithme népérien (e=2,718...).

· Leij : Longueur équivalente qui prend en considération la différence de l'altitude

entre l'amont et l'aval du tronçon.

L.(eseij - 1)

Leij = ,

seij

Transformation de l'équation de flux pour avoir la formule de chute de pression, pour déterminer le coefficient Rij.

1. On calcule Q2

Tb ) i - _eseijP 2

F?????? P 2 j ??????? D⁵.

Q2 = (5,747)² x 10-8 F2

Pb T_{m Leij} G Z

3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME

2. On fait sortir la formule de perte en charge

?

???????????????

2

P_i² - eseijP2 = Q2

j D5

On pose A = 10-⁸ × (5,747)² et B = Tb

Pb)

3. On fait sortir le coefficient Rij

?

????

.

G ·T_{m ·Leij} ·Z ?????

Tb !2 ????

(5,747)² ·10-⁸ · · F² ? ?

Pb

Rij =	G ·Tm ·Leij ·Z
	A·B·F2 .

D'où la perte de charge sera exprimée comme suit :

_Q2

P 2

i -eseijPj 2 =Rij.D5.

4. Le facteur de compressibilité

On dit qu'un fluide est compressible, si pour une quantité massique donnée de gaz qui occupe un volume donnée V1, dans les conditions de pression et de température(P1,T1), occupe un autre volume V2 en changent les conditions de (P1,T1) à (P2,T2). [12]

Cette propriété de gaz est représentée par le facteur de compressibilité Z qui est exprimé en fonction de la température, la pression et la composition de gaz.

Il exister plusieurs méthodes pour le calcul du facteur de compressibilité, on peut citer la méthode de CNGA (California Natural Gas Association), qui est la plus simple et rapide en termes de calcul.[11]

1

Z =

?

?????

1+

?

?????

P_m × 344,4(10)1,785×d

T 3,825 m

₁₁

,

avec :

.

40

P_m : Pression moyenne (Kpas).

. T_m : Température moyenne K (273,15+C^?).

. d : Densité relative du gaz.

41

3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME

5. Nombre de Reynolds

Un paramètre important pour caractériser le type de mouvement des fluides circulant dans un gazoduc, le nombre de Reynolds dépend du débit massique M, le diamètre intérieur du gazoduc, la densité et la viscosité du gaz, il peut être calculé par la relation: [11]

4M

Re = ðDu,

· Re : nombre de Reynolds (sans unité).

· M : Le débit massique, M = Q x ñ.

Q : Le débit volumique.

ñ : La masse volumique de gaz, (ñ = 0,78).

· ð = 3,14...

· D : Diamètre intérieur du gazoduc.

· u : La viscosité du gaz (Kg/m.s), (u = 1,25 x 10-⁵).

6. Coefficient de friction

Coefficient de résistance hydraulique établit par Darcy, il est calculé de la même manière que pour les liquides. Le calcul du coefficient de friction peut se faire par l'intermédiaire de la formule suivante : [11]

/158 \

Re + 2 · Rug

ë = 0,067 ,

D

· Re : nombre de Reynolds (sans unité).

· Rug: La Rugosité de la conduite (mm), Rug = 0,015.

42

3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME

7. Puissance de compression

La formule qui calcule la puissance d'un compresseur nécessaire pour comprimer un débit Q est la suivante : [11]

" _{/Pj !m j}

286,76

W_a = mG T1 - 1 ,

Pi

·

· m =

y

W_a : Puissance d'un compresseur (joule/kg). y -1 , avec

y : Le rapport de chaleur spécifique qui vaut 1,28.

· T1 : Température d'aspiration de gaz (K) .

· Pi : Pression d'aspiration (Kpas) .

· Pj : Pression de refoulement (Kpas).

8. Hauteur adiabatique

La Hauteur adiabatique caractérise la puissance absorbée par le compresseur pour comprimer le gaz en supposons que la transformation est adiabatique. [11]

" /Pj !m j 286,76 Had = mG T1.g - 1 Pi

.

Remarque:

On obtient la formule précédente en multipliant la formule de la puissance de compression par g, où g = 9, 81m³.kg-¹.s-².

43

3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME

3.6.3 Modélisation des courbes caractéristiques des compresseurs

Les différentes plages de fonctionnement des compresseurs centrifuges sont définies par la carte de compression, propre à chaque compresseur, dans notre cas tous les compresseurs sont identiques.

La carte de fonctionnement est donnée en fonction du débit volumique Q (axe des abscisses), de la hauteur adiabatique H (axe des ordonnées), la vitesse S et le rendement adiabatique ç.

FIGURE 3.4 - La carte de fonctionnement d'un compresseur

Interprétation

Les caractéristiques d'un compresseur sont limitées par:

- Sur la gauche du diagramme : Limitation par la zone de pompage (débit trop faible).

Le pompage se produit dans un compresseur centrifuge quand le débit est réduit à tel point que le compresseur, à une vitesse donnée, ne peut plus pomper contre la hauteur

44

3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME

de pression présente.

A ce moment, une inversion momentanée du sens d'écoulement se produit ainsi qu'une chute de la hauteur de pression normale et le cycle recommence. Cela provoque une impulsion et un choc dans l'ensemble du compresseur et des tuyauteries associées.

Le fonctionnement du compresseur à gauche de cette ligne se trouve dans une zone de pompage. Dans ce cas il faut soit diminuer la hauteur soit augmenter le débit, de façon à ce que le fonctionnement du compresseur retourne à droite de la ligne de pompage.

- Sur la droite du diagramme: Limitation par la zone de gavage (débit trop important). L'examen d'une courbe caractéristique à vitesse donnée montre qu'au delà d'un certain débit volumique, la hauteur utile diminue, de plus en plus vite, vers les hauts débits. A ce moment, le rendement diminue également très vite et toute augmentation de puissance ne permet qu'une très faible augmentation de débit: il s'agira ainsi d'une zone appelée zone de gavage du compresseur qui correspond aux débits limites réalisables pour la (les) roue(s) du compresseur.

- Vers le haut du diagramme : Limitation par la vitesse maximale admissibles.

- Vers le bas du diagramme : Limitation par la vitesse minimale que peut développer la turbine.

On définit la hauteur adiabatique d'un compresseur _Had par l'énergie qui resterait emmagasinée dans le fluide par suite d'un procédé de compression adiabatique qui a lieu entre la pression d'aspiration du compresseur et la pression de refoulement de ce dernier.

Les quantités reliées aux compresseurs centrifuges sont le débit Q, La vitesse S, La hauteur adiabatique _Had et le rendement adiabatique ç, ces relations sont représentées par les équations suivantes:

La hauteur adiabatique

) Had = a1 + a2 Q )2 Q )3! Q + a3 + a4 × S^2, S S S

(1)

Le rendement adiabatique

_Q ) _{Q )}2 _{Q )}3

ç = b1 + b2 + b3 + b4 , (2)

S S S

3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME

où les paramètres a1, a2, a3, a4,b1, b2, b3 et b4 sont des constantes qui dépendent du type du compresseur.

3.6.4 Estimation des valeurs de la hauteur adiabatique et du rendement adiabatique

Pour estimer les valeurs de la hauteur adiabatique et du rendement adiabatique théoriques, on doit trouver les valeurs des paramètres a1, a2, a3, a4 (pour la hauteur adiabatique) et b1, b2, b3, b4 (pour le rendement). La méthode des moindre carrées sera utilisée pour minimiser l'erreur entre les données observées à partir des courbes caractéristiques du compresseur et les données théoriques calculées à l'aide de formules exprimées ci-dessus.

Principe de la méthode des moindres carrées

La méthode des moindres carrés, indépendamment élaborée par Legendre et Gauss au début du XIXe siècle, permet de comparer des données expérimentales, généralement entachées d'erreurs de mesure, à un modèle mathématique censé décrire ces données.

Les modèles de régression linéaires multiples [1] contiennent k variables explicatives X1,...,Xk, ils sont définis comme suit :

Y = b0 + _b1X1 + _b2X2 + ... + _bkXk + e

où les constantes b0,b1,b2,...,bk sont des paramètres du modèle et e est une variable aléatoire non observable représente la différence entre la valeur de Y observée et sa valeur approxi-mée par la relation fonctionnelle suivante dite fonction de régression :

Y = (X1,X2,...,Xk;b0,b1,b2,...,bk);
= b0 + _b1X1 + _b2X2 +... + bkXk

Pour les n observations ou réalisation (x1i,...,xki), i = 1,2,...,n, des variables explicatives X1,X2,...,Xk, les valeurs yi, i = 1,2,...,n, de la variable aléatoire expliquée Y, sont données par :

45

yi = b0x1i + _b1x2i + ... + _bkxki + ei,i = 1,2,...,n,

3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME

Considérons les notations suivantes :

0

- y= (y1,y2,...,y_n), est le vecteur des n observation de la variable expliquée Y, ce vecteur peut être aussi comme une seule réalisation de vecteur aléatoire

_Y0 = (Y1,Y2,...,Y_n),

où les variables aléatoires Yi, i = 1,2,...,n, sont indépendante identiquement distribuées.

- e est un vecteur colonne des variables aléatoires (non observables) défini par :

0 e

= (e1,e2,...,en),

- b est un vecteur colonne des paramètres de régression : b⁰=(b0,b1,...,bk),

- X est une matrice, de dimension, n × (k + 1), dite matrice du plan d'expérience et elle est donnée par :

? 1 1 . X = ????????????????????????????????????????????? .	x11 x12 . . . x1n-1 x1n	x21 ... x22 ... . . . x2n-1 ... x2n ...	? xk1 xk2 . ?????????????????????????????????????????? . . xkn-1 ? ?? xkn
. 1 1

0

En utilisant ces notations, on peut regarder le vecteur y= (y1,...,y_n), comme une réalisation du vecteur aléatoire Y satisfaisant le modèle linéaire :

46

Y = X b +e.

47

3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME

Application

Notre modèle de régression est défini comme suit :

Q(Q²

QHad =SS) ,(S)3;a1,a2,a3,a4!;

= a1 + a2 ()+ a3 ( )2 + ^a4(Q)3 x _S2 S

pour la hauteur adiabatique.

et

çad =

Q2 Q 3 ! Q S , , ;b1,b2,b3,b4 ; S S

_{Q Q2 Q} 3

= b1 +b2 +b3 +b4

S S S

pour le rendement adiabatique.

On calcule le coefficient de corrélation entre les deux valeurs (valeur observée et valeur théorique), noté r qui est égale au rapport de leur covariance et du produit non nul de leurs écarts types (le coefficient de corrélation est compris entre -1 et 1).

óXóY

Cor(X,Y) =

Cov(X,Y)

où Cov(X,Y) désigne la covariance des variables X et Y, óX et óY leurs écarts types.

Les valeurs des paramètres a1, a2, a3, a4 pour la hauteur adiabatique (b1, b2, b3, b4 pour le rendement adiabatique) calculées avec le solveur de Microsoft Excel sont :

Pour la hauteur adiabatique :

a1 = 1,0000 x10³,

a2 = -1,9912 x 10-¹²,

a3 = -7,5939 x 10-¹²,

a4 = -2,9715 x 10-¹⁰.

Le coefficient de corrélation r=0.991.

48

3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME

Pour le rendement adiabatique:

b1 = 6,7363x10-¹,

b2 = -1,1512x10-²,

b3 = 4,9884x10-⁴,

b4 = -4,3506x10-⁶.

Le coefficient de corrélation r=0,976.

49

3.6. DONNÉES ET PARAMÈTRES DU PROBLÈME

Les valeurs de _Hth ^et _çth calculées à partir des résultats :

Les données de la courbe du compresseur				Le calcul par les moindres carrés
Vitesse	Débit	Hauteur adiabatique	Rendement observé	Hauteur théorique	Rendement théorique
S	Q	Hobs	çobs	Hth	çth
3250	126 139	13 244	0,77	10 379	0,724
3250	165 530	13 121	0,80	10 148	0,807
3250	207 577	12 385	0,81	9 744	0,840
3250	226 608	11 649	0,80	9 498	0,821
3250	255 377	10 178	0,77	9 039	0,738
3900	152 252	19 252	0,77	14 941	0,726
3900	197 840	18 639	0,80	14 620	0,805
3900	247 410	17 535	0,81	14 056	0,840
3900	273 081	16 432	0,80	13 658	0,820
3900	306 275	14 592	0,77	13 020	0,739
4550	174 382	26 119	0,77	20 356	0,720
4550	228 821	25 629	0,8	19 920	0,803
4550	287 244	23 789	0,81	19 154	0,840
4550	317 340	22 195	0,80	18 615	0,821
4550	356 731	19 497	0,77	17 737	0,741
5200	198 282	34 090	0,77	26 594	0,719
5200	260 245	33 477	0,80	26 032	0,802
5200	325 749	31 024	0,81	25 064	0,841
5200	362 042	28 817	0,80	24 327	0,822
5200	406 744	25 506	0,77	23 193	0,743
5850	221 297	43 164	0,77	33 672	0,716
5850	291 227	42 306	0,80	32 967	0,800
5850	366 468	39 240	0,81	31 722	0,841
5850	404 974	36 297	0,80	30 848	0,824
5850	456 315	32 005	0,77	29 395	0,749
6500	245 640	52 974	0,77	41 572	0,716
6500	323 979	52 238	0,80	40 695	0,800
6500	407 629	48 192	0,81	39 152	0,841
6500	449 676	44 758	0,80	38 092	0,824
6500	505 443	39 608	0,77	36 345	0,749
6825	259 360	58615	0,77	45 821	0,718
6825	340 355	57 266	0,80	44 863	0,801
6825	429 316	53 097	0,81	43 134	0,840
6825	474 018	49 295	0,80	41 942	0,823
6825	474 018	43 777	0,77	40 088	0,750

TABLE 3.1 - Résultats obtenue par estimation

50

3.7. FORMULATION MATHÉMATIQUE DU PROBLÈME

le rendement adiabatique;

FIGURE 3.5 - Le rendement adiabatique théorique en fonction du débit et de la vitesse

3.7 Formulation mathématique du problème

3.7.1 Les hypothèses du problème

· Dans une station de compression, le débit rentrant est égale au débit sortant de la station de compression.

· Chaque station de compression est constituée d'un nombre fixe de compresseurs centrifuges identiques (4 compresseurs ) montés en parallèle. Cette hypothèse nous a conduit à diviser le débit écoulé à travers la station de compression identiquement sur les compresseurs utilisés.

· Dans une station de compression, le nombre de compresseurs qu'on peut faire fonctionner est 3. Le quatrième reste en mode « standby ».

· La ligne étudiée admet un seul terminal départ et un seul terminal arrivé, donc le débit qui rentre en aval du gazoduc est égale au débit en amont du gazoduc.

· Le diamètre est le même pour tous les tronçons.

51

3.7. FORMULATION MATHÉMATIQUE DU PROBLÈME

3.7.2 Définition des données

Soient les données suivantes : Tronçons:

( )

- Q : Le débit dans le gazoduc m³/jour .

- Rij : Une constante de la formule de perte de charge liée aux caractéristiques du tronçon (i,j).

- D : le diamètre du gazoduc (mm).

Compresseurs:

- Pmin : La pression minimale de service (kpa) .

- Pmax : La pression maximale de service (kpa).

- Smin : La vitesse minimale du compresseur (RPM) (Tour Par Minute).

- Smax : La vitesse maximale du compresseur (RPM) (Tour Par Minute).

( )

- qmin : Le débit minimal du compresseur m³/h .

( )

- qmax : Le débit maximal du compresseur m³/h . 3.7.3 Paramètres du modèle

Pour simplifier la modélisation on définit les paramètres suivants:

· I : L'ensemble de tous les points du gazoduc ( Voir la figure 3.6) I = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

· E_c : L'ensemble des couples ordonnées (i,j) représentant les stations de compression. E_c = {(2,3), (4,5), (6,7), (8,9), (10,11)}

· E_p : L'ensemble des couples ordonnées (i,j) représentant les tronçons. E_p = {(1,2), (3,4), (5,6), (7,8), (9,10), (11,12)}

3.7. FORMULATION MATHÉMATIQUE DU PROBLÈME

FIGURE 3.6 - Représentation de la ligne étudiée

Variables de décision

Le problème posé se résume à :

Déterminer le nombre de compresseurs à mettre en fonction à la station (i,j) où (i,j) E E_c de telle sorte à minimiser la quantité de gaz consommée par cette station, en fonction des invariants, tout en respectant le domaine de fonctionnement des compresseurs.

Donc les variables de décision sont :

· Pi : pression au point i , i E I.

· wij=

? ? ??? ????

1 si la station (i,j) fonctionne. 0 sinon (i,j) E Ec

·

52

nij : Le nombre de compresseurs en fonction dans la station (i,j) , (i,j) E E_c.

· Sij : La vitesse de rotation du compresseur dans la station (i,j), (i,j) E E_c.

· hij : La hauteur adiabatique du compresseur dans la station (i,j), (i,j) E E_c.

· qij : Le débit volumique passé par le compresseur dans la station (i,j), (i,j) E E_c.

3.7.4 Contraintes

a- Contraintes relatives aux tronçons

1. Pour un tronçon (i,j) E E_p, il existe des règles de conservation en perte de charge à respecter. Ceci est exprimé à l'aide de la contrainte suivante (Voir calcul perte de charge page 40) :

2

P_i² - e^seijP_j² = Rij.D5, , (i,j) E E_p.

53

3.7. FORMULATION MATHÉMATIQUE DU PROBLÈME

2. La pression au point i doit être supérieure à la pression minimale de service _Pmin et inférieure à la pression maximale de service _Pmax, ce qui est exprimé à l'aide de la double contrainte suivante :

Pmin<Pi<Pmax ,i E I.

b- Contraintes relatives aux compresseurs

3. La pression de refoulement Pj d'une station de compression (i,j) est supérieure ou égale à la pression d'aspiration Pi de cette station. En effet, si la station de compression fonctionne alors Pj > Pi sinon Pj = Pi. Ce qui est présenté par la double contrainte suivante :

Pj ^1<Pi

Pmax , (i,j) E Ec. Pmin

Pour chaque station de compression en marche, le débit qui passe par elle est divisé identiquement sur les turbocompresseurs en fonction. D'où le débit qui passe par chaque tur-

bocompresseur est égal à

wij.Q nij

donc le triplet des variables

wij.Q nij

!,Pi,Pj doit satisfaire le

domaine de fonctionnement d'un turbocompresseur. Ce qui est présenté par les contraintes suivantes :

4. La hauteur adiabatique est constante entre les compresseurs de la même station :

hij =

qij qij qij )3) 2 ! !2 1( a1 + a2 S + a3 S + a4 S x Sij??.wij, (i,j) E Ec. ijij _

avec

"

286,76 P. m

hij m.G ^T1.g _p -1 , (i,j) E E_c.

5. La hauteur adiabatique _hij ne doit pas dépasser la hauteur adiabatique maximale et doit être supérieur ou égale à la hauteur adiabatique minimale, ce qui est présenté par la double contrainte suivante :

H^L.wij <_ hij.wij <_ H^U.wij , (i,j) E E_c.

54

3.7. FORMULATION MATHÉMATIQUE DU PROBLÈME

avec

2 3

HL = (a1 + a2 ^max! + a3 ^max! + a4 ^max )XSin,

2

Smax Smax Smax

?2 3

HU =^?a1 + a2 ^min! + a3 ^min! + a4 min!?????X Smax.

Smin Smin Smin

6. Le débit Q est partagé de manière équitable sur les compresseurs utilisés dans une même station de compression :

24 · wij · qij.nij + (1 - wij) = Q.w(i,j) (i,j) E E_c

7. Le rendement d'un compresseur dans la station de compression (i,j) doit être inférieur ou égale à 1 :

! _!2 _!3

qij qij qij

b1 + b2 + b3 + b4 C 1, (i,j) E E_c.

Sij Sij Sij

8. La vitesse de rotation _Sij d'un compresseur en marche dans la station(i,j) ne doit pas dépasser la vitesse maximale et doit être supérieur ou égale à la vitesse minimale. Ce qui est présenté par la double contrainte suivante :

Smin.wij C Sij.wij C Smax.wij.

9. Le débit _qij qui passe par un compresseur dans la station(i,j) ne doit pas dépasser le débit maximal et doit être supérieur ou égale au débit minimal. Ceci est exprimé par la double contrainte suivante :

qmin.wij C qij.wij C qmax.wij, (i,j) E E_c.

10. Le rapport entre le débit et la vitesse du compresseur doit être compris entre pompage et gavage.

avec

55

3.7. FORMULATION MATHÉMATIQUE DU PROBLÈME

qmin qmax

pompage = , gavage =

Smax

Smin

On peut exprimer ça par la double contrainte suivante :

S l S l S

qmin qij qmax

min
·

.wi
· < .wi
· < .wij, (i,j) E E_c.

i j
· max

3.7.5 L'objectif

Notre objectif est de minimiser la quantité du gaz consommée par toute les stations de compression du gazoduc. Cette quantité va être donc égale à la somme des quantités du gaz consommées par chaque station de compression . D'où :

Min(Z) = _X fij

(i,j) EE_c

avec : fij est la fonction qui calcule la quantité du gaz consommée par la station (i,j) , (i,j) E E_c, définie comme suit :

?

???????????

fij =

hij

1000

?

????????

? ??

. wij

Q
·ñ
·

24
·çij
· çT R
·çmc
·P CI

avec :

çT R = 0,35 : Le rendement de la turbine.

çmc = 0,95 : Le rendement mécanique.

PCI :Pouvoir Calorifique Inférieur du gaz ( PCI=36 000kj/m³).

! _!2 _!3

qij qij qij

· çij = b1 + b2 + b3 + b4 ,

Sij Sij Sij

56

3.7. FORMULATION MATHÉMATIQUE DU PROBLÈME

Donc on aura le modèle suivant :

? ? ????????????????????????????????????????????????????????????????????????????????????????????????

???

????????????????????????????????????????????????????????????????????????????????????????????????????

P =

Min(Z) = P(i,j) ?E_c fij s.c

P _i ²-e^seijP_j²= Rij.^Q2 ?(i,j)?E_p ...(1)

D5

Pi = Pmin ?i ? I ...(2)

Pi = Pmax ?i ? I ...(3)

Pi

Pj =

Pi

! _!2

qij qij qij !^3???_??? × _S2 ??????.wij ?(i,j) ? E_c ...(6)

+a₃ +a4 ij

Sij Sij Sij

Pmax ?(i,j) ? E_c ...(5)

Pmin

??

????

??

? ???

a1 + a2

Pj = 1 ?(i,j) ? E_c ...(4)

hij =

Pj _!m !

286,76

hij = mG T1.g - 1 ?(i,j) ? E_c

Pi

hij.wij = H^L.wij (i,j) ? E_c ...(7)

hij.wij = H^U.wij (i,j) ? E_c ...(8)

qij.n(i,j) = Q.w(i,j) ?(i,j) ? E_c ...(9)

! _!2 _!3

qij qij qij

b1 +b2 +b3 +b4 = 1 ?(i,j) ? E_c ...(10)

Sij Sij Sij

Sij.wij = Smin.wij (i,j) ? E_c ...(11)

Sij.wij = Smax.wij (i,j) ? E_c ...(12)

qij qmin ?(i,j) ? E_c ...(13)

wij = .wij

Sij Smin

qij qmax

.wij = .wij ?(i,j) ? E_c ...(14)

Sij Smax

qij.wij = qmin.wij ?(i,j) ? E_c ...(15)

qij.wij = qmax.wij ?(i,j) ? E_c ...(16)

Pi = 0 ?i ? I ...(17)

nij ? {0,1,2,3} ?(i,j) ? E_c ...(18)

qij = 0 ?(i,j) ? E_c ...(19)

hij = 0 ?(i,j) ? E_c ...(20)

Sij = 0 ?(i,j) ? E_c ...(21)

wij ? {0,1} ?(i,j) ? E_c ...(22)

57

3.7. FORMULATION MATHÉMATIQUE DU PROBLÈME

3.7.6 Evaluation du modèle

a- Nombre de variables

· |I| = 12 , alors nous avons :

- 12 variables de type Pi.

· |E_c| = 5, alors nous avons :

- 5 variables de type qij.

- 5 variables de type Sij.

- 5 variables de type hij.

- 5 variables de type nij.

- 5 variables de type wij.

Donc le nombre de variables est :12 + 5 + 5 + 5 + 5 + 5 = 37.

b- Nombre de contraintes

· |E_p| = 6 alors nous avons :

- 6 contraintes de type (1)

· |I| = 12, alors nous avons :

- 12 contraintes de type (2).

- 12 contraintes de type (11).

· |E_c| = 5 alors nous avons :

- 5 contraintes de type (3).

- 5 contraintes de type (4).

- 5 contraintes de type (5).

- 5 contraintes de type (6).

- 5 contraintes de type (7).

- 5 contraintes de type (8).

- 5 contraintes de type (9).

- 5 contraintes de type (10).

- 5 contraintes de type (12).

- 5 contraintes de type (13).

- 5 contraintes de type (14).

- 5 contraintes de type (15).

58

3.7. FORMULATION MATHÉMATIQUE DU PROBLÈME

- 5 contraintes de type (16).

Donc le nombre des contraintes est :6 + (2 * 12) + (13 * 5) = 95.

L'analyse du modèle mathématique du problème posé montre qu'on est en présence d'un problème non linéaire mixtes en nombre entiers MINLP (Mixed-Integer NonLineaire Programming), en fonction d'une variable bivalente (wij), une variable entière ( _nij) et des variables continues Pi, qij^, sij ^et hij.

Notre problème appartient à la famille des problèmes appelés "Gaz Pipeline Fuel Consumption Minimisation Problem (GPFCMP)". Dans ce qui suit, nous présenterons une petite bibliographie concernant les travaux réalisés liés au problème (GPFCMP).

59

3.8. L'ÉTAT DE L'ART

3.8 L'état de l'art

3.8.1 Introduction

Dans le monde technologique dans lequel nous vivons, la croissance de la demande des hydrocarbures en général et le gaz naturel en particulier, a créé une pression sur nombreuses entreprises. Ces dernières doivent résoudre des problèmes d'optimisation concernant le transport de gaz par canalisation. C'est ce besoin d'optimisation dans ce secteur très concurrentiel qui a enrichi la recherche en problème de "Gaz Pipeline Fuel Consumption Minimisation Problem (GPFCMP)".

3.8.2 Les différentes approches de modélisation et de résolution de "Gaz Pipeline Fuel Consumption Minimisation Problem (GPFCMP)"

Plusieurs points de vue ont été utilisés pour aborder ce problème, qui possède plusieurs invariants selon les hypothèses de modélisation et les décisions à prendre. Une de ces hypothèses réalisées dans beaucoup de travaux est que le nombre de compresseurs qui fonctionnent au sein de chaque station de compression est fixé et le débit qui passe par les tronçons et les stations de compression est considéré comme une variable, où la plupart des approches proposées ont été basées sur des technique de la programmation dynamique, citons les travaux de Wong et al. [12] et Carter [1] qui ont travaillé sur un algorithme de programmation dynamique lorsque le débit est fixé.

Pecell et al [8]. ont traité le problème tout en utilisant le gradient réduit généralisée (GRG) pour l'optimisation non linéaire. D'autre part, Wu et al [15]. ont proposé un modèle mathématique pour la minimisation du coût de carburant sur une seule station de compression.

60

3.8. L'ÉTAT DE L'ART

Le premier ouvrage qui prend en considération le nombre d'unités de compression comme une variable est celui de Wu et al [15], ils ont d'abord déterminé au premier lieu la quantité d'écoulement à travers la station de compression, puis, à une deuxième étape, de déterminer le nombre d'unité qu'il faut mettre en fonction pour ce flux particulier.

Ensuite en 2003, Zaleta a étudié ce problème sur une ligne [5] qui comporte une seule station de compression qui possède dix unités de compression (Voir la figure 3.7).

FIGURE 3.7 - Schéma de la ligne

Le débit qui passe par les tronçons et la station de compression est considéré comme une variable de décision, Zaleta prend en considération les contraintes relatives à la plage de fonctionnement des compresseurs et la contrainte concernant le débit qui passe par les deux tronçons (3,4) et (3,5) où leur somme est égale au débit au noeud 3. Pour la résolution elle utilise une démarche déterministe, où elle fait l'implémentation à l'aide de logiciel de modélisation GAMS (Algebraic modeling language ou AML). Il faut souligner que lorsque l'instance du problème augmente le solveur ne peut pas résoudre le problème.

Chebouba et al. proposent dans [3] un algorithme basé sur la technique de la programmation dynamique en première partie, et dans une deuxième partie un programme qui fait le choix automatique des compresseurs à utiliser.

61

3.8. L'ÉTAT DE L'ART

Les métaheuristiques n'étaient pas largement utilisées pour résoudre "Gaz Pipeline Fuel Consumption Minimisation Problem (GPFCMP)" :

- Les algorithmes génétiques ont été utilisés pour la première fois, en 1985 par Goldberg, où les contraintes concernant la plage de fonctionnement des compresseurs sont prise en considération.

- Chebouba et Smati [4] ont appliqué pour la première fois les algorithmes de colonies de fourmis pour la résolution de ce problème.

En 2011, et pour la première fois Rodriguez et al. [6] formulent le problème de façon multi-objectif en maximisant la quantité transportée et en minimisant la consommation des compresseurs.

Il est à noter qu'il existe d'autres travaux qui traitent ce problème mais il s'avère que ces recherches ont été si spécifiques où il est question de modéliser un problème de flux dans un réseau non linéaire. La plupart de ces travaux ne prennent pas en considérations toutes les contraintes du problème.

62

Chapitre 4

Méthode de résolution

4.1 Introduction

A l'heure actuelle, il est généralement admis de considérer la résolution de problèmes comme un processus complexe de modélisation mathématique. Ce processus complexe peut se traduire par la mise en oeuvre d'une démarche de résolution impliquant plusieurs phases. Résoudre des problèmes après la formulation mathématique nécessite un questionnement sur la nature du modèle. Ceci consiste à comprendre l'énoncé et à construire une modélisation, puis mettre en oeuvre des stratégies et des procédures de résolution. Ces phases sont indissociables, la démarche considérée pour analyser et résoudre un système est illustrée dans le schéma suivant:

FIGURE 4.1 - Le processus de l'analyse du système

63

4.2. LA PROGRAMMATION NON LINÉAIRE MIXTE EN NOMBRES ENTIERS

4.2 La programmation non linéaire mixte en nombres entiers

Les problèmes d'optimisation sont classés en grandes catégories, linéaire(LP), non li-néaire(NLP), programmation linéaire mixte en nombres entiers (MILP), en fonction de leurs caractéristiques mathématiques. La formulation la plus complexe, rencontrée fréquemment à l'ingénierie, relève des problèmes non linéaires mixte en nombres entiers « Mixed Integer Non Lineair Programming».

4.2.1 Qu'est ce qu'un programme MINLP?

Un programme non linéaire mixte en nombres entiers MINLP est un problème d'op-timisation consiste à minimiser une fonction objectif non linéaire à n variables mixtes, discrètes et continues soumises à un ensemble de contraintes non linéaire exprimées sous forme d'équations ou d'inéquations.

La formulation générale d'un problème MINLP est donnée par:

? ? ???????????????

???

???????????????????

Où

Min f (x,y) S.C :

h(x,y) = 0 g(x,y) 0

x ? X

y ? Y entier

- f (x,y) : fonction objectif.

- h(x,y) : Ensemble des contraintes égalité.

- g(x,y) : Ensemble des contraintes inégalité.

- X : Ensemble des variables continues.

- Y : Ensemble des variables entières.

64

4.2. LA PROGRAMMATION NON LINÉAIRE MIXTE EN NOMBRES ENTIERS

La variable x correspond généralement aux variables physiques (débit, pression, température, etc). Et la variable y correspond aux variables qui traduisent l'existence ou non d'une opération unitaire, le nombre d'unités d'une entité, etc.

4.2.2 Technique de résolution

La programmation non linéaire mixte en nombre entier combine la difficulté de l'opti-misation combinatoire sur des ensembles de variables entières avec la difficulté de la manipulation d'une fonction objectif non linéaire et des contraintes non linéaires. L'exécution des méthodes dites exactes (programmation dynamique, séparation et évaluation) pour la résolution de ce problème risque de prendre un temps de calcul considérable.

Afin d'éviter ce genre de situation, on se contente souvent d'une solution dite approchée données par certaines méthodes appelées « méthodes approchées» et dont la valeure de la fonction objectif correspondante se rapproche de celle de la solution exacte.

Vu qu'on est en présence d'un problème non linéaire en variables mixtes assez complexe, nous proposons d'utiliser une heuristique pour obtenir une solution réalisable et de l'amé-liorer avec deux métaheuristiques : Algorithme génétique et recuit simulé.

65

4.3. LES MÉTHODES APPROCHÉES

4.3 Les méthodes approchées

Face au caractère intraitable de certains problèmes d'optimisation combinatoire, où la solution optimale de ces problèmes est souvent hors d'atteinte en raison de l'explosion combinatoire de leur espace de recherche et vu la nécessité de fournir des solutions de "bonne" qualité en un temps "raisonnable", les heuristiques [9] deviennent l'unique moyen d'obtenir une bonne solution en un temps raisonnable.

4.3.1 Les heuristiques classiques

Heuristique « dérivée de mot grec heuriskêin, trouver » est un terme de didactique qui signifie l'art d'inventer, de faire des découvertes.

Une heuristique est une méthode spécifique développée pour résoudre un problème donnée, elle lui est intimement liée et conçue pour prendre en charge les caractéristiques de celui-ci et couvrir les propriétés de ses différentes instances. Ces méthodes sont généralement basées sur un raisonnement logique ou intuitif et se doivent d'être simples, rapide et bien sûr de fournir des solutions de bonne qualité. La difficulté majeur est toutefois de déterminer une garantie de performance d'une heuristique, aussi pour un même problème, il existe souvent plusieurs heuristiques et selon l'instance traitée, leurs performances peuvent varier, donc il est impossible de dire qu'une heuristique est meilleure qu'une autre.

Les heuristiques peuvent être classées en deux catégories :

· Les heuristiques de construction: sont des méthodes approchées qui démarrent d'une entité élémentaire quelconque et construisent de proche en proche une solution réalisable, par exemple la méthode de plus proche voisin pour le problème PVC.

· Les heuristiques d'amélioration : sont des méthodes approchées qui démarrent d'une solution réalisable (probablement moins intéressante), et l'améliorent de proche en proche. Par exemple, on trouve la méthode 2-opt (PVC).

66

4.3. LES MÉTHODES APPROCHÉES

On retrouve en général des principes de base utilisés dans ces heuristiques tels que :

- Principe glouton: ce principe repose sur le choix définitif des valeurs de la solution, ce qui interdit toute modification ultérieure. Autrement dit d'après Sakarovitch [9] « Il consiste à "manger" les élément de la solution dans un certain ordre sans jamais remettre en question un choix une fois qu'il est effectué ».

- Principe de construction progressive : c'est une extension du principe glouton dans la mesure où l'on s'autorise, cette fois-ci, à modifier des valeurs déjà assignées. On retrouve par exemple l'algorithme de Ford pour la recherche des chemins optimaux.

- Principe de partitionnement : ce principe repose sur le fait que résoudre le problème global se révèle souvent plus complexe que résoudre la somme des sous problèmes qui le composent. Toute la difficulté réside alors dans le fusionnement des solutions de chaque sous problème. On retrouve par exemple l'algorithme de Dichotomie.

67

4.3. LES MÉTHODES APPROCHÉES

4.3.2 Les métaheuristiques

Depuis environ, une quarantaine d'années, sont apparues des approches de résolution plus générale, qui peuvent donc, moyennant la fixation de certaines paramètres et quelques adaptations, s'appliquent à une large classe de problèmes d'optimisation, ces méthodes sont dites heuristiques de haut niveau ou métaheuristiques (dérivées de la composition de deux mots grecs : « heuriskien » qui signifie trouver, et « Méta » qui signifie dans un niveau supérieur).

La polyvalence, l'efficacité concrète et la relative simplicité des métaheuristiques, leur ont conféré une popularité et une extension remarquables durant ces 25 dernières années. Leur efficacité dépend néanmoins du soin apporté à la fixation des paramètres et à l'adap-tation du problème traité, leur principe et parfois inspiré d'observations réalisées dans des domaines totalement différents que celui de l'optimisation sous contraintes, c'est le cas pour les métaheuristiques de type « recuit simulé », « algorithme génétique » et « algorithme de colonies de fourmis ».

Les métaheuristiques sont des méthodes dites stochastiques, fondées sur des règles d'évo-lution probabilistes, contrairement aux méthodes déterministes qui s'appuient sur les propriétés mathématiques. On désigne deux stratégies de recherche des métaheuristiques :

L'intensification ou exploitation: on entend l'exploitation de l'information rassemblée par le système à un moment donné. C'est ce qui permet l'amélioration de la valeur d'une solution trouvée dans un certain voisinage, i.e, permet d'examiner en profondeur une zone particulier de l'espace de recherche.

La diversification ou exploration: on entend au contraire, l'exploration de l'espace de recherche encore inconnu. Elle est généralement obtenue par des processus stochastiques.i.e., permet d'orienter la recherche vers des nouvelles zones (autorisés) dans l'espace de recherche.

68

4.4. LE RECUIT SIMULÉ

Les métaheuristiques peuvent être classées de nombreuses façons. On peut cependant distinguer:

Les métaheuristiques à parcours

Les métaheuristiques les plus classiques sont celles fondées sur la notion de parcours. Ces algorithmes partent d'une solution initiale (obtenue par une méthode de résolution, ou par tirage aléatoire) et construisent une trajectoire dans l'espace des solutions en tentant de se diriger vers des meilleurs solutions. La méthode du recuit simulé (SA), recherche tabou (TS) et recherche à voisinage variables (VNS) sont des exemples typiques de ce type de métaheuristiques.

Les métaheuristiques à populations

Ces méthodes utilisent la notion de population: elles manipulent un ensemble de solutions en parallèle. Chaque élément de population parcourt un certain nombre de solutions dans l'ensemble local. Les algorithmes génétiques et Les algorithmes de colonies de fourmis présentent les exemples les plus connus des méthodes qui travaillent avec une population.

Dans ce qui suit, nous détaillerons la méthode recuit simulé et celle des algorithmes génétiques.

4.4 Le recuit simulé (Simulated Annealing)

4.4.1 Présentation

Comme son nom l'indique, cette métaheuristique RS simule une opération de "recuit" qui est courante, notamment en sidérurgie. De quoi s'agit-il? Un matériel, qui par exemple a subi des déformations, est chauffé afin de lui fournir un haut degré d'énergie susceptible de faire disparaitre. Puis le matériel est refroidi très lentement, afin qu'il puisse retrouver progressivement un équilibre, c'est-à-dire un état stable correspondant à un niveau minimum d'énergie. L'analogie est faite entre le niveau d'énergie et la valeur de la fonction à minimiser. Aussi, la simulation nécessitera d'introduire dans la méthode RS, un paramètre

69

4.4. LE RECUIT SIMULÉ

è appelé température.[13]

4.4.2 L'analogie entre le recuit physique et le recuit simulé

On résume dans le tableau suivant l'analogie qui se trouve entre les termes employés en recuit physique et ceux employés en recuit simulé :

Problème d'optimisation	Système physique.
fonction objectif de coût/objectif f(x)	énergie libre E(x).
variable de problème	"Cordonnées"des atomes.
trouver une bonne configuration	trouver un état de basse énergie.

TABLE 4.1 - Analogies recuit physique / recuit simulé

4.4.3 Paramètres opérationnelles

La fixation des paramètres

Déterminer la valeur la plus appropriée des paramètres est certainement l'aspect le plus délicat de l'implémentation du recuit simulé, qui sont choisi en fonction du problème considéré et de l'instance traitée.

a) La température initiale

Elle doit être élevée pour accepter suffisamment et facilement une solution moins bonne que la solution courante, donc tous les voisins de la solution courante ont la même probabilité d'être acceptés.

b) Le coefficient de refroidissement

Le paramètre á est à choisir avec précaution. En effet, s'il est choisi trop grand, la température baissera très rapidement et l'algorithme pourra être bloqué dans un minima local, si au contraire il est choisi trop petit, la température baissera très lentement et le temps de calcul sera très grand.

70

4.4. LE RECUIT SIMULÉ

c) Le nombre d'itérations à chaque palier de température

Un paramètre borne le nombre d'essais (itérations) par palier. A la fin d'un palier, le compteur est incrémenté si le pourcentage d'acceptation est inférieur à un seuil, remis à zéro si la qualité de la meilleure solution a évolué au cours du palier.

d) Critère d'arrêt

Tout au long du processus la température sera diminuée, il faudra donc déterminer une température finaleof telle que la procédure du recuit simulé se termine lorsque la température courante atteint la température finale.

4.4.4 Principe de RS :

Le principe du recuit simulé est de parcourir de manière itérative l'espace des solutions, on part d'une solution notée x initialement générée d'une manière aléatoire ( ou trouvée à l'aide d'une autre méthode approchée) qui correspond à une énergie initiale Z(x) et une température initiale o⁰, généralement élevée.

-AZ

o .

À chaque itération de l'algorithme un changement s'effectue sur la solution. Cette solution x^' fait varier l'énergie du système, AZ = Z(x^') - Z(x) si cette variation est négative ( la nouvelle solution améliore la fonction objectif) et permet de diminuer l'énergie du système, elle est acceptée. Si la solution trouvée est moins bonne que la précédente alors elle sera acceptée avec une probabilité calculée suivant y = e

En fonction du critère de Métropolis, un nombre p E [0,1] est comparé à la probabilité

y = e

-AZ o . Si y ~ p la nouvelle solution est acceptée.

Le fonctionnement de critère de Métropolis est interprété par:

- Si AZ = Z(x^') - Z(x) < 0, alors e-AZ

o > 1, donc p est toujours inférieure à cette valeur est

'

on accepte la solution x.

-AZ

- Si AZ > 0, alors eo ' 1, tout voisin est systématiquement acceptée.

- Si AZ > 0 et o <<<, alors e

-AZ o 0, une dégradation à peu de chance d'être accepté.

71

4.4. LE RECUIT SIMULÉ

4.4.5 Algorithme général du Recuit simulé

Algorithm 1 Recuit Simulé

ENTRéES: x := x⁰ ; Z = Z(x); xop := x ; Z(x_op); è := è⁰ ; n_r ; èf ; á

Début

tantque è > èf faire

tantque nb ~ n_r faire

x' := ô(x) ;

Z(x');

ÄZ = Z(x')-Z(x);

si ÄZ < 0 alors

x := x' ;

Z(x) := Z(x');

si Z(x') < Z(x_op) alors

xop := x' ;

Z(x_op) := Z(x'); finsi

sinon p E [0,1];

-ÄZ

y := eè ;

si p ~ y alors

x := x' ;

Z(x) := Z(x');

finsi

finsi

nb := nb +1;

fin tantque

è := á.è ;

fin tantque

Fin

72

4.5. LES ALGORITHMES GÉNÉTIQUES

4.5 Les algorithmes génétiques

Les algorithmes génétiques sont des algorithmes d'optimisation s'appuyant sur des techniques dérivées de la génétique et des mécanismes d'évolution de la nature : croisements, mutations, sélections, etc. Ils appartiennent á la classe des algorithmes évolutionnaires.

4.5.1 Présentation

Dans la nature, les êtres vivants croisent et interagissent les uns avec les autres. Chaque individu est caractérisé par un génotype indépendant de l'environnement où il vit. Les opérateurs génétiques fonctionnent au niveau génotypique tandis que le mécanisme de sélection opère au niveau phénotypique (le phénotype d'un individu est l'ensemble des traits caractéristiques d'un individu, alors que le génotype est le codage de ces traits en gènes). Les algorithmes génétiques sont à la base des algorithmes d'optimisation stochastiques, mais peuvent également servir pour l'apprentissage automatique, par exemple. Les principes fondamentaux des algorithmes génétiques dans le cadre de l'optimisation mathématique ont été développés entre 1960 et 1970 par John Holland. [13]

4.5.2 L'analogie entre la génétique biologique et algorithme génétiques

On résume dans le tableau suivant l'analogie qui se trouve entre les termes employés en génétique biologique et ceux employés pour les algorithmes génétiques:

Problème d'optimisation	Système biologique.
Ensemble des points de l'espace de recherche	Génotype.
Ensemble particulier de points de l'espace de recherche	Population.
Un point particulier de l'espace de recherche	Individu.
Ensemble de variables caractérisant un point de l'espace	Chromosome.
Une variable	Gène.
Valeur possible de la variable	Allèle.

TABLE 4.2 - Analogie génétique biologique/algorithme génétiques

73

4.5. LES ALGORITHMES GÉNÉTIQUES

4.5.3 Le principe d'un algorithme génétique

A. Initialisation

A.1. Codage des données

Le codage est une partie très importante des algorithmes génétiques, il permet de représenter une solution x du problème d'optimisation par une séquence (string) de caractères, cette séquence sera appelée individu, elle constitue l'ensemble des gènes du chromosome. Plusieurs codages sont employés. Voici quelques exemples. [13]

· Le codage binaire : représente une solution par une suite de variables binaires.

· Le codage par permutations de valeurs entières : le gène est codé par une valeur entière dans un ensemble de cardinalité égale au nombre de gènes.

A.2. Fonction fitness d'un individu

A un individu donné est associée une fonction fitness (forme physique), elle mesure la performance de cet individu et a pour but d'évaluer si un individu est mieux adapté qu'un autre à son environnement. Elle est évidemment étroitement liée avec la fonction objectif du problème d'optimisation. [13]

A.3. Population initiale

Différents individus sont considérés, souvent générés aléatoirement afin d'assurer une population diversifiée. La population initiale est ainsi constituée d'un ensemble d'individus {1,...,N} et le paramètre n est appelé taille de la population.

La taille N d'une population est un paramètre important d'un algorithme génétique. Elle doit être fixée en tenant compte de la longueur d'un individu, une taille grande favorise une meilleur diversification mais au prix d'un plus grand temps de calcul pour une itération. [13]

74

4.5. LES ALGORITHMES GÉNÉTIQUES

B. Itération d'un algorithme génétique

Sur base de la population courante, diverses opérateurs vont être appliqués successivement à des sous-ensembles d'individus, appelés des parents, pour générer de nouveau individus appelés enfants.

B.1. Opérateur de sélection

Il s'agit des pairs d'individus qui sont sélectionnées au sein de la population courante, une telle paire sera noté P1 et P2. Il convient donc de définir un mécanisme de sélection de paires de parents. Cet opérateur de sélection est généralement aléatoire mais doit néanmoins d'autant plus favoriser la sélection d'un individu que sa fonction fitness est meilleure. [13] Plusieurs méthodes existent et sont, généralement, basées sur la théorie de Darwin. Nous présenterons les deux plus connues:

· La roulette (roulette Wheel sélection) : [13] Cette méthode exploite la métaphore d'une roulette de casino. La roue est divisée en autant de secteurs que d'individus dans la population. La taille de ces secteurs est proportionnelle à l'adaptation de chaque individu (une probabilité pi). Un nombre aléatoire r E [0,1] désigne alors l'individu i* sélectionné par la formule :

? ? ???

????

0 < r < Pi*

i=1 pi, si i^* = 1.

_Pi^*-1

i=1 pi < r < Pi*

i=1pi, si non.

75

4.5. LES ALGORITHMES GÉNÉTIQUES

FIGURE 4.2 - Sélection par roulette

· Sélection par tournoi(tournatment selection) : [13] Plusieurs individus (classiquement deux) sont d'abord choisis totalement aléatoirement dans la population. Ils se confrontent alors sur base de leur valeur fitness et le meilleur est sélectionné.

FIGURE 4.3 - Sélection par tournoi (entre deux individus)

B.2. Opérateur de croisement

Un opérateur de croisement (crossover) consiste à créer de nouveaux individus -des enfants- en échangeant des caractères -des gènes- entre les deux parents. La zone de croisement est généralement choisie aléatoirement dans les chromosomes. Toutefois l'opérateur

4.5. LES ALGORITHMES GÉNÉTIQUES

de croisement n'est pas systématiquement appliqué à chaque paire de parents, mais avec une probabilité de croisement p_c (classiquement = 0.9, nous suivrons ici aussi le schéma classique où deux enfants (notés E1 et E2) sont créés par le croisement. [13]

76

FIGURE 4.4 - Croisement en un point

B.3. Opérateur de mutation

Pour des raisons de diversification, il est bon de temps en temps de modifier très légèrement un enfant créé. C'est le rôle de l'opérateur de mutation qui est appliqué à un enfant avec une petite probabilité p_m (classiquement= 0.01). [13]

FIGURE 4.5 - La mutation

C. Critère d'arrêt

Les critères les plus utilisés sont les suivants :

· Arrêt de l'algorithme après un certain nombre de générations, fixé au départ; c'est ce que l'on est tenté de faire lorsque l'on doit trouver une solution dans un temps limité.

· L'algorithme peut être arrêté lorsque la population n'évolue plus ou plus suffisamment rapidement, c.-à-d. les meilleurs individus ne s'améliorent plus depuis un certain nombre de générations. [13]

77

4.5. LES ALGORITHMES GÉNÉTIQUES

Paramètres internes de l'algorithme génétique

Les algorithmes génétiques possèdent des paramètres internes qui doivent être choisis avec les considérations suivantes :

· Taille de la population N : Elle doit être judicieusement choisie en fonction de la taille du problème.

· Probabilité de croisement : Plus le taux de croisement est élevé, plus il y aura de nouvelles structures qui apparaissent dans la population.

· Probabilité de mutation: la probabilité de mutation est généralement inférieur à 0.01, mais il n'est pas rare de voir dans d'autres applications un taux plus important, par exemple dans les problèmes d'ordonnancement.

4.6. SCHÉMA DES MÉTHODES APPROCHÉES

4.6 Schéma des méthodes approchées

4.7 Démarches Hybrides

Cette méthodologie combine différentes approches, elle permet d'amplifier les avantages de ces méthodes et d'autre part réduire les limites. Les algorithmes hybrides peuvent être classés en deux catégories :

1- Bas niveau d'hybridation: Ce type d'hybridation consiste à intégrer une méthode de résolution (méthode 2) dans une autre méthode (méthode 1) (Voir figure 4.6 ).

Par exemple on peut intégrer l'heuristique 2-OPT (méthode 2) dans le Récuit simulé (méthode 1) comme une transformation admissible.

78

FIGURE 4.6 - Schéma d'hybride de bas niveau

79

4.7. DÉMARCHES HYBRIDES

2- Haut niveau d'hybride (pipeline) : Ce type d'hybridation consiste à trouver une solution par une méthode, ensuite l'améliorer par une autre méthode ( Voir figure 4.6 ). Par exemple:

on peut utiliser une Recherche Locale dans les méthodes évolutives. L'avantage est que la Recherche Locale réduit le danger de passer à côté d'une solution optimale sans la voir. En règle générale, une méthode évolutive est excellente pour détecter de bonnes régions dans l'espace de recherche alors qu'une Recherche Locale explore efficacement les régions prometteuses, donc on peut utiliser l'algorithme génétique en première étape, ensuite en appliquant le Récuit simulé en démarrant de la solution trouvée par l'algorithme génétique.

FIGURE 4.7 - Schéma d'hybride de Haut niveau

80

Chapitre 5

Résolution du problème

5.1 Adaptation d'une heuristique au problème

Pour la résolution de notre problème, nous présentons une heuristique de type amélioration basée sur le principe de construction progressive. Cette heuristique se fera en deux étapes, une première pour l'initialisation, en démarrant d'une solution initial aléatoire réalisable, et une deuxième pour l'amélioration de la solution.

5.1.1 Principe de l'heuristique

1. Étape Initialisation:

1.1 Initialiser toutes les stations en marche.

1.2 Pour chaque station i générer aléatoirement:

a. Le nombre de compresseurs en marche entre (1, 3) tout en respectant le débit maximal rentrant à un compresseur _(qmax =530 000 m³/h).

b. Les vitesses de rotation des turbocompresseurs en marche comprises entre

(Smin = 3 250 et Smax = 6 825 ) tout en respectant les contraintes concernent la hauteur adiabatique _Had et le rendement adiabatique ç.

2. Étape Amélioration:

2.1 Pour chaque pression d'aspiration d'une station de compression i calculer sa valeur en supposant que la station de compression i -1 n'est pas en marche on aura deux cas: a.1 (Si Paspi = 45 bars ) alors la station i - 1 reste en marche.

81

5.1. ADAPTATION D'UNE HEURISTIQUE AU PROBLÈME

a.2. (Si Paspi > 45 bars ) alors changer l'état de la station i - 1 de 1 à 0. 5.1.2 Procédure de l'heuristique

82

5.1. ADAPTATION D'UNE HEURISTIQUE AU PROBLÈME

Procédure Heuristique NSCM ( E : Q : entier; a1, a2, a3, a4, b1, b2, b3, b4, T1, g, G, m : réel; S :w,n,q,s,H,e_ta,Pasp,Pref :vecteur)

Début

//Initialisation

Pour i := 1 à 5 faire w[i] := 1;

Q

l[i] := 24.530000 ; // Pour respecter les contraintes du débit max

n[i] := random(l,3);

Q

q[i] := n[i].24 ;

S[i] := random(3250,6825);

H[i] :=

? q[i] ! q[i] !2 ??q[i] !^3??????.S[i]^2; ???a1 + a2. + a3. + a4 S[i] S[i] S[i]

? q[i] ! q[i] !2

?!3?????? ; eta[i] := ???q[i]

_?b1 + b2. + b3. + b4

S[i] S[i] S[i]

Si ( (eta[i] < 0) ou (eta[i] > 1) ou ((H[i] < 9 092) ou (H[i] > 4 579) ) alors

Répéter S[i] := random(3 250, 6 825);

? q[i] ! _!2

? q[i]

H[i] := _????!^3???_???.S[i]² ;

q[i]

a1 + a2. + a3. + a4

S[i] S[i] S[i]

? q[i] !

? q[i] !2 !3??????
eta[i] := ????q[i]

b1 + b2. + b3. + b4

S[i] S[i] S[i]

jusqu'à ( ( eta[i] > 0) et ( eta[i] < 1) et ( H[i] > 4 5769) et (H[i] < 9 092) )

Fait;

5.1. ADAPTATION D'UNE HEURISTIQUE AU PROBLÈME

0.5

;

?

??????????????

?

???????????

? ??

Pasp[i] :=

2

(Pref [i - 1])² - r[i].₅!

_ese[i]

?

???????????

?

????????

? ??

m

.Pasp[i -1]

H[i -1]

~286,76.g.T1 ~ + 1

G.m

Sinon _Pref [i -1] :=

0.5

?

??????????????

?

???????????

? ??

Pasp[i] :=

(Pref [i - 1])² - r[i].Q2! D5

_ese[i]

H[i] !

n[i].q[i].ñ. 1000

eta[i].ç_mc.çT R.P CI

Sinon f [i] =

Fsi

Z := Z +f [i]

Fait

Fin.

//Amélioration

pour i := 2 à 5 faire

~ ~

Si Pasp[i] > 45 alors

w[i -1] := 0;S[i -1] := 0;n[i -1] := 0;H[i -1] := 0;eta[i -1] := 0; Pref [i -1] := Pasp[i -1]

1

Fsi

Fait;

Z := 0;

pour i := 1 à 5 faire

Si (w[i] = 0) alors f [i] := 0

83

5.1. ADAPTATION D'UNE HEURISTIQUE AU PROBLÈME

5.1.3 Organigramme de l'heuristique

Smin^, Smax^, max
a1, a2, a₃, 0₄
b1, b₂, b₃, b4

G

f ( sne) 1 Ft_if.

P + 1
(2876 X X T₁ x 1 y

x P_r, _p,

9(Pr.f,) --

2 (p,.1) -- rt X Q^2/D^5 eSe!

*

1. WJ:=1

2. l .-- Q
RmasX²⁴

3. n_tf := Tandom(l, 3)

4. ^ckJ 24Xn

S -- random(3250,6825)

l f }}2 ((( 7)ll3

H_Qd: ai+a2( ) ^+Q, () +a₄ xS^z_ï

(9~p} Ry}}^z /4e1}^a

n:=b1+b2(Sl+b1( ) ^+b4(7)

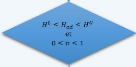
Non

k := k + 1

Oui

S_il := := Had

l

k := k + 1

Non

i := 1

w,1 := 0, nig := 0, [h_i := 0, S, := 0, h,₁ := 0

Pref^. i a p;, asp,+, := 9 (Prefi)

Oui

I			Prep; asp; ^Pa-sp,f, · tf (Prefi~

> 45 bars

^--"¹¹¹¹1.1¹P^-₁

^r Non

Oui

I-

i:=i+1

Pref; := f(asp,) ^P ni+1 := A(P ®fi)

i:=i+1

**

Solution X,

P,₁,11, ,,H, eta: vecteur

Non

Qui

84

r11111111.⁴ **

85

5.2. ADAPTATION DES ALGORITHMES GÉNÉTIQUES AU PROBLÈME

5.2 Adaptation des algorithmes génétiques au problème

5.2.1 Codage des données

Nous définissons le chromosome comme étant un vecteur V de taille 15, composé de trois parties :

- Partie une : Un vecteur de taille 5 de composante bivalentes ( 1 si la station de compression est en marche, 0 sinon).

- Partie deux: Un vecteur de taille 5 de composantes entières( le nombre de turbocompresseurs en marche dans la station de compression correspondante).

- Partie trois : Un vecteur de taille 5 de composantes entières( les vitesses de rotation des turbocompresseurs dans les stations de compression).

La structure d'un individu est présentée dans la figure ci-dessous.

FIGURE 5.1 - La structure d'un individu.

5.2.2 Population initiale

On génère n solutions réalisables du problème, obtenues par l'heuristique NSCM, qui constituera une population initiale pour l'algorithme génétique.

Vu que les constantes n'influencent pas sur la solution, on va pas les considérer dans l'éva-luation des individus, ce qu'on appelle fitness.

86

5.2. ADAPTATION DES ALGORITHMES GÉNÉTIQUES AU PROBLÈME

5.2.3 Évaluation

Procédure Évaluation ( E : nT C, S, q, H, Eta: matrice; S : f : matrice, Z : vecteur)

Début

Pour i := 1 à n faire

Y := 0

Pour j := 1 à 5 faire

f (i,j] :=

H [i,j] ! Q · 1000 24·Eta[i,j] ;

Y := Y +f [i,j];

Fait;

Z [i] := Y ;

Fait;

Fin.

5.2.4 Sélection

La sélection des individu pour la reproduction se fait par la sélection de deux individus aléatoirement. Pour chaque paire d'individus tirées aléatoirement on compare et on sélectionne le meilleur, ce qui produit deux parents P1 et P2. L'étape sélection est décrite dans la partie (1) de la procédure croisement.

5.2.5 Croisement

Dans notre cas, nous avons utilisé le croisement en un point. Pour effectuer ce type de croisement sur des chromosomes, on tire aléatoirement une position de croisement dans chacun des parents. On échange ensuite les deux chaînes terminales de chacun des deux chromosomes, ce qui produit deux enfants E1 et E2. Pour ce qui est du probabilité de croisement nous avons choisi P_c = 0.9.

87

5.2. ADAPTATION DES ALGORITHMES GÉNÉTIQUES AU PROBLÈME

Procédure Croisement ( E : P1, P2 : vecteur; S : P 1, P 2, E1, E2, H1, H2, q1, q2, Eta1, Eta2 : vecteur)

Début

Pour i := 1 à n faire /* Partie(1)*/

t := random(n);

u := random(n);

minimum :=min (Z [t],Z [u]);

Si (minimum=Z [t]) alors indice1 :=t Sinon indice1 :=u;

v := random(n);

w := random(n);

minimum :=min(Z [v],Z [w]);

Si (minimum=Z [v]) alors indice2 :=v

Si non indice2 :=w;

Pour k := 1 à 15 faire

P 1[k] := B[k,indice1];

P 2[k] := B[k,indice2];

Fait;

/* Partie(2)*/

r := random[0,1]; Si (r < p_c) alors

s := random(5);

Pour k := 1 à s - 1 faire E1[k] := P 1[k] ;

E2[k] := P 2[k];

E1[k + 5] := P 1[k +5] ; E2[k +5] := P 2[k +5]; E1[k + 10] := P 1[k + 10] ; E2[k +10] := P 2[k +10]; Fait;

Pour k := s à 5 faire E1[k] := P 2[k];

E2[k] := P 1[k];

E1[k +5] := P 2[k +5]; E2[k +5] := P 1[k +5]; E1[k +10] := P 2[k +10]; E2[k + 10] := P 1[k + 10] ;

Fait;

Pour k := 1 à 5 faire

P [i,2k] :=

'Q2 ' (P [i,2k - 1])^2- R[K] · D5 ; se[k]

y

	? ??????????????			? ??????????? ? ??				P [i,2k +1] :=
		+1

Fait; Si non

- Garder les deux parents P1 et P2; Fsi;

Fait; Fin.

88

5.2. ADAPTATION DES ALGORITHMES GÉNÉTIQUES AU PROBLÈME

89

5.2. ADAPTATION DES ALGORITHMES GÉNÉTIQUES AU PROBLÈME

On aura le résultat suivant:

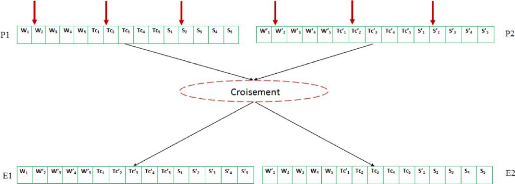
5.2.6 Mutation

On sélectionne un individu aléatoirement, selon la probabilité de mutation qui est égale à 0.002, un point (un gène) dans la troisième partie (vecteur des vitesses) sera choisi aléatoirement pour être changé.

La procédure de mutation est décrite ci dessous :

H [m,d] :=

?? 2 )3??????·

a1 +a2
·^q_[^m,d] +a_.^q[m,d]+a..^q[m,d] (B[m,á])² ;

B[m,á] ³ B[m,á] 4 B[m,á]

Procédure Mutation (E/S F : vecteur)

Début

Pour i := 1 à n faire

m := random(n) ; /* Soit l'individu F */

r := random[0,1];

Si (r < p_m) alors

á := random(10,15);

d := á -10;

Si (B[m,d] # 0) alors

B[m,á] := random(3250,6825);

q[m,d] ! _q[m,d] !2 _q[m,d] !3

Eta[m,d] := b1 +b2 · +b3 · +b4 · ;

B[m,á] B[m,á] B[m,á]

Si ((Eta[m,d] > 1)ou (Eta[m,d] < 0)) et ((H [m,d] > 45769.670)ou (H [m,d] < 9092.202)) alors Répéter

B[m,á] := random(3250,6825);

? 2 3

H [m,d] := a1 +a2 · q[m,d] +a3 · q[m,d] +a4 · q[m,d]

· (B[m,á])² ;

B[m,á] B[m,á] B[m,á]

q[m,d] ! _q[m,d] !2 _q[m,d] !3

Eta[m,d] := b1 +b2 · +b3 · +b4 · ;

B[m,á] B[m,á] B[m,á]

jusqu'à ((Eta[m,d] < 1)et (Eta[m,d] > 0)) et ((H [m,d] < 45769.670)et (H [m,d] > 9092.202))

Fsi; Fsi; Fsi; Fait ;

Fin.

90

5.2. ADAPTATION DES ALGORITHMES GÉNÉTIQUES AU PROBLÈME

91

5.3. HEURISTIQUE DE RÉPARATION

5.3 Heuristique de réparation

Après avoir utilisé et appliqué les procédures (croisement, mutation), l'admissibilité des individu n'est pas toujours assurée, pour cela nous proposons une heuristique de réparation pour rétablir l'admissibilité des individus qui a le même principe de l'heuristique NSCM décrite précédemment , cela ce fait de la manière suivante :

- Si la pression d'aspiration n'est pas vérifiée dans une station k ( inférieur à 45 bars) , nous proposons de revenir en arrière ( c'est à dire la station k-1) tout en vérifiant l'ajustement et le fonctionnement de cette station.

- En d'autre terme nous allons mettre en marche autant de stations afin de rétablir l'admis-sibilité des individu ayant perdu cette dernière.

92

5.3. HEURISTIQUE DE RÉPARATION

5.3.1 Organigramme de l'adaptation des AG au problème

93

5.4. ADAPTATION DU RECUIT SIMULÉ AU PROBLÈME

5.4 Adaptation du recuit simulé au problème

5.4.1 Initialisation

Cette étape consiste à déterminer une solution réalisable du problème, qui constituera une solution de départ pour l'algorithme du recuit simulé. l'initialisation est obtenue par l'heuristique NSCM (Nombre de Stations de Compression en Marche) décrite précédemment.

5.4.2 Paramètres opérationnelles

· O0 = 500.

· á = 0,5.

· n_r = 50.

· Of = 0,0006.

5.4.3 Voisinage

Pour définir une solution (X^',Z(X^')) a partir d'une solution (X,Z(X)), en considérant uniquement la partie 3 (le vecteur des vitesses), on génère aléatoirement une position entre 1 et 5, si la station correspondante à la position générée est en marche alors en génère aléatoirement (entre 3250 et 6825) une vitesse de rotation des compresseurs en marche dans cette station.

5.4.4 Principales étapes

(1). Choisir aléatoirement une position k entre 1 et 5 tel que la station k est en marche.

(2). Générer aléatoirement une vitesse de rotation S[k] entre _Smin ^et Smax.

(3). Si solution réalisable trouvée alors Fin, si non aller à (2).

5.4. ADAPTATION DU RECUIT SIMULÉ AU PROBLÈME

?

^???_??a1 + a2

H [k] :=

q[k] ! q[k] !2 q[k] !3?????? (S [k])² ;

+ a3 + a4

S [k] S [k] S [k]

Procédure Voisinage ( E : X : Vecteur, S : X^' : Vecteur)

Début

Pour k := random(1,5);

Si w[k] = 0 alors

Répéter

k := random(1,5);

Jusqu'à w [k] ~ 0;

Fsi;

S[k] := random(3250,6825);

? q[k] !

? q[k] !2 q[k]

H [k] := _????!^3????_?? (S [k])² ;

a1 + a2 + a3 + a4

S [k] S [k] S [k]

q[k] ! q[k] !2 q[k] !3

Eta[k] := b1 + b2 + b3 + b4 ;

S [k] S [k] S [k]

Si ((Eta[k] > 1)ou (Eta[k] < 0)) et ((H [k] > 45769.670)ou(H [k] < 9092.202)) alors Répéter

S[k] := random(3250,6825);

q[k] ! q[k] !2 q[k] !3

Eta[k] := b1 + b2 + b3 + b4 ;

S [k] S [k] S [k]

jusqu'à ((Eta[k] < 1)et (Eta[k] > 0)) et ((H [k] < 45769.670)et(H [k] > 9092.202))

Fsi; Fin.

94

5.4. ADAPTATION DU RECUIT SIMULE AU PROBLÈME

5.4.5 Organigramme d'adaptation de recuit simulé au problème

			^5mlm Smax^,a1, a2, a3, a4 61, 62, b3, b4 0^°, Of, a,Tt,
Solutions initiale X trouvée par l'heuristique, Z(X)
nb :=1

Choisir X' dans V(X), r :=random(1,5), si w[r] 0 alors S[r] :=random(3250,6825)

{/ {( `I 2 1j 3 \j 2

H[r].=(al+l1 S[r])^+c1(S[r]! +d'(S[r]l 1XS[l]

2 3

^{eta[r]:=a2+b2}(s~r])⁺(s~r]I ^+d2(S[r]~

J

I

Non

AZ := Z (X') -- Z (X)

Non			Oui
p := randoin[0,1]
	Oui
-BE p < e r				Non
						nb < 20

Non

Oui

nb := nb-F1

nb := nb+1

8 := a8

Oui

futioml X. Z(X) ,eta : vecteur

**

Non

4

95

Fin

FIGURE 5.2 -- Organigramme d'adaptation de récuit simulé au problème

96

Chapitre 6

Description informatique

6.1 Introduction

Nous aboutissons maintenant à l'étape finale à savoir l'élaboration d'une application aussi convivial que possible, munie d'une interface claire et accessible, facilitant ainsi son utilisation. Avant de procéder à la présentation de notre application, une description de l'environnement de programmation utilisé (DelphiXE3) s'avère nécessaire.

6.2 C'est quoi le Delphi?

Delphi est un environnement de développement de type RAD (Rapid Application Development). En utilisant Delphi, Il est possible de créer des applications Microsoft Windows très efficaces avec un minimum de codage manuel.

Delphi fournit tous les outils qui sont nécessaires pour développer, tester déboguer et déployer des applications incluant une importante bibliothèque de composants réutilisables, un ensemble d'outils de conception, des modèles d'application et de fiches, ainsi que des experts de programmation. Ces outils simplifient le prototype et réduisent la durée de développement. Ceci explique notre choix pour l'une des versions de Delphi pour créer notre application.

97

6.3. PRÉSENTATION DE L'APPLICATION

6.3 Présentation de l'application

Cette section comportera une description de l'application et des explications bien détaillées afin de permettre à l'utilisateur de connaître les étapes à suivre pour sa manipulation.

6.3.1 Description de l'application

- Nom de l'application: Gasline.

- Outil de développement: Delphi XE3. - Version du logiciel : V1.0.

- Logo:

FIGURE 6.1 - Logo

6.3.2 Utilisation de l'application

Lors du lancement de l'application, la fenêtre ci-dessous apparait :

98

6.3. PRÉSENTATION DE L'APPLICATION

FIGURE 6.2 - Fenêtre de lancement de l'application

Elle comporte une zone à écrire et deux boutons: - Zone à écrire : pour saisir le mot de passe

FIGURE 6.3 - Saisie du mot de passe

- Quitter: pour quitter l'application.

- Entrer : permet d'accéder à la fiche principale.

Une fois que le mot de passe saisi est correcte, la fenêtre suivante s'affiche :

99

6.3. PRÉSENTATION DE L'APPLICATION

FIGURE 6.4 - Fenêtre principale du l'application

La fenêtre principale comporte les menus suivants :

- Menu « Données » :permet à l'utilisateur de voir les données utilisée.

FIGURE 6.5 - Menu "Données"

Dans le menu « Données » : l'utilisateur trouve 4 sous-menus :

- Calcul moindres carrées:

100

6.3. PRÉSENTATION DE L'APPLICATION

FIGURE 6.6 - sous-menu "calcul moindres carrées"

En cliquant sur ce sous-menu un fichier Excel contenant les calculs concernant l'estima-tion des paramètres caratéristiques des compresseurs par la methode des moindres carrées s'ouvre :

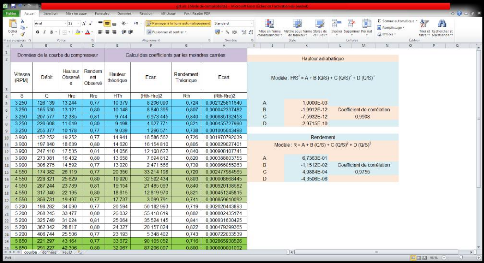
FIGURE 6.7 - Les calculs par moindres carrées

- Conditions opératoires:

FIGURE 6.8 - sous-menu "Conditions opératoires"

101

6.3. PRÉSENTATION DE L'APPLICATION

En cliquant sur ce sous-menu la fenêtre ci-dessous s'affiche :

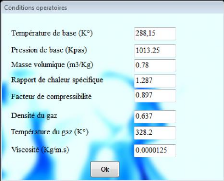
FIGURE 6.9 - Conditions opératoires

- Caractéristiques du gazoduc:

FIGURE 6.10 - sous-menu "Caractéristiques du gazoduc"

En cliquant sur ce sous-menu la fenêtre ci-dessous s'affiche :

102

6.3. PRÉSENTATION DE L'APPLICATION

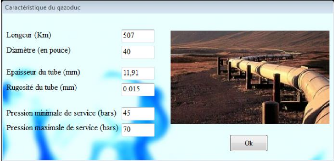
FIGURE 6.11 - Caractéristiques du gazoduc

- Caractéristiques des compresseurs:

FIGURE 6.12 - sous-menu "Caractéristiques des compresseurs"

En cliquant sur ce sous-menu la fenêtre ci-dessous s'affiche :

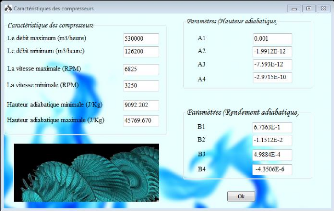
FIGURE 6.13 - Caractéristiques des compresseurs

103

6.3. PRÉSENTATION DE L'APPLICATION

- Menu « Calcul perte de charge»: permet à l'utilisateur de calculer la perte de charge pour différents débits.

FIGURE 6.14 - Menu "Calcul perte de charge"

En cliquant sur ce menu la fenêtre ci-dessous s'affiche :

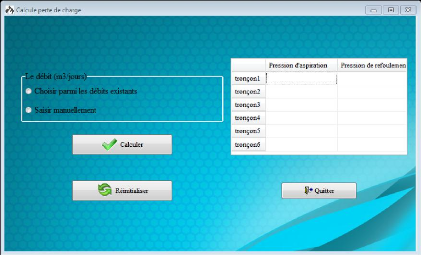
FIGURE 6.15 - fenêtre "Calcul perte de charge"

104

6.3. PRÉSENTATION DE L'APPLICATION

- Menu « Outils » : dans ce menu l'utilisateur trouve 2 sous-menus:

1 - Options: permet à l'utilisateur d'ouvrir "calculatrice" ou "bloc notes".

FIGURE 6.16 - sous-menu "Options"

2 - Sites web: permet à l'utilisateur d'acceder à quelque sites web utiles.

FIGURE 6.17 - sous-menu "Sites web"

La fenêtre principale comporte aussi 4 boutons:

- Bouton « Résolution »

FIGURE 6.18 - Bouton "Résolution"

6.3. PRÉSENTATION DE L'APPLICATION

En cliquant sur ce bouton la fiche suivante s'affiche:

FIGURE 6.19 - La fenêtre "Résolution"

Sur cette fiche, l'utilisateur doit "choisir" ou "saisir manuellement" le débit dont il veut calculer la configuration optimale correspondante:

FIGURE 6.20 - Le champ correspondant au débit

l'utilisateur doit aussi choisir la méthode de résolution parmi les méthodes suivantes :

105

FIGURE 6.21 - Le champ correspondant aux méthodes de résolution

106

6.3. PRÉSENTATION DE L'APPLICATION

En choisissant "Heuristique" une fenêtre pour la résolution s'affiche, en cliquant sur le boutons "Executer" on obtient la fiche suivante :

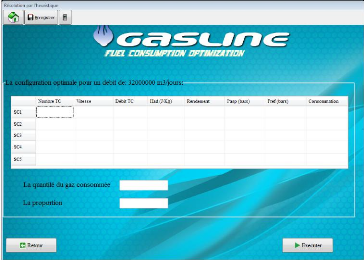
FIGURE 6.22 - Résolution par l'heuristique

6.3. PRÉSENTATION DE L'APPLICATION

De même pour l'algorithme génétique:

FIGURE 6.23 - Résolution par l'algorithme génétique

La même chose si l'utilisateur choisit "Recuit simulé" :

FIGURE 6.24 - Résolution par le récuit simulé

107

6.3. PRÉSENTATION DE L'APPLICATION

L'utilisateur trouve dans les trois fenêtres précédentes quartes boutons dans la barre d'ou-

tils :

· Accueil: permet à l'utilisateur d'aller à la fenêtre principale.

· Enregistrer: permet à l'utilisateur d'enregistrer les résultats obtenues dans un fichier Excel.

· Calculatrice : permet à l'utilisateur d'ouvrir "Calculatrice".

· Quitter: pour quitter l'application.

FIGURE 6.25 - Barre d'outils

Il trouve aussi deux boutons, un permet d'exécuter la méthode de résolution et l'autre pour le retour à la fenêtre de résolution.

Les résultats obtenus seront affichés dans les champs présentés dans les figures ci-dessous.

FIGURE 6.26 - Champ correspondant à l'affichage de la configuration optimale

108

6.3. PRÉSENTATION DE L'APPLICATION

FIGURE 6.27 - Affichage de la quantité consommée ainsi que sa proportion

Si l'utilisateur veut exécuter les deux méthodes "Algorithme génétique" et "Recuit simulé" alors il choisit "Executer AG et RS".

- Bouton « Voir la ligne » : permet à l'utilisateur de voir le tracé de la ligne étudiée (GZ1).

FIGURE 6.28 - Bouton "Voir la ligne"

En cliquant sur ce bouton la fiche suivante s'affiche:

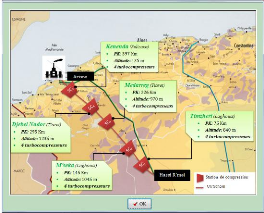
FIGURE 6.29 - La fenêtre "Voir la ligne"

109

110

6.3. PRÉSENTATION DE L'APPLICATION

- Bouton « Aide »

FIGURE 6.30 - Bouton "Aide"

En cliquant sur ce bouton la fiche suivante s'affiche:

FIGURE 6.31 - La fenêtre "Aide"

111

6.3. PRÉSENTATION DE L'APPLICATION

- Bouton « A propos »

FIGURE 6.32 - Bouton "A propos"

En cliquant sur ce bouton la fiche suivante s'affiche:

FIGURE 6.33 - La fenêtre "A propos"

6.4. RÉSULTATS DE L'APPLICATION

6.4 Résultats de l'application

Après avoir programmé les méthodes exposées dans le chapitre précédent, nous avons illustré nos résultats en choisissant comme exemple un débit de 32000000m³/jour :

- Résultats obtenus par l'heuristique NSCM pour le débit choisi:

FIGURE 6.34 - Résolution par l'heuristique

112

La quantité du gaz consommée: 11654.85m³/h

113

6.4. RÉSULTATS DE L'APPLICATION

- Résultats obtenus par l'algorithme génétique:

FIGURE 6.35 - Résolution par l'algorithme génétique

La quantité du gaz consommée: 11563.97m³/h

114

6.4. RÉSULTATS DE L'APPLICATION

- Résultats obtenus par le recuit simulé:

FIGURE 6.36 - Résolution par le recuit simulé

La quantité du gaz consommée: 11260.515m³/h

115

6.4. RÉSULTATS DE L'APPLICATION

Pour des débits entre 20 000 000 et 38 000 000 m³/jour, une exécution des trois méthodes a donné les résultats suivants:

Débit (m3/jour)	Configuration optimale					Quantité du gaz consommée	Trouvée par
	SC1	SC2	SC3	SC4	SC5
24000000	0	0	0	0	2	3000	NSCM
25000000	0	0	0	2	0	3400.454	RS
26000000	0	0	3	3	0	3659.55	RS
27000000	0	3	0	0	3	4814	AG
28000000	0	3	0	3	0	5873	NSCM
29000000	3	3	0	0	3	7048	AG
32000000	0	3	3	3	3	12520.84	RS
33000000	3	0	3	3	3	14484.93	AG
34000000	3	3	0	3	3	15889.013	RS
35000000	3	3	3	0	3	17843.95	RS
36000000	3	3	3	3	3	22276.31	AG
37000000	3	3	3	3	3	24946.32	AG
38000000	3	3	3	3	3	25826.92	AG

TABLE 6.1 - Résultats obtenus par l'application

116

6.4. RÉSULTATS DE L'APPLICATION

A partir du graphique, on remarque que l'algorithme génétique est plus performant que les deux autres méthodes pour certains débits, pour les autres débits, le recuit simulé devient plus efficace surtout en temps d'exécution, ce qui justifie l'utilisation des deux méta-heuristiques.

On peut illustrer le résultat des trois approches pour les débits entre 20 000 000 et 38 000 000 (m³/jour) à l'aide d'outil graphique sous MATLAB, qui exprime la quantité consommée en fonction des débit rentrants

Après l'exécution des trois méthodes pour différents débits entre 20 000 000 et 38 000 000 (m³/jour), les résultats obtenus montrent l'importance du choix des stations de compression à mettre en marche pour des débits importants.

En effet, l'augmentation du débit rentrant dans le gazoduc engendre une chute de pression importante (en dessous de la pression minimale 45 bars), ce qui conduit à augmenter le nombre de stations en marche ainsi que la vitesse de rotation des turbocompresseurs en fonction.

117

6.4. RÉSULTATS DE L'APPLICATION

6.4.1 Comparaison des résultats obtenus avec les données réelles

Une comparaison entre la quantité du gaz consommée pour le régime de fonctionnent usuel et la quantité de gaz consommée pour le régime de fonctionnent obtenue avec l'opti-misation pour les débits usuels est représentée dans le tableau ci-dessous.

Débit (m^3/jour)	Consommation	Régime usuel	Régime optimisé	Gain
26873129	Quantité (m^3/h)	19210,75	6025,85	13184,9 (m^3/h)
	Proportion	1.7%	0,54%	1,16%
27000893	Quantité (m^3/h)	23103,29	7440.79	15662,5 (m^3/h)
	Proportion	2,1%	0,66%	1,44%
26863871	Quantité (m^3/h)	24289	6006,74	18279,26 (m^3/h)
	Proportion	2,2%	0,54%	1,66%
27035567	Quantité (m^3/h)	19481,25	6905,54	12575,71 (m^3/h)
	Proportion	1,7%	0,61%	1,09%
25126400	Quantité (m^3/h)	18589,875	3849,43	14740,445 (m^3/h)
	Proportion	1,8%	0,36%	1,44%
23481194	Quantité(m^3/h)	14136,115	3036,463	11099,685 (m^3/h)
	Proportion	1,4%	0,31%	1,09%
25247167	Quantité (m^3/h)	13923	4006,98	9916,02 (m^3/h)
	Proportion	1,3%	0,38%	0,92%
25691742	Quantité (m^3/h)	14654,4	4159,15	10495,25 (m^3/h)
	Proportion	1,4%	0,39%	1,01%

TABLE 6.2 - Comparaison entre les données réelles et les résultats obtenus par l'optimisation

Conclusion générale

Notre projet de fin d'étude nous a permis de nous confronter pour la première fois à un problème du monde réel avec le bagage académique dont nous disposons.

L'entreprise SONAT RACH nous a confié une étude qui a pour titre "Optimisation de transport du gaz par canalisation".

Pour mener bien ce projet, il a fallu maîtriser et comprendre des notions hors notre domaine d'étude comme les données physiques techniques et économiques. Au-delà de la connaissance de ces données, nous avons essayé le calcul hydraulique avec différentes formules afin d'obtenir un résultat qui traduit la réalité.

Nous avons abouti l'élaboration d'un modèle mathématique qui est un problème non linéaire mixte en nombre entiers.

En ce qui concerne l'approche de résolution, nous nous sommes orientées en premier temps vers le solveur GAMS ( General Algabraic Modeling System) qui est une démarche déterministe, que nous avons bien maitrisé, mais vu la complexité de notre problème, GAMS n'a pas pu implémenté toutes les contraintes surtout celles qui définissent le domaine de fonctionnement d'un compresseur. Cette difficulté nous a incité vers une combinaison de l'algorithme génétique avec GAMS. Cette approche a éliminé la diversification de l'algo-rithme génétique , ce qui nous a conduit à abandonner cette approche.

Enfin, nous avons élaboré une heuristique qui permet de déterminer une solution réalisable, puis d'améliorer cette dernière à l'aide de deux metaheuristiques ( Algorithme génétique et Recuit simulé).

Par cette dernière approche nous pensons que notre objectif est atteint. Sachant que le manager suscite un grand intérêt pour la réalisation d'un outil d'aide à la décision et afin de concrétiser notre travail, nous avons élaboré une application qui porte le nom »GASLINE» et qui permet de déterminer le nombre de stations de compression à mettre en marche ainsi que le nombre de compresseurs qui marche dans chaque station à partir d'un débit injecté au gazoduc.

Au terme de notre travail, nous estimons que l'approche que nous avons adapté donne des résultats cohérents et satisfaisants. Notre grand souhait serait que notre travail soit bénéfique à SONAT RACH et qu'elle fasse l'objet de développement et de recherche plus approfondies.

Bibliographie

[1] M.Bentarzi, Régression multiple, Document non publié.

[2] R. G. Carter, Pipeline Optimization : Dynamic programming after 30 years, PSIG Annual Meeting, 28-30 October, Denver, Colorado 1998.

[3] A. Chebouba et A.Smati, Optimisation d'un pipeline de transport de gaz naturel par la programmation dynamique avec choix automatique, 2003; 39 1-14.

[4] A. Chebouba, Farouk Yalaoui, A. Smati, Lionel Amodeo, K. Younsi, A. Tairi, Optimization of Natural Gas Pipeline Transportation using Ant Colony, Optimization Algorithm Computers and Operations Research 06/2009 (19161923);

[5] D. Cobos Zaleta, Modelos de Optimización Entera Mixta no Lineal en Sistemas de Transporte de Gas Natural, tesis en opción al grado de mastero en ciencais en ingenía de sistemas, 2003.

[6] R.Hernandez, Optimization of Gas Transmission Networks under Energetic and Environmental Considerations, thèse doctorat en Génie de procédé et de l'environnement, 2011.

[7] S.Hocine, Identification de modèles de procedes par programmation mixte déterministe , thèse doctorat, 2006.

[8] H. S. Lall and P. B. Percell (1990). A dynamic programming based gas pipeline optimizer. In A. Bensoussan and J. L. Lions (editors), Analysis and Optimization Systems, Volume 144, Lecture Notes in Control and Information Sciences, pp. 123-132, Springer-Verlag, Berlin.

[9] S.Micheal, Technique Mathématique de la recherche opérationnelle Optimisation Combinatoire , Haermann, 1984.

[10] A. Rojey, Le gaz naturel Production traitement transport, Paris, Éditiond Tech-nip, 2008, 300 p.

[11] E.Shashi, Menon, Gas Pipeline Hydraulics, CRC Press, Boca Raton, FL 2005.

[12] SONATRACH, PetroGas Consult, Calcul thermohydraulique des gazoducs.

[13] J.Tegham, Recherche opérationnelle Tome1, Ellipses, 2012.

[14] P.J.Wong and R.E.Larson , Optimization of natural-gas pipeline systems via dynamic programming . IEEE Transactions on Automatic Control , AC-13 (5); 475-481, 1968.

[15] R. Z.Wu , Model relaxations for the fuel cost minimization of steady-state gas pipeline networks , Mathematical and Computer Modeling, 31(2-3); 197-220, 2000.

[16] Rapport annuel Sonatrach 2013.

[17] http :// www.GRTgaz.com.

[18] www.Sonatrach.dz.

Annexe

Les données	Les valeurs
Longueur (km)	507
Diamètre "en pouce"	40
Nuance d'acier	X60
Épaisseur du tube (mm)	11.9
Rugosité du tube (mm)	0.015
Nombre de station de compression	(05) Sc1,Sc2,Sc3,Sc4,Sc5
Nombre de turbocompresseurs (par station)	04 (3+1)
Mode d'assemblage des compresseurs	Parallèle
Pression maximale du service design (bars)	70
Capacité maximale réelle (10^9Sm^3 / ans)	13.679
Le débit maximum de gazoduc	(36.10^6m^3 / h)

TABLE 6.3 - Caractéristiques de la ligne GZ1.

	PK (km)	Altitude (m)
Terminal départ	0.000	749
Station 1	75	840
Station 2	149	1045
Station 3	226	970
Station 4	295	1235
Station 5	397	205
Terminal arrivée	507	56

TABLE 6.4 - Profil Altimétrie

Les données	la valeur	Unité
Type (km)	Centrifuge	/
débit maximale	530000	m^3/min
débit minimale	126200	m^3/min
La vitesse minimale du compresseur	3250	RPM (Rotation Par Minute)
La vitesse maximale du compresseur	6825	RPM (Rotation Par Minute)
Le rendement mécanique (çT R)	0.95	/
Le rendement de la turbine (çmc)	0.35	/
La pression minimale d'aspiration	45	bar
La pression maximale de refoulement	70	bar

TABLE 6.5 - Caractéristiques des compresseurs.

COMPOSITION DU GAZ NATUREL
Formules	Composés	%	Masse molaire
CH4	Méthane	0.862	16.04
C2H6	Ethane	0.093	30.07
C3 H 8	Propane	0.013	44.09
n^-C4H10	n-Butane	0.001	58.12
i^-C4H10	Isobutane	0.001	58.12
n^-C5H12	n-Pentane	-	72.15
i^-C5H12	Isopentane	-	72.15
n^-C6H14	n-Hexane	-	86.18
n^-C7H16	n-Heptane	-	100.21
H2S	Hydrogène sulfuré	-	34.08
CO2	Dioxyde de carbone	0.020	44.01
N2	Azote	0.010	28.01
Masse Molaire	18.47
Masse Volumique	0.78 kg / m3

TABLE 6.6 - Caractéristiques de gaz naturel.