|

GLOBAL PORTFOLIO DIVERSIFICATION WITH
CRYPTOCURRENCIES
Master thesis submitted to the Faculty of Economics and
Business
Institute of Financial Analysis
University of Neuchâtel
For the Master of Science in Finance
by
Salma OUALI
Supervised by:
Prof. Frédéric SONNEY,
University of Neuchâtel
Neuchâtel, August 2019
|
Faculté des sciences économiques Avenue du
1er-Mars 26 CH-2000 Neuchâtel
www.unine.ch/seco
|
|
1
Abstract
This study raises questions about the potential of
cryptocurrencies as a new alternative investment. I explore the ability to
which major cryptocurrencies endow diversification and hedging benefits to a
global investor. Using the dynamic conditional correlation model developed by
Engle (2002), I find evidence of effective diversification and weak hedging
effects against global traditional assets. Furthermore, I investigate the issue
using risk based portfolio optimization frameworks. I find enhanced performance
of the investor's portfolio when including Bitcoin to a well-diversified
portfolio. Likewise, later generation of cryptocurrencies Ripple, Dash and
Litecoin provide better improvement on a risk adjusted basis. Nonetheless,
their very high volatility worsen off the portfolio's downside risk.1
1 ACKNOWLEDGEMENTS: I would like to express
my gratitude to my supervisor Prof. Frédéric Sonney for his
guidance and valuable advice. I would like to thank my family for their love
and unconditional support. I am also grateful to my partner and my best friend
for brightening my life throughout the thesis process.
2
1. Introduction
The 2008 financial crisis led to growing skepticism around
traditional financial systems.
As a response to these backdrops, a programmer under the
pseudonym of Nakamoto introduced Bitcoin, a decentralized medium of exchange in
2009. The peer-to-peer electronic currency shows unique features. It is not
backed by any central authority, has a fixed supply set in advance of 21
million Bitcoins and is created via an innovative technology, Blockchain that
registers transactions and stows them into transparent blocks. These blocks are
completed once these transactions are verified and secured into a distributed
network. Therefore, this creation process is similar to gold mining, which led
to Bitcoin being called the «digital gold».
Following the inception of Bitcoin, many alternative
cryptocurrencies, using the same blockchain technology emerged. Whether
addressing same purposes as Bitcoin or providing innovative decentralized
solutions, they attracted investors' attention and gained growing market shares
with the most popular among them being Ethereum, Ripple, Dash, Stellar and
Litecoin.
Driven by high capital inflows, Cryptocurrencies witnessed
price rise in tandem. Market capitalization and volume traded continued growing
exponentially until the end of 2017, when Bitcoin realized its meteoric rise
before topping out in the following months.
This rapid surge in prices and the high volatility displayed
by the cryptocurrency market has attracted mostly speculators seeing
Cryptocurrencies as a speculative asset rather than a currency store of value.
Consequently, many investors question whether cryptocurrencies are just
fictitious currencies forming speculation bubbles or a valuable opportunity
investment.
The main purpose of this study is to explore Cryptocurrencies
as a new alternative investment.
The research is conducted from the perspective of a global
investor who considers diversification as of paramount importance. Considering
the excessive volatility encompassing
3
cryptocurrencies, I restrain cryptocurrencies to hedging and
diversification uses only. According to Baur and Lucey (2010), a hedge is an
asset that shows adverse correlation to another asset, whereas a diversifier
exhibits marginal positive price co-movements with the other asset.
Furthermore, this study sheds light on the use of the cryptocurrencies as
performance enhancers in a global portfolio while previous research focused
only on Bitcoin. I benchmark the cryptocurrency market with Bitcoin and three
major alternative cryptocurrencies: Ripple, Dash and Litecoin. Whilst among
traditional assets I consider stocks, bonds, real estate and gold.
In order to investigate the diversification and hedging traits
of the aforementioned cryptocurrencies and capture the co-movement between each
cryptocurrency and the traditional assets, I consider the multivariate dynamic
conditional correlation GARCH model of Engle (2002). The results offer
compelling evidence of cryptocurrencies as effective diversifiers, yet they
exhibit weak hedging properties. I find that Bitcoin acts as a strong hedge
only against price movements of Chinese equities, global real estate and
corporate bonds. Additionally, Litecoin qualifies as a hedge for global real
estate and Japanese equities. Whereas Dash is only a good hedge against global
bonds. Ripple, on the other side, does not possess any hedging properties since
it exhibits moderately positive correlation with all traditional assets.
I further examine the diversification perquisites of
cryptocurrencies in a portfolio comprising all traditional asset classes.
Bruder and Roncalli (2012) argue that risk aversion of institutional and
individual investors increased significantly after the 2008 financial crisis.
Thus, they prompt the use of investment strategies based on risk budgeting and
diversification instead of return forecasting ones.
Regarding this matter and the high volatility nature of
Cryptocurrencies, this study adopts four optimization frameworks that focus on
measuring risk: traditional minimum variance, minimum conditional value at
risk, inverse volatility and maximum diversification.
4
The out-of-sample performance of the optimal portfolios is
studied on a risk adjusted return basis. The back-testing results confirm the
evidence of cryptocurrencies being outstanding diversifiers. Regardless of the
strategy, I find that adding cryptocurrencies to the basic portfolio, the risk
return ratio increases significantly albeit at different magnitudes. On the
other side, the downside risk of the portfolio increases especially when
alternative tokens are included. Interestingly, Bitcoin succeeds to reduce the
downside risk under minimum variance and inverse volatility.
The research paper is structured as follow: Section 2 presents
the literature review, section 3 undergoes the methodology details, section 4
introduces the data, section 5 reports empirical results and robustness check
and section 6 provides conclusion.
2. Literature review
Despite the global financial instability, the strong past
financial performance of bitcoin (BTC) made it comparable to a digital gold.
Therefore, a strand of studies examined Bitcoin and its properties as an asset
class. Yermack et al. (2013) compare BTC's daily exchange rates with gold and
fiat currencies and argue that BTC is more comparable to a speculative
investment. Baur et al. (2015) investigate statistical properties and future
usage of bitcoin. They suggest that bitcoin is a hybrid between conventional
currencies and commodity currency. Dyhrberg et al. (2015) find similarities of
BTC with gold and USD and confirm the views of Baur et al. (2015). Ciaian,
Rajcaniova and Kancs (2016) go a step further and analyze the impact of BTC's
supply and demand on its price formation. Thus, they discover similar price
formation patterns with other currencies.
Whether considered as a medium of exchange or a highly
speculative asset, BTC's skyrocketing returns are the main reason of its
attractiveness. After being accepted as a method of payment, its use as a
financial investment vehicle has been thoroughly examined. In point of fact, a
broad
5
range of literature studied whether including bitcoin in a
traditional portfolio can enhance its return and reduce the risk.
Brière et al. (2015), using mean variance spanning
test, assert BTC's diversification benefits in an investment portfolio. They
conclude that BTC's low correlation with other assets enhances the portfolio's
performance and compensates for the increase in the overall risk. As returns of
BTC exhibit high kurtosis and low skewness, Eisl et al. (2015), proposes the
use of a CVaR framework as an alternative to mean variance analysis. Their
findings are in line with the ones of Brière et al. (2015). Indeed,
investing a small fraction in BTC enhances intensely the portfolio's risk
return tradeoff.
Kihoon Hang (2016), performs a trading strategy based on
momentum (TSMOM). By conducting a mean variance analysis, he demonstrates that
enhanced returns and reduced volatility can be achieved in a portfolio of
equities and TSMOM.
Diversification and hedging are characteristics of huge
importance when building a portfolio. Therefore, an investigation of
correlation between BTC and other financial assets is crucial. Following this,
Bouri et al. (2017), employed a dynamic conditional correlation model (Engle,
2002) to estimate correlation between BTC and other financial assets. They find
that Bitcoin does qualify as an effective diversifier. However, it can only
serve as a hedge or safe haven in few cases. On the contrary, Bouoiyour and
Selmi (2017), vindicate the hedge and safe haven role of bitcoin against oil
price movements. Moreover, by adding Bitcoin to a portfolio of oil only, they
observe an enhancement in performance and downside risk reduction.
Guesmi et al. (2018), consider DCC GJR GARCH as the suitable
model for modeling joint dynamics of different financial assets. They document
that Bitcoin can be a systematic hedge and that adding a small fraction of
bitcoin reduces considerably the portfolio's risk exposure.
6
They also stress that a short position in Bitcoin hedges the
risk for commodities, stocks and currencies.
Due to the high trading and predominant mining activity in
China, Kajtazi and Moro (2017), raise the question of whether BTC adds value in
a Chinese asset-based portfolio. They show significant but low correlation with
Chinese assets and argue that Bitcoin fails in enhancing portfolio's
performance over all periods.
Evidence that Bitcoin offers diversification benefits in a
traditional portfolio is abundant in literature and so far, research towards
altcoins remains infrequent.
Aiming to close this gap, Osterrieder et al. (2016), were
amongst the first to explore the interdependences between cryptocurrencies
(CCs). They demonstrate that low mildly correlation exist between most CCs
except for the ones sharing the same technology. Following this, Braineis and
Mestel (2018), expand the research by exploring the effects of diversified
cryptocurrency investments. Their empirical results show that adding several
CCs expands the efficient frontier of a bitcoin-based portfolio.
Further investigating the diversification effect, Chuen et al.
(2017), advocate the use of the CRIX index, which was developed by Trimborn and
Hardle (2016) to mimic the CCs market performance. When looking at static and
dynamic correlations between CRIX and traditional assets, they give evidence of
diversification benefits. However, the mean-variance spanning tests reveal
enhancement of global minimum variance only. In fact, the negative skewness of
CRIX and high risk makes it redundant in a tangency portfolio.
Klein et al. (2018), argue that Bitcoin is not the new gold.
According to their research results, Bitcoin is only suitable for
diversification benefits and does not display stable hedging
7
capabilities. Meanwhile, they find CRIX to display better
hedging effects. Yet, it still fails to be an effective hedge like gold.
3. Data
To conduct the analysis, I retrieve data from two different
sources. I retrieve daily closing prices for traditional assets in form of
indices from DataStream. While the data for cryptocurrencies are extracted from
coinmarketcap.
According to Abidin et Al. (2004), international
diversification is proven to yield higher returns and reduce risks and since
cryptocurrencies are global in nature, I decide to adopt the perspective of a
global investor. Therefore, I create a well-diversified international portfolio
composed of cryptocurrencies and traditional assets.
Emphasis lies on the largest cryptocurrency assets. Therefore,
I select four cryptocurrencies from the ten largest cryptocurrencies by market
capitalization. Bitcoin and three major alternative cryptocurrencies: Litecoin,
Ripple and Dash. These cryptocurrencies are portrayed as more suitable than
other major altcoins like Bitcoin cash and Ethereum, which were only introduced
in 2015 and 2017, respectively, and would not provide enough set of data to
conduct the research. Additionally, the selection is made based on the
underlying correlation of the alternative cryptocurrencies with Bitcoin. Ripple
and Dash are moderately correlated with Bitcoin while Litecoin is relatively
highly correlated with the latter.
Traditional and alternative assets comprise equity, fixed
income, real estate and gold. Each asset class is embodied by liquid financial
indices.
Equity indices are selected based on the four most important
markets of cryptocurrencies trading. I use four regional indices S&P 500,
Euro Stoxx 50, Nikkei 225, SSE (Shanghai Stock Exchange) as well as MSCI
Emerging Markets Index. Considering the global bond universe of fixed income, I
adopt the following indices: S&P Global Developed Sovereign Bond Index
and
8
IBOXX Liquid Investment Corporate Grade Index. Gold is added in
consonance with Dyhrberg et al. (2015) since the latter is typically depicted
as hedge. As of real estate, I use as a reference FTSE EPRA NAREIT global.
The sample contains daily price information from 30 July 2014 to
31 April 2019. I remove the daily data of cryptocurrencies during the weekends
in order to match the number of observations with traditional assets.
Furthermore, I compute daily log returns since they are deemed
more convenient for time series analysis and provide a better fit for
statistical models. Therefore, daily log returns are obtained using the
following formula:
Pi,t
rit = log Pi,t-1
4. Methodology
Modern portfolio theory states that correlation is the basis
of diversification in a portfolio. Accordingly, investing in low correlated or
negatively correlated assets can achieve efficient diversification (Bodie et
Al, 2014). Following this, I examine diversification capabilities of
cryptocurrencies as well as their ability to enhance the risk-return reward of
a global investor.
4.1. Correlation analysis
I perform a correlation analysis in order to assess if
cryptocurrencies can be a diversifier or a hedge. At first, I estimate
correlation coefficients of cryptocurrencies and other assets via a pairwise
correlation. However, the latter is only the average estimation and correlation
in general is known to display time varying properties.
Hence, I conduct the multivariate dynamic conditional
correlation (DCC) model by Engle (2002). The advantage of the model lies in its
limited number of estimated parameters, univariate GARCH flexibility and its
direct parameterization of conditional correlation.
9
The estimation of the DCC model is performed in three steps:
I estimate an ARMA (1, 1)2 mean equation to model the
conditional mean and deal with the autocorrelation in the time series
returns.
The conditional mean equation for each asset is presented in the
equation below:
?? ??
???? = ?? + E??+ ? ????????-?? + ? ???? E??-??
??=1 ??=1
Where c is a constant term, E?? is the white noise, p is the
autoregressive term, q the moving average term and ö, è are the
model parameters.
After deeming the conditional mean for each asset, the ARMA
residuals are used to estimate the GARCH (1, 1) variance model.
Therefore, conditional variances are implemented one by one using
the following formula:
????2= ??+ ?? E??2 +
??????-1
2
Where ??t is the conditional variance, ?? is the
intercept, ?? is the coefficient displaying the impact of previous shocks,
E??2 is the squared residual and ?? is a coefficient that transmits
the GARCH (1, 1) effect.
Afterward, I model conditional covariance of standardized returns
using computed variances from first step.
With ????,??,??+1 = ????????(????+1
?? , ????+1
?? ) and ????,?? = ??
1-??-??
The dynamic conditional correlation is computed as follows:
??
????,??,??+1 = ????,?? + ?? (????+1??????+1- ??????) +
?? (????,??,?? - ??????)
2 Autoregressive moving average (1,1) model
10
Once the auxiliary variable gi,j,t+i is forecasted, I compute the
dynamic conditional correlation
|
as follows:
|
Pi,j,t+i =
|
gi,j,t+i
.gi,i,t+i.gj,j,t+i
|
After studying the co-movement between the selected asset
classes and cryptocurrencies, I investigate the usefulness of cryptocurrencies
as a diversification tool from a portfolio perspective.
4.2. Portfolio optimization
I start by constructing a portfolio without cryptocurrencies,
which will be referred to as the basis portfolio. Furthermore, I investigate
the options of including cryptocurrencies to the traditional assets' portfolio.
I construct two sets of portfolios. The first portfolio includes traditional
assets and only Bitcoin and the second one includes traditional assets and the
four cryptocurrencies. The benefits of adding cryptocurrencies are assessed in
terms of risk-return profiles, cumulative wealth and downside risk.
In order to calculate these performance metrics, I use the
out-of-sample backtesting method, which evaluates trading strategies using
historical data. The models' parameters are assessed via a rolling window
approach under the following steps: I use the 200 last days observations before
the rebalancing date for the parameters' estimation. Then, the resulting
weights are rebalanced on a monthly basis for the whole out of sample
period.
Thus, the optimized weights are subject to different
parameters depending on the optimization frameworks presented below.
11
4.2.1. Minimum risk approaches
Minimum variance portfolio is the Markowitz least variance
framework. It is set out as the portfolio that maximizes the use of
diversification to achieve the lowest risk. The portfolio weights are optimized
for each point in time using the subsequent formula:
min 6P = En1 Ey 1 wiw1611 s. t.
wl >_ 0, En1 wl = 1 Where weights are estimated by using
the historical variance and covariance matrix.
Nevertheless, a strong shortcoming of the mean variance
analysis is the assumption of normal distribution of returns. In this context,
cryptocurrencies' excess volatility infers a heavy tail distribution as already
stated by Eisl et al. (2015) and Chuen et al. (2017).
To cope with this issue, I follow Rockafeller and Uryasev
(2002) to construct the conditional value at risk strategy (CVaR). The strategy
uses the expected shortfall, which is a more coherent risk measure contrasting
to the variance since it aims to quantify only the downside risk. Log returns
are simulated via a T-student distribution.
Therefore, conditional value at risk portfolio weights are
given by solving the following optimization problem:
min CVARa(wt) s. t. up,t(wt) = rtarget
; wt1p = 1 , wl,t » 0 wtERP
1
CVARa(w) = (1 - a) if(w,r)<VARa(w)
f(w,r)p(r)dr
Where f (w, r) is the probability density function of
portfolio returns with weights w, a is the confidence level,
VARa is the loss to be expected in a.100% of the
times.
Short selling is constrained under the two strategies since
Bitcoin futures were only introduced recently on Chicago Board Options Exchange
(CBOE) and Chicago Mercantile Exchange
12
(CME) in December 2017. In addition, I impose a maximum weight
constraint of 50% for each asset in order to omit extreme weight
allocations.
0% < ???? < 50%
4.2.2. Risk budgeting approaches
Requiring only the estimation of volatility, risk budgeting
approaches are becoming a popular solution for risk adverse investors. Booth
and Fama (1992) argue that these models put diversification at the heart of the
investment strategy and are a good alternative to Markowitz least variance
framework when the assumption of normal returns is not solid. Therefore, I
adopt the subsequent risk budgeting approaches:
The inverse of the volatility is used to determine the weight
of each asset. Highly volatile assets will be given a lower weight in
comparison to low volatility assets. Hence, each asset contributes different
amount of risk to the overall portfolio. The optimization problem takes the
following form:
1
|
???? =
|
????????
|
|
? ( 1
?? ??=1 ????????)
|
Introduced by Choueifaty and Cognard (2008) maximum
diversification seeks to maximize the diversification ratio of the weighted
average assets volatilities to the total portfolio volatility. The
diversification ratio is given as:
Maximize DR = ? ????????
??
??=1 s. t. ? ????
?? ??=1 = 1 and ???? = 0
? ????
??
??=1
13
4.3. Performance measurement
In order to measure the portfolios performance, I rely on
Sharpe ratio, which is a performance criteria widely used by practitioners and
in literature.
u,,
=
^ - Rf
o-^,,
Sharpe ratio is defined as follow:
^ SR,,
With û,, the portfolio sample mean returns and
o-^,, its sample standard deviation.
In addition, I compute the cumulative returns and the maximum
drawdown of the investment strategies for each of the optimal portfolios.
5. Empirical results
5.1. Sample Characteristics
Table 1 and table 2 display summary statistics of daily log
returns for cryptocurrencies and traditional assets.
Regarding traditional assets, equity indices exhibit slightly
positive mean returns with S&P 500 showing the highest average daily
returns and the lowest standard deviation. As expected, corporate and
government bonds indices have low mean returns and showcase the lowest standard
deviation among all financial assets. Commodities depicted by S&P GSCI gold
provide the worst reward to volatility with negative mean return and an
annualized Sharpe ratio of -0.04. On the other hand, real estate exhibit
promising performance with a favorable annualized Sharpe ratio of 0.44.
Meanwhile, in line with Chuen et Al. (2017), I find that
cryptocurrencies outperform traditional financial assets in terms of average
daily returns and have the highest standard deviation by far.
14
As can be noticed, the 1% and 99 % percentiles show that
extreme price movements are more severe for cryptocurrencies than for
traditional assets. Albeit, the higher magnitude of positive returns is
emphasized for cryptocurrencies when compared with negative ones.
In the case of skewness and kurtosis, I find Ripple, Dash and
Litecoin to be positively skewed, a significant characteristic rational
investors look for. In contrast, Bitcoin, equities, bonds and real estate
display a negative skewness that indicates a higher tail risk. Additionally, I
find that all-time series are leptokurtic. Eurostoxx 50 and Shanghai stock
exchange present high excess kurtosis but to a lesser extent than altcoins.
Apart from Bitcoin, cryptocurrencies have very high excess
kurtosis as the market for altcoins is still developing.
Therefore, the Jarque-Bera test supports the latter findings
by rejecting the normality for all assets at 1% significance level. All the
conventional assets and cryptocurrencies are not normally distributed.
Moreover, I conduct Ljung box test to check for serial correlation. Hence, I
find most conventional assets as well as Ripple to show significant
autocorrelation. Nevertheless, Bitcoin, Dash, S&P500, Sovereign bonds and
Gold display a low autocorrelation of daily returns, which suggests a lack of
predictability.
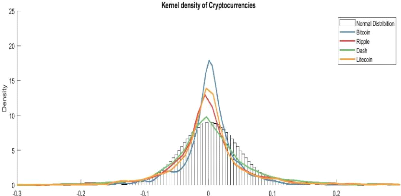
Cryptocurrencies pronounced deviation from normality is
visualized in Figure 1. The black line depicts a theoretical normal
distribution of Bitcoin. I observe that the latter is the least volatile with
more observations around the mean and a less pronounced tail than altcoins.
5.2. Correlation analysis
Accurate correlation assessment is one fundamental aspect in
portfolio theory. According to Corbet et Al. (2018), such important metric has
momentous implications on portfolio construction, diversification and
hedging.
15
Figure 2 illustrates pairwise correlation coefficients, which
give a first snapshot of average correlations between our different financial
assets. It is noteworthy that almost all correlation coefficients between
cryptocurrencies and traditional assets do not exceed 0.10. Regarding
cryptocurrencies, they range from 0.25 to 0.59 with Bitcoin and Litecoin
exhibiting the highest correlation. Relatively, traditional assets have more
varying correlations within themselves due to their global diversification.
Yet, this is only the average correlation for our sample period. That is why I
derive the multi-varying correlation through the Dynamic conditional
correlation model.
Tables 4, 5, 6 and 7 illustrate descriptive statistics of
dynamic conditional correlations between the innovations of each of the
cryptocurrencies and traditional assets. The multi-varying correlation analysis
will allow us to asses precisely the diversification and hedging benefits of
cryptocurrencies.
Table 4 depicts the DCC statistics for correlation pairs
within Bitcoin. The latter displays negative correlation among all the sample
period with the following asset categories: developed corporate bonds, global
real estate and Chinese equities. Hence, it acts as a strong hedge according to
the definition of Baur and Lucey (2010). Moreover, it has a correlation of
approximately zero with gold, MSCI emerging markets and sovereign bonds. It is
also notable that the standard deviation of those correlation pairs is very low
suggesting a stable correlation over time and high diversification benefits.
Regarding developed market equities, Bitcoin is negatively correlated to Nikkei
225 on average with a maximum value of 0.0194.
The highest average correlation from all conventional assets
is the pair with Eurostoxx 50 with a value of 0.0649. Nevertheless, it is very
stable among all the period. For S&P 500, DCC correlation is more dynamic
with a maximum spike of 0.27.
16
Table 5 reveals that Ripple cannot be regarded as a strong
hedge against any of the traditional assets. A further look into the
descriptive statistics of DCC correlations brings to light the noisy
correlation spikes. Moreover, the 25% and 75% quantiles show slightly positive
correlations with traditional assets over the whole sample period.
Table 6 shows that Dash has the highest correlation with
developed market equities within all the cryptocurrencies. Furthermore, dynamic
correlation is unstable for emerging markets equities and alternative
investments since it swings from negative to positive. Yet, it can be
considered as a strong hedge against developed corporate and sovereign bonds
only.
According to table 7, Litecoin possesses hedging capacities
against Japanese equities and global real estate. In addition, Low co-movements
with equity market indices are more persistent than for Ripple and Dash which
suggests better investment opportunities.
It is apparent that S&P 500 shows unstable dynamic
correlations with cryptocurrencies all over the sample period. For a better
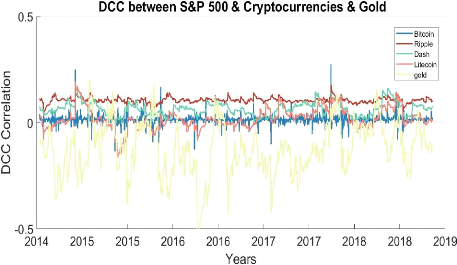
assessment of hedging capacities, figure 2 plots its DCC correlation with
cryptocurrencies as well as gold. The latter is added as a reference point
since it is depicted as a safe haven against S&P 500. (Baur & Mc
Dermott 2016).
Ripple and Dash show mostly positive correlations as already
stated. Meanwhile, Bitcoin and Litecoin exhibit a wide range of positive and
negative correlation values. Albeit, with small periods and no persistence
while being negative. Gold, on the contrary, shows negative dynamic correlation
for successive several months. In this regard, safe haven and strong hedge
attributes should be excluded for Bitcoin and Litecoin. They can only be very
effective diversifiers against S&P 500.
5.3. Portfolio performance
In this section, I discuss the results of the different
optimization frameworks performed for the three optimal portfolios: a portfolio
of traditional assets, a portfolio of traditional assets and
17
Bitcoin and finally, a portfolio of traditional assets,
Bitcoin and the three alternative cryptocurrencies: Ripple, Dash and
Litecoin.
Table 8 reports the performance of the optimal portfolios
under the Minimum Variance optimization. I find that allocating Bitcoin to the
basic portfolio slightly increases the annualized returns. Interestingly, the
volatility of the optimal portfolio remains unchanged and maximum drawdown is
even lower.
Likewise, the inclusion of alternative cryptocurrencies
increases a bit more the returns but at the cost of a slightly higher
volatility and a higher maximum drawdown. In fact, allocating even an
insignificant share into altcoins does not compensate for their very high
volatility. However, the higher returns seem to offset the evident increase in
risk and the risk return reward of 1.26 vindicates the importance of adding
Cryptocurrencies to the basic portfolio.
Due to the fat tail problem of cryptocurrencies, Conditional
Value at Risk emerges as more coherent risk measure than variance. Table 9
presents the performance of Minimum Conditional Value at Risk optimization. It
is important to note that the strategy's ability to focus on the expected
shortfall only brought higher returns for the portfolios with
cryptocurrencies.
When including Bitcoin in the basic portfolio, the strategy
shows a slight increase in the returns from 3.8% to 4.51%. The inclusion of
alternative cryptocurrencies improved more the returns with an annualized mean
of 5.08%. Once again, the high returns of cryptocurrencies offset their excess
volatilities. Despite the increase in standard deviation, annualized Sharpe
ratio increases from 1.05 to 1.17 when adding Bitcoin and to 1.29 when Altcoins
are included.
Skewness and kurtosis of the second and third portfolios are
slightly improved. Cumulative wealth increases as well. However, I observe a
higher maximum drawdown when including Bitcoin and the effect is more prominent
for the third portfolio.
18
Optimal portfolio weights is the main scope of the two
aforementioned risk strategies. Now, I switch to risk budgeting strategies
which impose constraints on the volatility contribution of each asset to the
total portfolio volatility.
Table 10 summarizes the results of the inverse volatility
strategy. I observe that diversification effects of this framework worsen off
the performance of the basic portfolio. In fact, all the indices in the
portfolio have positive weights in spite of their level of risk while the two
first strategies omit weight allocations for the riskiest assets. The basic
portfolio gives mean return of 2.9%, a standard deviation of 5.17% and a Sharpe
ratio of only 0.56. The effect of cryptocurrencies is more prominent here. When
adding Bitcoin, Sharpe ratio increased by 0.28 from 0.56 up to 0.85 that is
driven by a significant improve in returns and an insignificant increase in
volatility of 0.03%. The contribution of alternative cryptocurrencies is even
more significant. Portfolio III displays a risk return efficiency of 1.30 and a
cumulative wealth of 1.30. Contrariwise, maximum drawdown is again higher than
first and second portfolios. Lastly, table 11 illustrates the performance of
the maximum diversification strategy, which aims to maximize diversification
effects by creating a portfolio with minimally correlated assets. Effective
diversification benefits of cryptocurrencies are the most pronounced under this
strategy. In fact, adding cryptocurrencies increases drastically the
performance of the basic portfolio as Sharpe ratio increases from 0.73 to 1.22
with Bitcoin and up to 1.54 when adding Ripple, Dash and Litecoin. The strategy
displays the highest returns for the second and third portfolio as well as the
highest standard deviation. Once more, the skyrocket returns of
cryptocurrencies seem to outweigh their high volatility.
Portfolio III shows higher maximum drawdown of 9.46% and more
leptokurtic returns. However, it is important to pinpoint that this is the only
portfolio to display positive skewness, which means that the probability of
positive returns was higher than negative ones. Moreover, portfolio III hits
the highest level of cumulative wealth with 1$ turning into 1.37$.
19
So far, this study revealed crucial portfolio benefits when
adding cryptocurrencies to a traditional assets' portfolio independently of the
optimization strategy employed.
For further insights, a detailed analysis of portfolios weight
allocation is presented in the following section.
5.4. Portfolio weights analysis
As can be seen from the asset allocation weights graphs,
portfolios of traditional assets under inverse volatility and maximum
diversification strategies are more diversified. On the other hand, Conditional
Value at Risk strategy sets extreme weight allocations to bonds indices
followed by S&P 500 since they exhibit the least volatility. Therefore, the
C-var optimizer omits weighting other indices, which performed really bad and
were highly volatile during estimation periods. This results in the basis
portfolio exhibiting the best performance under this strategy with a Sharpe of
1.07.
When cryptocurrencies are included, I notice that the
weighting scheme of other asset classes fluctuates to compensate for the
additional volatility. Equity indices weights change the most during the sample
period. I observe a significant increase in S&P 500 proportion but also a
small position taken in gold. In addition, through the whole investment period,
optimal portfolios contain between 0 and 3% of cryptocurrencies with the higher
allocation share during the years 2016-2017, the period of tremendous growth
for cryptocurrencies. Indeed, cryptocurrencies are considered too risky for the
parameters of the optimization problem.
It is also noticeable that Bitcoin dominates over alternative
cryptocurrencies. In fact, none of the Altcoins is given more than 1% weight
during the whole optimization process.
Regarding risk budgeting approaches, I observe that portfolio
assets do not fluctuate that much when adding cryptocurrencies. Moreover, the
weight allocated to cryptocurrencies is larger under those two strategies.
Until 2017, there is an increasing allocation in cryptocurrencies. However, it
decreases drastically after the Bitcoin boom.
20
Furthermore, the Maximum Diversification strategy, which
boosted the performance of investments significantly, invests between 0 and 10%
in cryptocurrencies. Thus, the higher cryptocurrency exposure had a huge impact
on maximizing the portfolio performance.
5.5. Robustness check
To assess the robustness of the trading strategies results,
tables 12, 13, 14 and 15 present performance results using weekly data and
monthly rebalancing.
The results of the study are robust with regard to the asset
allocations employed. I find that cryptocurrencies always add substantial value
when included in the stocks-bonds-alternative investments portfolio. Sharpe
ratio increases significantly under the different optimization frameworks.
However, similar results regarding the downside risk of the basis portfolio are
found when using weekly data. Alternative cryptocurrencies worsen of the
maximum drawdown of the portfolio whereas Bitcoin increases slightly the
maximum drawdown under Inverse volatility and minimum variance strategies.
Interestingly, Minimum conditional value at risk performs
better than maximum diversification and yields the highest Sharpe Ratio when
cryptocurrencies are added.
6. Conclusion
This study seeks to address the possible hedging and
diversification benefits of cryptocurrencies as an alternative investment. From
the perspective of a global investor, I investigate the market linkages between
Cryptocurrencies and global asset indices as well as the benefits of their
inclusion within these assets.
21
Using the dynamic conditional correlation model, I find that
block-chain assets can act as effective diversifiers for the investment period
analyzed. I also detect that the correlation of traditional assets against
Bitcoin are closer to zero and more stable than against over crypto-tokens.
Moreover, I find that Bitcoin, Dash and Litecoin do possess hedging properties
against some assets' indices. However, none of the cryptocurrencies acts as
hedge against European, American and emerging market equities.
The resulting diversification properties further endorse the
cryptocurrencies use case in a diversified portfolio. These findings are useful
for global investors seeking protection from markets downward movements. I
examine the out of sample performance of portfolios with and without
cryptocurrencies via risk-based investment strategies: minimum variance,
minimum conditional value at risk, inverse volatility and maximum
diversification.
The results are in line with previous research regarding the
inclusion of Bitcoin in a global portfolio of equities, bonds and alternative
assets. I find that the risk return efficiency is enhanced under all
strategies. The small increase in volatility was compensated with
proportionally greater returns.
Despite their extreme volatility, the addition of alternative
cryptocurrencies to a global diversified portfolio, which already contains
Bitcoin, enhances the risk return reward. However, these crypto-assets yield
higher volatility and higher maximum drawdown under all strategies. Further,
the performance of the portfolio is boosted significantly under inverse
volatility and maximum diversification. In fact, these modern risk based
strategies prompt higher risk return reward via greater cryptocurrency exposure
and especially greater alternative cryptos exposure. On the other side, due to
their volatility structure, Minimum variance and Minimum C-var strategies
invested in cryptocurrencies and particularly in Bitcoin only in certain points
of time.
22
Moreover, the hedging properties of Cryptocurrencies are
analyzed via the portfolios maximum drawdown. When adding Bitcoin, I find that
it slightly drops under minimum variance and inverse volatility strategy.
However, when Dash, Ripple and Litecoin are further added, the maximum drawdown
increases under the four optimization models.
As robustness checking, I apply the aforementioned allocation
strategies using weekly data. Results persist robustly. Cryptocurrencies
enhance the portfolio performance on risk-adjusted basis but do not really
decrease the portfolio downside risk.
In a nutshell, the study evidence suggests that
cryptocurrencies can act as outstanding diversifier tools on a global
perspective but do not offer appealing hedging properties.
However, the results of this study should be interpreted with
caution. This analysis employs only limited asset allocation strategies. The
sample period is small due to the short history of cryptocurrencies and better
alternative to the selected cryptocurrencies might exist.
23
Appendix:
Table 1: Descriptive statistics of traditional
assets.
Summary statistics of daily log returns for traditional assets
from 31 July 2014 to 30 April 2019. (N=1238 observations). Results are reported
on a percentage basis apart from skewness, kurtosis, Sharpe ratio, the JB and
LJBox tests. In addition, Sharpe ratio is annualized.
|
S&P 500 Eurostoxx 50
|
SSE A
shares
|
Nikkei 225
|
MSCI Markets EM
|
IBOXX LIG
|
S&P GSD
|
FTSE EPRA NAREIT
|
S&P GSCI GOLD
|
|
Mean
|
0.042
|
0.008
|
0.027
|
0.030
|
0.011
|
0.014
|
0.002
|
0.022
|
-0.002
|
|
Standard Deviation
|
0.833
|
1.117
|
1.507
|
1.136
|
0.897
|
0.295
|
0.354
|
0.792
|
0.815
|
|
Skewness
|
-0.448
|
-0.786
|
-1.190
|
-0.261
|
-0.311
|
-0.332
|
-0.002
|
-0.748
|
0.271
|
|
Kurtosis
|
7.068
|
12.335
|
10.063
|
7.079
|
4.721
|
3.926
|
5.312
|
9.167
|
6.036
|
|
Minimum
|
-4.184
|
-11.102
|
-8.869
|
-5.742
|
-5.101
|
-1.451
|
-1.922
|
-6.912
|
-3.418
|
|
1% percentile
|
-2.520
|
-3.037
|
-6.109
|
-3.460
|
-2.330
|
-0.741
|
-0.950
|
-2.271
|
-2.252
|
|
5% quantile
|
-1.427
|
-1.709
|
-2.221
|
-1.791
|
-1.501
|
-0.492
|
-0.580
|
-1.235
|
-1.353
|
|
25% quantile
|
-0.255
|
-0.574
|
-0.473
|
-0.486
|
-0.511
|
-0.157
|
-0.187
|
-0.373
|
-0.404
|
|
Median
|
0.029
|
0.039
|
0.032
|
0.063
|
0.060
|
0.015
|
0.000
|
0.052
|
0.000
|
|
75% percentile
|
0.445
|
0.577
|
0.606
|
0.614
|
0.540
|
0.198
|
0.197
|
0.464
|
0.411
|
|
99% percentile
|
2.103
|
2.925
|
4.183
|
3.003
|
2.172
|
0.685
|
0.939
|
1.977
|
2.176
|
|
Maximim
|
4.842
|
5.567
|
5.599
|
6.414
|
3.228
|
0.938
|
1.802
|
3.622
|
4.590
|
|
Sharpe Ratio
|
0.800
|
0.117
|
0.285
|
0.414
|
0.193
|
0.767
|
0.013
|
0.442
|
-0.044
|
|
Jarque Bera Test
|
894.984
|
4622.047
|
2865.479
|
872.227
|
172.802
|
66.976
|
275.770
|
2077.435
|
490.681
|
|
Ljung Box Test
|
18.779
|
40.143
|
69.939
|
105.296
|
69.638
|
39.657
|
24.314
|
43.257
|
20.791
|
|
Critical Value Jarque Bera Test
|
5.943
|
|
|
|
|
|
|
|
|
Critical Value Ljung Box Test
|
31.400
|
|
|
|
|
|
|
|
24
Table 2: Descriptive statistics of
cryptocurrencies.
Summary statistics of daily log returns for cryptocurrencies from
31 July 2014 to 30 April 2019. (N=1238 observations).
|
Bitcoin
|
Ripple
|
Dash
|
Litecoin
|
|
Mean
|
0.179
|
0.330
|
0.242
|
0.185
|
|
Standard Deviation
|
4.394
|
7.513
|
7.522
|
6.945
|
|
Skewness
|
-0.210
|
2.381
|
0.015
|
1.000
|
|
Kurtosis
|
8.206
|
20.257
|
27.050
|
15.789
|
|
Minimum
|
-23.874
|
-35.328
|
-86.020
|
-51.393
|
|
1% percentile
|
-13.533
|
-18.051
|
-19.343
|
-15.550
|
|
5% quantile
|
-7.056
|
-9.364
|
-9.759
|
-8.994
|
|
25% quantile
|
-1.423
|
-2.430
|
-2.845
|
-2.138
|
|
Median
|
0.222
|
-0.345
|
-0.276
|
0.000
|
|
75% percentile
|
1.890
|
2.089
|
2.990
|
1.822
|
|
99% percentile
|
13.828
|
27.293
|
23.589
|
26.831
|
|
Maximim
|
22.512
|
75.083
|
76.818
|
53.980
|
|
Sharpe Ratio
|
0.645
|
0.698
|
0.511
|
0.422
|
|
Jarque Bera Test
|
1406.84
|
16530.00
|
29834.76
|
8643.49
|
|
Ljung Box Test
|
31.76
|
91.30
|
26.56
|
36.60
|
|
Critical Value Jarque Bera Test
|
|
5.94
|
|
|
|
Critical Value Ljung Box Test
|
|
31.40
|
|
|
25
Table 3: Correlation matrix
This table shows unconditional pairwise correlation coefficients
between cryptocurrencies and traditional assets from 31 July 2014 to 30 April
2019.
|
Bitcoin
|
Ripple
|
Dash
|
Litecoin
|
S&P500
|
Eurostoxx
50
|
SSE A
Shares
|
Nikkei
225
|
MSCI
EM
|
IBOXX
LIG
|
S&P
GSD
|
FTSE
EPRA
|
S&P
GSCI
GOLD
|
|
Bitcoin
|
1.000
|
0.330
|
0.485
|
0.592
|
0.039
|
0.036
|
0.012
|
-0.037
|
0.016
|
-0.023
|
0.010
|
-0.019
|
0.023
|
|
Ripple
|
|
1.000
|
0.254
|
0.332
|
0.053
|
0.030
|
-0.007
|
0.020
|
0.063
|
0.035
|
0.033
|
0.010
|
0.026
|
|
Dash
|
|
|
1.000
|
0.431
|
0.080
|
0.068
|
0.030
|
-0.013
|
0.049
|
-0.073
|
-0.037
|
-0.017
|
-0.006
|
|
Litecoin
|
|
|
|
1.000
|
0.026
|
0.004
|
-0.015
|
-0.026
|
0.007
|
-0.006
|
0.009
|
-0.015
|
-0.016
|
|
S&P500
|
|
|
|
|
1.000
|
0.493
|
0.162
|
0.065
|
0.441
|
-0.193
|
-0.214
|
0.515
|
-0.138
|
|
Eurostoxx 50
|
|
|
|
|
|
1.000
|
0.127
|
0.160
|
0.578
|
-0.125
|
-0.026
|
0.256
|
-0.099
|
|
SSE A Shares
|
|
|
|
|
|
|
1.000
|
0.211
|
0.413
|
0.013
|
-0.101
|
0.230
|
-0.058
|
|
Nikkei 225
|
|
|
|
|
|
|
|
1.000
|
0.416
|
0.203
|
0.124
|
0.181
|
0.102
|
|
MSCI EM
|
|
|
|
|
|
|
|
|
1.000
|
0.022
|
-0.032
|
0.435
|
0.018
|
|
IBOXX LIG
|
|
|
|
|
|
|
|
|
|
1.000
|
0.446
|
0.108
|
0.280
|
|
S&P GSD
|
|
|
|
|
|
|
|
|
|
|
1.000
|
-0.373
|
0.558
|
|
FTSE EPRA
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
NAREIT
|
|
|
|
|
|
|
|
|
|
|
|
1.000
|
-0.177
|
|
S&P GSCI
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
GOLD
|
|
|
|
|
|
|
|
|
|
|
|
|
1.000
|
26
Figure 1 : Density of
Cryptocurrencies.
The following figure illustrates Gaussian kernel density
estimators of cryptocurrencies against fitted normal distribution.
The subsequent tables summarize the dynamic conditional
correlations between daily returns of the four cryptocurrencies and traditional
asset class. Standard deviations are expressed in percentage.
Table 4: DCC statistics for traditional assets against
Bitcoin
|
Mean
|
Std.deviation
|
Minimum
|
Median
|
Maximum
|
25%
quantile
|
75% quantile
|
|
S&P 500
|
0.0146
|
2.2501%
|
-0.1343
|
0.0147
|
0.2738
|
0.0099
|
0.0194
|
|
Eurostoxx 50
|
0.0648
|
0.0022%
|
0.0648
|
0.0648
|
0.0649
|
0.0648
|
0.0648
|
|
SSE_A shares
|
-0.0056
|
0.0038%
|
-0.0061
|
-0.0056
|
-0.0052
|
-0.0056
|
-0.0056
|
|
Nikkei 225
|
-0.0374
|
3.2494%
|
-0.0977
|
-0.0317
|
0.0194
|
-0.0693
|
-0.0102
|
|
MSCI EM
|
0.0196
|
0.0002%
|
0.0196
|
0.0196
|
0.0196
|
0.0196
|
0.0196
|
|
IBOXX LIG
|
-0.0149
|
0.0002%
|
-0.0150
|
-0.0149
|
-0.0149
|
-0.0149
|
-0.0149
|
|
S&P GSD
|
0.0112
|
0.2561%
|
-0.0252
|
0.0112
|
0.0243
|
0.0106
|
0.0118
|
|
FTSE EPRA
|
|
|
|
|
|
|
|
|
NAREIT
|
-0.0320
|
0.2980%
|
-0.0541
|
-0.0321
|
-0.0029
|
-0.0331
|
-0.0310
|
|
S&P GSCI gold
|
0.0166
|
0.0002%
|
0.0165
|
0.0166
|
0.0166
|
0.0166
|
0.0166
|
27
Table 5: DCC statistics for traditional assets against
Ripple
|
Mean
|
Std.deviation
|
Minimum
|
Median
|
Maximum
|
25% quantile
|
75% quantile
|
|
S&P 500
|
0.064
|
3.12%
|
-0.009
|
0.064
|
0.173
|
0.040
|
0.082
|
|
Eurostoxx 50
|
0.044
|
0.00%
|
0.044
|
0.044
|
0.044
|
0.044
|
0.044
|
|
SSE_A shares
|
0.004
|
7.65%
|
-0.255
|
-0.002
|
0.337
|
-0.040
|
0.048
|
|
Nikkei 225
|
0.013
|
2.13%
|
-0.049
|
0.011
|
0.094
|
0.000
|
0.025
|
|
MSCI EM
|
0.073
|
2.56%
|
-0.010
|
0.071
|
0.200
|
0.059
|
0.084
|
|
IBOXX LIG
|
0.018
|
0.13%
|
0.007
|
0.018
|
0.026
|
0.018
|
0.018
|
|
S&P GSD
|
0.034
|
0.00%
|
0.034
|
0.034
|
0.034
|
0.034
|
0.034
|
|
FTSE EPRA
|
|
|
|
|
|
|
|
|
NAREIT
|
0.020
|
4.48%
|
-0.312
|
0.019
|
0.338
|
0.002
|
0.037
|
|
S&P GSCI gold
|
0.026
|
0.00%
|
0.026
|
0.026
|
0.026
|
0.026
|
0.026
|
Table 6: DCC statistics for traditional assets against
DASH.
|
Mean
|
Std.deviation
|
Minimum
|
Median
|
Maximum 25% quantile 75% quantile
|
|
S&P 500
|
0.11
|
1.4%
|
0.03
|
0.10
|
0.18
|
0.10
|
0.11
|
|
Eurostoxx 50
|
0.10
|
3.1%
|
-0.08
|
0.10
|
0.27
|
0.09
|
0.11
|
|
SSE_A shares
|
0.04
|
0.0%
|
0.04
|
0.04
|
0.04
|
0.04
|
0.04
|
|
Nikkei 225
|
0.02
|
0.7%
|
-0.03
|
0.02
|
0.11
|
0.02
|
0.03
|
|
MSCI EM
|
0.08
|
2.5%
|
0.00
|
0.08
|
0.18
|
0.07
|
0.10
|
|
IBOXX LIG
|
-0.07
|
0.0%
|
-0.07
|
-0.07
|
-0.07
|
-0.07
|
-0.07
|
|
S&P GSD
|
-0.04
|
0.0%
|
-0.04
|
-0.04
|
-0.04
|
-0.04
|
-0.04
|
|
FTSE EPRA
|
|
|
|
|
|
|
|
|
NAREIT
|
-0.01
|
8.2%
|
-0.45
|
-0.01
|
0.49
|
-0.05
|
0.03
|
|
S&P GSCI gold
|
-0.02
|
2.1%
|
-0.26
|
-0.02
|
0.10
|
-0.02
|
-0.01
|
28
Table 7: DCC statistics for traditional assets against
Litecoin
|
Mean
|
Std.deviation Minimum
|
Median
|
Maximum
|
25% quantile 75% quantile
|
|
S&P 500
|
0.018
|
4.89%
|
-0.164
|
0.011
|
0.192
|
-0.010
|
0.040
|
|
Eurostoxx 50
|
0.035
|
1.88%
|
-0.036
|
0.035
|
0.120
|
0.027
|
0.043
|
|
SSE_A shares
|
-0.027
|
2.90%
|
-0.099
|
-0.029
|
0.042
|
-0.044
|
-0.014
|
|
Nikkei 225
|
-0.021
|
0.00%
|
-0.021
|
-0.021
|
-0.021
|
-0.021
|
-0.021
|
|
MSCI EM
|
0.020
|
2.47%
|
-0.086
|
0.020
|
0.110
|
0.006
|
0.033
|
|
IBOXX LIG
|
-0.010
|
4.31%
|
-0.129
|
-0.009
|
0.181
|
-0.031
|
0.012
|
|
S&P GSD
|
0.001
|
0.00%
|
0.001
|
0.001
|
0.001
|
0.001
|
0.001
|
|
FTSE EPRA
|
|
|
|
|
|
|
|
|
NAREIT
|
-0.016
|
0.00%
|
-0.017
|
-0.016
|
-0.016
|
-0.016
|
-0.016
|
|
S&P GSCI gold
|
-0.016
|
5.46%
|
-0.207
|
-0.009
|
0.154
|
-0.046
|
0.018
|
Figure 2 : Dynamic conditional correlation plot of
S&P 500 against cryptocurrencies and gold.
29
The following tables present the performance of the three
optimal portfolios: Portfolio I: a portfolio of traditional assets, which
encompasses equities, bonds and alternative investments. Portfolio II: a
portfolio of traditional assets and Bitcoin. Portfolio III: a portfolio of
traditional assets, Bitcoin and alternative cryptocurrencies. Four different
optimization frameworks are performed subsequently: Minimum variance, Minimum
Conditional Value at Risk, Inverse Volatility and Maximum Diversification
frameworks. I use a 200 days moving window and the out of sample period ranges
from May-08-2015 to April-30-2019. Sharpe ratio, mean daily return and standard
deviation are annualized.
|
Table 8: Minimum Variance strategy
|
|
|
Portfolio I
|
Portfolio II
|
Portfolio III
|
|
Mean (%)
|
3.81%
|
4.14%
|
4.60%
|
|
Standard deviation (%)
|
3.62%
|
3.62%
|
3.64%
|
|
Skewness
|
-0.45
|
-0.44
|
-0.43
|
|
Kurtosis
|
5.30
|
5.24
|
5.06
|
|
Maximum drawdown (%)
|
5.43%
|
5.37%
|
5.45%
|
|
Cumulative wealth
|
1.16
|
1.17
|
1.19
|
|
Sharpe ratio
|
1.05
|
1.14
|
1.26
|
Table 9: Minimum conditional value at risk
strategy
|
Portfolio I
|
Portfolio II
|
Portfolio III
|
|
Mean (%)
|
3.80%
|
4.51%
|
5.08%
|
|
Standard deviation (%)
|
3.64%
|
3.85%
|
3.94%
|
|
Skewness
|
-0.41
|
-0.36
|
-0.37
|
|
Kurtosis
|
5.25
|
5.13
|
5.09
|
|
Maximum drawdown (%)
|
5.50%
|
5.70%
|
6.93%
|
|
Cumulative wealth
|
1.16
|
1.19
|
1.21
|
|
Sharpe ratio
|
1.04
|
1.17
|
1.29
|
30
|
Table 10 : Inverse volatility strategy.
|
|
|
Portfolio I
|
Portfolio II
|
Portfolio III
|
|
Mean (%)
|
2.91%
|
4.42%
|
7.67%
|
|
Standard deviation (%)
|
5.17%
|
5.20%
|
5.88%
|
|
Skewness
|
-0.39
|
-0.46
|
-0.45
|
|
Kurtosis
|
5.35
|
5.53
|
5.57
|
|
Maximum drawdown (%)
|
11.85%
|
10.39%
|
11.70%
|
|
Cumulative wealth
|
1.12
|
1.18
|
1.32
|
|
Sharpe ratio
|
0.56
|
0.85
|
1.30
|
Table 11 : Maximum diversification
strategy.
|
Portfolio I
|
Portfolio II
|
Portfolio III
|
|
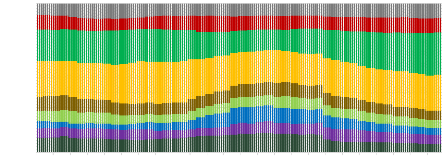
Mean (%)
|
3.31%
|
5.94%
|
8.75%
|
|
Standard deviation (%)
|
4.50%
|
4.86%
|
5.65%
|
|
Skewness
|
-0.37
|
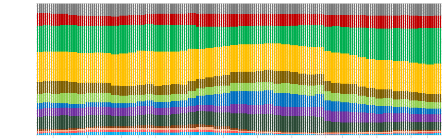
-0.31
|
0.07
|
|
Kurtosis
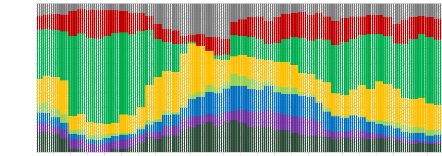
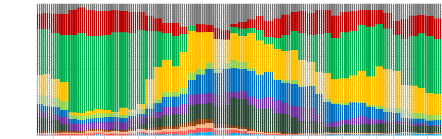
|
5.08
|
4.91
|
7.09
|
|
Maximum drawdown (%)
|
8.15%
|
9.40%
|
9.46%
|
|
Cumulative wealth
|
1.13
|
1.24
|
1.36
|
|
Sharpe ratio
|
0.73
|
1.22
|
1.54
|
FIGURES: Weight Allocation
The following graphs display the weight allocation for
traditional assets and cryptocurrencies from 8 May 2015 until 30 April 2019
under the following strategies: minimum conditional value at risk, inverse
volatility, and maximum diversification.
Minimum Conditional Value at Risk
Portfolio of traditional
assets
08.05.2015 08.07.2015 08.09.2015 08.11.2015 08.01.2016 08.03.2016
08.05.2016 08.07.2016 08.09.2016 08.11.2016 08.01.2017 08.03.2017 08.05.2017
08.07.2017 08.09.2017 08.11.2017 08.01.2018 08.03.2018 08.05.2018 08.07.2018
08.09.2018 08.11.2018 08.01.2019 08.03.2019
1,00
0,90
0,80
0,70
Weights
0,60
0,50
0,40
0,30
0,20
0,10
0,00
Year
S&P 500 Eurostoxx 50 SSE A Shares Nikkei 225 MSCI EM
IBOXX LIG S&P GSD FTSE EPRA NAREIT S&P GSCI GOLD
Minimum Conditional Value at Risk Portfolio of tradtional assets
and cryptocurrencies
08.05.2015 08.07.2015 08.09.2015 08.11.2015 08.01.2016 08.03.2016
08.05.2016 08.07.2016 08.09.2016 08.11.2016 08.01.2017 08.03.2017 08.05.2017
08.07.2017 08.09.2017 08.11.2017 08.01.2018 08.03.2018 08.05.2018 08.07.2018
08.09.2018 08.11.2018 08.01.2019 08.03.2019
1,00
0,90
0,80
0,70
Weights
0,60
0,50
0,40
0,30
0,20
0,10
0,00
31
Year
Bitcoin Ripple Dash Litecoin S&P500
Eurostoxx 50 SSE A Shares Nikkei 225 MSCI EM IBOXX LIG
S&P GSD FTSE EPRA NAREIT S&P GSCI GOLD
Inverse Volatility
Portfolio of traditional assets
08.05.2015 08.07.2015 08.09.2015 08.11.2015 08.01.2016 08.03.2016
08.05.2016 08.07.2016 08.09.2016 08.11.2016 08.01.2017 08.03.2017 08.05.2017
08.07.2017 08.09.2017 08.11.2017 08.01.2018 08.03.2018 08.05.2018 08.07.2018
08.09.2018 08.11.2018 08.01.2019 08.03.2019
1,00
0,90
0,80
0,70
Weights
0,60
0,50
0,40
0,30
0,20
0,10
0,00
Year
S&P 500 Eurostoxx 50 SSE A Shares Nikkei 225 MSCI EM
IBOXX LIG S&P GSD FTSE EPRA NAREIT S&P GSCI GOLD
Inverse Volatility
Portfolio of traditional assets and
cryptocurrencies
08.05.2015 08.07.2015 08.09.2015 08.11.2015 08.01.2016 08.03.2016
08.05.2016 08.07.2016 08.09.2016 08.11.2016 08.01.2017 08.03.2017 08.05.2017
08.07.2017 08.09.2017 08.11.2017 08.01.2018 08.03.2018 08.05.2018 08.07.2018
08.09.2018 08.11.2018 08.01.2019 08.03.2019
1,00
0,90
0,80
0,70
Weights
0,60
0,50
0,40
0,30
0,20
0,10
0,00
32
Year
Bitcoin Ripple Dash Litecoin S&P500
Eurostoxx 50 SSE A Shares Nikkei 225 MSCI EM IBOXX LIG
S&P GSD FTSE EPRA NAREIT S&P GSCI GOLD
Maximum Diversification
Portfolio of traditional
assets
08.05.2015 08.07.2015 08.09.2015 08.11.2015 08.01.2016 08.03.2016
08.05.2016 08.07.2016 08.09.2016 08.11.2016 08.01.2017 08.03.2017 08.05.2017
08.07.2017 08.09.2017 08.11.2017 08.01.2018 08.03.2018 08.05.2018 08.07.2018
08.09.2018 08.11.2018 08.01.2019 08.03.2019
1,00
0,90
0,80
0,70
Weights
0,60
0,50
0,40
0,30
0,20
0,10
0,00
Year
S&P 500 Eurostoxx 50 SSE A shares Nikkei 225 MSCI EM
IBOXX LIG S&P GSD FTSE EPRA NAREIT S&P GSCI GOLD
Maximum Diversification
Portfolio of traditional assets and
crytocurrencies
08.05.2015 08.07.2015 08.09.2015 08.11.2015 08.01.2016 08.03.2016
08.05.2016 08.07.2016 08.09.2016 08.11.2016 08.01.2017 08.03.2017 08.05.2017
08.07.2017 08.09.2017 08.11.2017 08.01.2018 08.03.2018 08.05.2018 08.07.2018
08.09.2018 08.11.2018 08.01.2019 08.03.2019
1,00
0,90
0,80
0,70
Weights
0,60
0,50
0,40
0,30
0,20
0,10
0,00
33
Year
Bitcoin Ripple Dash Litecoin S&P500
Eurostoxx 50 SSE A Shares Nikkei 225 MSCI EM IBOXX LIG
S&P GSD FTSE EPRA NAREIT S&P GSCI GOLD
34
The subsequent tables present the results obtained from the
robustness check. It reports the performance of the optimal portfolios when
using weekly data. I use 40 weeks (Equivalent of 200 trading days) moving
window and the out of sample period ranges from May-08-2015 to April-30-2019.
Sharpe ratio, mean daily return and standard deviation are annualized.
|
Table 12: Minimum variance strategy
|
|
|
Portfolio I
|
Portfolio II
|
Portfolio III
|
|
Mean (%)
|
3.38%
|
4.08%
|
5.64%
|
|
Standard deviation (%)
|
4.29%
|
4.31%
|
4.53%
|
|
Skewness
|
-1.17
|
-1.26
|
-1.01
|
|
Kurtosis
|
10.07
|
10.31
|
8.93
|
|
Maximum drawdown (%)
|
6.97%
|
6.50%
|
7%
|
|
Cumulative wealth
|
1.13
|
1.16
|
1.22
|
|
Sharpe ratio
|
0.79
|
0.95
|
1.24
|
Table 13: Minimum conditional value at risk
strategy
|
Portfolio I
|
Portfolio II
|
Portfolio III
|
|
Mean (%)
|
3.30%
|
4.36%
|
10.40%
|
|
Standard deviation (%)
|
4.45%
|
5.15%
|
6.07%
|
|
Skewness
|
-1.30
|
-2.54
|
-1.53
|
|
Kurtosis
|
14.30
|
21.90
|
14.09
|
|
Maximum drawdown (%)
|
7.00%
|
8.74%
|
9.00%
|
|
Cumulative wealth
|
1.14
|
1.17
|
1.39
|
|
Sharpe ratio
|
0.74
|
0.85
|
1.60
|
35
|
Table 14: Inverse volatility strategy
|
|
|
Portfolio I
|
Portfolio II
|
Portfolio III
|
|
Mean (%)
|
3.00%
|
4.59%
|
8.16%
|
|
Standard deviation (%)
|
6.15%
|
6.23%
|
6.85%
|
|
Skewness
|
-0.78
|
-0.83
|
-0.66
|
|
Kurtosis
|
5.75
|
5.81
|
4.73
|
|
Maximum drawdown (%)
|
10.83%
|
9.83%
|
11.0%
|
|
Cumulative wealth
|
1.11
|
1.18
|
1.32
|
|
Sharpe ratio
|
0.49
|
0.74
|
1.19
|
|
Table 15: Maximum diversification strategy
|
|
|
Portfolio I
|
Portfolio II
|
Portfolio III
|
|
Mean (%)
|
3.11%
|
6.55%
|
11.64%
|
|
Standard deviation (%)
|
5.76%
|
6.52%
|
8.83%
|
|
Skewness
|
-1.24
|
-1.20
|
0.36
|
|
Kurtosis
|
9.39
|
8.25
|
7.40
|
|
Maximum drawdown (%)
|
8.69%
|
10.02%
|
9.57%
|
|
Cumulative wealth
|
1.12
|
1.26
|
1.45
|
|
Sharpe ratio
|
0.54
|
1.00
|
1.31
|
36
Salma Ouali
References
Bouri, E., Molnár, P., Azzi, G., Roubaud, D., Hagfors,
L.I., 2017. On the hedge and safe haven properties of Bitcoin: Is it really
more than a diversifier? Finance Research Letters 20, 192-198.
Briere, M., Oosterlinck, K., Szafrz, A., 2015. Virtual
currency, tangible return: Portfolio diversification with bitcoin. Journal of
Asset Management, 16, 6, 365-373.
Brauneis, A., Mestel, R., 2019. Cryptocurrency-portfolios in a
mean-variance framework. Finance Research Letters 28, 259-264.
Dyhrberg, A. H., 2016. Bitcoin, gold and the dollar- A GARCH
volatility analysis. Finance Research Letters, 85-92.
Eisl, A., Gasser, S.M., Weinmayer, K., 2015. Caveat emptor:
Does bitcoin improve portfolio diversification?
Engle, E., 2000. Dynamic conditional correlation - A simple
class of multivariate GARCH models.
Guesmi, K. Samir Saadi, S., Abid, I., Ftiti, Z., 2018.
Portfolio diversification with virtual currency: Evidence from bitcoin.
International Review of Financial Analysis.
Henriques, I., Sadorsky, P., 2018. Can bitcoin replace gold in
an investment portfolio? Journal of Risk and Financial Management 11, 48.
Hong, K., 2016. Bitcoin as an alternative investment vehicle.
Springer Science+ Business Media
Kajtazi, A., Moro, A., 2017. Bitcoin, portfolio
diversification and Chinese financial markets
Klein, T., Thu, H.P., Walthe, T., 2018. Bitcoin is not the new
gold, a comparison of volatility, correlation, and portfolio performance.
Working paper.
Lee, D.K.K., Li Guo, L., Yu Wang, Y., 2017. Cryptocurrency: A
new investment opportunity? Liu, W., 2018. Portfolio diversification across
cryptocurrencies. Finance Research Letters.
Lorenz, J., Strika, M., 2017. Bitcoin and cryptocurrencies -
not for the faint-hearted. International Finance and Banking 4, 1.
Petukhina, A., Trimborn, S., Härdle, W.K., Elendner, H.,
2018. Investing with cryptocurrencies - evaluating the potential of portfolio
allocation.
Platanakis, E., Urquhart, A., 2018. Should investors include
bitcoin in their portfolios? A portfolio theory approach.
Rockafellar, R.T., Uryasev, S., 1999. Optimization of
conditional value at risk. Journal of Risk, 21-41.
37
Salma Ouali
Svärd, S., 2014. Dynamic portfolio strategy using
multivariate garch model. Working Paper
Symitsi, E., Chalvatzis, K.J., 2019. The economic value of
bitcoin: A portfolio analysis of currencies, gold, oil and stocks. Research in
International Business and Finance 48, 97-110.
Urquhart, A., Zhang, H., 2016. Bitcoin a hedge or safe-haven for
currencies? An intraday analysis.
| 


