|

Mémoire de MASTER ii MOUTNGUI SEE
c?UYI 2010-2011.
EXISTENCE GLOBALE DES SOLUTIONS
DU SYSTÈME COUPLÉ DE
MAXWELL-BOLTZMANN-EULER SUR UN
ESPACE-TEMPS DE BIANCHI I
Mémoire Présenté et soutenu
publiquement
en vue de l'obtention du MASTER
en Mathématiques
Option : Analyse
Par
MOUTNGUI SEE Timothée Raoul
Maître ès Sciences
Matricule: 08V 1011
Sous la direction de :
Pr. NOUTCHEGUEME Norbert
Professeur
Université de Yaoundé I
Année Académique 2010/2011
Mémoire de MASTER iii MOUTNGUI SEE c?UYI
2010-2011.
Mémoire de MASTER i MOUTNGUI SEE
c?UYI 2010-2011.
Dédicace
A` ma mère OBONO Philomène
félicité pour son soutien et sa forte contribution à
mon éducation et à ma réussite.
Mémoire de MASTER ii MOUTNGUI SEE
c?UYI 2010-2011.
Remerciements
Le travail que je présente aujourd'hui n'aurait jamais
atteint ce stade si je n'avais bénéficié de l'encadrement
du professeur NOUTCHEGUEME Norbert, pour nous avoir
fait l'honneur de diriger ce travail en y mettant beaucoup de rigueur et de
méthode. Sa disponibilité, son savoir et toute l'attention qu'il
a toujours accordé à ce travail nous a permis de le mener
à terme.
Je tiens à remercier tous les enseignants de la
faculté des sciences de l'Université de Yaoundé I, en
particulier les professeurs NGUETSENG,
DOSSA Marcel, WAMON
Francois, TONGA Marcel et les docteurs
NOUNDJEU Pierre, AYISSI Raoult
et FOMEKONG Christophe.
J'exprime ma reconnaissance à tous les enseignants du
département de Mathématiques de la faculté des sciences de
l'Université de Douala; particulièrement aux docteurs
IKOLLO NDOUMBE Moïse et NGAKEU
Ferdinang qui m'ont initié en Mathématiques.
Je remercie tous mes camarades de promotion, en particulier
YEMATA KEU-NANG Francis et SEUTCHE
Dietric qui m'ont été d'un grand secours pour
l'ac-complissement de ce travail. Je dis merci à mes amies
MPESSE AYISSI Danièle et MFOUMOU
Ginette pour leur soutien tant bien moral que financier.
Je remercie mon père ESSE
Benjamin, BITOUNI Elsie, mes petits
frères ESSE Christian Eloi et
NDIGUI Dimitri et mes petites soeurs NGO
MOUTNGUI Christine et NGO NDIGUI Corine
qui représentent tous ceux que j'ai de plus chers au
monde. Enfin j'exprime ma gratitude aux familles
MOUTNGUI, MBOUDOU et
EYIKE EBOBISSE.
Mémoire de MASTER iii MOUTNGUI
SEE c?UYI 2010-2011.
Résumé
On étudie l'existence globale des solutions du
système couplé de Maxwell-Boltzmann-Euler, qui gouverne en
théorie cinétique des plasmas relativistes, l'évolution
avec collisions d'un train de particules massives de matière pure
chargée dans un espace-temps de Bianchi I, en négligeant l'action
des forces de gravitation devant les forces
électromagnétiques.
Mémoire de MASTER iv MOUTNGUI SEE
c?UYI 2010-2011.
Table des matières
Dédicace i
Remerciements ii
Résumé iii
Introduction 1
1 FORMULATION DU PROBLÈME ET ÉQUATIONS 3
1.1 Espace-temps de base et fonctions inconnues 3
1.2 Le système de Maxwell en F 5
1.3 L'équation de Boltzmann en f 8
1.4 Équations d'Euler et système
différentiel en u = (uá) 11
1.5 Le système couplé à étudier
14
1.6 Les espaces de fonctions 16
2 EXISTENCE LOCALE DES SOLUTIONS 18
3 EXISTENCE GLOBALE DES SOLUTIONS 33
3.1 La méthode 33
3.2 Existence globale des solutions 39
Conclusion et perspectives 47
Annexes 48
Bibliographie 60
Mémoire de MASTER 1 MOUTNGUI SEE
c?UYI 2010-2011.
Introduction
Dans notre étude, nous étudions
l'évolution à très grande vitesse et avec collisions d'un
train de particules massives de matière pure chargée sous
l'action des forces électromagnétiques créées par
le mouvement des particules chargées. L'espace-temps étant celui
de Bianchi I qui est une généralisation de l'espace-temps de
Friedmann-Lemaitre-Robertson-Walker reconnu comme l'espace-temps de base de la
cosmologie, où les phénomènes homogènes tel que
nous les considérons ici sont importants. Notons que l'univers tout
entier est modelé et ce que nous appelons particules dans la description
cinétique, peuvent être des galaxies ou un groupe de galaxies,
raison pour laquelle seulement l'évolution dans le temps est
réellement significative, d'où l'importance des
phénomènes homogènes.
Les équations de Maxwell sont les équations de
base de l'électromagnétisme, elles déterminent le champ
électromagnétique créé par le mouvement des
particules chargées. Les équations de Maxwell dépendent du
courant de Maxwell définit par la fonction de distribution f,
la densité de charge e et le vecteur-vitesse matérielle
unitaire u supposé temporel futur.
L'équation de Boltzmann relativiste en f
considérée ici est l'une des équations de base de la
théorie cinétique relativiste. Cette équation
décrit la dynamique des particules massives et chargées en
déterminant leur fonction de distribution f qui est une
fonction scalaire positive de la position et de l'impulsion des particules.
L'équation de Boltzmann généralise l'équation de
Vlasov qui gouverne les cas sans collision en introduisant l'opéra-teur
de collision. Les équations d'Euler expriment la conservation du tenseur
d'impulsion-énergie Táâ qui
représente le contenu matériel et énergétique de
l'espace-temps. Le tenseur d'impulsion-énergie est défini en
fonction de la fonction de distribution f des particules, du champ
électromagnétique F, de la pseudo densité
constante P0 des particules et du vecteur-vitesse matérielle
u.
Mémoire de MASTER 2 MOUTNGUI SEE
c?UYI 2010-2011.
TABLE DES MATIÈRES
Quelques auteurs ont prouvé l'existence locale des
solutions pour l'équation de Boltzmann relativiste, en
considérant cette équation seule comme D. Bancel en [1], K.
Bichteler en [3] ou en la couplant à d'autres équations comme D.
Bancel et Y. Choquet-Bruhat en [2]; R. T. Glassey et W. Strauss ont obtenu un
résultat global en [4]. P.B. Mucha a étudié
l'équation de Boltzmann couplé à l'équation
d'Einstein en [7] et [8]. Récemment N. Noutchegueme et E. Takou en [11]
et N. Noutchegueme et D. Dongo en [9] ont étudié
l'équation de Boltzmann relativiste couplé à
l'équation d'Einstein dans l'espace-temps de Robertson-Walker et dans
l'espace-temps de Bianchi 1 respectivement, mais seulement N. Noutchegueme, D.
Dongo et E. Takou ont prouvé l'existence globale des solutions de
l'équation de Boltzmann en [10]. N. Noutchegueme et R.D. Ayissi ont
prouvé l'exis-tence globale des solutions du système
couplé Maxwell-Boltzmann sur un espace-temps de Bianchi I en [12].
L'objectif de notre travail est d'étendre le résultat de [12] au
système couplé Maxwell-Boltzmann-Euler. La méthode pour
prouver l'existence globale des solutions est similaire à celle faite en
[12]. Dans le cas des particules chargées, l'impulsion p =
(pá) des particules devient aussi une inconnue, et
l'étude se ramène à un système différentiel
du premier ordre non linéaire en (F, p, f, u), où nous
appliquons le théorème de Cauchy-Lipschitz.
Notre travail se présente de la manière suivante
:
Chapitre 1, on introduit les équations.
Chapitre 2, nous étudions l'existence locale.
Chapitre 3, nous prouvons l'existence globale.
Mémoire de MASTER 3
MOUTNGUI SEE c?UYI 2010-2011.
CHAPITRE UN
FORMULATION DU PROBLÈME
ET ÉQUATIONS
Tout indice grec á, â,
ry, ... varie de 0 à 3 et tout indice latin
i, j, k, ... varie de 1 à 3. On
adopte la convention de sommation d'Einstein
aábá = Eá
aábá.
1.1 Espace-temps de base et fonctions inconnues
On considère l'évolution à très
grande vitesse et avec collisions d'un train de particules massives et
chargées , de vecteur-vitesse matérielle u =
(uá), de pseudo-densité constante p0
> 0, de densité de charge e > 0, dans un
espace-temps de Bianchi I (1[84, g), orienté dans le
temps, où, en notant xá =
(x0, xi) = (t, xi)
les coordonnées usuelles de 1[84, avec t qui
représente le temps et (xi) l'espace, g est
une métrique donnée fixée de signature hyperbolique
(-, +, +, +) qui s'écrit :
2gëu
[?águâ +
?âgáu - ?ugáâ]
1
g = -dt2 +
a2(t)(dx1)2 +
b2(t) [(dx2)2 +
(dx3)2] (1.1)
où a >
0 et b > 0 sont deux fonctions données de classe
C1 sur 1R dont la variable est notée t. Les
symboles de Christoffel de la connexion de Levi-Civita V
associée à g sont définis par :
rë áâ =
Les seuls symboles rëáâ
non nuls sont les ri i0, r0 et on a :
ii
aÿa
r110 =, r220 =
r330 =b; r011 =
aÿa, r022 = r033
= bÿb. (1.2)
où aÿ = dt . On rappelle que
rëáâ = rëâá. On fait
l'hypothèse que les fonctions ÿaa et bb sont
bornées sur R i.e : C > 0 tel que :
Mémoire de MASTER 4 MOUTNGUI SEE
c?UYI 2010-2011.
1.1 Espace-temps de base et fonctions inconnues
????
< C;
bÿ b
????
???? a aÿ
????
< C (1.3)
On déduit de (1.3) que l'on a , Vt E
1[8+ :
{
a(t) < a0eCt;
b(t) < b0eCt; 1
a(t) < a01 eCt; 1
b(t) < b01 eCt (1.4)
o`u a0 = a(0) >
0,b0 = b(0) > 0.
D'après la loi de Laplace, les particules
chargées en mouvement créent un champ
électromagnétique représenté par une 2-forme
antisymétrique fermée F =
(F0i, Fij) où F0i et
Fij sont respectivement les composantes électrique
et magnétique de F. Nous considérons le cas
homogène où F dépend de la seule variable
t.
L'outil essentiel pour décrire la dynamique des
particules massives et chargées est une fonction scalaire positive
inconnue f de la position (xá) et de
l'impulsion
p = (pá) =
(p0, pi) = (p0,
p) où p = (pi), i = 1,
2, 3, des particules, appelée fonction de distribution des
particules massives et chargées ; f est donc définie sur
le fibré tangent T(1[84) de coordonnées
locales (xá, pá) :
f : T(1[84) ^'
1[84 x 1[84 ~ 1[8+,
(xá, pá) E-
f(xá, pá) E
1[8+.
On introduit un produit scalaire sur 1[83 en
posant, pour p = (pá) =
(p0, pi) = (p0,
p) et q = (qá) =
(q0, qi) = (q0,
q) :
p ' q =
a2p1q1+b2(p2q2+p3q3)
(1.5)
On suppose que les particules ont une masse propre au repos
m > 0. Les particules massives et chargées évoluent
sur la nappe future de l'hyperboloïde de masse d'équation
g(p, p) = -m2. Dans le but de simplifier
les notations, on suppose la masse m normalisée à
l'unité, i.e m = 1. On déduit alors de g(p,
p) = -1 que l'on a vu (1.1) :
v
p0 = 1 +
a2(p1)2 +
b2 [(p2)2 +
(p3)2] (1.6)
où le choix p0 > 0
s'explique par le fait que de façon naturelle, les particules
s'éjectent vers le futur. (1.6) montre que
p0 ne s'annule jamais et qu'en fait, f est
définie sur le sous-fibré de T(1[84) de
composantes locales xá et pi.
Nous considérons le cas homogène où f ne
dépend que de t et de pi.
Les trajectoires des particules sont les courbes s H
(xá(s),
pá(s)) dans le fibré tangent
T(1[84), solutions du système différentiel
:
dxá ds
dpá
= pá; = Pá
(1.7)
ds
Mémoire de MASTER 5 MOUTNGUI SEE
c?UYI 2010-2011.
1.2 Le système de Maxwell en F
où :
Pá = Pá(F) =
-Páëupëpu
+ep'F á (1.8)
'
où, dans le cas homogène
considéré, e > 0 est la densité de charge,
fonction inconnue de la seule variable t. Les formules (1.7)
et (1.8) montrent qu'en présence du champ
électromagnétique F, les trajectoires initiales des
particules sont déviées et ne sont plus les
géodésiques comme dans le vide, et que le champ de vecteurs :
X(F) = (pá,
Pá(F)) (1.9)
où Pá est donné par
(1.8), est tangent aux trajectoires.
1.2 Le système de Maxwell en F
Le système de Maxwell en F qui constitue les
équations de base de l'électromagnétisme peut
s'écrire, en notation covariante :
{
VáFá' = J'
(1.10)
V'Fãá
VãFá'
+
+
= 0 (1.11)
VáF'ã
J' =
'f(t,p)ab2dp1dp2dp3
p
(1.10) et (1.11) sont respectivement les
1er et 2e groupe des équations
de Maxwell, et Vá désigne la
dérivée covariante dans g. Dans (1.10) J'
représente le courant de Maxwell que nous prenons sous la forme
:
- eu' (1.12)
IIP3 p°
où ab2 =
|detg|12 , u = (u') est le
vecteur-vitesse matérielle unitaire supposé temporel futur,
fonction inconnue de la seule variable t. La relation
g(u, u) = -1 permet de déduire que l'on a, de
façon analogue à (1.6) :
|
vu° = 1 +
a2(u1)2 +
b2[(u2)2 +
(u3)2]
|
(1.13)
|
(1.13) montre que u° ne
s'annule jamais et que les ui déterminent
u°. Noter que l'analogie entre (1.6) et
(1.13) provient du choix m = 1. On suppose que u =
(u') ne dépend que de t.
Mémoire de MASTER 6 MOUTNGUI SEE
c?UYI 2010-2011.
1.2 Le système de Maxwell en F
Remarque 1.1.
· On vérifie
en utilisant (1.2) que :
?áFá0 = 0
(1.14)
En effet,
?áFá0 =
?áFá0 +
FááâFâ0 +
F0áâFáâ
= F0 F11 + F022 F22 + F033
F33 11
= 0
d'où :
?áFá0 = 0
Les équations de Maxwell (1.10)
imposent donc que l'on doit avoir :
J0 = 0 (1.15)
· On a toujours l'identité
?á?âFáâ
= 0. Les équations de Maxwell (1.10) imposent donc
que le courant de Maxwell J = (Jâ) est assujeti
à la loi de conservation :
?ëJë = 0
(1.16)
On a en effet de (1.2), J =
J(t) et (1.15) que :
?ëJë =
?ëJë +
FëëâJâ =
?0J0 + 110J0
= 0
d'où :
?ëJë = 0
Les équations de Maxwell (1.11) sont en fait
des identités exprimant la propriété que F est
fermée i.e : dF = 0.
Les équations de Maxwell (1.11) se scindent en
:
?0Fij + ?iFj0 +
?jF0i = 0 et ?iFjk +
?jFki + ?kFij = 0 (1.17)
En utilisant Fk ij= Fkji et Fij = -Fji,
(1.17) s'écrit :
?0Fij + ?iFj0 +
?jF0i = 0 et ?iFjk +
?jFki + ?kFij = 0 (1.18)
Mémoire de MASTER 7 MOUTNGUI SEE
c?UYI 2010-2011.
1.2 Le système de Maxwell en F
Le 2e groupe des équations (1.18)
est identiquement vérifié car Fij =
Fij(t) et pour cette même raison, le 1er
groupe des équations (1.18) se réduit à :
?0Fij = 0
D'où :
Fij = Fij(0) := öij
(1.19)
(1.19) montre que la partie magnétique
Fij n'évolue pas et reste constamment égale
à sa valeur (ou donnée) initiale, notée
öij.
Il reste donc à déterminer la partie
électrique (F0i) du champ
électromagnétique F. L'expression de
J0 fournie par (1.12) pour â = 0
donne alors vu (1.15) :
e(t) = u0 f3 f(t,
p)ab2(t)dp (1.20)
où dp =
dp1dp2dp3 ; ce qui montre que f
et les ui déterminent e. En posant
dans les équations de Maxwell (1.10) â =
i, on a :
V áFái =
Ji
or
V áFái =
?áF ái +
?ááâFâi +
?iáâFáâ
= ?0F0i +
?ááâFâi
= ?0F0i +
?00âFâi
+ ?kkâFâi
= ?0F0i +
?kkâFâi
= ?0F0i +
?kk0F0i
= ?0F0i +
(?110 + ?220 +
?330)F0i
= ?0F0i + + a 2
b/ F°i
(
ainsi V
áFái =
?0F0i + ( aÿ
+ 2 bl Fai
/
Par ailleurs, (1.12) donne, vu (1.20) :
Ji = f ~0 f(t,
p)ab2dp - eui
3
ui
= f3 P0f(t,p)ab2dp
- u0 f3 f(t,p)ab2dp
Mémoire de MASTER 8 MOUTNGUI SEE
c?UYI 2010-2011.
1.3 L'équation de Boltzmann en f
Le système ?áF ái =
Ji, s'écrit donc de façon explicite :
( aÿ ) ? ?
bÿ pi
?0F 0i+ a +2 F 0i =
p0 f(t, p)ab2dp- ui R3
f(t, p)ab2dp (1.21)
b u0
R3
C'est l'équation différentielle (1.21)
qui déterminera la partie électrique F0i du
champ électromagnétique F.
1.3 L'équation de Boltzmann en f
l'équation de Boltzmann relativiste en f, pour
les particules chargées dans l'espace-
temps de Bianchi I s'écrit en notation covariante :
LXf = Q(f,f)
(1.22)
où LXf désigne la
dérivée de Lie de f par rapport au champ de vecteurs
X défini par (1.9) et Q l'opérateur
des collisions que nous introduisons ci-après. (1.22)
s'écrit donc, vu (1.9) et avec P á
défini par (1.8) :
pá ?f
?xá + Pá ?f
?pá = Q(f,f)
(1.23)
Nous considérons, le cas des collisions binaires et
élastiques du à Lichnérowicz et Cher-nikov (1940)
où, à un instant donné t et à une position
donnée (xi) de R3, seules deux particules
rentrent en collision à la fois, sans se détruire l'une et
l'autre, la collision affectant seulement l'impulsion de chaque particule qui
n'est plus la même avant et après le choc, seule la somme des 2
impulsions est conservée, suivant le schéma:
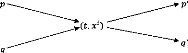
L'opérateur des collisions Q est alors
défini de la façon suivante, en prenant en compte cette situation
et en désignant par p, q les impulsions avant le choc, par
p', q' les impulsions après le choc et en utilisant
deux fonctions f et g sur R3 :
Q(f, g) = Q+(f,
g) - Q-(f, g) (1.24)
1.3 L'équation de Boltzmann en f
{ Q+(f, g)(p) = f
$3 abq0dq fS2
f(p')g(q')ó(t,
p, q, p', q')dù (1.25)
où : Q (f, g)(p) =
f$3 a q0
q fS2
f(p)g(q)ó(t, p, q,
p', q')dù (1.26)
formules dont nous présentons les
éléments étape par étape, en précisant les
hypothèses adoptées :
· S2 désigne la sphère
unité de R3 dont l'élément d'aire est
noté dù
· ó est une fonction positive et
régulière de tous ses arguments appelée noyau de la
collision ou section efficace de choc.
Nous faisons sur ó les hypothèses
suivantes. Il existe une constante C1 > 0 telle que :
{
0 < ó(t, p, q, p',
q') < C1
|ó(t, p1, q,
p', q') - ó(t,
p2, q, p', q')| <
C1|p1 - p2| (1.27)
3
où |p| = Ei)
[1(p2]
|
2
|
désigne la norme euclidienne sur R3
|
|
· Mémoire de MASTER 9
MOUTNGUI SEE c?UYI 2010-2011.
La loi de conservation p + q =
p' + q' se scinde en :
{
p0 + q0 =
p'0 + q'0
(1.28)
p + q = p' +
q' (1.29)
(1.28) exprime la conservation de la quantité
:
v v
?e = 1 +
a2(p1)2 +
b2[(p2)2 +
(p3)2] + 1 +
a2(q1)2 +
b2[(q2)2 +
(q3)2] (1.30)
appelée énergie élémentaire des
particules de masse propre au repos m = 1. Quant à
(1.29), on l'interprète en posant, suivant R. T. Glassey dans
[5] :
{
p' = p + C(p, q,
ù)ù (ù E S2)
(1.31)
q' = q -
C(p,q,ù)ù
où C(p, q, ù) est une fonction
scalaire de ses arguments.
On montre en utilisant (1.6) pour exprimer
p'0 et q'0, en
fonction de p' et q', puis
(1.31) pour exprimer p' et q'
en fonction de p et q que l'équation (1.28)
conduit à une équation du second degré en
C(p, q, ù), dont la seule solution non triviale est
donnée par :
2p0q0?e ù
· (?q - ?pl
C(p, q, ù) =
(1.32)
?e2 - [ù ·
(p + q)]2
Mémoire de MASTER 10 MOUTNGUI
SEE c?UYI 2010-2011.
1.3 L'équation de Boltzmann en f
où P = p0p,
é est donné par (1.30), et où le point
(· ) désigne le produit scalaire défini par
(1.5). ( La preuve est faite en Annexe 1. )
On déduit, en utilisant les propriétés
usuelles des déterminants, que le Jacobien du
changement de variables (p, q) (p',
q') défini par (1.31) est :
?(p', q')
?(p, q)
|
p'0q'0
= -(1.33)
p0q0
|
|
( La preuve est faite en Annexe 2. )
· Il apparait alors clairement, en utilisant
(1.6) et (1.31) que les fonctions qui apparaissent dans les
intégrales (1.25) et (1.26) qui définissent
Q+ et Q- s'expriment uniquement en
fonction de p, q et ù de sorte que les
intégrales qui sont prises par rapport à q et
ù laissent bien des fonctions Q+(f,
g) et Q-(f, g), de la seule variable
p. Dans la pratique, nous considérons des fonctions f
sur R4, (t, p) H f(t, p) qui
induisent pour t fixé dans R, des fonctions
f(t) sur R3 définies par
f(t)(p) = f(t, p).
· Maintenant, puisque f ne dépend que de
t et p = (pi), l'équation de
Boltzmann (1.23) en f s'écrit :
?f
+ ?t
|
Pi p0
|
?f ?pi
|
=
|
Q(f,f)
p0
|
(1.34)
|
|
De l'expression (1.2) des
?ëáâ et l'expression (1.8) de
Pá, on a pour i = 1, 2, 3
fixé :
P i ( )
1
â
p0 = - ?i
ëupëpu + epâF
i
p0
( )
1
= - ?i
0up0pu -
?ijupjpu +
ep0F0 i + epkF i
k
p0
( )
1
= - ?i
0up0pu - ?i
iupipu + ep0F0
i + epkF i
p0 k
( )
1
= - ?i
0ip0pi -
?i i0pip0 +
ep0g0áFái
+
epkgiáFká
p0
( )
1
= - 2?i
0ip0pi -
ep0F0i +
egijpkFkj
p0
( )
F0i + gij pk
= -2?i 0ipi - e
p0 Fjk
d'où :
Pi p0
( )
F0i + gij pk
= -2?i 0ipi - e
p0 Fjk (1.35)
1.4 Équations d'Euler et système
différentiel en u = (uá)
= p0
Dans le système différentiel des trajectoires
(1.7), on a, pour á = 0 et puisque x0
= t : dt
ds
d'où l'on déduit, que l'on peut prendre t
comme paramètre, pour i = 1, 2, 3, en
écrivant :
dpi
=
ds
1
= Pi ·
p0
Pi
= p0
(?)
dpi dt
ds
·
dt
d'où d'après (1.35), on a :
dpi
dt
k
= -2Pi0ipi
- e[F0i + gij
p0 Fjk], i = 1, 2, 3
api at
dpi
dt
af api
en plus on a, sur les trajectoires, en utilisant (1.34)
et (?) :
df
=
dt
=
=
=
af
+ at
af
+ at
af
+ at
af api ·
af api ·
Pi p0 ·
Mémoire de MASTER 11 MOUTNGUI SEE
c?UYI 2010-2011.
Q(f, f)
p0
Ainsi p = (pi) et f
satisfont au système différentiel suivant, où on
prend t comme para-
mètre :
{ dpi
dt = -2Pi0ipi
- e[F0i + gij pk
p0 Fjk], i = 1, 2,
3 (1.36)
dfdt = p0 Q(f, f)
1(1.37)
Bien noter que les deux membres de (1.37) sont
évalués sur les trajectoires (t,
pi(t)).
1.4 Équations d'Euler et système
différentiel en u = (uá)
Le contenu matériel et énergétique de
l'espace-temps (1184,g) est représenté par le
tenseur d'impulsion-énergie Táâ
défini en fonction de la fonction de distribution f des
particules, du champ électromagnétique F, de la
pseudo-densité constante ñ0 > 0 des
particules et du vecteur-vitesse matérielle u =
(uá) par :
Táâ =
T1áâ +
ôáâ +
ñ0uáuâ (1.38)
Mémoire de MASTER 12 MOUTNGUI SEE
c?UYI 2010-2011.
1.4 Équations d'Euler et système
différentiel en u = (uá)
où :
{ T1áâ = .IR3
p«psf(teab2dp (1.39)
ôáâ = -g??
4
FëuFëu +
FáëF ë (1.40)
â
ôáâ défini par
(1.40) est appelé tenseur de Maxwell associé au champ
électromagnétique F.
Lemme 1.1. Le tenseur de Maxwell
Táâ vérifie la relation :
?áTáâ
=
Fâë?áFáë
(1.41)
Preuve. (1.40) donne :
|
Táâ = -gáâ
4
|
FëuFëu +
FáëFâë
|
d'où
áâ
?áTáâ
= -g4 ?á
(FëuFëu) +
?á
(FáëFâë)
1
?â(FëáFëá)
+ ?á (F áëF â
)
ë
?â(FëáFëá)
+
Fáë?áFâë
+
Fâë?áFáë
4
1
4
= -
= -
Donc pour avoir (1.41), il nous suffit de montrer que
:
|
1 ) + Fáë?áF
â
-4?â(FëáFëá
ë =
D'après les équations de Maxwell (1.11),
on a :
|
0
|
|
?âFëá +
?ëFáâ +
?áFâë
|
=
|
0
|
|
|
|
d'où
|
|
|
|
|
|
|
Fëá?âFëá
+ Fëá?ëFáâ
+
Fëá?áFâë
|
=
|
0
|
|
|
|
Fëá?âFëá
+ Fáë?áFëâ
+
Fëá?áFâë
|
=
|
0
|
|
|
|
Fëá?âFëá
- Fáë?áFâë
-
Fáë?áFâë
|
=
|
0
|
|
|
|
2Fëá?âFëá
-
4Fáë?áFâë
|
=
|
0
|
|
|
|
?â
(FëáFëá) -
4Fáë?áFâë
|
=
|
0
|
(car
|
?â
(FëáFëá) =
2Fëá?âFëá
)
|
|
gâu?â
(FëáFëá) -
4gâuFáë?áFâë
|
=
|
0
|
|
|
|
?u(FëáFëá)
- 4Fáë?á
(gâuFâë)
|
=
|
0
|
|
|
|
?u(FëáFëá)
-
4Fáë?áFuë
|
=
|
0
|
|
|
Mémoire de MASTER 13 MOUTNGUI SEE
c?UYI 2010-2011.
1.4 Équations d'Euler et système
différentiel en u = (uá)
1 ) +
FáëVáFâ
d'où : -
4Vâ(FëáFëá ë
= 0
Ainsi nous avons :
VáTáâ
=
FâëVáFáë
Les équations d'Euler expriment la conservation du tenseur
d'impulsion-énergie Táâ qui s'écrit :
VáTáâ
= 0 (1.42)
Mais il est prouvé dans [6] que si f
vérifie l'équation de Boltzmann (1.23) alors
T1áâ défini par
(1.39) vérifie
VáT1,áâ = 0.
(1.42) se réduit donc, vue l'expression (1.38) de
Táâ et (1.41) à :
FâëVáFáë
+
Vá(ñ0uáuâ)
= 0 (1.43)
(1.43) s'écrit en utilisant les équations
de Maxwell (1.10) :
FâëJë
+
uâVá(ñ0uá)
+
(ñ0uá)Váuâ
= 0 (1.44)
La multiplication contractée de (1.44) par
uâ donne, compte tenu de : uâuâ =
-1 et uâVáuâ
= 0 :
Vá(ñ0uá)
=
FâëJëuâ
(1.45)
Puisque ñ0 > 0 est une constante,
(1.45) permet d'exprimer la quantité
Váuá. En reportant la
valeur de
Vá(ñ0uá)
fournie par (1.45) dans (1.44) on obtient :
FâëJë
+
uâ(FuëJëuu)
+
(ñ0uá)Váuâ
= 0
soit :
|
uáVáuâ
= - 1
ñ0
|
FâëJë
- 1
ñ0
|
FáëJëuáuâ
(1.46)
|
|
FâëJë
- 1
ñ0
|
FáëJëuáuâ
|
|
FâëJë
- 1
ñ0
|
FáëJëuáuâ
|
|
FâëJë
- 1
ñ0
|
FáëJëuáuâ
|
C'est (1.46) qui fournira le système
différentiel qui détermine le champ unitaire u =
(uá). En effet (1.46) donne :
uáVáuâ
= - 1
ñ0
uá(?áuâ
+ râáëuë) =
-
1
ñ0
1
u0?0uâ +
râáëuáuë
= -
ñ0
|
uáuë
?0u = -
â râáë
u0
|
ñ0u0 Fâ
1 ëJë - 1
ñ0u0 Fá
ëJëuáuâ
|
1.5 Le système couplé à
étudier
d'où :
1
ñ°u°FâëJë-
1
ñ°u°FáëJëuáuâ
(1.47)
_ uáu
r
uâ -- -aa
u°
Mémoire de MASTER 14 MOUTNGUI SEE
c?UYI 2010-2011.
Remarque 1.2. On sait que
J° = 0. Dans [12], l'hypothèse que f
est invariant par SO3 et que les particules sont supposées spatialement
au repos, entrainent que pour â = i, l'intégrale dans
(1.12) est nulle et ui = 0 ; d'où
Ji = 0.
L'équation (1.21) en
F°i correspondante était donc
homogène et se résolvait donc aussitôt pour donner
F°i = â°
F°i(0) ce qui avait permis de
découpler l'équation en F.
Ici la situation est très différente car
Ji =? 0 et les équations
(1.21) en F°i et
(1.47) en uâ doivent être
couplées au système du début à la fin.
1.5 Le système couplé à
étudier
· Il est fondamental de noter que, vu le système
différentiel (1.36)-(1.37), p =
(pi) qui était au départ une variable pour
f, est maintenant devenu une fonction inconnue de t, au
même titre que f. La variable pour la fonction f devra
donc être notée dorénavant par une autre lettre que
p, pour éviter toute confusion.
· Pour étudier (1.37), on s'interesse
d'une manière générale à l'équation
différentielle :
df 1
dt = p°
Q(f, f) (1.48)
pour une fonction, f : I c R -+ E, t H
f(t) E E, où E est un espace de Banach de
fonctions sur R3 à spécifier, avec pour q
E R3, q H
?f(t)(q) E R. La
restriction de f aux trajectoires (pi(t))
c R3 définies par le système
conjoint (1.36) donnera la solution cherchée f de
(1.37). L'étude de l'opérateur des collisions Q
faite par exemple dans [12] montre que l'espace de Banach approprié
est E = L1(R3). Maintenant
pour ne pas surcharger les notations, au lieu d'introduire (1.48) en
f on va toujours considérer (1.37) cette fois f
joue le rôle de f? ; de même, toutes les
intégrales en f sont en fait des
?f.
intégrales en
· L'équation (1.21) en
F°i s'écrira, vu l'expression
(1.20) de e :
i
Fÿ°i+HF°i
= J 3 qq°2
f(t)(q)dq- u° f3
f(t)(q)ab2dq, i = 1,
2, 3 (1.49)
1.5 Le système couplé à
étudier
où :
aÿ bÿ
H = +2 (1.50)
a b
H est une quantité appelée courbure
moyenne de l'espace-temps (1[84, g). H jouera un
rôle fondamental.
· Le système en p =
(pi) s'écrira vu (1.36) et l'expression
(1.20) de e :
{ ÿpi =
-2?i0ipi -
[F0i + gijpk
öpj0k ] o fR3
f(t)(q)ab2dq
(1.51)
i = 1,2,3
où ?i0i est donné par
(1.2) et d'après (1.19) öij =
Fij(0) = Cte.
· L'équation en f est donnée
(1.48) où pour simplifier f est notée
f.
· En ce qui concerne le système en u =
(uâ), on a le lemme suivant.
Lemme 1.2. En utilisant Fá
ëuáuë =
Fáëuáuë
= 0 (car Fáë = -Fëá) et
l'expression (1.12) de Jâ,
(1.47) donne le système en (uâ)
:
ñ0u0 Fâ ë [ I3
që.Î(tg(q)ab2
dq - û0 f3 f(t)
(q)ab2dql1
uáuë
ÿuâ =
-?âáë
u0
Mémoire de MASTER 15 MOUTNGUI SEE
c?UYI 2010-2011.
1
ñ0u0Fáëuáuâ
f3 g0
f(t)(q)ab2dq
(1.52)
De plus (1.52) s'écrit, en
explicitant les fonctions inconnues :
|
(ui)2
ÿu0 = -?0 ii 0
u
|
giiF0iab2
|
[/' 3 q0i I
f(t)(q)dq - u0 f3
f(t)(q)dql1
|
|
ñ0u0
|
|
ab2
+
ñ0
|
giiF0i (u0 l
f3 qo f(t)(q)dq-ui
f3 f(t)(q)dq
f --ab p ijui f3
q39
f(t)(q)dq
(1.53)
|
et :
ab2giiöii
qjf(t)(q)
ab2giiöij
ÿui = -2?i0iui 0
f (t)(q)dq
ñ0u f3 qo dg
ñ0(u0 )2
IIP3
|
ab2gjjF0jui
+
ñ0
|
2g
0juiuj
f3
g0f(t)(q)dq - ab
pou° f3
|
f(t)(q)dq
|
- ab2öjk p0u0
JR 3 g° f(t)(q)dq. (i
= 1, 2, 3) (1.54)
Mémoire de MASTER 16 MOUTNGUI SEE
c?UYI 2010-2011.
1.6 Les espaces de fonctions
Preuve. (Voir Annexe 3)
On sait d'après (1.13) que les
ui déterminent u0. On
étudiera donc le système (1.54) en
ui, i = 1, 2, 3, en prenant
l'équation (1.53) en u0 comme une
équation auxilliaire qui peut être éventuellement utile
pour l'étude du système (1.54).
On pose dans toute la suite :
fEi = F0i
E = (Ei), i = 1,
2, 3
En définitive le système différentiel
couplé à étudier en (Ei,
pi, f, ui) est le suivant :
(S) : {
Ei = - (a + 2)
Ei + ab2 fR3 qo fdq
a b abu0 i 1 R3 fdq
(1.55)
i i ab2Ei
ab2gijöjk pk
ÿpi = -2?0ip -
u0 fR3 fdq - u0 p0
fR3 fdq (1.56)
df dt =
ui
p0Q(f, f)
1 (1.57)
=i
uz - ab2giiöij qj
d ab2giiöijuj d
ab2gjjEjui qj fdq
ñ0u0 f][P3 q0 f q
+ ñ0(u0)2 f][P3 f q + P0
fR3 q0 f q
ab2gñ0u0uiuj fR3
fdq - ab2öjk P0u0 iuj fR3 q0 fdq, i
= 1, 2, 3 (1.58)
1.6 Les espaces de fonctions
- L1(1183) ; la norme dans
L1(1183) sera notée ? · ?
ou ? · ?L1(R3) ; ?r ?
118*+, on pose :
Xr = {f ?
L1(1183); f = 0, ?f? = r}.
(1.59)
Muni de la distance induite par ? · ?,
Xr est un sous-espace métrique complet et connexe de
L1(1183).
Soit I un intervalle de 118.
- C([I;
L1(1183)]) = {f : I -?
L1(1183); f continue et bornée}
C([I;L1(1183)]) est un
espace de Banach pour la norme |||f||| =
sup{?f(t)?, t ? I}.
- C([I; Xr]) =
{f ? C([I;
L1(1183)]); f(t)
? Xr, ? t ? I}. (1.60)
Muni de la
distance induite par la norme |||·||| de C([I;
L1(1183)]), C([I;
Xr]) est un espace métrique complet.
- 1183 est muni de la norme usuelle notée
? · ? ou ? · ?R3.
- C([I;1183]) = {p
: I -? 1183; p continue et
bornée}.
C([I;1183]) est un espace
de Banach pour la norme |||p||| = sup{?p(t)?, t
? I}.
- E = 1183 ×
1183 × L1(1183) ×
1183
Mémoire de MASTER 17 MOUTNGUI SEE
c?UYI 2010-2011.
1.6 Les espaces de fonctions
Nous munissons cet espace de la norme :
?(E,p, f, u)? = ?E?R3 +
?p?R3 + ?f?L1(R3) +
?u?R3 (1.61)
Nous considérons aussi l'espace
C([I;R3]) ×
C([I;R3]) × C([I;
L1(1183)]) ×
C([I;R3]) muni de la norme :
|||(E,p,f,u)||| = |||E||| +
|||p||| + |||f||| + |||u||| (1.62)
Ce qui en fait un Banach.
Remarque 1.3. Le système différentiel
(S) s'écrit :
Xÿ = G(t, X)
où :
X : I ? R -? E,
X=(E,p,f,u),
G(t, X) = (G1(t, X),
G2(t, X), G3(t, X), G4(t,
X))
avec :
?
?????????
?????????
( )
aÿ
G1(t,X) = - a +
2bÿ Ei + ab2 ? qi
q0fdq - ab2ui ?R3
fdq
b R3 u0
(1.63)
G2(t, X) =
-2Pi0ipi -
abuoi?R3
fdq - ab2
ui0öjk
P0 ?R3 fdq (1.64)
G3(t,X) =
p01Q(f,f) (1.65)
G4(tX =
-217iui -
ab2giiöij qj d ab2giiöijuj d
ab2gjjEjui qj fdq
) 0i
ñ0u0 ?R3 q0 f q + ñ0(u0)2
?R3 fdq + P0 f][P3 q0 f q
?
?
(1.66)
ab2gjjEjuiuj qk
-R3 fdq - ab2öjk uiuj
q0 fdq, i = 1,2,3
ñ0u0 ñ0u0 R3
Mémoire de MASTER 18 MOUTNGUI SEE
c?UYI 2010-2011.
CHAPITRE DEUX
EXISTENCE LOCALE DES
SOLUTIONS
Notre objectif est d'appliquer au système
différentiel (S) la théorie des systèmes
différentiels du premier ordre. A` cet effet, nous prouverons
que les fonctions définies par (S) sont continues par rapport à
la variable t et localement lipschitzienne par rapport à X
= (E, p, f, u) pour la norme de l'espace de Banach E =
1183 × 1183 ×
L1(1183) × 1183
Proposition 2.1. Soit f, g ?
L1(1183) ; alors
p01 Q+(f, g),
p01 Q-(f, g),
p01 Q(f, g) appartiennent
à L1(1183) et :
? p01 Q+(f, g)? =
C(t)?f??g?; ? p0 1
Q-(f, g)? = C(t)?f??g?
(2.1)
?
p01Q+(f, f)
- p0Q+(g,g)?
=C(t)(?f? + ?g?)?f - g?
1(2.2)
?p01Q-(f,f)
-p0Q-(g,g)?
=C(t)(?f? + ?g?)?f -g?
1(2.3)
? 11
p0Q(f, f) -
p0Q(g,g)? =
2C(t)(?f? + ?g?)?f - g?
(2.4)
où C(t) =
4ðC1ab2(t), C1 >
0 étant la constante fournie par (1.27).
Preuve.
1. L'expression (1.25) de Q+(f, g) donne, en utilisant la
majoration (1.27) de ó par C1 :
?p0Q+(f,g)?
= C1ab2(t)f3fR3
dp°d0q J s2 |f (a)
Le Jacobien (1.33) du changement de variables (p,
q) ? (p', q') donne p0e P
e dpg00 =
d2:0'
'0 q'0'
Mémoire de MASTER 19 MOUTNGUI SEE
c?UYI 2010-2011.
Nous avons de (a), en utilisant 1
p'0q'0 = 1
d'après (1.6) :
?p01Q+(f,g)?
= C1ab2(t)J
I.Î(P')I dP' f 3
I9(q')I dq'du)J 2 d
3
=
4ðC1ab2(t)?f??g?
d'où la première inégalité.
De même l'expression (1.26) de
Q-(f, g), l'inégalité
(1.27) et 1
p0q0 = 1 donnent :
J J J
? p0 1 Q-(f,g)? =
C1ab2(t) R3 |f(p)|dp
R3 |g(q)|dq S2
dù
=
4ðC1ab2(t)?f??g?
d'où (2.1)
2. Les expressions (1.25) et (1.26) de Q+ et Q- montrent
que Q+, Q- ainsi que Q sont des opérateurs bilinéaires.
? ?
p01Q+(f,f)-
p0Q+(g,g)?
=? 1
1 p0 Q+(f,f-g)+
p01Q+(f - g,
g)?
=?p01Q+(f,f-g)?+?p01Q+(f-g,g)?
= C(t)?f??f - g? +
C(t)?g??f - g?
= C(t)(?f? + ?g?)?f -
g?
d'où (2.2)
?
?p01Q-(f, f)
- p0Q-(g, g)?
= ?1
1 p0Q-(f, f -
g)
+ p01Q-(f
- g, g)?
=
?p01Q-(f, f -
g)? +
?p01Q-(f - g,
g)?
= C(t)?f??f - g? +
C(t)?g??f - g?
= C(t)(?f? + ?g?)?f - g?
d'où (2.3)
? ?
p01Q(f, f) -
p0Q(g, g)? =
?(1
1 p0Q+(f,
f) -
p01Q-(f, f))
- (p01Q+(g,
g) -
p01Q-(g,
g))?
= C(t)(?f? + ?g?)?f - g?
+ C(t)(?f? + ?g?)?f - g?
= 2C(t)(?f? + ?g?)?f -
g?
d'où (2.4)
Proposition 2.2. Soit p =
(pz), u = (uz), pi
= (pzi), ui =
(uzi) ? 1183, j =
1, 2, f ? L1(1183). Alors :
=
p0Q+(f, f) -
p0 Q+(g, g)) + (1
1 p0Q-(g, g)
- p01Q-(f,
f))?
= ? 1
p0 Q+(f, f) - p0
Q+(g, g)? + ? 1
1 p0 Q-(f, f) - p0
1Q-(g,g)?
?( 1
p0 = a|p1|; p0
= b|p2|; p0 =
b|p3| (2.5)
u0 = a|u1|; u0
= b|u2|; u0 =
b|u3| (2.6)
pk2
p02
uk
2
u0 2

????
pk1
p0 1
????
uk
1
u01
????
????
????
p0 1
1
p02
1
????
1
1
0
u0
2
u 1
?( )
??1 + a
? = 5 b + b ?p1 -
p2? (2.7)
a
?( )
??1 + a
= 5 b + b
? ?u1 - u2? (2.8)
a
=
pk1p02
- pk2p01
p01p02
pk1(p02
- p01) +
p01(pk1 -
pk2)
p01p02
|
????
|
pk1 p0 1
|
pk2
p02
|
????
|
=
=
|
????
????
|
????
????
(2a + 4b)?p1 -0
p2?, j = 1, 2
(2.9)
pi
= (2a + 4b)?u1 -0
u2?, j = 1, 2
(2.10)
ui
? 1 1
0Q(f, f,p1) -
0Q(f, f,p2)? =
8ðC1ab2?f?2?p1
- p2?, j = 1,2 (2.11)
pi pi
où C1 > 0 est la constante
donnée par (1.27).
Preuve. Remarquons que d'après
(1.6) et (1.13), il nous suffit de prouver les
inégalités en p et la proposition en
découlera.
1. (2.5) est une conséquence directe de
l'expression (1.6) de p0
2. Soit k ? {1, 2, 3}
Mémoire de MASTER 20 MOUTNGUI SEE
c?UYI 2010-2011.
En utilisant p02 = 1, on
déduit :
|pk1||p02
- p01|
=+|pk 1 -pk 2|
(a)
p01p02
????
pk2
pk1
p0 1
p02
????
En utilisant l'expression (1.6) de p0 :
2)2
p0 1 - p0 2 = (p0
1)2 - (p0 0
p01 + p2
a2(p1 1 +
p1 2)(p1 1 - p1
2) + b2(p2 1 +
p2 2)(p2 1 - p2
2) + b2(p3 1 +
p3 2)(p3 1 - p3
2)
=
(b)
p0 1 + p0 2
Nous avons de (a) et (b) :
|
????
|
pk1
p01
|
k
p2 p02
|
????
|
=
|
[a2(|pp11|
+
|pk1p12|)
+
b2(|pk1p21|
+
|pk1p22|)
+
b2(|pk1p31|
+ |pk1p32|) + 1]
?p1 - p2?(c)
p01p02(p01
+ p02) J
Nous avons en utilisant convenablement les
inégalités (2.5) : Pour k = 1 :
|
|p11|2 +
|p11p12|
p01p02(p01
+ p02) =
|
2
|p11p21|
+
|p11p22|
2 |p1
1p3
1| + |p1
1p3
2| 2
a2; p0
1p0 2(p0 1 +
p0 2) = ab; p0
1p0 2(p0 1 +
p0 2) = ab
|
Pour k = 2 :
|p21p11|
+
|p21p12|
p01p02(p01
+ p02) =
Pour k = 3 :
|p31p11|
+
|p31p12|
p01p02(p01
+ p02) =
(c) donne alors :
2 |p21|2 +
|p21p22|
2 |p2
1p3
1| + |p2
1p3
2| 2
ab; p0
1p0 2(p0 1 +
p0 2) = b2 ; p0
1p0 2(p0 1 +
p0 2) = b2
2
|p31p21|
+
|p31p22|
2 |p3
1|2 +
|p3
1p3
2| 2
ab; p0
1p0 2(p0 1 +
p0 2) = b2 ;
p01p02(p01
+ p02) =b2
????
p11
p01
p12
p02
????
2
p21
p 2
p0 1
p02
=(5 + 2)?p1 -
p2? b
????
3
p 2
p0 1
p31
p02
=
(3 + 4b)?p1 - p2? a (5 + 2)?p1 - p2?
b
Mémoire de MASTER 21 MOUTNGUI SEE
c?UYI 2010-2011.
|
or
|
3 + 4b
a
|
( )
1 + a
= 5 b + a b
|
( )
5 + 2a b = 5 + 5a 1 + a
b =5 b + a b
d'où :
?( )
??1 + a
= 5 b + b
? ?p1 - p2?, k =
1, 2, 3
a
????
pk2
pk1
p01
p02
????
3. Nous avons en utilisant l'expression (1.6) de
p0 et (b) :
???(p01)2
- (p02)2 ?=
???p01p02(p01
+ p02) ?
= ????
????
a2(p11 +
p12)(p11 -
p12) +
b2(p21 +
p22)(p21 -
p22) +
b2(p31 +
p32)(p31 -
p32)
p01p02(p01
+ p02)
a2(|p11|
+ |p12|)
+ b2(|p21| +
|p22|) +
b2(|p31| +
|p32|)
= ?p1 - p2?
(d)
p01p02(p01
+ p02)
En utilisant (2.5) et
p0j = 1, j =
1,2 :
|
|p11|
+ |p12|
p01p0 2(p01 + p0 2)
=
|
2 |p2 1| +
|p2 2| 2
|p3 1| +
|p3 2| 2
;
ap0 p0
1p0 2(p0 1 +
p0 2) = ;
bp0 2) = , j = 1,2
(e)
p0 1p0 2(p0
1 + p0 bp0
j j j
|
(d) et (e) donnent :
= (2a + 4b)?p1 -
p2? ,j = 1,2
p0j
??
??
?= ?
? ?
???????+ ?
4.
????
Q(f, f,p1) - Q(f,
f,p2)
p0j
Q+(f, f,p1) -
Q+(f, f,p2)
pj
0
Q-(f,f,p1) -
Q-(f, f,p2)
p0j
Mémoire de MASTER 22 MOUTNGUI SEE
c?UYI 2010-2011.
L'expression (1.25) de Q+ donne :
???? =
|
????
|
Q+(f, f,p1) -
Q+(f, f,p2)
|
|
pj
0
|
?? dù
|f(p')||f(q')|
??ó(t, p1, q,
p', q') ? ó(t,
p2, q, p', q')
1 /' ab2dq~
pj R3 g0 s2
En utilisant la seconde inégalité
(1.27) du noyau de la collision ó et en
procédant comme dans la preuve de la première
inégalité (2.1), on obtient :
|
? ?
? ?
?Q+(f,f,p1)
- Q+(f,f,p2) ?
? p0 ?
j
|
=
4ðC1ab2?f?2?p1
- p2?
|
|
De même on obtient :
? ?
? ?
?Q-(f, f,p1)
- Q-(f, f,p2) ?
? p0 ?
j
d'où :
|
=
4ðC1ab2?f?2?p1
- p2?
|
|
? ?
? ?
?Q(f, f, p1) -
Q(f, f, p2) ?
? p0 ?
j
|
=
8ðC1ab2?f?2?p1
- p2?, j = 1, 2
|
Proposition 2.3. Soit
X1 = (E1,p1,
f1, u1) ? E = 1183 × 1183
× L1(1183) ×
1[83
X2 = (E2, p2,
f2, u2) ? E
alors il existe des constantes C2, C3,
C4, C5, C6 telles que :
?G1(t,X1) -
G1(t,X2)?63 = C2(?E1 -
E2? + ?f1 - f2? + ?u1 -
u2?) (2.12) ?G2(t, X1) - G2(t,
X2)?63 = C3(?E1 - E2? +
?p1 - p2? + ?f1 -
f2? + ?u1 - u2?) (2.13)
?G3(t, X1) - G3(t,
X2)?L1(63) = C4(?p1
- p2? + ?f1 -
f2?) (2.14) ?G4(t, X1) - G4(t,
X2)?63 = C5(?E1 - E2? +
?f1 - f2? + ?u1 - u2?)
(2.15) ?G(t, X1) - G(t, X2)? =
C6?X1 - X2? (2.16)
où
{
?X1 - X2? = ?E1 -
E2? + ?p1 - p2?
+ ?f1 - f2? + ?u1 -
u2?
C2=10(1+C)(1+ab2)(1+ab+ab+1a+1b)(1+?f2?)
C3 = 10(1 + C)(1 + a +
b)4(1 + ab + ab + a1 +
1b)2(1 +?E1?)(1
+?f2?)(1 + ? ij |öij|)
C4 = 16ðC1ab2(1 + a
+ 2b)(1 + ?f1? + ?f2? +
?f2?2)
C5 = 200
ñ0 (1 + C)(1 + ñ0)(1 + a
+ b)5(1 + ab + ba + a1
+ 1b)2(1 + ?E1?
+?E2?)(1 + ?f1? +
?f2?)×
(1 + ?u1? + ?u2?)(1 + >ij
|öij|)
C6 = C2 + C3 + C4 +
C5
(2.17)
Preuve.
Mémoire de MASTER 23 MOUTNGUI SEE
c?UYI 2010-2011.
Mémoire de MASTER 24 MOUTNGUI SEE
c?UYI 2010-2011.
1. D'après (1.63) on a :
( aÿ bÿ )
G1(t, X1) - G1(t, X2) = a
+ 2 (Ei 2 - Ei 1)
b
fz ( [uJ
+ ab2J 3q(ff2)2 u23
f2dq u~ ][P3 f1dq] (1)
Pour le premier terme de (1) on a d'après (1.3)
:
????
( aÿ bÿ )
a + 2 (Ei 2 - Ei 1) ????
= 3C?E1 - E2? (2)
b
Pour le deuxième terme de (1) on a :
ab2 f
????
i R3 qo (fi -
f2)dq????= (b2
+ ab)?f1 - f2? (3)
Pour le troisième terme de (1) on a en utilisant
(2.6) et (2.8) :
|
????
|
ui1
ab2 [u2 JR3 f2dq -
u0 1J 3 f1dq]???? =???ab2
[(u2 u01 ) J3 f2dq + u0 1J
3(f2 - f1)dq]
|
[ ( ) (1 ) ]
= ab2 5 1+ a b +b
?f2??u1-u2? + a + 1
?f1 -f2?
a b
( )
= 5ab2 1+ a b + a b +
a 1 + 1
(1+?f2?)(?f1-f2?+?u1-u2?)
b
d'où :
ab2
[uo J f2dq - uo
J f1dq]????=
u2 R3 U 3
( )
5ab2 1+a b +a b +1 a
+1
(1+?f2?)(?f1-f2?+?u1-u2?)
(4) b
De (1), (2), (3) et (4) on obtient
(2.12) et l'expression de C2 dans (2.17).
Remarquons que :
- (ab2g11 = b2 a ;
ab2g22 =
ab2g33 = a)
(ab2gii = b2 a + a, i
= 1,2,3)
- D'après (2.5) on a :
???= a1+1
?b, k = 1,2,3 et j = 1,2
pkj p0j
????
- (ab2g11 =
a3b2;
ab2g22 = ab2g33 =
ab4) (ab2gjj =
ab2(a2 + b2), j
= 1, 2, 3).
2. L'expression (1.64) de G2 donne :
r Ei f E f 1
G2(t, X1) - G2(t, X2) =
2?i0i(pi2 - pi1) + ab2 L 0
J f2dq fidq]
U2 R3 u1 R3
2 iipk 1pk 1
+ ab g öik [p2
u2 3 f2dq p° u ~3
f1dq]
(5) 1
?101 = ÿaa , ?202 =
?303 = bÿb et en utilisant (1.3) on a :
|?i0i| = C
d'où le premier terme de (5) donne :
|2?i0i(pi2
- pi1)| = 2C?p1 -
p2? (6)
Ei
? ????
ab2 [ 1
ô J f2dq -- 0
fldq] =
2 R3 u1 R3
i
ab2 [ 10 (Ei2
- El)/ f2dq +
0 0) E1 f f2dq
+
E01 (1
2 - f1)dq]
u2 R3 ( u2
u1 R3 u1 R3
= ab2 (?f2??E1 -
E2? + (2a +
4b)?E1??f2??u1 - u2? +
?E1??f1 - f2?)
=
K3(?E1-E2?+?f1-f2?+?u1-u2?)
( En utilisant (2.10) )
où :
K3 = 4(1 + a + b)4(1 +
?E1?)(1 + ?f2?)
d'où :
????
ab2 [uL
Ei E f
f2dq -- u0 3
f1dq]????=K3(?E1 -
E2? + ?f1 - f2? + ?u1 -
u2?) (7)
2 1
? Écrivons le troisième terme de (5) comme
suit :
|
????
|
p2 1 f pi
ab2giiöik[
f2dq0 0 p0 10p2
u2 R3 u1
fR
3
|
]???? =
f1dq
|
Mémoire de MASTER 25 MOUTNGUI SEE
c?UYI 2010-2011.
|
????
|
2 ii ( k kl 1 (u0
1 1 l k1 k(lab g cpik [1
P200J 0f2dq
+0JPf2dq0PO
(12 - f1)dqJ\p2 p1
u2 R3 2 u1 P1 R3
u1 p1 R3
|
(b2 ) ? [ ( ) (1 )
1 + a
= a + a |öik| 5 b +
b ?f2??p1 - p2? +
(2a + 4b) a + 1 ?f2??u1
- u2?
a b
i,k
(1 ) ]
+ a + 1 ?f1 - f2?
b
=
K'3(?p1-p2?+?f1-f2?+?u1-u2?)
( En utilisant (2.7) et (2.10) )
où :
/ l2
K'3=5(1+a+b)2I
1+ b+a+ 1 + 1)
(1+?f2?)?|öik|
\\ ab
d'où :
????
i,k
ab2giiöik
[p2 2 20 0 JR3 f2dq
-p1 1 JR3 f1
q]???? =
KW?p1 - p2? + ?f1 -
f2? + ?u1 - u2?) (8)
de (5), (6), (7) et (8) on obtient
(2.13) et l'expression de C3 dans (2.17). 3. L'expression
(1.65) de G3 donne :
G3(t, X1) - G3(t, X2) =
1
1
p0Q(f1, f1,
p1) -p0 Q(f2,
f2, p2)
1 2
1 1
= (Q(f1, f1, p1)
- Q(f2, f2,p1)) +
(Q(f2, f2,p1) -
Q(f2, f2,p2))
p0 p0
1 1
( 1 )
- 1
+ Q(f2, f2,p2)
(9)
p0 p0
1 2
Pour le premier terme de (9) dans lequel p1
est fixé, utilisons (2.4) avec f1 = f,
f2 = g pour obtenir :
? 10 (Q(f1,
f1,p1) - Q(f2,
f2,p1))? =
8ðC1ab2 (?f1? +
?f2?) ?f1 - f2? (10)
p1
Pour le deuxième terme de (9) dans lequel f2 est
fixé, utilisons l'inégalité (2.11) avec j
= 1, f = f2 pour obtenir :
? 10 (Q(f2,
f2,p1) - Q(f2,
f2,p2))? =
8ðC1ab2?f2?2?p1
-p2? (11)
p1
Pour le troisième terme de (9) dans lequel f2 est
fixé utilisons (2.9) avec j = 2 :
? )? ?
? ( 1 ?
? ? ?
? - 1 Q(f2,
f2,p2) ?
? Q(f2, f2,p2) ? ?=
(2a+4b)?p1 -p2?
?
p0 p0 ?
p0 ? (12)
1 2 2
Mémoire de MASTER 26 MOUTNGUI SEE
c?UYI 2010-2011.
Nous déduisons de (12) en utilisant
l'inégalité (2.4) dans laquelle on pose f =
f2, g = 0 que :
|
? (? ? ?
|
) ?
1 1 ?
- Q(f2, f2, p2) ? =
(2a + 4b)?p1 -
p2?(8ðC1ab2?f2?2)
?
p0 p0
1 2
|
Soit :
? ? ( 1 ) ? ?
?- 1 ? ? =
16ðC1ab2(a +
2b)?f2?2?p1
-p2? (13)
? Q(f2, f2,p2)
p0 p0
1 2
de (9), (10), (11) et (13) on obtient
(2.14) et l'expression de C4 dans (2.17). 4.
L'expression (1.66) de G4 donne :
G4(t, X1)-G4(t, X2) =
2?i0i(ui2-ui1)
|
ab2giiöij
+
ñ0
|
r i+ab2 ii j /' 9 /'
Lu0 J gp f2dq - 0 J g0
f1dq g ö [(u01)2 fJ f1dq
-22J f2dq
R3 q R3 qñ0 R3 (u2) R3
|
+ ab2gjj
ñ0
[Ej1ul f qj
f1dq - Ej2u2 q~ l
ab2gjj u2 j
ui
J

0
q0
1
R3 u
R3
ñ0
-0
j1
1
R3 q
R3

f2dq +
u2E2u2 f2dq
E
ui f
[ ]
abñ0jk uou2 f
3 ~0f2dq -
uoui f3
g0f1dq (a)
2 1
on a ainsi :
|2?i0i(ui2
- ui1)| = 2C?u1 - u2?
(b)
Pour le deuxième terme de (a) on a :
|
????
|
ab2giiöij
ñ0
|
1qj1 q~fidq
0 nof2dq
- 0 0
[u2R3q u1J3q
|
|
????
|
ab2giiöij
ñ0
|
[(
|
u? - ) fR30f2dq
+0fq(f2 q u1
~3 q
|
) ]
?f1 - f2?
2
) ? ) (1
+a ?f2??u1 - u2? + a
+ 1
a b
i
(b [ (1
1
? |öij| (2a + 4b) a
+ 1
ñ0 b
,j
= K5(?f1 -f2?+?u1
-u2?) ( En utilisant (2.10))
où :
4 ?
(1 + a + b)2(1 + a
K5 = b + a b + a 1 + 1 b
)2(1 + ?f2?) |öij|
,j
ñ0 i
dq
Mémoire de MASTER 27 MOUTNGUI SEE
c?UYI 2010-2011.
d'où :
????
ab2giiöij
ñ0
[ 1 ?qj 1 20
q0f2dq u1 J
f1dq]????=K5(?f1
- f2? + ?u1 - u2?)
(c)
Pour le troisième terme de (a) on a :
|
?????
|
ab2giiöij
ñ0
|
[(u01)2 ~ f1dq -( 2
u0) IR3 f2dq]?????=
2
|
|
?????
|
ab2giiöij
ñ0
|
[(uuj01
1 - uu0)
u10
1 fIIt 3 f1dq + ( u10
1 - u1 2j I3 f1dq +
(uu
2 f3(f1 - f2)dq
2 2
|
(b2 )? [ ( ) (1 )
1 1+ a
= a +a |öij| 5 b+
b
?f1??u1-u2?+(2a+4b)
a+ 1 ?f1??u1-u2?
ñ0 a b
i,j
+(a+b)
?f1-f2?]
=
K'5(?f1-f2?+?u1-u2?)
( En utilisant (2.8) et (2.10) )
où :
K5 = 20(1 + a +
b)2(1 + a +a
+a + b)2(1+ñ0
,j
?f1?)? |öij| i
d'où :
?????
|
ab2giiöij
ñ0
|
[(u01)21IIt3 J
fldq - (u2) p 2 f2dq
K5(?f1-f2?+?u1-u2?)
(d)
R
|
|
Pour le quatrième terme de (a) on a :
????
|
ab2gjj
ñ0
|
[Ej1ul I3 qqjn
of1dq -
Ej2u2?3qpf2dq]??=
|
|
ab2gjj
ñ0
????
LEj1(ui1
- ui2) I
q0 f1dq +
(Ej1 - Ej2)u J
gp f1dq + Ej2u J
gp(f1 - f2)d]L3 q3 q R3
q
Mémoire de MASTER 28 MOUTNGUI SEE
c?UYI 2010-2011.
[(1 ) (1 )
ab2
= (a2+ b2)
a+1
?E1??f1??u1-u2?+
a+1
?f1??u2??E1-E2?
ñ0 b b
+(a+b)?E2??u2??f1-f2?]
=
K''5(?E1-E2?+?f1-f2?+?u1-u2?)
où :
2
K'' 5 =
ñ0
|
(1 + a + b)5(1 + ab +
ab + a1 + 1b)(1 +
?E1? +?E2?)(1 + ?f1?)(1
+?u2?)
|
|
d'où :
ab2gjj
ñ0
????
[Ej1uiJ 3
q0f1dq - Ej2u2 J 3
q0f2dq]????
= K5
(?E1-E2?+?f1-f2?+?u1-u2?)
(e)
Pour le cinquième terme de (a) on a :
????
|
ab2gjj
ñ0
|
L2 j i 1 j i
uj f
uj f ab2gjj r
(u2 ul j i
f
u2 E2u2 3 f2dq -
u0 E1u11 3
f1dq]??=?ñ0 L 1 u2 -
u10 ) E2u2 J 3 f2dq
|
|
+ (Ej2 -
Ej1)u0u2 J 3 f2dq +
(ui2 - u1)Ei o f 3
f2dq + uôEiui J
3(f2 - f1)dql
1 1 1 R J
[ ( ) (1 )
ab2
= (a2 +b2) 5 1+ a b
+ b ?E2??u2??f2??u1
-u2?+ a + 1
?f2??u2??E1 -E2?
ñ0 a b
(1 ) (1 ) ]
+ a + 1
?E1??f2??u1-u2?+ a +
1 ?E1??u1??f1-f2?
b b
= C'
(?E1-E2?+?f1-f2?+?u1-u2?)
( En utilisant (2.8) )
5
où :
C5= po(1+a+b)5(1+ ab +
a+1a+1b)(1+?E1?+?E2?)(1+?f2?)(1+?u1?+?u2?)
d'où :
[
ab2gjj
ñ0
????
uEj2u
u02 f2dq-0Ej1ui J 3
f1dq]????=
C5(?E1-E2?+?f1-f2?+?u1-u2?)
(f)
2iI3u1
pour le sixième terme de (a) on a :
????
|
ab2öjk
ñ0
|
f3q0f2u1
k[uu;
jf ~kuui f qqo
q u JR3 fldq] =ab2 [(-
)u J f2du2 1 qk R3
qo ñ0 u2
u12
|
|
j fk j f k
i2-ui1
1
+ (u) u J 3 q0
f2dq+uul 0 J 3 q0
(f2-f1)dq]
[ ( )(1 ) (1 )2
ab2 ? ?
= ?öjk ?? 5 1+a b
+b a +1
?f2??u2??u1-u2?+ a +1
?f2??u1 -u2?
ñ0 a b b
j,k
(1 )2 ]
+ a+1
?u1??f1-f2? b
=
C''5(?f1-f2?+?u1-u2?)
( En utilisant (2.8) )
Mémoire de MASTER 29 MOUTNGUI SEE
c?UYI 2010-2011.
Mémoire de MASTER 30 MOUTNGUI SEE
c?UYI 2010-2011.
où :
2
C''5 =
ñ0(1+a+b)3(1+b+ab+a+b)
(1 + ?f2?)(1 + ?u1? +
?u2?) öjk
\\ j,k
d'où :
|
????
|
ab2öjk
ñ0
|
[u202 ui2
f 0f2dq
- uoui f 0f1dq]
????= C5(?f1 - f2?
+ ?u1 - u2?) (g)
|
ainsi de (a), (b),
(c), (d), (e),
(f) et (g), on obtient (2.15) et l'expression
de C5 dans (2.17).
5. Additionnons (2.12), (2.13),
(2.14) et (2.15) et utilisons la définition
(1.61) de la norme de l'espace E pour avoir
(2.16).
D'où la proposition.
Nous sommes maintenant en mesure de prouver le
théorème suivant :
Théorème 2.1. Soit T >
0, t0 ? [0, T], Xt0 =
(Et0, pt0, ft0, ut0) ? E.
Alors il existe un nombre réel ä > 0 tel que le
système différentiel (S) ait une unique
solution
X = (E, p, f, u) ? F satisfaisant
X(t0) = Xt0. De plus, f satisfait la relation
:
|||f||| = sup {?f(t)?, t ?
[t0, t0 + ä]1 =
?ft0?L1(R3) (2.18)
où F = C([t0, t0 +
ä];103) × C([t0, t0 +
ä];103) × C([t0, t0 +
ä]; L1(1[83)) ×
C([t0, t0 +
ä];103).
Preuve. Nous appliquons la
théorie des systèmes différentiels du premier ordre au
système (S).
1. Puisque toutes les fonctions apparaissant dans (S) a,
b, ÿa, ÿb,
1a, 1b, ó,
... sont continues par rapport à t, il vient que G
= (G1, G2, G3, G4) l'est aussi.
Par la continuité des fonctions z = a, b,
1a, 1b à t = t0, il existe
ä0 > 0 tel que :
(1)
t ?]t0?ä0,
t0+ä0[ |z(t)| =
|z(t0)|+1
(1) implique, en utilisant (1.4) pour borner z,
que :
t ?]t0 - ä0, t0 +
ä0[ |z(t)| = (a0 +
b0 + 1+ 1)eCt0 + 1 (2)
a0 b0
Mémoire de MASTER 31 MOUTNGUI SEE
c?UYI 2010-2011.
Posons
B(Et0,1) = {E
E 1[83,IIE - Et0II < 1}
B(ft0, 1) = {f E
L1(1[83), IIf - ft0II <
1} B(ut0,1) = {u E
1R83, IIu - ut0II < 1}.
Alors :
{ E E B(Et0,1)
= IIEII < IIEt0II + 1
f E B(ft0,1) =
IIfII < IIft0II + 1 (3)
u E
B(ut0,1) = IIuII <
IIut0II + 1
Considérons le voisinage Vt0 =]t0 -
80, t0
+80[xB(Et0,1)
x 1[83 x B(ft0, 1)
x B(ut0,1) de (t0,
Xt0) dans le Banach 1[8 x 5, soit donc :
(t, X1), (t, X2) E Vt0
(4)
où :
Xi = (Ei, pi,
fi, ui), i = 1, 2
|
(3) implique :
|
{ IIEiII < IIEt0II
+ 1 IIfiII < IIft0II + 1
IIuiII < IIut0II + 1
|
i = 1, 2 (5)
|
On déduit de (2.16), des définitions
(2.17) de C2, C3, C4, C5 et C6, de la relation (2)
de z = a, b, 1a,
1b, de la relation (5) de Ei,
fi, ui, i = 1, 2, qu'il existe une constante
C7 = C7(ñ0, a0, b0, t0, Et0,
ft0, ut0, öij) telle que :
IIG(t, X1) - G(t, X2)II
<-- C7IIX1 - X2II (2.19)
Ce qui montre que G est localement lipschitzienne par
rapport à X = (E, p, f, u). L'existence d'une unique
solution X = (E, p, f, u) du système (S) sur
un intervalle [t0, t0 +8], 8 > 0 telle que
X(t0) = Xt0 est ainsi garantie par le
théorème de Cauchy-Lipschitz.
La relation (2.18) de f est établie
dans la reférence [10] qui étudie l'existence globale des
solutions pour l'équation de Boltzmann relativiste.
Mémoire de MASTER 32 MOUTNGUI SEE
c?UYI 2010-2011.
Le résultat suivant est une conséquence
immédiate du Théorème 2.1 pour (t0 =
0).
Théorème 2.2. Soit X0 = (E0,p0,f0,u0) E 5,
öij E R donnés, alors il existe T
> 0 tel que :
Le système différentiel (S) a une unique
solution X = (E,p, f, u) E C([0, T];R3) x C([0,T];R3) x
C([0,T];L1(R3)) x C([0,T];R3) telle que X(0) =
X0. De plus, f satisfait la relation :
fffffff = f0 (2.20)
CHAPITRE TROIS
EXISTENCE GLOBALE DES
SOLUTIONS
?p,
f,
u)
3.1 La méthode
Notons par [0, T[ le domaine maximal d'existence de
la solution notée (E, donnée par le
théorème 2.2 du système (S) avec pour
donnée initiale
X0 = (E0, p0,
f0, u0) ? R3 ×
R3 × L1(R3) ×
R3 = E.
Nous voulons prouver que T = +8.
· Si nous avons déjà T =
+8, le problème d'existence globale est résolu.
· Nous allons montrer que si nous supposons T <
+8, la solution (E,
|
?p,
|
T?u) = X peut
|
|
Mémoire de MASTER 33
MOUTNGUI SEE c?UYI 2010-2011.
être prolongée au delà de T, ce qui
contredit la maximalité de T.
· La stratégie est comme suit :
Supposons 0 < T < +8, soit t0
? [0, T[. Nous montrerons qu'il existe ä
> 0 indépendant de t0 tel que le
système (S) ait une unique solution X = (E, p, f,
u) sur [t0, t0 + ä] avec la condition
initiale
?X(t0) =
(?E(t0), ?p(t0),
h0), u(t0)).
Alors, en prenant t0 suffisamment proche de T
tel que 0 < T - t0 <
ä2, il s'ensuit que T < t0 +
ä2, nous pouvons ainsi prolonger la solution X
= (?E,?p, ?f,?u) sur
[0, t0 + ä2] qui contient strictement
[0, T[ et ceci contredit la maximalité de T. Dans le
but de simplifier les notations se sera suffisant si nous pouvons chercher
ä tel que 0 < ä < 1.
· Dans ce qui suit nous fixons un nombre r >
0 et nous prenons f0 tel que ?f0? = r, par
(2.20) nous avons :
??f(t0)? = ?f0?
(3.1)
Mémoire de MASTER 34 MOUTNGUI SEE
c?UYI 2010-2011.
3.1 La méthode
Nous déduisons de (2.18) et (3.1) que
toute solution f de l'équation de Boltzmann sur
[t0, t0 + ä] telle que f(t0)
= ?f(t0) satisfait :
I If(t)I I < r , Vt E
[t0, t0 + ä] (3.2)
Notons que (3.2) montre que toute solution X =
(E, p, f, u) du système (S) sur [t0,
t0 +ä] telle que :
|
satisfait :
|
(E, p, f, u)(t0) = (
|
?E(t0),
|
p(t0), h0),
|
-u-(t0))
|
X = (E, p, f, u) E C([t0,
t0+ä];1[83)xC([t0,
t0+ä];1[83)xC([t0,
t0+ä]; Xr)xC([t0,
t0+ä];1[83)
où Xr est défini par
(1.59), C([t0, t0 + ä];
Xr) par (1.60), avec I =
[t0, t0 + ä]. Dans ce qui suit, [0, T[
désigne le domaine maximal d'existence de la solution
X = (E, p, ?f, u) de (S)
telle que :
(
?E(0),?p(0),
?f(0), u(0)) = (E0,
p0, f0,u0) E S, I If0I I <
r.
Nous prouvons le résultat suivant qui sera utile dans la
suite.
Lemme 3.1. Les applications t
E(t) ; t p(t) ; t ' u(t)
sont uniformement
bornées sur [0, T[ et on a :
| Éi(t)| <
(|Ei
0|+Ci
8T)e3CT, V t E [0, T[
, i = 1, 2, 3 (3.3)
|P(t)| <
(|pi0|+Ci11T)e2CT,
Vt E [0, T[ , i = 1, 2, 3
(3.4)
|i(t)| <
(|ui0|+Ci12T)e(2C+Ci13)T,
Vt E [0,T[ , i = 1, 2, 3
(3.5)
où
|
{
|
Ci8 =
Ci8(a0, b0, r, T)
(3.3 bis)
Ci11 = Ch (a0, b0, r, T,
|Ei0|, ~i,j |öij|)
(3.4 bis)
Ci12 = 02 (ñ0,
a0, b0, r, T, Ei,j
|öij|) (3.5 bis)
Ci13 = Ci (ñ0,
a0, b0, r, T, |Ei 0|, ?i,j
|öij|) (3.5 bis)
13
|
Preuve. 1) Considérons
(1.55) dans lequel on pose E = E, f = f
et u = u i.e, l'égalité :
Ei = - +2 b Ei+ab2 J
gni fdq- ui ab2
J f dq , sur [0, T[. (1)
C a b) R3
u°(u)
q R3
Mémoire de MASTER 35 MOUTNGUI SEE
c?UYI 2010-2011.
3.1 La méthode
????
+ 2
aÿ a
bÿ b
????
de (1.3), on a :
= 3C (2)
1
|?u3|
|?u2|
1, b
,
a
1 b
=
?u)
?u) =
=
)
u0(
u0(
Nous avons de (1.4) et (2.6) :
|?u1|
?
?
?
et
u0(?u
( 1 )
z(t) = a0 + b0 1 +
a0 + b0 eCT, ?t ? [0,
T[ , où :
z=a, b, 1a, 1b
|
En utilisant (2.20) (|||
|
?f||| = ?f0? = r), on obtient :
ab2 Jqo fdq- ô
Z ab2 J f dq???= Cs (3)
R3 q u (u) R3
|
où :
Ci8 =
Ci8(a0, b0, r,
T).
(1), (2) et (3) donnent alors :
|ÿ?Ei| =
3C|?Ei|+Ci8
, i = 1,2,3 (4)
Intégrons (4) sur [0, t] (t ? [0,
T[), on obtient :
|
|
?Ei(t)|
= (|
|
? t
?Ei(0)| +
Ci 8T) + 3C |
?Ei(s)|ds
0
|
où ?Ei(0) =
Ei0 , i = 1,2,3
donc :
? t
| ?Ei(t)| =
(|Ei
0|+Ci 8T)+3C |
?Ei(s)|ds (5)
0
d'après le lemme de Gronwall on a :
| ?Ei(t)|
= (|Ei0| +
Ci8T)e3CT, ? t
? [0, T[ , i = 1,2,3 (3.3)
|
?E, p = ?p,
f =
|
f? et u = ?u i.e,
l'égalité :
|
D'où t ?-? ?E(t)
est uniformement bornée.
2) Considérons (1.56) dans lequel on pose
E =
|
ÿ?pi
=
-2?i0i?pi
|
ûi 2 ? ~c1?
0 (T) f3
fdq-ab2giip0(?p)öik
u0(?u) f 3 fdq (6)
|
3.1 La méthode
|
?101 =
|
aÿ a
|
, ?202 =
?303 =
|
bÿ b
|
de (1.3) on a :
|2?i0i?pi|
= 2C|?pi| (7)
d'après (3.3) et en procédant comme
ci-dessus, on a avec 1
u0(?u) = 1 :
????
où :
?Eiab2 ?fdq??
u0(
u) I3? = Cs (8)
Ci9 = Ci
(a0, b0, r, T, |Ei
0|). 9
ab2g33 = a
|?p1| < 1 |P|
< 1
b2
ab2g22
De même avec ab2g11
=
a g = g , p0(?p) -- a, p0(?p)
-- b
pO(P) = b et 1
u0(?u) = 1, on a
:
|
????
|
ab2gii
|
?pk
?
p0(p)öik
|
1? f fdq????=
Ci0 (9)
u0(u)3
|
où :
Ci10 = Ci (a0,
b0, r, T, ? 10
i,k
|öik|).
On déduit de (6), (7), (8), (9) et (3.3) que :
|ÿ?pi|=
2C|?pi|+Ci
(10)
11
où :
?
Ci 11 = Ci
(a0,b0,r,T, |Ei 0|,
11
i,k
|öik|).
Mémoire de MASTER 36 MOUTNGUI SEE
c?UYI 2010-2011.
En intégrant (10) on obtient ?t ? [0, T[
:
? t
|?pi(t)| =
(|?pi(0)| +
Ci11T) + 2C
|?pi(s)|ds , ?t ? [0, T[
, i = 1, 2, 3
0
En appliquant le lemme de Gronwall nous avons avec
?pi(0) = pi0, i =
1,2,3 :
|?pi(t)| =
(|pi0| +
Ci11T)e2CT, ?t
? [0, T[ , i = 1, 2, 3 (3.4)
3.1 La méthode
|
3) Considérons (1.58) dans lequel nous posons
E = l'égalité :
|
E, f =
|
f, u =
|
?u et u0 =
u0(?u) i.e,
|
ab2giiqj
ab2giiöij ~
·
ab2gjP0 JR3
jEui qjui =
-2ri0iû -ñ0u R 0
öijf3 q0 fdq + P0(u0)2
u' f fdq + q0?fR3
|
ab2gjjûiûj?Ej
|
L2 ui?uj qk 3
fdq - ab çjk ñ0u0
JR3 q0?fdq
(11)
|
|
ñ0u0
|
De la même façon que ci-dessus on déduit
les inégalités suivantes, pour les 2e et 3e
termes de (11) :
{
|ri0i| = C
?? (12)
-
ii
j
ii
iñ0
0
0
ñ0
0
ab2g
fr q
f ab2g
r
u
JR3 q
" dq +
(u
)2 u JR3 fdq C12
où :
Ci 12 = Ci (ñ0,
a0, b0, r, T, ? 12
i,j
|öij|).
Mémoire de MASTER 37
Intégrons (14) sur [0, t] (t ? [0, T[), ce qui donne :
MOUTNGUI SEE c?UYI 2010-2011.
Pour les 4e, 5e et 6e termes de (11), on a
:
ab2gjj?Ej / q
ô fdq-ab2gjj
Ejlj f fdq-ab2öjk ~ 0
f q0 fdq û? ??=
Ci13|?u | (13)
C Po JR3 q ñ0u
R3ñil-ri
R3 q
où :
|
Ci113 = C13
(ñ0, a0, b0, r, T,
|Ei0LE
I E
i,j
|
|öij|).
|
de (11), (12) et (13) on obtient :
| ÿûi| =
2C|?ui| +
Ci13|u| + Ci12
i.e.
| ÿûi| =
(2C+Ci13)|i|+Ci12
, i = 1, 2, 3 (14)
t
û(t)
|
|=(|?ui(0)| +
Ci12T) + (2C +
Ci13)/ |û(s)|ds , i
= 1, 2,3
0
Le lemme de Gronwall donne avec ûi(0) =
ui0, i = 1, 2, 3 :
|iii(t)| =
(|ui0| +
Ci12T)e(2C+Ci13)T, ?t ?
[0, T[, i = 1,2,3 (3.5)
De
(3.3), (3.4) et (3.5) on obtient le lemme.
Le lemme 3.1 nous permet de déduire la
proposition suivante :
Mémoire de MASTER 38 MOUTNGUI SEE
c?UYI 2010-2011.
3.1 La méthode
Proposition 3.1. Il existe 3
constantes R1 > 0, R2 > 0,
R3 > 0 telles que :
||| ?E||| = R1,
|||?p||| = R2, |||?u||| =
R3.
où
R1 = R1(a0, b0, r, T,
E0)
R2 = R2(a0, b0, r, T,
öij, E0,
p0)
R3 = R3(ñ0,
a0, b0, r, T,
öij, E0,
u0).
Preuve. On pose
|
Ri 1 = Ci 8 + (|Ei
0| + Ci e3C(T+1), i =
1, 2, 3.
[ 8T)e3CT]
En prenant :
3
R1 = Ri
? 1 i=1
On déduit de (3.3) que :
|||?E||| = R1
On pose :
Ri2 = [C1 +
(|pi0| +
Ci11T)e2CT1
e2C(T+1), i = 1, 2,
3
3
R2 = Ri
? 2 i=1
Et on déduit de (3.4) que :
|||?p||| = R2
En posant :
R3 = [Ci12 +
(|ui0| +
Ci12T)e(2C+Ci131
e(2C+C13)(T+1), i = 1,
3
R3 = Ri
? 3
|
2,
|
3.
|
(3.6)
(3.7)
(3.8)
(3.9)
(3.10)
(3.11)
|
i=1
On déduit de (3.5) que :
||| ?u||| = R3
d'où la proposition.
Comme nous le verrons les nombres R1,
R2, R3 sont pris suffisamment grands, pour borner non seulement
X mais aussi, toute solution X du problème de Cauchy
sur [t0, t0+ä] avec la donnée initiale
en t0 ? [0, T[.
Mémoire de MASTER 39 MOUTNGUI SEE
c?UYI 2010-2011.
3.2 Existence globale des solutions
3.2 Existence globale des solutions
Dans ce qui suit nous posons :
B(R1) = {E E
R3;IIEII < R1}
B(R3) = {u E
R3;IIuII < R3}
Pout tout t0 E [0, T[ et ä
> 0, on pose :
Yä = C([t0, t0 +
ä]; B(R1)) x C([t0,
t0 + ä];R3) x C([t0,
t0 + ä]; Xr) x
C([t0, t0 + ä];
B(R3)).
Soit (E, p, f, u) E Yä, on obtient du
système (S) défini par
(1.55)-(1.56)-(1.57)-(1.58) en posant dans
G = (G1, G2, G3, G4) donné
par (1.63)-(1.64)-(1.65)-(1.66) : f
= f, u = u dans G1, E = E, f
= f, u = u dans G2, p = p
dans G3 et E = E, f = f dans
G4, le système différentiel suivant :
?
????????
????????
ÿEi = G1(t, E, f,u)
(3.12)
ÿpi = G2(t, E, p, f,
u) (3.13)
dfdt = G3(t, p, f) (3.14)
ÿui = G4(t, E, f, u)
(3.15)
où :
|
?
??????????? ?
????????????
|
( aÿ ) ?
qi
G1(t, E, f,u) = - a +
2ÿb Ei + ab2 ? q0 fdq -
ab2ui R3 fdq (3.16)
b R3 u0(u)
G2(t, E,p, f, u) =
-2Pii0pi -
u0(u) ?R3 fdq - g p°(p)öjk u0(u) ?R3
fdq (3.17)
G3(t,p, f) = 1
p0(p)Q(f, f,p) (3.18)
G
(t E, f u)-- ab2g0(uiiöij) II$ f3 qjq0
fdq + ab2giiöijuj2?R3 fdq
, = --2Pi i0ui P0u
4
ñ0 (u0(u))
+ab2gjjEjui ? q0 fdq -
ab2gjjEjuiuj ? ?
qj qk
R3 fdq - ab2öjk uiuj q0
fdq, i = 1, 2, 3 (3.19)
ñ0 R3 ñ0u0(u) ñ0u0(u)
R3
|
Nous prouvons :
Proposition 3.2. Soit t0 E
[0, T[, ä E]0, 1[ et (E, p,
f, u) E Yä donnés. Alors le système
différentiel
(3.12)-(3.13)-(3.14)-(3.15)
a une unique solution (E,p, f, u) E Yä
telle que
(E, p, f, u)(t0) = (
?E(t0),
?p(t0),
?f(t0),
?u(t0)).
Mémoire de MASTER 40 MOUTNGUI SEE
c?UYI 2010-2011.
3.2 Existence globale des solutions
Preuve. Puisque a, b,
ÿa, ÿb,
1a, 1b, E, p, f,
u sont des fonctions continues en t, les fonctions G1,
G2, G3 et G4 le sont aussi.
1) Considérons l'équation (3.12) en
E avec G1 défini par (3.16) dans laquelle
f, u sont fixés. Nous déduisons de
(2.12) dans lequel on pose f1 = f2 = f et
u1 = u2 = u que :
?G1(t, E1,
f,u)-G1(t,E2,f,u)? =
C2?E1-E2? (a)
où :
C2 = 10(1+C)(1+ab2)(1+a b
+b a+1 a+1
)(1+?f?) (b)
b
utilisons (1.4) pour borner z = a, b,
1a, 1b, nous obtenons
alors, en utilisant 0 < ä < 1 :
( + 1 )
|z(t)| = a0+b0+ 1
eC(T+1), ?t ? [t0,t0+ä]
(c)
a0 b0
(d)
Nous déduisons de (b), en utilisant ?f? =
r(car f ? C([t0, t0 + ä];
Xr)) et (c) que : C2 =
C'2, où C'2
= C'2(a0, b0, r,
T)
de (a) et (d), G1 est globalement
lipschitzienne par rapport à E et l'existence locale d'une
solution E de (3.12) est ainsi garantie.
Puisque E satisfait (3.12), en suivant le
même procédé que dans le Lemme 3.1 en
remplaçant E par E, f par f et u
par u, on obtient en procédant comme dans la preuve du
Lemme 3.1 plus précisement numero (4) :
|ÿEi| =
3C|Ei| + Ci8
, i = 1,2,3
En intégrant sur [t0, t0 + t]
où t ? [0, ä[, on a :
fto+t
(t0 + t)| =
(|Ei(t0)| + C8) +
3CJIEi(s)|ds
to
?
|
or d'après (3.3) et la condition initiale
E(t0) =
|
E(t0), on a :
|
|Ei(t0)| =
|?Ei(t0)| =
(|Ei0| +
Ci8T)e3CT
|
d'où :
|
t0+t
|Ei(t0 + t)| =
[Ci8 +
(|Ei0| +
Ci8T)e3CTl + 3CJ
|Ei(s)|ds
to
J
|
3.2 Existence globale des solutions
Le lemme de Gronwall donne :
[ 8T)e3CT]
|Ei(t0+t)| = Ci 8
+(|Ei 0|+Ci e3C(T+1), ?t ?
[0, ä[, i = 1, 2, 3
(3.20)
Ce qui montre que toute solution E de (3.12)
satisfaisant E(t0) = ?E(t0) et
définie sur [t0, t0 + ä[ est
uniformement bornée. Par la théorie standard des systèmes
différentiels du premier ordre, la solution E est
définie sur l'intervalle [t0, t0 + ä]
tout entier, et d'après (3.6), (3.7) et
(3.20) on a E ? C([t0, t0 +
ä]; B(R1)).
2) Considérons l'équation (3.13) en
p avec G2 défini par (3.17) dans laquelle
E, f, u sont fixés. Nous déduisons de
(2.13) dans lequel on pose E1 = E2 = E,
f1 = f2 = f et u1 = u2 = u
que :
?G2(t, E, p1, f, u) -
G2(t, E, p2, f, u)?|
=C3?p1 - p2?
(e)
où :
|
?
C3 = 10(1 + C)(1 + a +
b)4(1 + a + b + 1 + 1
b a a b)2(1 +?E?)(1
+?f?)(1
+
ij
|
|öij|) (f)
|
Nous déduisons de (f), en utilisant (c),
?f? = |||f||| = r et ?E? = |||E|||
= R1
(car (E, f) ? C([t0, t0 +
ä]; B(R1)) × C([t0,
t0 + ä]; Xr)) que :
C3 = C'3,
où C'3 = C'
(a0, b0, r, R1, T,
|öij|) (g)
3
,
|ÿpi|=2C|pi|+Ci11
i = 1,2,3
Intégrons sur [t0, t0 + t]
où t ? [0, ä[ :
t0+t
|pi(t0 + t)| =
(|pi(t0)| +
Ci11ä) +
2CJIpi(s)|ds
to
or d'apres (3.4), et pi(t0)
= ?(t0), on a :
|pi(t0)| =
|P(t0)| = (|pi0|
+
Ci11T)e2CT
d'où :
t0+t
|pi(t0 + t)| =
[C1 + (|pi1
i0| +
Ci11T)e2CT1 +
2C |pi(s)|ds
JJ t0
Nous déduisons de (e) et (g) que G2 est globalement
lipschitzienne par rapport à p et
l'existence locale d'une solution p de (3.13) est ainsi
garantie.
De façon analogue à (10) dans la preuve du lemme
3.1 on a :
Mémoire de MASTER 41 MOUTNGUI SEE
c?UYI 2010-2011.
Mémoire de MASTER 42 MOUTNGUI SEE
c?UYI 2010-2011.
3.2 Existence globale des solutions
et le lemme de Gronwall donne :
[ 11T)e2CT]
|pi(t0 + t)| = Ci 11
+ (|pi 0| + Ci
e2C(T+1), ?t ? [0, ä[, i =
1,2,3
Ce qui montre que toute solution p de (3.13)
satisfaisant p(t0) =
?p(t0) et définie sur [t0, t0
+ ä[ est uniformement bornée et on a ainsi p ?
C([t0, t0 + ä];
1183).
3) Il est prouvé dans [9] que l'équation
(3.14) en f a une unique solution f ? C([t0, t0
+ ä]; Xr) telle que
f(t0) = 7(t0).
4) Considérons l'équation (3.15) en u
avec G4 défini par (3.19) dans laquelle
E, f sont fixés. Par la continuité des
fonctions z = a, b, 1a, 1b à t =
t0, il existe ä0 > 0 tel que :
t ? ]t0 ? ä0, t0 + ä0[=
|z(t)| = |z(t0)| + 1 d'après
(1.4) et t0 < T, on a :
( + 1 )
t ? ]t0?ä0, t0+ä0[=
|z(t)| = a0+b0+ 1 eCT+1
(h)
a0 b0
Soit :
B(?u(t0),1) =
{u ? 1[83; ?u - ?u(t0)?
< 1}
alors :
u ? B(?u(t0),1)
= ?u? = ??u(t0)? + 1
la proposition 3.1 donne :
u ? B(?u(t0), 1) = ?u? =
R3 + 1 (i)
Considérons le voisinage Wto
=]t0 ? ä0, t0 +
ä0[×B(?u(t0),1)
de (t0, u(t0)) dans le Banach II8 ×
1183, soit donc :
(t, u1), (t, u2) ? Wto
(j)
Nous déduisons de (2.15) dans lequel on pose
E1 = E2 = E, f1 = f2 = f
:
?G4(t, E, f, u1)-G4(t, E, f,
u2)? = C5?u1-u2? (k)
Mémoire de MASTER 43 MOUTNGUI SEE
c?UYI 2010-2011.
3.2 Existence globale des solutions
où :
C5 =
200(1 + C)(1 + ñ0)(1 + a
+ b)5(1 + a + b + 1 +
1)2(1+2?E?)(1+2?f?)×
ñ0 b a a b
(1+?u1?+?u2?)(1+E
|öij|)(l) i,j
Nous déduisons de (l), en utilisant
(h), (i), (j), ?f? = |||f||| = r et ?E?
= |||E||| = R1 que :
C5 = C'5,
où C'5 =
C'5(a0, b0,
ñ0, r, R1, R3, T, öij)
(m)
De (k) et (m), G4 est localement
lipschitzienne par rapport à u et l'existence locale d'une
solution u de (3.15) telle que u(t0) =
?u(t0) est garantie.
Puisque u satisfait (3.15), en suivant le
même procédé que dans le Lemme 3.1 en
remplaçant E par E, f par f et u
par u, on obtient en procédant comme dans la preuve du
Lemme 3.1 plus précisement numero (14) :
|ÿui| = (2C +
Ci13)|ui| +
Ci12 , i = 1,2,3
Intégrons sur [t0, t0 + t]
où t ? [0, 8[, on a :
f t0+t
|ui(t0 + t)| =
(|ui(t0)| +
Ci128) + (2C +
Ci13)JIui(s)|ds
to
|
or (3.5) et la condition initiale
u(t0) =
|
?u(t0) donne :
|
13)T
|ui(t0)| =
|?ui(t0)| =
(|ui 0| +
Ci 12T)e(2C+Ci
d'où :
f
to+tui(t0 +
t)| =[Ci12 +
(|ui0| +
Ci12T)e(2C+Ci13)Tl
+ (2C + Ci13) I
u(s)|ds
o
JJ
En appliquant le lemme de Gronwall, on obtient :
|ui(t0+t)| =
[C12+(|ui0|+Ci12T)e(2C+Ci13)T]
e(2C+C13)(T+1), ?t ? [0, 8[,
i = 1, 2, 3 (3.21)
Ce qui montre que toute solution u de (3.15)
satisfaisant u(t0) = ?u(t0) et
définie sur [t0, t0 + 8[ est uniformement
bornée. Par la théorie des systèmes différentiels
du premier ordre la solution u est définie sur l'intervalle
[t0, t0 +8] tout entier, et d'après
(3.10), (3.11)
Mémoire de MASTER 44 MOUTNGUI SEE
c?UYI 2010-2011.
3.2 Existence globale des solutions
et (3.21), on a u E C([t0, t0
+ 8]; B(R3)).
D'où la proposition
Notons que Yä défini
précédemment est un sous-espace métrique complet de
l'espace de Banach C([t0,t0
+8];1[83) xC([t0,t0
+8];1[83) xC([t0,t0
+8];L1(1[83))
xC([t0,t0 +8];1[83)
la proposition 3.2 nous permet de définir
l'application :
g : Yä -- Yä
(3.22)
(E,p,f,u) (E,p,f,u)
Nous prouvons :
Proposition 3.3. Soit t0 E
[0, T[, Il existe un nombre réel 8
E]0,1[, indépendant de t0, tel que le
système (S) défini par
(1.55)-(1.56)-(1.57)-(1.58)
ait une unique solution (E,p, f, u) E Yä
satisfaisant :
(E,p, f, u)(t0) = (
?E(t0), p(t0), h0),
?u(t0)).
Preuve. Nous prouverons qu'il existe
8 E]0,1[, indépendant de t0
tel que l'appli-cation g définie par (3.22) soit une
application contractante de l'espace métrique complet Yä,
ainsi elle admettra un unique point fixe (E,p, f, u) solution du
système (S).
|
Avec la donnée initiale
(?E(t0),
|
p(t0), h0),
|
u(t0)) à t = t0, le
système différentiel (3.12)-
|
(3.13)-(3.14)-(3.15) avec
G1, G2, G3 et G4 donnés par
(3.16)-(3.17)-(3.18)-(3.19) équivaut
au système intégral suivant :
|
{
|
Ei(t0 + t) =
?Ei(t0) + ? t0+t
t0 G1(ô, E, f, u)dô
(3.23)
pi(t0 + t) =
.1-3i(t0) + ? t0+t
t0 G2(ô, E, p, f, u)dô
(3.24)
f(t0 + t) = h0) + ? t0+t
t0 G3(ô, p, f)dô
(3.25)
ui(t0 + t)
=?ui(t0) + ? t0+t
t0 G4(ô, E, f,u)dô, t E
[0, 8], i = 1, 2, 3 (3.26)
|
À (Ej, pj,
fj, uj) E Yä, correspond une solution
(Ej, pj, fj, uj) E
Yä avec j = 1, 2, leur
existence est prouvée dans la proposition 3.2.
Écrivons le système intégral
(3.23)-(3.24)-(3.25)-(3.26) pour j
= 1 et j = 2, et prenons la
Mémoire de MASTER 45 MOUTNGUI SEE
c?UYI 2010-2011.
3.2 Existence globale des solutions
différence, nous obtenons avec i = 1,
2, 3 :
{ Ei1(t0 + t)
- Ei2(t0 + t) = ? t0+t
{G1(ô, E1, f1, u1) -
G1(ô, E2, f2,
u2)}(ô)dô (3.27)
t0
pi1(t0 + t)
- pi2(t0 + t) = ?t0+t
{G2(ô, E1,p1,
f1, u1) - G2(ô,
E2,p2, f2,
u2)}(ô)dô (3.28)
t0
f1(t0 + t) - f2(t0 +
t) = ? t0+t {G3(ô,p1, f1)
- G3(ô,p2,
f2)}(ô)dô (3.29)
t0
ui1(t0 + t)
- ui2(t0 + t) = ?t0+t
{G4(ô, E1, f1, u1) -
G4(ô, E2, f2,
u2)}(ô)dô (3.30)
t0
Maintenant nous avons d'après la proposition 2.3
:
IIG1(ô, E1, f1,
u1)-G1(ô, E2, f2,
u2)II <- C'
(IIE1-E2II+IIf1-f2II+IIu1-u2II)(ô)
(3.31)
2
IIG2(ô, E1,p1,
f1, u1)-G2(ô,
E2,p2, f2, u2)II
<-
C'
(IIE1-E2II+IIp1-p2II+IIf1-f2II+IIu1-u2II)(ô)
(3.32)
3
IIG3(ô,p1,
f1)-G3(ô,p2, f2)II <-
C'
(IIp1-p2II+IIf1-f2II)(ô)
(3.33)
4
IIG4(ô, E1, f1,
u1)-G4(ô, E2, f2,
u2)II <- C'
(IIE1-E2II+IIf1-f2II+IIu1-u2II)(ô)
(3.34)
5
où, en utilisant (Ej, pj,
fj, uj),
(Ej,pj, fj, uj) E
Yä, j = 1, 2, on a :
C2 =
C2(a0,b0,r,T)
C3 =
C3(a0,b0,r,R1,T,öij)
C4 =
C4(a0,b0,r,T)
C5 =
C5(a0,b0,ñ0,r,R1,R3,T,öij)
Notons déjà que les constantes C2,
C3, C4 et C5 sont indépendantes de
t0.
Maintenant en utilisant les inégalités
(3.31)-(3.32)-(3.33)-(3.34), nous
déduisons de
(3.27)(3.28)-(3.29)-(3.30) en utilisant la
norme ||| ·||| et le fait que t E [0, ä]
:
|
|||E1
|
-
|
E2|||
|
<- C2ä(|||E1 - E2|||
+ |||f1 - f2||| +
|||u1 - u2|||)
|
|
|
(3.35)
|
|
|||p1
|
-
|
p2|||
|
<-
C'3ä(|||E1 -
E2||| + |||p1 - p2|||
+ |||f1 - f2||| +
|||u1
|
-
|
u2|||)
|
(3.36)
|
|
{
|
|||f1
|
-
|
f2|||
|
<- C ä(|||p1 -
p2||| + |||f1 - f2|||)
|
|
|
(3.37)
|
|
|||u1
|
-
|
u2|||
|
<-
C'5ä(|||E1 -
E2||| + |||f1 - f2|||
+ |||u1 - u2|||)
|
|
|
(3.38)
|
Mémoire de MASTER 46 MOUTNGUI SEE
c?UYI 2010-2011.
3.2 Existence globale des solutions
Additionnons pour obtenir :
|||E1-E2|||+|||p1-p2|||+|||f1-f2|||+|||u1-u2|||
<
(C2 + C3 + C4 +
CDä(|||E1 - E2||| +
|||p1 - p2||| + |||f1
- f2||| + |||u1 - u2|||)
+(C'2 + C3 + C4
+ C'5)ä(|||E1 -
E2||| + |||p1 - p2|||
+ |||f1 - f2||| +
|||u1 - u2|||) (3.39)
Si on prend
ä tel que :
0 < ä <
InfS1,4(C2+ Cg+ C4+
C5)} (3.40)
(3.40) implique en particulier que 0 <
(C2 +C3 +C4 +C5)ä <
14, on obtient ainsi de (3.39) que :
3 (|||E1 - E2||| + |||p1
- p2||| + |||f1 -
f2||| + |||u1 - u2|||) < 1
(|||E1 - E2||| + |||p1 -
p2|||
4 4
+|||f1
-f2|||+|||u1 -u2|||)
|||E1-E2|||+|||p1-p2|||+|||f1-f2|||+|||u1-u2|||
<
1(|||E1 - E2||| +
|||p1 - p2||| +
|||f1 - f2||| + |||u1
- u2|||) (3.41)
3
ce qui donne :
(3.41) montre que l'application g
définie en (3.22) est une application contractante dans
l'espace métrique complet Y8, qui admet un unique point fixe
(E, p, f, u) E Y8 solution du système intégral
(3.23)-(3.24)-(3.25)-(3.26) et delà,
solution du système différentiel (S) défini par
(1.55)-(1.56)-(1.57)-(1.58) tel que :
(E, p, f, u)(t0) = (
?E(t0), p(t0),
?f(t0),
-u-(t0))
D'où la proposition
Basé sur la méthode détaillée dans la
section 3.1, nous avons prouvé le résultat suivant :
Théorème 3.1. Soit X0
= (E0, p0, f0,u0) E S =
1[83 x 1[83 x
L1(1183) x 1183,
öij E IR donnés tel que I If0I I < r,
où r > 0 est un nombre réel donné. Alors le
système différentiel (S) défini par
(1.55)-(1.56)-(1.57)-(1.58)
a une unique solution globale X = (E, p, f, u)
définie sur tout l'intervalle [0, +oo[ et
telle que :
(E, p, f, u)(0) =
(E0,p0, f0, u0).
D'où l'existence globale des solutions du
système couplé de Maxwell-Boltzmann-Euler sur un espace-temps de
Bianchi I.
Mémoire de MASTER 47 MOUTNGUI SEE
c?UYI 2010-2011.
Conclusion et perspectives
Dans ce travail nous avons étudié l'existence
globale des solutions du système couplé de
Maxwell-Boltzmann-Euler, qui gouverne l'évolution à très
grande vitesse d'un train de particules massives de matière pure
chargée, soumises à la seule action des forces
électromagnétiques créées par les particules
chargées, et en négligeant l'action des forces de gravitation. Le
cadre géométrique choisi était l'espace-temps courbe de
Bianchi de type I de la cosmologie.
Une étude complète de la situation consisterait
à prendre également en compte l'ac-tion du champ de gravitation.
Il faudrait alors coupler le système étudié aux
équations d'Einstein qui sont un système non-linéaire du
second ordre en a et b.
C'est ce que nous envisagerons de faire dans nos prochaines
investigations.
Mémoire de MASTER 48 MOUTNGUI SEE
c?UYI 2010-2011.
Annexes
Annexe 1
Preuve que dans (1.31) on a :
2p0q0?e ù
· (?q - p)
Cp
(, q,ù) = (1.32)
F2 - [ù · (p
+ q) 2 1.32
Remarquons que (1.5) et (1.6) nous donnent les
relations suivantes :
|
(p0)2
|
=
|
1 + p · p
|
|
|
(p'0)2
|
=
|
1 + p' · p'
|
|
|
{
|
|
|
|
(1)
|
|
(q0)2
|
=
|
1 + q · q
|
|
|
(q'0)2
|
=
|
1 + q' · q'
|
|
(1.28) et (1.30) donnent :
é = p'0 + q'0
|
é =
|
(p'0 +
q'0)2
|
|
|
=
|
(p'0)2
|
+ (q'0)2
|
+
2p'0q'0
|
|
=
|
(p'0)2
|
+ (q'0)2
|
+ 2(-6-- -
q'0)q'0
|
|
=
|
(p'0)2
|
- (q'0)2
|
+ 2-6-q'0
|
= 1 + p' · p' - 1 -
q' · q' +
2éq'0 d'après (1)
= p' · p' - q' ·
q' + 2eq'0
d'où :
-2éq'0 =
p'·p'-q'·q'-e
(2)
Mémoire de MASTER 49 MOUTNGUI SEE
c?UYI 2010-2011.
3.2 Existence globale des solutions
Calculons p' · p' - q'
· q' en utilisant (1.31), où pour
simplifier les notations C(p, q, w) sera noté C :
p' · p' = (p + Cw) · (p + Cw)
= p · p + 2Cp · w + C2w · w
= p · p + 2Cp · w + C2 (car w ?
S2)
de même :
q' · q' = q · q - 2Cq · w +
C2
ainsi :
p'·p'-q'·q'
= 2Cw·(p+q)+p·p-q·q (3)
En remplaçant (3) dans (2) on obtient
:
|
-2?eq'0 =
|
2Cw · (p + q) + p · p - q · q -
?e2
|
|
|
|
=
|
2Cw · (p + q) + (p0)2 -
|
1 - (q0)2 + 1
|
- ?e2
|
(d'après (1))
|
|
=
|
2Cw · (p + q) + (p0)2 -
|
(q0)2 - ?e2
|
|
|
= 2Cw · (p + q) + (p0 +
q0)(p0 - q0) - ?e2 = 2Cw · (p
+ q) + ?e(p0 - q0) - ?e2 = 2Cw · (p + q)
+ ?e(p0 - q0 - ?e) = 2Cw · (p + q) -
2q0?e
d'où :
-2?eq'0 = 2Cw · (p + q) -
2q0?e
En élevant au carré on a :
4?e2(q'0)2 = (2Cw ·
(p + q) - 2q0?e)2
(1) donne:
4?e(1 + q' · q') =
4C2(w · (p + q))2 - 8q0?e(w · (p +
q))C + 4(q0?e)2
or
1 + q' · q' = 1 + q · q -
2Cq · w + C2
Mémoire de MASTER 50 MOUTNGUI SEE
c?UYI 2010-2011.
3.2 Existence globale des solutions
ainsi on a :
4é(1 + q · q - 2Cq ·
ù + C2) = 4(ù · (p
+ q))2C2 -
8q°?e(ù · (p +
q))C +
4(q°?e)2
ce qui donne :
2
4 [ù·(p+q)]
-é
)C2+4(2éq·ù?2q°éù·(p+q))C
+4(q°Z)2-4é(1+q·q)
= 0 (4)
Le calcul des coefficients de l'équation (4) donne :
? 2éq · ù -
2q°é ù · (p
+ q) = 2é ù · (éq -
q°(p + q)) = 2é
ù · (p°q +
q°q - q°p -
q°q) = 2é ù ·
(p°q - q°p) =
2p°q°?e ù ·
(?q - ?p)
où ?p =; .
?
4(q°)2é -
4é(1 + q · q) =
4é(q°)2 -
4-62(q°)2
= 0
d'où l'équation (4) devient :
|
2 ~
4 [ù·(p+q)]
-é)C2+8p°q°é
ù·(-?p) = 0
|
(5)
|
l'équation du second degré en C(p,
q, ù) est ainsi obtenue en (5), elle admet pour solution non
triviale :
2p°q°?e
ù · (?q - ?p)
,..2
C(p,q,ù __
) - [ù · (p +
q)]2
d'où le résultat.
3.2 Existence globale des solutions
Annexe 2
Preuve que le Jacobien du changement de variables (1.31)
est :
?(p', q')
?(p, q)
p'0q'0
= _(1.33)
p0q0
Le Jacobien du changement de variables (p, q)
(p', q') défini par (1.31)
est donné par :
|
?(p', q')
?(p,q)
|
=
|
????????????????
|
?p'1 ?p1
?p'2 ?p1
?p'3 ?p1
?q'1 ?p1
?q'2 ?p1
?q'3 ?p1
|
?p'1 ?p2
?p'2 ?p2
?p'3 ?p2
?q'1 ?p2
?q'2 ?p2
?q'3 ?p2
|
?p'1 ?p3
?p'2 ?p3
?p'3 ?p3
?q'1 ?p3
?q'2 ?p3
?q'3 ?p3
|
?p'1 ?q1
?p'2 ?q1
?p'3 ?q1
?q'1 ?q1
?q'2 ?q1
?q'3 ?q1
|
?p'1 ?q2
?p'2 ?q2
?p'3 ?q2
?q'1 ?q2
?q'2 ?q2
?q'3 ?q2
|
?p'1 ?q3
?p'2 ?q3
?p'3 ?q3
?q'1 ?q3
?q'2 ?q3
?q'3 ?q3
|
????????????????
|
|
?(p',
q')
?(p, q)
|
=
|
????????????????
|
1 + ?C
?p1 ù1 ?p2 ù1
?C ?p3 ù1
?C ?q1 ù1
?C ?q2 ù1
?C ?q3 ù1
?C
?p1 ù2 1 + ?C
?C ?p2 ù2 ?p3 ù2
?C ?q1 ù2
?C ?q2 ù2
?C ?q3 ù2
?C
?p1 ù3
?C ?p2 ù3 1 + ?C
?C ?p3 ù3 ?q1 ù3
?C ?q2 ù3
?C ?q3 ù3
?C
_ ?C w1 _
aCwi _
aCù1 1 _
?C _ ?Cwi _
aCù1
?p1 a,2 ap3 ?q1
?q2 aq3
_ ?C ù2 _ ?C
ù2_ ?Cù2 _
?Cù2 1 _
?C ù2 _ ?C
ù2
?p1 ?p2 ap3 aq1
?q2 ?q3
_ ?Cw3
_aCw3
_aCw3
_aCù3
_?Cù3 1 _
?C ù3
?p1 a,2 aP3 aq1
?q2 ?q3
|
????????????????
|
où C(p, q, ù) est tout
simplement noté C, ù =
(ù1, ù2, ù3). En
effectuant les opérations élémentaires L4 - L1 +
L4 ; L5 - L2 + L5 ; L6 - L3 + L6,
on obtient :
?(p', q')
?(p, q)
= ????????????????
1 + ?C
?p1 ù1 ?p2 ù1
?C ?p3 ù1
?C ?q1 ù1 ?C
?C ?q2 ù1 ?C
?q3 ù1
?C
????????????????
?p1 ù2 1 + ?C
?p2 ù2 ?p3 ù2
?C ?q1 ù2 ?C
?C ?q2 ù2 ?C
?q3 ù2
?p1 ù3
?C ?p2 ù3 1 + ?C
?C ?p3 ù3 ?q1 ?C
ù3 ?q2 ?C ù3
?C
?q3 ù3
1 0 0 1 0 0
0 1 0 0 1 0
0 0 1 0 0 1
Mémoire de MASTER 51 MOUTNGUI SEE
c?UYI 2010-2011.
3.2 Existence globale des solutions
Des opérations élémentaires C1
?- C1 -C4 ; C2 ?- C2 -C5 ;
C6 ?- C3 -C6, on obtient:
|
?(p',
q')
?(p, q)
|
=
|
????????????????
|
1 + ( ?C
?p1 - ?C )ù1 ( ?C
?p2 - ?C )ù1 ( ?C
?p3 - ?C )ù1 ?C
?q1 ù1 ?q2 ?C
ù1 ?C
?q3ù1
?q1 ?q2 ?q3
( ?C
?p1 - ?C )ù2 1 + ( ?C
)ù2 ?q1ù2 ?C
?C
?p2 - ?C )ù2 ( ?C
?p3 - ?C ?q2ù2 ?C
?q3ù2
?q1 ?q2 ?q3
( ?C
?p1 - ?C )ù3 ( ?C
?p2 - ?C )ù3 1 + ( ?C
?p3 - ?C )ù3 ?C
?q1 ù3 ?q2 ?C
ù3 ?C
?q3 ù3
?q1 ?q2 ?q3
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
|
????????????????
|
[ (?C ) ][
(?C ) ( ?C ) ]
= 1+ ù1 1+ ù3
?p1 - ?C ?p2 - ?Cù2+
?p3 - ?C
?q1 ?q2
?q3
(?C ) )( ?C
-ù1ù2 ?p1 - ?C
)( ?C (?C
-ù1ù3 )
?p2 -?C ?p1 - ?C ?p3 - ?C
?q1 ?q2
?q1 ?q3
( ?C ) ( ?C ) (
?C )
= 1 + ù3
?p1 - ?C ù1 + ?p2 - ?C
ù2 + ?p3 - ?C
?q1 ?q2
?q3
|
d'où :
|
?(p',
q')
?(p, q)
|
( ?C ) ( ?C ) ( ?C
)
= 1+ ù1+ ù2+
ù3 (1)
?p1 - ?C ?p2 - ?C ?p3 -
?C
?q1 ?q2
?q3
|
( ) ( ) ( )
?C
Calculons ?p1 - ?C ?C ?C
, ?p2 - ?C et ?p3 - ?C .
?q1 ?q2 ?q3
On pose :
A=2p0q0?eù·(?q-?p)et
B=?e2- [ù · (p +
q)]2
(1.32) donne :
A
C = B
d'où :

?C
?C
?pi
?qi =
i = 1, 2, 3 (2)
B(aP - aq) - A(ap
- aq)
,
B2
or
A = 2p0q0?e
ù · (?q - ?p)
= 2?e ù · (p0q -
q0p)
=
2?e[a2ù1(p0q1
- q0p1) +
b2ù2(p0q2
- q0p2) +
b2ù3(p0q3
- q0p3)]
Mémoire de MASTER 52 MOUTNGUI SEE
c?UYI 2010-2011.
3.2 Existence globale des solutions
En dérivant :
a2p1
;
p0
??e ?p0 ?p1
?p1
??e a2q1
?q1 q0
?A ?p1
= 2a2p1
p0ù ·(p0q
-q0p)-2a2?e
ù1q0 +2a2?e p1
p0(ù · q) (3)
de même :
?A ?q1
2 q1 0 0 2?1 0 2?q1
Et :
= 2a 0ù · (p q - q
p) + 2a e ù p ? 2a e q0 (ù ·
p) (4)
1
?p1 = 2a2?e ~0
?B
-2a2ù1ù·(p+q)
(5)
?q1 = 2a2?e q1
q0
?B
2a2ù1ù
·(p+q) (6)
(3) et (4) donnent :
?A ?A ?p1 ?q1
)
=
2a2(ù·(p0q-q0p))(p1
(p1 )
p0 - q1 -2a2?e
ù1(p0
+q0)+2a2?e p0(ù
·q)+ q1
q0 (ù·p)
q0
d'où :
?A
?p1

) )
?q1 =
2a2(ù·(p0q-q0p))(p1
(p1
?A p0 -q1
-2a2?e2ù1+2a2?e p0
(ù·q)+q1
q0 (ù·p) (7)
q0
(5) et (6) donnent :
?B ?B ?p1 ?q1
(p1 )
= 2a2?e p0 - q1q0

(8)
En procédant comme ci-dessus, on a :
?A
? ?p2
= 2b2p2
p0ù · (p0q
- q0p) - 2b2?e
ù2q0 + 2b2?e p2
p0 (ù · q) (9)
?A ?q2
= 2b2 q2
q0 ù · (p0q
- q0p) + 2b2?e
ù2p0 - 2b2?e
q2
q0 (ù · p) (10)
= 2b2?e p
p0
-2b2ù2ù·(p+q)
(11)
?B ?p2
2
= 2b2?e q
q0
2b2ù2ù·(p+q)
(12)
?B ?q2
2
Mémoire de MASTER 53
MOUTNGUI SEE c?UYI
2010-2011.
(9) et (10) donnent :
?A ?A ?p2 ?q2
)
= 2b2(ù ·
(p0q - q0p))(p2
(p2 )
p0 - q2 -
2b2?e2ù2
+ 2b2?e p0 (ù · q) + q2
q0 (ù · p) (13)
q0
3.2 Existence globale des solutions
(11) et (12) donnent :
?B ?B
?p2 ?q2
(p2 )
= 2b2?e p0 - q2 (14)
q0
?A
? ?p3
?A ?q3
2 p3
0 0 2? 3 0 2? 3
= 2bp0ù ' (pq - qp) -
2be ùq + 2bep0(ù
' q) (15)
2 q3 0 0 ~ 2~ q3
= 2bq0ù ' (pq - qp) +
2b2eù3P0
- 2beq0(ù ' p) (16)
|
?B ?p3
|
= 2b2?e p3
p0
|
-2b2ù3ù'(p+q)
(17)
|
|
?B ?q3
|
= 2b2?e q3
q0
|
2b2ù3ù'(p+q)
(18)
|
Mémoire de MASTER 54 MOUTNGUI SEE
c?UYI 2010-2011.
(15) et (16) donnent :
?A ?A ?p3 ?q3
= 2b2(ù '
(p0q - q0p))(p0 3 -
q0 ) -
2b2?e2ù3
+ 2b2?e (P0 (ù ' q) +
q0 (ù ' p)) (19)
(17) et (18) donnent :
?B ?B ?p3 ?q3
(p3 )
= 2b2?e p0 - q3 (20)
q0
De (1), (2), (7), (8), (13), (14), (19) et (20) on obtient :
|
?(p', q')
?(p, q)
|
= 1+
|
( [ ( ?A ) ( ?A ) (
?A )]
1 B ù1
+ù2 +ù3
?p1 - ?A ?p2 - ?A ?p3 -
?A
B2 ?q1 ?q2
?q3
[ (?B )
(?B ) (?B
)])
-A ù1 ?p1 - ?B +
ù2 ?p2 - ?B + ù3 ?p3
- ?B
?q1 ?q2
?q3
|
|
= 1 +
|
[ 1
B
|
?e2 A2
2p0q0(ù '
(?q - p))2 2?e2 +
Pq0(ù ' p)(ù ' q)] +
B2p0q0
|
|
C2
= 1 + p0q0 +
|
Bp0q0 [ -
(p0)2(q0)2((ù
' p
)2 +(ù'?q)2
2(ù ' ?p)(4,0
)(w
|
- p0q0
?e2 (p +
q))2 -
p0q0(ù (p +
q))2 + ?e2(ù '
p)(ù ' q)]
|
C2
= 1 + p0q0
|
2p0q0
Bp0q0 [e - (ù ' (p
+ q))2] Bp0q0 [ -
(q0)2(ù ' p)2
-
(p0)2(ù
|
+ 2p0
q0(ù'p)(ù'q)-p0
q0(ù'p)2-p0q0(ù'q)2-2p0
q0(ù'p)(ù'q)+?e2(ù'p)(ù'q)]
3.2 Existence globale des solutions
|
C2
= 1+ p°q°
|
2+
|
2
Bp°q°
[-q°(ù
·p)2?e-p°(ù
·q)2?e+?e2(ù·p)(ù·q)]
|
|
2
_ -1+P q°+
|
Bp°q°
[-q°p°(ù·p)(ù·?p)-p°q°(ù·q)(ù·?q)+p°(ù·p)(ù·q)+q°(ù·p)(ù·q)]
|
|
2
= -1 + pq°+
|
Bpq ((w'P) °° [ù ·
(q - p)] + (ù
·?q)[ù · (p -
q)])
|
|
2
_ -1+P q° +
|
2?ep°q°(ù
· (?q - ?p))(ù
· (p - q))
Bp°q°
|
|
d'où :
|
2
= -1 + pq +
°
|
C
(ù · (p - q))
p°q°
|
?(p', q')
?(p,q)
2
= -1+ pq° +
C
(ù·(p-q)) (21)
p°q°
Mémoire de MASTER 55 MOUTNGUI SEE
c?UYI 2010-2011.
Par ailleurs, (1.6) et (1.31) donnent :
(p'°)2 = 1 +
p' · p'
= 1 + p · p + 2C(ù ·
p) + C2 = (p°)2 +
C2 + 2C(ù · p)
d'où :
(p'°)2 =
(p°)2 + C2 +
2C(ù · p)
de même on a :
(q'°)2 =
(q°)2 + C2 -
2C(ù · q)
or
?e2 =
(73'0)2
P0)2 +
(q'°)2 +
2p'°q'°
= (p°)2 +
(q°)2 +
2p°q°
ainsi
2p'°q'°
= ?e2 -
(p'°)2 -
(q'°)2
= ?e2 -
[(p°)2 +
(q°)2 + 2C2 +
2Cù · (p - q)] = ?e2 -
[?e2 -
2p°q° +
2C2 + 2Cù · (p - q)] =
2p°q° -
2C2 - 2Cù · (p -
q)
d'où :
|
p'°q'°
|
C2
= -1 + p°q° +
|
C
(ù · (p - q)) (22)
p°q°
|
|
p°q°
|
Mémoire de MASTER 56 MOUTNGUI SEE
c?UYI 2010-2011.
3.2 Existence globale des solutions
|
de (21) et (22), on conclut que :
|
8(p',
q')
8(p,q)
|
p'°q'°
= -
p°q°
|
d'où le résultat.
3.2 Existence globale des solutions
Annexe 3
Preuve du Lemme 1.2
|
(1.47) donne :
uáuë
ÿuâ =
-?âáë u0
|
ñ0u0 Fâ
1 ëJë - 1
ñ0u0FáëJëuáuâ
|
|
= -?âáë
|
uáuë
|
1që
ñ0u0 Fâë (f3 q0 f(t,
q)ab2dq - euë
|
|
u0
|
1/ a
ñ0u0
Fáëuáuâ (JJ3 q0
f(t, q)ab2dq - euë
|
= -?âáë
|
uáuë
|
uë
ñ0u0Fâë(~3
qëf(o
)ab2dq - u0 ?3 f(t,q)ab2dq)
|
|
u0
|
1 ë
ñ0u0
Fáëuáuâ R3 q0
f(t, q)ab2dq +
ñ0eu0uâFáëuáuë
|
= -?âáë
|
uáu°ë -
ñou0Fâ(f3
qëf(qo
q)ab2dq - uë
3 fut,q)ab2dq)
|
1/ a
0
Fáëuáuâ J q0 f(t,
q)ab2dq
ñ0u R3 q
d'où le système (1.52).
En explicitant les fonctions inconnues on a :
uáuë
ÿu0 =
-?0áë
u0
ñ0 ttë
F0 [ f3 q0.Î(t,
q)ab2dq - u0 JR 3 f(t,
q)ab2dq]
?
1 që
ñ0u0 Fáëuáu0
q0 f(t, q)ab2dq
R3
(ui)2
= -?0
ii u0
ë
ñ0u 10gëâF0 (?3
g0 f(t, q)ab2dq - u0
?f(t,q)ab2dq)
1
ñ0
(ui)2
ÿu0 = -?0 ii
0
u
giiF0iab2
ñ0u0
f
Faauá J
gaof(t,
q)ab2dq
R3 q
[ ? ? ]
q0f(t)(q)dq- ui
qi
R3 f(t)(q)dq
u0
R3
Mémoire de MASTER 57
MOUTNGUI SEE c?UYI
2010-2011.
(F0ëu0 +
Fiëui)
ab2
ñ0
ab2
= +
ñ0
3.2 Existence globale des solutions
|
or
|
(F0ëu0 +
Fiëui)
|
që F0iu0 /
qi 2 F0iui /
?3 ° f(t)(q)ab2 dq = - J
o f(t)(q)ab dq+ J f
(t)(q)ab2dq
q
ñ0 ~3 q ñ0 R3
|
|
ñ0
|
ab2 ñ0
j
öijui
fq0f(t)(q)dq
R3
i f
FOiab2
=
ab2 j
ñ0 (u0 f g0 f(t)(q)dq -
uz f(t)(q)dq) - po
~Zjui q° f(t)(q)dq
3 3 3
i f
l ab2 qj
g0ágiâFáâ
(u0 f 3 q0 f(t)(q)dq - ui f(t)(q)dq)
- po ö f q° f(t)(q)dq
3 3
l / 9
giiFoi (u0 Jl[~ g0 f(t)(q)dq -
ui J f (t)(q)dq) - ab
poz'uz J~ q0 f(t)(q)dq
3 R3 3
on obtient ainsi (1.53).
En plus on a de (1.52) avec â = i :
uáuë
ÿui =
-Piáë u0
1
ñ0u0Fi ë (? 3
qëf(q~q)ab2 dq - u0 f
3 f(t)(q)ab2dq)
1 /
N
1 O Fáëuaui J R3 q0
f(t)(q)ab2dq
Calcule de A, B et D où
:
· A = -Piáë
|
uáuë
|
ujuë
i ë i i i
=
-ri - Pjë
u0 = = --POiu -- POiu
--2Poiu
|
|
u0
|
donc A =
-2Pi0iui
(1)
ëë
· B = ñ0u0 Fi ë ( f q0
f(t)(q)ab2dq - u0R J 3 f(t)(q)ab2dq)
1
= ñ0u0Fi 0(f3
f(t)(q)ab2dq - f3 f dq)
+ ñ0u0 Fi j ( R3 q0 f(t)(q)ab2dq
- u0 R3 f(t)(q)ab2dq)
( f3 q0 f(t)(q)dq - 0f f (t)(q)dq)
qj
u
( f3 q0 f(t)(q)dq - u0 f f(t)(q)dq)
u
giáFájab2
ñ0u0
ab2giiFij
ñ0u0
R3
R3
Mémoire de MASTER 58
MOUTNGUI SEE c?UYI
2010-2011.
ab2giiöij qj
ab2giiöijuj
donc B = ñ0u0 f3 q0f(t)(q)dq
ñ0(u0)2 f3 f(t)(q)dq (2)
Mémoire de MASTER 59
MOUTNGUI SEE c?UYI 2010-2011.
3.2 Existence globale des solutions
1
ë
· D = ñ0u0
Fáëuáui R3 q0
f(t)(q)ab2dq
ab2 = ñ0u0 (F0ëu0 +
Fjëuj)ui f3 q0 f(t)(q)dq
ab2F0ëui f 3 qA0 f(t)(q)dq +
ab2ñ0u0jui f3 q0 f(t)(q)dq
ñ0
= ab2F0juiq
f q0f(t)(q)dq +
ab2Fj0 ab2F
0u~uz f Î(t)(q)dq +
jk0ujui f
of(t)(q)dq
ñ0 R3 q ñ0u R3 ñ0u
JR3 q
|
ab2gjjF0jui
|
fj ab2
F0juiuj uiuj
k
3 g0 f(t)(q)dq+ 9 p0u0 f3
f(t)(q)dq+ab2öjk ñ0u0 fR3 q0
f(t)(q)dq
|
|
ñ0
|
|
ab2gjjF0jui
donc D = -
ñ0
|
f3 qj
f(t)(q)dq+ab2gjjF0
uiuj R3 f(t)(q)dq
ñ0u0
|
2 uiuj qk
+ ab
öjkñ0u0 JR3
q0f(t)(q)dq (3)
De (1), (2), (3) et du fait que
ÿui = A - B - D, on obtient
(1.54).
Mémoire de MASTER 60
MOUTNGUI SEE c?UYI
2010-2011.
Bibliographie
[1] D. Bancel, Problème de Cauchy
pour l'équation de Boltzmann en Relativité
Générale. Ann. Henri Poincaré, Vol XVIII, 3,
263, (1973).
[2] D. Bancel ; Y. Choquet-Bruhat,
Uniqueness and local stability for the Einstein-Maxwell-Boltzmann system.
Comm. Math. Phys, 33, 87 (1973).
[3] K. Bichleter, On the Cauchy problem
for relativistic Boltzmann equation. Comm. Math. Phys, 4, 352
(1967).
[4] R. T. Glassey ; W. Strauss,
Asymptotic stability of the relativistic Maxwellian.
Publ. Math. RIMS Kyoto, 29, 301 (1992).
[5] R. T. Glassey, The Cauchy problem in
kenetic theory, SIAM, Indiana University, Bloomington, Indiana
(1996).
[6] Jurgens Eulers, A survey of General
Relativity theory. Astrophysics and Cosmology. Ed. W. Israel (14),
(26).
[7] P. B. Mucha, Global existence for
the Einstein-Boltzmann equation in the flat Robertson-Walker space-time.
Comm. Math. Phys. 203, 107, (1999).
[8] P. B. Mucha, Global existence of
solutions of the Einstein-Boltzmann equation in the spatially homogeneous case
in Evolution Equation, Existence, Regularity and Singularities,
Banach Center publications, volume 52, Institute of Mathematics,
Polish Academy of Science, Warzawa (2000).
[9] N. Noutchegueme, D. Dongo, Global
existence of solutions for the Einstein-Boltzmann system in a Bianchi type 1
space-time for arbitrarily large initial data. Class Quantum Grav.
23, 2979-3003 (2006).
BIBLIOGRAPHIE
[10] N. Noutchegueme, D. Dongo, E. Takou,
Global existence of solutions for the relativistic Boltzmann
equation with arbitrarily large initial data on a Bianchi type 1 space-time.
Gen. Relat. Grav (2005), 37 (12) 2047-2062.
[11] N. Noutchegueme, E. Takou, Global
existence of solutions for the Einstein-Boltzmann system with cosmological
constant in a Robertson-Walker space-time. Commun. Math. Sci, vol.
4, no. 2, pp 291-314, (2006), International Press.
[12] N. Noutchegueme, R. D. Ayissi, Global
existence of solutions to the Maxwell-Boltzmann system in a Bianchi type 1
space-time. Adv. Studies Theor. Phys, Vol. 4, 2010, no. 18,
855-878.
Mémoire de MASTER 61 MOUTNGUI SEE
c?UYI 2010-2011.
| 


