4.2 Description de l'application
Afin de comparer les deux fonctions de prédiction des
liens, il est nécessaire de les appliquer sur les mêmes
données et dans le même contexte, pour cela, nous avons
4.2.1 Algorithmes et explications
Chapitre 4. Implémentation et Expérimentations
43
choisi d'utiliser le même réseau social. Comme le
langage que nous avons utiliséest un langage objet, nous avons
profitéde cet aspect de programmation durant
le développement de l'outil d'expérimentation.
L'organigramme global suivant 4.2 présente les
différentes étapes de l'implémentation :
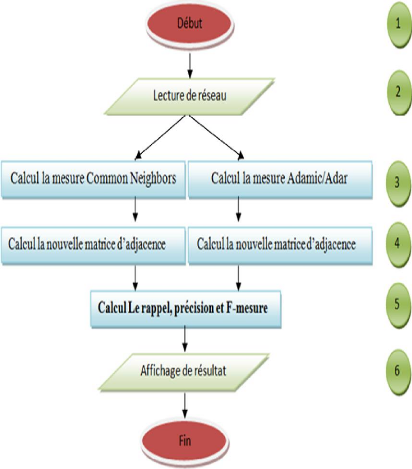
FIGURE 4.2 - L'organigramme de l'application
L'étape (2) : C'est une étape
très importante, il s'agit des opérations d'entrée/sortie
dans laquelle le programme lit le réseau social à partir du
fichier texte, notre réseau social est stockésous une forme
matricielle, ce qu'il facilite son interprétation.
L'étape (3) : Ce niveau de calcul est
distinguéen deux étapes indépendantes,
Chapitre 4. Implémentation et Expérimentations
44
une étape consiste à appliquer la fonction qui
calcul la matrice de similaritéAda-mic/Adar et l'autre consiste à
appliquer la fonction de similaritéVoisins communs, à partir de
la matrice d'adjacence.
L'étape (4) : consiste à
recalculer la nouvelle matrice d'adjacence pour chaque algorithme en ajoutant
les liens prédits.
L'étape (5) : Cette étape
consiste à mesurer les performances de nos algorithmes
de prédiction des liens, nous prenons les deux matrices
d'adjacence construit àpartir de l'étape
précédente et nous les comparons avec une nouvelle capture de
ce même réseau social.
Dans la suite nous allons voir les fonctions et les
procédures qui sont incluent dans chaque étape.
4.2.1.1 Construire la matrice de Adamic et Adar
Le pseudo code suivant [1] représente
l'exécution de l'algorithme de Adamic et Adar. la fonction Adamic et
Adar commence par récupérer la matrice d'adjacence de
réseau social, puis elle recherche pour tous pairs de noeuds non
connecté, leurs voisins commun, s'ils existent elle fait appel à
une autre fonction (degreenoeud(k)) qui calcul le degréde
chaque voisin commun en lui passant comme paramètre, puis
elle calcul l'inverse de log de degréde ce
dernier. A la fin la matrice de similaritéreçoit la somme des
inverses delog dégrée de tous les voisins communs pour
tous les
pairs non connecté, par convention la
similaritéentre deux noeuds
déjàconnecté(dans la matrice d'adjacence
(M(i, j) = 1)) est égal à 0, ainsi la
similaritéentre un noeud et le même noeud est aussi égal
à 0.
Chapitre 4. Implémentation et Expérimentations
45
Algorithm 1 Algorithme de Adamic et Adar
1: function DEGREE
NOEUD(adj,k)
2: entier degree +- 0
3: entier N +- adj.length
4: fori +- 1 to N
do
5: if adj(k, i) = 1
then
6: degree +- degree + 1
7: end if
8: end for
9: return degree
10: end function
11: function ADAMIC ET ADAR(adj)
12: Output matrice de similarité:
adamicAdar
13: double freq +- 0
14: entier N +- adj.length
15: fori +- 1 to N
do
16: forj +- 1 to N
do
17: if i = j
then
18: adamicAdar(i, j) +- 0
19: else
20: if adj(i, j) = 1
then
21: adamicAdar(i, j) +- 0
22: else
23: for k +- 1 to N
do
24: if adj(i, k) = 1 ?
adj(k, j) = 1 then
1
25: freq +- freq + ln(DEGREE NoEUD(M,k))
26: adamicAdar(i, j) +- freq
27: end if
28: end for
29: freq +- 0
30: end if
31: end if
32: end for
33: end for
34: return adamicAdar
35: end function
Chapitre 4. Implémentation et Expérimentations
46
4.2.1.2 Construire la matrice de Commons
Neighbors
la multiplication matricielle est la solution la plus
intuitive pour trouver les voisins communs entre chaque deux noeuds non
connecté, si M est la matrice d'adjacence qui indique les chemins de
longueurs 1 (voisin directe), alors M2 est la matrice qui
indique les chemins de longueur 2 entre chaque deux noeuds, c'est-à-dire
se sont voisins des voisins, si nous trouvons par exemple
M2(i, j) = 2 ça veux dire qu'il existe deux
chemins de longueur 2 entre i et j et donc forcement il
existe 2 voisins communs entre i et j, nous avons effectuer
une modification dans laquelle M2(i, i) = 0 et
M2(i, j) = 0 si i et j sont des
voisins directe dans la matrice d'adjacence c'est-à-dire M(i,
j) = 1, le pseudo code[2] résume ce calcul :
Algorithm 2 Algorithme de Commons Neighbors
1: function COMMON NEIGHBORS(adj)
2: Input matrice: adj
3: Output matrice de similarité:
commonNeighbors
4: entier N +- adj.length
5: for i +- 1 to N do
6: for j +- 1 to N do
7: if i = j V
adj(i,j) = 1 then
8: commonNeighbors(i, j) +- 0
9: else
10: fork+-1toNdo
11: commonNeighbors(i, j) +- CN(i, j) +
adj(i, k) x adj(k, j)
12: end for
13: end if
14: end for
15: end for
16: return commonNeighbors
17: end function
| 


