|
RÉPUBLIQUE ALGÉRIENNE DÉMOCRATIQUE
ÉT POPULAIRE
MINISTÈRE DE L'ENSEIGNEMENT SUPÉRIEUR ET
DE LA RECHERCHE SCIENTIFIQUE
UNIVERSITÉAMAR TELIDGI - LAGHOUAT

Facultédes sciences
Département de mathématiques et d'informatique
MÉMOIRE DE MASTER
DOMAINE : MATHÉMATIQUES ET INFORMATIQUE.
FILIÈRE : INFORMATIQUE.
OPTION : SYSTÈMES D'INFORMATION ET DE
DÉCISION.
Mémoire de fin d'étude en vue d'obtention de
diplôme
Master en systèmes d'information et de
décision
RÉALISÉPAR : ROUANE
OUSSAMA
THÈME :
ÉTUDE COMPARATIVE ENTRE DEUX ALGORITHMES DE
PRÉDICTION DES LIENS DANS LES RÉSEAUX SOCIAUX
Soutenu publiquement devant le jury composéde
:
|
Mr
|
Y. GUELLOUMA
|
Universitéde Laghouat
|
(Président)
|
|
Mr
|
B. ZIANI
|
Universitéde Laghouat
|
(Examinateur)
|
|
Mr
|
A. LAKHDARI
|
Universitéde Laghouat
|
(Examinateur)
|
|
Mr.
|
Y. OUINTEN
|
Universitéde Laghouat
|
(Encadreur)
|
|
Mr.
|
M. BOUAKKAZ
|
Universitéde Laghouat
|
(Co-Encadreur)
|
Année universitaire : 2014/015
Dédicaces
«
JE dédie affectueusement ce modeste travail
:
A mes chers parents :
- A mon cher père Rouane
Ali, c'est à toi que je dois tout. Ce travail est le fruit de la rigueur
de ton éducation.Que Dieu le garde et protège pour moi.
- A ma chère mère Rouane Zohra qui m'a
éclairée mon chemin et qui m'a encouragée et soutenue tout
au long de mes études. Que Dieu la garde et protège pour moi
aussi.
A mon frère et mes soeurs : Abd
Eslam, Saida , Nour el houda et Rihem auxquels je souhaite tout le bonheur, le
succès et la réussite.
A tous mes amis : en particulier
à Gasmi Aissa , Bakha Abesse, Khorsi Ahmed, Benlehbib Abd
essatar.
A tous mes enseignants : qui ne
m'ont guère privéde leur savoir et de leur
bienséance.
Enfin à tous qui portent le nom Rouane et à
tous ceux qui connaissent.»
Rouane Oussama
Remerciements
«
JE remercie tout d'abord ALLAH, le tout puissant
de m'avoir donnéla force et la patience et de m'avoir rapprocher des
personnes qui m'ont soutenu et aidépour accomplir ce travail.
Mes remerciements s'adressent également à tous
les personnes qui ont contribuéde près ou de loin avec leurs
conseils ou avec leurs encouragements à l'accomplis-sement de ce
travail.
Je tiens à exprimer ma sincère
reconnaissance et remerciements à Mr. Ouinten
Youcef, professeur à l'universitéde Laghouat d'avoir
acceptéd'encadrer et de diriger mes travaux. Mes remerciement vont aussi
à mon co-encadreur Mr.Bouakkaz Mustapha qui n'a pas
cesséde m'aider et de m'encourager pour l'accomplissement de ce
mémoire.
Je remercie tous le personnel de l'universitéAmar
telidgi de Laghouat ,l'univer-sitéqui m'a accueilli bras ouvert, mes
remerciements vont particulièrement aux enseignants et administrateurs
du département de mathématique et informatique.
Enfin, j'exprime mes vifs remerciements à toute ma
famille et spécialement àmes parents ,que je leurs
souhaite une longue vie pleine de bonheur, de santéet de
prospérité, c'est à eux que je dois tout . "
Rouane Oussama
Résumé
E mémoire présente une étude comparative
entre deux algorithmes de prédictions Cdes liens dans
les réseaux sociaux en se basant sur les motifs topologiques d'un
réseau social.
Nous commençons ce mémoire par une petite
introduction sur les réseaux sociaux, ensuite nous présentons une
vision globale sur le domaine de l'analyse des réseaux sociaux. Enfin
nous présentons un état de l'art sur les différentes
techniques proposées pour résoudre le problème de
prédiction des liens.
Nous nous focalisons dans ce travail sur les mesures de
similarités topologique. nous avons choisi d'expérimenter les
deux mesures : Adamic/Adar et voisins communs.
Nous avons implémenté, comparéet
mesuréles performances de chacun de ces deux algorithmes.
Mots-clés : Analyse des réseaux sociaux,
prédiction des liens dans les réseaux sociaux, mesure de
similaritétopologique, Adamic/Adar, Voisins communs.
Abstract
HIS dissertation presents a comparative study between two
algorithms of link Tprediction in social networks based on
topological motifs of social network.
We begin this dissertation by a small introduction about
social networks, then we present a global vision about social network analysis
domain's. We present a state of art for different technics proposed to resolve
the link prediction problem.
We focus in this work on topological mesures of similarity, we
chose to experiment two mesures of simiarity : Adamic/Adar and Commons
Neighbors.
We implemented, compared, mesured, the preformances of each of
these two functions.
Keywords : social networks analysis, link
prediction in social networks, topological mesures of similarity, Adamic/Adar,
Commons Neighbors.
iii
Table des matières
|
Résuméi Abstract
Introduction
1 Généralités sur les réseaux
sociaux
1.1 Historique des réseaux sociaux
1.1.1 Panorama des réseaux sociaux
1.1.1.1 1997-2001 :les réseaux sociaux foisonnent
1.1.1.2 2002-2003 :Les réseaux sociaux envahissent la
toile
1.1.1.3 Myspace
1.1.1.4 Facebook
1.2 Types des réseaux sociaux
|
ii ix
1
1
2
2
3
3
4
4
|
|
1.2.1
|
Réseaux sociaux professionnelles
|
5
|
|
|
1.2.1.1 LinkedIn
|
5
|
|
|
1.2.1.2 Viadeo
|
6
|
|
1.2.2
|
Les réseaux sociaux grands publics
|
7
|
|
|
1.2.2.1 Facebook
|
7
|
|
|
1.2.2.2 Twitter
|
7
|
|
|
1.2.2.3 Google+
|
8
|
|
2
|
État de l'art
|
10
|
|
2.1 Analyse des réseaux sociaux
|
10
|
|
2.1.1
|
Définition
|
10
|
|
2.1.2
|
Représentation d'un réseau social
|
11
|
|
2.1.3
|
Indicateurs d'un réseau social
|
13
|
|
|
2.1.3.1 Densité
|
13
|
|
|
2.1.3.2 Centralité
|
13
|
|
2.1.4
|
Caractéristiques d'un réseau social
|
14
|
|
|
2.1.4.1 Six degrés de séparation (petit monde)
|
14
|
|
|
2.1.4.2 Coefficient de Clustering élevé
|
15
|
|
|
2.1.4.3 Structure en communautés
|
16
|
|
|
2.1.4.4 Distribution de degréen loi de puissance
|
16
|
|
2.2 Prédiction des liens
|
17
|
|
2.2.1 Problématique
|
17
|
Table des matières iv
Bibliographie 58
2.2.2 Domaines d'applications 18
2.3 Techniques de prédiction des liens 18
2.3.1 Les approches non supervisé 19
2.3.1.1 Mesures basées sur le contenu d'un noeud 19
2.3.1.2 Mesures basées sur les motifs topologiques 20
· Mesures de similaritélocales 21
· Mesures de similaritéglobales 24
· Mesures basées sur les marches aléatoires
25
2.3.1.3 Mesures basées sur la théorie social
25
2.3.2 Méthodes basées sur l'apprentissage
supervisé 26
2.3.2.1 Classification binaire 26
3 Les fonctions : Adamic/Adar et voisins communs
28
3.1 La fonction de similarité: Adamic/Adar 28
3.1.1 Origine de la méthode 28
3.1.2 Principe de la méthode 29
3.1.2.1 Calcul de la matrice de similarité 29
3.1.3 Exemple pratique 29
3.2 La fonction de similarité: Voisins communs 34
3.2.1 Origine de la méthode 34
3.2.2 Principe de la méthode 34
3.2.2.1 Calcul de la matrice de similarité 34
3.3 Mesures de performances 37
3.3.1 Le rappel 38
3.3.2 La précision 39
3.3.3 La F-mesure 39
4 Implémentation et Expérimentations
40
4.1 Environnement de travail 40
4.2 Description de l'application 42
4.2.1 Algorithmes et explications 42
4.2.1.1 Construire la matrice de Adamic et Adar 44
4.2.1.2 Construire la matrice de Commons Neighbors . . 46
4.2.1.3 Construire la nouvelle matrice d'adjacence 46
4.2.1.4 Calculer les mesures de performance 47
4.2.2 Représentation de l'application 49
4.3 Expérimentations et résultats 50
4.3.1 Interprétation des résultats 55
4.3.1.1 Point de vue temps d'exécution 55
4.3.1.2 Point de vue Rappel 55
4.3.1.3 Point de vue Précision 55
4.3.1.4 Point de vue F-mesure 56
Conclusion 57
v
Table des figures
|
1.1
|
Chronologie des réseaux sociaux
|
5
|
|
1.2
|
Logo de LinkedIn
|
6
|
|
1.3
|
Logo de Viadeo
|
6
|
|
1.4
|
Logo de Facebook
|
7
|
|
1.5
|
Logo de Twitter
|
8
|
|
1.6
|
Logo de Google+
|
9
|
|
2.1
|
Représentation d'un réseau social avec une matric
d'adjacence . . .
|
13
|
|
2.2
|
Théorie de six degrés de séparation
|
15
|
|
2.3
|
Coefficient de clustering élevée
|
15
|
|
2.4
|
Structure en communautés
|
16
|
|
2.5
|
Distribution de degrés en loi de puissance
|
16
|
|
2.6
|
Problématique
|
17
|
|
3.1
|
Exemple d'une capture d'un reseau social
|
30
|
|
3.2
|
L'état du réseau aprés l'exécution
de Adamic/Adar
|
33
|
|
3.3
|
L'état de réseau social aprés
l'exécution de Common Neighbors. . .
|
37
|
|
3.4
|
Les différents types des liens : TP, FP, FN
|
38
|
|
4.1
|
L'interface de NodeXL
|
42
|
|
4.2
|
L'organigramme de l'application
|
43
|
|
4.3
|
L'interface globale de l'application
|
49
|
|
4.4
|
Capture du réseau de collaboration construite en 2011
|
50
|
|
4.5
|
Capture du réseau de collaboration construite en 2015
|
51
|
Liste des tableaux vi
4.6 Réseau social obtenu après
l'exécution de la fonction : Adamic/Adar 52
4.7 Réseau social obtenu après
l'exécution de la fonction : Commons
neighbors 53
4.8 Représentation graphique du rappel,
précision, F-mesure et temps
d'exécution 54
vii
Liste des tableaux
2.1 Quelques caractéristiques des mesures de
similaritélocale [Wp15] . 23
3.1 Représentation du réseau social par une
matrice d'adjacence . . . . 31
3.2 Matrice de similarité: Adamic/Adar 31
3.3 Liste de similaritéde Adamic/Adar 32
3.4 Nouvelle matrice d'adjacence aprés
l'exécution de Adamic/Adar . 33
3.5 Matrice de similarité: common Neighbors 35
3.6 Liste de similaritéde Common Neighbors 36
3.7 Nouvelle matrice d'adjacence aprés
l'exécution de Common Neighbors 36
3.8 Matrice de confusion 38
4.1 Mesures de performances 54
viii
Liste des algorithmes
|
1
|
Algorithme de Adamic et Adar
|
45
|
|
2
|
Algorithme de Commons Neighbors
|
46
|
|
3
|
Construction de la nouvelle matrice d'adjacence
|
47
|
|
4
|
Précision, Rappel et F-mesure
|
48
|
ix
Introduction
ES réseaux sociaux sont omniprésents depuis
l'avènement d'Internet. Ils per-Lmettent aux
différents utilisateurs d'interagir en communautés et de se
regrouper selon des critères qui leur sont importants.
Ces réseaux sociaux sont de différents types.
Certains sont connus de tous et comptent des millions de membres. D'autres
exploitent des niches moins connus et peuvent passer relativement
inaperçus ou rester confidentiels, tels les réseaux
d'entreprise.
Tous ces réseaux sociaux amassent de très
nombreuses données : les amis, les messages, les images, la
fréquence d'utilisation.. . tous ces échanges et informations
sont soigneusement enregistrés. Dès lors se pose le
problème de l'exploitation de cette masse d'informations.
L'analyse de ces réseaux et l'exploration de cette
énorme quantitéde données peut permettre de chercher
à détecter des groupes d'acteurs fortement connectés entre
eux. On peut aussi prédire des caractéristiques des acteurs ou de
liens entre eux. C'est ce sujet qui est au coeur de ce mémoire,
oùnous nous intéressons à la prédiction des liens
dans les réseaux sociaux.
Le problème de prédiction des liens dans les
réseaux sociaux est un sujet central de la recherche pour l'ensemble de
la théorie des réseaux sociaux. On s'intéresse souvent
à la dynamique d'un réseau par rapport aux arêtes. Dans les
réseaux sociaux, non seulement des nouveaux noeuds apparaissent mais
aussi les interactions entre les personnes changent et il serait de savoir
estimer l'état de ce réseau à un instant
ultérieur.
INTRODUCTION x
L'objectif de ce travail est de présenter un
état de l'art sur ce domaine et d'ef-fectuer une étude
comparative entre deux algorithmes de prédiction des liens en
présentant en détail les principes de chacune de ces algorithmes.
Nous avons or-ganiséce mémoire en quatre chapitres, qui
commenceront tous par quelques mots introductifs :
Dans LE PREMIER CHAPITRE, nous présentons des
généralités sur les réseaux sociaux.
LE DEUXIÈME CHAPITRE sera consacréà
un état de l'art sur l'analyse des réseaux
sociaux, comment ils ont modélisé, leurs
caractéristiques et indicateurs, une grande partie
consacréau problème de prédiction des liens. Nous
citons les différents travaux de recherches qui ont
étémenés autour de ce problème, et surtout les
algorithmes basésur la topologie d'un réseau social.
Dans LE TROISIÈME CHAPITRE, nous avons
expérimentéles deux algorithmes qui sont basées sur la
topologie d'un graphe : Adamic/Adar et Voisins Communs en
donnant des exemples pour faciliter leurs compréhensions.
Dans LE QUATRIÈME CHAPITRE, nous présentons
l'environnement de travail que nous avons choisi. Nous décrivons le
réseau social que nous avons expérimenté, c'est un
réseau de collaboration des chercheurs au sein de laboratoire de
mathématiques et d'informatique de l'université»Amar
Telidgi-Laghouat», ainsi l'application que nous avons
développé. Puis nous présentons les résultats
d'expérimentation. Nous essayons d'interpréter, comparer et juger
la performance de chacune des algorithmes que nous avons abordés.
Nous concluons ce travail par une vision globale et
synthétique sur le travail que nous avons fait en particulier et sur le
domaine de prédiction des liens en général. Nous parlons
de l'expérience que nous avons acquise à travers ce
mémoire.
Nous pouvons remarquer finalement que dans ce travail, nous
analysons l'effica-citédes méthodes de prédiction de liens
en termes d'un ensemble de mesures. Nous n'effectuons pas une étude de
complexitédes algorithmes et nous ne concentrons pas ce travail sur la
meilleure façon pour implémenter ces méthodes. Les
méthodes ont étéimplémentées en JAVA d'un
point de vue pragmatique, sans optimiser les codes au point de vue de
complexitéou de stockage des données...
1
Chapitre 1
Généralités sur les
réseaux
sociaux
A
CTUELLEMENT, avec le développement rapide de
l'Internet, les réseaux sociaux en ligne deviennent un partie importante
de la vie des personnes. Ils sont caractérisés par des ensembles
de sites Internet axés sur des communautés. Mais le terme de
réseau social provient initialement d'une théorie sociologique.
Le terme de réseau social est souvent employépour désigner
les médias sociaux qui regroupent les médias intégrant
[Pat10] technologies et interactions sociales. Ce sont
généralement un ensemble de sites Internet qui permettent de se
constituer un réseau d'amis, ou de relations professionnelles, et qui
proposent des interactions entre ses membres via des moyens de communication.
Le réseau social permet aussi d'échanger du contenu
multimédia comme des images ou des liens hypertextes. Les
médias sociaux permettent à l'utilisateur de se
créer un profil, une carte d'identitévirtuelle, qui lui permet
d'échanger avec les autres. Basés sur la création de
liens,
souvent virtuels, les réseaux sociaux ont tendance
à regrouper des communautés en fonction de leurs centres
d'intérêts, opinions politiques, religions, relations
professionnelles ou autre.
1.1 Historique des réseaux sociaux
La place importante des réseaux sociaux aujourd'hui
n'est pas simplement due au hasard, elle est inscrite dans l'évolution
technologique de ces quarante dernières années. Pour comprendre
l'apparition des réseaux sociaux il faut avant tout faire un petit
éclairage rétrospectif sur l'être humain. Se souvenir que
l'Homme a
Chapitre 1. Généralités sur les
réseaux sociaux 2
génétiquement tendance à se
regrouper en sociétés plus ou moins structurées.
Ce mode de fonctionnement existe depuis toujours et il est
constituéd'un ensemble de moyens et d'outils de liens sociaux autour
d'un thème fédérateur (religion, loisir,
activitéprofessionnelle.. .). Souvent assimilés au
développement du Web 2.0, les sites de réseaux sociaux voient le
jour durant les années 90. Aujour-d'hui, les utilisateurs de
réseaux sociaux se comptent en centaines de millions pour certains
sites. Mais, comment cela a débuté.
1.1.1 Panorama des réseaux sociaux
C'est en 1995 que le premier réseau social voit le jour
[Pat15] .Classmates 1, fondépar »Ranry
Conrad» est lancésur l'Internet. Le site permet de retrouver ses
amis
d'écoles, du primaire au lycée, et ses
collègues abandonnés. La plate forme a une très forte
connotation nostalgique. Mais Il n'offre pas cependant toutes les
possibilités des réseaux sociaux actuels.
Sixdegrees2 Lancéen janvier
1997 par la sociétéMacroview [Pat15], fondée par Andrew
Weinreich, est le premier réseau social dont la forme se rapproche
réellement de ce que nous connaissons aujourd'hui. Basésur le
concept des six degrés de séparation, ce réseau social
permet de créer un profil et une liste d'amis. Les utilisateurs peuvent
envoyer des messages mais aussi poster des messages sur leur propre profil, qui
seront visibles jusqu'au troisième degré, c'est-à-dire par
les amis des amis de leurs amis. Il est possible d'accéder aux
connexions de tous les utilisateurs. Malgréses millions d'utilisateurs,
le site dûfermer en 2000 faute de viabilitééconomique.
1.1.1.1 1997-2001 :les réseaux sociaux
foisonnent
Entre 1997 et 2001 [Pat15] , de nouvelles plateformes de
réseaux sociaux se sont développées, permettant des
combinaisons variées de profils et la publication de réseaux
d'amis. nous notons :
1. AsianAvenue : communautéasiatique.
2. BlackPlanet : communauténoire.
3. MiGente communautélatino.
Une nouvelle vague de sites de réseaux sociaux
tournés vers le développement de réseaux d'affaires
permettaient aux utilisateurs de créer des profils personnels,
1. www.classmates.com
2. www.sixdegrees.com
Chapitre 1. Généralités sur les
réseaux sociaux 3
professionnels ou de faire des rencontres. Arriva avec le
lancement de Ryze3 en 2001. Mais, ce réseau
ne connut pas de succès, c'est LinkedIn qui devient un
solide réseau d'affaires et un réseau professionnel très
actif aujourd'hui.
1.1.1.2 2002-2003 :Les réseaux sociaux
envahissent la toile
Entre 2002 et 2003, les réseaux sociaux deviennent le
premier courant du web et peuvent apparaître comme une réponse
à l'explosion de l'internet en 2000 .L'avènement de site comme
Friendster4 fondépar »Jonathan
Abrams» à Santa Clara en 2002, lancéen 2003, marque le
phénomène de petit monde aussi connu sous la
formulation, et le modèle de réseautage social du cercle
d'amis. Lin-kedIn5, le premier réseau professionnel
en ligne, permet aux professionnels du monde entier de mettre en avant leur
parcours, de développer leur réseau et de rester
informésur leur secteur d'activité. L'entreprise a vu le jour en
2002 dans le salon de Reid Hoffman, co-fondateur, et a
étélancéofficiellement le 5 mai 2003. Le siège
social est situéà Mountain View en Californie, mais l'entreprise
possède des bureaux dans plus d'une vingtaine de villes aux Etats-Unis
et dans le monde. Aujourd'hui on compte plus de 200 sites de réseaux
sociaux qui font référence au phénomène de
YASNS : Yet Another Social Networking Service, dont les plus
significatifs dans l'histoire d'Internet sont Facebook et Myspace. Il convient
donc de faire un rapide historique de ces deux sites de réseaux sociaux
qui sont aujourd'hui les plus populaires au monde.
1.1.1.3 Myspace
Peu de journalistes notèrent le lancement en 2003 de
MySpace6 à Santa Monica, Californie, à quelques
centaines de miles de la Silicon Valley [Pat15]. Un des fondateurs Tom Anderson
expliquait que MySpace a pu récupérer les utilisateurs du site
»Friendster» qui avait perdu son audience après des rumeurs
prétendant qu'il voulait adopter un système d'abonnement payant.
Les premiers utilisateurs furent des groupes de musiciens rocks
indépendants de la région de Los Angeles. Ce succès attira
les clubs de musique populaire qui utilisèrent MySpace pour faire de la
publicité. Puis l'expansion de MySpace se confirma en devenant une
plate-forme de contact entre les groupes et leurs fans.
Le site qui, au départ, était conçu pour
tous les publics, acquit très vite une
3.
www.ryze.com
4.
www.friendster.com
5.
www.linkedin.com
6.
www.myspace.com
Chapitre 1. Généralités sur les
réseaux sociaux 4
spécificitéde réseau social du milieu
artistique, ce qui est encore vrai aujourd'hui. L'autre particularitéde
MySpace fut d'offrir la possibilitéà ses utilisateurs de
créer le design de leur page en leur permettant d'entrer du code
spécifique.
Les jeunes commencèrent à rejoindre MySpace en
masse à partir de 2004. A cause du manque de couverture de la presse en
2004, peu de personnes remarquèrent la popularitégrandissante du
site.
1.1.1.4 Facebook
Facebook7 est lancéle 4
février 2004 par »Mark Zuckerberg» [Pat15] . Alors encore
étudiant à Harvard, Mark Zuckerberg décide de créer
un site de réseau social ferméréservéaux
étudiants de l'université, l'utilisateur devait avoir une adresse
e-mail universitaire
Harvard.edu. Mais c'est entre 2005 et
2006, sous l'influence de Sean Parker (fondateur de Napster), que le nom de
domaine est achetéet que facebook élargi son audience et autorise
l'inscription a toute personne âgée d'au moins 13 ans. En 2007
Facebook connaît une ascension phénoménale grâce
à son système de micro-blogging.
Le nom du site s'inspire d'ailleurs des albums photo
trombinoscopes ou facebooks en anglais regroupant les photos des
visages de tous les élèves prises en début d'année
universitaire.
Aujourd'hui, D'après les taux de fréquentation
fournis par le site Alexa8 : Facebook est le réseau social
numéro 1 dans le monde, en février 2015, les statistiques parlent
de plus de 1,393 milliard utilisateurs .
1.2 Types des réseaux sociaux
Le monde des réseaux sont très
diversifiés, il existe de ce fait plusieurs plateformes de
réseaux sociaux, parmi ces plateformes, il faut distinguer deux
catégories, ceux à usage exclusivement professionnel,
orientésur la mise en valeur et les échanges professionnels de
ses membres, et ceux à usage privé, ceux qui sont devenus grand
public comme MySpace (construit au départ pour favoriser la mise en
relation d'artistes) ou Facebook (conçu à l'origine par et pour
des universitaires).
7.
www.facebook.com
8.
www.alexa.com

Chapitre 1. Généralités sur les
réseaux sociaux 5
FIGURE 1.1 - Chronologie des réseaux sociaux [Pat15]
1.2.1 Réseaux sociaux professionnelles
Parmi les principales fonctionnalités et ou raisons de
créer son compte sur un réseau social professionnel, nous notons
[Har12] :
- trouver du travail ou recruter.
- s'ouvrir de nouvelles perspectives d'affaires.
- disposer d'un carnet d'adresse en ligne accessible et à
jour.
Ainsi, la première action et finalitédes
réseaux sociaux professionnels est de remplir sa fiche personnelle sur
le réseau, et d'indiquer ainsi que l'on existe professionnellement.
Cette mise en avant de son profil professionnel, régulièrement
mise à jour, permet aux potentiels recruteurs de prospecter et recruter,
privilégiant même les réseaux sociaux professionnels aux
sites d'emploi.
1.2.1.1 LinkedIn
LinkedIn9 est un réseau
social professionnel . Il est l'un des leaders sur ce créneau. Une des
finalités de LinkedIn est de rechercher un emploi, des contacts ou des
opportunités de business, et d'être recommandépar
quelqu'un. Enfin, les employeurs peuvent y diffuser des offres d'emplois.
Depuis peu, vous pouvez d'ailleurs recevoir des listes personnalisées
d'offres d'emplois [Har12].
LinkedIn a aussi lancédes pages de profils de
sociétés : elles permettent aux
9. www.linkedin.com
Chapitre 1. Généralités sur les
réseaux sociaux 6
10. www.viadeo.com
sociétés de se présenter, de
connaître les connexions avec les membres de linkedIn. Ces pages
privées, accessibles aux inscrits, présentent des informations
telles que la description de la société, le type d'industrie, les
statuts officiels, et son adresse. LinkedIn utilisera ces données pour
publier aussi les récentes embauches, promotions, et offres d'emplois.
Aujourd'hui , LinkedIn compte plus de 400 millions de membres dans plus de 200
pays et territoires.

FIGURE 1.2 - Logo de LinkedIn
1.2.1.2 Viadeo
Le premier réseau social professionnel français,
a étéco-fondéen 2004 par Dan Serfaty [Har12]. Il
revendique en tout 2 millions de membres. C'est en fait le prolongement d'un
club d'entrepreneurs crééen 2000.
Une de ses particularités réside dans ses
»hubs», sortes de forums de discussion communautaires et
thématiques, publics (lisibles par tous les membres de Viadeo) ou
privés (réservés à une poignée
d'inscrits).
Viadeo 10 propose un service de
base gratuit mais, en fait, il faut souscrire au service payant premium pour
accéder à la plupart des fonctionnalités (consulter le
profil et contacter sans limites les autres membres, partager et
échanger sur les hubs, publier ses événements, discuter en
temps réel avec les autres membres...). Par ailleurs, Viadeo offre la
possibilitéd'abonner à des flux d'informations provenant du site
(offres d'emploi, messages hubs, etc.).

FIGURE 1.3 - Logo de Viadeo
Chapitre 1. Généralités sur les
réseaux sociaux 7
1.2.2 Les réseaux sociaux grands publics
L'objectif des réseaux sociaux est de connecter les
individus, de partager de l'in-formation, des liens et de créer du
contenu qui sera ainsi partagé. Selon la version imaginée par les
créateurs de ces réseaux sociaux, chaque contact qui accepte
l'in-vitation accroît le réseau de nouveaux contacts. Les
arrivants inscrivent à leur tour leurs contacts et ainsi de suite...
jusqu'àce le monde entier soit relié. En réalité,
la plupart d'entre nous n'invite personne, mais recherche quelles sont ses
connaissances déjàprésente dans le réseau,
principalement des individus que l'on connaît par Internet
interposé.
1.2.2.1 Facebook
Le réseau social le plus connu , dépasse du
milliard de membres d'inscrits (àl'heure du post). Le principe est
d'échanger avec sa communautéd'amis sur tout et n'im-porte quoi.
L'inscription est obligatoire pour l'utiliser. Pour être amis sur
Facebook avec une personne, il faut lui envoyer une demande et que cette
dernière l'accepte. Facebook permet également de réagir
sur les commentaires et news postés par ses amis via le »Like»
ou J'aime. C'est un moyen pour dire que l'on a trouvéun commentaire ou
un post à son goût. Il est devenu fréquent d'entendre le
verbe »like» dans une conversation. Facebook permet beaucoup d'autres
choses : discussion instantanée, envoi de message direct, identifier des
amis sur une photo[Har12]...

FIGURE 1.4 - Logo de Facebook
1.2.2.2 Twitter
Bien que ne partageant pas la plupart des
caractéristiques des autres réseaux sociaux, Twitter s'en
apparente de par son nombre d'utilisateurs (232 millions de membres en octobre
2013) et de son utilisation finale. Crééen 2006, Twitter
11 est un site de microblogging qui permet à ses utilisateurs
de faire part à leur »suiveurs» (followers) d'informations
courtes (»tweets») ne dépassant pas 140 signes, un peu comme
les statuts sur Facebook (qui eux ne sont pas limités en longueur).
11. www.twitter.com
Chapitre 1. Généralités sur les
réseaux sociaux 8
Ces »tweets» peuvent également contenir des
liens externes renvoyant sur des articles, des photos, des vidéos, etc,
Les abonnés peuvent être des individus ou des raisons sociales,
comme des entreprises, des organisations, etc. Suite à l'arrivée
de personnes célèbres ou ayant une grande autorité, il
offre la possibilitéde suivre d'autres comptes, pas de demande
d'invitation, il permet de suivre n'importe qui, et être suivi par
n'importe qui. le site a développéune fonction permettant de
certifier l'identitédu tweeter et « »retweeter», et donc
par exemple de reconnaître la vrai personne parmi les dizaines de
contrefaçons [Har12].

FIGURE 1.5 - Logo de Twitter
1.2.2.3 Google+
Google+ 12 est l'application de
réseau social de l'entreprise américaine Google lancée le
28 juin 2011, et accessible pendant près de 90 jours sur invitation, il
est conçu comme une couche supplémentaire sur des services Google
existants et fonctionnant avec un compte Google. Google met en avant trois
nouveaux services [dLP13] :
· Les (circles), des groupes de contact
différents que l'utilisateur peut créer et au sein desquels il
décide des informations qu'il souhaite partager, proche des
»Aspects» de Diaporama. Organisés via une interface en
»drag and drop», les contacts font partie de cercles dont ils peuvent
connaître les membres mais dont
ils ne connaissent pas le nom, les paramètres de vie
privée permettent aussi àchacun de cacher les membres
de ses cercles ainsi que ceux dont ils font partie. Ce
système remplace la »liste d'amis» typique
d'autres sites comme Facebook.
· Les (hangouts), un système de chat vidéo
collectif et spontané, réunissant entre 2 à 10 personnes
en simultané. Chaque bulle peut potentiellement être rejointe par
quiconque en possèderait l'URL unique. Le 18 août 2011, Google a
ajoutéune fonction au bouton »Partage» des vidéos
YouTube, permettant de suggérer à un ami de venir regarder la
vidéo en simultané, dans une bulle.
· Les (sparks), un système de suggestion et de
partage de contenu par thème avec ses contacts, proche de la section
»Recommandations» de Google Reader.
12. plus.google.com
Chapitre 1. Généralités sur les
réseaux sociaux 9
Le lancement s'est dérouléaprès celui de
Google +1, une fonctionnalitéqui permet à un utilisateur d'un
compte Google de cliquer sur un bouton disponible sur la plupart des sites
internet afin d'indiquer qu'il aime l'article.

FIGURE 1.6 - Logo de Google+
Conclusion
Dans ce chapitre, nous avons vu quelques concepts et
définitions liées aux réseaux sociaux, leurs historique,
leurs types en donnant quelques exemples sur les réseaux les plus
populaires dans le monde qui comptent des centaines de millions
d'uti-lisateurs, Tous ces réseaux sociaux amassent de très
nombreuses données. Ce problème a obligéaux chercheurs de
différents domaines comme la sociologie, les mathématiques, et
l'informatique de développer des méthodes d'exploration et
d'analyse de cette grande masse de données, c'est ce que nous allons
voir dans le deuxième chapitre.
10
Chapitre 2
État de l'art
Nous présentons dans ce chapitre quelques approches et
techniques qui ont étéproposées dans le cadre
de prédiction des liens dans les réseaux sociaux issues de
différentes sources. Nous expliquons les principes de
ces approches en définissant quelques concepts liés à ces
techniques pour avoir une idée générale sur le domaine de
prédiction des liens. Pour l'organisation de cet état de l'art,
nous avons introduit le domaine de l'analyse des réseaux sociaux, nous
avons aussi définit quelques concepts et propriétés
liées aux réseaux sociaux avant de rentrer sur le fond de notre
état de l'art, enfin nous avons choisis de classer les
différentes approches de prédiction des liens que nous sommes en
mesure de présenter selon des principales catégories que nous
allons les définir brièvement.
2.1 Analyse des réseaux
sociaux
2.1.1 Définition
Les interactions des utilisateurs au travers les
réseaux sociaux amassent de très nombreuses données : les
amis, les messages, les images, la fréquence d'utilisation, les Hashtags
... tous ces échanges et informations sont soigneusement enregistres.
Des lors se pose le problème de l'exploitation de cette masse
d'informations. Ces interactions amènent la
communautéscientifique à réfléchir sur les moyens
de capter ces usages pour y appliquer les techniques d'analyse des
réseaux sociaux. L'analyse des réseaux sociaux est définie
comme étant l'étude des entités sociales (les personnes
dans les organisations qu'on appelle acteurs) ainsi que leurs interactions et
leurs relations [GE09]. Ces interactions et relations peuvent être
représentées par un graphe, dans lequel chaque noeud
représente un acteur et chaque lien est une
Chapitre 2. État de l'art 11
relation. Nous pouvons étudier les
propriétés de la structure et son rôle ainsi que la
position et le prestige de chaque acteur social. Nous pouvons rechercher aussi
les différents types de sous-graphes comme par exemple les
communautés formées par des groupes d'acteurs ayant des
intérêts communs, en isolant le groupe d'individus ayant une
densitéélevée. Les réseaux sociaux peut être
aussi une source permettant l'élaboration de recommandations : trouver
un expert dans un domaine donné, suggérer des produits à
vendre, proposer un ami, etc. Cette élaboration peut être
fondée sur des algorithmes d'exploration de chemins, d'analyse de
degrés...
2.1.2 Représentation d'un réseau social
La première personne à avoir
représentéun réseau social est[Mor33]. Son objectif
étant de visualiser graphiquement un réseau social, il a
représentéles personnes par des points et une relation entre deux
personnes par des flèches. Cette représentation est depuis
désignée par le terme sociogramme, mais on parlait
également de toiles en raison de leur aspect en toile d'araignée.
Cette forme de visualisation, aussi peu innovante qu'elle puisse paraître
de nos jours, fut un premier outil d'identification rapide des
caractéristiques d'un réseau social. Moreno a ainsi introduit le
concept d'étoile pour désigner les personnes ayant le plus de
relations dans un réseau social, en référence à
l'étoile formée par un point et ses connections. Les
mathématiciens ont rapidement fait le rapprochement entre les
représentations sociogrammes et la théorie des graphes au sens
mathématique. [Sco00] passe en revue l'évolution de la
représentation des réseaux sociaux. Au milieu du vingtième
siècle. Le graphe est devenu par la suite la représentation
adoptée par toutes les sciences manipulant l'analyse des réseaux
sociaux, dont la sociologie, les mathématiques et l'informa-tique. Les
définitions suivantes listent quelques notions manipulées par la
théorie des graphes pour les réseaux sociaux [GE09] :
1. Un noeud est l'unitéde base d'un réseau, il
en représente une ressource. Dans un réseau social on parle
d'acteur.
2. Une arête est une connexion entre
deux noeud. On parle également d'arc ou de lien.
3. Une arête est orientée si
elle ne s'utilise que dans une seule direction. Inversement, on parle
d'arête non orientée pour une arête qui s'utilise dans les
deux directions.
4. Une arête est pondérée
lorsqu'on lui attribue un poids.
5. Une arête est étiquetée
lorsqu'on lui attribue un label.
6.
Chapitre 2. État de l'art 12
Un graphe est défini par un ensemble de
noeuds et un ensemble d'arêtes.
7. Un graphe orientédésigne un
graphe avec des arêtes orientées.
8. Un graphe
pondérédésigne un graphe avec des arêtes
pondérées.
9. Un graphe étiquetédésigne
un graphe avec des arêtes étiquetées.
10. Un graphe multipartite désigne un
graphe avec des noeuds de types différents.
11. Le degréd'un noeud est le nombre
de ses arêtes adjacentes.
12. Un chemin est une séquence
d'arêtes qui relie deux noeuds.
13. Un chemin orientéest une
séquence d'arêtes qui relie deux noeuds en respectant
l'orientation du parcours à chaque arrête.
14. Une géodésique est l'un
des plus courts chemins entre deux noeuds donnés.
15. Le diamètre d'un graphe est le
plus long chemin géodésique de ce graphe.
16. Un graphe est complet lorsqu'il existe
une arête entre toute paire de noeuds.
17. Un graphe est dit connexe lorsqu'il
existe un chemin entre toute paire de noeuds.
Les graphes non orientés sont adaptés pour les
réseaux sociaux avec des relations non orientés. Les graphes
orientés sont adaptés pour représenter des relations non
symétriques comme les réseaux des »followers» par
exemple. Les graphes pondérés sont adaptés aux
réseaux sociaux qui contiennent différents niveau
d'intensités dans les relations. Les graphes étiquetés
permettent de représenter différents types de relations. Les
graphes multipartites sont adaptés pour des réseaux sociaux
incluant différent types de ressources manipulées par les acteurs
et qui sont le support d'interactions [GE09].
La matrice est l'objet mathématique le plus
utilisépour manipuler ces concepts. On distingue deux types de matrices
dans un réseau social, les matrices d'inci-dence et les matrices
d'adjacence. On parle de matrice d'adjacence lorsqu'on a les mêmes
ressources en ligne et en colonne, on obtient ainsi une matrice carrée
avec la ligne i et la colonne i représentant la même ressource
comme il est indiquédans la figure 2.1.

Chapitre 2. État de l'art 13
FIGURE 2.1 - Représentation d'un réseau social
avec une matric d'adjacence
Un graphe peut ainsi être représentésous
la forme d'une matrice M à n lignes et n colonnes représentant un
tableau. Chaque case de ce tableau est notée M(i, j) avec i et
j les numéros respectifs de ligne et de colonne de la case. La valeur
contenue dans la case M(i, j) est le poids de la relation entre les
ressources vi et v (égal à 1 dans le
cas d'un graphe non pondéré), 0 correspond à une absence
de relation. Les matrices d'incidence contiennent deux types de ressources, les
lignes représentent un type et les colonnes un autre type[GE09].
2.1.3 Indicateurs d'un réseau social
2.1.3.1 Densité
La Densitéindique la quantitéde liens au sein
d'un réseau et permet de définir la cohésion d'un
réseau social. Selon [Sco00] cette mesure peut-être
utilisée dans l'op-tique d'une analyse socio-centrée ou
égocentrée. Une analyse centrée sur l'individu consiste
à mesurer la densitédes liens autour d'un noeud donné. Une
telle analyse montre notamment l'influence du noeud analysésur la
densitédu sous graphe au-
quel il appartient avec ses voisins. Une analyse
socio-centrée considère la densitésur l'ensemble du graphe
et mesure la contrainte du réseau sur ses membres. Ainsi toute
comparaison de densitéentre graphes ne fournit aucun résultat
significatif.
2.1.3.2 Centralité
La centralitéest une
caractéristique de la position d'un noeud dans un réseau. Elle se
mesure par des indices évalués sur les sommet du graphe du
reseau. Il en existe plusieurs,[Fre79] reprend l'ensemble de ces approches et
en extrait trois principales : la centralitéde degré(degree
centrality), la centralitéde proximité
Chapitre 2. État de l'art 14
(closeness centrality) et la
centralitéd'intermediarité(betweenness centrality). La
première approche appelée centralitéde
degré, considère comme centraux les noeuds qui
possèdent les degrés les plus élevés du graphe. En
effet, ces noeuds suscitent un grand intérêt, sont très
visibles, et ont un potentiel élevéà faire circuler
l'information, par leur forte connectivitéaux autres
éléments du réseau, un noeud moins central plus il
dépend de un ou plusieurs voisins pour établir des nouvelles
relations.
La centralitéd'intermédiaritése
concentre sur la capacitéd'un noeud à servir
d'intermédiaire dans un graphe. Un noeud situésur un chemin
géodésique possède une position stratégique dans la
cohésion d'un réseau et dans la circulation de l'information,
d'autant plus si ce chemin est unique. Par exemple, un noeud situésur
l'unique chemin reliant deux ensembles connectés de noeuds
possède un fort contrôle sur la communication de ces deux groupes.
Plus un noeud est intermédiaire, plus le réseau est
dépendant de lui et plus il a de pouvoir.
Enfin, la centralitéde proximitépour
un noeud, dépende inversement de la somme des chemins
géodésique entre ce sommet-làet touts les autres. Dans
le
domaine des réseaux sociaux, Cette mesure
représente la capacitéd'un noeud àse connecter
rapidement avec les autres noeuds du réseau .D'une autre façon,
elle peut répondre à la question : quel est l'acteur le plus
indépendant.
2.1.4 Caractéristiques d'un réseau social
Ils existent beaucoup de propriétés des
réseaux sociaux, nous citons dans ce mémoire les
caractéristiques les plus populaires :
2.1.4.1 Six degrés de séparation (petit
monde)
Cette théorie s'appuie sur les travaux de [Mil67], qui
avaient demandédans les années 1960 à 300 personnes vivant
dans le Nebraska (centre des Etats-Unis) de faire parvenir une lettre à
quelqu'un à Boston (Massachusetts, nord-est) par l'in-termédiaire
de connaissances. Un ami représentait un degréde
séparation, l'ami d'un ami deux degrés, etc... Les lettres
parvenues à leur destinataire avaient franchi en moyenne 6, 2
degrés de séparation.
Ainsi toute personne dans un réseau social est
connectée à toute autre personne par un chemin de courte
distance. Le plus court chemin entre deux sommets dans un réseau social
de taille n est de l'ordre de log(n). Ainsi lorsque la taille du réseau
augmente, la longueur des plus courts chemins n'augmente que très peu
2.2.

Chapitre 2. État de l'art 15
FIGURE 2.2 - Théorie de six degrés de
séparation
En 2008 [S08], une équipe de chercheurs travaillant
pour Microsoft, étudiant 30 milliards de messages instantanés
envoyés par 240 millions de personnes en juin 2006, avaient
établi qu'en moyenne, deux personnes peuvent être reliées
en 6, 6 étapes. L'étude ayant bénéficiéen
2011 du concours de Facebook et Twitter montre quant à elle que des
utilisateurs des sites peuvent se connecter avec un autre internaute, via des
connaissances, en 4.74 étapes seulement[Cas14].
2.1.4.2 Coefficient de Clustering
élevé
Une autre caractéristique est issue de la tendance de
l'homme à se socialiser en groupe ce qui donne aux réseaux
sociaux une forte tendance au clustering et une structure en communautés
[Kan10]. La question qui se pose Les amis de mes amis tendent-ils à
devenir mes amis?
Autrement dit, un réseau montre du clustering si un
noeud X est connectéà un noeud Y et que ce noeud Y est
connectéà un noeud Z, alors X et Z ont une forte
probabilitéd'être également connectés, on parle
aussi de transitivité2.3 :

FIGURE 2.3 - Coefficient de clustering élevée
Chapitre 2. État de l'art 16
2.1.4.3 Structure en communautés
Une autre caractéristique des réseaux sociaux
c'est la structure en communautés [Kan10], à savoir des groupes
de noeuds avec une forte densitéd'arêtes et reliés entre
eux par des ponts. Ce phénomène peut être exprimépar
des individus ayant des intérêts communs ou de fortes relations
entre eux. Donc, cette socialisation s'effectue avec une tendance à
l'affiliation entre des noeuds ayant des propriétés quasi
équivalentes.

FIGURE 2.4 - Structure en communautés
2.1.4.4 Distribution de degréen loi de
puissance
On constate également que la distribution des
degrés suit une loi de puissance [Kan10] , à savoir que plus on
considère un degréélevé, plus le nombre de sommets
qui ont ce degrédans un même réseau est faible. Le
réseau est alors dit invariant d'échelle (scalefree), dans
l'équation suivante : P(K) = K-8, K
: le nombre de noeuds qui ont le degréa
comme il est indiquédans la figure 2.5

FIGURE 2.5 - Distribution de degrés en loi de
puissance
Chapitre 2. État de l'art 17
2.2 Prédiction des liens
Les réseaux sociaux sont très dynamique, des
nouveaux noeuds et des liens sont ajoutés aux graphes d'une instant
à une autre, comprendre cette évolution est un problème
très complexe dûà l'existence d'un nombre important de
paramètres. Ce problème peut être simplifiési nous
pouvons trouver des associations entre les noeuds, et à quel niveau,
l'évolution d'un réseau social peut être influx par ces
associations, dans la suite du chapitre nous présentons en détail
ce problème.
2.2.1 Problématique
Considérant une capture d'un réseau social
représentépar un graphe G =< V, E c V x V
> à l'instant t, tel que V et E sont des ensembles des
noeuds et des liens respectivement, la prédiction des liens consiste
à prédire l'apparition
des nouveaux liens qui peuvent être apparaitre à
l'instant t' tel que t' > t
c'est àdire pendant l'intervalle [t,
t'] [Wp15]. plus formellement nous définissons
le sous graphe temporel G =< G1, . . . , Gi, .. . , GT
>, tel que Gi est le sous graphe àl'instant
j, la tâche de prédiction des liens consiste à
prédire pour chaque couple
x, y E flT i=1 Vi : (x, y) E/
ET?(x, y) E ET+1 [Kan10] . Nous notons que les noeuds sont
statiques dans tous les instants de l'évolution d'un réseau
social, c'est-à-dire pas d'apparition ou de disparition des noeuds dans
ce cas, ce qu'il n'est pas le cas dans les réseaux sociaux réels
qui sont dynamique par rapport aux noeuds aussi. La figure 2.6 illustre ce
problème :

FIGURE 2.6 - Problématique
Chapitre 2. État de l'art 18
Le problème de prédiction des liens est
également liée au problème de détections des liens
cachés [Wp15], dans un certain nombre de domaines comme les
réseaux sociaux des terroristes ,l'un construit un réseau
d'interactions basées sur des données observables et essaie
ensuite de déduire des liens supplémentaires qui ne sont pas
directement visibles à la même instant t, sont
susceptibles d'exister. Ce problème peut-être résolu si
nous pouvons exploiter les caractéristiques des noeuds dans un
réseau social, au lieu d'évaluer des méthodes de
prédiction basées uniquement sur la structure d'un graphe.
2.2.2 Domaines d'applications
La prédiction des liens apparaît dans de nombreux
domaines d'applications [Wp15] la construction d'un système de
recommandation dans les réseaux sociaux est vue comme un problème
de prédiction de liens, il peut aider les personnes à trouver des
nouveaux amis, dans les réseaux académiques, comme par exemple
les réseaux de co-publication ou de co-citation entre les auteurs, il
permet au chercheurs de trouver des bons collaborateurs ou des co-auteurs. La
plus part des sites e-commerce aujourd'hui utilisent la prédiction des
liens pour fournir au acheteurs des nouveaux produits intéressants en
fonction de leurs préférences ou leurs achats, il peut être
aussi utilisépour aider les entreprises à trouver des
partenaires, attirer plus des clients. Finalement, en bioinformatique, ce
problème a étéétudiépar exemple dans le
cadre de l'inférence des réseaux biologiques, et en particulier
pour la prédiction des interactions protéine-protéine,
dans les domaines reliés à la sécurité, comme les
réseaux terroristes par exemple, il peut être utilisépour
identifier les communications anormales . . .
2.3 Techniques de prédiction des liens
Dans un réseau social, il existe deux façons
pour prédire l'évolution des liens [Wp15] : les approches non
superviséet les approches basées sur l'apprentissage
supervisé. Les approches non supervisécalculent une valeur de
similarité,c'est un score attribuéà chaque paire de noeuds
non connectés (x, y), un score élevéindique une grande
probabilitéque x et y seront liés dans le futur et vice versa,
après une liste des scores ordonnées est construite et les liens
qui ont des grandes valeurs de similaritésont les plus susceptibles
d'être liée.
Les approches basées sur l'apprentissage
supervisétraitent ce problème comme un
Chapitre 2. État de l'art 19
problème de classification binaire, par
conséquent, nombreux modèles d'appren-tissage et de
probabilitépeuvent être utilisépour résoudre ce
problème.
2.3.1 Les approches non supervisé
Ils existent beaucoup de méthodes de prédiction
des liens non supervisés, simples et basiques, utilisent l'information
de noeuds, la topologie et la théorie social pour
calculer la similaritéentre les paires de noeuds non
connectés, les méthodes basésur l'apprentissage
supervisésont les plus complexe, mais ils ont composépar des
mesures de cette classe, nous allons présentéune vue
systématique des ces mesures.
2.3.1.1 Mesures basées sur le contenu d'un
noeud
Le calcul de la similaritéentre les pairs de noeuds est
une solution intuitive dans la tâche de la prédiction des liens.
Il est basésur une idée simple : les paires les plus similaires
sont des noeuds ayant une grande vraisemblance et donc se sont les plus
susceptibles d'être reliéet vice versa.
Cette hypothèse conforme au concept que les personnes
tendent à créer des relations avec d'autres personnes qui sont
similaires dans l'éducation, religions, les intérêts et
localisation... ces caractéristiques peuvent être mesurées
par une si-milaritéattribuée à chaque pair de noeuds, une
grande valeur de similaritéentre deux noeuds indique qu'ils ont une
grande probabilitéd'être liée dans le futur.
Dans les réseaux sociaux réels, un noeud est
généralement à un ou plusieurs attributs qui le
caractérisent comme les profiles des utilisateurs dans les
réseaux sociaux, nom d'un email dans les réseaux des emails, des
publications dans les réseaux sociaux académiques, ces
informations peuvent être exploitées directement pour calculer la
similaritéentre les pairs de noeuds. Dans la plus part des cas, les
valeurs de ces attributs ayant une forme textuelle ce qu'il facilite le calcul
de la similarité.
Bhattacharyya et Garg [BP11] ont remarquépar exemple
qu'une personne dans
un réseau social aime le football et une autre aime le
soccer ou bien sport, malgréqu'ils n'ont aucune relation directe ils ont
une similaritépar ce qu'ils aiment le
même contexte c'est le sport, en se basant sur cette
idée, ils ont construit plusieurs modèles d'arbres de
catégorisation pour étudier les mots-clés de profile des
utilisateurs puis, ils ont définit des distances entre les mots
clés pour déterminer la similaritéentre les pairs
d'utilisateurs. Leur observation la plus importante est que, sauf pour les amis
directs, la similaritéentre les utilisateurs sont approximativement la
même, quelles que soient les paramètres topologiques de
réseau. Ils
Chapitre 2. État de l'art 20
montrent également que l'augmentation du nombre d'amis
et les mots clés diminue la similaritéentre une personne et leurs
amis...
Anderson et Huttenlocher [And12] Utilisent principalement les
intérêts des utilisateurs comme une mesure de similarité,
ces intérêts sont présentés par des
activités, par exemple éditer un article dans WIKIPEDIA, poser
une question dans StackOverflow, commenter un statu dans Facebook,
évaluer des produits d'un site e-commerce, évaluéune
application dans le PlayStore... tous ces actions sont présentées
dans un vecteur de poids en calculant les nombres d'interactions par rapport
aux interactions avec d'autres groupes, personnes etc. une grande valeur
indique que cette personne favorise par exemple des status d'une telle page,
produits, d'autres utilisateurs. . .
En conclusion, ils existent des dizaines de méthodes
qui utilisent comme référence les attributs et les
activités des utilisateurs dans les réseaux sociaux, ces
approches donnent des très bons résultats si nous pouvons
capturer le maximum de ceux-ci, ce qui nous permettre de connaitre de plus en
plus les comportements et les personnalités des internautes dans les
réseaux sociaux.
2.3.1.2 Mesures basées sur les motifs
topologiques
Considérant un simple réseau social qui ne
contient aucun attribut sur les noeuds ou sur les liens, ils existent beaucoup
de mesures qui permettent de calculer les similarités entre les paires
de noeuds, la plupart concentrent sur l'information de
la structure ou bien de la topologie d'un réseau social.
Les auteurs ont montréque la structure joue encore un
rôle important sur l'évolution des liens dans un
réseau social, par conséquent, beaucoup de
mesures de similaritéen se basant sur la topologie d'un réseau
social ont étéproposé, dans la section suivante, nous
donnons une vue systématique sur les mesures les plus populaires dans la
prédiction des liens. Ce qu'il nous faut prendre en considération
que ces mesures se distinguent en trois grandes catégories :
1. Les mesures locales basées sur le voisinage des
noeuds.
2. Les mesures globales basées sur les distances entre les
noeuds.
3. Les mesures basées sur les marches
aléatoires.
· Chapitre 2. État de l'art 21
Mesures de similaritélocales
Dans les réseaux sociaux, les personnes tendent de
créer des relations avec des personnes proche de celui-ci, les voisins
sont les plus proches, pour cela, les chercheurs ont définit beaucoup de
mesures basées sur les voisins d'un noeud, ces mesures attribuent des
scores aux paires de noeuds non connectés seulement en fonction de leurs
voisins et ne considèrent pas l'information sur tous les noeuds de
réseau social, une grande valeur de similaritéentre les noeuds
non connectésignifie qu'il y a une grande probabilitéque ce pair
soit connectédans le futur.
Attachement préférentiel (PA)
:[New01] et [Ba02] considèrent qu'il existe une forte
probabilitéque deux noeuds se connectent, si ces noeuds, appelés
également «hubs», sont déjàconnectés
à un nombre élevéde noeuds . Cette idée rejoint le
principe du «rich-get-richer». Le score associéà la
possibilitéd'existence d'un lien entre x et y est le suivant :
L'attachement préférentiel a toutefois
l'inconvénient d'obtenir des valeurs de similarités
élevées concernant les utilisateurs non connectés, au
détriment des utilisateurs peu connectés dans le réseau.
Cet inconvénient relève du fait que les relations entre les
utilisateurs dépendent uniquement de leur connectivité. Or, notre
but est de trouver de nouveaux voisins aux noeuds qui en ont peu. En outre, une
autre limite de cette méthode est la création de plusieurs liens
entre les noeuds et la maximisation de la connectivitédu
réseau.
Voisins communs (CN) :[New01] définit
une mesure qui est l'une les plus utilisées dans le problème de
prédiction des liens principalement en raison de sa simplicité.
Pour les deux noeuds, x et y, le CN est définie comme le nombre de
noeuds que x et y ont une interaction directe c'est-à-dire sont des
voisins communs. Un plus grand nombre des voisins communs facilite l'apparition
d'un lien entre X et Y, cette mesure est définie comme suit :

Chapitre 2. État de l'art 22
Comme nous avons dit, cette méthode considère
que plus les utilisateurs partagent des voisins, plus ils sont
corrélés. Or, comme pour l'attachement
préférentiel, l'in-convénient de cette méthode est
sa tendance à attribuer des similarités élevées aux
utilisateurs ayant de nombreux voisins. De ce fait, la similaritéentre
les utilisateurs disposant de peu de voisins tend à être faible,
voire nulle.
Coefficient de Jaccard (JC) : le coefficient
de Jaccard est une amélioration de la méthode voisins communs, Il
mesure la similaritéentre deux noeuds par le nombre de voisins en commun
divisépar le nombre total de voisins de ces noeuds. Il affecte des
valeurs plus élevées aux paires de noeuds qui ont une grande
proportion de voisins communs par rapport au total du nombre de voisins qu'ils
ont. Cette mesure est définie comme suit :

Comparéaux deux méthodes
précédentes, Jaccard a l'avantage de ne pas augmenter l'influence
des utilisateurs disposant d'un grand nombre de voisins.
Adamic et Adar (AA) : [Ada03] à
l'origine, cette une méthode est pour calculer la similaritéentre
deux pages Web au premier à travers ces items en prenant en compte les
items que ces deux utilisateurs ont en commun. La particularitéde cette
méthode est que les items qui sont partagés par peu
d'utilisateurs, ont un poids plus important que les items dont les occurrences
sont élevées (i.e. les items
qui sont communs à plusieurs paires d'utilisateurs),
après il a étélargement utilisédans les
réseaux sociaux :

Selon l'équation, au lieu de considérer les
items, nous considérons les voisins qu'au x et y ont en commun.
L'idée de cette mesure consiste à introduire une
pondération en fonction du nombre de voisins des voisins communs. Ainsi
les voisins communs les moins connectés sont associés à un
poids plus important.
Chapitre 2. État de l'art 23
Dans le tableau 2.1, nous comparons les mesures les plus
populaires qui sont basées sur le voisinage selon trois principaux
critères : la normalisation, la com-plexitétemporelle et leurs
caractéristiques. Il existe en effet 3 mesures qui ne sont pas
normalisées, c'est-à-dire la similaritéest
calculéen utilisant ces mesures ayant une signification seulement si on
construit une liste des scores ordonnées et il nous ne donne aucune
information sur la topologie par exemple leurs degrés, proportion de
leurs voisins communs par rapport aux tous les voisins etc.
La complexitétemporelle est un facteur important pour
choisir des mesures en fonction de la taille d'un réseau social.
Supposant que la moyenne de nombre de voisins d'un noeud dans un réseau
social est n, pour deux noeuds x et y, la com-plexitétemporelle pour
trouver tous les voisins d'un noeud est O(n), et la
com-plexitétemporelle de l'intersection ou l'union de deux ensembles est
O(n2). CN (Voisins communs) , AP (Attachement
préférentiel) , JC (Coefficient de Jaccard) ont O(n2)
par ce qu'ils ont besoin de calculer l'intersection et l'union de deux
ensembles. AA (Adamic et Adar) a besoin de calculer l'intersection de deux
ensembles et de trouver les voisins des voisins communs, par conséquent,
la complexitétem-porelle sera O(2n2). Les
caractéristiques de ces mesures sont aussi discutédans le tableau
suivant.
Mesure
|
ou non
|
NormaliséComplexitéCaractéristiques
|
|
AP
|
Non
|
O(n2)
|
Simple, des noeuds ayant des degrés élevés
sont plus susceptible d'être liée
|
CN
|
Non
|
O(n2)
|
Simple et intuitive
|
JC
|
Oui
|
O(n2)
|
Proportion des voisins communs sur les voisins total
|
AA
|
Non
|
O(2n2)
|
Voisins communs ayant moins de voisins sont
pondérées plus lourdement
|
|
TABLE 2.1 - Quelques caractéristiques des mesures de
similaritélocale [Wp15]
Finalement, nous devons prendre en compte qu'il existe un
nombre important des algorithmes de prédiction de liens qui sont
basés sur le voisinage, mais pour des expérimentations
réels, plusieurs études ont montréqu'il n'existe pas une
mesure de similaritéabsolu donne des bonnes prédictions pour
n'importe quel réseau social.
· Chapitre 2. État de l'art 24
Mesures de similaritéglobales
Contrairement aux mesures de similaritélocales, les
mesures globales nécessitent de connaître toute l'information
topologique du réseau social. Ces approches se basent
généralement sur l'hypothèse que dans le cas oùil
existe plusieurs relations de longueurs différentes
(3ème degréou plus), cela peut
conduire à une relation entre ces deux personnes dans le futur.
Plus court chemin :[Win14] La mesure la plus directe pour
calculer la simila-ritéentre deux noeuds est la distance entre eux. Il
est défini comme la plus courte distance qui sépare x à y.
Plus précisément, nous initialisons S = {x} et D = {y} . A chaque
étape, nous élargissons les deux ensembles en incluant les
voisins directes pour chaque noeud de manière récursive. Nous
arrêtons si nous trouvons au moins un élément appartient
à ces deux ensembles: S et D c'est-à-dire S nD =6 Ø, le
plus court chemin dans ce cas est le nombre d'itérations. Une grande
distance indique une faible similaritétandis qu'une courte distance
indique une grande similarité.
Local path : [Lu09] Cette mesure prend en
considération l'information des chemins locales entre les noeuds de
longueurs 2 et 3 contrairement aux mesures qui prennent en compte que les
voisins les plus proches, cette mesure exploite des informations additionnelles
avec un chemin de longueur 3 depuis le noeud courant, évidement, les
chemins de longueur 2 sont plus importants par rapport aux chemins de longueur
3 donc il y a un facteur d'ajustement appliquédans cette mesure.
Katz :[Kat53] Cette mesure basésur le principe que
deux personnes dans un réseau social peuvent utiliser tous les chemins
qui les relie surtout si ses chemins sont nombreux par rapport aux chemins de
longueur inferieur, donc elle compte tous les chemins de différentes
longueurs qui relient les pairs de noeuds, en utilisant une pondération
en fonction de la longueur d'un chemin, tel que les chemins courts ont un poids
élevépar rapport aux chemins longs qu'en lui affectant des poids
faible.
·
Chapitre 2. État de l'art 25
Mesures basées sur les marches
aléatoires
Les interactions entre les noeuds au sein d'un réseau
social peuvent être aussi modélisées par des chaines
Markoviennes, en affectant une probabilitéde transition a chaque lien
entre chaque deux noeuds, la marche aléatoire saute d'un noeud à
un autre et ce dernier représente un état d'une chaine de Markov,
il existe un nombre assez important de mesures pour calculer la
similaritéentre deux noeuds en se basant sur les marches
aléatoires.
Hitting Time (HT) : [Fou07] Ht(x,y) est le
nombre des étapes pour effectuer une marche aléatoires en partant
d'un noeuds x à un noeud y.
Commute time(CT) : puisque la mesure Hitting
time n'est pas symétrique, la mesure CT est symétrique
c'est-à-dire elle considère le nombre des étapes pour
partir d'un x jusqu'au noeud y est le même pour une marche
aléatoire allant de y à x. CT(x,y) : Ht(x, y) = Ht(y,
x)
SimRank (SR) : [JG02] est une adaptation de
l'algorithme de Google qui permet de trier les pages web en selon leurs
importance en fonction du nombre de pages qu'ils la référence.
simRank est une mesure de similaritédans un graphe orienté, elle
est basésur une idée simple : deux noeuds sont similaire s'ils
référencent des noeuds qui sont aussi similaires, sachant que la
similaritéd'un seul noeud égal à 1, elle calcule ce score
à travers le nombre de leur voisins entrants et ces voisins à
travers leurs voisins entrants et ainsi de suite jusqu'àarriver à
un seul noeud.
La valeur de simRank peut être calculéavec deux
marches aléatoires, l'une part d'un noeud x et l'autre à partir
un noeud y, elle mesure après combien de temps les deux marches
aléatoire stationnent sur le même noeud, le cas le plus favorable
c'est que ce dernier est un voisin commun directe et dans ce cas la
similaritéest maximale.
2.3.1.3 Mesures basées sur la théorie
social
Dans de nombreux travaux récents, un nombre important des
algorithmes développés, sont basés sur les théories
sociaux classiques comme les communautés, les cen-tralités des
noeuds, triades etc. ont étéproposépour résoudre le
problème de prédiction des liens.
Chapitre 2. État de l'art 26
Chapitre 2. État de l'art 27
Valverde et Lopes [VJ13] ont combinéles informations
topologiques avec la détection des communautés en prenant en
considération les intérêts des utilisateurs, puis, ils ont
essayéde prédire les futures liens dans le réseau social
Twitter , ils ont définit la similaritéentre deux noeuds x et y
qui appartiennent à deux communautés différentes Cx
et Cy en fonction du nombre des voisins communs qu'ils les partagent dans
la même communautédivisésur le nombre de leurs voisins
communs total, ils ont montréque cette méthode est efficace et
donne des bonnes prédictions.
Liu , Huz et Haddadi [Liu13] ont proposéun
modèle de prédiction des liens basésur la combinaison des
noeuds ayant des liens faible et les trois types de centralité(de
degrés, intermédiaritéet proximité) des voisins
communs, ils ont découvrit dans le contexte de leur travaille, que les
noeuds centraux sont aussi important pour la prédiction des liens, les
noeuds de degrés faible préfèrent établir des
relations avec des noeuds centraux par rapport aux noeuds similaires. Ils ont
proposéaussi un ensemble d'algorithmes qui peuvent capturer ces noeuds
centraux dans les réseaux sociaux.
2.3.2 Méthodes basées sur l'apprentissage
supervisé
Les méthodes d'apprentissage sont basés sur des
nombreuses méthodes fournit par des mesures de similarités
basiques comme les mesures topologiques ou les mesures qui exploitent les
contenus des noeuds, les attributs internes et les informations externes,
nombreux méthodes ont étéproposéces
dernières années en citant par exemple la classification binaire
supervisé[MH13]
2.3.2.1 Classification binaire
Supposant que nous avons deux noeuds x, y E V dans le
réseau social G(V,E) et considérant L(x,y) est une
étiquette de ce pair de noeuds (x,y), dans la prédiction des
liens chaque paire de noeuds non connectécorrespond à une
instance inclut la classe et un ensemble des caractéristique
décrits les pair de noeuds, en plus , le pair
étiquetécomme négative s'il n'existe pas un lien entre ces
deux noeuds, s'il existe déjàun lien, il est
étiquetécomme positif, l'étiquette (x,y) est
définit comme suit :
f
+1 si (x,y)E E
l(x,y) =
-1 si (x,y)/E E
Ensuite nous pouvons construire un vecteur d'informations qui
contient un ensemble des valeurs (poids) des mesures de similaritéentre
tous les noeuds dans un réseau social plus une étiquète de
chaque paire, ensuite, nous utilisons n'importe quelle méthode
d'apprentissage supervisépour résoudre ce modèle en
l'occurrence les SVM, les réseaux de neurones et les méthodes
probabilistes comme les réseaux bayésiens...
Pour construire un classifieur efficace et donne des bonnes
prédiction de liens, il est important de définir et extraire un
ensemble de caractéristiques appropriépour chaque réseau
social, les caractéristiques fournit par les noeuds, la topologie et la
théorie social sont populaires et important pour les modèles de
classification, en plus, plusieurs études expérimentaux ont
montréque la combinaisons entre des attributs fournit par des noeuds et
des liens (comme l'âges ,les intérêts, nombres
d'interactions...) peuvent améliorer la précision d'un
classifieur, cependant ces informations ne sont pas toujours accessible pour
les fouilleurs.
Conclusion
Nous avons introduit dans ce chapitre l'analyse des
réseaux sociaux, parmi les méthodes d'analyse des réseaux
sociaux nous avons présentéun état de l'art qui
résume les principaux travaux qui ont étémenés
autour le problème de prédiction des liens qui est au coeur de ce
mémoire. Nous avons présentéles principales approches
existantes pour résoudre ce problème, en l'occurrence des
approches basée sur le contenu des noeuds, des approches exploitant des
propriétés topologiques du réseau et des méthodes
d'apprentissage supervisé.
Pour nos travaux, nous avons choisi deux mesures de
similaritéqui ont basésur les motifs topologique d'un
réseau social, la première mesure c'est la mesure de
Adamic et Adar et la deuxième c'est
voisins communs.
Dans le chapitre qui suit, nous allons expliquer en
détail les principes de fonctionnement de chacune de ces deux mesures de
similarité. Ensuite nous implémentons ces deux fonctions dans le
but est de faire une comparaison basée sur les résultats de cette
implémentation.
28
Chapitre 3
Les fonctions : Adamic/Adar et
voisins communs
Dans ce chapitre, nous allons présenter en
détail les principes des deux approches de prédiction des liens
que nous avons choisi, voire la mesure de similaritéAda-mic/Adar et
Voisins Communs, nous présentons des exemples simples pour bien
comprendre leur fonctionnement.
3.1 La fonction de similarité:
Adamic/Adar
3.1.1 Origine de la méthode
Cette mesure à étéproposépar
[Ada03], est une méthode d'extraction des réseaux d'amis des
universités de Stanford et du MIT, à partir des pages
personnelles des étudiants. Les étudiants de ces
universités, au moment de l'étude, avaient pour usage de mettre
des items textuels comme par exemple leurs intérêts, les groupes
ou ils appartiennent, leurs localisations géographiques, des hyperliens
de leur page personnelle vers les pages personnelles de leurs amis. Ainsi, dans
un premier temps, les auteurs démontrent que le graphe formépar
la structure en hyperliens de ces pages possède les
propriétés des réseaux sociaux : »small world»,
distribution des degrés en loi de puissance, et un taux de clustering
élevé. Ensuite, un indice de simi-laritéentre les pages
personnelles est défini à partir de la co-occurrence
d'éléments textuels et de la présence d'hyperliens entre
les pages.
Les auteurs ont trouvéque deux étudiants plus
qu'ils mentionnent des items communs dans leurs pages web, plus ils sont
similaires dans leurs vie réel et donc, il existe une relation forte
entre eux. Ils ont prouvéaussi que par exemple un
Chapitre 3. Les mesures : Adamic/Adar et voisins communs
29
item commun mentionnépar deux étudiants
seulement à une similaritéplus élevéqu'un item
commun partagépar 5 étudiants, pour cela, ils ont choisi une
formule mathématique pour attribuer des poids aux items communs en
fonction du nombre de personne qu'ils les partagent, ils ont
utilisél'inverse de ln x pour attribuer des poids élevéau
items rarement partagé, par exemple un item partagépar deux
étudiants à un poids égal à 1
ln 2, un item partagépar 1000
étudiants sera égal à1
ln 1000.
3.1.2 Principe de la méthode
Comme nous avons citéprécédemment, au
lieu de considérer les items, nous considérons les voisins
communs dans un réseau social, pour chaque paire de noeuds
(x, y) non connecté, nous calculons la
similaritéentre x et y en fonction de degréde leurs voisins
communs. Cette mesure est similaire à la mesure Common Neigh-
bors que nous avons la défini dans le chapitre
précédent mais elle est adaptée à la tâche
d'attribution des poids élevéaux noeuds rarement
partagédans un réseau social. Après avoir
calculéles similarités entre toutes les pairs de noeuds dans le
réseau social, ces derniers sont stockés de manière
ordonnés en ordre décroissant dans une liste. Le résultat
de la prédiction sera tout simplement les K premiers pairs de noeuds qui
ont des valeurs de similaritéles plus élevé.
3.1.2.1 Calcul de la matrice de similarité
Cette mesure de similarités'obtient en
calculant la somme de l'inverse de logarithme de dégrées des
voisins communs pour chaque paire non connectéet qui partagent un
ensemble de voisins comme il est indiquée dans la formule suivante:

3.1.3 Exemple pratique
Supposons que nous avons une capture d'un réseau social
constituéde 15 noeuds et 15 liens à l'instant t, tel que les
noeuds sont des personnes et les liens indiquent qu'il existe une relation
d'amitiéentre eux, comme il est illustrédans la figure 3.1 :

Chapitre 3. Les mesures : Adamic/Adar et voisins communs
30
FIGURE 3.1 - Exemple d'une capture d'un reseau social
Sur cette figure, nous cherchons à inférer les
nouveaux liens qui peuvent être apparaissent à l'instant
t' > t , pour cela nous allons calculer la
similaritéentre chaque paire non connecté, premièrement
par l'algorithme de Adamic/Adar. Les étapes d'exécution de
l'algorithme de Adamic/Adar est illustrédans la figure suivante, nous
allons détailler par la suite chaque étape :
· Etape 1 : nous construisons la matrice d'adjacence de
ce petit réseau social, tel que les lignes et les colonnes sont des
personnes et leurs intersections indiquent s'il existe une relation
d'amitiéentre eux ou non, la valeur 1 indique que ces deux personnes
sont des amis, 0 sinon. 3.1
Chapitre 3. Les mesures : Adamic/Adar et voisins communs
31
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
L
|
M
|
N
|
O
|
A
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
B
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
C
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
D
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
E
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
F
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
G
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
H
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
I
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
J
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
K
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
L
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
M
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
N
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
O
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
|
TABLE 3.1 - Représentation du réseau social par
une matrice d'adjacence
· Etape 2 : En utilisant la formule de
Adamic/Adar, on peut facilement calculer la matrice de similarité, les
intersections entre des lignes et des colonnes indiquent la
similaritéentre les deux personnes(x, y) qui ne sont pas des amis
3.2.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
L
|
M
|
N
|
O
|
A
|
0.0
|
0.0
|
1.34
|
0.0
|
0.0
|
0.0
|
0.72
|
0.72
|
0.62
|
0.0
|
0.62
|
0.62
|
0.0
|
0.0
|
0.0
|
B
|
0.0
|
0.0
|
0.0
|
1.44
|
0.72
|
0.72
|
0.0
|
0.0
|
0.0
|
0.72
|
0.0
|
0.0
|
0.72
|
0.91
|
0.91
|
C
|
1.34
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.72
|
0.72
|
0.62
|
0.0
|
0.62
|
0.62
|
0.0
|
0.0
|
0.0
|
D
|
0.0
|
1.44
|
0.0
|
0.0
|
0.72
|
0.72
|
0.0
|
0.0
|
0.0
|
0.72
|
0.0
|
0.0
|
0.72
|
0.0
|
0.0
|
E
|
0.0
|
0.72
|
0.0
|
0.72
|
0.0
|
0.72
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
F
|
0.0
|
0.72
|
0.0
|
0.72
|
0.72
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
G
|
0.72
|
0.0
|
0.72
|
0.0
|
0.0
|
0.0
|
0.0
|
0.72
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
H
|
0.72
|
0.0
|
0.72
|
0.0
|
0.0
|
0.0
|
0.72
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
I
|
0.62
|
0.0
|
0.62
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.62
|
0.62
|
0.0
|
0.0
|
0.0
|
J
|
0.0
|
0.72
|
0.0
|
0.72
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.72
|
0.0
|
0.0
|
K
|
0.62
|
0.0
|
0.62
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.62
|
0.0
|
0.0
|
0.62
|
0.0
|
0.0
|
0.0
|
L
|
0.62
|
0.0
|
0.62
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.62
|
0.0
|
0.62
|
0.0
|
0.0
|
0.0
|
0.0
|
M
|
0.0
|
0.72
|
0.0
|
0.72
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.72
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
N
|
0.0
|
0.91
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.91
|
O
|
0.0
|
0.91
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.0
|
0.91
|
0.0
|
|
TABLE 3.2 - Matrice de similarité: Adamic/Adar
·
Chapitre 3. Les mesures : Adamic/Adar et voisins communs
32
Etape 3 : Nous stockons dans une liste
ordonnée de manière décroissante toutes les valeurs de
similarités obtenus à travers la matrice de
similaritéAda-mic/Adar. Puis en se basant sur le principe que plus la
similaritéest élevée plus il y a de chance pour que les
paires de noeuds soient connectés dans le futur, pour cela nous
choisissons les k premiers pairs qui ont des valeurs de similarités les
plus élevés. pour notre exemple, nous avons choisi les 5
premières paires qui ont des valeurs de similaritéles plus
élevés 3.3 :
(x,y)
|
Similarité(x,y)
|
(1,3)
|
1.44
|
(0,2)
|
1.34
|
(1,13)
|
0.91
|
(1,14)
|
0.91
|
(13,14)
|
0.91
|
(0,6)
|
0.72
|
(0,7)
|
0.72
|
(1,4)
|
0.72
|
. . .
|
. . .
|
(0,8)
|
0.62
|
. . .
|
. . .
|
(10,11)
|
0.62
|
|
TABLE 3.3 - Liste de similaritéde Adamic/Adar
· Etape 4 : nous construisons la
nouvelle matrice d'adjacence tout simplement à travers l'ancienne
matrice en ajoutant les 5 nouveaux liens choisi comme il est indiquédans
la matrice 3.4 :
Chapitre 3. Les mesures : Adamic/Adar et voisins communs
33
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
L
|
M
|
N
|
O
|
A
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
B
|
1
|
0
|
1
|
|
100
|
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
C
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
D
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
E
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
F
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
G
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
H
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
I
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
J
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
K
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
L
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
M
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
N
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
O
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
|
TABLE 3.4 - Nouvelle matrice d'adjacence aprés
l'exécution de Adamic/Adar
· Finalement, nous pouvons visualiser notre nouveau
réseau social après la prédiction sur cette figure3.2 :

FIGURE 3.2 - L'état du réseau aprés
l'exécution de Adamic/Adar
3.2 Chapitre 3. Les mesures : Adamic/Adar et voisins communs
34
La fonction de similarité: Voisins
communs
3.2.1 Origine de la méthode
[New01] a étudiéles réseaux de
collaboration scientifique en physique et en biologie, pour cela, il a
utilisédeux bases de données bibliographiques :
1. The Los Alamos E-print Archive : est une
base de données bibliographique contient les prépublications
soumis par leurs co-auteurs.
2. Medline : est une base de donnes des
articles publiéen biologie et en médecine.
Ainsi, dans un premier temps, l'auteur démontre que le
graphe formépar la structure des noeuds qui l'ont
considérécomme des co-auteurs et les liens indiquent s'ils ont
publiéau moins un article ensemble, cette structure a les
propriétés des réseaux sociaux : »small world»,
distribution des degrés en loi de puissance, et un taux de clustering
élevé. Ensuite, son contribution est que la
probabilitéd'apparition des nouvelles collaborations entre les auteurs
qui n'ont pas encore publiéensemble augmente en fonction du nombre de
collaborateurs qu'ils ont en communs.
3.2.2 Principe de la méthode
Au lieu de considérer les réseaux de
collaboration scientifique, nous pouvons appliquer la mesure de voisins communs
sur la relation d'amitiédans notre réseau social, pour chaque
paire de noeuds (x, y) non connecté, la similaritéentre deux
personnes est tout simplement le nombre de leurs voisins communs. La fonction
CommonsNeighbors utilise une matrice d'adjacence qui représente une
capture d'un réseau social à une instant donnée ou les
lignes et les colonnes représentent des personnes. Après avoir
calculéles similarités entre toutes les paires de noeuds non
connectés de ce petit réseau social. Le résultat de la
prédiction sera tout simplement les K premières paires qui ont
les valeurs de similarités les plus élevés.
3.2.2.1 Calcul de la matrice de similarité
Cette mesure consiste à calculer le
nombre des voisins communs pour chaque pair non connectéet qui partage
un ensemble de voisins comme il est indiquédans la formule suivante :
Avec le même exemple, nous calculons la similaritéentre les
personnes à partir la matrice d'adjacence de notre réseau social,
comme nous avons indiquéprécédemment, nous avons
résumél'exécution de cette algorithme en seulement 3
étapes comme il est indiquédans la figure suivante :

·
Chapitre 3. Les mesures : Adamic/Adar et voisins communs
35
Etape 1 : c'est tout simplement la
création de la matrice d'adjacence de notre réseau social
· Etape 2 : Cette étape consiste
à calculer la similaritétopologique entre chaque paire non
connecté, la similaritédans ce cas est le nombre de voisins
communs de ce pair 3.5
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
L
|
M
|
N
|
O
|
A
|
0
|
0
|
2
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
B
|
0
|
0
|
0
|
2
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
C
|
2
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
D
|
0
|
2
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
E
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
F
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
G
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
H
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
I
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
J
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
K
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
L
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
M
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
N
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
O
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
|
TABLE 3.5 - Matrice de similarité: common Neighbors
· Etape 3 : de la même
manière, nous avons construit une liste qui contient toutes les valeurs
de similaritétrouvé, nous allons trier cette dernière en
ordre décroissant, ensuite nous choisissons les k
premières paires qui ont des valeurs de similaritémaximum,
puisque l'idée c'est plus la similaritéest
élevéentre un pair non connectéplus nous allons une forte
probabilitéque ce pairs liée dans le futur, par exemple, nous
allons choisi k = 5, c'est le même nombre des pair choisi pour
l'algorithme précédent afin de voir les différences entre
les deux algorithmes 3.6 :
Chapitre 3. Les mesures : Adamic/Adar et voisins communs
36
TABLE 3.7 - Nouvelle matrice d'adjacence aprés
l'exécution de Common Neigh-
bors
(x,y)
|
Similarité(x,y)
|
(0,2)
|
2
|
(1,3)
|
2
|
(0,6)
|
1
|
(0,7)
|
1
|
(0,8)
|
1
|
(0,10)
|
1
|
(0,11)
|
1
|
(1,4)
|
1
|
. . .
|
. . .
|
(3,12)
|
1
|
. . .
|
. . .
|
(13,14)
|
1
|
|
TABLE 3.6 - Liste de similaritéde Common Neighbors
· voici la nouvelle matrice d'adjacence de ce réseau
social 3.7 :
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
L
|
M
|
N
|
O
|
A
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
B
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
C
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
D
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
E
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
F
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
G
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
H
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
I
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
J
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
K
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
L
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
M
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
N
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
O
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
|
·
Chapitre 3. Les mesures : Adamic/Adar et voisins communs
37
Finalement, nous pouvons visualiser notre nouvelle état du
réseau social après la prédiction sur cette figure 3.3
:

FIGURE 3.3 - L'état de réseau social aprés
l'exécution de Common Neighbors
3.3 Mesures de performances
Nous avons choisis comme mesures de performance : le rappel,
la précision ainsi que le rapport entre les deux
caractérisépar la F-mesure [LC12] , nous allons voir en
détail le principe de chaque mesure de performance dans le contexte de
la prédiction des liens, dont le but est de faire une comparaison entre
les résultats de ces deux algorithmes Adamic/Adar et Commons
Neighbors.
Notant que nous pouvons mesurer les performances de nos
algorithmes seulement si nous prendrions une nouvelle capture de notre
réseau social, ce qui nous permet de voir les différences entre
le réseau social réel et le réseau sociaux
prédit.
Nous distinguons 4 types des liens dans un réseau
social :True Positif (TP), False
Chapitre 3. Les mesures : Adamic/Adar et voisins communs
38
Positif (FP), False Negatif (FN) et True Negatif (TN),
nous les représentons dans la matrice suivante 3.8 :
|
Nouvelle capture : +
|
Nouvelle capture : -
|
|
Prédit à: +
|
TP
|
FP
|
|
Prédit à : -
|
FN
|
TN
|
TABLE 3.8 - Matrice de confusion
- TP : sont des liens ajoutés
après la prédiction, et ils ont apparut aussi dans la nouvelle
capture de réseau social.
- FP : sont des liens
ajoutéaprès la prédiction, et qui ne sont pas inclut dans
l'ensemble des liens de la nouvelle capture de réseau social.
- FN : sont des liens qui ne sont pas
ajoutés après la prédiction, et ils sont ajoutés
dans le nouvel état de réseau social.
- TN : sont des liens qui n'ont pas
ajoutéaprès la prédiction, et qui n'existent pas dans la
nouvelle état de réseau social.
la figure 3.4 illustre les différents types des liens
pour calculer les performances d'un algorithme de prédiction des liens
:

FIGURE 3.4 - Les différents types des liens: TP, FP,
FN
Dans notre contexte, le rappel correspond au rapport du nombre
des liens ajoutéaprès la prédiction et ils ont
inclut aussi dans l'ensemble des liens observédans la
3.3.1 Le rappel
Chapitre 3. Les mesures : Adamic/Adar et voisins communs
39
nouvelle capture d'un réseau social, sur le nombre
total des liens ajoutédans la nouvelle capture de ce même
réseau social, ce rapport a étécalculéà
l'aide de la formule :
Rappel = T P
TP+FN
3.3.2 La précision
La précision correspond au rapport du nombre des liens
ajoutéaprès la prédiction et observéaussi dans la
nouvelle capture d'un réseau social, sur le nombre total des liens
ajoutéaprès la prédiction, nous l'avons
calculéà l'aide de la formule :
Précision = T P
TP+FP
3.3.3 La F-mesure
Une mesure qui combine entre le rappel et la précision en
effectuant une moyenne entre ces deux, plusieurs variantes de cette mesure ont
étéproposées, la variante la plus populaire est
définie par la formule :
F-mesure = 2×Rappel×Précision
Rappel+Précision
Conclusion
Dans ce chapitre, nous avons vu la motivation et les principes
de fonctionnement de chacune des deux mesures de similarité: Adamic/Adar
et Commons Neighbors. Nous avons également présentédes
exemples illustrant d'avantage ces deux techniques.
Dans le chapitre suivant nous allons présenter
l'application que nous avons développéainsi notre processus
expérimental pour comparer ces deux mesures.
40
Chapitre 4
Implémentation et
Expérimentations
Dans ce chapitre nous visons à présenter notre
projet, l'outil que nous avons développéainsi que les
différentes expérimentations que nous avons effectuépour
évaluer et comparer les deux mesures de similaritéAdamic/Adar et
Common Neighbors dans le contexte de la prédiction des liens dans les
réseaux sociaux, l'ensemble de données utiliséest
construite à partir d'un réseau de collaboration scientifique des
chercheurs de laboratoire de Mathématiques et d'informatique de
l'universitéAmar Telidgi.
4.1 Environnement de travail
Nous avons implémentéles deux algorithmes de
prédiction des liens en JAVA, il s'agit d'un langage de programmation
objet, gratuit et portable, ce qui lui a permis d'être parmi les langages
les plus utilisé. Il a étédéveloppépar la
firme Sun Microsystems en 1995, cette dernière a
étérachetée en 2009 par Oracle. Le JDK (Java Development
Kit) et le JRE (Java Runtime Environnent) peuvent être gratuitement
téléchargés sur le site officiel
1 .
Nous avons utiliséla version JDK1.8 dans un ordinateur
portable dotéd'un processeur Intel R Dual core @ 2.00 GHz (2 CPUs), avec
une mémoire vive (RAM) de 2GO qui fonctionne sur le système
d'exploitation Microsoft Windows 7 Professional 32 bits. Pour l'éditeur,
nous avons choisi L'IDE (Integrated Development Environment) NetBeans IDE 8. Il
s'agit de la dernière version de Netbeans, ce dernier est parmi les
éditeurs java les plus appréciés, cette forte
appréciation est
1. http ://
www.oracle.com/technetwork/java/javase/downloads/index.html
Chapitre 4. Implémentation et Expérimentations
41
due à de multiples avantages notamment les simplifications
d'édition et la facilitéde la création des interfaces
graphiques par l'option drag and drop. Ils intègrent
les fonctionnalités suivantes :
1. Éditeur de textes avec coloriage syntaxique
2. L'option auto Complète (menus contextuels
suggère de multiples choix).
3. Génération automatique des conteneurs et
dossiers nécessaires à l'organisa-tion d'un projet et des
paquetages des classes.
4. Intégration des commandes Java et de leurs options
dans des menus et des boîtes de dialogue appropriés.
5. Débogueur pour corriger les erreurs.
6. Proposition pour la résolution automatique de
quelques erreurs de programmation
Nous avons visualiser notre réseau social avec NodeXL,
c'est un outil gratuit d'ex-ploration et d'analyse des réseaux sociaux.
En effet, NodeXL est facile d'utilisation et simple à assimiler. Il
permet à l'utilisateur de s'initier à l'analyse des
réseaux sociaux et manipuler des graphes sociaux. Parmi la panoplie
d'outils disponibles sur le marché, nous avons trouvéque NodeXL
est le mieux adaptéà un public large.
Celui-ci reprend l'utilisation de feuilles de calcul du
tableur pour y afficher dans un premier temps des données qui
permettront de produire un graphe sous la forme noeud-lien. L'utilisation des
feuilles de calcul permet un import souvent direct ou plus aisée des
données.
Toutefois, comme il s'agit de produire un graphe relationnel
sous la forme noeud-lien, il est demandéà l'utilisateur de mettre
en évidence les relations (arêtes) entre les entités. Pour
cela, les données doivent être présentées suivant un
format strict. Chaque ligne de la table décrit une arête qui sera
identifiéa l'aide des deux entités (sommets) qu'elle met en
relation. Les sommets sont stockées dans les deux premières
colonnes de la ligne puis suit une liste d'attributs qui seront affectés
àl'arête.
Pour ce qui est de la présentation du réseau
sous forme noeud-lien, l'utilisateur a le choix entre plusieurs algorithmes de
dessin qu'il peut relancer à chaque fois qu'il apporte une modification
au graphe. Ces modifications peuvent être faite soit directement dans la
représentation noeud-lien soit dans la table. Ce module permet
Chapitre 4. Implémentation et Expérimentations
42
donc d'importer un réseau social, d'en construire une
représentation et enfin de pratiquer une analyse visuelle. Les points
forts du module nodeXL sont :
1. la construction d'un graphe noeud-lien a partir d'une
table.
2. le calcul automatique de métriques grâce a la
puissance du tableur.
3. analyse visuelle du réseau.
4. un module intégrée au Microsoft Excel. la
figure 4.1 résume tous ce que nous avons dit :

FIGURE 4.1 - L'interface de NodeXL
4.2 Description de l'application
Afin de comparer les deux fonctions de prédiction des
liens, il est nécessaire de les appliquer sur les mêmes
données et dans le même contexte, pour cela, nous avons
4.2.1 Algorithmes et explications
Chapitre 4. Implémentation et Expérimentations
43
choisi d'utiliser le même réseau social. Comme le
langage que nous avons utiliséest un langage objet, nous avons
profitéde cet aspect de programmation durant
le développement de l'outil d'expérimentation.
L'organigramme global suivant 4.2 présente les
différentes étapes de l'implémentation :
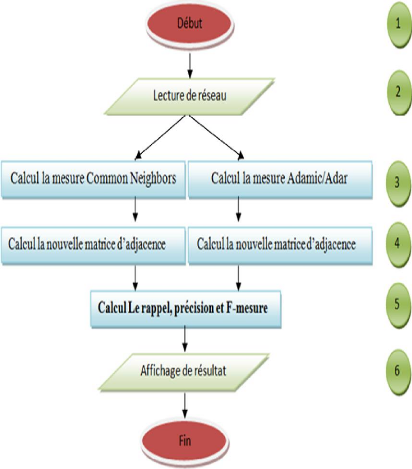
FIGURE 4.2 - L'organigramme de l'application
L'étape (2) : C'est une étape
très importante, il s'agit des opérations d'entrée/sortie
dans laquelle le programme lit le réseau social à partir du
fichier texte, notre réseau social est stockésous une forme
matricielle, ce qu'il facilite son interprétation.
L'étape (3) : Ce niveau de calcul est
distinguéen deux étapes indépendantes,
Chapitre 4. Implémentation et Expérimentations
44
une étape consiste à appliquer la fonction qui
calcul la matrice de similaritéAda-mic/Adar et l'autre consiste à
appliquer la fonction de similaritéVoisins communs, à partir de
la matrice d'adjacence.
L'étape (4) : consiste à
recalculer la nouvelle matrice d'adjacence pour chaque algorithme en ajoutant
les liens prédits.
L'étape (5) : Cette étape
consiste à mesurer les performances de nos algorithmes
de prédiction des liens, nous prenons les deux matrices
d'adjacence construit àpartir de l'étape
précédente et nous les comparons avec une nouvelle capture de
ce même réseau social.
Dans la suite nous allons voir les fonctions et les
procédures qui sont incluent dans chaque étape.
4.2.1.1 Construire la matrice de Adamic et Adar
Le pseudo code suivant [1] représente
l'exécution de l'algorithme de Adamic et Adar. la fonction Adamic et
Adar commence par récupérer la matrice d'adjacence de
réseau social, puis elle recherche pour tous pairs de noeuds non
connecté, leurs voisins commun, s'ils existent elle fait appel à
une autre fonction (degreenoeud(k)) qui calcul le degréde
chaque voisin commun en lui passant comme paramètre, puis
elle calcul l'inverse de log de degréde ce
dernier. A la fin la matrice de similaritéreçoit la somme des
inverses delog dégrée de tous les voisins communs pour
tous les
pairs non connecté, par convention la
similaritéentre deux noeuds
déjàconnecté(dans la matrice d'adjacence
(M(i, j) = 1)) est égal à 0, ainsi la
similaritéentre un noeud et le même noeud est aussi égal
à 0.
Chapitre 4. Implémentation et Expérimentations
45
Algorithm 1 Algorithme de Adamic et Adar
1: function DEGREE
NOEUD(adj,k)
2: entier degree +- 0
3: entier N +- adj.length
4: fori +- 1 to N
do
5: if adj(k, i) = 1
then
6: degree +- degree + 1
7: end if
8: end for
9: return degree
10: end function
11: function ADAMIC ET ADAR(adj)
12: Output matrice de similarité:
adamicAdar
13: double freq +- 0
14: entier N +- adj.length
15: fori +- 1 to N
do
16: forj +- 1 to N
do
17: if i = j
then
18: adamicAdar(i, j) +- 0
19: else
20: if adj(i, j) = 1
then
21: adamicAdar(i, j) +- 0
22: else
23: for k +- 1 to N
do
24: if adj(i, k) = 1 ?
adj(k, j) = 1 then
1
25: freq +- freq + ln(DEGREE NoEUD(M,k))
26: adamicAdar(i, j) +- freq
27: end if
28: end for
29: freq +- 0
30: end if
31: end if
32: end for
33: end for
34: return adamicAdar
35: end function
Chapitre 4. Implémentation et Expérimentations
46
4.2.1.2 Construire la matrice de Commons
Neighbors
la multiplication matricielle est la solution la plus
intuitive pour trouver les voisins communs entre chaque deux noeuds non
connecté, si M est la matrice d'adjacence qui indique les chemins de
longueurs 1 (voisin directe), alors M2 est la matrice qui
indique les chemins de longueur 2 entre chaque deux noeuds, c'est-à-dire
se sont voisins des voisins, si nous trouvons par exemple
M2(i, j) = 2 ça veux dire qu'il existe deux
chemins de longueur 2 entre i et j et donc forcement il
existe 2 voisins communs entre i et j, nous avons effectuer
une modification dans laquelle M2(i, i) = 0 et
M2(i, j) = 0 si i et j sont des
voisins directe dans la matrice d'adjacence c'est-à-dire M(i,
j) = 1, le pseudo code[2] résume ce calcul :
Algorithm 2 Algorithme de Commons Neighbors
1: function COMMON NEIGHBORS(adj)
2: Input matrice: adj
3: Output matrice de similarité:
commonNeighbors
4: entier N +- adj.length
5: for i +- 1 to N do
6: for j +- 1 to N do
7: if i = j V
adj(i,j) = 1 then
8: commonNeighbors(i, j) +- 0
9: else
10: fork+-1toNdo
11: commonNeighbors(i, j) +- CN(i, j) +
adj(i, k) x adj(k, j)
12: end for
13: end if
14: end for
15: end for
16: return commonNeighbors
17: end function
4.2.1.3 Construire la nouvelle matrice d'adjacence
Comme nous avons citédans les chapitres
précédents, les algorithmes de prédiction des liens
calculent des scores selon un paramètre topologique entre chaque deux
noeuds non connecté, un score élevéindique une
probabilitéélevéque cette paire soit connectédans
le futur, en se basant sur ce principe, nous avons construit une liste contient
toutes les valeurs de similaritétrouvéaprès
l'exécution d'un tel algorithme, cette liste est ordonnée de
manière décroissante, ensuite la spécification
Chapitre 4. Implémentation et Expérimentations
47
des nouveaux liens prédit dépend seulement de
l'utilisateur, donc il a le choix sur les K premiers liens dans la
liste qui ont les valeurs de similaritéles plus élevé,
à la fin il nous reste qu'àrécupérer les indices
des ces valeurs choisi ( c'est-à-dire le pair (i, j) ) en
mettant un 1 dans la nouvelle matrice d'adjacence et ainsi de suite, nous
notons aussi que nous avons gardétous les liens qu'ils existent dans la
matrice d'adjacence en leurs mettant dans la nouvelle matrice d'adjacence[3]
:
Algorithm 3 Construction de la nouvelle matrice
d'adjacence
1: Input matrice : ancien,
similarite
2: entier K, N +-
ancien.length
3: Output matrice : nouvelle
· Stocker toutes les valeurs (6= 0) de
similarités calculés dans une liste.
· Trier la liste en ordre décroissant selon les
valeurs de similarités.
4: for i +- 1 to
N do
5: for j +- 1 to
N do
6: if ancien(i,j) = 1
then
7: nouvelle(i,j) +- 1
8: else
9:
fork+-1toKdo
10: if i = indice
i de kiéme
élément dans la liste ?
j = indice j de
kiéme élément
dans la liste then
11: nouvelle(i,j) +- 1,
nouvelle(j,i) +- 1
12: end if
13: end for
14: end if
15: end for
16: end for
4.2.1.4 Calculer les mesures de performance
Cette étape consiste à voir les
différences entre la matrice d'adjacence calculés en lui
comparant avec une nouvelle matrice d'adjacence qui représente une
capture de ce même réseau social, pour cela nous avons
utiliséles mesures que nous avons définit dans le chapitre 3 : Le
rappel, la précision et la F-mesure, pour le rappel nous avons
calculéla quantitédes liens prédit correctement sur le
nombre de tous les nouveaux liens qui sont apparut dans la nouvelle capture, la
précision indique seulement le nombre des liens prédit
correctement sur les K liens spécifiés par l'utilisateur,
finalement la F-mesure est une moyenne entre la précision et le
rappel[4] :
Chapitre 4. Implémentation et Expérimentations
48
Algorithm 4 Précision, Rappel et F-mesure
1: function
PR'EcIsIoN(avant,apres,snapshot)
2: Output : double precision
3: entier tp +- 0
4: entier fp +- 0
5: entier N +- avant.length
6: for i +- 1 to N do
7: for j +- i + 1 to N do
8: if avant(i, j) = 0 ? apres(i,
j) = 1 ? snapshot(i, j) = 1 then
9: tp +- tp + 1
10: end if
11: if avant(i, j) = 0 ? apres(i,
j) = 1 ? snapshot(i, j) = 0 then
12: fp+-fp+1
13: end if
14: end for
15: end for
16: return precision +- tp
tp+fp
17: end function
18: function
RAPPEL(avant,apres,snapshot)
19: Output : double rappel
20: entier tp +- 0
21: entier fn +- 0
22: entier N +- avant.length
23: for i +- 1 to N do
24: for j +- i + 1 to N do
25: if avant(i, j) = 0 ? apres(i,
j) = 1 ? snapshot(i, j) = 1 then
26: tp +- tp + 1
27: end if
28: if avant(i, j) = 0 ? apres(i,
j) = 0 ? snapshot(i, j) = 1 then
29: fn+-fn+1
30: end if
31: end for
32: end for
33: return rappel+- tp
tp+fn
34: end function
35: function F-MEsuRE(Precision, Rappel)
36: Output : double fmesure
37: fmesure +-
2×PR'EcIsIoN(avant,apres,snapshot)×RAPPEL(avant,apres,snapshot)
PR'EcIsIoN(avant,apres,snapshot)+RAPPEL(avant,apres,snapshot)
38: return fmesure
39: end function
Chapitre 4. Implémentation et Expérimentations
49
4.2.2 Représentation de l'application
La figure 4.3 représente une capture
d'écran de l'application, l'outil que nous avons
développépour évaluer et comparer les deux fonctions de
prédiction des liens.
· Menu de l'application : pour quitter
ou voir quelques informations sur l'ap-plication.
· Paramétrage :
Représente les différents paramètres nécessaires
pour l'exécution des deux fonctions, on distingue un menu
déroulant pour préciser le réseau so-cial,(nous avons
expérimenter seulement un réseau social), Il existe aussi deux
zones de texte pour spécifier le nombre des liens choisi
»K» pour les deux algorithmes de prédiction.
· Résultats et mesures de performances
: Un simple tableau qui affiche l'ordre des liens qui ont
étéprédit par les deux algorithmes en fonction de K,
il existe aussi un autre espace oùles différents mesures de
performances, un tableau affiche le rappel, la précision ainsi que la
F-mesure pour les deux fonctions.
· Temps d'exécution : dans cet
espace, le temps d'exécution est affichépour comparer les deux
fonctions en point de vue de complexité.

FIGURE 4.3 - L'interface globale de l'application
Chapitre 4. Implémentation et Expérimentations
50
4.3 Expérimentations et résultats
Pour assurer une comparaison efficace entre les deux
fonctions, nous avons les testés sur un réseau de collaboration
scientifique au laboratoire de mathématiques et d'informatique de notre
université, pour cela nous avons essayer de construire deux captures de
ce réseau, l'une à 2011 et la deuxième à
2015, ensuite nous allons essayer de prédire l'apparition des
nouveaux liens pendant la période [2011,2015]. Pour effectuer
la prédiction par les deux fonctions que nous avons
présenté, Nous avons envisagéune opération de
pré-traitement, cette dernière consiste à effectuer sur
l'ensemble des noeuds et des liens les opérations suivantes :
1. Nous allons assurer de prendre les mêmes noeuds
(représentent des chercheurs) pour les deux captures (2011 et
2015).
2. Nous avons assurer aussi de garder les liens
(représentent des collaborations entre les chercheurs) en 2011
même s'ils sont disparu dans le réseau de collaboration en
2015.
les figures 4.4 et 4.5 représentent
les deux captures que nous avons construit en 2011 et en 2015
respectivement :

FIGURE 4.4 - Capture du réseau de collaboration
construite en 2011

Chapitre 4. Implémentation et Expérimentations
51
FIGURE 4.5 - Capture du réseau de collaboration
construite en 2015
Nous avons utilisél'outil NodeXL pour visualiser les
résultats de chacune de ces deux fonctions pour les 70 premiers liens
que nous avons choisi dans les figures 4.6 et 4.7, Nous notons que avons
visualiser que les liens prédit correctement puisque les deux fonctions
ajoutent 96 liens. Nous pouvons remarquer que l'algorithme Adamic/Adar a
prédit correctement 1 lien plus par rapport à l'algorithme Common
Neighbors.

Chapitre 4. Implémentation et Expérimentations
52
FIGURE 4.6 - Réseau social obtenu après
l'exécution de la fonction: Adamic/A-
dar

Chapitre 4. Implémentation et Expérimentations
53
FIGURE 4.7 - Réseau social obtenu après
l'exécution de la fonction: Commons
neighbors
Le tableau 4.1 résume les différentes
mesures que nous avons effectuées pour juger les performances des deux
fonctions. Nous avons fait varier K (nombre des liens) de 10
jusqu'à90.
Chapitre 4. Implémentation et Expérimentations
54
|
Adamic/Adar
|
Commons Neighbors
|
|
K
|
Temps
|
Rappel
|
Précision
|
F-mesure
|
Temps
|
Rappel
|
Précision
|
F-mesure
|
|
10
|
1208526
|
0.0%
|
0.0%
|
0.0%
|
631793
|
0.0%
|
0.0%
|
0.0%
|
|
20
|
1151133
|
0.0%
|
0.0%
|
0.0%
|
627128
|
0.0%
|
0.0%
|
0.0%
|
|
30
|
1069943
|
0.0%
|
0.0%
|
0.0%
|
634593
|
0.0%
|
0.0%
|
0.0%
|
|
40
|
1148800
|
40.0%
|
5.0%
|
8.9%
|
628527
|
20.0%
|
2.5%
|
4.4%
|
|
50
|
1240723
|
40.0%
|
4.0%
|
7.3%
|
632727
|
20.0%
|
2.0%
|
3.6%
|
|
60
|
1150200
|
60.0%
|
5.0%
|
9.2%
|
629460
|
40.0%
|
2.9%
|
6.2%
|
|
70
|
1083008
|
80.0%
|
5.7%
|
10.7%
|
629461
|
40.0%
|
2.9%
|
5.3%
|
|
80
|
1151601
|
80.0%
|
5.1%
|
9.4%
|
649992
|
60%
|
3.8%
|
7.6%
|
|
90
|
1154867
|
80.0%
|
4.8%
|
8.9%
|
628527
|
60%
|
3.5%
|
6.7%
|
TABLE 4.1 - Mesures de performances
Nous avons également
représentégraphiquement nos résultats par rapport à
notre réseau social, la figure 4.8 montre le rapport, la
précision, le temps d'exécution ainsi que le F-mesure par rapport
à K .

FIGURE 4.8 - Représentation graphique du rappel,
précision, F-mesure et temps
d'exécution
Chapitre 4. Implémentation et Expérimentations
55
4.3.1 Interprétation des résultats
Dans le but de comparer et juger les performances de chacune
des deux fonctions en détectant leurs différents avantages et
inconvénients à travers les mesures que nous avons
effectué, voire, le temps d'exécution, le rappel, la
précision ainsi que le rapport entre ces deux derniers qui est la
F-mesure.
4.3.1.1 Point de vue temps d'exécution
Nous pouvons voir à partir le graphes de temps
d'exécution dans la figure 4.8 que la mesure de
similaritéAdamic/Adar prend un temps plus considérable par
rapport à la mesure de similaritéCommons Neighbors. Cela
s'explique par le fait que Adamic/Adar fait beaucoup d'opérations
supplémentaires, voire l'extraction des voisins communs, le calcul de
degrés des ces voisins communs. ce qui consomme plus de temps. Par
contre la fonction Commons Neighbors calcule simplement le nombre de voisins
communs entre chaque pair non connecté.
4.3.1.2 Point de vue Rappel
Nous rappelons qu'une forte valeur de rappel se traduit par un
taux de résultat pertinent élevéet vice versa. Nous
apercevons clairement les performances de la fonction Adamic/Adar à
travers la courbe du rappel qui s'est montrétrès
considérable par rapport à la fonction Commons Neighbors surtout
quand le nombre des liens choisi k est important. ce qui est un
remarquable avantage. Le rappel est restéfixéà zéro
pour tout k ? [10, 30] et pour les deux fonctions, cela
s'interprète par le fait qu'il n'existe aucun lien prédit
correctement, ce qu'il présente un inconvénient pour ces deux
mesures.
4.3.1.3 Point de vue Précision
Nous rappelons également qu'une forte valeur de
précision s'interprète par une bonne qualitéde
prédiction. Dans notre cas, nous avons marquéun écart de
presque 2% privilégiant la fonction Adamic/Adar par rapport à la
fonction Commons Neibhbors, cela s'exprimer que la fonction Adamic/Adar
prédit correctement 1 lien plus par rapport à la fonction Commons
Neighbors (Voir les figures : 4.6 et
4.7). Pour un k ? [10, 30] la précision
est la même que le rapport est
restéfixéàzéro pour les deux mesure ce
qui représente aussi un inconvénient.
Chapitre 4. Implémentation et Expérimentations
56
4.3.1.4 Point de vue F-mesure
Nous rappelons que la F-Mesure est la moyenne entre le rappel
et la précision. Nous remarquons que les deux mesures ont
marquéun très mauvais F-mesure qui est
restéfixéà zéro pendant l'intervalle k ? [10, 30] ,
cela est dûaux valeurs du rappel, et précision cependant nous
pouvons constater. clairement que la fonction Adamic/Adar a donnéde
très bon résultats par rapport à la fonction Commons
Neighbors,
Enfin nous pouvons conclure que la performance de la fonction
Adamic/Adar est supérieure à celle de la fonction Commons
Neighbors, cette dernière prends plus de temps à
l'exécution mais elle reste très efficace surtout quand le nombre
de liens choisi est grand car elle donne la prioritéaux voisins qui sont
rarement partagédans un réseau social, ce qui représente
un grand manque dans la fonction Commons Neighbors.
57
Conclusion
UiTE à l'importance de la prédiction des liens
opérant sur les réseaux sociaux. SActuellement, de nombreux
auteurs se sont intéressés à ce nouveau domaine
.Récemment, beaucoup des travaux de recherche proposant d'avantage de
techniques et de fonctions de prédiction des liens dans les
réseaux sociaux sont entrain de se faire.
Notre but à travers ce mémoire est d'effectuer
une étude comparative entre deux algorithmes de prédiction des
liens. Pour cela, nous avons choisi les fonctions Adamic/Adar et Voisin
Communs, nous avons implémentéles deux fonctions en langage
JAVA.
Nous avons appliquéles deux fonctions sur un
réseau de collaboration scientifique
au sein de laboratoire de Mathématiques et
d'Informatique de notre universitéAmar Telidgi, ainsi, nous
avons visualiséle réseau de collaboration avec l'outil
NodeXL.
Les différentes mesures que nous avons
effectuées sur ces fonctions nous ont permis de conclure que la fonction
Adamic/Adar est plus performante que Voisin commun, malgréle fait
qu'elle nécessite un peu de temps d'exécution
supplémentaire.
Ce travail nous a permis également de savoir ce qu'est
les domaines d'analyse des réseaux sociaux et surtout la
prédiction des liens dans les réseaux sociaux.
L'implémentation que nous avons effectuée en langage JAVA nous a
permis de nous familiariséd'avantage avec la programmation
orientéobjet.
Enfin, Ce travail est une expérience très
enrichissante qui nous a permis d'acquérir une
quantitéappréciable de connaissances très utiles...
58
Bibliographie
[Ada03] Adar Adamic. Friend and neighbors on the web.
Social Networks, 2003.
[And12] Kleinberg J et al Anderson, Huttenlocher D. Effects of
user similarity in social media. In Proceedings of the 5th ACM
International Conference on Web Search and Data Mining (WSDM'12), 2012.
[Ba02] Neda Z Barabasi, Jeong H and al. Evolution of the
social network of scientic collaborations. Physica A, pages 590-616,
2002.
[BP11] Wu F S Bhattacharyya P, Garg A. Analysis of user
keyword similarity in online social networks. Social Network Analysis and
Mining, 2011.
[Cas14] Jean-Laurent Cassely. Sur twitter et facebook, la
théorie des «six degrés de séparation» ne
fonctionne pas. 2014.
[dLP13] Xavier de La Porte. Google+ : bienvenue dans la matrice.
2013.
[Fou07] Renders J M et al Fouss, Pirotte A. Random-walk
computation of similarities between nodes of a graph with application to
collaborative recommendation. IEEE Transactions on Knowledge and Data
Engineering, 2007.
[Fre79] L. Freeman. Centrality in social networks : Conceptual
clarification.social network. 1979.
[GE09] Michel B Patrick G Guillaume E, Fabien G. Analyse des
réseaux sociaux et web sémantique : un état de l'art.
ISICIL, 2009.
[Har12] Jean Harrold. Les types de réseaux sociaux les
réseaux sociaux. 2012.
[JG02] Widom J Jeh G. Simrank : a measure of
structural-context similarity. In : Proceedings of the Eighth ACM SIGKDD
International Conference on Knowledge Discovery and Data Mining (KDD'02),
2002.
[Kan10] R Kanawati. Prédiction de liens dans les
réseaux sociaux. UniversitéParis 13, 2010.
[Kat53] Katz. A new status index derived from sociometric
analysis. Psychome-trika, 1953.
BIBLIOGRAPHIE 59
[LC12] Ryan Lichtenwalter and Nitesh V. Chawla. Link
prediction : fair and effective evaluation. Department of Computer Science
The University of Notre Dame, 2012.
[Liu13] Haddadi H et al Liu, Hu Z. Hidden link prediction
based on node centrality and weak ties. EPL (Europhysics Letters),
2013.
[Lu09] Zhou T Lu, Jin H. Similarity index based on local paths
for link prediction of complex networks. Physical Review E, 2009.
[MH13] Zaki M Hasan, S Saeed. Link prediction using supervised
learning. Machine Learning and Applications (ICMLA), 2013 12th
International Conference, 2013.
[Mil67] S. Milgram. The small world problem. Psychology
Today, 1967. [Mor33] Jacob Moreno. Emotions mapped by new geography.
1933.
[New01] Newman. Clustering and preferential attachment in
growing networks. Physical Review Letters E, 2001.
[Pat10] Elodie Patenotte. Les media sociaux. 2010.
[Pat15] Elodie Patenotte. Les réseaux sociaux, cultures
numériques remasterisées. 2015.
[S08] David S. Proof! just six degrees of separation between
us. Microsoft
researchers, 2008.
[Sco00] Scott. Social network analysis,a handbook. second
edition. 2000.
[VJ13] Lopes A Valverde J. Exploiting behaviors of communities
of twitter users for link prediction. Social Network Analysis and Mining,,
2013.
[Win14] Andrew Winslow. Link prediction algorithms. 2014.
[Wp15] Z Xiaoyu W peng, W yurong. Link prediction in social
networks : the state-of-the-art. Science China, 2015.
| 


