Recherche bibliographique portant sur la " Contribution à la réalisation du problème d'emploi de temps par une approche évolutionnaire "

CHAPITRE II. METHODES D'OPTIMISATION

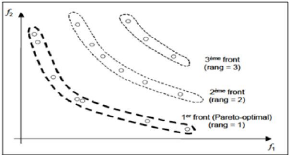
Figure II.3 - Rand de Parito .

I(A, B) = inf(?R){Vz² E B, z¹ E A : z¹ < z²}

Où z représente un vecteur objectif et < la relation de l'epsilon-dominance multiplicative.

De la même façon un indicateur un-aire d'un ensemble A, I(A) peut être défini comme suit : I(A) = I(A, R).

Où R représente un ensemble de solutions de Référence.

Par analogie, l'indicateur epsilon additif peut être obtenu en remplaçant la relation I par _I+ .

II.4.3 Procédures de comparaison et de classement

Plusieurs procédures de comparaison et de classement des individus ont été proposées. Elles sont basées soit sur la dominance comme le rang de Pareto et le Strength, soit sur la densité ou sur les indicateurs de performance comme le critère d'encombrement, le critère du kime voisin et le critère de contribution à l'hyper-volume.

- Rand de Pareto.Consiste à déterminer à chaque étape i les d'individus non dominés d'un ensemble A (sauf les individus qui ont déjà un rang) et de les attribuer le rang i qui doit être incrémenté à chaque étape. (voir figure II.3)

- Le Strength.Chaque individu domine un nombre fini d'individu, ce nombre représente le Strength qui doit être attribué à celui-ci et qui est la base de classement.

- Le critère d'encombrement. La distance de crowding d'une solution i se calcule en fonction du périmètre formé par les solutions du même front les plus proches de i sur chaque objectif. Le principe est de tri les solutions selon chaque objectif dans un ordre ascendant. Ensuite, pour chaque objectif, les individus possédant les valeurs limites (la plus petite et la plus grande valeur de fonction objective) se voient associés à une distance infinie. Pour les autres solutions intermédiaires, la distance de crowding égale à la différence normalisée des valeurs de fonctions objectives de deux solutions adjacentes. Ce calcul est réalisé pour chaque fonction objective. Le critère d'encombrement d'une solution est calculée en sommant les distances de crowding corresponds à chaque objectif. [15](voire figure II.4).

20