CHAPITRE 4 : METHODOLOGIE
Notre étude sera basée sur une démarche
hypothético-déductive. Il est question pour nous de partir d'un
ensemble de travaux existants dans le domaine de notre recherche afin
d'élaborer des hypothèses qui seront testées par la suite
au travers des multiples tests statistiques correspondant. A partir des
données provenant des sources secondaires, on estimera à l'aide
de la méthode économétrique (régression
linéaire) les paramètres significatifs de notre modèle.
Avant de spécifier le modèle et de parler des éventuels
tests statistiques à appliquer, nous allons d'abord décrire la
source de nos données.
4.1. PRESENTATION DES VARIABLES ET METHODE DE COLLECTE
DES DONNEES
4.1.1. Présentation des variables
- La consommation des particuliers : il s'agit de la
quantité annuelle d'eau utilisée par les ménages. Le choix
de cette variable est évident dans la mesure où l'augmentation de
la consommation d'eau dans un ménage est supposée entrainer une
augmentation de l'offre dans la même proportion.
- Les investissements en eau : il s'agit de la
dépense annuelle faite par la société distributrice d'eau
pour la production annuelle de l'eau offerte dans les secteurs ménagers,
industriels et administratifs
- La production totale annuelle d'eau : cette variable
constitue la variable déterminante (variable à expliquer) de
notre étude. Il s'agit d'une approximation de la production annuelle
d'eau par la société publique en charge de sa gestion. Il est
question pour nous d'analyser les sources de variations de l'offre d'eau par la
société distributrice d'eau au Cameroun.
- La taille de la population urbaine : cette variable a
été introduite pour étudier l'effet de l'évolution
démographique de la population urbaine sur l'offre d'eau. Nous avons en
effet constaté que la taille de la population urbaine oblige la
société distributrice à accroître sa production
totale d'eau.
- Le prix de l'eau : après un parcours de la
littérature sur l'eau au Cameroun, on a supprimé cette variable
de l'analyse à cause de sa forte corrélation avec certaines
variables explicatives telles que la consommation d'eau par les particuliers,
les industries et les administrations.
- La consommation des industries : il s'agit de la
quantité annuelle d'eau utilisée par les industries. Le choix de
cette variable est évident dans la mesure où l'augmentation de la
consommation d'eau dans une industrie est supposée impacter l'offre
d'eau.
- La consommation de l'administration : il s'agit de la
quantité annuelle d'eau utilisée par l'administration. Le choix
de cette variable est évident dans la mesure où l'augmentation de
la consommation d'eau dans l'administration est supposée entrainer une
augmentation de l'offre dans la même proportion.
4.1.2. Méthode de collecte des
données
Nous nous sommes proposé dans le cadre de ce travail
d'étudier les facteurs qui déterminent l'offre d'eau potable et
ceci principalement par la société chargée de sa gestion
au Cameroun. A cet effet, nous avons retenu cinq variables qui peuvent avoir
une influence significative sur l'offre d'eau à savoir : la
consommation d'eau des particuliers, la consommation d'eau des industries, la
consommation d'eau de l'administration, l'investissement en eau et
l'évolution de la population urbaine. En dehors de ce dernier où
la base de données de la banque mondiale nous a permis d'avoir son
évolution durant les 50 dernières années, pour les autres
variables nous avons obtenu des données sur une période beaucoup
plus restreinte. En effet, un parcours sur les bases de données du
MINEE, de la Banque Mondiale, de l'INS, de la CDE et de la littérature
dans ce domaine au Cameroun ne nous a permis que d'avoir des valeurs sur 10 ans
sur les autres variables y compris sur la variable dépendante. Il
était dès lors impossible pour nous de réaliser un
modèle de régression avec ces données surtout qu'elles
n'étaient pas désagrégés ni en mois ni en
semestres. Nous nous sommes ainsi proposé de calculer pour les variables
dont nous avons les données sur 10 ans le taux de croissance moyen
annuel afin de reconstituer les données pour les autres années
suivant la formule ci-après :
Yn = (1 + t)nY0 t =
  1 1
Où : Yn représente la valeur de
la variable à l'année n
Y0 représente la valeur de la
variable à l'année 0
t est le taux de croissance moyenne pour la variable
choisie.
n est le nombre d'année qui sépare
l'année de la dernière valeur de la variable de la
première valeur.
Ainsi pour les ces variables, on a obtenu les valeurs
suivantes :
- Pour la production annuelle d'eau
t = 2.12%
- Consommation particuliers
t = 1.22%
- Consommation industries
t = -9.08%
- Consommation administration
t = 4.54%
- Investissements
t = 1.5%
Il existe en réalité une forte
corrélation entre ces variables indépendantes et la variable
dépendante.
4.2. PRESENTATION DU MODELE THEORIQUE ET TESTS A
EFFECTUER
4.2.1. Présentation du modèle
théorique
A partir d'une revue générale de la
littérature sur la gestion de l'eau au Cameroun, nous allons extraire
des données nécessaires pour l'estimation de notre modèle.
Nos données proviendront par conséquent principalement des
sources secondaires à savoir des documents obtenus de la SNEC et de
quelques ouvrages sur l'eau au Cameroun mais elles proviendront
également de quelques calculs effectués par nous. Nous nous
proposons d'étudier les facteurs déterminants l'offre en eau
potable dans le secteur des industries, des ménages et de
l'administration du Cameroun. L'analyse économétrique offre des
possibilités quant à l'analyse des variables quantitatives et
qualitatives ou dichotomiques. Le modèle choisi est celui de la
régression linéaire classique. Mais compte tenu du fait que la
variable à expliquer à savoir l'offre moyenne d'eau est
quantitative et est expliquée par des variables quantitatives, on va se
borner à une régression multiple. Mais avant d'effectuer cette
régression, il est important de vérifier si les variables sont
stationnaires. Si elles ne le sont pas, on pourra pallier à ce
problème grâce à un modèle de cointégration
ou un modèle VAR. Il nous conduira à analyser les sources de
variation de l'offre en eau dans les industries et les ménages du
Cameroun.
Pour ce faire, nous avons retenu cinq variables quantitatives
comme ayant a priori une influence sur l'évolution de l'offre d'eau dans
les secteurs retenus dans notre analyse.
Ces variables sont les suivantes :
Ø Les investissements en eau : variable quantitative
Ø La consommation d'eau dans le secteur industriel:
variable quantitative
Ø La consommation d'eau par les particuliers :
variable quantitative
Ø La consommation d'eau par l'administration :
variable quantitative
Ø L'évolution démographique de la
population urbaine : variable quantitative
Notre méthode d'analyse consistera à faire une
régression sur les variables correspondant aux sources ci-dessus
identifiées.
On a par conséquent le modèle d'analyse de
régression multiple suivant :
Y = u + a1X1 +
a2X2 + a3X3 +
a4X4 + a5X5 + 
Où :
Y représente la production totale d'eau.
u est la constance.
X1 représente les investissements.
X2 représente la consommation des
particuliers.
X3 représente la consommation des
industries.
X4 représente la consommation de
l'administration.
X5 représente l'évolution de la
population urbaine.
å est le terme d'erreur.
a1, a2, a3, a4 et
a5 sont des coefficients.
Le tableau suivant définit les modalités des
variables de la régression.
TABLEAU 17 : présentation
des variables.
|
Nom de la variable
|
Identification
|
Nature de la variable
|
Unité
|
Signes attendus
|
|
Production totale d'eau
|
Y
|
Dépendante
|
m3
|
|
|
Investissement
|
X1
|
Indépendante
|
Fcfa
|
+
|
|
Particuliers
|
X2
|
Indépendante
|
m3
|
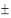 ? ?
|
|
Industries
|
X3
|
Indépendante
|
m3
|
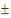 ? ?
|
|
Administration
|
X4
|
Indépendante
|
m3
|
 ? ?
|
|
Population urbaine
|
X5
|
Indépendante
|
|
+
|
Source : l'auteur.
4.2.2. Les différents tests à
effectuer
Il s'agit des moyens par lesquels les données sont
recueillies et ont été mises sous une forme
synthétisée et facile d'analyse. Les travaux liés aux
traitements économétriques ont été effectués
grâce au logiciel économétrique e-views 5.0.
Des résultats de nombreux travaux empiriques
révèlent que les séries temporelles sont la plupart du
temps non stationnaires, c'est-à-dire qu'elles admettent une moyenne et
souvent, une variance qui croît sans limite avec le temps. Or, les
techniques statistiques classiques ne s'appliquent qu'à des
séries stationnaires. La présence de racine unitaire dans les
séries temporelles, loin de constituer une pathologie, est devenue une
caractéristique commune des séries économiques.
La construction d'un modèle avec des séries
chronologiques impose de tester
une éventuelle cointégration
entre les variables. Le concept de cointégration, auquel nous aurons
peut-être recours dans nos résultats, fournit donc un cadre de
référence théorique pour étudier les situations
d'équilibre et de déséquilibre, qui pourraient
prévaloir respectivement, à long terme et à court terme.
Si les variables ne sont pas stationnaires, la cointégration permettra
de rationaliser la modélisation à court et long termes,
après avoir vérifié le même ordre
d'intégration entre les différentes variables d'une
équation. Et ainsi de suite, si les variables sont
cointégrées, elles admettent une spécification dynamique
de type correction d'erreur. Le modèle ECM (Error Correction Mecanism)
permet donc de réconcilier dans un même cadre, les comportements
de court et long termes, qui sont calés sur des horizons temporels
à priori antinomiques.
Selon Engle et Granger (1987), une combinaison
linéaire de deux ou plusieurs variables peut être stationnaire
(I(0)). Si une telle combinaison stationnaire existe, alors les variables
non-stationnaires (I(1)) sont dites cointégrées. Ainsi la
combinaison linéaire stationnaire est appelée équation de
cointégration et peut être interprétée comme une
relation de long-terme entre les variables. Or nos tests de racine unitaire
nous donnent l'évidence de la stationnarité de nos deux variables
dépendantes (voir annexe) que sont le taux d'inflation et le taux de
croissance, ce qui nous permet de savoir que nous avons des combinaisons
linéaires stationnaires. Dans ce cas, un test de cointégration
serait superflu. C'est pourquoi nous procéderons à une estimation
par la méthode des moindres carrés ordinaires, qui pourra
éventuellement être améliorée par la méthode
des doubles moindres carrés,ce qui est faisable parce que notre
modèle comporte deux équation dont les variables
expliquées reviennent de part et d'autres des deux équations
(c'est-à-dire un modèle à équations
simultanées).
Les tests appliqués sont les suivants :
* Le test de racine unitaire pour déterminer le
degré d'intégration des variables du modèle. Nous
utiliserons pour ce fait, le test de stationnarité de Dickey Fuller
Augmenté (ADF). Ce dernier consiste à faire le test
d'hypothèse :
H0 : présence de racine unitaire (série non
stationnaire)
H1 : absence de racine unitaire (série stationnaire)
Si ADFcalculé > ADFThéorique
alors la variable est stationnaire.
Pour vérifier qu' n'y a pas de bias pour ce test, on
lui associera le test de Phillipe-Perron.
Une fois cette régression effectuée, il faudra
tester si tous les coefficients diffèrent de manière
significative pour tous les groupes et le test correspondant s'effectue
à travers la régression suivante :
Y = u + a1X1 +
a2X2 + a3X3 +
a4X4 + a5X5 + 
Les tests de significativité à effectuer seront
les tests de Fisher.
a. Test d'égalité des coefficients
L'hypothèse nulle notée H0
H0 : a1= a2=
a3= a4 = a5
Contre l'hypothèse alternative notée Ha
Ha: a1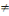 a2 a2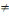 a3 a3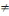 a4 a4  a5 a5
A travers ce test, on va vérifier s'il existe ou par
une différence significative entre les contributions des facteurs. En
d'autres termes, ce test va permettre de savoir si la consommation d'eau par
les ménages, la consommation d'eau par les industries, la consommation
d'eau par l'administration, les investissements et l'évolution
démographique urbaine expliquent dans les mêmes proportions ou pas
l'offre annuelle en eau.
b. Test sur la contribution des investissements
L'hypothèse nulle est H0 :
a1=0
Contre l'hypothèse alternative Ha: a1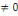
Ce test permet de capter l'effet investissement
c. Test sur la contribution de la consommation des
ménages ou particuliers
L'hypothèse nulle est H0 :
a2=0
Contre l'hypothèse alternative Ha: a2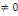
Ce test permet de capter l'effet de la consommation de l'eau
par les ménages.
d. Test sur la contribution de la consommation des
industries
L'hypothèse nulle est H0 :
a3=0
Contre l'hypothèse alternative Ha: a3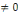
Ce test permet de capter l'effet de la consommation des
industries
e. Test sur la contribution de la consommation de
l'administration
L'hypothèse nulle est H0 :
a4=0
Contre l'hypothèse alternative Ha: a4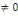
Ce test permet de capter l'effet de la consommation de
l'administration
f. Test sur la contribution de la population urbaine
L'hypothèse nulle est H0 :
a5=0
Contre l'hypothèse alternative Ha: a5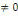
Ce test permet de capter l'effet de la population urbaine
Pour réaliser ces différents tests, on
procède de la manière suivante :
Ø On estime le modèle par la méthode des
moindres carrés ordinaires.
Ø On récupère la somme des carrés
des résidus sous l'hypothèse nulle (SCR0), puis sous
l'hypothèse alternative (SCRa)
Ø On calcule le degré de liberté sous
l'hypothèse nulle (DDL0), puis sous l'hypothèse
alternative (DDLa)
Où DDLi = nombre total d'observation - nombres de
paramètres à estimer (avec i= 0, a)
Ø On détermine ensuite la statistique de Fisher
calculée notée (Fcal)
Fcal = 
Où : CMR représente le carré moyen
régression
CME représente le carré moyen erreur
Ø Décision
On comparera le Fisher calculé (Fcal) au Fisher
théorique (Fthéo).
A un seuil  donné, on a : donné, on a :
Fthéo = FDDLo-DDLa (1-  ). On rejettera Ho si Fcal > Fthéo au seuil donné. ). On rejettera Ho si Fcal > Fthéo au seuil donné.
En se servant du logiciel Eviews on a pu estimer cette
équation et effectuer ces différents tests ce qui nous a permis
d'aboutir aux résultats qui sont présentés au chapitre
suivant.
| 


