Stochastic differential equations involving the two- parameter fractional brownian motion

MINISTERE DE L'ENSEIGNEMENT SUPERIEUR ET DE LA RECHERCHE SCIENTIFIQUE

UNIVERSITE Dr. MOULAY TAHAR DE SAÏDA
FACULTE DES SCIENCES & TECHNOLOGIE
DEPARTEMENT DE MATHEMATIQUES & INFORMATIQUE

Mémoire de MASTER

Système d'études: LMD-Master 2 Recherche Spécialité: Probabilités & Applications

Intitulé

Stochastic Differential Equations Involving

The Two-parameter Fractional Brownian Motion

Présenté par

Mr. Iqbal HAMADA Soutenu publiquement le: 18/06/2012

Devent le jury composé de:

Président	A. Kandouci	Maître de conférences	(Univ.Saïda)
Rapporteur	T. Guendouzi	Maître de conférences	(Univ.Saïda)
Examinateurs	O. Benzatout	Maître assistant classe A	(Univ.Saïda)
	N. Ait Ouali	Maître assistant classe B	(Univ.Saïda)

Promotion 2011/2012

Si tu veux courir, cours un kilomètre, si tu veux
changer ta vie, cours un marathon
Emil Zatopek1.

REMERCIEMENT

Il m'est agréable, avant de commencer la partie purement mathématique de ce mémoire, d'adresser quelques remerciements. Je demande par avance à ceux que je vais oublier de bien vouloir me le pardonner.

Mon premier ira à Guendouzi Toufik , à qui j'ai demandé il y a deux ans de m'encadrer. Il a accepté de bon coeur et déjà pour ça je l'en remercie. Il m'a proposé un sujet riche et fertile et est à l'origine d'un certain nombre d'idées contenues dans ce mémoire. De plus, c'est entre autres lui, grâce à ses qualités pédagogiques et à la clarté de ses différents cours, qui m'a donné l'envie de me lancer dans les probabilités et d'en faire mon métier.

Kandouci Abdeldjebbar a accepté la lourde tâche d'être président de ce mémoire.

O. Benzatout, N. Ait Ouali je suis conscient de l'honneur qu'elles me font en me permettant d'associer leurs noms à ma modeste contribution scientifique .

Mon sujet de mémoire m'a naturellement amené à faire la connaissance de plusieurs personne.

En général, au début de son mémoire, on est un peu perdu. Pour ma part, je crois avoir eu beaucoup de chance en travaillant avec Jérome. Car trouver une personne qui, malgré son emploi du temps chargé, se propose de vous montrer l'attirail du chercheur et comment on s'en sert, tout le monde n'a pas ce privilège. Bien entendu, son rôle ne s'est pas arrêté là. Nous avons beaucoup travaillé ensemble et c'est d'ailleurs avec lui que j'ai construit une bonne partie du contenu de ce mémoire.

Enfin, je n'ai pas abordé le cas de mes proches. Quand on dit qu'on est en train de préparer un mémoire en mathématiques, cela procure en général chez son interlocuteur un sentiment ambigu. Tout d'abord, je pense ne pas manquer de modestie en disant que souvent ça impressionne. Et puis, immanquablement on a droit à la question "Mais à quoi ça sert la recherche en maths?". Il y a alors une stratégies est celle consiste à répondre "à rien pardi!" et à passer à autre chose.

Pourtant (enfin, je m'avance peut-être en écrivant ces lignes) ça n'a pas em-
pêché mes amis et mes proches de venir assister à ma soutenance. Ils n'auront
rien compris, j'en suis sûr, mais n'est-ce pas un bon moyen de tester les liens

4

du sang ou d'amitiés? Plus nommément, je voudrais déjà en premier lieu remercier Soufiane, qui m'a souvent remonté le moral lors de mes baisses de régime et de motivation récurrentes. On finit ensemble nos études cette année et je la felicite pour sa brillante réussite.

Ensuite, j'adresse un vif remerciement à ma famille.

A mon frère, qui doit être l'un des seuls lycéens à avoir "appris" ce qu'était le MBF avant de connaître l'intégrale classique de terminale.

Enfin, j'ai une pensée pour Emilie et Morais, qui ont toujours montré un grand intérêt pour ce que je faisais.

Ouaf!: ça, c'était pour Amine... il comprendra!

Contents

Introduction 7

1 The Elements of Fractional Brownian Motion 9

1.1 Fractional Brownian Motion 9

1.1.1 Self-similarity 9

1.1.2 Hölder Continuity 10

1.1.3 Path Differentiability 11
1.1.4 The Fractional Brownian Motion is not a Semimartin-

galeforH=61 ₂ 11
1.1.5 Fractional Integral and Fractional Derivative of Function 12

1.2 Two-parameter Fractional Brownian Motion 13

1.2.1 The Main Definition 13

1.2.2 Fractional Integrals and Fractional Derivatives of Two-

parameter Functions 14

1.2.3 Hölder Properties of Two-parameter fBm 16

1.2.4 Fractional Generalized Two-parameter Lebesgue-Stieltjes Integrals 17

2 Stochastic Integration with Respect to Two-parameter Fractional Brownian Motion 19

2.1 Pathwise Integration in Two-parameter Besov Spaces 19

3 Existence and Uniqueness of the Solutions of SDE with Two-Parameter Fractional Brownian Motion 29

Bibliography 35

Introduction

In problems of stochastic analysis and in the investigation of certain physical problems -in particular, in hydromechanics-, it is necessary to construct a field, i.e., two-parameter random functions with stationary increments. Fractional Brownian fields may serve as an example of such functions. To consider, stochastic differential equations with fractional Brownian fields, it is necessary to construct first a theory of integration with respect to those fields, witch is done in the present Master thesis.

The main objective of this thesis is to study the so-called Equations Differentials Stochastics Involving Two-parameter Fractional Brownian Motion. This thesis consist of three chapters, Element of Fractional Brownian Motion, Stochastic Integration with Respect to Two-parameter Fractional Brownian Motion, Existence and Uniqueness of the Solutions of SDE with Two-Parameter Fractional Brownian Motion. The first chapter is divide in two section, in the first we give the definition of Fractional Brownian Motion (case of one parameter), and some properties; in the second section we give the necessary notion of Two-parameter Fractional Brownian Motion and Hölder properties of Two-parameter Fractional Brownian Motion. In the second chapter we study Pathwise Integration in Two-parameter Besov Spaces of Two-parameter Fractional Brownian Motion. The Existence and Uniqueness of the Solutions of SDE with Two-Parameter Fractional Brownian Motion are given in last chapter.

Chapter 1

The Elements of Fractional

Brownian Motion

1.1 Fractional Brownian Motion

Definition 1.1.0.1. The (two-sided, normalized) fractional Brownian motion (fBm) with Hurst index H E (0, 1) is a Gaussian process B^H = {BH _t , t E R} on (Ù, F, P), having the properties:

1. BH 0 = 0,

2. EBH t = 0; t E R,

1 (|t|^2H + |s|^2H - |t - s|^2H) ; t, s E R,

3. EBH t BH s = 2

1.1.1 Self-similarity

Definition 1.1.1.1. We say that an R^d-valued random process X = (Xt)t=0 is self-similar or satisfies the property of self-similarity if for every a > 0 there exist b > 0 such that:

law (Xat, t = 0) = law (bXt, t = 0) (1.1)

Note that (1.1) means that the two process _Xat and bXt have the same finite-dimensional distribution functions, i.e., for every choice t1, ..., t_n E R,

P (Xat0 = x0, ..., Xat_n = x_n) = P(bXt₀ = x0, ..., bXt_n = x_n) For every x0, ..., x_n E R.

Definition 1.1.1. A stochastic process X = {Xt, t E R} is called b-selfsimilar if

{X_at,t E R} ^d ={a^bXt,t E R} in the sense of finite-dimensional distributions.

1.1.2 Hölder Continuity

We recall that according to the Kolmogorov criterion [13], a process X = (Xt)t?R admits a continuous modification if there exist constants á = 1, â > 0 and k > 0 such that

E [|X(t) - X(s)|^á] = k|t - s|^1+â

for all s,t E R.

Theorem 1.1.2.1. Let H E (0, 1). The fractional Brownian motion BH admits a version whose sample paths are almost surely Hölder continuous of order strictly less than H.

Proof. We recall that a function f : R -? R is Hölder continuous of order á, 0 < á = 1 and write f E C^á(R), if there exists M > 0 such that

|f(t) - f(s)| = M|t - s|^á,

For every s, t E R. For any á > 0 we have

E ~|BH t - BH _s |á] = E [|BH 1 |á] |t - s|^áH;

Hence, by the Kolmogorov criterion we get that the sample paths of B^H are almost everywhere Hölder continuous of order strictly less than H. Moreover, by [1] we have

lim t-+0+	sup	~~BH ~~ t	= CH
		t^Hs/log log t-1

with probability one, where CH is a suitable constant. Hence B^H can not have sample paths with Hölder continuity's order greater than H.

1.1.3 Path Differentiability

By[9] we also obtain that the process B^H is not mean square differentiable and it does not have differentiable sample paths.

Proposition 1.1.3.1. Let H E (0, 1). The fractional Brownian motion sample path B^H(.) is not differentiable. In fact, for every t0 E [0, 8)

~~~~

sup

lim

t--+t0

~~~~ = 8

BH t - BH t0

t - t0

With probability one.

1.1.4 The Fractional Brownian Motion is not a Semi-martingale for H =6 1 2

The fact that the fractional brownian motion is not a semimartingale for
H =61 ₂ has been proved by several authors. In order to verity B^H is not a
semimartingale for H =6¹ ₂, it is sufficient to compute the p-variation of B^H.

Definition 1.1.4.1. Let (X(t))tE[0,T ] be a stochastic process and consider a partition ð = {0 = t0 < t1 < ... < t_n = T}. Put

8_p(X,ð) := _Xn |X(ti) - X(ti_1)|^p

i=1

The p-variation of X over the interval [0, T] is defined as

Vp(X, [0, T]) := sup ð

8p(X, ð),

where ð is a finite partition of [0, T]. The index of p-variation of a process is defined as

I(X, [0, T]) := inf {p > 0; V_p(X, [0, T]) < 8}.

We claim that

I(B^H, [0, T ]) = 1H .

In fact, consider for p > 0,

Yn,p = npH_1

Xn i=1

~~'~~ ^p ~BH ( ^i n) - B^H . (i-1 n )

12

1.1.5 Fractional Integral and Fractional Derivative of Function

Since B^H has the self-similarity property, the sequenceY_n,p, m ? N has the same distribution as

^eYn,p = m-1

Xn i=1

~'Ip . ~BH i - BH i-1

And by the Ergodic theorem [3] the sequence _eYn,p converges almost surely and in L¹ to E [~~BH ~~p] as n tends to infinity. It follows that

1

Vn,p =

Xn i=1

~~'~I ^p ~BH ( ^i n) - BH (i_1 n )

converges in probability respectly to 0 if pH > 1 and to infinity if pH < 1 as

1

n tends to infinity. Thus we can conclure that I(B^H, [0, T]) = H . Since for

every semimartingale X, the index I(X, [0, T]) must belong to [0, 1]?{2}, the

1

fractional brownian motion B^H can not be a semimartingale unless H = ₂.

1.1.5 Fractional Integral and Fractional Derivative of Function

Let á > 0 (and in most cases below á < 1 though this is not obligatory). Define the Riemann-Liouville left- and right-sided fractional integrals on (a, b) of order á by

Z x

1

(I^á _a+f)(x) := f(t)(x - t)^á?1dt,

['(á) a

and

Z b

1

(I^á _b_f)(x) := f(t)(t - x)^á-1dt,

['(á) x

respectively.

We say that the function f ? D(Iá _{a+(b_))} (the symbol D(.) denotes the domain of the corresponding operator), if the respective integrals converge for almost all (a.a.) x ? (a, b) (with respect to (w.r.t.) Lebesgue measure).

The Riemann-Liouville left and Right sided fractional integrals on R are defined as

J x

1

(I^á ₊f)(x) := f(t)(x - t)^á-1dt,

['(á) -8

and

J 8

1

(I^á _-f)(x) := f(t)(t - x)^á?1dt,

['(á) x

respectively.

The Riemann-Liouville left and Right sided fractional derivatives of f of order á on IR are defined by

(I^-á + f)(x) = (D^á+f)(x) :=			Z x 1 d f(t)(x - t)^-ádt, (1 - á) dx -8
and	(I^-á -f)(x) = (D^á-f)(x) :=	-1		Z 8 d f(t)(t - x)^-ádt, dx x
		(1 - á)

respectively.

For f ? I^á#177;(L_p(118)) with p > 1 the Riemann-Liouville left and Right sided derivatives coincide with the Marchaud fractional derivatives

( 15á+f)(x) := (1 1 á) /L#177; (f(x) - f(x- y))y^-á-1dy,

and

( fi^áf)(x) := (1 1 á) L_#177; (f(x) - f(x+ respectively.

Proposition 1.1.5.1. [4] Assume that f,g are C¹([a, b])-function with f(a) = 0. Let á, â ? (0,1] be such that á+ â > 1 and let ä := {a = t0 < ... < t_n = b} be a partition of [a, b] with the norm 1ä1 = max (tj+1 - tj). Then for

j

every 0 < å < á + â - 1 the following estimates hold:

~~~~	fb f(t)dg(t) = C(á, â)1fk[a,b],álgk[a,b],â(b - a)^1+å, (1.2) a

^~~Z^~~_~ a b

~

f (t)dg(t) - E f (ti)[g(ti+1) - g (ti)] ~= C(á, â)1f [a,b],á1g1[a,b],â(b - a)^å.

~

i

(1.3)

1.2 Two-parameter Fractional Brownian Motion

1.2.1 The Main Definition

For technical simplicity we consider two-parameter fBm (fBm field) {B^H_t , t ? 118²₊}, where t = (t1, t2). We suppose that s = t if s = (s1, s2), t = (t1, t2) and si = ti, i = 1, 2.

1.2.2 Fractional Integrals and Fractional Derivatives of 14 Two-parameter Functions

Definition 1.2.1. The two-parameter process {B^H_t ,t ? R²₊} is called a (normalized) two-parameter fBm with Hurst index H = (H1, H2) ? (0,1)², if it satisfies the assumptions:

(a) B^H is a Gaussian field, Bt = 0 for t ? ?R²₊;

(b) EBtⁱ = 0, EBt ^HB^H = 1 11

4

(ti ^2Hi si 2Hi ti si

i=1,2

Evidently, such a process has the modification with continuous trajectories, and we will always consider such a modification. Moreover, consider "two-parameter" increments:Ä_sB^H_t := B^H_t - BHs1t2 - BHt1s2 + B^H_s for s = t. Then they are stationary. Note, that for any fixed ti > 0 the process B^H

(ti,.)

will be the fBm with Hurst index Hj, i = 1,2, j = 3 - i, evidently, nonnormalized.

1.2.2 Fractional Integrals and Fractional Derivatives of Two-parameter Functions

For á = (á1, á2) denote (á) =

(á1)¹(á2)

Definition 1.2.2. [12] Let f ? T := [a, b] := 11 [ai, bi], a = (a1, a2),

i=1,2

b = (b1, b2). Forward and backward Reimann-Liouville fractional integrals of orders 0 < ái < 1 are defined as

(I_a^á_r¹² f)(x) := (á) f (u) ?(x, u, 1 - á) du,

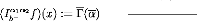
and

(Ir2 f)(x) := (á) f (u)

du

lx,b] ?(x, u, 1 - á) ,

correspondingly, where [a, x] = 11 [ai, xi], [x, b] = 11 [xi,bi],du = du1du2,

i=1,2 i=1,2

?(u, x, á) =| u1 - x1 |^á1| u2 - x2 |^á2, u, x ? [a, b].

Definition 1.2.3. Forward and backward fractional Liouville derivatives of orders 0 < ái < 1 are defined as

2

(Dr² f)(x) := (1 f (u) a) \ du

?x1?x2 ?(x, u, á)

and

?2 f (u) , du, x ? [a, b]

(Dr :á2 x)

:= (1 - á) ?x1?x2 i[x,b] ?(x, u, á)

1.2.2 Fractional Integrals and Fractional Derivatives of Two-parameter Functions 15

Definition 1.2.4. Forward fractional Marchaud derivatives of orders 0 < ái < 1 are defined as

~ f Ä_u xdu

( 15r² f)(x) :=(1 - á) f (x) +

?(x, u, á) á1á2 ./[a,x] ?(x, u,⁽ 1 )+ á)

+ E i=1,2,j=3-i	ái	áj	ix% f (x) - f (ui, x j) dui) a% (xi - ui)^1+^á%
	xj - aj

and the backward derivatives can be defined in a similar way

Let 1 = p = 8, the classes Iá1á2

+ (L_p(T )) := ~f|f = Iá1á2

_a+ ?, ? ? L_p(T )~,

_I

á1á2 - (L_p(T )) := ~f|f = Iá1á2 b- ?, ?? L_p(T)1 Further we denote Dá1á2

_a+ := Ia-+ á1á2). Of course, we can introduce the notion of fractional integrals and fractional derivatives on R² +. For exemple, the Riemann-Liouville left and Right sided fractional integrals and derivatives on R²₊ are defined by the formulas

(If+ l1á2 f)(x) := (á) L8 f(t) ,x] cp(x , u, á)^dt

f (t)

(I21á2 f)(x) := (á) 48) ?(x,u, á) dt,

2

(c^á

^(á12)f)(x) = (DT^á2 f)(x) := (1 - á) ? x1?x2

?I f(t)

(,_,x] (p(x ,t, á) dt

and

2

f ft)

(I^-(á1á2)f)(x) (D^á1á2f)(x)

:= (1 - á) ?x1?x2 _i[x,8) ?(x( t, á)^dt,

0 < ái < 1. Evidently, all these operators can be expanded into the product

of the form Iá1á2

+ = Iá+ 1 ? I^á2 +, and so on. In what follows we shall consider

only the case Hi ? (1/2, 1). Define the operator

YM#177; 1 H2 f := i=1,2

C(3) H%I^á1á2 #177; f.

1.2.3 Hölder Properties of Two-parameter fBm

We fix á = (á1, á2), ái ? (0,1] and let T = [a1, b1] × [a2, b2]. Let f the Riemann-Liouville fractional integral of order á i.e

1

x1 Ix2

₂ (x1 - t1) 1-- f (át1,t21 (x2 )- t2)--á2

f)(x1, x2) = (al)F(a2) dt1dt2, (x1, x2) ? T

vx1)^v.1^ritc:E2) a1 . a

p

The space Ëá,p = (I_a^á+)(L_p(T)) is called the Liouville space (or Besov space) and it becomes separable Banach space with respect to the norm WEc+fllá,p = IIfII

Proposition 1.2.3.1. [6] For every á, â

Iá _a+I^â a+= Iá+â

_a+ ,

If f ? C²_b (T) and f = 0 on ?1T = ([a1,b1] × {b1}) ? ({a1} × [a2,b2])then the function

1 f x1 14+ f (x1, x2) = r2 ?²f(t1,t2) dt1dt2

(1 - á1)(1 - á2) _L1 J_a2 ?t1?t2 (x1 - t1)^á1 (x2 - t2)^á2

(1.4)

is the unique function from L₈(T) such that

I^á_a+D^á_a+f = f.

For a rectangle D = [s1, t1] × [s2, t2] ? T we define the increment on D of the function f : T ? R by

f(D) = f(t1,t2) - f(t1, s2) - f(s1,t2) + ^f(s1, s2).

We denote by _C[ai,bi],ái the space of all ái-Hölder functions on [ai, bi] and

kfk[ai,bi],ái = sup u6=v,ai=u,v=bi

|f(u) - f(v)| (u - v)ái .

Also, we denote by CT,á1,á2 the space of all (á1, á2)-Hölder functions on T, i.e., f ? CT,á1,á2 if f is continuous,

If(a1, .)k[a2,b2],á2 < 8, f(., a2)k[a1,b1],á1 < 8

and

|f([u1, v1] × [u2, v2])|

< 8.

|u1 - v1|^á1|u2 - v2|^á2

kfkT,á1,á2 = sup

ui6=vi

Proposition 1.2.3.2. [4] Let 0 < â1 < á1,0 < â2 < á2 and p = 1. Then we have the continuous inclusions Ëá,p ? Ëâ,p,

Ëá,p ? Cá1-p^-1,á2-p^-1, Câ1,â2 ? Ëã,p if áip > 1, âi > ãi > 0

1.2.4 Fractional Generalized Two-parameter Lebesgue-Stieltjes Integrals 17

1.2.4 Fractional Generalized Two-parameter LebesgueStieltjes Integrals

Let 0 = ái = 1, i = 1, 2 be fixed. In what follows, we assume that all functions considered belong to the space D(T), i.e., at every point (x1, x2) ? T, they have limits in the four quadrants

Q⁺⁺(x1, x2) = {(s1, s2) ? T : s1 = x1, s2 = x2} , Q^+-(x1, x2) = {(s1, s2) ? T : s1 = x1, s2 < x2} , Q^-+(x1, x2) = {(s1, s2) ? T : s1 < x1, s2 = x2} , Q^--(x1, x2) = {(s1, s2) ? T : s1 < x1, s2 < x2} ;

furthermore,

f(x1, x2) lim f (s1, s2)

=

(s1,s2)?Q++?(x1,x2)

and, on the sides of the rectangle, the limits that can be defined are supposed to exist and denoted as f(x1, b^-₂ ), f(b^-₁ , x2), f(b^-).Denote f_a+(x) = Ä_af(x), x ? T, and fb-(x) := f(x) - f(x1, b^-₂ ) - f(b-1 , x²) + f(b-),

a := (a1, a2), b := (b1, b2).

Definition 1.2.5. Let f, g : T -? R. The generalized two-parameter LebesgueStieltjes integral of the function f w.r.t to the function g is defined by

_{Z Z}

f(x, y)dg(x, y) :=

K(D:1+ á2 _a+)(x, y)(D¹T^á11?á2 gb-)(x, y)dxdy

+ I (D^á+ f_a+ ) (x, a2) (D- ^á1) (g_b- (x, b₂ ) - g_b- (x, a2)) dx

a₁

^a b2

+ (DZ f_a+₂ ) (a1, y)(D1bá2) (gb-(b1 ,y) - g_b-(a1, y)) dy + f (a)Ä_ag(b)

a2

Where

fa⁺₁ (x, a2) = f(x, a2) - f(a), f_a+₂ (a1, y) = f(a1, y) - f(a),

gb-1 (x, b^-₂ ) = g(x, b^-₂ ) - g(b-), gb^-₁ (x, a2) = g(x, a2) - g(b^-₁ , a2),

gb- _2(b-1 , y) = g(b^-₁ , y) - g(b^-), gb- _2(a1, y) = g(a1, y) - g(a1, b- 2 ).

1.2.4 Fractional Generalized Two-parameter Lebesgue-Stieltjes 18 Integrals

Chapter 2

Stochastic Integration with

Respect to Two-parameter

Fractional Brownian Motion

2.1 Pathwise Integration in Two-parameter Besov Spaces

The next result gives an estimate of the Stieltjes integral for smooth functions in terms of Hölder norms and represents the essential step for extending the Stieltjes integral to Hölder functions of two variables.

Proposition 2.1.1. Let ái + âi > 1, ái, âi ? (0, 1], f, g ? C²(T) and let 0 < åi < ái + âi - 1. Then

_iab1 b2
¹

a

2

~~

f(t1, t2)dg(t1, t2) ~~

~~~~

= C(ái, âi)1gkT,â1,â2 {1f1T,á1,á2(b1 - a1)^á1+â1(b2 - a2)^á2+â2 +kf(., a2)1[a1,b1],á1(b1 - a1)^1+å1(b2 - a2)^â2 +1f(a1, .)1[a2,b2],á2(b1 - a1)^â1(b2 - a2)^1+å2 + |f(a1, a2)| (b1 - a1)^â1(b2 - a2)^â2~

(2.1)

Moreover, for every partition A = (si, _tj)i,j, a1 = s1 < ... < sn1 = b1, a2 = t1 < ... < t_n2 = b2, 1A1 = max(si+1 - si) + max(tj+1 - tj) , we have

i j

X 1

j

~~Z _b1 Z b2 n1-1_X n2-

f(si, tj)g ([si, si+1] × [tj, tj+1])

~_~f(u1, u2)dg(u1, u2) -

~ a1 a2 i=1 =1

Z _b1 Z b2 ~~~~ = (b1 - a1)^å1(b2 - a2)^å2

f(t1, t2)dg(t1, t2) å1å2(å1)(å2)

a1 a2

~~~~

kf1 * h1k8

(b1 - a1)^1+å1(b2 - a2)^1+å2

=

å1å2(å1)(å2) kf1k8kh1k8.

(2.2)

+ C(ái,âi)11fIIT,á1,á2 [11g1IT,â1,â211Äll^{á1+â1+á2+â2} (11g11T,â1,â2 .)1[a2,b2],â2) 1ÄM^á1

+ (1g1T,â1,â2 + kg(., _{a2)k[a1,b1],â1)} 1Ä1^á2] .

Proof. Assume first that f = 0 on ?1T and define

h(t1, t2) = g(b1 - t1, b2 - t2) - g(b1 - a1, b2 - t2) (2.3)

-g(b1 - t1, b2 - a2) + g(b1 - a1, b2 - a2).

Then

Z _b1 Z b2 f(t1, _t2)?²g(t1, t2) dt1dt2 = ?²(f * h)(b1, b2) .
?t1?t2 ?t1?t2

a1 a2

Choose åi > 0, 0 < á⁰_i < ái, 0 < â⁰_i < âi withá0 _i + â0 i = 1 +åi. By proposition 1.2.3.1 the function f1 = D_a^á+^' f, h1 = D_a^â+^' h are in L₈ and satisfy

I

á⁰ _Iâ⁰
_a+f1 = f, _a+h1 = h. (2.4)
Then by proposition 1.2.3.1, (2.3) and (2.4) we have

Z _b1 Z b2 Z _b1 Z b2 f(t1, _t2)?²g(t1, t2)

f(t1, t2)dg(t1, t2) = dt1dt2

?t1?t2

a1 a2 a1 a2

?²(f * h)(b1,b2)

=

?2

?t1?t2

_{h i}

_Iá⁰

=

?t1?t2
?2

=

_a+f1 * Iâ0

_a+h1 (b¹, b2)

_{h i}

_Iá⁰+â⁰

_a+ (f1 * h1) (b1, b2)

?t1?t2

?2 ~I1

= _a+I^å a+(f1 * h1) (b1, b2)

?t1?t2

= Iå _a+(f1 * h1)(b1, b2), such that I¹_a+ = I(1,1) _a+, I^å_a+ = Iå1,å2

_a+

and then

Next, the integration by parts for functions of two variables (see[14]) yields

(1 - á0(1 - á^'₂) _a2

(x1, x2) =

x1 1 r2 df ([t1,x1] × [t2, x2])

(x1 - t1)^{á 4} (x2 - t2)^{á 4}

1 f ([t1,x1] × [t2, x2]) lim (1 - á0(1 - á^'₂) t%?x% (x1 - t1)^á4 (x2 - t2)^á4

lirn

x1 f ([t1, x1] [t2, )

dt

t2?x2 x21,

- j_{a1 (x1 toá,} (x2 _t2)^j ál 2 1

- lim

f ([t1,x1]×[t2, x2]) dt2 j_a2 (x1 - t1)^á4 (x2 - t2)^á4

+áV1á^02

x1 r2 f ([t1,x1] × [t2, x2]) dt1dt2 a1 } Ja2 (x1 - t1)^á4+1(x2 - t2)^á2+1

r2 f ([t1,x1] × [t2, x2]) dt dt

(1 - áo(1 - _a1 J_a2 (x1 - t1)^á1+1(x2 - t2)^á2+1

i 2,

so that

₂₎kfkT,á1,á2

(1 - á⁰ ₁)(1 - á0

á0 1á0 2

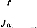
x1 Ix2

Ja1 a

2

(2.6)

× (x1 - t1)^á1?á01-1(x2 - t2)^á2?á02-1dt1dt2

= ckfkT,á1,á2(b1- a1)^á1?á01(b2 - a2)^á2?á02.

Similary

kh1k8 = c1kgkT,â1,â2(b1- a1)^â1?â01(b2 - a2)^â2?â02. (2.7)

By using (2.6) and (2.7) in (2.5) we obtain (2.1) if f = 0 on ?1T. If f is not necessarily null on ?1T then we define

f(t1, t2) = f ([a1, t1] × [a2, t2]) .

Then f = 0 on ?1T and f, f have the same increments. Then we have

Z _b1 Z b2 f(t1, _t2)?²g(t1, t2) dt1dt2

?t1?t2

a1 a2

Z _b1 Z b2 Z _b1 Z b2

f(t1, _t2)?²g(t1, t2) f(a1, _t2)?²g(t1, t2)

= dt1dt2 + dt1dt2

?t1?t2 ?t1?t2

a1 a2 a1 a2

2

a

Z _b1 Z b

+

a1 2

=

Z _b1 Z b2

a1 a2

f(t1, _a2)?²g(t1, t2) dt1dt2 + f(a1, a2)g ([a1, b1] × [a2, b2]) ?t1?t2

Z b2 ~

f(t1, _t2)?²g(t1, t2) ~?g(b1, t2) - ?g(a1, t2)

dt1dt2 + f(a1, t2) dt2

?t1?t2 ?t2 ?t2

a2

Z b1 ~?g(t1, b2) ~

- ?g(t1, a2)

+ f(t1, a2) dt1 + f(a1, a2)g ([a1, b1] × [a2, b2])

?t1 ?t1

a1
4

=

X k=1

Jk.

(2.8)

From the previous reasoning we have

~~Z _b1 Z b2 ~~~~

~f(t1, _t2)?²g(t1, t2)

~ dt1dt2

?t1?t2

a1 a2

= C(ái, âi)kfkT,á1,á2kgkT,â1,â2(b1 - a1)^á1+â1(b2 - a2)^á2+â2. (2.9)

Next by using (1.2) we have

|J2| =

~~Z b2 ~~ a2

r?g(b1, t2) ?g(a1, t2) 1 dt2 [f (a1, t2) - f(a1, a2)] ?t2 - ?t2

+ |f(a1, a2)g ([a1, b1] × [a2, b2])|

= C(ái, âi) kf(a1, _{.)1[a2,b2],á2} kg(b1, .) - g(a1, .)k[a2,b2],â2 (b2 - a2)^1+å2

+ |f(a1, a2)| 1g1T,â1,â2(b1 - a1)^â1(b2 - a2)â2,

so that

11J211ái,âi)11g1IT,â1,â2 {11f(a1,.)1[a2,b2],á2 (b1 -a1)^â1(b2 -a2)^1+å2 + |f (a1, a2)| (b1 - a1)^â1(b2 - a2)^â2}.

(2.10)

Similarly

11J311 = C(ái, âi)11g11T,â1,â2{11f(., _{a2)k[a1,b1],á1} (b1 - a1)^1+å1(b2 - a2)^â2 +|f(a1, a2)|(b1 - a1)^â1(b2 - a2)^â2}.

(2.11)

Replacing (2.10) and (2.11) in (2.8) we obtain (2.2). Next we have

Z _b1 Z b2 _X

IÄ = f(u1, u2)dg(u1, u2) - f(si, tj)g ([si, si+1] × [tj, tj+1])

a1 a2 i,j

X=

[f(u1, u2) - f(si,tj)] dg(u1,u2)

Z _si+1 Z tj+1

i,j

X=

si tj

Z _si+1 Z tj+1

si tj

[f(u1, u2) - f(u1, tj) - f(si, u2) + f(si,tj)] dg(u1,u2)

i,j

+E

Z _si+1 Z tj+1

i,j

+E

si tj [f(u1, tj) - f(si,tj)] dg(u1, u2)

Z _si+1 Z tj+1

i,j

= I¹ _Ä+ I²_Ä + I³ _Ä.

si tj [f(si, u2) - f(si,tj)] dg(u1, u2)

(2.12)

From (2.1) it follows that

|I^1Ä| = ClIfIlT,á1,á211g1IT,â1,â2E i,j

(si+1 - si)^á1+â1(tj+1 - tj)^á2+â2

(2.13)

=C1kfkT,á1,á2kgkT,â1,â2kÄM^{á1+â1+á2+â2-2}.

Next define

Then (1.2),(1.3) imply

= E

= E

Z b1

^i,j X ~?g(u1, tj+1)?g(u1,tj)] = f1(u1, tj)du1

?u1 ?u1

a1j

Z _si+1 Z tj+1 [f(u1, tj) - f(si, tj)] ?²g(u1, u2) du1du2

?u1?u2

i,j si tj

[f (u1 , tj) - f (si, tj)] ?u1

? g (u1 , _tj+1) ?g(u1 1 tj)1 du1

?u

Z si+1

si

~~I2 ~~ = C Z b1 kf1(u1, _{.)k[a2,b2],á2} kg(u1, _{.)k[a2,b2],â2} du1. (2.14)

Ä

a1

Since u1 ? [si, si+1) we have

kf1(u1, .) [a2,b2],á2 = 1f1T,á1,á2 (u1 - si)^á1 = IfkT,á1,á2 kÄká1

and

Mg(u1,.)1[a2,b2],â2 = (b1 - a1)â1 ,gkT,â1,â2 + 1g(a1,.)1[a2,b2],â2 (2.15)

It follows by replacing in (2.14) that

~|I² Ä| = C1kfkT,á1,á2kÄká1 ~ kgkT,â1,â2 + kg(a1, _{.)k[a2,b2],â2} . (2.16)

Similarly

~|I³ Ä| = C1kfkT,á1,á2kÄká2 ~ kgkT,â1,â2 + kg(., _{a2)k[a1,b1],â1} . (2.17)

Finally using (2.13),(2.16) and (2.17) in (2.12) we (2.2).

Next we define CT,á1,á2,8 the space _CT,á1,á2 endowed with the norm

kxkT,á1,á2,8 = 1x1₈+ sup

a1=t1=b1

kx(t1, .) _[a2,b2],á2+ sup

a2=t2=b2

1x(., t2)1[a1,b1],á1+1xIT,á1,á2.

The space (CT,á1,á2,8, k.kT,á1,á2,8) is a Banach space.

The convergence of Riemann-Stieltjes sums to the integral for Hölder functions of one variable in shown in [[4],[15],[16]]. The corresponding result for functions of two variables is given in the next theorem.

Theorem 2.1.1. Let T0 = [a1 - å0, b1 + å0] × [a2 - å0, b2 + å0], å0 > 0, and let

á1, á2, â1, â2 ? (0, 1] be such that ái + âi > 1. If f ?CT0,á1,á2, g ? CT0,â1,â2,

Z _b1 Z b2

a1 a2

every sequence of partitions Äⁿ = (sⁿ_i ,tⁿ_j ), a1 = s0 < ... < sk(n) = b1, a2 = t0 < ... < tk(_n) = b2, with 1Äⁿ1 ? 0, the Riemann-Stieltjes sums

then there exists a unique real number f(u, v)dg(u, v) such that for

Sog= E i

X~ × ~tn ~~ , f(sn i , tn j )g ~~sn i , sn j , tn i+1 j+1 j

Z _b1 Z b2

converge to f(u, v)dg(u, v). Moreover, the following estimate holds:

a1 a2

_/b1 f

_a f (u, v)dg(u, v) f - a1)^â1(b2 - a2)^â2.

1 a2

(2.18)

Proof. It is enough to prove that for every ä > 0 there exist ç > 0 such that for every two partitions (Äi)i=1,2, ai = uⁱ₀ < ... < uim(i) = bi with kÄik < ç we have

S _,^f4 - = ä. (2.19)

Let J ? C^°°(R²) be such that J = 0, J(x) = 0 if 114 = 1 and J(x)dx = 1

_R2

and define J_å(x) = å^-2 J (^x). Consider the regularizations of f_å, g_å of f,g. å

Recall that

f_å(x) =_R J_å(x - y)f(y)dy = f (x - åy)J(y)dy,

²

and for g_å similarly (as usual f,g are extended as 0 on R² \ T0). It is well known that f_å ? f,g_å ? g uniformly on T. Also it is easily seen that

få ? CT,á1,á2, g_å ? CT,â1,â2.

Next we show that if 0 < á⁰_i < ái, 0 < â0 i < âi, then

f_å ? f in CT,á⁰ (2.20)

1,á0 ₂, g_å ? g in CT,â⁰ 1,â0 2,

f_å(a1, .) ? f(a1, .) in C[a2,b2],á⁰₂,

g_å(a1, .) ? g(a1, .) in C[a2,b2],â0 ₂, (2.21)

f_å(., a2) ? f(., a2) in C[a1,b1],á^'₁,

g_å(.,a2) ? g(., a2) in C[a1,b1],â⁰₁. (2.22)

We have

(f_å - f) ([s1,t1] × [s2, t2]) = J(u,v){f([s1 - åu, t1 - åu] × [s2 - åv, t2 - åv])

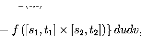
(0,1)

and then for every å, ä > 0,

sup

si6=ti

|(f_å - f) × [s2, t2])|

|s1 - t1|^á01|s2 - t2|^á02

= sup

{ | (få - f)([s1,t1]× [s2,t2])| , |si - ti| > ä, i = 1,2} - t1|^á4|s2 - t2|^á4

+ sup {|(f_å - f)([s1,t1] × [s2,t])|

₂ , |s1 - t1| > ä or |s2 - t2| > ä

|s1 - t1|^{á0 1}|s2 - t2|^á0

1

= sup {|f(u1, v1) - f (u2, v2)| , |ui- vi|< å, ? T0, i = 1, 2}

äá1+á2

- f ([s1, t1] × [s2, t2])} dudv,

? 0 as å ? 0,ä ? 0.

+CU max(äá1-á'1, äá2-á2)

Similarly one prove(2.21),(2.22).

Next we choose 0 < á⁰_i < ái, 0 < â0 i < âi with á⁰_i + â⁰ _i> 1. Then from (2.20),(2.22) and (2.12) we obtain

~~~~~ - ₌f ^,gå +

Ä1 Ä2 ^,g - S^feS^f,g - Sfå,gå

Ä2 Ä2

+Saf-å;gå- _fb1 b2

dg_å Skf^å - fådgå

d

b1 b2

a,

1

a

2

fa

1

a

2

=- S;^t6,.^å;^gå + - S kf^å

+C (II fåIIT,á4,á4 + IlgålITAA) {(1 + 11Ä21e^+â1+á4+%-2

+ + 11Ä21)^á4 + _(llÄ1ll + 11Ä21e}

=

f,g- S;^t6_,.^å;^gå + - gå

st

+C1 {(11Ä1ll + 11Ä211)^{á4+â1+á4+â?2} + _(11Ä1ll + 11Ä211)^á4

+ (kÄ1k + kÄ21)^á02o ?0,

as å ? 0 and then IÄiI ? 0. The previous computation also shows that

lim b1b2 b1b2

fådgå =

f dg,

å?0

la

¹

12

²

1

¹

12

2

and this fact and(1.2) imply (2.18).

28 2.1 Pathwise Integration in Two-parameter Besov Spaces

Chapter 3

Existence and Uniqueness of the

Solutions of SDE with

Two-Parameter Fractional

Brownian Motion

Next for K > 0 we define the closed sets

C[_a,b],H(K) = {(P ? C[_a,b],H :1(PI[a,b],H = K}, and for (Pi ? C[ai,bi],ái,

(

CT,á1,á2,00(K, (P1, (P2) = x ? CT,á1,á2,00 : x(a1, .) = (P1, x(., a2) = (P2, Ix1T,á1,á2 = K,

sup a1<t1<b1

kx(t1, .)I[a2,b2],á2 = K, a2<sut2p<b2

}11x(., t2) 11 [a1 ,b1],á1 = K .

By using the Hölder spaces of functions we obtain the following local contraction property of an integral operator between such spaces, which is useful in the next existence and uniqueness result.

Proposition 3.1. Let â1, â2 ? (1/2, 1] and á1, á2 be such that âi > ái > 1 - âi.Let g ? CR²,â1,â2 and b, ó : R ? Rbe such that b is bounded and Lipschitz and ó ? C²_b(R) with ó^" Lipschitz. Then for every K > 0 and ai, bi ? R,ai < bi, i = 1, 2, there exists å0 > 0 independent of ai, bi, such that for every (Pi ? C[ai,ai+å0],ái(K) the operator

F : C[a1,a1+å0]x[a2,a2+å0],á1,á2,00(2K, ^(P1, (P2) ? C[a1,a1+å0]x[a2,a2+å0],á1,á2,00(2K, (P1, (P2)

defined by

Existence and Uniqueness of the Solutions of SDE with 30 Two-Parameter Fractional Brownian Motion

Z _s Z t Z _s Z t

(F x)s,t = ?1(s) + ?2(t) + b(x_u,v)dudv + ó(x_u,v)dg(u, v),

a1 a2 a1 a2

is a contraction.

Proof.(We refer to read [8] for more detail.) Clearly we have

~ ~ ~ ~

Z . Z . a1 a2

~ ~ b(xu,v)dudv ~ = kb18(b1 - a1)^1-á1(b2 - a2)^1-á2 ~T,á1,á2,8 × [(b1 - a1)^á1(b2 - a2)^á2 + 1] .

(3.1)

By using (2.18) it follows

~ Z. ~Z. ~~ a1a2

~ ó(xu,v)dg(u, v) ~= (x)11T,á1,á2,811g11T,â1,â2 T,á1,á2,8

×(b1 - a1)^â1?á1(b2 - a2)^â2?á2 [(b1 - a1)^á1(b2 - a2)^á2 + 1] . (3.2)

Next

ó(x) ([s1, t1] × [s2, t2]) = (xt1,t2 - xt1,s2)

-(xs1,t2 - xs1,s2)

ó0 (ëxt1,t2 + (1 - ë)xt1,s2) dë
ó0 (ëxs1,t2+ (1 - ë)xs1,s2) dë

1

_J

0 1

Z0

Z0 1 ó0 (ëxt1,t2 + (1 - ë)xt1,s2) dë

Then

ó(x) ([s1, t1] × [s2, t2]) = (xt1,t2 - xt1,s2 - xs1,t2 + xs1,s2)

Z 1

+(xs1,t2 - xs1,s2) [ó⁰ _(ëxt1,t2 + (1 - ë)xt1,s2)

0

-ó^' _(ëxs1,t2 + (1 - ë)xs1,s2)] dë.

(3.3)

Then (3.3) implies

{|ó(x) ([s1, t1] × [s2, t2])| = 1ó¹181x1T,á1,á2 + Ió^'IL1x(s1, .)1[a2,b2],á2

)

Z 1 ~ dë

× ~ëkx(., _{t2)k[a1,b1],á1} + (1 - ë)kx(., s2)k[a1,b1],á1 (t1-s1)^á1(t2-s2)^á1,

0

Existence and Uniqueness of the Solutions of SDE with Two-Parameter Fractional Brownian Motion 31

and hence, if x ? CT,á1,á2,8(K, ?1, ?2), then

Ió(x)1T,á1,á2 = K (1ó¹1₈ + kó⁰k_L) . (3.4)

From (3.2),(3.2) and (3.4) it follows that

Fx ? C[a1,b1]×[a2,b2],á1,á2,8

a

if x ? C[a1,b1]×[a2,b2],á1,á2,8nd also for å1 > 0 enough small,
Fx ? C[a1,a1+å1]×[a2,a2+å1],á1,á2,8(2K, ?1, ?2)
if x ? C[a1,a1+å1]×[a2,a2+å1],á1,á2,8(2K, ?1, ?2).

Next we have

[ó(x) - ó(y)] ([s1, t1] × [s2, t2])

1

= (x - y)([s1,t1] × [s2, t2]) J ó0 (ëxt1,t2 + (1 - ë)yt1,t2) dë

+[(xs1,t2 -ys1,t2) -(xs1,s2 -ys1,s2)]

1

0

Z× [ó⁰ _(ëxt1,t2 + (1 - ë)yt1,t2) - ó0 (ëxs1,t2 + (1 - ë)ys1,t2)] dë

0 Z

1

+(xs1,s2 - ys1,s2) [ëx ([s1, t1] × [s2, t2]) + (1 - ë)y ([s1, t1] × [s2, t2])]

Z 1 0

× ó00 (u(ëxt1,t2 + (1 - ë)yt1,t2) + (¹ - u) (ëxs1,t2 + (1 - ë)ys1,t2)) dudë

+(

_Z

× [ó⁰⁰ (u _(ëxt1,t2 + (1 - ë)yt1,t2) + (1 - u) (ëxs1,t2 + (1 - ë)ys1,t2))

0

-ó^" (u _(ëxt1,s2 + (1 - ë)yt1,s2) + (1 - u) (ëxs1,s2 + (1 - ë)ys1,s2))] dudë.

(3.5)

0 Z 1
xs1,s2 - ys1,s2) [ë(xt1,s2 - xs1,s2) + (1 - ë)(yt1,s2 - ys1,s2)]
0 1

If x, y ? C[a1,a1+å1]×[a2,a2+å1],á1,á2,8(K, ?1, ?2), then (3.5) yields

kó(x) -ó(y)1T,á1,á2 = C (K, kól₈, Mó^tkL, kó^itkL)

Mx - ylT,á1,á2. (3.6)

From (3.1), (3.2) and (3.6) it follows that there exists å2 > 0 enough small, independent of ai, bi, such that

11^F x-Fyl[a1,a1+å2]×[a2,a2+å2],á1,á2,8 = dlx-yl[a1,a1+å2]×[a2,a2+å2],á1,á2,8, (3.7)

for some 0 < d < 1, and hence, denoting å0 = min(å1, å2), we obtain that

Existence and Uniqueness of the Solutions of SDE with 32 Two-Parameter Fractional Brownian Motion

F : C[a1,a1+å0]x[a2,a2+å0],á1,á2,00(2K, ?1, ?2) ? C[a1,a1+å0]x[a2,a2+å0],á1,á2,00(2K, ?1, ?2)

is a contraction. 111

An existence and uniqueness result for ordinary differential equations with Hölder continuous forcing is obtained in [11]. The global solution is constructed, first in small time interval, when the contraction principle can be applied, by using estimates in terms of Hölder norms. For the two-parameter case we have the following result.

Theorem 3.1. Let â1, â2 ? (1/2, 1] and á1, á2 be such that âi > ái > 1- âi. Let g ? CR²,â1,â2 and b, ó : R ? R be such that b is bounded and Lipschitz and ó ? C2 b (R) with ó^" Lipschitz. Then for every a1 < b1, a2 < b2 and ?i ? C[ai,bi],ái with ?1(a1) = ?2(a2), the equation

t

x st=?1(s) ? 2(t) - ?1 (a1) + f i

b(x_u,v)dudv

l a

2

(3.8)

+ _Is ft

j_a1 ó(x_u,v)dg(u,v), (s, t) ? T,

has a unique solution in CT,á1,á2,00.

Proof. Let K > 0 be such that ?i ? C[ai,bi],ái(K). Then from Proposition 3.1 we obtain the existence of the solution x of (3.8) on the rectangle

[a1, a1 + å0] × [a2, a2 + å0], å0 independent of ai, bi (but dependent on K). If a1 + å0 < b1, let n0 be the biggest integer such that n0å < b1. Then x ? CT,á1,á2,00(2K) and inductively we obtain the existence of the solution on

[a1 + å0, a1 + 2å0] × [a2, a2 + å0], ..., [a1 + n0å0, b1] × [a2, a2 + å0], and then on

[a1, a1 + å0] × [a2 + å0, a2 + 2å0], ..., [a1 + n0å0, b1] × [a2 + å0, a2 + 2å0],

and continuing again by induction we obtain the existence on T . Let now x1, x2 be two solutions of (3.8). In particular, there is K > 0 such that x1, x2 ? CT,á1,á2,00(K). From (3.7) we deduce the existence of å0 > 0 (which does not depend on ai, bi) and 0 < d < 1 such that

1x1 - x21[a1,a1+å0]x[a2,a2+å0] = d1x1 - x21[a1,a1+å0]x[a2,a2+å0],

and therefore x1 = x2 on [a1, a1 + å0] × [a2, a2 + å0].Inductively (see the existence part) we obtain that x1 = x2 on T. 111

Existence and Uniqueness of the Solutions of SDE with Two-Parameter Fractional Brownian Motion 33

Theorem 3.2. Let (B^H_{t )tE[0,1]2} be a two-parameter fractional Brownian motion with Hi ? (1/2,1) and let ái,âi > 0 be such that 1/2 < âi < Hi,

âi > ái > 1-âi, i = 1, 2. Let b, ó : R ? R be such that b is bounded and Lipschitz and ó ? C²_b (R) with ó^" Lipschitz and let be the processes {?i(t)}tE[0,1] such that almost surely ?1(0) = ?2(0) and ?i ? C[0,1],á,. Then with probability one the stochastic equation

s t

Xs,t = ?1(s) + ?2(t) - ?1 (0) + b(X_u,v)dudv

f

0 0 (3.9)

+ ₁s _ft

0 ft (s,t)? [0,1]²,

has a unique solution _{{Xu,v}(u,v)E[0,1]2} with the paths in C[0,1]²,á1,á2,00.

Proof. From the Kolmogorov criterion (see [2, 7]) it follows that B^H has â-Hölder paths, i.e., there exists a random variable C such that for all ù ? Ù

2

(B^H ([t, s])) (ù) ~~ = C(ù)

II j=1

(sj - tj)^â' . (3.10)

s pt

Therefore almost surely we have by Theorem 2.1.1 and (3.10) that the Stieltjes integral

10 0 f (u, v)dBuH,v

is well defined for f ? C[0,1]²,á1,á2. Now the result is a consequence of Theorem 3.1 applied pointwise.

Existence and Uniqueness of the Solutions of SDE with 34 Two-Parameter Fractional Brownian Motion

Bibliography

[1] M. ARcoNEs, On the law of iterated logarithm for Gaussian processes, JouRNAL of ThEoRETicAL PRobAbiLiTy 8 (4) 877-904 (1995).

[2] A. AyAchE, S. LEgER, M. PoNTiER, Drap brownian fractionnaire,PoTENTiAL ANAL. 17 31-43 (2002).

[3] G. DA PRATo, J. JAbczyk, Ergodicity for infinte dimensional systems, CAmbRidgE UNivERsiTy PREss,(1993).

[4] D. FEyEL, A. DE LA PRAdELLE, On fractional Brownian processes, PoTENTiAL ANAL. 10 273-288 (1999).

[5] A.KAmoNT,On the fractional anisotropic Wiener field, PRobA. MATh. STAT., 16, 85-98 (1996).

[6] F. KLiNgENhöfER, M. ZähLE, Ordinary differential equations with fractal noise, PRoc. AmER. MATh. Soc. 127 1021-1028(1999).

[7] S. LEgER, M. PoNTiER, Drap brownian fractionnaire,C. R. AcAd. Sci. PARis 329 893-898 (1999).

[8] Y. MAshuRA, Stochastic calculus for fractional Brownian motion and related processes, SpRiNgER-VERLAg BERhim HEidELbERg (2008).

[9] B. MAsLowski, D. NuALART, Evolution equations deriven by fractional Brownian motion, J. FuNcT. ANAL. 202 277-305 (2003).

[10] D. NuALART, A. RAscANu, Differential equations driven by fractional Brownian motion, CoLLEcT. MATh. 53 55-81 (2002).

[11] A.A. RuzmAikiNA, Stieltjes integrals of Hölder continuous functions with applications to fractional Brownian motion,J. STAT. Phys. 1000 1049-1069 (2000).

[12] S.G. Samko, A.A. Kilbas, O.I. MarichEv, Fractional Integrals and Derivatives. Theory and Applications, Gordon and BrEach SciEncE PublishErs, NEw York (1993).

[13] A.D. VEnttsEl,A course in the theory of stochastic processes, McGraw Hill, NEw York (1981).

[14] J. YEh, CamEron-Martin, Translation theorems in the Wiener space of functions of two-variables,Trans. AmEr. Math. Soc. 107 409-420 (1963).

[15] L.C. Young, An inequality of the Hölder type connected with Stieltjes integration, Acta Math. 67 251-282(1936).

[16] M. ZählE, Integration with respect to fractal functions and stochastic calculus I,Probab.ThEory RElatEd FiElds 111 333-374 (1998).