|
N° d'ordre : 03/2009-M/G.C
REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET
POPULAIRE
MINISTERE DE L'ENSEIGNEMENT SUPERIEUR ET
DE LA RECHERCHE
SCIENTIFIQUE
UNIVERSITE DES SCIENCES ET DE LA TECHNOLOGIE « HOUARI
BOUMEDIENE »
FACULTE DE GENIE CIVIL

MEMOIRE
Présenté pour l'obtention du
diplôme de MAGISTER
EN : GENIE CIVIL
Spécialité :
CONSTRUCTION
Par : OUALI Nabil
Sujet
Effets des Dispositifs D'amortissement sur les
Déplacements,
Vitesses et Accélérations des
Structures
Soutenu le 18/01/2009, devant le jury composé de
:
Mr CHABAAT. M Professeur, FGC/USTHB
Président
Mr BOUKHALED.A Maître de Conférences,
FGC/USTHB Directeur de thèse
Mr BENYAHIA A Professeur, FGM/USTHB
Examinateur
Mr ZERZOUR. A Maître de Conférences,
ENTP Examinateur
Mr DJAKAB. E Maître de Conférences,
FGC/. USTHB Examinateur

REMERCIEMENTS
Avant tout, je remercie Dieu le tout puissant de m'avoir donner
le courage et la volonté pour mener à terme ce travail.
J'adresse mes sincères remerciements à mon
encadreur monsieur A.BOUKHALED, Maître de conférences à
l'USTHB et mon co encadreur monsieur F.CHALAH , Chargé de recherches
à l'USTHB , pour avoir dirigé ce travail et qui, malgré
les multiples obligations, n'ont jamais ménagé aucun effort pour
suivre de près cette étude.
Je tiens à remercier Monsieur M. CHABAAT, Professeur
à l'USTHB, mon enseignant et président de jury, qui m'a fait le
grand honneur de présider le jury.
Mes remerciements vont également à Monsieur
BENYAHIA. A, Professeur à l'USTHB qui a accepté d'examiner mon
travail.
J'adresse également mes remerciements à Monsieur
A. ZERZOUR, Directeur de ENTP, qui me fait l'honneur d'examiner mon travail,
qu'il trouve ici, l'expression de ma considération distinguée.
Mes remerciements sont destinés également à
Monsieur DJAKAB. E, Chargé de cours à l'USTHB qui a
accepté d'examiner mon travail.
Enfin, je remercie toutes les personnes qui ont contribué
de près ou de loin à la réalisation de ce travail.
0 2øÎáã
äíÈ Çã
íÑÆÇÒÌáÇ
áÇãÔáÇ ÏÌæí
ËíÍ ÉíáÇÚ
ÉíáÇÒáÒ ÊÇÐ
ÉÞØäã í ÚÞÊ
ÉáæÏ
ÑÆÇÒÌáÇ
ÑÇÈÊÚÇÈ
`w
áæ?Ç
|
Éíí í
ÇøíáÌ Ñßä ä
ÇäíáÚ ÈÌí
íæÇíÓæÑæ?Ç
ÍØÓáÇ
íäÇËáÇæ
íÞíÑ?Ç
ÍØÓáÇ
|
|
9
|
..u4???
|
ÉÏÇÖã
ÉÏíÏÌ
ÊÇíäÞÊ
áÇãÚÊÓÇ
íáÇÊáÇÈæ
ÉíÚíÈØáÇ
ÉËÑÇßáÇ åÐå
äã ÉíÏÚÇÞáÇ
ÊÇÔäãáÇæ
ÊÇÑÇãÚáÇ
ÉíÇãÍ
.
ÊÇßáÊããáÇæ
ÍÇæÑ?Ç
ÉíÇãÍá
ÇäíáÚ ÖæÑã
Ñã æå
áÒ?Òáá
|
ÑæÏáÇ
ÑíÈßÊÈ
íáÇÒáÒáÇ
áÒÚáÇ ÍãÓí
ËíÍÈ
ÊÇÏãÎãáÇæ
íáÇÒáÒáÇ
áÒÚáÇ ÉíäÞÊ
ÊÇíäÞÊáÇ
åÐå
|
C.I.? ??
|
ÉÞÇØáÇ í
ÉÑÔÇÈã ÑËÄÊ
ÉäæÑãáÇ
åÐåæ ÉÑÇãÚ æ
ÑÓÌ äÇ ÁÇæÓ
ìäÈãáá
ÉÑíÈ ÉäæÑã
ÁÇØÚÅ
íáÇÊáÇÈæ
|
ÖÚÈ Çåá
íáÇÒáÒáÇ
áÒÚáÇ íåæ ?
ÉíäÞÊáÇ
|
åÐå äßá
|
Çå41Óã ÖÎÈ
ãæL. 4L? ?4
..411ããáÇ É.4Ç
ÒáÒáÇ
9
|
ÇÐå Ïå æåæ
ÊÇÏãÎãáÇ
áÇãÚÊÓÇ
ÈÌí ßÑÍÊáÇ
ÇÐå íÏÇÊáæ
ìäÈãáá
ÑíÈßáÇ
ßÑÍÊáÇ
ÇåäíÈ äãæ
ÊÇíÈáÓáÇ
.
íãáÚáÇ
ËÍÈáÇ í
ÉãÏÞã ÑÇØÅ í
áãÚáÇ
Résumé :
L'Algérie, par sa situation géographique, est un
pays de grande sismicité du faîte qu'elle est située entre
deux plaques tectoniques, la plaque Africaine et la plaque Euro- Asiatique.
Pour cela, on doit élaborer une méthode de protection de
structures contre les catastrophes. L'utilisation de nouvelles techniques
parasismiques devient donc une nécessité pour la protection des
vies humaines et de sauvegarder les biens matériels.
Parmi ces techniques, on trouve la technique d'isolation
sismique et celle des amortisseurs. La première permet d'augmenter la
période et la souplesse de la structure. Cette souplesse influe
directement sur l'énergie sismique absorbée. Cependant,
l'inconvénient majeur que présente cette technique est le
déplacement important de la structure. Pour réduire ces effets
néfastes, l'une des solutions efficaces est celle d'incorporer dans la
structure des dispositifs d'amortissement. Ceci constitue l'objet principal de
cette étude.
Mot clés ; Amortisseur, amortissement,
isolation sismique
Abstract:
Based on the geographical situation, Algeria is categorized as
a high seismic activity zone. Algeria is located between two tectonic plates;
The African Plate and the Eurasian Plate. The African Plate which includes the
continent of Africa, as well oceanic crust lies between the continent and
various surrounding ocean ridges. The African Plate's speed is estimated at
around 2.5cm per year. When structures are build in a high seismic activity
zones, structural engineers have to elaborate:
1- Safety provisions suitable for use throughout the specific
region;
2- Design and building practices that address the earthquake
hazard and minimize the resulting damage.
Among these practices, we can find the seismic isolation. The
seismic isolation is a technology that protects the structure from the
destructive effects of an earthquake. The seismic isolation decouples the
structure from the ground and provides it with dampening. Seismic isolation is
physically achieved by placing the structure on isolators. The isolators are
laterally flexible elements, yet the are able to carry the vertical loads on
the structure. Since the isolators are more flexible than the structure, most
of the lateral movements occur in the isolators. As result, the isolated
structure experiences less motion and reduced forces. One of the disadvantages
of these systems is the relatively high permanent displacements. In order to
soften this effect, isolators can be coupled with special shock absorbers, to
form a dual system meeting the resistance and service requirements.
The aim of the thesis presented by the author is to bring some
clarification related to these systems.
Notations
ÄU: Energie dissipée par cycle,
æ: Valeur d'amortissement
A: Amplitude de mouvement.
c: Constante d'amortissement visqueux,
Ù: Fréquence de la force d'excitation. A
l : : Amplitude initiale
An + 1 :Amplitude après n
cycles.
Ùr : Fréquence de
résonance
ä : Décroissance logarithmique
équivalente
Q : Largeur de bande
ÄE : Energie transformée en chaleur
ou énergie de contrainte interne E : Energie de
déformation à l'amplitude maximale.
ó : Contrainte
å : Déformation
ö : Angle de phase
îeq : Valeur d'amortissement équivalente
îi : Valeur d'amortissement du
matériaux i
Ei : Energie élastique de
déformation emmagasinée dans chacun des matériaux
Fm : Force d'inertie.
Fc : Force d'amortissement due
à la structure.
Fm : Force de rigidité.
P(t) : Charge dynamique (variable en fonction du
temps).
M : Matrice de la masse de la structure
C : Matrice d'amortissement
K : Matrice de rigidité
U&& :
Accélération du système
U& : Vitesse du système
U : Déplacement du
système
V : Vitesse du piston (soupape)
C et á : paramètres
dépendants de la loi de comportement du fluide F'c :
Force de l'amortisseur ajouté au système
U& & g :
Accélération sismique du sol
á ,â : Paramètres
employés par la méthode d'intégration de NEWMARK.
T : Période propre de la structure
d : Déplacement élastique
Sa ( T, æ) : Accélération du
spectre élastique du règlement ñ :
Coefficient de réduction
înl : Amortissement dû à
l'amortisseur
îvisqueux : Amortissement visqueux de la
structure
h(á) : Fonction de
linéarisation
F : Force maximale de l'amortisseur
Liste des tableaux
Tableau I.1 : classement de
l'amortissement. Tableau I.2 : définition de
l'amortissement. Tableau I.3 : mesure de
l'amortissement - Bibliothèque Millikan
Tableau I.4 : valeurs
caractéristiques d'amortissement (en pourcentage)
Tableau III.1 : différents types
d'amortisseurs selon les différentes valeurs de l'exposant
á Tableau IV.1 : valeur du déplacement
maximal
Tableau IV.2 : valeur du déplacement
maximal Tableau IV.3 : valeur du déplacement
maximal
Tableau IV.4 : récapitulatif des
valeurs du déplacement maximal
Tableau V.1 : tableau récapitulatif
du model 1 (portique sans amortisseur)
Tableau V.2 : tableau récapitulatif
du model 1 (portique avec amortisseur)
Tableau V.3 : tableau récapitulatif
de comparaison entre portique avec ou sans amortisseur Tableau V.4
: tableau récapitulatif du model pont sans
amortisseur
Tableau V.5 : tableau récapitulatif
du model pont avec amortisseur
Tableau V.6 : tableau récapitulatif
du model pont avec appareils d'appuis glissants et un amortisseur du model pont
avec amortisseur
Tableau V.7 : tableau récapitulatif
de comparaison entre pont avec ou sans amortisseur
Liste des figures
Figure I.1 : Différents types
d'amortissement. Figure I.2 Réponses libres de
vibration Figure I.3 Spectre de réponse en
fréquence.
Figure I.4. Diagramme de
contrainte-déformation sous chargement cyclique.
Figure I.5 : Vibrations harmoniques
forcées de la bibliothèque de Millikan
Figure I.6 : Réponse sismique de la
bibliothèque Millikan
Figure I.4 : Systèmes à
amortissement contrasté FigureI.8 :
Amortissement de Rayleigh
Figure I.9 : Amortissement de Caughey
Figure II.1 : Appui en caoutchouc fretté
Figure II.2 : Appui en pendule glissant
Figure II.3 : Appuis à
déformation et à glissement
Figure II.4 : Appui à billes
Figure II.5 : Caoutchouc fretté avec
amortisseur en barreau de plomb
Figure II.6 Coupe transversale d'un
amortisseur type visqueux à liquide
FigureII.7 Illustration des contreventements
par amortisseur visqueux d'un bâtiment
FigureII.8 Utilisation des amortisseurs dans les
bâtiments
FigureII.9 Système de contreventement
en acier avec amortisseurs visqueux
Figure II.10 : Coupe transversale d'un
amortisseur visqueux
Figure II.11 : Montage d'amortisseurs
visqueux en superstructure
FigureII.12 Système d'amortisseurs
actifs FigureII.13 Utilisation des amortisseurs
FigureII.14 Amortisseurs dans les ponts
Figure II.15: Amortisseur à frottement
Figure II.16: Comportement d'un ressort
élastique
Figure II.17: Comportement d'un
fusible
Figure II.18 : Comportement d'un amortisseur
visqueux
Figure II.19 : Comportement d'un fusible/
amortisseur élastoplastique
Figure III.1 : Lois de comportements de
différents types d'amortisseurs Figure IV.1
Oscillateur simple
Figure V.1 : Modèle portique sans
amortisseur Figure V.2 : Modèle portique avec
amortisseur Figure V.3 : Modèle pont en
élévation
Figure V.4 : Section transversale du
pont
Figure V.5 : Pont courant avec appareils
d'appuis néoprène
Figure V.6 : Pont courant avec appareils
d'appuis néoprène en service
Figure V.7 : Pont courant avec appareisl
d'appuis néoprène en séisme
Figure V.8 : Période
Figure V.9 : Spectre de
réponse
Figure V.10 : Déformation de la
pile
Figure V.11 : Pont avec appareils d'appuis
glissants
Figure V.12 : Pont avec appareils d'appuis
glissants en service
Figure V.13 : Pont avec appareils d'appuis
glissants sous séisme
Figure V.14 : Période
Figure V.15 : Spectre de
réponse
Figure V.16 : Pont avec appareils d'appuis
glissants et des amortisseurs
Figure V.17 : Pont avec appareils d'appuis
glissants et des amortisseurs en service
Figure V.18 : Pont avec appareils d'appuis
glissants et des amortisseurs sous séisme
Figure V.19 : Période
Figure V.20 : Spectre de
réponse
Figure V.21 : Spectre de réponse de
comparaison
Figure V.22 : L'utilité des organes
parasismique pour un bâtiment
Figure V.23 : Fenêtre d'introduction
des données Figure V.24 : Fenêtre des
résultats
Figure V.25 : Fichier résultat,
relatif au : calcul des paramètres de l'amortisseur
Liste des graphes
Graphe IV.1 : Signal séismique d' El-
centro
Graphe IV.2 : Variation de
déplacement en fonction du temps avec ù=1 et î=0%
Graphe IV.3 : Variation de
déplacement en fonction du temps avec ù=1 et î=5%
Graphe IV.4 : Variation de
déplacement en fonction du temps avec ù=1 et î=10%
Graphe IV.5 : Variation de
déplacement en fonction du temps avec ù=1 et î=20%
Graphe IV.6 : Variation de
déplacement en fonction du temps avec ù=1 et î=50%
Graphe IV.7 : Variation de
déplacement en fonction du temps avec ù=1 et î=100%
Graphe IV.8 : Comparaison des
déplacements de différentes valeurs de î avec ù=1
Graphe IV.9 : Variation de déplacement en
fonction du temps avec ù=5 et î=0%
Graphe IV.10 : Variation de
déplacement en fonction du temps avec ù=5 et î=5%
Graphe IV.11 : Variation de déplacement en fonction
du temps avec ù=5 et î=10% Graphe IV.12 :
Variation de déplacement en fonction du temps avec
ù=5 et î=20% Graphe IV.13 : Variation de
déplacement en fonction du temps avec ù=5 et î=50%
Graphe IV.14 : Variation de déplacement en fonction
du temps avec ù=5 et î=100% Graphe IV.15 :
Comparaison des déplacements de différentes valeurs
de î avec ù=5 Graphe IV.16 : Variation
de déplacement en fonction du temps avec ù=10 et î=0%
Graphe IV.17 : Variation de déplacement en
fonction du temps avec ù=10 et î=5% Graphe IV.18 :
Variation de déplacement en fonction du temps avec
ù=10 et î=10% Graphe IV.19 : Variation
de déplacement en fonction du temps avec ù=10 et î=20%
Graphe IV.20 : Variation de déplacement en
fonction du temps avec ù=10 et î=50% Graphe IV.21 :
Variation de déplacement en fonction du temps avec
ù=10 et î=100% Graphe IV.22 :
Comparaison des déplacements en fonction de î avec
ù=5
Graphe V.1 : Déplacement du portique
sans amortisseur
Graphe V.2 : Vitesse du portique sans
amortisseur
Graphe V.3 : Accélération du
portique sans amortisseur
Graphe V.4 : Déplacement du portique
avec amortisseur
Graphe V.5 : Vitesse du portique avec
amortisseur
Graphe V.6 : Accélération du
portique avec amortisseur
Graphe V.7 : Comparaison des
déplacements entre portique avec et sans amortisseur
Graphe V.8 : Comparaison des vitesses entre
portique avec et sans amortisseur Graphe V.9 :
Comparaison des accélérations entre portique avec et
sans amortisseur Graphe V.10 : Déplacement du
pont sans amortisseur
Graphe V.11: Vitesse du pont sans
amortisseur
Graphe V.12 : Accélération du
pont sans amortisseur
Graphe V.13 : Déplacement du pont
avec amortisseur
Graphe V.14: Vitesse du pont avec
amortisseur
Graphe V.15 : Accélération du
pont avec amortisseur
Graphe V.16 : Comparaison des
déplacements entre pont avec et sans amortisseur Graphe
V.17 : Comparaison des vitesses entre pont avec et sans
amortisseur Graphe V.18 : Comparaison des
accélérations entre pont avec et sans amortisseur
Graphe V.19 : Déplacement du pont
avec appareils d'appuis glissants et un amortisseur Graphe V.20 :
Vitesse du pont avec appareils d'appuis glissants et un
amortisseur Graphe V.21 : Vitesse du pont avec
appareils d'appuis glissants et un amortisseur
SOMMAIRE
Introduction générale .1
Chapitre I : Amortissement, théories et
concepts
I.1. Introduction 4
I.2. Définition de l'amortissement 4
I.3. Classification de l'amortissement 5
I.3.1. la position de l'amortissement .5
I.3.2. Nature de l'amortissement 5
a- L'amortissement matériel 5
b- L'amortissement de système .6
c- L'amortissement de rayonnement .6
I.3.3. Aspect physique 7
A. Amortissement visqueux 7
B. Amortissement de Coulomb ..7
C. Amortissement par hystérésis 8
I.4. Mesure de l'amortissement 9
I.4.1. Méthode de courbe d'affaiblissement 9
I.4.2. Méthode de largeur de bande ..10
I.4.3. Méthode de l'énergie ..11
I.4.4. Méthode de déphasage 12
I.5. Mesure de l'amortissement modal 13
I.5.1. Principe de l'amortissement modal ..13
I.5.2. Valeurs caractéristiques de l'amortissement
..15
I.6. Amortissement non classique 15
I.7. Construction de la matrice d'amortissement .17
I.7.1. Amortissement de Rayleigh ...17
I.7.2. Amortissement de Caughey 18
I.7.3. Matrice d'amortissement modal .19
|
Chapitre II : Identification et typage des
parasismiques
|
organes et dispositifs
|
|
II.1.Introduction
|
..22
|
|
II.2.Les appuis parasismiques
|
.22
|
|
II.2.1.Appuis à déformation
|
23
|
|
II.2.2.Appuis à glissement
|
24
|
|
II.2.3.Appuis à déformation et à glissement
|
25
|
|
II.2.4.Appuis à roulement
|
25
|
|
II.3.Le choix entre ces types
|
26
|
|
II.4. Dispositifs d'amortissement
|
26
|
|
II.5.Addition des amortisseurs parasismiques aux structures
|
.27
|
|
II.6.Types d'amortisseurs parasismiques
|
27
|
|
II.6.1.Amortisseurs hystérétiques
|
27
|
|
II.6.2.Amortisseurs visqueux
|
..28
|
|
II.6.3 Amortisseur à frottement
|
32
|
|
II.7. Conditions d'addition des amortisseurs aux constructions
|
33
|
II.8. Différents appareils disponibles permettent
d'obtenir les relations force-déplacement
.34
II.8.1. Ressort élastique 34
II.8.2. Fusible 35
II.8.3. Amortisseur visqueux 35
II.8.4. Fusible/amortisseur élasto-plastique 36
II.8.5. Coupleur dynamique 36
Chapitre III : Formulation du problème
d'amortissement et méthode de dimensionnement des
amortisseurs
III.1. Introduction 37
III.2. Caractéristiques des amortisseurs visqueux 37
III.3. Formulation des amortisseurs dans l'équation du
mouvement .38
III.4. Méthode de dimensionnement des amortisseurs
visqueux non linéaire a partir d'un spectre de réponse 44
Chapitre IV : Application numérique sur un
oscillateur simple
IV.1. Introduction 51
IV.2. Formulation mathématique du problème 51
IV.3. Application 52
Chapitre V : Application (pont et portique) et
développement d'un logiciel de dimensionnement des
amortisseurs
|
V.1. Introduction
|
62
|
|
V.3. Exemples étudiés
|
.63
|
|
V.3.1. Cas d'un portique
|
...63
|
|
V.3.1.1. Portique sans amortisseur
|
63
|
|
V.3.1.2. Portique avec amortisseur
|
66
|
|
V.3.1.3. Comparaison des valeurs du déplacement, vitesse
et accélération entre portique sans et avec amortisseur
|
68
|
|
V.3.2. Cas d'un pont
|
70
|
|
V.3.2. 1. Pont sans amortisseurs
|
.71
|
|
V.3.2. 2. Pont avec amortisseurs
|
74
|
|
V.3.2.3. Comparaison
|
76
|
V.3.2.4. pont avec amortisseurs et appareils d'appuis glissants
sur les culées et la
|
pile
|
77
|
|
V.3.3. Interprétation
|
80
|
|
V.4. Exemple de conception
|
81
|
|
V.4. 1.Cas d'un pont
|
.81
|
|
V.4. 1.Cas d'un bâtiment
|
88
|
V.5. Dimensionnement d'amortisseurs visqueux non linéaires
pour les ouvrages de génie civil 89
Conclusion générale ..96
Références bibliographiques
Introduction générale
Introduction générale
I. Introduction générale
Les tremblements de terre les plus récents, survenus
dans le monde et en particulier en Algérie ont causé la mort de
milliers de personnes et de graves dommages matériels. L'exemple qui
reste gravé dans notre mémoire est le dernier séisme qui a
touché les régions de Boumerdes et d'Alger (Séisme de
Boumerdes du 21 Mai 2003). Pour l'ensemble des acteurs participant à
l'acte de construire, le séisme est l'épreuve de
vérité pour une construction. L'objectif que l'on se fixe est de
contribuer à la mise en oeuvre d'une démarche
réfléchie dans la protection parasismique des structures.
Pour un grand nombre d'ingénieurs, l'approche la plus
conventionnelle de protection des ouvrages (bâtiments et ponts) des
effets des tremblements de terre consiste à augmenter leur
rigidité. Cette approche n'est pas toujours efficace surtout quand il
s'agit d'un contexte qui favorise le phénomène de
résonance et d'amplification des forces sismiques.
Par conséquent, le domaine du génie parasismique
a connu des percées importantes catalysées entre autres par le
développement des techniques de calcul sur support informatique et
l'utilisation des installations d'essais puissantes. Ceci a favorisé
l'émergence de plusieurs technologies innovatrices telles que
l'introduction des dispositifs spéciaux d'isolation entre
l'infrastructure et la superstructure. Cette approche, communément
connue sous le nom " isolation sismique " permet d'absorber les efforts
importants sans que la structure ne soit endommagée et ainsi assurant la
protection des vies humaines et des biens matériels [14].
En outre, les déplacements imposés à la
construction par les secousses du sol se localisent principalement au niveau
des appuis. Grâce à ces déplacements, la période
propre de la construction s'allonge et les charges sismiques sont
réduites. Il y a donc une atténuation du mouvement sismique
[4].
De même, ce mécanisme d'isolation de la base peut
être utilisé en association avec des amortisseurs parasismiques
dans le but de contrôler la déformation du système
d'isolation et le déplacement absolu de la superstructure située
au dessus de l'interface d'isolation. D'autre part, on peut utiliser seulement
ces amortisseurs parasismiques pour atténuer les amplitudes
d'oscillations et par conséquent réduire les charges sismiques.
L'utilisation des dispositifs d'amortissement représente une solution
efficace pour la réhabilitation des structures existantes. Compte tenu
de tous ces moyens de réduction d'accélération
considérés comme passifs, de nombreuses recherches ont
été menées durant plusieurs années pour mettre au
point un système de maîtrise actif de la réponse des
bâtiments aux séismes [3].
En effet, au cours des vingt dernières années,
ces technologies innovatrices de dissipation d'énergie et d'appuis
parasismiques ont été développées et
proposées pour améliorer la performance sismique des
bâtiments. Certains de ces appuis parasismiques ont déjà
été utilisés tandis que d'autres sont restés au
stade d'études théoriques ou d'essais. Par la suite, cette
technique des appuis parasismiques, avec plusieurs variantes, a suscité
par le passé et actuellement, un intérêt pour la plupart
des pays concernés par le risque sismique. Par conséquent, une
attention considérable est accordée à cette technologie
principalement au Japon et aux États-Unis, qui ont introduit
l'installation de ces systèmes non seulement dans les nouveaux
bâtiments mais aussi pour la réhabilitation des bâtiments
existants.
En outre, des séismes ont déjà
frappés des structures de constructions récentes, tels que les
séismes dévastateurs de Northridge (Californie, 1994) et de Kobe
(Japon, 1995). On a constaté que les structures isolées
sismiquement se sont très bien comportées [13]. A cet effet, la
réalisation d'ouvrages avec des systèmes d'isolation sismique
suscite un intérêt certain pour les pays sujets à
l'activité sismique. En l'Algérie, ces dispositifs sont en cours
d'utilisation par des entreprises étrangères dans les autoroutes
et dans un bâtiment en cours de réalisation. Notons aussi la
rédaction en cours du 'Règlement Parasismique des Ouvrages d'Art'
(RPOA).
Notre travail consiste à faire dans un premier temps,
un bilan bibliographique portant aussi bien sur les plans théorique et
conceptuel de l'amortissement et d'appareils d'amortissement. Nous
procédons dans un deuxième temps à des applications
concrètes pour montrer l'intérêt de l'incorporation de ces
appareils aux structures (portique et pont). Cet intérêt est mis
en évidence par la réduction des grandeurs tels le
déplacement, la vitesse et l'accélération de ces
structures supposées soumises à un signal sismique.
Le mémoire est subdivisé en cinq chapitres :
Le premier chapitre a pour but de présenter les concepts
et les théories de l'amortissement,
Le deuxième chapitre porte sur l'identification et typage
des organes et dispositifs parasismiques,
Le troisième chapitre présente les étapes et
les formules nécessaires à la résolution du
problème de l'amortissement,
Le quatrième chapitre porte sur une application
numérique programmée en fortran consistant à mettre en
évidence l'importance de l'amortissement,
Le cinquième chapitre présente une application
numérique réalisée par un programme informatique pour
montrer la pertinence des structures avec des amortisseurs comparativement
à des structures sans amortisseur ainsi de développer un logiciel
du dimensionnement des amortisseurs visqueux nommé DAV 2007
v.1.0.
Ce modeste travail se termine par une conclusion
générale portant sur les résultats obtenus et certaines
recommandations concernant l'utilisation et le dimensionnement des
amortisseurs.
Chapitre I : Amortissement, théories et
concepts
Amortissement, théories et concepts
I.1. Introduction
La notion d'amortissement constitue un sujet très
important dans les études de structures soumises à des
excitations dynamiques. Mais, elle a besoin d'être maîtrisée
pour être incorporée efficacement dans l'analyse des structures.
Il existe relativement peu de littérature traitant le sujet dans la
profondeur qu'il mérite.
L'amortissement est un paramètre important dans
l'analyse des structures sous chargement dynamique. Un ensemble de valeurs des
coefficients d'amortissement issu d'une base expérimentale est
proposé pour mener une analyse structurelle selon le type de
matériaux.
Le but de ce chapitre est de définir l'amortissement et
d'en discuter les bases conceptuelles et théoriques.
I.2. Définition de l'amortissement
La consultation du dictionnaire Larousse donne les
définitions suivantes de
l'amortissement :
Amortissement n. m. diminution d'amplitude d'un mouvement
ondulatoire. (Prélèvement annuel sur les bénéfices
d'une entreprise pour compenser la diminution de valeur subie par les
immobilisations du fait de leur vétusté) : amortissement
industriel. (Extinction graduelle d'une dette) : amortissement
financière.
Quelques synonymes de l'amortissement ;
amortissement : adoucissement, affaiblissement,
apaisement, assourdissement, atténuation, extinction, rendement,
travail, utilisation.
Des définitions par domaine sont données dans le
tableau ci-après :
Tableau I.2 : différentes
définitions pour l'amortissement.
|
Domaine
|
Définition
|
|
- électricité
|
Diminution progressive dans le temps de certaines grandeurs
caractéristiques d'un phénomène
|
|
- géologie
|
Diminution progressive de l'amplitude d'un déplacement
tectonique au sein des terrains voisins.
|
|
- physique
|
Terme qui caractérise la rapidité de l'extinction
graduelle d'une vibration.
Affaiblissement progressif des mouvements vibratoires sonores
dans un corps, par suite de la dissipation de l'énergie.
|
L'amortissement définit les propriétés de
dissipation d'énergie d'un matériel ou d'un système sous
un effort cyclique, pour notre cas dynamique. L'amortissement dans une
structure vibrante est associé à la dissipation de
l'énergie mécanique, habituellement par conversion en une
énergie thermique. La dissipation d'énergie est égale au
travail effectué par la force d'amortissement. Ainsi, l'amortissement
est fondamentalement la dissipation de l'énergie qui se produit dans les
systèmes vibrants [1].
I.3. Classification de l'amortissement
L'amortissement peut être identifié et
caractérisé par trois paramètres qui sont directement
liées à son environnement, à savoir sa localisation, sa
nature matériels et son aspect physique.
I.3.1. la position de l'amortissement
La position de l'amortissent est le lieu où se produit
l'amortissement ; ceci nous permet de distinguer deux types, amortissement
interne qui se produit à l'intérieur du système et
l'amortissement externe qui se produit aux limites du système
(interface).
I.3.2. Nature de l'amortissement
La nature de l'amortissement est généralement
décrite comme suit: - Amortissement matériel ;
- Amortissement de système ;
- Amortissement de rayonnement.
a- Amortissement matériel
L'amortissement matériel est l'énergie
absorbée dans les matériaux de construction. Il est du à
l'hystérésis interne des matériaux résultant du
comportement non linéaire des contrainte- déformation, du
frottement inter granulaire et de la thermo élasticité. Celui-ci,
existe généralement pour la plupart des aciers de construction et
de béton armé, cependant l'amortissement pour certain
matériaux comme le bois de construction stratifié peut être
important.
b- Amortissement de système
L'amortissement de système est l'énergie
absorbée au niveau des discontinuités structurales, par exemple
les raccordements boulonnés ou rivetés et les joints de
construction des structures en béton armé. Ceci résulte du
frottement dans le glissement ou le rongement des joints, des appuis, du
revêtement ou des diverses autres parties de la structure pendant le
mouvement relatif. Il est également connu sous le nom d'amortissement de
discontinuité. On considère que l'amortissement matériel
peut être prévu et mesuré par des essais, alors qu'il est
beaucoup plus difficile de prévoir le niveau de l'amortissement de
système où le degré peut changer considérablement
même pour les structures qui sont identiques.
c- Amortissement de rayonnement
L'amortissement de rayonnement est l'énergie
absorbée par l'environnement de la structure, par exemple la
résistance de l'air, de l'eau et des fondations qui sont difficilement
prévisible. La dissipation de l'énergie dans les fondations se
produit même lorsque le matériel de fondation est
linéairement élastique en raison de la propagation des ondes
d'effort par la fondation [1].
L'organigramme suivant résume les différents
types d'amortissements (figure I.1).

Amortissement

Hystéries
(Visqueux, friction.)
Matériel
Interne
Mouvement relatif entre les
sous- structures
(roulements,
joints, etc...)
Système
Surfaces de contact des
structures
Rayonnement
Contact externe (élément
non
structurel, rayonnement
d'énergie au sol).
Externe
Position
Natures
Physique
Figure I.1 : classification de
l'amortissement.
I.3.3. Aspect physique
L'amortissement, comme décrit précédemment,
est représenté par trois familles (pas nécessairement et
spécifiquement liées à une méthode
particulière de dissipation d'énergie):
- Amortissement visqueux.
- Amortissement de Coulomb.
- Amortissement par hystérésis.
On doit noter que ceci correspond à une
représentation modérée n'impliquant pas un
mécanisme pour l'amortissement [1].
A. Amortissement visqueux
Les forces d'amortissement dans l'analyse dynamique des
structures sont supposées habituellement proportionnelles à
l'amplitude de la vitesse et opposées à la direction du
mouvement. Ce type d'amortissement est connu en tant qu'amortissement visqueux.
Il est analogue à l'amortissement produit par le mouvement des
fluides.
Bien que l'amortissement de type visqueux peut être
exprimé de manière mathématique simple, d'autres types
d'amortissement plus complexes sont souvent exprimés en tant
qu'amortissement visqueux équivalent en analyse. L'analogie avec
l'amortissement visqueux est souvent faite indépendamment des
caractéristiques dispersives réelles du système. En fait,
il est admis que si la nature brute de la dissipation est expliquée, les
détails réels sont non pertinents pour des calculs de
technologie. C'est-à-dire, le concept de prise en compte d'amortissement
visqueux équivalent est mitigé [1].
B. Amortissement de Coulomb
L'amortissement de Coulomb ou amortissement de friction peut
être considéré comme existant quand la force
d'amortissement est constante (dépendant seulement de la réaction
normale) et s'oppose au mouvement du corps en mouvement.
L'amortissement des structures réelles n'est pas
strictement dû à la viscosité mais dans la plupart du temps
est provoqué par le frottement aux interfaces comme dans les assemblages
boulonnés, dans les joints du revêtement et dans les fissures du
béton armé. Ces forces de friction sont indépendantes de
l'amplitude et de la fréquence, elles s'opposent toujours au mouvement
et leur grandeur, à une première approximation, peut être
considérée constante.
Les expériences prouvent que les vibrations des
structures réelles se trouvent habituellement entre les réponses
visqueuses et de friction. Cependant, la prétention visqueuse est
commode pour l'employer analytiquement et est suffisamment précise pour
la plupart des objectifs [1].
C. Amortissement par hystérésis
Les expériences sur l'amortissement qui se produit dans
les matériaux solides des structures qui ont été soumises
à une contrainte cyclique ont montré que la force d'amortissement
peut être indépendante de la fréquence de la force
d'excitation. Afin de modéliser cet amortissement interne ou
matériel, la limite de l'amortissement par hystérésis de a
été définie telle que :
ÄU = ð æ A2 (I.1)
Cette définition de l'amortissement par
hystérésis s'avère justement coïncider avec celle de
l'amortissement structural comme indiqué par Clough et Penzien (1975)
pour l'excitation d'état d'équilibre.
Clough et Penzien (1975) définissent l'amortissement
structural pour un système à un seul degré de
liberté en tant que tel, tant que la force d'amortissement est
proportionnelle au déplacement et s'oppose au mouvement. Sous toute
condition autre que celle de l'excitation d'état d'équilibre,
cette définition est quelque peu douteuse. Néanmoins, à
l'état d'équilibre, elle donne le même résultat que
l'amortissement par hystérésis comme dans l'équation.
(I.1).
L'amortissement par hystérésis est le
résultat du frottement entre les plans internes qui glissent les uns sur
les autres pendant la déformation du corps. L'énergie
absorbée dans cette déformation est dissipée sous forme de
chaleur [1].
L'origine principale de l'amortissement est toujours le
frottement par exemple l'oscillation d'un pendule s'atténue
progressivement après un certain nombre de cycles à cause des
frottements entre l'air le pendule et le frottement de la rotule.
I.4. Mesure de l'amortissement
Comme discuté précédemment, il y a
plusieurs manières de définir mathématiquement la
capacité d'amortissement matériel et/ou de structure. Dans une
situation donnée le procédé utilisé dépendra
principalement de la méthode de mesure adoptée.
La mesure de l'amortissement dans le béton a toujours
posé des difficultés parce que le béton est un
matériau hétérogène avec un amortissement
relativement bas. Les procédures expérimentales ont
généralement favorisé l'essai par des méthodes
résonnantes et en particulier l'affaiblissement d'un système
libre vibrant. Il y a une variété de techniques qui sont
généralement utilisées pour mesurer la capacité
d'amortissement [1].
I.4.1. Méthode de courbe d'affaiblissement ` courbe
d'atténuation'
Elle est connue comme étant la méthode
d'affaiblissement libre. Elle compte parmi les méthodes directes.
L'amortissement est obtenu en mesurant la diminution de l'amplitude de
vibrations libres (voir figure I,2) et puis en calculant la décroissance
logarithmique ä [1].
1 ? A ?
(I.2)
1
ä= . ln
+1
n ??An ??
Figure I.2 Réponses libres de
vibration.
Les structures sont excitées par un marteau pour des
vibrations libres, et les réponses sont enregistrées à un
ou plusieurs points par des accéléromètres. (FigureI.2)
I.4.2. Méthode de largeur de bande
Pour un amortisseur idéal et pour de petites valeurs
d'amortissement la constante d'amortissement peut être obtenue par la
différence entre les valeurs Ù2 etÙ1 de la courbe de
résonance due à une fonction harmonique (voir figure I.3).
Selon la réponse du spécimen autour de sa
fréquence de résonance (Cole, 1965), la " largeur de bande " est
dénotée par Q, où :
(I.3)
1 Ù - Ù
2 1
=

r
Q 3Ù
Dans laquelle Ùr, est la fréquence de
résonance et Ù1 et Ù2 sont les fréquences se
trouvant respectivement à gauche et à droite, leur
amplitude est égale à la moitié de la fréquence de
la résonance (voir figure I.3).


Figure I.3 spectre de réponse en
fréquence.
Au lieu d'utiliser la courbe d'amplitude de
déplacement, la vitesse ou les courbes d'amplitude
d'accélération peuvent être également
employées dans les cas où l'amortissement est faible. Pour des
valeurs relativement petites de la capacité d'amortissement, la
décroissance logarithmique équivalente ä peut être
obtenue à partir de l'expression:
Q = ð (I.4)
ä
Dans la plupart des cas pratiques l'amortissement est
évalué par la méthode de la courbe d'affaiblissement
(comme discuté dans la section précédente) plutôt
que par la méthode de la largeur de bande [1].
I.4.3. Méthode de l'énergie
L'amortissement peut être également mesuré
au moyen de la capacité d'amortissement spécifique S
définie comme étant le rapport de l'énergie de
déformation perdue par cycle à toute l'énergie de
déformation du modèle pour ce cycle :
S Ä E
= (I.5)
E
ÄE : est l'énergie qui est transformée en
chaleur ou énergie de contrainte interne et E est l'énergie
de
déformation à l'amplitude maximale. La valeur de S peut
être déterminée directement en
mesurant le secteur de la boucle d'hystérésis du
diagramme de contrainte-déformation du modèle sous le chargement
cyclique, comme indiqué sur la figure2.4. De nouveau, selon Cole et
Spooner (1968), pour de petites valeurs de l'amortissement, le
décrément logarithmique, ä, est obtenu par[1]. :
S
ä = (I.6)
2
Contrainte ó
Figure I.4. Diagramme de
contrainte-déformation sous chargement cyclique.
I.4.4. Méthode de déphasage
Dans le cas de fonctions de forces oscillatoires, la
contrainte (ou les forces internes) est trouvée pour mener la
déformation (ou le déplacement). L'angle de phase ö qui
représente le retard de la contrainte derrière l'effort
appliqué dans les oscillations forcées d'un spécimen, peut
être employé pour évaluer la capacité
d'amortissement.
Selon Cole et Spooner (1968), la décroissance
logarithmique, ä, peut être liée à cet angle de phase
ö comme indiqué par l'expression suivante[1].:
ä = ð tan ö (I.7)
I.5. Mesure de l'amortissement modal
I.5.1. Principe de l'amortissement modal
La bibliothèque Millikan, sur le campus de
l'université de Caltech (Californie), fournit un exemple de mesures de
l'amortissement sur une structure réelle.
Cet ouvrage a été sollicité à
l'aide de vibreurs harmoniques convenablement disposés sur sa hauteur
pour exciter son mode fondamental. Par ailleurs, on dispose sur le même
ouvrage d'enregistrements accélérométriques recueillis
lors des deux séismes l'ayant sollicité : séisme de Lytle
Creek de magnitude 5.4 sur l'échelle de Richter et
d'accélération maximale au sol égale à 0.05g et
séisme de San Fernando de magnitude 6.4 sur l'échelle de Richter
et d'accélération maximale au sol égale à 0.20g. La
figure I.5 présente, pour l'excitation par vibreur, la réponse en
accélération au sommet de l'immeuble en fonction de la
fréquence d'excitation des vibreurs. L'enregistrement fait clairement
apparaître un pic marqué à la fréquence de 1.49 Hz
correspondant à la fréquence du mode fondamental.
Pour le mode fondamental de vibration, la structure
répond comme un oscillateur à un seul degré de
liberté. Une méthode d'identification inverse permet donc de
déterminer le pourcentage d'amortissement critique reproduisant au mieux
la courbe de la figure I.5 La valeur obtenue est donnée dans le tableau
I.3.

Figure I.5 : Vibrations harmoniques
forcées de la bibliothèque de Millikan
La figure I.6 représente pour le séisme de San
Fernando les accélérations enregistrées à la base
et au sommet de l'ouvrage à partir desquelles le déplacement
différentiel sur la hauteur peut être calculé (figure I.5).
En reproduisant des résultats analogues à plusieurs niveaux, il
est
possible d'identifier les deux premiers modes de vibration de
l'ouvrage et de calculer le pourcentage d'amortissement critique associé
à chacun de ces modes. Les résultats obtenus sont donnés
dans le tableau I.3

Figure I.6 : Réponse sismique de la
bibliothèque Millikan
Le tableau I.3 fait apparaître des résultats
importants, qui ont une portée plus générale que ceux
relatifs à cet ouvrage. La période du mode fondamental
croît lorsque l'amplitude de la sollicitation augmente depuis
l'excitation par vibreur jusqu'au séisme le plus fort.
Corrélativement l'amortissement du mode fondamental croît de 1%
à 7%. On constate également que l'amortissement modal n'est pas
constant et peut être plus élevé ou plus faible sur le
deuxième mode que sur le premier. Ces mesures confirment en particulier
que l'amortissement dépend de l'amplitude de la déformation
[2].
Tableau I.3 : Amortissement
mesurés- Bibliothèque Millikan
|
Excitation
|
Accélération (g)
|
Mode fondamental
|
Seconde mode
|
|
Période (s)
|
Amortissement (%)
|
Période (s)
|
Amortissement (%)
|
|
Générateur
Vibrations
|
3.10-3 à 17.10-3
|
0.66 - 0.68
|
0.7-1.5
|
-
|
-
|
|
Lytle Creek
|
0.035
|
0.71
|
2.2
|
0.18
|
3.6
|
|
San Fernando
|
0.348
|
0.98
|
7.0
|
0.20
|
5.9
|
I.5.2. Valeurs caractéristiques d'amortissement
Hormis des cas exceptionnels comme celui de la
bibliothèque Millikan, on ne dispose pas de mesures de l'amortissement
sur l'ouvrage à étudier. L'analyste doit s'en remettre à
son propre jugement ou à des valeurs conventionnelles publiées
par voie réglementaire. Ces valeurs sont généralement
rattachées à un type de matériau (béton, acier,
bois, etc...). Le tableau I.4 présente un tel ensemble de valeurs dans
lequel une distinction a été introduite en fonction du niveau de
sollicitation atteint dans l'ouvrage [2].
Tableau I.4 : Valeurs
caractéristiques d'amortissement ( en pourcentage)
|
Déformation
Matériau
|
< 0.5 limite élastique
|
Voisinage limite élastique
|
|
Béton arme
|
3-5
|
7-10
|
|
Béton précontraint
|
2-3
|
7-10
|
|
Acier soudé
|
2-3
|
5-7
|
|
Acier boulonné
|
5-7
|
10-15
|
|
Bois cloué
|
5-7
|
15-20
|
I.6. Amortissement non classique
Certains systèmes conduisent à des valeurs
d'amortissement très contrastées entre les différentes
parties de l'ouvrage. Cette situation se rencontre par exemple pour
l'étude des phénomènes d'interaction sol-structure ou
fluide-structure (figure I.4). Généralement les structures
présentent des pourcentages d'amortissement équivalents
relativement faibles, de l'ordre de quelques pourcents (tableau I.4), alors que
le milieu avec lequel elles interagissent peut présenter des
amortissements plus élevés (cas du sol où la valeur peut
atteindre plusieurs dizaines de pourcents) ou du fluide dans lequel il est au
contraire très faible (inférieur à 1 %)[2].

Figure I.4 : Systèmes à
amortissement contrasté
Dans le même ordre d'idée, l'utilisation
d'amortisseurs concentrés conduit également à des valeurs
contrastées de l'amortissement entre les différentes parties du
système. Cette technique est utilisée par exemple pour
l'isolation vibratoire des machines vibrantes, la conception ou le renforcement
de structures en zone sismique, l'idée étant d'accroître la
dissipation d'énergie et donc de limiter la part de l'énergie
transmise à l'ouvrage. Lorsqu'une structure est composée d'un
assemblage de plusieurs matériaux, l'usage veut que l'amortissement
modal équivalent soit calculé au prorata de l'énergie
élastique de déformation Ei emmagasinée dans chacun des
matériaux [2].
? î E
i i
î = (I.8)
eq
i
? E
Il peut cependant être nécessaire de construire
une matrice d'amortissement lorsque le recours à des calculs par
intégration temporelle s'avère indispensable pour la prise en
compte de systèmes partiellement non linéaires.
Plusieurs techniques sont envisageables: définir a
priori la forme de la matrice d'amortissement, construire cette matrice
à partir de la donnée de l'amortissement modal ou, lorsque cela
est possible, construire la matrice d'amortissement à partir des
données géométriques et mécaniques du
système (amortisseurs localisés). Les deux premières
approches conduisent à un amortissement qualifié d'orthogonal car
la diagonalisation de la matrice d'amortissement sur la base des modes propres
est préservée. La dernière approche conduit
généralement à un amortissement non classique qui
nécessite le recours à des techniques de résolution
spécifiques pour la résolution sur la base des modes [2].
I.7. Construction de la matrice d'amortissement
I.7.1. Amortissement de Rayleigh
On se donne à priori la structure de la matrice
d'amortissement sous la forme d'une combinaison linéaire de la matrice
de masse et de la matrice de rigidité [2].
C =á?M
+â K (I.9)
·
·
·
M U + CU +KU = F(t)
(I.10)
Il est évident que dans ce cas, la
propriété d'orthogonalité de la matrice d'amortissement
par rapport aux modes propres est préservée. En reportant
l'équation (I.9) dans l'équation générale de la
dynamique (I.10) et en faisant usage de cette propriété,
l'équation du mouvement s'écrit :
|
m y t
& & + á + â & +
m k y t k t y p t j N
j j ( ) ( j j j
) ( ) ( ) =
j j j ( ) , = 1,
D'où il ressort que le pourcentage d'amortissement
critique équivalent s'exprime par[2] :
|
(I.11)
|
|
1 ? á
î = +âù
j 2 ?? ? ù j
|
j
|
?
?? ?
|
(I.12)
|
L'amortissement donné par l'équation (I.12) se
compose de deux termes, l'un proportionnel à la pulsation et l'autre
inversement proportionnel à celle ci. Comme en général,
il
est souhaitable de représenter la dissipation
d'énergie dans le système par un amortissement indépendant
de la fréquence, un choix approprié des valeurs de a et â
permet de satisfaire, de façon approximative, cette condition. La
détermination de a et â est illustrée sur la figure I.9
pour le portique de la figure I.8 : en se fixant deux valeurs de pulsations, w1
et w 2, pour lesquelles l'amortissement donné par l'équation
(I.12) prend la valeur recherchée, il s'ensuit qu'entre w1 et w2
l'amortissement est sensiblement égal, quoique légèrement
inférieur, à la valeur recherchée. La première
pulsation w1 est prise égale à celle du mode fondamental du
système et la seconde w2 à la plus grande pulsation ayant un
intérêt pour cette modélisation de l'amortissement est
classiquement utilisée pour la réalisation de calculs temporels
sur des systèmes comportant une partie pseudo-élastique, pour
laquelle il est nécessaire de spécifier un amortissement
équivalent, et une partie non linéaire dans laquelle la
dissipation d'énergie est directement prise en compte par la loi de
comportement du matériau.

FigureI.8 : Amortissement de
Rayleigh
On notera que seule la combinaison linéaire de la
matrice de masse et de la matrice de rigidité permet de donner un
amortissement sensiblement indépendant de la fréquence.
L'utilisation d'un seul de ces termes donnerait naissance à un
amortissement dépendant de la fréquence dont la
réalité physique est généralement prise en
défaut [2].
I.7.2. Amortissement de Caughey
Il s'agit d'une généralisation de
l'amortissement de Rayleigh dans laquelle la matrice d'amortissement s'exprime
comme une combinaison linéaire de p termes constitués du produit
de la matrice de masse et de l'inverse de la matrice de rigidité [2].
En procédant comme pour l'amortissement de Rayleigh, on
montre que le pourcentage d'amortissement critique du mode j s'exprime par :
Ainsi en choisissant p égale à N-1, où N
est le nombre de modes, il est théoriquement possible de respecter la
valeur de l'amortissement modal pour chacun des modes du système. Dans
la pratique en retenant un nombre de termes nettement inférieur, p= N-1,
on obtient une approximation suffisante. La figure I.9 illustre l'application
de la formulation (I.13) au cas du portique de la figure I.8, avec dans ce cas
p égal à N-1 [2].

Figure I.9 : Amortissement de
Caughey
I.7.3. Matrice d'amortissement modal
Il est également possible à partir de la
donnée des amortissements modaux de construire directement la matrice
d'amortissement associée. Soit C cette matrice et
F la matrice d'ordre N
constituée des N vecteurs modaux [2] :

(I.15)
La matrice C doit satisfaire la relation :

Dans laquelle la matrice a la structure suivante :


Avec des coefficients égaux à :
c j = 2 m j ù j î
j (I.18)
L'inversion de la relation (I.16) fournit l'expression de la
matrice C :
= Ö T ? ÎÖ
[ ] 1
1
C - (I.19)
Le calcul de C par la relation (I.19) nécessite
l'inversion de deux matrices d'ordre N
n'est pas efficace d'un point de vue numérique. Tenant
compte de la relation d'orthogonalité de l'expression I.20 , dans
laquelle la matrice m est diagonale avec des coefficients
égaux aux masses généralisées j m, on en
déduit en prenant l'inverse de la relation (I.20) et en pré-
multipliant ou post-multipliant par les quantités MF et TM F , les
relations I .21 et I.22
Ö T Ö = (I.20)
M m
|
(I.21) (I.22)
|
|
En reportant les relations (I.21) et (I.22) dans la relation
(I.19), il vient :
|
|
(I.23)
|
Les matrices m et E etant diagonales ( equ I.16 et I.20) le
produit m-1Em est immédiat ; c'est une matrice diagonale k
dont les termes valent :
La matrice C s'exprime alors comme le simple produit de matrices
:
En notant symboliquement C= A x B la matrice
carrée dont les termes gk1 sont les produits ak b1 des
composantes des deux vecteurs A et B la relation (I.25) peut alors se
développer sous la forme :
Sous cette forme, le jème terme de la somme
apparaît comme la contribution du jème mode,
d'amortissement æj , à la matrice d'amortissement globale. Si ce
terme est nul, alors le mode j ne contribue pas à l'amortissement global
du système [2].
Chapitre II : Identification et typage des
organes et dispositifs parasismiques
Identification et typage des organes et dispositifs
parasismiques
II.1.Introduction
Pour atténuer les effets dynamiques (sismiques) nous
pouvons agir par l'adoption d'un système de contrôle actif ou
passif.
Le système de contrôle passif se compose de deux
types de procédés : procédé par l'isolation
sismique, procédé par l'amortissement.
L'organigramme ci après résume les
différents types de systèmes de contrôle de structures :

Système d'isolation sismique
Systèmes de contrôle passif

Systèmes de
contrôle actif

Amortisseurs
parasismiques

Systèmes de
contrôle
Système de contrôle de
structures
L'utilisation des organes parasismiques dans les structures de
génie civil notamment dans les ponts pour réduire l'effort
sismique devient de plus en plus une nécessité afin de construire
des structures qui résistent aux séismes violents.
On peut adopter une conception optimale en employant des
appareils spéciaux qui permettant de changer le schéma statique,
afin de mieux répartir les efforts entre les appuis et de les
réduire globalement.
Cette réduction d'efforts peut s'effectuer de deux
manières différentes :
- Soit on conserve au pont un comportement sensiblement
élastique linéaire et on adapte la rigidité des appuis ou
l'amortissement, seuls paramètres qui, avec la masse, conditionnent la
réponse dynamique. Les efforts maximums dans les piles et les
déplacements du tablier sont alors pratiquement proportionnels á
l'accélération du sol.
- Soit on confère au pont un comportement
élastoplastique en limitant les forces horizontales transmises par les
piles au tablier. Les efforts dans les piles sont alors peu dépendants
du niveau sismique contrairement aux déplacements.
Pour réaliser ces objectifs, on dispose de plusieurs
solutions qui sont généralement fondées sur l'utilisation
des appareils d'appuis (spéciaux ou parasismique) ou des amortisseurs
bien adopté au contexte du projet.
Ce chapitre sera consacré à l'identification, le
fonctionnement et le domaine d'utilisation des différents organes
parasismiques et dispositifs d'amortissement.
II.2. Organes parasismiques
Les organes parasismiques sont des dispositifs
caractérisés par une grande souplesse horizontale et une
rigidité verticale, ils sont placés entre l'infrastructure et la
superstructure pour dissiper le maximum d'énergie.
Il existe plusieurs types d'organes parasismiques. Certains
ont été déjà utilisés, d'autres sont
restés au stade d'études théoriques ou d'essais. Parmi ces
plusieurs catégories et selon leur mode de fonctionnement, on peut citer
[14]:
II.2.1.Appuis à deformation
Les appuis à déformation, utilisés pour
isoler les constructions sont analogues aux appuis couramment utilisés
pour les ponts et ont toujours montré un comportement satisfaisant. Ils
sont en général constitués d'un empilement de feuillets
d'élastomère naturel (caoutchouc) ou synthétique
(Néoprène) séparés par des frettes
métalliques.
La présence des frettes confère aux appuis une
grande rigidité verticale alors que les feuillets
d'élastomère peuvent se déformer facilement en
cisaillement horizontal, permettant aussi d'obtenir une grande souplesse
vis-à-vis des efforts horizontaux agissant sur le bâtiment et
autorisent des déplacements notables de la superstructure.
Par conséquent, ces appuis en élastomère
fretté fournissent une solution efficace et simple à mettre en
oeuvre pour la protection parasismique des bâtiments. Ils permettent une
réduction sensible des sollicitations sismiques subies par les
structures.
On distingue différents types d'appuis à
déformation, tels que les appuis en caoutchouc fretté (figure
II.1), les appuis en néoprène fretté et les appuis en
caoutchouc fretté avec amortisseur en barreau de plomb.

Figure II.1 : Appui en caoutchouc
fretté
II.2.2.Appuis a glissement
Le système d'appuis à glissement est
constitué d'une part de plaques solidaires de la superstructure et
d'autre part, de plaques fixées aux fondations. Leur interface constitue
le plan de glissement.
Ces systèmes permettent le découplage des
mouvements horizontaux et verticaux de la superstructure de ceux des
éléments de fondations qui est dû à la
différence importante des fréquences d'oscillation dans les deux
directions. La réponse à l'excitation sismique d'une structure
reposant sur des plaques de glissement ne dépend que de sa masse et du
coefficient de frottement entre les plaques.
Parmi ces appuis, on peut citer les appuis en pendules
glissants qui utilisent une interface de glissement sous forme de cuvette
(portion d'une sphère) qui confère à la structure un
mouvement global similaire à un pendule (figure II.2).

Rotule glissante
Surface sphérique concave
Figure II.2 : Appui en pendule glissant
II.2.3.Appuis à déformation et à
glissement
Ces appuis résultent de l'association de plaques de
glissement et des appuis élastomères (figure II.3). Dans un
premier temps, le système se déforme latéralement
grâce à la distorsion de l'élastomère. Lorsque la
force nécessaire à l'accroissement de la distorsion devient
supérieure à la force de frottement entre les plaques, ce qui se
produit lors des séismes de très forte intensité, le
glissement commence à se produire. Ce système de protection
sismique est très efficace et entraîne une réduction
à la fois des accélérations et des déplacements en
superstructure et conduit ainsi à une diminution importante des efforts
tranchants à la base.
|
Appui
à déformation
|
|
Plaques de glissement
|
|
|
|
Figure II.3 : Appuis à
déformation et à glissement
II.2.4.Appuis à roulement
Bien que plusieurs systèmes d'appuis à roulement
aient été proposés, il n'existe que très peu de
réalisations de ce type en raison des inconvénients (durée
de vie limité
maintenance difficile et coûteuse) qu'ils
présentent. Pour permettre des mouvements dans les deux directions
horizontales, on utilise des billes sphériques (fig. II.4) ou deux
couches orthogonales de rouleaux cylindriques. Un dispositif de blocage
vis-à-vis de l'action du vent ainsi que des amortisseurs parasismiques
peuvent être prévus.

Figure II.4 : Appui a billes
II.3.Choix entre les types d'appuis parasismiques
Le choix de types d'appuis appropriés pour isoler la
base des constructions nécessite une évaluation des
caractéristiques, des normes de performance parasismique et des
coûts de ces appuis parasismiques. Il est par ailleurs nécessaire
de prendre en considération le rendement et l'entretien à long
terme de ces appuis. Puisque le caoutchouc peut durcir ou s'étirer, il
est nécessaire d'effectuer des inspections périodiques afin de
s'assurer en tout temps de sa souplesse. Par contre, les appuis à
glissement ne nécessitent généralement aucun entretien.
En plus, une autre considération qui régit le
choix des appuis est l'état du sol. Les appuis à
déformation perdent en grande partie leur efficacité dans les
sols mous, à longue période d'oscillation. En effet, leurs
périodes propres sont dans ce cas proches de la période
d'excitation, donc proche de la résonance. Sur ces sols, les appuis
à glissement conviennent mieux car pour les faibles coefficients de
frottement des plaques, la réponse de la superstructure est
indépendante du contenu fréquentiel du mouvement sismique.
D'autre part, l'association de plaques de glissement et d'appuis à
déformation supprime les inconvénients que représentent
ces appuis à déformation dans les sols meubles.
Les appuis à roulement sont très peu
utilisés en raison de leurs inconvénients, dont les principaux
sont le grippage éventuel du système en l'absence durable de
mouvement, et leur faible capacité d'amortissement.
II.4. Dispositifs d'amortissement
Les amortisseurs dynamiques sont des dispositifs
utilisés pour atténuer des mouvements oscillatoires
gênants, souvent dus à des phénomènes de
résonance, qui peuvent apparaître dans des tours de grande hauteur
(World Financial Center à Shangai) ou dans des passerelles minces et
souples (Passerelle de Solferino à Paris) ou encore dans des ponts de
longue portée (Pont de Normandie). Ils peuvent être causés
par les effets des vents ou des séismes, le mouvement d'une foule de
piétons ou les effets du trafic sur un pont.
L'utilisation des amortisseurs dynamiques n'est pas
récente, mais la nécessité de trouver une solution pour
augmenter l'amortissement des structures est un problème qui se pose
même à présent.
Citons par ordre chronologique certains projets
déjà réalisés pour les quels ce souci d'amortisseur
à été pris en compte :
1978 : Pose d'un des tous premiers amortisseurs dynamiques dans
l'immeuble de la Citicorp à New-York (279m de haut).
1986 : Pose du premier amortisseur dynamique au Japon dans la
Tour du Port de Chiba (125m de haut).
1992 : Apparition des premiers amortisseurs actifs,
c'est-à-dire contrôlés par ordinateur pour optimiser leurs
performances.
Ces systèmes ont été largement
utilisés au Japon ; pays qui compte beaucoup de tours de grande hauteur,
soumises à des vents forts, à de nombreux typhons et à des
sollicitations d'origine sismique.
Ce sont essentiellement les Japonais qui ont
développé cette technique au cours des vingt dernières
années, jusqu'aux systèmes très sophistiqués
utilisant actuellement des amortisseurs contrôlés par
ordinateur.
II.5.Addition des amortisseurs parasismiques aux
structures
Dans la technologie de la construction, l'amortissement peut
être défini comme une caractéristique d'un système
structurel, qui s'oppose au mouvement en tentant à ramener le
système au repos.
La technique d'amélioration du comportement de la
structure par l'addition des dispositifs d'amortisseurs parasismiques est
semblable à celle d'un amortisseur dans un véhicule. De la
même façon que l'amortisseur réduit les chocs causés
par les mauvais états
des routes, ces amortisseurs parasismiques réduit aussi
l'incidence des mouvements du sol sur l'ouvrage et sur ses occupants [4].
Ces dispositifs d'amortisseurs permettent de dissiper une
quantité d'énergie élevée et d'atténuer les
amplitudes des oscillations sismiques. Ils convertissent l'énergie
cinétique des charges externes en énergie thermique (chaleur)
[3], généralement par des déformations inélastiques
ou de frottement concentré dans ces dispositifs, protégeant de ce
fait les autres éléments structuraux [5]. En outre, ces
amortisseurs n'ont aucune fonction porteuse dans le domaine statique et peuvent
être dimensionnés pour supportés une charge dynamique.
II.6.Types d'amortisseurs parasismiques
Un certain nombre de dispositifs d'amortisseurs sont
actuellement en service ou proposés pour l'usage en structures
conventionnelles ou en association avec des appuis parasismiques dans les
structures isolées. Ils sont plus souvent hystérétiques,
visqueux ou à frottement.
II.6.1.Amortisseurs hystérétiques
Les éléments dissipateurs peuvent être en
acier spécial dont le rôle est d'absorber les efforts sismiques et
de dissiper l'énergie par plastification alternée. Ces
éléments peuvent être combinés avec un appareil
d'appui classique acier téflon destinée à transmettre
uniquement les charges verticales. Il peut également s'agir d'un
appareil en élastomère fretté avec un noyau cylindrique en
plomb [6].

Figure II.5 : Caoutchouc fretté
avec amortisseur en barreau de plomb
II.6.2.Amortisseurs visqueux
En termes simples, les amortisseurs visqueux sont des tiges
qui se déplacent selon un mouvement de va-et-vient dans un cylindre de
liquide visqueux et qui absorbe l'énergie induite lors d'un
séisme au moyen d'une friction entre la tige, le cylindre et le liquide.
Les pièces communes d'un amortisseur visqueux sont une tige de piston
solide en acier inoxydable imprégnée de téflon, un
cylindre fermé et un liquide de travail, qui est
généralement un liquide de silicone inerte placé en
permanence dans une chambre étanche de l'amortisseur (Taylor et
Constantinou, 2000). La figure 3 présente une illustration d'un
amortisseur visqueux.
On peut fixer les amortisseurs, comme les vérins
à force, à une structure au moyen d'une chape de type montage sur
goujons filetés ou d'un montage de plaque de base. La figure II.6
présente un schéma d'un système de contreventement par
amortisseur d'un bâtiment (Keller). Dans la figure II.8, on
présente un système de contreventement avec deux amortisseurs
visqueux visibles à la base du contreventement (photographie fournie par
Craig Keller de Taylor Devices, N. Tonawando, New-York).
La force d'un amortisseur visqueux est fonction de la vitesse
de course et peut être déphasée par des contraintes
produites par le mouvement de la structure. La force de l'amortisseur diminue
lorsque le déplacement de la structure est maximal
(accélération nulle). On obtient le maximum de force de
viscosité lorsque le déplacement de la structure est minimal ou
que la structure reprend sa position initiale. La réponse en opposition
de phase est une caractéristique très importante d'un amortisseur
visqueux à liquide puisqu'elle aide à réduire
simultanément les contraintes et la déformation d'un
bâtiment.
Ces dispositifs sont des tiges qui se déplacent selon
un mouvement de va-et-vient dans un cylindre rempli avec un liquide visqueux et
qui absorbe l'énergie induite lors d'un séisme au moyen d'une
friction entre la tige, le cylindre et le liquide
Les amortisseurs visqueux sont également très
efficaces et permettent une dissipation d'énergie très
significative où les diagrammes `'charges-déformations»
montrent une boucle d'hystérésis s'approchant d'un rectangle. La
quantité maximale d'énergie que ce type d'amortisseurs peut
dissiper dans un temps très court n'est limitée que par la
capacité thermique du plomb et du tube en acier. En plus, ils peuvent
être montés plus facilement en superstructure.

Figure II.6 Coupe transversale d'un
amortisseur type visqueux à liquide
Quelques exemples d'utilisations pratiques de ces amortisseurs
sont présentés ci-après :

FigureII.7 Illustration des contreventements
en V par amortisseur visqueux d'un bâtiment

FigureII.8 utilisation des amortisseurs en
diagonale dans les bâtiments

Figure II.9 Système de
contreventement en acier avec amortisseurs visqueux
disposés
horizontalement

Figure II.11 : Montage d'amortisseurs
visqueux en superstructure

FigureII.12 système d'amortisseurs
actif

FigureII.13 utilisation des
amortisseurs

FigureII.14 amortisseurs dans les
ponts
II.6.3 Amortisseur à frottement
Le frottement est un phénomène qui est en
relation avec les transformations de l'énergie mécanique
(énergie cinétique ou de mouvement) en énergie thermique
(chaleur). Habituellement, dans les systèmes mécaniques (machines
par exemple), le frottement constitue une entrave à leur fonctionnement
idéal et engendre une dissipation d'une partie d'énergie fournie,
dissipation qui apparaît comme une perte pour ces systèmes et par
voie de conséquence, entraînant une diminution de leur rendement
mécanique.
Dans les études de machines, le frottement est donc
considéré et traité comme un phénomène
nuisible. En revanche, dans le cas de la présente étude le
frottement est considéré comme un avantage et donc un atout.
Les amortisseurs à friction comprennent une
série de plaques fixées les unes aux autres par des boulons en
acier à haute résistance et spécialement traitées
pour produire un degré de friction maximale. Le principe de ces
amortisseurs repose sur le phénomène de dissipation de
l'énergie par friction qui apparaît sur les boucles
d'hystérésis du diagramme charges- déformations, qui
peuvent être rectangulaires.
Plusieurs dispositions de ces types d'amortisseurs sont possibles
: les amortisseurs pour le contreventement transversal et le contreventement
diagonal (fig. II.15).
|
|
|
Détail du dispositif d'amortissement
à
frottement
|
|
Ossature contreventée par des
Amortisseurs à
frottement
|
Figure II.15: Amortisseur à
frottement
II.7. Conditions d'addition des amortisseurs aux
constructions
L'addition des amortisseurs parasismiques dans les
constructions pour assurer une bonne performance de dissipation
d'énergie est difficile. Ils sont seulement adaptés à un
nombre limité de structures. Par conséquent, il est d'une
importance capitale de sélectionner les projets nécessitant
l'addition des amortisseurs parasismiques dans la phase de conception.
La technique d'incorporer ou d'installer en parallèle
des amortisseurs parasismiques aux structures isolées permet de
contrôler la déformation du système d'isolation et de
garder les déplacements de ce dernier et de la superstructure dans des
limites admissibles [8]. En outre, les niveaux élevés
d'amortissement supplémentaire ne sont pas nécessaires dans les
systèmes d'isolation car ils provoquent des accélérations
plus élevées dans la superstructure [7].
Les bâtiments souples conviennent à l'addition de
l'amortissement supplémentaire plus que les bâtiments rigides.
Plus le bâtiment est flexible plus la quantité d'amortissement est
faible pour réduire la réponse sismique [9].
L'amortissement supplémentaire peut de manière
significative réduire les mouvements sismiques et éloigner la
période de la structure par rapport à la période de
mouvement du sol afin d'éviter la résonance. Mais si la
période de la structure et la période du mouvement du sol sont
largement distinctes, l'amortissement supplémentaire peut avoir
seulement un effet marginal sur la réponse. Les structures avec
amortisseurs ne doivent pas être implantées dans les sites proches
de failles sismiques [5].
Les limitations de la hauteur des bâtiments ne devraient
pas excéder les limites recommandées pour les systèmes
structuraux. Les systèmes structuraux appropriés à
l'addition des amortisseurs sont les ossatures contreventées par des
portiques autostables et les autres systèmes qui ne conviennent pas sont
ceux où les déformations seront trop petites comme par exemple
les contreventements en voiles [9].
Bien que le renforcement des bâtiments existants par les
amortisseurs parasismiques limite les dommages et les coûts de
réparation, une évaluation de ces bâtiments sans
amortisseurs doit précéder avant que l'on considère
l'addition d'amortissement.
Remarque : Les propriétés de
quelques dispositifs de dissipation d'énergie peuvent varier en fonction
des effets du vieillissement, de la température, de la fatigue et
d'autres conditions environnementales. Par conséquent, ces dispositifs
exigent des inspections régulières et des programmes d'essais
rigoureux de contrôle de qualité afin d'éviter des ruptures
prématurées [9].
II.8. lois de comportement des différents
organes :
L'objectif attendu pour chacun des appareils parasismiques est
étroitement lié a son comportement une fois soumis a une source
de vibration.
L'analyse des différents appareils d'appuis disponibles
permet d'obtenir la relation force-déplacement définie comme suit
:
II.8.1. Ressort élastique
Les déplacements aller et retour suivent sensiblement la
même trajectoire. Il n'y a donc pas d'énergie
dépensée pendant un cycle, donc pas d'amortissement
[4].
La courbe force-déplacement peut être proche d'une
droite et d'un palier horizontal.

Figure II.16: comportement d'un ressort
élastique
II.8.2. Fusible

Figure II.17: comportement d'un
fusible
Il s'agit d'un ressort élastique dont la
résistance disparaît complètement dés que cette
dernière dépasse un certain seuil. Cette fonction est par exemple
obtenue avec une goupille métallique qui périt par cisaillement.
Elle permet de supprimer la liaison du tablier avec un appui et donc passer
d'une configuration en service á une configuration spécifique au
séisme.
II.8.3. Amortisseur visqueux
Les cycles force-déplacement dépendent de la
vitesse. Chaque cycle dépense de l'énergie, d'oú un
amortissement du mouvement.Cette fonction est réalisée par des
amortisseurs contenant un fluide plus ou moins visqueux.

Figure II.18 : comportement d'un amortisseur
visqueux
II.8.4. Fusible/amortisseur élasto-plastique
La relation force déplacement, indépendante de la
vitesse, est du type élasto-plastique avec (p2 = 0) ou sans (p2 = 0)
écrouissage.
Les cycles dépensent de l'énergie dés que la
limite élastique est dépassée.
Cette fonction est assurée par des amortisseurs visqueux
pilotés par des soupapes et des dispositifs á frottement.

Figure II.19 : comportement d'un fusible/
amortisseur élastoplastique
II.8.5. Coupleur dynamique
Le déplacement est libre pour une vitesse très
lente, très faible pour une vitesse au-delàd'un
certain seuil. Cette fonction est remplie par des dispositifs
métalliques et des
amortisseurs visqueux réglés spécialement.
Elle permet en cas de séisme de réaliser des liaisons
supplémentaires entre les piles et le tablier.
Chapitre III : Formulation du problème
d'amortissement et méthode de
dimensionnement des amortisseurs
Formulation du problème d'amortissement et
méthode de
dimensionnement des amortisseurs
III. 1. Introduction
L'équation du mouvement dynamique est fondée sur
trois composantes principales qui caractérisent une construction et sa
structure : la masse mise en mouvement, la rigidité des
éléments structuraux et les différents systèmes
d'amortissement.
Ces composantes sont reliées respectivement aux grandeurs
du mouvement : le déplacement, la vitesse et
l'accélération.
Notre travail porte sur l'impact de l'addition de nouvel appareil
d'amortissement sur le mouvement.
Nous allons ainsi procéder dans ce chapitre à la
formulation de l'équation de mouvement avec intégration des
amortisseurs, ensuite au dimensionnement des amortisseurs ;
III.2. Caractéristiques des amortisseurs
visqueux
Ces dispositifs sont assimilables à un vérin
hydraulique à doubles effets et à forte capacité de
dissipation d'énergie. Ils comportent couramment deux chambres remplies
d'un fluide (huile hydraulique ou pâte silicone). Celles-ci sont
reliées l'une à l'autre par des soupapes calibrées de
façon à permettre des déplacements lents et une
dissipation d'énergie générée par frottement
visqueux du fluide sous l'effet du mouvement sismique (rapide).
La relation entre la force d'amortissement et la vitesse relative
V peut s'écrire comme suit [6]:
F = C Vá (III-3)
V : la vitesse du piston (soupape),
C et á : sont des paramètres qui dépendent
de la loi de comportement du fluide.
Tableau III.1 : différents types
d'amortisseurs selon les différentes valeurs de l'exposant á
[6].
|
Type
d'amortisseur
|
Valeur
de á
|
Force
d'amortissement
|
Remarques
|
|
Amortisseur linéaire
|
á =1
|
F = C V
|
Amortisseur hydraulique classique
|
|
Amortisseur non linéaire
|
á =0
|
F = C
|
Amortisseur idéal à frottement sec
|
|
Amortisseur non linéaire
|
á ? 0, 1
|
F = C Vá
|
Amortisseur visqueux intermédiaire
|
En général la valeur de l'exposant á varie
entre 0.1 et 1.8 [6].
Les figures suivantes, montrent la loi de comportement des
différents types d'amortisseurs soumis à une excitation
sinusoïdale.
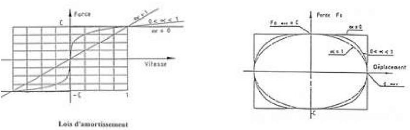
Figure III.1 : lois de comportements de
différents types d'amortisseurs
Remarque
L'amortisseur liquide assure seulement l'amortissement dans sa
direction axiale.
III.3. Formulation de l'équation du mouvement
avec des amortisseurs
Le problème posé par les déplacements
excessifs peut être résolu par l'augmentation de
l'amortissement
En général l'équation d'équilibre
dynamique de n'importe quel modèle est sous la forme suivante:
Fm + Fc + Fk= P(t) (III-1)
Fm : Force d'inertie.
Fc : Force d'amortissement due à la
structure.
Fm : Force de rigidité.
P(t) : Charge dynamique (variable en fonction du temps).
On peut donc écrire l'équation comme suit :
& & &
M U + CU +
KU = P( t ) (III-2)
M : matrice de la masse de la structure,
C : matrice d'amortissement,
K : matrice de rigidité,
U&& ,U& etU
sont respectivement l'accélération, la vitesse et les
déplacements du système.
La force d'amortissement due à un amortisseur est
donnée par l'expression suivante [11] :
F = C Vá
Pour un système où l'on utilise des amortisseurs
l'équation de mouvement devient :
Fm + Fc +Fc' +Fk= P(t)
(III-4)
F'c : force d'amortissement due à l'amortisseur ajouté
au système, d'où l'équation de mouvement devient [11] :
.. .
M U +
Cs
U+CaVá + K U
= P t (III-5)
( )
Lors de mouvement de système, la vitesse du piston V est
égale à la vitesse de mouvement du
.
système, donc U = V
D'où l'équation devient [11] :
M U & & + C
s U & + CaU &
á + KU = P(t)
(III-6)
Et pour une excitation sismique l'équation s'écrit
[11]:
M U s U C a U
+ C + á + K
= -
U MUg (III-7)
& & &
U& & g : Accélération
sismique du sol
On remarque bien que si á est égal à
l'unité l'équation devient linéaire comme suit [11]:
& & & & &
M U + ( C
s +Ca)U
+KU=MUg (III-8)
La résolution de cette équation devient classique
comme elle a été introduite dans le chapitre IV par la
méthode de Newmark ou par d'autres méthodes [11].
Si a ? 1 l'équation du mouvement
précédente reste non linéaire et parmi les nombreuses
méthodes d'intégration directe pour résoudre cette
équation, la méthode d'intégration de Newmark semble
être la plus efficace avec de très petites erreurs
numériques. Dans la méthode de Newmark, on supose que
l'accélération est linéaire pendant le temps à
t + Ä t . Pour l'intervalle de temps Ät,
les relations sont [11]:
. . .. ..
|
Ut +Ä t = Ut + -
â + â +Ä Ä
[(1 ) U t U t t t
]
|
(III-9)
|
. .. ..
U t +Ä t = Ut
+Ut Ät + [( 2 -á
)U t+áUt+Ät]Ät
2 (III-10)
á et â sont les paramètres
employés pour obtenir l'exactitude et la stabilité
d'intégration. Dans le cas oil 4
á = et 2
1 â = , la méthode
d'accélération moyenne constante rapportera la
1
stabilité sans conditions dans le procédé
d'itération.
. ..
Les équations précédentes, Ut
+Ät et Ut +Ät
peuvent être résolues en termes de Ut + Ä t
comme
U t + Ä t t + Ä t (1 -
â )U t+âÄtUt
+Ät
&&
( U t+Ä t - Ut
-Ut- - 1U t
1 1
1
&&

áÄ
t áÄt
2
á
(III-11)
(III-12)
Pour obtenir le déplacement, la vitesse et
l'accélération au temps t + Ä t ,
l'équation d'équilibre est écrite comme [11]:
|
M U & & C
s U & C K (
g ) t t
t t t t a t t
U +
& á
+ + U = - M & U &
+ Ä + Ä + Ä t t
+ Ä +Ä
|
.
|
(III-13)
|
C & : Terme de la non
linéairité.
á
aUt +Ä t
Pour éviter d'employer la technique d'itération
pour détérminer le vecteur de déplacement à
á
chaque étape, le terme non linéaire Ut
+Ä t est développé par une série de
Taylor comme montré dans l'équation suivante: [11]
& á t +Ä t = U
tá+r · diag
( 1 )(
á
U & - U & - U & )
t t t
+ Ä t
U
(III-14)
On suppose que les limites d'ordre supérieur peuvent
être négligées sans perte d'exactitude
diag : Opérateur de diagonalisation d'un vecteur
à une matrice. Les étapes de résolution sont comme suit
[11] :
~ ~
|
~
|
..
|
|
P M U g t t Ma M C
s a C C a C
+ +
t t
+ Ä = - ( ) + Ä + a a
s
|
(III-17)
|
K Ut +Ä t =
Pt+Ät
.
~ 1 â r â
K K
= + + + C a diag U t
á
M C m (
t 2
á Ä á Ä t á
Ä t
(III-15)
(III-16)
)
-1

1 t 2 U t +áÄt
Ut+( 2á 1) Ut
1 . 1
â
Ut + ( á
2á-1)U t + Ä t( -1)
Ut
& .. .
..
â U
t - U t á + râ diag(
Ut á-
)Wt + â Ä t(
1 - 1) U t - rÄ t(1 - â )
diag( Uá t )U t
2á
·
·
a Cd
á Ä
â â
..
áÄt
. .
áÄ t
·
=
aM
=
aCs
(III-18)
(III-19)
(III-20)
La vitesse U
t+ Ät et
l'accélération U t+ Ät peuvent
être obtenues à partir des équations III-11 et
4-12 [11].
Nous présentons sous forme d'organigramme le cheminement
des étapes de déterminations des grandeurs déplacements,
vitesses et accélérations.
1
n
ö
ö j n
ö n n
Détermination de la matrice modale Ö
1 j n
ö ö ö
1 1 1
? ? ? ? ? ? ? ??
j n
ö ö
j j
Ö
1
ö
j
Détermination de la matrice d'amortissement diagonale
|
C m
|
=
|
ci
|
c
j
|
?
?
?
?
?
?
cn ?
|
1

ORGANEGRAMME DE DETERMINATION DES
DEPLACEMENTS,
VITESSES ET ACCELERATIONS
Début
Lecture des données
Matrices de masse et de rigidité
Détermination des pulsations propre du
système
det(K-ù2M)=0

|
Détermination des modes propres du système (K-
ù j2M)Öj=0
|


Chapitre III Formulation du problème d'amortissement et
méthode de dimensionnement des amortisseurs
Détermination de la matrice d'amortissement
modale
Cs=(MÖ[ÖTMÖ]-1)Cm
([ÖTMÖ]-1 ÖTM)
Calcul de la rigidité effective Keff
1 â r â .
Keff = K+ ( )
r -
+ 1
M C + C d diag U
P t + Ä t = -
M(Ug) t +Ä t
MaM + C sa C
+C aa C
s
&& 1
1- t + Ä t = 2 (
U t+Ä t U t) - 1 U t
2á 1) U t
~
Détermination du déplacement Ut+Ät
acs=
U t + Ä t = U t
+Ä t (1 -â )U t
+âÄ tUt+Ät
Calcul de la charge effective Peff
aM=
Détermination de l'accélération
áÄ
. .
â
Ut + ( -1) Ut + Ä
t( -1) U t
áÄ t á 2á
Détermination des coefficients
. t 2 m
á Ä á . Ä t
á . Ä t t
Détermination de la vitesse
acd=
â â
áÄ t
1
áÄ
..
r
âut - u
t+
.
1 1
U t + U t + ( - 1)
2 áÄt 2á
K Ut + Ät =
Pt+Ät
~ ~
t
Résultats
1
.
râ
..
..
á
táÄt&
diag(u
.
Ut
..
..
a
III.4. Méthode de dimensionnement des
amortisseurs visqueux non linéaire à partir d'un spectre de
réponse
Le dimensionnement de ponts utilisant des amortisseurs
visqueux non linéaires pour diminuer les effets du séisme, en
termes de forces ou de déplacements, ne peut se justifier, à
l'heure actuelle, que par des simulations non linéaires temporelles.
Nous proposons ici une méthode de dimensionnement extrêmement
simple qui ne fait appel qu'au spectre de réponse élastique
fourni par le règlement. Cette méthode s'appuie sur une technique
de linéarisation des lois de comportement des amortisseurs. Elle rend
compte, de façon approchée, des mouvements sous séisme
d'oscillateurs simples dotés de tels dispositifs
III.4.1. Démarche de dimensionnement
La démarche de dimensionnement des amortisseurs
fondée sur un spectre de réponse se compose de plusieurs
étapes (voir organigramme page 47) [12] :
A. Evaluation de la période propre de la
structure

T=
2ð
M
K
(III-21)
T la période propre de la structure M masse du
système
K rigidité du système
B. Evaluation du déplacement
élastique
T ?
2 ??
ð
d =
?
??
2
Sa ( T, æ)
(III-22)

0 . 07
ñ
(III-23)
0. 02
+ îeq
d : déplacement élastique
Sa ( T, æ) : accélération du spectre
élastique du règlement
C. Choix du coefficient de réduction de
l'amplitude des déplacements
La valeur du coefficient de réduction ñ de
l'amplitude des déplacements est donnée par le
règlement [AFPS 95] :
îeq : Amortissement équivalente du
système
Cette formule est acceptable pour des valeurs d'amortissement
comprises entre 2% et 30% D. Déduction d'un taux d'amortissement
équivalant
îeq
0.02
(III-24)
0. 07
ñ 2
E. déduction du taux d'amortissement
înl provenant des amortisseurs seuls
(III-25)
înl = îeq - îvisqueux
înl Amortissement des amortisseurs
îeq Amortissement équivalente
îvisqueux Amortissement visqueux de structure ( 5 à
7 %) Dans le cas où l'amortissement visqueux égale à 5
%
0 . 07 1
(III-26)
înl = îeq -0.05 = 0. 07
2 - = 0 . 07 ( 2 -1)
ñ ñ
F. Détermination du paramètre
d'amortissement c a mettre en oeuvre :
(III-27)
C =( M 4ð ænl 1
[ñ T Sa ( T, æ)]1-á )
T h(á) 2ð
á :exposent de la vitesse lié aux lois de
comportement de l'amortisseur h(á) : fonction de linéarisation
h(á) =0.0892 á2 -0.3583 á
+1.2699
G. Détermination de la force maximale
supportée par les amortisseurs
F = C Vá = C. [ñ
T Sa ( T, æ)]á
(III-28)
2ð
F : force maximale de l'amortisseur
L'organigramme suivant résume les différentes
étapes de dimensionnement des amortisseurs
Paramètre d'amortissement C =( M 4ð
ænl 1 [ñ T
Sa ( T, æ)]1-á )
T h(á) 2ð

Force de l'amortisseur F = C Vá = C.
[ñ
T Sa ( T, æ)]á

2ð

FIN
ORGANIGRAMME DE DIMENSIONNEMENT DES
AMORTISSEURS


Début
Matrices, K, M

Période T

Accélération de la zone A

Périodes caractéristiques associées à
la catégorie de site T1, T2

Spectre Sa ( T, æ)

Coefficient de réduction ñ

L'exposant á

|
Déplacement d =
|
?
??
|
T ?
2 ??
ð
|
2
|
Sa ( T, æ)
|

|
0. 07
Taux d'amortissement équivalant æeq = ( 2
ñ
|
-0.02 )
|

Taux d'amortissement provenant de l'amortisseur ænl=
æeq - æ

Chapitre IV : Application numérique sur
un oscillateur simple
Application numérique sur un oscillateur
simple
IV.1. Introduction
Ce chapitre est consacré à une application
portant sur un oscillateur simple. Nous nous intéressons plus exactement
à la variation du déplacement en fonction de la variation de
l'amortissement en considérant comme source d'excitation le signal
sismique d'El Centro.
Nous présentons d'abord l'aspect théorique, suivi
d'un organigramme qui résume les étapes de calcul des
déplacements.
L'exploitation de cet organigramme nous a permis
d'élaborer un programme en FORTRAN dont les résultats de
simulation sont représentés graphiquement.
IV.2. Formulation mathématique du
problème
On considère un oscillateur simple lié au sol et
caractérisé par sa pulsation ù et son coefficient
d'amortissement î. Il est soumis aux effets d'un séisme, c'est
à dire que son point d'appui se déplace avec une
accélération du sol donnée par un
accélérogramme, comme par exemple celui d'El Centro du 18 mai
1940.

Figure IV.1 Oscillateur simple
chapitre IV Application numérique sur un oscillateur
simple

0 5 10 15 20 25 30 35
acceleration m/s2
-0,1
-0,2
-0,3
-0,4
0,3
0,2
0,1
0,0
tem ps s
Graphe IV.1 : Signal séismique d'
El- centro
On calcule les déplacements dus au signal sismique avec
différentes valeurs
d'amortissement à l'aide de l'intégral du Duhamel
:
1
u(t) = ? - (t - )
p îù ô
( ) e
ô sin ( )
ù t d
- ô ô
D
mùD
t
0
(IV-1)
Cette équation est appelée intégrale de
Duhamel, qui est basée sur le principe de superposition. Elle n'est
applicable qu'à des systèmes linéaires.
Pour calculer numériquement cette réponse, on a
:
sin (ùDt- ùDô)=sinùDt
cosùDô - cosùDt sinùDô
Donc :
t t
sin t
(IV-2)
ù c os ù D t -
(t - )
u(t) = D ? - (t- )
îù ô
ô ( ) e îù ô
ù ô ô
( ) e
p cos( ) d - ? p ô sin( )
ù ô d ô
D D
m ù m ù
D 0 D 0
t îùô
1 e
(IV-3)
Posons : A(t)= p ( )
ô ù ô d ô
îù D
? t cos( )
m ù e
D 0
et
t îùô
1 e
(IV-4)
B(t)= p ( )
ô ù ô d ô
îù D
? t sin( )
m ù e
D 0
L'équation IV-2 prend la forme suivante:
u(t)= A(t) sinùDt - B(t) cosùDt (IV-5)
En résolvant ces intégrales, on détermine
la réponse u(t). Le chargement dynamique p(t)
..
est dû à une accélération ( )
a t d'un signal sismique (El-centro 18 mai 1940
composante SO-
OE par exemple),
Notons que la force effective due à cette
accélération est donnée par :
..
Peff(ô)=-m ( )
a ô
Donc :
t
1 .. - (t- )
u(t) = - ? a îù ô
( ) e
ô sin ùD ( t
d
- ô ô
ùD
0
(IV-6)
|
1 t..eùô
A(t)= - ? a ( )
ô cos( )
ù ô ô
D d
îù t
ù e
D 0
1 t..eùô
B(t)= - ?a (ô ) sin( )
ù ô ô
D d
îù t
ùe D 0
|
(IV-7)
(IV-8)
|
On ne peut pas résoudre ces intégrales par les
méthodes classiques. On utilise alors un procédé de
sommation :
Ät 1 A
Donc :
A(t)= -
××Ó (t)
ù D ò
(IV-9)
|
Ät 1 A B(t)= - ×
×Ù (t)
ùD ò
|
(IV-10)
|
Parmi les méthodes de résolution, il existe trois
qui sont les plus souvent utilisées : méthode par simple
sommation, méthode de trapèze et méthode de Simpson.
1. Simple sommation (q=1) :
A A ..
? ?(îù t )
Ó = Ó - Ä + - Ä ×
( ) ( ) ( ) cos ( )
t t t a t t ù t t e - Ä
- Ä × (IV-11)
D
?? ?? 1 1
A A ..
? ? ( - Ä
îù t )
( ) ( ) ( (IV-12)
Ù = Ù - Ä +
t t t a t t ) sin (
- Ä × ù t t
- Ä ) × e
D
?? ??
1 1
2. Méthode des trapèzes
(ò=2)
A ? A ? ..
..
( ) ( ) ( ) cos ù ( ) îù (
) cos ù
? Ä t
t = ? t t a t t D t t e ( )
Ó Ó ? Ä + ? Ä × ? Ä ? × +
×
a t D t (IV-13)
? ?
2 ? 2 ?
A A ....
? ? ? Ä
îù t
Ù ( )
t = ( t t a t t
) ( ) sin ù ( t t ) e ( ) a
t
( ) sin ù t (IV-14)
D D
Ù ? Ä + ? Ä × ? Ä × + ×
?? ??
2 2
3. Méthode de Simpson (G=3)
A
Ó
(t)
3
A ..
? Ó ( 2 ) ( 2 ) cos
t ? Ä + ? Ä ×
t a t t
?? 3
? îù t t
t t e a t t t t e ( ? Ä
îù
ù ù
D ( 2 ) + ? ? Ä ×
..
( 2 )
)
? Ä 4 ( ) cos ( ) ?
? Ä ? Ä
× ×
D
?? ?? ??
|
..
+ a(t) × cos
ùDt
|
(IV-15)
|
..
-
2) sin
Ä ×
t

(t-2Ä t) + a(t
A? A
Ù Ù
( )
t = ?
?
3 ? 3
? ? ..?
)
t t e ( 2 )
- Ä
îù t îù t
ù D ( 2 ) 4 ( ) sin ( )
a t t ù D t t e (
- Ä - Ä
? × + ? - Ä × - Ä ? ×
? ? ? ? ? ?
|
..
+ a(t) × sin ùDt
|
(IV-16)
|
La précision attendue ici de la solution dépend
évidemment de la durée de l'intervalle At. En
général, cet intervalle doit être choisi suffisamment court
à la fois pour que la fonction de
T
chargement et les fonctions trigonométriques soient bien
définies : Ät10 .C'est la règle
pratique qui est largement utilisée et qui donne de bons
résultats.
La précision et le volume des calculs
nécessaires augmentent avec l'ordre du procédé de
sommation. En règle générale, la précision accrue
que procure la méthode de Simpson justifie son utilisation en
dépit d'une plus grande complexité numérique.
Les résultats obtenus sont représentés dans
les graphes suivants avec différentes valeurs de coefficients
d'amortissements et pulsations :
L'organigramme suivant résume les différentes
étapes de résolution de ce problème
Organigramme de résolution

m
ùD
Lecture des données
t t
u(t) = sinùD t) e
-îù (t- ô) cos( ùD
ô)dô- cosùDt ?
?
ùD
0
- (t- )
p ( ) e îù ô
ô sin( )
ù ô d ô
D
Intégral DUHAMEL
u(t) = 1 ? p (ô )
e- 4o(t- ô) sin
ùD ( t -
mùD
t
0
t1
e4oô
A(t)= p ( )
ô ù ô d ô
îù D
? t cos( )
mùe
D 0
t1
e4°ô
B(t)= ? t
p ( )
ô sin( )
ù ô d ô
îù D
m ù e
D 0
Ät 1 A A(t)= - × × Ó
(t)
ùòò
D
Peff(ô)=-m ( )
a ô
Ät 1 A B(t)= - ×
×Ù (t)
ùD ò
A
Ó
(t)
cos
3
..
? A
Ó ( 2 ) ( 2 )
t ? Ä + ? Ä ×
t a t t
??
3
? îù t ( - î
ù t t e a t t ù t t e
D ( 2 ) + ? - Ä ×
..
( 2 )
- Ä 4 ( ) cos ( ) ?
- Ä - Ä
× ×
D
?? ?? ??
..
+ a(t ) ×
cos
ùD t
u(t)= )= A(t) sinùDt - B(t) cosùDt
A? A
Ù Ù
( )
t = ?
?
3 ? 3
? ? .. ?
t t e ( 2 )
- Ä
îù t îù t
ù D ( 2 ) 4 ( ) sin ( )
a t t ù D t t e (
- Ä - Ä
? × + ? - Ä × - Ä ? ×
? ? ? ? ? ?
)
..
+ a(t) × sin ùDt
(
sin
..
t - 2Ä t ) + a(t -Ä
t) ×
2
FIN
Début
IV.3. Application (oscillateur simple)
Pour mettre en évidence le lien qui existe entre la
souplesse de la structure et l'amortissement qu'il faut avoir pour
réduire les déplacements qui en sont engendrés, nous
allons faire variées le taux d'amortissement en adoptants comme
paramètre la pulsation ù.
Les résultats de cette étude sont
représentés par les graphes illustratifs présentés
ci après. Nous faisons varier le taux d'amortissement î pour
différentes valeurs de pulsationù, les résultats
représentés par les graphes ci après :

1. pulsation ù=1 :

Graphe IV.2 : variation de
déplacement en fonction du temps avec ù=1 et î=0%
Graphe IV.3 : variation de
déplacement en fonction du temps avec ù=1 et î=5%


Graphe IV.4 : variation de
déplacement en fonction du temps avec ù=1 et î=10%

Graphe IV.5 : variation de
déplacement en fonction du temps avec ù=1 et
î=20%
Graphe IV.6 : variation de
déplacement en fonction du temps avec ù=1 et î=50%

Graphe IV.7 : variation de
déplacement en fonction du temps avec ù=1 et î=100%

Graphe IV.8 : comparaison des
déplacements de différentes valeurs de î avec
ù=1
Tableau IV.1 valeur du
déplacement maximal
|
Pulsation ù=1
|
|
Taux d'amortissement î (%)
|
Déplacement maximal (cm)
|
|
0
|
4.68
|
|
5
|
3.23
|
|
10
|
2.36
|
|
20
|
2.07
|
|
50
|
1.68
|
|
100
|
1.23
|

2. Pulsation ù=5 :

Graphe IV.9 : variation de
déplacement en fonction du temps avec ù=5 et
î=0%
Graphe IV.10 :
variation de déplacement en fonction du temps avec
ù=5 et î=5%

Graphe IV.11 : variation de
déplacement en fonction du temps avec ù=5 et î=10%


Graphe IV.12 : variation de
déplacement en fonction du temps avec ù=5 et
î=20%
Graphe IV.13 : variation de
déplacement en fonction du temps avec ù=5 et î=50%

Graphe IV.14 : variation de
déplacement en fonction du temps avec ù=5 et î=100%

Graphe IV.15 : comparaison des
déplacements de différentes valeurs de î avec
ù=5
Tableau IV.2 valeur du
déplacement maximal
|
Pulsation ù=5
|
|
Taux d'amortissement î (%)
|
Déplacement maximal ( cm)
|
|
0
|
0.66
|
|
5
|
0.28
|
|
10
|
0.24
|
|
20
|
0.24
|
|
50
|
0.21
|
|
100
|
0.19
|
3. Pulsation ù=10 :

Graphe IV.16 : variation de
déplacement en fonction du temps avec ù=10 et î=0%


Graphe IV.17 : variation de
déplacement en fonction du temps avec ù=10 et
î=5%
Graphe IV.18 : variation de
déplacement en fonction du temps avec ù=10 et î=10%

Graphe IV.19 : variation de
déplacement en fonction du temps avec ù=10 et î=20%

Graphe IV.20 : variation de
déplacement en fonction du temps avec ù=10 et î=50%

Graphe IV.21 : variation de
déplacement en fonction du temps avec ù=10 et
î=100%

Graphe IV.22 : comparaison des
déplacements en fonction de î avec ù=5
Tableau IV.3 valeur du déplacement
maximal
|
Pulsation ù=10
|
|
Taux d'amortissement î (%)
|
Déplacement maximal (cm)
|
|
0
|
0.46
|
|
5
|
0.25
|
|
10
|
0.21
|
|
20
|
0.20
|
|
50
|
0.17
|
|
100
|
0.11
|
Tableau IV.4 récapitulatif des
valeurs du déplacement maximal
|
Pulsation ù=1
|
Pulsation ù=5
|
Pulsation ù=10
|
|
Taux d'amortissement
î (%)
|
Déplacement
maximal (cm)
|
Déplacement
maximal (cm)
|
Déplacement
maximal (cm)
|
|
0 %
|
4.68
|
0.66
|
0.46
|
|
5 %
|
3.23
|
0.28
|
0.25
|
|
10 %
|
2.36
|
0.24
|
0.21
|
|
20 %
|
2.07
|
0.24
|
0.20
|
|
50 %
|
1.68
|
0.21
|
0.17
|
|
100 %
|
1.23
|
0.19
|
0.11
|
Conclusion :
On peut tirer comme conclusion que les déplacements
augmentent lorsque la période augmente (principe de l'isolateur
sismique) et que les déplacements diminuent quand l'amortissement
augmente. Ceci montre bien l'utilité d'incorporer ces genres des
dispositifs dans des structures de grande ampleur afin de diminuer
considérablement les déplacements et aussi bien les
sollicitations.
Chapitre V : Application (pont et
portique) et développement d'un logiciel
de dimensionnement des amortisseurs
Applications (pont et portique) et dimensionnement des
amortisseurs
V.1. Introduction
La prise en compte du risque sismique pour les structures
conduit à des actions horizontales de dimensionnement qui peuvent
être très importantes. On est parfois amené à
changer le schéma de fonctionnement de la structure pour diminuer les
efforts induits. Il s'agit, par exemple, d'assouplir la structure en isolant la
superstructure (isolateur sismique) et de diminuer ainsi les efforts au niveau
des appuis, aux prix de déplacements relatifs plus importants de la
superstructure sur ceux-ci. On peut encore diminuer forfaitairement ces efforts
en acceptant un certain niveau d'endommagement (notion de la rotule
plastique et coefficient de comportement) des dispositifs parasismiques.
Les structures équipées d'appareils d'appuis spéciaux
(fusible, amortisseur, etc...) destinés à améliorer le
comportement de ces ouvrages sous sollicitations sismiques connaissent un
développement important. Ces dispositifs sont utilisés aussi bien
dans la réalisation de structures neuves que dans la
réhabilitation sismique d'ouvrages existants.
Parmi les dispositifs spéciaux, les amortisseurs ont pour
objectif de diminuer à la fois les efforts et les déplacements en
dissipant l'énergie induite dans l'ouvrage.
Dans ce chapitre, on se propose de faire une application de
l'utilisation des amortisseurs dans le domaine du génie civil notamment
le domaine des ouvrages d'arts qui sont très sensibles au
séisme.
Parmi les rares outils automatiques qui traitent de ce genre
d'organes parasismiques, le SAP2000 qui permet d'analyser des structures avec
amortisseurs (damper) à travers une interface graphique
puissante et facile d'utilisation. Cette facilité est rendue possible
par le fait que la création du modèle structurel, son analyse et
ses résultats sont réalisés à l'aide des interfaces
simples et conviviales. De même plusieurs fonctions relatives aux
éléments non linéaires tels que les dispositifs
d'isolation et les amortisseurs sont disponibles.
L'utilisation des amortisseurs nécessite la
caractérisation de la capacité portante de ces derniers.
Motivés pour ce souci, nous allons développer un logiciel de
dimensionnement des amortisseurs.
V.3. Exemples étudiés
Nous nous proposons donc comme modèles à
étudier un portique en béton armé et un pont caisson
à deux travées de 60 m chacune
V.3.1. Cas d'un portique
Nous considérons un portique (figure V.1) en béton
armé de 5 m de hauteur et de 4 m de portée et de section
transversale constante égale 30x30 cm2.
Ce portique est considéré soumis au signale de
référence d'El Centro. Nous allons déterminer les
diagrammes des réponses déplacements, vitesses et
accélérations pour les deux cas de figures : portique sans
amortisseur et portique avec amortisseur.
V.3.1.1. Portique sans amortisseur
Les réponses sont représentées graphiquement
et suivies d'un tableau récapitulatif de leurs valeurs maximales.

Figure V.1 : modèle d'un portique
sans amortisseur
A. Déplacement :

Graphe V.1 : déplacement du
portique sans amortisseur
B. Vitesse :

Graphe V.2 : vitesse du portique sans
amortisseur
C. Accélération :

Graphe V.3 : accélération du
portique sans amortisseur
Tableau V.1 : tableau
récapitulatif du model 1 (portique sans amortisseur)
|
valeurs
|
|
Déplacement maximal (cm)
|
1.62
|
|
Vitesse maximale (cm/s)
|
28.26
|
|
Accélération maximale
(cm/s2)
|
914.55
|
V.3.1.2. Portique avec amortisseur
Dans ce cas, le portique plan, soumis au séisme d'El
Centro a été pourvu d'un amortisseur disposé en diagonale.
Nous avons fait un choix délibéré des
caractéristiques de cet amortisseur C=
100 KN/m/s et á=0.5
Les digrammes des accélérations, des vitesses et
des déplacements ainsi obtenus sont représentés par des
graphes. La comparaison entre les résultats obtenus pour le cas de
portique sans amortisseur et le cas de portique avec amortisseur est
présentée sous forme graphique et tabulée.

Figure V.2 : modèle d'un portique
avec amortisseur
A. Déplacement

Graphe V.4 : déplacement du
portique avec amortisseur
B. Vitesse

Graphe V.5 : vitesse du portique avec
amortisseur
C. Accélération

Graphe V.6 : accélération du
portique avec amortisseur
Tableau V.2 : tableau
récapitulatif du model 1 (portique avec amortisseur)
|
valeurs
|
|
Déplacement maximal (cm)
|
1.05
|
|
Vitesse maximale (cm/s)
|
15.71
|
|
Accélération maximale
(cm/s2)
|
654.47
|

V.3.1.3. Comparaison des valeurs du déplacement,
vitesse et accélération entre portique sans et avec amortisseur
:

Graphe V.7 : comparaison des
déplacements du portique avec ou sans amortisseur
Graphe
V.8 : comparaison des vitesses du portique avec ou sans
amortisseur

Graphe V.9 : comparaison des
accélérations du portique avec ou sans
amortisseur
Tableau V.3 : tableau
récapitulatif de comparaison du portique avec ou sans
amortisseur
|
Modèle1
(sans amortisseur)
|
Modèle 2
(avec amortisseur)
|
pourcentage de gain
|
|
Déplacement maximal (cm)
|
1.62
|
1.05
|
35.18 %
|
|
Vitesse maximale (cm/s)
|
28.26
|
15.71
|
44.40 %
|
|
Accélération maximale
(cm/s2)
|
914.55
|
654.47
|
28.44 %
|

V.3.2. Cas d'un pont
Les ponts constituent généralement des ouvrages
de grande importance et de grande ampleur, le maintien de leur
fonctionnalité après un quelconque séisme est absolument
vital pour garantir la continuité et la fluidité de la
circulation des secours aux endroits sinistrés.
C'est pourquoi nous nous intéressons à l'analyse de
ce type d'ouvrages. Cette analyse à pour objet de déterminer les
réponses de la structure (déplacements, vitesses et
accélérations) supposées soumise au séisme
référentiel d'El Centro. A titre de comparaison, nous
considérons deux variantes pont avec appareil d'appuis et pont avec
appareils d'appuis et amortisseurs.
Pour ce cas, nous commençons d'abord par la
modélisation de la structure du pont puis nous procédons a son
analyse pour déterminer graphiquement les repenses :
déplacements, vitesses et accélérations, leurs valeurs
maximales seront données dans le tableau récapitulatif.

Figure V.3 : modèle d'un pont en
élévation


Figure V.4 : section transversale du
pont
Pour monter l'influence des conditions d'appuis sur les ponts
nous avons proposé plusieurs variantes :
- pont sans amortisseurs
Nous distinguons dans cette variante quatre sous variantes :
1- pont avec des appareils d'appuis fixes.
2- pont avec des appareils d'appuis en élastomère
frété.
3- Pont avec des appareils d'appuis en élastomère
frété sur la pile et glissant sur les culées
4- Pont avec des appareils d'appuis glissants
- pont avec amortisseurs
Nous distinguons dans cette variante deux variantes :
1- pont avec amortisseurs et appareils d'appuis glissants sur
les culées et en élastomère frété sur la
pile.
2- pont avec amortisseurs et appareils d'appuis glissants sur
les culées et la pile.
V.3.2. 1. Pont sans amortisseurs
A. pont avec appareils d'appuis fixes
Ce type d'appuis est à éviter à cause de
l'énergie sismique qui est totalement absorbé par l'ouvrage (T =
0.0955 s) et de l'effet thermiques dont il faut tenir compte.
Avantage :
- Déplacement négligeable.
Inconvenants :
- Efforts thermiques à prendre en compte
- Énergie sismique importante ( T = 0.0955 s)
B. pont avec appareils d'appuis en
élastomère frété
Ce type de conditions d'appuis est couramment utilisé pour
les ouvrages courants à cause de leur efficacité sismique
(isolateur sismique).
Avantage :
- Absorbation de l'effet thermique.
- Déplacement tolérable pour les ouvrages
courants
- Énergie sismique moyennement importante (T = 0.9645 s
)
Inconvenant :
- Limitation de l'utilisation aux les ouvrages courants
C. Pont avec appareils d'appuis en
élastomère frété sur la pile et glissants sur les
culées
Avantage :
- Énergie sismique faible (T = 3.4269 s)
Inconvenant :
- Déplacement important
Les résultats concernant les déplacements,
vitesses et accélérations sont représentés par les
graphes suivants :
Déplacement

Graphe V.10 : déplacement du pont
sans amortisseur
Vitesse

Graphe V.11: vitesse du pont sans
amortisseur
Accélération

Graphe V.12 : accélération
du pont sans amortisseur
Tableau V.4 : Tableau
récapitulatif du modèle pont sans amortisseur
|
valeurs
|
|
Déplacement maximal (cm)
|
29.05
|
|
Vitesse maximale (cm/s)
|
68.45
|
|
Accélération maximale
(cm/s2)
|
331.1
|
D. Pont avec appareils d'appuis glissants
:
Dans ce cas le tablier est totalement isolé des appuis
du point de vue efforts. Ce cas est idéal, mais l'inconvenant ici est
que les déplacements tendent vers l'infini ; ceci nous oblige à
limiter ces déplacements par addition d'amortisseurs.
V.3.2. 2. Pont avec amortisseurs
Les caractéristiques de l'amortisseur pris en compte
dans cette application sont : C= 1000 KN/m/s á=0.5
V.3.2.2.1. pont avec amortisseurs et appareils
d'appuis glissants sur les culées et en élastomère
frété sur la pile.
Avantage :
Déplacement faible.
Énergie sismique faible (T = 3.4269 s)
Inconvenant :
Coût et maintenance relativement élevés
Les résultats trouvées de déplacement,
vitesse et accélération sont représentés par les
graphes suivants :
Déplacement

Graphe V.13 : déplacement du pont
avec amortisseur
Vitesse

Graphe V.14: vitesse du pont avec
amortisseur
Accélération

Graphe V.15 : accélération
du pont avec amortisseur
Tableau V.5 : Tableau
récapitulatif du model pont avec amortisseur
|
valeurs
|
|
Déplacement maximal (cm)
|
6.31
|
|
Vitesse maximale (cm/s)
|
24.48
|
|
Accélération maximale
(cm/s2)
|
298.2
|
V.3.2.3. Comparaison graphiques des réponses


Graphe V.17 : comparaison des vitesses entre
pont avec et sans amortisseur
Graphe V.16 : comparaison des
déplacements entre pont avec et sans amortisseur

Graphe V.18 : comparaison des
accélérations entre pont avec et sans amortisseur
V.3.2.4. pont avec amortisseurs et appareils d'appuis
glissants sur les culées et la pile (tablier totalement
isolé)
Avantages :
- Déplacement faible.
- Énergie sismique très faible (T = 5.4110 s)
Inconvenant :
- Coût et maintenance élevée
Les résultats trouvés des déplacement,
vitesse et accélération sont représentés par les
graphes suivants :
Déplacement

Graphe V.19 : déplacement du pont
avec appareils d'appuis glissant et un amortisseur
Vitesse

Graphe V.20 : vitesse du pont avec appareils
d'appuis glissant et un amortisseur
Accélération

Graphe V.21 : vitesse du pont avec appareils
d'appuis glissants et un amortisseur
Tableau V.6 : Tableau récapitulatif
du modèle pont avec appareils d'appuis glissants et
un
amortisseur
|
valeurs
|
|
Déplacement maximal (cm)
|
7.63
|
|
Vitesse maximale (cm/s)
|
27.26
|
|
Accélération maximale
(cm/s2)
|
300.03
|
Tableau V.7 : tableau récapitulatif
de comparaison entre pont avec et sans amortisseur
|
Pont pile fixe
culées libres
(sans
amortisseur)
|
Pont à pile fixe et
culées
libres
(avec amortisseur)
|
Pont avec
Tablier libre
(avec
amortisseur)
|
gain
(%)
|
|
Déplacement maximal (cm)
|
29.05
|
6.31
|
7.63
|
73.73
|
|
Vitesse maximale (cm/s)
|
68.45
|
24.48
|
27.26
|
60.17
|
|
Accélération maximale
(cm/s2)
|
331.1
|
298.2
|
300.03
|
9.94
|
|
Période (s)
|
3.4269
|
3.4269
|
5.411
|
-
|
V.3.3. Interprétation des résultats
On constate après un cycle de mouvement une
réduction dans un rapport égal à 1/3 de la valeur des
amplitudes des pics successifs, alors que sans amortisseur plusieurs pics sont
mis en évidence, ce qui sollicite grandement les éléments
résistants et altère fortement les appuis dans leur
constitution
L'amortisseur fait chuter brutalement les réponses en
épargnant les dispositifs isolateurs ainsi que les fixations
On remarque également que l'utilisation des
amortisseurs ne modifie pas la période de la structure. L'amortisseur
est donc généralement associé à des isolateurs
sismiques pour qu'ils se complètent mutuellement. Les isolateurs
sismiques (appareils d'appuis en néoprène fretté) ont pour
but d'augmenter la période, ce qui engendre des déplacements
importants.
Pour cela, l'utilisation des appareils d'appuis glissants
réalise l'isolement total de la structure (sauf frottement entre les
plaques de glissement) mais engendre des déplacements très
importants. Le système le plus efficace est donc celui qui incorpore des
appareils glissants pour rendre libre ou isoler sismiquement la structure (
c.à.d que la période devient très grande) en association
avec des amortisseurs pour gêner et enfin réduire les amplitudes
du mouvement en s'y opposant par une force proportionnelle à sa
vitesse.

V.4. Exemple de conception
V.4. 1.Cas d'un pont
Pour mieux faire valoir l'utilité des amortisseurs, les
trois modèles de ponts sont analysés :
- Pont courant avec appareils d'appuis en
néoprène,
- Pont avec appareils d'appuis glissants,
- Pont avec amortisseurs.
1- Modèle pont courant avec appareils d'appuis
néoprène
Nous considérons ici que tous les appuis sont
constitués d'appareils d'appuis en néoprène qui
présentent une certaine rigidité dans le plan horizontal.
Celle-ci sera modélisée par un système de ressort.

Figure V.5 : pont courant avec appareils
d'appuis en néoprène
Le pont sera bien entendu dimensionné pour résister
dans les deux situations : situation durable et transitoire et situation
accidentelle.
Le modèle structurel sera représenté par la
figure suivante :

Figure V.6 : modèle d'un pont courant
avec appareils d'appuis néoprène
a- Situation durable et transitoire
:
Le déplacement horizontal est principalement dû
dans ce cas aux effets thermiques et au freinage de véhicules.
b- situation accidentelle :
Dans ce cas, le déplacement est dû uniquement aux
effets sismiques.
Calcul de la période fondamentale :

m
T 1= 2ð
k
Soit k la rigidité globale des piles k = k1 +k2+k3
Où ki = k i pile + ki appareil d'appuis.
La période T1 a été déterminée
par la formule ci-dessus. Le spectre de réponse
(FigV.9) permet de déterminer
l'accélération sismique:
Accélérationã (g)
T1
Période T (s)
Figure V.9 : spectre de
réponse

Figure V.10 : déformation de la
pile
On remarque bien que la déformation de l'appui est
composée de deux déplacements, le premier est celui de la
déformation intrinsèque de la pile et le deuxième est la
déformation de l'appareil d'appuis en élastomère
fretté, qui donne une certaine souplesse à la pile et par
conséquent diminution de l'effort sismique.
2- Modèle pont avec appareils d'appuis
glissants

Figure V.11 : pont avec appareils d'appuis
glissants
Nous considérons ici que tous les appuis sont
constitués d'appareils d'appuis glissants sauf le deuxième appui
qui est considéré fixe.
Le modèle structural sera représenté par la
figure suivante :

Figure V.12 : modèle de pont avec
appareils d'appuis glissants
Calcul de la période fondamentale :
La période fondamentale est donnée par la formule
suivante :

m
T = ð
2 2
k2
k2 : rigidité de la pile P2
La période T2 étant évaluée, le
spectre de réponse nous permet de déterminer
l'accélération sismique ã2 tel que le
montre le schéma suivant :
Accélérationã (g)
T2 Période T (s)
Figure V.15 : spectre de
réponse
On remarque bien que l'accélération sismique
ã2 donnée par la période T2 est
plus
faible que celle donnée par T1. Par voie de
conséquence, l'effort sismique engendré sera moins important.
3- Modèle pont avec addition
d'amortisseurs
Nous considérons ici que tous les appuis sont
constitués d'appareils d'appuis glissants sauf pour le deuxième
appui auquel on va associer un amortisseur.

Figure V.16 : pont avec appareils d'appuis
glissants et amortisseurs
Le modèle structural sera représenté par la
figure suivante :

Figure V.17 : modèle d'un pont avec
des appareils d'appuis glissants et des amortisseurs
La période fondamentale est obtenue par
:

m
T = ð
3 2 = T2
k 2
k2 : rigidité de la pile P2
Le calcul de la période T3 nous donne une valeur
égale à T2, mais une accélération sismique
ã3 plus faible que ã2 .
Cela s'explique par le fait que l'addition d'un amortisseur
n'influe pas sur la période de vibration d'une structure ;
mais elle fait diminuer les sollicitations dynamiques par le biais de
l'augmentation de l'amortissement [10].
Accélérationã (g)

î
5%
ã3
î
> 5 %
T3=T2 Période T (s)
Figure V.20 : spectre de
réponse
Le spectre de réponse suivant montre l'influence de
l'addition des différents organes parasismiques et dispositifs
d'amortissement sur l'effort sismique.

ã1
5 %
î
Période T (s)
T1
T3=T2
Accélérationã (g)
ã2
ã3
î
> 5%
Figure V.21 : comparaison des spectres de
réponse
Paramètre d'amortissement C =( M 4ð
ænl 1 [ñ T Sa ( T,
æ)]1-á )
T h(á) 2ð

Force de l'amortisseur F = C Vá = C.
[ñ
T Sa ( T, æ)]á
2ð

FIN
V.4. 1.Cas d'un bâtiment
Cet exemple montre l'utilité de l'addition des
différents organes parasismiques dans le domaine bâtiment.
La figure suivante retrace les différentes étapes
du comportement de la structure d'un bâtiment supposée d'abord
courante, puis munie progressivement d'organes parasismiques.

Figure V.22 : comportement structurel d'un
bâtiment avant et après additions
d'organes
parasismiques
Commentaire
Pour mettre en évidence l'intérêt de combiner
les différents systèmes de contrôle, nous allons mener un
raisonnement virtuel qui retrace les états d'équilibre dans
différentes situations.
Nous considérons tout d'abord que le bâtiment est
au repos : le déplacement horizontal est donc nul. Nous supposons
ensuite que ce même bâtiment est soumis à une excitation
dynamique (séisme) qui provoque un déplacement horizontal D
acceptable, mais engendrant des efforts assez importants. Pour les
réduire, on incorpore dans la structure un système de
contrôle passif du type isolateur sismique qui aura pour
conséquence non seulement la réduction attendue des efforts mais
aussi l'augmentation du déplacement horizontal parfois excessive et donc
non souhaitable ou non admissible. Pour contrecarrer cet inconvénient
nous devons combiner à cela un système de contrôle passif
du type amortisseur. Cette dernière solution permet de réduire
considérablement le déplacement horizontal et par voie de
conséquence d'absorber l'énergie sismique. Il demeure comme
même nécessaire d'évaluer les différents
paramètres qui permettent la justification de la structure sous ces
différents aspects.
Une bonne conception structurale qui intègre l'addition
des amortisseurs reste une opération tés importante, mais pas
très bien maîtrisée par les professionnels. Pour mener une
telle étude parasismique, le critère économique nous
interpelle et nous pousse à faire le dimensionnement de ces
amortisseurs, qui tient compte des données réelles du projet. Les
outils existants dans ce domaine ne permettent pas de dimensionner ces derniers
sur la base d'un spectre de réponse. Ils considèrent des valeurs
d'amortissement forfaitaire en pourcentage du poids selon la zone sismique.
Nous nous proposons de combler ce vide moyennant l'élaboration d'un
logiciel de dimensionnement des amortisseurs selon le règlement
parasismique algérien en vigueur (RPA) .
V.5. Dimensionnement des amortisseurs visqueux non
linéaire pour les ouvrages de génie civil
La partie théorique relative au dimensionnement des
amortisseurs a été développée dans le chapitre III
intitulé « formulation du problème d'amortissement et
méthode de dimensionnement des amortisseurs »
Nous avons réalisé à cet effet un logiciel
de dimensionnement des amortisseurs visqueux non linéaire que nous avons
dénommé DAV2007 v1.0,
Les différentes étapes de dimensionnement sont
représentées par l'organigramme suivant :
Début

Matrices, K, M

Période T

Accélération de la zone A

Périodes caractéristiques associées à
la catégorie de site T1, T2

Spectre Sa ( T, æ)

Coefficient de réduction ñ

L'exposant á

|
Déplacement d =
|
?
??
|
T ?
2 ??
ð
|
2
|
Sa ( T, æ)
|

|
0 .07
Taux d'amortissement équivalant æeq = ( 2
ñ
|
-0.02 )
|

Taux d'amortissement provenant de l'amortisseur ænl=
æeq - æ

Exemple
Données
Les données nécessaires à l'exécution
de ce programme sont :
- Période T = 0.90 seconde
- Accélération de la zone A = 0.4g
- Masse du système M = 82000 kg
- Amortissement critique æ = 5 %
- T1, T2 périodes caractéristique associées
a la catégorie de site
T 1 = 0.15 seconde
T 2 = 0.40 seconde
- Coefficient de réduction ñ = 0.50
- Exposant á = 0.60
Résultats
Les résultats obtenus par ce programme sont

7
- Correction d'amortissement ç =
2+ î
h(á) =0.0892 á2 -0.3583 á
+1.2699
Sa ( T, æ) = 1.25 A ( 1+ T (2.5
ç-1)) 9,81 si 0 = T= T1
T1
Sa ( T, æ) = 2.5 ç (1.25. A) 9.81
si T1 < T= T2
2
Sa ( T, æ) = 2.5 ç (1.25 A)
9,81 si T2 < T= 3 sec
? T 2 ? 3
?? ??
T

2 5
? T 3
2 ? 3 ?
?? ?? ?? 3 ?? ?
3 T
Sa ( T, æ) = 2.5 ç (1.25 A)

9,81 si T > 3 sec
- Déplacement d =
Sa ( T, æ)/100 = 14.661 cm
?
??
T ?
2 ??
ð
2

|
0. 07
- Taux d'amortissement équivalant æeq = ( 2
ñ
|
-0.02 )100 = 26 %
|
Taux d'amortissement provenant de l'amortisseur ænl=
æeq - æ = 21 %
- Paramètre d'amortissement C = (M 4ð
ænl 1 [ñ T
Sa (T, æ)] 1-á) /100 =169.14 N /
T h(á) 2ð
(m/s)á
- Force de l'amortisseur F = C Vá = C.
[ñ
T Sa ( T, æ)]á = 113.192 N

2ð
Interfaces du logiciel
a. Fenêtre d'introduction des
données
Dans cette partie du déroulement de l'exécution
du logiciel, les informations issues d'un calcul de la structure objet de
l'étude, sont introduites comme des données de départ
c'est-à-dire en input

Figure V.23 : Fenêtre d'introduction
des données
b. Fenêtre de résultats
Après un calcul comme explicité
précédemment, les résultats sont données en valeurs
numériques et enfin complétée par un graphe de
fonctionnement de l'amortisseur

Figure V.24 : Fenêtre des
résultats
c. Exemple illustratif : Fiche de données et de
résultats
Les fichiers de données et de résultats peuvent
être affichés et enregistrés en fichiers texte sous format
.doc, comme le montre l'exemple suivant :

Figure V.25 : Fichier données et
résultats, relatif au calcul des paramètres de
l'amortisseur

Graphe V.1. Force de l'amortisseur en fonction de la
vitesse.
Ce graphe représente la loi de comportement ainsi
calculé ; Force de l'amortisseur en fonction de la vitesse et sert
à la formulation d'une exigence de caractéristiques. Chaque
amortisseur possède ses paramètres propres,
Conclusion générale
CONCLUSION GENERALE
Le séisme est un phénomène naturel
complexe qui se produit en différents moments et dans différents
lieux dans le monde. Il engendre plusieurs victimes et il détruit
beaucoup de biens. Malgré le progrès scientifique, on ne peut
prévoir avec certitude ni où ni quand il peut se produire.
Les tremblements de terres reste donc un
phénomène très aléatoire et leurs effets sont
dévastateurs et incontournables. Il s'agit donc de
réfléchir aux méthodes et aux moyens pour atténuer
leurs impacts. Pour atteindre cet objectif qui constitue pour l'heure une part
importante de leurs préoccupations, des chercheurs et des politiques
tentent de trouver à ce problème des réponses rationnelles
et optimales. Ce « raisonnement parasismique » doit s'étaler
à toutes les phases du cycle de la vie d'un ouvrage,
c'est-à-dire, depuis le début de sa conception, en passant par la
phase de sa réalisation et en terminant par sa mise en service
(entretien). Ceci se traduit par le fait qu'une attention particulière
doit être portée sur la conception architecturale et structurale
de l'ouvrage, et qu'il faut veiller au choix de la nature et de la
qualité des matériaux de construction, au suivi régulier ,
voire même rigoureux des étapes de réalisation, et à
la mise en place des services d'entretien compétents.
Notre travail se veut d'être une modeste contribution
à ce vaste domaine du « parasismique » Notre
préoccupation était donc l'atténuation des effets
sismiques moyennant l'incorporation des dispositifs d'amortissement (appuis et
amortisseurs) à des structures de grandes dimensions. Nous nous sommes
particulièrement intéressés à l'effet de
l'amortissement sur les paramètres ou réponses qui sont le
déplacement, la vitesse et l'accélération des structures
dont dépendent bien évidement les sollicitations. Les
études théoriques et les applications concernant cet axe sont
très récentes, et quasi absentes à l'échelle
nationale.
Nous avons ainsi réalisé dans un premier temps
une prospection, une analyse et une synthèse des informations
bibliographiques (données et connaissances) inhérentes au domaine
étudié. La première étape de cette partie a
porté sur les notions et les concepts relatifs à l'amortissement.
Un classement de « l'amortissement » selon plusieurs critères
a été fait. Des méthodes d'évaluation de
l'amortissement ont été présentées et
discutées.
La deuxième étape à été
consacrée aux différentes techniques de l'isolation sismique
parmi les quelles l'utilisation des amortisseurs.
La troisième étape a été
réservée pour la formulation mathématique (construction du
modèle) de l'équation de mouvement avec amortisseur.
Nous nous sommes intéressés dans un second temps
à des applications pour mettre en évidence l'intérêt
de l'addition à des structures des dispositifs d'amortissement. Pour ce
faire, nous avons réalisé un programme informatique pour
l'évaluation des réponses (déplacements) d'un oscillateur
simple supposé soumis au séisme de référence
d'El-Centro. Nous avons ainsi montré que les déplacements
diminuent considérablement avec l'augmentation de l'amortissement.
Une deuxième application concernant un portique et un
pont a été réalisée pour mettre en évidence
l'influence de l'introduction des amortisseurs sur les réponses de ces
structures. La comparaison des résultats relatifs à une structure
munie d'un amortisseur et ceux de la même structure sans amortisseur a
bien montré qu'il y a un gain important dans la quantité de
mouvement (déplacements, vitesses et accélérations).
Nous avons dans le même ordre d'idées conçu
et réalisé un programme informatique de dimensionnement des
amortisseurs.
Comme conclusion, l'utilisation des amortisseurs et les
techniques d'isolation sismique, surtout dans les constructions
stratégiques (hôpital, bâtiment important, pont, etc.)
peuvent contribuer d'une manière efficace à l'atténuation
des sollicitations sismiques, et par voie de conséquence, à la
réduction du risque sismique.
Les modèles de structures munies d'appareils
d'amortissement ne sont pas encore pris en charge par les règlements et
les codes Algérien ( RPA, RPOA) Notant aussi l'absence des DTR
concernant les aspects pratiques de ces dispositifs d'amortissement. Il est
temps d'y réfléchir sérieusement à ce
problème afin d'intégrer cette nouvelle composante technologique
tant sur le plan conceptuel, théorique que pratique.
Perspectives
Il demeure comme perspective l'évaluation de l'impact
économique dans le sens le plus large (coût matériel,
coût de réalisation, coût d'entretien...) dû à
l'intégration de ces dispositifs d'amortissement dans une structure.
Autrement dit, il s'agit de procéder à une étude
technicoéconomique comparative entre une structure munie de dispositifs
d'amortissement et la solution équivalente sans dispositifs.
Références bibliographiques
Références bibliographiques
[1].SANAUL (hyq chonwdhury) - Damping
characteristics of reinforced and partially prestressed concrete beams, Faculty
of Engineering-GRIFFITH UNIVERSITY- GOLD COAST CAMPUS, 1999, 283P.
[2].PECKER (Alain)- Cour de dynamique des
structures- ENPC Paris, 2004.
[3]. Zacek M- Construire parasismique- Edition
Parenthèses, (1996).
[4]. Ministre des travaux publics et services
gouvernementaux -Aléas sismiques, codes du bâtiment et
options d'atténuation des risques pour les immeubles canadiens, N°
du catalogue : D82-73/2002F-IN, gouvernement du Canada, (2001).
[5]. US Army Corps of Engineers (USACE) -Sismic
design for building- Engineering Division Directorate of Military
Programs-washington-DC, (1998).
[6]. SETRA -Pont courant en zone sismique guide
de conception -janvier 2000, 140p
[7] Kelly J.M-The implementetion of base
isolation in the United States, Proceedings of tenth world conference on
Erthqauke-Balkema, Rotterdam 1994, pp 6507-6514.
[8]. Kelly.J.m & Jose. A -Optimum damping
in base-isolated structures, Proceedings of tenth world conference on
Earthquake Engineering-Madrid-1992.
[9]. -Trevor E Kelly - « In-structure
damping and energy dissipation; design guidelines `` Holmes Consulting Group,
New Zealand-(2001);
www.holmesgroup.com
[10]. A.Capra & D Amir Mazaheri
-Séminaire sur les ponts en zone sismiques -Alger, juin 2006
[11]. A.Parvin -The use of helical spring and
fluid damper isolation systems for structures subjected to vertical ground
acceleration, july 2001,12p
[12]. M. Kahan- Dimensionnement
simplifié d'amortisseurs visqueux non linaires pour les ponts en zone
sismique , Revue française de génie civil - SETRA 2000
pp35-55.
[13]. MCM Cabinet Conseil (2003)- '` Les appuis
parasismiques en caoutchouc », catalogue, journées scientifiques et
techniques, Algérie.
[14]. Ikhlef Boualem -Mémoire de
magister -Technique d'isolation sismique : analyse et comparaison des codes
existants, USTHB 2005.
| 


