III.4.6.3. Fonction d'impulsion
Les fonctions de réponses impulsionnelles permettent en
vertu du théorème de Wald, d'analyser l'effet d'un choc d'une
innovation sur les valeurs courantes et futures des variables endogènes
du modèle VAR. Cette approche pose néanmoins un certain nombre de
problèmes méthodologiques dus notamment à la très
probable corrélation des innovations du modèle. Une fonction
d'impulsion trace l'effet d'un choc d'un écart-type d'une des
innovations sur les valeurs courantes et futures des variables
endogènes. Un choc de la ième variable se transmet
aussi à toutes les autres variables à travers la structure
dynamique du VAR.
Prenons l'exemple d'un VAR(1) composé de la production
et du stock de monnaie. On peut l'écrire sous forme d'un système
de la façon suivante :
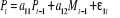

Une variation de å1t changera
immédiatement la valeur courante de P. Mais elle modifiera aussi toutes
les valeurs de P car les valeurs retardées de P apparaissent dans les
deux équations. Les innovations sont généralement
corrélées de sorte qu'elles ont une composante commune qui ne
peut pas être associée à une variable spécifique. La
solution arbitraire à ce problème est d'attribuer tout l'effet de
la composante commune à la variable qui vient en premier dans le
système VAR.
Ainsi, dans notre exemple, la composante de å1t et
å2t est attribuée totalement à
å1t car å1t précède
å2t et donc l'innovation de Pt et l'innovation
de Mt est transformée de sorte que la composante commune
est enlevée. Les graphiques des fonctions de réponses aux chocs
représentent les réponses à des chocs sur les
résidus structurels des trois variables dans les trois équations
du modèle. Pour chaque variable, le choc est égal à
l'écart-type des résidus. Pour les variables de notre
étude, l'horizon représentant le délai nécessaire
pour que les variables retrouvent leur niveau de long terme est
supérieur ou égal à 10ans. Les mouvements positifs et
négatifs observés à travers les fonctions de
réponses aux chocs des prix des produits pétroliers sur le PIB,
l'IPC et RF peuvent avoir la même explication que celle du signe du
coefficient de corrélation.
| 


