Tableau no5 : Test de
Stationnarité des résidus
|
Variable s Modèle [1]
Modèle [2] Modèle [3]
ADF PP ADF
PP ADF PP
|
|
RELIPC -1,586 -2,182 -1,283
-1,826 -1,623 -2,221
(-2,624) (-2,622) (-3,223)
(-3,220) (-1,622) (-1,621)
RELRF -2,636 -3,096 -2,606
-3,139 -2,707 -3,188
(-2,624) (-2,622) (-3, 223)
(-3,220) (-1,622) (-1,621)
RELPIB -2,383 -2,782 -2,363
-2,767 -2,427 -2,849
(-2,975) (-2,970) (-3,586)
(-3,579) (-1,954) (-1,953)
Les valeurs critiques au seuil de 5% sont entre
parenthèses.
Source : Nous-mêmes à
partir des tests de stationnarité.
|
En analysant ce tableau, pour les trois séries
estimées, nous en déduisons que tous les résidus sont
stationnaires en niveau. En effet, les valeurs d'ADF et de PP calculées
sont inférieures aux valeurs critiques.
III.4.3. Définition du Modèle Vectoriel
Autorégressif (VAR)
Un modèle VAR est un outil économétrique
particulièrement adapté pour mesurer et utiliser en simulation,
l'ensemble des liaisons dynamiques à l'intérieur d'un groupe de
variables données. Toutes les variables sont initialement
considérées comme étant potentiellement endogènes.
En règle générale, la modélisation VAR
« standard » consiste à modéliser un vecteur
de variables stationnaires à partir de sa propre histoire et chaque
variable est donc expliquée par le passé de l'ensemble des
variables.
La forme standard de ce type de modèle est
caractérisée par les points suivants :
- les variables à modéliser sont toutes
stationnaires ;
- les variables à modéliser sont toutes
potentiellement endogènes ;
- le nombre de décalages associés à
chaque variable dans chaque équation est identique.
III.4.4. Choix du nombre de retards
Le choix du nombre de retards des variables est très
important pour un modèle vectoriel autorégressif dans ce genre
d'étude. Il est difficile d'estimer un modèle VAR sans que les
réponses aux problèmes de retards et de causalité ne
soient trouvées. Généralement, selon Régis
BOURONNAIS (1993), un des problèmes principaux inhérents à
ce modèle est la détermination du nombre de retards à
considérer.
En effet, en admettant qu'une variable endogène
dépend de ses propres innovations (ou d'autres variables) à des
périodes différentes, le problème qui se pose est de
savoir à quelle période s'arrêter. Il est difficilement
concevable que ces variables aillent jusqu'à l'infini.
Pour détecter l'influence d'une variable sur une
autre, une certaine période de retard est nécessaire. Selon
Boswijk et Franses (1992), Gonzalo (1994) ainsi que Ho et Sorensen (1996), le
choix du nombre de retards peut affecter sensiblement les résultats des
tests du maximum de vraisemblance pour la coïntégration.
Ainsi, plusieurs travaux (voir notamment Deniau et Alii, 1992)
ont permis d'estimer le nombre de retards « p » sans
tâtonnement. D'où plusieurs critères de choix de retards
existent. Il arrive que tous les critères ne convergent pas vers la
même solution et le choix du «bon» critère est
laissé au soin de l'utilisateur.
Pour déterminer le nombre de retards d'un VAR, on
utilise plusieurs critères d'informations comme notamment :
· Le critère d'information du Final Predictor
Error (FPE) avec une formule relative suivante :
FPE =  
· Le critère d'information d'Akaike (AIC) avec la
formule relative suivante :
AIC = 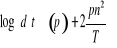
· Le critère d'information de Schwarz (SC) avec
une formule relative suivante :
SC = 
· Le critère d'information d' Hannan-Quinn (HQ)
avec la formule relative suivante :
HQ = 
Avec :
dét ?(p) : le déterminant de la matrice de
variance-covariance des innovations obtenues à partir d'un VAR(p) ;
n : le nombre des variables ;
p : le nombre de décalages ;
T : la taille de l'échantillon.
| 


