Conception et modélisation d'un capteur acoustique

2.2.3 Interaction du faisceau ultrasonore avec la matière

1.2.3.1 Réflexion et réfraction d'u4eI14d1 ultrasonore

Lorsqu'une onde ultrasonore rencontre une interface séparant deux milieux de caractéristiques physiques différentes, une partie de son énergie est transmise d'un milieu à l'autre, alors que l'autre est réfléchi (cf. figure 2.2).

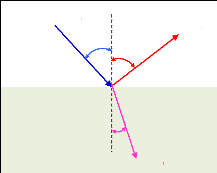
Milieu 1 ; Za1
Milieu 2 ; Za2

Onde incidente

èi

Onde transmise

è_t

è_r

Onde réfléchie

Fig. 2.2 - Réflexion et réfraction d'une onde ultrasonore sur une interface

5 L'unité de mesure de l'impédance acoustique est le : Rayl ; 1Rayl =1kg.m^-2s^-1; exemple pour l'air : 415 Rayls.

D'un point de vue énergétique, le coefficient de réflexion «???? » et le coefficient de transmission «????» peuvent être donné par les relations suivantes [64,68,69]:

Iar

Iai

????=

et

Iat
Iai

???? =

2

(2.4)

Z_a2 _cosèi-Za1 cos è_t

Z_a2 cos _èi+Za1 cos è_t
⁴Za1 Z_a2cos² èi

Za2 cos _èi+Za1 cos è_t~²

(2.5)

où _Za1 et Za2 sont respectivement les impédances acoustiques des milieux 1 et 2;

èi , è_r et è_t sont respectivement l'angle d'incidence, de réflexion et transmise de l'onde ultrasonore ;

Iai, Iaret Iat représentent respectivement l'intensité de l'énergie incidente, réfléchie et transmise.

Si nous considérons que l'onde ultrasonore atteint l'obstacle perpendiculairement (èi=è_r=è_t=0 ). Les coefficients de réflexion et transmission peuvent donc s'écrire :

	????=	Za2^-Za1		2	(2.6)
et		Za2+Za1
????=^1-????=			^4Za1Za2 Za1+Za2)^2			(2.7)

On constate que si les impédances acoustiques des deux milieux sont très différentes l'énergie réfléchie sera très élevée. C'est ainsi qu'une couche d'air, meme très fine, dans le champ de propagation des ultrasons agit comme un écran infranchissable. C'est pour cette raison qu'il est nécessaire d'utiliser un milieu de couplage entre le transducteur et le milieu dans lequel on souhaite faire propager l'onde acoustique.

Dans le tableau 2.3 nous présentons quelques valeurs des coefficients de réflexion et de transmission pour quelques interfaces acoustiques typiques.

Milieu 1	Milieu 2	Za1^(MRayl)	Za2 (MRayl)	????(%)	????(%)
Air	Aluminium	0.00043	17.06	99.99	0.01
Air	Plexiglas	0.00043	4	99.99	0.01
Air	Muscle	0.00043	1.64	99.95	0.05
Air	Eau	0.00043	1.48	99.88	0.12
Eau	Aluminium	1.48	17.06	84.03	15.97
Eau	Plexiglas	1.48	3.30	38.08	61.92

Tab. 2.3 - Valeurs de l'interface acoustique entre quelques milieux [64,67]

1.2.3.2 Atténuation d'une onde ultrasonore

L'atténuation d'une onde ultrasonore dépend principalement de la fréquence considérée. Pour la plupart des matériaux, plus la fréquence est haute plus l'atténuation est importante. La theorie prevoit que l'attenuation est directement proportionnelle au carre de la frequence pour une onde plane.

Considerons une onde plane se propageant suivant la direction « z », la pression acoustique est donnee par la formule [70]:

P_a =P??0exp(^--???? z) (2.8)

oil _P??0 est la pression initiale (z=0) et a_s est le coefficient d'attenuation.

Pour les liquides, le coefficient d'atténuation est donné par la relation [71]:

2çù²

????= 3ñva3 (2.9)

oil ç est le coefficient de viscosite et ù est la pulsation.