Conception et modélisation d'un capteur acoustique

République Algérienne Démocratique et Populaire

0 TQTNWE dE l(QNETI QEmEQN6DSpITEDr EtEEM 5EFhEIFhEI6FTEQtTfTqDE

UNIVERSITE DES SCIENCES ET DE LA TECHNOLOGIE D'ORAN
- MOHAMED BOUDIAF -

FACULTE DE GENIE ELECTRIQUE

(3$57(0 (17 0(/ (&7521,48(

Mémoire en vue de l'obtention du diplôme de Magister

Spécialité : Electronique
Option : Composants et Systèmes de la Microélectronique Avancée

Présenté par :

SLIMANI ABDOUN

Sujet du mémoire :

Conception et Modélisation d'un

Capteur Acoustique

Soutenue le 15 / 03 / 2010 devant le jury composé de :

M^r	M. LOUNIS	Maître de conférences (USTO-MB)	Président
M^r	T. BOUTCHACHA	Professeur (USTO-MB)	Rapporteur
M^r	D. BENBEKRITE	Chargé de cours (USTO-MB)	Co-rapporteur
M^r	A. KADDOUR	Maître de conférences (USTO-MB)	Examinateur

Remerciements

Le travail présenté dans ce mémoire a été réalisé au Laboratoire d'Étude des Composants Electroniques au Silicium de l'Université des Sciences et de la Technologie d'Oran - Mohamed Boudiaf dirigé par le professeur Touati BOUTCHACHA.

Je tiens tout d'abord à remercier le professeur Touati BOUTCHACHA, pour la confiance qu'il m'a accordée en me proposant de réaliser ce mémoire au sein de son équipe de recherches « Composants et Systèmes de la Microélectronique Avancée ». J'ai été très sensible à ses remarques et recommandations. Il m'a permis par ses critiques d'améliorer ce travail qu'il trouve ici l'expression de ma profonde gratitude pour l'honneur qu'il m'a fait d'avoir bien voulu être rapporteur de ce travail, et de participer au jury.

Je remercie vivement monsieur Djamel BENBEKRITE, chargé de cours à l'USTO-MB. Je le remercie d'avoir codirigé ce travail et de m'avoir fait profiter de ses compétences et de ses conseils efficaces et d'avoir apporté la rigueur scientifique nécessaire à son bon déroulement, je tiens également à le remercier pour sa gentillesse et sa grande disponibilité.

J'adresse toute ma gratitude à monsieur Mourad LOUNIS, maître de conférences à l'USTO-MB, pour avoir accepté d'être le président du jury de cette soutenance.

Je remercie également monsieur Abdelhafid Kaddour, maître de conférences à l'USTOMB, pour l'intérêt qu'il a porté à mon travail en acceptant de participer au jury.

Pour vous laisser le loisir d'apprécier ce mémoire, je terminerai ici, mais je n'oublie évidemment pas ceux que je n'ai pas nommés ici et aussi ma famille et tous mes amis qui m'ont apporté leur soutien dans la réalisation de ce modeste travail.

₄Üi ÜÜÜi cÜÜÜ`~^õ .ÜÜ~ÐÜaÜ~ æ fÜ..6:

·

1_,.c₉.,.=a Sa~~ . 11Ç ^..}1.6. A4Ç..1Ç á1~~ ^cri _A4Ç..1Ç A₄c.₃.1 æ _~~~1Ç á~~-1Ç _cfi Ñ3-~Ç r7F3: ~~~~i äÅ ÌÇi&i.14 111 ä1.A^,y Êii_.1Ç b3å Ú1 aÇæ É ÐÜ.. . ~~~~~~~~Ç ~~~~~~Ç *~) :#li~Ç Êv_-~ 0-⁶¹--a cD:L.^---'^.. .1.₄ All. áj_~1 Ï~.4tÇ A,Ï~? 4:A.1Ç A.ÇÑÏ ₄~Å 3.~1Ç b0å áN~ ₄).. .81 . l,1ÇÏ -"_..).,_?.
·12,5 æ 4_641:11.6d cittn..4^-

Ç3+I

. ì.~

Ai+ CiA

"

PSPICE

"

F!)

AL.Ç3. A9l11Ç á -~

Ú1-3~Ç L.Åæ :4÷ (:)"3 íÏ~i÷Å 1.0  cf.-4

ÏÇi.1Çæ A,Ï~i#7Ç Á14.4SIÇ á.? Ê1,.i..1 ₄1Ç3:~Ç ^ulc. ÉJÂ:
·1Ç b0å ^c).4 ₄3111Çæ áæ>Ç a..Ñ,_.1Ç ^11,......& Ö.;iÇ

c.111Ç Ñi_-1Ç c_y
· áæ>Ç Á.4Ç t.u.a..et& P' . ~~~~~~Ç bl"-.1 Êi9.~ ÚÇ9- `1:6 æ Ê1."A-1Ç bl"-.1 A7Ï~84Ç ;70-.41Ç

_c
·-
·31:3 _j..1 1:~.:IAÇ

₄3111Ç Á.,~Ç

. Ú4:4 æ Ú1.6 äæ
·. All~Ç á9--1 ArÏl- 43-3.Ç A"ÇÑ
·1

"

"

PSPICE

æ

cri

ÑÇ_,4 )Å 6416 )1 641.1Ç Ñ9..1Ç _vi ÉÑ9Âa.1Ç Ï~.4tÇ r_Ï~. ÌÐ~.11Ç äÅ . Aill,1Ç á _j_N..41 ZA_LASIÇ Z
·14.41Ç Útli.,...V 1.A.1,1.1.. ZIA .~ 43Ï~4#7Ç A,114 €S1Ç ÉÏ~.114 :À:~Ç ÒÇ:~åNÇ á11^, äl4 1_,:c_ui _J.S.I.,i l+1 ₄1Å ^AIL:=714 .W~ ..Çæ ÏÏ.~ -_.4j4.
·_₄ 3&.1:1 ₄11Ç Ï~.4tÇ ^A3.1:'.Nli "0~.4~~Ç 43..1Ç '7ÇÑ.1 &ÇilÇ Ñj_-1Ç 1:.a Ê1~:~1Ç b3å J₄111 . A1.d~ Z#ÇilÇ ^cci ₄å Aye ÊÇÑ14c 1'411 -11Âæ ÊÇÏÏ511Ç _.t.₄... _4.5.1c. 6₄1,5 l+1 ₄~Å ^'AIL:414 ÒÇ_5åVÇ áLS. ^ap. á1_VÇ Ñ14.1c.iÇ A_Ï~.#7Ç '4114)41Ç ÊZ1~. æ Z1æ..1Ç Ê.~tz. ₀.eix₄ 110.14 ÇÐÅ Ï~~)7Ç r.Ï1? ÊÇÑ14c ₄1Å 1..1 ^ciS.4,1 ₄11Ç Ï~
·4tÇ

. t÷Ç..1Ç `.L ^vi ÉtIm.1Ç

0~-~~~~1Ç cZ'.11Ç áN.~.14 ^lili ~ja.1Ç^LiNkl ula c. ~JÇ Öiii ãti&1Ç viæ

L.:cui .

'..Ü4. _ce-Alul ...).-₄ :LS^-Uzi á ÜÜ-~ PZT rlÏ~d÷7Ç ro(14)ÜÜÜ41Ç ÏÇ-AlÇ :7Ï~84Ç Á~).ÜÜÜÜ41Ç : ZyjÜåi~1Ç Ê44,~~Ç . PSPICE Ï~.4tÇ A.1.1 43Ü.. Ï~.4tÇ A3Ï~.

Conception et modélisation d'un capteur acoustique

Résumé

L'amélioration de la qualité des images dans le domaine de l'imagerie médicale et qualité des contrôles dans le domaine du contrôle non destructif est liée en particulier à celle des transducteurs ultrasonores piézoélectriques utilisés. La modélisation et la simulation de transducteurs permettent de les caractériser et optimiser. L'objectif de ce travail est d'une part de traiter la modélisation unidimensionnelle et tridimensionnelle d'un transducteur ultrasonore piézoélectrique, et d'autre part de simuler le transducteur avec PSPICE. À cet effet, des généralités sur la piézoélectricité et matériaux piézoélectriques, ultrasons et transducteurs ultrasonores sont respectivement décrits dans le premier et deuxième chapitre. Ensuite, la modélisation unidimensionnelle du transducteur sans et avec pertes est traitée dans la première partie du troisième chapitre. Dans la deuxième partie, le logiciel PSPICE est utilisé pour simuler l'impédance électrique du transducteur. Les modèles unidimensionnels décrits dans le chapitre précédent ne sont applicables uniquement qu'autour d'une fréquence de résonance particulière, ainsi ils supposent que les modes de vibrations d'une céramique piézoélectrique sont découplés, cependant, il existe des couplages entre ces modes. Afin de surmonter ces difficultés, nous traitons dans le quatrième chapitre une modélisation analytique tridimensionnelle qui prend en compte le couplage entre les modes de vibration et qui est valable à toutes les fréquences. De plus, elle nous donne des expressions tridimensionnelles qui se réduisent aux expressions simplifiées unidimensionnelles lorsque certains coefficients élastiques et piézoélectriques sont supposés nuls. Enfin, dans le but de valider nos résultats de simulation, des résultats expérimentaux extraits de la littérature sont exploités.

Mots-clefs : Piézoélectricité, matériaux piézoélectriques, PZT, transducteur ultrasonore modélisation unidimensionnelle, modélisation tridimensionnelle, PSPICE.

Table des matières

Remerciements i

Résumé ii

Table des matières iv

Liste des figures viii

Liste des tableaux x

Principales notations, symboles et constantes physiques xi

Introduction générale 1

1 Principes fondamentaux de la piézoélectricité 3

1.1 Introduction 4

1.2 Historique de la piézoélectricité 4

1.3 Effet piézoélectrique 6

1.4 Symétrie et piézoélectricité 6

1.5 Equations de la piézoélectricité 8

1.6 Caractéristiques électriques et mécaniques des matériaux piézoélectriques ........ 10

1.6.1 Permittivité « åij » 10

1.6.2 Compliance élastique « sij » 10

1.6.3 Constante de charge piézoélectrique « dij » 10

1.6.4 Constante de tension piézoélectrique « gij » 11

1.6.5 Coefficient de couplage électromécanique « k ij » 11

1.6.6 Facteur de qualité « Q » 11

1.7 Les matériaux piézoélectriques 12

1.7.1 Les principaux matériaux piézoélectriques 12

1.7.1.1 Les cristaux piézoélectriques 12

1.7.1.2 Les céramiques piézoélectriques 13

1.7.1.2.1 Généralités 13

1.7.1.2.2 Les zircono titanates de plomb (PZT) 14

1.7.1.2.2.1 Structure et polarisation des PZT 14

1.7.1.2.2.1.1 Structure des PZT 14

1.7.1.2.2.1.2 Polarisation des PZT 14

1.7.1.2.2.2 Matrice élasto-piézo-diélectrique des PZT 17
1.7.1.2.2.3 Caractéristiques des céramiques piézo-

électriques PZT 17

1.7.1.3 Les polymères piezoelectriques 18

1.7.1.3.1 Generalites 18

1.7.1.3.2 Origine de la piezoelectricite dans le PVDF .... 19

1.7.1.3.3 Caracteristiques des polymères piezoelectriques 19

1.7.2 Autres materiaux piezoelectriques 20

1.7.2.1 Les composites piezoelectriques 20

1.7.2.1.1 Classification 20

1.7.2.1.2 Caracteristiques des piezocomposites 1-3 ..... 21

1.7.2.2 Les couches epaisses piezoelectriques 21

1.7.3 Choix du materiau piezoelectrique .... 22

1.8 Modes de déformation d'un matériau piézoélectrique 22

1.8.1 Modes de deformation fondamentaux 23

1.8.1.1 Mode longitudinal {33} 23

1.8.1.2 Mode transversal {31 ou 32} 23

1.8.1.3 Mode cisaillement {15} 23

1.8.2 Autres modes de deformation 24

1.9 Quelques applications des materiaux piezoelectriques 24

1.9.1 Transformateurs piezoelectriques 24

1.9.2 Chaussures piezoelectriques 25

1.9.3 Actionneurs bilames 26

1.9.4 Imprimantes à jet d'encre 27

1.10 Conclusion 28

2 Différents types de transducteurs ultrasonores 29

2.1 Introduction 30

2.2 Theorie des ultrasons 30

2.2.1 Definition et applications des ultrasons ... 30

2.2.2 Parametres de l'onde ultrasonore 31

2.2.2.1 Longueur d'onde et vitesse de propagation 31

2.2.2.2 Impedance acoustique 32

2.2.2.3 Pression et intensite acoustiques 32

2.2.3 Interaction du faisceau ultrasonore avec la matière 32

2.2.3.1 Réflexion et réfraction d'une onde ultrasonore 32

2.2.3.2 Atténuation d'une onde ultrasonore 34

2.3 Differents types de transducteurs ultrasonores et leurs principes de fonctio-

nnement 34

2.3.1 Transducteur piezoelectrique 34

2.3.1.1 Structure d'un transducteur piézoélectrique 34

2.3.1.2 Description du faisceau ultrasonore emis par un transducteur

piezoelectrique 35

2.3.2 Transducteur capacitif 37

2.3.3 Transducteur piezoresistif 38

2.3.4 Transducteur impulsion-echo 38

2.4 Conclusion 39

3 Modélisation unidimensionnelle et simulation d'un transducteur ultrasonore piézoélectrique 40

3.1 Introduction 41

3.2 Modelisation unidimensionnelle d'un transducteur ultrasonore piezoelectrique 41

3.2.1 Transducteur sans pertes 41

3.2.1.1 Transducteur comme un système lineaire à trois ports 41

3.2.1.2 Impedance electrique du transducteur 43

3.2.1.2.1 Expression de l'impédance électrique .................... 43

3.2.1.2.2 Caractérisation du transducteur .... 44

3.2.1.2.3 Simulation de l'impédance électrique .... 46

3.2.1.2.4 Validation des résultats de simulation .................... 48

3.2.1.3 Schémas électriques équivalents 49

3.2.1.3.1 Schéma électrique équivalent de Mason .......... 49

3.2.1.3.2 Schéma électrique équivalent KLM .... 50

3.2.1.3.3 Schéma électrique équivalent de Leach ..... 51

3.2.2 Transducteur avec pertes 52

3.2.2.1 Différents types de pertes 52

3.2.2.1.1 Pertes diélectriques 52

3.2.2.1.2 Pertes mécaniques 53

3.2.2.2 Impédance électrique avec pertes du transducteur 53

3.2.2.2.1 Expression de l'impédance électrique avec pertes 53

3.2.2.2.2 Simulation de l'impédance électrique avec pertes 53

3.2.2.3 Schéma électrique équivalent simplifié du transducteur ..... 55

3.2.2.3.1 Schéma électrique équivalent simplifié . 55

3.2.2.3.2 Identification des paramètres du schéma électrique équivalent simplifié 56

3.2.2.3.2.1 Procédé d'identification 56

3.2.2.3.2.2 Simulation de l'admittance électrique .... 58

3.2.2.3.2.3 Identification des paramètres 59

3.3 Simulation d'un transducteur ultrasonore piézoélectrique .... 59

3.3.1 Caractérisation de la ligne de transmission et analogie électroacoustique ... 59

3.3.2 Sous-circuit PSPICE du modèle de Leach 62

3.3.3 Simulation de l'impédance électrique du transducteur 63

3.3.3.1 Procédé de simulation 63

3.3.3.2 Résultats de simulation 64

3.3.3.3 Validation des résultats de simulation 65

3.3.3.4 Paramètres utilisés pour la simulation 66

3.4 Conclusion .... 67

4 Modélisation tridimensionnelle d'un transducteur ultrasonore piézoélectri-

que 68

4.1 Introduction 69

4.2 Hypotheses générales 70

4.3 Expression tridimensionnelle de l'impédance électrique d'une céramique

piézoélectrique .... 72

4.3.1 Céramique piézoélectrique de forme parallélépipédique 72

4.3.2 Céramique piézoélectrique de forme cylindrique 74

4.3.3 Discussion 76

4.4 Simulation de l'impédance électrique d'une céramique piézoélectrique 76

4.4.1 Résultats de simulation 76

4.4.1.1 Céramique de forme parallélépipédique 76

4.4.1.2 Céramique de forme cylindrique 78

4.4.2 Validation du modele tridimensionnel de l'impédance électrique d'un

disque céramique 79

4.5 Conclusion 80

Conclusion générale et perspectives 81

Bibliographie 83

Annexes 93

Annexe A : Notions fondamentales d'élasticité 94

Annexe B : Piézoélectricité et matériaux piézoélectriques 96

Annexe C : Analogie électro-acoustique 101

Annexe D : Modèles unidimensionnels et hypothèses 102

Annexe E : Photographies 104

Annexe F : Fonctions de Bessel de première espèce 105

Liste des figures

1.1 Illustration des effets piézoélectriques [12] ~~~. ~~~~ .~~~~ ~ ~ 6

1.2 Organisation des différentes classes cristalline [24] .......... ..................... ... 7
1.3 Représentation schématique de l'apparition de la piézoélectricité : (a) Cristal centro-

symétrique (ou isotrope), (b) Cristal non centrosymétrique (ou anisotrope) [33] ~ 8
1.4 Microstructure typique d'une surface céramique polie qui illustre les grains monocri-

stallins, joints de grains et pores [31] .......... ...................... ... 13
1.5 Représentation de la structure pérovskite de PZT:(a) cubique (T=Tc), (b) tétragonale

(T<Tc) [46] ............................................ .... .............................. ... 14

1.6 Microstructure d'une céramique PZT montant les domaines ferroélectriques [42,46] 15
1.7 Représentation du processus de polarisation dans une céramique ferroélectrique

(a) Domaines aléatoirement distribués avant la polarisation, (b) application

d'un champ électrique, (c) champ électrique supprimé [20,46] ................ ... 15

1.8 Cycle d'hystérésis d'un matériau ferroélectrique [48] ............. ............ ... 16
1.9 Diagramme schématique d'un sphérolite montrant la disposition radiale de ses lamel-

les cristallines et localisation des phases amorphes [56] ........................... ... 18

1.10 Schémas de connectivité pour un composite à deux phases [19] ................. ... 20

1.11 Vue schématique d'un piézocomposite de connectivité 1-3 [2] ....... .... ... 21

1.12 Modes de déformation principaux d'un matériau piézoélectrique [47] ... ... 23

1.13 Déformation parasite par conservation du volume. Pour une déformation longitudina-

le, la conservation du volume introduit un mode transversal mécanique [42] ...~ 24

1.14 Transformateur piézoélectrique « Type de Rosen » [60] ......... ............. ... 25
1.15 (a) Quelques valeurs de puissances produites par le corps humain, (b) implantation

du matériel piézoélectrique dans une chaussure et vue d'un convertisseur de remise

en forme de la tension [61] .......... ......... .................. .... ... 26
1.16 (a) déformation d'une poutre par application d'une tension (b) bilame couplé à une

petite plaque métallique très fine [12] .......... ..................... .... ... 27

1.17 Principe d'une imprimante à jet d'encre [63] ....................................... ... 27

2.1 (a) Onde longitudinale, (b) Onde transversale [66] ......... .... ...... .... ... 30

2.2 Réflexion et réfraction d'une onde ultrasonore sur une interface ............ .... ... 32

2.3 Constitution d'un capteur acoustique piézoélectrique [73] .................. .... ... 35

2.4 Faisceau ultrasonore émis par un transducteur piézoélectrique ...... .......... ... 36

2.5 Intensité acoustique sur l'axe du faisceau en fonction de la distance au transducteur ... 36
2.6 Principe de fonctionnement d'un transducteur capacitif : (a) Membrane au repos, (b)

Application d'une tension de polarisation continue, (c) Superposition d'une tension

alternative, (c) application d'une pression acoustique [64,75] ....... ... ....... ... 37

2.7 Schéma de principe d'un transducteur piézorésistif à membrane silicium [78] ~~ 38

2.8 Vue en coupe d'un dispositif impulsion-écho [6] ......... ................... ... ... 39

3.1	(a) Diagramme d'une céramique piézoélectrique vibrant en épaisseur, (b) Le transd-
	ucteur comme un système linéaire à trois ports [19,81] ............ ... ...	42
3.2	Variation du coefficient de couplage en fonction de «fr/fa » ... ...	45
3.3	Variation de la fréquence d'antirésonance en fonction de l'épaisseur ............ ....	46
3.4	Courbe simulée de l'impédance ; (a) Module; (b) Phase .......... ... ...	47
3.5	Courbes simulée et expérimentale de l'impédance;(a) Module, (b) Phase ....... ...	48
3.6	Modèle de Mason d'un transducteur ultrasonore piézoélectrique [86] ............ ...	50
3.7	Modèle KLM d'un transducteur ultrasonore piézoélectrique [5] ......... ...	51
3.8	Modèle de Leach d'un transducteur ultrasonore piézoélectrique [97] ...	52
3.9	Courbe simulée de l'impédance;(a) Résistance, (b) Réactance ............ ... ...	54
3.10	Schéma électrique équivalent simplifié du transducteur [93] ............... ...	55
3.11	Tracé théorique de l'admittance électrique du transducteur : (a) Dans le diagramme
	de Bode, (b) Dans le plan de Nyquist [94] ...................... ... ... ...	57
3.12	Tracé simulé de l'admittance électrique: (a) Dans le diagramme de Bode, (b) Dans le
	plan de Nyquist .......... ... ...	58
3.13	Schéma électrique équivalent d'une ligne de transmission de longueur dx ...........	60
3.14	Sous-circuit PSPICE du modèle de Leach [96] ...................... ... ...	63
3.15	Circuit PSPICE pour simuler l'impédance électrique du transducteur ......... .....	63
3.16	Variation de l'impédance en fonction de la fréquence:(a) Partie réelle (ou résistance)
	;(b) Partie imaginaire (ou réactance) ................................................ ...	64
3.17	Courbes simulée et expérimentale de l'impédance;(a) Résistance, (b) Réactance .~	65
4.1	Dimensions et système de coordonnées d'une plaque céramique .............. ...	72
4.2	Dimensions et système de coordonnées d'un disque céramique ................ ...	74
4.3	Courbe simulée de l'impédance électrique d'une plaque céramique ............ .....	77
4.4	Courbe simulée de l'impédance électrique d'un barreau céramique ............. ...	77
4.5	Courbe simulée de l'impédance électrique d'un disque céramique .....................	78
4.6	Courbe simulée de l'impédance électrique d'un cylindre céramique ......... ...	78
4.7	Courbes simulée et expérimentale de l'impédance électrique d'un disque céramique	79
A	Notation des contraintes sur un volume élémentaire ....... ............... ....... ...	94
B.1	Cycle de fabrication des céramiques PZT par voie solide [114] ...... .......... ...	97
B.2	(a) Coefficient de couplage électromécanique en mode épaisseur. (b) permittivité
	relative, en fonction de l'impédance acoustique [5] ....... .......... ...	97
E.1	Céramiques piézoélectriques PZT: plaques, disques émaillés, anneaux, tubes,
	rondelle, portions de sphères [39] .......... ...................... ................. ...	104
E.2	Film PVDF [119] ....................................................................... ...	104
E.3	Composites 1.3 fabriqués (sans métallisation à gauche) [2] ....................... ...	104
E.4	Transducteurs ultrasonores piézoélectriques [120,121] ....... ................... ...	104
F	Fonctions de Bessel de première espèce ....... ................... ................ .....	105

Liste des tableaux

1.1	Équations de la piézoélectricité	9
1.2	Grandeurs électriques, mécaniques et piézoélectriques	9
2.1	Principales applications des ultrasons en fonction de leur fréquence ....	31
2.2	Vitesse de propagation des ultrasons dans les différents milieux [65,67]	31
2.3	Valeurs de l'interface acoustique entre quelques milieux [64,67]	33
3.1	Comparaison des valeurs des fréquences théoriques et expérimentales	49
3.2	Facteurs de couplage et vitesse acoustique théoriques et expérimentaux .....	49
3.3	Paramètres du schéma électrique équivalent simplifié	59
3.4	Paramètres du transducteur ultrasonore piézoélectrique	66
3.5	Paramètres des milieux avant et arrière	66
3.6	Paramètres du circuit d'excitation électrique	66
4.1	Caractérisation tridimensionnelle: hypothèses et principaux résultats [104]	71
4.2	Comparaison des valeurs de fréquences d'antirésonance théoriques et expérimentales	80
A	Notation matricielle	95
B.1	Échantillons pour la caractérisation des modes de déformations fondamentaux d'une
	céramique piézoélectrique [39,115,116,117]	98
B.2	Caractéristiques des céramiques piézoélectriques utilisées [108,116,118]	99
C	Analogie entre les grandeurs électriques et acoustiques [5]	101
D	Caractérisation unidimensionnelle: hypothèses et principaux résultats ..........	103

Principales notations, symboles et constantes

physiques

Symbole	Description		Unité
a	Rayon de la céramique piézoélectrique		m
a1,a2,a3	Dimensions géométriques de la céramique piézoélectrique
A	Section de la céramique piézoélectrique		m^2
ci7	Constante élastique		N.m^-2
C	Capacité linéique		F.m^-1
Cm	Capacité liée à l'élasticité de l'élément vibrant		F
C0	Capacité statique du transducteur rigidement lié
C0	Capacité d'un disque en mode radiale (1D)
C0^"	Capacité d'un barreau (1D)
di7	Constante de charge		C.N^-1
Dt	Diamètre du transducteur		m
D1, D2, D3	Composantes du vecteur induction électrique		C.m-2
D0	Module du vecteur induction électrique
E	Terme relatif au mode en épaisseur		-
E1, E2, E3	Composantes du vecteur champ électrique		V.m^-1
f	Fréquence caractérisant l'onde ultrasonore		Hz
fa	Fréquence d'antirésonance
fc	Fréquence centrale du matériau piézoélectrique
fe	Fréquence de la source d'excitation
fP	Fréquences de résonance du circuit oscillant parallèle
fr	Fréquence de résonance
fs	Fréquences de résonance du circuit oscillant série
fL,	Fréquence d'antirésonance des modes latéraux (3D)
fE	Fréquence d'antirésonance des modes en épaisseur (3D)
F1, F2	Forces acoustiques sur les faces de la céramique		N
gi7	Constante de tension		V.m.N^-1
G	Conductance linéique		S.m^-1
hi7	Constante piézoélectrique		V.m^-1
Ia	I ntensité acoustique sur l'axe du faisceau à une distance z du transducteur		kg.m^-1.s^-2
Ia0	Intensité acoustique sur l'axe au niveau du transducteur
Iai, Iar, Iat	Intensité de l'énergie incidente, réfléchie et transmise
Im		Courant motionnel		A
1(x, t)		Courant d'entré de la ligne de transmission
1(x + dx,t)		Courant de sortie de la ligne de transmission
I3		Courant électrique d'excitation
kt		Coefficient de couplage électromécanique en épaisseur		-
kerr		Coefficient de couplage électromécanique effectif		-
kp		Coefficient de couplage électromécanique du mode radial		-
L		Inductance linéique		H.m^-1
L		Terme relatif aux modes latéraux		-
Lm		Inductance liée à la masse vibrante		H
NK		Rapport de transformation (modèle de KLM)		^-
NM		Rapport de transformation (modèle de Mason)		N.V^-1
N		Extension du champ proche d'un transducteur piézoélectrique		m
Np		Constante de fréquence (Mode radial)		Hz. in
N1		Constante de fréquence (Mode latéral)
N5		Constante de fréquence (Mode de cisaillement)
N3a		Constante de fréquence (Mode barreau)
N3t		Constante de fréquence (Mode en épaisseur)
P		Polarisation		C.m^-2
pa		Pression acoustique		W.m-2
Pa0		Pression initiale (z=0)
Q		Charge totale sur les électrodes		C
Qe		Facteur de qualité électrique		-
Qin		Facteur de qualité mécanique		-
R		Résistance linéique		Ù.m^-1
R		Terme relatif aux modes radiaux		-
Rm		Résistance liée aux pertes par déformation
R0		Résistance traduisant les pertes diélectriques
s		Opérateur de Laplace		-
sij		Compliance élastique		m^2.N^-1
Si;		Tenseur des déformations		-
Tc		Température de Curie		°C
Ti;		Tenseur des contraintes		N.m^-2
ui		Vecteur de déplacement		m
va		Vitesse des ondes ultrasonores dans le milieu de propagation		m.s^-1
vP3		Vitesse des ondes ultrasonores dans la céramique selon l'axe de polarisation « x3»
vP		Vitesse des ondes ultrasonores dans la céramique selon une direction quelconque dans le plan « x1-x2 »
vPr		Vitesse des ondes ultrasonores dans la céramique selon le rayon « a » (cas d'un disque)
' vP3		Vitesse des ondes ultrasonores dans la céramique selon l'axe de polarisation « x3» (cas d'un barreau)
vel		Vitesse de propagation d'une impulsion sur une ligne de transmission électrique
v1, v2, v		Vitesses de déplacements des particules
V3		Tension électrique d'excitation		V
V(x, t)		Tension d'entrée de la ligne de transmission
?? (x + dx , t)		Tension de sortie de la ligne de transmission
XK		Réactance (modèle de KLM)

??

	Admittance électrique d'entrée du transducteur	S
z	Axe de propagation de l'onde ultrasonore	-
??	Impédance électrique du transducteur	Ù
Ze	Impédance caractéristique de la ligne de transmission
????	Impédance acoustique de la céramique métallisée	Rayl
??0	Impédance acoustique spécifique de la céramique
??1	Impédance acoustique du milieu arrière (ou backing)
??2	Impédance acoustique du milieu avant (ou milieu de propagation)
??	Nombre d'onde dans la céramique selon une direction quelconque dans le plan « x1-x2 »	rad.m-1
????	Nombre d'onde dans la céramique selon le rayon « a » (cas d'un disque)
??3	Nombre d'onde dans la céramique selon l'axe de polarisation «x3»
' ??3	Nombre d'onde dans la céramique selon l'axe de polarisation «x3» (cas d'un barreau)
????	Coefficient d'atténuation	Np.m-1
??????	Atténuation linéique
??????	Coefficient d'atténuation dû aux pertes visqueuses
??????	Coefficient d'atténuation dû à la conduction thermique
??????	Déphasage linéique	rad. m-1
??????	Constante d'imperméabilité diélectrique	m.F^-1
ã	Constante de propagation de la ligne de transmission	-
åij	Permittivité électrique	F.m^-1
æ1, æ2 , æ	Déplacement de particules	m
ç	Coefficient de viscosité	-
èi, èr ,èt	Angle d'incidence, de réflexion et transmise de l'onde ultrasonore	rad
????	Demi-angle de divergence du faisceau ultrasonore
ë	Longueur d'onde du milieu de propagation	m
ël	Longueur d'onde de la lame d'adaptation d'impédance
ëP	Longueur d'onde du matériau piézoélectrique
??0	Longueur d'onde de la source d'excitation
ñ	Masse volumique du matériau	kg.m^-3
????	Coefficient de réflexion	-
????	Coefficient de transmission	-
????	Coefficient de Poisson	-
ô	Temps de relaxation	s
ù	Pulsation	rad.s^-1
dx	Longueur élémentaire	m
??????????	Tangente de l'angle de pertes diélectriques	-
??????????	Tangente de l'angle de pertes diélectriques	-
R?? ??~	Partie réelle de la variable x	-
I?? ??)	Partie imaginaire de la variable x	-
???? ??~	Fonctions de Bessel de premiere espèce d'ordre « n » de la variable « x »	-
??, ??, ??)	Cordonnées cylindriques	-

L'acoustique recouvre plusieurs disciplines dont l'élément commun est l'étude des ondes sonores, incluant non seulement les sons audibles, mais aussi tous les phénomènes vibratoires non audibles : infrasons et ultrasons [1].

Les transducteurs¹ ultrasonores piézoélectriques sont étudiés et développés depuis de nombreuses années pour la génération ou la détection des ondes acoustiques dans de nombreux domaines tels que l'imagerie médicale et le contrôle non destructif² [2,3,4]. Ces deux domaines ont connu un développement important ces dernières décennies. Les nombreuses publications et innovations attestent que ces domaines ont engendré un grand intérêt aussi bien en recherche que pour le développement de produits commerciaux. Les transducteurs ultrasonores piézoélectriques sont au coeur de ces innovations et leurs performances sont régulièrement améliorées afin d'obtenir des images ou des contrôles de meilleure qualité. L'aptitude d'un transducteur ultrasonore à satisfaire les exigences de l'application envisagée est conditionnée en grande partie par les performances électroacoustiques de sa partie active. Cette fonction de conversion étant généralement réalisée par un matériau piézoélectrique, dont les performances intrinsèques doivent être choisies en fonction de l'application [5].

La modélisation a toujours été très importante pour la conception de transducteurs ultrasonores piézoélectriques. Grâce à la connaissance du modèle précis, un dispositif qui vérifie les spécifications souhaitées peut être conçu de façon rapide [6].

Le travail effectué au cours de ce mémoire a pour objectif la modélisation unidimensio- nnelle et tridimensionnelle d'un transducteur ultrasonore piézoélectrique et simulation du transducteur avec PSPICE, afin de pouvoir le caractériser et optimiser.

1 Le transducteur est un dispositif qui transforme une forme d'énergie en une autre. Le transducteur relatif à la transformation d'énergie électrique en énergie acoustique et vice-versa est appelé transducteur électro-acoustique. L'une des principales applications du transducteur est le capteur. La différence entre le capteur et transducteur est souvent très légère : Le transducteur est l'élément « mesureur » ; Le capteur est l'élément protecteur qui contient le transducteur, il assure parfois également une part du conditionnement. En pratique, on fait souvent l'amalgame entre les deux notions [6,7].

2 La méthode de contrôle non-destructif (CND) par ultrason permet la détection et localisation de défauts dans le volume d'une pièce sans l'altérer [8].

Ce mémoire est réparti en quatre chapitres dont nous présentons brièvement les lignes principales ci-après :

Le premier chapitre est consacré à la description des propriétés de la piézoélectricité, à la présentation des différents matériaux piézoélectriques et de leurs caractéristiques.

Le second chapitre présente les différents types de transducteurs ultrasonores et leurs principes de fonctionnement.

Le troisième chapitre est consacré à la modélisation unidimensionnelle et simulation avec PSPICE d'un transducteur ultrasonore piézoélectrique.

Le quatrième chapitre traite la modélisation analytique tridimensionnelle d'un transduct- eur ultrasonore piézoélectrique.

Nous terminerons ce mémoire par une conclusion générale qui englobera l'ensemble des travaux effectués et les perspectives envisagées pour la continuité de ce travail.

Chapitre 1

Principes fondamentaux de la piézoélectricité

Sommaire
1.1 1.2 1.3 1.4 1.5 1.6	Introduction .. Historique de la piézoélectricité Effet piézoélectrique Symétrie et piézoélectricité Équations de la piézoélectricité Caractéristiques électriques et mécaniques des matériaux piézoélectriques .		4 4 6 6 8 10
	1.6.1	Permittivité « åij » ..	10
	1.6.2	Compliance élastique « sij » ..	10
	1.6.3	Constante de charge piézoélectrique « dij » ..	10
	1.6.4	Constante de tension piézoélectrique « gij » ..	11
	1.6.5	Coefficient de couplage électromécanique « kij » .	11
	1.6.6	Facteur de qualité « Q » .	11
1.7	Les matériaux piézoélectriques		12
	1.7.1	Les principaux matériaux piézoélectriques .	12
	1.7.2	Autres matériaux piézoélectriques ..	20
	1.7.3	Choix du matériau piézoélectrique .	22
1.8	Modes de déformation d'un matériau piézoélectrique		22
	1.8.1	Modes de déformation fondamentaux .	23
	1.8.2	Autres modes de déformation .	24
1.9	Quelques applications des matériaux piézoélectriques		24
	1.9.1	Transformateurs piézoélectriques .	24
	1.9.2	Chaussures piézoélectriques .	25
	1.9.3	Actionneurs bilames	26
	1.9.4	Imprimantes à jet d'encre ..	27
1.10	Conclusion		28

1.1 Introduction

Les matériaux intelligents s'imposent aujourd'hui dans les secteurs les plus divers, allant du bâtiment aux équipements sportif en passant par la biomédecine, la robotique ou le secteur militaire [9]. Le terme « matériau intelligent » indique généralement un matériau capable de modifier spontanément un ou plusieurs de ses propriétés physiques, par exemple sa forme, sa connectivité, sa viscoélasticité ou sa couleur, en réponse à des excitations naturelles ou provoquées venant de l'extérieur ou de l'intérieur du matériau : variations de température, contraintes mécaniques, champs électriques ou magnétiques. Le matériau va donc adapter sa réponse, signaler une modification apparue dans l'environnement et dans certains cas, provoquer une action de correction. Un matériau intelligent est sensible, adaptatif et évolutif. Il possède des fonctions qui lui permettent de se comporter comme un capteur (détecter des signaux), un actionneur (effectuer une action sur son environnement) ou parfois comme un processeur (traiter, comparer, stocker des informations). Les matériaux les plus populaires sont : les alliages à mémoire de forme (AMF), les matériaux piézoélectriques, électrostrictifs et magnétostrictifs [10].

Dans ce chapitre nous allons rappeler les définitions, les propriétés et les équations associées à la piézoélectricité. Nous présentons également les grandes familles de matériaux piézoélectriques en détaillant plus particulièrement les zircono titanates de plomb (PZT). Puis, après avoir cité les différents modes de déformation d'un matériau piézoélectrique, nous présentons quelques applications des matériaux piézoélectriques.

1.2 Historique de la piézoélectricité

L'observation qualitative du phénomène piézoélectrique a été faite au milieu du XIXe siècle (1817) par un minéralogiste français l'abbé René Just Haûy (d'après ses théories cristallographiques) [11,12]. Ce fondateur de la cristallographie a en effet par ses observations de la matière (étude systématique de la morphologie générale des cristaux) apporté de grandes connaissances au niveau de la géométrie atomique des cristaux et participé à en déterminer des lois structurales.

La piézoélectricité a été mise en évidence à Paris en 1880 par les frères Pierre et Jacques Curie. Ces derniers montrèrent que les cristaux de quartz, topaze, tourmaline, niobate de lithium, cane à sucre et sel de Rochelle génèrent une polarisation électrique sous contraintes mécaniques c'est à dire la production d'une charge électrique sous contraintes mécaniques [13,14]. Cette découverte attira immédiatement l'attention des scientifiques : le français Gabriel Lippmann (1845-1921), Prix Nobel de physique en 1908 et inventeur de la photographie couleur, démontra de son côté l'année suivante que le phénomène était réversible et déduira mathématiquement du principe fondamental de la thermodynamique la théorie des cristaux piézoélectriques ; ainsi si des signaux électriques sont appliqués sur le cristal, celui-ci se dilate et se comprime dans une certaine direction, sa résonance mécanique favorisant les vibrations à une fréquence donnée. C'est grace à cette dernière propriété que le quartz a atteint une telle notoriété [11,15]. Immédiatement les frères Curies confirmèrent l'existence de l'effet piézoélectrique inverse. Ils apportèrent une preuve

quantitative de la réversibilité complète de la déformation électro-élasto-mécanique dans les cristaux piézoélectriques.

La piézoélectricité n'était qu'une curiosité de laboratoire mais la première guerre mondiale (1914-1918) la fit entrer dans la voie des applications pratiques. En 1917, Paul Langevin eut l'idée d'exciter des lames de quartz par un signal électrique alternatif pour créer des ultrasons ; ceux-ci, réfléchis sur la coque des sous-marins ennemis, retournent vers d'autres cristaux piézoélectriques et y font naître des tensions électriques alternatives aisées à détecter. Ce générateur d'ondes ultrasonores « Sonar » est la première utilisation conjuguée des effets piézoélectriques direct et inverse. Cependant, cette invention ne s'est pas perfectionnée jusqu'à la fin de la guerre [16,17].

Le succès du sonar a stimulé l'activité intense de développement sur toutes sortes de dispositifs piézoélectriques, résonnant et non-résonnant. Walter G. Cady, en 1918, réalisa le premier oscillateur électronique stabilisé par un cristal de quartz [11]. Il établit le schéma électrique équivalent du résonateur piézoélectrique. Dès lors, la piézoélectricité devint l'associée de l'électronique naissante. Elle permit la génération de fréquences électriques, donc d'échelles de temps, extrêmement stables.

La Seconde Guerre mondiale vit naître l'industrie moderne de la piézoélectricité. Cinquante millions de résonateurs à quartz piézoélectriques furent alors fabriqués aux ÉtatsUnis. A la même époque furent étudiés : des cristaux synthétiques, parfois décevants à l'usage ; mais surtout certaines céramiques, dites ferroélectriques, rendues anisotropes par un champ électrique au cours de leur élaboration et présentant ensuite un effet piézoélectrique intense [17].

En 1954, les zircono titanates de plomb (PZT) ont été élaborés, et se sont répandus très rapidement, car leurs propriétés supplantent de loin celles de toutes les autres familles de composés [12].

En 1969, Kawai a été le premier à découvrir les remarquables propriétés piézoélectriques du polyvinylidène difluoré (PVDF). Ce polymère piézoélectrique est le plus étudié et utilisé [18].

Depuis le début des années 80, différents nouveaux matériaux piézoélectriques ont été élaborés. En particulier les composites piézoélectriques qui ont vu jour peu après l'apparition du titanate de barium comme céramique piézoélectrique lorsque les chercheurs du Naval Research Laboratory ont voulu intégrer le titanate de barium dans une matrice de polymère afin d'obtenir un hydrophone flexible. D'autres tentatives ont consisté à combiner des poudres de PZT avec un polymère, toujours afin d'obtenir des matériaux piézoélectriques flexibles. Les premières communications montrant le potentiel de ces matériaux pour les applications sous-marines ont déclenché l'attrait des chercheurs pour les composites piézoélectriques, notamment à Pennsylvania State University [19,20].

1.3 Effet piézoélectrique

La piézoélectricité, du grec "piézo" signifiant presser ou serrer [21], certains matériaux (cristaux, céramiques ou polymères) ont la propriété de se polariser sous l'influence d'une contrainte mécanique : c'est l'effet piézoélectrique direct. Cette polarisation est proportionnelle à la contrainte et change de signe avec elle. Ce phénomène est réversible : une polarisation électrique résultant de l'application d'un champ électrique entraînera une déformation du méme matériau. On parle alors d'effet piézo-électrique inverse [22,23] (cf. figure 1.1).

L'application d'un champ électrique variable (champ électrique alternatif) entre les faces d'un matériau piézoélectrique, va exciter une onde acoustique dans le matériau. Cette onde acoustique est la résultante d'une déformation mécanique (déformation variable) du réseau cristallin qui oscille alors à une fréquence donnée, dite fréquence de résonance et c'est typiquement l'application exploitée dans les oscillateurs à quartz [24,25].

Générateur
de tension

Effet piézoélectrique inverse

D

E

F

O
R

M
A
T

I
O

N

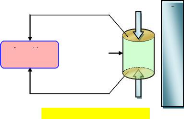
Apparition
de charges

Effet piézoélectrique direct

Mat6riau
piezo6lectrique

C O N T R A

I N T E

Fig. 1.1 - Illustration des effets piézoélectriques [12]

1.4 Symétrie et piézoélectricité

L'effet piézoélectrique a été mis en évidence principalement dans les solides cristallins anisotropes (absence de centre de symétrie dans la maille cristalline) [27,28,29]. En cristallographie, on classe toutes les structures répertoriées selon 32 classes de symétrie définies comme étant toutes les combinaisons distinctes possibles entre les éléments de symétrie que sont les plans, les axes et les centres de symétrie. Onze de ces classes sont dites centrosymétriques et ne peuvent donc pas présenter des propriétés polaires ou aucune polarisation spontanée. L'une des 21 autres classes (la classe cubique 432) possèdent des éléments de symétrie lui interdisant de présenter des caractéristiques polaires. Les 20 classes restantes possèdent au moins un axe polaire et les matériaux qu'elles caractérisent peuvent donc posséder des caractéristiques polaires telles la piézoélectricité, la pyroélectricité³ et la ferroélectricité⁴ [30,31].

3 Les cristaux pyroélectriques ont une polarisation électrique spontanée qui dépend de leur température ; ils portent en surfaces des charges électriques proportionnelles à cette polarisation et de signe contraire sur les faces opposées [34].

4 Les cristaux ferroélectriques possèdent un moment dipolaire (polarisation permanente) électrique même en l'absence d'un champ électrique extérieur [35].

La Figure 1.2 précise la place qu'occupent les matériaux piézoélectriques dans la hiérarchie des solides cristallins.

32 Classes cristallines

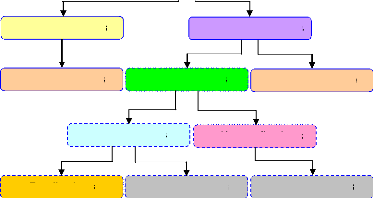
11 Centrosymétriques

21 Non centrosymétriques

Non piézoélectriques

20 Piézoélectriques

1 Non piézoélectrique

10 Pyroélectriques

10 Non pyroélectriques

Ferroélectriques

Non ferroélectriques

Non ferroélectriques

Fig. 1.2 - Organisation des différentes classes cristalline [24]

A l'échelle cristalline, la piézoélectricité se manifeste par une polarisation de la maille tandis qu'à l'échelle de la maille, ce sont les propriétés de symétrie des cristaux qui déterminent leur caractère piézoélectrique ou non. Tout corps présentant un centre de symétrie ne peut pas être piézoélectrique alors que les cristaux ne possédant pas de centre de symétrie peuvent l'être [32].

Un cristal possédant un centre de symétrie ne peut pas être déséquilibré électriquement et par conséquent il ne peut pas avoir de propriété piézoélectrique (cf. figure 1.3.a) [33]. En effet, lorsqu'il est soumis à une contrainte (flèches jaunes ou vertes), le déplacement des charges positives et négatives est identique dans toutes les directions et par conséquent la structure reste équilibrée (i.e. on observe toujours le même centre de symétrie).

Maintenant, si ce cristal ne possède pas de centre de symétrie les phénomènes présentés sur la figure 1.3.b peuvent être observés. Notons que cette structure de cristal est formée par deux triangles équilatéraux dont les sommets disposent de charges positives pour l'un et négatives pour l'autre. Tant que le cristal n'est soumis à aucune contrainte, les deux centres des triangles équilatéraux sont identiques et on ne dispose d'aucun effet piézoélectrique. Dès lors qu'une contrainte est appliquée, soit suivant X, soit suivant Y, les centres des deux triangles équilatéraux se déplacent en sens inverse et déséquilibrent la structure du cristal. L'effet piézoélectrique est lié à cette possibilité de déséquilibrer la structure et par conséquent, seuls les cristaux dont la structure ne possède pas de centre de symétrie sont piézoélectriques. De plus, comme on peut le constater les deux centres se déplacent suivant

l'axe des X quelque soit la contrainte appliquée (suivant Y ou suivant X). Par conséquent l'axe des X est appelé axe électrique et l'axe des Y est appelé axe mécanique. Perpendiculairement à ces deux axes se trouve l'axe des Z qui lui sera appelé l'axe optique car des techniques optiques sont utilisées pour le localiser. De plus il n'y a aucun effet piézoélectrique qui soit associé à l'axe optique.

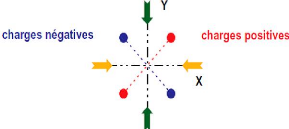
(a)

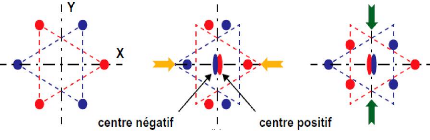
(b)

Fig. 1.3 - Représentation schématique de l'apparition de la piézoélectricité : (a) Cristal
centrosymétrique (ou isotrope), (b) Cristal non centrosymétrique (ou anisotrope) [33]

1.5 Équations de la piézoélectricité

L'effet piézoélectrique est la conséquence d'un couplage entre le comportement électrique et mécanique d'un matériau piézoélectrique. Lorsque le phénomène de la pyroélectricité est négligeable (i.e. l'effet thermique est négligeable), l'effet piézoélectrique peut se traduire par les 8 équations fondamentales reliant les grandeurs électriques (champ électrique "E" et induction "D") aux grandeurs mécaniques (contrainte "T" et déformation "S") comme indiqué dans le tableau 1.1 [20,36].

Variables indépendantes	Type	Relation piézoélectrique	Forme
T,E	Extensives	S=s^E . T + d ??.E D=d .T + å^T.E	Forme-d
S,D	Intensives	T=c^D . S -h ??.D E=-h. S +â1^S .D	Forme-h
T,D	Mixtes	S=s^D.T +g ^??.D E=-g.T + â^T.D	Forme-g
S,E	Mixtes	T=c^E. S .E - e^t . D=e. S + å^S.E	Forme-e

Tab. 1.1 -- Équations de la piézoélectricité

Le tableau 1.2 récapitule les différentes grandeurs électriques, mécaniques et piézoélectriques ainsi que leurs significations.

Symbole	Signification	Unité	Dimension
D	Déplacement électrique ou induction	C/m^2	(3×1)
E	Champ électrique	V/m
å	Permittivité électrique	F/m	(3×3)
â	Constante d'imperméabilité diélectrique	m/F
S	Déformation relative	--	(6×1)
T	Contrai nte mécanique	N/m2
s	Compliance ou susceptibilité élastique	m2/N	(6×6)
c	Raideur ou constante élastique	N/m2
d	Coefficient piézoélectrique traduisant la proportionnalité entre l'induction et la contrainte à champ électrique constant	C/N	(3×6)
e	Coefficient piézoélectrique traduisant la proportionnalité entre l'induction et la déformation à champ électrique constant	C/m^2
g	Coefficient piézoélectrique traduisant la proportionnalité entre la contrainte et le champ résultant à induction constante	V.m/N
h	Coefficient piézoélectrique traduisant la proportionnalité entre la déformation et le champ résultant à induction constante	V/m

Tab. 1.2 - Grandeurs électriques, mécaniques et piézoélectriques

avec :

· X ^t est la transposé de la matrice X.

· X^E indique que la grandeur X est considérée à champ électrique constant.

· X^D indique que la grandeur X est considérée à induction électrique constante.

· X^T indique que la grandeur X est considérée à contrainte constante.

· X^S indique que la grandeur X est considérée à Déformation constante.

Remarques :

· Le coefficient piézoélectrique d (ou e,g,h ) est identique pour le comportement électrique et le comportement mécanique du matériau piézoélectrique. Ceci signifie que la piézoélectricité requiert l'interaction entre ces deux comportements.

· Comme cas particulier, si le matériau est non piézoélectrique (d=e=g=h=0), le comportement électrique et le comportement mécanique sont découplés.

1.6 Caractéristiques électriques et mécaniques des maté- riaux piézoélectriques

Les matériaux piézoélectriques possèdent des performances différentes d'un matériau à un autre. Pour quantifier ces performances, plusieurs coefficients sont définis. Parmi eux, nous citerons :

1.6.1 Permittivité << åij »

La permittivité « åij » d'un matériau piézoélectrique détermine la charge par unité de surface due au champ électrique appliqué [37,38]. Elle est suivie de deux indices. Le premier indice désigne la direction du déplacement électrique ; le second celui du champ électrique.

· åij T est la permittivité à force constante caractérisant un échantillon libre.

· åij S est la permittivité à déformation constante caractérisant un échantillon encastré.

1.6.2 Compliance élastique << sij »

La compliance élastique « sij» est définie comme le rapport de la déformation relative sur la contrainte mécanique appliquée [39]. Elle est suivie de deux indices. Le premier indice désigne la direction de la déformation relative ; le second celui de la contrainte mécanique.

· sij E est la compliance à champ électrique constant.

· sij D est la compliance à déplacement électrique constant.

1.6.3 Constante de charge piézoélectrique << dij »

Le coefficient de charge « dij» est la constante de proportionnalité entre le déplacement électrique et la contrainte mécanique (ou la déformation relative et le champ électrique). Il est suivi de deux indices. Le premier indice désigne la direction du déplacement électrique (ou du champ électrique) ; le second celui de la contrainte mécanique (ou déformation relative). Puisque la contrainte induite dans un matériau piézoélectrique par application d'un champ électrique est le produit de la valeur du champ électrique et de la valeur du coefficient de charge, les matériaux piézoélectriques qui se caractérisent par des coefficients de charges élevés sont plus souvent utilisés comme actionneurs que comme capteurs [37,40].

1.6.4 Constante de tension piézoélectrique << gij >>

Le coefficient de tension « ?????? » est la constante de proportionnalité entre le champ électrique et la contrainte mécanique (ou la déformation relative et le déplacement électrique). Il est suivi de deux indices. Le premier indice désigne la direction du champ électrique (ou du déplacement électrique) ; le second celui de la contrainte mécanique (ou déformation relative). Puisque le champ électrique induit dans un matériau piézoélectrique par application d'une contrainte mécanique est le produit de la valeur de la contrainte mécanique et de la valeur du coefficient de tension, les matériaux piézoélectriques qui se caractérisent par des coefficients de tension élevés sont plus souvent utilisés comme capteurs que comme actionneurs [37,40].

1.6.5 Coefficient de couplage électromécanique << kij >>

Un matériau piézoélectrique est caractérisé dynamiquement par son coefficient de couplage c'est-à-dire sa capacité à transformer l'énergie électrique en énergie mécanique et réciproquement. Cette transformation d'énergie est utilisée dans les capteurs et actionneurs à base de matériaux piézoélectriques. Ce paramètre est toujours inférieur à 1 parce que la conversion d'énergie est toujours inachevée [40,41]. 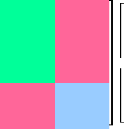Il s'écrit :

Énergie transformée

kij 2=

Energie appliquée

Le coefficient de couplage peut s'exprimer en fonction des paramètres électromécaniques du matériau et selon le mode de déformation considéré [37]:

dij 2

kij 2= E (1.1)

åij ^T sij

1.6.6 Facteur de qualité << Q >>

Pour les matériaux piézoélectriques, nous définissons deux facteurs de qualité qui permettent de mesurer l'influence des pertes diélectriques et mécaniques [24,42,43]. Le facteur de qualité mécanique « Q_m» est relié à la résistance « R_m », la capacité « C_m », l'inductance « L_m » et la pulsation « ?? » tel que :

Qm=

1 Lmù = (1.2) RmCmù Rm

Ce paramètre est égal aussi au rapport de la fréquence centrale sur la largeur de bande :

f_c

Q_m= (1.3)

f₂- f1

avec :

· f_c est la fréquence centrale du matériau piézoélectrique.

· f₁ et f₂ sont les fréquences à -3dB en dessous et au dessus de f_c.

Le facteur de qualité électrique « Q_e » qui correspond au rapport entre la capacité ??0 du matériau piézoélectrique et la résistance R0 symbolisant les pertes diélectriques tel que :

1

Q_e= R0C0ù (1.4)

Ces facteurs aussi appelés facteurs de surtension donnent le taux d'amplification de la structure à la résonance mécanique ou électrique. En effet, les matériaux piézoélectriques peuvent résonner électriquement ou mécaniquement. Ces fréquences de résonance ne sont pas forcément confondues. Un facteur de qualité élevé traduit un amortissement de la structure faible et donc une minimisation des pertes.

1.7 Les matériaux piézoélectriques

1.7.1 Les principaux matériaux piézoélectriques

Les matériaux piézoélectriques peuvent se regrouper en trois classes principales : les cristaux, les céramiques et les polymères.

1.7.1.1 Les cristaux piézoélectriques

Le quartz et la tourmaline sont sans doute les cristaux naturels les mieux connus découverts respectivement par Matthias et Aurivillus en 1949. Ils ont des caractéristiques stables dans le temps, mais ils présentent des impédances acoustiques relativement élevées et des coefficients de couplage très faibles. Ainsi qu'il faut couper les cristaux le long de certaines directions cristallographiques, ce qui limite le nombre possible de figures géométriques. Il existe d'autres monocristaux synthétisés en laboratoire comme le niobate de lithium (LiNbO3) ou le tantalate de lithium (LiTaO3) qui affichent des valeurs de coefficient plus élevées. Le coût élevé et la fragilité de ces cristaux expliquent qu'on ne les retrouve que très peu dans les produits actuels [43].

Il est actuellement possible de fabriquer de nombreux monocristaux de même composition que les céramiques, mais les techniques mises en jeu sont délicates et coûteuses. Il s'agit de cristaux « nouveaux » de type (1-x)PMN-xPT et (1-x)PZN-xPT. Ces derniers présents des propriétés extraordinaires par rapport aux céramiques piézoélect- riques ou cristaux naturels. Par rapport aux meilleures céramiques de PZT (les plus utilisés des matériaux ferroélectriques), le gain en terme de couplage atteint un facteur 3 en mode latéral, et les coefficients piézoélectriques dépassent 2000pC/N alors qu'ils sont limités à 700pC/N pour les céramiques les plus douces. Par exemple, la composition 0,67PMN0.33PT présente de forts coefficients ??33(2500pC/N) et ??33(>0.9). À présent, ces matériaux bénéficient d'importants efforts de recherche dans leurs procédés d'élaborations et de

caractérisations, car ils pourraient remplacer dans des applications d'actionneurs et de capteurs, les céramiques PZT [18,44].

1.7.1.2 Les céramiques piézoélectriques

1.7.1.2.1 Généralités

Le terme céramique évoque souvent des objets rustiques comme des poteries, des briques et des tuiles, mais le terme de céramique signifie plus généralement un solide qui n'est ni un métal ni un polymère. Une céramique est un matériau solide de synthèse qui nécessite souvent des traitements thermiques pour son élaboration. La plupart des céramiques modernes sont préparées à partir de poudres consolidées (mise en forme) et sont densifiées par un traitement thermique (frittage). Les procédés de fabrication des céramiques sont ajustables afin de pouvoir adapter leurs propriétés diélectriques, mécaniques et piézoélectriques à la demande. La plupart des céramiques sont des matériaux polycristallins, c'est à dire comportant un grand nombre de microcristaux bien ordonnés (grains) reliés par des zones moins ordonnées (joins de grains) comme illustré en figure 1.4 [31,21].

Fig. 1.4 - Microstructure typique d'une surface céramique polie qui illustre les grains
monocristallins, joints de grains et pores [31]

Les céramiques piézoélectriques sont apparues dans les années quarante. Par leurs coefficients piézoélectriques bien supérieurs à ceux des cristaux, elles ont permis un élargissement des applications du phénomène de piézoélectricité. Les céramiques piézoélectriques sont incontestablement les matériaux les mieux adaptés à l'heure actuelle. Ils sont souvent utilisés tels quels, mais entrent également dans la fabrication des composites que nous décrivons plus loin.

La famille des céramiques piézoélectriques comporte de nombreux éléments, citons entre autres, les titanates de baryum (BaTiO3) qui sont les ancêtres des céramiques actuelles, les Zircono Titanates de Plomb, d'où leur appellation abrégée PZT, qui sont les plus répandus et qui comptent à eux seuls cinq à six compositions différentes [29,30].

On distingue ainsi deux familles de céramique : les céramiques dites douces et celles dites dures, selon la propension que présente le matériau à se dépolariser [43]:

· Les matériaux doux sont généralement utilisés dans les applications à bas niveau d'excitation, notamment détecteurs (hydrophones, sondes échographiques...). Ils présentent en effet des couplages électromécaniques et des permittivités élevées.

· Les applications de puissance (piézomoteurs, transducteurs pour nettoyage par ultrasons...) nécessitent l'utilisation de céramiques dures pour leurs faibles pertes mécaniques et diélectriques.

1.7.1.2.2 Les zircono titanates de plomb (PZT) 1.7.1.2.2.1 Structure et polarisation des PZT 1.7.1.2.2.1.1 Structure des PZT

Le matériau PZT, de formule générale Pb _(ZrxTi1-x)O3 cristallise dans la structure de type pérovskite ABO3. Au dessus d'une certaine température appelée température de Curie " T_c ", c'est dans le système cubique que les PZT cristallisent (cf. figure 1.5.a). La polarisation du milieu est nulle, car dans chaque maille, le barycentre des charges positives correspond à celui des charges négatives. À des températures inférieures à Tc, une distorsion de la maille cubique apparaît. Les barycentres des charges positives et négatives ne sont plus confondus. Ceci a pour conséquence un dipôle et une structure tétragonale (cf. figure 1.5.b) [35,45].

		+

(a) (b)

Fig. 1.5 - Représentation de la structure pérovskite de PZT : (a) cubique (T=T_c), (b)
tétragonale (T<T_c) [46]

1.7.1.2.2.1.2 Polarisation des PZT
> Processus de polarisation

Les PZT sont des céramiques polycristallines ferroélectriques. Ils sont formés de grains et de joints de grains. Chaque grain est divisé en domaines au sein desquels les dipôles sont orientés dans la même direction. Chaque domaine présente une polarisation microscopique spontanée, mais leur répartition dans le matériau est aléatoire : le matériau est donc globalement non polaire. La frontière entre les domaines est appelée mur de domaine (cf.

figure 1.6). Pour que le matériau ferroélectrique devienne piézoélectrique, on doit le polariser [12,47].

Domaines

Murs de domaines

Fig. 1.6 - Microstructure d'une céramique PZT montant les domaines
ferroélectriques [42,46]

L'orientation des domaines dans une direction donnée par application d'un champ électrique intense est une étape importante. Après cette étape et lorsque le champ est supprimé, une polarisation rémanente et une déformation rémanente subsistent dans le matériau et le matériau devient piézoélectrique (cf. figure 1.7).

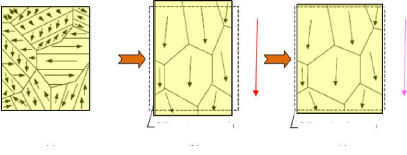
Champ el ectrique

Pol ari sdi on remanente

Déformation provoquée par le champ électrique

(a) (b)

Déformation rémanente

(c)

Fig. 1.7 - Représentation du processus de polarisation dans une céramique ferroélectrique : (a) domaines aléatoirement distribués avant la polarisation, (b) application d'un champ électrique, (c) champ électrique supprimé [20,46]

> Cycle d'hystérésis

Si un champ extérieur suffisamment intense est appliqué au matériau, il se polarise : les domaines, orientés dans le sens du champ, grossissent au détriment des autres. Plus le champ n'est élevé, plus le nombre de dipôles orientés est grand, ce qui contribue à l'augmentation progressive de la polarisation. Ce phénomène se manifeste par un cycle d'hystérésis P=f(E) (cf. figure 1.8). P représente la polarisation moyenne de l'ensemble des domaines et E est le champ extérieur appliqué au matériau ferroélectrique. La polarisation est saturée à #177;Ps pour des valeurs de champ très importantes et la polarisation rémanente #177;Pr correspond à la valeur de la polarisation à champ nul. La valeur du champ à polarisation nulle est le champ coercitif noté Ec qui définit un nouvel axe de polarisation [12,22,30].

P

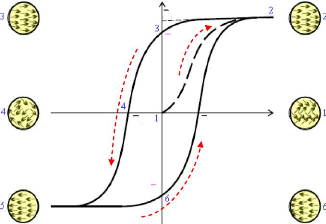
E

E_c

-E_c

P_s

P_r

-P_r

Fig. 1.8 - Cycle d'hystérésis d'un matériau ferroélectrique [48]

> Température de Curie

La polarisation rémanente induite par orientation des dipôles n'est stable que dans un domaine de température donné. Au-delà de la température de Curie " T_c", il se produit une transition de phase. Le matériau passe de l'état ferroélectrique à l'état paraélectrique et il ne présente plus alors l'effet piézoélectrique. Cette température est l'un des critères de choix de céramiques piézoélectriques ; en fait, plus le point de Curie est grand, plus la gamme en température d'utilisation de la céramique est importante [12,49].

1.7.1.2.2.2 Matrice plasto-pipzo-diplectrique des PZ T

La matrice élasto-piézo-diélectrique décrit le comportement électromécanique global d'une céramique piézoélectrique. Pour les PZT qui sont assimilables aux cristaux de la classe de symétrie 6mm du système hexagonal, cette matrice s'écrit [50,51]:

d15

0

0 0 0 0

d15

0
0
0

0
0

d13
d13
d33

0
0
0

0

T E11

0

T E11

0
0

0
0

T

E33

0
0
0

T1

T2

T3

T4

. T5

T6

E1

E2

E3

S55

S55

S66

d15

0

0
0

0

d15

0
0
0

E

0

0

0 0 0 0

E

0

0 0 0 0 0

E

(1.5)

??1

S2

S3 S4 S5 S6 D1 D2 D3		SE 11 E S12 E S13 0 0 0		E SE S12 13 E E S11 S13 E E S13 S33 0 0 0 0 0 0

1.7.1.2.2.3 Caractéristiques des céramiques piézoélectriques PZT

Les avantages des céramiques PZT peuvent être regroupés comme suit [34,52,53]:

· Possibilité d'usinage ou moulage dans une grande variété de formes et de tailles.

· Coût abordable ; coefficient de couplage électromécanique très élevé par rapport à d'autres matériaux piézo-électriques. Cela nécessite une application d'une énergie électrique moyenne pour obtenir une énergie mécanique.

· Pertes électriques sont faibles, elles ne s'échauffent donc presque pas et leur rendement acoustique est très bon.

· Robustesse mécanique, elles peuvent supporter des déformations beaucoup plus grandes que la plupart des autres céramiques, c'est pourquoi on peut obtenir la même puissance, avec un cristal de plus faible volume.

· Permittivités diélectriques relatives fortes.

· Constantes de charges piézoélectriques élevées.

· Température de curie ajustable selon la composition.

A cause de leurs excellentes propriétés piézoélectriques (bons coefficients de couplages électromécaniques), les PZT sont largement utilisés dans les capteurs et les actionneurs.

Leurs principaux inconvénients sont :

· Impédances acoustiques très élevées par rapport à d'autres matériaux piézoélectriques. Elles sont donc plus difficiles à coupler aux autres matériaux.

· Coefficients pyroélectriques importants.

· Variation thermique des constantes piézoélectriques et des permittivités diélectriques.

1.7.1.3 Les polymères piézoélectriques

1.7.1.3.1 Généralités

Le terme " polymère" signifie littéralement « plusieurs parties». Les polymères solides peuvent être divisés en deux catégories : amorphes et semi-cristallines. Le polyfluorure de vinylidène "PVDF" étant un polymère semi-cristallin, il présente une phase cristalline et une phase amorphe [10,54,55,56].

· La phase amorphe est constituée de chaînes moléculaires désordonnées, qui représentent environ la moitié du volume du matériau et déterminent l'essentiel de ses propriétés mécaniques.

· La phase cristalline peut présenter quatre structures distinctes dont trois polaires (â, ã, ä) et une non polaire a.

La phase cristalline la plus fréquente est la lamelle qui résulte des replis successifs de chaînes polymères sur elles-mêmes. Une chaîne polymère peut participer à plusieurs lamelles, de la même façon qu'une lamelle peut être constituée de plusieurs chaînes différentes. Les lamelles ont la possibilité de s'organiser en une structure semi-cristalline nommée sphérolite (diamètre de l'ordre du ìm). Les sphérolites sont constituées par un arrangement radial des lamelles à partir d'un centre de nucléation. Bien que les sphérolites soient une structure semi-cristalline, elles ne sont pas elles-mêmes totalement cristallines. Il y a toujours, une phase amorphe présente, notamment entre les lamelles constituant les sphérolites (cf. figure 1.9).

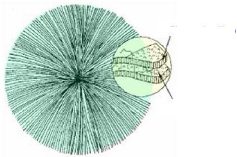
Phase cristalline
(Lamelle)

Phase amorphe

Fig. 1.9 - Diagramme schématique d'un sphérolite montrant la disposition radiale de ses
lamelles cristallines et localisation des phases amorphes [56]

Le polymorphe du PVDF le plus couramment obtenu est la phase a. A partir de la structure cristalline a centrosymétriques, qui ne présente pas de propriétés piézoélectriques, on peut obtenir une structure cristalline non centrosymétriques (â) par étirement uniaxial ou biaxial ou par compression sous haute pression hydrostatique. La phase â présente la plus grande activité piézoélectrique par rapport aux phases ã, ä.

Quelle que soit la phase polaire obtenue, le moment dipolaire de chacun des cristaux est orienté de façon aléatoire dans le matériau, de sorte que la polarisation macroscopique est nulle. Ainsi, pour obtenir une bonne activité piézoélectrique, le PVDF orienté (en phase â) doit être polarisé électriquement : il s'agit d'orienter la polarisation ferroélectrique des cristaux suivant un champ électrique appliqué perpendiculairement au plan du film. L'un des procédés courants consiste à appliquer à haute température (typiquement 80 a 130 ^oC), et pendant 15 a 120 minutes, un champ électrique proche (mais inférieur) au champ coercitif maximal, de l'ordre de 30 a 120 V/ìm, entre les électrodes métalliques déposées sur les faces du film polymère. Il est à noter que les propriétés piézoélectriques dépendent fortement de la polarisation rémanente du matériau.

1.7.1.3.2 Origine de la piézoélectricité dans le PVDF

Les origines physiques des propriétés piézo-électriques de ce matériau sont restées longtemps controversées [43]. De nombreux modèles ont été avancés afin d'expliquer ces propriétés. Le modèle couramment admis est celui de cristallites ferroélectriques noyées dans une matrice amorphe. Il apparaît que l'activité piézoélectrique de ces matériaux provient à la fois :

· Des variations de leurs dimensions géométriques dues à la contrainte ou à la température.

· Des variations de la polarisation des cristallites dues à la contrainte ou à la température.

· Des variations de permittivité dues à la déformation.

1.7.1.3.3 Caractéristiques des polymères piézoélectriques PVDF

Les films piézoélectriques PVDF présentent plusieurs avantages [18,27,34]:

· Bonne flexibilité : possibilité d'adaptation à des surfaces non planes et possibilité de fabrications dans une variété de formes.

· Légèreté et coût abordable.

· Épaisseurs possibles de quelques micromètres à une centaine de micromètres.

· Possibilité d'utilisation dans une large gamme de fréquence s'étendant de 0,001 Hz à 10⁹ Hz.

· Impédance acoustique faible, proche de celle de l'eau, tissu humain et systèmes adhésifs.

· Coefficient de tension piézoélectrique élevé.

· Haute stabilité : il présente une très faible absorption d'humidité (inférieur à 0.02%) ainsi qu'une très bonne résistance aux agressions extérieures (agents chimiques, oxydants, rayons ultraviolets et radiations nucléaires).

· Possibilité de collage avec les adhésifs commerciaux.

Leurs principaux inconvénients sont :

· Coefficients de couplage plus faible que celle des céramiques piézoélectriques.

· Coefficients de charges piézoélectriques plus faibles que celle des céramiques piézoélectriques.

· Constantes diélectriques plus faibles que celle des céramiques piézoélectriques.

· Coefficients de pertes diélectriques plus élevés que celle des céramiques piézoélectriques.

1.7.2 Autres matériaux piézoélectriques

D'autres matériaux piézoélectriques font l'objet de recherche et de développement visant des applications plus spécifiques compte tenu de leurs remarquables propriétés.

1.7.2.1 Les composites piézoélectriques

Le terme « composite » dans le domaine des matériaux signifie que deux ou plusieurs matériaux sont associés à l'échelle macroscopique afin de développer un matériau ayant de nouvelles propriétés [2]. Un composite piézoélectrique, encore appelé piézocomposite par abus de langage, est la combinaison d'une céramique piézoélectrique et d'un polymère non piézoélectrique. Le fait d'associer plusieurs constituants, appelés phases, permet de combiner leurs propriétés physiques [57].

1.7.2.1.1 Classification

Les piézocomposites ont été classés par Newnham suivant la connectivité de chacune de leurs phases et on caractérise ainsi leur structure tridimensionnelle [19]. On désigne un composite constitué de deux phases par deux entiers "i-j" qui précisent le nombre de directions suivant lesquelles chaque phase établit une liaison ou connectivité. Différentes combinaisons sont décrites sur la figure 1.10.

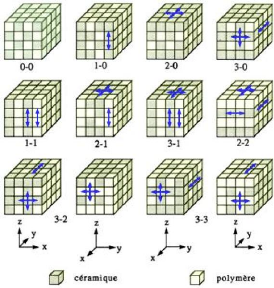
Fig. 1.10 - Schémas de connectivité pour un composite à deux phases [19]

Si les piézocomposites ont pris de multiples formes, les composites dits de connectivité 1-3, ont le plus retenu l'attention. Un piézocomposite 1-3 se compose de barreaux ou fibres de PZT qui sont arrangés en parallèle suivant la direction de polarisation et un polymère constituant la matrice (cf. figure 1.11).

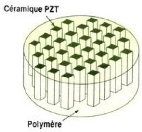
Fig. 1.11 - Vue schématique d'un piézocomposite de connectivité 1-3 [2] 1.7.2.1.2 Caractéristiques des piézocomposites 1-3

Les avantages d'un composite, en général, sont de présenter de meilleures performances en de nouvelles propriétés par rapport à ces constituants. Par exemple, pour les piézocomposites 1-3, les propriétés essentielles du composite sont [18,25,26]:

· Impédance acoustique se situe entre celle de la céramique piézoélectrique et celui du polymère.

· Coefficient de couplage électromécanique élevé.

· Le choix judicieux de ces constituants et de leur fraction volumique permet d'ajuster son impédance électrique.

· Souplesse de mise en forme liée aux propriétés thermiques et mécaniques du polymère.

· Les modes latéraux sont fortement atténués et par conséquent les effets parasites associés sont réduits.

1.7.2.2 Les couches épaisses piézoélectriques

Depuis les années 70, l'industrie des microtechniques a connu un essor très important. Les techniques de fabrication ont évolué et ont ainsi permis une réduction du coût de production. Aujourd'hui, de nombreuses applications intègrent des dispositifs de taille réduite. En effet, les industries automobile, aéronautique et biomédicale cherchent à miniaturiser et alléger leurs produits tout en demandant une fiabilité accrue. La demande est également très forte dans le domaine des télécommunications ou de l'électronique grand public [12].

Les couches épaisses sont une alternative intéressante pour remplacer les céramiques massives amincies traditionnellement employées dans les systèmes de petite taille. Il permet la diminution de la taille de ces systèmes tout en offrant la possibilité de les réaliser

rapidement par des techniques de fabrication collective. Des épaisseurs d'une centaine de micromètres peuvent être atteintes à partir d'usinages de céramiques massives. Pour obtenir de plus faibles épaisseurs (plusieurs dizaines de micromètres), une solution consiste à venir déposer le matériau actif (films céramiques) sur un substrat comme l'alumine. Viennent ensuite les étapes de dépôt de l'électrode d'alimentation et de polarisation. Le coefficient ??33 est inférieur à celui du même matériau en configuration massique. La diffusion de l'électrode d'alimentation et la porosité du matériau actif limitent les performances du système couche+substrat.

1.7.3 Choix du matériau piézoélectrique

La comparaison des caractéristiques de matériaux piézoélectriques permet de choisir le matériau le plus adapté à l'application visée. Pour le transducteur ultrasonore piézoélectrique, c'est le matériau piézoélectrique qui conditionne ses performances. Donc alors le choix du matériau piézoélectrique devient nécessaire.

Dans ce mémoire, les PZT ont été choisis, car :

· Ils présentent des excellentes propriétés piézoélectriques (surtout des bons coefficients de couplage).

· Ils sont très utilisés dans les équipements ultrasonores du commerce.

· On a suffisamment de propriétés diélectriques, mécaniques et piézoélectriques de ces matériaux qui sont nécessaires pour réaliser nos simulations.

1.8 Modes de déformation d'un matériau piézoélectrique

Le matériau piézoélectrique se déforme dans différentes manières à différentes fréquences. Ces diverses déformations s'appellent les modes de déformation [58]. Du fait de l'anisotropie des matériaux piézoélectriques, leur déformation se fait selon une direction

privilégiée sous l'action d'un champ électrique E . Une étude des propriétés de ces matériaux nécessite donc une identification des directions. La figure 1.12 illustre ces modes dans le cas d'un barreau parallélépipédique de céramique piézoélectriques. D'une manière générale, une céramique piézoélectrique est référencée par un trièdre (o,x1,x2,x3). Par convention, la direction et le sens de la polarisation sont confondus avec l'axe 3, pour un mode ië~, i correspond à l'axe d'orientation du champ électrique appliqué et ë à l'axe de la déformation mécanique générée (i=1,2,3, ë=1,2,3,4,5,6) [42,47,59].

1.8.1 Modes de déformation fondamentaux

1.8.1.1 Mode longitudinal {33]

Le mode longitudinale traduisant des déformations dans la même direction que l'axe du champ électrique. Ce mode possède un bon coefficient de couplage, cependant le placement des électrodes sur les surfaces vibrantes les fragilise.

1.8.1.2 Mode transversal {31 ou 32]

Le mode transversale traduisant des déformations perpendiculaires à l'axe du champ électrique. Dans ce mode, les électrodes ne sont pas placées sur les surfaces subissant les déformations, donc offrant l'avantage de ne pas soumettre les électrodes à la contrainte. En revanche, il possède un coefficient de couplage moindre que le mode longitudinal.

1.8.1.3 Mode cisaillement {15]

Le mode de cisaillement traduisant des déformations perpendiculaires à la direction de polarisation ou autour d'un axe. La céramique subit alors un phénomène de torsion autour de l'axe choisi. Elle est obtenue lorsque le champ appliqué est perpendiculaire à la polarisation du matériau. Par exemple, si le champ est appliqué sur l'axe 1, la déformation se fera autour de l'axe 2 (rotation associée à l'indice 5).

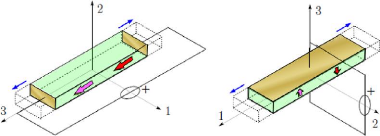
(a) Mode longitudinal {33} (b) Mode transversal {31 ou 32}

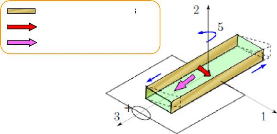
Position des électrodes Champ électrique (E ) Polarisation (P )

(c) Mode de cisaillement {15}

1.8.2 Autres modes de déformation

D'autres modes de déformation « parasites » résultant de la forme particulière de l'échantillon peuvent apparaître [42]. Ils sont d'origine mécanique par exemple, des déformations perpendiculaires à l'épaisseur (mode radial traduit par le coefficient de Poisson comme présenté sur la figure 1.13) ou d'origine électrique par déplacement dipolaire (modification des parois de blocs). En jouant sur la forme de l'échantillon (plaque, tube, ...) et sur sa polarisation (uniforme, radiale,...), une grande variété de déformations peuvent être exploitées. Il est à noter que lors de l'utilisation d'une céramique piézoélectrique, plusieurs modes interagissent simultanément. Ces modes parasites sont souvent négligés : les dimensions des structures sont choisies pour que ces hypothèses soient vérifiées. Par exemple, il est préférable de privilégier une longueur nettement supérieure à l'épaisseur pour utiliser le mode 33.

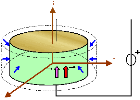
2

P

E

1

3

Fig. 1.13 - Déformation parasite par conservation du volume. Pour une déformation longitudinale, la conservation du volume introduit un mode transversal mécanique [42]

1.9 Quelques applications des matériaux piézoélectriques

Nous allons à présent citer quelques applications des matériaux piézoélectriques actuellement développées.

1.9.1 Transformateurs piézoélectriques

Dans un transformateur électromagnétique, l'énergie électrique d'entrée est convertie en énergie magnétique, puis l'énergie magnétique est reconvertie en énergie électrique de sortie. Le transformateur piézoélectrique a un principe de fonctionnement analogue. Il convertit l'énergie électrique d'entrée en une énergie mécanique (i.e. ondes acoustiques) et puis reconvertit l'énergie mécanique en une énergie électrique de sortie [37,60].

Le transformateur piézoélectrique est une combinaison d'un actionneur et d'un transducteur piézoélectriques, qui servent de primaire et de secondaire respectivement comme le montre la figure 1.14. L'actionneur convertit la tension V_e en vibration mécanique, cette dernière est ensuite reconvertie en tension V_s par le transducteur. Le rapport de V_s sur V_e dépend des dimensions géométriques, facteur de couplage électromécanique, facteur de qualité mécanique et la résistance de charge RL .

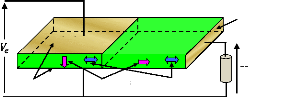
Electrode de sortie

Actionneur Transducteur

V_s

RL

Electrodes d'entrée

Polarisations

Contraintes

Le transformateur piézoélectrique a plusieurs avantages par rapport au transformateur électromagnétique, tel que le poids et le volume inférieurs, le meilleur isolement et l'absence du bruit électromagnétique.

Fig. 1.14 - Transformateur piézoélectrique « Type de Rosen » [60]

1.9.2 Chaussures piézoélectriques

Le corps humain stocke, dissipe et peut produire une énergie considérable eu égard à la consommation de nos appareils électroniques portables habituels. Il convertit de l'énergie constamment (mouvements, respiration, chaleur...), et on peut considérer qu'il s'agit d'une énergie renouvelable, gratuite, non polluante et de durée de vie élevée (cf. figure 1.15.a). Méme si, bien sûr, une faible part de cette énergie est exploitable, il semble que l'énergie associée aux mouvements du corps humain peut permettre d'approvisionner bon nombre d'applications et de réduire, voire supprimer les problèmes de recharge et de dépendance aux réseaux électriques ou aux piles. Cela requiert de convertir en électricité une partie de l'énergie dépensée, par des moyens à déterminer en fonction des ressources, des solutions technologiques envisageables et des besoins. Les dispositifs piézoélectriques permettent de convertir en électricité l'énergie des mouvements humains [61,62].

La figure 1.15.b montre une chaussure piézoélectrique capable de convertir en électricité l'énergie générée lors de la marche. Deux dispositifs piézoélectriques sont implantés dans la chaussure :

· Un dispositif formé de deux rubans précontraints et incurvés de céramique PZT, placé dans le talon. L'énergie récupérée (charge adapté de 500kg) : 8.4mw.

· Une feuille de PVDF flexible, placée dans la semelle, récupère l'énergie des mouvements de flexion pendant chaque pas. L'énergie récupérée (charge 250kg) : 1.3mW.

Chapitre 1. Principes fondamentaux de la piézoélectricité 26

(b)

(a)

Chaleur humaine 2.4-4.8W
(Tête seulement)

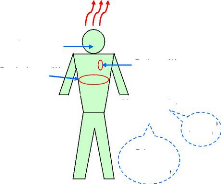
Respiration 0.42W
(0.83W)

Mouvements des
doigts 0.76-2.1mW
(6.9-19mW)

Souffler 0.4W

(0.83W)

Mouvements des

bras 0.33W

(60W) Puissance

fournie

Puissance
Calorifique
consommée

Pouls 0.37W
(0.93W)

Mouvement du
pied 5-8.3W
(67W)

Fig. 1.15 - (a) Quelques valeurs de puissances produites par le corps humain, (b) Implantation du matériel piézoélectrique dans une chaussure et vue d'un convertisseur de remise en forme de la tension [61]

1.9.3 Actionneurs bilames

Les actionneurs à base des couches épaisses piézoélectriques sont employés dans de nombreux microsystèmes. L'actionneur bilame est le système le plus simple : la couche épaisse piézoélectrique est déposée sur un substrat [12]. Suivant le sens de la tension appliquée, le substrat se déforme comme l'illustre la figure 1.16.a.

Quelques systèmes sont présentés avec des céramiques massives de fine épaisseur. Pour remplacer les ventilateurs rotatifs encombrants et bruyants, une équipe américaine propose l'utilisation d'un bilame couplé à une petite plaque métallique très fine pour ventiler certains composants électroniques placés dans les ordinateurs. Ce bilame est actionné grâce à deux céramiques massives amincies à 300um environ, puis collées de chaque coté de la plaque métallique à faire vibrer (cf. figure 1.16.b).

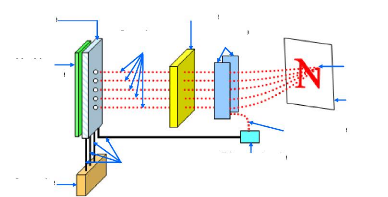
Générateur de
gouttelettes

Matériau

piézoélectrique

Cartouche
d'encre

Gouttelettes
d'encre projetées

Canalisations Récupération de

l'encre utilisée

Chargeur
électrostatique

Plaques de
déviation

Encre inutilisée

Formation
de l'image

Papier

+ V --

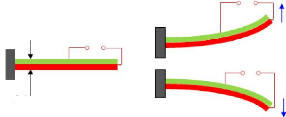
Couche de PZT
électrodée

Substrat

0 V

- V +

(a)

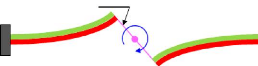
Plaque métallique

(a)

Fig. 1.16 -- (a) Déformation d'une poutre par application d'une tension (b) Bilame couplé à
une petite plaque métallique très fine [12]

1.9.4 ,P SUP DcNIs Ei jINEd9IcRIE

L'imprimante à jet d'encre est une imprimante sans impact. Elle imprime ligne par ligne à l'aide d'une tête d'impression montée sur un chariot mobile. Cette tete utilise de l'encre qu'elle conserve dans un générateur d'encre. L'encre stockée A dans une cartouche est amenée dans le générateur d'encre par des canalisations. A l'arrière du générateur se trouve un matériau piézoélectrique qui permet de faire vibrer l'encre afin de le propulser sous forme de gouttelettes à travers les buses (trous de la tête de l'imprimante). Les gouttelettes d'encre (toutes de la meme taille) passant par un chargeur électrostatique qui va les charger positivement pour les faire dévier par deux plaques de déviation traversées par un champ électrique, ce qui permet de projeter les goulettes avec une grande précision sur le papier. Un caractère est imprimé point par point, colonne par colonne (cf. figure 1.17) [63].

1.10 Conclusion

Les principales propriétés de la piézoélectricité, ainsi que les différents types de matériaux piézoélectriques ont été décrits dans ce chapitre. De cette étude, il ressort les points suivants :

· Les propriétés de symétrie des cristaux déterminent leur caractère piézoélectrique ou
non. Un cristal présentant un centre de symétrie ne peut pas être piézoélectrique.

· Chacun de matériaux piézoélectriques dispose de caractéristiques différentes qui conditionnent leur utilisation. Il faut donc faire un choix judicieux en fonction des applications visées.

· Du fait de l'anisotropie des matériaux piézoélectriques, ils se déforment selon des directions privilégiées sous l'action d'un champ électrique.

Chapitre 2

Différents types de transducteurs ultrasonores

Sommaire

2.1 Introduction . 30

2.2 Théorie des ultrasons .. 30

2.2.1 Définition et applications des ultrasons ... 30

2.2.2 Paramètres de l'onde ultrasonore 31

2.2.3 Interaction du faisceau ultrasonore avec la matière ... 32
2.3 Différents types de transducteurs ultrasonores et leurs principes de fonc-

tionnement .. 34

2.2.1 Transducteur piézoélectrique 34

2.2.2 Transducteur capacitif 37

2.2.3 Transducteur piézorésistif 38

2.2.4 Transducteur impulsion-écho 38

2.4 Conclusion . 39

2.1 Introduction

Ce chapitre débute par une brève description de la théorie des ultrasons. Nous présentons ensuite les différents types de transducteurs ultrasonores et leurs principes de fonctionnement, en détaillant le transducteur ultrasonore piézoélectrique, qui fera par la suite l'objet de l'étude de modélisation et simulation décrites dans ce mémoire.

2.2 Théorie des ultrasons

2.2.1 Définition et applications des ultrasons

Contrairement aux ondes électromagnétiques, les ondes ultrasonores ont besoin d'un support matériel (i.e. les ultrasons ne se propageant pas dans le vide) car elles sont liées au déplacement des particules du matériau dans lequel elles se propagent [65,66]. Parmi les différents types d'ondes, on distingue deux modes d'ondes principaux :

· Les ondes longitudinales (ou ondes de compression) pour lesquelles les vibrations des particules ont lieu parallèlement à la direction de propagation de l'onde (cf. figure 2.1.a).

·

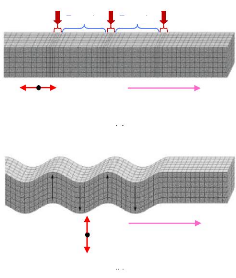
Compression

Compression

Compression

Direction de propagation

(a)

Direction de vibration
des particules

(c)

Direction de vibration
des particules

Direction de propagation

Expansion

Expansion

Les ondes transversales (ou ondes de cisaillement) pour lesquelles les vibrations des particules ont lieu perpendiculairement à la direction de propagation de l'onde (cf. figure 2.1.b).

Les ultrasons sont de même nature que les sons audibles, mais sont inaudibles pour l'oreille humaine. Le domaine fréquentiel des ultrasons s'étend de la frontière avec l'acoustique audible, fixée arbitrairement à 16 kHz, jusqu'aux fréquences d'agitation thermiques des molécules aux environs 10¹³ Hz. On désigne aussi sous le terme d'hypersons les ultrasons dont la fréquence est supérieure à 100 GHz [19].

Les principales applications des ultrasons sont présentées dans le tableau 2.1 en fonction de la fréquence de ces derniers.

Plage de fréquence	Applications
10-50kHz	Nettoyage, soudage, usinage, collage par ultrasons, émulsification...
10-100kHz	Acoustique sous-marine, analyse des sous-sols
1-20MHz	Acoustique médicale, échographie, contrôle non destructif
100MHz-10GHz	Acousto-optique, acousto-électronique
10-1000GHz	Étude de la matière

Tab. 2.1 - Principales applications des ultrasons en fonction de leur fréquence

2.2.2 Paramqtres de l'onde ultrasonore

Cette section présente les différents paramètres nécessaires à la caractérisation de l'onde ultrasonore.

1.2.2.1 Longueur d'onde et vitesse de propagation

L'onde ultrasonore en déplacement dans un milieu donné se caractérise par sa fréquence « f » et sa longueur d'onde « ë ». Ces deux caractéristiques permettent de déterminer la vitesse de propagation des ultrasons v_a dans le milieu [65]:

v_a=ë f (2.1)

La vitesse de propagation des ultrasons dans la matière dépend essentiellement des caractéristiques du milieu (élasticité, densité). À titre d'exemple, quelques vitesses de propagation des ultrasons dans différents milieux sont répertoriées dans le tableau 2.2.

Milieu	va (m/s)
Acier	5900
Aluminium	6320
Os	3500
Caoutchouc	2300
Eau	1480
Air	334

Tab. 2.2 - Vitesse de propagation des ultrasons dans les différents milieux [65,67]

1.2.2.2 Impédance acoustique

Le comportement du milieu vis-à-vis des ultrasons est exprimé par une constante appelée impédance acoustique⁵ Z_a. Elle est définie comme le produit de la masse volumique et de la vitesse du son du milieu et donnée par la relation suivante [67]:

Z_a=ñ v_a (2.2)

1.2.2.3 Pression et intensité acoustiques

La pression acoustique varie selon la fréquence de l'onde ultrasonore. L'énergie délivrée dans le milieu dépend de ces variations de pression qui soumettent les particules du milieu à des mouvements vibratoires.

On définit l'intensité acoustique comme le flux d'énergie acoustique traversant une unité de surface perpendiculaire à la direction de propagation de l'onde par unité de temps. Elle est reliée à la pression acoustique par la formule suivante [43] :

Ia=	???? 2 (2.3) 2 ñva

où P_a et I_a sont respectivement la pression et l'intensité acoustique.

2.2.3 Interaction du faisceau ultrasonore avec la matière

1.2.3.1 Réflexion et réfraction d'u4eI14d1 ultrasonore

Lorsqu'une onde ultrasonore rencontre une interface séparant deux milieux de caractéristiques physiques différentes, une partie de son énergie est transmise d'un milieu à l'autre, alors que l'autre est réfléchi (cf. figure 2.2).

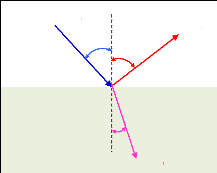
Milieu 1 ; Za1
Milieu 2 ; Za2

Onde incidente

èi

Onde transmise

è_t

è_r

Onde réfléchie

Fig. 2.2 - Réflexion et réfraction d'une onde ultrasonore sur une interface

5 L'unité de mesure de l'impédance acoustique est le : Rayl ; 1Rayl =1kg.m^-2s^-1; exemple pour l'air : 415 Rayls.

D'un point de vue énergétique, le coefficient de réflexion «???? » et le coefficient de transmission «????» peuvent être donné par les relations suivantes [64,68,69]:

Iar

Iai

????=

et

Iat
Iai

???? =

2

(2.4)

Z_a2 _cosèi-Za1 cos è_t

Z_a2 cos _èi+Za1 cos è_t
⁴Za1 Z_a2cos² èi

Za2 cos _èi+Za1 cos è_t~²

(2.5)

où _Za1 et Za2 sont respectivement les impédances acoustiques des milieux 1 et 2;

èi , è_r et è_t sont respectivement l'angle d'incidence, de réflexion et transmise de l'onde ultrasonore ;

Iai, Iaret Iat représentent respectivement l'intensité de l'énergie incidente, réfléchie et transmise.

Si nous considérons que l'onde ultrasonore atteint l'obstacle perpendiculairement (èi=è_r=è_t=0 ). Les coefficients de réflexion et transmission peuvent donc s'écrire :

	????=	Za2^-Za1		2	(2.6)
et		Za2+Za1
????=^1-????=			^4Za1Za2 Za1+Za2)^2			(2.7)

On constate que si les impédances acoustiques des deux milieux sont très différentes l'énergie réfléchie sera très élevée. C'est ainsi qu'une couche d'air, meme très fine, dans le champ de propagation des ultrasons agit comme un écran infranchissable. C'est pour cette raison qu'il est nécessaire d'utiliser un milieu de couplage entre le transducteur et le milieu dans lequel on souhaite faire propager l'onde acoustique.

Dans le tableau 2.3 nous présentons quelques valeurs des coefficients de réflexion et de transmission pour quelques interfaces acoustiques typiques.

Milieu 1	Milieu 2	Za1^(MRayl)	Za2 (MRayl)	????(%)	????(%)
Air	Aluminium	0.00043	17.06	99.99	0.01
Air	Plexiglas	0.00043	4	99.99	0.01
Air	Muscle	0.00043	1.64	99.95	0.05
Air	Eau	0.00043	1.48	99.88	0.12
Eau	Aluminium	1.48	17.06	84.03	15.97
Eau	Plexiglas	1.48	3.30	38.08	61.92

Tab. 2.3 - Valeurs de l'interface acoustique entre quelques milieux [64,67]

1.2.3.2 Atténuation d'une onde ultrasonore

L'atténuation d'une onde ultrasonore dépend principalement de la fréquence considérée. Pour la plupart des matériaux, plus la fréquence est haute plus l'atténuation est importante. La theorie prevoit que l'attenuation est directement proportionnelle au carre de la frequence pour une onde plane.

Considerons une onde plane se propageant suivant la direction « z », la pression acoustique est donnee par la formule [70]:

P_a =P??0exp(^--???? z) (2.8)

oil _P??0 est la pression initiale (z=0) et a_s est le coefficient d'attenuation.

Pour les liquides, le coefficient d'atténuation est donné par la relation [71]:

2çù²

????= 3ñva3 (2.9)

oil ç est le coefficient de viscosite et ù est la pulsation.

2.3 Différents types de transducteurs ultrasonores et

leurs principes de fonctionnement

2.3.1 Transducteur piézoélectrique

2.3.1.1 Structure d'un transducteur piézoélectrique

Le transducteur piezoelectrique convertit l'énergie électrique en énergie acoustique et inversement et son fonctionnement fait appel à la piezoelectricite. Il est constitue de trois elements de base qui sont : l'élément piezoelectrique, le materiau absorbant (ou backing) et lame d'adaptation d'impédance (ou lame quart d'onde) (cf. figure 2.3) [5,65,72].

> L'élément piézoélectrique est généralement composé d'un simple disque (ou plaque) de céramique piézoélectrique qui permet la conversion d'un signal electrique en vibration mecanique ou reciproquement.

> 3/1 %47,4i1M1Vs4VH/t est un materiau dense et très attenuant sert d'amortisseur aux vibrations de l'élément piézoélectrique après l'excitation et absorbe également une partie de l'énergie rayonnée vers l'arrière de l'élément piézoélectrique. Plus l'impédance acoustique du materiau absorbant est proche de celle de l'élément piezoelectrique, plus la quantite d'énergie absorbee est elevee (amortissement fort), favorisant la création d'impulsions courtes d'où une meilleure résolution axiale⁶ du transducteur, au prix d'une dégradation de sa sensibilite⁷.

6

La resolution axiale est le pouvoir de separer dans le temps des ondes reflechies respectivement par deux reflecteurs très voisins situes sur une direction axiale [1].

7 La sensibilité est l'aptitude de détecter des réflecteurs, plus le signal qui est reçu de ces reflecteurs est grand, plus la sensibilite est meilleure [73].

> Lame d'adaptation d'impédance sert de protection contre les chocs mécaniques et permet un transfert maximal de l'énergie issue de l'élément piézoélectrique au milieu de propagation. Elle peut agir aussi comme lentille acoustique focalisatrice placée en avant de l'élément piézoélectrique et il sert à modifier la géométrie du faisceau ultrasonore. L'impédance acoustique de la lame d'adaptation d'impédance est comprise entre celle de l'élément piézoélectrique et celle du milieu de propagation permettant d'éviter une trop forte réflexion du faisceau ultrasonore vers le transducteur. L'énergie transmise sera maximale si l'épaisseur de lame d'adaptation d'impédance est égale ël/4 (ël étant la longueur d'onde de la lame à la fréquence de fonctionnent du transducteur) et son impédance est égale à la moyenne quadratique de l'impédance acoustique de l'élément piézoélectrique et celle du milieu de propagation.

Connecteur

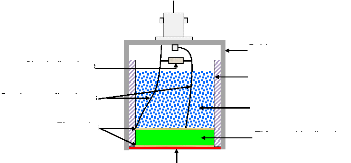
Circuit électrique

Conducteurs électriques

Electrodes

Elément piézoélectrique

Boitier

Housse isolante

Matériau absorbant

Lame d'adaptation
d'impédance

Fig. 2.3 - Constitution d'un capteur acoustique piézoélectrique [73]

2.3.1.2 Description du faisceau ultrasonore émis par un transducteur piézoélectrique

Le faisceau ultrasonore émis par un transducteur piézoélectrique est constitué d'un lobe principal formant un cône dans lequel la plus grande partie de l'énergie est concentrée et de lobes secondaires d'énergie beaucoup plus faible (cf. figure 2.4). Il comprend deux régions distinctes. La première appelée zone de Fresnel (ou champ proche) où le faisceau est quasiment cylindrique. La seconde appelée zone de Fraunhofer (ou champ lointain) se caractérise par une divergence du faisceau selon un demi-angle «????» par rapport à l'axe ??. La limite entre les deux régions, pour un transducteur de diamètre ???? et de longueur d'onde ë dans le milieu de propagation, se situe à une distance [73,74]:

????²

N??= 4ë (2.10)

L'angle de divergence est donné par la relation [72]:

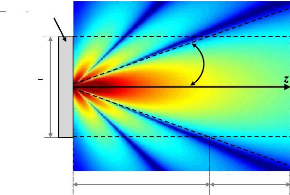
Transducteur

è??

D??

Champ proche Champ lointain

Fig. 2.4 - Faisceau ultrasonore émis par un transducteur ultrasonore piézoélectrique

L'intensité acoustique le long de l'axe du faisceau à une distance z du transducteur est donnée par la formule suivante [74]:

2

I_{a =Ia0} sin2 ð ë ???? 4 +z²-z ~ (2.12)

avec _Ia0 est l'intensité acoustique sur l'axe du faisceau au niveau du transducteur.

La figure 2.5 montre la variation sur l'axe de l'intensité acoustique en fonction de la distance pour un transducteur de 50 mm de diamètre vibrant à 0.76 MHz et rayonnant des ondes acoustiques dans l'eau. Nous remarquons que l'intensité acoustique décroît régulièrement dans la zone du champ lointain à cause de la divergence de faisceau.

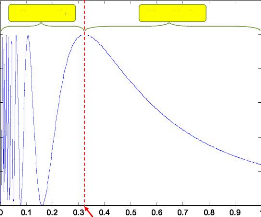
Champ proche

Champ lointain

Nt =0.32

2.3.2 Transducteur capacitif

Les transducteurs capacitifs (ou électrostatiques), dans leur principe comportent deux armatures, une fixe et l'autre mobile, séparées par une couche d'air. Le déplacement de l'armature mobile peut-être provoqué soit par une pression acoustique externe (ultrasons) si le transducteur fonctionne comme capteur, soit par la tension électrique si le transducteur est utilisé comme actionneur [6].

La figure 2.6 montre le principe de fonctionnement d'un transducteur capacitif. Quand une tension statique (tension de polarisation) est appliquée entre les deux armatures, la membrane est attirée vers le substrat par la force colombienne. Quand un voltage alternatif est superposé à la tension de polarisation, la membrane va se mettre en mouvement et une onde ultrasonore est générée et envoyée dans l'air [64]. De même en mode réception, si un ultrason approche, la membrane va se déformer ce qui entraine la variation de la capacité formée entre les deux armatures. En conservant une charge électrique constante entre les armatures, la tension électrique entre ces armatures varie selon le mouvement de l'électrode mobile engendré par la pression acoustique.

Les transducteurs capacitifs possèdent les avantages suivants : une faible sensibilité aux variations de température, une grande sensibilité à la pression acoustique et une bonne performance en terme de bruit [75,76].

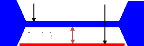
Armature
mobile

Cavité Armature
fixe

d

Substrat isolant
S b t t

(a) Pression

acoustique

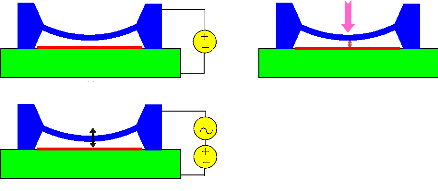
(b)

(d)

Déplacement
de l'armature

d-w

(f)

Fig. 2.6 - Principe de fonctionnement d'un transducteur capacitif : (a) Membrane au repos, (b) Application d'une tension de polarisation continue, (c) Superposition d'une tension alternative, (c) application d'une pression acoustique [64,75]. d et w sont respectivement la distance interarmatures et la déflexion de la membrane.

2.3.3 Transducteur piézorésistif

La piézorésistivité est la capacité que possède un matériau à changer ses propriétés de conductivité électrique lorsqu'il est soumis à une contrainte mécanique [77]. Cet effet est surtout utilisé dans les accéléromètres, les capteurs de pression et également dans les capteurs ultrasonores dans le domaine de mesure de distance ou la détection d'obstacle [64].

Les transducteurs piézorésistifs utilisent des matériaux piézorésistifs comme le silicium monocristallin ou polysilicium. Ces matériaux sont utilisés pour constituer des résistances communément appelées jauges de contrainte. Les transducteurs piézorésistifs sont idéalement composés de 1,2 ou 4 jauges piézorésistives diffusées, pour détecter avec la meilleure sensibilité les contraintes longitudinales et transversales subies par le matériau. Sous l'effet d'une pression acoustique, la membrane de silicium se déforme, ce qui entraine la déformation des jauges piézorésistives et par conséquent il apparait une variation de résistivités à leurs bornes proportionnelle à la déformation. Grâce à un pont de Wheatstone, il est très simple de mesurer et traiter cette variation de résistance. Donc alors on peut déterminer facilement la pression acoustique appliquée sur la membrane de silicium (cf. figure 2.7) [78].

Les transducteurs piézorésistifs sont extrêmement sensibles à la température (i.e. la valeur de la résistance dépend de la température) et ne peuvent fonctionner correctement sans l'addition de circuits de compensation onéreux [75,76].

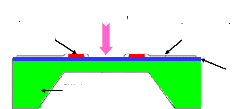
Silicium

Couche d'oxyde

Jauge
piézorésistive

Pression
acoustique

Interconnexion
en aluminium

Fig. 2.7 - Schéma de principe d'un transducteur piézorésistif à membrane silicium [78]

2.3.4 Transducteur impulsion-écho

Le transducteur impulsion-écho utilise l'effet piézorésistif pour la détection de l'onde acoustique, et l'effet bimétallique⁸ pour la génération vu que l'effet piézorésistif est irréversible [6,64].

La figure 2.8 illustre une vue en coupe d'un dispositif contenant le transducteur impulsion-écho, ce dernier est formé d'une plaque composée de plusieurs couches issues du procédé de fabrication CMOS. La couche de nitrure de silicium (Si3N4) est mécaniquement la plus importante. La couche de polysilicium⁹ (SiO2) utilisée pour l'intégration des

8 Effet bimétallique : une simple structure formée de deux matériaux ayant des coefficients de dilatation différents exerce, sous un changement de température, un déplacement dans le sens perpendiculaire au plan de séparation de deux matériaux [6].

9 Le polysilicium ou le silicium polycristallin est un matériau déposé à basse pression et haute température. Cependant, il se distingue du
silicium par sa structure amorphe, puisque composé d'un agrégat de grains de silicium formant ainsi un matériau non cristallin [77].

composants nécessaires pour le fonctionnement du dispositif (résistances de chauffe, jauges piézorésistives et thermopiles). La résistance de chauffe en polysilicium est placée au centre de la membrane pour produire l'excitation thermomécanique de celle-ci. La membrane encastrée à son extrémité est déformée en flexion par le couplage thermoélectrique dans le régime de génération. En réception, la détection du mouvement de la plaque se fait par les jauges piézorésistifs intégrées dans la couche de polysilicium. On note aussi la présence de quatre thermopiles placées entre le sommet et le centre de la membrane permettant de mesurer la température moyenne au sein de la membrane.

Résistance de
chauffe

Thermopiles

Membrane
carrée

Jauges
piézorésistives

Fig. 2.8 - Vue en coupe d'un dispositif impulsion-écho [6]

2.4 Conclusion

Dans ce deuxième chapitre, nous avons tout d'abord décrit brièvement quelques définitions, et propriétés physiques et applications des ultrasons. Nous avons ensuite présenté les différents types de transducteurs ultrasonores. Il s'agit de transducteurs : piézoélectrique, capacitif, piézorésistif et impulsion-écho. Les transducteurs : piézoélectrique et capacitif permettent la détection et la génération des ultrasons par l'exploitation de deux effets réversibles : piézoélectrique et capacitif respectivement. Les transducteurs piézorésistifs utilisent l'effet piézorésistif pour la détection des ultrasons. Cependant, l'effet piézorésistif est irréversible. Il faut donc générer les ultrasons par un autre moyen. A cet effet, l'effet bimétallique est utilisé par les transducteurs impulsion-écho afin de générer les ultrasons.

Dans le chapitre suivant, nous allons présenter la modélisation unidimensionnelle et la simulation d'un transducteur ultrasonore piézoélectrique.

Chapitre 3

Modélisation unidimensionnelle et simulation

d'un transducteur ultrasonore piézoélectrique

Sommaire
3.1 3.2	Introduction ............................................ .......... ............. . Modélisation unidimensionnelle d'un transducteur ultrasonore piézoélect- rique....... ............... ................................ .... .............		41 41
	3.2.1	Transducteur sans pertes ............................... ................	41
	3.2.2	Transducteur avec pertes ............................... ................	52
3.3	Simulation d'un transducteur ultrasonore piézoélectrique ................ 59
	3.3.1	Caractérisation de la ligne de transmission et analogie électroaco-
		stique...................... ............................................	59
	3.3.2	Sous-circuit PSPICE du modèle de Leach .......................... .	62
	3.3.3	Simulation de l'impédance électrique du transducteur ....... ...	63
3.4	Conclusion ........................................................ ............. .		67

3.1 Introduction

La modélisation du transducteur ultrasonore piézoélectrique est une étape nécessaire pour la compréhension de son comportement, pour l'estimation de ses caractéristiques et pour son optimisation [6].

Le succès de l'électronique moderne est construit sur la possibilité de prédire avec précision le comportement d'un système par le recours à des outils de simulation. Ce paradigme peut être prolongé aux composants tels que les transducteurs ultrasonores piézoélectriques associent à leur électronique. La capacité de simuler le transducteur ultrasonore piézoélectrique et leur électronique rend possible l'ensemble des optimisations efficaces au niveau de système réduisant la taille, le coût et la consommation d'énergie [79].

Le présent chapitre est dédié à la modélisation unidimensionnelle et à la simulation avec PSPICE d'un transducteur ultrasonore piézoélectrique.

3.2 Modélisation unidimensionnelle d'un transducteur

ultrasonore piézoélectrique

3.2.1 Transducteur sans pertes

3.2.1.1 Transducteur comme un système linéaire à trois ports

Si le transducteur considéré comme une plaque piézoélectrique assez large pour ne pas avoir de vibrations parasites suivant les dimensions latérales, on utilise alors une modélisation à une dimension, en ne considérant que l'axe de propagation de l'onde ultrasonore : z. Ce type de modélisation considère une plaque d'épaisseur « a3 » composée d'une céramique piézoélectrique, avec une électrode de chaque coté, à z = - a3/2 et à z = a3/2, comme illustré sur la figure 3.1.a. Le système mécanique considéré peut être facilement mis en analogie avec un système électrique, ou schéma équivalent. C'est pourquoi on peut considérer notre transducteur comme un système linéaire à trois ports (ou accès) (cf. figure 3.1.b) [19,80]:

· Un port électrique alimenté par une intensité I3, sous une tensionV3.

· Deux ports acoustiques alimentés par les vitesses v1 et v2 analogues à des intensités sous l'action des forces F1 et F2 analogues à des tensions.

Chapitre 3. Modélisation unidimensionnelle et Simulation d'un transducteur ultrasonore piézoélectrique 42

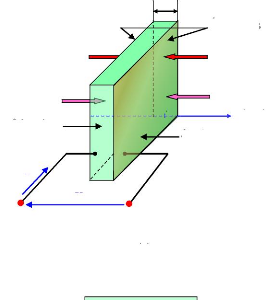
v2=- v (a3/2)

v1= v (-a3/2)

a3

Electrodes

F1= -AT (-a3/2) F2= -AT (a3/2)

Céramique

piézoélectrique

z (ou 3)

0

I3

V3

(a)

v1 v2

Section A

Port
acoustique

F1

Port
acoustique

F2

Transducteur

Port
électrique

I3

V3

(b)

Fig. 3.1 - (a) Diagramme d'une céramique piézoélectrique vibrant en épaisseur, (b) Le
transducteur comme un système linéaire à trois ports [19,81]

Une excitation du port électrique, à l'aide d'un générateur de tension, provoque une sollicitation mécanique sous la forme d'une onde ultrasonore. Les deux ports acoustiques représentent en fait les faces arrière et avant du transducteur. L'effet inverse se traduit par une sollicitation mécanique mettant le transducteur en résonance et excite le port électrique.

3.2.1.2 Impédance électrique du transducteur

3.2.1.2.1 Expression de l'impédance électrique

En utilisant les équations de la piézoélectricité (cf. § 1.5), on peut mettre en relation les grandeurs électriques et mécaniques (cf. figure 3.1) sous forme matricielle [82,83]:

??1 ~ ??2 ~ = -?? ??3

????0?????? ??3??3 ????0??????????(??3??3) h33

????0?????????? ??3??3 ????0?????? ??3??3 h33

h33 ?? h33 ?? 1

??11 ??2 (3.1) ??3

?? ?? ????0

Dans le cas d'un transducteur (matériau piézoélectrique métallisé d'impédance Z_p) ,dont on néglige l'épaisseur des électrodes et chargé par deux milieux d'impédances Z1 et Z2 respixtivement en face arrière et en face avant du transducteur, l'impédance électrique d'entrée se calcule á partir de la matrice des impédances (cf. équation (3.1)) [84] :

où

??=

??3 ??3

1

????0 ??

1 +

??

(3.2)

Id 2?? ?? 1 - cosö) ? j Z1 + Z2)sinö

???? 2

- ???? + ??1??2)???????? + ^??????(??1 + ??2)????????)

· ??0 est l'impédance acoustique spécifique du matériau piézoélectrique.

· ??3 est le nombre d'onde associé à la pulsation «ù» et á la vitesse des ondes ultrasonores dans la céramique«????3» selon l'axe de polarisation «x3» (??3 = ??/????3).

· L'angle ö est défini comme ?? = ??3??3.

· h33est la constante piézoélectrique.

· ???? est le coefficient de couplage électromécanique en épaisseur.

· ??0 est la capacité statique du transducteur rigidement lié (clampé) définie par [6] :

??33 ?? ??

??0 = (3.3)

??3

Remarque :

La relation (3.2) souligne l'importance de la constante de couplage comme le principal paramètre piézo-électrique caractérisant le transducteur. Il est aussi clair que le rapport 1/????0 module l'impédance électrique du transducteur en fonction de la fréquence.

3.2.1.2.2 Caractérisation du transducteur

Pour caractériser le transducteur, on peut utiliser une configuration mécanique du type résonateur libre [80]. Dans ce cas, le transducteur est sans charge avant et arrière (i.e. Z1=Z2=0 ). L'impédance électrique s'écrit d'après l'équation (3.2):

1 1 - ????2 tan ??/2~

(3.4)

?? = ??/2 ~

??????0

L'impédance tend vers l'infini (i.e. admittance ?? = 1/?? s'annule) pour chaque multiple de ???? , la fréquence d'antirésonance :

????(??) = 2?? + 1)??_?? ; avec ???? = ????3 (2??3) et ?? ? N (3.5)

L'impédance s'annule (i.e. admittance tend vers l'infini) pour les fréquences de résonances ????(??) avec ?? ? N, ce qui d'après l'équation (3.4) nous donne :

(??) (??)

????2?????? ~?? ???? ~ = ?? ???? 2 f_a 2 fa (3.6)

Le mode fondamentale est donné par ?? = 0 et les harmoniques sont de fréquences multiples impaires de la fréquence fondamentale.

Pour caractériser un transducteur, on mesure les fréquences de résonance et d'antirésonance, ce qui donne la vitesse acoustique et le coefficient de couplage électromécanique ???? :

????3 = ²??????3 (3.7)

???? = ~?? ???? ?????? ?? ????-???? (3.8)

2 ???? 2 ????

Il est important de noter que l'épaisseur de la céramique piézoélectrique fixe la fréquence d'antirésonance et non la fréquence de résonance. La fréquence de résonance est elle-même liée au coefficient de couplage électromécanique du matériau piézoélectrique.

En pratique, c'est la mesure des fréquences de résonance et d'antirésonance qui fournit la valeur du coefficient de couplage électromécanique [24]:

· Coefficient de couplage en fonction du rapport Ir/Ia

La figure 3.2 montre la variation du coefficient de couplage électromécanique en fonction du rapport «f??/f?? » (cf. équation (3.8)). On peut observer que plus le rapport «f??/f?? » est faible (i.e. l'intervalle de fréquence entre la résonance et l'antirésonance est élevé) plus le coefficient de couplage est grand.

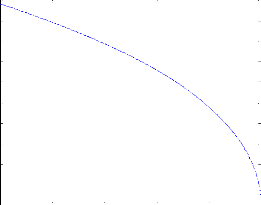
Fig. 3.2- Variation du coefficient de couplage en fonction de «f??/f?? »

· Influence de l'épaisseur de la céramique sur la fréquence d'antirésonance

La figure 3.3 montre pour une céramique piézoélectrique de type PZT503, l'évolution de la fréquence d'antirésonance définie par l'équation 3.7. On comprend facilement qu'une montée en fréquence nécessite une diminution de l'épaisseur. L'utilisation des céramiques massives permet de couvrir une gamme de fréquence qui s'étend du « kHz » à la centaine de « MHz ». Pour des fréquences de l'ordre du « GHz », l'épaisseur de la céramique s'amenuise à quelques microns. Donc alors, il est nécessaire d'avoir recours à des couches (ou films) piézoélectriques déposées par des techniques relevant du domaine de la microélectronique, tout en gardant des propriétés électromécaniques équivalentes à celles obtenues par les procédés classiques.

a3 (m)

Fig. 3.3 - Variation de la fréquence d'antirésonance en fonction de l'épaisseur Remarque :

Pour obtenir une puissance acoustique convenable, il faut travailler dans des conditions de résonance. Pour cela, il faut choisir la fréquence f0 de la source d'excitation de telle sorte que l'épaisseur de la céramique piézoélectrique soit [33]:

a3 = (2n + 1)

A0 2

= (2n + 1) Vp3 (3.10) 2f0

Le fondamental A0/2 est le plus recherché, car il correspond aux pertes les plus faibles dans le matériau piézoélectrique, puisque le parcours des ondes acoustiques y est le plus réduit.

3.2.1.2.3 Simulation de l'impédance électrique

La figure 3.4 montre, pour une plaque céramique de type PZT503, la variation du module et phase de l'impédance en fréquence. On constate que pour le mode de résonance fondamental ils associent des modes parasites (ou partiels).

· Pour le mode fondamental, les fréquences de résonances et d'antirésonances sont respectivement : 5.5MHz, 7.7 MHz.

· Pour les modes parasites :

- Les fréquences de résonances sont : 22.5 MHz, 38 MHz, 53.9 MHz, 69.1 MHz, 5 84.5 MHz.

- Les fréquences d'antirésonance sont : 23.1 MHz, 38.5 MHz, 53.9 MHz, 69.3 MHz, 84.7 MHz.

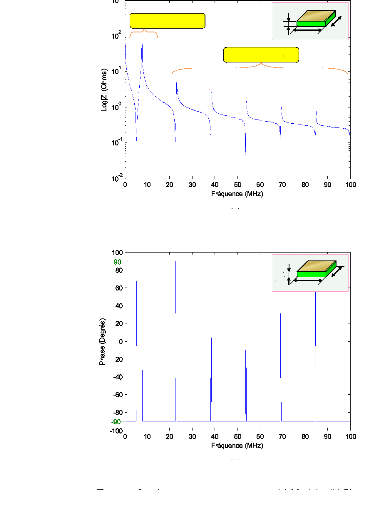
(a)

PZT503

20

mm

20

(b)

Fig. 3.4 - Courbe simulée de l'impédance ; (a) Module; (b) Phase

0.3

mm

mm

PZT503

Mode fondamental

20

0.3

mm

mm

20

mm

????

Modes parasites

???? (1)

???? (2)

???? (3)

???? (1) ???? (2)

????

???? (3) ???? (4) ???? (5)

(5)

???? (4) ????

3.2.1.2.4 Validation des résultats de simulation

Pour permettre la validation des résultats de simulation précédents, les résultats expérimentaux (courbe de l'impédance et celle de la phase) donnés dans la référence [85] sont utilisés. La figure 3.5 illustre les variations du module et phase de l'impédance en fonction de la fréquence. Nous remarquons que la concordance entre les positions des fréquences de résonance et d'antirésonance est bonne.

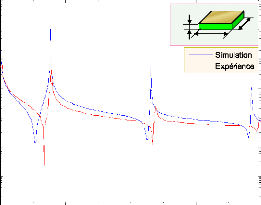
0.3

mm

20

PZT503

mm

mm

20

(a)

(b)

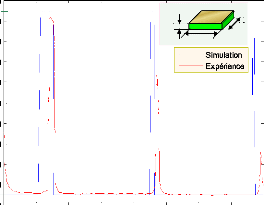
0.3

mm

20

PZT503

mm

mm

20

Les valeurs des fréquences de résonances et d'antirésonances expérimentales sont comparées celles issues de l'approche analytique et résumées dans le tableau 3.1. Nous constatons que les fréquences expérimentales sont cohérentes avec celles théoriques :

Fréquences (MHz)	Théorie	Expérimentale	Erreur relative (%)
????	5.5	6.9	20
???? (1)	22.5	23.5	4
???? (2)	38	39.3	3
????	7.7	7.9	2.5
???? (1)	23.1	23.8	3
???? (2)	38.5	39.7	3

Tab. 3.1 - Comparaison des valeurs des fréquences théoriques et expérimentales

A partir des résultats précédents, le facteur de couplage électromécanique et vitesse acoustique (cf. équations : 3.7, 3.8 et 3.9) sont déduits et récapitulés dans le tableau 3.2.

Paramètres	Théorie	Expérimentale
????	0.73	0.49
????3	4620	4740

Tab. 3.2 - Facteurs de couplage et vitesse acoustique théoriques et expérimentaux

3.2.1.3 Schémas électriques équivalents

Il est souvent pratique d'utiliser un schéma électrique équivalent pour modéliser le comportement d'un transducteur [19]. Il est plus facile alors d'analyser les interactions entre le transducteur, les lames d'adaptation d'impédance et le milieu de propagation, dès lors que l'on se ramène à un schéma électrique équivalent familier. Divers schémas équivalents sont connus tels que le modèle de Mason, le modèle KLM et le modèle de Leach.

3.2.1.3.1 Schéma électrique équivalent de Mason

Mason, dans les années 40, a démontré que pour une analyse unidimensionnelle, la plupart des difficultés rencontrées dans l'obtention d'une solution analytique de l'équation (3.1) peuvent être surmontées en utilisant une analogie avec des circuits électriques [6,18]. Il a présenté le circuit analogique qui sépare un matériau piézoélectrique dans un port électrique relié par un transformateur électromécanique avec deux portes acoustiques (cf. figure 3.6). La piézoélectricité est prise en compte par le transformateur de rapport ???? = h33??0.

F2

v1 ZM1 ZM1 v2

B F

ZM2

F1

1:NM

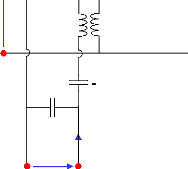
C0

C0

I3

E

V3

Fig. 3.6 -- Modèle de Mason d'un transducteur ultrasonore piézoélectrique [86]. Les lettres B, F désignent Back et Front respectivement (c'est-à-dire la face arrière et la face avant du transducteur) et la lettre E désignent Electrical port (c'est-à-dire le port électrique du transducteur)

Les impédances ZM1 et ZM2 sont données par les relations suivantes [81]:

ZM1 = ./Z0A tan	??3??3	)	(3.11)
	2

ZM2 = --./Z0A casec(a3a3) (3.12)

3.2.1.3.2 Schéma électrique équivalent KLM

Un des inconvénients du modèle de Mason repose sur l'introduction du terme de la capacité négative qui n'a pas de sens physique. Dans l'effort d'enlever cette capacité du circuit et alimenter directement le centre de la structure mécanique par un transformateur, Krimholtz, Leedom et Matthaei ont publié en 1970 un modèle alternatif. Ce modèle se déduisant de l'équation (3.1) est couramment appelé modèle KLM (cf. figure 3.7). Il s'agit d'une ligne de transmission, qui traduit la propagation, au centre de laquelle est injecté un courant à la sortie d'un transformateur électromécanique dont le coefficient de transformation varie en fonction de la fréquence [87,88].

Chapitre 3. Modélisation unidimensionnelle et Simulation d'un transducteur ultrasonore piézoélectrique 51

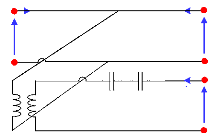
v1

F1 F2

E

XK C0 I3

V3

B

1:NK

F

v2

Fig. 3.7 - Modèle KLM d'un transducteur ultrasonore piézoélectrique [5]

Le rapport de transformation « ??K » et la réactance « XK » sont donnés par les relations suivantes [85]:

NK =	Z0??0 cosec 2h33	??3??3	)	(3.13)
		2

hi3 _r

XK = sink_.a3a3) (3.14)

Z0ik⁰²

3.2.1.3.3 Schéma électrique équivalent de Leach

La figure 3.8 montre le circuit équivalent de Leach d'un transducteur ultrasonore piézoélectrique. Ce circuit consiste en deux parties, une partie électrique (i.e. la capacité entre les deux électrodes « C0 ») et une partie mécanique (i.e. la ligne de transmission). Le couplage entre les deux parties est réalisé par deux sources contrôlées [79].

· La source de tension contrôlée dans partie mécanique a la tension « h33.I3/s », où s est l'opérateur de Laplace. Elle est commune entre les deux ports de la ligne de transmission. Puisque la charge sur les électrodes de transducteur est liée au courant par: Q=I3/s, la tension de la source devient h33.Q .Donc la source de tension est contrôlée par la charge sur les électrodes.

· La source de tension contrôlée dans partie électrique a la tension «h33. (v1 -- v2)/s ». Puisque le déplacement de particules est lié à la vitesse de particules par: c=v/s, la tension de la source devient _h33.(c1-c2). Donc la source de tension est contrôlée par la différence entre les déplacements de particules sur les deux faces du transducteur.

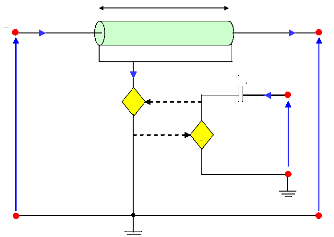
-I-

h33.(v1-v2)/s

-

v1 v2

B

F

v1-v2

h33.I3/s

-I-

-

C0

I3

F1

F2

E

V3

Fig. 3.8 - Modèle de Leach d'un transducteur ultrasonore piézoélectrique [97]

Parmi d'autres chercheurs qui ont proposé des modèles décrivant le comportement des transducteurs ultrasonores piézoélectriques citons au moins les travaux de Redwood, Brown et Carlson, Gonnard, Hsueh, Morris et Hutchens, Dion, Püttmer, Emeterio, Hirsekon.

3.2.2 Transducteur avec pertes

La modélisation d'une façon précise d'un système de transduction électromécanique exige l'ensemble des propriétés électromécaniques pour chacun des éléments constitutifs du système. La réponse dynamique d'un tel système ne sera caractérisée avec précision que si les propriétés électromécaniques avec pertes pour chacun des éléments constitutifs de ce système ont introduit dans le modèle [89]. Le transducteur ultrasonore piézoélectrique est soumis à un ensemble de pertes d'une grande importance lors de la modélisation. Il s'agit notamment de pertes mécaniques et diélectriques dans le matériau actif (i.e. céramique piézoélectrique), pertes mécaniques dans les matériaux passifs tels que le matériau absorbant et lame d'adaptation d'impédance.

3.2.2.1 Différents types de pertes

3.2.2.1.1 Pertes diélectriques

Lors de leur fonctionnement, les céramiques piézoélectriques dissipent une puissance non négligeable, correspondant aux pertes d'origine diélectrique. Ces pertes se traduisent sous forme de chaleur, ce qui, à terme, provoque la perte des propriétés piézoélectrique [42]. Elles sont souvent représentées au travers de la tangente de l'angle de pertes diélectriques « ?????????? ». Dans ce cas, on définit une permittivité complexe, dont la partie

imaginaire est fonction de ?????????? [90] :

??33^??' = ??33^?? 1 - ????????????) (3.15)

où ??33^??' et ??33^?? sont respectivement les permittivites de la ceramique avec et sont pertes. 3.2.2.1.2 Pertes mécaniques

Les pertes mecaniques, qui sont une consequence de la propagation de l'onde acoustique dans les materiaux actifs ou passifs et sont dues aux frottements internes generes dans ces materiaux. Elles sont quantifiées par la tangente de l'angle de pertes mécaniques ??????????. Dans ce cas, on definie une constante elastique complexe dont la partie imaginaire est fonction de ?????????? [91] :

??33^??' = ??33^?? 1 + ????????????) (3.16)

où ??33^??' et ??33^?? sont respectivement les constants elastiques de la ceramique avec et sont pertes.

3.2.2.2 Impédance électrique avec pertes du transducteur

3.2.2.2.1 Expression de l'impédance électrique avec pertes

Pour modeliser les pertes dans le transducteur (resonateur libre), nous introduisons les parties imaginaires des paramètres complexes (equations (3.15) et (3.16)) dans la relation (3.4), ceci nous permet d'expliciter l'impédance electrique avec pertes¹⁰ :

1

??=

1 - ????2 1 - ????????????

??????0(1 - ????????????)

1 + ?? ??????????

2

?????? (?????? ?? 1 - ?? ?????????? ))

(3.17)

2 2

??
2

3.2.2.2.2 Simulation de l'impédance électrique avec pertes

La figure 3.9 montre pour une ceramique piezoelectrique de type PZT503, l'évolution de la résistance et réactance de l'impédance electrique d'une plaque de dimensions 20 × 20 × 0.3 ????. Nous constatons que les pertes dielectrique et mecanique entrainent la variation de la resistance. Il nous faut donc completer le modèle du transducteur sans pertes en y ajoutant des elements electriques resistifs.

10 Le developpement limite de Taylor d'ordre "1" est utilise afin d'effectuer des approximations sur les differents paramètres de notre modèle et par consequent un modèle simple est obtenu.

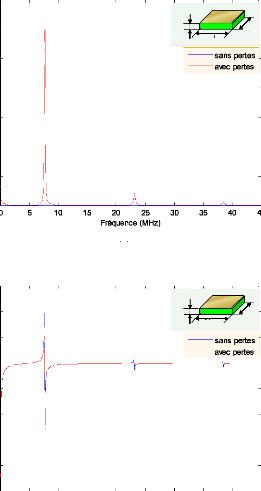
0.3

mm

20

PZT503

mm

mm

20

(a)

0.3

mm

20

PZT503

mm

mm

20

(b)^pert
Fig. 3.9 - Courbe simulée de l'impédance;(a) Résistance, (b) Réactance

3.2.2.3 Schéma électrique équivalent simplifié du transducteur

3.2.2.3.1 Schéma électrique équivalent simplifié

D'une manière générale, au voisinage d'une de ses fréquences de résonance, le comportement du transducteur de faible charge acoustique est décrit par le schéma équivalent simplifié illustré sur la figure 3.10 [92].

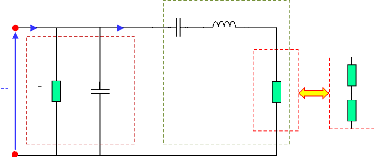
V3

I3

I_m

C_m L_m

Branche statique

Branchgclynamique
ou motionnelle

R0

C0

R_m

R_a

Rb

Fig. 3.10 - Schéma électrique équivalent simplifié du transducteur [93]

où

· R0 est une résistance représentant les pertes diélectriques. Elles se relié à la tangente l'angle de pertes diélectrique par [39]:

1

R0 = (3.18)

C0o.tanS_e

· R_a est une résistance dans laquelle se dissipe une énergie égale à l'énergie mécanique rayonnée par la céramique.

· Rb est une résistance qui traduit les pertes mécaniques dans le matériau.

· La résistance : R_m= R_a+Rb.

· L'inductance « L_m » est proportionnelle à la masse de la céramique.

· La capacité « C_m » est proportionnelle à l'élasticité de la céramique.

· I_m est le courant motionnel.

La branche statique du schéma équivalent traduisant les propriétés purement diélectriques, formée par la mise en parallèle de R0 et C0. La valeur très élevée de R0 permet dans la plupart des cas de négliger cette branche.

La branche motionnelle du schéma équivalent traduisant les propriétés mécaniques de l'élément vibrant constituée par la mise en série de R_m, C_m et Lm.

Les fréquences de résonance « ????, ????» associées respectivement au circuit oscillant série (formé par la branche motionnelle) et au circuit oscillant parallèle (formé par l'association de la branche électrique et motionnelle) sont donnés par les relations [39]:

		1
???? =			(3.19)
	2?? ????	????
		1
???? =			(3.20)
	2?? ????	??0????
					Le coefficient de couplage électromécanique est donné par [18]:
???? =	~????		(3.21)

3.2.2.3.2 Identification des paramètres du schéma électrique équivalent simplifié 3.2.2.3.2.1 Procédé d'identification

L'identification des paramètres du schéma équivalent simplifié se fait à partir du tracé de l'admittance électrique du transducteur « Y » dans le diagramme de Bode (cf. figure 3.11.a) et dans le plan de Nyquist (cf. figure 3.11.b).

Le tracé de l'admittance dans le plan de Bode fait apparaitre les phénomènes de résonance (admittance maximale pour « ???? ») et d'antirésonance (admittance minimale pour « ???? ») qui sont respectivement proches des fréquences ???? et ????.

Les éléments du circuit équivalent sont déterminés à partir du tracé de l'admittance dans le plan de Nyquist avec les relations [47,94]:

· Résistance ??0 :

· · · ·	Résistance ???? : Capacité ??0 : Capacité ???? : Inductance ???? :	??0 ???? ??0 ???? ????	1	?? ; ????????	« ???? (3.22) (3.23) 3.24) (3.25) (3.26)
			= R?? (??(??)) 1 =
			R?? ?? ????~ - I?? ?? ????)
				1 ??0
			= ???? 2 ??0 ????^2 - ???? 2 ~
			= ???? 1 =
			??0 (????^2 - fs2)

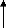
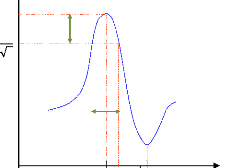
YM

Y_m

Ym

2

3dB

Af

Résonance

Antirésonance

f

f M		f m
fs		f p

(a)

C0

L_m C_m

??0

f 2

??0 + Rm

f 1

f

f M

fs

f p Conductance R_e (Y)

1

f

1

f m

f a f r

(b)

Susceptance 3_m(Y)

3.2.2.3.2.2 Simulation de l'admittance électrique

La figure 3.12 montre le tracé de l'admittance électrique d'un disque céramique de type PZT503 dans le plan de Nyquist.

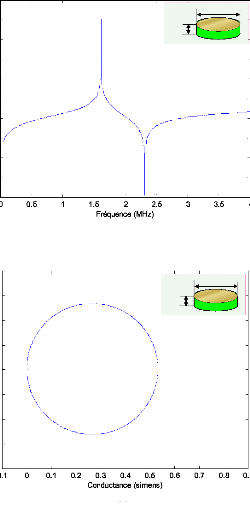
1mm

16mm

PZT503

(a)

(c)

1mm

16mm

PZT503

Fig. 3.12 - Tracé simulé de l'admittance électrique: (a) Dans le diagramme de Bode, (b)
Dans le plan de Nyquist

^{3 35} 4

3.2.2.3.2.3 Identification des paramètres

A partir des résultats de simulation précédents, les différents paramètres du schéma électrique équivalent simplifié sont déduits et résumés dans le tableau 3.3.

Paramètres	valeur	Unité
fr	1.61	MHz
fa	2.31
R0	1.98	kÙ
C0	989	pF
Rm	1.21	Ù
Lm	9330	mH
Cm	1050	pF

Tab. 3.3 - Paramètres du schéma électrique équivalent simplifié

3.3 Simulation d'un transducteur ultrasonore piézoélec-

trique

Dans cette partie, parmi les schémas équivalents que nous avons décrits (cf. § 3.2.1.3), le modèle de Leach à été choisi pour réaliser nos simulations, car il utilise des sources contrôlées au lieu du transformateur. L'utilisation des sources contrôlées entraîne la disparition de la capacité négative comme dans le modèle de Mason et du transformateur dont le rapport de transformation varie en fonction de la fréquence comme dans le modèle KLM.

3.3.1 Caractérisation de la ligne de transmission et analogie électroacoustique

Une onde ultrasonore se propageant dans un milieu peut être décrite comme une perturbation à laquelle le milieu réagit. De même, dans une ligne de transmission électrique une impulsion électrique peut se propager à travers elle. Cette impulsion est reçue à l'autre extrémité de la ligne après un temps très court, mais fini et une certaine vitesse. Par analogie à l'onde ultrasonore, l'impulsion électrique est la concentration et raréfaction des électrons à l'intérieur d'une ligne de transmission électrique [98].

Une ligne de transmission acoustique est caractérisée de façon similaire à une ligne de transmission électrique. Une analogie électro-acoustique (cf. annexe C) établit une correspondance entre une ligne de transmission électrique et une transmission d'onde acoustique. Cette correspondance permet ainsi de modéliser simplement le comportement d'une ligne de transmission [5].

La ligne de transmission avec pertes est modélisée par un quadripôle, avec une tension et un courant d'entrée et de sortie [79]. Ce quadripôle est lui-même constitué de plusieurs dipôles passifs appelés paramètres primaires de ligne comme le montre la figure 3.13.

I(x,t) R.dx L.dx I(x+dx,t)

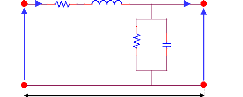
V(x,t) G.dx C.dx V(x+dx,t)

dx

Fig. 3.13 - Schéma électrique équivalent d'une ligne de transmission de longueur ????

avec

· R est la résistance linéique.

· L est l'inductance linéique.

· C est la capacité linéique.

· G est la conductance linéique.

· ??(??, ??)et ?? ??, ??) sont respectivement le courant et tension d'entré de la ligne.

· ??(?? + ????, ??)et ?? ?? + ????, ??) sont respectivement le courant et tension de sortie de la

ligne.

Les paramètres secondaires (Z_e,ã), sont exprimés en fonction des paramètres primaires de la ligne (R,L,C,G). Ainsi, l'impédance caractéristique électrique et la constante de propagation sont respectivement données par [99]:

₇ R+jùL

(3.27)

Ze iG+jùC

et

ã = R+jùL~(G+jùC) =?????? +j?????? (3.28)

Pour un milieu acoustique avec pertes, l'impédance caractéristique acoustique est exprimée par la relation [96]:

Z_a=ñv_a 1+jùô (3.29)

avec ô est le temps de relaxation.

En faisant un développement limité sur les équations (3.27) et (3.28), on obtient :

Ze?JL _C 1+ 1

2jù ^R L - G C (3.30)

et

1

ã? 2 LC

+jù LC (3.31)

R G
L + C

1

2 LC

1

+ ₂ LC

G

C (3.36)

?????? =

R

L

Dans le cas de pertes faibles, mais non négligeables où R«ùL et G«ùC et ùô«1, les impédances caractéristiques : électrique (équation 3.30) et acoustique (équation 3.29) sont

respectivement approximée par : Z_e? L ?? et Z_a? ñv_a. Pour corréler les deux impédances caractéristiques, on utilise l'analogie entre les grandeurs électriques et acoustiques (cf. annexe C). L'équivalence entre les deux systèmes est donnée par [98]:

Z_e= Z_aA (3.32)

avec A est la section de la céramique piézoélectrique perpendiculaire au sens de la propagation des ondes acoustiques.

La vitesse de propagation dans le milieu acoustique s'écrit [95]:

1

v_a = LC (3.33)

En utilisant les équations (3.32) et (3.33), on obtient les relations suivantes:

L? Añ (3.34)

1

C= Añv_a (3.35)

La partie réelle de l'équation (3.31) est la constante d'atténuation :

Dans la théorie classique de l'atténuation acoustique, la constante d'atténuation s'écrit [79]:

aaclassique =????v +????t (3.37)

avec _aav est le coefficient d'atténuation dû aux pertes visqueuses, et a_at est le coefficient d'atténuation dû à la conduction thermique.

En utilisant les équations (3.34), (3.35), (3.36) et (3.37), les relations suivantes peuvent être obtenues :

R= ²ñvaA????v (3.38)

2

G= ñAva aat (3.39)

3.3.2 Sous-circuit PSPICE du modèle de Leach

Les sources contrôlées du modèle de Leach que nous avons décrit (cf. § 3.2.1.3.3), ont des gains qui varient en fonction de la fréquence. Or, PSPICE n'accepte pas la fréquence comme paramètre à ses modèles de sources contrôlées [70]. Pour cela, la dépendance en fréquence est modélisée utilisant les différentes approches représentées dans la figure 3.14. Dans la partie électrique du modèle, ceci est accompli par l'utilisation d'un circuit équivalent de Norton qui consiste en une source de courant contrôlée par courant « F1 » en parallèle avec la capacité « C0 ». Ce circuit équivalent accomplit la nécessité d'intégration¹¹

de « v1^-v2 ». Dans la partie mécanique du modèle une source de courant contrôlée par courant « F2 » est utilisée avec une capacité « C1 » pour accomplir l'intégration du courant« /3 » [100].

Les deux parties : électrique et mécanique interagissent par de deux sources de courant contrôlées par courant« F1 » et «F2 ». Dans la partie mécanique, la déformation elle-même n'est pas mesurée, mais le courant «v1-v2 » qui représente le taux de déformation est mesuré. Ce courant contrôle la source contrôlée « F1 » de gain « h33C₀». Dans la partie électrique, le courant « /3 » contrôle la source contrôlée « F2 » de gain «h33». Les noeuds de sorties de la source contrôlée doivent être intégrée pour obtenir une charge totale sur les électrodes. Pour assurer l'isolation de l'intégrateur, une source de tension contrôlée par tension de gain « 1 » est utilisée. La résistance « R1» sert à éviter le cas des noeuds flottants12.

11

Une multiplication par s dans le domaine du transformer de Laplace représente l'opérateur dérivé dans le domaine temporel et une division par s dans le domaine du transformer de Laplace représente l'opérateur intégrale dans le domaine temporel [95].

12 Pour le logiciel PSPICE, les noeuds de sortie de la source contrôlée ne doivent pas etre flottants. Ils doivent etre relies à la masse (noeud 0) d'une manière ou d'une autre, éventuellement par de fortes résistances.

Chapitre 3. Modélisation unidimensionnelle et Simulation d'un transducteur ultrasonore piézoélectrique 63

-

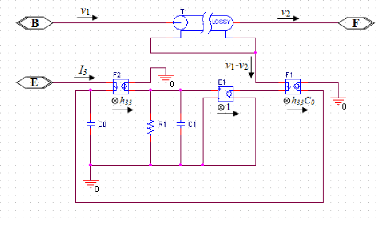
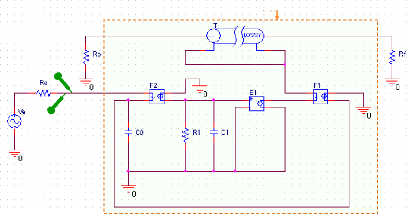
I

V

Transducteur

Fig. 3.14 - Sous-circuit PSPICE du modèle de Leach [96]

3.3.3 Simulation de l'impédance électrique du transducteur

3.3.3.1 Procédé de simulation

Pour simuler l'impédance électrique du transducteur, en excitant le transducteur (résonateur libre) par une tension sinusoïdale et déduisant le rapport ente la tension et courant d'entrée du transducteur (i.e. ?? = ??/??) (cf. figure 3.15). Le matériau absorbant (air) et le milieu de propagation (air) sont modélisés comme étant des résistances.

3.3.3.2 Résultats de simulation

Les résultats de simulation sont représentés sur la figure 3.16. La fréquence d'antirésonance du transducteur a lieu pour 7.7MHz.

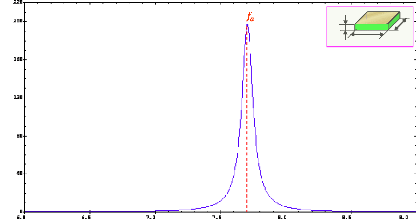
Re(Z) (Ohms)

7.7

0.3

mm

20

PZT503

mm

20

mm

Fréquence (MHz)

(a)

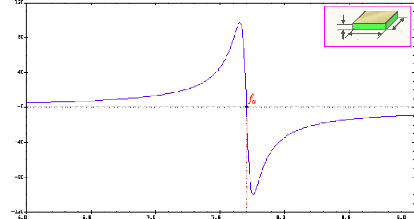
Im(Z) (Ohms)

7.7

0.3

mm

20

PZT503

mm

20

mm

Fréquence (MHz)

(b)

Fig. 3.16 - Variation de l'impédance en fonction de la fréquence : (a) Partie réelle (ou
résistance) ;(b) Partie imaginaire (ou réactance)

3.3.3.3 Validation des résultats de simulation

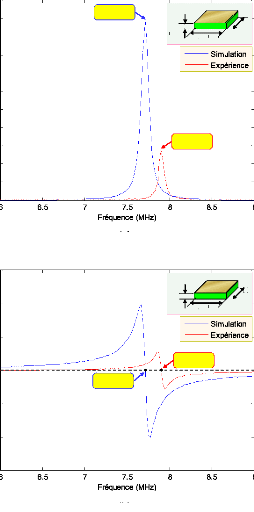
(a)

(c)

7.7 MHz

0.3

mm

7.9 MHz

20

PZT503

mm

20

mm

7.7 MHz

imulati

0.3

mm

7.9 MHz

20

PZT503

mm

20

mm

Afin de vérifier la validité des résultats de simulation précédents, nous avons exploité les résultats expérimentaux donnés dans la référence [85] et effectué une comparaison entre les courbes expérimentales de l'impédance et celles issues de la simulation (cf. figure 3.17). On peut observer une bonne correspondance entre les positions de fréquences d'antirésonances.

3.3.3.4 Paramètres utilisés pour la simulation

Les différents paramètres utilisés pour la simulation sont résumés dans les tableaux cidessous :

Céramique piézoélectrique
de type < PZT503 "

Ligne de transmission

Gains des sources contrôlées

Paramètre

	Valeur	Unité
a1	20×10^-3	m
a2	20×10^-3	m
a3	0.3×10^-3	m
A	4×10-4	m2
ñ	7.8×10^3	kg.m^-3
????	4622.5	m/s
fa	7.7	MHz
h33	5.91×10^9	V/m
S å33	4.69×10^-9	F.m^-1
C0	6.26	nF
Qm	75	-
L	3.12	H
C	15	nF
R	2.01	MÙ
G	0	s
F1	37	V.F/m
F2	5.91×10^9	V/m
E1	1	-
R1	1	kÙ
C1	1	F

Tab. 3.4 - Paramètres du transducteur ultrasonore piézoélectrique

	Paramètre	Valeur	Unité
Milieu avant < air "	Zf	0.00043	Mrayl
	Rf	0.17	Ù
Milieu arrière < air "	Zb	0.00043	Mrayl
	Rb	0.17	Ù

Tab. 3.5 - Paramètres des milieux avant et arrière

Paramètre		Valeur	Unité
Ve (tension sinusoïdale)	Amplitude : VAMPL	7.5	V
	Fréquence : FREQ	7.7	MHz
	Offset : VOFF	0	V
	AC	1	V
Re		50	Ù

Tab. 3.6 - Paramètres du circuit d'excitation électrique

3.4 Conclusion

Pour pouvoir caractériser le transducteur ultrasonore piézoélectrique, la détermination de ses fréquences de résonances et d'antirésonances à partir du tracé de son impédance électrique devient nécessaire. À cet effet, dans ce chapitre, le tracé de l'impédance électrique est obtenu par deux méthodes : par simulation du modèle unidimensionnel et par utilisation d'un circuit PSPICE. Les résultats de simulation sont ensuite validés. Une bonne correspondance est constatée entre la simulation et l'expérience.

Ainsi, dans ce chapitre, nous avons simulé le modèle de l'impédance électrique avec pertes du transducteur et identifié les paramètres de son schéma électrique équivalent simplifie.

Chapitre 4

Modélisation tridimensionnelle d'un transdu-

cteur ultrasonore piézoélectrique

Sommaire

4.1 Introduction . 69

4.2 Hypothèses générales .. 70

4.3 Expression tridimensionnelle de l'impédance électrique d'une céramique

piézoélectrique 72

4.3.1 Céramique piézoélectrique de forme parallélépipédique . 72

4.3.2 Céramique piézoélectrique de forme cylindrique .. 74

4.3.3 Discussion . 76

4.4 Simulation de l'impédance électrique d'une céramique piézoélectrique 76

4.4.1 Résultats de simulation . 76

4.4.2 Validation du modèle tridimensionnel de l'impédance électrique

d'un disque céramique .. 79

4.5 Conclusion 80

4.1 Introduction

Les modèles unidimensionnels sont très utilisés pour déterminer le comportement des transducteurs ultrasonores piézoélectriques utilisés en médecine notamment en imagerie médicale et ont conduit au développement considérable de l'échographie ultrasonore. L'amélioration de la qualité des images obtenues par cette technique est liée en particulier à celle des transducteurs utilisés [101]. Toutefois le couplage des modes en épaisseur et latéraux (ou radiaux) fait apparaître des images fantômes ou artefacts qui ne peuvent être interprétées qu'en faisant appel à des modèles bi-ou tridimensionnels. Les méthodes numériques (méthode des éléments finis par exemple) permettant de déterminer tous les modes de vibrations d'une céramique piézoélectrique sont très efficaces et donnent de bons résultats. En contrepartie, elles sont très lourdes et ne donnent pas aisément une vision synthétique de l'influence des différents paramètres. Seuls les modèles analytiques permettront de pallier ces inconvénients.

La céramique piézoélectrique est l'élément principal constituant le transducteur et sa caractérisation tensorielle (i.e. la détermination des ses paramètres : diélectriques, élastiques et piézoélectriques) nécessite habituellement l'utilisation de plusieurs échantillons dont la forme et les dimensions sont définies dans les normes IEEE [102,103]. La réalisation de ces échantillons est une opération longue et bien qu'ils proviennent du méme lot, il peut, lors de la polarisation, se produire une petite dispersion des résultats. Il serait plus judicieux de pouvoir déterminer tous les paramètres à partir d'un méme échantillon. Les modèles unidimensionnels décrits dans les normes supposant que les modes de vibration sont découplés ne permettent pas de réaliser la caractérisation complète au moyen d'un seul échantillon, car pratiquement il existe des couplages dus à la fois aux effets piézoélectriques et élastiques par effet de Poisson. Dans ce cas, la modélisation unidimensionnelle ne s'applique plus.

La modélisation tridimensionnelle que nous allons présenter dans ce chapitre permet de surmonter les difficultés précédentes. Elle fournit l'ensemble des modes de vibration de type longitudinale relatifs à une céramique piézoélectrique de forme donnée : parallélépipédique ou cylindrique et conduit à des expressions des impédances électriques applicables à toutes les fréquences. Celles.ci se réduisent aux expressions simplifiées unidimensionnelles lorsque sont introduites les conditions de vibration unidimensionnelle. De plus, la modélisation tridimensionnelle proposée reposant sur des hypothèses indépendantes du mode et de la géométrie considérés, fait intervenir pour une géométrie donnée, l'ensemble des paramètres liés aux ondes de type longitudinal. Il est par exemple possible à partir d'un disque céramique d'obtenir les quatre constantes élastiques à

induction constante (c11 ?? , c12 ?? , c13 ?? et c33 ?? ).

4.2 Hypothèses générales

Contrairement aux modèles unidimensionnels pour lesquels les hypothèses simplificatrices varient avec le mode et la géométrie considérés (cf. annexe D), les modèles tridimensionnels utilisent les mêmes hypothèses pour les géométries : parallélépipédique (plaque ou barreau) et cylindrique (disque ou cylindre) (cf. tableau 4.1). Elles se rapportent l'une au type d'onde se propageant dans les matériaux piézoélectriques et l'autre aux conditions aux limites sur les faces latérales des échantillons [102,104] :

· La céramique piézoélectrique est sans pertes.

· La vibration globale de la céramique piézoélectrique s'effectue sous l'action de trois ondes planes couplées se propageant chacune selon un axe de coordonnées. Les couplages s'effectuent par l'intermédiaire des coefficients de Poisson et les paramètres piézoélectriques de la céramique. Cette hypothèse entraîne l'absence de vibrations de cisaillement et on peut alors prendre en compte l'ensemble des paramètres relatifs aux modes longitudinaux. Tout se passe finalement comme si trois modes pistons étaient couplés par les constantes élastiques et piézoélectriques de la céramique. Par suite, tous les points d'une face vibrent en phase et les déplacements correspondants sont indépendants des deux autres coordonnées, soit :

u1 = U1 (x1) _exp (jcut)

u2 = U2 (x2) _exp (jcut) (4.1)

u3 = U3 (x3) exp (j cut)

· Du fait de la propagation d'ondes planes selon les axes de coordonnées, les termes d'indices croisés (13,31 ou 23,32 ou 12,21) du tenseur des déformations sont nuls : S4 = S5 = S6 = 0. Il s'ensuit que les composantes du tenseur des contraintes correspondant au cisaillement sont aussi nulles : T4 = T5 = T6 = 0.

· Les faces latérales sont libres quelle que soit la géométrie des échantillons, ce qui n'est pas toujours le cas pour les modèles-unidimensionnels :

Tij nj = 0 (4.2)

· Les déplacements s'effectuant toujours parallèlement à eux-memes, il n'y a pas de distorsion des lignes de champ électrique. Les composants E1 et E2 du champ électrique sont donc consentement nulles soit : E1 = E2 = 0 Vxi .

· Du fait de l'écriture de u1 et u2 on a 8ui/8xj = 0 quand i * j et puisque E1et E2 sont nuls on aura aussi D1 = D2 = 0 dans le matériau. Par suite la relation de Gauss ( divD = 0) se réduira à 8D3/8x3 = 8[D0 exp (jcut)]/8x3 = 0 sera constante et

égale à D0 .

· La mise en oscillation de la céramique piézoélectrique est réalisée par l'application d'une différence de potentiel sur les électrodes déposées sur les faces supérieures et inférieures perpendiculaires à l'axe de polarisation x3 ou z :

??3 = ??0exp ??????) (4.3)

Les conditions de fonctionnement portant sur les déplacements et sur l'induction nous les choisirons comme variables indépendantes. Sous forme matricielle les équations de la piézoélectricité (cf. tableau 1.1) seront [101]:

??1 ??2 ??3 ??4 ??3

= ??11^????1 + ??12^????2 + ??13^????3 - h31??3 = ??12^????1 + ??11^?? ??2 + ??13^????3 - h31??3 = ??13^????1 + ??13^????2 + ??33^????3 - h33??3 = ??5 = ??6 =^0; ??4 = ??5 = ??6 =^0 = -h31^??1 + ??2) - h33??3 + ??33????3 ??1 = ??2 = 0; ??1 = ??2 = 0

(4.4) (4.5)

Geometrie

Hypothèses

Résultats

Mécaniques

Electriques

V i tesse

Permittivite

N.0^,00^,1 . 1^,401 WI 1^,1. de coup! age

Plaque rectangul ai re a1,a2,a3 qUQIconques

??1, ??1, ??4 ??4

??2, ??3 ??2, ??3 = ??5 = ??5

? 0 ? 0 = ??6 = ??6

= =

0 ^0

??1 = ??1 = ? ??1,

??2 = 0 ??2 = 0 ??2 ??3 ? 0, ??3

?

0

2 ????3 ???? 2

= =

??33 ??

??33 ??

????^2 2

???? = =

2 ~33 2 ~31

?? ??33

Di sque ou cyl i ndre a,a3 quel conques

????, ????, ??4 ??4

????, ???? ????, ???? = ??5 = ??5

? 0 ? 0 = ??6 = ??6

= =

0 ^0

???? = ???? = ? ??, ??

???? = 0 ???? = 0 ??3 ? 0, ??3

?

0

2 ???? 2

????3 = =

?? ??33

??33 ??

????^2 2 ????

= =

2 ~33 2 ~31

?? ??33

Tab. 4.1 - Caractérisation tridimensionnelle: hypothèses et principaux résultats [102]

4.3 Expression tridimensionnelle de l'impédance électri-

que d'une céramique piézoélectrique

4.3.1 Céramique piézoélectrique de forme parallélépipédique

Considérons la céramique piézoélectrique de la figure 4.1.

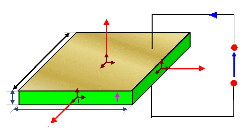
x3

a1

T4

T5

T6

T3

T4

T2

x2

V3

a3

T5 T6_T

P +

-

1

a2

I3

x1

Fig. 4.1 - Dimensions et système de coordonnées d'une plaque céramique

D'après [101], l'expression (4.1) peut s'écrire :

u1 = U1sin(ax1) exp (jcut)

u2 = U2sin(ax2) exp (jcut) (4.6)

u3 = U3sin(a3x3) exp (jcut)

avec a = cu/vp est le nombre d'onde dans la céramique selon une direction quelconque dans le plan « x1-x2 ».

Les différentes conditions aux limites mécaniques sur les faces permettent de calculer les valeurs des amplitudes : U1, U2 et U3 des ondes en fonction des coefficients élastiques et piézoélectriques.

Sous la forme développée la relation (4.2) s'écrit:

· T1 = 0 , pour x1 = #177;a1/2 et x2 et x3 arbitraires, mais x2 E [--a2/2, a2/2 et x3 E [--a3/2, a3/2 ].

· T2 = 0 , pour x2 = #177;a2/2 et x1 et x3 arbitraires, mais x1 E [--a1/2, a1/2 et x3 E [--a3/2, a3/2].

· T3 = 0 , pour x3 = #177;a3/2 et x1 et x2 arbitraires, mais x1 E [--a1/2, a1/2 et x2 E [--a2/2, a2/2].

En reportant les relations (4.6) dans les expressions (4.4), les polarisations des diverses ondes sont :

??1 =

??2 =

??3 =

avec

??1 =

??3 =

??1??0

??cos ????1/2)

(4.7)
(4.8)

??1??0

??cos ????2/2)

??3??0

??3cos ??3??3/2)

??

~31??33 ?? - ~33??13

?? 2

??11 ?? + ??12 ?? ~??33 ?? - 2??13

??

~33 ??11 ?? + ??12 ?? ~ - ²31??13

?? 2

??11 ?? + ??12 ?? ~??33 ?? - 2??13

En reportant les relations (4.6) dans la relation (4.5) et en prenant la ligne de champ correspondant à ??1 = ??2 = 0, on obtient :

1

+

????1

2 ~

?? ??3 _~??3 - ~33 + ??33 ?? ??3 (4.9)

????2 ????3

2 ~

cos

??3 = -~31??1

cos

1

En intégrant le champ électrique on obtiendra le potentiel « ??3 » appliqué d'où :

[??3 = ??33^?? - h31??1

1 1 ~ ??3 - 233??3 tan ??3??3 + cos^????1 cos ????2 2 ~ ??3 2 ~ 2 ~

??3 (4.10)

La charge totale sur les électrodes s'écrit [101]:

?? = ??1??2??3 (4.11)

Le courant électrique est lié à la charge totale sur les électrodes par la relation :

?? ??

??3 = = ????1??2????3 (4.12)

????

Par suite, l'expression de l'impédance électrique «??» de la céramique piézoélectrique sera :

1 - 2 ~31??13 ??

?? (4.13)

~31 ~33(??11 ?? + ??12 ?? )

??3 ?? =

1 1 - ~31??33 ?? - ~33??13

=

??3 ????0?? ?? 2

??11 ?? + ??12 ?? ~??33 ?? - 2??13

??

?? ~ ?? + ???? 2

??33 ??13 ?? 2

1 - 2 ??

??11 ?? + ??12 ?? ~??33

avec

1 1

L=

cos

cos

aa2)
2

aa1) + 2

tan

E=

a3

a3a3\

2 )

??3a3

2

S a1 a2

C0 = 633

(4.14)

L'expression de l'impédance électrique (relation 4.13) montre que le couplage des modes se manifeste par la présence de deux termes : l'un est relatif aux modes latéraux (L) et l'autre au mode en épaisseur (E).

Les fréquences d'antirésonance des modes latéraux et en épaisseur sont respectivement données par les relations :

VP

fL_i = (2n + 1) 2a ; i = 1 ou 2, n E N (4.15)

i

fE = (2n + 1)

VP3 ; n E N (4.16) 2a3

4.3.2 Céramique piézoélectrique de forme cylindrique

Considérons la céramique piézoélectrique de la figure 4.2.

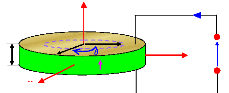
X3 z

I3

a3

X2

V3

a

r

P + -

X1

Fig. 4.2 -- Dimensions et système de coordonnées d'un disque céramique

Les hypothèses précédentes sont les mêmes. Seules changent les écritures des déplacements afin de tenir compte de la géométrie particulière de la céramique piézoélectrique. Dans le cas de vibrations radiales, on a [104]:

où (r, e, z) sont les cordonnées cylindriques.

La loi de newton est donnée par la relation [101] :

??T??j = ?? ??xj

a2ui at2 (4.18)

En introduisant les équations (4.17) dans l'équation (4.18), on obtient :

u_r = U_r?? 1(????)exp (j cut)

u_z = U_z sin(a3a3) exp (j cut) (4.19)

ue = 0

En reportant les expressions des déplacements selon r et z dans les relations (4.4) et (4.5), l'expression de l'impédance électrique « Z » de la céramique piézoélectrique sera :

Z=	1 j??0cu[^1	?? h31	h31 C^133 h33 C1^D3 R 2 ac/C33 43 aa0(aa)	h33		fl33 ?? ah33 h31C13D???? 0(????) El (4.20) ????C33^D 43 2????0(????)

avec

R = (70(aa)

tan

a3 a3

2 J

E=

a3 a3

(4.21)

2

c0 = Eg3n- a3

_a2

3a = aC ⁱf1a0 (aa) CD _a CD

12

- (aa)

et a0(aa) et a1(aa) sont respectivement les fonctions de Bessel de première espèce d'ordres 0 et1 de la variable « aa ».

L'expression de l'impédance électrique (relation 4.20) comporte deux termes : l'un est relatif aux modes radiaux (R) et l'autre au mode en épaisseur (E).

Les fréquences d'antirésonance pour le mode en épaisseur ont la meme expression que pour la céramique piézoélectrique en forme de plaque (cf. équation (4.16)).

4.3.3 Discussion

Du fait des hypothèses générales utilisées, les résultats de la modélisation tridimensionnelle (cf. tableau 4.1) sont valables quelques soient les dimensions de l'échantillon céramique :

· Pour la géométrie parallélépipédique, les résultats sont applicables aux cas d'une plaque ou barreau.

· Pour la géométrie cylindrique, les résultats sont applicables aux cas d'un disque ou cylindre.

De plus, ces résultats mettent clairement en évidence l'influence des couplages piézoélectrique ( _h31 ) et élastique ( c12 ?? , c13 ?? ) sur le comportement de la céramique piézoélectrique et montrent que les vitesses acoustiques et permittivités ne dépendent pas de la géométrie de l'échantillon.

Contrairement aux modèles unidimensionnels qui étaient applicables seulement autour d'une fréquence de résonance particulière, les modèles tridimensionnels sont valables à toutes les fréquences.

Remarquons que les expressions (4.13) et (4.20) se simplifient lorsque l'on considère que certains coefficients élastiques et piézoélectriques sont nuls. On retrouve alors les expressions unidimensionnelles correspondantes. Ce qui montre, a contrario, que pour établir les relations simplifiées, il faut supposer nuls les coefficients correspondants.

· Si on suppose c12 ??= c13 ??= 0 et h31 = 0, les expressions (4.13) et (4.20) se réduisent et on retrouve les expressions (3.4) et (D.2).

· Si on suppose c33 ?? = 0 et h33 = 0, l'expression (4.20) se réduit et on retrouve l'expression (D.1).

4.4 Simulation de l'impédance électrique d'une cérami-

que piézoélectrique

Les modèles unidimensionnels permettent de situer les fréquences relatives à un mode particulier alors que les modèles tridimensionnels fournissent l'ensemble du spectre de fréquences correspondant à une géométrie donnée (plaque, barreau, disque ou cylindre). Afin de vérifier cette propriété, nous avons effectué une simulation des expressions tridimensionnelles des impédances électriques pour une céramique piézoélectrique de type PZT802.

4.4.1 Résultats de simulation

4.4.1.1 Céramique de forme parallélépipédique

Les figures 4.3 et 4.4 montrent les évolutions tridimensionnelles des impédances électriques relatives à respectivement une plaque et un barreau. Nous constatons que, par rapport au modèle unidimensionnel qui ne fait apparaitre que les fréquences relatives au mode en épaisseur, le modèle tridimensionnel fait apparaitre en plus de ces fréquences, les fréquences relatives aux modes latéraux.

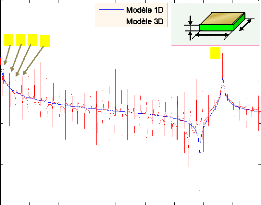
L1 L2 L3 L4

0.3

mm

20

E1

PZT802

mm

20

mm

Fig. 4.3 - Courbe simulée de l'impédance électrique d'une plaque céramique

E1

L1

E2

15mm

5mm

L2

PZT802

5mm

Fig. 4.4 - Courbe simulée de l'impédance électrique d'un barreau céramique

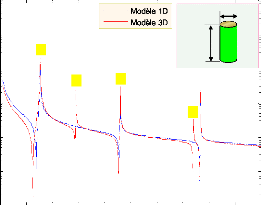
E1

R1

E2

15mm

R2

5mm

PZT802

4.4.1.2 Céramique de forme cylindrique

Les figures 4.5 et 4.6 montrent les évolutions tridimensionnelles des impédances électriques relatives à respectivement un disque et un cylindre. Nous constatons que, par rapport au modèle unidimensionnel qui ne fait apparaitre que les fréquences relatives au mode en épaisseur, le modèle tridimensionnel fait apparaitre en plus de ces fréquences, les fréquences relatives aux modes radiaux.

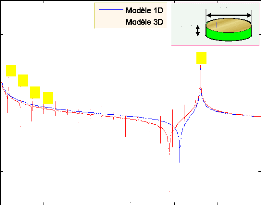
R1

R2

R3 R4

1mm

E1

16mm

PZT802

Fig. 4.5 - Courbe simulée de l'impédance électrique d'un disque céramique

4.4.2 Validation du modèle tridimensionnel de l'impédance élec- trique d'un disque céramique

Afin de valider notre étude, nous avons exploité les courbes expérimentales de l'impédance électrique d'un disque céramique de type « PZT802 » données dans les références [105,106].

La figure 4.7 montre les évolutions théorique et expérimentale de l'impédance électrique. La comparaison entre les deux courbes montre que notre modèle permet de retrouver avec un bon accord les positions relatives de fréquences d'antirésonances radiales et en épaisseur. Par contre, le modèle étant sans pertes, les amplitudes exactes des pics sont erronées. Remarquons ainsi que la courbe expérimentale de l'impédance présente d'autres modes de résonances qui peuvent provenir de vibrations de cisaillement. Ces modes ont été négligés dans notre modélisation et n'apparaissent pas dans notre modèle.

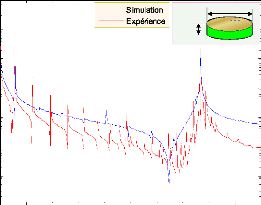
3mm

25mm

PZT802

Fig. 4.7 - Courbes simulée et expérimentale de l'impédance électrique d'un

Expérence

disque céramique

Les valeurs de fréquences d'antirésonances expérimentales et théoriques sont comparées et reportées dans le tableau 4.2. Nous remarquons que les valeurs des fréquences d'antirésonance théoriques et expérimentales sont cohérentes.

Fréquences (kHz)	Théorie	Expérimentale		Erreur relative (%)	fR1
58.6	52.3	12		fR2
151.8	122.8	23		fR3
237.4	193.3	22		fR4
325.1	242.1	34		fE1
767.6	770.2	0.3

Tab. 4.2 - Comparaison des valeurs de fréquences d'antirésonance théoriques et
expérimentales

4.5 Conclusion

Dans ce chapitre, après une description des hypothèses générales de la modélisation tridimensionnelle, les expressions des impédances électriques pour les échantillons céramiques de forme : parallélépipédique (plaque et barreau) et cylindrique (disque et cylindre) sont données. Ensuite, ces expressions ont fait l'objet de simulations, afin de montrer l'apport de la modélisation tridimensionnelle par rapport à la modélisation unidimensionnelle. Enfin, pour valider notre étude, une comparaison du modèle de l'impédance électrique d'un disque céramique de type PZT802 aux résultats expérimentaux est effectuée.

Le travail de recherche présenté dans ce mémoire traite la modélisation et simulation d'un transducteur ultrasonore piézoélectrique.

Le premier chapitre a porté tout d'abord sur des rappels concernant la piézoélectricité qui ont permis une meilleure compréhension de ce phénomène et de ces grandeurs physiques. Ensuite, un tour d'horizon des différentes familles de matériaux piézoélectriques disponibles à ce jour est présenté, suivi d'une description de modes de déformation d'un matériau piézoélectrique. Enfin, quelques applications des matériaux piézoélectriques sont présentées : Transformateurs piézoélectriques, chaussures piézoélectriques, actionneurs bilames et imprimante à jet d'encre.

Dans le deuxième chapitre, les propriétés des ultrasons et leurs interactions avec la matière sont décrites. Puis les différents types de transducteurs ultrasonores sont présentés : transducteur piézoélectrique, transducteur capacitif, transducteur piézorésistif et transducteur impulsion-écho.

Le troisième chapitre est consacré à la modélisation unidimensionnelle et simulation avec PSPICE d'un transducteur ultrasonore piézoélectrique. Dans la première partie de ce chapitre, le modèle unidimensionnel de l'impédance électrique sans pertes du transducteur est simulé. Ensuite, trois schémas électriques équivalents du transducteur ont été décrits. Enfin, après la simulation de l'impédance électrique avec pertes, les paramètres du schéma électrique équivalent simplifié du transducteur sont identifiés à partir du tracé de son admittance électrique dans le diagramme de Bode et dans le plan de Nyquist. Dans la deuxième partie, l'impédance électrique du transducteur est simulée avec PSPICE.

Les modèles unidimensionnels décrits dans le chapitre précédent supposent que les modes de vibration (modes latéraux ou radiaux et mode en épaisseur) d'une céramique piézoélectrique sont découplés. Or, en effet, il existe des couplages dus aux effets élastiques et piézoélectriques. Le quatrième et dernier chapitre présente une modélisation analytique tridimensionnelle pour les échantillons céramiques de forme : parallélépipédiques (plaque et barreau) et cylindriques (disque et cylindre), prenant en considération les couplages entre les modes de vibration. De plus, elle fournit l'ensemble du spectre de fréquences

correspondant à une céramique piézoélectrique et conduit à des expressions tridimensionnelles qui se réduisent à celles déduites de la modélisation unidimensionnelle lorsque certains coefficients élastiques et piézoélectriques sont supposés nuls.

Concernant la validation de nos résultats de simulations, les résultats expérimentaux (courbes de l'impédance électrique) donnés dans les références [85,105,106] sont utilisés. Une bonne correspondance est observée entre la simulation et l'expérience.

Finalement, les perspectives à envisager au terme de cette étude sont nombreuses et alléchantes :

· Conception de transducteurs ultrasonores piézoélectriques pour l'application en imagerie médicale et le contrôle non destructif.

· Modélisation bidimensionnelle de transducteurs ultrasonores piézoélectriques avec PSPICE.

· Modélisation tridimensionnelle de transducteurs ultrasonores piézoélectriques en utilisant l'expression l'impédance électrique universelle. Cette dernière est valable pour toutes les géométries : plaque, barreau, disque et cylindre. Ainsi, elle permet d'obtenir les fréquences de résonances et d'antirésonances relatives aux modes de vibration : latéraux ou radiaux et en épaisseur d'un matériau piézoélectrique de façon précise. De plus, à partir de l'expression tridimensionnelle de l'impédance, les expressions unidimensionnelle et bidimensionnelle peuvent être déduites. D'après la référence [108], le modèle de l'impédance électrique universelle nous donne des résultats au moins 50 % meilleurs que ceux donnés par les autres modèles décrits dans la littérature.

· Modélisation numérique tridimensionnelle de transducteurs ultrasonores piézo- électriques en utilisant la méthode des éléments finis «FEM» et méthode des éléments frontières «BEM».

Bibliographie

[1] A. Kaddour, «Etude, modélisation et visualisation des champs acoustique rayonnés par des transducteurs électroacoustiques circulaires et sphériques», Thèse de doctor- at, Université des Sciences et de la Technologie d'Oran - Mohamed Boudiaf, Juin 2004.

[2] H. -s. Lee, «Etude et réalisation de sources acoustiques de puissance en composite piézoélectrique 1.3 pour applications thérapeutiques », Thèse de doctorat, Institut National des Sciences Appliquées de Lyon, France, Février 2003.

[3] J. Kocbach, «Finite element modeling of ultrasonic piezoelectric transducers: influ- ence of geometry and material parameters on vibration, response functions and radi- ated field», dr. scient thesis, University of Bergen, September 2000.

[4] H. Jensen, «Calculations for piezoelectric ultrasonic transducers», Lic-Techn thesis, Technical University of Denmark, Roskilde, Denmark, May 1986.

[5] P. Maréchal, «Transducteurs mono-éléments pour l'imagerie ultrasonore haute rés- olution : modélisation, réalisation et caractérisation», Thèse de doctorat, Université de Tours, France, Décembre 2004.

[6] L. Rufer, « Transducteurs électroacoustiques et ultrasonores: des macro- aux micro- systèmes », Habilitation à Diriger des Recherches, Université Joseph Fourier de Grenoble, France, Novembre 2007.

[7] I. R. Sinclair, «Sensors and transducers», Newnes, Great Britain, 2001.

[8] K. Jezzine, «Approche modale pour la simulation globale de contrôles non-destruct- ifs par ondes élastiques guidées», Thèse de doctorat, Université Bordeaux 1, France , Novembre 2006.

[9] J. De Rosnay, «Les matériaux intelligents», 278^e conférence de l'Université de Tous Les Savoirs, Octobre 2000.

[10] J. S. Harrison, Z. Ounaies, « Piezoelectric polymers», Phosphorus-containing pol- ymers and oligomers, Vol. 3, Encyclopedia of Polymer Science and Technology, John Wiley & Sons, New York, USA, pp. 474-498.

[11] F. Giraud, «Modélisation causale et commande d'un actionneur piézoélectrique à onde progressive», Thèse de doctorat, Université Lille I, France, Juillet 2002.

[12] S. Le Dren, «Elaboration de couches épaisses piézoélectriques déposées sur substra- ts pour des applications microtechniques», Thèse de doctorat, Institut National des Sciences Appliquées de Lyon, France, Septembre 2000.

[13] A. R. Streett, «Preliminary finite element modeling of a piezoelectric actuated mari- ne propulsion fin», Master of science thesis, Rochester Institute of Technology, New York, USA, September 2006.

[14] PIEZOCRYST advanced sensors GMBH, www.piezocryst.com, «Introduction to pi- ezoelectric sensors», Austria, August 2005.

[15] R. Periasamy, « Shape control of composite structures with optimally placed piézo- electric patches», Master of science thesis, University of Waterloo, Ontario, Canada, 2008.

[16] Measurement Specialties, www.msiusa.com, «Piezo film sensor-technical manual», April 1999.

[17] L. Delmas, «Etude et réalisation de capteurs à sortie fréquentielle en orthophosphate de gallium (GaPO4)», Thèse de doctorat, Université de Franche-Comté, France, Sep- tembre 2005.

[18] H. Frayssignes, «Etude des effets non-linéaires et des pertes dans les moteurs ultras- onores : Introduction au problème de couplage mécanique entre les voies», Thèse de doctorat, Institut National des Sciences Appliquées de Lyon, France, Novembre 2001.

[19] M. Wilm, «Etude et réalisation de transducteurs composites pour l'imagerie acoust- ique et le contrôle non-destructif», Thèse de doctorat, Université de Franche-Comté, France, Novembre 2004.

[20] A. V. Carazo, «Novel piezoelectric transducers for high voltage measurements», do- ctoral thesis, Universitat politècnica de catalunya, Barcelona, Spain, January 2000.

[21] James R. Phillips, «Piezoelectric technology primer», Albuquerque, New Mexico.

[22] C. Millon, «Contribution à l'étude de procédés de réalisation de structures métal/ PZT/métal sur silicium pour microsystèmes piézoélectriques», Thèse de doctorat, Institut National des Sciences Appliquées de Lyon, France, Juillet 2003.

[23] N. S. Almind, S. H. Brodersen, «MEMS PZT based accelerometer: design, fabric- ation and characterization», Bachelor thesis, Technical University of Denmark, Den- mark, October 2007.

[24] E. Gaboriaud, «Etude des résonateurs piézoélectriques dans le domaine des micoon- des : application au filtrage», Thèse de doctorat, Université de Limoges, France, Oc- tobre 2004.

[25] M. Hubain, «Capteurs de pression et de force», http://perso/orange.fr/michel.hubain /capteurs/phys/chap-p3.htm. (Consulté le 12.04.2007).

[26] G. Fleury, C. Gondard, «Improvements of ultrasonic inspections through the use of piezocomposite transducers», 6^th European Conference on Non Destructive Testings, France, May 1995.

[27] Wenkang Qi, Wenwu Cao, «Finite element analysis and experimental studies of the thickness resonance of piezocomposite transducers», Ultrasonic imaging, Vol. 18, 1996.

[28] N. J. Renault, C. Martelett, P. Clechet, «Capteurs chimiques et biochimiques», Te- chniques de l'Ingénieur, Doc. R 420 ; P 360, France.

[29] C. A. Paget, «Active health monitoring of aerospace composite structures by embe- dded piezoceramic transducers», Doctoral thesis, Royal Institute of Technology, St- ockholm, Sweden, November 2001.

[30] J. M. Haussonne, «Céramiques pour l'électronique et l'électrotechnique», Presses Polytechniques et Universitaires Romandes, Lausanne, Suisse, 2002.

[31] A. Aydi, «Elaboration et caractérisations diélectriques de céramiques ferroélectriqu- es et/ou relaxeur de formule MSnO3-NaNbO3 (M = Ba, Ca) », Thèse de doctorat, Faculté des Sciences de Sfax, Tunisie, Mars 2005.

[32] A. Faiz, «Amortissement vibratoire et anéchoïsme par traitement non-linéaire d'élé- ments piézoélectriques», Thèse de doctorat, Institut National des Sciences appliqués- de Lyon, France, Mai 2006.

[33] C. Tilhac, «Développement d'architectures de filtres à base de résonateurs à ondes acoustiques de volume et contribution à l'intégration dans une technologie avancée silicium industrielle pour des applications radiofréquences», Thèse de doctorat, Uni- versité de Franche-Comté, France, Juillet 2007.

[34] J. Fraden, « Handbook of modern sensors : physics, designs, and applications», Springer-Verlag, New York, USA, 2004.

[35] P. Paruch, «Atomic force microscopy studies of ferroelectric domains in epitaxial PbZr0.2Ti0.8O3 thin films and the static and dynamic behavior of ferroelectric domain walls», Doctoral thesis, Université de Genève, Genève, Switzerland, 2003.

[36] B. Fu, « Piezoelectric actuator design via multiobjective optimization methods »,
Doctoral thesis, Universität Paderborn, Germany, June 2005.

[37] J. F. Lopez, «Modeling and optimization of ultrasonic linear motors», Doctoral th- esis, Ecole Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, November 2006.

[38] S. O. Reza Moheimani and Andrew J. Fleming, « Piezoelectric transducers for vibration control and damping», Springer-Verlag, London, UK, 2006.

[39] Saint-Gobain Quartz, www.quartz.saint-gobain.com, «Céramique piézoélectriques», France, 2004.

[40] T. L. Jordan, Z. Ounaies, «Piezoelectric ceramics characterization», ICASE, NASA Langley Research Center, Hampton, Virginia, USA, September 2001.

[41] M. Malhis, «Contrôle actif modal flou des rotors flexibles par plan d'action piézo- électrique », Thèse de doctorat, Institut National des Sciences Appliquées de Lyon, France, Décembre 2002.

[42] L. Garbuio, « Etude du phénomène de lubrification électroactive à l'aide d'actionn- eurs piézoélectriques : application à la réduction des forces de frottement sec dans dans un moteur à combustion interne», Thèse de doctorat, Institut National Polytec- hnique de Toulouse, France, Juin 2006.

[43] Z. Ghalmi, «Contribution au développement d'un capteur ultrasonique pour mesurer l'épaisseur de la glace», Mémoire de la maîtrise en ingénierie, Université du Québec, Chicoutimi, Canada, Mars 2006.

[44] G. Sebald, «Nouveaux monocristaux à forte conversion piézoélectrique: croissance, modélisation et caractérisation », Thèse de doctorat, Institut National des Sciences Appliquées de Lyon, France, Septembre 2004.

[45] N. G. Ledermann, « Piezoelectric acoustic sensors and ultrasonic transducers based on textured PZT thin films», Doctoral thesis, Ecole Polytechnique Fédérale de lausa- nne, Lausanne, Switzerland, 2003.

[46] J. Brünahl, «Physics of piezoelectric shear mode inkjet actuators», Doctoral thesis, Royal Institute of Technology, Stockholm, Sweden, 2003.

[47] C. Viguier, « Contribution au développement d'actionneurs électroactifs pour l'assi- stance circulatoire : application à la mise au point d'une fonction antithrombotique», Thèse de doctorat, Institut National Polytechnique de Toulouse, France, Décembre 2005.

[48] M. Kaltenbacher, «Numerical simulation of mechatronic sensors and actuators», Springer-Verlag, Berlin Heidelberg, Germany, 2007.

[49] A. Benayad, «Matériaux monocristallins à forte activité piézoélectrique: élaboration , caractérisation et application», Thèse de doctorat, Institut National des Sciences Appliquées de Lyon, France, Décembre 2005.

[50] A. M. Abdel Fattah, M .G. S .Ali, N. Z. Elsyed, Gharieb. A. Ali, «Piezoceramic materials for ultrasonic probes», J. Solids, Vol. 28, No. 2, Egypt, 2005.

[51] E. Dieulesaint, D. Royer, « Ondes élastiques dans les solides », Masson, Paris, France, 1974.

[52] G. Asch, « Les capteurs en instrumentation industrielle », Bordas, Paris, France 1987.

[53] T. Omori, H. Makita, M. Takamats, K. Hashimoto, M. Yamaguchi, M. Sato, « Prep- aration of piezoelectric PZT micro-discs by sol-gel method», T.IEE Japan, Vol. 121- E, No.9, pp.496-500, 2001.

[54] P. Anbalagan, «Radiation damage of polymers in ultrasonic fields», Doctoral thesis, Rheinischen Friedrich-Wilhelms-Universität Bonn, Bonn, Germany, April 2008.

[55] C. Dutriez, «Corrélations entre les propriétés diélectriques et mécaniques des poly- mères ; influence de la température», Thèse de doctorat, Ecole Centrale de Lyon et Ecole Doctorale des Matériaux de Lyon, France, Octobre 2004.

[56] N. Noury, «Du signal à l'information : le capteur intelligent ; exemples industriels et en médecine», Habilitation à Diriger des Recherches, Université Joseph Fourier de Grenoble 1, France, Avril 2002.

[57] W. A. Smith, «The role of piezocomposites in ultrasonic transducers», IEEE procee- dings ultrasonics symposium, pp. 755-766, 1989.

[58] J. M. Gallière, P. Papet, L. Latorre, «A unified electrical SPICE model for pie- zoelectric transducers», IEEE, 978-1-4244-1567-0/07, pp. 138-142, 2007.

[59] F. Pigache, «Modélisation causale en vue de la commande d'un translateur piézoé- lectrique plan pour une application haptique», Thèse de doctorat, Université des Sciences et Technologies de Lille, France, Mars 2005.

[60] W. Huang, «Design of a radial mode piezoelectric transformer for a charge pump electronic ballast with high power factor and zero voltage switching», Master of sci- ence thesis, Virginia Polytechnic Institute and State University, Blacksburg, Virginia , USA, April 2003.

[61] S. Turri, G. Poulin, « Dispositifs électromécaniques permettant l'exploitation de l'énergie des mouvements humain», Colloque Energie portable : autonomie et intég- ration dans l'environnement humain (Journées Electrotechniques du Club EEA), Ca- chan, France, Mars 2002.

[62] B. Multon, S. Turri, M. Ruellan, D. Miller, H. Ben Ahmed, «Produire de l'énergie pour les appareilles électroniques portables grâce aux ressources disponibles dans l'environnement humain», AS n°106CNRS-STIC(Conception faible consommation) , Paris, France, Mai 2004.

[63] M. C. Belaid, «Unité d'entré/sortie et périphériques», Les Pages Bleues Sarl RIMS Raffor , Bouira, Octobre 2001.

[64] C. C. Domingues, «Conception de transducteurs acoustiques micro-usinés», Thèse de doctorat, Institut National Polytechnique de Grenoble, France, Avril 2005.

[65] A. Kassem, « Contributions à la faisabilité d'un système sur puce dédié à l'imagerie par ultrasons», Thèse de doctorat, Université de Montréal, Canada, Décembre 2004.

[66] D. Maillard, « Ondes élastiques dans les solides », Cours de vibrations et ondes, Université Paris7-Denis Diderot, France.

[67] P. B. Nagy, «Introduction to ultrasonics», 20-251-728, 2001.

[68] M. Ribault, «Caractérisation ultrasonore de lésions induites par ultrasons focalises de haute intensité», Thèse de doctorat, Université Claude Bernard - Lyon 1, France, Janvier 1999.

[69] J. E. Wilhjelm, O. T. Andersen, «Medical diagnostic ultrasound», Technical Unive- rsity of Denmark, Denmark, 2004.

[70] J. Johansson, «Microelectronics for the thumb-size ultrasound measurement system », Luleå University of Technology, Luleå, Sweden, 2004.

[71] E. Molz, D. Canny, E. Evans, «Ultrasonic velocity and attenuation measurements in high density drilling muds», Baker Hughes INTEQ , Houston, Texas, USA.

[72] K. K. Shung, « Diagnostic ultrasound: imaging and blood flow measurements », Taylor & Francis Group. LLC, USA, 2006.

[73] Panametrics, www.panametrics.com, « Technical notes », pp. 32-40.

[74] M. Wanin, «Evaluation non destructive de la qualité des matériaux», Technique de l'Ingénieur, Doc. M 4 130, France, Décembre 2001.

[75] M. Al Bahri, «Influence de la température sur le comportement statique et dynamiq ue des capteurs de pression capacitifs au silicium», Thèse de doctorat, Institut Nati- ional des Sciences Appliquées de Toulouse, France, Mai 2005.

[76] A. Chaehoi, «Conception et modélisation de MEMS monolithiques CMOS en tech- nologie FSBM: application aux accéléromètres», Thèse de doctorat, Université Mo- ntpellier II, Sciences et Techniques du Languedoc, France, Octobre 2005.

[77] J. -B. Bureau, «Conception, realisation de micro-capteurs de force à base de jauges piezoresistives pour la caracterisation mecanique d'assemblages cellulaires en milieu liquide», Thèse de doctorat, Universite des Sciences et Technologies de Lille, France , Decembre 2006.

[78] C. Malhaire, «Caracterisation et modelisation de microtransducteurs de pression à hautes performances integres sur silicium», Thèse de doctorat, Institut National des Sciences Appliquees de Lyon, France, Janvier 1998.

[79] Y. B. Gandole, S. P. Yawale, S. S. Yawale, « Simulation of pulser receiver system for ultrasonic measurments», International Journal of Pure and Applied Physics,

ISSN 0973-1776, Vol. 2, No. 2, pp.167-186, India, 2006.

[80] O. Guedes, « Generation et propagation ultrasonore», orland.guedes@freeir, septe- mbre 2005.

[81] K . W. Tay, « The analysis and design of film bulk acoustic-wave resonators», Doctoral thesis, National Cheng Kung University Tainan, Taiwan, China, January 2005.

[82] M. Engholm, «A narrowband ultrasonic spectroscopy technique for the inspection of layered structures», Technical Licentiate thesis, Uppsala University, Uppsala, Sweden, August 2006.

[83] K. Sadasing, «Transducteur piezoceramique large bande», Laboratoire d'acoustique appliquee, Ecole d'ingenieurs-HES, Genève, Suisse, 2001.

[84] J. David N. Cheeke, «Fundamentals and applications of ultrasonic waves», CRC Press LLC, USA, 2002.

[85] E. Dijkstra, «Ultrasonic distance detection in spinal cord stimulation», Doctoral thesis, University of Twente, Enschede, the Netherlands, February 2003.

[86] E. Dieulesaint, D. Royer, «Propagation et generation des ondes elastiques », Tech- nique de l'Ingénieur, Doc. E 3 210, France.

[87] S. Sherrit, S. P. Leary, B. P. Dolgin, Y. B-Cohen, «Comparison of the Mason and KLM equivalent circuits for piezoelectric resonators in the thickness mode», IEEE Ultrasonics Symposium, 1999.

[88] S. A. Morris, «Equivalent circuit modeling for thin disk and bar type piezoelectric transducers», Master of science thesis, the University of Tulsa, Ok, 1986.

[89] D. J. Powell, J. Mould, G. L. Wojcik, «Dielectric and mechanical absorption mec- hanisms for time and frequency domain transducer modeling», A preprint of an article to appear in the 1998 IEEE Ultrasonic Symposium Proceedings.

[90] T. Ritter, K. K. Shung, W. Cao, T. R. Shrout, «Electromechanical properties of thin strip piezoelectric vibrators at high frequency», Journal of Applied Physics,

Vol. 88, No. 1, pp.394-397, USA, July 2000.

[91] S. Sherrit, V. Olazábal, J. M. Sansiñena, X. Bao, Z. Chang, Y. Bar- Cohen, «

The use of piezoelectric resonators for the characterization of mechanical properties of polymers», Proceedings of the SPIE Smart Structures Conference, Vol. 4695, No. 35, San Diego, CA, March 2002.

[92] Morgan Electro ceramics, www.morganelectroceramics.com, «Technical informati- on: introduction to piezoelectric ceramics», USA, May 2001.

[93] D. Benbekrite, «Caractérisation d'un capteur piézoélectrique ultrasonore», Mémoire de magister, Université des Sciences et de la Technologie d'Oran-Mohamed Boudiaf , Juillet 1999.

[94] W. Szlabowicz, «Contribution au dimensionnement et à la réalisation d'actionneur Piézoélectrique à rotation de mode fort couple pour applications aéronautiques», thèse de doctorat, Institut National Polytechnique de Toulouse, France, Novembre 2006.

[95] W. M. Leach, «Controlled-Source analogous circuits and SPICE models for piezo- electric transducers», IEEE transactions on ultrasonics, ferroelectrics, and frequency control, Vol. 41, No. 1, pp. 60-66, January 1994.

[96] J. V. Deventer, T. Löfqvist, J. Delsing, «PSPICE Simulation of ultrasonic systems Systems», IEEE transactions on ultrasonics, ferroelectrics, and frequency control, Vol. 47, No. 4, pp. 1014-1024, July 2000.

[97] R. S. Dahiya, M. Valle, D. Caviglia, G. Metta, L. Lorenzelli, «Modeling of lossy piezoelectric polymers in SPICE», University of Genoa, Italy.

[98] J. V. Deventer, «Modeling an Ultrasonic Transducer with SPICE», In First annual conf. on CSEE», Luleå University of Technology, Sweden, May 2000.

[99] G. Asch, «Acquisition de données du capteur à l'ordinateur», Dunod, 1999.

[100] J. V. Deventer, «Material investigations and simulation tools towards a design strategy for an ultrasonic densitometer», Doctoral thesis, Luleå University of Tech- nology, Sweden, 2001.

[101] M. Brissaud, L. Eyraud, H. Kleimann, «Modélisation analytique tridimensionnelle des modes de vibrations des éléments céramiques piézoélectriques utilisés en image-

rie acoustique», Acustica, Vol. 66, No. 2, pp. 62-72, Juillet 1988.

[102] M. Brissaud, «Nouvelles procédures tridimensionnelles de caractérisation des mat- ériaux piézoélectriques», Colloque de physique, Colloque , supplément au No. 2, Tome 51, pp. 879-582, Février 1990.

[103] S. El Nachef, M. Brissaud, «Modélisation tridimensionnelle : identification et infl- uence du couplage sur les paramètres complexes des matériaux piézoélectriques», Journal de physique IV, Colloque Cl, supplément au Journal de physique III, Vol. 2, pp. 369-372, Avril 1992.

[104] M. Brissaud, L. Eyraud, H. Kleimann, «Modélisation analytique tridimensionnelle du comportement vibratoire d'un élément piézoélectrique», J. Acoustique, pp. 437- 448, Décembre 1989.

[105] Dragan Manèiæ, Violeta Dimiæ, Milan Radmanoviæ, «Resonance frequencies of PZT piezoceramic disks : a numerical approach», Facta Universitatis, Series: Mechanics, Automatic Control and Robotics, Vol. 3, No. 12, pp. 431-442, Yugoslavia, 2002.

[106] L. Peric, «Coupled tensors of piezoelectric materials state and applications», MP In- terconsulting: ultrasonics-sonochemistry-innovation, Switzerland, 2005.

[107] N. Ratier, «Physique des micro-capteurs», Ecole Nationale Supérieure de Mécanique et des Microtechniques de Besançon, France.

[108] S. Chaussedent, «Cours de physique ondulatoire pour les sciences de la terre», Université d'Angers, France, Année 2001-2002.

[109] F. Lakestani, « Etude théorique et expérimentale des transducteurs ultrasonores piézoélectriques fonctionnant dans le domaine du mégahertz», Thèse de doctorat, Institut National des Sciences Appliquées de Lyon, France, Juin 1984.

[110] S. Kim, « Low power energy harvesting with piezoelectric generators», Doctoral thesis, University of Pittsburgh, December 2002.

[111] IEEE Standard on Piezoelectricity (IEEE Std 176-1978), Institute of Electrical and Electronic Engineers, New York, USA, pp. 10-14.

[112] N. RIZET, «Contrôle actif de vibrations utilisant des matériaux piézoélectriques», Thèse de doctorat, Institut National des Sciences Appliquées de Lyon, France, Janvier 1999.

[113] S. Sherrit, B. K. Mukherjee, «Characterization of piezoelectric materials for transd- ucers», Jet Propulsion Laboratory, California Institute of Technology, Pasadena, California, USA.

[114] Morgan Electro ceramics, www.morganelectroceramics.com, «Piezoelectric cerami- cs», USA, November 2007.

[115] L. Khadir, « Etude du phénomène de résonance des pièces complexes en aluminium », Mémoire de la maîtrise en ingénierie, Université du Québec, Chicoutimi, Canada, Août 2007.

[116] Morgan Electro ceramics, www.morganelectroceramics.com, «Technical-publication TP-226: properties of piezoelectricity ceramics», USA.

[117] V. Pommier, M. Budinger, B. Mouton, S. Leleu, «Contrôle actif de vibrations», CETSIS'2005, Nancy, 25-27 octobre 2005.

[118] http://www.ndt-ed.org

[119] http://www.directindustry.fr

[120] F. Bowman, «Introduction to Bessel functions», Dover Publications Inc, New York, USA, 1958.

Annexes

Annexe A

Notions fondamentales d'élasticité

Une déformation produite en un point d'un milieu élastique se transmet de proche en proche dans ce milieu et ce phénomène de propagation met en jeu les propriétés élastiques du milieu, propriétés que nous allons maintenant rappeler.

A.1 Contraintes

Une contrainte est une force par unité de surface qui agit sur un élément de volume élémentaire, sa notion permet de décrire la répartition des forces à l'intérieur d'un solide soumis à une charge [107].

Considérons un parallélépipède élémentaire. Sur chacune de ces faces s'exerce une contrainte qui peut se décomposer en trois composantes selon les axes du trièdre (????1??2??3) (cf. figure A). Ces composantes, notées ?????? ; ??, ?? = 1 a 3), sont les sont les éléments du tenseur des contraintes« ?? ^a , l'indice «??» repérant la direction dans laquelle s'exerce la contrainte et l'indice « ?? ^a~ se référant à la face sur laquelle elle s'exerce. Les éléments ?????? sont dites contraintes normales, car elles agissent perpendiculairement à la face. Les éléments ?????? = ?????? ; ?? ? ??~ sont dites contraintes tangentielles (ou de cisaillement) puisqu'elles agissent dans le plan de la surface. Le tenseur^I des contraintes est donc symétrique et s'écrit [108]:

		??11	??12	??13
??????	=	??21	??22	??23	(??. 1)
		??31	??32	??33

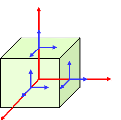
??12

??11

??21

??

??31

??22

??32

??13

??23

??33

??3

??2

??1

Fig. A - Notation des contraintes sur un volume élémentaire

I Le concept du tenseur à été introduit, à la fin du dix-neuvième siècle, par le physicien W.Voigt pour définir l'état de tension

mécanique d'un solide (le mot tenseur vient de tension), sa notation apparaît dis qu'on cherche à établir des relations linéaires entre effets et causes dans les milieux anisotropes. Dans un cristal, une cause appliquée suivant une direction donne en générale naissance à un effet orienté suivant une autre direction. Le rang d'un tenseur correspond au nombre d'indices nécessaires pour définir un de ses éléments : un tenseur de rang « r » est un ensemble de 3r éléments repérées par « r » indices [51].

A.2 Déformations

Lorsque des forces extérieures sont appliquées à un solide, celui-ci se déplace et se déforme. Cette déformation est décrite au moyen du tenseur des déformations « S » qui lui aussi est symétrique. Les éléments de ce tenseur peuvent s'écrire [109]:

1 +??????

?????? = 2 ?????? (??. 2) ?????? ??????

Ou (???? ??

?????? ???? ???? ??

??????) sont les gradients des déplacements.

Les éléments Sii représentent l'allongement dans chacune des directions des axes principaux et les éléments Sij ; i ? j~ représentent les déformations de cisaillement.

A.3 Relation entre contraintes et déformations

En régime élastique, le milieu satisfait la loi de Hooke qui exprime la proportionnalité entre contrainte et déformation (i.e. les composantes du tenseur des contraintes sont une combinaison linéaire de toutes les composantes du tenseur des déformations), d'où la formulation [5]:

?????? = ?????????? ?? ???? (??. 3)

Les coefficients « cijkl » sont les constantes élastiques, ils constituent un tenseur de rang 4 comprenant 81 éléments. En fait par suite de la symétrie du tenseur des contraintes et du tenseur de déformations il y a seulement 36 éléments indépendants. Néanmoins, le produit tensoriel reste très à manipuler ; c'est pourquoi nous allons faire appel à une écriture matricielle (c'est-à-dire un artifice de calcul qui va permettre de simplifier les choses).À cet effet, une notation contractée des indices est adoptée [108,110]:

???? ???? ????	?? ???? ??
11	1
22	2
33	3
23 ou 32	4
13 ou 31	5
12 ou 21	6

Tab. A - Notation matricielle

Les notations tensorielles sont réduites à une notation matricielle pour _cijkl qui devient c_pq et vectorielle pour _Tij et _Skl qui deviennent T_p et S_q (S_q = Skl si k = l et S_q = ²Skl si k ? l).

En notation contractée (i.e. produit matriciel), la loi de Hooke s'exprime alors :

Annexe B

Piezoelectricite et materiaux piezoelectriques

B.1 Relation entre les differentes constantes dielectriques mecaniques et piezoelectriques

Les differentes constantes dielectriques, mecaniques et piezoelectriques sont reliees par les relations suivantes [1111:

· Constantes mecaniques

cEr _47" s^E = 8_P4 (B.1)

P

CDr _47" S^D = 8_P4 (B.2)

P

D E

^CP4 = ^CP4 + ^e kP hk_q (B. 3)

sgi = sP^Eq -- dkpgkg (B.4)

· Constantes diélectriques

A^sicEj^sic = 8ii (B.5)

gkEjic = 8ii (B. 6)

T S

£L - = E - - + d ^-14 1 e-₄ (B.7)

11 11

1³11 = 1³ fj g iq hi q (B.8)

· Constantes piazoilectriques

dip = Eric .9kp (B.9)

eiP = digcrip (B.10)

tip = filic dkp (B.11)

hip = gig e (B.12)

ip

avec i,j, k = 1,2,3 : Indices electriques.

p, q, r = 1,2,3,4,5,6 : Indices mecaniques. S_ij : Matrice unite de type (3 x 3).

opq : Matrice unite de type (6 x 6).

B.2 Fabrication des céramiques piézoélectriques PZT

La figure B.1 illustre le cycle de fabrication des céramiques piézoélectriques PZT par voie solide.

Fabrication d'une poudre
PZT à partir d'oxydes
chauffés à 900°C

Obtention d'une céramique crue par
pressage d'un mélange (poudre
PZT+ liant) dans une matrice

Déliantage à 600°C

Polarisation par application d'un champ électrique continu (plusieurs kV/mm)

Dépôt des électrodes par sérigraphie

Frittage de la céramique crue à plus de 1200°C

Fig. B.1 - Cycle de fabrication des céramiques PZT par voie solide [112]

B.3 Coefficient de couplage électromécanique et permittivitéen fonction de l'impédance acoustique pour une large gamme de matériaux piézoélectriques disponibles

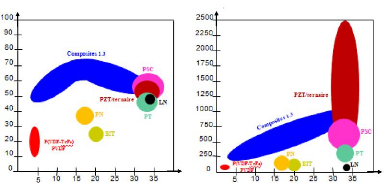
kt(%) å33,r

S

Z(MRa) Z(MRa)

(a) (b)

PZT : Zircono Titanate de Plomb PVDF : Polymère P(VDF-TrFe) : Copolymère Composites 1.3 : Composites PZT et polymère PSC : Monocristaux à base de Plomb

BIT : Titanate de Bismuth LN : Niobate de Lithium PN : Niobate de Plomb PT : Titanate de Plomb

B.4 Echantillons pour la caractérisation des modes de défor- mation fondamentaux

Forme d'échantillon

Mode de deformation

Direction polarisation

Excitation

Direction de vibration

Coefficients utiles

Frequence de resonance

Coefficient de couplage

a3

a3 a1

D

Barreau

??33 ??33 ??33 ??33 ??

??3?? =

2 ??33 2 =

a2^3 a3>5.a1 ; a3>5.a2 a3>5.D 2 1

Transverse (lateral)

??31 ??31 ??31 ??33 ??

??1 ???? = ??2

a1

Epaisseur

??33 ??33 ???? ?? 33

??3?? ???? = ??3

D

a3 a1 a3 a2 3 a1 et a2>10.a3 1

D

Radial (planaire)

??31

??31 ???? T å33

?? ?? ???? = ??

2 k ^2 =k 2 1 1 -ó^E

D>20.a3

Cisaillement

d15 ??15 ??15 ??11 ??

??5 ???? = ??3

a3

a2 a1 et a2>10.a3

B.5 Caractéristiques des céramiques piézoélectriques utili- sées

	Symbole	Unité	PZT503 (ou PXE5) <<Céramique douce>>		PZT802 (ou PZT8) <<Céramique dure>>	Caractéristiques électriques à faible champ
Constantes diélectriques relatives (å0 = 8.85 x 10-12F.m -1)
T ^år11	-	1800	1290
			1150
			900
			600		Tangente de l'angle de pertes diélectriques
??????????			0.003		Résistivité (à 25 °C)
??????	-	50^10	10^10		Caractéristiques électromécaniques
Coefficients de couplage
??15	-	0.66	0.55
			0.3
			0.64
			-
			0.54		Constantes de charge
??15	10^-12??. ??^-1	515	300
			-97
			250
			31		Constantes de tension
??15	10^-3??. ??. ??^-1	33	-28.9
			-10.9
			24.6
			3.6		Constantes de pression
h 15	10^8??. ??^-1	-	12.9
			-7.8
			26.9		Coefficients piézoélectriques <<eij>>
e15	??. ??^-2	-	10.3
			-4
			13.8		Constantes de fréquence
??1	????. ??	1450	1700
			-
			-
			2070
			2000
			-
			2285

Facteur de qualité	Qm	-	75		1000	Caractéristiques mécaniques
Compliances à champ constant
?? ??11	10^-12??^2.??^-1	15	11.5
			-3.7
			-4.8
			13.5
			31.9
			30.4		Compliances à induction constante
?? ??11			10.1
			-4.5
			-2.5
			8.5
			22.6
			30.4		Constantes élastiques à champ constant
?? ??11	10^10??. ??^-2	-	13.7
			6.97
			7.16
			12.4
			3.13
			3.40		Constantes élastiques à induction constante
?? ??11			14
			7.28
			6.08
			16.1
			4.46
			3.40		Coefficient de Poisson
???? = -??12^??/??11^??	-	0.3	0.32		Masse volumique
??	10^3????.??^-3	7.8	7.6		Caractéristiques thermiques
Température de Curie
????	°??	285	300		Conductivité thermique
-	??. ??^-1. ??^-1	1.2	-

Tab. B.2 - Caractéristiques des céramiques piézoélectriques utilisées [106,114,116]

Annexe C

Analogie électro-acoustique

Par une analogie électro-acoustique (cf. tableau C), les expressions des grandeurs acoustiques sont identifiées à des variables électriques.

Domaine électrique	Unité	Domaine mécanique		Unité	Courant << I >>
A	Vitesse << Va >>	m.s^-1		Tension << v >>
V	Force << F >>	N		Impédance électrique << Ze>>
Ù	Impédance acoustique << Za>>	Rayl		Puissance électrique << Ps >>
W	Intensité acoustique << Ia >>	kg.m^-1.s^-2

Tab. C - Analogie entre les grandeurs électriques et acoustiques [5]

Annexe D

Modèles unidimensionnels et hypothèses^[104]

Les expressions unidimensionnelles des impédances électriques des céramiques piézoélectriques en forme de disque (mode radiale) et de barreau (mode barreau) sont respectivement données par les relations :

?? = ????0 '

?? 1 +

????^2 1 - ????^2

1 + ??^??)??1(??????) ???? ????0 ???? ??) - (^1 - ??^??)??1(???? ??) 1

-1

(??.1)

1 2

?? = ????0 "?? 1 - ??33

'

tan ??3 ??3

2

'

??3 ??3

2

)

(??. 2)

avec

??0 ' ??0 " ??1	?? = ??33 ?? (???? ??)	= ??33 1 1 =		????2	??1		(???? ??)
			??3 ??1??2
			- ????

(??. 3)
(??. 4)

(??. 5)

??

???? = (??. 6)

??????

'

??3

??

= ' (??.7)

????3

·

oil

???? est le nombrl R3'Rna dans la céramique selon le rayon « a ».

· ??3 ' UND KRP HI R'RnIe dans la céramique selon l'axe de polarisation «x3».

· Capacité du disque en mode radiale.

· Capacité du barreau.

Les hypothèses et résultats concernant les différentes géométries des céramiques piézoélectriques sont récapitulés dans le tableau D :

Geometrie

Hypothèses

Résultats

Mécaniques

Électriques

Vitesse

Permiftivite

Coefficient de couplage

Plaque mince a3 a2

??1 = ??5 = ??4 = ? ??1, ??3 ?

??2 ??6 ??5 ??2 0,

= = = ??3

??4 ^0 ??6 ?

= = 0

0 0

??1 = ??2 = 0 ??1 = ??2 =0 ? ??1, ??2 ??3 ? 0, ??3 =

??????

?? ??33 2

?? ??33

????^2

2 ??33 ?? ??33 =

= ????3 ??

?? ??33

Barreau long a3 >> a1, a2

??1 = ??5 = ??4 = ? ??1, ??3 ?

??2 ??6 ??5 ??2 0,

= = = ??3

??4 ^0 ??6 ?

= = 0

0 0

??1 = ??2 = 0 ??1 = ??2 =0 ? ??1, ??2 ??3 ? 0, ??3 =

??????

'2 = 1

EL (1. - kh)

2 ??33

2 ??33 =

?? ?? ??33 ??33

????3 ?? ????33

Disque mince a3 << a

??3 = ???? = ???? = ??3 = ??6 =

0 ???? ???? ??4 ^0

? ? =

0 0 ??5

=

0

???? = ???? = 0 ???? = ???? =0 ? ??, ?? ??3 = ??????, ??3

? 0

2 ??????

1

E^T (1 k) -33 - P

2 ??31 ???? 2 =

2 ??31 =

= ????11 ?? 1 - ??12 ?? ???? = -

????~

?? ??33 ?? ??11 2 2

??31 1 - ????

?? ??11

Tab. D - Caractérisation unidimensionnelle : hypothèses et principaux résultats

Annexe E

Photographies

Fig. E.1 - Céramiques piézoélectriques PZT : plaques, disques émaillés, anneaux, tubes,
rondelle, portions de sphères [39]

Fig. E.2 - Film PVDF [117] Fig. E.3 - Composites 1.3 fabriqués

(sans métallisation à gauche) [2]

Fig. E.4 - Transducteurs ultrasonores piézoélectriques [118,119]

Annexe F

Fonctions de Bessel de première espèce

Les fonctions de Bessel de premi~re esp~ce d'ordre « n » de la variable « x » sont calculées à partir de la suite suivante [120]:

Co

)

(2). an, _x, (x\ⁿ (-1)p . x 2p
LA 2²p. p! (n + p)! (F)
p =0

Les tracés des fonctions de Bessel de premiqre espqce d'ordres 0 à 8 sont montrés sur la figure F :

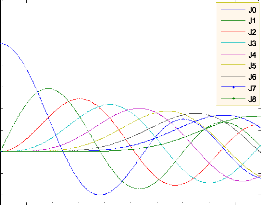
Fig. F - Fonctions de Bessel de première espèce