|

REPUBLIQUE DU CAMEROUN UNIVERSITE DE DOUALA
REPUBLIC OF CAMEROON UNIVERSITY OF DOUALA
ECOLE DOCTORALE DES SCIENCES
FONDAMENTALES ET
APPLIQUEES.
LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Matricule : 05UD038
ETUDE AB-INITIO DE LA
STABILITE OU DE LA METASTABILITE
D'UN ANION TETRATOMIQUE .
CAS DU SYSTEME N2O2 -
/ N2O2 .
MEMOIRE
Présenté en vue de
l'obtention du
DIPLOME DE D.E.A. DE PHYSIQUE ET SCIENCES
DE
L'INGENIEUR
OPTION
PHYSIQUE
Spécialité
PARTICULES ET
RADIATIONS
Par
Jean Jules FIFEN
Maître ès Sciences
Sous la direction de :
Dr. Mama NSANGOU et Dr. Ousmanou
MOTAPON de cours. Chargé
Faculté des Sciences.
Chargé de cours. Faculté des Sciences.
Université de Douala.
Université de
Ngaoundéré.
Supervisé par :
Professeur Louis Max AYINA
OHANDJA.
Maître de conférences
Année académique 2005 -
2006 Go to Home page
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
REMERCIEMENTS
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Ce travail de première année de Doctorat a
été réalisé au laboratoire de Physique fondamentale
de l'Université de Douala, sous la direction de M. Mama
Nsangou et M. Ousmanou Motapon respectivement
Docteurs de Physique à l'Université de Ngaoundéré
et de Douala.
Je leur adresse ma profonde gratitude de m'avoir aidé avec
patience à mener à bien cette étude.
Je tiens à remercier très sincèrement le
professeur Louis Max AYINA OHANDJA, directeur de l'IUT et
coordonnateur de l'unité de Formation Doctorale de Physique et Sciences
de l'ingénieur de l'Université de Douala., pour avoir
supervisé ce travail. Je suis également très honoré
qu'il ait accepté de présider mon jury.
Je tiens également à remercier M.
Kenfack Cyrill, Docteur en Physique au Centre de Physique
Atomique et d'Optique Quantique de l'Université de Douala, pour avoir
accepté avec plaisir d'examiner ce travail.
Je remercie M. Mbaze, Docteur en Chimie pour
avoir également accepté avec plaisir d'examiner ce travail.
Je remercie très sincèrement M. Robert
Mbiake, Docteur en Physique au Centre de Physique Atomique et
d'Optique Quantique de l'Université de Douala, pour ses conseils et ses
encouragements. Sa disponibilité et son amitié m'ont
été très précieuses.
Je pense en ce moment à tous mes enseignants de
l'Université de Douala ayant participé à
l'édification de mon savoir.
Je remercie toute la famille Motapon pour la
convivialité de leur accueil et leur grande sympathie.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Je remercie très profondément mon amie
Khalie Ahmat pour son aide financière à
l'élaboration de ce travail.
Je remercie mes camarades Moustatapha et Ndoumbé
pour avoir mis leurs ordinateurs à ma disposition.
Je remercie Mbatchania et Hyeudip
pour avoir accepté de relire mon travail pour en corriger le
style.
Je pense tendrement à Chimène pour
sa grande et sincère amitié.
Je remercie également mes amis, Brice,
Carline, Coby, Dorothée,
Edith, Epée, Emma,
Lucrèce, Khalie,
Nathalie, Sonia, Simon,
Willy pour leur compagnie et leur soutient moral permanent.
Je souhaite aussi remercier toutes les personnes dont j'ai
croisé le chemin, amis, collègues, étudiants et qui m'ont
prodigué leur aimable soutien. Je ne veux oublier personne et je suis
certain que chacun se reconnaîtra.
Enfin, je pense à ma famille pour laquelle j'ai, sans
doute, manqué de disponibilité et qui m'a non seulement
supporté mais soutenu. Je remercie chacun pour sa compréhension
et son affection.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
A mes parents...
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
TABLE DES MATIERES.
|
Remerciements p.1
Introduction générale p.8
1. METHODES DE CALCUL DES FONCTIONS D'ONDES ET DES
ENERGIE
|
|
ELECTRONIQUES.
|
.p.12
|
|
1.1. Introduction
|
p.13
|
|
1.1.1. Hamiltonien et fonction d'onde
|
p.13
|
|
1.1.2. Approximation diabatique, adiabatique et de Born
Oppenheimer
|
p.15
|
|
1.1.3. Limité de validité de l'approximation de
Born-Oppenheimer
|
.p.17
|
|
1.2. Méthodes de calcul des fonctions d'onde et des
énergie électroniques
|
.p.19
|
|
1.2.1. Exposé des méthodes de champ
auto-cohérent de base
|
p.20
|
|
1.2.1.1. Méthode de Hartree
|
p.20
|
|
1.2.1.2. Méthode de Hartree-Fock
|
..p.22
|
|
1.2.1.3. Méthode de Roothaan et Hall (LCAO)
|
..p.27
|
|
1.2.2. Les bases de calcul
|
p.31
|
|
1.2.2.1. Les fonctions de Slater
|
..p.31
|
|
1.2.2.2. Les fonctions Gaussiennes
|
.p.33
|
|
1.2.2.3. Classification des bases contractées
|
..p.36
|
|
1.2.2.3.1. Bases de Pople
|
.p.38
|
|
1.2.2.3.2. Bases de Dunning-Husinaga
|
p.40
|
|
1.2.3. Limites de la méthode LCAO-SCF
|
..p.41
|
1.2.4. Méthodes d'approche de l'énergie de
corrélation ou méthodes post-
Hartree-Fock p.43
1.2.4.1. Introduction p.43
1.2.4.2. Méthode d'Interaction de Configuration (CI)
p.46
1.2.4.3. Méthode du champ auto-cohérent
multiconfigurationnelle (MCSCF) .p.49
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
1.2.4.4. Méthode d'Interaction de Configuration
Multiréférence (MRCI). 1.2.4.5. Méthode des Clusters
Couplés (CC) .p.51
1.3. Bref résumé des méthodes de
corrélation électroniques p.53
2. RESOLUTION DE L'EQUATION DE SCHRÖDINGER
NUCLEAIRE. ...p.57 2.1. Introduction p.58 2.2. Résolution de
l'équation de Schrödinger nucléaire par la méthode
des
|
perturbations
2.2.1. Vibrations moléculaires
|
p.58 p.58
|
|
2.2.1.1. Cas simple d'une molécule diatomique
|
.p.60
|
|
2.2.1.2. Potentiel anharmonique
|
.p.60
|
|
2.2.1.3. Vibrations moléculaires en mécanique
quantique
|
.p.58
|
|
2.2.1.3.1. Coordonnées normales
|
p.62
|
|
2.2.1.3.2. Classification des vibrations moléculaires
|
..p.63
|
|
2.2.1.3.3. Coordonnées internes
|
..p.64
|
|
2.2.1.3.4. Coordonnées de symétrie
|
.p.65
|
|
2.2.2. Rotations moléculaires (rotateur rigide)
|
p.66
|
|
2.2.2.1. Molécules linéaires
|
p.66
|
|
2.2.2.2. Molécules non linéaires
|
.p.66
|
|
2.2.3. Solution du problème nucléaire
|
p.68
|
3. COURBES ET SURFACES DE POTENTIEL p.69
3.1. Introduction p.70
3.2. Etude des fragments NO, NO- et N2O p.70
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
|
3.2.1. Bases utilisées
|
..p.70
|
|
3.2.2. Méthodes de calcul utilisées
|
p.73
|
|
3.2.3. Structure électronique du NO, NO- et N2O
et courbes de potentiel.....
|
p.75
|
|
3.3. Etude de l'état fondamental des systèmes
tétratomiques N2O2 - et N2O2 p.78
3.3.1. Modes de vibration des molécules
N2O2 et N2O2 - en symétries C2v et
Cs.
|
|
3.3.2. Géométries optimisées des
molécules N2O2 et N2O2-
|
..p.81
|
|
3.3.3. Stabilité ou métastabilité d'un
système moléculaire
|
p.85
|
|
3.3.4. Bases et Méthodes de calcul utilisées
|
..p.87
|
|
3.3.5. Courbes de potentiel électroniques
|
..p.87
|
|
Conclusion générale
|
.p.90
|
|
Références
|
.p.93
|
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
INTRODUCTION
GENERALE
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Jusqu'à nos jours, la spectroscopie moléculaire
reste le moyen le plus performant pour sonder un milieu inaccessible au
laboratoire, tel qu'une zone polluée de l'atmosphère terrestre,
le milieu interstellaire, une étoile, ou plus généralement
une région bien déterminée d'une galaxie ou de
l'univers.
L'enregistrement puis l'interprétation du spectre
d'émission ou d'absorption du milieu en question, peut renseigner de
façon précise l'expérimentateur, sur les différents
constituants de ce milieu , leurs concentrations, les conditions physiques dans
lesquelles ils se trouvent et éventuellement leurs vitesses de
déplacement par rapport à un référentiel
donné.
L'interprétation des spectres revient en premier lieu
à l'analyse des positions, des intensités et des profils de raies
spectrales et de leur comparaison à ceux obtenus à partir des
« spectres témoins » réalisés en laboratoire.
Cependant, les conditions physiques de certains milieux, sont
très différentes de celles de nos laboratoires terrestres (Par
exemple, température et pression très basses dans les milieux
interstellaires, ou très hautes dans les étoiles,...) et font
que, de nombreux radicaux ou ions moléculaires instables en laboratoire,
y soient relativement très abondants. Alors, faute de spectres
témoins, l'identification de telles espèces ne peut se faire que
grâce aux données spectroscopiques calculées
théoriquement. Quand bien même ces espèces sont
identifiables, on fait toujours recours aux calculs théoriques dans un
souci de modélisation.
Parmi ces espèces, citons les molécules
NO, NO- , N2O, et qui sont
N 2 O- 2 N 2 O 2
ici sujets de nos intérêts.
Le N 2 O- 2 et le sont considérés en termes de
leurs rôles comme des
N 2 O 2
produits intermédiaires des réactions [1]
O- + N2O et N + NO2. Après de longues
années d'étude, Arnold et Newmark[1] ont montré
théoriquement que ces réactions peuvent se produire suivant
plusieurs chemins.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
NO NO , H 2.8Kcal/ mol.
-
? + Ä = -
-
? ? +
NO NO e , H 2.3Kcal/ mol.
+ Ä = -
En effet, O N O
- + ? ? (a)
2 O N , H 55.6Kcal/ mol.
- + Ä = -
? 2 2
? ?
O N e , H 45.4Kcal/ mol.
-
+ + Ä = -
2 2
?
? ?
? ?
2
N O O H 42Kcal/ mol.
+ Ä = -
2
NO NO H 42Kcal/ mol
N NO
+
(b)
+ Ä = -
N O H 42Kcal/ mol
2 +
? Ä = -
2
? ? +
N 2O H 42Kcal/ mol
Ä = -
2
Jusqu'à présent, aucune expérience n'a
encore été faite pour prouver les chemins de
l'équation
(b). Néanmoins, Paulson, Moruzzi et al[2-3] ont pu observer
le premier
chemin de l'équation (a). Ils ont montré que les
produits de ce chemin de réaction
résultent des structures NNO- 2 et
ONNO- résultant à leurs tours de l'attaque de l'anion
O- respectivement sur l'azote central ou l'azote terminal du
N2O[2-3].
Ainsi, les molécules NO, NO-
et N2O seraient des fragments du N 2 O- 2 .
Une récente étude ab-initio sur plusieurs
isomères du effectuée par
N 2 O- 2
Hiraoka et al [4] prévoit que l'état
fondamental de cette molécule appartient au
groupe . En supposant que
la molécule est formée en enlevant un électron à
C2 v N 2 O 2
une orbitale de la moléculeN 2 O- 2 , Arnold et
Neumark[1] ont montré que la molécule N 2 O
2 a deux géométries d'équilibre (A) et (B) en
symétrie et une géométrie
C2 v
d'équilibre en symétrie Cs.
Le but de ce travail est d'abord de maîtriser les
méthodes de calcul ab-initio et leur application à l'étude
de la stabilité ou métastabilité du système N 2 O-
2 / N 2 O2. Ensuite, de fournir des données spectroscopiques
suffisamment précises sur ce système
et sur les fragments NO, NO- et
N2O susceptibles d'aider à affirmer ou infirmer la
présence de ces espèces dans le milieu étudié et de
contribuer à mieux comprendre la chimie des NOx qui existent
en tant que polluants de l'atmosphère terrestre.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
De part ces objectifs, nous structurons ce travail comme suit
:
· Dans le premier chapitre, nous présentons les
méthodes de détermination des surfaces de potentiel
d'énergies électroniques ; en passant au peigne fin les bases de
fonctions d'ondes sur lesquelles ces méthodes peuvent être
projetées. A l'issue de l'exposé de cette partie, nous serons
à mesure de choisir de manière optimale, une méthode et
une base de calcul des surfaces de potentiel des énergies
électroniques adaptées à un système
moléculaire donné.
· Dans le deuxième chapitre, dans le but de
décrire les mouvements des noyaux au sein des surfaces de potentiel
décrites plus haut, nous présentons la détermination de
l'énergie nucléaire d'un système moléculaire par la
méthode des perturbations. Par la suite, nous caractérisons ses
modes de vibration en nous servant des outils de la théorie des groupes
de symétrie.
· Enfin, dans le troisième chapitre, nous
présentons et discutons les résultats de calculs liés aux
fragments NO, NO- , N2O et aux
molécules N 2 O- 2 , N 2 O2. Les
calculs menés dans cette section sont dans un premier
temps relatifs aux effets des
bases et des méthodes de calcul pour
les systèmes étudiés. Dans un second temps,
ils sont liés à la stabilité ou la
métastabilité du système /
N 2 O- 2 N 2 O2.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
CHAPITRE 1
METHODES DE CALCUL DES
FONCTIONS D'ONDE ET DES
ENERGIES ELECTRONIQUES
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
1.1 INTRODUCTION
Etudier un système moléculaire revient à
résoudre l'équation de Schrödinger qui régit
l'ensemble de ses électrons et de ses noyaux. Or la résolution de
l'équation de Schrödinger pour un système moléculaire
n'est pas aisée. Pour cela, on fera une première approximation
dite de Born-Oppenheimer, qui va permettre de découpler le mouvement
électronique du mouvement nucléaire.
Dans ce chapitre, on se concentrera sur la résolution
de l'équation de Schrödinger électronique. Pour cela, un
exposé des méthodes de chimie quantique sera fait en passant au
peigne fin les méthodes ab-initio.
Au sorti de cet exposé, il serait nécessaire de
savoir laquelle des méthodes abinitio est la mieux adaptée
à la description d'un système moléculaire.
1.1.1 Hamiltonien et fonction
d'onde.
Considérons un système moléculaire
formé de noyaux et n électrons. A ce
N
système, on associe un repère orthonormé(o
, i , j , k). Dans la
description quantique non relativiste où le spin est
négligé, l'Hamiltonien de ce système peut s'écrire
:
H = Te ( r )
+ TN ( R ) + V
NN ( R ) + VeN
( R,r ) + Vee( r)
(1.1)
Où et r désignent respectivement
l'ensemble des coordonnées des noyaux et des
R
électrons par rapport à l'origine du
repère. Les différents termes constituants cet Hamiltonien sont
définis en unités atomiques comme suit :
· Te ( r) est
l'énergie cinétique totale des électrons :
n
1
T e r = - ?? r
(1.2)
2
( )
i
2 =
i 1
ri étant la position de
l'électron numéro i par rapport à l'origine du
repère.
· TN ( R) est
l'énergie cinétique des noyaux :
N
1 1
TN R = - ? ? R
(1.3)
( )
i
2 = M
i 1 i
Mi étant la masse du noyau numéro i et
sa position par rapport à l'origine du
Ri
repère.
· VNN ( R) est
l'énergie potentiel de répulsion entre noyaux :
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
1N N Z Z
VNN R = ?? (1.4)
i j
( )
2 = = R
i 1 j 1 ij
j i
?

Où R ij = R i - R
j est la distance entre les noyaux de charge Zi
et Zj .
· VeN ( R,r)
est l'énergie potentielle totale d'attraction entre électrons et
noyaux :
n N
Z
VeN R,r ?? R r (1.5)
j
( ) = -
i 1 j 1 j i
-
= =
· Vee ( r) est
l'énergie potentielle totale de répulsion entre électrons
:
1 n n 1
Vee r = ?? (1.6)
( )
2 = = r
i 1 j 1 ij
j i
?
rij étant la distance entre les électrons i et
j.
Chaque état moléculaire peut être
représenté par une fonction d'onde qui est
ØT
solution de l'équation de Schrödinger :
HØT =E
TØT (1.7)
Où est l'énergie totale du système.
L'observation de l'Hamiltonien de ce système
E T
montre que dépend de et . Et quant à lui
dépend seulement de R . L'équation
ØT r R E T
(1.7) peut donc s'écrire :
HØT ( R ,
r ) = E T ( R
)ØT( R , r )
(1.8)
Rappelons que L'équation de Schrödinger est le
postulat de première quantification. La seconde quantification quant
à elle tient lieu des effets relativistes, de la création et de
la destruction des particules. Ce que nous négligerons dans toute notre
étude.
La résolution analytique exacte de l'équation
(1.8) est impossible. On ne peut qu'approcher la solution de par des
considérations physiques simplificatrices. L'approximation fondamentale
qu'on effectue ici est celle de Born Oppenheimer ; qui quant à elle
permet de découpler le mouvement des électrons de celui des
noyaux. Ce qui engendre deux sous problèmes :
v' La résolution de l'équation de Schrödinger
électronique,
v' La résolution de l'équation de Schrödinger
nucléaire.
Bien entendu, chaque sous-problème nécessite des
approximations optimisant la solution du problème global.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
1.1.2. L'approximation diabatique, l'approximation
adiabatique et l'approximation de Born - Oppenheimer.
L'Hamiltonien du système décrit peut encore
s'écrire sous la forme :
H = TN + H
e +H pm (1.19)
OA He est l'Hamiltonien
électronique et Hpm la polarisation de masse
définis par :
H e = Te
( r ) + Vee ( r )
+ VeN ( R , r )
+ VNN( R ) (1.10)
2
? ?
n
1
H pm = - ? ? ?
? (1.11)
i
2M =
tot i 1
? ?
Mtot étant la masse totale de tout le système.
En supposant connus les vecteurs et valeurs propres de
He , on a :
H e Øi ( R
, r ) = E i ( R
)Øi ( R , r ), i =
1, 2,..., 8 (1.12)
L'hermiticité de H permet de choisir les
solutions orthonormales :
?R r R r r = ä =
* i j ij { 1 si i=j
Ø ( , )Ø ( , )d (1.13)
0 sinon
La base ainsi construite, il est clair que (sans aucune
approximation), la fonction d'onde totale du système peut
s'écrire comme une combinaison linéaire des différents
vecteurs de base. Les coefficients de combinaison étant évidement
des fonctions de R .
8
Ø ( , ) Ø ( )Ø ( , )
R r =? R R r (1.14)
T Ni i
i =1
En introduisant (1.14) dans (1.7), on obtient :
8( VN ØNi ) + 2 ( VN Ø i )( VN Ø Ni ) +
Ø Ni ( VNØ i + Ø Ni E i Ø
i + Ø Ni Hpm Øi = E
T ?Ø Ni Øi (1.15) ? ? ? i 1 = i
1 =
OA nous avons tenu compte du fait que
He et Hpm agissent
seulement sur la fonction d'onde électronique Maintenant, multiplions
l'équation (1.15) à gauche par 'Pj* et
intégrons sur tous les coordonnées électroniques. On
exploitera ici la notation bra-ket :
|
? Ø ØdV Ø Ø
* H =
? ? ? H
Ø *ØdV = Ø Ø
? Ø Ø= ä
i j ij
??
|
(1.16)
|
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Ainsi, l'équation (1.15) devient :

ur 2
? N Nj
Ø E Ø
+ +
j Nj
8
?
i 1
=
?
??
ur ur ur 2

(1.17)
2 Ø ? N Ø ( )
? N Ø + ?
Ø N Ø Ø + Ø H
j i Ni j i Ni j pm Øi Ø ? = E
Ø
Ni ? T Nj
?
L'équation (1.17) montre que ses deux premiers termes
sont dépourvus de la fonction d'onde électronique ; tandis que
les autres contiennent des termes de couplage de deux états
électroniques différents .Les deux premiers termes de ces
derniers sont des éléments de couplage non
adiabatique, respectivement du premier et du deuxième
ordre. Tandis que le dernier est la polarisation de masse. Le couplage non -
adiabatique est important pour les systèmes à plus d'une surface
électronique, telles que les réactions photochimiques.
Dans l'approximation adiabatique, la
forme de la fonction d'onde totale est restreinte à une surface
électronique ; ce qui signifie que tous les éléments de
couplage contenus dans l'équation (1.17) sont négligés (
seules les termes avec i=j survivent).
ur ? ? ? ?
ur

2 2
N + + ? N
E j Ø j Ø j Ø j pm Ø j Ø Nj E
T Ø N
+ H ? = j (1.18)
? ?
En négligeant la polarisation de masse, (1.18) devient
:
ur
2 + E j + Ø j ? Øj ?
ØNj = E T ØN 2
N N ? ? j
ur ? ? ? ?

(1.19)
Ou plus explicitement :
|
ur ? ? ? ?
|
2
R R R
N + E ( ) + U( ) ? Ø Nj ( ) = E T
Ø ( )
Nj R
j ? ?
|
(1.20)
|
2
U( R ) = Ø ? Ø i
N
est connu comme une « correction diagonale » et il est
plus
Où

j
ur
petit que E j ( R) . En effet,
d'après le théorème d'équipartition
d'énergie,
m 1
U( R ) = áE j ( R
) avec á = . A étant le nombre de charge moyen d'un
M 1836 xA
atome de la molécule (Il est donc clair que les effets
relativistes sont plus marqués
lorsque A est élevé).
Ainsi, la forme de la surface d'énergie est déterminée
presque
exclusivement par Ej ( R) .
L'approximation de Born - Oppenheimer consiste
à
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
négliger la « correction diagonale ». Ce qui
revient à découpler le mouvement des noyaux des atomes de celui
des électrons. Physiquement, ceci se traduit par le fait que la
mobilité des électrons étant beaucoup plus importante que
celle des noyaux, ils s'adaptent adiabatiquement à toute modification de
la position des noyaux en des temps beaucoup plus courts que ceux typiques du
mouvement des noyaux. Du point de vue des noyaux, l'adaptation est quasi
instantanée. L'approximation de Born-Oppenheimer est donc une
approximation adiabatique.
|
|
2
l'équation de Schrödinger
N
|
|
Du point de vu de cette approximation, en posant
|
TN = ?
|
devient :
? T N + V j ( ) ? Ø Nj (
) = E T Ø Nj ( )
R R R (1.21)
? ?
(C'est l'équation de Schrödinger nucléaire
où V j ( R ) = E j ( R
) est l'énergie électronique
et joue le rôle d'énergie potentiel
électronique.) La représentation de est une courbe
Vj
de potentiel (cas d'une molécule diatomique) ou une
surface de potentiel ?-
dimensionnelle (cas d'une molécule à
plus de deux atomes ; étant le nombre de
?
degrés de liberté de vibration de cette
molécule.)
En général, l'approximation de Born- Oppenheimer
(et adiabatique) est une bonne approximation. Mais elle a des limites.
1.1.3. Limites de validité de l'approximation
de Born - Oppenheimer.
L'approximation de Born - Oppenheimer n'est plus valable dans les
situations ci-dessous mentionnées :
> Au niveau de la description des états de Rydberg
où la vitesse des électrons est de l'ordre de celle des
noyaux.
> Lors de croisements évités, quand le couplage
entre deux états électroniques de même symétrie
devient grand devant l'écart en énergie.
En effet, considérons une molécule diatomique
pour simplifier l'étude. Dans ce
cas, les termes de couplage de
premier et de second ordre de l'équation (1.17)

2
? ?
peuvent respectivement s'écrire : i
ø ø et ø ø .
j i 2 j
? R ? R
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Par ailleurs,


(i)
?ø i ? rid wi vj wj )
wi
? R . = ø
? R ?Røj
? ? ? r`T in \ In ?
? ?

= ø ø V R V R V R
( ) ( ) ( )
+ ? - ? ø ø
i j j ? j i ? i j
? R ?R
Or L? ? R ,Helj= ??R V(R,r i) avec
cf( R, ri)= VeN ( R,
ri )+VNN(R) (ii)
Ainsi, l'équation (i) donne :

?
ø i ø j =
? R
? c ? R
i j
? - ?
j ( ) ( )
? V R V R
i ?
Quant au terme de couplage de second ordre, en introduisant la
relation de fermeture, on obtient :

(iv)
(5i)
ø i ? R2 ø j = ? ? R ? ø k
øk ? ? Røjj
? 2
? ?
= ? ?


øi ø k øk ?
xi, .)+ ? i ? xi, k Wk ? øj
R ? R ? ? R ?R

? ? ? ? ? ?
= ?? R ?R
+ ? ? R ø k ø k ?R ø
j


Or les fonctions øi étant
orthonormées, on a : ø i ø i = 1 Soit :
ø ?i ? R ø i = 0
Compte-tenu de (iii) et (5i), (iv) devient :



)?? (6i)
? 2 ? ??ø i ? R øj
??øi ? V ? R Wk ? V ? R ø? R 2
øj --( 1 - ä ij )?R ? i[V j ( R ) - V i ( R))
?k ? ij??V k ( R ) - V i ( R ) ??[V j ( R ) -V k(R
pour i ? j (iii)
Ainsi, les expressions (iii) et (6i) des termes de couplages
montrent qu'ils dépendent de manière critique de la
différence d'énergie potentiel ? V j ( R ) - V i ( R ) ? ?
?
entre deux états électroniques donnés. On
peut donc s'attendre à des erreurs importantes dans l'approximation de
Born-Oppenheimer chaque fois que deux courbes se trouverons très
près en énergie l'une de l'autre
(quasi-dégérescence).
> Dans les systèmes Renner -Teller.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Une fois l'approximation de Born - Oppenheimer établie,
il reste à résoudre l'équation de Schrödinger
électronique (Comme nous l'avons déjà mentionné)
pour un ensemble de géométries nucléaires
données.
1.2. METHODES DE CALCUL DES FONCTIONS D'ONDE ET DES
ENERGIES ELECTRONIQUES.
Parlant de ces méthodes, on peut citer principalement :
> Les méthodes ab - initio.
> Les méthodes semi - empiriques.
Toutes ces méthodes ont pour but de résoudre
l'équation de Schrödinger électronique (1.12).
Les méthodes ab - initio, qui
signifient du tout début, des premiers principes, ont pour base la
méthode Hartree-Fock. A cause de la complexité des calculs et des
limites (fréquences CPU et capacité RAM) des supercalculateurs,
elles ne s'appliquent que sur des systèmes moléculaires de
petites tailles (quatre atomes au maximum).
Quant aux méthodes semi -
empiriques, elles sont également basées sur les
équations de Hartree - Fock ; mais ne les résolvent pas de la
même façon. Dans ces méthodes, on fait les approximations
suivantes :
v' La matrice de recouvrement S est
équivalente à la matrice unité.
v' Les intégrales mono - électroniques engageant
trois centres (deux des fonctions de base et un de l'opérateur) sont
nuls.
v' Les intégrales bi - électroniques à trois
ou quatre centres sont négligées. Pour compenser ces
approximations, le reste d'intégrales est déterminé sous
la base des paramètres expérimentaux liés à des
systèmes de référence.
Le but principal de ces méthodes étant la
description des liaisons chimiques, elles ne s'occupent que des
électrons de valence. Etant donné le grand nombre
d'approximations effectuées au niveau de ces méthodes, il ne
reste plus que peu d'intégrales à calculer ; ainsi, ces
méthodes sont rapides et nécessitent moins d'espace
mémoire dans un ordinateur.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Par rapport aux objectifs, nous nous limiterons aux
méthodes ab-initio que nous présenterons par la suite.
1.2.1. Exposé des méthodes de champ
auto - cohérent de base.
C'est en utilisant l'Hamiltonien ainsi simplifié
qu'historiquement fut mené le tout premier calcul de chimie quantique
dont la paternité revient à Walter Heitler et Fritz
London qui, en 1927, dans le but de vérifier la validité des
équations de la toute jeune mécanique quantique,
calculèrent l'énergie de la molécule la plus simple, H2.
Au-delà de cet exemple extrêmement simple, le grand nombre
d'électrons qui compose les systèmes chimiques
d'intérêt et la taille des bases d'orbitales nécessaires
à une description adéquate font que les calculs exacts sont
généralement hors de portée des calculateurs même
les plus puissants. C'est dans le but de trouver une bonne approximation
à ces impossibles diagonalisations que de nombreuses méthodes de
chimie quantique ont été mises au point. La plus
célèbre d'entre elles est sans conteste la méthode
Hartree-Fock, qui a été proposée sous une forme
primitive par Douglas Hartree en 1928 et qui a pris sa forme définitive
dans les travaux de Vladimir Fock en 1930[5]. Elle consiste à
chercher une fonction d'onde monoélectronique, c'est-à-dire
où chaque électron est traité indépendamment des
autres, même s'il est sensible à leur potentiel moyen ;
d'où son appellation de méthode de champ moyen ou SCF (pour "Self
Consistent Field").
1.2.1.1. Méthode de Hartree.
Hartree considère que les électrons sont
indépendants les uns des autres : C'est le premier niveau de
l'approximation orbitale. En plus, l'interaction entre un électron et
l'ensemble des autres électrons du système est
considérée comme une interaction entre cet électron et un
« champ moyen » crée par l'ensemble de tous les autres corps
du système.
En effet, le premier niveau de l'approximation orbitale (un
modèle à particules indépendantes) laisse comprendre que
chaque électron agit dans un sous espace vectoriel qui lui est propre.
Et ces sous espaces vectoriels ne s'emboîtent pas. Ainsi, l'espace
d'état décrivant le système total est un produit tensoriel
des sous espaces
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
d'états engendrés par des électrons pris
individuellement. Ainsi, la fonction d'onde électronique s'écrit
:
n
H =??á i (i) = ?á 1 (1)
?á2 (2)... ?án (n) . (1.22)


i =1
En projetant cette relation dans la base spatiale
électronique, on obtient :
n
|
H ( r , R )= ??
ái( ri)
|
.
|
(1.23)
|
i =1
Où (pá i (ri ) représente
l'orbitale moléculaire du i -ième électron. ai
est un indice composite représentant l'ensemble des nombres quantiques
associés à cet orbitale. 'PH
représente la fonction d'onde de Hartree. Ainsi,
l'énergie électronique est alors définie par :

E H = ØH H e
ØH . ( 1 .24)
Soit :
n
E H = ? (i)... ?á n (n)
hi ?á 1 (1)... ?á i
(i)..Ván (n)



(1.25)
i =1

i = 1 j = 1
+ 2n
1



(1)... ?á i (i)... ?á n (n)
1 ?á 1 (1)... ?á (i)... ?á
n (n) + VNN
j i
?
= - ?r-
2
i
est la somme de l'énergie cinétique d'un
électron peuplant
h i
1
2
N Zj
j =1 R j - ri
?

l'orbitale ?á et de l'énergie potentiel
de son attraction par les noyaux. Les fonctions ?á
étant orthonormées, il est clair que :





i = 1i = 1 j = 1
-- E (i) hi
EH -- (Pá i (Pá i (i) + 1
alo) ajo 1
E 0) jo +VNN
. (P.J (Pi (Pa.J
. (1.26)
2 ?? rij
En plus, on remarque que les intégrales
biélectroniques sont indépendantes des numéros des
électrons considérés. Ainsi, dans les écritures, on
pourra seulement considérer les électrons 1 et 2. De ces
considérations, l'équation (1.26) devient :
i = 1i = 1 j = 1
n n



E H = (Pá E (1) h 1
?á (1)
(Pa
, (1.27)
1 ?? (1) ?a (2) 1 á (1) ?á
(2) + V
NN
2 r (P

ij
que l'on peut encore écrire :
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
n n n
1
E = ? + ?? + NN , (1.28)
h J V
H i ij
2
i 1
= i 1 j 1
= =
j i
?
où

h i = ? á i (1) h 1 ? á i (1) est
l'énergie orbitalaire du i-ième électron,
|
1
J = ? á (1) ? á (2) ? á (1) ? á
(2)
ij i j i j
r ij
|
|
est l'énergie d'interaction coulombienne entre les
|
électrons i et j. Pour déterminer cette
énergie, Hartree utilise le principe variationnel repris par Vladimir
Fock[6].
Au niveau de sa fonction d'onde, la méthode de Hartree
traite mal la corrélation électronique (Parlant de
corrélation électronique, deux électrons
sont dits corrélés lorsque le mouvement de l'un
influence celui de l'autre. Dans le cas contraire, les électrons sont
dits indépendants. Nous reviendrons sur cet aspect au paragraphe
1.2.3.). Elle ne prend pas en compte le spin électronique. Ce qui
est une violation du postulat de symétrisation, plus
particulièrement le principe d'exclusion de Pauli (Deux électrons
de même spin ne peuvent occuper le même état quantique).
C'est pour lever ce dernier échec que Fock proposa une fonction d'onde
monodéterminentale dite slaterienne construite à l'aide de spin -
orbitales.
1.2.1.2. Méthode de Hartree -
Fock
Afin de corriger la fonction d'onde de Hartree, Fock proposa une
fonction d'onde du type :
n
Ø = A? ? á (i) s (i)
m , (1.29)
H i i


i 1
=
telle que : 1 ( 1)
A = ? - P est
l'opérateur d'antisymétrisaton ; P est
l'opérateur de
ó
ó
n!
permutation et est la fonction d'onde spinorielle de
l'électron i. Par la suite, il
smi (i)
définit l'énergie électronique comme
étant :

E HF = ØHF H e ØHF .
(1.30)
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
En tenant compte des propriétés de
l'antisymétriseur A et en posant :
Ö qi (i) = ? á i ( ri)s
mi (i) avec q i = (ái,mi) ,
on a :

Ö q l (i) Ö qk (j) = ä ij
ä m i mj, (1.31)
et
n n
? ? ? ?
= ? ? ? ? ? ? ?
2
E HF q e q
? Ö (i) H A ? Ö (i) ?
i i
? i 1
= ? ?
(1.32)
i =1 ?
n n nn n n
? ? ? ? 1 ? ? ? ? ? n
A ?
= ? [ ]
h A ? +
q i q ? q q
? ? ? ?
Ö (i) ? Ö (i) ?? ? Ö (i) ? ? ? ? ? Ö (i)
V
? + NN
i i i i
2 r
i 1
= ? i 1
= ? ? i 1
= ? i i 1
= = ? i 1 ? ? ? ? ? ?
= ij i 1
= ?


Par définition, h i Ö
qi(i) = h i Ö qi (i) . Ainsi, en raison de
l'orthogonalité des
fonctionsÖ , le premier terme de l'équation (1.32)
n'est non nul que lorsque P=1 (application
identique) . En effet, toute permutation peut être
décomposée en un nombre fini de transpositions [7], et
dans chaque permutation différente de l'identité, il existe au
moins une transposition qui permettra d'annuler ce premier terme. Quant au
deuxième terme contenant l'opérateur
biélectronique 1 , il est non nul seulement
rij
lorsque l'opérateur P représente
soit la permutation identique (1), soit la transposition entre
les électrons i et j (Pij). Ainsi, l'équation
(1.32) devient :
n n n



1 1 P
- ij
E = ? Ö (i) Ö (i)
h + Ö (i)Ö (j) V
HF q i q q q q q NN
?? Ö (i)Ö (j) +
i i i j i j
2 r
i 1
= i 1 j 1
= = ij
j ?i



n 1 n n 1
= ?
h ?? Ö (i)Ö (j) Ö (i)Ö (j)
i +
q q q q
i j i j
2
(1.33)
=
i
=
1 i
=
1 j
1
rij
j ?i
n n
1 2 ?? Öqi (i)Öqj(j)
i = 1 j =1

1
rij
Ö q (j)Ö (i) +VNN
q j

n n n
= ?
1
h J
i + ij
??
2
i =1 i = 1 j =1
j ?i
n n
1 ?? +
K V
ij NN
2
i = 1 j =1
j ?i
??K
avec
Ji


1
Ö (2) Ö (1) Ö (1) Ö (2)
=
q q q q
j i i j
r12
Ö (2) = Ö (1) 1 Ö (2) Öq j
(1)
r 12
? =

J Ö (2) Ö (2)
J
(1.34)
ij q i q j
et j
?? ?? =
K Ö (2) Ö (1)

K
ij q i qj j
A partir des définitions des Öch , on peut
réécrire Ji et Kij comme suit :
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

J = ? (2) J ? (2
ij q i q
j j
K = ? (2) K ? ( 1)
ij q i q
j j
?
?? ??
)
(1.35)
Dans le but de déterminer les variations de
l'énergie, il est convenable d'exprimer l'énergie en fonction des
opérateurs de Coulomb :
n n n


1
(1.36)
E = ? Ö (i) Ö (i)
h + ?? i - K
+
( Ö (2) Ö (2) Ö (2) Ö (1) V
J )
HF q i q q q q i q NN
i i j j j j
2
i 1
= i 1 j 1
= =
j i
?
La famille de fonctions d'ondes étant inconnue, le nouveau
problème à
? ?
? ?
Ö =
qi i 1,...n
résoudre est de déterminer une base de
spinorbitale qui minimise l'énergie, ou la rend au moins stationnaire
par un changement de spinorbitale. Les nouvelles spinorbitales restant toujours
orthogonales et normées : Il s'agit donc ici d'une optimisation par
contrainte [8]. Ce principe peut donc être mis en
évidence par la méthode des coefficients de Lagrange. En bref, la
condition est qu'une légère variation des orbitales de base ne
puisse modifier la fonction de Lagrange ; ce qui signifie que la fonction de
Lagrange ainsi définie doit être stationnaire par rapport à
une variation d'orbitales de base. On définit donc la fonction de
Lagrange comme suit :
n n

? =
L E - ë ? ? Ö (i) Ö (j) - ä ? ?
? HF ij q q
?? ij
i j
(1.37)
i 1 j 1
·
= =
??
n n

? et L E
ä = ä - ë ä
? Ö (i) Ö (j) Ö (i) Ö (j) 0
- ä ? =
HF ij q q q q
?? i j i j
?? ? ?
i 1 j 1
= =
Où les ë ij sont les multiplicateurs de
Lagrange. De la relation (1.36), on a :
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
n nn n
ä



1 1
E = ä
? Ö (i) Ö (i)
h + Ö (i) Ö (i)
h ä + ?? ä Ö (i)Ö (j) Ö
(i)Ö (j)
HF q i q q i q q q q q
?
i i i i i j i j
2 r
i =1 i =1
i = 1 j = 1 ij
j i
?
n n n n


1 1 1 1
+ ?? Ö (i) Ö (j) Ö (i)Ö (j)
ä + Ö (i)Ö (j) Ö (i)Ö (j)
ä
q q q q q q q q
??
i j i j i j i j
2 r 2 r
i 1 j 1
= = ij i 1 j 1
= = ij
j i
? j i
?

n n

1 1
+ q q
?? Ö (i)Ö (j)
i j
2 r
i 1
= j 1
= ij
1 1

n n
Ö (i) Ö (j)
q q q q q q
i j i j i j
2 r
= =
i 1 j 1 ij
ä - ?? ä Ö (i)Ö (j) Ö (j)Ö (i)
j ? i j i
?
n n n n


1 1 1 1
Ö (i) Ö (j) Ö (j)Ö (i)
ä - Ö (i)Ö (j) Ö (j) Ö (i)
ä
q q q q q q q
?? q
i j i j i j i j
2 2 ??
r r
i 1 j 1
= = ij i 1 j 1
= = ij
j i
? j i
?
j i
?
n ?n
2 i 1 j 1
1
Ö (i)Ö (j) Ö (j) Ö
(i
ä
q q q q
i j i j
r ij


=
=

Les indices i et j étant muets, cette relation devient
alors :
n n

E = ä
? Ö (i) Ö (i)
h + ? Ö (i) Ö (i)
h ä
HF q i q q i q
i i i i
ä
i 1
= i 1
=
n n


?
?
? ?
?
?
? ?
1 ? 1 1
+


?? ? ä Ö (i)Ö (j) Ö (i)Ö (j) Ö
(i)Ö (j) Ö (j)Ö (i)
- ä
q q q q q q q q
i j i j i j i j
2 ? r r
= =
i 1 j 1 ? ij ij
j i
n n
1 ?
+ 2 ?? ? ?
i 1 1
= =
i ?
j i
?

?


1 1
Ö (i)Ö (j) Ö (i) Ö (j) Ö (i)Ö (j)
Ö (j) Ö (i)
ä - ä
r ij rij
q q j q j q j i j
Remarquons de plus que pour i=j, les deux derniers termes de
l'équation précédente sont nuls. Ainsi, on peut se passer
de la condition i ?j et l'on obtient donc :
n n
E = ä
? Ö (i) Ö (i)
h + ? Ö (i) Ö (i)
h ä
HF q i q q i q
i i i i
ä
i 1
= i 1
=
n n






1 ? 1 1 ?
+ ? Ö (i)Ö (j) Ö (i)Ö (j) Ö (i)Ö
(j) Ö (j)Ö (i) ?
q q q q q q q q
i j i j i j i j
2 ?? - ä
ä
? r r
i 1 j 1
= = ? ij ij ? ?

n n
1 ?
+ ?? ?
2 ?
i 1=j 1
= ?
1 1 ?



Ö (i) ä Ö q j ( j) - (i)Ö q j (j) (j) ä
Ö qj (i)
r ql r
ij ij ? ?
En vertu de leur qualité muets, les indices i et j peuvent
être permutés. Donc
n n

ä = ? ä
E Ö (i) Ö (i)
F + ? F ä
Ö (i) Ö (i) , (1.38)
HF q i q q i q
i i i i
i 1
= i 1
=

UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
n
avec F = h i + ?(
J j - Kj). (1.39)
j =1
Fi est appelé
opérateur de Fock ou
Fockien.
Par suite, la variation de la fonction de Lagrange dans
l'équation (1.37) devient :


??
nn n ä L = ? F
? ä Ö (i) Ö (i) Ö (i) Ö (i)
+ F ä ? - ë ? ä + ä
q i q q i q ij q q q
? ?? ? Ö (i) Ö (i) Ö (i) Ö (i)
i i i i i i i i
? q
i =1 i = 1 j =1
En utilisant les relations :
* *
Ö ä Ö = ä Ö Ö , Ö F
ä Ö = ä Ö F Ö et ä L =
0, nous avons :
n? n ?


ä = ? ä
L - ë ä
q i q ij q
? Ö (i) Ö (i)
F Ö (i) Ö (i) ?
q
?
i i i i
i 1
= ? ? j = 1 ? ?
n ? n


* * ?
+ ? ä - ë ä ? =
q i q ij q q
? Ö (i) Ö (i)
F ? Ö (i) Ö (i) 0
i i i i
i 1
= ? ? j = 1 ? ?

Cette relation devant être vérifiée quelque
soit äÖ et *
äÖ , il est clair que :
n




ä Ö(i) Ö (i)
F - ë ä
? ?? ? Ö (i) Ö (i) 0
q =
q i q ij q
i i i i
j 1
=
n
?




* *
Ö(i) Ö (i)
F ä - ë =
q i q ij q
? Ö (i) Ö (i) 0
ä q
i i i i
j =1
En prenant le conjugué complexe des deux derniers termes
du système précédent, et en
les soustrayant des deux
premiers termes, on obtient :

n

? ë - ë ä
( ) i
* Ö (i) Ö (i) 0
= . Soit *
ë ij = ë ji indépendamment de ä
Ö qi (i) . Ainsi,
ij ji q q i
j =1
la matrice des coefficients de Lagrange X est
une observable. Les ont donc un sens ij
physique que nous préciserons dans la suite. On arrive
alors à l'équation :

n
= ?ë
Ö q j (j)
(1.40)
F
ij
i Ö qi (i)
j=1 i =1,...,n
Cette équation constitue l'ensemble des
équations de Hartree - Fock. Pour simplifier son écriture, on
choisit une transformation unitaire qui diagonalise la matrice des
multiplicateurs de Lagrange. Ainsi, les vecteurs de base de cette
transformation unitaire sont ceux qui diagonalisent le Fockien. On les
appellera donc les spinorbitales
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
moléculaires canoniques. Remarquons que réaliser
cette opération revient à choisir les ë ij tels
que ë ij = å i äij. Ainsi, dans la base canonique,
l'équation (1.40) s'écrit :

F Ö (i) Ö (i)
~ ~
q = å
i q i
i i
(1.41)
.
i
1,...,n = Les équations (1.41), dites de Hartree - Fock
seront donc appelées les équations aux
pseudo-valeurs propres. Et les coefficients de Lagrange peuvent
être interprétés dans la base canonique Fockienne comme les
énergies spin-orbitalaires monoélectroniques.
En tenant compte des équations (1.39) et (1.41), on peut
écrire :
n
å = + ? - , (1.42)
h ( )
J K
i i ij ij
j 1
=
Soit enfin,
n n n n n
? ?? ??K V . (1.43)
? 1 1 ?
E J +
HF = å -
i ij - ij NN
2 2
i 1
= ? i 1 j 1
= = i 1 j 1
= = ?
j i
? j i
?
? ?
En définitive, l'énergie électronique
proposée par Fock diffère de celui de Hartree par le terme
d'échange qui n'est effectif que pour deux électrons de
même spin. Ainsi, dans le formalisme de Fock, chaque électron est
entouré par un double trou :
· Un trou de fermi : Deux
électrons de même spin ne s'approchent pas.
· Un trou de Coulomb : Deux
électrons se repoussent en tant que particules de même charge.
1.2.1.3. Méthode de Roothaan et Hall (LCAO)
Rappelons tout d'abord qu'une orbitale atomique (OA) permet de
décrire la distribution des électrons autour d'un atome ; alors
qu'une orbitale moléculaire (OM) permet de décrire la
distribution des électrons autour d'une molécule.
Dans une molécule, l'électron appartient
à l'ensemble des atomes et il ne peut plus être décrit par
une OA, mais par une OM. En effet, au sein d'une molécule,
les atomes ne perdent pas complètement leurs
identités (c'est l'idée forte de la LCAO) qui sont
justement à l'origine de la liaison chimique. Ainsi, les OA de cette
molécule sont une information clé ou mieux les acteurs de la
liaison ; pour tout dire la base de la
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
molécule. Donc une orbitale moléculaire est une
combinaison linéaire d'orbitales atomique.
Ainsi, on peut écrire les ?ái (OM) sous
la forme :
? á (i) = ? ÷
C â â ?
(i) (1.44)
i i n
[ ]
i
[ m]


â?
Où m est la dimension de la base d'OA (nombre de fonctions
÷â ) et Câ i ? 0 ? â? [ m ] , i?[ n] .
Introduisons l'opérateur densité de charge
défini en un point r de l'espace par,
|
ñr = ? ? r ? r
= ?? ? ÷ r ÷ r = ? ?
÷ r ÷
* * *
( ) á ( ) á ( ) C C ( ) ( )
* P ( ) ( )
r
ì í ì
i i í ìí ì í
i i
i n
? [ ]i n
? ì? í?
[ ] [ ] [ ]
m m ì? í?
[ ] [ ]
m m
|
(1.45)
|
|
Où
|
Pìí = ? í (1.46)
C ì * i C i
|
i ?[ n]
Développons les équations de Hartree-Fock dans la
base de Roothaan et Hall.

( j)
Fj ?á j (j) =
å j ?áj (j)
? 1 1 ?
h

? (j) + ? ? (i) ? (i) (j)
? - ? (i) ? (j) (i)
ë
? ä = å
? ÷
j m m j j
? C
á á á á á á á
ë
?
j i i j i i j i j
r
i ? ? r ij ij ? ? ë

?
s i ìíó
? 1 1
( j) * (i) (i) ( j) * ÷ (i) ( j) (i)
C j j
h ÷ + i i j i j i m m
? C C C ÷ ÷ ÷ - ÷ ÷ ä
C C C
s ó ì í ó ì í ó
ì í ó ì í i
? ó
r r
? ij ij



?
j ?
?
j) (1.48)
= å C ÷
j j
? ó

(
ó
ó
En projetant dans la base d'OA, on arrive à :
1
En posant : (2) (1) ÷ í ÷
ó
(1) (2)
÷ ô ÷ ì
, l'équation (1.50) devient:


r12

= ìí ôó
?1 1 ?


* ( j) (i) ÷ ÷ -
(i) ( j) * ( j) (i) ( j) (i)
C (h )
j j i i j i j i m m
? ? C C C ÷ ÷ ÷ ÷
C C C ÷ ÷ ä
ó ôó + ì í ó
ô ì í ó ì í ó ô ì
í ó i j
? r r ?
s
(1.49)
i ìíó ? ij
ij ?
= å
j j
? C S
ó ôó
ó
Soit :
?
? 1 1





(2) (1) (1) (2) ÷ ÷
(2) (1) (2) (1)
+ ?
C (h ) ÷ ÷ ä
j j j j m m
? P C ÷ ÷ ÷ ÷ - P C
ó ôó ìí ó ô
ì í ó ìó í ô ì í
ó 1 2
s ìíó
(1.50)
? r 12 r12
= å
ôó
j j
? C S
ó
ó
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
|
? ?
C (h ) P C j (
ó j j ôó ìí ó m m j
j
1 2 ) = C S
ó ôó
? ? + ? ìí ôó - ìó
ôí ä ? ? å
ó ? ?ìí ?? ó
|
, (1.51)
|
soit :
avec
? - å
C ó i F ôó
( )
(i) i S ôó =0 . (1.52)
ó


F ôó (i)÷ ô (i)F
÷ ó(i) (h i )
ôó + ? PìíCói ( ìí
ôó - ìó ôí ä 1 m2) . (1.53)
m
ìí
La forme matricielle de l'équation (1.52) est donc :
( F - åS ) C
= 0. (1.54)
L'approximation LCAO a donc converti les équations aux
dérivées partielles complexes de Hartree-Fock en un
système d'équations algébriques simple. Dans cette
approximation, on a :
*
h i = Ö (1) h i
Ö q i (1) =?C ìi C í i (h i)ìí
, (1.55)







ìí


ìí ëó , (1.56)
J = Ö (1)Ö (2) 1 Ö (1)Ö (2) = ? C
ì C í C ó C ë
* *
ij q q q q i j i j
i j i jr
12 ìíóë
1
K Ö (1)Ö (2) Ö (2)Ö (1)
= = ? C ì C í C
ó C ë
* * ìó ëí ä . (1.57)
ij q q q q i j i j m m
i j i j i j
r 12 ìíóë
Par la suite, en substituant (1.55), (1.56) et (1.57) dans
l'équation (1.33), on arrive à :
E = ? + ? ìí ëó - ìó
ëí ä (1.58)
P ìí h ìí
( i ) P ìí P ëó
(
HF m m
i j )ìí
ìíëó
Ainsi, déterminer l'énergie électronique
d'un système moléculaire revient à procéder comme
suit :
1) Choisir les fonctions d'essai constituantes la base
d'orbitales atomiques.
2) Calculer la matrice densité
Pìí .
3) Calculer l'énergie électronique ( )
E (1) = ? + ? ìí ëó - ìí
ëó ä m
P ìí h ìí P
ìí P ëó (
i m i j )
ìí ìíëó
4) Calculer le Fockien (
F ôó (h i ) ôó
(i) = + ? ìí ôó - ìó
ôí äm m
P ìí C ó i 1 2 )
ìí
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
5) Diagonaliser le Fockien afin d'en extraire les vecteurs
propres qui constitueront une nouvelle base de combinaisons linéaires
d'orbitales atomiques.
6) Calculer la nouvelle énergie électronique
E(2)

Si le rapport (2)
E - E E est supérieur à la précision
fixée, on recommence les
(1) (1)
étapes 2) à 6).
On résume tout ceci par le graphique ci-dessous :
Obtain initial guess for density
matrix


False
Form new density matrix
Diagonalize Fock matrix
Test convergence
Form Fock matrix
True
E=En
Jusqu'à lors, nous avons décrit la
méthode Hartree-Fock sans aucune restriction sur la forme de la fonction
d'onde spatiale. Ainsi, les fonctions d'onde d'essai sont dites de type
«unrestricted Hartree-Fock» (UHF).
Si le système étudié possède un
nombre d'électrons pair, la fonction d'onde du système est un
singulet. On dit alors qu'il s'agit d'un système à couches
fermées. La
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
restriction qu'un tel système impose est que chaque
orbitale spatiale devrait avoir deux électrons, un de spin á (up)
et l'autre de spin â (down). Les fonctions d'onde ainsi construites sont
de type <<restricted Hartree-Fock» (RHF).
1.2.2. Les bases de calculs.
Comme nous l'a déjà appris la méthode
LCAO, les fonctions d'onde moléculaires peuvent s'écrire comme
des combinaisons linéaires d'orbitales atomiques (OA) formant une base
de représentation pour ces OM. En principe, n'importe quel type de
fonction de base peut être utilisé pour la description d'une OM :
exponentiel, gaussien, polynomial, onde plane, ...etc. Mais, tous ces types ne
sont pas bien adaptés. Pour choisir le type de fonction d'onde de base
à utiliser pour la description optimale d'un système
moléculaire, on se base sur deux critères fondamentaux :
Premier critère : Le type de base choisi doit
avoir un comportement en accord avec la physique du problème
étudié. Ceci assure une convergence rapide des calculs lorsque
plusieurs fonctions de base sont ajoutées. En d'autres termes, les
fonctions de base choisies doivent s'annuler pour des électrons
très éloignés des noyaux.
Deuxième critère : Les fonctions d'onde
choisies doivent faciliter le calcul de toutes les intégrales requises.
Le premier critère suggère fortement l'usage des fonctions
exponentielles pour chaque noyau. L'inspiration vient du fait que ces fonctions
décrivent bien l'atome d'hydrogène, surtout le comportement au
voisinage de zéro. Elles ont été par ailleurs mises en
évidence par Slater. D'où leur nom de fonctions de Slater
1.2.2.1. Les fonctions de Slater.
Comme nous l'avons déjà mentionné, les OA
fonctions propres de l'opérateur de Fock atomique, peuvent être
représentées par des fonctions de Slater STO (<<Slater Type
Orbitals»).Les fonctions de Slater étant de même type que les
fonctions hydrogénoïdes, une STO centrée sur l'atome a
s'écrit[4] :
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
|
n 1 ra m
*
÷ = Cr e Y
- -î
a a l
|
( )
è a
, ?
a
|
*
-ó
Z Z
eff
î = =
*
n n
(1.59)
où ( est l'harmonique sphérique liée
à l'atome a.
Y l è a , ? a
m )
C est une constante de normalisation,
ra est la distance de l'électron à
l'atome a.
Z est le nombre d'électrons de l'atome
considéré.
ó est l'effet d'écran des électrons les plus
internes de l'atome considéré.
Dans le cas des hydrogénoïdes, on a î = 1 .
Pour un atome différent d'un hydrogénoïde, les fonctions de
base sont construites à partir des combinaisons linéaires de
fonctions de Slater. Cependant, lorsque dans un système, chaque orbitale
atomique est représentée par une seule fonction de Slater, la
base des fonctions utilisée est dite minimale
ou Single Zéta (SZ). Dans le cas
contraire, on parle de base étendue. Une base
étendue peut être du type :
Double Zêta (DZ) : Chaque
sous-couche d'orbitales atomique est représentée par deux
fonctions de Slater.
Triple Zêta (TZ) : Chaque
sous-couche d'orbitales atomique est représentée par trois
fonctions de Slater.
Quadruple Zêta (QZ) : Chaque
sous-couche d'orbitales atomique est représentée par quatre
fonctions de Slater.
Quintuple Zêta (5Z) : Chaque
sous-couche d'orbitales atomiques est représentée par cinq
fonctions de Slater.
...etc. Ici, l'expression Zêta est liée à
l'argument grec î de l'exponentiel; nommé zêta. Les
fonctions de Slater telles que décrites respectent bien le premier
critère de choix d'une fonction de base ; mais, elles violent le second
critère. Ceci dans le sens que le calcul des intégrales
biélectroniques à deux centres ou plus, rend l'utilisation de ces
fonctions très lourde et très coûteuse en temps de calcul.
C'est pour cette raison que l'usage de ces fonctions reste très
limité aux atomes et aux molécules diatomiques.
Pour surmonter les difficultés rencontrées dans les
calculs des intégrales multicentres, Boys[10]a introduit les
fonctions gaussiennes pour remplacer les slateriennes.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
1.2.2.2. Les fonctions gaussiennes.
Les fonctions gaussiennes GTO («Gaussian type
orbitals») sont le produit d'une harmonique sphérique et d'une
fonction radiale. Les GTO habituellement utilisées sont de la forme :
|
2
÷ a = Nx l x y l y z lz e-áa
ra
|
.
|
(1.60)
|
L'indice a permet de repérer l'atome a ; á
a est le coefficient de la gaussienne traduisant la
diffusivité de l'orbitale : Plus á a est petit, plus
l'orbitale décrite est diffuse. Par contre, lorsque á
a est grand, on parle d'orbitale polarisée. N est un facteur
de normalisation. On montre qu'il est défini par :


3 ( ) ( 2l 2m 2n 3 4
+ + + )
l m n
+ +
4
? ?
2 2 á
1 2 , (1.61)
N = ? ?
? ð ? ? -
? ( ) ( ) ( )
2l 1 ! 2m 1 ! 2n 1 !
- - ? ?
où n, l et m sont respectivement les nombres quantiques
principal, secondaire et azimutal. La somme donne le type angulaire de
l'orbitale. Ainsi, si
l x + l y + l z
lx + l y + lz=0, 1, 2,.. .,il
s'agit respectivement d'une orbitale de type s, p, d, f,.... Nous avons alors
respectivement les orbitales ÷ as , ÷ ap ,
÷ ad ,... définies comme suit :
÷=
asN se
-á
as r:
2
N xe áap a = p p x
2
?÷ ap = ?N ye áap ra = py
2
? -á ap r a
N ze = p
p z
??
?
?
?
?
?
÷ ad =
?
2
N d x 2e -áad ra = dxx
2
2 -á ad a
N y e r = d
d yy
2
N d z 2e -áadra = dzz
r 2
ad a
N xye -á = d
d ' xy
r 2
ad a
N xze -á = d
d ' xz
r 2
ad a
N yze -á = d
d ' yz
?
? ?
? ?
(1.62)
Pour une orbitale de type d, on peut former les combinaisons
linéaires suivantes : d x 22 -y - 2 , d 2z -2 - 2 - y2 ,
dxy , d, dyz qui représentent bien les cinq
orbitales d disponibles dans
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
une couche électronique de nombre quantique principal
supérieur ou égal à trois. Les fonctions définies
par l'équation (1.62) ont une propriété avantageuse : Le
produit de deux gaussiennes centrées sur deux noyaux A et B
différents est équivalent à une gaussienne centrée
en un point C situé entre A et B et d'exposant á C = á
A+ áB. Ainsi,
toutes les intégrales biélectroniques à
plusieurs centres se ramènent à une somme d'intégrales
monocentriques qui se calculent aisément. Remplacer une orbitale de
Slater par une gaussienne simplifie énormément les calculs, mais
présente quelques inconvénients. En effet, une gaussienne ne
reproduit pas correctement le comportement de la fonction d'onde au voisinage
du noyau, ni à l'infini. Les exponentielles en
e-á r2 constituent donc une
approximation moins bonne que les exponentielles en e-î
r pour la représentation des orbitales atomiques. Ainsi, le
développement des orbitales moléculaires en série de
fonctions de gaussiennes nécessite donc beaucoup plus de termes que leur
développement en fonctions de Slater. Il faut utiliser environ trois
fois plus de GTO que de STO pour atteindre une énergie donnée.
Ainsi, si le calcul des intégrales biélectroniques est
facilité par l'utilisation des fonctions gaussiennes, le nombre de ces
intégrales augmente. Pour décrire au mieux une slaterienne, il
faut combiner linéairement au minimum trois GTO (Voir figure 1.1).
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

Figure 1.1 Représentation d'une orbitale
de Slater STO ( î = 1 ) par une, deux et trois fonctions
gaussiennes, dont les paramètres sont optimisés par
recouvrement maximal avec l'orbitale de Slater.
La qualité d'une base de gaussienne dépend donc de
trois facteurs :
-Le nombre de fonctions primitives (étendue de la
base).
-La méthode utilisée pour l'optimisation des
coefficients de combinaison et des exposants de la
gaussienne[11].
-Le nombre et le type de contractions[12-13].
Dans la pratique, pour le choix des exposants des gaussiennes,
on a recours à la littérature où sont tabulées des
bases dites standard, de tailles différentes pour plusieurs atomes.
Pour se rapprocher le plus possible de la solution
Hartree-Fock, la base d'orbitales doit être suffisamment étendue
dans des limites raisonnables, afin de ne pas dépasser la
capacité des ordinateurs. Pour les calculs SCF, nous utiliserons des
gaussiennes contractées (CGTO), c'est-à-dire des combinaisons
linéaires des gaussiennes primitives (PGTO) de la base standard :
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
÷ = ? ÷ g (1.63)
(k)
t
a ak
k [N ]
? g
|
Où :
· ( )
k
÷g
|
k ? [N ]
g
|
sont les gaussiennes définies par l'équation
(1.60).
|
·

t ? sont des coefficients supposés connus au départ
du calcul variationnel
ak k [N ]
g
moléculaire ; et peuvent être optimisés sur
les atomes séparés.
· Ng est le Nombre de fonctions primitives.
Pour un atome donné, Ng est plus grand pour
les OA des couches internes que pour celles des couches externes à cause
de leur grande contribution à l'énergie électronique de la
molécule et de la variation rapide des orbitales atomiques près
du noyau.
La base d'orbitales atomique doit bien décrire le
système à toutes les distances interatomiques et pour tous les
degrés d'excitation intervenants dans les calculs. C'est la raison pour
laquelle on ajoutera aux bases standard des orbitales plus diffuses, pour bien
décrire les couches de valence ; et des orbitales de corrélation
ou de polarisation non occupées dans l'état fondamental de
l'atome pour décrire les phénomènes relatifs à la
corrélation électronique ou à la déformation des OA
dans la molécule.
Dans une base, pour un atome donné, lorsqu'on
représente les orbitales s, p, d, ... par n1, n2, n3, ... PGTO, cette
base est notée (n1s, n2p, n3d, ...) pour cet atome.
Si par la suite, cette base est contractée en m1, m2,
m3, ... CGTO, elle est alors notée (n1s, n2p, n3d, ...)/[m1s, m2p, m3d,
...]. Cette notation a l'avantage d'indiquer directement les tailles des bases
contractées et non contractées. Mais, elle ne permet pas de
comprendre comment les contractions sont effectuées. Dans la suite, nous
verons comment les bases contractées sont classifiés.
1.2.2.3. Classification des bases
contractées.
Pour comprendre les stratégies d'amélioration des
bases, on peut découper
l'espace en Trois zones comme l'indique la figure 1.2.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
|
Orbitales internes
Orbitales de valence
Orbitales diffuses
|
|
Fig 1.2 : les zones à considérer
dans la conception d'une base.
Après avoir décidé du type de fonctions
de base à utiliser, le facteur le plus important est le nombre de ces
fonctions à prendre en compte. Ainsi, comme nous l'avons
mentionné plus haut, on pourra construire une base minimale ou
étendue.
La base minimale est formée
d'orbitales entrant dans la configuration électronique du fondamental de
chaque atome. Ainsi, par exemple pour les éléments de la
deuxième ligne du tableau périodique (n = 2 , doncl = 0 ou 1), la
base minimale sera
construite de deux orbitales s (1s et 2s) et d'un ensemble
d'orbitales p ( px , p y , p z ) pour
chaque atome.
La base étendue quant à elle
est construite en multipliant toutes les orbitales de la base minimale par un
coefficient constant. Ainsi, lorsque le coefficient vaudra 2, 3, 4, 5, ..., on
aura ainsi construit respectivement les bases DZ, TZ, QZ, 5Z,... Ainsi, la base
QZ pour un élément de la deuxième ligne du tableau
périodique contient huit orbitales s (4 orbitales 1s et 4 orbitales 2s)
et quatre ensembles d'orbitales p (soit 12 orbitales p). En principe l'effet de
la multiplication des orbitales de la base minimale est négligeable sur
les orbitales de coeur, et plus marqué sur les orbitales de valence. On
pourra donc ainsi construire de nouvelles bases suivant le même principe
que précédemment, mais en gardant le nombre de fonctions
décrivant les orbitales de coeur constant (ce nombre est celui de la
base minimale). Elles seront par la suite dénommées
VDZ (pour valence double zêta), VTZ
(pour valence triple zêta), VQZ (pour valence quadruple
zêta),... Dans la littérature, on laisse souvent de
côté la lettre V et ces bases sont
délibérément appelées DZ, TZ, QZ, 5Z,... Notons
qu'une base étendue a l'intérêt de pouvoir décrire
les systèmes pour lesquels la distribution des électrons est
différente dans plusieurs directions[14]. Mais cette base
devient insuffisante lorsqu'il faut décrire
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
des liaisons polarisées ou diffuses. Il faudra donc
introduire les orbitales de polarisation et diffuses.
Intuitivement, pour polariser une orbitale s, on lui
associera une orbitale p ; on associera une orbitale d à une orbitale p
pour la polariser et ainsi de suite. On retient donc que les orbitales de
polarisation d'une orbitale atomique de moment angulaire l sont les orbitales
de moment angulaire l + 1 qu'on pourrait lui associer. Par définition,
les orbitales de polarisation permettent de bien décrire la
corrélation électronique (corrélation statique, radiale et
angulaire) ; c'est pourquoi elles seront aussi appelées
orbitales de corrélation. Ainsi, par exemple, une base
VQZ enrichie d'un, de deux ensembles de fonctions de polarisation sera
respectivement dénommée VQZP (pour valence
quadruple zêta plus polarization), VQZ2P (pour valence
quadruple zêta plus double polarization). Contrairement aux orbitales de
polarisation, les orbitales diffuses sont
caractérisées par un coefficient de gaussienne á plus
petit, permettant ainsi une bonne description des anions et des états
excités.
Les bases contractées les plus utilisées sont
celles de pople, de DunningHuzinaga, ....
Comment ces bases se présentent-elles ?
1.2.2.3.1. Bases de Pople.
Se sont des bases de type STO-nG et
k-nlmG développées par Pople et
al[15]. Bases de type STO-nG
Se sont des bases d'orbitales de Slater construites à
l'aide de n fonctions gaussiennes primitives. Les
inconvénients de ce type de base est qu'elle détermine les
coefficients de ces PGTO par un fitting sur les STO au lieu de les optimiser
via une procédure variationnelle et considère les mêmes
exposants de PGTO pour les orbitales s que pour les orbitales p. Ce qui
réduit la flexibilité de la base bien que le temps de calcul se
voit réduit. La base minimale la plus utilisée ici est la base
STO-3G et la plus étendue est la base STO-6G.
Pour montrer comment les fonctions sont réparties dans
ce type de base, prenons l'exemple d'un atome de la deuxième ligne du
tableau périodique décrit dans la base STO-6G et consignons ceci
dans le tableau 1.1.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Orbitale
|
Contractions
|
Primitives
|
1s
|
1
|
1 x 6 = 6
|
2s
|
1
|
1 x 6 = 6
|
2p
|
1
|
3 x 6 = 18
|
Total
|
3
|
30
|
|
Tableau 1.1 : Présentation de la base
STO-6G pour un atome de la deuxième ligne du tableau
périodique.
Un atome de la deuxième ligne du tableau
périodique dans cette base est donc représenté par 30 PGTO
contractées en 3 CGTO. Ainsi, cette base pour l'atome
considéré est équivalente à la base
(12s6p)/[2s1p].
Base de type k-nlmG
Se sont des bases de démultiplication des couches de
valence notées :
· k-nlG pour les bases VDZ.
· k-nlmG pour les bases VTZ.
Où k est le nombre de primitives utilisées pour
représenter les orbitales de coeur. Les indices n, l, m indiquent
respectivement le nombre de primitives entrant dans chaque contraction pour les
orbitales de valence.
Ces bases ont l'avantage de lever le problème
d'optimisation posé par leurs prédécesseurs en
déterminant les coefficients des PGTO par des procédures
variationnelles. Mais, ne résolvent pas le problème d'exposants
identiques pour les orbitales s et p. Comme exemple, disséquons la base
6-311G pour un atome de la deuxième ligne du tableau périodique.
On a alors le tableau 1.2 suivant :
Orbitale
|
Contractions
|
Primitives
|
|
1s
|
1
|
1 x 6 = 6
|
|
2s
|
3
|
1 x (3+1+1)
|
=5
|
2p
|
3
|
3 x (3+1+1)
|
= 15
|
Total
|
7
|
26
|
|
|
Tableau 1.2 : Présentation de la base
6-311G pour un atome de la deuxième ligne du tableau
périodique.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Un atome de la deuxième ligne du tableau
périodique dans cette base est donc représenté par 26 PGTO
contractées en 7 CGTO. Ainsi, cette base pour l'atome
considéré est équivalente à la base
(11s5p)/[4s3p].
Dans chacune de ces bases, on peut ajouter des fonctions
diffuses et/ou de polarisation. Les fonctions diffuses sont
généralement des fonctions s et p. Elles sont marquées par
un plus (+) ou deux plus (++) avant le symbole G. Lorsqu'elles sont
marquées par +, les fonctions diffuses sont ajoutées sur les
atomes lourds. Lorsqu'elles sont marquées par ++, la fonction diffuse s
est aussi ajoutée. Quant aux fonctions de polarisation, elles sont
marquées après le symbole G, par les fonctions concernées
ou par une ou deux étoiles suivant qu'on ait respectivement un ou deux
ensembles de polarisation. La base standard de Pople la plus large est la base
6-311++G (3df, 3pd). C'est une base triple zêta
enrichies des fonctions diffuses sp, de trois ensembles de fonctions d et d'un
ensemble de fonctions f toutes sur les atomes lourds et d'un ensemble de
fonctions diffuses s, de trois ensembles de fonctions p et d'un ensemble de
fonctions d toutes sur les hydrogènes.
Comme exemple, présentons la base 6-311+G* pour un atome
de la deuxième
ligne du tableau périodique. On a alors le tableau 1.3
suivant :
|
|
Orbitale
|
Contractions
|
Primitives
|
|
1s
|
1
|
1 x 6 = 6
|
|
2s
|
3
|
1 x (3+1+1)
|
=5
|
2p
|
3
|
3 x (3+1+1)
|
= 15
|
s diffuse
|
1
|
1 x 1 = 1
|
|
pdiffuse
|
1
|
3 x 1 = 3
|
|
d polarisante
|
1
|
5 x 1 = 5
|
|
Total
|
10
|
35
|
|
|
Tableau 1.3 : Présentation de la base
6-311+G* pour un atome de la deuxième ligne du tableau
périodique.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
1.2.2.3.2. les bases de Dunning-Huzinaga.
Les bases de Dunning sont affranchies des restrictions
imposées par les bases de Pople. Elles sont par la suite très
flexibles, mais très coûteuses en temps de calcul. Les plus
utilisées sont les bases « correlation consistent
» en abrégé cc. Ces bases ont
l'avantage de réduire le nombre de fonctions de base utilisées
par les bases d'orbitales atomiques naturelles en produisant
des résultats très comparables. Elles sont
dénommées par cc-pVDZ, cc-pVTZ, cc-pVQZ, cc-pV5Z et cc-pV6Z
(correlation consistent polarized Valence
Double/Triple/Quadruple/Quintuple/Sextuple Zeta). Leurs structures sont
présentées dans le tableau 1.4a[16]. Pour obtenir des
énergies optimales, on ajoute à ces bases des fonctions diffuses.
Ceci se fait en ajoutant, à chaque fonction de moment angulaire
l une fonction de même moment angulaire, mais d'exposant
plus petit. Pour dénommer de telles bases, on ajoute simplement le
préfixe aug- (pour Augmented) devant la
dénomination de leurs bases parentes. Leurs structures sont
présentées dans le tableau 1.4b.
Bases Fonctions primitives Fonctions
contractées
cc-pVDZ 9s4p1d 3s2p1d
cc-pVTZ 10s5p2d1f 4s3p2d1f
cc-pVQZ 12s6p3d2f1g 5s4p3d2f1g
cc-pV5Z 14s9p4d3f2g1h 6s5p4d3f2g1h
cc-pV6Z 16s10p5d4f3g2h1i 7s6p5d4f3g2h1i
Tableau 1.4a : Les bases correlation
consistent.
Bases Fonctions primitives Fonctions
contractées
aug-cc-pVDZ 10s5p2d 4s3p2d
aug-cc-pVTZ 11s6p3d2f 5s4p3d2f
aug-cc-pVQZ 13s7p4d3f2g 6s5p4d3f2g
aug-cc-pV5Z 15s10p5d4f3g2h 7s6p5d4f3g2h
aug-cc-pV6Z 17s11p6d5f4g3h2i 8s7p6d5f4g3h2i
Tableau 1.4b : Les bases augmented correlation
consistent.
La plus grande base de Dunning est la base aug-cc-pV7Z.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
1.2.3 Limites de la méthode
LCAO-SCF.
De ce qui précède, une base idéale
devrait avoir une dimension infinie. Les capacités des ordinateurs
imposent une réduction de l'espace vectoriel où on se place. De
ce fait, la limite Hartree-Fock (EHF) n'est jamais atteinte. La
taille de la base et la qualité des fonctions la constituant en
constitue une limite.
Par ailleurs, la méthode LCAO-SCF donne une fonction
d'onde décrite par un seul déterminant de Slater ; ce qui revient
à obliger chaque électron à rester dans une spin-orbitale
Ö á , et à négliger ainsi « une
partie >> de la corrélation entre électrons. De
plus, de part son caractère variationnel, cette
méthode ne peut que permettre d'atteindre l'état le plus bas
(fondamental) d'un système. Elle est donc inadaptée pour
l'étude des états excités. Ceci bien entendu, n'est pas
sans conséquence négative sur l'évaluation des
différentes grandeurs physiques déduites de la fonction d'onde de
Hartree-Fock telles que les énergies de dissociation, d'excitation, les
sections efficaces, les moments dipolaires, la polarisabilité, etc.
C'est ainsi par exemple que les longueurs de liaison ont tendance à
être plus courtes dans un calcul SCF. Il est donc nécessaire
d'aller au-delà de ce modèle à particules
indépendantes, et d'évaluer l'énergie de
corrélation non prise en compte.
Parlant de corrélation, deux électrons sont
dits corrélés lorsque la probabilité de trouver l'un
à une position quelconque dépend de la position de l'autre. En
général, la corrélation électronique est à
double titre :
- Les électrons se repoussent d'abord comme fermions de
même spin,
- Les électrons se repoussent ensuite comme particules de
même charge.
Cette corrélation à double titre est souvent
interprétée par une représentation imagée où
l'électron est entouré d'un « trou de Coulomb >> et
d'un « trou de Fermi >> qui annihilent plus ou moins, respectivement
l'apparition dans son voisinage d'une particule négative et d'une
particule de même spin.
La corrélation électronique peut être
classée en deux groupes : La corrélation
dynamique et la corrélation statique.
La corrélation dynamique est due à la
répulsion de courte portée, de deux électrons, qui
entraîne leur éloignement l'un de l'autre (i.e. Diminution de
l'énergie).
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Quant à la corrélation statique, elle est
dûe aux effets de longues portées (états excités,
rupture de liaison,...).
La méthode de Hartree traitait déjà une
partie de l'énergie de corrélation de part sa description de
l'Hamiltonien du système où les électrons se repoussent
entre eux en tant que particules de même charge. Quant à la
méthode de Hartree-Fock, non seulement elle récupère
l'énergie de corrélation de Hartree, mais aussi, de part sa
fonction d'onde qui interdit la cohabitation de deux électrons de
même spin, elle récupère une autre partie de
l'énergie de corrélation. Malgré l'énergie de
corrélation récupérée par la méthode de
Hartree-Fock, l'énergie électronique totale donnée par
cette méthode reste inférieure à la valeur
expérimentale et vaut 99 % de celle-ci. Il reste donc 1% de
l'énergie expérimentale à récupérer. Cette
énergie s'appelle énergie de corrélation ;
bien entendu en prenant le niveau d'énergie HF comme
référence. Ainsi, l'énergie de corrélation peut
s'exprimer comme la différence entre l'énergie
expérimentale et l'énergie de Hartree-Fock :
E corr = E éxacte - EHF (1.64)
Dans les paragraphes suivants, nous exposerons les
méthodes (méthodes PostHartree-Fock) qui permettent de lever les
difficultés posées par la méthode LCAO qui jusqu' à
lors, est la mieux adaptée. Ces méthodes auront donc pour
objectifs de récupérer l'énergie de corrélation et
de traiter les états excités.
1.2.4. Méthodes d'approche de
l'énergie de corrélation ou méthodes
Post-Hartree-Fock
1.2.4.1. Introduction.
Les méthodes de corrélation électronique
peuvent être classées en deux grands groupes : Les
méthodes variationnelles et les méthodes
de perturbation.
Parlant des méthodes variationnelles, on peut
citer :
· L'Interaction de configuration,
(CI pour configuration interaction).
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
· La Méthode du Champ autocohérent
multiconfigurationnelle, (MCSCF pour
Multi-Configuration Self-Consistent Field ).
· L'Interaction de Configuration
Multi-Référence (MRCI pour
Multi-Reference Configuration Interaction ).
· La Théorie de la Fonctionnelle de la
Densité (DFT pour Density Functional
theory).
· Les méthodes Monte Carlo.
Les deux dernières ne sont pas des méthodes
post-HF et ne seront pas exposées explicitement dans ce travail.
Parlant des méthodes de perturbation, on peut
citer :
· La méthode des perturbations multi
corps (MBPT pour Many Body Perturbation Theory) ou
plus précisément MPn (Moller Plesset d'ordre
n).
· La méthode des clusters
couplés (CC pour Couplet Clusters).
Rappelons que le point de départ de toutes ces
méthodes de corrélation est la fonction d'onde de HF. Par
conséquent, pour tout traitement de la corrélation, la fonction
d'onde s'écrira :
8

Ö = ø + ? ø , (1.65)
a a
0 HF i i
i 1

=
avec a 0 1 , et déterminé par la
condition de normation de la fonction d'onde Ö . Les

méthodes de corrélation diffèrent dans la
manière de calculer les coefficients ai. Les øi sont
les déterminants additionnels et s'appellent encore
déterminants de Slater
excités.
Comment les déterminants de Slater
excités sont-ils construits ?
Les øi sont construits par excitation des
électrons des orbitales occupées de la
fonction d'onde HF (déterminant de
référence) vers les orbitales virtuelles
(orbitales
inoccupées). En effet, avec un système à n
électrons construit à l'aide de M fonctions
de base, on a n 2
( resp. (n + 1) 2) occupées dans le cas RHF (resp. ROHF) et
M - n 2 ( resp. M - (n + 1) 2) orbitales virtuelles, qui vont
recevoir les électrons issus
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
des orbitales occupées après être
excités. On pourra donc exciter 1,2,3,... électrons
des
orbitales occupées vers les orbitales virtuelles. Ce qui conduira
aux déterminants de
Slater simplement, bi-, tri-,... excités
respectivement. L'équation (1.65) pourra donc
8 8 8

+...
encore s'écrire : 0 HF
Ö = ø + ? ø + ? ø + ? ø
a a a a
s s D D T T
s D T
Les indices S, D,T,... sont respectivement liés aux
déterminants de Slater simplement, bi-, tri-,... excités.
Illustrons ceci par le diagramme de la figure 1.3.
En considérant le cas où n = 6 et M = 8

HF Simples excitations(S) Doubles excitations (D) (T)
(Q)
Fig 1.3 Déterminants de Slater
excités.
On comprend ainsi que le nombre de déterminants
excités générables dépend de la dimension de la
base de fonctions décrivant le système considéré.
Il faut donc prendre en compte dans une base donnée, tous ces
déterminants de Slater excités, afin d'espérer
évaluer complètement l'énergie de corrélation. Par
ailleurs, à l'aide d'une base infinie, l'équation de
Schrödinger est résolue de façon exacte dans l'approximation
de Born Oppenheimer et non relativiste. De ceci, il découle que les
méthodes de corrélation électronique ont deux
degrés de liberté : La dimension de la base utilisée et le
nombre de déterminants de Slater excités. En effet, plus la
dimension de la base utilisée et le nombre de déterminants sont
élevés, meilleurs sont les résultats.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Pratiquement, les changements chimiques importants prennent
naissance seulement dans les orbitales de valence. Les orbitales de coeur sont
presque constantes. Ainsi, dans plusieurs situations, on s'intéresse
seulement au calcul de l'énergie de corrélation associée
aux électrons de valence : C'est l'approximation du coeur
gelé.
1.2.4.2. Méthode d'Interaction de Configuration
(CI).
Dans la méthode CI, les ai sont calculés de
manière variationnelle [17]. En effet, on définit
comme pour la méthode SCF, une fonctionnelle

L = Ö Ç Ö - ë ? Ö Ö - 1 ? ? ,
CI e CI ? CI CI
8
où CI
Ö = ? ai ø . (1.66) i
i =0
La condition de minimisation de l'énergie impose :

?
L =0
, (1.67)
? ai
soit :
a i( E i -ë) + ? a j
ø Ç e ø j = 0 . (1.68)
j ?i
Le problème variationnel posé conduit donc
à résoudre le système d'équations séculaires
suivant :
?-
H E H ... H ... a
? ? ? ? ?
0
00 01 0j 0
? ... a
? ? ? ?
H E ... H ?
H -
10 11 1j ? ? ? ? ?
0
? 1
(1.69)
? ... ... ... ... ......
? =
? ? ? ?
...
? ? ? ? ? ?
H ... ... H E ... a
- 0
? j0 jj ? ? ? ? ?
j
?... ... ... ... ......
? ? ? ? ?
? ? ? ? ? ?
...

Où H ij = ø i Ç
e ø j. Ce qui est équivalent
à l'équation matricielle :
Ç a = Ea
Ç = ( ij ) i,j ( i ) i
H a a
=
???
??
(1.70)
Il est donc clair que (de part 1.66), pour déterminer les
coefficients , il suffit juste
( i ) i
a
de diagonaliser la matrice CI, Ç = H .
L'énergie donnée par la méthode CI est la
( ij ) i,j
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
plus petite valeur propre pour le fondamental ; les autres
valeurs propres sont les énergies des états excités.
Remarquons que la matrice CI a beaucoup d'éléments nuls :
· Les éléments matriciels ( ij ) i,j
H issus de deux déterminants de spins total
différents sont nuls. Ceci se justifie par le simple fait
que l'Hamiltonien du système ne contient pas de spin.
· Si de plus, le système étudié
possède une symétrie donnée, on aura encore sans doute
d'autres éléments nuls dans ladite matrice. En effet, les
éléments de H issus des déterminants
n'admettant pas des projections nulles suivant les représentations
irréductibles du système sont tout aussi nuls.
· Les éléments issus des déterminants
de symétries différentes sont
( Hij )
également nuls. En effet, l'Hamiltonien du
système considéré appartient
toujours à la
représentation totalement symétrique. Par suite,
l'intégrale


ø i Ç e
ø j serait non nulle si et seulement si, øi
et ø j appartiennent à la
même représentation
irréductible[18] : C'est la règle
générale de sélection.
· Les éléments ( issus des
déterminants qui diffèrent de plus de deux orbitales
Hij )
=
0
moléculaires (spatiales) sont aussi nuls. En effet,
l'Hamiltonien du système est constitué seulement
d'éléments à un et deux corps. Ainsi, on aura :


° 1 2
Ö Ö Ö Ö Ö
... ... ... ... h Ö Ö Ö Ö Ö = ?
ä
... ... ... .. h
i j k i 1 2 i ' j' k ' i áá '
á? I
car cardI = 1 . Où I est l'ensemble des indices des
orbitales à gauches de h i qui diffèrent de leurs homologues
à droite.

° 1 2
Ö Ö Ö Ö Ö
... ... ... ... g Ö Ö Ö Ö Ö = Ö
Ö
... ... ... .. g
i j k ij 1 2 i' j' k ' i j ij i' j'
Ö Ö ? ä =
áá 0
'

á?I'
avec I ? I ' tel quecardI = cardI'+ 2 = 3. En conclusion,
ø ì Ç e ø
í = 0 lorsque card I = 3 . Ce résultat est d'ailleurs la
règle de Slater-Condon.
· Les éléments de matrice ( Hij )
issus de l'état de référence HF et d'un
déterminant mono excité sont nuls : C'est le
théorème de Brillouin. En effet,
pour un déterminant mono-excité, on excite un électron de
l'orbitale i de la configuration de référence ( ø
0 ) vers une orbitale a. On alors :
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

a
ø H ø = Ö Ö +
h
0 e i i a i j a j i j j a
? ? ? Ö Ö Ö Ö - Ö Ö Ö Ö
? ?
j

(1.71)
= F
Ö Ö
i a

= puisque les
å ä Ö sont fonctions propres de F.
i ia i
= 0 car i a.
?
Remarquons de plus que d'après le résultat de
Slater-Condon, et du résultat précédent, l'état de
référence ne produira des éléments de matrice non
nuls qu'avec des déterminants bi-excités. Et on aura :

ø 0 H e ø ij = Ö
i Ö j Ö a Ö b - Ö
i Ö j Ö b Ö a (1.72)
ab
De part cette multitude d'éléments nuls dans la
matrice CI, elle acquière une structure diagonale par blocs. Cette
matrice est par ailleurs symétrique et définie positive. Ce qui
simplifiera davantage les calculs ! La matrice CI a donc la structure finale
suivante :
|
ø HF
|
ø S
|
ø D
|
ø T
|
ø Q
|
ø Q5
|
...
|
...
|
...
|
ø HF
|
EHF
|
Ï
|
|
Ï
|
Ï
|
Ï
|
LÏ
|
|
Ï
|
ø S
ø D
ø T
ø Q
ø Q5
|
Ï
Ï
Ï
Ï
|
Ï
Ï
|
Ï
|
|
Ï
|
Ï
Ï
|
LÏ
L
Ï
|
Ï
L
Ï
|
Ï Ï Ï Ï Ï
|
M
|
M
|
M
|
M
|
O
|
|
|
|
|
|
M
|
Ï
|
Ï
|
Ï
|
Ï
|
Ï
|
|
|
|
|
M
|
Ï
|
Ï
|
Ï
|
Ï
|
Ï
|
Ï
|
|
|
|
|
Dans cette matrice, les représentent des matrices nulles
de dimension p.q où p et q
Ï
représentent respectivement les nombres de fonctions
de base du sous-espace vectoriel engendré par les excitations
électroniques d'un type donné (S, D, T, Q,...), respectivement
d'un autre type donné (S, D, T, Q,...) afin de former la matrice Hpq.
Par ailleurs, de part la limite des supercalculateurs, aucun
calcul ne peut être effectué dans une base infinie ; et le full CI
n'est possible que sur des systèmes de très petites tailles. On
comprend donc la nécessité de tronquer la méthode CI. Ceci
se fait en se limitant aux excitations doubles, triples, quadruples ou plus. Ce
qui conduira respectivement aux méthodes CIS, CISD, CISDT, CISDTQ,...
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
De part les théorèmes de Slater-Condon et
Brillouin, on comprend que plus on prendra en compte de type d'excitations,
mieux on traitera la corrélation et les états excités.
Cependant, la méthode CI généralement applicable à
une très grande variété des systèmes est la
méthode CISD ; bien que la méthode CISDTQ donne des
résultats généralement très proches du full CI.
Les méthodes CI ne connaissent pas de succès
sans échecs. En plus de leur temps de calcul relativement long, elles
souffrent du problème de contamination de
spin.
1.2.4.3. Méthode du champ autocohérent
multiconfigurationnelle (MCSCF).
La méthode MCSCF peut être
considérée comme une CI où les coefficients ai ne sont pas
les seuls à être optimisés par le principe variationnel,
mais aussi les orbitales moléculaires entrant dans la construction des
déterminants excités[19]. Ces méthodes plus
rapides que les précédentes, ne soufrent pas de la contamination
de spin. Elles sont généralement utilisées pour
générer des fonctions d'ondes assez flexibles et permettant ainsi
de récupérer l'énergie de corrélation statique.
Elles ont l'inconvénient de ne pouvoir pas traiter la corrélation
dynamique d'une part, et de ne pas converger d'autre part. On utilise la
méthode de Newton-Raphson pour forcer sa convergence.
Le problème majeur avec la méthode MCSCF est la
sélection manuelle des configurations nécessaires à
introduire lorsqu'on s'intéresse à des propriétés
bien précises du système à étudier. L'approche la
plus populaire pour résoudre ce problème est la méthode
CASSCF (Complete Active Space Self-Consistent Field) encore
appelée FORS (Full Optimised Reaction Space). Dans
cette méthode, la sélection des configurations se fait en
partitionnant l'espace des orbitales moléculaires en trois sous espaces
:
· L'espace interne ou
espace de coeur, où les OM restent
doublement occupées. Généralement, les électrons de
ces OM sont gelés. On n'y effectue donc aucune excitation. C'est donc un
espace inactif.
· L'espace actif,
où les OM peuvent être occupées ou inoccupées. Cet
espace est constitué de quelques HOMO (Highest occupied Molecular
orbitals) et de quelques LUMO (Lowest unoccupied Molecular orbitals). C'est
dans cet espace qu'ont lieu toutes les excitations possibles.



UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
· L'espace externe situé
au-dessus de l'espace actif. Cet espace est inactif. Donc l'espace externe et
l'espace de coeur constituent l'espace inactif.
Dans la méthode CASSCF, l'espace actif coïncide avec
l'espace de valence formé à partir des OA de valence des atomes
qui forment la molécule.
Une fois le partitionnement effectué, les
configurations utilisées sont construites en considérant les
différentes possibilités de répartir les électrons
peuplant les orbitales actives dans leur propre sous espace. Ainsi, dans le
sous espace des orbitales actives, la méthode CI est complète.
D'où l'appellation « Complete active Space ».
La figure 1.4 montre le partitionnement de l'espace des OM dans
le cas de la molécule de NO dans une base de dimension 15.
N : 1s2 2s2 2p3
O : 1s2 2s2 2p4
Core
Valence
Espace externe.

Orbitales virtuelles
Espace de valence = Espace actif.
2s2(O) + 2p4(O)
+ 2s2(N) + 2p3(N)
Orbitales occupées.
Espace interne = Espace de coeur 1s2(N) +
1s2 (O)
Fig 1.4 Partitionnement de l'espace des
orbitales moléculaires du système NO.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
1.2.4.4. Méthode d'interaction de configuration
multiréférence
La méthode d'interaction de configuration
multiréférence appelée par les anglosaxons multireference
configuration Interaction (MRCI) est une approximation dans laquelle la
fonction d'onde est encore une combinaison linéaire de
déterminants de Slater. Elle utilise comme référence la
fonction d'onde MCSCF et n'autorise que les simples et doubles excitations
à partir de cette dernière. On a ainsi :
+ ?? c Ö + ?? c Ö . (1.73)
a a ab ab
ø = ø
MRCI MCSCF s s D D
s a D ab
Les et sont des fonctions de configurations
générées à partir de la fonction
a Ö D ab
Ö S
multiconfigurationnelle MCSCF.
L'un des avantages majeur de la méthode MRCI est que
la fonction d'onde correspondante permet une meilleure prise en compte de la
corrélation. Cependant, le nombre de configurations
généré est souvent trop élevé. Ce qui a pour
effet d'alourdir les calculs, notamment en termes de temps machine. Pour rendre
les calculs faisables, on a souvent recours à de nouvelles
approximations. En général, on ne choisit que les configurations
dont le poids statistique dans la fonction d'onde est important. On peut aussi
associer à cela la contraction des configurations dans le but d'en
diminuer le nombre .
Les différentes approximations effectuées dans
la méthode MRCI diminuent la quantité d'énergie que l'on
peut récupérer par corrélation. Par ailleurs, le fait de
ne pas inclure les excitations quadruples diminue également la
flexibilité de la fonction d'onde. Pour remédier à ces
inconvénients, Davidson propose la correction qui porte son nom et qui
consiste à prendre en compte les excitations quadripolaires à
l'aide de l'approximation
Ä E Q = 1 - a 0 Ä E CISD .
(1.74)
( 2 )
ÄECISD est la correction en énergie due aux simples
et doubles excitations.
1.2.4.5. La méthode des clusters
couplés.
Dans cette méthode, la fonction d'onde
électronique décrivant un système de N électrons
est écrite sous la forme suivante[20] :
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

Ø cc = e Ø 0 (1.75)
T
Où Ø 0 est la solution de Hartree-Fock
et est un opérateur défini par son
e T
développement de Taylor :
e 1 T T ...
T 1 2
= + + +
2!
, (1.76)
k
8
T
=?
k!
k 0
=
avec T un opérateur cluster (ou d'excitation) qui peut
s'écrire :
N
T T T
= + + L + = ? i , (1.77)
T T
1 2 N
i 1
=
Où N est le nombre d'électrons du
système.
L'opérateur Ti agît sur la fonction d'onde de
référence de Hartree-Fock et génère tous les
déterminants de Slater excités i fois. Ainsi,
occ vir
a a
T Ö
Ö =
1 0 ?? t i i


ab ab
T Ö =
2 0 ?? t ij ij
Ö


i j a b
p p
T1 et T2 donnent respectivement toutes les excitations
simples et doubles. De la même manière, on peut construire des
opérateurs pour les excitations triples, quadruples, etc...
On peut remarquer que :
e = 1 + T + T + T + T + T T + T + T + T T + 2 T +
2 T T + 24 T +L T 1

( ) ( ) (
1 2 4
1
3 2 1 1
2
) ( ) (1.79)
1 2 2 1 3 2 1 6 1 4 3 1 1 2 1 1
Les couples de parenthèses 1, 2, 3, 4,... donnent
respectivement tous les états simplement, doublement, triplement,
quadruplement,... excités.
Avec la fonction d'onde « clusters » couplés,
l'équation de Schrödinger devient :

He Ø 0 = E cc e Ø 0 .
(1.80)
T T
Ce qui conduit à :

Ø 0 He Ø 0 = E cc Ø
0 e Ø 0 = E cc . (1.81)
T T
Par la suite, on a :
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
E = Ø H 1 T T T
1 2
( + + + ) Ø
cc 0 1 2 2 1 0


occ vir occ vir
b a
=E t a a ab a b
H ( t t t t t ) Ø
0 + ?? Ø Ø + ?? + -
i 0 i ij i j i j 0
(1.82)
H
Ø
a i

i a i j a b
-< -<
D'après le théorème de Brillouin, on a
finalement :
occ vir

. (1.83)
ab a b b a
E E
= + ( )
cc 0 ij i j i j i j a b
?? ?
t t t t t ?
+ - Ö Ö Ö Ö - Ö Ö Ö Ö
?
i j b a ?
i j a b
-< -<
Les équations des clusters couplés sont
résolues de façon itérative en utilisant E cc = E
0 comme point de départ.
Si tous les opérateurs Ti sont introduits dans
l'équation de cluster T, tous les déterminants possibles seront
générés et la fonction d'onde Ø cc est
équivalente à une
fonction d'IC complète. Pour limiter le
développement (1.77), on utilise dans la
méthode des clusters
couplés, comme dans les méthodes d'IC, une base des
OM
tronquée. Si l'on fait les restrictions T = T1 et T =
T1 + T2,... on, obtient respectivement
les méthodes CCS, CCSD
et ainsi de suite. L'aspect important dans ces méthodes
CC
est que les excitations d'ordres supérieurs
à ceux correspondant à la coupure de T
entrent dans les
équations des amplitudes. Ce qui rend la théorie CC
extensive en taille.
1.3. RESUME DES METHODES DE CORRELATION
ELECTRONIQUES
Les méthodes de corrélation
généralement utilisées sont : CISD, CCSD, CCSD
(T), MPn, MCSCF et MRCI.
En termes de précision, avec des bases de dimensions
moyennes, on a l'ordre suivant :
HF CISD < MCSCF < MP4(SDQ) CCSD < CCSD(T) < MRCI
En termes de temps de calculs, le tableau 1.5 compare les
méthodes CI, CC et MP. Le temps de calcul avec les méthodes HF
est de l'ordre de M4. M étant la taille de la base.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Temps proportionnel à
|
Méthodes CI
|
Méthodes MP
|
Méthodes CC
|
M5
|
|
MP2
|
C
|
M6
|
CISD
|
MP3, MP4 (SDQ)
|
CCSD
|
M7
|
|
MP4
|
CCSD(T),CC3
|
M8
|
CISDT
|
MP5
|
CCSDT
|
M9
|
|
Mp6
|
|
M10
|
CISDTQ
|
MP7
|
CCSDTQ
|
|
Tableau 1.5: Ordre de grandeur des
coûts informatiques des méthodes CI, MP et CC.
On peut comparer ces différentes méthodes de part
leurs avantages et leurs inconvénients par le tableau 1.6.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Méthodes Avantages
Inconvénients
HF
· Temps de calcul apaisé
· Ne prend pas en compte la
corrélation statique.
· États excités non décrits.
· Size extensivity*
· Fonctions d'onde peu
·
flexibles.
Non size consistency*. CI
·
Bonne précision
· Temps de calcul élevé.
· polyconfigurationnelle
· Non size
consistency.
· Non size extensitivity.
· Contamination de Spins.
MCSCF
MRCI
CC MP
|
·
·
·
·
·
·
·
·
·
·
|
Pas de contamination de
Spins
Fonctions d'onde flexibles Récupère
l'énergie de
corrélation statique.
Bonne précision.
Très grande précision
Très précise (CCSDTQ).
«Size extensitivity et size
consistency»
Très précise (MP6).
«Size extensitivity».
|
·
·
·
·
·
·
·
·
·
·
|
Convergence difficile
Temps de calcul élevé. Sélection des
configurations difficile.
Fonctions d'onde moins
flexibles.
Nombre de configuration
très élevé.
Temps de calcul très élevé.
Pas variationnelle. Monoréférentielle. Temps de
calcul prohibitif.
Pas variationnelle.
|
|
Tableau 1.6: Avantages et inconvénients
des méthodes HF et post-HF.
* Une méthode est dite << size extensive
>> lorsque l'énergie qu'elle fournie est proportionnelle
au nombre d'atomes du système (idem qu'en thermodynamique) à
toutes les géométries du système étudié.
Une méthode est dite << size consistency
>> lorsqu'il donne l'énergie EA+E B pour deux
sous systèmes A et B bien séparés.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
La différence entre ces deux qualités de
méthode est donc que la size extensitivity se vérifie à
toutes les géométries alors que la size consistency n'est valable
qu'à la limite de dissociation du système moléculaire.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
CHAPITRE 2
RESOLUTION DE L'EQUATION DE
SCHRÖDINGER NUCLEAIRE.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
2.1. INTRODUCTION.
Après avoir déterminé les puits de
potentiel sur lesquels se meuvent les
électrons, il est tout aussi très
intéressant de maîtriser les mouvements des noyaux. Dans cette
section, la théorie des groupes nous sera d'une très grande
utilité.
2.2. RESOLUTION DE L'EQUATION DE SCHRÖDINGER
NUCLEAIRE PAR
LA METHODE DES PERTUBATIONS.
L'étude de la dynamique des noyaux revient à la
résolution l'équation de Schrödinger nucléaire (1.21)
:
? T N + V j ( ) ? Ø Nj
( ) = E T Ø Nj ( ) .
R R R
? ?
Pour résoudre cette équation, on fait en plus
de l'approximation de Born-Oppenheimer, une deuxième approximation
d'ordre zéro qui suppose que le mouvement de rotation de la
molécule est indépendant de ses mouvements de vibration ; de
sorte que l'on peut étudier la vibration de la molécule en ne
tenant pas compte de sa rotation, puis la rotation globale de la
molécule supposée indéformable.
2.2.1. Vibrations moléculaires.
2.2.1.1. Cas simple d'une molécule
diatomique.
2 2
? ?
h ?
? - 2 U(R) n E
+ ? Ø = n
Ø . (2.1)
? ì ?
2 R ?
Considérons le cas d'une molécule diatomique
qu'on assimilera à un système constitué de deux atomes de
masses ponctuelles M1 et M2 séparées par une distance R et
interagissant par l'intermédiaire d'un potentiel U(R). Le système
ainsi formé a une énergie totale E et vérifie
l'équation de Schrödinger suivante :
Le premier terme dans (2.1) est l'énergie
cinétique de vibration ; est la masse réduite
ì
du système.
Un développement en série de Taylor de U au
voisinage de son minimum ( R = R e)
donne :
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
(2.2)
? ?
dU 1 d U
? ?
2 2 1 d U
? ?
3
3
U(R R )
- = ? ? - + ? ? -
( )
R R ( )
R R + ? ? -
( )
R R + ...
e e 2 e 3 e
? ?
dR 2! dR
R ? ? 3! dR
? ?
e R R

e e
2! ?dR
1 d 2 U (R -R e)2 + 1 d3U1 ( R
-R e)3 +...
2 R 3! ? dR3 R
e e
Les mouvements moléculaires étant de faible
amplitude, on peut, dans l'approximation harmonique, négliger les termes
de degré supérieur à deux. Ainsi, on a :
U(R - R e ) = 21k ( R
-Re)2
Où k = C1.2U
dR2 est la constante de force harmonique. Ainsi, la
résolution de

Re
l'équation (2.1) conduit aux solutions suivantes :
[ Ø n p) C p e 2 á ( R -Re) 2H p (
á ( R - Re ))
(2.4)
E ( p) = ( p+ 12 )hù
1
Lì 1 dRd 2 U2 ?2
03 = Avec p ? 0 , =pulsation de l'oscillateur. ; H
p=polynôme
Re
d'Hermite ;
( 2 p p! á ð) 2
ìù
= Constante de normalisation et .
á =
h
Cp =

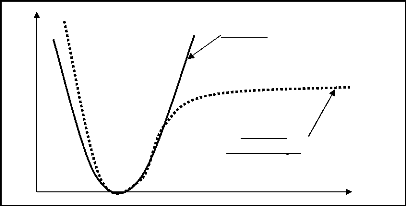
Potentiel
Potentiel
anharmonique
Figure 2.1 : Potentiel harmonique et
anharmonique.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Physiquement, le potentiel harmonique ne parvient pas
à expliquer la dissociation des molécules et certaines
transitions vibroniques. En effet, l'approximation harmonique devient
très vite insuffisante dès que l'on s'éloigne de la
position d'équilibre. D'où l'idée de l'approximation
anharmonique.
2.2.1.2. Potentiel anharmonique.
Pour un tel potentiel, on ne néglige plus les termes
de degré supérieur à 2 dans l'équation (2.2). Toute
fois, comme ils sont très inférieures au terme quadratique, on
peut considérer la correction qu'ils apportent à l'hamiltonien
total du système comme une perturbation stationnaire. Ainsi, en
première approximation, on peut écrire :
1 2 1 d U
? ?
3
3
U(R R ) k R R
- ( )
- + ? ? -
( )
R R
e e 3 e
2 6 dR
? ? R e
Par suite, au second ordre de perturbation, on a :
|
. (2.5)
|
|
( )
p ? ? ?
1 1
E = ? + ? ù - ? +
p h p
? ? ?
2 2
? ? ù x
h . (2.6)
e
?
2
Où xe est une constante positive
appelée constante d'anharmonicité. L'écart entre deux
niveaux consécutifs d'énergie n'est plus constant et vaut :
E E
( p ) ( p 1 )
- ? ?
- = ù ? - ? +
h 1 x p
e
? ?
Ainsi, les niveaux se resserrent lorsqu'on monte en
énergie.
Une des formes analytiques de potentiel anharmoniques la plus
couramment utilisée est le potentiel de Morse[21] (fig. 2.2)
:
U R D e 1 e-â -
( e ) 2
R R
( ) = ? - ? ? . (2.8)
?
.
hùe
=
x e
(2.11)
4D
e
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
.
.
(a)
.
.
.
De
D0
.
(b)
2 hù
1
Figure 2.2 : Potentiel de Morse. (a)
Continuum, (b) Limite de dissociation
Où De est l'énergie de dissociation et
â une constante caractéristique de la molécule
considérée.
En faisant un développement limité à
l'ordre 3 au voisinage de la position d'équilibre Re, on
trouve :
( ) ( ) ( ) ( ( ) )
â 3
2 2 3 3
U R D e R R e
= â - - R R e
- + Ï -
R R . (2.9)
e
2
En identifiant cette relation à la relation (2.5), on
arrive à :
1
? ì ? 2
â = ? ? ù . (2.10)
e
? ?
2De
Et l'énergie du système est donnée par la
relation (2.6) avec
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
2.2.1.3. Vibrations moléculaires en
mécanique quantique[22].
Dans une molécule polyatomique, les atomes
constitutifs subissent des oscillations autour de leur position
d'équilibre. Au cours de ces oscillations, les longueurs des liaisons et
les angles intramoléculaires changent de façon
périodique.
En posant

q i = Miri,
n
M M
% = +? m
i i i
. (2.12)
i 1
=
L'énergie totale de vibration s'écrit :
N 1 N
= ? % r & = ? & qi .
(2.13)
1 2 2
E M
V i i
2 = 2 =
i 1 i 1
L'énergie potentiel de vibration V(q), où q
désigne l'ensemble des coordonnées qi, peut
être
développée en série de Taylor au voisinage de la position
d'équilibre de chaque
qi0
atome ; soit :
N ? ? ?
V 1 N N ? ? ?
2 V
V q V q
( ) ( )
= + ? ? +
? q ?? ? ? +
q q ...
0 i i j
i 1
= q
? ? ? 2
i i 1 j 1 ? ? ? ? ? ?
q q
= =
q i j
i0 q i0
|
(2.14)
|
|
En prenant l'origine de l'énergie potentiel à
l'équilibre, on a ; la courbe
V ( q 0 ) = 0
d'énergie potentiel passe par un minimum
pourqi = q 0 . Ainsi, le second terme du
i
membre de droite de (2.14) est nul. En se limitant à
l'approximation harmonique, on a :
N N ? ? ?
2
1 V
V q
( ) = ?? á q q , á = ? ?
ij i j ij
2 i 1 j 1
= = ? ? ? ? ? ?
q q
i j q
i0
|
. (2.15)
|
|
Pour étudier complètement le mouvement
vibratoire d'un système, nous devons préciser ses
coordonnées normales, ses coordonnées internes et ses
coordonnées de symétrie.
2.2.1.3.1 Coordonnées normales
Les coordonnées normales sont les nouvelles
coordonnées qui conservent la forme
Qi
de l'énergie cinétique, tout en permettant
d'exprimer l'énergie potentiel sous une forme quadratique. En effet,
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
1 1
2 2
E = ? ?
q & = Q&
V i i
2 2
i i
1 1 2 2
V q
( ) = ? á q q = ? ù Q
ij i j k k
2 2
i, j k
(2.16)
?
Où est une fréquence propre du système.
Dans ce cas, une énergie propre du
ùk
système est donnée par
3N 6
-? ?
1
E = ? + ? ù +
? h ? ? xij
n
k k
k 1 ? ?
2
= j j i
<
L'intérêt des coordonnées normales
réside dans le fait qu'elles permettent de réaliser une
représentation irréductible du groupe de symétrie du
système étudié. En effet, à chaque fréquence
propre du système, on peut toujours associer une coordonnée
normale. Ce qui caractérise un mode propre de vibration précis,
qu'on peut aisément associer à une représentation
irréductible du groupe de symétrie du système global. On
comprend donc que les coordonnées normales d'un système
permettent de classifier ses vibrations. Mais, la détermination
explicite de ces coordonnées normales est assez épineuse. Pour
s'affranchir de cette difficulté, on utilisera la théorie des
groupes.
2.2.1.3.2. Classification des vibrations
moléculaires.
Pour classifier les vibrations moléculaires, on
procède comme suit :
· On détermine la représentation totale
engendrée par les 3N coordonnées de déplacement des atomes
de la molécule.
· On détermine la représentation vibratoire
totale v en éliminant dans les
représentations associées aux translations et
rotations d'ensemble.
· On décompose ensuite v en
représentations irréductibles.
óv
C2
O
H H
Figure 2.3 La molécule d'eau
Etudions par exemple le cas de la molécule d'eau (H2O)
dont la structure géométrique est représentée par
la figure 2.3.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Compte tenu de ses éléments de symétrie,
cette molécule appartient au groupe C2v. Sa
représentation vibratoire totale est donc :
Ainsi, T = 3A 1 ? A 2 ? 2B 1 ? 3B2 (2.17)
La représentation engendrée par
les
translations et les rotations d'ensemble
C 2v
E
|
C 2
|
óv
|
'
ó v
|
T
|
9
|
-1
|
3
|
-1
|
|
est :
T + R = A 1 ? A 2 ? 2B 1 ? 2B2 (2.18)
Par suite, la représentation vibratoire totale est : V =
2A1 ? B2 (2.19)
On conclut donc que la molécule d'eau a :
9 2 modes de vibrations complètement symétriques
(A1).
9 1 mode de vibration complètement antisymétrique
(B1).
Parlant des modes de vibrations, on distingue :
9 Stretching mode (allongement)
9 Bending mode (courbure)
9 Twisting mode (torsion)
9 Wagging mode (hochement)
9 Scissoring mode (cisaillement)
9 Rocking mode (rotation plane)
De part cet exemple, on constate que la détermination
du nombre de fréquences fondamentales d'une molécule ainsi que
leur classement selon le type de symétrie correspondant aux
représentations irréductibles contenues dans la
représentation vibratoire totale, ne nous apprend rien sur le mouvement
réel des atomes. Il faut donc penser à introduire les
coordonnées internes et les coordonnées de symétrie.
2.2.1.3.3. Coordonnées internes.
Les déplacements des atomes dans une molécule
peuvent en effet être repérés en
considérant les
allongements des liaisons, ainsi que les variations des angles entre
qi â i
les axes de liaison des atomes. Ces variations de longueur et
d'angle sont appelées coordonnées internes de la
molécule.
Pour illustration, reprenons l'exemple du H2O.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
H H
Figure 2.4. coordonnées internes de la
molécule d'eau.
O
â
q1 q2
Ainsi, on a : v = q ? â , (2.20)
avec q = A 1 + B 2 et â =
A1. (2.21)
2.2.1.3.4. Coordonnées de
symétrie.
Les coordonnées de symétrie sont des fonctions
de base des représentations figurant dans une décomposition
canonique. Elles sont des combinaisons linéaires d'un seul type de
coordonnées internes. Elles ont l'avantage de livrer le secret des
mouvements réel des atomes dans une symétrie donnée.
Pour déterminer ces coordonnées de
symétrie, on applique sur tous les coordonnées internes,
l'opérateur projecteur Pá défini par :
n
á = ? ÷
á
P
g G
|
*
( ) ( )
á G
|
.
|
(2.22)
|
|
Où ÷ est le caractère associé à
la représentation irréductible du groupe de
( á )
á
symétrie G ; ( G) est le caractère de la
représentation totale de ce groupe ; ná est la
dimension de á et g est l'ordre du groupe G.
Ainsi, les coordonnées de symétrie de la
molécule de H2O sont :
( )
q q
1 + 2
2
? ? S A
2 ( ) = â
1
1
( ) ( )
= q q
-
1 2
2
1
S A
1 ( ) =
1
?
?
?
?
S A
3 1
(2.23)
Maintenant, on sait comment les atomes bougent dans un mode de
vibration donnée.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
2.2.2. Rotations moléculaires (rotateur
rigide)
2.2.2.1. Molécules linéaires.
Si on assimile la molécule à un rotateur rigide,
l'Hamiltonien Hr relatif à la rotation s'écrit :
I est le moment d'inertie du système par rapport à
son centre d'inertie G. L étant
l'opérateur moment cinétique dont les composantes
, , dans un repère mobile
L x L y L z
(Gxyz) et , , dans un repère fixe (OXYZ) vérifient
la relation :
LX LY LZ
L L L L L L L
2 = + + = + + Z
2 2 2 2 2 2 . (2.25)
x y z X Y
{ }
L , L z
2 Constitue un E.C.O.C. Donc les fonctions J,M , sont
les bonnes fonctions

propres associées à Hr ; et on a :
H r J,M = E r J,M . (2.26)
En remplaçant Hr par son expression en (2.24),
on obtient :
E J = hcB eJ(J + 1). (2.27)
h
Où =
B est la constante de rotation.
e 8 cI
ð 2
Pour une valeur de J, il existe (2J+1) harmoniques
sphériques è ?
Y , =-
M ( ) . Donc
J M J,...,J
chaque valeur propre EJ est (2J+1) fois
dégénérée.
2.2.2.2. Molécules non
linéaires.
Si on assimile la molécule à un rotateur rigide,
l'Hamiltonien Hr relatif à la rotation s'écrit :
H r
2 2 2
1? L L L ? x y

= + + z . (2.28)
2 I I I
? ?
? xx yy zz ?
Par ailleurs, { }
L , L z , L
Z
2 est un E.C.O.C. D'où la base J,K,M est une
base propre
associée à Hr telle que :
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

J 0,1,...
=
2
? J,K,M J J 1 J,K,M
2
L = +
( ) h


? L J,K,M K J,K,M
?
?
??
(2.29)
K J,...J
=-
= h
z


M J,...J
=-
LJ,K,M M J,K,M
= h
Z
LZ
Les fonctions propres correspondant aux vecteurs propres
simultanés de , et
L 2 Lz
sont de la forme [23] :
Ö ( ) È è
J iK
J,K,M , ,
è ? ÷ = N J,K,M K,M e ÷ eiM ?
( )
|
.
|
(2.30)
|
|
Où est la constante de normation, et est un
polynôme de Legendre. ,
J
N J,K,M È K , M Ixx
Iyy
|
et sont les moments principaux d'inertie dans les directions
(Gx), (Gy) et (Gz)
Izz
|
|
respectivement. Ils permettent de caractériser la
molécule :
· Si les trois moments principaux d'inertie sont
égaux, la molécule est une toupie sphérique.
· Si I xx = I yy ? I zz , la molécule est
une toupie symétrique.
· Si I xx ? I yy ? I zz, la molécule est
dite toupie asymétrique.
Par ailleurs, l'énergie de rotation du système est
donnée par l'équation :


H r J,K,M = E J J,K,M . (2.31)
Ainsi,
V' Dans le cas d'une toupie
sphérique, on a :
E J = hcB e J ( J + 1). (2.32)


Et, pour chaque valeur de J ; K et M prennent chacun (2J+1)
valeurs. Par suite, à
chaque niveau d'énergie EJ correspond
(2J+1)2 valeurs de J,K,M différentes. EJ
est alors (2J+1)2 fois
dégénérée.
V' Dans le cas d'une toupie
symétrique, on a :
E J, K hc ? B e J J 1 A e B e
K

= ( ) ( ) 2
+ + - ? . (2.33)
? ?
B
|
|
h
|
|
h
et sont les constantes rotationnelles à
l'équilibre.
A =
e 8 cI
ð 2
zz
|
|
|
|
|
xx
|
|

Pour une valeur donnée de J, le nombre quantique M peut
prendre (2J+1)
valeurs différentes ; et comme EJ, K dépend de
la valeur absolue de K, il lui
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.


correspond 2(2J+1) valeurs de J,K,M différentes. E J, K
est donc 2(2J+1)
fois dégénérée.
v' Dans le cas d'une toupie
asymétrique, plusieurs calculs ont été faits
pour obtenir une formule donnant les énergies EJ. Nous donnons
l'expression proposée par Wang[24] :
? 1 1
E hc B C J J 1 A
J ( e
= ? + e ) ( ) e ( e
? ? ?
+ + - B C W
+ e ) ? ? , (2.34)
? ô
? 2 ? 2 ? ?
h
avec C = .
yy
e 8 cI
ð 2
Pour J donnée, prend (2J+1) valeurs différentes ;
et par conséquent, on a (2J+1)
Wô
états différents [23].
2.2.3. Solution du problème
nucléaire.
Le mouvement nucléaire peut se décomposer en
vibrations, rotations et translations. Dans un premier temps, on se place dans
le référentiel du centre de masse de la molécule. Ce qui
revient à ne plus percevoir le mouvement de translation. Par ailleurs,
les vibrations et les rotations sont faiblement couplées. On
néglige donc ce couplage. Ce qui revient à exprimer la fonction
d'onde nucléaire comme un produit de fonctions d'onde vibrationnelle et
rotationnelle.
La fonction d'onde vibrationnelle est le produit d'une vibration
d'élongation et d'une vibration angulaire.
Ainsi, la fonction d'onde vibrationnelle peut s'exprimer :
2
( ( ) ) ( ) ( )
1 R R
á - e l
Ö = 2
vib A H n á -
R R e e P n cos ã . (2.35)
Par suite, la fonction d'onde nucléaire pourra être
écrite comme suit :
2
( ( ) ) ( ) ( ) ( )
2 1 R R
á - e l J iK
N A H n R R e e ã È è
P n cos K,M e e
÷ iM ?
Ö = á - . (2.36)
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
CHAPITRE 3
COURBES ET SURFACES DE
POTENTIEL.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
3.1. INTRODUCTION
L'étude théorique d'un spectre
moléculaire nécessite, comme nous l'avons montré dans le
premier chapitre, la détermination précise des courbes
d'énergie potentiel des états électroniques
étudiés.
La fiabilité des résultats spectroscopiques
obtenus dépend de la qualité de ces courbes ou de ces surfaces
qui dépendent elles même essentiellement de la qualité de
la base d'OA et de la performance des méthodes de calcul
utilisées. Pour cela, nous les testons en essayant de reproduire
quelques résultats expérimentaux.
3.2. ETUDE DES FRAGMENTS NO, NO - ET N2O.
3.2.1. Bases utilisées
Les molécules NO et NO- sont diatomiques
hétéronucléaires. Elles appartiennent donc au groupe de
symétrie C8 v . Quant à la molécule N2O, elle
est linéaire et ne
possède pas de centre d'inversion. Elle appartient donc
également au même groupe de
symétrie . Comme les calculs
doivent être effectués dans une base finie, nous
C8 v
choisissons de les mener dans le groupe de symétrie qui
est un sous-groupe
C2 v
distingué de .
C8 v
Nous avons par la suite utilisé plusieurs bases
optimisées par Dunning . Il
[16]
s'agit notamment des bases aug-cc-avtz,
aug-cc-avqz et aug-cc-av5z auxquelles on a associé les
ensembles de fonctions spd, spdf, spdfg et spdfgh.
Pour mettre en évidence l'effet d'une base
donnée, nous avons effectué des calculs au niveau MCSCF avec des
bases différentes. Les résultats sont illustrés par les
courbes des figures 3.1, 3.2, 3.3, et 3.4.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

-128
-129
-130
1 2 3 4 5 6
Energie (u.a.)
-126
-127
-123
-124
-125
2Ó+ (avtz/spdf) 2Ä
(avtz/spd) 2Ó+ (avtz/spdf) 2Ä (avtz/spd)
Distance internucléaire (Bohr)
Figure 3.1 : Deux états
électroniques du NO ( 2 Ó+ ,1Ä )
calculés au niveaux MCSCF/avtz/spd et
MCSCF/avtz/spdf.

-123
-124
1 2 3 4 5 6
Distance internucléaire (Bohr)
-129
-130
-125
-126
-127
Energie (u. a.)
-128
2Ó+ (avtz/spd) 2Ä
(avtz/spd) 2Ó+ (avtz/spdf) 2Ó+
(avqz/spdf)
Figure 3.2 : Deux états
électroniques du NO ( 2 Ó+ ,1Ä )
calculés au niveaux MCSCF/avtz/spdf et
MCSCF/avqz/spdf.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2
Distance internucléaire (Ang)
-123
-124
-125
Energie (u.a.)
-126
-127
-128
-129
-130
B2Ð avqz (spdf) B2Ð avtz (spdf)
Figure 3.3 : premier état excité
doublet 2Ð du NO calculé au niveau MCSCF/avtz/spdf et
MCSCF/avqz/spdf.

1Ó+ (av5z) 1Ó+ (avqz)
1Ó+ (avtz)






0,0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5
Distance internucléaire (Bohr)
-124
-125
-129
-130
-126
Energie (u. a.)
-127
-128
Figure 3.4 : Etat
1Ó+ du NO-
déterminé au niveau de calcul MCSCF/avtz, MCSCF/avqz et
MCSCF/av5z.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Observations et
interprétations.
· La figure 3.1 montre que les effets de l'ajout des
fonctions f sur une triple zêta pour le monoxyde d'azote bien que
négligeables, sont plus marqués aux grandes distances. Ce qui est
très normal, puisque l'ajout de ces fonctions augmente la
flexibilité de la base.
· Les figures 3.2 et 3.3 montrent que pour un
état excité, les bases triple et quadruple zêta donnent les
mêmes résultats aux grandes distances, et des résultats
différents aux courtes distances. La différence étant
assez notable, le système NO est bien décrit au moins dans une
base quadruple zêta.
· La figure 3.4 quant à elle montre que dans le cas
de l'ion, il n'y a pratiquement pas de différence à travailler
dans une base triple zêta que dans une quadruple zêta. Une
différence notable aux très grandes distances n'apparaît
que lorsque les calculs sont effectués dans la base av5z. Compte tenu de
la croissance du coup informatique avec la base de calcul, si on
s'intéresse aux grandeurs énergétiques (énergie
totale, énergie d'ionisation et affinité électronique d'un
système moléculaire) ou aux grandeurs géométriques
(longueurs et angles de liaison, conformations), on peut sans erreurs notables
effectuer les calculs dans la base avqz. Il serait prudent d'effectuer les
calculs au moins dans une base av5z si on s'intéresse aux
propriétés électriques (moments dipolaires, multipolaires,
polarisabilités et
hyperpolarisabilités), magnétiques
(déplacement chimique et constantes de couplage de RMN) et
spectroscopiques.
3.2.2. Méthodes de calcul
utilisées.
Pour ces trois fragments du N 2 O 2 ou
duN 2 O- 2 , nous avons utilisé
successivement les méthodes HF, MCSCF, MRCI, MP4 et CCSD
(T) dans la base avqz.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

Figure 3.5 : Etat 2 II de la
molécule NO donnés par les méthodes HF, MCSCF et MRCI.
MRCI MRCI+Q MCSCF SCF-HF
-121
-122
-123
-124
-125
-126
-127
-128
-129
-130
Energie (u.a.)
0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2
Distance internucléaire (Ang)
-124
-125
-126
-127
-128
-129
Energie (u. a.)
R-HF MCSCF MRCI MD4 CCSD(T)
-130
0,0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5
Distance interatomique (Bohr)
Figure 3.6 : Etat 2 II de la
molécule NO donnés par les méthodes HF, MCSCF et MRCI, MP4
et CCSD. Observations et interprétations.
La figure 3.5 montre que la correction de Davidson
apportée à la méthode MRCI peut
être
négligée pour les états du NO .Les figures 3.5 et 3.6
montre qu'en terme de
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
précision, on a l'ordre suivant : HF <<
MCSCF < CCSD(T) < MP4
< MRCI. Ce quiest bien en accord avec les
prévisions faites au chapitre 1.
3.2.3. Structure électronique du NO, NO- et
N2O.
Commençons par présenter quelques états
électroniques des systèmes étudiés.
Energie (u.a.)
|
-127
-128
-129
|
|
|
X2Ó+
A2Ä
A2Ó+
B2Ó+
2Ä
X2Ð
A2Ð
B2Ð
C2Ð
D2Ð
|
|
|
-130
0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2
Distance internucléaire (Ang)
Figure 3.7 : les dix états
électroniques les plus bas du NO dans ses deux premières
symétries au niveau MCSCF/avqz.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

3Ä 3Ó+ 3Ä
3Ó+
X3Ð
3Ð 3Ð 3Ð
3Ó- 3Ó-
3Ä

0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6
Distance internucléaire (Ang)
-127
-130
-128
Energie (u.a.)
-129
Figure 3.8 : les onze états
électroniques les plus bas du NO- au niveau MCSCF/avqz.

-183,2
-183,3
1Ó+ 1Ä
1Ó+ 1Ó+
-183,4
Energie (u. a.)
-183,5
-183,6
-183,7
-183,8
-183,9
0,5 1,0 1,5 2,0 2,5 3,0 3,5
RN-N (Ang)
Figure 3.9 : les quatre états
électroniques les plus bas du N2O lorsqu'on tire sur la liaison N-N.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
|
-183,2
|
|
|
|
1Ó+ 1Ä
1Ó+
|
|
|
|
|
|
|
-183,3 -183,4 -183,5 -183,6 -183,7
|
|
|
|
|
|
|
|
|
|
|
-183,8
|
|
|
|
|
|
|
|
|
-183,9
|
|
|
|
|
|
0,5 1,0 1,5 2,0 2,5 3,0 3,5
RN-O (Ang)
Figure 3.10 : les trois états
électroniques les plus bas du N2O lorsqu'on tire sur la liaison N-O.
Observations et interprétations.
· Les figures 3.7 et 3.8 montrent respectivement que les
états fondamentaux du NO et du NO- sont
respectivement2 Ð et 3Ð. Il ressort des courbes
3.9 et 3.10 que le fondamental du N2O est l'état 1 .
Ó+
· Les états excités du N2O sont
très éloignés de leur fondamental, contrairement à
ceux du NO et du NO-. Ce qui signifie que les molécules NO et
NO- sont facilement excitables par rapport à la
molécule N2O.
· On observe également sur les figures 3.7 et 3.8
les croisements évités entre les états
2Ó d'une part et les états d'autre part.
2Ð
· Les énergies au seuil de dissociation des
systèmes NO et NO- sont respectivement -128. 569
eV et -129. 1746 eV.
· Les calculs montrent que le protoxyde d'azote N2O est
linéaire. Ce résultat était prévisible suivant la
règle de Walsh : La géométrie d'une molécule est
déterminée par le nombre d'électrons de valence. Les
molécules triatomiques ne contenant pas l'hydrogène et
possédant au plus 16 électrons de valence sont linéaires.
C'est bien le cas du N2O qui
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
posséde 5 électrons de valence par atome d'azote
et 6 électrons de valence par atome d'oxygène.
3.3. ETUDE DE L'ETAT FONDAMENTAL DES SYSTEMES
N 2 O- 2 ET N 2 O2 Comme nous l'avons
mentionné à l'introduction générale, les
molécules N 2 O- 2 et N 2 O 2 appartiennent au
groupe ponctuel de symétrie . Nous présentons ci-dessous
C2 v
leurs structures géométriques. Par la suite, nous
déterminerons leurs modes de vibrations et leurs activités en
spectroscopie Raman et infrarouge.

O
Cs
O
O
C2 v
N
O
N
N
O
O
N
N
N
Figure 3.11 : Structures
géométriques du et du
N 2 O 2 N 2 O- 2 en symétrie C2v et
Cs.
3.3.1. Modes de vibration des molécules
N 2 O 2 et en symétries
et
N 2 O- 2 C2 v Cs
Chacune des molécules N 2 O 2 et
possède 4 atomes ; soit 6 modes
N 2 O- 2
normaux de vibrations indiquant ainsi que les vibrations de
chacun de ces deux systèmes sont décrites par 6
coordonnées internes ( r1 ,r2 ,r 3
,â 1, â 2, â 3) (voir figure
3.2) et 6 coordonnées de symétrie.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

â 1
â3
r3
r2
O
O
â2
N
r1
N
Figure 3.12 : coordonnées internes du
ou .
N 2 O 2 N 2 O- 2
Par ailleurs, on montre que la représentation
irréductible qui engendre les vibrations de chacun de ces
systèmes est :
v = 3A 1 ? B 1?2B2 . (3.3)
Ainsi, celles engendrant les vibrations d'allongement et
angulaires sont données respectivement par :
r = 2A1 ? B 2 , (3.4)
= ? ? 2 . (3.5)
â A 1 B 1 B
Chacun de ces deux systèmes possède donc en
symétrie C 2v :
· Deux modes de vibration d'allongement complètement
symétriques suivant A 1.
· Un mode de vibration d'allongement complètement
antisymétrique suivant B2.
· Un mode de vibration angulaire complètement
symétrique suivant A1.
· Un mode de vibration angulaire complètement
antisymétrique suivant B2.
· Un mode de vibration angulaire antisymétrique
suivant B1.
Tous ces 6 modes de vibration sont actifs en spectroscopie
Infrarouge et Raman. Les fonctions d'onde de symétrie adaptées
à ces modes de vibration sont :
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Ø 1 (A 1 ) = r 1
|
|
Symmetric stretching
mode
|
|
1
Ø (A ) =
2 1 2

(r 2 r + 3 )

Symmetric stretching
mode
1
Ø (B ) =
3 2 2

(r 2 r - 3 )

asymmetric stretching
mode
1
Ø (A ) =
4 1 2
Ø 5 (B 1 ) = â 1

scisoring mode
Bending mode...
(1 â +â3)

1
Ø (B ) =
6 2 2

(1 â -â 3 )

Bending mode
En symétrie Cs pour le N 2
O2 , nous obtenons:
v = 5A ? A"' (3.6)
Ainsi, dans ce groupe, la molécule a :
· 5 modes de vibration suivant actifs en spectroscopie
infrarouge et Raman.
A '
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
· 1 mode de vibration suivant actif en spectroscopie
infrarouge et Raman.
A "Contrairement aux calculs effectués par
Arnold et Neumark, où ils trouvent qu'en
symétrie C , toutes les vibrations ont lieu dans le plan
de la molécule, soit suivant .
A '
s
3.3.2. Géométries optimisées des
molécules N 2 O2 et .
N 2 O- 2
Nous présentons ci-dessous les géométries
optimisées sous Gaussian 03W[25].
méthode Energie RN-N RN-O1 RN-O2 < NNO1 <NNO2
UHF/6-31+G*
|
-258.493 764
|
1.2531
|
1.2541
|
1.2541
|
119.2542°
|
119.2542°
|
UMP2/6-31+G*
|
-259.165 960
|
1.2704
|
1.2528
|
1.2528
|
120.2575°
|
120.2575°
|
UMP2/6-311+G*
|
-259.274 329
|
1.2726
|
1.2402
|
1.2402
|
120.1256°
|
120.1256°
|
|
Tableau 3.1 : Résultats
ab-initio de l'anion N 2 O- 2 c
méthode
|
ù1
|
ù2
|
ù3
|
ù4
|
ù5
|
ù6
|
théorie
|
|
|
|
|
|
|
UMP2/6-31+G*
|
1411.3928
|
1243.0460
|
679.7760
|
997.7958
|
1539.0959
|
609.0024
|
UMP2/6-311+G* expérience
|
1421.1382
|
1222.9497
|
695.2410
|
1000.9260
|
1543.1580
|
623.7265
|
Ar matrix a
|
1356
|
1004
|
...
|
...
|
1199
|
...
|
Ne matrix b
|
1359
|
1008
|
...
|
...
|
1205.5
|
...
|
|
a Références [26] et
[27].
b Référence [26].
c Les énergies sont
données en u.a., les longueurs de liaison en angströms et les
fréquences vibrationnelles en cm-1
Tableau 3.2 : Fréquences
propres de vibration de l'anion N 2 O- 2 c
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Etat
|
paramètre
|
HF/6-31+G*
|
MP2/6-311+G*
|
Mode
|
HF/ 6-31+G*
|
MP2/ 6-311+G*
|
1
|
|
|
|
|
|
|
A1
|
RN-N
|
1.3021
|
1.2525
|
ù1
|
1534.5804
|
1391.6340
|
(A)
|
RN-O
|
1.1895
|
1.2299
|
ù2
|
1178.1499
|
1108.9664
|
|
<NNO1
|
114.3236°
|
114.0619°
|
ù3
|
691.8905
|
600.2176
|
|
<NNO2
|
114.3236°
|
114.0619°
|
ù4
|
875.5625
|
742.1835
|
|
Energie
|
-258.332 951
|
-259.123 993
|
ù5
|
1761.1334
|
1689.8163
|
|
|
-258.390 078e
|
|
ù6
|
175.8113i
|
800.7031i
|
1
A1
|
RN-N
|
1.127
|
1.1302
|
ù1
|
2196.3178
|
2318.5474
|
(B)
|
RN-O
|
1.3502
|
1.4735
|
ù2
|
1179.6093
|
1071.1945
|
|
<NNO1
|
146.8211°
|
147.4966°
|
ù3
|
895.7086
|
637.9780
|
|
NNO2
|
146.8211°
|
147.4966°
|
ù4
|
510.5793
|
520.0772
|
|
Energie
|
-258.293 542
|
-259.133 323
|
ù5
|
668.7958
|
983.2470
|
|
|
-258.332 402e
|
|
ù6
|
461.6837
|
51.6401
|
|
c Les énergies sont
données en u.a les longueurs de liaison en angströms et les
fréquences vibrationnelles en cm-1.
e Résultat HF dans la base
6-311+G*
c
Tableau 3.3 : Résultats ab-initio
des états singulets du en symétrie C
N 2 O 2 .
2v
|
Energie
|
RN-N
|
RN-O1
|
RN-O2
|
< NNO1
|
<NNO2
|
3
A1
|
|
|
|
|
|
|
UHF/6-31+G*
|
-258.426 981
|
1.225
|
1.270
|
1.270
|
127.5°
|
127.5°
|
MP2/6-31+G*
|
-258.998 122
|
1.182
|
1.294
|
1.294
|
129.6°
|
129.6°
|
3
|
|
|
|
|
|
|
B1
|
|
|
|
|
|
|
UHF/6-31+G*
|
-258.374 977
|
1.282
|
1.280
|
1.280
|
122.2°
|
122.2°
|
MP2/6-31+G*
|
-258.952 149
|
1.248
|
1.301
|
1.301
|
123.6°
|
123.6°
|
3
|
|
|
|
|
|
|
B2
|
|
|
|
|
|
|
UHF/6-31+G*
|
-258.341 847
|
1.144
|
1.388
|
1.388
|
127°
|
127°
|
MP2/6-31+G*
|
-258.953 932
|
1.188
|
1.311
|
1.311
|
116.6°
|
116.6°
|
3
|
|
|
|
|
|
|
A2
|
|
|
|
|
|
|
UHF/6-31+G*
|
-258.412 978
|
1.405
|
1.185
|
1.185
|
115.3°
|
115.3°
|
MP2/6-31+G*
|
-259.058 994
|
1.441
|
1.230
|
1.230
|
115.1°
|
115.1°
|
|
c Les énergies sont données en u.a.,
les longueurs de liaison en angströms .
c
Tableau 3.4 : Résultats ab-initio
des états triplets du en symétrie C
N 2 O 2 .
2v
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
|
ù1
|
ù2
|
ù3
|
ù4
|
ù5
|
ù6
|
3
A1
|
|
|
|
|
|
|
UHF/6-31+G*
|
1543
|
1038
|
608
|
608
|
1288
|
576
|
MP2/6-31+G*
|
1972
|
1142
|
649
|
819
|
1776
|
585
|
3
|
|
|
|
|
|
|
B1
|
|
|
|
|
|
|
UHF/6-31+G*
|
1634
|
1032
|
657
|
437
|
923
|
545
|
MP2/6-31+G*
|
1467
|
1022
|
618
|
627
|
571
|
1180i
|
3
|
|
|
|
|
|
|
B2
|
|
|
|
|
|
|
UHF/6-31+G*
|
2037
|
869
|
495
|
618
|
977
|
561
|
MP2/6-31+G*
|
1646
|
959
|
611
|
541
|
1164
|
312
|
3
|
|
|
|
|
|
|
A2
|
|
|
|
|
|
|
UHF/6-31+G*
|
1576
|
1050
|
716
|
777
|
1868
|
565
|
MP2/6-31+G*
|
1431
|
902
|
625
|
638
|
1815
|
483
|
|
c Les fréquences vibrationnelles sont en
cm-1.
c
Tableau 3.5 : Résultats ab-initio
des fréquences de vibration des états triplets du en
symétrie C
N 2 O 2 .
2v
Observations et
interprétations.
L'analyse des tableaux 3.1, 3.2, 3.3, 3.4 et 3.5 montre que :
· Les résultats de calculs effectués dans la
base 6-31+G* sont en parfait accord avec ceux effectués par Arnold et
Neumark[1].
· L'optimisation de géométrie aux niveaux
HF/6-31+G* et MP2/6-311+G* prévoit que l'ion moléculaire N2O2 -
est plan. Il appartient au groupe de symétrie C2v et son fondamental est
l'état 2BB2 pour lequel la molécule a des longueurs et
des angles de liaison presque égaux. Ses angles de valence valent
environ 120° et Ses longueurs de liaison sont angström et
R N - O = 1.254
R N - N = 1.253 angström au niveau HF/6-31+G*. Au niveau
MP2/6-311+G*, ces longueurs valent respectivement 1.24 angström et 1.27
angström. Remarquons que la valeur calculée pour R N - N au niveau
HF/6-31+G* est caractéristique d'une double liaison ; par exemple ,
[28] R N - N = 1.252 Angström.
· Quant à la molécule neutre
N2O2, elle est également plane et possède deux
géométries d'équilibre (A et B) en symétrie
C2v et une en symétrie Cs. Son état
fondamental est l'état 1A1. Les calculs effectués au
niveau MP2/6-311+G*
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
montrent que l'angle de valence <ONO vaut seulement
65° pour la structure B contre 132° pour la structure A. aussi, cet
angle est le paramètre géométrique qui varie le plus
lorsqu'un photodétachement sur l'anion conduit aux états triplets
de la molécule neutre. En plus, R N - N ne change pas beaucoup via un
photodétachement sur le N 2 O- 2 conduisant aux
états triplets
3 A 1 , B 1 , et B 2
3 3
|
.Ainsi,la liaison N-N dans ces états est
fondamentalement une
|
|
double liaison juste aussi comme dans l'anion.
Cependant, la longueur R N - N pour l'état triplet de la molécule
neutre mesure 0.17 angström de plus que
3 A2
dans l'anion. La valeur calculée (1.441 angström au
niveau MP2/6-31+G*) est
caractéristique d'une liaison simple N-N. par
exemple, angström
R N - N = 1.449
dans le [29]
N 2 H 4 .
· Par ailleurs, les énergies des molécules et
à leurs limites de
N 2 O- 2 N 2 O 2
dissociation sont respectivement -258.921eV et
-258.363 eV au niveau HF/avqz-spdf.
· En symétrie C2 V , La structure B de la
molécule neutre N 2 O2 est la plus stable.
· Lorsqu'on ne prend pas en compte la corrélation
statique, on peut classer les états triplets du comme suit : . Cet ordre
s'estompe
3 A 1 < A 2 < B 1 < B 2
3 3 3
N 2 O 2
lorsqu'on prend en compte ce type de corrélation (la
bonne description). Dans
ce cas, ces états sont classés comme
suit : au niveau MP2/ 6-
3 A 2 < A 1 < B 2 < B
3 3 3
1
31+G*. Notons que cet ordre pourrait bien changer en fonction du
niveau de calcul. En effet, les calculs effectués par Arnold et Neumark
[1] au niveau MP4/6-311+G* les classent comme suit : .
3 A 2 < A 1 < B 1 < B
3 3 3
2
· Les états triplets de la molécule N
2 O2 sont « en général » plus
hauts
énergétiquement que les états singulets
des trois géométries de cette molécule. Ce résultat
nous permettra certainement de simplifier l'étude de la
métastabilité de notre système.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
· L'optimisation de géométrie au niveau
HF ou MP2 surestime les fréquences des modes propres de vibrations de la
molécule et s'accorde raisonnablement avec les résultats
expérimentaux.
La molécule sous l'effet de ses vibrations, peut perdre
son état après un temps relativement court ou long. On dira ainsi
qu'elle présente des états métastables...
3.3.3. Stabilité ou métastabilité
d'un système moléculaire.
Un anion moléculaire est dit stable ou métastable
dans un état électronique donné lorsqu'il satisfait les
trois critères ci-dessous [30] :
1) L'affinité électronique de l'anion
relativement à cet état est positive. Par
définition, contrairement au potentiel d'ionisation, l'affinité
électronique X
A - d'un
anion traduit la difficulté à enlever un
électron d'une couche électronique de cet
X-
anion pour former la molécule neutre . C'est donc la
différence entre l'énergie de X
l'état fondamental de la molécule neutre (parent)
et celle de l'état fondamental de l'anion correspondant. Elle s'exprime
donc comme suit :

A - E (X) E (X )
-
= 0 - 0 . (3.7)
X
Ainsi, une affinité électronique positive
signifie physiquement qu'à partir des courbes de potentiel
électroniques, l'anion est en dessous de son neutre parent, plus
précisément dans la région d'équilibre de leurs
états fondamentaux respectifs.
Donnons une expression plus explicite de l'affinité
électronique. Pour cela, considérons la représentation
schématique ci-dessus.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.

E
0
E-0
E0
A -
X
2 ù
1
0
2
1
ù0
-
Courbe de potentiel de la
molécule neutre.
Courbe de potentiel de
l'anion
R
Figure 3.13 : Illustration de
l'affinité électronique.
Ainsi, la relation de Chales permet d'écrire :
A + ù = E - + ù (3.8)
1 ( )
- 1
E 2 0
-
X - 2 0 0 0
Soit donc :
( 1 ) ( )
E E 1
-
A + (3.9)
X - 0 2 0
ù - 2 ù
-
= + 0 0
E0 et étant respectivement les énergies
électroniques des fonds des puits de
Å0 -
potentiel de la molécule neutre et de l'anion.
ù0 et 0
ù sont respectivement les fréquences
-
propres de vibration de la molécule neutre et de
l'anion en cm-1 , dans leurs états fondamentaux. 2 1 ù
0 et 1 2 ù- 0 sont appelées «
zero-point correction » respectivement de la molécule neutre et de
l'ion.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
2) La fonction d'onde associée à cet
état doit présenter de faibles interactions avec les états
du continuum électronique. Physiquement, ceci signifie que
le puit de potentiel électronique de l'anion doit être
suffisamment profond afin que la moindre excitation du système ne
l'amène hors de cet état.
3) Le couplage spin-orbite entre cet état
et un état de transition possible est pratiquement nul.
Physiquement, ceci se traduit par le non croisement de la courbe de potentiel
électronique de cet état et de celles des états du neutre
ayant une multiplicité de spin différente d'une unité de
celle de l'anion.
Pour étudier la stabilité ou la
métastabilité de l'anion N 2 O- 2 , nous avons effectué
des investigations sur cet anion et sur la molécule
neutre associée aux mêmes géométries. Dans la suite,
nous préciserons les bases et les méthodes de calcul
utilisées pour mener cette étude tout en présentant les
différents résultats obtenus.
3.3.4. Base et méthode de calcul
utilisée.
Michels et Montgomery[31], à partir des
investigations au niveau HF/6-31G* ont trouvé que l'état
fondamental du N 2 O 2 est l'état
1A1. En tenant compte de ce
résultat
Nous avons effectué des calculs dans les bases
aug-cc-pVTZ et aug-cc-pVQZ de Dunning au niveau HF vu nos limites dans les
outils informatiques. Les résultats sont présentés
à travers les courbes de potentiel ci-dessous.
3.3.5. Courbes de potentiel
électroniques.
Les calculs présentés ici ont été
faits pour les variations d'angles.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
112 113 114 115 116
Angle <NNO (°)


-258,1324
-258,1300
-258,1302
|
Energie (u.a)
|
-258,1304 -258,1306 -258,1308 -258,1310 -258,1312 -258,1314
-258,1316 -258,1318 -258,1320 -258,1322
|
|
|
Figure 3.14 : Etat fondamental
X1 du
A1 N 2 O2 pour des variations
d'angles /HF /avqz/spdf.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
-258,30

|
Energie (eV)
|
-258,32 -258,34 -258,36 -258,38 -258,40
|
|
|
90 95 100 105 110 115 120 125
Angle (dégrés)

-258,42
Figure 3.15 : Etat fondamental X
du
2 B2 N 2 O- 2 pour des variations d'angles
/HF/avqz/spdf
Après une étude minutieuse des configurations
dominantes des états représentés
sur les figures 3.14 et 3.15, il en ressort que l'état
X1 est le neutre parent associé à
A1
l'état . L'état est bien en dessous de son neutre
parent. Ainsi, l'ion
X B 2
2 X B 2
2 N 2 O- 2 a
une affinité électronique positive. En effet,
compte tenu des optimisations de
géométries
récapitulées dans les tableaux 3.1, 3.3 et de la formule (3.9),
l'affinité
électronique de la molécule N 2 O- 2 est :
A - = -259.133 323+0.012605 -259.274
329+0.014824 0.138787u.a. 0
( ) (
- ) = >
N 2 O2
Donc l'anion N 2 O- 2 existe bel et bien. Il est situé
à environ 3.8 eV en dessous du neutre.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
CONCLUSION
GENERALE
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
L'étude menée dans ce travail nous permet de
comprendre que les méthodes post-Hartree-Fock pourraient être
classées comme suit :
HF CISD < MCSCF < MP4(SDQ) CCSD < CCSD(T) < MRCI
. Ainsi, la méthode MRCI est la méthode
ab-initio la plus précise. Pour des systèmes de petites tailles,
les bases de Dunning sont les meilleures, et la plus précise est la base
aug-ccpV7Z enrichie de toutes ses fonctions primitives. Donc un système
moléculaire serait décrit « parfaitement » si les
calculs sont effectués au niveau MRCI/aug-cc-pV7Z. Mais, compte tenu de
son temps de calcul très élevé, il nous est difficile
d'effectuer des études à ce niveau de précision.
Les résultats issus de nos calculs de structures
électroniques au niveau HF/avqzspdf montrent, qu'à la limite de
dissociation, les énergies E(NO) + E(NO) et E(NO) + E(NO-)
sont respectivement proches de E(N2O2) et E(N2O2 -). Ceci permet d'affirmer que
les molécules N2O2 et N2O2 - peuvent bien se
fragmenter respectivement en NO + NO et NO + NO- . L'analyse des
courbes de potentiel liées aux fragments de N2O2 - montre
également que leurs niveaux d'énergie fondamentaux sont
respectivement les états et pour le NO et le NO-. Le
protoxyde d'azote N
2Ð 3Ð 2O quant à lui est
linéaire
et son fondamental est l'état 1 .
Ó +
La deuxième partie des calculs basée sur les
systèmes tétratomiques montre que l'ion moléculaire N2O2 -
est plan. Il appartient au groupe de symétrie C2v et son
fondamental est l'état 2B2 pour lequel la molécule a
des longueurs et des angles de liaison presque égaux. Ces angles de
valence valent environ 120°. Les liaisons N-O mesurent 1.24 angström
et la liaison N-N est une double liaison mesurant 1.27 angström. Quant
à la molécule neutre N2O2, elle est également
plane et possède deux géométries d'équilibre (A et
B), l'une en symétrie C2v et l'autre en symétrie
Cs. Son état fondamental est l'état A
1 1. Les calculs effectués au niveau MP2/6-311+G*
montrent que l'angle de valence <ONO vaut seulement 65° pour la
structure B contre 132° pour la structure A.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Concernant la métastabilité, l'anion N2O2 -
présente un état métastable qui est un état
intermédiaire de la réaction -
O N 2 O NO NO-
+ ? + . L'état fondamental de cet
anion est situé à 3.8 eV en
dessous de son neutre parent (géométrie B).
Cette étude préliminaire pourra être
approfondie par une exploration plus précise des états
excités en vue d'une étude spectroscopique de l'anion N2O2 -.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
Références.
[11 D. W. Arnold and Daniel M. Neumark, J.
Chem. Phys. 102, 18 (1995).
[21 J. F. Paulson, Adv. Chem. Ser. 58, 28
(1966) ; J. Chem. Phys. 52, 959 (1970).
[31 J. L. Moruzzi and J. T. Dakin, J. Chem.
Phys. 49, 5000 (1968).
[41 K. Hiraoka, S. Fujimake, K. Aruga, and S.
Yamabe, J. Phys. Chem. 98, 8295
(1994).
[51 D.R. Hartree, Proc. Cambridge Phil Soc.
24, 89 (1928).
[61 V. Fock, Z. Phys. Rev. 36,
57 (1930).
[71 A. Donedou. Dénombrements - Groupes
symétriques. Paris : Librairie Vuibert
1984, p.123.
[81 F. Jensen, Introduction to computational
chemistry, Electronic structure
methods. Odence University, Odence, Denmark, P.61 (1999), 429.
[91 J. C. Slater, Phys. Rev.
36, 57 (1930).
[101 S. F. Boys, Proc. Roy. Soc. A
200, 542 (1950)
[111 C.M. Reeves et R. Fletcher, J.Chem. Phys.
42 (12) 4073 (1965).
[121 T. H. Dunning, Jr., J. Chem. Phys.
53 (7) 2823 (1970).
[131 T. H. Dunning, Jr., J. Chem. Phys.
55 (2) 716 (1971).
[141 F. Jensen, Introduction to Computational
Chemistry, Basis sets. Odense University, Odense, Denmark, P.152 (1999),
429.
[151 R. Krishnan, J. S. Binkley, R. Seeger and
J. A. Pople, J. Chem. Phys. 72, 650 (1980).
[161 D. E. Woon and T. H. Dunning, Jr. J. Phys.
Chem. Vol 103. N° 11, 15, 4572 (1995).
[171 F. Jensen, Introduction to Computational
Chemistry, Electron correlation methods. Odense University, Odense, Denmark,
101 (1999), 429.
[181 J. HLADIK, Règles de
sélection en spectroscopie moléculaire. La théorie des
groupes en Physique et chimie quantiques. Paris, Milan, Barcelone : Masson,
1995, P. 119-120.
[191 B.O. Roos, in lecture notes in Quantum
Chemistry, Ed. B.O. Roos, SpringerVerlag, 1992.
UNIVERSITE DE DOUALA /ECOLE
DOCTORALE DES SCIENCES FONDAMENTALES ET APPLIQUEES/ UFD PHYSIQUE ET SCIENCES DE
L'INGENIEUR / LABORATOIRE DE PHYSIQUE FONDAMENTALE.
[20] A Karpfen, P. Schuster, J. Petkov, H. Lischka,J. Chem.
Phys. 68, 3884 (I978).
[21] J.M. Dyke, A Morris, I.RTrickle, J.Chem. Soc. Faraday
Trans. II 73 147 (1977).
[22] J. HLADIK, Vibrations moléculaire. La théorie
des groupes en Physique et chimie quantiques. Paris, Milan, Barcelone : Masson,
1995, P. 95-107.
[23] S. Lahmar, Etude Théorique de la spectroscopie des
molécules triatomiques, Thése présentée à la
FST, Tunis (1995).
[24] S.C. Wang, Phys. Rev, 38, 1432 (1931).
[25] M. J. Frich et al, Gaussian 98 (Gaussian, Inc., Pittsburgh,
PA, 1998).
[26] M.E. Jacox, J. Chem. Phys. 93, 7622 (1990).
[27] J. Hacaloglu, S. Suzer, and L. Andrews, J. Phys. Chem. 94,
1759 (1990)
[28] M. Carlotti, J.W.C. Johns, and A. Trombetti, Can. J. Phys.
52, 340 (1974).
[29] Y. Morino, T. Iijima, and Y. Murata, Bull. Chem. Soc. Jpn.
33, 46 (1960).
[30] M. Nsangou, N. Jaidane and M. Hochlaf, preprint submitted
to Elsevier Science. (2006).
[31] H. H. Michels and J. A. Montgomery, Jr., J. Chem. Phys. 88,
7248 (1988).

Go to Home page
Go to Home page
| 


