Simulation et optimisation de la combustion isobare des hydrocarbures saturés CnH2n+2 par deux approches de résolution

République Algérienne Démocratique et Populaire
Ministère de l'Enseignement Supérieur et de la Recherche Scientifique
Université Ibn Khaldoun - Tiaret
Faculté des Sciences et des Sciences de l'Ingénieur
Département de Génie Mécanique
Laboratoire de Recherche des Technologies Industrielles

MÉMOIRE

pour obtenir le Diplôme

d'Ingénieur

Spécialité : Génie Mécanique Option : Energétique

Thème

Simulation et optimisation de la combustion isobare
des hydrocarbures saturés _CnH2n+2 par
deux approches de résolution

Présenté par:
Monsieurs KHERRIS Sahraoui et KHARROUBI Ahmed

Soutenu le : 07 /07 / 2002

Devant le jury: MM.

SAD CHEMLOUL Noureddine	Chargé de Cours	Université de Tiaret	Président
GUERRI Mohamed	M. A. C. de Cours	Université de Tiaret	Examinateur
ABED Belkacem	M. de Conférences	Université de Tiaret	Examinateur
ASNOUN Ahmed	Chargé de Cours	Université de Tiaret	Rapporteur

Nous tenons à présenter nos vifs remerciements à Monsieur ASNOUN Ahmed pour l'honneur qu'il nous a accordé de proposer ce projet de fin d'étude et de nous avoir encadré et prodigué ses précieux conseils durant toute la période de notre étude.

Nous tenons aussi à lui exprimer notre profonde et gratitude respect pour sa sympathie; sa modestie et son encouragement lors de la réalisation de ce travail.

Nous remercions très sincèrement tous les nombres de jury d'avoir accepté de juger ce travail.

Nous adressons nos vifs remerciements à tous nos professeurs qui ont contribués à notre formation sur tous:

Chemloul.S, Haddouche.K, Abed.B, Madani.A, particulièrement Monsieur M.Guerri et Mzad.H; ainsi qu'à l'ensemble de personnel de l'institut.

Nous adressons aussi nos remerciements à tout le personnel de la bibliothèque de l'institut de Génie Mécanique.

Nous adressons nos remerciements à tout le personnel de la boite informatique (HIDHEB Computer) en particulier:

Khaled. Miloudi et Mustapha. Akermi pour leurs gentillesses et leurs encouragements.

En fin, nous n'oublions pas de remercier tout nos amis:

Selam.Laid, Mekroussi .s, debeh.M, safa.A, rabeh.H, Bendbiza.H, chatouane.M, Guetaf.AEK, Mahrouz.AEK, Deouiyeb.H, Belabass.S ects.

A toutes les personnes qui, de prés ou de loin nous ont soutenu lors de ce travail, nous adressons nos sincrères remerciements.

Je dédie cette oeuvre à mes très chers parents qui m'ont soutenu au cours de mes études.

Je la dédie également à mes frères et mes soeurs surtout Mansour et Bendhiba.

Je la dédie à:

ZIAINA. Ahmed NOUAR. Lakhdar MIL YANI. Habchi ZIAINA. Aissa

FETEH. Benaissa GAÂMOUCI. Lakhdar

HADJI. Brahime AKERMI.Maidi

ainsi, qu'a mes amis sans exception.

Également je la dédie à tous les étudiants et les étudiantes de l'institut de Génie Mécanique.

Et en particulier à une personne qui m'est très chère et qui a toujours su m'aider.

KHERRIS. Sahraoui

Je dédie cette oeuvre à:

Mes très chers parents qui m'ont soutenu au cours de mes études. Mes frères et mes soeurs.

Mes amis:

KRAKRIA. Ahmed, B.AEK, G.Sassi, B.Abderrahmane, B.Kadoure, B.Mohamed, B.Mohamed, BOUDJLALE. Mohamed, K.Mohamed, MORDJANI.M, K.Hassane, Rachdi.B, B.Sâad, Mostfaoui.A ..ect.

Mes professeurs.

A tous mes camarades de la promotion Génie Mécanique.

KHARROUBI. Ahmed

Introduction CHAPITRE I : potentiel chimique	.1
I-1 - Notion de potentiel chimique	2
I-2- Potentiel chimique d'un gaz parfait	4
I-3- Potentiel chimique d'un mélange	6
I-4- Mélange comporte plusieurs phases	7
I-5- Degré d'avancement d'une réaction	7
I-5-1- Expression de la condition d'équilibre	...8
I-6- Affinité des réactions chimiques	.9
I-6-1- Définition	...9
I-6-2- Expression de la condition d'équilibre	...9

CHAPITRE II: Calcul de la composition chimique d'un mélange gazeux

II-1- Introduction 10

II-2- 1^ere méthode « annulation des affinités » .10

II-2-1-Méthode de résolution 11

II-2-2-Calcul de l'affinité chimique 13

II-2-3-Algorithme 14

II-2-4-Déterminationde la chaleur molaire à pression constante, de l'enthalpie,

de l'entropie, et par suite de l'enthalpie libre des produits de combustion	.15
I-3-2^eme Méthode « constante d'équilibre »	...15
II-3-1-Constante d'équilibre de réactionë*R	....17
II-3-2-Expression logarithmique de la constante d'équilibre	17
II-3-3- Variation de la constante d'équilibre avec la température	..17
II-3-4- Méthode de résolution	20
II-3-5-Méthode de newton	...22
II-3-5-1- Principes	.22
II-3-5-2-Algorithme de résolution du système(S)	..24
II-4-Calcul de la température de flamme adiabatique	.25
II-4-1-Hypothèses générales	25
II-4-2- Principe de calcul de la température adiabatique	..26
CHAPITRE III: Résultats et interprétations
III-1- Influence de la richesse	29

III-1-1- La variation de la composition des produits de combustion en fonction de la richesse 29
III-1-2- La variation de la température de flamme adiabatique en fonction de la

richesse 34

Conclusion 35

Listes des symboles.

Listes des symboles :

Symboles	Nomenclatures	Unité
U	Energie interne	J
S	Entropie	J/K°
H	Enthalpie	J
G	Enthalpie libre	J
F	Énergie libre	J
ii	Potentiel chimique	J/ mole
y	Coefficient stoechiométrique	mole
xi	Fraction molaire	/
Aff	Affinité des réactions chimiques	J/ mole
d)r	Degré d'avancement	mole
K	Constante thermodynamique d'équilibre	/
Cp f	Chaleur massique isobare des gaz frais	J / K° Kg
R	Constante des gaz parfaits	J/ K° mole
Mf	Masse molaire des gaz frais	Kg / mole
Hf	Enthalpie de formation	J/ mole Kg
P	Pression	Atm
Hm	Enthalpie de mélange	J
G ~	Grandeur molaire	/ mole.
ù	Nombre de mole de N2	mole

Introduction

Introduction

INTRODUCTION

Il y a des millénaires, l'homme acquérait «l'art du feu ». Ce n'est qu'au cours de l'essor industriel du 19^éne siècle que la combustion vive commençait à être valablement utilisée dans des machines pour répondre aux besoins énergétiques.

De notre jour, la combustion occupe une place prépondérante pour satisfaire aux besoins énormes de notre monde économique, dans des domaines aussi divers que:

La production d'énergie électrique;

Le chauffage des locaux;

L'élaboration des matériaux de combustion;

La sidérurgie;

Les transports terrestres, aériens, cosmiques;

La production des hydrocarbures à partir du pétrole brut dans les raffineries etc.

L'importance de notre étude portera sur l'élaboration d'un programme pour le calcul de certains paramètres de la combustion isobare et adiabatique des hydrocarbures saturés.

Dans le premier chapitre, on fera une étude sur le potentiel chimique. Ce paramètre est essentiel dans l'étude des équilibres chimiques des mélanges réactifs.

Le second chapitre sera consacré au calcul de la composition chimique d'un mélange gazeux, dans ce chapitre, nous exposeront les deux méthodes de calcul des concentrations des espèces chimiques dans la zone de combustion.

La première méthode est basée sur l'annulation des affinités chimiques et la seconde sur le calcul des constantes d'équilibres des réactions chimiques.

Les différents paramètres entrant en jeu dans les réactions chimiques et les relations qui les relient, seront présentés dans chaque méthode.

L'analyse et l'interprétation des résultats feront l'objet de notre dernier chapitre.

En fin, on donnera une conclusion générale sur notre étude.

Chapitre I

Potentiel chimique

I-1- Notion de potentiel chimique :[1J

Soit un système à n composants en une phase, par exemple un mélange de gaz ou une solution liquide ou solide.

Si l'on introduit ou si l'on enlève une petite quantité de l'un des composants, l'énergie interne de la phase va varier.

Considérons alors l'expression de la différentielle dU de l'énergie interne obtenue par application simultanée des deux principes à un système fermé, soit:

dU = TdS - PdV (I-1)

Si _m1,m2,... ,mi,... ,m_n représentent les masses respectives des différents composants présents dans la phase, il faut écrire:

dU = TdS-PdV+a ^U dm ... U

? ? a dm ... U

i + ? a

1dmn

a m 1 a m i a m n

Ou plus simplement:

dU = TdS - PdV +i

?a a (I-2)

U idm

i i

m

Les quantités telles que? ? ij a U ?lu ami s,v,mj composants dans le système.

sont les potentiels chimiques des

Le potentiel chimique interne, défini par «GIBBS », est une mesure de l'influence de l'énergie interne de la phase considérée, sur l'influence de la masse du constituant (i).

Si l'on envisage maintenant l'enthalpie, l'énergie libre et l'enthalpie libre de la phase considérée et comme on a par définition respectivement:

H = U+ PV

F = U-TS

G = H- TS

Leurs différentielles sont:

dH = dU+ d(PV)

D'où dH = dU+PdV+VdP (I-3)

dF = dU- d(TS)

D'où dF= dU- TdS- SdT ....(I-4)

dG= dU+ PdV+ VdP- d(TS)

D'où: dG= dU+ PdV+ VdP- TdS- SdT (I-5)

En substituant, la nouvelle expression de dU:

dU= TdS- PdV+ ?

i

Il vient:

dH= TdS+ VdP+ ?

i

dF= -SdT- PdV+ ?

i

dG= -SdT+ VdP+ ?

i

Et par conséquent:

tidmi ..(I-6)

ti dmi ..(I-7)

ti dmi (I-8)

ti dmi ..(I-9)

v,mj

,p, mj

?

v,mj

? aU ?

t_i

? ?

? ami s ,

)

? a H ?

? ?

? a m i )_s

? a F ?

? ? ?

? ami t ,

)

? aG ?

? ?

mj

? a m i t ,p ,

)

Il est souvent commode de définir la composition d'un mélange par le nombre de moles ni des composants. Les dérivées partielles à introduire sont alors :

? a U ? a H ? ? a F ? ? a G ?

? ? ? ? ? ? ? ? ? ? ?

? a n n n n

i s , v,nj

,p , nj

) a

i s ,p ,nj

) a i t , v,nj

) a i ) t

On les désigne sous le nom de potentiels chimiques molaires ? ~ i, ou

~ encore de quantités molaires partielles (Ui

~ , H i

~ ,G i

, Ui ~). Elles sont liées

aux potentiels chimiques définis précédemment par la relation: ? ~ i =Mi ? i

Ou Mi est la masse molaire du composant i.

I-2- Potentiel chimique d'un gaz parfait: [2]

Soit un système homogène constitué par un mélange de gaz. On peut caractériser la composition du mélange par les nombres de moles n1,... ,ni_.,... ,n_n des différents composants. Dans ces conditions on utilisera, pour mesurer l'influence d'une variation de la quantité d'un composant présent dans le mélange sur l'énergie interne, l'enthalpie, l'énergie libre ou l'enthalpie libre de celui-ci, les potentiels molaires ? ~ i et l'on écrira:

dU=TdS-PdV+ ? i dH = TdS+ VdP+ ? i dF = -PdV- SdT+ ? i dG = VdP- SdT+ ? i

? ~ i dni (I-10) ? ~ i dni .(I-11) ?~ i dni ..(I-12) ?~ i dni (I-13)

Alors que les fonctions (U,H,F,G) dépendent des nombres de moles des différents composants, les potentiels chimiques ne sont fonction que des rapports de ces nombres entre eux, autrement dit que de la composition et sont indépendants des constituants du mélange. Considérons d'abord un gaz parfait à l'équilibre ; la formule de Massieu:

??? a

G ?

a = V (I-14)

P )? T

donne pour une évolution isotherme du gaz entre un état de référence de pression P0 et un état de pression P, en désignant par g l'enthalpie libre d'une mole de gaz:

P

g~ -- J

g~ 0 VdP

P0

Soit, compte tenu de l'équation d'état: PV=RT

~ -- ^P

~

g dp

g RT

⁰ P

RTln P

P0 0

p

Ou:

~ + .(I-15)

~

g g RT ln P

0

P 0

Où,g⁰

~ fonction de la température seulement, représente l'enthalpie libre d'une mole de gaz dans l'état de référence, sous la pression P0 et a la température T.

Si l'état de référence choisi est un état de pression unité : P0=1 (atm) on peut écrire :

~ = g0

g ~ +RT ln Pi (I-16)

L'enthalpie libre, comme l'énergie interne ou l'énergie libre, est une grandeur extensive, l'enthalpie libre d'un mélange de gaz parfaits est la somme des enthalpies libres des composants, chacun d'eux étant toutefois pris sous sa pression partielle, soit:

G n (g RT ln (I-17)

P

~ 0 ⁱ )

i i+

i P 0

La différentielle de cette fonction G calculée à pression totale et température constantes, a pour expression:

dG (g RT ln

~ 0 i

~~ ~~~

P i

)dn _n RT dP (I-18)

ii i

P

i 0 i i

P

D'après l'équation d'état: PiV n _i RT ,V étant le volume total, on a:

dP i

dP

~ ~ ~

n RT

i VdP V

i

i

P

i i

i i

Puisque la pression totale ~ P i

Pi a été supposée constante.

P

RT ln ⁱ )dn i

P 0

L'expression (I-18) s'écrit donc

dG (g

= -

0_i

i

Soit en comparant avec l'expression générale:

d= ? G ~ i

J1~ i dni .(I-19)

J1 ~ i =0

~ + RT ln (Pi/P0)

gi

que l'on peut écrire aussi :

J1 + RT ln (Pi/P0) ou encore:

~ 0

i

~

J1 i =

~

J1 ~ i = 0

J1+RTlnPi (I-20)

i

J1 , Désignant alors le potentiel chimique d'une mole de gaz Gi à l'état

~ 0

i

pur sous la pression d'une atmosphère et à la température actuelle T, identique à l'enthalpie libre molaire et à cette température seulement.

I-3- Potentiel chimique d'un mélange:

Soit un système constitué par un mélange de gaz; on a vu que le potentiel chimique molaire de l'un des constituants du mélange, dans l'hypothèse où ceux-ci sont assimilables à des gaz parfaits, est relié à sa pression partielle Pi = Xi P par la relation:

J1 (T)+ RT ln(Pi/P0)

~ 0

i

~

J1 i=

Ou _Xi=ni/nT (fraction molaire), avec nT le nombre total des moles. J1 (ou 0

~ 0 ~ ) désigne le potentiel chimique d'une mole du gaz(i)à l'état pur

gi

i

sous la pression de référence Pi⁰ (ou P0 ) pression prise le plus souvent égale à une atmosphère;⁰

J1 est une fonction de la température T ~

i

seulement.

En remplaçant Pi par Xi P, il vient:

~i= ⁰

P (T)+ RT ln(P/P0)+RT ln Xi (I-2 1)

P

~

i

I-4- Mélange comporte plusieurs phases:

La variation de l'enthalpie libre G de la phase j ; dans la quelle le nombre du constituant i est ni _j et son potentiel chimique _ìij, pour des transformations élémentaires isobares et isothermes est:

dG

~ dG_j

j

Soit:

dG= ij

.. _ijdn .(I-22)

ij

Il y a égalité du potentiel chimique de i dans chaque phase à l'équilibre si le système est globalement fermé dG=0, c'est-à-dire :

~P~ ij (I-23)

ij

dnij 0

I-5- Degré d'avancement d'une réaction:

Considérons une phase déterminée d'un système homogène et supposons qu'une réaction chimique soit susceptible de s'y produire.

Au cours d'une telle réaction certains corps disparaissent, d'autre apparaissent et les variations des nombres de moles des corps sont liées par l'équation stoechiométrique de la réaction.

Par exemple pour la réaction d'équation

VAA+VBB ? VCC+VDD

Le degré d'avancement élémentaire de la réaction est:

_r dn dn dn dn dn

^{A B C}

d O ^{D i} (I-24)

D D D D D

A B C D i

Où les íi sont les coefficients stoechiométriques négatifs pour les corps réagissants, positifs pour les produits de la réaction.

Par exemple Soit la réaction d'équilibre :

CO2 ? CO + 1/2O2

à t=t1 XCO2 XCO XO2

à t=t2 X_CO2 - î XCO+ î XO2+1/2 î

donc: ?

XCO2 =XCO2 ^(t2)- XCO2 (t1)

?XCO2 =XCO2 - î -XCO2 ?XCO2 =-î

Alors : AX CO 2 ?

U

de même:

? XO2= î

? XO2= 1/2 î

-î/-1= î

co

2

AXCO î /1= î
?

U co

? ? ?

? X (1 / 2)

O2 =

U_O 2 1/2

I-5-1- Expression de la condition d'équilibre:

D'après l'équation (I-24) et par conséquent

r

dn _i =?v d X

r r

i

i

C'est-à-dire, la variation du nombre de moles du constituant i dans la réaction r est la somme des produits des coefficients stoechiométriques par le degré d'avancement de la réaction r.

De l'équation (I-13) on trouve:

? ?? ?

~ r

dG VdP SdT

= _ + r ?? ? v ? r

?? i i d .(I-26)

i

Nous savons qu'un système fermé et en équilibre thermodynamique interne s'il est en équilibre thermique, mécanique et chimique, donc:

dG= ?? ~ i

i

dni=0

Finalement une nouvelle expression de la condition d'équilibre (I-26):

G= ?r

(:JI ~ i

i

v i )dër. (I-27) r

I-6- Affinité des réactions chimiques:

I-6-1- Définition:

Par définition, la quantité [-?? ~ r

v _i ] est appelée affinité chimique

i

i

(introduite en 1922 de DONDER [5]) de la réaction chimique r.

Aff=-?JI ~ i

v i ..(I-28) r i

II-6-2 Expression de la condition d'équilibre:

D'où la nouvelle expression de la condition d'équilibre (I-27):

(dG)p ,t=^-? Affd)r (II-29).

Chapitre II

Calcul de la composition

chimique d'un mélange

gazeux

II-1- Introduction:

Deux méthodes illustrent le calcul de la composition.

La première est fondée sur l'annulation des affinités des réactions chimiques considérées au sein des produits de combustion [4], quant à la deuxième, elle est basée sur le calcul des constantes d'équilibre.

Considérons le cas d'un hydrocarbure de formule _CnHm dont la combustion est effectuée dans l'air sous pression constante; les produits de la combustion comprennent essentiellement du:

(CO2, H2O, O2, N2 ,CO, H2 , OH, NO, H, O, NO2, N).

A haute température, le mélange sera le siège des réactions d'équilibre: R[0]= 2CO2 ? 2CO+O2

R[1]= 2H2O ? 2OH+H2

R[2]= 2H2O ? 2H2+O2

R[3]=H2? 2H R[4]= O2? 2O R[5]=N2+ O2 ? 2NO

R[6]=N2? 2N

R[7]= NO+ 1/2 O2 ? NO2

II-2- 1^ére méthode - annulation des affinités:

Pour un mélange constitué de N composants et M espèces atomique (C,H,N,O, on a ici M= 4); il faut compléter les M équations de conservation des espèces atomiques par (N-M) réactions d'équilibre dont l'affinité _Affj peut s'écrire :

Affj =-? v ijt i (j= 1,... ,N-M) (II-1)

Où v _ij représente le coefficient stoechiométrique du i^ème composant dans la j^ème réaction et ti le potentiel chimique de ce composant.

ti est définit par:

ti	?	G (T 0	) +	ln	? P ? ? ? ? P 0 ?	+	ln	? n ? i ? ? 1nb ?	(II-2)
RT		RT

Où G⁰ (T) est l'enthalpie libre à température T.

G ⁰ (T)

i =

RT

H ⁰ (T)S⁰ (T) ⁱ - ⁱ

RT R

D'où:

(II-3)

avec: ni : le nombre de moles du composant i.

nb : le nombre total de moles du mélange. P0 : la pression de référence égale à 1 atm.

II-2-1- Méthode de résolution :

Soit [M] la matrice des espèces atomiques et [D] celle de la composition initiale d'un mélange quelconque d'hydrocarbure et d'air de richesse Ri.

On a l'équation suivant:

Ri _CncHnh+Zst (O2+ù N2)

ù est le nombre de mole de N2.

Avec : Zst = n_c +nh/4 (coefficient stoechiométrie).

C				nR c i
Donc: [M] =	H O	et [D] =			n R h i 2Z st
N			2 Z w st

Dans le cas d'un mélange pauvre, les 4 premiers ( CO2, H2O, O2, N2); dits de base sont affectés de l'indice O et les autres composants non de base sont affectés de l'indice 1.

Ces composants, représentés par des matrices [R0] et [R1], s'expriment respectivement en fonction des espèces atomiques à l'aide des matrices [A0] et [A1], et ont des nombres de moles [X_o] et [X1] et des potentiels chimiques [G_o] et [G1].

On a:

1

?

?

?

?

J

2

1

?

?

?

?

J

H

			1020
?		0210
		0020
			0002

CO

O₂

N₂

[Ro]=

H O

2

= [R0]=[A0][M] éléments de base

1

?

?

?

?

J

C

O

N

[ ]

R 1

? CO1

? ?

H

? 2 ?

? OH ?

? ?

NO

? ? ? ?

? NO ?

2

? ?

? H ?

? O ?

?? ??

? N J

? ? ? ? ? ?

? 0110 ? 0011 ? 0021 ? 0100 ? 0010 ?? 0001

?

?

? = [R1]=[A1][M]éléments non de base

?

?

?

1

?

?

?

?

?

?

?

?

?

?? J

C
H

N

O

1

?

?

?

?

J

Dans le cas d'un mélange riche, on permute O2 avec CO entre [RO] et [R1] ; Soit [X_n] la matrice des coefficients stoechiométriques qui relie la masse molaire des éléments non de base à celle des composants de base.

[R1]=[X_n][R0] (II-4)

avec:

[X_n]=[A1][A0]^-1 (II-5)

[ ]

X_n

1 ?

?

?

?

?

?

?

?

?

?? J

2

1 0 1 2 0

--

0 1 1 2 0

--

40

001

?

0 0 1 12

01

21

21

0 12 1 4 0

--

0

00

00

12 0

12

La conservation du nombre de moles s'exprime: ^t[A0][X0]+^t[A1][X1]=[D] (II-6).
que nous écrivons:

[X0]= ^t[A0]^-1([D]-^t[A1] [X1]) (II-7)

D 'ou: [X0]= ^t[A0]^-1 [D]-^t[X_n] [X1] .(II-8)
II-2-2- Calcul de l'affinité chimique:

Soient [G0] la matrice des potentiels chimiques des éléments de base et [G1] celle des éléments non de base.

? J-tCO21

?J-tH2O ?? ? [G1
? J-tO2 ?? ? J-tN2?J

[G0

J-t

J-t

CO

H2

J-t

OH

J-t

NO

1=

NO2

J-t

H

J-t

O

J-t

1 ?

?

?

?

?

?

? J

N

J-t

donnent pour l'affinité des réactions la matrice [Aff]: [Aff]=[X_n][G0]-[G1] (II-9)
Où l'indice supérieur ^t désigne la transposition de la matrice.

III-2-3- Algorithme:

Pour déterminer la composition, on suit l'algorithme suivant:

1- on initialise les matrices: [A0], [A1], [X_n]

2- on se donne les valeur de n_c, nh et Ri ce qui permet le calcul de [D].

3- on calcule successivement: [A0]^-1, ^t[A0]^-1 , [X_n],^t[A1].

4- Si le mélange est riche (Ri>1), [A0]^-1 et [X_n] seront recalculées, à partir de leurs valeurs initiales données et en tenant compte de la permutation de O2 avec CO.

G ⁰ (T) P

5- calcul de [A0]^-1 et ⁱ +ln

RT P₀

6- on initialise [X1] (X1(i)=0.001, i=1.....8)

7- on commence alors le cycle itératif:

a- on calcule [X0] à partir de l'équation (II-8) avec la condition Suivante: Si X0(i) < 0 Alors X0(i) = 1 0-8

b- on calcule nb le nombre de moles total,[G0] et [G1]

c- on déduit: [Aff]= [X_n]-[G1]

d- on effectue le test de convergence:

Si _[Aff] <0.01

Alors la composition est donnée par [X1] et [X0]

Si non, on recommence une nouvelle itération

e- On calcule les nouveaux nombres de moles [X1] à l'aide de la loi empirique:

[ ] [ ] [ ] ?

' ?

x x ₁ exp

1 .(II-10)

p ? 1 = ?_

p ff i

?

i i ? ? ?

Où p désigne le numéro de l'itération.

a: est un paramètre empirique que l'on doit diminuer au cours du calcul pour accélérer la convergence.

a varie de(2~100) [3]

II-2-4- Détermination de la chaleur molaire à pression constante, de l'enthalpie, de l'entropie et par suite de l'enthalpie libre des produits de combustion:

Pour des températures comprises entre 1000 et 5000 K°, les polynômes de GORDON et MAC BRIDE [3], permettant le calcul de ces grandeurs sans dimension pour chaque composant.

Cp ⁰ (T)

ⁱ =a1+a2T+a3T²+ a4T³+ a5T⁴

R

H⁰(T)

i = a1+ T

a 2 ? 3 2 ? 4 3 ? 5 4 ? 6

a a a a

T T T T

RT 2 3 4 5

S0 (T)

ⁱ =a1 ln T+ a2T +7

a + + +

3 2 4 3 ⁵ T ⁴ a

a a

T T

R 2 3 4

Par suite:

G ^0 (T) i =	H ^0 (T) i	-	S0 (T) i
RT	RT		R

Les valeurs des coefficients ai, des principaux produits de combustion d'hydrocarbures sont données dans l'annexe (A).

II-3- 2^ème méthode - Constante d'équilibre: [4]

Soit la réaction d'équilibre R sous la forme générale suivante:

R: í1A1+ + ínAn ? w1B1+ + wmBm

Avec : (íi, i=1.... n,wi= 1 m) sont les coefficients stoechiométriques ;

(Ai ,i=1 n ; Bi ,i=1 m) constituants chimiques.

On définit la constante d'équilibre K:

m

?

wi

P Bi

K (II-11)

1

?

? P ^Di

Ai

Avec : ( P_Bi , P_Ai ) les pressions partielles des constituants Bi, Ai

respectivement.

L'équation (II-11) devient:

m

w

wi_m

n

wi

Bi

rI

1

i ?

? V )?

?

( n RT ?

? ?

?

? V )

m Bi ( RT ? 1

K ?

1

D

n ( n RT ? rI ?

Ai

'

1 ? V )

n

? D

?? V )?

i

( RT ? 1

i n

i

D

n

Ai

rI

1

On à : PTV = nT RT

m

n

P Ai

1

avec : = ?

1

P T P _Bi + ?

m

n

et ? ?

n T n _Bi + ?

n

1

Ai

1

et donc: ?

( RT (

P ?

? )? ? ?

V ? nT )

m n ( ^m I ? ?? n wi ? wi i ? ? ? ?? ? Bi ? K ? ? P 1 1 1 n n ^T n ?? 1I ^i Ai ? 1 )

(II-12)

Exemple :

Soit la réaction d'équilibre :

3 ?

0. 5

CO O2

?? )? ?? ??

n n

?

( P ? ( n n ?

? CO2 )

CO2 ? CO+ 2 1 O2.

K ?

1

n

( P ? ( ?

2 CO O2

n

?? )? ?? ??

n CO

n 2 )

avec: n = n_CO2 + n_O2 + nCO

II-3-1- Constante d'équilibre de réaction ë*R avec ë R La réaction ë*R s'écrit sous la forme:

ë*R:ë í1A1+ + ë ínA n ? ë ù1B1+ + ë wmBm

D'après l'équation (II-12) :

m

m n ? wi

wi ? r' n ?

i

= ??

( ? ? ?

? - ?? Bi

P

K ? 1 1 1

n n

^T n

?? i

?

r' Ai 1 D'où:

m n

E ?V

wi -
1 1

??

?

?

P

=

K ?

n

T

?

?

i

m

r'

1

i

n

n

r'

1

Ai

V

??

wi
Bi

n

Donc:^..

K ? = K (II-13)

II-3-2- Expression logarithmique de la constante d'équilibre: D'après l'équation (II-12) :

m( '\ m

= ?? V - ?

n n

P

ln K w ln

?

?? ) ? I I - ? - ?V ...(II-14)

i i w ln(n ) ln(n )

1 i Bi 1 i Ai

1 1 1 n T )

II-3-3- Variation de la constante d'équilibre avec la température : [1] La constante K est définie par:

lnK= -

A ..(II-15) G0 RT

Ses variations avec la température s'étudient grâce à la formule de Van't Hoff obtenue en appliquant la formule de Gibbs Helmholtz à l'équation stoechiométrique de la réaction, chacune des espèces étant prise dans l'état de référence.

( A

d( G ⁰ ) 0 0

? ( A ? A

G H "

La relation ? ? ? ? ? s'écrit aussi :

? dT ? ? T ?

( A (II-16)

G 0 0

? ( A H ?

?

d 2

? = _ ? ? dT

? T ? ? T ?

D'où en tenant compte de : ?G⁰= -RT lnK

( d(ln K) ?

?? ??

dT

0

? ?

(A H ?

? RT 2 ?

(II-17)

On en déduit aisément l'influence d'une augmentation de température sur l'équilibre :

a- AH >0, la réaction est endothermique et la constante d'équilibre

0

augmente avec la température ; la réaction progresse de gauche à droite lorsqu'on augmente la température.

b- 0 AH <0, la réaction est exothermique. La réaction régresse de

droite à gauche pour une élévation de température.

c- AH =0, la constante d'équilibre K est indépendante de la

0

température. La réaction elle-même est indifférente à une variation de température.

On notera que dans le cas d'une réaction entre gaz parfaits, AH ne dépend que de la température.

ln K = -	A G0
	RT

où: AG⁰ = AH⁰ - TAS⁰ .(II-18)

T

AH , est la chaleur de réaction dans les conditions correspondant à l'état

0

de référence; 0

ASest la différence des entropies des produits de la réaction et des corps initiaux, avec les nombres de moles figurant dans l'équation stoechiométrique, chacun d'eux étant pris dans l'état de référence, soit à l'état pur, et sous la pression d'une atmosphère, en général, pour les gaz, la température étant la température actuelle T.

La constante d'équilibre résulte alors de l'équation:

= -- .(II-19)

H ⁰ A ⁰

A S

ln K .

RT R

En introduisant la température T0 pour laquelle sont données les enthalpies et les entropies dans les tables, il vient, d'après la formule de Kirchhoff:

A ? A +

H 0T H (Cp) dT

0 n Jv i Xi

T0

T0 1

De même, pour la variation d'entropie :

T ( \î ?

S S

0 0 i Xi

(Cp)

A = A + n J ?

I dT

T T0 1 T0 ? T ?

on en déduit:

0 0

A H A S

T0 T0

+

RT R

T n 1 T n ? ? (Cp)

(Cp) dT ?

i Xi

J J

v +

i Xi

RT T0 1 R T0 1 ? T

lnK

?

dT

?

?

1

(II-20)

Les deux derniers termes sont de signes contraires, et se compensent plus ou moins. C'est pourquoi, en première approximation, on prend souvent :

RT

R

lnK =

A H

T0 A

0

?

S 0

T0

II-3-4- Méthode de résolution:

Les chaleurs absorbées par les réaction R[i] (i= 0 7), obtenues

à partir des chaleurs de formation.

Les réactions R[i] ne sont pas indépendantes et influent les unes sur les autres. C'est ce qui rend relativement difficile la détermination de la composition du mélange de gaz brûlés dans des conditions données de température et de pression.

Désignons les nombres de moles dans le mélange en équilibre par:

(

n , n , n , n , n , n , n , n , n , n , n , n . )
CO2 H2O O2 N2 CO H2 OH NO H O NO2 N La détermination de ces 12 inconnues s'effectue au moyen des 12

équations obtenues en exprimant, d'une part l'équilibre pour les réactions R[i], et d'autre part, les bilans du carbone, de l'hydrogène, l'oxygène et d'Azote.

Pour le carbone, on doit avoir:

nCO2+nCO= nc^*Ri

pour l'hydrogène_:

nH2O+nOH+2nH2+nH=nh Ri

Pour l'oxygène:

2nCO2+nH2O+2nO2+nCO+nOH+2nO+nO+2nNO2=2Zst

Pour l' azote:

2nN2+nN0+nNO2+nN=ù .Zst

le nombre total de moles est:

N=nco2+nH2o+no2+nN2+nco+nH2+noH+nNo+nH+no+nNo2+nN

Désignons par K[i] (i=0,7), les constantes d'équilibre des réactions R[i] (i=0... 7), et par P la pression totale dans l'hypothèse de gaz parfaits, généralement justifiée.

D'après l'équation (II-12) :

L

KI-0b P N n no2 => lnK[0]= ln ^P +2ln(nco)+ln(no2)-2ln(nco2).

-- nL2 N

K1-i N = P n²OHnH2

lnK»ln ^P +2ln(nOH)+ln(H2)-2ln(nH2O).

-I nî,2O N

K?2?=^P n?-12nH2N lnK[2bln^P +2ln(nH2)+ln(nO2)-2ln(nH2O) n^2N H2O

.

KI-3'1= ^{P nîï} lnK[3ln ^P +2ln(nH)-ln(nH2)

' N nH2 N

KI^-4_'1 = P n° lnK[4]ln ^P +2ln(nO)-ln(nO2)

' N nO2 N

145]=(P ² nNO lnK[52ln(nNO)-ln(nN2)-ln(nO2)

N nN2nO2

K[6]= ^{P n?"}' lnK[6ln ^P +2ln(nN)-ln(nN2)

N

' N nN2

,_1

KM = V ) 3 nNO2

lnK[7-- ¹ _ln ^P +ln(nNO2)-ln(nNO)-- ¹ ln(nO2) N nNOnm 2 N 2

On pose les symboles suivants:

1°- f(i):est le vecteur de la composition X2[i], (i = 0...11)

2°-X2:(nCO2 ,nH2O,nO2 ,nN2,nCO,nH2,nOH,nNO,nH,nO,nNO2,nN.)

Alors le système d'équation (S) obtenue: ( f(i) i= 0...11) est :

f(0)= X2 (0)+ X2(4)-n_c Ri =0

f(1)= X2 (1)+2 X2 (5)+ X2 (6)- X2 (8) _-nhRi =0

f(2)=2X2(0)+X2( 1 )+2X2(2)+X2(4)+X2(6)+2X2(7)+X2(9)+ 2X2( 1 0)-2Z_st=0

f(3)=2 X2 (3)+ X2 (7)+ X2 (10)+ X2 (11)- ù Zst=0

f (4)=ln N P +2 ln X2 (4)+ ln X2 (2)-2 ln X2 (0)- ln K[0] =0 f(5)= ln N P +2 ln X2 (6)+ln X2 (5)-2 ln X2 (1)- ln K[1] =0 f(6)= ln N P +2 ln X2 (5)+ ln X2 (2)-2 ln X2 (1)- ln K[2] =0 f(7)= ln N P +2 ln X2 (8)- ln X2 (5)- ln K[3] =0

(S)

f(8)= ln N P +2 lnX2 (9)- lnX2 (2)- ln K[4] =0

f(9)=2 ln X2 (7)- ln X2 (3)- ln X2 (2)- ln K[5] =0 f(10)= ln N P +2 ln X2 (11)- ln X2 (3)- ln K[6] =0

f (11)=- ₂ 1ln N P +lnX2(10)-lnX2(7)- ₂ ¹lnX2(2)-ln K[7] =0

La résolution du système d'équations précédentes n'est possible que pour une méthode d'approximations successives; en effet la valeur des constantes d'équilibre K dépend de la température, on utilise la méthode de Newton pour résoudre ce système

II-3-5- Méthode de Newton : [6] II-3-5-1- Principes:

Notons x*= [x*1,x*2, x*_n]^t le vecteur solution du système

non linéaire :

fi(x) =0 (i= 1,...,n.) .(II-21)

Si chaque fonction fi est continue et continûment différentiable, alors, par développement en série de Taylor dans le voisinage d'un estimé _xK proche de x* on obtient:

fi( x*) = fi [ x^K+ (x*-x^K)] fi(x*)=fi(x^K)+

*j

x K j

)(xx *r r -- K

0 f (x )

K

n ? i ? n n

? J -- + ??

1

? (x x )

K

*_j (x

j

0 x 2

j 1

= = = =

j

? ? j 1 r 1

x x K

2

+.... 0......(II-22)

= x K

? 0 f (x)

i ?

0 0

x x

j r

? ? x

) ? J

Pour i=1,....,n.

Si x^K est un estimé proche de x*, les éléments ( x*i- xj ^K)² sont négligeables, ainsi que les termes de degré supérieur.

Le système (II-22) s'écrit donc:

? ⁱ _?J -- =--

n ? 0 f (x) K

? (x x ) f (x )

K K

j j i

j 1 j

x

= ?? .(II-23)

0 x x K

=

Définition la matrice E^K des dérivées premières telles que : ? 0 f (x)

i ?

E K ij x

= (II-24)

?? 0 ?J

i x x K

=

Le vecteur d'erreur ?x^K par:

A x j = x -- x (II-25)

K K

*j j

Puis le vecteur F^K par

Fi ^K=-fi(x^K) (II-2 6)

Alors la Relation matricielle (III-23) s'écrit:

E^K. ?x^K = F^K (II-2 7)

?x^' =F' 1

E ? (II-28)

(')

La méthode de newton présentée ci- dessus génère souvent une correction

?x^' telle que l'approximation de (II-22),par (II-23) n'est pas valable dans

[x', x^' + ?x^' ].

Toutefois, on se satisfait souvent de trouver une correction ?x^' telle que:

f(x^('+1)) < (f(x)^') (

est une norme quelconque)

C'est pourquoi on choisit souvent de se déplacer dans la direction ?x^' de Newton d'un pas:

(x^('+1)) = (x)^') + ë ' ?x^' .(II-29)

ouë^' < 1 est choisi tel que:

f(x^('+1)) < f(x)^'

II-3-5-2- Algorithme de résolution du système (s):

Pour le calcul de la composition on adopte l'algorithme suivant:

1. On se donne la matrice Ei _j (x),(i=1... .1 1,j=1.....11 )

2. On se donne le vecteur des constantes d'équilibre : K[i](en fonction de la température)

3. On se donne le vecteur Fi(x),( i = 0.....11 )

4. On initialise le vecteur de la composition estimée X 2[i] ,(i = 0... 1 1),proche de la solution

5. On commence le cycle itératif.

6. On calcule la matrice E(X2) à partir de l'équation (II-24).

7. On calcule le vecteur K(T) à partir de l'équation (II-14).

8. On calcule le vecteur F(x) à partir du système (S).

9. On calcule le nouveau vecteur X2[i] à partir de l'équation (II-28).

Si X2 [i] ~0 on prend X2 [i] =||X2[i] ||, On effectue le test de Convergence.

> Si Äx^k <1 0^-2; la valeur de Äx^k est calculée à partir de l'équation (II-29).

> Si non, on calcule les nouveaux nombres des moles X2 à partir de la loi:

X2K=X2K? ¹ +Ax

Et on effectue une nouvelle itération avec X2^K où K désigne le numéro de l'itération.

II-4- Calcul de la température de flamme adiabatique:

II-4-1- Hypothèses générales : [3]

Les hypothèses fondamentales sur les quels seront basés nos calculs sont:

1°- Le mélange de gaz frais est assimilable à un gaz calorifiquement parfait, c'est-à-dire, si U et H représentent respectivement l'énergie interne et l'enthalpie, on à:

PV=nRT

dU=nCvdT

dH=nCpdT

Avec: Cp- Cv= R= 8.32 (j/mole K^°)

CP ??? ( Constante des gaz parfait )

1 .4

CV

2°- Les mélanges des réactifs et les produits de combustion sont assimilables à des gaz parfaits. Cette hypothèse est valable tant que les pressions ne soient pas très élevées

.

3°- La combustion est isobare et adiabatique donc les échanges thermiques ne sont pas pris en considération.

4°- On suppose que la composition T

nfi d'un constituant i du mélange frais à une température et une pression donnée, est égale à sa composition nf⁰i aux conditions de référence (P0=1 atm, T0=298 K°),

nfi = nf⁰i .(II-30)

T

5°- Les chaleurs spécifiques d'un constituant i du mélange frais ont été supposées indépendantes de la température.

Cp _fi =Cp .(II-31)

T 0

fi

et par suite on a pour le mélange

? n Cp

T 0

fi fi

Cp (II-32)

T

^f n

= i

? T fi

i

6°- L'enthalpie des gaz frais à la température T est donnée par:

H f H Hà T T 0 = ? fi +? fi i i

(II-33)

H0 fi est l'enthalpie de formation du constituant (i) du mélange, au conditions de référence;

HàTfi est l'enthalpie sensible à la température T.

à T ⁰fi 0fi ( 0)

fi = n Cp T -- T

(II-43)

H

7°- On a tenu compte que de 12 éléments chimiques

Les enthalpies de formation et la chaleur spécifique des constituants sont données par les tableaux (voir annexes B et C).

Le calcul détaillé de l'enthalpie des gaz frais est donné en annexe E. II-4-2-principe du calcul de la température adiabatique:

Lors d'une combustion isobare et adiabatique l'enthalpie des gaz, avant et après leur combustion, se conserve.

H H ^Tb

f = (II-34)

Tf

b

L'enthalpie Tf

Hfest déterminée à partir de Tf et de l'équation (II-32).

La pression dans la chambre étant connue, on cherche ensuite la température Tb qui donne la composition et les enthalpies des composants de produits de combustion, conduisant à l'égalité des enthalpies des gaz avant et après combustion.

-Il faut d'abord choisir la méthode de calcul.

-Cette méthode permet pour une température et une pression donnée des gaz brûlés, de déterminer leur composition.

-La composition étant évaluée, on peut alors, en utilisant les polynômes de GORDEN et MAC BRIDE [3], calculer l'enthalpie de chaque constituant et par suite l'enthalpie totale des produits de combustion.

-Enfin, on évalue la température Tb des gaz brûlés, en utilisant la méthode itérative des sécantes, qui permet dans ce cas une convergence rapide et dont le principe est le suivant:

-On se donne alors deux températures T1 et T2 arbitraires et à l'aide de la méthode choisie, on déterminer les compositions et par suites les enthalpies _H ^et H ^T2

f correspondantes à T1 et T2.

T 1

b

L'intersection de la droite joignant les points A1(T1, T1

H ) et A2 (T2, T2

Hb )

b

avec la droite Tf

Hf= constante: (Fig :II-1) donne une première température Tb que l'on considère comme étant acceptable si :

Tb-T < æ Si non, on pose T1=T et _T2=Tb et on recommence. T étant la température correspondante à l'enthalpie, ( _H ^ou H T 2

b ) dont la valeur

T1

b

algébrique est la plus proche de celle de T 1

Hf .

H

H2 Hf H1

T1 TfT2 T

(Fig :II-1): principe du calcul de la température adiabatique

Chapitre III

Résultats et interprétations

Dans ce chapitre, on va représenter les différents résultats obtenus par les deux méthodes, essayer de les interpréter et de les comparer.

III-1- Influence de la richesse:

III-1-1- La variation de la composition des produits de combustion en fonction de la richesse:

Les figures [(III-1), (III-8)], représentent la variation de la composition

des produits de combustion isobare du méthane et du propane, (CO2, H2O, CO, N2, O2, H2, OH et NO). Deux cas sont à distinguer:

1er Cas : Ri<1

On constate, qu'en milieu pauvre la quantité de O2 produit est inversement proportionnelle à la richesse ceci est dû à la quantité d'air exedante.

L'excès de comburant diminue nettement l'intensité des réactions d'équilibres (dissociation).

D'autre part, il implique la décroissance du nombre de moles des gaz CO2 et H2O. Aussi, on note que la proportion négligeable du CO, OH, NO et le H2, est le résultat de l'activité trop faible des réactions d'équilibres.

2^émeCas :Ri>1

Dans ce cas, on a un défaut d'air, l'oxygène disponible étant insuffisant, ce qui explique sa quantité négligeable. Cette dernière est produite par les réactions d'équilibres (dissociation), devenues très vives à cause du manque de comburant. Cette vivacité des réactions d'équilibres dissocie un nombre important des molécules du (CO2, H2O), en (CO, H2) ce qui explique la décroissance des premières et l'augmentation des dernières.

Remarque:

Pour les gaz (NO, NO2, OH, H, O et N), leurs réactions d'équilibre sont intenses, seulement à des hautes températures, qu'on ne peut pas les atteindre avec les hydrocarbures saturés, ce qui indique leur faible quantité et par conséquent, la quantité d'azote N2 reste pratiquement constante.

Chapitre III Résultats et interprétations

3.00

----- CH4 ___ C3H8

0.00

2.00

1.00

0.80 0.90 1.00 1.10 1.20 1.30

Richesse Ri

Fig III.1: Variation de la composition de CO2 en fonction de la richesse

4.00

----- CH4

___ C3H8

3.00

2.00

1.00

0.80 0.90 1.00 1.10 1.20 1.30

Richesse Ri

Fig III.2: Variation de la composition de H2O en fonction de la richesse

0.25

0.20

0.05

0.00

----- CH4

___ C3H8

0.15 0.10

0.80 0.90 1.00 1.10 1.20 1.30

Richesse Ri

Fig III.3: Variation de la composition de CO en fonction de la richesse

20.00

----- CH4 ___ C3H8

16.00

12.00

8.00

4.00

0.80 0.90 1.00 1.10 1.20 1.30

Richesse Ri

Fig III.4: Variation de la composition de N2 en fonction de la richesse

1.00

----- CH4 ___ C3H8

0.80

	0.60 0.40
0.20 0.00

0.00

0.80 0.90 1.00 1.10 1.20 1.30

Richesse Ri

Fig III.5: Variation de la composition de O2 en fonction de la richesse

3.00

----- CH4 ___ C3H8

2.00 1.00

0.80 0.90 1.00 1.10 1.20 1.30

Richesse Ri

Fig III.6: Variation de la composition de H2 en fonction de la richesse

0.12

----- CH4

___ C3H8

0.08 0.04 0.00

0.80 0.90 1.00 1.10 1.20 1.30

Richesse Ri

Fig III.7: Variation de la composition de OH en fonction de la richesse

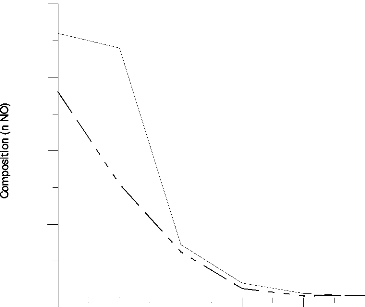
0.16

----- CH4 ___ C3H8

0.12

0.04

0.00

0.08

0.80 0.90 1.00 1.10 1.20 1.30

Richesse Ri

Fig III.8 Variation de la composition de NO en fonction de la richesse

Ri / ni	nCO2	nH2O	nCO	nN2	nO2	nH2	nOH	nNO
0.8	0.739	1.477	0	7.463	0.318	0.054	0.093	0.112
0.9	0.831	1.676	0.0001	7.492	0.173	0.08	0.066	0.062
1	0.996	1.887	0.0012	7.511	0.025	0.092	0.04	0.025
1.1	0.082	1.791	0.0035	7.521	0.017	0.399	0.018	0.005
1.2	0.066	1.623	0.0141	7.523	0.033	0.772	0.008	0.001
1.3	0.049	1.445	0.0238	7.523	0.05	1.152	0.004	0.001

Tableau III.1 a : La variation de la composition des produits de combustion
pour le méthane CH4

Ri / ni	nCO2	nH2O	nCO	nN2	nO2	nH2	nOH	nNO
0.8	2.45	3.093	0	18.73	0.8077	0.045	0.106	0.144
0.9	2.515	3.465	0.0001	18.738	0.446	0.059	0.1	0.136
1	2.998	3.881	0.0013	18.795	0.026	0.099	0.039	0.029
1.1	2.535	3.422	0.001	18.805	0.064	0.962	0.031	0.008
1.2	2.27	2.913	0.105	18.809	0.129	1.879	0.0129	0.0024
1.3	2.198	2.394	0.2	18.815	0.201	2.802	0.005	0.0008

Tableau III.1 b : La variation de la composition des produits de combustion pour le Propane C3H8

III-1-2- La variation de la température de flamme adiabatique en fonction de la richesse:

· a) première méthode

La figure (III-2- a) représente la variation de la température de fin de combustion du méthane et du propane en fonction de la composition initiale des gaz frais.

- On remarque que les courbes présentent un maximum au voisinage du mélange stoechiométrique, cette constatation se rencontre chez la plupart des hydrocarbures.

- En milieu pauvre (Ri<1), la décroissance de Tf s'explique comme nous l'avons vu précédemment, par l'augmentation de la quantité (nombre de moles) des produits

gazeux au sein desquels va se dissiper l'enthalpie initiale ?H i.

- En milieu riche (Ri>1), la décroissance de Tf quand la richesse augmente est due à l'activité importante et accrue des réactions d'équilibres, dont le caractère endothermique arrive à l'emporter sur l'échauffement des produits formés

· b) deuxième méthode

La comparaison des graphes III.2.a et III.2.b et des tableaux III.1.a et III.1.b montre que les résultats obtenus par la méthode des constantes d'équilibres sont très proches de ceux calculés par la première méthode pour les mélanges pauvres. L'écart relatif maximal de deux valeurs correspondantes ne dépasse pas les 7% pour le méthane et reste inférieur à 4% pour le propane. Par contre, au-delà de la richesse stoechiométrique, les valeurs obtenues par les deux méthodes divergent, et ce sont les résultats de la seconde méthode qui sont incompatibles avec la réalité. Cette incompatibilité est due peut être à une erreur dans notre programme. Il faut noter aussi que pour avoir une bonne convergence de la seconde méthode il faut que les valeurs initiales des racines soient proches de la solution.

			---- C3H8 ___ CH4

2500.00

2400.00

2300.00

2200.00

2100.00

2000.00

0.60 0.80 1.00 1.20 1.40

Richesse Ri

Fig III.2.a: La variation de la température de flamme adiabatique (1ère méthode).

3000.00

2800.00

2200.00

2000.00

----- C3H8
___ CH4

2600.00 2400.00

0.60 0.80 1.00 1.20 1.40

Richesse Ri

Fig III.2.b: La variation de la température de flamme adiabatique ( 2ème méthode).

Ri		Tf (CH4)		Tf (C3H8)
0.7		2037.09		201 6.12
0.75		2115.39		2093.66
0.8		2151.73		2119.54
0.85		2260.85		2149.34
0.9		2329.17		2241.22
0.95		2394.72		2407.34
1		2455		2470.33
1.05		2515.49		2532.07
1.1		2573.63		2617
1.15		2629.65		2692.76
1.2		2683.63		2704.28
1.25		2735.7		2757.51
1.3		2785.95		2809.05
Ri	Tf(CH4)		Tf(C3H8)
0.7	2063.53		2063.22
0.75	2080.73		21 00.09
0.8	2151.73		2192.33
0.85	2193.91		2197.18
0.9	2213.42		2245.82
0.95	2233.84		2271 .72
1	2426.17		2430.93
1.05	2420.27		2423.46
1.1	2416.5		2406.62
1.15	2386.83		2373.79
1.2	2359.4		2341.04
1.25	2326.9		2305.73
1.3	2063.34		2272.16

Tableau (III.1 .b) la variation de la Température Tableau (III.1 .a) la variation de la Température

de flamme adiabatique de flamme adiabatique

deuxième méthode première méthode

Conclusion

Conclusion

CONCLUSION

Notre étude est une initiation aux calculs par ordinateur des paramètres d'un phénomène physico-chimique très complexe qui est la combustion.

Dans le temps qui nous a été alloué, on n'a pas pu tenir compte de tous les phénomènes influents sur le déroulement de la combustion, d'ou l'utilisation de certaines hypothèses simplificatrices pour nous faciliter la tâche.

Les résultats obtenus restent des valeurs approchées.la première méthode donne des résultats quantitatifs conformes à la réalité quelque soit la richesse du mélange.

Pour la seconde méthode si les valeurs obtenues pour les mélanges pauvres sont valables dans l'ensemble, celles des mélanges riches sont en contradiction avec la réalité. Nous pensons qu'il y a une erreur qu'on n'a pas pu déceler à temps pour palier à cet inconvénient.

Notre programme peut calculer à la demande en plus de la température de flamme et de la composition, d'autres paramètres tel que: les chaleurs spécifiques, l'enthalpie, l'entropie et l'enthalpie libre.

En fin dans cette étude nous avons amélioré nos connaissances dans le domaine de la combustion et appris à manipuler le logiciel de la

programmation avancé qui est le «DELPHI».

Annexes

Annexe A-1: [3]

	CO2	H2O	N2	O2
Hf(298) So(298)	-94.054 +51.070	-57.798 +45.106	+0.000 +45.770	+0.000 +49.000
a1	+4.460041E+00	+2.7167633E+00	+2.8963194E+00	+3.6219535E+00
a 2	+3.0981719E-03	+2.9451374E-03	+1.5154866E-03	+7.3618264E-04
a 3	-1.239257 1E-06	-8.0224374E-07	-5.7235277E-07	-1 .965222E-07
a 4	+2.2741325E-10	+1.022666E-10	+9.907393E-11	+3.620155E-11
a5	-1.5525954E-14	-4.8472146E-15	-6.5223555E-15	-2.8945627E+15
a6	-4.8961442E+04	-2.9905826E+04	-9.0586184E+02	1.2019825E+03
a7	-9.8635982E-01	+6.6305671E+00	+6.1615148E+00	+3.6150960E+00

Annexe A-2:

	CO	H2	OH	NO
Hf(298) So(298)	-26.420 +47.210	+0.000 +31.210	+9.432 +43.880	+21.580 +50.347
a 1	+2.9840696E+00	+3.1001901E+00	+2.9106427E+00	+3.1890000E+00
a 2	+1.4891390E-03	+5.1119464E-04	+9.5931650E-04	+1.3382280E-03
a 3	-5.7899684E-07	+5.2644210E-08	-1.9441702E-07	-5.2899318E-07
a 4	+1.0364577E-10	-3.4909973E-11	+1.3756646E-11	+9.5919332E-11
a5	-6.9353550E+15	+3.6945345E-15	+1.4114542E-16	-6.4847932E-15
a 6	-1.4245228E+04	-8.7738042E+02	+3.935315E+03	+9.8283290E+03
a 7	+6.34791 56E+00	-1.962942 1E+00	+5 .4423445E+00	+6.74581 26E+00

Annexe A-2:

	H	O	NO2	N
Hf(298) So(298)	+52.100 +27.392	+59.559 +3.470	+7.910 -57.340	+113.000 +36.610
a 1	+2.5000000E+00	+2.5420596E+00	+4.6240771E+00	+2.4502682E+00
a2	+0.0000000E+00	-2.7550619E-05	+2.5260332E-03	+1.0661458E-04
a 3	+0.0000000E+00	-3.1028033E-09	-1.0609498E-06	-7.4653373E-08
a4	+0.0000000E+00	+4.5510674E-12	+1.9879239E-10	+1.8796524E-11
a5	+0.0000000E+00	-4.3680515E-16	-1.3799384E-14	-1.0259839E-15
a6	+2.5471627E+04	+2.9230803E+04	+2.2899900E+03	+5.6116040E+04
a7	-4.6011763E-01	+4.9203080E+00	+1.332413E+00	+4.448758E+00

Remarque : Hf et SO en (cal/mole).

Annexe B: [7]

Les enthalpies de formation de diverse substance dans l'état standard de référence, [Hf] 298 ⁰ K

Substance	[Hf]298 0 K (Kcal/mole)		Substance	0 [Hf] 298 K (Kcal/mole)
O(g)	59.148		CH1(g) .	-17.889
O2(g) .....	0		C2H6(g) ...	-20.236
H(g) .	52.082		C3H8(g) .	-24.820
H2(g)	0		C4H12(g)... .	-29.812
OH(g)	9.402		C5H14(g)	-35.00
N(g) ...	112.482		C6H14((g) .	-39.96
N2(g)	0		C7H16(g)	-44.89
NO(g) .	21.595		C8H18(g) ..	-49.82
NO2(g) ...	8.090		C6H6(g) .	19.820
CO(g)	-26.412		C2H2(g)	54.194
CO2(g) .	-94.040		C2H4(g)...	12.496
H2O(g)	-57.790
H2O(l) .	-68.309

Légende: (g): gaz.

(l): liquide.

Annexe C: [7]

C-1-Chaleur Spécifique à Pression Constante Cp Des Gaz

Température
t	T
C°	K°
0	273
100	373
200	473
300	573
400	673
500	773
600	873
700	973
800	073
900	1173
1000	1273
1100	1373
1200	1473
CH4				C2H6		C3H8
CP				CP		CP
Kcal/Kg°K		Kcal/Kg°K		Kcal/Kg°K	Kcal/Kg°K	Kcal/Kg°K	Kcal/Kg°K
0.5172		2.1654		0.3934	1.6471	0.3701	1.5495
0.5848		2.4484		0.493	2.0674	0.4817	2.0168
0.6704		2.8068		0.5947	2.4899	0.5871	2.4581
0.7584		3.1753		0.6814	2.8696	0.6770	2.8345
0.8430		3.5295		0.7676	3.2138	0.7550	3.1610
0.9210		3.8560		0.8405	3.5190	0.8237	3.4487
0.9919		4.1529		0.9045	3.770	0.8831	3.6974
1.0560		4.4213		0.3607	4.0223	0.9357	3.9159
1.1129		4.6595		1.0069	2.2157	0.9175	4.0926
1.1638		4.8726		1.0483	4.3890	1.0151	4.2500
1.2089		5.0614		1.0863	4.5481	1.0495	4.3945
1.2483		5.2264		1.1209	4.6930	1.0811	4.5263
1.2820		5.3675		1.1521	4.8236	1.1094	4.6448

C-2-

Température
t	T
C°	K°
0	273
100	373
200	473
300	573
400	673
500	773
600	873
700	973
800	073
900	1173
1000	1273
1100	1373
1200	1473
CH4							C2H6				C3H8
CP							CP				CP
Kcal/Kg°K			Kcal/Kg°K				Kcal/Kg°K		Kcal/Kg°K		Kcal/Kg°K		Kcal/Kg°K
0.3486			1.4395				0.38447		1.6007		0.2253		0.9433
0.4363			1.267				0.44669		1.8702		0.3189		1.3352
0.5197			2.1759				0.48817		2.0439		0.4003		1.6760
0.5918			2.4777				0.51928		2.1714		0.4673		1.9565
0.6334			2.7357				0.54501		2.2818		0.5213		2.1826
0.7065			2.9580				0.56756		2.3763		0.5659		2.3693
0.7532			3.1535				0.58784		2.4612		0.6029		2.5242
0.7942			3.3252				0.60643		2.5390		0.6342		2.6553
0.8295			3.4730				0.62337		2.6099		0.6609		2.7671
0.8609			3.6044				0.63881		2.6746		0.6834		2.8613
0.8887			3.7208				0.65279		2.7331		0.7029		2.9429
0.9126			3.8209				0.66542		2.7860		0.7196		3.0128
0.9336			3.9088				0.67672		2.8333		0.7340		3.0731
Température
T		T
C°		K°
0		273
100		373
200		473
300		573
400		673
500		773
600		873
700		9731
800		073
900		1173
1000		1273
1100		1373
1200		1473
1300		1573
1400		1673
1500		1773
1600		1873
1700		1973
1800		2073
1900		2173
2000		2273
2100		2373
2200		2473
2300		2573
2400		2673
2500		2773
2600		2873
2700		2973
2800		3073
2900		3173
3000		3273
O2								N2
CP								CP
Kcal/Kg°K					Kcal/Kg°K			Kcal/Kg°K		Kcal/Kg°K
0.2185					0.9148			0.2482		1.0392
0.2230					0.9337			0.2489		1.0421
0.2300					0.9630			0.2512		1.0517
0.2376					0.9948			0.2554		1.0693
0.2445					1.0237			0.2607		1.0915
0.2504					1.0484			0.2664		1.1354
0.2533					1.0869			0.2721		1.1392
0.2593					1.0856			0.2774		1.1614
0.2627					1.0999			0.2822		1.1815
0.2656					1.1120			0.2864		1.1991
0.2682					1.1229			0.2902		1.2150
0.2703					1.1317			0.2935		1.2280
0.2723					1.1401			0.2964		1.2410
0.2743					1.1484			0.2989		1.2514
0.2762					1.1564			0.3011		1.2606
0.2780					1.1639			0.3030		1.2686
0.2797					1.1710			0.3048		1.2761
0.2815					1.1786			0.3063		1.2824
0.2832					1.1857			0.3077		1.281
0.2849					1.1928			0.3089		1.2933
0.2867					1.2004			0.3100		1.2979
0.2884					1.2075			0.3110		1.3021
0.2900					1.2142			0.3120		1.3063
0.2917					1.2213			0.3128		1.3096
0.2933					1.2280			0.3136		1.3130
0.2948					1.2343			0.3143		1.3150
0.2964					1.2410			0.3155		1.3209
0.2979					1.2472			0.3162		1.3239
0.2984					1.2493			0.3170		1.3272
0.2997					1.2548			0.3173		1.3285
0.3010					1.2602			0.3180		1.3314

C-3-

Annexe D: [1] Constantes d'équilibres.

T(°K) K[i]	H2 = 2H	O2=2O	O2= 2N	N2+ O2 = 2NO	2CO2= 2CO +O2	2H2O= 2H2+O2	2H2O=2OH+H2
1000	5.121 10^-18	3.63 10^-20	8.2 10^-32	7.3 10 -9	4.00 10^-21	7.5 10^-21	1.310-^23
1100	6.682 10^-18	8.8 10^-18	2.26 10^-28	5.3 10 -8	1.92 10^-18	1.71 10^-18	710^-21
1200	3.889 10^-14	8.6 10^-16	1.67 10^-26	2.77 10 -7	3.28 10^-16	1.59 10^-16	1.410^-18
1300	1.221 10^-12	4.19 10^-14	4.50 10^-24	1.11 10^-6	2.52 10^-14	7.46 10^-15	1.210^-16
1400	2.361 10^-11	1.17 10^-12	5.5 10^-21	3.68 10^-6	1.00 10^-12	2.02 10^-13	610^-15
1500	3.090 10^-10	2.11 10^-11	5.610^-19	1.04 10^-5	2.58 10^-11	3.54 10 -11	1.610-13
1600	2.956 10^-9	2.66 10^-10	1.3 10^-17	2.58 10 -5	4.26 10^-10	4.35 10 -11	3.010-12
1700	2.166 10^-8	2.48 10 -9	3.40 10^-16	5.76 10^-5	5.05 10 -9	3.98 10^-10	410^-11
1800	1.279 10 -7	1.82 10^-8	6.0 10^-15	1.17 10 -4	4.5 10 -8	2.8 10 -9	410-10
1900	6.287 10 -7	1.08 10 -7	7.8 10^-14	2.22 10 -4	3.2 10 -7	1.7 10^-8	3.010^-9
2000	2.634 10^-6	5.38 10 -7	7.8 10^-13	3.93 10 -4	1.9 10^-6	8.2 10^-8	1.910^-8
2100	9.684 10^-6	2.31 10^-6	6.4 10^12	6.6 10 -4	9 10 -6	3.4 10 -7	110-7
2200	3.163 10 -5	8.7 10^-6	4.26 10^-10	1.06 10 -3	3.8 10 -5	1.3 10^-6	4.510^-7
2300	8.367 10 -5	2.90 10 -5	2.45 10^-11	1.63 10 -3	1.4 10 -4	4.2 10^-6	1.810^-6
2400	2.512 10^-4	8.8 10^-5	1.20 10^-9	2.42 10^-3	4.8 10^-4	1.3 10^-5	610^-6
2500	6.295 10^-4	2.43 10^-4	5.20 10^-8	3.48 10^-3	1.4 10^-3	3.5 10^-5	2.110^-5
2600	1.468 10^-3	6.24 10^-4	7.11 10^-7	4.86 10^-3	3.9 10^-3	8.9 10^-5	610^-5
2700	3.216 10 -3	1.48 10 -3	2.28 10 -7	6.62 10 -3	1 10^-2	2.1 10 -4	1.610-4
2800	6.668 10^-3	3.36 10^-3	6.80 10^-7	8.8 10^-3	2.2 10^-2	4.7 10^-4	4.210^-4
2900	1.256 10^-2	7.14 10^-3	1.88 10^-6	1.15 10^-2	4.8 10^-2	1.0 10^-2	110^-3
3000	2.483 10^-2	1.44 10^-2	2.44 10-^6	1.48 10^-2	0.11	2.0 10 -3	2210-3

Annexe E: [7]

Calcul de l'enthalpie du mélange frais:

L'enthalpie HT fdu mélange frais à la température T est donnée par:

à

T
fi

H f H H
T = ? 0 fi +?

i i

Hf⁰i , est l'enthalpie de formation du constituant i aux conditions de référence. à

?fi H T

? ? n T fi

Cp(T T 0 )
T --

fi

i i

Compte tenu des relations (II-3 0) - (II-31) - (II-32) on à: à

?fi H T

? ? n 0 fi

Cp(T T 0 )
0 --

fi

i i

Si on considère le mélange suivant:

Ri CncHnh +Zst (O2 + ù N2) avec Zst = n_c+( nh/4) Sachant que: _H (O ) _H (N 2 ) 0

0 f = =

0

2 f

On aura:

H H (C H ) (R 4.762 Z ) Cp (T T )

T 0 0

f ? + + --

f nc nh i st 0

f

l'enthalpie massique du mélange frais devient:

H ^T

h T f

^f (R 4. 762 Z ) .M --

i st

f

+

Organigramme

H1

Méthode 1 Méthode2

T₁

H2

Méthode 1

Méthode2

T₂

Initialisation T1 et T2

Calcul de la température de flamme par la méthode de la
sécante

Procédure graphe ( Tb , Xb , H_x )

Début

composition

T_f =T₁

Température de flamme

T1=T2 T₂ = Tb

Non

Non

| T1 -T2 | < 1

|H₂-Hf | > |H₁-Hf|

Oui

Oui

T₂ = T₁ T1=Tb

Fin

T (H H ) T (H H )

2 1 f 1 2 2

-- -- --

T_b =

H H

1 2

--

METHODE (1)

Procédure matrice X_b (T , X_b , H_b)

I=0

Début

X1(I)=0.0 1

I=I+1

Oui Non

I<7

A₀

Inverse

		Ai
A0,Ai,X n

Transpose

At n , At , i Xt 0
A t , 0		D

Produit M.V

R_s= * D

A ^t

0

T

G_rTT

G_rT0=G0+ln GrT1= G1+ln

p

p 0

p

p 0

Produit M-V

DC

Rs1= Xt * X₁

n

D

C

Rs -Rsi

DIFFRENCE

GrT0 , GrT1							X0= R s - Rs1
Calcul G
						( ) ( ) X 0 i G 0 ~ G r T 0 i + ln Xb ( ) ( ) X 1 i G 1 ~ G r T 1 i + ln Xl
			G0 , G1
Aff

Test 2

bool

Faux

bool

Vrai

Prod HK

Fin

Hb

Fin

CALCUL DE L'AFFINITE CHIMIQUE

Procédure Aff (Go , G1 , Aff )

X_n, G0

Début

Prod M-V

G1,Xn G

X_nG= X _n *G0

DiffAff

Aff= G1-XnG

TEST DE CONVERGENCE

Procédure test 2(Aff,bool )

Bool=Faux

i=0

Non

E_r<0.01

Non

Er=Er+Aff(i)

I<7

Oui

Oui

Bool = vrai

i=i+1

X1(i) = x1 (i)* exp _(-Aff (i) /2)

Non

Oui

i=i+1

I<7

Fin

E_r = 0

I=0

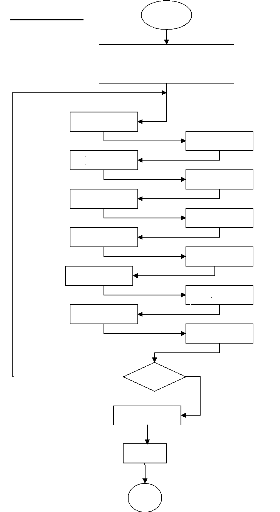
? Méthode (2)

Début

Initialisation X₂
E(X₂) , F(X₂) , K(T)

prod HK

Prod M-V

Calcul E

Faux

Const K

Calcul f

Inverse

Test 3

bool

X₂

K,X₂

E^-1,f(i)

T

test

Vrai

E(X₂)

bool

K(T)

f(i)

E-1

dx i

Hm

Fin

Enthalpie du mélange

Procédure (nor ,V1,V2,V3, bool)

P=1

Bool = false
SV=0

V(i)=V₁(i)

V2(i)=V1 (i)-V(i)

V3(i)=V1(i)

non

V(i)=V1(i) +PV2(i)

X1(i)~ 0

non

P=P-0, 1

V1(i)=

Norm (f,norm2)

calcul f(V3 ,K,f)

oui

norm2 <nor

oui

V1(i

)

V2(i)

SV=SV+

oui non

SV<0,1

bool = true

FIN

TEST 3

Bibliographie

Bibliographie

[1] : Thermodynamique générale et applications Par:R.KLING (1980);

[2] : Cours de sciences physiques thermodynamiques Par: R. Annequin et Boutigny (1979);

[3] : Simulation de la combustion dans un moteur alternatif à combustion interne Par: P. BANER et O. HEUZE (1986);

[4] : La combustion industrielle Par: E. PERTHUIS (1983);

[5] : Thermodynamique (6ème édition) Par : A. KASTLER (2000);

[6] : Méthodes Numériques Appliquées Par : A. GOURDIN et M. BOUMAHRAT (1988);

[7] : Simulation de la Combustion Interne : Modélisation et Expérémentation Par : ASNOUN AHMED, Thèse de doctorat (1997);

[8] : Thermodynamique et Equilibre Chimique Par : ALAIN GRUGE (1997);

[9] : Thermodynamique, Physique et Chimique Par: PAUL Roux et JEAN Robert (1998).