IV. BIBLIOGRAPHIES
Davis J. C. - (1973) - Statistics and Data
Analysis in Geology. John Wiley & Sons, inc., New York
Gilabert M.A., Maselli F., Conese C., Bindi M.
- (1995) - Charaterization of primary productivity levels in Niger
by means of NOAA NDVI variations. Geocarto Interational, 10, 31-41
Groten S.M.E. - (1993) - NDVI-crop
monitoring and early yield assessment of Burkina Faso. International
Journal of Remote Sensing, 8, 1945-1515
Hayes M.J., and Decker W.L. - (1996) -
Using NOAA AVHRR data to estimate maize production in the United States
Corn Belt. International Journal of Remote Sensing, 17, 3189-3200
Huete A. R. and Turker C. J. - (1991) -
Investigation of soil influences in AVHRR red and near-infrared vegetation
index imagery. International Journal of Remote Sensing. 12, 1223-1 242
Hutchinson C.F. - (1991) - Uses of satellite
data for famine early warning system in sub-Saharan Africa. Intenational
Journal of Remote Sensing, 12, 1405-1421.
Maselli F., Conese C., Petkov L., Gialabert
M.A. - (1993) - Environmental monitoring and crop forecasting in
the Sahel trought the use of NOAA NDVI data. A case study: Niger 1986-89.
International Journal of Remote Sensing, 14, 3471-3487.
Sivakumar M. V. K. - (1988) - Predicting
rainy season potential from the oneset of rains in Southern Sahelian and
Sudanic climatic zones of West Africa. Agricoltural and Forest
Meteorology. 42: 295-305
Begué. A., 1991. Estimation de la
production primaire en zone sahélienne à partir de données
radio métriques. Cas d'un couvert discontinu : le mil. Thèse de
l'université de Paris VII, 139pp.
SCOT, CNES : Développement de nouveaux
produits issus de capteur basse résolution : SPOT4/VEGETATION (OSS,
Centre Agrhymet et CSE) 85pages.
H. KONTONGOMDE et I. ALFARI
1991. Modélisation de la prévision des rendements de mil à
partir NDVI et de la Pluviométrie au Niger.
DE FILIPPIS, T., VIGNAROLY, P., DJABY., B., KONE,
B., and DI VECCHIA, A., 1988, AP3A : Agrhymet Projet
Alerte Précoce et Prévision des Productions Agricoles. Final
Repport, Agrhymet Center, Niamey, NIGER.
V. TERMES DE REFERNCE DU CONTRAT
V.TERMES DE REFERENCE DE PRESTATION DE
SERVICE
APPLICATION DES METHODES D'EVALUATION DE RENDEMENTS
AGRICOLES A L'AIDE DES IMAGES NDVI AUX.
1. Contexte
Dans le cadre de l'amélioration des dispositifs de
prévention et de gestion des crises conjoncturelles, le Programme Majeur
information a entrepris depuis plusieurs années de développer des
outils pour l'alerte précoce et la prévision des productions
agricoles.
La disponibilité de l'imagerie satellitale basse
résolution au CRA tout au long de la campagne agricole a permis de
mettre en place des outils pour le suivi de la végétation
naturelle ou cultivée en vue de suivre l'état d'installation des
cultures et des pâturages. Afin d'améliorer ce suivi qualitatif,
le CRA a participé plusieurs initiatives visant à
améliorer les prévisions quantitatives liées à la
production agricole et en particulier les rendements avec plusieurs centres de
recherches européens, CESBIO, IBIMET et SCOT. Ces travaux ont
été concluants sur le plan des résultats et depuis 2003,
des actions sont en cours pour rendre opérationnels les
résultats. Les premiers résultats testés sur le Niger ont
été présentés à la réunion de suivi
à mi-parcours de juin 2004 à Dakar. Afin de mettre en place ces
outils pour la campagne 2004 - 2005 et de les rendre opérationnels au
sein de la chaîne de production d'informations du CRA, le Programme
Majeur Information se propose de tester les méthodologies de
détermination des rendements agricoles à l'aide de l'imagerie
base résolution sur un plus grand nombre de pays du CILSS.
2. Objectifs de la prestation de service
La présente prestation de service a pour objectif de
poursuivre l'amélioration et le test des modèles d'estimation des
rendements agricoles par les méthodes qui utilisent l'imagerie
satellitale basse résolution NDVI provenant de NOAA et de Spot
Vegetation. Ces méthodes ont été déjà
utilisées par le CRA pour des tests sur le Niger en 2003 et
résultent des collaborations déjà menées par le CRA
avec le CeSIA, l'ITC et le CeSBIO.
3. Tâche du prestataire
Depuis 2003, le CRA utilise les méthodes
développées par l'ITC (Méthode Groten) et par le CeSIA
(Méthode Maselli) pour l'évaluation des rendements agricoles. Ces
méthodes testées sur le NIGER ont été concluantes
et les premiers résultats ont été présentés
à la réunion de suivi à mi parcours de la campagne
agricole 2004.
Les taches du prestataire sont d'appuyer le CRA dans le test et
l'application des méthodes retenues sur les autre pays du CILSS par :
- Le test des méthodologies développées
par S. Groten et F. Maselli sur les autres pays du CILSS. Ce test sera
mené sur la période 1995 à 2003 sur tous les pays du CILSS
en utilisant différents types d'images NDVI à savoir la
série GAC corrigée fournie par la NOAA jusqu'en 2002, la
série NOAA LAC du CRA, la série SPOT Végétation
disponible sur la période 2002 - 2004 dans le cadre des collaborations
avec le CESBIO et le projet GMFS
- L'application de la méthodologie SCOT sur le Niger
sur 3 années retenues sur la base d'une considération qu'une des
années est moyenne, une excédentaire et une déficitaire
par rapport à une situation normale.
4. Résultats attendus.
Le prestataire devra produire à la fin de la prestation
un rapport détaillé présentant la méthodologie de
travail, les résultats obtenus qui mettront en relief pour chaque type
d'image, les méthodes qui présentent les meilleurs
résultats, une analyse critique des résultats en mettant l'accent
sur l'opérationnalisation des méthodes au cours de la prochaine
campagne agricole. Le rapport décrira aussi les procédures de
mise en oeuvre des différentes méthodologies
Le Rapport sera accompagné d'un CD comprenant les
données utilisées, les résultats sous forme
numérique et les procédures proposées.
Une présentation des résultats de la prestation
sera faite en présence des experts du PMI 15 Jours avant la fin de la
prestation.
4. Modalités particulières.
Le CRA mettra à la disposition du prestataire un
micro-ordinateur, les données satellitales et les données de
rendements agricoles nécessaires à la réalisation de la
prestation
L'activité est placée sous la
responsabilité du programme majeur information au sein de l'unité
méthodes et applications qui en assure la supervision technique en
collaboration avec les autres unités du Programme.
L'activité démarrera le 15 Novembre 2004 et se
terminera le 28 Février 2005.
Tous les coûts relatifs à la prestation de service
seront pris en charge par le budget USAID, 2004.
VI. ANNEXES
Principe de la validation
croisées
La validation croisées s'appuie non seulement sur des
hypothèses théoriques de distribution des données mais
également sur le fait que plusieurs estimations à partir de
portions indépendantes d'un échantillon sont plus fiables qu'une
estimation sur la totalité. Cette méthode détermine la
valeur probable du pouvoir prédictif en utilisant le paramètre "
crossvalidated r squared". Elle permet de définir différents
ensemble de données: un pour l'apprentissage et l'autre pour la
validation croisée. Ces deux ensembles sont nécessaires pour
étudier la généralisation de manière
systématique.

Echantillon issue de la
Echantillon initiale validation croisée
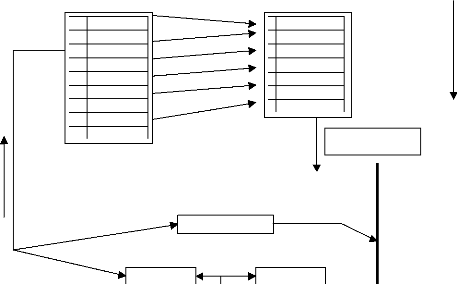
Rangée des
composés exclus
Equation de
corrélation dérivée
Y = ax+b
Propriétés prédites pour les rangées
des composés exclues
Mesurées
Prédites
Propriétés exclues
?
|
Répété jusqu'à m fois
|
|
|
Différences
|
|
|
Déviation standard

Principe de l'analyse de la validation
croisée
A partir d'une table initiale de données, on construit
une autre table dite de validation croisée résultant du
croisement des données initiales et de l'omission d'une où de
plusieurs rangées. Le nouveau modèle ainsi obtenu donne une
nouvelle équation de corrélation qui permet de déduire
l'activité résultante de l'exclusion de ou des rangées. La
différence entre l'activité mesurée et celle
prédite donne la déviation standard et la proportion de
l'incertitude originale crossvalidated r carré de la validation
croisée qui évaluent le modèle ainsi obtenu.
Le cycle de déviation/prédiction est poursuivi
jusqu'à ce que les valeurs obtenues pour l'activité cible soient
constantes. Notons que la validation croisée est un processus
contrôlé par le nombre de composé dans la table. Ainsi si
le nombre de groupe de la validation croisée est posé égal
au nombre de composés de façon à ce que toutes les
activités cibles soient prédites par toutes les données,
le processus de validation permettant d'obtenir des valeurs constantes dans des
séries consécutives se produira pendant un temps très long
car le modèle est réalisé autant de fois qu'il y a de
composés dans la table.
Principe de la méthode appliquée pour la
correction de l'effet sol

La valeur de NDVI corrigée par l'effet sol est:
NDVI = NDVIx - Dx
Où:
NDVI = NDVI corrigé
NDVIx = NDVI des données brutes
Dx = effet des sols
a = NDVIx - NDVIsx
A = NDVIc - NDVIsx
D = NDVIsx - NDVIsd
NDVIsx = valeur de NDVI d'un pixel avec un type de sol avec une
couverture végétale = 0
NDVIc = valeur de NDVI au point où la couverture
végétale = 0
NDVIsd = valeur de NDVI avec couverture végétale =
0 et sols clairs (DC = 0)
On fait l'approximation des courbes Sd C et Sb C à deux
droites. Sd représente la valeur de NDVI quand le pourcentage de
couverture végétale P est égal à zéro pour
les sols foncés et Sb représente la valeur des sols clairs. C'est
le seuil au-delà duquel les sols n'ont plus d'effet.
La surface à l'intérieur du triangle Sb C Sd
représente donc l'aire dans laquelle un pixel peut retomber avec un
pourcentage déterminé de couverture végétale,
inférieur à 100%. Par approximation linéaire on reporte le
point x sur l'axe y (Sx). En considérant les deux triangles Sx C F et SX
X E on établit la proportion
Sx E: Sx F= a : A
d'où P = Sx E / Sx F = a / A.
Considérant maintenant les triangles G X H et Sd Sx I on
établit la proportion
D : Dx = 1: (1-P)
de sorte que Dx =(1-P)D. [0, 0.2]
La valeur corrigée de NDVI résulte donc :
NDVI = NDVIx - Dx
Prenons par exemple deux valeurs de NDVI 0.7 et 0.4
Appliquons la formule pour calculer la valeur de NDVI
corrigée :
|
NDVI = 0.7 - Dx = 0.7
|
- (1-P) D =
|
0.7
|
-(1-0.7)*0.2
|
= 0.64
|
|
NDVI = 0.4 - Dx = 0.4
|
- (1-P) D =
|
0.4
|
-(1-0.4)*0.2
|
=0.28
|
| 


