Application des methodes d'évaluation de rendements agricoles à l'aide des images NDVI

CILSS

Comite Permanent Inter-Etats de Lutte
contre la Sécheresse dans le Sahel

CILSS

Permanent Interstates Committee for
Drought Control in Sahel

Centre Régional AGRHYMET

Application des Méthodes d'évaluation de Rendements
Agricoles à l'aide des images NDVI

Présenté par :

Mr MAI MOUSSA MOURIMA

Janvier 2005

Remerciements

Au terme de cette consultation nous tenons à remercier très vivement toutes les personnes qui ont participé à la préparation de ce document a travers leurs suggestions et leurs conseils. Il s'agit en particulier de :

> Mr Brahima SIDIBE chef du Programme Majeur Information (PMI) > Dr Bakary DJABY chef de l'Unité Méthode Application (UMA)

> Mr Issifou ALFARY chef de l'Unité Gestion des Naturelles(GRN)

> Mr Alkhalil ADOUM Unité Gestion des ressources Naturelles (GRN) > Mr Ado DAN KARAMI Unité Gestion des ressources naturelles (GRN) Qu'ils trouvent ici l'expression de ma très haute gratitude.

SOMMAIRE

I. LISTE DES SIGLES ET ABREVIATIONS 4

II PREAMBULE 5

III TACHES SPECIFIQUES DU CONSULTANT ET RESULTATS ATTENDUS 7

3.1 Méthodes S.Groten et F.Maselli d'estimation des rendements agricoles 7

3.11Introduction 7

3.12 Présentation et caractérisation de la zone d'étude 7

3.13 Méthodologie 10

3.131 Les outils utilisés 10

3.132 Données utilisées et sources d'acquisition 10

3.134Rappel sur l'indice de végétation à différence normalisée (NDVI) 10

3.134 Elimination de l'effet de sol 13

3.135 Etalonnage géographique des valeurs NDVI et rendements 15

3.136 Caractérisation de la zone agricole sur la zone d'étude 18

3.14 Résultats, analyses et discussions 20

3.141 Méthode Fabio Maselli 20

3.142 Méthode Susanne Groten 28

3.15 Validation des résultats 31

3.16 Conclusion 34

3.2 Méthodologie SCOT d'évaluation des rendements 36

i Modèle semi- déterministe 36

3.21 1Introduction 36

3.212 Méthodologie 37

3.213 Résultats et analyses 38

3.214 Validation 42

3.214 Conclusion 44

IV. BIBLIOGRAPHIES 45

V.TERMES DE REFERENCE DE PRESTATION DE SERVICE 48 VI. ANNEXES 51

I. LISTE DES SIGLES ET ABREVIATIONS

AP3A Projet Alerte Précoce et Prévision des Productions Agricoles

AVHRR Advanced Very High Resolution Radiometer

CILSS Comité Inter-Etats pour la Lutte contre la Sécheresse au Sahel

IBIMET Instutute of Agrometeorology and Environmental Analysis for agriculture

FAO Food and Agricultural Organization

FMA Fondation pour la Metéorologie Appliquée

GAC Global Area Coverage

GIMMS Global Inventory and Modeling Studies

LAC Local Area Coverage

MVCs Maximum Value Composite

NASA National Aeronautics and Space Administration

NDVI Normalized Difference Vegetation Index

NOAA National Oceanic and Atmospheric Administration

OMM Organisation Météorologique Mondiale

RMSE Root Mean Square Error

II PREAMBULE

Le Centre Régional AGHRYMET (CRA) est une structure créé en 1974 par le Comité Inter états de lutte contre la Sécheresse au Sahel (CILSS) dans le but de faire face aux problèmes dérivant des sécheresses qui ont sévi depuis 1969 dans la zone Soudano- sahélienne de l'Afrique Occidentale et qui ont atteint des proportions catastrophiques après la saison de pluies de 1972 et 1973.

A travers ces Programmes Majeurs Formation et Information, le CRA a entre autre objectif de rechercher une méthodologie fiable et opérationnelle qui puisse servir de support à un Système d'Alerte Précoce dans les centres nationaux du CIL SS. Car à défaut de pouvoir changer les conditions climatiques des pays du Sahel, il faut pouvoir prévoir et quantifier les déficits et les excédents agricoles afin d'organiser au mieux les secours alimentaires en cas de mauvaise production et la gestion des excédents en cas de bonne production.

L'imagerie satellitaire a été utilisée dans plusieurs travaux pour tenter une telle approche (Barthomé, E. 1988 ; Rudorf B.F.T. 1989 ; Ahscroft P.M. et al 1990).

Dans le cadre de l'amélioration des dispositifs de prévention et de gestion des crises conjoncturelles, le Programme Majeur Information a entrepris depuis plusieurs années de développer des outils pour l'alerte précoce et la prévision des productions agricoles. La disponibilité de l'imagerie satellitaire basse résolution au CRA tout au long de la campagne agricole a permis de mettre en place des outils pour le suivi de la végétation naturelle ou cultivée en vue de suivre l'état d'installation des cultures et des pâturages. Afin d'améliorer ce suivi qualitatif, le CRA a participé à plusieurs initiatives visant à améliorer les prévisions quantitatives liées à la production agricole et en particulier les rendements avec plusieurs centres de recherches européens, CESBIO, IBIMET et SCOT.

Ces travaux ont été concluants sur le plan des résultats et depuis 2003, des actions sont en cours pour rendre opérationnels les résultats. Les premiers résultats testés sur le Niger ont été présentés à la réunion de suivi à mi-parcours de juin 2004 à Dakar. Afin de mettre en place ces outils pour la campagne 2004-2005 et de les rendre opérationnels au sein de la chaîne de production d'informations du CRA, le Programme Majeur Information se propose de tester les méthodologies de

détermination des rendements agricoles à l'aide de l'imagerie base résolution sur un plus grand nombre de pays du CILSS.

La présente prestation de service a pour objectif de poursuivre l'amélioration et le test des modèles d'estimation des rendements agricoles par les méthodes qui utilisent l'imagerie satellitaire basse résolution NDVI provenant de NOAA et de Spot Végétation.

Ces méthodes ont été déjà utilisées par le CRA pour des tests sur le Niger en 2003 et résultent des collaborations déjà menées par le CRA avec le CESIA, l'ITC et le CESBIO.

Depuis 2003, le CRA utilise les méthodes développées par l'ITC (Méthode GROTEN) et par le CESIA (Méthode MASELLI) pour l'évaluation des rendements agricoles. Ces méthodes testées sur le NIGER ont été concluantes et les premiers résultats ont été présentés à la réunion de suivi à mi-parcours de la campagne agricole 2004.

Notre tache sera d'appuyer le CRA dans le test et l'application des méthodes retenues sur les autres pays du CILSS par :

· d'une part le test des méthodologies développées par S.GROTEN et F.MASELLI sur les autres pays du CILSS. Ce test sera mené sur la période de 1995 à 2003 sur tous les pays du CILSS en utilisant différents types d'images NDVI à savoir la série GAC corrigée fournie par la NOAA jusqu'en 2002, la série NOAA LAC du CRA, la série SPOT Végétation disponible sur la période 2002-2004 dans le cadre des collaborations avec le CESIA et le projet GMFS.

· D'autre part l'application de la méthodologie SCOT sur le Niger sur 3 années retenues sur la base d'une considération qu'une des années est moyenne, une excédentaire et une déficitaire par rapport à une situation normale

III TACHES SPECIFIQUES DU CONSULTANT ET RESULTATS ATTENDUS

3.1. Méthodes S.Groten et F.Maselli d'estimation des rendements

agricoles

3.1.1. Introduction

Tucker (1979) fut l'un des premiers à examiner les relations entre le NDVI développé dés le début des années 1970 et les paramètres biophysiques de couverts végétaux tels que la biomasse sèche, verte (photosynthétique), brune ( sénescente),etc. De nombreuses études par la suite ont été basées sur les capacités des indices de végétation à prédire la production agricole et le rendement.

L'utilisation des données NOAA- AVHRR NDVI pour la prévision des récoltes, a une importance particulière dans les régions semi-arides où les fluctuations inter annuelles de rendement dues aux caprices météorologiques sont fortes.

Ainsi, l'ITC et Le CESIA à travers S.GROTEN et F.MASELLI ont mis en place des méthodes opérationnelles pour le traitement des données NDVI visant le contrôle de l'environnement et plus spécifiquement à l'évaluation et la prévision des rendements des récoltes dans les régions du Sahel. Les deux méthodologies se basent sur le même principe. Il s'agit de s'appuyer sur des études expérimentales pour chercher une relation utilisant les données satellitaires et la pluviométrie ou le rendement afin de travailler de façon opérationnelle pour la prévision des rendements agricole à l'échelle des entités administratives pour lesquelles les données de rendement des années antérieures existent. Nous utiliserons d'une part pour la méthode de S. Groten la valeur de l'indice de végétation maximum estimée pendant la troisième décade d'Août et le cumul pluviométrique à la première décade d'Août, et d'autre part pour la méthode de F.Maselli le NDVI maximum relevé en fin septembre et le cumul pluviométrique à la fin de la première décade de septembre.

3.1.2. Présentation et caractérisation de la zone d'étude
· Le Sénégal

Situé entre 12° et 16° 30 de latitude nord et 11°3 et 17° 30 de longitude ouest, le
Sénégal couvre une superficie de 196 722 km². Il est limité au Nord par la Mauritanie,

à l'Est par le Mali, au Sud par la Guinée Bissau et la Guinée Conakry et à l'Ouest par l'Océan Atlantique.

Le climat est soudano sahélien de type semi-aride tropical avec une amplitude de température relativement peu importante, et des températures moyennes comprises entre 20° C de novembre à avril et 35°C de mai à octobre. Le régime climatique du Sénégal est caractérisé par l'existence de deux saisons : une saison chaude et pluvieuse (hivernage) marquée par la circulation de mousson de juin à octobre, et une saison sèche durant laquelle soufflent les alizés continentaux.

La pluviométrie a baissé de façon significative depuis les six dernières années. Elle varie fortement d'une région à une autre, passant de plus de 1000 mm/an dans le Sud à moins de 300 mm dans le Nord.

La Végétation évolue du Nord au Sud en suivant le gradient pluviométrique. Selon les zones, on distingue :

- les steppes arbustives et les steppes arborées du domaine sahélien ;

- les savanes arbustives et savanes arborées appartenant au domaine sahélosoudanien;

- les forêts claires caractéristiques du domaine guinéen ;

- les forêts du domaine guinéen.

Le Sénégal est subdivisé en trente cinq départements administratifs comprenant une variété de paysages (figure n°1)

· Le Burkina faso

Le Burkina Faso est un pays sahélien enclavé d'Afrique de l'Ouest, sa superficie est de 274 000 km². Il est encadré, au Nord et à l'Ouest par le Mali ; à l'Est par le Niger ; au Sud, ses frontières longent le Bénin, le Togo, le Ghana et la Côte d'Ivoire. Le climat du pays est chaud et sec, les pluies sont rares et mal réparties (350 mm au nord contre 1000 mm au sud-ouest). La flore Burkinabé est riche de plus d'un million d'espèces réparties en deux sous ensemble principaux : la fore sèche saharienne et sahélienne (la steppe) et la flore soudanienne (la savane). Il faut aussi noter une flore guinéenne le long des cours d'eau (FONTES et GINKO, 1995).

Le pays est subdivisé en une trentaine de provinces avec une variété de paysages (figure 2)

Figure n°1 : La zone d'étude du Sénégal divisée en trente cinq départements

Figure n°2 : La zone d'étude du Burkina Faso divisée en trente provinces

9

3.1.3. Méthodologie
3.1.3.1. Les outils utilisés

Les logiciels qui ont été utilisés sont :

· Le logiciel WINDISP3.5 pour l'extraction des valeurs d'indice de végétation NDVI pour les différentes zones d'études.

· Le logiciel SURFER qui a servi à l'interpolation et la spatialisation des données ;

· Le logiciel IDRISI3.2 et ARCVIEW3.2 pour l'établissement et la finalisation des différentes cartes ;

· Le logiciel EXCEL qui a servi aux traitements des données, les divers calculs et la confection des tableaux et graphiques.

3.1.3.2. Données utilisées et sources d'acquisition

Les données de base qui ont été utilisées étaient constituées de :

· Les données GAC (Global Area coverage) d'indice de végétation par la différence normalisée (NDVI) couvrant l'Afrique occidentale provenant de la base des données du Centre Régional pour les années de 1990 à 2002 avec une résolution d'environ 4 km au nadir ;

· Les données LAC (Local Area coverage) couvrant également l'Afrique Occidentale provenant de la base des données du CRA avec une résolution de 1.1 km au nadir pour la période de 1990 à 2002.

· Les données de pluviométrie décadaire de la période 1990 à 2002 pour le Sénégal et le Burkina faso provenant de la base des données du logiciel SPM (Suivi des Pluies par Metéosat) du CRA.

· Les données de rendements proviennent de la base des données TDBASE (Système de Gestion de la Base de données Thématique) du Centre Régional AGRHYMET ;

· Les cartes vectorielles des différentes zones d'études proviennent du Centre Régional AGRHYMET.

3.1.3.4. Rappel sur l'indice de végétation à différence normalisée (NDVI)

Depuis 1973, l'indice de végétation à différence normalisée (NDVI) est utilisé pour étudier la végétation. Son existence est due à la télédétection, ensemble de techniques employées pour acquérir des informations à distance qui fournit les mesures de réflectance ou rayonnement électromagnétique émis ou réfléchi par les corps terrestre dans différentes longueurs d'onde (de 0.4 um à 14 um) effectuées par les satellites à défilement. Plus de 90% de l'information spectrale sur un couvert végétal est contenue dans les bandes rouge du visible ® et proche infra rouge (PIR), d'où leur utilisation pour le calcul des indices de végétation (Baret et Guyot, 1991, repris par Guyot, 1996).

Le NDVI est le rapport de la différence des réflectances des canaux PIR et R sur leur somme :

NDVI= PIR - R / PIR + R

Sa valeur varie de -1 à 1 et n'a pas d'unité. Selon Tucker et al (1981) cités par Hiermaux et al (1986), la valeur de 0.05 est le seuil indiquant une présence minimale de végétation correspondant à 100 kg de matière sèche par hectare avec une couverture de 1 %. Son utilisation est avantageuse, son calcul est simple et sa normalisation réduit les effets d'arrière plan tout en discriminant le spectre de la végétation (Justice, 1986, repris par Djaby, 2000). En effet, selon Hiernaux (1988) cité par Djaby (2000), l'intensité du rayonnement de la matière verte augmente beaucoup dans le rouge(R) à cause de la chlorophylle qui l'absorbe, tandis qu'elle augmente légèrement dans le proche infra rouge (PIR), à cause de la diffusion des radiations par les parois hydratées des cellules foliaires. Il est donc un bon indicateur de la vigueur de la végétation.

Inconvénients de l'interprétation

Le NDVI est sensible :

> A la couleur du sol sous-jacent qui l'affecte ;

> Aux couverts végétaux denses qui saturent l'indice et le rendent insensible aux variations de la quantité de phytomasse verte ;

> Au très bas niveau de la couverture végétale verte qui le rend aussi insensible : 1% est le recouvrement minimal visible par le radiomètre AVHRR de NOAA ;

> Aux conditions atmosphériques telles les nuages, la poussière, la brume, la vapeur d'eau et d'autres aérosols qui diminuent la valeur du NDVI ;

> Aux problèmes liés au capteur qui font que les pixels éloignés du nadir ont une résolution plus basse que celles qui en sont proches, et ceux liés à l'âge du satellite (dérive).

Pour toutes ces raisons, des corrections doivent être appliquées aux données avant leur utilisation.

3.1.3.4. Elimination de l'effet de sol

D'une analyse préliminaire, les images NDVI apparaissent fortement conditionnées par les variations dues aux différents types de sols. Selon Huete et Tuker (1991) les différents types de sols peuvent causer des variations de NDVI de 0.2 dans les zones semi-arides où la couverture végétale est faible.

Le modèle permet la réduction du pourcentage d'influence du sol sur l'NDVI pour chaque pixel. De cette façon, et tenant compte également du traitement particulier auquel ont été soumises les images, les valeurs digitales de chaque pixel doivent être considérées en pratique comme l'expression du seul apport de la végétation.

Le fonctionnement du modèle est schématisé en Figure 3.

Figure N°3 : Schéma du modèle de correction pour l'effet des sols.

NDVIsx = valeur de NDVI d'un pixel pour un type déterminé de sol rapporté à une couverture végétale nulle ;

NDVIc = valeur de NDVI au point où la couverture végétale est nulle ;

NDVIsd = valeur de NDVI avec une couverture végétale nulle et sols clairs.

En pratique un pixel sans végétation peut retomber dans l'intervalle Sd-Sb. Alors que lorsque la végétation recouvre complètement le terrain dans l'un et l'autre cas on atteint le point C du graphique, c'est-à-dire le point au-delà duquel les sols n'ont aucun effet dans le calcul du NDVI. Entre ces deux extrêmes un pixel peut retomber dans le triangle Sd Sb C.

Pour corriger les images il faut enlever à la valeur digitale de chaque pixel le segment Dx qui représente la valeur à imputer à l'effet des sols.

La valeur de NDVI corrigée par l'effet sol est donc :

NDVI = NDVIx - Dx

Où :

NDVI = NDVI corrigé

NDVIx = NDVI des données brutes

Dx = effet des sols

Dx = (1-P)*D représente l'effet sol

Cette méthodologie de correction de l'effet des sols a été appliquée uniquement sur les images NDVI GAC parce que selon son auteur Fabio Maselli pour qu'elle puisse être appliquée aux autres images, il faut un travail préalable de réadaptation.

3.1.3.5. Etalonnage géographique des valeurs NDVI et rendements

Des études récentes ont démontré que la méthode d'étalonnage géographique des valeurs NVDI et des rendements des cultures est très efficace pour dissocier les informations non intéressantes liées à la différence spatiales des ressources (types de végétation, topographie, sol, etc., Kogan 1990, Maselli et al. 1993, Hayes and Decker 1996) qui peuvent influencer l'interprétation des différents résultats.

Pour appliquer cette procédure, nous avons calculé les valeurs moyennes des NDVI pour chaque circonscription (départements pour le Sénégal et provinces pour le Burkina faso) sur les douze années d'études et les résultats ont été utilisés pour estimer les valeurs géographiques standardisées S_NDVI (Maselli et al. 1993) à travers la formule suivante :

S_NDVI= (NDVI - M_NDVI) / SD_NDVI

Où
S_NDVI = NDVI standardisé pour chaque année par circonscription administrative
NDVI=valeur de NDVI maxi pour chaque année par circonscription administrative
M_NDVI = moyen des douze années de NDVI par circonscription (figure 4,5)
SD_NDVI = écart type des NDVI maxi pour les douze années d'études par
circonscription (table 1)

Une formule semblable d'étalonnage a été appliquée pour chaque circonscription pour calculer le rendement standardisé S_YIELD selon :

S_YIELD = (YIELD - M_YIELD) / SD_YIELD

Où
S_YIELD=rendement final standardise par circonscription administrative et par année
YIELD = rendement final par circonscription et par année
M_YIELD=moyen des douze années de rendement par circonscription administrative
SD_YIELD=écart type des rendements pour les douze années par circonscription

Les précipitations ont aussi été soumises au même processus d'étalonnage pour avoir des précipitations standardisées S_PRECI PITATION :

S_PRECIPITATION = (PRECIP - M_PRECIP)/SD_PRECIP

Les valeurs (NDVI et précipitation) utilisées dans ce processus d'étalonnage sont relatives :

· aux valeurs relevées à la fin du mois d'août pour les NDVI maxima et au cumul des précipitations jusqu'à la fin de la première décade d'août (méthode de Susanne GROTEN)

· aux valeurs relevées à la fin du mois de Juillet pour les NDVI maxima et au cumul des précipitations jusqu'à la première décade de Juillet (Méthode de Fabio MASELLI)

Cette procédure a été appliquée aux valeurs NDVI de toutes les circonscriptions (provinces et départements) des différentes zones d'études. Ainsi ces valeurs étalonnées (S_NDVI) ont été comparées aux données collectées (précipitations et rendements) qui ont été également soumises à un processus semblable d'étalonnage à travers les valeurs moyennes multi annuelles et les écart types des NDVI (table N°1).

Figure N°4 : Valeur moyenne des NDVI maxi mesurée en fin Août de 90 à 02 au Burkina

Figure N°5 : Valeur moyenne des NDVI maxi mesurée en fin Août de 90 à 02 au Sénégal

17

Table 1 : Valeur moyennes (M_NDVI) et écart type (SD_NDVI) des valeurs NDVI LAC
mesurées à la fin Août de 1990 à 2002 pour le Sénégal et le Burkina Faso

Burkina Faso				Sénégal			Provinces
SD_NDVI		M_NDVI	Départements	SD_NDVI	M_NDVI	BAM
0.046721004		0.39811057	BAKEL	0.064767391	0.57109649	BAZEGA
0.093790876		0.49616595	BAMBEY	0.037931789	0.37776378	BOUGOURI BA
0.124512044		0.54020115	BIGNONA	7.45058E-09	0.42575	BOULGOU
0.131684304		0.54421206	DAGANA	0.125386114	0.30753667	BOU LKI EMDE
0.005773503		0.42008367	DAKAR		0.186305	COMOE
0.128960469		0.52063168	DIOURBEL	0.041049381	0.37066505	GANZOURGOU
0.07369869		0.46682892	FATICK	0.070354253	0.29359992	GNAGNA
0.138129627		0.49228252	FOUNDIOUGN E	0.100759879	0.46069732	GOURMA
0.111858291		0.57169717	GOSSAS	0.063245553	0.40842	HOU ET
0.074996393		0.51303835	KAFFRI N E	0.040535657	0.47495637	KADIOGO
0.116681444		0.4280865	KAOLACK	0.048914948	0.44408304	KENEDOUGOU
0.119696057		0.55904323	KEBEMER	0.101527814	0.33161129	KOSSI
0.002006581		0.46801825	KEDOUGOU	0.087424554	0.55147684	KOURITENGA
0.109663808		0.46164944	KOLDA	0.057231933	0.5807584	MOUHOUN
0.086525293		0.5193552	LINGUERE	0.084899936	0.36273943	NAHOURI
0.078733038		0.49730327	LOUGA	0.05710042	0.2810059	OUBRITENGA
0.09777014		0.45379381	MATAM	0.060607379	0.38499417	OUDALAN
0.023918784		0.35928576	MBACKE	0.054494924	0.38395074	PONI
0.051844721		0.49644772	MBOUR		0.394914	SANGUIE
0.003041683		0.43361506	NIORO DU RIP	0.096763046	0.53016644	SANMATENGA
0.016466292		0.39988095	OUSSOUYE	0.153486024	0.41476964	SOUM
6.35388E-09		0.379585	PIKINE		0.227806	SOUROU
0.057514453		0.45945384	PODOR	0.067550871	0.30196597	TAPOA
0.072094219		0.52109881	RUFISQUE	0.065800006	0.33870726	YATENGA
0.108430047		0.41957106	SEDHIOU	0.031622777	0.546631	ZOUNDWEOGO
0.132791227		0.55431875	TAMBACOUN DA	0.060383437	0.56995517
			THIES	0.042163702	0.365079
			TIVAOUANE	0.044789512	0.31438508
			VELINGARA	0.071101126	0.61133418
			ZIGUINCHOR	0.129992728	0.47002626

3.1.3.6. Caractérisation de la zone agricole sur la zone d'étude

Pour caractériser notre zone agricole sur le Sénégal et le Burkina Faso, à l'absence d'une carte d'occupation des sols, nous nous sommes servis des cartes indiquant la longueur moyenne de la saison de l'année 1971 à l'année 2000 d'une part et d'autre part leur variabilité saisonnière et interannuelle des NDVI (Tucker et al 1991). Ainsi sont considérées comme zone agricole, les régions dont la longueur moyenne de la saison pluviales va au moins à quatre vingt dix jours (figure N° 6 et figure N°7) et puis ses zones ne soient pas complètement boisées.

Figure N°6 : Longueur moyenne de la saison pluviale de 1971 à 2000 pour le Sénégal

Figure N°7 : Longueur moyenne de la saison pluviale au Burkina Faso de 1971 à 2000

Ainsi les départements de Podor, Dagana et Louga (sénégal) avec une longueur moyenne saisonnière inférieure à quatre vingt dix jours et les zones de Kedougou et Velingara pour le Sénégal et Comoe, Poni et Bougouriba pour le Burkina Faso, régions boisées ont été exclues de la présente étude.

3.1.4. Résultats, analyses et discussions

Le NDVI (Normalised Difference Vegetation Index) est un bon indicateur de la productivité des récoltes surtout dans les zones ou il dépend fortement des conditions environnementales. Ainsi comme dans le cas de la première étude, les comparaisons entre NDVI, précipitations et rendements ont été limitées aux circonscriptions (provinces pour le Burkina et départements pour le Sénégal) qui sont caractérisées par une forte variabilité. Le choix des différentes circonscriptions s'est basé sur leurs variabilités saisonnières et interannuelles des NDVI (Gilabert et al.1993), ainsi que sur la durée moyenne de la saison pluviale qui nous ont permis de caractériser les zones agricoles.

Le traitement des données a été fait en utilisant différents types d'images NDVI à savoir la série GAC corrigée fournie par la NOAA jusqu'en 2002 et la série NOAA LAC du CRA sur la même période.

3.1.4.1. Méthode Fabio Maselli

Il convient tout d'abord de faire un bref aperçu sur le principe même de cette méthodologie. Il consiste à considérer le NDVI maxi relevé en fin Juillet, le cumul de précipitations à la première décade de Juillet et le rendement final. Ce choix s'explique pour plusieurs raisons. En effet la troisième décade de juillet est considérée comme étant la période la plus variable en terme de précipitation et précède juste le mois d'août où l'activité végétative est importante. En général, si la saison des pluies commence tardivement ou si la précipitation est au dessous de la moyenne, il n y a plus assez de temps pour le développement complet des plantes vers la fin de la saison de croissance et la production finale est basse (Sivakumar, 1989). En conséquence, l'hypothèse est que l'état de la végétation en fin juillet est fortement sensible aux précipitations des mois précédent et est lié à la production finale.

Ainsi pour la corrélation, nous considérons le NDVI maxi relevé en fin Juillet, le cumul des précipitations jusqu'à la première décade de Juillet et le rendement final.

~ Comparaison entre NDVI et données au sol

Cette comparaison a été faite, d'une part entre les images NDVI à savoir la série GAC fournie par la NOAA corrigée et non corrigée, la série NOAA LAC de la troisième décade de juillet et les précipitations recueillies deux décades au paravent, et d'autre part entre ces mêmes valeurs de NDVI et le rendement final.

Les figures 8 et 9 nous donnent le rapport existant entre les valeurs de NDVI maximum relevées en fin juillet et les cumuls de précipitation recueillis jusqu'à la première décade de Juillet.

Nous récapitulons les résultats de cette première analyse dans les tableaux 2et 3.

Tableau N°2 : cas du Sénégal

Type d'images NDVI	Relation NDVI/Pluies(x/y)	Coefficient de corrélation(r)		Erreur standard	LAC
Y= 311.59X - 6.1973	0.7048	41.97mm		GAC corrigées
Y=212.81X+16.179	0.7193	42.47mm		GAC non corrigées
Y= 418.89X+57.21	0.6843	44.34mm

Tableau N°3 : cas du Burkina Faso

Type d'images NDVI	Relation NDVI/Pluies	Coefficient de corrélation(r)		Erreur standard	LAC
Y= 582.87X-15.142	0.8046	51.08mm		GAC corrigées
Y=586.16X+93.848	0.7237	59.56mm		GAC non corrigées
Y=511.01X-75.802	0.7192	59.699mm

Les variables NDVI et précipitation sont liés entre elles avec un coefficient de corrélation de 0.7048 pour le Sénégal et 0.8046 pour le burkina Faso pour ce qui est des images LAC. Ceci confirme les résultats des autres recherches que pendant cette date, le NDVI est fortement lié aux précipitations antérieures dans les régions semi-arides (Seguin et al.1989, Malo and Nicholson ).

350

300

250

200

150

100

50

0

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

y = 212.81x + 16.179
R2 = 0.5175

NDVI GAC corrigées fin Juillet

350

300

250

200

150

100

50

0

y = 311.59x - 6.1973
R2 = 0.4968

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

NDVI LAC fin Juillet

600

500

400

300

200

100

0

y = 418.89x + 57.21
R2 = 0.4684

0 0.2 0.4 0.6 0.8 1 1.2

NDVIgac non corrigées fin Juillet

Figure N°8 : Régression linéaire entre les images NDVI fin Juillet et le cumul de précipitations à la
première décade de Juillet pour le Sénégal pendant la période de 1990 à 2002

y = 582.87x - 15.142
R2 = 0.6475

0 0.2 0.4 0.6 0.8 1

NDVI Lac fin Juillet

700

600

500

400

300

200

100

0

700

600

500

400

300

200

100

0

y = 428.11x + 8.233
R2 = 0.51 94

0 0.2 0.4 0.6 0.8 1

NDVIgac corrigées fin Juillet

700

600

500

400

300

200

100

0

y = 511.01x - 75.802
R2 = 0.5173

0 0.2 0.4 0.6 0.8 1

NDVI Gac non corrigées Juillet

Figure N°9 : Régression linéaire entre les images NDVI fin Juillet et le cumul de précipitations à la
première décade de Juillet pour le Burkina Faso pendant la période de 1990 à 2002

Le rapport existant entre les valeurs de NDVI maximum et le rendement final des différents départements du Sénégal et des provinces du Burkina Faso est représenté sur les figures 10 et 11. Nous constatons que le rapport entre le NDVI et le rendement des récoltes n'est pas très bien défini (tableaux 4 et 5), avec coefficient de corrélation qui varie de 0.6496 pour les images LAC à 0.560 pour les images GAC non corrigées. Cette différence observée entre les deux variables peut avoir probablement une origine géographique, dérivant des conditions environnementales différentes. En effet, il a été démontré que le NDVI mesuré à un moment précis d'une saison est linéairement corrélé à la production végétale totale et au rendement des récoltes (Tucker et al. 1985, Prince 1991).

Tableau N°4 : cas du Sénégal

Type d'images NDVI	Relation NDVI/Rendements(x/y)	Coefficient de corrélation(r)		Erreur standard	LAC
Y= 2755.2X - 296.25	0.6496	101 kg/ha		GAC corrigées
Y=1678.9X+570.22	0.5982	108kg/ha		GAC non corrigées
Y= 1711.9X+357.78	0.560	156kg/ha

Tableau N°5 : cas du Burkina Faso

Type d'images NDVI	Relation NDVI/Rendements(x/y)	Coefficient de corrélation(r)		Erreur standard	LAC
Y= 2802.6X-337.75	0.6353	96.8kg/ha		GAC corrigées
Y=2325.1X+323.08	0.6426	91 .7kg/ha		GAC non corrigées
Y=2735.6X-1 10.92	0.6321	11 0kg/ha

3000

2500

2000

1500

1000

500

0

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

y = 1678.9x + 570.22
R2 = 0.3579

NDVI GAC corrigées fin Juillet

3000

2500

2000

1500

1000

500

0

y = 2755.2x + 296.25
R2 = 0.4221

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

NDVIlac fin Juillet

3000

2500

2000

1500

1000

500

0

y = 1711.9x + 357.78
R2 = 0.3137

0 0.2 0.4 0.6 0.8 1 1.2

NDVI GAC non corrigées fin Juillet

Figure N°10 : Régression linéaire entre NDVI à la fin du mois de juillet et le rendement final
des récoltes dans les différents départements du Sénégal pendant la période 1990-2002

y = 2802.6x + 337.75
R2 = 0.4037

0 0.2 0.4 0.6 0.8 1

NDVI en fin Juillet

4000

3500

3000

2500

2000

1500

1000

500

0

4000

3500

3000

2500

2000

1500

1000

500

0

y = 2325.1x + 323.08
R2 = 0.413

0 0.2 0.4 0.6 0.8 1

NDVI Gac corrigées fin Juillet

y = 2735.6x - 110.92
R2 = 0.3996

0 0.2 0.4 0.6 0.8 1

NDVI Gac non corrigées fin juillet

4000

3500

3000

2500

2000

1500

1000

500

0

Figure N°10 : Régression linéaire entre NDVI à la fin du mois de juillet et le
rendement final des récoltes dans les différentes provinces du Burkina Faso
pendant la période 1990-2002

Pour pallier aux problèmes d'origine géographique qui affectent considérablement les différentes valeurs des NDVI, une autre méthode a été appliquée. Celle-ci consiste à standardiser les différentes valeurs avant le traitement.

~ Comparaison entre NDVI standardisée et données au sol

Nous récapitulons les résultats de cette opération de standardisation dans deux tableaux différents, l'un pour le Sénégal (tableau N°6) et l'autre pour le Mali (tableau N°7). Pour ce qui des courbes représentatives des différentes fonctions, se référer à l'annexe du document.

Tableau N°6 : Relations entre variables normalisées (NDVI, précipitation et
rendement) pour le cas du Sénégal

Types d'image NDVI	Valeurs non Standardisées					Valeurs standardisées
	NDVI/Rendements			Pluies/NDVI		NDVI/Rendements
	Erreur standard		Coef de corrélation	Erreur standard	Coef de corrélation	Erreur standard	Coef de corrélation	Erreur standard	LAC
0.7048	41.97mm		0.6496	101 kg/ha	0.723	0.394	0.687	0.102	GAC corrigées
0.7193	42.47mm		0.5982	108kg/ha	0.721	0.411	0.613	0.104	GAC non corrigées
0.6843	44.34mm		0.560	156kg/ha	0.691	0.443	0.601	0.128

Tableau N°7 : Relations entre variables normalisées (NDVI, précipitation et
rendement) pour le cas du Burkina Faso

Types d'image NDVI	Valeurs non Standardisées					Valeurs standardisées
	NDVI/Rendements			Pluies/NDVI		NDVI/Rendements
	Erreur standard		Coef de corrélation	Erreur standard	Coef de corrélation	Erreur standard	Coef de corrélation	Erreur standard	LAC
0.8046	51.08mm		0.6353	96kg/ha	0.812	0.580	0.682	0.0761	GAC corrigées
0.7237	59.56mm		0.6426	91kg/ha	0.740	0.579	0.674	0.0906	GAC non corrigées
0.7192	59.69mm		0.6321	110kg/ha	0.7204	0.561	0.6410	0. 1021

Ainsi, l'étalonnage géographique adoptée nous permis de réduire de façon significative l'influence des facteurs environnementaux en améliorant considérablement les corrélations existantes entre les différentes variables.

3.1.4.2. Méthode Susanne Groten

Dans cette partie, nous allons insister beaucoup sur la méthodologie d'estimation des rendements développée par Dr Susanne M. E. Groten. Cette méthodologie nous a permis d'avoir des résultats satisfaisant lors des premières expériences appliquées dans le cas du Niger.

Ainsi les hypothèses du départ ont été relativement maintenues comme dans le cas de la première étude (méthodologie de F.Maselli) à la seule différence que, nous allons utilisé dans le cas présent, le cumul pluviométrique jusqu'à la première décade d'Août et l'indice de végétation maximum estimé à la fin du mois d'août. Ce choix est motivé par plusieurs raisons fondamentales. Entre autre, nous savons que dans le Sahel, le mois d'Août correspond plus généralement au mois le plus pluvieux de l'année et l'activité végétative est plus importante.

Les résultats de l'étude sont récapitulés dans deux tableaux différents l'un pour le Sénégal (tableau N°8) et l'autre pour le Burkina Faso (tableau N°9).

Tableau N°8 : Relations entre variables (NDVI, précipitation et rendement) pour le
cas du Sénégal

Types d'image NDVI	Valeurs non Standardisées					Valeurs standardisées
	NDVI/Rendements			Pluies/NDVI		NDVI/Rendements
	Erreur standard		Coef de corrélation	Erreur standard	Coef de corrélation	Erreur standard	Coef de corrélation	Erreur standard	LAC
0.7785	70mm		0.7542	78kg/ha	0.807	0.575	0.794	0.0646	GAC corrigées
0.7584	76.07mm		0.734	101kg/ha	0.757	0.692	0.721	0.0875	GAC non corrigées
0.7145	81.64mm		0.583	108kg/ha	0.730	0.764	0.6505	0.117

A travers les résultats du tableau ci-dessus relatifs au Sénégal, nous remarquons que les coefficients de corrélation sont assez significatifs surtouts comparés à ceux calculés avec la méthode de F.Maseli (voir tableau N°6). Ceci confirme l'efficacité de la méthodologie de Dr Susanne M.E. Groten par rapport à celle de Fabio Maselli dans le cas Sénégal. Ces différents résultats obtenus varient aussi en fonction du type d'image. Ainsi à travers le tableau N°8, les coefficients de corrélations obtenus avec les images de la série NOAA LAC du CRA sont supérieurs à ceux calculés avec

la série GAC corrigée ou non. Cependant, nous remarquons l'effet dû à la correction apportée à la série Gac qui a permis l'amélioration du coefficient de corrélation (voir tableau N°8).

Pour pouvoir une fois de plus améliorer, la corrélation entre les différentes valeurs, nous avons appliqué la méthode de l'étalonnage géographique. Cette méthode permet de réduire les effets dus aux différences géographiques qui influencent les résultats. Ceci a permis d'améliorer le coefficient de corrélation (tableau N°8).

En définitif, nous pouvons dire que parmi toutes les images utilisées, la série LAC du CRA présente les meilleurs résultats pour la prévision des rendements (figure N°11)

Tableau N°9 : Relations entre variables (NDVI, précipitation et rendement) pour le
cas du Burkina Faso

Types d'image NDVI	Valeurs non Standardisées					Valeurs standardisées
	NDVI/Rendements			Pluies/NDVI		NDVI/Rendements
	Erreur standard		Coef de corrélation	Erreur standard	Coef de corrélation	Erreur standard	Coef de corrélation	Erreur standard	LAC
0.816	54.72mm		0.706	70kg/ha	0.8252	0.584	0.7238	0.0671	GAC corrigées
0.723	66.07mm		0.667	88kg/ha	0.7368	0.671	0.665	0.1022	GAC non corrigées
0.721	65.64mm		0.652	74kg/ha	0.7325	0.681	0.6584	0.1018

Le résultat du tableau N° 9, confirme aussi notre analyse comme dans le cas du Sénégal. Les coefficients de corrélation (NDVI/rendements) sont assez significatifs variant de 0.701 à 0.652 pour les valeurs non standardisées à 0.8252 à 0.7325 pour les valeurs standardisées. Ainsi, les corrélations entre les deux variables considérées (précipitation et rendement) sont beaucoup plus remarquables et significatives quand on utilise des données standardisées.

Ceci confirme l'hypothèse selon laquelle, le NDVI est linéairement corrélé au rendement des récoltes à un moment précis de la saison (Tucker et al. 1985, Prince 1991).

600

500

400

300

200

100

0

y = 731 .96x - 56.129
R2 = 0.6061

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

NDVIlac fin Aout

3000

2500

2000

1500

1000

500

0

y = 3564.5x - 353.33
R2 = 0.5689

0 0.2 0.4 0.6 0.8

NDVI Lac fin Août

3

2

1

0

-1

-2

-3

y = 0.7348x - 0.0214
R2 = 0.6404

-4 -3 -2 -1 0 1 2 3 4

NDVI lac fin Août*

3

2

1

0

-1

-2

-3

-4

-4 -3 -2 -1 0 1 2 3 4

NDVIlac fin Aout*

y = 0.792x + 0.01
R2 = 0.6342

Figure N°11 : Régression linéaire (pluies, rendements, NDVI lac) standardisés et non standardisés pour le Sénégal de 1990 à
2002

Figure N°12 : Régression linéaire (pluies, rendements, NDVI lac) standardisés et non standardisés pour le Burkina Faso de
1990 à 2002

y = 774.93x + 45.571
R2 = 0.6668

0 0.2 0.4 0.6 0.8 1

NDVI lac fin Août

800

700

600

500

400

300

200

100

0

y = 3703x - 304.24
R2 = 0.4998

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

NDVI en Ao ût

4000

3500

3000

2500

2000

1500

1000

500

0

4

3

2

1

0

-1

-2

-3

NDVIlacfinAout*

-2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 4

y = 0.8198x + 0.0138
R2 = 0.6811

4

3

2

1

0

-1

-2

-3

NDVIlacfin Août*

-2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 4

y = 0.6283x - 0.01 95
R2 = 0.5239

3.1.5. Validation des résultats

Pour valider les résultats auxquels nous nous sommes aboutis, plusieurs méthodes peuvent être utilisées. Cependant, une fois de plus notre choix s'est porté comme dans le cas de la première étude sur la validation croisée. Cette méthode détermine la valeur probable du pouvoir prédictif en utilisant le paramètre " crossvalidated r squared". Elle permet de définir différents ensemble de données : un pour l'apprentissage et l'autre pour la validation croisée. Ces deux ensembles sont nécessaires pour étudier la généralisation de manière systématique.

Les figures ci-dessous représentent les résultats de la validation. A la figure N°13 et N°14, nous avons représenté respectivement les différents profils de rendements pour le Sénégal et pour le Burkina Faso. Pour chaque année choisie, nous avons représenté deux profils. Le premier profil représente le rendement réel et le second celui du rendement estimé. A chaque représentation, nous relevons le coefficient de corrélation et l'erreur standard. Les différents résultats obtenus issues de ces validations sont récapitulés dans les tableaux N°10 et N°11.

Tableau N°10 : Résultats du test de validation pour le Sénégal

Années		Types d'images
		GAC corrigées		GAC non corrigées
		Erreur standard kg/ha	Coef de corrélation	Erreur standard	Coef de corrélation	Erreur standard	1997
0.60		279.02	0.51	280.3	0.51	278.5	1998
0.69		237.64	0.41	277	0.40	301	1999
0.67		232	0.47	260	0.47	306	2000
0.65		236	0.40	195	0.40	238

Tableau N°11 : Résultats du test de validation pour le Burkina Faso

Années		Types d'images
		GAC corrigées		GAC non corrigées
		Erreur standard kg/ha	Coef de corrélation	Erreur standard kg/ha	Coef de corrélation	Erreur standard	1999
0.50		151	0.327	198	0.26	182.51	2000
0.75		116	0.56	187	0.54	181	2001
0.43		158	0.36	225	0.326	250	2002
0.66		133.14	0.66	276	0.62	276

Nous remarquons que sur toute la période de validation les images NDVI lac présente les meilleurs résultats pour le Sénégal ainsi que pour le Burkina faso. Ceci démontre une fois de plus la précision des ces images lac vis-a vis de la série gac corrigée ou non corrigée.

A travers la figure N°13 relative au Sénégal, nous pouvons dire que le résultat de la validation pour l'année 1998 se rapproche beaucoup de l'allure du rendement réel. Nous relevons un coefficient de corrélation de 0.69 pour une erreur standard de 237 kg/ha.

Pour le Burkina Faso(figure N°14), c'est l'année 2000 qui se rapproche beaucoup de l'allure du rendement réel avec un coefficient de corrélation de 0.75 pour une erreur standard estimée à 11 6kg/ha.

Nos résultats ont été validés sur quatre années différentes donc ce qui nous donne quatre résultats différents. Le résultat final sera la moyenne de ses différents résultats. En définitif, nous relevons comme résultat final de notre validation un coefficient de corrélation moyen de 0.65 pour une erreur standard moyenne d'environ 200 kg/ha pour le Sénégal et d'une part et d'autre part pour le Burkina Faso une corrélation d'environ 60% pour une erreur moyenne de 1 39kg/ha.

2500

2000

1500

1000

500

0

13579111315171921232527

Rendements réels Rendements estimés

Différentes localités

2000

1800

1600

1400

1200

1000

400

200

800

600

0

1 3 5 7 9 11 13 15 17 19 21 23 25 27

Rendements réels Rendements estimés

différentes localités

Rendements

réels Rendements estimés

2500 2000 1500 1000 500 0

Différentes localités

Rendements réels rendements estimés

3000 2500 2000 1500 1000 500 0

1 3 5 7 9 11 13 15 17 19 21 23 25 27

Différentes localités

Figure N°13 : Profils des différents rendements réels et estimés pour le Sénégal pendant la période de validation (images LAC)

2500

2000

1500

1000

500

0

2000

1800

1600

1400

1200

1000

800

600

400

200

0

2500

2000

1500

1000

500

0

3500

3000

2500

2000

1500

1000

500

0

Rendements réels Rendements estimés

1 357911131517192123252729

Différentes localités

Rendements réels Rendements estimés

1 35 7911131517192123252729

Différentes localités

Rendements réels rendemnts estimés

1 357 911131517192123252729

Différentes localités

Rendements réels Rendements estimés

1 3 5 7 9 11 13 15 17 19 21 23 25 27 29

Différentes localités

Figure N°14 : Profils des différents rendements réels et estimés pour le Burkina Faso pendant la période de validation (images LAC)

3.1.6. Conclusion

Le développement des moyens efficaces de prévision des rendements de récolte est un défi pour les pays du Sahel, où la productivité de l'agriculture de subsistance est toujours assujettie à des adversités atmosphériques ou des attaques parasites. En effet, plusieurs études ont été menées sur la possibilité d'utiliser des données NDVI convenablement traitées pour faire des prévisions. Ainsi dans le présent travail deux méthodes ont été développées. Celle de l'ITC à travers Dr Susanne Groten et celle du Cesia par Fabio Maselli. Ces méthodes utilisées nous ont permis d'effectuer une estimation précoce des productions au niveau des provinces pour le Burkina Faso et des départements pour le Sénégal. Cette estimation est de très grande importance pour les pays en question ou la productivité de l'agriculture de subsistance peut être très fortement influencé par des conditions météorologiques variables. La lenteur de la circulation de l'information à l'intérieur de ces pays et la rareté de celles qui parviennent aux pays développés aggrave encore le problème.

La méthodologie appliquée est basée sur la corrélation entre les valeurs de NDVI maximum par décade et les rendements finaux. La procédure de standardisation utilisée, élimine la majeure partie des informations qui ne sont pas intéressante, liées aux variations spatiales du territoire.

A travers l'analyse des corrélations, la meilleure période pour la prévision des rendements a été identifiée à la fin Août ( méthode S.Groten).

On observe une assez bonne corrélation entre les NDVI Lac et la pluviométrie d'une part et les rendements d'autre part avec la méthode développé par l'ITC (Méthode GROTEN). Ceci peut s'expliquer à la résolution relativement faible des images NDVI lac 1.1km*1.1km et à leur fréquence d'acquisition élevée par rapport à celle des NDVI Gac.

Cependant l'influence de la correction sur l'effet sol apportée aux images NDVI Gac se fait fortement sentir parce ça a permis d'améliorer les différentes corrélations. L'application de la procédure de corrélation des images NDVI Lac avec les rendements a permis d'obtenir des valeurs de r tournant autour de 70% avec une erreur approximative de 80 kg /ha. Des tels résultats peuvent être considérés suffisant pour des applications opérationnelles dans des cas de système d'alerte précoce (Hutchison,1991).

Ce modèle de prévision pourra cependant être amélioré en utilisant des données NDVI Lac corrigées de l'effet sol et une carte d'occupation des sols permettant de discriminer les zones occupées par les cultures.

En définitif, il serait hasardeux de comparer les deux méthodes. En effet pour les systèmes de l'alerte précoce la méthode qui donne les résultats dès le mois de juillet sur les rendements peut aussi être intéressante. Compte tenu que les périodes sur lesquelles portent les deux méthodes sont différentes, il ne faut pas les comparer. En effet la méthode Groten s'avance plus dans la campagne pour les prévisions, et au mois d'août concerné, il y a aussi d'autres outils pas des moindres. Donc loin de pouvoir dégager la suprématie d'une méthode sur l'autre nous suggérons au Centre Régional Agrhymet de prendre en compte ses deux méthodes dans le calendrier des crises alimentaires afin d'avoir une confirmation des estimations faites en juillet dès le mois d'Août.

3.2.6. Méthodologie SCOT d'évaluation des rendements

L'élaboration de l'information " production de biomasse -rendement " fait à plusieurs approches. Trois classes de modèles de production - rendement se distinguent par les approches suivantes :

~ Modèle empirique (corrélation statistique) qui est facile à mettre en oeuvre mais relativement imprécis, utilisant une carte d'occupation des sols et un indice de végétation (NDVI) : voire méthodes F. Maselli ; Docteur Susanne Groten...;

~ Modèle déterministe très précis mais nécessite beaucoup de données raison pour laquelle son utilisation reste cantonnée aux parcelles expérimentales ;

~ Modèle semi- déterministe qui est à cheval entre les deux modèles. Ce modèle intermediare sera développé dans la présente étude. Ainsi nous pouvons tester l'applicabilité de cette méthode sur le Niger sur trois années retenues sur la base d'une considération qu'une année est moyenne (l'année 2001), une excédentaire (1998) et une moyenne (1994).

i Modèle semi- déterministe

(Modèle de production de Monteith simplifié)

3.2.1.1. Introduction

C'est une méthode couramment utilisée à l'échelle régionale et globale, son succès est dû à sa relative facilité de mise en oeuvre et aux faibles nombres des coefficients et variables utilisées. Il offre aussi l'avantage d'utiliser des pas de temps de l'ordre de dix jours. Mais cette méthode présente un certain nombre d'inconvénients qui limitent son application comme par exemple la non connaissance précise des valeurs d'efficience de conversion et les facteurs intervenant dans cette approche ne peuvent être déterminés que de façon empirique. Par ailleurs elle ne tient pas compte des effets de stress environnementaux (essentiellement le stress hydrique) qui peuvent affecter le fonctionnement des couverts végétaux.

3.2.1.12. Méthodologie

Le modèle de production de Monteith simplifié utilise trois efficiences. La matière sèche totale (MST) produites s'exprime suivant la relation suivante :

MST= ?e_a eb e_c RG dt = e_a eb e_c Ó (N DVI - NDVI sol nu)k RG ( k nbre de décades)

· ea, L'efficience d'interception ou d'absorption représente la fraction du rayonnement photo- synthétiquement actif incident absorbé par le couvert. Elle est déterminée de manière empirique par la relation qui consiste à faire correspondre au NDVI du sol une absorption nulle et à un NDVI maximal de 0.7, une absorption maximale de 0.95,

· eb, l'efficience de conversion est le rapport entre la matière sèche produite pendant un laps de temps donné At, et l'énergie photo-synthetiquement active absorbée pendant la même période de temps. Ce coefficient n'est pas normalement constant mais par manque de données terrain, nous avons utilisé une valeur moyenne sur la saison de 1.2g.MJ^-1 (Bégué et Myneni, 1996).

· °_c , l'efficience climatique est souvent peu variable au cours de la saison. Elle correspond à une valeur moyenne de 0.466 (valeur souvent comprise entre 0.4 et 0.5),

· RG, le rayonnement global (MJ.m^-2) supposé constant à l'échelle du pays,

La période d'intégration pour l'application correspond à 15 décades chacune. Elle débute de la deuxième décade de mai et se termine à la première décade d'octobre. La date correspondant la période végétative s'est déduite de l'analyse des profils de NDVI.

L'analyse des profils de NDVI couplée à des données météorologiques (rayonnement global incident, efficience climatique) et agronomiques (efficience photo-chimique) permet ainsi de prévoir les rendements agricoles selon le schéma suivant :

3.2.1.3. Résultats et analyses

Les figures N°15, 16 et puis 17 illustrent respectivement pour les années 1994, 1998 et 2001 respectivement année déficitaire, année excédentaire et année moyenne les résultats des différents rendements obtenus par ce modèle. On remarque que la distribution des valeurs les plus faibles (200 à 450 kg/ha pour l'année déficitaire, de 450 à 650 kg/ha pour l'année moyenne et l'année excédentaire) suit un gradient du nord au centre du pays, et celle des valeurs relativement fortes (450 à 800kg/ha année 1994, 650 à 1000kg/ha année 2001 et 650 à 850 kg/ha année 1998) suit un gradient du centre au sud.

41

Figure N°15 : Niger 1994 (année déficitaire). Rendements estimés (en Kg/ha) avec le modèle semi- déterministe de Monteith

Figure N°17 : Niger 2001 (année moyenne). Rendements estimés (en Kg/ha) avec le modèle semi- déterministe de Monteith

3.2.1.4. Validation

Pour pouvoir bien juger les résultats obtenus à travers le modèle de Monteith, nous avons comparé les différentes sorties du modèle avec les relevés du terrain au niveau des différents départements du Niger. La figure N° 18 nous donne les résultats issus de cette comparaison. Ainsi pour chaque année particulière, nous avons relevé le coefficient de corrélation et l'erreur standard (Tableau N° 12).

Tableau N°12 : Résultats de la validation

Images Années	ND VI lac
	Coefficient de corrélation	Erreur standard
1994 (année déficitaire)	0.74	147.56kg/ha
1998 (année excédentaire)	0.45	256kg/ha
2001 (année moyenne)	0.60	201kg/ha

Nous remarquons que l'année déficitaire 1994 présente le meilleur résultat avec un coefficient de corrélation de 0.74 pour erreur estimée à 147.56kg/ha. Par la suite, nous avons l'année moyenne 2000 avec une corrélation moins bonne de 0.6 pour une erreur de 201 kg/ha et en dernière position l'année excédentaire 1998 avec une faible corrélation de moins de 50% pour une erreur de 201 kg/ha.

1600

1400

1200

1000

400

200

800

600

1600

1400

1200

1000

400

200

800

600

1400

1200

1000

0

400

800

600

200

0

0

1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 192021 22 23 24 252627

Réels Estimés ANNEE 1998

7 9 11 13 15 17 19 21 23 25 27 29 31

Réels Estimés ANNEE 1994

Réels Estimés ANNEE 2001

Departements

Departements

Departements

Figure N°18 : Comparaison entre rendements réels et rendements estimés

3.2.1.4. Conclusion

D'une manière générale, à travers les résultats obtenus (figure N°18), nous pouvons dire que le modèle simplifié de Monteith permet de sous dimensionner la prévision des rendements agricoles.

Ainsi selon notre étude, l'utilisation du modèle de Monteith serait plus efficace pour des prévisions des rendements sur des années déficitaires (coefficient r >70%). Cependant pour les trois années particulières nous relevons un coefficient de corrélation moyen de 0.59 pour une erreur de 201 kg/ha.

Le résultat de ce modèle peut bien sure être utilisé pour la prévision et alerte précoce en ce sens qu'il permet de prévoir relativement plus ce qu'il faut pour les aides d'urgence mettant à l'abri les populations vulnérables.

IV. BIBLIOGRAPHIES

Davis J. C. - (1973) - Statistics and Data Analysis in Geology. John Wiley & Sons, inc., New York

Gilabert M.A., Maselli F., Conese C., Bindi M. - (1995) - Charaterization of primary productivity levels in Niger by means of NOAA NDVI variations. Geocarto Interational, 10, 31-41

Groten S.M.E. - (1993) - NDVI-crop monitoring and early yield assessment of Burkina Faso. International Journal of Remote Sensing, 8, 1945-1515

Hayes M.J., and Decker W.L. - (1996) - Using NOAA AVHRR data to estimate maize production in the United States Corn Belt. International Journal of Remote Sensing, 17, 3189-3200

Huete A. R. and Turker C. J. - (1991) - Investigation of soil influences in AVHRR red and near-infrared vegetation index imagery. International Journal of Remote Sensing. 12, 1223-1 242

Hutchinson C.F. - (1991) - Uses of satellite data for famine early warning system in sub-Saharan Africa. Intenational Journal of Remote Sensing, 12, 1405-1421.

Maselli F., Conese C., Petkov L., Gialabert M.A. - (1993) - Environmental monitoring and crop forecasting in the Sahel trought the use of NOAA NDVI data. A case study: Niger 1986-89. International Journal of Remote Sensing, 14, 3471-3487.

Sivakumar M. V. K. - (1988) - Predicting rainy season potential from the oneset of rains in Southern Sahelian and Sudanic climatic zones of West Africa. Agricoltural and Forest Meteorology. 42: 295-305

Begué. A., 1991. Estimation de la production primaire en zone sahélienne à partir de données radio métriques. Cas d'un couvert discontinu : le mil. Thèse de l'université de Paris VII, 139pp.

SCOT, CNES : Développement de nouveaux produits issus de capteur basse résolution : SPOT4/VEGETATION (OSS, Centre Agrhymet et CSE) 85pages.

H. KONTONGOMDE et I. ALFARI 1991. Modélisation de la prévision des rendements de mil à partir NDVI et de la Pluviométrie au Niger.

DE FILIPPIS, T., VIGNAROLY, P., DJABY., B., KONE, B., and DI VECCHIA, A., 1988, AP3A : Agrhymet Projet Alerte Précoce et Prévision des Productions Agricoles. Final Repport, Agrhymet Center, Niamey, NIGER.

V. TERMES DE REFERNCE DU CONTRAT

V.TERMES DE REFERENCE DE PRESTATION DE SERVICE

APPLICATION DES METHODES D'EVALUATION DE RENDEMENTS AGRICOLES A L'AIDE DES IMAGES NDVI AUX.

1. Contexte

Dans le cadre de l'amélioration des dispositifs de prévention et de gestion des crises conjoncturelles, le Programme Majeur information a entrepris depuis plusieurs années de développer des outils pour l'alerte précoce et la prévision des productions agricoles.

La disponibilité de l'imagerie satellitale basse résolution au CRA tout au long de la campagne agricole a permis de mettre en place des outils pour le suivi de la végétation naturelle ou cultivée en vue de suivre l'état d'installation des cultures et des pâturages. Afin d'améliorer ce suivi qualitatif, le CRA a participé plusieurs initiatives visant à améliorer les prévisions quantitatives liées à la production agricole et en particulier les rendements avec plusieurs centres de recherches européens, CESBIO, IBIMET et SCOT. Ces travaux ont été concluants sur le plan des résultats et depuis 2003, des actions sont en cours pour rendre opérationnels les résultats. Les premiers résultats testés sur le Niger ont été présentés à la réunion de suivi à mi-parcours de juin 2004 à Dakar. Afin de mettre en place ces outils pour la campagne 2004 - 2005 et de les rendre opérationnels au sein de la chaîne de production d'informations du CRA, le Programme Majeur Information se propose de tester les méthodologies de détermination des rendements agricoles à l'aide de l'imagerie base résolution sur un plus grand nombre de pays du CILSS.

2. Objectifs de la prestation de service

La présente prestation de service a pour objectif de poursuivre l'amélioration et le test des modèles d'estimation des rendements agricoles par les méthodes qui utilisent l'imagerie satellitale basse résolution NDVI provenant de NOAA et de Spot Vegetation. Ces méthodes ont été déjà utilisées par le CRA pour des tests sur le Niger en 2003 et résultent des collaborations déjà menées par le CRA avec le CeSIA, l'ITC et le CeSBIO.

3. Tâche du prestataire

Depuis 2003, le CRA utilise les méthodes développées par l'ITC (Méthode Groten) et par le CeSIA (Méthode Maselli) pour l'évaluation des rendements agricoles. Ces méthodes testées sur le NIGER ont été concluantes et les premiers résultats ont été présentés à la réunion de suivi à mi parcours de la campagne agricole 2004.

Les taches du prestataire sont d'appuyer le CRA dans le test et l'application des méthodes retenues sur les autre pays du CILSS par :

- Le test des méthodologies développées par S. Groten et F. Maselli sur les autres pays du CILSS. Ce test sera mené sur la période 1995 à 2003 sur tous les pays du CILSS en utilisant différents types d'images NDVI à savoir la série GAC corrigée fournie par la NOAA jusqu'en 2002, la série NOAA LAC du CRA, la série SPOT Végétation disponible sur la période 2002 - 2004 dans le cadre des collaborations avec le CESBIO et le projet GMFS

- L'application de la méthodologie SCOT sur le Niger sur 3 années retenues sur la base d'une considération qu'une des années est moyenne, une excédentaire et une déficitaire par rapport à une situation normale.

4. Résultats attendus.

Le prestataire devra produire à la fin de la prestation un rapport détaillé présentant la méthodologie de travail, les résultats obtenus qui mettront en relief pour chaque type d'image, les méthodes qui présentent les meilleurs résultats, une analyse critique des résultats en mettant l'accent sur l'opérationnalisation des méthodes au cours de la prochaine campagne agricole. Le rapport décrira aussi les procédures de mise en oeuvre des différentes méthodologies

Le Rapport sera accompagné d'un CD comprenant les données utilisées, les résultats sous forme numérique et les procédures proposées.

Une présentation des résultats de la prestation sera faite en présence des experts du PMI 15 Jours avant la fin de la prestation.

4. Modalités particulières.

Le CRA mettra à la disposition du prestataire un micro-ordinateur, les données satellitales et les données de rendements agricoles nécessaires à la réalisation de la prestation

L'activité est placée sous la responsabilité du programme majeur information au sein de l'unité méthodes et applications qui en assure la supervision technique en collaboration avec les autres unités du Programme.

L'activité démarrera le 15 Novembre 2004 et se terminera le 28 Février 2005.

Tous les coûts relatifs à la prestation de service seront pris en charge par le budget USAID, 2004.

VI. ANNEXES

Principe de la validation croisées

La validation croisées s'appuie non seulement sur des hypothèses théoriques de distribution des données mais également sur le fait que plusieurs estimations à partir de portions indépendantes d'un échantillon sont plus fiables qu'une estimation sur la totalité. Cette méthode détermine la valeur probable du pouvoir prédictif en utilisant le paramètre " crossvalidated r squared". Elle permet de définir différents ensemble de données: un pour l'apprentissage et l'autre pour la validation croisée. Ces deux ensembles sont nécessaires pour étudier la généralisation de manière systématique.

Echantillon issue de la

Echantillon initiale validation croisée

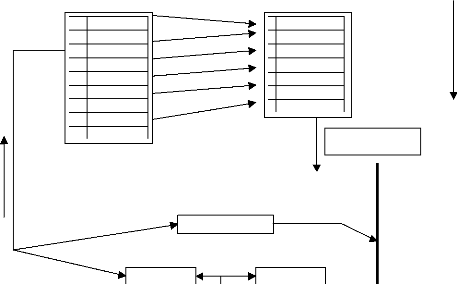
Rangée des
composés exclus

Equation de
corrélation dérivée

Y = ax+b

Propriétés prédites pour les rangées des composés exclues

Mesurées

Prédites

Propriétés exclues

?

Répété jusqu'à m fois
	Différences

Déviation standard

Principe de l'analyse de la validation croisée

A partir d'une table initiale de données, on construit une autre table dite de validation croisée résultant du croisement des données initiales et de l'omission d'une où de plusieurs rangées. Le nouveau modèle ainsi obtenu donne une nouvelle équation de corrélation qui permet de déduire l'activité résultante de l'exclusion de ou des rangées. La différence entre l'activité mesurée et celle prédite donne la déviation standard et la proportion de l'incertitude originale crossvalidated r carré de la validation croisée qui évaluent le modèle ainsi obtenu.

Le cycle de déviation/prédiction est poursuivi jusqu'à ce que les valeurs obtenues pour l'activité cible soient constantes. Notons que la validation croisée est un processus contrôlé par le nombre de composé dans la table. Ainsi si le nombre de groupe de la validation croisée est posé égal au nombre de composés de façon à ce que toutes les activités cibles soient prédites par toutes les données, le processus de validation permettant d'obtenir des valeurs constantes dans des séries consécutives se produira pendant un temps très long car le modèle est réalisé autant de fois qu'il y a de composés dans la table.

Principe de la méthode appliquée pour la correction de l'effet sol

La valeur de NDVI corrigée par l'effet sol est:

NDVI = NDVIx - Dx

Où:

NDVI = NDVI corrigé

NDVIx = NDVI des données brutes

Dx = effet des sols

a = NDVIx - NDVIsx

A = NDVIc - NDVIsx

D = NDVIsx - NDVIsd

NDVIsx = valeur de NDVI d'un pixel avec un type de sol avec une couverture végétale = 0

NDVIc = valeur de NDVI au point où la couverture végétale = 0

NDVIsd = valeur de NDVI avec couverture végétale = 0 et sols clairs (DC = 0)

On fait l'approximation des courbes Sd C et Sb C à deux droites. Sd représente la valeur de NDVI quand le pourcentage de couverture végétale P est égal à zéro pour les sols foncés et Sb représente la valeur des sols clairs. C'est le seuil au-delà duquel les sols n'ont plus d'effet.

La surface à l'intérieur du triangle Sb C Sd représente donc l'aire dans laquelle un pixel peut retomber avec un pourcentage déterminé de couverture végétale, inférieur à 100%. Par approximation linéaire on reporte le point x sur l'axe y (Sx). En considérant les deux triangles Sx C F et SX X E on établit la proportion

Sx E: Sx F= a : A

d'où P = Sx E / Sx F = a / A.

Considérant maintenant les triangles G X H et Sd Sx I on établit la proportion

D : Dx = 1: (1-P)

de sorte que Dx =(1-P)D. [0, 0.2]

La valeur corrigée de NDVI résulte donc : NDVI = NDVIx - Dx

Prenons par exemple deux valeurs de NDVI 0.7 et 0.4

Appliquons la formule pour calculer la valeur de NDVI corrigée :

NDVI = 0.7 - Dx = 0.7	- (1-P) D =	0.7	-(1-0.7)*0.2	= 0.64
NDVI = 0.4 - Dx = 0.4	- (1-P) D =	0.4	-(1-0.4)*0.2	=0.28